- 1Institute for Mathematics and Computing, Ludwigsburg University of Education, Ludwigsburg, Germany
- 2Grupo Signos, Departamento de Matemáticas, Universidad el Bosque, Bogotá, Colombia
- 3School of Informatics, University of Edinburgh, Edinburgh, United Kingdom
We report on a study on syllogistic reasoning conceived with the idea that subjects' performance in experiments is highly dependent on the communicative situations in which the particular task is framed. From this perspective, we describe the results of Experiment 1 comparing the performance of undergraduate students in 5 different tasks. This between-subjects comparison inspires a within-subject intervention design (Experiment 2). The variations introduced on traditional experimental tasks and settings include two main dimensions. The first one focuses on reshaping the context (the pragmatics of the communication situations faced) along the dimension of cooperative vs. adversarial attitudes. The second one consists of rendering explicit the construction/representation of counterexamples, a crucial aspect in the definition of deduction (in the classical semantic sense). We obtain evidence on the possibility of a significant switch in students' performance and the strategies they follow. Syllogistic reasoning is seen here as a controlled microcosm informative enough to provide insights and we suggest strategies for wider contexts of reasoning, argumentation and proof.
Introduction
The acquisition of reasoning proficiency according to logical standards is a central topic in regard to the development of critical thinking competencies. It inheres also in the development of mathematical argumentation and proof. Even so, the experimental evidence from the psychology of reasoning and from mathematics education has widely documented well-rooted difficulties concerning the reasoning skills of students (and humans, in general). In this context, syllogistic reasoning is a paradigmatic case which can provide pre-eminent insights for several reasons: first, the study of the topic accumulates more than a 100 years of experimental study [starting with (Störring, 1908)] with the corresponding corpus of experimental approaches, robustness of observed phenomena and variety of theoretical explanations (Khemlani and Johnson-Laird, 2012). Second, syllogisms clearly illustrate the dichotomy between normative standards and the actual performance of subjects. Moreover, even in this very restricted context, it is possible to observe a full spectrum of diversity in performance, from some syllogisms that are almost always correctly answered, to some others that are practically always wrong. Third, from a historical perspective, the topic has clearly emerged in a very specific context of argumentation and disputation and has been for centuries a characteristic model for this kind of reasoning. Finally, during more than two millennia, we can see a diversity of theoretical, and didactic approaches to the subject including a diversity of semiotic registers.
Given the relevance of the subject to the issues alluded to before, and the experimental evidence so far, two natural questions emerge: what can explain the fact that typical performance in the usual syllogistic tasks does not adhere to Classical Logic? Are there other situations or experimental settings which can elicit reasoning closer to this logical standard?
Following the path of Vargas et al. (submitted), the proposal of the present paper is to show how, even if we have chosen a tiny fragment of full first-order classical logic, in regard to syllogisms we can already see important changes in reasoning tied to the use of representations and the pragmatic situations from which particular reasoning mechanisms emerge. We report on two subsequent experiments. In the first one we compare how undergraduate subjects perform on 5 different tasks intended to understand how different thinking strategies are followed by subjects depending on the communicative situations. The second experiment, more educationally oriented, is based on the insights provided by the first experiment. It studies the trajectories of students in a sequence of tests and short interventions. These are intended to lead them to a shift in their performance based on their understanding of the kind of reasoning that they are expected to attain normatively.
In what follows, we first elaborate on the theoretical background just outlined focusing on the two fundamental aspects which support the design: the importance of communicative settings for reasoning, and the use of the construction of counterexamples in argumentation and proof (Sections Plurality of Goals in Communication and Reasoning and Construction of Counterexamples: Modeling and Countermodeling as Tools for Syllogistic Reasoning). We describe and report then on Experiments 1 and 2 (Sections Experiment 1: Recognizing the Diversity of Communication Contexts and Goals and Experiment 2: Integrating the Tasks as a Didactic Sequence). In the final discussion (Section Results) we develop connections with the psychology of reasoning and the implications for education, particularly in regard to the literature on argumentation and proof in mathematics education.
Plurality of Goals in Communication and Reasoning
Experimental study of Aristotelian syllogisms has led to a very neat conclusion: answers of untrained subjects in the customary tasks are very far from being correct from the point of view of the intended, classical interpretation. There have been different kinds of explanations in the psychological literature that try to give an account of experimental data [see (Khemlani and Johnson-Laird, 2012) for an overview].1 A natural suggestion is that syllogisms are a kind of task limited to academic environments and for which we show no capacity beyond this, i.e., without instruction or specific training. An extreme illustration is offered by Luria (1976) experiments in the 1930s showing how illiterate subjects had a tendency to refuse the endorsement of any conclusion at all about facts not known to them beforehand, just from the information provided by premises. According to him, they tended not to rely on information beyond their personal experience (as is essential in hypothetical reasoning) and not to accept premises as having general validity. Furthermore, they even conceived syllogisms not as unified wholes, but as unintegrated pieces of information. A later study carried on in Liberia by Scribner (1975), showed similar dispositions, which were in fact interpreted as a case of an “empirical bias” (Scribner, 1977). This illustrates how syllogisms (and logic in general) are not context independent mechanisms but emerge from the analysis of particular communicative/pragmatic situations. It therefore seems natural to consider experimentally the kind of situation and discourse in which syllogistic arguments first appeared in philosophy, namely, the context of argumentation, discussion and refutation. They are not, in short, a description of deductive processes executed in abstracto by individual minds. Syllogistic arguments are originally about a context of adversarial communication. What we do primarily in communication, instead, has a cooperative character determined by a fundamental “verbal contract.” Hence, very commonly, we are not strictly limited by what the speaker makes explicit, but most of the times we “complete” the message with a background given by intended common assumptions. We do not communicate just what is explicit or concluding what is “entailed” (in the strict sense) by the externalized sentences. We infer, in addition to this, also a series of “implicatures,” as they are known after Grice (1975) and, more widely, we frame the information in order to convey a message or interpret available information. Here we take the general view that different communicative or pragmatic demands may put into action different reasoning strategies and mechanisms, and that considering a plurality of logics may give us appropriate tools for their description (Stenning and van Lambalgen, 2008). From this point of view, what are often considered simply as “mistakes” are frequently sensible conclusions which may even adhere to the rules of a particular logic. This is highly relevant for educational purposes because of the prevalence of categories such as “correct” or “incorrect” often used as if having absolute character.
The previous discussion connects at different points with research in education. On one side, the general view that human cognition, and mathematical cognition, in particular, happens as a social and communicational phenomenon, challenges more traditional, internalistic views on thinking and learning which ignore, both experimentally and educationally, their essential character. Inspired largely by Vigotsky, this view has been stressed repeatedly in mathematics education research, since its “social turn” (Lerman, 2000; Sfard, 2008; Roth and Radford, 2011).
On the other side, an important point of connection relates to the literatures on argumentation and proof. Our view on the context/communicational dependency of reasoning is in line in fact with integrating the “social dimension” of proof (Balacheff, 1987) and with the “shift to a pragmatic view of proof” (Hanna and Jahnke, 1993). Which particular communicational activities relate to the logic behind argumentation and proof? How can we contextualize proof so that it emerges more in continuity with other human practices, and not as an epistemological rupture with them (Duval, 1991, 1992)? Even if the birth of the concept of mathematical proof in Ancient Greece is still debated, philological evidence suggests that it originated from the development of argumentative and dialogic discourse as seen in philosophy and that “the practice of a rational discourse provided a model for the organization of a mathematical theory according to the axiomatic-deductive method. In sum, proof is rooted in communication” (Jahnke, 2010).2 This communication, given its dialectical nature, is adversarial at a fundamental level and in a technical sense. These historical origins continue to be present in the practice of proof production, which requires a dialectics with (real or potential) refutations (Lakatos, 1976). In this sense, an adversarial disposition is skeptically oriented leading an “opponent” to look for countermodels or counterexamples to what the “proponent” says (Dutilh Novaes, 2018). It is in fact, primarily, through the exhibition of individual counterexamples that an argument is refuted, as we will elaborate next.
Construction of Counterexamples: Modeling and Countermodeling as Tools for Syllogistic Reasoning
As noted before, in syllogistic reasoning the usual instructions do not prompt answers according to what “logically follows.” As with many other reasoning tasks, simple rephrasing or emphasis in the instructions do not lead to substantial changes in performance. This way, asking for “necessary conclusions” or deductions “valid in general” does not usually lead to substantial improvement or disambiguation. We propose a change in the contextualization of the materials which may encourage an integration of what precisely “logically” or “necessary” means in this practice. Even if experimental evidence seems to indicate that we are not “naturally” capable of syllogistic reasoning in general, we are more inclined to see here what may be expressed using the competence vs. performance dichotomy, but with more than one competence possible. Actual low performance may be caused because performance deviates from the competence that is normatively established. But performance has to be measured against the right competence, and performance aimed at other norms may be successfully elicited by appropriate contexts which invoke their ecological source (Simon, 1956, 1990).
What do we logically expect when asking if a conclusion “logically follows” from some premises? Even if in some traditions still influential in education “logical” is conceived from this definition of a deductive system or a set of syntactic transformations (or inference rules), we believe that, in the context of ‘naive' untrained reasoners, a more accessible approach is semantic. In classical logic (Tarski, 1936), the definition of the entailment relation establishes that a sentence ϕ follows from set of sentences Γ (indicated as Γ⊨φ) if and only if every model of Γ is also a model of ϕ.3 This may be rephrased by saying that there is not a model for Γ that is a countermodel for ϕ (a counterexample). The validity of a deduction is equivalent to the impossibility of getting a counterexample for it.
The problem of the exploration of possible counterexamples and their generation may not be finite or even decidable in general. This may be overcome in the particular case of syllogistic reasoning where we deal only with a vocabulary of three monadic predicates. In this case models are sets of a certain number of individuals, with interpretations for the predicates.4 Problems with valid conclusions have always 1-element models.5 This property (“case identifiability”), leads in fact to an algorithm for extracting conclusions from a pair of premises (Stenning and Yule, 1997). In this way, for valid problems we limit ourselves to the case of 1-element models. This is not the case in general for the premises of non-valid problems: pairs of premises here may need 2-elements to be modeled. Therefore, when we come to the problem of the construction of counterexamples, at least 2 elements may be indispensable. In general, in fact, we have that a conclusion fails to follow from a pair of premises if and only if there is a countermodel. And we also know that countermodels never require more than 2 elements (1-element models would not suffice, in general). Moreover, if there is not such a countermodel, as can be established by an exhaustive examination, the inference is valid (the conclusion follows from the premises). It is worth noticing that refutation by countermodeling is in general a separate and distinct process from proof. Syllogisms are exceptional in that examination of 2-element models leads both to a refutation method and to a decision method for validity. We propose that psychologically, these processes remain distinct for naive subjects in the syllogism.
Despite this crucial role that the construction of counterexamples may play in regard to the analysis of syllogistic thinking, the topic has been almost completely absent from experimental testing in the psychology literature. One exception is Bucciarelli and Johnson-Laird (1999) where the authors performed an experiment asking for the construction of counterexamples. In fact, according to the basic tenets of mental models theory, people make deductions by building “models” and searching for counterexamples (Johnson-Laird and Byrne, 1991). Bucciarelli and Johnson-Laird consider the counterexamples of their experiment as a means to “externalize the process of thought” concluding that individuals are capable of generating them. Our results suggest that beyond being a simple externalization of internal processes, asking for this kind of external representation may modify strategies of reasoning or, even more, the goals themselves pursued in reasoning and the corresponding logic. This is more clearly the case if, as in our case, the counterexamples construction is embedded in adversarial communication (in contrast to cooperative communication that, we claim, usually predominates in the conventional experiments). As we will see, results show a remarkable difference of performance between our counterexample tasks and more traditional ones.
Besides psychological experiments and theories, the use of examples (and counterexamples) in the learning and teaching of mathematics has been widely acknowledged (as well as in mathematicians' practices). The mathematics education literature has recently addressed the role of examples and counterexamples [see, e.g., (Watson and Mason, 2005), or the special issues on “The Role and Use of Examples in Mathematics Education” (Bills and Watson, 2008) and “Examples in mathematical thinking and learning from an educational perspective” (Antonini et al., 2011)]. The formation and exploration of an “example space” (Watson and Mason, 2005) is essential to mathematical thought, and fundamental for learning:
“Examples can therefore usefully be seen as cultural mediating tools between learners and mathematical concepts, theorems, and techniques. They are a major means for ‘making contact' with abstract ideas and a major means of mathematical communication, whether ‘with oneself', or with others. Examples can also provide context, while the variation in examples can help learners distinguish essential from incidental features and, if well-selected, the range over which that variation is permitted.” (Goldenberg and Mason, 2008).
A change in disposition already occurs when we deal with the exploration of examples and counterexamples. This is reflected in our Experiment 1 results. Nevertheless, grasping the sense of counterexamples and adjusting the relevant conventions in the semiotic representation used in each particular situation is not something automatic or easy. This is the case in mathematical contexts, in general, but we will face the same obstacles in our study. Our Experiment 2 addresses these difficulties proposing strategies on how they can be dealt with.
Experiment 1: Recognizing the Diversity of Communication Contexts and Goals
The aim in Experiment 1 was to explore the effects that countermodeling in an adversarial setting produces in syllogistic reasoning. This is done comparing performance across 5 tasks described below. Most of the studies of syllogistic reasoning present pairs of premises and ask the subject for a conclusion of syllogistic form from a menu including the option “none of the above” either explicitly from a menu presented in each trial, or from instructions at the beginning about the constraints on the form of conclusions (the generation paradigm). In some cases experiments propose, besides the pair of premises, a conclusion whose validity, given the premises, is to be judged (the evaluation paradigm). We use both approaches in our tasks.
Methods
Materials and Procedure
Each subject answered a booklet in just one of the conditions described next. Subjects were assigned conditions in a random order. So, these five conditions are essentially separate experiments with random subject sampling from the same population. They had 60 min to do this even if in practice many of the participants finished before, predominantly around 45 min. The booklets had 16 problems for all tasks, aside from the evaluation task which was substantially less demanding. For this task, participants had to answer the whole set of 32 problems studied. The order of presentation of the problems was also random, with three different such orders for each set of problems. The tasks studied are the following (for the exact phrasing of the instructions see the Supplementary Material):
• Conventional (CV): The draw-a-conclusion task usually considered in the literature [see e.g., (Johnson-Laird and Steedman, 1978) or (Khemlani and Johnson-Laird, 2012)]. Given a pair of premises, participants are asked to decide what follows. Conclusions are selected from a menu offering the eight classical possibilities plus a “none of the above” option.
• Evaluation task (EV): This task has been also extensively present in the literature (see, for example, Rips, 1994 for a large experiment comprising 256 of the 512 possible syllogisms). The two premises of a syllogism and a conclusion are presented to participants. They are asked to evaluate whether the conclusion follows or not. Here the proposed conclusions are the same as in the CMA and CMA2 tasks described next. The aim here is to provide a task that is similar to CV, in the sense that no countermodel construction is asked and that is not an adversarial situation, but that at the same time is directly comparable with the results of the countermodels tasks. In this sense, the EV task is crucial in the experiment because it can either confirm or disconfirm the differences already noticed between CV and other tasks (Vargas et al., submitted) and see if they are really attributable to other differences such as the collaborative/ adversarial context, the active construction of models, the subjects' involvement in justifying their own judgment, or if they are only by-products of the format of the questions (e.g., nine options choice vs. a Yes/No answer).
• Countermodels Adversarial (CMA): This is essentially the “Syllogistic Dispute” task in Vargas et al. (submitted) which proposes the construction of countermodels in a betting situation against Harry-the-snake. Participants are presented a pair of premises and a proposed conclusion. They have to bet whether this conclusion is valid or not. They are thus in competition with Harry, the nefarious character who proposes the bets and who is trying to empty their wallets. We apply a small variation to the countermodel construction: 2-element countermodels were requested. Syllogism AI3 will serve as an example. Suppose the following premises are given:
All the students taking linguistics are taking Arabic.
Some of the students taking geometry are taking Arabic
Harry proposes the following bet:
Some of the students taking geometry are taking linguistics.
Besides having to judge whether this follows or not, participants must provide the counterexample in this last case by ticking or crossing each course if the student is taking it or not:
Student 1:
Linguistics
Arabic
Geometry
Student 2:
Linguistics
Arabic
Geometry
• Countermodels Adversarial 2 (CMA2): With the same structure of CMA (a proposed conclusion from two given premises, and the construction of counterexamples when possible) but in this case with another story/context. Instead of a betting situation and Harry-the-snake, participants are asked to play the role of a professor who must correct the answers (conclusions) offered by students as valid inferences in an exam. If the conclusion does not follow (i.e., if the exam script that they are correcting presents a mistake) participants must provide a counterexample as a didactic tool for their imaginary pupil in order to explain why it does not follow. This is a familiar, technically adversarial, situation: an examination.
• Communication-conclusions task (COMM-C) This task is proposed with the idea that what participants actually do in CV is to play a cooperative game which the task is an attempt to mimic. Here subjects are introduced into a game: each participant has an imaginary team-mate who wants to communicate to her an assigned statement. Following the syllogistic structure (with b the middle term and a and c the other ones) this statement is about terms a and c. This communication cannot be done directly: the team-mate can only express something about a and b, and something about b and c. The participant is presented with two statements (which play the role of “premises”) which “come from her teammate.” The task is to decide which sentence is it most likely that the team-mate is trying to communicate from a menu of nine possibilities (a possibility for: “no favorite guess” is included). It is emphasized that this is a cooperative task in the precise sense that the subject should think of him or herself as working in a team with the source of the premises. The team-mate is trying to communicate a sentence, and our participant is trying to guess it. Both of them are scored as teams (pairs) according to how often they succeed in their mutual goal. The instructions assert that “If you can guess what sentence he has in mind from the pair of premises (s)he gives you, then your team win five points. If you guess wrong, then you both lose 1 point. There is also the option: ‘Have no preferred guess,' in which case you neither win, nor lose any points.” In this game the points are established in order to encourage a preferred option rather than “Have no preferred guess” if the participant is not sure. But in the case of total indifference, choosing this last option has greater expected value than random selection of some other answer.
It is important to emphasize, for comparison purposes, that, in their structure, CV and COMM-C tasks follow the generation paradigm, whereas EV, CMA, and CMA2 tasks follow the evaluation paradigm.
Tasks CMA and CMA2 require, besides an evaluation of validity, the construction of counterexamples. For the reason explained in Section Construction of Counterexamples: Modeling and Countermodeling as Tools for Syllogistic Reasoning (with two elements it is always possible to construct a counterexample, if one exists), we standardized the required countermodels to 2-element ones.
Problem Selection
As indicated above, beyond purely historical interest, syllogisms constitute a microcosm complex enough to reveal wide variation in typical performance from subjects. So, it is a topic revealing a wide spectrum at the level of misalignment from normative expectations. Studying the whole set of 512 possible pairs of premises and proposed conclusions was not feasible in the time. We limited ourselves to a subset of 32 of these possibilities, presenting 16 to each of our participants. The selection of these problems was heavily biased toward the ones which could reveal the use or absence of classically valid reasoning, and therefore, those which turn out to be solved by other strategies. This is revealed by traditional performance in the CV task, already well-documented in the literature. Our choice was therefore focused on those problems which turn out to be “difficult” in the CV task. A prominent phenomenon in this task is a clear incapacity for detecting that the majority of the problems (out of 64 pairs of premises) have no valid conclusions. Those problems with no valid conclusions which are judged by subjects as having one, reveal a tendency to reason cooperatively. Table 1 rehearses the basic properties that motivated the selection of the 32 problems used. They were divided in two sets (indicated in the last column of the table), balanced according to these properties, both logical and psychological, namely:
• Validity rate: an equal number of logically valid and non-valid problems in both sets. This number is in proportion with the number of valid/non valid problems among the 64 problems (seven valid and nine with no valid conclusion in each set, which reflects the fact that among the 64 possible pairs of premises there are 27 with valid and 37 with no valid conclusions). In the 4th column of Table 1 (“VC/NVC”), we indicate for each problem if it has any valid conclusion (a “VC problem”) or if it has no valid conclusion (an “NVC problem”).
• Difficulty: the main measure of this is given by the typical performance of subjects in the conventional task. We used for this the results from the meta-analysis in Khemlani and Johnson-Laird (2012) which are reported in the 6th column in the table. This performance motivates also the “empty-sets”6 classification (ES classification) introduced in Vargas et al. (submitted). This classification reflects and provides explanations for the variation of VC problem difficulty in the drawing of valid conclusions in the CV task (NVC problems are all classified 0 by ES). This will be also used repeatedly in our graphs. The ES classification sorts all syllogisms with any valid conclusions into five classes7 on the basis of their quantifiers and whether the conclusion quantifier is already used in one or more premises. Starting from the “easiest,” problems with:
1. one existential and one universal premise and a valid conclusion with a positive quantifier from a premise;
2. two universal quantifiers and a valid universal conclusion;
3. one existential premise and one universal premise, and a conclusion with a negative quantifier from a premise;
4. one existential and one universal premise with a valid conclusion requiring a quantifier not in the premises; and
5. two universal premises, but only existential valid conclusions.8
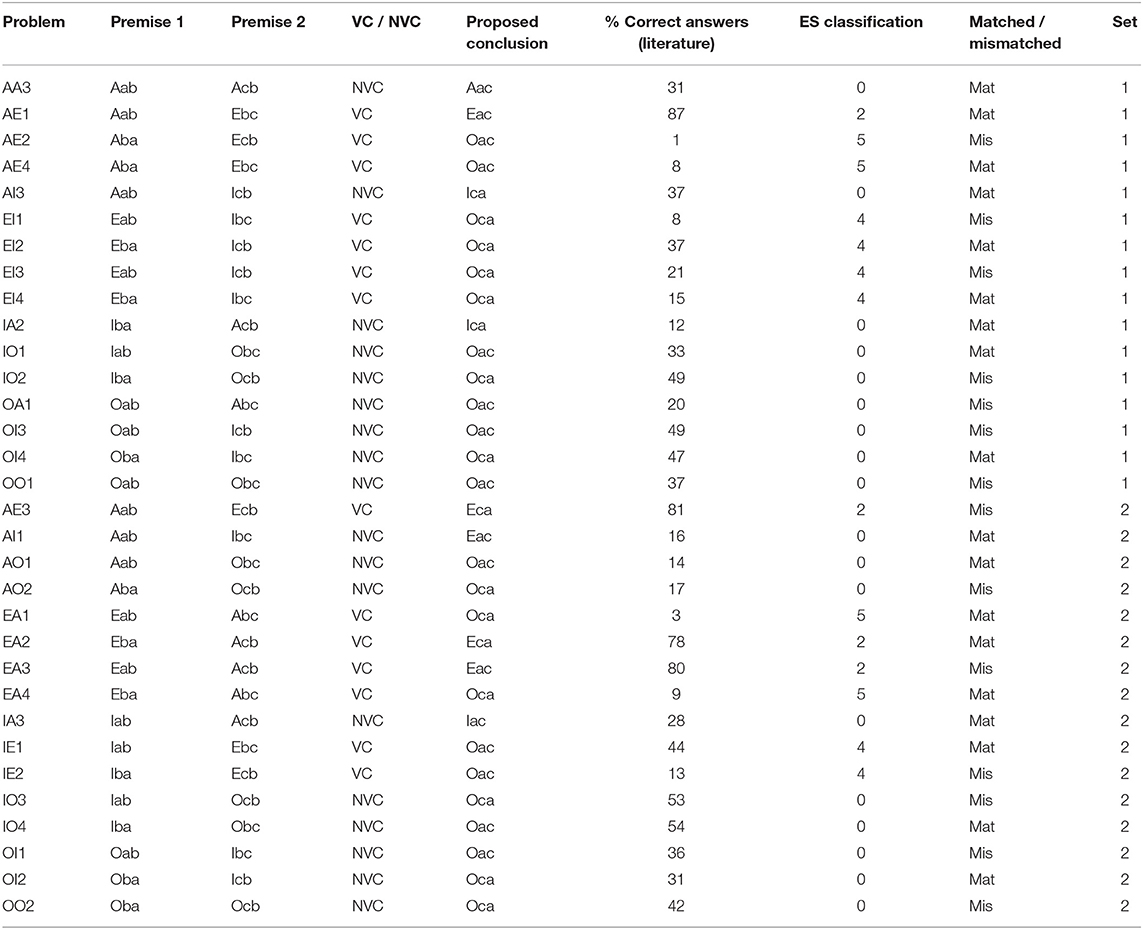
Table 1. The 32 problems selected in the study, their premises, existence, or absence of valid conclusions, the proposed conclusions in the tasks following the evaluation paradigm, percentage of correct answers in the literature CV task, the ES classification, the matched vs. mismatched classification and our two sets subdivision.
Matched/mismatched rate: a pair of premises is matched if the middle term is either positive in both premises or negative in both premises. Otherwise it is mismatched. Problem AE2, for instance, is mismatched because in the premises All b are a, No c are b, the term b appears, respectively, as positive and negative (rephrasing No c are b as “c implies not b”). We considered this property to be important in the problems selection and balancing because it is related to the ease in constructing counterexamples. With matched problems we can naturally produce 1-element models9 of the two premises in which the conclusions proposed are automatically also true, so changes are necessary in order to produce counterexamples. These 1-element models can be produced for mismatched problems only by using the truth of universal statements with antecedents defining empty sets, i.e., by rejecting the existential import of universal statements. The 1-element models that result from integrating the premises using empty-antecedent reasoning are immediately countermodels of the most popular conclusions. This regularity holds only because the bets were chosen as the commonest invalid conclusions in the meta-analysis data, and those have a particular property of “figurality” defined in Vargas et al. (submitted).
The conclusions in the table (5th column) were used in tasks under the evaluation paradigm, namely, EV, CMA, and CMA2, where they are proposed after the two premises. Participants should either accept or reject that the conclusion necessarily follows from the premises. The conclusions presented were selected according to the following criteria: for VC problems the conclusion is chosen to be valid. If more than one conclusion is valid, we chose the most frequently selected in the CV task, according to the meta-analysis in Khemlani and Johnson-Laird (2012). This last criterion was also applied for non-valid problems, namely, we chose the most popular specific conclusion for each problem, in this case obviously a non-valid one. This makes it as difficult as possible for our subjects to detect the invalidity of the proposed conclusions.
Participants
A total of 244 undergraduate students (mean age = 22.4) from first to third-year courses in the Ludwigsburg University of Education distributed thus: CV: 82, EV: 22, CMA: 54, CMA2:44 COMM-C: 42. The difficulty of the two countermodeling tasks (CMA and CMA2) led in some cases either to the non-comprehension of the task or to failure to comply with instructions. We excluded from all our analyses the answers of a total of 3 and 5 participants, respectively, in CMA and CMA2. These are subjects who did not provide any complete construction of countermodels. We did not consider their answers evaluating the validity of the conclusion because the counterexamples part was crucial in our experiment as an exploration of the effects obtained with this construction. This made these data uninterpretable for us. We take the systematic failure to provide counterexamples in these subjects as a clear indication that it was by far more demanding than the other tasks, but also more difficult to grasp without further indications or explanations.10
Evaluation of Problems and Countermodels
Universal statements can be interpreted in different ways and models can be considered to be adequate for them according to two well-known options. On one hand, since Aristotle, a long-established convention determines that universal statements are false when the antecedent property is empty in the domain because they are considered to have existential import. So, a universal statement does presuppose in this interpretation the existence of something to which the predicate is applicable. On the other hand, according to modern semantics, truth does not require existence for universal statements. Given, e.g., the syllogistic problem AA1 (All A are B, all B are C) the universal conclusion All A are C is a valid one (the type Barbara). Now, if we consider the particular conclusion Some A is C, it is validly inferred only if the universal first premise has existential import leading to type Barbari. This inference is not valid under the modern interpretation and, from this perspective is an example of the “existential fallacy.”
The traditional Aristotelian view is adopted in most of the psychological literature, notably in the criterion for scoring accuracy. We follow this convention even if it is not clear that either of the interpretations should be adopted from a psychological point of view, or that it should be absolutely mandatory in education from a normative stance. For this reason, we will consider the modern interpretation in some of our analyses and will emphasize that some of our subjects in Experiment 2 do follow it explicitly.11 Even if our focus here will be on the evaluation judgment of the tasks and not on the counterexamples produced, the construction of counterexamples allows us to observe where the divergence between the interpretations is present, since we can see where subjects use empty sets for interpreting their terms (see Vargas et al., submitted).
Results
The CV Task
As a first consideration Figure 1 compares the performance in the CV task across the 32 problems of our experiment 1 subjects with what we know from the meta-analysis (Khemlani and Johnson-Laird, 2012). Our participants present similar patterns in their answers in comparison with the literature, as seen by the high correlation (Spearman coefficient of 0.78, p < 0.001). As seen in the scatterplot, our participants have a performance slightly lower in most of the problems, but the tendencies are clearly the same. We may also see in the figure different clusters of problems confirming that the ES classification captures to a great extent the degree of difficulty of the problems in this task remaining stable across groups. This stratified analysis of the problems based on their structural characteristics gives us suggestive insights into the different strategies used by subjects. Problems in group 5, for instance, have a valid conclusion whose type (kind of quantifier) is an existential one not present in the premises (both universal) i.e., they require existential presuppositions. This makes these problems particularly difficult in this task leading to correct answers being practically absent, according to the traditional scoring with existential presuppositions, both in the literature and in our subjects, as is evident in Figure 1. The commonest responses in these problems are actually universal, which are invalid.
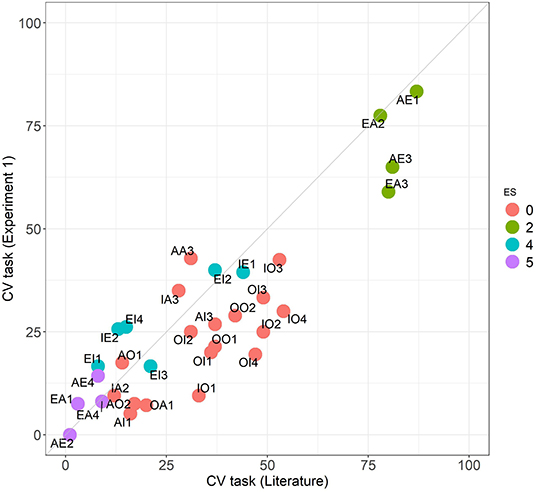
Figure 1. Comparison of the CV task performance across the 32 problems between the literature and Experiment 1 groups. Colors follow the ES classification.
The EV Task
This task is also present in the literature (Rips, 1994). Our results indicate that, as expected, there are important differences with the CV task even if conclusions must be drawn with care given their different structure. In principle the tasks are not comparable, so it is difficult to interpret the apparent increase in the overall accuracy between CV and EV from 27.6 to 46.4 % (see Figure 2). The difference in performance between both tasks is more evident in groups 4 and 5 of the ES-classification (see Figure 3) for natural reasons: these problems are commonly incorrect in CV because participants prefer to generate conclusions different from the correct ones (which are not valid with the premises). In EV, instead, these conclusions are presented without other possible options which enter in competition with them. In the class 2 of the ES-classification, the two tasks are closer.
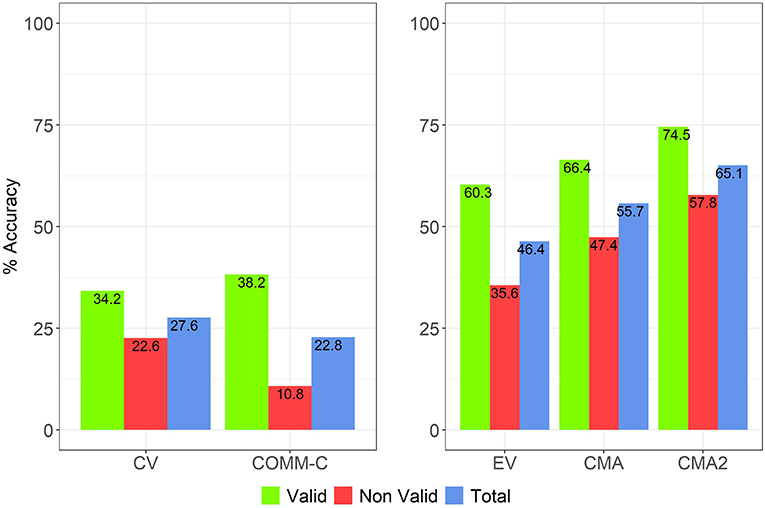
Figure 2. Five tasks comparison in performance. Generation paradigm (left) and evaluation paradigm tasks (right).
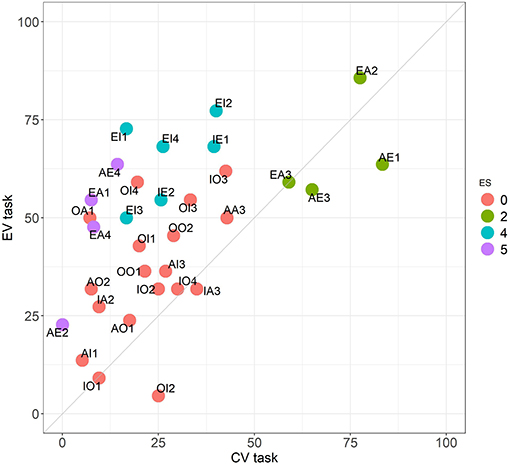
Figure 3. Comparison between the CV and the EV tasks. Performance across the 32 problems. Colors follow the ES classification.
It is worth also noticing that there is in EV a strong asymmetry between valid and non-valid problems which is reflected in a percentage difference of almost 25 points in favor of the former.
The CMA and CMA2 Tasks
As explained before, the CMA and CMA2 tasks share the same structure: a deduction evaluation, followed by counterexample construction when possible, in an adversarial setting. In them we obtained an overall improvement in accuracy and reduction of the imbalance in determining the validity vs. non-validity of conclusions, as seen in Figure 2. We have an accuracy improvement in regard to the EV task: mean scores pass from 46.4 in EV to 55.7 and to 65.1, respectively, in CMA and CMA2 (p = 0.0004348 between EV and CMA and p = 1.598e-11 between EV and CMA2). The difference between valid and invalid problems decreases from 24.7 to 19 and to 16.7 points in EV, CMA and CMA2. This reduction in the imbalance is also significant: p = 0.004586 between EV and CMA and p = 0.0002718 between EV and CMA2.
We compare CMA and CMA2 with EV, respectively, in Figures 4, 5. It is noticeable here that the improvement is not just in the means, but also present for almost all problems taken individually.
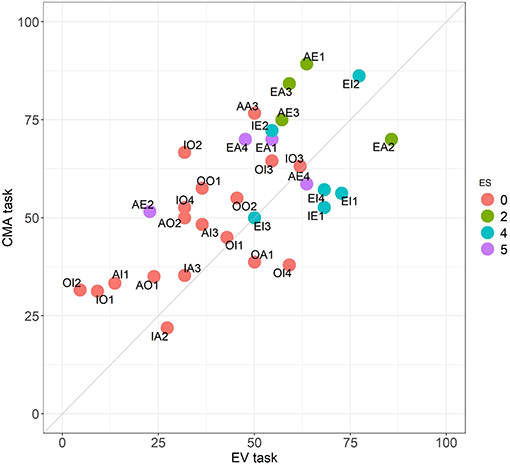
Figure 4. Comparison between the EV and the CMA tasks. Performance across the 32 problems. Colors follow the ES classification.
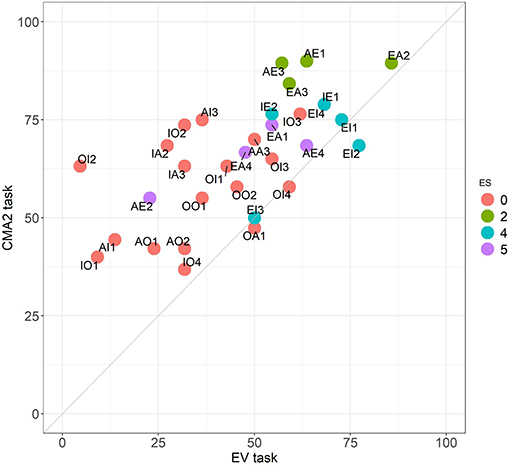
Figure 5. Comparison between the EV and the CMA2 tasks. Performance across the 32 problems. Colors follow the ES classification.
CMA and CMA2 offer the additional countermodel data which deserves separate analysis which will not be done here. Nevertheless, it is worth mentioning that, despite the improvement in conclusion evaluation, the generation of countermodels is far from perfect: in these tasks the percentage of correct countermodels is 20 and 31% of possible ones (namely, for each participant the 9 non-valid problems out of 16 presented to her). Calculating the chance levels of correct countermodeling is complex. There are 64 possible 2-element models different in principle among which 28 avoiding reorderings and repetitions of elements. For each problem there are different subsets which are correct. On the other hand there are relatively simple properties of problems that will filter out possibilities. The psychological process of countermodel construction is also complex the most direct evidence being that participants take around three to four times as long per problem. The analysis in Vargas et al. (submitted) provides strong evidence that its subjects are trying to do classical logical countermodeling despite their many errors. The construction of counterexamples poses difficulties due to high demands on executive functions (working memory in particular). Besides this, it poses a number of problems difficult to clarify by means of test instructions alone. This motivated a different approach in Experiment 2.
The COMM-C Task
The purpose of this task was to substantiate the idea that what participants do in the CV task is essentially framed in a context of cooperative communication. If instructions ask subjects explicitly to do precisely this, we obtain in fact very similar results. Correlation between CV and COMM-C is 0.75 (Spearman coefficient, p < 0.00005). This is in fact the highest correlation obtained between all tasks (Table 2). As shown in the scatterplot in Figure 6, the ES classification is also essentially respected. Subjects perform similarly as in CV, only that the collaborative attitude leads even more to the extreme, so to speak. We can see this in the fact that the conclusions of the problems in ES class 2 are endorsed even more frequently. In general, subjects extract more valid conclusions for VC problems in COMM-C than in CV (average scores 38.2 and 34.2% in generating valid conclusions). Similarly, a conclusion for NVC problems is “guessed” even more frequently without exception in any of the problems, a characteristic collaborative strategy. This leads to an even increased asymmetry between VC and NVC problems. According to our instructions for COMM-C, under a situation of complete uncertainty, the payoffs of selecting “no preferred guess” would be larger. This means that the conclusions they select seem at least to some extent plausible for them in the communicative game.
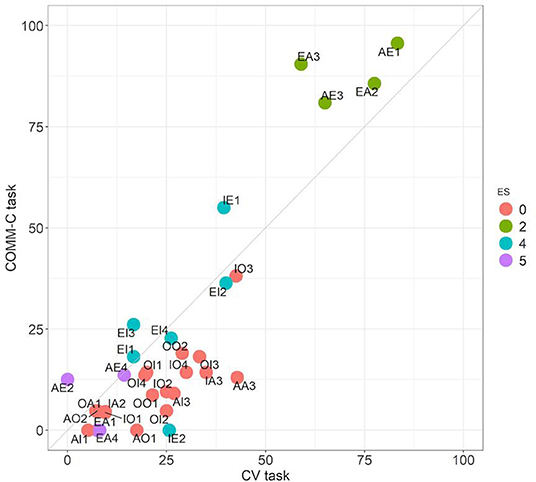
Figure 6. Comparison between the CV and the COMM-C tasks. Performance across the 32 problems. Colors follow the ES classification.
What Does Countermodeling Elicit?
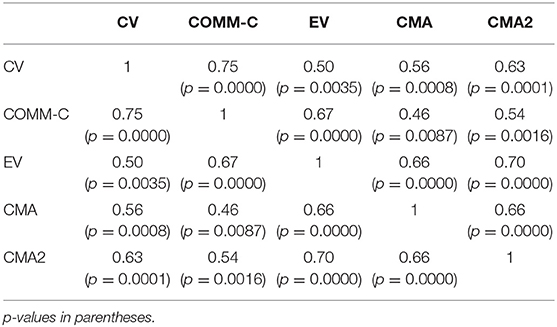
Our comparison across tasks is guided by the idea that there is a change in disposition: CV, EV, and COMM-C tasks on the one hand (cooperative), and CMA and CMA2 on the other (adversarial). From the point of view of the answer format we have on the one hand the CV and COMM-C tasks (choose from a menu of conclusions), and on the other, the CMA, CMA 2, and EV tasks (determine the validity given a proposed conclusion). Even if all tasks are all positively correlated (Table 2), some significant differences are obtained as can be seen in Figure 2. On the one hand, both in CMA and CMA2 we see an improvement in the overall accuracy across problems. Here, the more direct comparison is with EV. Particularly salient is the improvement with regard to NVC problems (red columns) which leads to a large reduction of the VC/NVC performance asymmetry. The spectrum varies from large differences in the COMM-C and CV tasks. In these we see differences of 27.4 and 11.6 percentage points, but the strong asymmetry in these tasks is more evident if we re-score these tasks in a way that bisects the possibilities (any valid conclusion vs. no valid conclusion). This is designed to capture the over-inferencing which is so characteristic of the NVC problems in the conventional task. In this way, the generation paradigm tasks are evaluated in a bivalent way which makes them at least approximately comparable with those of the evaluation paradigm. If we consider the judgment that “something follows” in valid problems, accuracy rates for CV and COMM-C are of 84.2% and 93.8%. The difference between valid and non-valid problems is therefore striking: 61.6 and 83 percentage points.
Under the evaluation paradigm the differences range from 24.7 (EV task) to 19 (CMA task) and 16.7 (CMA2 task). These effects of countermodeling are significant, as reported in subsection The CMA and CMA2 Tasks.
Back to the comparison between CV and COMM-C, we noticed in subsection The COMM-C Task how close they are. Participants in the conventional task do not answer following classical norms consistently, leading to an extremely irregular performance across problems (Figure 1). This may be attributed to a great extent to the fact that they do not interpret the task goal in the same way the experimenter does. The purpose of the COMM-C task is to clarify what those aims may be. The very large correlation between the two tasks indicates that what subjects do in both is very similar: they understand the CV task essentially as a communication task, from a cooperative stance. As may be expected, this cooperative disposition is more extreme in COMM-C: a higher tendency to believe that valid conclusions do follow from premises, and the correspondent difficulty of refraining from endorsing conclusions from the menu (low performance in NVC problems). We see COMM-C as a caricature of CV in the sense that its more striking characteristics are exaggerated, though perhaps not by much. This tells us that participants in CV are not attempting but failing to do the intended task, but that they are really doing another, fundamentally different task. To get them to do the required classical logical task is an important educational goal, but one first has to communicate the goal, before resorting to accusations of poor performance.
The cooperative task of interpreting and understanding discourse can be approached through logical tools (van Lambalgen and Hamm, 2005; Stenning and van Lambalgen, 2008). We interpret the data as indicating that subjects understand the CV task by assimilating it to this logic of discourse interpretation which radically differs from classical logic. Nevertheless, results are usually evaluated from the perspective of the latter which leads to the conclusion that subjects have “poor reasoning” competence. The COMM-C task attempts to understand what the team-mate is conveying. This is something very close to cooperative discourse interpretation: an attempt to reconstruct the intended situation described (the intended or “preferred” model, in the technical sense).12
Experiment 2: Integrating the Tasks as a Didactic Sequence
The effects obtained in Experiment 1 indicate clear tendencies when we take (as experimenters and educators usually do) classical logic as our benchmark. The results obtained comparing the spectrum of tasks suggest that there are good reasons why “naive” subjects deviate from this particular logic and suggest also in which direction we should move if our goal is to obtain results according to it. Again, the goals pursued matter. Experiment 2 explores what we can obtain from an intervention designed in this direction. We implement three successive tests (pretest, posttest 1, and posttest 2) with the idea of facilitating the transition from an initial (cooperative) point, toward an adversarial classical logic one.
We start from the observation that, as noticed in subsection The CMA and CMA2 Tasks, the countermodeling tasks are highly demanding and that even if we see a change in disposition and performance, correct countermodel production is generally not attained. Understanding the construction of counterexamples needs in general more than the bare written instructions of the usual experiments. We focus then on the clarification of this notion, crucial for us as an external tool supporting the definition of the (classical) inference relation, as already explained in Section Construction of Counterexamples: Modeling and Countermodeling as Tools for Syllogistic Reasoning.
Methods
Materials
We focused here on a within-subjects comparison of the tasks EV and CMA2 (the one that seemed most promising from Experiment 1 to obtain a shift toward classical reasoning). The instructions were the same as in Experiment 1 but in this case instructions (including the countermodeling explanation) were carefully explained and not just provided in the booklets: see the procedure.
The problem selection was the same as in Experiment 1. In the pretest and posttest 1 the problems were the 16 of set 1 (see Table 1). In posttest 2 we applied the problems both of set 1 and set 2, each to half of the participants. This allowed us to test the trajectories of problems of set 1 (comparing along the three tests). At the same time, we applied set 2 problems in the third test in order to control for possible plain memory or training effects along the three trials with the same set of problems, using a set with similar characteristics (as discussed above in section Materials and Procedure). As in Experiment 1, the order of presentation of the problems in all the booklets was randomly generated and different these orders were randomly distributed to the participants.
Participants
These were 36 1st and 2nd year mathematics students at University El Bosque in Bogotá. The mean age was 20.3. They were beginning their studies with introductory courses. From the point of view of logic, their knowledge was limited to a basic semi-formal logic course (partially or totally completed by the time of the experiments), mostly focused on propositional logic, truth tables and quantifiers notation for mathematical statements. The experiment was conducted separately in a total of 5 small groups (from 5 to 9 students each) during class hours with students from different courses.
Procedure
The sequence was designed with alternating tests and short interventions over three sessions based on the following stages:
• First session: After a very short, 5 min introduction the pretest was administered. The purpose was explained as to complement their knowledge of logic with learning about syllogisms. The starting point was the EV task. As we explained, we were interested in their initial answers previous to any instruction. Typically, students finished the 16 problems within 30 min.
• Second session: We implemented the first intervention, comprising some quick history of Aristotelian logic and syllogisms. We provided instructions on the countermodeling technique, which were explained in detail. We passed then to some practice with 2 or 3 example problems which they worked on individually. Their counterexample proposals were discussed and corrected in the group. Questions were clarified by the experimenter. This intervention took around 45 min. We then conducted posttest 1 with the framework of CMA2. In this experiment we introduced a variation with regard to Experiment 1: in order to emphasize that the source of the answers was really a student, we selected some of the answered booklets from the first session and presented them in an anonymized and randomized way. An hour was assigned for the test but most of the students finished in 40 min.
• Third session: A second intervention consisted in giving back to participants their corrected pretest and posttest 1. Special attention was given to providing individual feedback on the counterexamples constructed. This was facilitated by the fact that the groups were small. Pretest and posttest 1 were given back not only in order to correct the mistakes and clarify concepts, but also with the didactic aim of making participants aware of how far their starting point was from classical validity, and how substantial improvement could be attained by the use of counterexamples (a means for reaching the concept of entailment, as explained in Section Construction of Counterexamples: Modeling and Countermodeling as Tools for Syllogistic Reasoning). Additional time for questions was given. In total, this took around 30 min. Next, posttest 2 was administered, again asking to evaluate the validity of a deduction, and to construct a counterexample when possible. Here again, an hour was assigned for the 16 problems. Most of the students took around 40 min in order to complete the test. A total of four participants missed this last session.
The three sessions were held a week apart. At the end, all the results of the three tests were shown to the participants, with a reflection on the didactic effect obtained by them individually and as a group.
Results
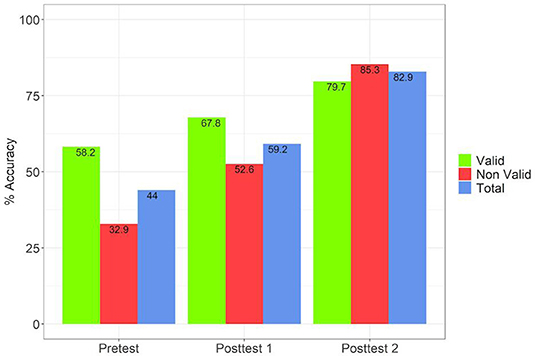
If we take the mean performance, we have a mean of 44, 59.2, and 85.3% for validity judgements, respectively, in the pretest, posttest 1 and posttest 2 (Figure 7).
We interpret these results as a progressive attainment of our intended target. This can be seen also examining the distribution of individual scores (over 16 problems) attained by each of the participants on each of the tests (Figure 8; see also the table in the Supplementary Material).
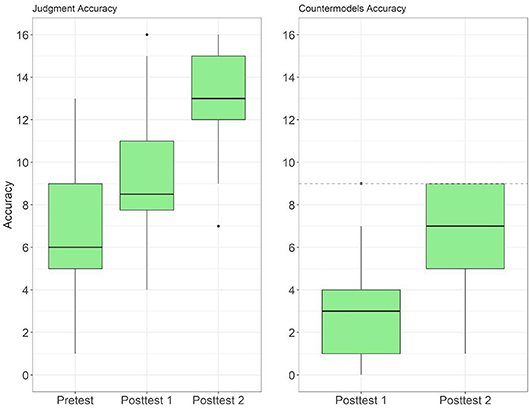
Figure 8. Boxplots showing the subjects' performance distribution in the three stages of Experiment 2. Left: performance in problems evaluation. Right: performance in correct countermodel construction in the two last stages.
In the pretest the mean score (7.04), the median (6), and 22 out of 36 participants had scores not greater than 8. With 16 problems, this means chance level or below. There were extreme cases of seven students with 25% or less correct answers, reflecting how misleading intuition can be in this task (they were providing answers almost opposite to the task that was required).
In posttest 1 we obtain a large improvement in the evaluation of the conclusions (Figures 7, 8). We attribute this, in part, to the change of perspective by taking over the position of a professor correcting a test from a student. This, together with the countermodel construction, led, as expected, to results similar to the ones observed in Experiment 1 comparing EV with CMA2 (44 and 59.2% of pretest, and posttest 1 are very close to the 46.4 and 65.1% obtained in EV and CMA2 in Experiment 1).
As observed in Experiment 1, this is an already important change which reflects an adversarial context. Even so, there is still clearly place for improvement. Above all, countermodeling constructions in posttest 1 are very frequently wrong. Seven participants provided two or less correct countermodels (out of nine possible); four did not construct even one. This alone confirms the difficulties involved in the process of understanding and performing well with the notion of counterexample, as already observed in Experiment 1. This motivated the necessity of a further stage for feedback and clarification, as addressed in our third session. The results obtained confirm this hypothesis and are close to being optimal. In posttest two we achieved another important improvement in evaluating the validity of the proposed conclusions, but more revealing than this, an improvement in the construction of the countermodels (mean score = 6.47 over nine possible countermodels with nine subjects having all of them correct; see also Figure 8-right). This improvement was present both with the same set of problems (set 1), or with a changed one (set 2). There is no significant difference between students with the two sets (p = 0.5178).
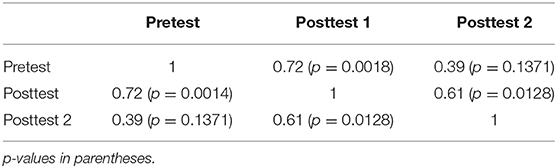
Figures 9, 10 provide a comparison between the different stages across the 16 problems of set 1. The first one is a close analog of comparing EV with CMA2 in Experiment 1 (Figure 4). In contrast, the comparison in Figure 10 shows an improvement absent in all the other tests considered in both experiments. On the one hand, all the problems have mean scores above 65%, with OI3 and OI2 having even 100%. On the other hand, we can see that all invalid problems clearly “move upwards” As we see in Figure 7, accuracy differences between valid and invalid problems decline from round 25–15 percentage points between the pretest and posttest 1. In posttest 2 the asymmetry is completely eliminated (with mean performance in non-valid problems even higher). This is supported by the fact that the pretest and posttest 2 are uncorrelated (Table 3).
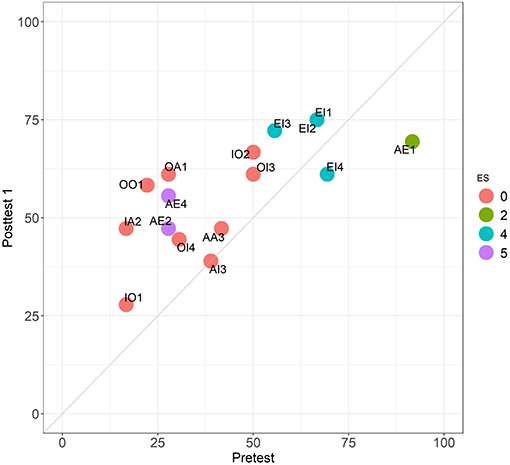
Figure 9. Comparison between the pretest (EV task) and posttest 1 (CMA2 task) in Experiment 2. Performance across the 16 problems of set 1. Colors follow the ES classification.
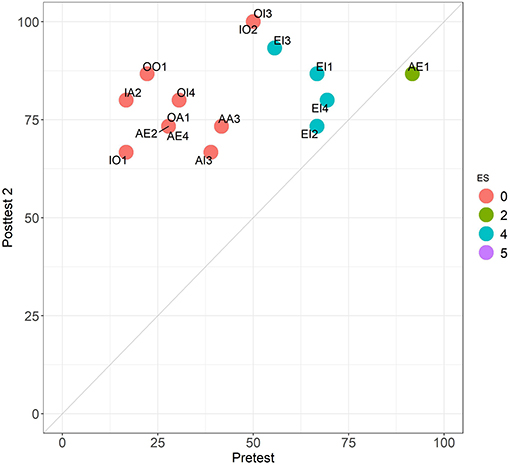
Figure 10. Comparison between the pretest (N = 36) and posttest 2 (N = 15) in Experiment 2. Performance across the 16 problems of set 1. Colors follow the ES classification. Problems in class 5 (AE2 and AE4) are hidden behind OA1.
With few exceptions participants presented a sustained improvement in evaluating correctness of problems across the three trials (see the table in the Supplementary Material). Even the clearest exception (student S05) was an extremely revealing case. He was the oldest student (45), well above all the others (mean age = 20.3). He already had a professional qualification and had some knowledge of the topic. In the first test, in fact, he made use of Euler-Venn diagrams as a support and obtained the highest score. In the second test, he performed worse than before. In the third session, when receiving his feedback, he manifested his discomfort with having to use a different technique from that already known to him in dealing with syllogistic reasoning. In posttest 2 he performed even worse. He passed successively from 13 to 11 and to 9 correct answers. From the conversation with him, it was clear that he was trying to accommodate our counterexamples construction within the scheme of his knowledge of diagrams, already consolidated. What the other students learned along the process is apparently more directly acquired starting only from their intuitive knowledge, than with a previously existing scheme which could not easily be abandoned because the participant already felt confident using it.
Some Typical Strategies, Interpretation Obstacles, and Disambiguations
Experiment 2 allowed us also to obtain further information besides that provided from the data from the tests. After each session, notes on the arguments and questions from the students were taken. We present next some of the more salient phenomena revealed.
Strategies of Countermodeling Construction
Among the notions introduced in the tests, probably the most difficult one to acquire fully is that of countermodeling and how it can be used in regard to validity: a deduction is not valid if there is a model of the premises which is not a model of the conclusion. The double negative character of this procedure places heavy demands on subjects' attention needed for forcing premises to be true, forcing the conclusion to be false, and integrating the existence of such a construction with a judgment of the invalidity of the deduction. In fact, two salient tendencies in countermodeling (Vargas et al., submitted) are either, (1) to provide a model of the premises forgetting that the conclusion should not hold in order to have a countermodel, or (2) to then change the model to make the bet false, but not notice that one of the premises is then not true, so the countermodel fails because it is not a premise model. These can be calculation problems without conceptual confusion.
Another kind of misunderstanding observed here was about what a countermodel (or a counterexample) is. Given that we asked for universes with two elements, participants often considered that the validity or invalidity of the statements should be evaluated on each of the elements of the structure or the universe, and not globally. Typically, in their first encounter with having to construct counterexamples (in the intervention of our session 2) a conclusion such as Some of the students taking geometry are taking linguistics, was confronted with a situation such as:
Student 1:
Linguistics ✗
Arab ✓
Geometry ✓
Student 2:
Linguistics ✓
Arab ✓
Geometry ✓
In this case, some participants understand that Student 1 constitutes a counterexample whereas Student 2 constitutes an example, leading to the belief that a counterexample is provided. This is incorrect because the particular affirmative statement is true in the model: there is some student taking both geometry and linguistics, namely, Student 2. In the vocabulary of model theory, they are confusing the notion of a structure not being a model for a statement, with the notion of there being an instance, within the structure, of the negation of the statement. An explanation emphasizing that truth in a structure must take it as a whole turns out to be very useful in clarifying such misconceptions.
Which algorithm do individuals follow for countermodeling construction? Participant S20 was very conscious about what he did, and about the fact that he switched during posttest 1. First, he began constructing a model of the premises and only then tried to provide a countermodel of the conclusion. At the end, he noticed that for him it was easier to begin countermodeling the conclusion and then try to satisfy the premises. In fact, there was an improvement over the test: his only three mistakes were in the problems presented in position 3, 5, and 12, with no mistakes in his last 4 problems. Also, in his final test, after making this explicit remark, he performed perfectly both in conclusions evaluation (16/16) and correct countermodeling construction (9/9 possible countermodels). He changed his strategy because, as he indicated, it was easier, then, to remember that the conclusion had to be false in order to obtain a countermodel. We point to this case because, even if we believe that such a conscious metalevel monitoring as exhibited by S20 was not generally present, it indicates that countermodel construction may put into action clearly different algorithmic strategies even with such simple models as these.
Interpretation of the Quantifiers
Two well-known concerns regarding the interpretation of the quantifiers involved in the statements were posed by our students.
The first was about the “conversational” use of the existential (or “particular”) statements. Student S33 said, during the feedback on session 3, that some of his “mistakes” in posttest 1 were occasioned because he interpreted all existential assertions (Some A are B) as affirming also that Some A are not B. This implicature (Grice, 1975), is usually explained in terms of informativeness (“Make your contribution as informative as is required”).
Student S29 made explicit the same interpretation during the feedback session. In fact, she did so as an explanation of the fact that in some cases she added a third element to the countermodels. Two elements, in fact, are not always enough when assuming such an interpretation.
A second perplexity was about universal statements. For example, during the explanation of session 2, we used Syllogism AI3 as an example:
All the students taking linguistics are taking Arabic.
Some of the students taking geometry are taking Arabic
Conclusion:
Some of the students taking geometry are taking linguistics.
Participant S25 proposed the following counterexample:
Student 1:
Linguistics ✗
Arabic ✓
Geometry ✓
Student 2:
Linguistics ✗
Arabic ✓
Geometry ✓
She argued that the first premise is true in this case, because if there is no student taking linguistics, then the universal statement holds. This led to a debate in class. It is well-known that this is the key feature that distinguishes the Aristotelian and the modern interpretation of the universal quantifier. As explained in section “Evaluation of Problems and Countermodels,” for Aristotle, universal statements have existential import whereas modern interpretations do not require this. Was the premise true or not? We clarified the point emphasizing the historical development just mentioned. We did not commit to any of these conventions as “the correct” one, explaining that the interest of their answers in the tests was not in adhering to one or other of these normative positions, but to analyze how they reason. Educationally, it was an opportunity for us for emphasizing the conventional and historical character of some logical rules. Therefore, they were “allowed” to construct counterexamples according to their choice. Interestingly, in both posttest 1 and posttest 2 student S25 presented a systematic tendency in modeling all the universal affirmative statements in the premises using “empty antecedents” (interpreting the universal as an implication). This one was an extreme case, but seven other participants stated explicitly (when interrogated) that they had used this feature in at least some of the problems. In the table in the Supplementary Material we report in separate columns the scores from the two normative standpoints (“traditional” vs. “modern”). The countermodels data provide us here with strong evidence of reasoning with empty sets, indicating that a unique logical standpoint (as traditionally used) may hide other reasoning strategies equally legitimate.
Decidability and Proof
A final aspect that emerged during the discussions with participants that we want to emphasize, is that some of the questions and concerns reflected their conceptions about proof and mathematical procedures.
Student S09, for instance, was looking for an algorithmic mechanism for constructing counterexamples. He realized that at some point not everything was completely determined at each step of the construction about the two elements of the models. Some of the features were usually underdetermined by the premises. Part of the work was an exploration, sometimes hypothetical, which could eventually lead to a counterexample. The fact of having two or more possibilities and having to suppose something without knowing the final result produced a manifest anxiety in him. His conception about mathematics was procedural and he expected to reduce argumentation and proof to this level.
Two different students commented independently that a procedure for establishing validity of conclusions is needed. Counterexample construction is in fact a means which in principle leads only to showing invalidity.
As student S01 asked in session 3: “Professor: is there any way to be sure that the conclusion follows? Counterexamples tell you that a conclusion does not follow, but what about correct conclusions?” From this, it could be made clear to them that in this particular case, the combinatorial exhaustive search in the space of models with two elements led to the establishing of validity (as explained in Section Construction of Counterexamples: Modeling and Countermodeling as Tools for Syllogistic Reasoning), and that this was feasible in a reasonable time. In this case, the situation led naturally to the implicit understanding of the metalogical notions we wanted to reach such as the concept of logical necessity.13
General Discussion
The fields of cognitive psychology and mathematics education meet at different points in their subject of study. Even if their particular aims do not always coincide and mutual communication is not straightforward, there is a recognized need for interaction between them [see e.g., (Gillard et al., 2009; Star and Rittle-Johnson, 2016)].
The present study is an attempt at such an interaction. Its focus is on the crossroad of cognitive psychology (the topic of study, the design of the tests), educational psychology (class-based interventions, the learnability and teachability of a topic) and mathematics education (the role of counterexamples for mathematical reasoning, the emergence of the notion of proof and refutation). We see the two experiments presented as complementing each other taking into account the strengths and weaknesses of each discipline.
We see such an interaction taking place at the fundamental levels that guided our study: the role of counterexamples in reasoning, and the communicative goals pursued at the base of this process.
On the one hand, as already indicated in Section Construction of Counterexamples: Modeling and Countermodeling as Tools for Syllogistic Reasoning, the theme of examples and counterexamples plays a role both in psychology and mathematics education and can be addressed from the logical point of view, where “models” and “countermodels” have a precise definition. We addressed the problem here, in a very constrained situation, with this level of precision. This allows us to conclude that the process of generating a preferred model12 in reasoning is not necessarily accompanied by a subsequent search for counterexamples (as proposed by the mental models theory). And that mental models explanations of the conventional tasks do not fit the evidence—it is not just that countermodeling does not take place—what does take place is interpretable as inference in a different logic. The explicit generation of counterexamples leads in our experiments to completely different results compared with tasks which do not require this generation. It leads also, in our view, to a completely different notion of deduction and the logic underlying it.14 We think that this difference is more generally crucial in mathematical reasoning.
As we can infer from our second experiment, the generation of counterexamples requires in many respects a process of familiarization, disambiguation and mastery. We could see this process in a relatively simple situation (2-element models, 3 monadic predicates, a limited non-recursive syntax). It is even more necessary in the far more complex range of mathematical contexts.
On the other hand, context and communication determine the kind of reasoning that is elicited. The issue of context dependency has been widely documented in the psychological literature, and acknowledged in different ways from approaches such as ecological rationality or situated cognition. It is also present to a large extent in educational contexts, in particular in mathematics. The communicational situations may vary the goals pursued to the point of representing completely different “games” (Wittgenstein, 2003). The game of cooperative communication and construction of an intended model, differs completely from the adversarial search for possible counterexamples that attempt to defeat a statement or argument, as illustrated by the results presented here. We interpret these results as suggesting that adversarial argumentation, classical logic deduction, and mathematical proof may be seen as linked in a continuum if appropriate contextual prompts are provided. These prompts can materialize in communities of practice as emerging from particular communicative situations and dispositional attitudes. In this sense, the question of whether there is continuity or rupture between argumentation and proof (Duval, 1991, 1992) cannot be answered in general terms, but only within a context. The answer is contingent on how the kind of communication and argumentation operating in a particular setting is interpreted by subjects. If this interpretation is based on a cooperative disposition or “game”15, then there is indeed a rupture. The contrary occurs if it is experienced as an adversarial one. In this case we obtain a skeptically guided, oppositional search in the “example space.” As Balacheff (1987) put it: “intellectual proof mobilizes a meaning against another, a relevance against another, a rationality against another”.16 We see in the different tasks studied here indications of the presence of these two dispositions: CV, COMM-C, and EV show a primary tendency toward a cooperative setting, whereas our countermodeling tasks are tied to an adversarial stance, both when it is a manifest competition (CMA) or when it is an “adversarial cooperation” (CMA2). These are, even in the limited contexts of our experimental settings, cases of “engagement structures” (Goldin et al., 2011). We see in particular the “Let Me Teach You” structure operating in CMA2 in order to help students grasp the game being played from a situation that they know well.
Given this contextual character of communication and reasoning and how the diversity of situations leads to different processes and outcomes we want to stress that it inheres not only the descriptive, but also the normative aspect of logic and its role in psychology. We believe that both the cognitive psychology and the mathematics education literatures still miss and require pluralistic accounts on how we reason. These should go beyond the crude dichotomy between “correct” and “incorrect”17 answers in reasoning tasks, usually evaluated exclusively by standards of classical logic. This manifests itself in psychological experiments, where participants may well be trying to do a task different from the one intended by experimenters (Stenning and van Lambalgen, 2008). The situation is analogous in education, where the notion of “error” is often considered as more clear-cut than it is. Reasoning is a manifold process which may require different norms18 in different situations and, accordingly, “errors” may be sensible inferences depending on the interpretation adopted. They are not primarily something to be “eliminated,” an attitude that in traditional education often involves emotional and even moral implications (Oser and Spychiger, 2005). We believe, on the contrary, that to a large extent, learning to reason is learning the particular communicative conventions at use in a particular discourse, a process which usually also requires appropriate support through modes of representation.19 From this perspective we believe that pluralistic accounts which integrate this diversity of communication and cognitive situations are needed. The results of our study indicate how tasks comparable from their “formal” structure prompt in practice different kind of answers. Rationality should not be thought of just as something abstractly and generally either possessed or not, but as emerging in particular ecological contexts (Simon, 1956), here of a communicational kind.
Data Availability Statement
The datasets generated for this study are available on request to the corresponding author.
Ethics Statement
Ethical review and approval was not required for the study on human participants in accordance with the local legislation and institutional requirements. Written informed consent for participation was not required for this study in accordance with the national legislation and the institutional requirements.
Author Contributions
FV performed the interventions in Experiment 2, organized the databases, performed the statistical analysis, and wrote the first draft of the manuscript. FV and KS contributed conception, design of the study, contributed to manuscript revision, read, and approved the submitted version.
Funding
Funding was received from the SPP 15–16 New Frameworks of Rationality.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors thank the two reviewers for their help in improving the clarity of the paper. Special thanks to Dr. Laura Matignon for her collaboration in the data collection of Experiment 1 at Ludwigsburg University of Education.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2020.00028/full#supplementary-material
Footnotes
1. ^Among these different accounts of performance in syllogistic reasoning there is probability, see e.g., (Chater and Oaksford, 1999). Our general attitude to this is “the more the merrier”: classical logic, preferred model nonmonotonic logic, probability, … A multiple logics approach can embrace other bits of mathematics too. Probability is often taken to be a monolithic replacement for classical logic as a normative standard. This we absolutely reject. But there are also often misinterpretations of probability going on. A probabilistic interpretation of a situation is very close to a classical logical one. From our point of view, the most important point is that it cannot be the logic within which interpretations are developed— that requires a logic like the version of LP used in (Stenning and van Lambalgen, 2008), which can model our narrative ability to accommodate new information into the interpretation at every sentence by importing general knowledge (see Stenning and van Lambalgen, 2010 for extended discussion). A further general issue is whether the full force of probability is required to model what may be conditional frequency reasoning. If the mathematical/logical framework is taken to be involved in the mental computations (not merely providing some externally imposed normative standard), then there are real issues how these probabilities are computed, whereas conditional frequencies could be made available in, for example, the LP nets of semantic memory in (Stenning and van Lambalgen, 2008), and may well be the basis of the judgements made in experiments on “probabilistic models” of the syllogism, and possibly the explanation of the well-known frailties of naive probabilistic reasoning.
2. ^See also, e.g., (Lloyd, 1979) and, more recently, (Netz, 2003) on this topic.
3. ^The notion has been further elaborated more recently through Etchemendy (1990) distinction between “interpretational” and “representational” semantics. The approach in our experiments is closer to the last one. See also the distinction between formal vs. material consequence in (Read, 1994).
4. ^The fact that the identification of individuals with a particular one of eight possible types (corresponding to the assertions and negations of the three monadic predicates present in a syllogism) may be used to decide the validity of an argument is in fact already present in Aristotle's works, namely through the ekthesis technique of proof [(Kneale and Kneale, 1962), p. 77]. According to Hintikka (2004), ekthesis operates like the rules of instantiation in modern logic. It consists of choosing a particular individual (or, in another interpretation, a sub-class) to represent a general term. This is the sense that “ekthesis” also had in geometry, extensively used by Euclid in passing from a general statement into consideration of a particular object be it a point, a line or a triangle. Once this step is done, it is usually followed by the characteristic use of auxiliary constructions.
5. ^See Section Problem Selection for this notion.
6. ^The name is explained by the fact that a first criterion for the classification of problems arises from the observation that existential presuppositions are traditionally assumed in the field and this leads to a clear performance divergence from problems that require this assumption in order to have a valid conclusion and problems that do not. This substantial difference occurs with double universal problems (our classes 2 and 5).
7. ^All problems without any valid conclusions are conventionally assigned the number “0.”
8. ^This simple classification is motivated by the fact that it correlates highly with the percentage of correct answers of the valid problems in the Conventional Task meta-analysis 0.94, p = 2.288e-12.
9. ^Logical models are here sets of elements, each element of which represents a type of individual defined by the three properties and their negations. This is because the syllogism has no identity relation to distinguish individuals of the same type. So there are eight types of element which can be notated: ABC, ¬ABC, A¬BC, AB¬C, ¬A¬BC, A¬B¬C, ¬AB¬C, ¬A¬B¬C. Because these are types of thing, repetition of the same type in a model is redundant. So, there are just these eight types of element in any models of the syllogism. 1-element models contain just one of these eight types; 2-element models contain two (distinct types), up to a maximum of eight types i.e. the single 8-element model. We are only concerned with models of up to two elements because they are always sufficient for countermodeling. NB. Models and elements are semantic objects—sets of things. But they can either be thought of as collections of things (shoes and ships and tins of sealing wax …) with their relevant element labels from the possibilities above stuck on. Or their elements can be represented by sentences composed of conjunctions of three atomic propositions, such as say (¬A∧B∧¬C). Models are then sets of these sentences. The syllogism is so simple a fragment of classical logic that syntactic representation in the mind is hard to distinguish from semantic representation. This becomes important for assessing some psychological theories of the syllogism.
10. ^It is also worth clarifying that in EV we had only 22 participants, given that (as planned in the design) booklets included twice the number of problems in comparison to the other tasks. We used this design since EV was by far the less demanding task in time. Finally, the sample size in the CV task is remarkably larger because in this case we could include the data from a previous experiment. In this experiment we had a booklet generation mistake in the tasks different from CV. This experiment was conducted a semester before in the same institution and courses at the same university level (from first to third year).
11. ^Vargas et al. (submitted) presents some evidence, based on counterexample analysis, that existential presuppositions are not compatible with the results of the CMA task (compatible instead with modern interpretation of classical logic). Even so, they can well be present in the Conventional Task.
12. ^Here the term is used informally, but we mention that it has a technical counterpart in the preferential semantics (Shoham, 1987) for non-monotonic logics.
13. ^This was probably obtained owing to the fact that our participants were mathematics students and their particular involvement with mathematical proofs even at their early stage.
14. ^It is clear, as also confirmed here, that participants do not primarily follow classical logic in traditional syllogistic tasks. Actual performance on them may be approached more properly with non-monotonic logics (Stenning and van Lambalgen, 2008).
15. ^“Game” not only in Wittgenstein's sense, but also in the Games Theory sense that it can be cooperative or adversarial (zero-sum or non-zero-sum).
16. ^Our translation and emphasis.
17. ^Other labels such as “biases” or “fallacies” are equally contestable when understood in absolute terms.
18. ^These diverging norms may be approached through different logical systems. This presupposes logical pluralism: “the view that there is more than one genuine deductive consequence relation, and that this plurality arises not merely because there are different languages, but rather arises even within the kinds of claims expressed in the one language.” (Beall and Restall, 2006, p. 3)
19. ^This is far from conceptions in math education which see, for example, an opposition between “Child's Logic” and “Math Logic” (O'Brien et al., 1971) as if students' naïve performance were only a poor man's version of a supposedly ideal stage. We also deviate from the search for “The right notion” of logical concepts (Durand-Guerrier, 2003). Different logical interpretations are required in reasoning and even in mathematical practice.
References
Antonini, S., Presemeg, N., Mariotti, M. A., and Zaslavsky, O. (2011). Special issue: on examples in mathematical thinking and learning. ZDM – Zentralblatt fuer Didaktik der Mathematik 43, 191–194.
Balacheff, N. (1987). Processus de preuve et situations de validation. Educ. Stud. Math. 18, 147–176. doi: 10.1007/BF00314724
Beall, J. C., and Restall, G. (2006). Logical Pluralism. Oxford: Oxford University. doi: 10.1093/acprof:oso/9780199288403.001.0001
Bills, L., and Watson, A. (2008). Special issue: the role and uses of examples in mathematics education. Educ. Stud. Math. 69, 77–79. doi: 10.1007/s10649-008-9147-z
Bucciarelli, M., and Johnson-Laird, P. N. (1999). Strategies in syllogistic reasoning. Cogn. Sci. 23, 247–303. doi: 10.1207/s15516709cog2303_1
Chater, N., and Oaksford, M. (1999). The probability heuristics model of syllogistic reasoning. Cogn. Psychol. 38, 191–258. doi: 10.1006/cogp.1998.0696
Durand-Guerrier, V. (2003). Which notion of implication is the right one? From logical considerations to a didactic perspective. Educ. Stud. Math. 53, 5–34. doi: 10.1023/A:1024661004375
Dutilh Novaes, C. (2018). “A dialogical conception of explanation in mathematical proofs,” in The Philosophy of Mathematics Education Today, ed P. Ernest (Cham: Springer), 81–98.
Duval, R. (1991). Structure du raisonnement déductif et apprentissage de la démonstration. Educ. Stud. Math. 22, 233–262. doi: 10.1007/BF00368340
Duval, R. (1992). Argumenter, démontrer, expliquer: continuité ou rupture cognitive. Petit x 31, 37–61.
Gillard, E., Van Dooren, W., Schaeken, W., and Verschaffel, L. (2009). Dual processes in the psychology of mathematics education and cognitive psychology. Hum. Dev. 52, 95–108. doi: 10.1159/000202728
Goldenberg, P., and Mason, J. (2008). Shedding light on and with example spaces. Educ. Stud. Math. 69, 183–194. doi: 10.1007/s10649-008-9143-3
Goldin, G. A., Epstein, Y. M., Schorr, R. Y., and Warner, L. B. (2011). Beliefs and engagement structures: behind the affective dimension of mathematical learning. ZDM 43, 547–560. doi: 10.1007/s11858-011-0348-z
Grice, H. P. (1975). “Logic and conversation,” in Syntax and Semantics: Speech Acts, Vol. 3, eds P. Cole and J. Morgan (London: Academic Press), 41–58.
Hanna, G., and Jahnke, H. N. (1993). Proof and application. Educ. Stud. Math. 24, 421–438. doi: 10.1007/BF01273374
Hintikka, J. (2004). “Aristotles incontinent logician,” in Analyses of Aristotle. Jaakko Hintikka Selected Papers, Vol. 6 (Dordrecht: Springer), 139–152.
Jahnke, H. N. (2010). “The conjoint origin of proof and theoretical physics,” in Explanation and Proof in Mathematics, eds G. Hanna, H. N. Jahnke, and H. Pulte (Boston, MA: Springer), 17–32.
Johnson-Laird, P. N., and Byrne, R. M. J. (1991). Essays in Cognitive Psychology. Hillsdale, NJ: Deduction.
Johnson-Laird, P. N., and Steedman, M. (1978). The psychology of syllogisms. Cogn. Psychol. 10, 64–99. doi: 10.1016/0010-0285(78)90019-1
Khemlani, S., and Johnson-Laird, P. N. (2012). Theories of the syllogism: a meta-analysis. Psychol. Bull. 138, 427–457. doi: 10.1037/a0026841
Lakatos, I. (1976). Proofs and Refutations: The Logic of Mathematical Discovery. Cambridge: Cambridge University Press. doi: 10.1017/CBO9781139171472
Lerman, S. (2000). “The social turn in mathematics education research,” in Multiple Perspectives on Mathematics Teaching and Learning, ed J. Boaler (Westport, CT: Ablex Publishing), 19–44.
Lloyd, G. E. R. (1979). Magic, Reason and Experience: Studies in the Origin and Development of Greek Science. Cambridge: Cambridge University Press.
Luria, A. R. (1976). Cognitive Development: Its Cultural and Social Foundations. Cambridge, MA: Harvard University Press.
Netz, R. (2003). The Shaping of Deduction in Greek Mathematics: a Study in Cognitive history. Cambridge: Cambridge University Press.
O'Brien, T. C., Shapiro, B. J., and Reali, N. C. (1971). Logical thinking - language and context. Educ. Stud. Math. 4, 201–219.
Oser, F., and Spychiger, M. (2005). Lernen ist schmerzhaft. Zur theorie des negativen wissens und zur praxis der fehlerkultur. Weinheim: Beltz.
Read, S. (1994). Formal and material consequence. J. Philos. Log. 23, 247–265. doi: 10.1007/BF01048482
Rips, L. J. (1994). The Psychology of Proof: Deductive Reasoning in Human Thinking. Cambridge, MA: MIT Press.
Roth, W. M., and Radford, L. (2011). A Cultural-Historical Perspective on Mathematics Teaching and Learning. Rotterdam: Sense Publishers.
Scribner, S. (1975). “Recall of classical syllogisms: a cross cultural investigation of error on logical problems,” in Reasoning: Representation and Process, eds R. J. Fallmagne (Hillsdale, NJ: Lawrence Erlbaum Associates), 153–573.
Scribner, S. (1977). “Modes of thinking and ways of speaking: culture and logic reconsidered,” in Thinking: Readings in Cognitive Science, eds P. N. Johnson and P. C. Wason (New York, NY: Cambridge University Press), 483–500.
Sfard, A. (2008). Thinking as Communicating: Human Development, the Growth of Discourses, and Mathematizing. Cambridge: Cambridge University Press.
Shoham, Y. (1987). “A semantical approach to non-monotonic logics, in Proceedings of the Tenth International Joint Conference on Artificial Intelligence (IJCAI), 1987. (1987, October),” in Readings in Non-monotonic Reasoning, ed M. L. Ginsberg (San Francisco, CA: Morgan Kaufmann Publishers Inc.), 227–250.
Simon, H. A. (1956). Rational choice and the structure of the environment. Psychol. Rev. 63, 129–38. doi: 10.1037/h0042769
Simon, H. A. (1990). Invariants of human behavior. Annu. Rev. Psychol. 41, 1–20. doi: 10.1146/annurev.ps.41.020190.000245
Star, J., and Rittle-Johnson, B. (2016). “Toward an educational psychology of mathematics education,” in Handbook of Educational Psychology, 3rd Edn, eds L. Corno and E. Anderman (New York, NY: American Psychological Association; Routledge), 257–268.
Stenning, K., and van Lambalgen, M. (2008). Human Reasoning and Cognitive Science. Cambridge, MA: MIT Press.
Stenning, K., and van Lambalgen, M. (2010). “The logical response to a noisy world,” in Cognition and Conditionals: Probability and Logic in Human Thinking, eds M. Oaksford and N. Chater (Oxford: Oxford University Press), 85–102.
Stenning, K., and Yule, P. (1997). Image and language in human reasoning: a syllogistic illustration. Cogn. Psychol. 34, 109–159. doi: 10.1006/cogp.1997.0665
Störring, G. (1908). Experimentelle untersuchungen ber einfache schlussprozesse. Arch. für die Gesamte Psychol. 11:1127.
van Lambalgen, M., and Hamm, F. (2005). The Proper Treatment of Events. Oxford: Blackwell Publishing.
Watson, A., and Mason, J. (2005). Mathematics as a Constructive Activity: Learners Generating Examples. Mahwah, NJ: Erlbaum.
Keywords: syllogisms, deductive reasoning, logic, counterexamples, argumentation, situated cognition, mathematics education, proof
Citation: Vargas F and Stenning K (2020) Communication, Goals, and Counterexamples in Syllogistic Reasoning. Front. Educ. 5:28. doi: 10.3389/feduc.2020.00028
Received: 30 November 2019; Accepted: 11 March 2020;
Published: 17 April 2020.
Edited by:
Karin Binder, University of Regensburg, GermanyReviewed by:
Niki Pfeifer, University of Regensburg, GermanyCatarina Dutilh Novaes, University of Groningen, Netherlands
Copyright © 2020 Vargas and Stenning. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Francisco Vargas, Zmp2YXJnYXNtQHVuYm9zcXVlLmVkdS5jbw==
 Francisco Vargas
Francisco Vargas Keith Stenning
Keith Stenning