- 1Embodied Design Research Laboratory, Graduate School of Education, University of California, Berkeley, Berkeley, CA, United States
- 2Department of Educational Psychology, University of Wisconsin–Madison, Madison, WI, United States
- 3College of Information Studies, University of Maryland, College Park, College Park, MD, United States
- 4Department of Teaching & Learning, Southern Methodist University, Dallas, TX, United States
- 5Department of Social Science and Policy Studies, Worcester Polytechnic Institute, Worcester, MA, United States
- 6Department of Mathematics, Colorado State University, Fort Collins, CO, United States
A rising epistemological paradigm in the cognitive sciences—embodied cognition—has been stimulating innovative approaches, among educational researchers, to the design and analysis of STEM teaching and learning. The paradigm promotes theorizations of cognitive activity as grounded, or even constituted, in goal-oriented multimodal sensorimotor phenomenology. Conceptual learning, per these theories, could emanate from, or be triggered by, experiences of enacting or witnessing particular movement forms, even before these movements are explicitly signified as illustrating target content. Putting these theories to practice, new types of learning environments are being explored that utilize interactive technologies to initially foster student enactment of conceptually oriented movement forms and only then formalize these gestures and actions in disciplinary formats and language. In turn, new research instruments, such as multimodal learning analytics, now enable researchers to aggregate, integrate, model, and represent students’ physical movements, eye-gaze paths, and verbal–gestural utterance so as to track and evaluate emerging conceptual capacity. We—a cohort of cognitive scientists and design-based researchers of embodied mathematics—survey a set of empirically validated frameworks and principles for enhancing mathematics teaching and learning as dialogic multimodal activity, and we synthetize a set of principles for educational practice.
Introduction
Philosophy of cognitive science is undergoing considerable change. This change, dubbed the embodiment turn in the history of philosophy (Nagataki and Hirose, 2007, pp. 223–224; see also Zlatev, 2007), challenges the classical Cartesian mind–body divide (Merleau-Ponty, 1945/2005), which dominated 20th century perspectives on the fundamental infrastructure and mechanism of the human mind. Scholars of embodiment seek to evaluate the intriguing hypothesis that thought—even thinking about would-be abstract ideas—is inherently modal activity that shares much neural, sensorimotor, phenomenological, and cognitive wherewithal with actual dynamical corporeal being in the world. By this token, higher-order reasoning, such as solving an algebra equation, analyzing a chemical compound, editing a journal manuscript, or engineering a spacecraft, transpires not in some disembodied cerebral space and not as computational procedures processing symbolic propositions but, rather, by operating on, with, and through actual or imagined objects. Sprouting in the late 20th century as the confluence of intellectual efforts from philosophy, cognitive psychology, robotics, movement scholarship, and linguistics, the embodiment turn has now come of age, priding its own societies, conferences, and handbooks (Shapiro, 2014; Newen et al., 2018).
The embodiment turn in philosophy entertains a spectrum of perspectives on the mind, which range from relatively conservative views of cognition as amodal cerebral activity grounded on traces of multimodal sensorimotor activity (Barsalou, 2008) to radical views of cognition as, by and large, content-less integrated simulations of multimodal sensorimotor activity (Hutto and Myin, 2013, 2017). The mind, per some of the more pioneering suggestions, is more than the brain organ—it extends from the brain, through the sensing-cum-actuating body, and into natural and cultural ecology, where it entangles reciprocally with fellow humans, artifacts, media, and symbolic systems (Hutchins, 1995; Clark and Chalmers, 1998; Melser, 2004).
Empirical evidence has been accruing in support of embodiment theories of cognition. When, in conversation, we refer to our relationship with another person in terms of journeying together (e.g., “We had a rough start, but we’ve come a long way”), we coopt schematic images of mundane experience (a journey) to express the states of intangible ontologies (a relationship; Lakoff and Johnson, 1980). When we read, we form meanings from words via tacitly activating their motor implication (Hauk et al., 2004) and via imaginarily configuring spatial relationships (Glenberg and Kaschak, 2002). When we write with keyboards, we implicitly form negative vs. positive valence toward affect-neutral words, such as “drawer” or “linkup,” depending on how many of their characters are keyed with the left or right hand, respectively (Jasmin and Casasanto, 2012). And interfering with the gestures of abacus experts, as they solve a problem without an abacus, compromises their performance (Brooks et al., 2018). It appears, thus, that many of our cognitive faculties are constituted as situated activities. Cognition develops in context—Varela et al. (1991) contend that cognitive structures emerge from recurrent patterns in perceptually guided action (see also Piaget, 1968).
The embodiment turn has impacted the field of educational research (Abrahamson and Lindgren, 2014; Pouw et al., 2014; Lee, 2015; Shapiro and Stolz, 2019). In particular, the emergence of theoretical and empirical support for central tenets of the embodiment turn has resonated strongly with educational researchers already committed to foregrounding the role of physical activity, such as manipulation, in cognitive development (Allen and Bickhard, 2015). Thus, the embodiment turn helped educational researchers braid together a robust intellectual strain with roots in genetic epistemology (Piaget, 1968), enactivism (Varela et al., 1991), phenomenology (Merleau-Ponty, 1945/2005), pragmatism (Dewey, 1944), pedagogy literature (Montessori, 1967; Skemp, 1976; Rousseau, 1979; Freudenthal, 1983; Froebel, 2005), and their various historical elaborations and embroideries (e.g., Papert, 1980; von Glasersfeld, 1987; Wilensky, 1991; Pirie and Kieren, 1992; Steffe and Kieren, 1994; de Freitas and Sinclair, 2014).
Invigorated by this paradigmatically converging body of literature, scholars of teaching and learning have sought to interpret implications of the embodiment turn for theorizing, designing, and practicing education in a range of disciplines. These have included literacy (Glenberg et al., 2004), chemistry (Scherr et al., 2013; Flood et al., 2015a), astronomy (Gallagher and Lindgren, 2015; Rollinde, 2019), kinematics (Zohar et al., 2018); mathematics (Núñez et al., 1999; Roth, 2009; Nemirovsky et al., 2013; Nathan et al., 2014; Smith et al., 2014; Hutto et al., 2015), and moral development (Antle et al., 2013). Our article focuses on mathematics, where there has been significant interest in embodiment among educational researchers (Radford et al., 2009; Hall and Nemirovsky, 2012; Schoenfeld, 2016).
Educational research inspired by the embodiment turn often looks to understand new forms of teaching and learning enabled by educational design that caters to multimodal situated activity. These have included interactive technologies responding to kinetic qualities of students’ motor actions, such as moving virtual objects, whether by on-screen manipulation (Leung et al., 2013; Sinclair and Heyd–Metzuyanim, 2014) or remote-sensed gesture (Abrahamson and Trninic, 2011), as well as ambulatory motion (Nemirovsky et al., 1998; Ma, 2017; Marin et al., 2020). Research studies evaluating these embodied designs typically gather and analyze participants’ multimodal behaviors, using technology for tracking eye gaze (Duijzer et al., 2017), gesture (Nathan et al., 2014), whole-body movement via GPS (Hall et al., 2015) or motion sensors (Nemirovsky et al., 1998), computer interaction logs via telemetry (Pardos et al., 2018), brain activity (Lyons and Beilock, 2012), and multi-variate speech patterns (Levine and Scollon, 2004), often triangulated with qualitative analyses or audio–video data. These multimodal data may then be mined using machine-learning algorithms (Ochoa and Worsley, 2016; Worsley et al., 2016).
Research efforts to create and evaluate learning environments that implement embodiment theory to practice have, in turn, resulted in a set of empirically validated practicable methodologies for building and facilitating instructional activities. The rationale of creating and offering practicable sets of principled educational methodologies is hardly new. Recently, these “manuals” have variably been called design principles (Kali et al., 2009), design heuristics (Nielsen, 1994; Pratt and Noss, 2010), design guidelines (Antle et al., 2011), design issues or points (Dillenbourg and Evans, 2012), design and evaluation themes (Klemmer et al., 2006), design frameworks (Abrahamson, 2014), theory–practice intermediate frameworks and design tools (Ruthven et al., 2009), conjectures (Nemirovsky, 2003), hypothesized affordances (Sarama and Clements, 2009), and precepts (Lindgren and Johnson–Glenberg, 2013). The objective of this article is to introduce a set of heuristic design frameworks and related principles, emphases, and issues for consideration in building mathematics learning activities where enacting physical movement is taken as constitutive of conceptual reasoning. Whereas these frameworks and related issues all cohere around the broad intellectual sway of embodied cognition, they should be regarded as complementary, reflecting the range and nuances of embodied-cognition literature (Abrahamson, 2018; Johnson–Glenberg, 2018; Nathan et al., 2019). Furthermore, whereas the intellectual grounds and practicable products of our collective work represent broad territories of current educational research on mathematics teaching and learning motivated by the embodiment turn, we make no claims for exhaustive coverage of this dynamic field of scholarship and practice. Rather, we characterize and demonstrate several notable dimensions of current work in this field so as to chart directions for its future development.
Our set of design principles are organized in the next section around six research programs on embodiment and mathematics learning. The programs differ in nuanced ways with respect to the researchers’ assumptions concerning mathematical epistemology, ontology of mathematical objects, and the role of social interaction in enacting and understanding mathematical concepts. We view these differences as important both for honing our collective research efforts and for charting these efforts toward shaping a shared field of study. Our design-based research programs are as follows:
1. Embodied design. How should embodiment inform the design of STEM educational experiences? Embodied design, a pedagogical framework, draws on principles of genetic epistemology, Enactivism, ecological dynamics, and cultural–historical psychology to engage students’ naturalistic sensorimotor capacity and stage opportunities for guided negotiation between grounded ways of knowing and mathematical forms and practices.
2. Action–cognition transduction. How do actions change one’s mind? Action–cognition transduction explains how body movement can induce mental states that mediate sense making, inference, and proof.
3. Gesture and multimodality studies. How do gestures influence STEM teaching and learning? Do people studying mathematics gesture together and, if so, how does doing this support learning? Gesture and multimodality studies reveal how mathematics teaching and learning is embodied and used to ground formalisms and abstractions to the physical environment, support simulated action of mathematical ideas, and invoke conceptual blends and metaphors.
4. Graspable math. How does abstract thinking arise from concrete experiences? Graspable math engages the perceptual–motor system to reify the hierarchical structure of algebraic formalisms.
5. Playful learning. Why might STEM education need opportunities for playful learning? Playful learning constitutes a set of principles for motivating content learning through engaging in technology-based joyful challenging tasks.
6. Embodiment perspectives on teacher education. How should embodiment inform the design of teacher education and professional development? Embodiment perspectives on teacher education looks to involve multiple stakeholders, including university professors, who should all be informed by the promise of embodiment pedagogy.
The paper ends with a synthetic summary of these frameworks, where we chart exponents of these frameworks with respect to the ontology of manipulated objects and the role of sociality in mathematics learning.
Theoretically Informed and Empirically Validated Frameworks for the Design of Future Mathematics Education
This paper proposes the framework of embodied design (Abrahamson, 2009a, 2014) as means of implementing the embodiment turn in the form of mathematics learning activities. The framework of embodied design applies to “tools whose operatory function is engineered specifically so as to … cultivate … the development of particular sensorimotor schemes as a condition for masterful control of the environment in accord with task demands,” sensorimotor schemes that thereby “come to ground the mathematical concepts we want these students to learn” (Abrahamson and Bakker, 2016, p. 5). Below, we elaborate on the framework and then discuss affiliated research programs.
Embodied Design: A Research-Based Framework for Building Mathematics-Education Resources
Embodied design is a theory-to-practice approach to mathematics education that draws on the embodiment turn in the philosophy of cognitive sciences as well as on cognitive-developmental and sociocultural theory to articulate integrated guidelines for building and facilitating pedagogical materials and activities. The framework has been evolving through decades of numerous empirical-research projects all investigating mathematical cognition, teaching, and learning. Embodied-design studies have utilized diverse media—mechanical, electronic, and hybrid—to tackle enduring didactical challenges respecting a range of curricular subject-matter content, such as probability, proportionality, and algebra. Operating in the design-based orientation to educational research (Collins, 1990; Edelson, 2002; Easterday et al., 2016; Bakker, 2018), embodied-design investigations seek both to evaluate the purchase of embodiment theory in educational research and, reciprocally, to utilize the iterative, cyclic method of design practice—ideate, build, implement, evaluate, re-theorize, and over again—as an empirical context for conducting studies poised to elaborate on embodiment theory. Through these studies, a set of heuristic design guidelines were articulated, generalized, and refined.
The phrase “embodied design” was, perhaps, first coined by van Rompay and Hekkert (2001), Dutch industrial designers who used the cognitive-semantics theory of conceptual metaphor (Lakoff and Johnson, 1980) to predict emotional affects humans would attribute to architectural structures, such as bus stops (see also Kim and Maher, 2020). Thecla Schiphorst also used the phrase “embodied design,” first circa 2007 in an unarchived online site and, later, in a co-authored ethnographic study of “strategies for embodied design,” which surveyed HCI expert techniques for accessing and modeling users’ movement experiences with interactive products (Alaoui et al., 2015). Abrahamson, who founded the Embodied Design Research Laboratory at UC Berkeley in 2005, recycled the phrase “embodied design” into the learning sciences literature with his paper, Embodied Design: Constructing Means for Constructing Meaning (Abrahamson, 2009a). As such, a particular conceptualization of embodied design for STEM education was branded, pioneered, and formulated by the Berkeley cohort. This paper, however, presents the work of scholars who may use the phrase more loosely, bringing to bear a spectrum of philosophical and theoretical commitments from cognitive-science scholarship related to multimodal interaction.
At its broadest, the embodied-design framework outlines an approach for creating STEM learning environments that stage mediated negotiations between intuitive and disciplinary orientations toward phenomena relevant to targeted conceptual learning. For example, students who judge correctly, if qualitatively, that some diagonal line is “steeper” than another line should come to accept the rise-over-run geometrical comparison analysis of these same two lines, which yields a compatible quantitative inference. Through participating in embodied-design activities, teachers and students therefore experience opportunities to surface their tacit sensorimotor orientation to situations in juxtaposition with proposed cultural forms, such as mathematical models, that reframe these situations (Abrahamson, 2004, 2007a,b, 2013, 2015a,b, 2019; Abrahamson and Wilensky, 2007). Importantly, embodied designs set students up for correct intuitive responses or performances before presenting them with analytic procedures that validate yet enhance these intuitions. Embodied-design research studies focus on tutor–student collaborative pedagogical negotiations at the conceptual epicenter of struggling to perceive a proposed disciplinary display, such as a diagram, as signifying or facilitating the enactment of intuitive know-how respecting a source phenomenon in question. This struggle requires perceptual re-orientation toward the source phenomenon. We ask how teachers and learners reconcile these socio-cognitive tensions and what epistemic resources they bring to bear in so doing.
Whereas Abrahamson’s earlier investigations of embodied design sought to build activities that draw on students’ innate or early perceptual capacity—specifically their mathematically correct intuitive qualitative judgments in comparing two a/b intensive quantities, such as ratio (Abrahamson, 2002), probability (Abrahamson, 2009b,2012a,b), or slope (Thacker, 2010, Thacker, 2019; Lee et al., 2013)—later studies focused on students’ capacity to achieve new motor coordination for enacting solutions to manual-control problems (Abrahamson and Trninic, 2011, 2015; Howison et al., 2011). As such, Abrahamson refers, respectively, to two genres within embodied design—a perception-based genre, and an action-based genre (Abrahamson, 2014). Below, we offer brief design examples of each genre and discuss general principles for its implementation. These designs were each evaluated empirically with several dozen middle-school students, who participated individually or in pairs in task-based semi-structured clinical interviews.
Perception-Based Embodied Design
Perception-based embodied designs target a/b concepts, such as likelihood (favorable events/possible events), slope (rise/run), density (total object area/total area), and proportional equivalence in geometrical similitude (a:b = c:d). Further common to these designs is a general lesson plan by which students are invited first to articulate their naïve view with respect to a situation and only then to engage in modeling, reflecting, and discussing, by which to negotiate and reconcile the formal view as complementary to, and empowering of their naïve view (Abrahamson, 2009b). This collaborative achievement of teacher and student depends on students coming to see the proposed model as expressing, validating, and explaining their own intuitive judgment of the target properties in the situation. Abrahamson (2014) has named this perceptual accomplishment inferential parity. Figure 1 demonstrates the case of probability.

Figure 1. Selected materials from a design for the binomial: (A) an open urn full of green and blue marbles with a scooper for drawing out four marbles; (B) a card for indicating possible outcomes using green and blue crayons (the thick line indicates “this side up” so as to distinguish rotations); and (C) the sample space of all possible experimental outcomes, made up of 16 such cards.
As a rule, all participants anticipated that the plurality of scoops would bear 2 green and 2 blue marbles, with 4 green or 4 blue scoops being rarest, and so on. However, in building the sample space with cards and crayons, they generally argued that there are only five things you can get (the combinations) and did not initially appreciate why the different arrangements (variations on each combination) might be relevant. Yet once the full sample space was completed and then arranged as an iconic bar chart (Abrahamson, 2006), all study participants were eventually able to perceive the distribution of variations on each combination (1–4–6–4–1 in the five columns) as resonant with their own intuitive judgment respecting the relative likelihood of actual experimental outcomes. That is, they achieved a sense of inferential parity between their perceptions of a situation and its proposed mathematical model (cf. “More-A, More-B,” Tirosh and Stavy, 1999).1
Action-Based Embodied Design
Similar to perception-based embodied design, action-based embodied design, too, seeks to ground mathematics concepts in students’ innate/early capacity. Here, the capacity in question recruited by the pedagogical design is humans’ ecologically adaptive sensorimotor facility of coordinating the enactment of goal-oriented physical interaction. Participants in action-based embodied designs tackle motor-control problems: They are assigned the task of performing a technologically mediated manipulation of material or virtual objects, in an attempt to achieve a specified goal state. Action-based embodied designs are predicated on the research-based general hypothesis that, in the course of attempting to perform complex movements, such as simultaneous orthogonal bimanual manipulations, people spontaneously discern new sensorimotor perceptual structures that facilitate and regulate effective motor control; with appropriate intervention, these new structures, in turn, can become signified as mathematical objects. Empirical implementations of these designs serve as contexts for evaluating and elaborating this general hypothesis.
Intellectually, the action-based genre of embodied design draws on genetic epistemology, and in particular the notion of reflective abstracting (Piaget, 1968; Abrahamson et al., 2016c), as well as on various dynamic-systems ecological theories of sensorimotor and cognitive development (Kelso, 1984; Thelen and Smith, 1994, Smith, 2006; Mechsner et al., 2001; Chow et al., 2007; Kostrubiec et al., 2012; Wilson and Golonka, 2013). Within educational theory, action-based embodied design’s implication of mathematical notions as grounded in kinesthesia affiliates the framework with various dynamical models of cognition, such as in the literatures on concept image (Tall and Vinner, 1981) or enactivist theories of conceptual growth (Pirie and Kieren, 1994). We will illustrate the genre in broad strokes with a paradigmatic case of the Mathematics Imagery Trainer (Abrahamson and Trninic, 2015).
Students working with the Mathematics Imagery Trainer for Proportion (see Figure 2) are asked to move two cursors up and down so as to find locations that make the screen green. Once they succeed, they are asked to move both hands, keeping the screen green. The system is set so that the screen becomes green only when the right and left hands’ respective heights above the base relate by a particular ratio. Here the system is set at a 1:2 ratio, so that green feedback is activated only when the right hand is twice as high along the monitor as the left hand (see Abrahamson et al., 2014, for the case of other ratios).

Figure 2. The Mathematics Imagery Trainer for Proportion: schematic activity sequence (Art credit: Virginia J. Flood). (A) while exploring, the student first positions the hands incorrectly (red feedback); (B) stumbles upon a correct position (green); (C) raises the hands, maintaining a fixed interval between them (red); and (D) corrects the position (green). Note in B and D the different spatial intervals between the cursors or hands.
Figure 2 sketches out our Grade 4–6 study participants’ common four-step interaction sequence toward discovering an effective operatory scheme: (Figure 2A) while exploring, the student first positions the hands incorrectly (red feedback); (Figure 2B) stumbles upon a correct position (green); (Figure 2C) raises the hands, maintaining a fixed interval between them (red); and (Figure 2D) corrects the position (green). Note in Figures 2B,D the different spatial intervals between the cursors or hands.
Whereas the instructor never draws students’ attention to the interval, they construct this interval spontaneously as a new operable ontology, a perceptual means of solving the motor-control problem (Abrahamson et al., 2011). Engaging this affordance facilitates and regulates the bimanual enactment of a movement pattern that satisfies the task specifications. Specifically, students discover that the higher they raise their hands, the larger the interval should be, and vice versa.
Once students have both determined an effective means of enacting the target movement and articulated their strategy (see Figure 3A), we overlay symbolic artifacts onto the screen—first a grid (see Figure 3B) and then numerals (see Figure 3C). In response, the students utilize these artifacts as frames of reference to enhance the enactment, explanation, or evaluation of their manipulation strategies (Abrahamson et al., 2011). In so doing, the students shift from qualitative to quantitative language. These shifts in perceptual and semiotic orientation toward the sensory display are often accompanied by changes in bimanual action schemes, for example, students switch from raising both hands simultaneously to scaling the hands sequentially, 1 grid unit on the left, 2 on the right. Abrahamson (2014) has named this strategic cognitive accomplishment of reconfiguring interaction forms functional parity.
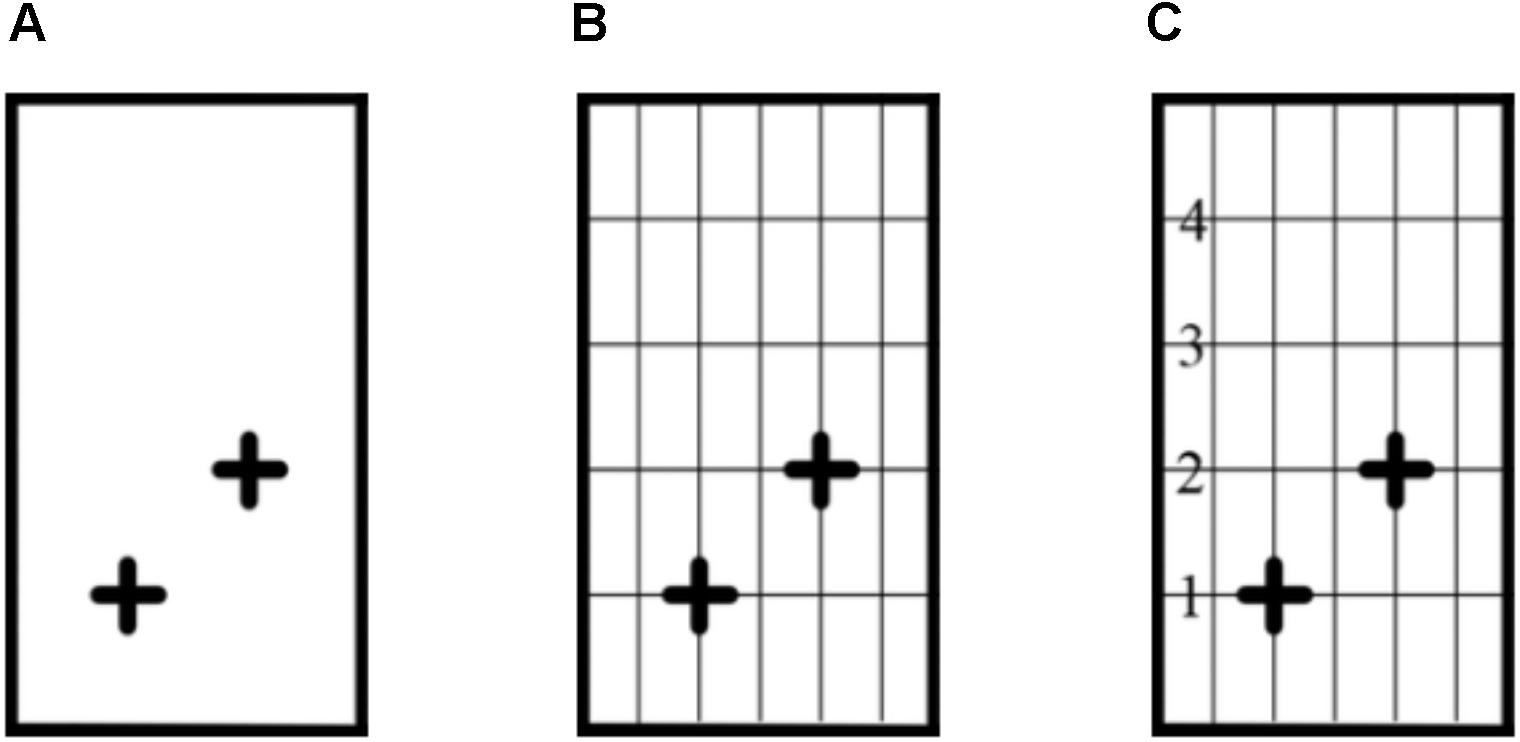
Figure 3. Symbolic artifacts overlaid onto the Mathematics Imagery Trainer activity space: (A) the two cursors; (B) a grid; (C) numerals.
Eye-tracking studies of students’ interactions both in this activity and other action-based embodied designs that use Mathematics Imagery Trainers for a variety of concepts have validated the general hypothesis: (a) students construct new perceptual structures—attentional anchors—as their means of performing the assigned motor-control tasks (Hutto and Sánchez-García, 2015; Abrahamson and Sánchez-García, 2016b; Abrahamson et al., 2016c; Shvarts and Abrahamson, 2019); and (b) these attentional anchors emerge as mathematical ontologies that students can describe, measure, reconstruct, and symbolize in other media, such as paper and pencil.2
In an AI-embedded version of the Mathematics Imagery Trainer, a virtual pedagogical tutor with naturalistic speech-and-gesture capabilities, “Maria,” responds to students’ manipulations with individualized prompts that summarize students’ actions, draw their attention to particular screen regions, encourage them, and offer new challenges (Flood et al., 2015b, c; Abdullah et al., 2017). The utility of the AI-tutor’s responses depends on the capability of machine-learning algorithms to emulate human-tutors’ real-time intuitive inference from the student’s actions to the student’s thoughts (Pardos et al., 2018). Given the increasing access of young students to interactive technologies (“apps”), developing Maria and her like could be one major frontier of embodied design-based research efforts.
The embodied-design framework has been expanded by Abrahamson, his students, and international collaborators to formulate the framework’s theoretical and practicable approach to multiple aspects of sensation, perception, cognition, and social interaction. Appendix A lists further readings pertaining to these research efforts.
Summary of Design Rationale and Principles
Mathematics imagery trainer
Moving in a new way
Working individually or in pairs, students tackle an interactive motor-control problem. The solution emerges as a particular attentional orientation, by which students coordinate the motor enactment of a movement form that instantiates the activity’s targeted mathematical concept.
Signifying the movement
Students adopt elements of mathematical instruments newly interpolated into the work space. Initially, they adopt the elements as means of enhancing the enactment, evaluation, or explanation of their solution strategy; yet in so doing, they shift into perceiving their own actions through a mathematical frame of reference.
Reconciling
Finally, students reflect on logical–quantitative relations between their conceptually complementary informal and formal perceptions-for-action.
Action–Cognition Transduction: How Performing Motor Actions Impacts Mathematical Reasoning
In this section, the focus is on whether and how actions that are initiated by the motor system lead to changes in cognitive processes—in essence, how actions change our minds—and how this would influence our reasoning about mathematics knowledge and mathematics education.
Action-Cognition Transduction: Reciprocity Between Doing and Thinking
That our mental faculties influence our motor behaviors is well established, since the thoughts I have can direct me to act: I can reach for a glass of water to satisfy my goal of obtaining something to drink (e.g., Wolpert et al., 2003). By acknowledging that the cognitive and motoric systems are coupled, we can ask whether and how the effects run the other direction. Indeed, the reciprocity of input and outputs in both directions is a common property of many physical devices and biological systems. Speakers (sound out/electrical signal in) and microphones (sound in/electrical signal out) are the same devices; as are LEDs (light out/electrical signal in) and optical sensors (light in/electrical signal out); and motors (rotation out/electrical signal in) and generators (rotation in/electrical signal out). In biological transduction, movement can induce cognitive states. For example, directing people’s eyes to trace a specific pattern can help solve Dunker’s classic tumor–radiation problem (Thomas and Lleras, 2007). The hypothesized theoretical basis for action–cognition transduction (ACT) is the proposed notion that actions can themselves induce cognitive processes and effectively change how we think. Through ACT, the eye gaze action pattern of convergence induces the convergence idea that will destroy the tumor. Coming at this another way, interfering with motor responses can impair cognitive functions selectively. Botox injections, which paralyze the currogator supercilli muscles between the eyebrows—the muscles we wrinkle when experiencing anger and frustration—selectively interferes with reading comprehension of emotionally angry sentences, but not of happy or neutral sentences (Havas et al., 2010).
Is There Evidence That Learners’ Actions Influence Their Cognitive Processes?
There are several means by which our actions influence our cognitive processes. How children categorize and compare unfamiliar objects can be influenced by how they hold and move them (Smith, 2005), but not how they observe the object being held or moved. People’s thoughts about familiar objects include the motor information for how they have handled those objects in the past and plan to use them in the future (Yee et al., 2013). For example, it was harder for people to think about familiar objects (but not unfamiliar objects) when performing secondary movements designed to be incompatible with typical object use. Indeed, many models of memory retrieval posit the re-enactment of object-related actions that were performed during initial learning (Damasio, 1989; McClelland et al., 1995). Together, these results suggest two ideas central to ACT: (1) that our memories for objects, both real and imagined, are constituted, in no small part, by motor schemas for past and future handling of the objects; and (2) that performing actions may induce (or interfere with) memories of these objects, as hypothesized by ACT, even when the objects are not present, and, as with mathematical objects, even when they are imaginary (Nemirovsky and Ferrara, 2009).
What Does a Theory of ACT Offer for Learning Environment Design? the ACT of Mathematics Education
For mathematics education, we may extend ACT to formal, mathematical objects such as shapes, graphs, and symbols. This is because, psychologically, we treat mathematical objects as physical objects through mechanisms such as analogical mapping and conceptual metaphor (Lakoff and Núñez, 2000; Nathan and Alibali, in press). People perceive and manipulate algebraic symbols as though they were objects that can be picked up and moved (Alibali and Nathan, 2007; Landy and Goldstone, 2007; Ottmar and Landy, 2017). Students’ self-imposed restrictions on their gestures can also limit their performance on generalization and prediction tasks. Middle school algebra students (n = 38) who confined their gestures to the frames of graphs of linear functions struggled to generalize to distal values that exceeded the frame (Bieda and Nathan, 2009). Once those same gestures revealed larger values, through transformations such as rescaling the axes, students were able to generalize to greater X-Y values, X2(1) = 12.6, p < 0.001. In geometry, people’s (n = 90) depictive gestures while reasoning geometrically predicted mathematical insight (d = 0.44, p < 0.05) and intuition (d = 0.65, p < 0.05) over and above contributions of spoken language, suggesting that gestures may facilitate reasoning and that its contribution may partly be non-verbal (Nathan et al., in press). However, the production of dynamic depictive gestures—gestures that both represented the objects and simulated transformations (e.g., dilating triangles, skewing quadrilaterals) and explored their generalized properties—most strongly predicted mathematically valid proof production (d = 1.40, p < 0.001), even when controlling for participants’ spatial ability and math expertise.
ACT can inform design of embodied interventions. Directed body movements of high school students produced greater learning gains than mathematically comparable non-body-based activities in tests of understanding mathematical similarity [F(1,162)56.4, p < 0.05, η2 = 0.04; Smith, 2018). Elsewhere, directed actions also led to superior geometry proof performance (n = 120; d = 0.62, p < 0.05), prompting the investigators to conclude that “actions can induce cognitive states … Furthermore, the experimental design we used allows us to conclude that it is specific actions—those we deemed grounding actions—that cause these benefits, rather than performing actions more generally” (Nathan et al., 2014, p. 192, original italics). The ACT approach has been extended to the design of an embodied video game, The Hidden Village (Nathan and Walkington, 2017; Walkington et al., 2019a), which tracks players’ movements in real time as it prompts players to make mathematically relevant actions that foster superior intuitions, insights, and proof performance (see Figure 4). Dynamic gestures of object transformations led to more successful geometric reasoning, especially when the gestures were made collaboratively and distributed across the hands and arms of multiple participants (Walkington et al., 2019a).
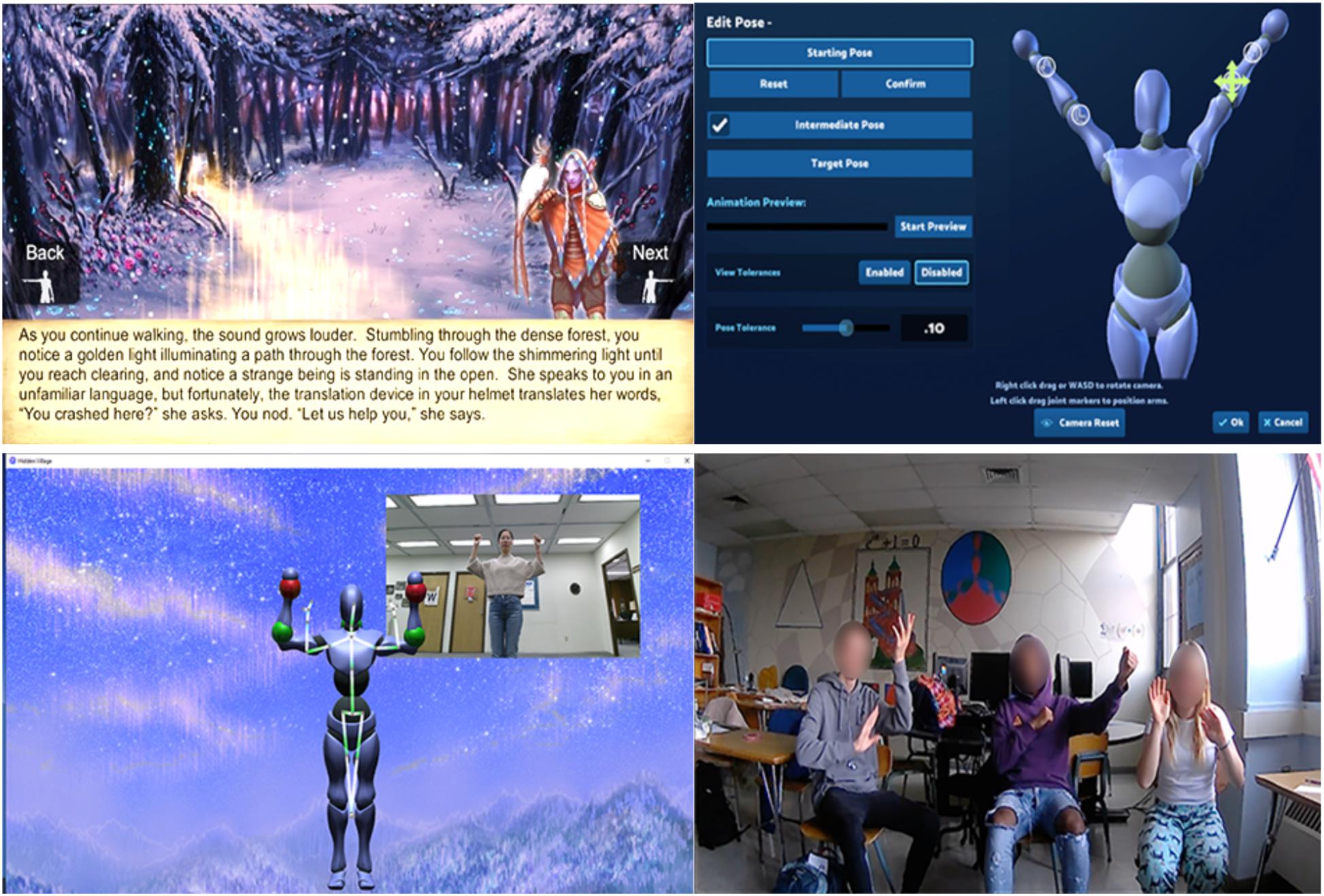
Figure 4. The Hidden Village is a video game that elicits and tracks players’ mathematically relevant actions in support of their subsequent mathematical reasoning. (Top-left) Players engage with the game narrative, and (Top-right) can create their own math content with poses (Bottom-left) that are tracked in real time (with an optional skeleton overlay, as shown). (Bottom-right) Students engage in collaborative gestures during game play and while reasoning mathematically.
How Do Learners’ Actions Influence Their Cognitive Processes? an Emerging Theory
There are two general ways within ACT that movement can influence cognition and benefit mathematics thinking and learning: cognitive offloading and simulation. These theoretical accounts are not mutually exclusive and employ cognitive rather than behaviorist mechanisms. With cognitive offloading, actions extend working memory and attention limits of an otherwise highly constrained cognitive system. Findings that collaborative gestures are extended over multiple people’s bodies offer one of the best illustrations of this (Walkington et al., 2019a). These extended collaborative gestures help people manage the complexity of a cognitively demanding task, thus freeing up resources used for mathematical reasoning and learning.
Simulation provides another locus of cognitive support. Dynamic gestures directly support students’ investigation of generalizable properties of space and shape through body movements by enacting various transformations on simulated mathematical objects. Movement, such as dynamic gesture production, depends on the generation of goal-directed motor programs, which activate predictors (feedforward mechanisms) for many or all plausible outcomes of the proposed actions so that during movement execution the system can make rapid course corrections or quickly determine goal achievement (Wolpert et al., 2003). These predictors perform like mental models that “run through” the steps toward plausible outcomes, and in so doing, support model-based reasoning and inference making (Nathan and Martinez, 2015), which can enhance scientific and mathematical learning.
Theory-Driven Design for Embodied Mathematics Education
Mathematically relevant actions can be a useful ideomotor resource for improving mathematics reasoning. Interventions that promote task-related movements, including implicit directed movements from video game play, explicit instructions, and collaborative contexts, all potentially contribute to improved mathematics performance through ACT by offloading or through simulation of object-related actions (Nathan, 2017). Mathematically relevant depictive gestures foster intuition and insight about basic properties. Dynamic depictive gestures appear to be critical for producing mathematically valid proofs regarding generalized spatial properties by enacting simulated transformations of the objects. Observing these same actions is less effective, suggesting that motoric image schemas may have primacy for making certain general conjectures. The research also clarifies that it is not simply that all actions facilitate thinking and learning. Actions that are not conceptually relevant exhibit few if any benefits for mathematical thinking and learning, while those that enact the relevant conceptual relations show improvements in cognitive performance, including mathematical intuition, insight, proof production, problem solving and learning (Lindgren and Johnson–Glenberg, 2013; Nathan et al., 2014; Walkington et al., 2020a). Action–Cognition Transduction offers a promising new framework for understanding how actions shape thought and for designing interventions that elicit directed actions as a viable channel for the future of embodied mathematics education.
Summary of Design Rationale and Principles
Action–cognition transduction
Action-cognition transduction
Action and cognition enjoy reciprocity: Just as cognitive processes can induce motor behaviors for performing goal-directed actions, performing actions can induce cognitive states that perform reasoning, problem solving and learning.
Fostering abstr-action
Actions that are either self-generated or externally directed can facilitate mathematical intuition and proof. The most effective actions are those that are relevant to the mathematical principles of interest.
Extended embodiment
People explore mathematical ideas deeply when they are encouraged to collaboratively co-construct body movements.
The Roles of Gesture, Collaborative Gesture, and Multimodality in Mathematics Teaching and Learning
In this section, we first give a general overview of research on gesture, and then we discuss a specific design-based research program, in which learners engage in collaborative gestures within a mathematics learning game.
Background: Research on Gesture, Teaching, and Learning
Gestures are movements of the hands, arms, and body that are produced in the effort of thinking and/or communicating. From a semiotic perspective, gestures are signs that people use to make meaning in the three ways that Charles Sanders Peirce (1894; see also Atkin, 2013) described: as indices, icons, or symbols. Indices make meaning by being connected to things, for example, pointing to an element in an equation. Icons make meaning by resembling things, for example, tracing a triangle in the air to refer to that triangle. Symbols make meaning by being associated with particular meanings, for example, making a “thumbs up” gesture to mean good. Thus, people use gesture to indicate objects and locations, to represent objects, events and ideas, and to symbolize ideas in agreed-upon ways (Clark, 1996). Mathematics teaching and learning commonly occur in rich environments that include a wide range of physical objects, tools, 3-dimensional models, diagrams, sketches, and symbolic inscriptions. Communication that occurs in such rich settings is usually multi-modal and grounded in the environment, and gesture is an integral part of such communication (e.g., Nathan et al., 2017c). Gesture is also intimately tied to action (Hostetter and Alibali, 2008), and, as such, gestures are ubiquitous in learning settings that involve actions, including working with physical manipulatives and constructing models. In mathematics education settings, both teachers and students regularly use gestures in all of these ways, as previous studies have richly documented (e.g., Flevares and Perry, 2001; Arzarello et al., 2008; Arzarello and Robutti, 2008; Nemirovsky and Ferrara, 2009; Alibali and Nathan, 2012).
This sub-section reviews research about (1) teachers’ gestures in mathematics instruction and their roles in student learning, and (2) students’ gestures in mathematics education settings and the ways in which they inform teachers’ instructional practices.
Teachers’ gestures and their role in students’ learning
Teachers use gestures in many different ways during instruction. They point to physical objects and to inscriptions on the board or in students’ work; they represent actions and objects that are not physically present; and they invoke ideas with movements that refer to ideas and concepts in agreed-upon ways. Different sorts of gestures contribute in distinct and important ways to students’ learning (Alibali et al., 2011).
Teachers regularly use pointing gestures to guide students’ attention to elements of the instructional context, and to support students’ focus on relevant information. Indeed, some research suggests that pointing gestures are the most frequent type of gesture that teaches use during mathematics instruction (Alibali et al., 2011).
Classrooms and other settings in which mathematics learning takes place are perceptually rich, and many of the objects and inscriptions that are used in these settings are visually complex. Teachers use gestures to guide students’ attention to elements in the instructional context that are relevant in the moment. Experimental evidence demonstrates that pointing gestures influence speech comprehension, especially when the verbal message is degraded (Thompson and Massaro, 1986, 1994), and that pointing gestures can influence the information that people encode from visuospatial representations, such as graphs of linear equations (Yeo et al., 2017).
Representational gestures express information via resemblance—that is, such gestures resemble, in some respect, their intended meanings. Representational gestures can represent via handshapes (e.g., using the hands to form a triangle) or via motion trajectories (e.g., tracing a triangle in the air with a finger). Some scholars have argued that such gestures arise from mental simulations of actions or perceptual states (Hostetter and Alibali, 2008, 2019). As such, representational gestures reflect—and may evoke in others—representations of visual, spatial, and motoric information. For example, a teacher might simulate taking objects off the two sides of a pan balance with her gestures (Alibali and Nathan, 2007), or a teacher might depict different sorts of angles using the position of her hands (Alibali et al., 2014). Such gestures may serve to highlight or schematize particular elements of a complex perceptual–motor event or situation, both for the gesture producer and for the recipient of the gesture (Kita et al., 2017).
Some gestures have forms and meanings that are “agreed upon” by members of a community. Some examples include the thumbs-up gesture and the “OK” gesture. Conventional gestures can also emerge in smaller communities, such as classrooms. For example, Rasmussen et al. (2004) describe the emergence and use of a gesture for the concept of slope invariance in a differential equations course. They describe how the gesture, which they term slope-shifting gesture, comes to be used to invoke a particular meaning within the classroom community—a form of local conventionalization. Another example is the gesture used in classroom activities termed “slope aerobics” or “algebra aerobics” (Carter, 2014; Lamb, 2014). In these activities the teacher calls out a category of slopes or functions (e.g., “positive slope!” or “y = x!”) and students produce a gesture with their arms that depicts that slope or the graph of the function. The gestures are agreed-upon and practiced by the students, so that the teacher’s commands elicit particular sorts of body movements.
All of these types of gestures may be used by teachers as part of their efforts to establish and maintain shared understanding, or common ground, with their students. Common ground refers to the knowledge, beliefs, and assumptions that are shared by participants in an interaction (Clark and Schaefer, 1989). Of course, the goal of instruction is often to help students build new knowledge, but this is generally accomplished by connecting to prior, shared knowledge.
Teachers establish and maintain common ground to support students in building new knowledge in several key ways: (1) by managing attention to shared referents, which may be accomplished with pointing gestures); (2) by connecting to already-shared prior knowledge, which may be expressed in representational gestures or conventional gestures; and (3) by implementing classroom practices that provide students with common experiences, and then re-invoking these shared experiences, which can be accomplished by pointing to aspects of the environment that may reactivate those ideas, or by simulating actions that reinvoke prior actions. As should be clear, teachers’ gestures can play key roles in each of these ways of fostering common ground (Nathan et al., 2017a; Alibali et al., 2019).
Students’ gestures and their role in teachers’ instruction
Students also commonly use gestures in mathematics learning settings, so any consideration of gesture in mathematics teaching and learning must also take students’ gestures into account. Students often produce gestures as part of their effort to communicate, whether they are asking questions, explaining their reasoning, or interacting with peers. In most cases, students’ gestures express information that is redundant with their speech, but, at times, students’ gestures express information that they do not express in speech. These gestures can reveal important information about students’ thinking.
Non-redundant or “mismatching” gestures are common when people talk about knowledge that is based in perception or action (Hostetter and Alibali, 2019). People may express their perceptual or action-based knowledge in their gestures, while at the same time expressing some aspects of that knowledge in verbal form. If learners are unable to fully articulate their perceptual or action-based knowledge in words, some of that knowledge may be expressed uniquely in gesture. Non-redundant gestures have been documented in students’ explanations in a wide range of mathematics domains, including early number (Gunderson et al., 2015), quantity (Church and Goldin–Meadow, 1986), equations (Perry et al., 1988), mathematical proof (Nathan et al., 2014), control of variables tasks (Stone et al., 1991), balance tasks (Pine et al., 2004), seasonal change explanations (Crowder and Newman, 1993; Crowder, 1996), and plate tectonics explanations (Singer et al., 2008).
When students express some aspects of their knowledge uniquely in gestures, then teachers who wish to obtain a complete picture of those students’ knowledge must attend to those gestures. In this respect, attention to students’ gestures is critical for accurate assessment of student knowledge. However, most standard assessment practices do not incorporate opportunities for expressing knowledge in gestures, and many assessment approaches actively inhibit gesture, for example, by requiring students to write or type.
Learners may express knowledge uniquely in gestures at an early point in the learning process, and, at a later point, they may express those same ideas in verbal form (e.g., Singer et al., 2008). In this sense, the knowledge that learners express uniquely in gestures may reflect new ideas that learners are “working on”—ideas that they are considering, evaluating, or consolidating. When learners express aspects of their knowledge in gesture but not in speech, they are often highly responsive to instruction or feedback (Church and Goldin–Meadow, 1986; Perry et al., 1988). In this sense, learners’ gestures reveal that their knowledge is in transition (Alibali and Goldin-Meadow, 1993).
Given that gestures reflect learners’ emerging knowledge, learners’ gestures may reveal aspects of knowledge that are not fully developed and that may require support from teachers or more advanced peers. Thus, teachers may draw on or interpret students’ gestures as indicators of areas in which they need scaffolding or direct instruction (Goldin–Meadow et al., 1993). Indeed, teachers do adjust their instruction based on the nature of students’ gestures, for example, by offering a wider variety of problem-solving strategies to learners who produce mismatching gestures (Goldin–Meadow and Singer, 2003).
Learners may use gestures to highlight certain aspects of complex perceptual or spatial tasks when they think or communicate about those tasks. These gestures may reveal the aspects of those tasks that learners are focusing on. In this way, students’ gestures may reflect their schematization of complex tasks—that is, their tendency to focus on some elements of the task and to neglect others (Kita et al., 2017). Thus, teachers may be able to infer students’ focus of attention by attending to their gestures. In this way, students’ gestures provide teachers valuable information about how best to engage or intervene with them.
The previous sub-section provided a general introduction to gestures, how they arise, and how they are used by students and teachers. In this section we use these ideas, as well as research on embodied learning, to motivate design-based research on a collaborative embodied game that leverages student action and gesture. Our design processes interleaved the development of a theory of how learners gesture in collaborative settings with the iterative development of digital mathematics game experiences to facilitate collaborative uses of gesture.
Gesture and collaborative embodiment
Current theories of embodiment and gesture (e.g., Hostetter and Alibali, 2008; Abrahamson and Sánchez-García, 2016b; Nathan and Walkington, 2017) have not yet fully addressed the collaborative nature of embodiment that occurs in classrooms as students are learning in physical proximity. This is in part because much of the experimental work on embodiment and gesture in mathematics has been conducted through laboratory studies with individual participants (e.g., Cook et al., 2008; Edwards, 2009; Nathan and Walkington, 2017; Pier et al., 2019). Research on gesture in multi-party interactions (e.g., Goldin–Meadow, 1999; Walkington et al., 2019a) presents evidence and synthesizes prior studies showing that the presence of multiple learners fundamentally changes the nature of how mathematical ideas can be embodied, in a way that is not describable as the sum of each individual’s actions. A theory of collaborative embodiment in mathematical domains is vital to understand mathematical cognition as it unfolds in classrooms and with increasingly prevalent technological innovations for collaborative learning.
Gesture studies offer an important link between individualized and social forms of embodiment. This is because, while gesture production has well-established cognitive benefits for the individual actor (e.g., Goldin–Meadow, 2005), gesture production is facilitated when speakers operate in a social context (e.g., Vygotsky, 1978; Goodwin, 2000; Moll and Tomasello, 2007), even when the speakers cannot see one another (Alibali et al., 2001). One hypothesis is that humans are motivated toward social interactions through a process of shared intentionality, a fundamental disposition toward having shared experiences with interlocutors (Tomasello and Carpenter, 2007). Because of shared intentionality, we can elevate mutual gaze to joint attention, turn mere social coexistence to cooperative communication, and transform group activity from parallel actions into collaboration (Shvarts and Abrahamson, 2019). Shared intentionality allows us to build on our capacities for biological adaptation to form cultural practices, and co-construct and preserve knowledge that can be shared socially and passed across generations (Tomasello, 2009). Gesture scholars have shown how shared intentionality contributes to fostering common ground during classroom discourse by drawing attention to shared referents that may be physically present or invoked through metaphoric gesture (Nathan and Alibali, 2011; Alibali et al., 2013a). In one study, desire for intersubjectivity led students in a middle school classroom to refine their idiosyncratic representations of 3D objects so others could apprehend and use them during group problem solving (Nathan et al., 2007).
Research on collaborative gesturing
When students work together to solve mathematics problems, they build and manage collaboration through multiple modalities. Gestures operate synchronously with speech, acting as a key mechanism to create cohesion and bind conversational elements during collaborative work (Koschmann and LeBaron, 2002; Enyedy et al., 2015). Singer et al.’s (2008) study of 6th graders engaging in an earth science project found that gestures were used collaboratively to foreshadow ideas not yet reflected in speech, and that they helped students both to communicate their new ideas and to engage with each other’s understandings. Group members engaged in multimodal co-construction, such that the external nature of gestures allowed students to copy, extend, correct, and revise each other’s conceptions through gesture. Flood (2018), through an analysis of a middle school student’s interactions with tutors around concepts of speed and ratio, demonstrates how multimodal revoicing—using gesture in conjunction with speech to reproduce, elaborate, or selectively modify an idea presented by a learner—can be used by tutors to move students toward conventional or culturally appropriate forms of reasoning. Another line of work (Hall et al., 2015; Ma, 2017; Ma and Hall, 2018) has explored ensemble routines, in which high school students learn to position and orient their bodies and coordinate their perspectives to accomplish a collective goal (e.g., formulating marching band patterns or large-scale geometric constructions), sometimes with the assistance of GPS technologies. This is similar to the work of Kelton and Ma (2018), which calls for considering “whole bodies” (rather than just hands) as instruments for embodied mathematical interaction and the development of mutual interdependence and shared sense-making among collaborators (see also Marin et al., 2020).
Two prior studies of teachers (Walkington et al., 2019a) and high school students (Walkington et al., 2020b) presented a taxonomy for learners’ use of collaborative gestures—jointly enacted physical movements demonstrating mathematical relationships. By jointly enacted, we mean that when gesturing collaboratively, a learner makes a gesture whose meaning is explicitly related to and inextricably tied to the gestures of a different learner. These studies found that when proving geometric conjectures, learners repeat one another’s gestures through echoing gestures (one gesture occurs after another) or mirroring gestures (gesturing at the same time). Learners respond to one another’s gestures through alternation gestures, in which they use gesture to build on or refute an idea communicated by an interactional partner through gesture. And learners can physically co-represent a single object using joint gestures, in which they operate in and build representations in a shared gesture space. Figure 5 shows groups of pre-service and in-service teachers working together to create a dynamic mathematical diagram for a geometry conjecture about an angle inscribed in a circle, as they formulate a joint gesture. These teachers are playing a computer-supported learning game, in which they are presented with geometric conjectures to prove without using pencil or paper. Although they were not specifically told to gesture, many gestures emerged, as they jointly constructed mathematical explanations.
Walkington et al. (2019a) found that although collaborative gestures were used in the majority of teachers’ proof attempts, less experienced teachers tended to make fewer collaborative gestures and were more likely to struggle with formulating a proof. They also found that some learners were quite central to collaborative gesture activity—they both initiated collaboration via gestures (e.g., echoed someone else’s gesture) and received gestural collaboration from others (e.g., someone echoed a gesture they had made)—while others were less balanced in terms of giving and receiving, and still others remained on the fringes of gestural activity. Follow-up analyses (Schenck et al., in press) suggested that the teachers were more likely to make collaborative gestures if their interactional partners did, if they were in smaller groups, or if they believed gestures had a positive impact on instruction. The average number of collaborative gestures made by group members significantly positively predicted correct proof.
Another study with high-school students playing the learning game in the same circumstances (Walkington et al., 2020b) found similar results, although high-school students had a lower tendency to produce collaborative gestures (approximately one quarter of geometry proofs). Students used such gestures in the establishment of common ground or intersubjectivity (Nathan and Alibali, 2011). Some categories of what were termed “collaborative talk moves” (e.g., learners agreeing, making an assertion, or rephrasing a contribution) were related to learners’ tendency to produce collaborative gestures and to their success at solving problems together.
Across both studies, gesturing collaboratively was generally associated with more valid geometric reasoning than making non-collaborative gestures or no gestures. Figure 6 shows the accuracy of groups in the teacher study (left) and the high school study (right), when no gestures were made proving conjectures, when gestures were made that were not collaborative, and when collaborative gestures were used. Learners’ accuracy is shown for three outcomes: intuition, or whether they were correct in their judgment of whether the conjecture was true or false; insight, or an understanding of the “gist” of the conjecture and the key mathematical ideas (Zhang et al., 2016); and whether they formulated a valid transformational proof (Harel and Sowder, 1998) of why the conjecture was always true or false. The trends in the graphs show that not gesturing during a proof attempt is associated with low levels of performance, while making any kind of gesture is often associated with substantially higher performance. In some cases, making collaborative gestures seems to be associated with even higher performance than non-collaborative gestures. These trends support other research suggesting that gestural mimicry improves learning (Vest et al., under review). Although here the relationship between collaborative gesture and valid mathematical reasoning is correlational, a growing body of research suggests that gesturing can itself change learners’ reasoning and support learning (Novack and Goldin-Meadow, 2015). However, findings for the causal role of gesture in directly supporting reasoning are mixed (e.g., Walkington et al., 2019b), and the facilitative effect of interventions intended to allow learners to leverage body movements may occur only under certain circumstances (Walkington et al., 2019b).
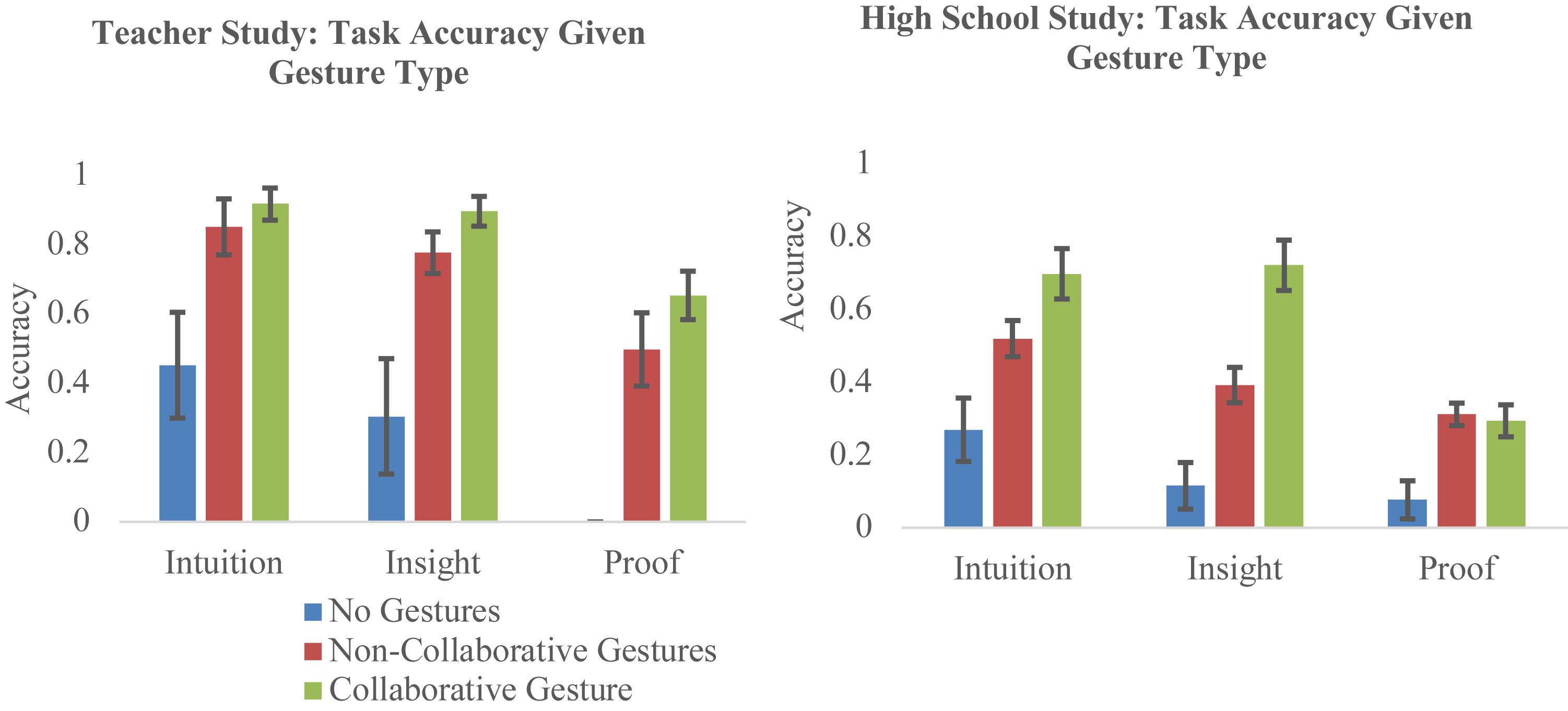
Figure 6. Bar graphs depicting differences in performance when proving geometric conjectures depending on whether and how learners in a group gestured.
The research reviewed here can provide the basis for a theory of collaborative embodiment, which recognizes that joint mathematical activity is a complex endeavor, in which interactional partners use shared multimodal resources, including speech, body position, gesture, writing, diagrams, and manipulatives (Arzarello et al., 2009). During collaboration, learners align their gesture spaces (i.e., the physical space in which they gesture and the socially constructed mathematical meaning of the space) and, in some cases, their body position and orientation (e.g., Kelton and Ma, 2018), in order to facilitate shared interpretation of mathematical ideas (Nathan et al., 2007; Yoon et al., 2014). Collaborative gesture specifically, and collaborative embodiment more generally, can become an interactional resource for meaning-making that can operate without technical language (Flood et al., 2015a). Collaborative gesture can be potentially powerful for establishing common ground and jointly advancing a group’s geometric understanding through embodied exploration together. Understanding ways to leverage this tendency to jointly embody, particularly in the context of motion-based, GPS, and holographic technology tools, may create novel opportunities for learners to come to understand mathematical ideas together in meaningful, embodied ways.
Summary of Design Rationale and Principles
Gesture, collaborative gesture, and multimodality in mathematics
Teacher gestures
Teachers use pointing, representational, and conventional gestures to establish and maintain common ground.
Student gestures
Learners’ gestures can reveal knowledge not in speech, emerging or transitional knowledge, and how learners schematize information.
Collaborative embodiment
The presence of multiple learners fundamentally changes the nature of gestures, as learners leverage shared multimodal resources.
Gestures during collaboration
Learners can jointly embody ideas using gestures that build off one another, and these gestures may facilitate mathematical learning, particularly in the context of action-based technology tools for learning.
Graspable Math: Concretizing Algebraic Solution Procedure
Over the past several decades, there have been significant advances in our understanding of how grounded and embodied cognition can help facilitate abstract learning. Theorists have argued that grounding abstraction in perceptual–motor-based actions offers an alternative to representing symbols as purely amodal, abstract, and arbitrary symbol systems, where the focus is on interpretation and rote manipulation of symbols (cf. Barsalou, 2008). Principles of grounded and embodied cognition suggest that successful perceptual practice and manipulation of algebraic structures uses cognitive systems that correctly embody mathematical rules and turn action into meaning (Dourish, 2004). Grounding one’s mathematical knowledge and reasoning has also been shown to support the transfer of knowledge to new situations (Landy and Goldstone, 2007; Goldstone et al., 2010).
At first look, it might seem that symbolic notation is intangible and not naturally given to embodiment. However, prior work in cognitive science has established that algebraic reasoning is rooted in at least three basic perceptual processes (Landy et al., 2014a; Goldstone et al., 2017). First, abstract symbols are treated as physical objects distributed in space (Dörfler, 2003; Nogueira de Lima and Tall, 2008; Landy and Goldstone, 2009; Landy, 2010). Second, seeing symbols involves perceptual processes such as grouping and attention (Kirshner, 1989; Landy and Goldstone, 2007, Landy and Goldstone, 2010; Murayama et al., 2013; Landy et al., 2014b). Third, learning to operate on algebraic notations involves learning attentional tendencies (Landy et al., 2008; Goldstone et al., 2010; Marghetis et al., 2016). For example, Landy and Goldstone (2007) demonstrated how perceptual grouping based on Gestalt principles affects how people interpret algebraic symbols in ways that may either adhere to or conflict with order-of-operations rules. Together, this suggests that students rely on the visual patterns available in notation clusters to learn reasonable patterns of mathematical behaviors taken upon symbolic objects. These findings have implications for research and practice, where turning algebraic notations into tangible objects that enforce their own rules through physical movements may help improve mathematics learning. In turn, this research on learning within dynamic systems could help transform many of the traditional distinctions between abstract and concrete knowledge. Perhaps, if students could actually—not only imaginatively—manipulate mathematical symbols, as though these were worldly objects, this could help tap into students’ perceptual learning systems and provide unique opportunities for students to explore the inherent structure of algebra physically and visually.
Graspable Math: The Interactive Math Notation
Building on this theoretical conjecture, Ottmar et al. (2015a) have explored how virtual tools can be designed to reify theory of embodied cognition in the form of dynamic algebra interfaces, where symbols can be picked up and rearranged. Over the past several years, they have developed Graspable Math (GM), an innovative dynamic learning technology that utilizes gesture-initiated actions to explore algebraic structure (Ottmar et al., 2015a). In GM, symbols are tactile virtual objects that can be flexibly picked up, manipulated, and rearranged through specified gesture–actions. In this approach, mathematical structure can be appreciated through exploration and manipulation. GM makes the implicit structure of mathematical objects overtly visual by grounding algebraic expressions and transformations in space and action. Through these physical manipulations of virtual objects, GM transforms algebra from a set of arbitrary rules for transforming symbolic statements to intuitive notions of manipulating concrete objects in quasi-natural ways.
In GM, the actions are called “gesture–actions” to distinguish them from gestures as they are often used in the psychological sense (Alibali and Nathan, 2012; Alibali et al., 2013b; Novack et al., 2014). These gesture–action routines were designed as dynamical virtual embodiments of imaginary symbolic manipulations people typically experience in performing algebraic transformation. For example, to simulate the imaginary perception of “moving the +3 over to the other side of the equal sign, making it −3,” GM lets students literally swing a digital “+3” over the equal sign, where it becomes “−3” (Ottmar et al., 2015a). Through gesture–actions, users can combine terms, apply operations to both sides of an equation, and rearrange terms through commutative, associative, and distributive properties (see Figure 7).

Figure 7. The Graspable Math dynamic algebra notation interface: examples of gesture–actions for factoring, rewriting equations, and inverting powers with negative exponents. Results of gesture–actions are depicted in gray.
It is hypothesized that as users engage with the GM system, the actions enable students to develop new sensorimotor schemes that can help facilitate mathematical reasoning by fostering grounded understandings of the mathematical properties and operations that the actions embody. In turn, these can facilitate learning new mathematical concepts. The actions taken are bound to a virtual visualization that reflects one way of imagining the corresponding mathematical transformation. For example, touching a term and moving it leftward will apply the commutative property, with the result that the term will literally move leftward. Gesture–actions are designed to emulate engaging in an appropriate physical action, and for each action there is a corresponding visualization. Ultimately, GM’s dynamic transformations and gesture–actions facilitate the exploration of algebraic structure in a low-risk learning environment and can provide opportunities to experience fluid, distinctive visualizations and fast feedback (Ottmar and Landy, 2017).
Empirical Support for Dynamic Notation Systems
Graspable Math has shown potential as a tool that provides opportunities for students to play with the structure of algebra in ways that are unavailable through traditional classroom tools. Below we highlight some of our empirical findings that demonstrate the usefulness of this approach for learning and engagement.
Perceptual-motor training in GM can have impacts on student outcomes
In several studies, GM has been shown to increase student performance and engagement compared to static methods of instruction (Landy and Goldstone, 2007, Landy and Goldstone, 2010; Ottmar et al., 2015b; Weitnauer et al., 2016; Manzo et al., 2017; Ottmar and Landy, 2017; Sawrey et al., 2019). One study using a puzzle-based version of GM (From Here to There) found that a 2.5-h intervention in intact classrooms with no instruction led to gains on a comprehensive test of procedural fluency covering all basic algebra identities and transformations (effect size of 0.82 improvement over regular classroom instruction; Ottmar et al., 2015b). A second RCT with 500 6–7th grade students found improvements on measures of conceptual understanding over traditional problem sets with hints and immediate feedback (effect size = 0.18; Sawrey et al., 2019).
Perceptual–motor training in GM before instruction can better prepare students for future learning
In a classroom study, using GM to explore concepts before instruction led to greater learning gains over the reverse order (Ottmar and Landy, 2017). These findings are in line with other work that shows that using concrete analogies or examples first and then fading these supports over time leads to stronger learning outcomes (Fyfe et al., 2014).
Dynamic algebra tools like GM can vastly increase efficiency and success in problem-solving by decreasing cognitive load
After a brief training, students were able to solve difficult equations using dynamic support available in GM more efficiently than on paper (Weitnauer et al., 2016). Students’ increased outcomes were partially attributable to the speed and fluency with which they moved through the content itself (Ottmar et al. (2015b); Hulse et al., 2019). These results suggest that GM’s dynamics may play a valuable role, comparable in ways to calculators, not as a replacement for paper-and-pencil solving but as a supportive scaffold that allows students to cope with more challenging situations by carrying less cognitive load (Sweller, 1994).
Distributed dynamic algebras may increase engagement and ameliorate the negative effects of math anxiety
Graspable Math was designed with the goal of making students more familiar with algebraic notations while providing scaffolding and feedback, thus increasing their confidence and comfort in dealing with equations. GM does not allow for simple transcription errors of the kind many students find particularly frustrating, and thus it decreases math anxiety. While higher math anxiety typically relates to lower math achievement, these relations have not been found when students use GM (Ottmar et al., 2020).
We also have evidence that dynamic touch-screen systems help increase students’ engagement and interest in learning algebra: students overwhelmingly reported that they enjoyed solving problems and learned more through the app than traditional instruction (Ottmar et al., 2012, 2015a).
Dynamic technologies like GM can provide insight into students’ mathematical problem solving and thinking
Graspable Math logs all user interactions and behaviors, when students are solving problems, providing rich information about student problem-solving process, mathematical strategy, behaviors, and errors. These in-app measures, such as resetting and exploration, have been found to predict learning gains (Hulse et al., 2019). Further, recent work has demonstrated that pause time before solving predicts the efficiency and flexibility of the mathematical strategy that students use (Chan et al., 2019). More research is underway to examine the mechanisms by which GM facilitates learning, engagement, and mathematical problem-solving strategies.
Conclusion
Graspable Math is an innovative, research-based software platform intended to supplement regular mathematics instruction. GM: (1) integrates formal syntax and grounded semantics; (2) is suitable for use by teachers in classrooms and by a large proportion of struggling students; and (3) can be used as a framework for exploring fundamental issues in mathematics learning. GM is a promising educational tool that addresses a relatively untapped area of practice-focused, cognitively motivated, perceptually guided instructional technology. GM focuses on the perceptual strategies successful students use to read and transform equations and develops an intervention to connect these experiences to meaningful structures in a precise and fluid interface. GM allows the procedural advantages of physically moving symbols to seamlessly integrate into conceptually challenging lessons. It is anticipated that this increase in familiarity and strong grounding in perceptual learning that underlies procedural fluency will better prepare students for future instruction and improve learning in advanced areas that assume the ability to read and manipulate equations. GM represents a first step at moving beyond static abstract symbols toward a dynamic concrete interface that provides an integrated, embodied notation experience capable of supporting a variety of mathematics curricular needs.
Summary of Design Rationale and Principles
Graspable math
Grounding of abstraction in perceptual-motor actions
Algebraic reasoning is rooted in basic perceptual processes.
Embedding action and perception into new technology tools
Dynamic notation systems that integrate embodied, perceptual-motor training in notation can support mathematics teaching and learning.
Insight into students problem solving and thinking
Data logged in technologies can be used to unpack mechanisms by which embodiment and action relate to student thinking, problem solving processes, and learning.
Playful Mathematics: Why Games Count
Previous sections have argued for a theorization of mathematics teaching-and-learning as a collaborative, multimodal, perceptual–motor phenomenon; and, accordingly, for educational designs that create opportunities for students to ground mathematical notions in embodied enactment of conceptually oriented movement forms. This section focuses, specifically, upon how the design of digital game-based environments can provoke embodied mathematics learning through play and gesture (for more general reviews of game-based mathematics learning, the reader is referred to the numerous works cited below).
Motivating Games for Mathematics Learning
The fundamental rationale for gamifying education is that games increase players’ motivation, engagement, and learning (e.g., Gee, 2005; Steinkuehler and Duncan, 2008; Martin, 2011). In mathematics in particular, well-designed games can provoke players to voluntarily mathematize the digital context in a process called theorycrafting (e.g., Steinkuehler and Williams, 2009; Devlin, 2011). Consequently, numerous educational designers—academic (e.g., Barab et al., 2010; Gresalfi and Barnes, 2016; Zandieh et al., 2018; Kang et al., 2020) as well as commercial (e.g., Ritzhaupt et al., 2009)—have therefore developed learning games. However, the quality of these games is inconsistent: too many learning games mix the “entertainment value of a bad lecture with the educational value of a bad game” (Squire and Jenkins, 2003, p. 8). Designers of mathematics learning games, in particular, often struggle to integrate curricular content into game mechanics and experiences, instead merely intjecting comic relief into calculation tedium. Consequently, students’ playful physical/digital actions are not semiotic enactments, that is, they do not constitute, bear, or otherwise suggest enactment of the targeted mathematical notions. An embodied perspective, whereby motor actions enact prospective concepts, offers new horizons for game-based learning, as discussed earlier (e.g., From Here to There, The Hidden Village).
We focus here on an exemplar of embodied playful mathematics design, a videogame titled Rolly’s Adventure (RA; Williams, 2015; Williams-Pierce, 2017), that requires players to engage in co-speech gesture when describing their experience and learning. Such descriptive co-speech gesture occurs during communication with others, whether a researcher or fellow players (Stevens et al., 2008; Williams-Pierce, 2017). Playing on one’s own is considerably less likely to elicit gesture. As discussed in earlier sections, gestures can express information related to mathematical reasoning that are not contained within the accompanying speech. Accordingly, the goal of this section is to describe how mathematics teaching in multimodal game-based environments requires attending to such gestures. Digital environments that use novel interactive representations of mathematical notions may provoke non-redundant gestures at a particularly high rate, such that teachers and researchers must attend to gesture to gain a comprehensive view of the playful mathematical learning.
Playful Mathematics Learning With Rolly’s Adventure
Rolly’s Adventure (see Figure 8) was designed to require manual actions both when playing the game (physical manipulation that results in digital action) and when discussing it (co-speech gestures). The design employed novel, non-standard mathematical representations and interactions to mitigate students’ mathematics anxiety (Papert, 1980; Williams-Pierce, 2016).
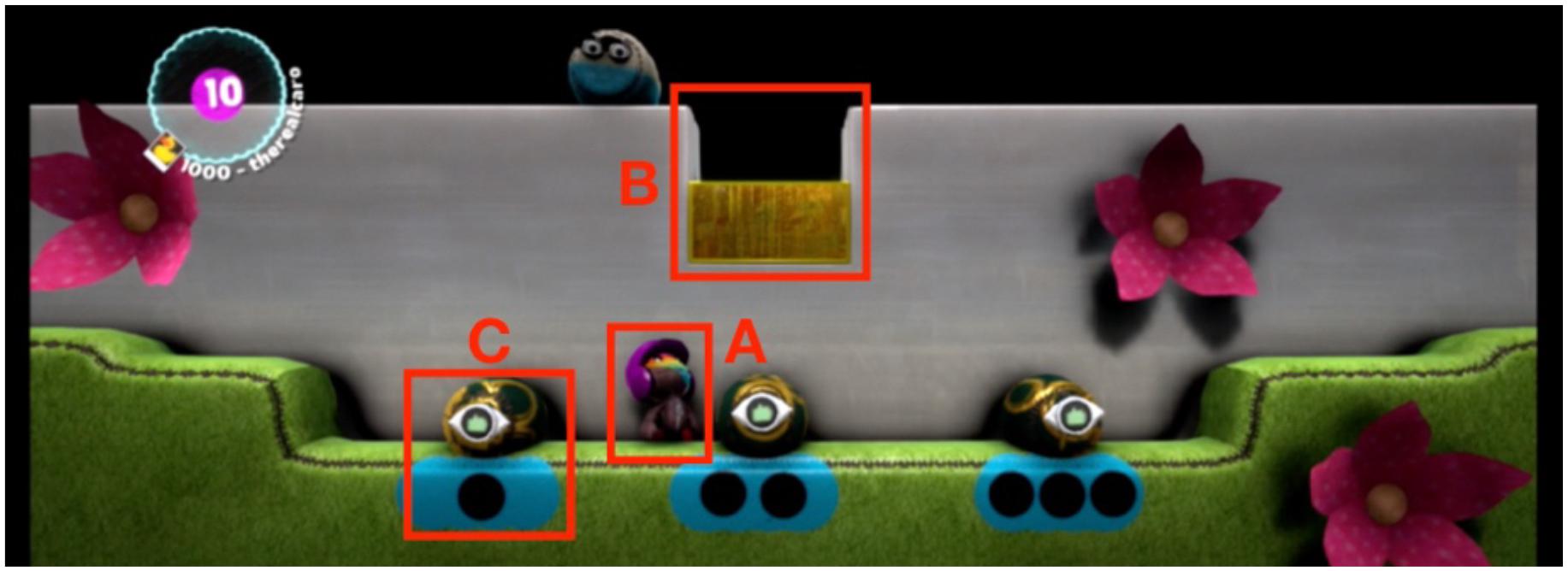
Figure 8. The first puzzle in RA, with red annotations. (A) The player’s avatar; (B) the fraction (the golden block) that must be operated upon in order to fill the unit (the hole that the golden block is within); (C) the primary interaction method (a round button) and its attendant label (the single black dot). The player must determine which round button will perfectly fill the unit: activating (C) enacts “1 × 1/2,” which replicates (B); whereas activating the middle button enacts “2 × 1/2,” perfectly filling the (w)hole unit.
Players enter RA without being told the underlying mathematical structures, interactions, or desired learning content, similar to both the Mathematics Imagery Trainer and The Hidden Village, but contrasting with Graspable Math, where the mathematics is overt. Only through iterative action–reflection cycles, experiencing failure and feedback, do they discover that the game is designed to enact fraction multiplication (Williams-Pierce, 2019). In making sense of the game, students must draw on their mathematical knowledge to model the situation in ways that are advantageous to solving the embedded and emerging problems. Figure 9 shows Christian’s verbal–gestural utterance, as he describes the game objects mathematically, including quantitative relationships between those objects and operations that transform one object into the other in RA (Williams-Pierce, 2016). Christian began by giving a specific example of a game puzzle, where the block is an improper fraction, 1 1/2, nested within the unit hole. He then treated that block as a unit, with his gestures indicating that he is smoothly re-unitizing (Hackenberg, 2007; Steffe and Olive, 2010): from the block as an improper fraction in relation to the unit hole, to the block as the unit whole that can then be acted upon (Williams-Pierce, 2017). Christian’s verbal–gestural utterance reveals the mental model he has developed of the game and the underlying mathematical structures, and it illustrates a form of transfer through reflection generalizations (Ellis, 2007; Williams-Pierce and Thevenow-Harrison, under review).
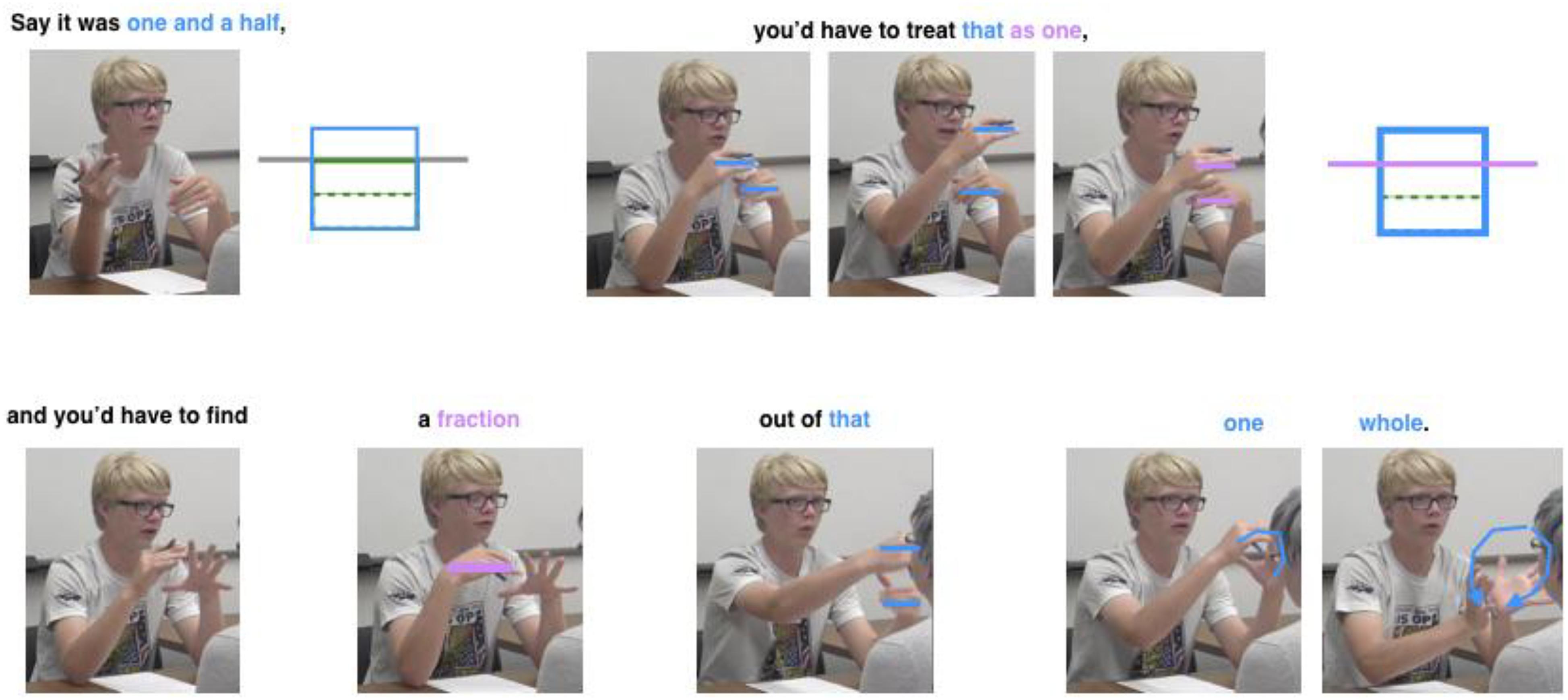
Figure 9. Christian (pseudonym) using a mathematical model to explain his game tactics. Gestures have been enhanced in blue (the improper fraction quantity that represents a gold block) and purple (the unit whole that represents the hole containing the block) to connect Christian’s gestures more clearly with his spoken language; independent images of his referents have been supplemented.
Designers seeking to integrate mathematical content into game mechanics should consider creating realistic situations that afford both proximal actions (manipulation) and distal actions (the digital outcome) that enact normative dynamics of mathematical transformations (Abrahamson and Bakker, 2016; Dittman et al., 2017). Students’ gestures demonstrate their productive struggle to coordinate between features of the situation and elements of mathematical forms (Abrahamson, 2004; Nemirovsky et al., 2020). As such, teachers who incorporate games into their curriculum are encouraged to facilitate classroom discussions that legitimate gestural utterance, so that they can support students’ mathematical modeling.
Summary of Design Rationale and Principles
Designing for voluntary mathematization
Novel non-standard mathematical representations and interactions can provoke voluntary mathematization by the player–learner.
Designing for semiotic enactments
Semiotic enactments can be supported by designing a game that requires players–learners to use co-speech gestures to communicate about the underlying mathematical patterns.
Learning as a multimodal synthesis
Understanding the processes of learning within a mathematical game requires synthesizing the player–learner’s digital actions, spoken language, and physical gesture.
Embodiment Perspectives on Teacher Education
A current movement in K–16 mathematics education is for instructors to teach using student-centered techniques that help make content accessible to students, especially students from historically underrepresented (HU) groups. Although an agreed-upon definition of student-centered learning does not exist, a unifying theme entails students developing their own knowledge, where “learning is personalized to the students’ unique needs, interests, and aspirations, and designed with their ideas and voices at the table” (Kaput, 2018, p. 10). Neumann (2013) encapsulates these various characteristics by describing student-centeredness as a process of focusing on students, in students, and with students. Instructors create lessons based on students’ educational needs and course goals, where students organically react to the lesson’s activities, engage in their own sense-making, and where instructors work in partnership with students. Although instructors generally have good intentions of implementing student-centered learning that emphasizes conceptual understanding, inservice K-12 teachers (Yurekli et al., 2020), prospective K–12 teachers (Loughran and Hamilton, 2016), and collegiate faculty (Estrada et al., 2018) do not always enact their intended teaching methods.
In this section, we describe barriers that prevent K–16 instructors from integrating student-centered teaching, summarize effective professional development (PD) strategies, and offer examples of how embodiment can support student-centered learning, be integrated as part of teacher education or professional development, and foster equitable instruction.
Toward Student-Centered Pedagogy Informed by Embodiment Perspectives
Whereas prospective K–12 teachers study student-centered instructional methodologies in their university preparation courses, they are generally challenged in implementing these methodologies in the school classroom. Given that some education faculty, mathematics faculty, university supervisors, and K-12 in-service supervisors have differing views on concept-based and student-centered teaching and learning, K-12 teachers struggle to transform their teaching (Simon, 2013, 2018). Researchers have implicated a theory–practice divide (Loughran and Hamilton, 2016), whereby university courses provide intellectual theory, while field-based practices provide authentic experiences (Horn and Campbell, 2015)—prospective teachers are not equipped to bridge this divide without guidance from university faculty and cooperating teachers. Worse, prospective teachers receive inconsistent views from university faculty and K–12 teachers about mathematics content, teaching, and learning. Zeichner et al. (2015) claim that, “too often these [elements] are not in dialogue and leave the novice teacher as the sole mediator of multiple knowledge sources” (p. 124).
In-service teachers likewise struggle to integrate research-to-practice, even after they partake in PD. Richards and Skolits (2009) cite teachers’ “unfamiliarity with instructional strategies promoting student engagement, inadequate training regarding these strategies, and insufficient support in the classroom” (p. 41) as reasons for the persistence of teacher-centered classroom practices. Moreover, teachers may perceive their school environment as unsafe for change, believe that administrators are unsupportive of such teaching, and fear violating state or national mandates (Greenberg and Baron, 2000; Fullan, 2001; Goleman et al., 2002).
Collegiate faculty, too, are slow to adopt student-centered teaching, despite the call for faculty to make STEM courses more inspiring, to assist students facing mathematical challenges, and to create an atmosphere of a community of STEM learners (PCAST, 2012). Handelsman et al. (2004) attribute this predicament to faculty being unaware of evidenced-based teaching methods. Yet even faculty who are aware of the research may distrust its findings, and in particular those who themselves learned via lecture. Furthermore, some faculty fear losing their identity and credibility as a researcher, if they focus on their teaching (Brownell and Tanner, 2012). Finally, transforming one’s teaching is effortful and cumbersome, requiring time, support from faculty and administrators, and resources.
In their synthesis of the literature, Richards and Skolits (2009) delineate that PD designed to integrate new teaching strategies must “incorporate hands-on, experiential learning opportunities, that are embedded in authentic contexts in which teachers can thoroughly connect with the new strategies” (p. 42). Experiences such as these allow teachers to better understand and connect the content and strategies by taking time to apply, analyze, and synthesize the strategies in ways that will be meaningful in the teachers’ classrooms. In their own research, Richards and Skolits found that teachers were more likely to integrate a new teaching strategy if they understood the educational theory behind the strategy, observed the strategy modeled, related the new strategy to existing teaching practices, and received on-site support as they integrated the new strategy for the first time. Some researchers (Speer et al., 2005, 2010; Deshler et al., 2015) have investigated effectiveness of PD for collegiate instructors, but the research remains minimal in this domain and much of the work is with graduate students. Given the wide range of research demonstrating that embodiment facilitates mathematics learning (Abrahamson, 2009a; Radford et al., 2009; Hall and Nemirovsky, 2012; Schoenfeld, 2016; Oehrtman et al., 2019; Soto–Johnson and Hancock, 2019) and the call for student-centered learning in K–16 mathematics education (Conference Board of the Mathematical Sciences [CBMS], 2016), the time is ripe to educate prospective teachers, in-service teachers, and collegiate instructors regarding embodiment.
Embodiment can inform teacher education and PD in the same way that it informs mathematics educational experiences, as long as these experiences are designed for students, in students, and with students in mind. Content courses designed for prospective teachers or as part of PD can be designed with activities that require play or action in either the physical or virtual world. Embodied, authentic, hands-on, body-on, activities intentionally designed based on the learning goals, the students’ needs, and the students’ background knowledge Abrahamson et al. (2012a) satisfy PD recommendations. Furthermore, as part of lessons instructors might intentionally gesture for students and convey how the gesturing exemplifies some aspect of the content. Given learning dwells in the student, instructors must learn to become attuned to students’ gesturing, motor-actions, and accompanied verbiage and be prepared to help them become conscious of their unconscious actions. Such observing and reporting students’ actions back to them may help students to begin to build intuition and to transform their physical or virtual experiences to abstract concepts. This is the juncture where instructors collaborate with students and help them bridge the experience, the play, the motor-actions, the verbiage, and the abstract concepts. Such facilitation requires modeling in prospective teachers’ collegiate mathematics content courses and PD designed to introduce embodiment to in-service mathematics teachers.
Embodiment in Professional Practice: A Design for Teacher Education
Figure 10 illustrates how embodiment has been used with prospective K–12 mathematics teachers as they learn properties of Euclidean transformations. In this activity, learners embody points on the Cartesian plane. They hold onto rope, which represents the segments of a polygon, and collaboratively engage in translating along the plane, rotating 45°, 60°, and 90° about a given point, and determining the image of their polygon when it is reflected about parallel lines and intersecting lines. Besides learning properties of these transformations, the students come to realize that Euclidean transformations are rigid motions on the plane. Realizing this via paper-and-pencil media is difficult, because one transforms a single point at a time (Yanik, 2014). The action of moving simultaneously, the gestures that materialize via student–student conversations, and the teacher–student dialogues that emerge during such an activity epitomize student-centeredness through embodiment. This activity has also been used as part of PD for K-12 teachers and collegiate instructors (Soto–Johnson, 2016; Nathan et al., 2017b; Soto, 2019).

Figure 10. Enacting Euclidean transformations: Guided by a university instructor, three mathematics teachers study a tarped Cartesian coordinate system in preparation for rotating a rope triangle over the plane. They current occupy (–1, –1), (1, 4), and (2, –2).
Prospective teachers are generally trained to inform their students about the choices that are made in the classroom, as such, integrating embodiment into teacher education and professional development should begin with regular brief introductions to embodied cognition. This can be as simple as stating that body movement can be a first sign that learning is occurring and that learners can demonstrate their understanding via multimodal utterances, which include eye motion, facial expressions, gesture, gaze, body poise, body motion, tone of voice, etc. (Nemirovsky and Ferrara, 2009). This is a good first step for audiences to understand the educational theory behind an activity, as suggested by Richards and Skolits (2009).
These utterances can also display what Estrada et al. (2018) refer to as micro/macro affirmations, which are particularly relevant for HU students. The authors promote micro/macro affirmations such as space left between people when interacting (e.g., physical closeness), eye contact, subtle teasing, voice tone, and actions that convey vulnerability and constitute utterances. Embodied activities that deliberately attend to these characteristics can serve as steppingstones toward such affirmations and support equity. Another benefit of embodiment is that it can provide a non-linguistic on-ramp to mathematics concepts, which can facilitate learning for students who may have a language barrier. Embodiment provides such learners access to concepts through body-based interventions and ways to express their reasoning in non-verbal ways. Given gestures can suggest learner readiness (Goldin–Meadow et al., 1993), practitioners’ abilities to attend to learners’ gestures may serve as micro-affirmations and give students confidence and make them feel more included. Through embodied activities that support micro/macro affirmations, HU learners or learners who consider themselves “unteachable” may experience new points of access to content presented through movement, concrete experiences, and body-based forms of engagement, which are all forms of student-centered learning.
Summary of Design Rationale and Principles
Embodiment perspectives on teacher education
K-16 student-centered teaching and learning
K-16 teachers should teach using student-centered techniques, where students can create and share their own knowledge.
Teacher education on embodiment
Embodiment can be integrated via content courses and K–16 PD, where learners engage in physical or virtual play. Learning to be attuned to students’ gesturing, motor-actions, and accompanied verbiage and helping students become conscious of their unconscious actions may help students build intuition and transform their actions to abstract concepts. Important for instructors to become cognizant of their own gestures and intentionally convey their gesturing to students.
Students develop a multimodal voice
Embodiment provides learners access to concepts through body-based interventions and can frame teachers’ formative assessments of students’ reasoning that is expressed in non-verbal ways.
General Summary and Implications for Mathematics Education Design and Research
These are exciting times for cognitive scientists investigating the futures of mathematics education. An interdisciplinary research intersection has formed, where three frontiers—paradigm-changing theory of human learning (embodied cognition), new human–computer interaction platforms (e.g., with gesture or gaze sensors), and powerful methods for measuring, coding, modeling, and monitoring individual and collective student activity in real time (multimodal data analytics, artificial intelligence, machine learning, and visualization)—converge to innovate learning environments offering naturalistic experiences that foster conceptual knowledge grounded in sensorimotor cognitive and affective processes. We, a cohort of collaborating learning scientists and mathematics educators and teacher educators who practice embodied design-based research, have surveyed some of the perspectives, evidence, and principles we bring to bear in working with the multiple stakeholders of mathematics educational enterprises—primarily students, teachers, and technology experts—to explore the futures of mathematics education. Whereas technology is rapidly evolving, we hope that some of the heuristic design principles we have demonstrated and delineated will endure and prove useful to our colleagues and fellow scholars.
As a cohort, we continue to investigate these tenets of embodied design:
• The meaning of mathematical concepts is grounded in individuals’ cognition in the form of modal processes, which are non-verbal and non-symbolic. This enactive know-how (System 1; Kahneman, 2011) may complement, be redundant with, or be totally distinct from our linguistic and inscriptional formalisms.
• Participants in embodied-design activities discover and develop concept-grounding enactive processes, even when they are not aware that or what they are learning (Abrahamson et al., 2016c; Nathan and Walkington, 2017; Mathayas et al., 2019).
• Mathematics knowledge can cross the epistemic divide from enactive to linguistic–symbolic through mediational processes that include discourse, reflection, expression, and argumentation, using a variety of modalities and media (Abrahamson, 2009b; Trninic and Abrahamson, 2012; Morgan and Abrahamson, 2016). Gesture, in particular, is instrumental in sounding pre-semiotic processes into social interaction.
These educational potentials of the embodiment turn favor approaches such as concreteness fading (Fyfe et al., 2014) as well as sociocultural models of guided mediation (Abrahamson et al., 2012b), and a rejection of formalisms first approaches to curriculum design and instruction (Nathan, 2012). Approaches to instruction that foreground embodied forms of knowing have implications also for assessment of knowledge that is encoded in non-verbal form (Pardos et al., 2018). See Appendix B for a summative list of the design principles emanating from the six research programs surveyed in this article.
Figure 11 plots the designs exponents of the six research programs discussed in this paper with respect to two axes: (1) the ontology of objects in the enactment domain; and (2) the social coordination of the solution enactment. As the figure demonstrates, the designs differ in their foci either on pre-symbolic or symbolic objects as the things that students manipulate. For example, in the Mathematics Imagery Trainer, students manipulate generic acontextual icons, such as empty circles, whereas in Graspable Math they manipulate numerical symbolic notations, such as the digit “7.” Designers’ selection of interactive digital objects may reflect their philosophical and theoretical positions concerning the epistemic function of working with pre-symbolic objects, their assumptions respecting students’ entering knowledge of a domain, and their instructional objectives for specific projects. These decisions can be of moment: research has demonstrated that images carry implicit semiotic content that may constrain their apparent affordances and therefore may either enhance or compromise the designers’ goals for students’ interactions (Rosen et al., 2018).
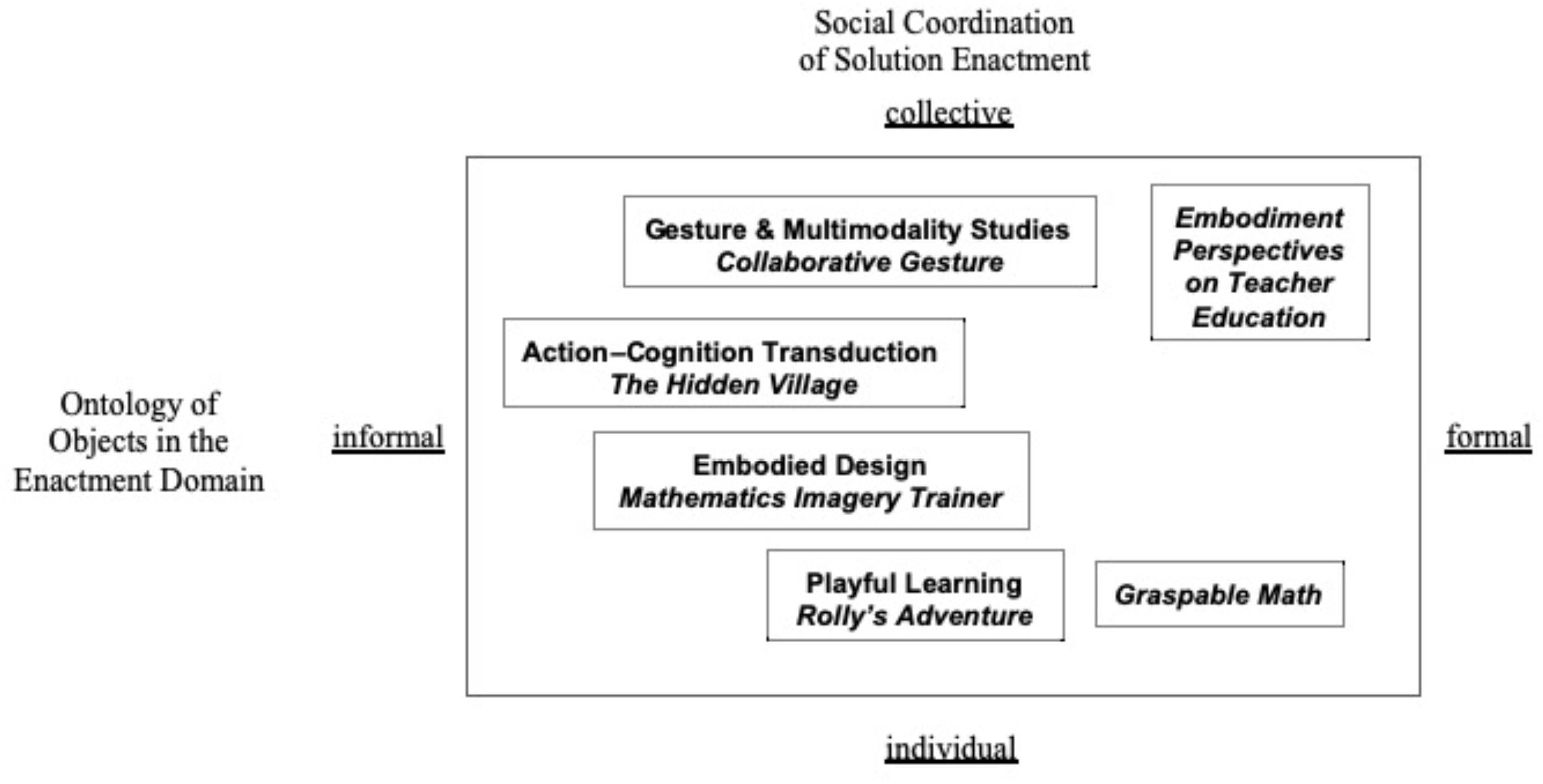
Figure 11. Plotting the six embodied designs along two axes: (x) the manipulatives’ ontological status; and (y) the social participation of solution enactment.
The designs also differ with respect to the contributions and prominence of fellow learners in the process of determining, coordinating, and enacting the physical actions that solve the problem encountered therein. For example, Rolly’s Adventure is designed to maximize outreach—any individual child with access to a digital device and internet could play this game, whereas Collaborative Gesture is designed explicitly to solicit disciplinary discourse among a cohort of co-present classroom students attempting to solve a collective problem. Designers’ choices respecting the collaborative quality of an educational activity are closely related to the perceived epistemic function of enactment, the available media, the instructional settings, and the desired roles of socialization. For further reviews of designers’ beliefs respecting the epistemic role of movement in embodied design, readers are referred to Abrahamson and Bakker (2016), Abrahamson (2018), and Abrahamson and Abdu (2020). Notably, designs premised on a conceptualization of the mathematics learning process as the development of a new sensorimotor perceptual structure may yield different learning outcomes whether a two-handed interaction is performed by an individual student or distributed over two students (Abrahamson et al., 2011). Finally, other potential dimensions of comparison among embodied designs could include: types of technological media supporting the activities; forms and degrees of pedagogical support proffered by teachers or avatars in the learning environment; and student opportunities to discover how to enact the movement forms necessary for completing the tasks.
Whereas the perspectives presented in this paper varied in their interpretations of embodiment, they all highlighted the role of physical movement in conceptual development (Abrahamson, 2018). And yet, by and large, the field of mathematics education research has not investigated the sensorimotor production of physical movement. Being informed of research on how we learn to move in new ways could help us better design, measure, and theorize the enactment of physical movements grounding mathematics learning (Beilock, 2008, 2015; belcastro and Schaffer, 2011; Abrahamson et al., 2016a). More broadly, inasmuch as we theorize perceptual–motor activity as constitutive in the development of mathematical cognition, our field should form interdisciplinary communities of educational research that cross traditional boundaries and bring in ideas from scholars in dance, kinesiology, sports science, somatics, and related fields (Mechsner et al., 2001; Thelen and Smith, 2006; Kelso, 2016; Adolph et al., 2018; Sheets-Johnstone, 2018; Cappuccio, 2019). The movement sciences, we maintain, have much to contribute to emerging theories of conceptual development in mathematics and beyond.
Data Availability Statement
The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.
Ethics Statement
The studies involving human participants were reviewed and approved by the IRB/CHPS at the authors’ respective universities. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin. Written informed consent was obtained from the individual(s) for the publication of any potentially identifiable images or data included in this article.
Author Contributions
DA initiated and led the effort, with MN making significant contributions to the opening and closing sections. CW-P, CW, EO, HS, and MA wrote a segment in the central section, which DA and MN reviewed. All authors contributed to the article and approved the submitted version.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Footnotes
- ^ For further details on this project, including a cluster of computer-based simulated experiments used in the studies, the reader is referred to https://edrl.berkeley.edu/projects/seeing-chance/.
- ^ For further details on this project, the reader is referred to https://edrl.berkeley.edu/projects/kinemathics/
References
Abdullah, A., Adil, M., Rosenbaum, L., Clemmons, M., Shah, M., Abrahamson, D., et al. (2017). “Pedagogical agents to support embodied, discovery-based learning,” in Proceedings of the 17th International Conference on Intelligent Virtual Agents (IVA 2017), eds J. Beskow, C. Peters, G. Castellano, C. O’Sullivan, I. Leite, and S. Kopp (New York, NY: Springer International Publishing), 1–14. doi: 10.1007/978-3-319-67401-8_1
Abrahamson, D. (2002). “When “the same” is the same as different differences: aliya reconciles her perceptual judgment of proportional equivalence with her additive computation skills,” in Proceedings of the 24th Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, Vol. 4, eds D. Mewborn, P. Sztajn, E. White, H. Wiegel, R. Bryant, and K. Nooney (Columbus, OH: Eric Clearinghouse for Science, Mathematics, and Environmental Education), 1658–1661.
Abrahamson, D. (2004). “Embodied spatial articulation: a gesture perspective on student negotiation between kinesthetic schemas and epistemic forms in learning mathematics,” in Proceedings of the 26th Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, Vol. 2, eds D. E. McDougall and J. A. Ross (Toronto, ON: Preney), 791–797.
Abrahamson, D. (2006). The shape of things to come: the computational pictograph as a bridge from combinatorial space to outcome distribution. Int. J. Comp. Math. Learn. 11, 137–146. doi: 10.1007/s10758-006-9102-y
Abrahamson, D. (2007a). “Both rhyme and reason: toward design that goes beyond what meets the eye,” in Proceedings of the 29th Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, eds T. Lamberg and L. Wiest (Stateline (Lake Tahoe), NV: University of Nevada, Reno), 287–295.
Abrahamson, D. (2007b). “Handling problems: embodied reasoning in situated mathematics,” in Proceedings of the 29th Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, eds T. Lamberg and L. Wiest (Stateline (Lake Tahoe), NV: University of Nevada, Reno), 219–226.
Abrahamson, D. (2009a). Embodied design: constructing means for constructing meaning. Educ. Stud. Math. 70, 27–47. doi: 10.1007/s10649-008-9137-1
Abrahamson, D. (2009b). Orchestrating semiotic leaps from tacit to cultural quantitative reasoning—the case of anticipating experimental outcomes of a quasi-binomial random generator. Cogn. Instru. 27, 175–224. doi: 10.1080/07370000903014261
Abrahamson, D. (2012b). Rethinking intensive quantities via guided mediated abduction. J. Learn. Sci. 21, 626–649. doi: 10.1080/10508406.2011.633838
Abrahamson, D. (2012c). “Seeing chance: perceptual reasoning as an epistemic resource for grounding compound event spaces,” in Probability in Reasoning about Data and Risk [Special issue]. ZDM Mathematics Education, Vol. 44, eds In R. Biehler and D. Pratt (Berkeley, CA: UC Berkeley), 869–881. doi: 10.1007/s11858-012-0454-6
Abrahamson, D. (2013). “Toward a taxonomy of design genres: fostering mathematical insight via perception-based and action-based experiences,” in Proceedings of the 12th Annual Interaction Design and Children Conference (IDC 2013) (Vol. “Full Papers,” pp. 218-227), eds J. P. Hourcade, E. A. Miller, and A. Egeland (New York, NY: The New School & Sesame Workshop).
Abrahamson, D. (2014). Building educational activities for understanding: an elaboration on the embodied-design framework and its epistemic grounds. Int. J. Child Comp. Interact. 2, 1–16. doi: 10.1016/j.ijcci.2014.07.002
Abrahamson, D. (2015b). “The monster in the machine, or why educational technology needs embodied design,” in Learning Technologies and the Body: Integration and Implementation, ed. In V. R. Lee (New York, NY: Routledge), 21–38.
Abrahamson, D. (2015a). Reinventing learning: a design-research odyssey. ZDM Math. Educ. 47, 1013–1026. doi: 10.1007/s11858-014-0646-3
Abrahamson, D. (2018). “Moving forward: in search of synergy across diverse views on the role of physical movement in design for STEM education [symposium],” in “Rethinking Learning in the Digital Age: Making the Learning Sciences Count,” Proceedings of the 13th International Conference of the Learning Sciences (ICLS 2018), Vol. 2, eds J. Kay and R. Luckin (London: International Society of the Learning Sciences), 1243–1250.
Abrahamson, D. (2019). “A new world: educational research on the sensorimotor roots of mathematical reasoning,” in Proceedings of the Annual Meeting of the Russian Chapter of the International Group for the Psychology of Mathematics Education (PME) & Yandex, ed. A. Shvarts (Moscow: Yandex), 48–68.
Abrahamson, D. (2020a). Embodied Design: Bringing Forth Mathematical Perceptions. Invited Lecture accepted for presentation at the 14th International Congress of Mathematics Education (ICME14), Shanghai. (Postponed due to COVID-19), Shanghai.
Abrahamson, D. (2020b). Strawberry feel forever: understanding metaphor as sensorimotor dynamics. Senses Soc. 15, 216–238. doi: 10.1080/17458927.2020.1764742
Abrahamson, D., and Abdu, R. (2020). “Towards an ecological-dynamics design framework for embodied-interaction conceptual learning: the case of dynamic mathematics environments,” in Embodied Cognition and Technology for Learning [Special issue]., Educational Technology Research and Development, eds T. J. Kopcha, K. D. Valentine, and C. Ocak. doi: 10.1007/s11423-020-09805-1
Abrahamson, D., and Bakker, A. (2016). Making sense of movement in embodied design for mathematics learning. Cogn. Res. Princ. Implic. 1:33.
Abrahamson, D., and Chase, K. (in press). “Syntonicity and complexity: a design-based research reflection on the Piagetian roots of Constructionism,” in Designing Constructionist Futures: The art, Theory, and Practice of Learning Designs, eds N. Holbert, M. Berland, and Y. Kafai (Cambridge, MA: MIT Press).
Abrahamson, D., Flood, V. J., Miele, J. A., and Siu, Y.-T. (2019). Enactivism and ethnomethodological conversation analysis as tools for expanding universal design for learning: the case of visually impaired mathematics students. ZDM Math. Educ. 51, 291–303. doi: 10.1007/s11858-018-0998-1
Abrahamson, D., Gutiérrez, J. F., and Baddorf, A. K. (2012a). Try to see it my way: the discursive function of idiosyncratic mathematical metaphor. Math. Think. Learn. 14, 55–80. doi: 10.1080/10986065.2012.625076
Abrahamson, D., Gutiérrez, J. F., Charoenying, T., Negrete, A. G., and Bumbacher, E. (2012b). Fostering hooks and shifts: tutorial tactics for guided mathematical discovery. Tech. Knowled. Learn. 17, 61–86. doi: 10.1007/s10758-012-9192-7
Abrahamson, D., Lee, R. G., Negrete, A. G., and Gutiérrez, J. F. (2014). Coordinating visualizations of polysemous action: values added for grounding proportion. ZDM Math. Educ. 46, 79–93. doi: 10.1007/s11858-013-0521-7
Abrahamson, D., and Lindgren, R. (2014). “Embodiment and embodied design,” in The Cambridge Handbook of the Learning Sciences (2nd ed), ed. R. K. Sawyer (Cambridge: Cambridge University Press), 358–376. doi: 10.1017/cbo9781139519526.022
Abrahamson, D., Sánchez-García, R., and Smyth, C. (2016a). “Metaphors are projected constraints on action: an ecological dynamics view on learning across the disciplines,” in “Transforming Learning, Empowering Learners,” Proceedings of the International Conference of the Learning Sciences (ICLS 2016) (Vol. 1, “Full Papers,” pp. 314–321), eds C.-K. Looi, J. L. Polman, U. Cress, and P. Reimann (Singapore: International Society of the Learning Sciences).
Abrahamson, D., Sánchez-García, R., and Trninic, D. (2016b). “Praxes proxies: revisiting educational manipulatives from an ecological dynamics perspective,” in Sin fronteras: Questioning Borders with(in) Mathematics Education – Proceedings of the 38th annual meeting of the North-American Chapter of the International Group for the Psychology of Mathematics Education (PME-NA) (Vol. 13, “Theory and research methods”, pp. 1565-1572), eds In M. B. Wood, E. E. Turner, M. Civil, and J. A. Eli (Tucson: University of Arizona).
Abrahamson, D., and Sánchez-García, R. (2016b). Learning is moving in new ways: the ecological dynamics of mathematics education. J. Learn. Sci. 25, 203–239. doi: 10.1080/10508406.2016.1143370
Abrahamson, D., Shayan, S., Bakker, A., and van der Schaaf, M. F. (2016c). Eye-tracking Piaget: capturing the emergence of attentional anchors in the coordination of proportional motor action. Hum. Dev. 58, 218–244. doi: 10.1159/000443153
Abrahamson, D., and Shulman, A. (2019). Co-constructing movement in mathematics and dance: an interdisciplinary pedagogical dialogue on subjectivity and awareness. Feldenkrais Res. J. 6, 1–24.
Abrahamson, D., and Trninic, D. (2011). “Toward an embodied-interaction design framework for mathematical concepts,” in Proceedings of the 10th Annual Interaction Design and Children Conference (IDC 2011) (Vol. “Full papers,” pp. 1–10), eds P. Blikstein and P. Marshall (Ann Arbor, MI: IDC).
Abrahamson, D., and Trninic, D. (2015). Bringing forth mathematical concepts: signifying sensorimotor enactment in fields of promoted action. ZDM Math. Educ. 47, 295–306. doi: 10.1007/s11858-014-0620-0
Abrahamson, D., Trninic, D., Gutiérrez, J. F., Huth, J., and Lee, R. G. (2011). Hooks and shifts: a dialectical study of mediated discovery. Technol. Knowled. Learn. 16, 55–85. doi: 10.1007/s10758-011-9177-y
Abrahamson, D., and Wilensky, U. (2007). Learning axes and bridging tools in a technology-based design for statistics. Int. J. Comp. Math. Learn. 12, 23–55. doi: 10.1007/s10758-007-9110-6
Adolph, K. E., Hoch, J. E., and Cole, W. G. (2018). Development (of walking): 15 suggestions. Trends Cogn. Sci. 22, 699–711. doi: 10.1016/j.tics.2018.05.010
Alaoui, S. F., Schiphorst, T., Cuykendall, S., Carlson, K., Studd, K., and Bradley, K. (2015). “Strategies for embodied design: the value and challenges of observing movement,” in Proceedings of the 2015 ACM SIGCHI Conference on Creativity and Cognition, eds T. Mayer and E. Y.-L. Do (Glasgow: ACM), 121–130.
Alibali, M. W., and Goldin-Meadow, S. (1993). Gesture-speech mismatch and mechanisms of learning: what the hands reveal about a child’s state of mind. Cogn. Psychol. 25, 468–523. doi: 10.1006/cogp.1993.1012
Alibali, M. W., Heath, D. C., and Myers, H. J. (2001). Effects of visibility between speaker and listener on gesture production: some gestures are meant to be seen. J. Mem. Lang. 44, 169–188. doi: 10.1006/jmla.2000.2752
Alibali, M. W., and Nathan, M. J. (2007). “Teachers’ gestures as a means of scaffolding students’ understanding: evidence from an early algebra lesson,” in Video Research in the Learning Sciences, eds R. Goldman, R. Pea, B. Barron, and S. J. Derry (Mahwah, NJ: Lawrence Erlbaum Associates), 349–365
Alibali, M. W., and Nathan, M. J. (2012). Embodiment in mathematics teaching and learning: evidence from learners’ and teachers’ gestures. J. Learn. Sci. 21, 247–286. doi: 10.1080/10508406.2011.611446
Alibali, M. W., Nathan, M. J., Boncoddo, R., and Pier, E. (2019). Managing common ground in the classroom: teachers use gestures to support students’ contributions to classroom discourse. ZDM Math. Educ. 51, 347–360. doi: 10.1007/s11858-019-01043-x
Alibali, M. W., Nathan, M. J., Church, R. B., Wolfgram, M. S., Kim, S., and Knuth, E. J. (2013a). Teachers’ gestures and speech in mathematics lessons: forging common ground by resolving trouble spots. ZDM Math. Educ. 45, 425–440. doi: 10.1007/s11858-012-0476-0
Alibali, M. W., Nathan, M. J., and Fujimori, Y. (2011). “Gestures in the mathematics classroom: what’s the point?,” in Developmental Cognitive Science Goes To School, eds N. Stein and S. Raudenbush (Abingdon: Taylor and Francis), 219–234.
Alibali, M. W., Nathan, M. J., Wolfgram, M. S., Church, R. B., Jacobs, S. A., Johnson Martinez, C., et al. (2014). How teachers link ideas in mathematics instruction using speech and gesture: a corpus analysis. Cogn. Instruc. 32, 65–100. doi: 10.1080/07370008.2013.858161
Alibali, M. W., Young, A. G., Crooks, N. M., Yeo, A., Wolfgram, M. S., Ledesma, I. M., et al. (2013b). Students learn more when their teacher has learned to gesture effectively. Gesture 13, 210–233. doi: 10.1075/gest.13.2.05ali
Allen, J. W. P., and Bickhard, M. H. (2015). Stepping back: reflections on a pedagogical demonstration of reflective abstraction. Hum. Dev. 58, 245–252. doi: 10.1159/000443713
Antle, A. N., Corness, G., and Bevans, A. (2013). “Balancing justice: exploring embodied metaphor and whole body interaction for an abstract domain,” in Whole Body Interaction [Special issue]., International Journal of Arts and Technology, Vol. 6, eds D. England and N. Bryan-Kinns. 388–409.
Antle, A. N., Wise, A. F., and Nielsen, K. (2011). “Towards utopia: designing tangibles for learning,” in Proceedings of the 10th Annual Interaction Design and Children Conference (IDC 2011) (Vol. “Full papers,” pp. 11–20), eds P. Blikstein and P. Marshall (Ann Arbor, MI: IDC).
Arzarello, F., Paola, D., Robutti, O., and Sabena, C. (2008). Gestures as semiotic resources in the mathematics classroom. Educ. Stud. Math. 70, 97–109. doi: 10.1007/s10649-008-9163-z
Arzarello, F., Paola, D., Robutti, O., and Sabena, C. (2009). Gestures and multimodality in the construction of mathematical meaning. Educ. Stud. Math. 70, 97–109.
Arzarello, F., and Robutti, O. (2008). “Framing the embodied mind approach within a multimodal paradigm,” in Handbook of International Research in Mathematics Education, ed. L. D. English (Abingdon: Routledge), 720–749.
Atkin, A. (2013). “Peirce’s theory of signs,” in The Stanford Encyclopedia of Philosophy (Summer 2013), ed. E. N. Zalta (Cambridge: Cambridge University Press).
Bakker, A. (ed.) (2018). Design Research in Education: A Practical Guide for Early Career Researchers. Abingdon: Routledge.
Barab, S., Gresalfi, M., and Ingram-Goble, A. (2010). Transformational play: using games to position person, content, and context. Educ. Res. 39, 525–536. doi: 10.3102/0013189x10386593
Beilock, S. L. (2008). Beyond the playing field: sport psychology meets embodied cognition. Int. Rev. Sport Exerc. Psychol. 1, 19–30. doi: 10.1080/17509840701836875
Beilock, S. L. (2015). How the Body Knows its Mind: The Surprising Power of the Physical Environment to Influence How You Think and Feel. New York, NY: Atria Book.
belcastro, S. M., and Schaffer, K. (2011). Dancing mathematics and the mathematics of dance. Math. Horizons 18, 16–20. doi: 10.4169/194762111x12954578042939
Bieda, K. N., and Nathan, M. J. (2009). Representational disfluency in algebra: evidence from student gestures and speech. ZDM Math. Educ. 41, 637–650. doi: 10.1007/s11858-009-0198-0
Brooks, N. B., Barner, D., Frank, M., and Goldin–Meadow, S. (2018). The role of gesture in supporting mental representations: the case of mental abacus arithmetic. Cogn. Sci. 42, 554–575. doi: 10.1111/cogs.12527
Brownell, S. E., and Tanner, K. D. (2012). Barriers to faculty pedagogical change: lack of training, time, incentives, and tensions with professional identity. CBE Life Sci. Educ. 11, 339–346. doi: 10.1187/cbe.12-09-0163
Cappuccio, M. L. (ed.) (2019). Handbook of embodied cognition and sport psychology. Cambridge, MA: The MIT Press.
Carter, S. (2014). Yarrrrrrr! Math = Love (Blog). Available online at: https://mathequalslove.blogspot.com/2014/06/yarrrrrrr.html (accessed June 11, 2014).
Chan, J. Y. –C., Hulse, T., Sawrey, K., and Ottmar, E. (2019). “Students’ behavior in a dynamic algebra notation system as indicators of their algebra skills,” in Against New Horizons—Proceedings of the 41st Annual Conference of the North-American Chapter of the International Group for the Psychology of Mathematics Education (PME-NA), eds S. Otten, A. G. Candela, Z. de Araujo, C. Haines, and C. Munter (St. Louis, MO: University of Missouri), 222–223.
Chase, K., and Abrahamson, D. (2015). Reverse-scaffolding algebra: empirical evaluation of design architecture. ZDM Math. Educ. 47, 1195–1209. doi: 10.1007/s11858-015-0710-7
Chase, K., and Abrahamson, D. (2018). Searching for buried treasure: uncovering discovery in discovery-based learning. Instruct. Sci. 46, 11–33. doi: 10.1007/s11251-017-9433-1
Chen, R. S. Y., Ninh, A., Yu, B., and Abrahamson, D. (2020). “Being in touch with the core of social interaction: embodied design for the nonverbal,” in Proceedings of the Annual Meeting of the International Society of the Learning Sciences, eds M. Gresalfi and I. Horn (Nashville, TN: Vanderbilt University).
Chow, J. Y., Davids, K., Button, C., Shuttleworth, R., Renshaw, I., and Araújo, D. (2007). The role of nonlinear pedagogy in physical education. Rev. Educ. Res. 77, 251–278.
Church, R. B., and Goldin–Meadow, S. (1986). The mismatch between gesture and speech as an index of transitional knowledge. Cognition 23, 43–71. doi: 10.1016/0010-0277(86)90053-3
Clark, H. H., and Schaefer, E. F. (1989). Contributing to discourse. Cogn. Sci. 13, 259–294. doi: 10.1207/s15516709cog1302_7
Collins, A. (1990). Toward a Design Science of Education—Technical Report No. 1. New York, NY: Center for Technology in Education.
Conference Board of the Mathematical Sciences [CBMS] (2016). Active Learning in Post-Secondary Mathematics Education. Washington, DC: Conference Board of the Mathematical Sciences.
Cook, S. W., Mitchell, Z., and Goldin–Meadow, S. (2008). Gesturing makes learning last. Cognition 106, 1047–1058. doi: 10.1016/j.cognition.2007.04.010
Crowder, E. M. (1996). Gestures at work in sense-making science talk. J. Learn. Sci. 5, 173–208. doi: 10.1207/s15327809jls0503_2
Crowder, E. M., and Newman, D. (1993). Telling what they know: the role of gestures and language in children’s science explanations. Pragm. Cogn. 1, 339–374.
Damasio, A. R. (1989). Time-locked multiregional retroactivation: a systems-level proposal for the neural substrates of recall and recognition. Cognition 33, 25–62. doi: 10.1016/0010-0277(89)90005-x
de Freitas, E., and Sinclair, N. (2014). Mathematics and the Body: Material Entanglements in the Classroom. New York, NY: Cambridge University Press.
Deshler, J. M., Hauk, S., and Speer, N. (2015). Professional development in teaching for mathematics graduate students. Notices Am. Math. Soc. 62, 638–643. doi: 10.1090/noti1260
Devlin, K. (2011). Mathematics Education for a New era: Video Games as a Medium for Learning. Natick, MA: A.K. Peters, Ltd.
Dewey, J. (1944). Democracy and Education. (Originally published 1916). New York, NY: The Free Press.
Dillenbourg, P., and Evans, M. (2012). Interactive tabletops in education. Int. J. Comp. Supported Collab. Learn. 6, 491–514. doi: 10.1007/s11412-011-9127-7
Dittman, M., Soto–Johnson, H., Dickinson, S., and Harr, T. (2017). Game building with complex-valued functions. PRIMUS 27, 869–879. doi: 10.1080/10511970.2016.1234527
Dörfler, W. (2003). Mathematics and mathematics education: content and people, relation and difference. Educ. Stud. Math. 54, 147–170. doi: 10.1023/b:educ.0000006118.25919.07
Dourish, P. (2004). Where the Action is: The Foundations of Embodied Interaction. Cambridge, MA: MIT press.
Duijzer, A. C. G., Shayan, S., Bakker, A., van der Schaaf, M. F., and Abrahamson, D. (2017). Touchscreen tablets: coordinating action and perception for mathematical cognition. Front. Psychol. 8:144.
Easterday, M. W., Rees Lewis, D. G., and Gerber, E. M. (2016). The logic of the theoretical and practical products of design research. Aust. J. Educ. Technol. 32, 125–144.
Edelson, D. C. (2002). Design research: what we learn when we engage in design. J. Learn. Sci. 11, 105–121. doi: 10.1207/s15327809jls1101_4
Edwards, L. D. (2009). Gestures and conceptual integration in mathematical talk. Educ. Stud. Math. 70, 127–141. doi: 10.1007/s10649-008-9124-6
Ellis, A. B. (2007). A taxonomy for categorizing generalizations: generalizing actions and reflection generalizations. J. Learn. Sci. 16, 221–262. doi: 10.1080/10508400701193705
Enyedy, N., Danish, J. A., and DeLiema, D. (2015). Constructing liminal blends in a collaborative augmented-reality learning environment. Int. J. Comp. Supported Collab. Learn. 10, 7–34. doi: 10.1007/s11412-015-9207-1
Estrada, M., Eroy-Reveles, A., and Matsui, J. (2018). The influence of affirming kindness and community on broadening participation in STEM career pathways. Soc. Issues Policy Rev. 12, 258–297. doi: 10.1111/sipr.12046
Flevares, L. M., and Perry, M. (2001). How many do you see? The use of nonspoken representations in first-grade mathematics lessons. J. Educ. Psychol. 93, 330–345. doi: 10.1037/0022-0663.93.2.330
Flood, V. J. (2018). Multimodal revoicing as an interactional mechanism for connecting scientific and everyday concepts. Hum. Dev. 61, 145–173. doi: 10.1159/000488693
Flood, V. J., Amar, F. G., Nemirovsky, R., Harrer, B. W., Bruce, M. R., and Wittmann, M. C. (2015a). Paying attention to gesture when students talk chemistry: interactional resources for responsive teaching. J. Chem. Educ. 92, 11–22. doi: 10.1021/ed400477b
Flood, V. J., Neff, M., and Abrahamson, D. (2015b). “Boundary interactions: resolving interdisciplinary collaboration challenges using digitized embodied performances,” in Exploring the Material Conditions of Learning: Opportunities and Challenges for Computer Supported Collaborative Learning (CSCL) Conference, Vol. 1, eds O. Lindwall, P. Häkkinen, T. Koschmann, P. Tchounikine, and S. Ludvigsen (Gothenburg: The International Society of the Learning Sciences), 94–100.
Flood, V. J., Schneider, A., and Abrahamson, D. (2015c). “Moving targets: representing and simulating choreographies of multimodal pedagogical tactics for virtual agent mathematics tutors,” in Paper Presented at the Annual Meeting of the American Educational Research Association,, April 16-20, Chicago.
Freudenthal, H. (1983). Didactical Phenomenology of Mathematical Structures. Dordrecht: Kluwer Academic Publishers.
Froebel, F. (2005). The Education of Man (W. N. Hailmann, Trans.). New York, NY: Dover Publications. Original work published 1885.
Fyfe, E. R., McNeil, N. M., Son, J. Y., and Goldstone, R. L. (2014). Concreteness fading in mathematics and science instruction: a systematic review. Educ. Psychol. Rev. 26, 9–25. doi: 10.1007/s10648-014-9249-3
Gallagher, S., and Lindgren, R. (2015). Enactive metaphors: learning through full-body engagement. Educ. Psychol. Rev. 27, 391–404. doi: 10.1007/s10648-015-9327-1
Gee, J. P. (2005). Learning by design: good video games as learning machines. E-Learning 2, 5–16. doi: 10.2304/elea.2005.2.1.5
Glenberg, A. M., Gutierrez, T., Levin, J. R., Japuntich, S., and Kaschak, M. P. (2004). Activity and imagined activity can enhance young children’s reading comprehension. J. Educ. Psychol. 96, 424–436. doi: 10.1037/0022-0663.96.3.424
Glenberg, A. M., and Kaschak, M. P. (2002). Grounding language in action. Psychon. Bull. Rev. 9, 558–565.
Goldin–Meadow, S. (1999). The role of gesture in communication and thinking. Trends Cogn. Sci. 3, 419–429. doi: 10.1016/s1364-6613(99)01397-2
Goldin–Meadow, S. (2005). Hearing Gesture: How our Hands Help us Think. Cambridge, MA: Harvard University Press.
Goldin–Meadow, S., Alibali, M. W., and Church, R. B. (1993). Transitions in concept acquisition: using the hand to read the mind. Psychol. Rev. 100, 279–297. doi: 10.1037/0033-295x.100.2.279
Goldin–Meadow, S., and Singer, M. A. (2003). From children’s hands to adults’ ears: Gesture’s role in the learning process. Dev. Psychol. 39, 509–520. doi: 10.1037/0012-1649.39.3.509
Goldstone, R. L., Landy, D. H., and Son, J. Y. (2010). The education of perception. Topics Cogn. Sci. 2, 265–284.
Goldstone, R. L., Marghetis, T., Weitnauer, E., Ottmar, E., and Landy, D. (2017). Adapting perception, action, and technology for mathematical reasoning. Curr. Direct. Psychol. Sci. 26, 434–441. doi: 10.1177/0963721417704888
Goleman, D., Boyatzis, R., and McKee, A. (2002). Primal Leadership: Realizing the Power of Emotional Intelligence. Boston: Harvard Business School Publishing.
Goodwin, C. (2000). Gesture, aphasia, and interaction. Lang. Gesture 2, 84–98. doi: 10.1017/cbo9780511620850.006
Greenberg, J., and Baron, R. A. (2000). Behavior in Organizations, 7th Edn. Upper Saddle River, NJ: Prentice Hall.
Gresalfi, M. S., and Barnes, J. (2016). Designing feedback in an immersive videogame: supporting student mathematical engagement. Educ. Technol. Res. Dev. 64, 65–86. doi: 10.1007/s11423-015-9411-8
Gunderson, E. A., Spaepen, E., Gibson, D., Goldin–Meadow, S., and Levine, S. C. (2015). Gesture as a window onto children’s number knowledge. Cognition 144, 14–28. doi: 10.1016/j.cognition.2015.07.008
Hackenberg, A. J. (2007). Units coordination and the construction of improper fractions: a rivision of the splitting hypothesis. J. Math. Behav. 26, 27–47. doi: 10.1016/j.jmathb.2007.03.002
Hall, R., Ma, J. Y., and Nemirovsky, R. (2015). “Re-scaling bodies in/as representational instruments in GPS drawing,” in Learning Technologies and the Body: Integration and Implementation in Formal and Informal Learning Environments, ed. V. R. Lee (New York, NY: Routledge), 112–131.
Hall, R., and Nemirovsky, R. (eds). (2012). Modalities of body engagement in mathematical activity and learning [Special issue]. J. Learn. Sci. 21, 1–9.
Handelsman, J., Ebert-May, D., Beichner, R., Bruns, P., Chang, A., DeHaan, R., et al. (2004). Scientific teaching. Science 304, 521–522.
Harel, G., and Sowder, L. (1998). “Students’ proof schemes,” in Research on Collegiate Mathematics Education, Vol. III, eds E. Dubinsky, A. Schoenfeld, and J. Kaput (Providence, RI: American Mathematical Society), 234–283. doi: 10.1090/cbmath/007/07
Hauk, O., Johnsrude, I., and Pulvermüller, F. (2004). Somatotopic representation of action words in human motor and premotor cortex. Neuron 41, 301–307. doi: 10.1016/s0896-6273(03)00838-9
Havas, D. A., Glenberg, A. M., Gutowski, K. A., Lucarelli, M. J., and Davidson, R. J. (2010). Cosmetic use of botulinum toxin-A affects processing of emotional language. Psychol. Sci. 21, 895–900. doi: 10.1177/0956797610374742
Horn, I. S., and Campbell, S. S. (2015). Developing pedagogical judgment in novice teachers: mediated filed experience as a pedagogy for teacher education. Pedagogies Int. J. 10, 149–176. doi: 10.1080/1554480x.2015.1021350
Hostetter, A. B., and Alibali, M. W. (2008). Visible embodiment: gestures as simulated action. Psychon. Bull. Rev. 15, 495–514. doi: 10.3758/pbr.15.3.495
Hostetter, A. B., and Alibali, M. W. (2019). Gesture as simulated action: revisiting the framework. Psychon. Bull. Rev. 26, 721–752. doi: 10.3758/s13423-018-1548-0
Howison, M., Trninic, D., Reinholz, D., and Abrahamson, D. (2011). “The mathematical imagery trainer: from embodied interaction to conceptual learning,” in Proceedings of the annual meeting of The Association for Computer Machinery Special Interest Group on Computer Human Interaction: “Human Factors in Computing Systems” (CHI 2011) (Vol. “Full Papers,” pp. 1989–1998), eds G. Fitzpatrick, C. Gutwin, B. Begole, W. A. Kellogg, and D. Tan (New York, NY: ACM Press).
Hulse, T., Daigle, M., Manzo, D., Braith, L., Harrison, A., and Ottmar, E. (2019). From here to there! elementary: a game-based approach to developing number sense and early algebraic understanding. Educ. Technol. Res. Dev. 67, 423–441. doi: 10.1007/s11423-019-09653-8
Hutchins, E. (1995). How a cockpit remembers its speeds. Cogn. Sci. 19, 265–288. doi: 10.1207/s15516709cog1903_1
Hutto, D. D., Kirchhoff, M. D., and Abrahamson, D. (2015). The enactive roots of STEM: rethinking educational design in mathematics. Educ. Psychol. Rev. 27, 371–389. doi: 10.1007/s10648-015-9326-2
Hutto, D. D., and Myin, E. (2013). Radicalizing Enactivism: Basic Minds Without Content. Cambridge, MA: MIT Press.
Hutto, D. D., and Myin, E. (2017). Evolving Enactivism: Basic Minds Meet Content. Cambridge, MA: MIT Press.
Hutto, D. D., and Sánchez-García, R. (2015). Choking RECtified: embodied expertise beyond Dreyfus. Phenomenol. Cogn. Sci. 14, 309–331. doi: 10.1007/s11097-014-9380-0
Jasmin, K., and Casasanto, D. (2012). The QWERTY effect: how typing shapes the meanings of words. Psychon. Bull. Rev. 19, 499–504. doi: 10.3758/s13423-012-0229-7
Johnson–Glenberg, M. C. (2018). Immersive VR and education: embodied design principles that include gesture and hand controls [Hypothesis and Theory]. Front. Robotics AI 5:81. doi: 10.3389/frobt.2018.00081
Kali, Y., Levin-Peled, R., Ronen-Fuhrmann, T., and Hans, M. (2009). The design principles database: a multipurpose tool for the educational technology community. Design Principles Pract. Int. J. 3, 55–65.
Kang, S., Shokeen, E., Byrne, V. L., Norooz, L., Bonsignore, E., Williams-Pierce, C., et al. (2020). “ARMath: augmenting everyday life with math learning,” in Proceedings of the annual meeting of The Association for Computer Machinery Special Interest Group on Computer Human Interaction: “Human Factors in Computing Systems” (CHI 2020), eds R. Bernhaupt and F. Mueller (New York, NY: ACM Press).
Kaput, K. (2018). Evidence for Student-Centered Learning. Technical Report #ED581111. Education Evolving. Available online at: https://files.eric.ed.gov/fulltext/ED581111.pdf (accessed March 27, 2018).
Kelso, J. A. S. (1984). Phase transitions and critical behavior in human bimanual coordination. Am. J. Physiol. Regul. Integr. Comp. 246, R1000–R1004.
Kelso, J. A. S. (2016). On the self-organizing origins of agency. Trends Cogn. Sci. 20, 490–499. doi: 10.1016/j.tics.2016.04.004
Kelton, M. L., and Ma, J. Y. (2018). Reconfiguring mathematical settings and activity through multi-party, whole-body collaboration. Educ. Stud. Math. 98, 177–196. doi: 10.1007/s10649-018-9805-8
Kim, J., and Maher, M. L. (2020). Conceptual metaphors for designing smart environments: device, robot, and friend [Review]. Front. Psychol. 11:198. doi: 10.3389/fpsyg.2020.00198
Kita, S., Alibali, M. W., and Chu, M. (2017). How do gestures influence thinking and speaking? The gesture-for-conceptualization hypothesis. Psychol. Rev. 124, 245–266. doi: 10.1037/rev0000059
Klemmer, S. R., Hartmann, B., and Takayama, L. (2006). “How bodies matter: five themes for interaction design,” in Proceedings of the 6th Conference on Designing Interactive Systems: ACM, New York, NY.
Koschmann, T., and LeBaron, C. (2002). Learner articulation as interactional achievement: studying the conversation of gesture. Cogn. Instruc. 20, 249–282. doi: 10.1207/s1532690xci2002_4
Kostrubiec, V., Zanone, P.-G., Fuchs, A., and Kelso, J. A. S. (2012). Beyond the blank slate: routes to learning new coordination patterns depend on the intrinsic dynamics of the learner—experimental evidence and theoretical model. Front. Hum. Neurosci. 6:222. doi: 10.3389/fnhum.2012.00222
Lakoff, G., and Johnson, M. L. (1980). Metaphors We Live by. Chicago, IL: The University of Chicago Press.
Lakoff, G., and Núñez, R. E. (2000). Where Mathematics Comes from: How the Embodied Mind Brings Mathematics into Being. New York, NY: Basic Books.
Lamb, J. (2014). Algebra Aerobics. Available online at: http://okmathteachers.com/algebra-aerobics/ (accessed June 30, 2014).
Landy, D. (2010). “Toward a physics of equations,” in Proceedings of “Diagrammatic Representation and Inference”: The 6th International Conference on the Theory and Application of Diagrams, eds A. K. Goel, M. Jamnik, and N. H. Narayanan (New York, NY: Springer), 160–166. doi: 10.1007/978-3-642-14600-8_16
Landy, D., Allen, C., and Zednik, C. (2014a). A perceptual account of symbolic reasoning. Front. Psychol. 5:275. doi: 10.3389/fpsyg.2014.00275
Landy, D., Brookes, D., and Smout, R. (2014b). Abstract numeric relations and the visual structure of algebra. J. Exp. Psychol. Learn. Mem. Cogn. 40, 1404–1418. doi: 10.1037/a0036823
Landy, D., and Goldstone, R. L. (2007). How abstract is symbolic thought? J. Exp. Psychol. Learn. Mem. Cogn. 33, 720–733. doi: 10.1037/0278-7393.33.4.720
Landy, D., and Goldstone, R. L. (2009). “How much of symbolic manipulation is just symbol pushing?,” in Proceedings of the 31st Annual Conference of the Cognitive Science Society, eds N. A. Taatgen and H. van Rijn (Austin, TX: Cognitive Science Society), 1072–1077.
Landy, D., and Goldstone, R. L. (2010). Proximity and precedence in arithmetic. Q. J. Exp. Psychol. 63, 1953–1968. doi: 10.1080/17470211003787619
Landy, D., Jones, M. N., and Goldstone, R. L. (2008). “How the appearance of an operator affects its mathematical precedence,” in Proceedings of the 30th Annual Conference of the Cognitive Science Society, eds B. C. Love, K. McRae, and V. M. Sloutsky (Austin, TX: Cognitive Science Society), 2109–2114.
Lee, R. G., Hung, M., Negrete, A. G., and Abrahamson, D. (2013). “Rationale for a ratio-based conceptualization of slope: results from a design-oriented embodied-cognition domain analysis,” in Paper Presented at the Annual Meeting of the American Educational Research Association (Special Interest Group on Research in Mathematics Education), San Francisco, April 27 – May 1, San Francisco, CA.
Lee, V. R. (2015). Learning Technologies and the Body: Integration and Implementation in Formal and Informal Learning Environments. New York, NY: Routledge.
Leung, A., Baccaglini-Frank, A., and Mariotti, M. A. (2013). Discernment of invariants in dynamic geometry environments. Educ. Stud. Math. 84, 439–460. doi: 10.1007/s10649-013-9492-4
Levine, P., and Scollon, R. (eds). (2004). Discourse and Technology: Multimodal Discourse Analysis. Washington, DC: Georgetown University Press.
Lindgren, R., and Johnson–Glenberg, M. (2013). Emboldened by embodiment: six precepts for research on embodied learning and mixed reality. Educ. Res. 42, 445–452. doi: 10.3102/0013189x13511661
Loughran, J., and Hamilton, M. L. (2016). “Developing an understanding of teacher education,” in International Handbook of Teacher Education, eds J. L. Loughran and M. L. Hamilton (Singapore: Springer).
Lyons, I. M., and Beilock, S. L. (2012). When math hurts: math anxiety predicts pain network activation in anticipation of doing math. PLoS One 7:e48076. doi: 10.1371/journal.pone.0048076
Ma, J. Y. (2017). Multi-party, whole-body interactions in mathematical activity. Cogn. Instruct. 35, 141–164. doi: 10.1080/07370008.2017.1282485
Ma, J. Y., and Hall, R. (2018). Learning a part together: ensemble learning and infrastructure in a competitive high school marching band. Instruct. Sci. 46, 507–532. doi: 10.1007/s11251-018-9455-3
Manzo, D., Ottmar, E., Landy, D., Weitnauer, E., and Achgill, C. (2017). “Assessing variation in mathematical strategies using dynamic technology at scale,” in AERA Online Paper Repository Paper Presented at the Annual Meeting of the American Educational Research Association (San Antonio, TX, Apr 27-May 1, 2017), San Antonio, TX.
Marghetis, T., Landy, D., and Goldstone, R. L. (2016). Mastering algebra retrains the visual system to perceive hierarchical structure in equations. Cogn. Res. Principles Implic. 1:25.
Marin, A., Taylor, K. H., Shapiro, B. R., and Hall, R. (2020). Why learning on the move: intersecting research pathways for mobility, learning and teaching. Cogn. Instruct. 38, 265–280. doi: 10.1080/07370008.2020.1769100
Martin, C. (2011). An information literacy perspective on learning and new media. On Horizon 19, 268–275. doi: 10.1108/10748121111179394
Mathayas, N., Brown, D. E., Wallon, R. C., and Lindgren, R. (2019). Representational gesturing as an epistemic tool for the development of mechanistic explanatory models. Sci. Educ. 103, 1047–1079. doi: 10.1002/sce.21516
McClelland, J. L., McNaughton, B. L., and O’Reilly, R. C. (1995). Why there are complementary learning systems in the hippocampus and neocortex: insights from the successes and failures of connectionist models of learning and memory. Psychol. Rev. 102:419. doi: 10.1037/0033-295x.102.3.419
Mechsner, F., Kerzel, D., Knoblich, G., and Prinz, W. (2001). Perceptual basis of bimanual coordination. Nature 41, 69–73. doi: 10.1038/35102060
Merleau-Ponty, M. (1945/2005). Phenomenology of Perception (C. Smith, Trans.) (Original work published 1945). New York, NY: Routledge.
Moll, H., and Tomasello, M. (2007). Cooperation and human cognition: the Vygotskian intelligence hypothesis. Philos. Trans. R. Soc. B Biol. Sci. 362, 639–648. doi: 10.1098/rstb.2006.2000
Montessori, M. (1967). The Absorbent Mind. (E. M. Standing, Trans.). (Original work published 1949). New York, NY: Holt, Rinehart, and Winston.
Morgan, P., and Abrahamson, D. (2016). Cultivating the ineffable: the role of contemplative practice in enactivist learning. For Learn. Math. 36, 31–37.
Morgan, P., and Abrahamson, D. (2018). Applying contemplative practices to the educational design of mathematics content: report from a pioneering workshop. J. Contemp. Inquiry 5, 107–119.
Murayama, K., Pekrun, R., Lichtenfeld, S., and Vom Hofe, R. (2013). Predicting long−term growth in students’ mathematics achievement: the unique contributions of motivation and cognitive strategies. Child Dev. 84, 1475–1490. doi: 10.1111/cdev.12036
Nagataki, S., and Hirose, S. (2007). Phenomenology and the third generation of cognitive science: towards a cognitive phenomenology of the body. Hum. Stud. 30, 219–232. doi: 10.1007/s10746-007-9060-y
Nathan, M. J. (2012). Rethinking formalisms in formal education. Educ. Psychol. 47, 125–148. doi: 10.1080/00461520.2012.667063
Nathan, M. J. (2017). “One function of gesture is to make new ideas: evidence for reciprocity between action and cognition,” in Why Gesture? How the Hands Function in Speaking, Thinking and Communicating, eds R. B. Church, M. W. Alibali, and S. D. Kelly (Philadelphia, PA: John Benjamins Publishing Company), 175–196. doi: 10.1075/gs.7.09nat
Nathan, M. J., and Alibali, M. W. (in press). “An embodied theory of transfer of mathematical learning,” in Transfer of Learning: Progressive Perspectives for Mathematics Education and Related Fields, eds C. Hohensee and J. Lobato (Berlin: Springer).
Nathan, M. J., and Alibali, M. W. (2011). “How gesture use enables intersubjectivity in the classroom,” in Integrating Gestures: The Interdisciplinary Nature of Gesture, eds G. Stam and M. Ishino (Amsterdam: John Benjamins), 257–266. doi: 10.1075/gs.4.23nat
Nathan, M. J., Church, R. B., and Alibali, M. W. (2017a). “Making and breaking common ground: how teachers use gesture to foster learning in the classroom,” in Why Gesture? How the Hands Function in Speaking, Thinking and Communicating, eds R. Breckinridge Church, M. W. Alibali, and S. D. Kelly (Amsterdam: John Benjamins), 285–316. doi: 10.1075/gs.7.14nat
Nathan, M. J., Eilam, B., and Kim, S. (2007). To disagree, we must also agree: how intersubjectivity structures and perpetuates discourse in a mathematics classroom. J. Learn. Sci. 523–563. doi: 10.1080/10508400701525238
Nathan, M. J., and Martinez, C. V. (2015). Gesture as model enactment: the role of gesture in mental model construction and inference making when learning from text. Learn. Res. Pract. 1, 4–37. doi: 10.1080/23735082.2015.1006758
Nathan, M. J., Schenck, K., Vinsonhaler, R., Michaelis, J., Swart, M., and Walkington, C. (in press). Embodied geometric reasoning: dynamic gestures during intuition, insight, and proof. J. Educ. Psychol.
Nathan, M. J., and Walkington, C. (2017). Grounded and embodied mathematical cognition: promoting mathematical insight and proof using action and language. Cogn. Res. Principles Implicat. 2:9.
Nathan, M. J., Walkington, C., Boncoddo, R., Pier, E., Williams, C. C., and Alibali, M. W. (2014). Actions speak louder with words: the roles of action and pedagogical language for grounding mathematical proof. Learn. Instruct. 33, 182–193. doi: 10.1016/j.learninstruc.2014.07.001
Nathan, M. J., Williams-Pierce, C., Walkington, C., Abrahamson, D., Ottmar, E., Soto, H., et al. (2019). The Future of Embodied Design for Mathematical Imagination and Cognition. Available online at https://circlcenter.org/events/synthesis-design-workshops/ (accessed June 6, 2019).
Nathan, M. J., Williams-Pierce, C., Abrahamson, D., Ottmar, E. R., Landy, D., Smith, C., et al. (2017b). “Embodied mathematical imagination and cognition (EMIC) working group,” in “Synergy at the Crossroads”—Proceedings of the 39th annual Conference of the North-American chapter of the International Group for the Psychology of Mathematics Education (Vol. 14 [Working groups], pp. 1497–1506), eds E. Galindo and J. Newton (Indianapolis, IN: Hoosier Association of Mathematics Teacher Educators).
Nathan, M. J., Wolfgram, M., Srisurichan, R., Walkington, C., and Alibali, M. W. (2017c). Threading mathematics through symbols, sketches, software, silicon, and wood: teachers produce and maintain cohesion to support STEM integration. J. Educ. Res. 110, 272–293. doi: 10.1080/00220671.2017.1287046
Nemirovsky, R. (2003). “Three conjectures concerning the relationship between body activity and understanding mathematics. (Coordinators), Perceptuo-motor activity and imagination in mathematics learning (Research Forum),” in Proceedings of the 27th Annual Meeting of the International Group for the Psychology of Mathematics Education, Vol. 1, eds R. Nemirovsky, M. Borba, N. A. Pateman, B. J. Dougherty, and J. T. Zilliox (Columbus, OH: Eric Clearinghouse for Science, Mathematics, and Environmental Education), 105–109.
Nemirovsky, R., and Ferrara, F. (2009). Mathematical imagination and embodied cognition. Educ. Stud. Math. 70, 159–174. doi: 10.1007/s10649-008-9150-4
Nemirovsky, R., Ferrara, F., Ferrari, G., and Adamuz-Povedano, N. (2020). Body motion, early algebra, and the colours of abstraction. Educ. Stud. Math. 104, 261–283. doi: 10.1007/s10649-020-09955-2
Nemirovsky, R., Kelton, M. L., and Rhodehamel, B. (2013). Playing mathematical instruments: emerging perceptuomotor integration with an interactive mathematics exhibit. J. Res. Math. Educ. 44, 372–415.
Nemirovsky, R., Tierney, C., and Wright, T. (1998). Body motion and graphing. Cogn. Instruct. 16, 119–172. doi: 10.1207/s1532690xci1602_1
Neumann, J. W. (2013). Developing a new framework for conceptualizing “student-centered learning.” Educ. Forum 77, 161–175. doi: 10.1080/00131725.2012.761313
Newen, A., Bruin, L. D., and Gallagher, S. (eds). (2018). The Oxford Handbook of 4E Cognition. Oxford: Oxford University Press.
Nielsen, J. (1994). “Enhancing the explanatory power of usability heuristics,” in Proceedings of the 1994 ACM SIGCHI Conference, Boston: ACM, 152–158.
Nogueira de Lima, R., and Tall, D. (2008). Procedural embodiment and magic in linear equations. Educ. Stud. Math. 67, 3–18. doi: 10.1007/s10649-007-9086-0
Novack, M., and Goldin-Meadow, S. (2015). Learning from gesture: How our hands change our minds. Edu. Psychol. Rev. 27, 405–412. doi: 10.1007/s10648-015-9325-3
Novack, M. A., Congdon, E. L., Hemani–Lopez, N., and Goldin–Meadow, S. (2014). From action to abstraction: using the hands to learn math. Psychol. Sci. 25, 903–910. doi: 10.1177/0956797613518351
Núñez, R. E., Edwards, L. D., and Matos, J. F. (1999). Embodied cognition as grounding for situatedness and context in mathematics education. Educ. Stud. Math. 39, 45–65.
Ochoa, X., and Worsley, M. (2016). Augmenting learning analytics with multimodal sensory data. J. Learn. Anal. 3, 213–219. doi: 10.18608/jla.2016.32.10
Oehrtman, M., Soto, H., and Hancock, B. (2019). Experts’ construction of mathematical meaning for derivatives and integrals of complex-valued functions. Int. J. Res. Undergraduate Math. Educ. 5, 394–423. doi: 10.1007/s40753-019-00092-7
Ottmar, E., Chan, J. Y. C., Iannacchione, A., and Drzewiecki, K. (2020). “Examining relations of math anxiety and algebra performance in two technology interventions,” in Poster Submitted for Presentation at the 2020 Mathematical Learning and Cognition Society Conference, Dublin.
Ottmar, E., and Landy, D. (2017). Concreteness fading of algebraic instruction: effects on learning. J. Learn. Sci. 26, 51–78. doi: 10.1080/10508406.2016.1250212
Ottmar, E., Landy, D., and Goldstone, R. L. (2012). “Teaching the perceptual structure of algebraic expressions: preliminary findings from the pushing symbols intervention,” in Proceedings of the 34th Annual Conference of the Cognitive Science Society, eds N. Miyake, D. Peebles, and R. P. Cooper (Austin, TX: Cognitive Science Society), 2156–2161.
Ottmar, E. R., Landy, D., Goldstone, R. L., and Weitnauer, E. (2015a). “Getting from here to there: testing the effectiveness of an interactive mathematics intervention embedding perceptual learning,” in Proceedings of the Thirty-Seventh Annual Conference of the Cognitive Science Society, eds D. C. Noelle, R. Dale, A. S. Warlaumont, J. Yoshimi, T. Matlock, C. D. Jennings, et al. (Pasadena, CA: Cognitive Science Society), 1793–1798.
Ottmar, E. R., Landy, D., Weitnauer, E., and Goldstone, R. (2015b). “Graspable mathematics: using perceptual learning technology to discover algebraic notation,” in Integrating Touch-enabled and Mobile Devices into Contemporary Mathematics Education, eds M. Meletiou-Mavrotheris, K. Mavrou, and E. Paparistodemou (Pennsylvania: IGI Global), 24–28.
Palatnik, A., and Abrahamson, D. (2018). Rhythmic movement as a tacit enactment goal mobilizing the emergence of mathematical structures. Educ. Stud. Math. 99, 293–309. doi: 10.1007/s10649-018-9845-0
Pardos, Z. A., Hu, C., Meng, P., Neff, M., and Abrahamson, D. (2018). “Characterizing learner behavior from high frequency touchscreen data using recurrent neural networks,” in Adjunct Proceedings of the 26th Conference on User Modeling, Adaptation and Personalization (UMAP ’18), eds D. Chin and L. Chen (New York, NY: Association for Computing Machinery).
PCAST (2012). Engage to Excel: Producing one Million Additional College Graduates with Degrees in Science, Technology, Engineering, and Mathematics. Washington, DC: The White House.
Peirce, C. S. (1894). “What is a sign?,” in The Essential Peirce, Volume 2: Selected Philosophical Writings (Chapter 2), ed. Peirce edition project (Bloomington, IN: Indiana University Press).
Perry, M., Church, R. B., and Goldin–Meadow, S. (1988). Transitional knowledge in the acquisition of concepts. Cogn. Dev. 3, 359–400. doi: 10.1016/0885-2014(88)90021-4
Piaget, J. (1968). Genetic Epistemology (E. Duckworth, Trans.). New York, NY: Columbia University Press.
Pier, E. L., Walkington, C., Clinton, V., Boncoddo, R., Williams-Pierce, C., Alibali, M. W., et al. (2019). Embodied truths: how dynamic gestures and speech contribute to mathematical proof practices. Contemp. Educ. Psychol. 58, 44–57. doi: 10.1016/j.cedpsych.2019.01.012
Pine, K. J., Lufkin, N., and Messer, D. (2004). More gestures than answers: children learning about balance. Dev. Psychol. 40, 1059–1067. doi: 10.1037/0012-1649.40.6.1059
Pirie, S. E. B., and Kieren, T. E. (1992). Creating constructivist environments and constructing creative mathematics. Educ. Stud. Math. 23, 505–528. doi: 10.1007/bf00571470
Pirie, S. E. B., and Kieren, T. E. (1994). Growth in mathematical understanding: how can we characterize it and how can we represent it? Educ. Stud. Math. 26, 165–190. doi: 10.1007/bf01273662
Pouw, W. T. J. L., van Gog, T., and Paas, F. (2014). An embedded and embodied cognition review of instructional manipulatives. Educ. Psychol. Rev. 26, 51–72. doi: 10.1007/s10648-014-9255-5
Pratt, D., and Noss, R. (2010). Designing for mathematical abstraction. Int. J. Comp. Math. Learn. 15, 81–97. doi: 10.1007/s10758-010-9160-z
Radford, L., Edwards, L., and Arzarello, F. (eds). (2009). Gestures and multimodality in the construction of mathematical meaning [Special Issue]. Educ. Stud. Math. 70, 143–157.
Rasmussen, C., Stephan, M., and Allen, K. (2004). Classroom mathematical practices and gesturing. J. Math. Behav. 23, 301–323. doi: 10.1016/j.jmathb.2004.06.003
Richards, J., and Skolits, G. (2009). Sustaining instructional change: the impact of professional development on teacher adoption of a new instructional strategy. Res. Sch. 16, 41–59.
Ritzhaupt, A. B., Higgins, H. J., and Allred, S. B. (2009). Evaluation of the DimensionM Game Series in the Middle school Mathematics Classroom. Tabula Digita: Educational Gaming Company.
Rollinde, E. (2019). Learning science through enacted astronomy. Int. J. Sci. Math. Educ. 17, 237–252. doi: 10.1007/s10763-017-9865-8
Rosen, D. M., Palatnik, A., and Abrahamson, D. (2018). “A better story: an embodiment argument for stark manipulatives,” in Using Mobile Technologies in the Learning of Mathematics, eds N. Calder, N. Sinclair, and K. Larkin (Berlin: Springer), 189–211. doi: 10.1007/978-3-319-90179-4_11
Roth, W.-M. (2009). The emergence of 3d geometry from children’s (teacher-guided) classification tasks. J. Learn. Sci. 18, 45–99. doi: 10.1080/10508400802581692
Rousseau, J.-J. (1979). Emile or on Education (A. Bloom, Trans.). (Originally published 1762). New York, NY: Perseus, Basic Books.
Ruthven, K., Laborde, C., Leach, J., and Tiberghien, A. (2009). Design tools in didactical research: instrumenting the epistemological and cognitive aspects of the design of teaching sequences. Educ. Res. 38, 329–342. doi: 10.3102/0013189x09338513
Sarama, J., and Clements, D. H. (2009). “Concrete” computer manipulatives in mathematics education. Child Dev. Perspect. 3, 145–150. doi: 10.1111/j.1750-8606.2009.00095.x
Sawrey, K., Chan, J. Y. –C., Ottmar, E., and Hulse, T. (2019). “Experiencing equivalence with graspable math: results from a middle-school study,” in Against New Horizons—Proceedings of the 41st Annual Conference of the North-American Chapter of the International Group for the Psychology of Mathematics Education (PME-NA), eds S. Otten, A. G. Candela, Z. de Araujo, C. Haines, and C. Munter (St. Louis, MO: University of Missouri), 1738–1743.
Schenck, K., Walkington, C., and Nathan, M. J. (in press). “Groups that move together, prove together: collaborative gestures and gesture attitudes among teachers performing embodied geometry,” in Movement Matters: How Embodied Cognition Informs Teaching and Learning, eds S. L. Macrine and J. M. Fugate (Cambridge, MA: MIT Press).
Scherr, R. E., Close, H. G., Close, E. W., Flood, V. J., McKagan, S. B., Robertson, A. D., et al. (2013). Negotiating energy dynamics through embodied action in a materially structured environment. Phys. Rev. Special Topics Phys. Educ. Res. 9:020105.
Shapiro, L., and Stolz, S. A. (2019). Embodied cognition and its significance for education. Theor. Res. Educ. 17, 19–39. doi: 10.1177/1477878518822149
Sheets-Johnstone, M. (2018). Why kinesthesia, tactility and affectivity matter: critical and constructive perspectives. Body Society 24, 3–31. doi: 10.1177/1357034x18780982
Shvarts, A., and Abrahamson, D. (2019). Dual-eye-tracking Vygotsky: a microgenetic account of a teaching/learning collaboration in an embodied-interaction technological tutorial for mathematics. Learn. Cult. Soc. Interact. 22:100316. doi: 10.1016/j.lcsi.2019.05.003
Simon, M. (2013). Promoting fundamental change in mathematics teaching: a theoretical, methodological, and empirical approach to the problem. ZDM 45, 573–582. doi: 10.1007/s11858-013-0486-6
Simon, M. A. (2018). “Challenges in mathematics teacher education from a (mostly) constructivist perspective,” in Building Support for Scholarly Practices in Mathematics Methods, eds S. E. Katsberg, A. M. Tyminski, A. E. Lischka, and W. B. Sanchez (Charlotte, NC: Information Age Publishing, Inc), 39–48.
Sinclair, N., and Heyd–Metzuyanim, E. (2014). Learning number with TouchCounts: the role of emotions and the body in mathematical communication. Technol. Knowled. Learn. 19, 81–99. doi: 10.1007/s10758-014-9212-x
Singer, M., Radinsky, J., and Goldman, S. R. (2008). The role of gesture in meaning construction. Discourse Process. 45, 365–386.
Skemp, R. R. (1976). Relational understanding and instrumental understanding. Math. Teach. 77, 20–26.
Smith, C. (2018). Body-based activities in secondary geometry: an analysis of learning and viewpoint. School Sci. Math. 118, 179–189. doi: 10.1111/ssm.12279
Smith, C. P., King, B., and Hoyte, J. (2014). Learning angles through movement: critical actions for developing understanding in an embodied activity. J. Math. Behav. 36, 95–108. doi: 10.1016/j.jmathb.2014.09.001
Smith, L. B. (2005). Action alters shape categories. Cogn. Sci. 29, 665–679. doi: 10.1207/s15516709cog0000_13
Soto, H. (2019). “Equity in teaching collegiate mathematics: the possible role of embodied cognition,” in Invited Presentation in M. Bonett–Matiz (Org.), Colloquia Series, Poorvu Center for Teaching and Learning, Yale University and University of Bridgeport, CT, October 4, 2019, Bridgeport, CT.
Soto–Johnson, H. (2016). “Moving and learning: embodying mathematics workshop,” in Invited Workshop in D. Kung (MAA Project NExT, Director), MathFest, Columbus, OH, August 4, 2016, Columbus, OH.
Soto–Johnson, H., and Hancock, B. (2019). Research to practice: developing the amplitwist concept. PRIMUS 29, 421–440. doi: 10.1080/10511970.2018.1477889
Speer, N., Gutmann, T., and Murphy, T. J. (2005). Mathematics teaching assistant preparation and development. College Teaching 53, 75–80. doi: 10.3200/ctch.53.2.75-80
Speer, N., Smith, J. P.III, and Horvath, A. (2010). Collegiate mathematics teaching: An unexamined practice. J. Math. Behav. 29, 99–114. doi: 10.1016/j.jmathb.2010.02.001
Steffe, L. P., and Kieren, T. (1994). Radical constructivism and mathematics education. J. Res. Math. Educ. 25, 711–733.
Steffe, L. P., and Olive, J. (eds). (2010). Children’s Fractional Knowledge. Berlin: Springer–Verlag. doi: 10.1007/978-1-4419-0591-8
Steinkuehler, C., and Duncan, S. (2008). Scientific habits of mind in virtual worlds. J. Sci. Educ. Technol. 17, 530–543. doi: 10.1007/s10956-008-9120-8
Steinkuehler, C., and Williams, C. (2009). Math as narrative in WoW forum discussions. Int. J. Learn. Media 1. doi: 10.1162/ijlm_a_00028
Stevens, R., Satwicz, T., and McCarthy, L. (2008). “In-game, in-room, in-world: reconnecting video game play to the rest of kids’ lives,” in The Ecology of Games: Connecting Youth, Games, and Learning, ed. K. Salen (Cambridge, MA: MIT Press), 41–66.
Stone, A., Webb, R., and Mahootian, S. (1991). The generality of gesture-speech mismatch as an index of transitional knowledge: evidence from a control-of-variables task. Cogn. Dev. 6, 301–313. doi: 10.1016/0885-2014(91)90041-b
Sweller, J. (1994). Cognitive load theory, learning difficulty, and instructional design. Learn. Instruc. 4, 295–312. doi: 10.1016/0959-4752(94)90003-5
Tall, D., and Vinner, S. (1981). Concept image and concept definition in mathematics with particular reference to limits and continuity. Educ. Stud. Math. 12, 151–169. doi: 10.1007/bf00305619
Tancredi, S., Chen, R. S. Y., Krause, C., and Siu, Y. T. (in press). “The need for SpEED: reimagining accessibility through special education embodied design,” in Movement Matters: How Embodied Cognition Informs Teaching and Learning, eds S. L. Macrine and J. M. Fugate (Cambridge, MA: MIT Press).
Thacker, I. E. (2010). Not too Slippery a Slope: Fostering Student Grounding of the Mathematics of Slope in Perceptions of Steepness. Unpublished MA thesis, University of California, Berkeley, Berkeley, CA.
Thacker, I. E. (2019). An embodied design for grounding the mathematics of slope in middle school students’ perceptions of steepness. Res. Math. Educ. doi: 10.1080/14794802.2019.1692061 [Epub ahead of print].
Thelen, E., and Smith, L. B. (1994). A Dynamic Systems Approach to the Development of Cognition and Action. Cambridge, MA: MIT Press.
Thelen, E., and Smith, L. B. (2006). “Dynamic systems theories,” in Handbook of Child Psychology Vol. 1: Theoretical Models of Human Development, ed. R. M. Lerner (Hoboken, NJ: Wiley), 258–312.
Thomas, L. E., and Lleras, A. (2007). Moving eyes and moving thought: on the spatial compatibility between eye movements and cognition. Psychon. Bull. Rev. 14, 663–668. doi: 10.3758/bf03196818
Thompson, L. A., and Massaro, D. W. (1986). Evaluation and integration of speech and pointing gestures during referential understanding. J. Exp. Child Psychol. 42, 144–168. doi: 10.1016/0022-0965(86)90020-2
Thompson, L. A., and Massaro, D. W. (1994). Children’s integration of speech and pointing gestures in comprehension. J. Exp. Child Psychol. 57, 327–354. doi: 10.1006/jecp.1994.1016
Tirosh, D., and Stavy, R. (1999). Intuitive rules: a way to explain and predict students’ reasoning. Educ. Stud. Math. 38, 51–66. doi: 10.1007/978-94-017-1584-3_3
Tomasello, M. (2009). The Cultural Origins of Human Cognition. Cambridge, MA: Harvard university press.
Tomasello, M., and Carpenter, M. (2007). Shared intentionality. Dev. Sci. 10, 121–125. doi: 10.1111/j.1467-7687.2007.00573.x
Trninic, D., and Abrahamson, D. (2012). “Embodied artifacts and conceptual performances,” in Proceedings of the 10th International Conference of the Learning Sciences: Future of Learning (ICLS 2012) (Vol. 1: “Full papers,” pp. 283–290), eds J. V. Aalst, K. Thompson, M. J. Jacobson, and P. Reimann (Sydney: University of Sydney/ISLS).
van Rompay, T., and Hekkert, P. (2001). “Embodied design: on the role of bodily experiences in product design,” in Proceedings of the International Conference on Affective Human Factors Design, Singapore, 39–46.
Varela, F. J., Thompson, E., and Rosch, E. (1991). The Embodied Mind: Cognitive Science and Human Experience. Cambridge, MA: M.I.T. Press.
von Glasersfeld, E. (1987). “Learning as a constructive activity,” in Problems of Representation in the Teaching and Learning of Mathematics, ed. C. Janvier (Hillsdale, NJ: Lawrence Erlbaum), 3–18.
Walkington, C., Nathan, M. J., and Wang, M. (2020a). “The effect of relevant directed arm motions on gesture usage and proving of geometry conjectures,” in Paper Accepted for Presentation at the Annual Meeting of the American Educational Research Association, San Francisco, April 17–21. (Modified format due to COVID-19), San Francisco, CA.
Walkington, C., Wang, M., and Nathan, M. J. (2020b). “Collaborative gestures among secondary students conjointly proving geometric conjectures,” in Paper Accepted for Presentation at the 14th International Congress on Mathematical Education, Shanghai, China. (Modified format due to COVID-19), Shanghai.
Walkington, C., Woods, D., Nathan, M. J., Chelule, G., and Wang, M. (2019b). Does restricting hand gestures impair mathematical reasoning? Learn. Instruc. 64:101225. doi: 10.1016/j.learninstruc.2019.101225
Walkington, C., Chelule, G., Woods, D., and Nathan, M. J. (2019a). Collaborative gesture as a case of extended mathematical cognition. J. Math. Behav. 55:100683. doi: 10.1016/j.jmathb.2018.12.002
Weitnauer, E., Landy, D., and Ottmar, E. O. (2016). “Graspable math: towards dynamic algebra notations that support learners better than paper,” in Future Technologies Conference, (San Francisco, CA: IEEE), 406–414.
Wilensky, U. (1991). “Abstract meditations on the concrete and concrete implications for mathematics education,” in Constructionism, eds I. Harel and S. Papert (Norwood, NJ: Ablex Publishing Corporation), 193–204.
Williams, C. (2015). Rolly’s Adventure [software]. Available on LittleBigPlanet via the Community Levels. Available online at: https://www.mediamolecule.com/games/littlebigplanet2
Williams-Pierce, C. (2016). “Rolly’s adventure: designing a fractions game,” in Proceedings of the 38th Annual Conference of the North-American Chapter of the International Group for the Psychology of Mathematics, eds M. B. Wood, E. E. Turner, M. Civil, and J. A. Eli (Tucson, AZ: The University of Arizona), 1690–1697.
Williams-Pierce, C. (2017). “Fractions, mental operations, and a unique digital context. brief research report,” in Proceedings of the 39th Annual Conference of the North American Chapter of the International Group for the Psychology of Mathematics Education, eds E. Galindo and J. Newton (Indianapolis, IN: Hoosier Association of Mathematics Teacher Educators), 1349–1352.
Williams-Pierce, C. (2019). Designing for mathematical play: failure and feedback. Inform. Learn. Sci. 120, 589–610. doi: 10.1108/ils-03-2019-0027
Wilson, A. D., and Golonka, S. (2013). Embodied cognition is not what you think it is. Front. Psychol. 4:58. doi: 10.3389/fpsyg.2013.00058
Wolpert, D. M., Doya, K., and Kawato, M. (2003). A unifying computational framework for motor control and social interaction. Philos. Trans. R. Soc. Lond. B Biol. Sci. 358, 593–602. doi: 10.1098/rstb.2002.1238
Worsley, M., Abrahamson, D., Blikstein, P., Bumbacher, E., Grover, S., Schneider, B., et al. (2016). “Workshop: situating multimodal learning analytics,” in Transforming Learning, Empowering Learners,” Proceedings of the International Conference of the Learning Sciences (ICLS 2016), Vol. 2, eds C.-K. Looi, J. L. Polman, U. Cress, and P. Reimann (Singapore: International Society of the Learning Sciences), 1346–1349.
Yanik, H. B. (2014). Middle school students’ concept images of geometric translations. J. Math. Behav. 36, 33–50. doi: 10.1016/j.jmathb.2014.08.001
Yee, E., Chrysikou, E. G., Hoffman, E., and Thompson-Schill, S. L. (2013). Manual experience shapes object representations. Psychol. Sci. 24, 909–919. doi: 10.1177/0956797612464658
Yeo, A., Cook, S. W., Nathan, M. J., Popescu, V., and Alibali, M. W. (2017). “Instructor gesture improves encoding of mathematical representations,” in Proceedings of the 40th Annual Conference of the Cognitive Science Society, eds T. T. Rogers, M. A. Rau, X. Zhu, and C. W. Kalish (Austin, TX: Cognitive Science Society), 2723–2728.
Yoon, C., Thomas, M. O., and Dreyfus, T. (2014). “The role of conscious gesture mimicry in mathematical learning,” in Emerging Perspectives on Gesture and Embodiment in Mathematics, eds L. D. Edwards, F. Ferrara, and D. Moore-Russo (Charlotte, NC: Information Age Publishing), 175–195.
Yurekli, B., Stein, M. K., Correnti, R., and Kisa, Z. (2020). Teaching mathematics for conceptual understanding: teachers’ beliefs and practices and the role of constraints. J. Res. Math. Educ. 51, 234–247. doi: 10.5951/jresematheduc-2020-0021
Zandieh, M., Williams-Pierce, C., Plaxco, D., and Amresh, A. (2018). “Using three fields of education research to frame the development of digital games,” in Proceedings of the 42nd Conference of the International Group for the Psychology of Mathematics Education, Vol. 4, eds E. Bergqvist, M. Österholm, C. Granberg, and L. Sumpter (Umeå: PME), 459–466.
Zeichner, K., Payne, K. A., and Brayko, K. (2015). Democratizing teacher education. J. Teacher Educ. 66, 122–135. doi: 10.1177/0022487114560908
Zhang, Z., Lei, Y., and Li, H. (2016). Approaching the distinction between intuition and insight. Front. Psychol. 7:1195.
Zlatev, J. (2007). “Embodiment, language and mimesis,” in Body, Language, Mind (Vol. 1, “Embodiment,” pp. 297-337), eds T. Ziemke, J. Zlatev, and R. Franck (Boston: Mouton de Gruyter).
Zohar, R., Bagno, E., Eylon, B., and Abrahamson, D. (2018). Motor skills, creativity, and cognition in learning physics concepts. Funct. Neurol. Rehabil. Ergon. 7, 67–76.
Appendix A—Embodied Design Literature
Suggested further readings on embodied design include publications pertaining to the following dimension of mathematics-education theory and practice:
• “how-to” heuristic principles for building embodied designs (Abrahamson, 2009a,2012c,2014,2015a);
• positioning embodied-design research projects as settings for investigating problems of empirical philosophy (Hutto et al., 2015)
• rethinking models of discovery learning (Abrahamson, 2012a; Chase and Abrahamson, 2015; Abrahamson, 2018);
• reconciling Piaget’s genetic epistemology and Vygotsky’s cultural–historical psychology (Abrahamson et al., 2011, 2012b,2016c; Abrahamson, 2015a);
• developing a complex dynamic-systems reading of Vygotskian theory (Shvarts and Abrahamson, 2019);
• theorizing students’ epistemic grounds for accepting cultural forms (Abrahamson et al., 2011; Abrahamson, 2014);
• situating the framework within historical approaches to intuition (Abrahamson, 2015b);
• discussing traditional and future uses of pedagogical artifacts that shape the normative enactment of disciplinary movement forms (Abrahamson et al., 2016b);
• analyzing the phenomenology of movement (Abrahamson and Bakker, 2016);
• determining the effect of context richness on movement-based learning (Rosen et al., 2018);
• investigating the role of rhythmic movements in the discovery of mathematical forms (Palatnik and Abrahamson, 2018);
• highlighting the centrality of perception in mathematics learning (Abrahamson, 2020a, b)
• pioneering the design-based research of interactive virtual pedagogical avatars with capacity for naturalistic speech and gesture (Abdullah et al., 2017; Pardos et al., 2018);
• identifying the framework’s roots in Seymour Papert’s educational vision (Abrahamson and Chase, in press);
• relating the framework to metaphor studies (Abrahamson et al., 2012a; Abrahamson et al., 2016a; Abrahamson, in press);
• discussing the framework in light both of dance (Abrahamson and Shulman, 2019) and somatic–contemplative practices (Morgan and Abrahamson, 2016; Abrahamson, 2018);
• dialoguing with special education (Chen et al., 2020; Tancredi et al., in press) and Universal Design for Learning (Abrahamson, 2019); and
• expanding the framework so as to include the treatment of science content (Abrahamson and Lindgren, 2014).
Appendix B—Embodied-Design Activity Architectures: Summary of Principles, Procedures, and Outcomes
Embodied Design: Mathematics Imagery Trainer
Moving in a New Way
Working individually or in pairs, students tackle an interactive motor-control problem. The solution emerges as a particular attentional orientation, by which students coordinate the motor enactment of a movement form that instantiates the activity’s targeted mathematical concept.
Signifying the Movement
Students adopt elements of mathematical instruments newly interpolated into the work space. Initially, they adopt the elements as means of enhancing the enactment, evaluation, or explanation of their solution strategy; yet in so doing, they shift into perceiving their own actions through a mathematical frame of reference.
Reconciling
Finally, students reflect on logical–quantitative relations between their conceptually complementary informal and formal perceptions-for-action.
Action–Cognition Transduction: The Hidden Village
Action-Cognition Transduction
Action and cognition enjoy reciprocity: Just as cognitive processes can induce motor behaviors for performing goal-directed actions, performing actions can induce cognitive states that perform reasoning, problem solving and learning.
Fostering abstr-Action
Actions that are either self-generated or externally directed can facilitate mathematical intuition and proof. The most effective actions are those that are relevant to the mathematical principles of interest.
Extended Embodiment
People explore mathematical ideas deeply when they are encouraged to collaboratively co-construct body movements.
Gesture, Collaborative Gesture, and Multimodality in STEM
Teacher Gestures
Teachers use pointing, representational, and conventional gestures to establish and maintain common ground.
Student Gestures
Learners’ gestures can reveal knowledge not in speech, emerging or transitional knowledge, and how learners schematize information.
Collaborative Embodiment
The presence of multiple learners fundamentally changes the nature of gestures, as learners leverage shared multimodal resources.
Gestures During Collaboration
Learners can jointly embody ideas using gestures that build off one another, and these gestures may facilitate mathematical learning, particularly in the context of action-based technology tools for learning.
Graspable Math
Grounding of Abstraction in Perceptual-Motor Actions
Algebraic reasoning is rooted in basic perceptual processes.
Embedding Action and Perception Into New Technology Tools
Dynamic notation systems that integrate embodied, perceptual-motor training in notation can support mathematics teaching and learning.
Insight Into Students Problem Solving and Thinking
Data logged in technologies can be used to unpack mechanisms by which embodiment and action relate to student thinking, problem solving processes, and learning.
Playful Learning: Rolly’s Adventure
Designing for Voluntary Mathematization
Novel non-standard mathematical representations and interactions can provoke voluntary mathematization by the player–learner.
Designing for Semiotic Enactments
Semiotic enactments can be supported by designing a game that requires players–learners to use co-speech gestures to communicate about the underlying mathematical patterns.
Learning as a Multimodal Synthesis
Understanding the processes of learning within a mathematical game requires synthesizing the player–learner’s digital actions, spoken language, and physical gesture.
Embodiment Perspectives on Teacher Education
K-16 Student-Centered Teaching and Learning
K-16 teachers should teach using student-centered techniques, where students can create and share their own knowledge.
Teacher Education on Embodiment
Embodiment can be integrated via content courses and K–16 PD, where learners engage in physical or virtual play. Learning to be attuned to students’ gesturing, motor-actions, and accompanied verbiage and helping students become conscious of their unconscious actions may help students build intuition and transform their actions to abstract concepts. Important for instructors to become cognizant of their own gestures and intentionally convey their gesturing to students.
Students Develop a Multimodal Voice
Embodiment provides learners access to concepts through body-based interventions and can frame teachers’ formative assessments of students’ reasoning that is expressed in non-verbal ways.
Keywords: cognition, design, embodiment, gesture, mathematics, multimodality, teaching, technology
Citation: Abrahamson D, Nathan MJ, Williams-Pierce C, Walkington C, Ottmar ER, Soto H and Alibali MW (2020) The Future of Embodied Design for Mathematics Teaching and Learning. Front. Educ. 5:147. doi: 10.3389/feduc.2020.00147
Received: 25 February 2020; Accepted: 23 July 2020;
Published: 25 August 2020.
Edited by:
Subramaniam Ramanathan, Nanyang Technological University, SingaporeReviewed by:
Christian Bokhove, University of Southampton, United KingdomJana Trgalova, Université Claude Bernard Lyon 1, France
Copyright © 2020 Abrahamson, Nathan, Williams-Pierce, Walkington, Ottmar, Soto and Alibali. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Dor Abrahamson, ZG9yQGJlcmtlbGV5LmVkdQ==
 Dor Abrahamson
Dor Abrahamson Mitchell J. Nathan
Mitchell J. Nathan Caro Williams-Pierce
Caro Williams-Pierce Candace Walkington
Candace Walkington Erin R. Ottmar
Erin R. Ottmar Hortensia Soto
Hortensia Soto Martha W. Alibali
Martha W. Alibali