Playing Entropy Mastermind can Foster Children’s Information-Theoretical Intuitions

Conceptual descriptions and measures of information and entropy were established in the twentieth century with the emergence of a science of communication and information. Today these concepts have come to pervade modern science and society, and are increasingly being recommended as topics for science and mathematics education. We introduce a set of playful activities aimed at fostering intuitions about entropy and describe a primary school intervention that was conducted according to this plan. Fourth grade schoolchildren (8–10 years) played a version of Entropy Mastermind with jars and colored marbles, in which a hidden code to be deciphered was generated at random from an urn with a known, visually presented probability distribution of marble colors. Children prepared urns according to specified recipes, drew marbles from the urns, generated codes and guessed codes. Despite not being formally instructed in probability or entropy, children were able to estimate and compare the difficulty of different probability distributions used for generating possible codes.

Introduction

Information is a concept employed by everyone. Intuitively, the lack of information is uncertainty, which can be reduced by the acquisition of information. Formalizing these intuitive notions requires concepts from stochastics (Information and Entropy). Beyond the concept of information content itself, the concept of average information content, or probabilistic entropy, translates into measures of the amount of uncertainty in a situation.

Finding sound methodologies for assessing and taming uncertainty (Hertwig et al., 2019) is an ongoing scientific process, which began formally in the seventeenth and eighteenth centuries when Pascal, Laplace, Fermat, de Moivre and Bayes began writing down the axioms of probability. This early work set the foundation for work in philosophy of science and statistics toward modern Bayesian Optimal Experimental Design theories (Chamberlin, 1897; Good, 1950; Lindley, 1956; Platt, 1964; Nelson, 2005). Probabilistic entropy is often defined as expected surprise (or expected information content); the particular way in which surprise and expectation are formulated determines how entropy is calculated. Many different formulations of entropy, including and beyond Shannon, have been used in mathematics, physics, neuroscience, ecology, and other disciplines (Crupi et al., 2018). Many different axioms have been employed in defining mathematical measures of probabilistic entropy (Csiszár, 2008). Examples of key ideas include that only the set probabilities, and not the labeling of possible results, affects entropy (these are sometimes called symmetry or permutability axioms); that entropy is zero if a possible result has probability one; and that addition or removal of a zero-probability result does not change the entropy of a distribution. An important idea is that entropy is maximum if all possible results are equally probable. This idea traces back to Laplace's recommendation for dealing formally with uncertainty, known as the principle of indifference:

If you have no information about the probabilities on the results of an experiment, assume they are evenly distributed (Laplace, 1814).

This principle is fundamental for establishing what is called the prior distribution on the results of experiments before any additional information or evidence on these results leads to an eventual updating of the prior, typically by means of Bayesian inference. However, in most experimental situations there is already some knowledge before the experiment is conducted, and the problem becomes how to choose an adequate prior that embodies this partial knowledge, without adding superfluous information. One and a half centuries later, Jaynes in 1957 observed that Entropy is the key concept for generalizing Laplace’s attitude, in what is today called the Max-Ent principle:

If you havesomeinformation about a distribution, construct your a priori distribution to maximize entropy among all distributions that embody that information.

Applying this principle has become possible and extremely fruitful since the discovery of efficient, implementable algorithms for constructing Max-Ent distributions. These algorithms began being developed already in the early twentieth century without rigorous proofs. Csiszár (1975) was the first to prove a convergence theorem of what is now called the “iterative proportional fitting procedure”, or IPFP, for constructing the Max-Ent distribution consistent with partial information. Recently computers have become powerful enough to permit the swift application of the Max-Ent Principle to real world problems both for statistical estimation and pattern recognition. Today maximum-likelihood approaches for automatically constructing Max-Ent models are easily accessible and used successfully in many domains: in the experimental sciences, particularly in the science of vision; in language processing; in data analysis; and in neuroscience (see, for instance, Martignon et al., 2000). The real-world applicability of the Max-Ent Principle is thus an important reason for promoting teaching information, entropy, and related concepts in school.

Today there is agreement in Germany that the concepts of “information”, “bit”, and “code” are relevant and should be introduced in secondary education, and that first intuitions on these concepts should be fostered even earlier in primary education (Ministerium für Kultus and Jugend und Sport, 2016). However, this is not easy. Given that mathematically simpler ideas, for instance of generalized proportions, can themselves be difficult to convey (see, for instance, Prenzel and PISA Konsortium Deutschland, 2004), how can one go about teaching concepts of entropy and information to children? Our work is guided by the question of how to introduce concepts from information theory in the spirit of the “learning by playing” paradigm (Hirsh-Pasek and Golinkoff, 2004). We describe playful exercises for fostering children’s intuitions of information content, code, bit and entropy. In previous work (Nelson et al., 2014; Knauber et al., 2017), described in Asking Useful Questions, Coding and Decoding, we investigated whether fourth graders are sensitive to the relative usefulness of questions in a sequential search task in which the goal is to identify an unknown target item by asking yes-no questions about its features (Nelson et al., 2014). The results showed that children are indeed sensitive to properties of the environment, in the sense that they adapt their question-asking to these properties. Our goal is now to move on from information content to average information content, i.e., entropy; we develop a more comprehensive educational intervention to foster children’s intuitions and competencies in dealing with the concepts of entropy, encoding, decoding, and search (for an outline of the success of this kind of approach, see Polya, 1973). This educational intervention is guided and inspired by the Entropy Mastermind game (Özel 2019; Schulz et al., 2019). Because the requisite mathematical concept of proportion largely develops by approximately fourth grade (Martignon and Krauss, 2009), we chose to work with fourth-grade (ages 8–10) children. The intervention study we present here is in the spirit of (Bruner, 1966; Bruner, 1970) enactive-iconic-symbolic (E-I-S) framework. In the E-I-S framework, children first play enactively with materials and games. Then they proceed to an iconic (image-based) representational phase on the blackboard and on notebooks. Finally, they work with symbolic representations again on the blackboard and notebook.

Information and Entropy

Information, as some educational texts propose (e.g., Devlin, 1991, p.6), should be described and taught as a fundamental characteristic of the universe, like energy and matter. Average information, i.e., entropy, can be described and taught as a measure of the order and structure of parts of the universe or of its whole. Thus, information can be seen as that element that reduces or even eliminates uncertainty in a given situation (Attneave, 1959). This description is deliberately linked with the physical entropy concept of thermodynamics. The more formal conceptualization of this loose description corresponds to Claude Shannon’s information theory (Devlin, 1991, p.16).

Thus, a widely used educational practice, for instance in basic thermodynamics, is to connect entropy with disorder and exemplify it by means of “search problems”, such as searching for a lost item. This can be modeled using the concept of entropy: a search is particularly complicated when the entropy is high, which means that there is little information about the approximate location of the searched item and the object can therefore be located at all possible locations with approximately the same probability. At the other extreme, if entropy is low, as for a distribution that is 1 on one event and 0 on all others, we have almost absolute certainty. Another educational approach is to describe information as a concept comparable to matter and energy. In this approach matter and energy are described as carriers of information.

A slightly more precise way of thinking about information is by imagining it as transported through an information channel. A communication system, also called channel, can be described by its four basic components, namely a source of information, a transmitter, a possible noise source, and a receiver. This is illustrated in Figure 1.

FIGURE 1

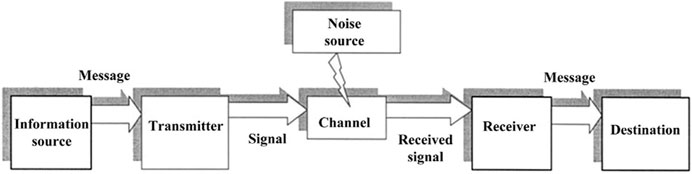
FIGURE 1. Diagram of an information channel (this is an adaptation of the standard diagram that goes back to Shannon and Weaver, 1949; from Martignon, 2015).

What is the information contained in a message that is communicated through the channel? This depends on the distribution of possible messages. An important approach to information theory, understood as a component of the science of communication, was formulated by Shannon in the late forties (Shannon and Weaver, 1949). We illustrate this approach as follows:

The basic idea behind Shannon’s information is inspired by the “Parlor game”, the classical version of the “Guess Who?” game we play today see Figure 2, below, which was well-known at the beginning of the 20th century. In this game a player has to guess a certain item by asking Yes-No questions of the other player, who knows what the item is. Consider an example: If the message describes one of the locations of a chess board then the player needs 6 questions to determine the field, if the questions she asks are well chosen. The same applies for guessing an integer between 1 and 64 if the player knows that the numbers are all equally probable. The first question can be: “Is the number larger than or equal to 32?”. According to the answer, either the interval of numbers between 0 and 31 or the interval between 32 and 64 will be eliminated. The next question will split the remaining interval in halves again. In 6 steps of this kind the player will determine the number. Now, 6 is the logarithm in base 2 of 64, or –log₂ (1/64). This negative logarithm of the probability of one of the equally probable numbers between 1 and 64 allows for many generalizations. Shannon’s definition of information content is illustrated in Figure 2:

FIGURE 2

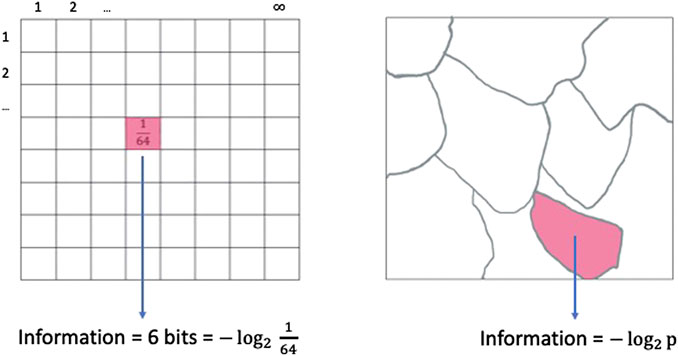
FIGURE 2. Generalizing the paradigm for defining information (from Martignon, 2015).

Here the event with probability p has an information content of -log p, just like one square of the chess board has an information content of −log (1/64) = 6.

The next step is to examine the expected information content of a distribution on a finite partition of events. This best-known formulation of average information is what Shannon called entropy. One of the fundamental outcomes of information theory was the derivation of a formula for the expected value of information content on the background of a probabilistic setting delivered by the information source. For a given probability distribution p and partition F, the Shannon entropy is

$H\left(F\right)= -{\displaystyle \sum }_{i=1}^n{p}_i \mathit{lo}{\mathit{g}}_2 p_{i }$

Shannon entropy is habitually written with the above formula; note that it can be written equivalently as follows:

$H\left(F\right)= -{\displaystyle \sum }_{i=1}^n{p}_i lo{g}_2 p_{i }={\displaystyle \sum }_{i=1}^n{p}_i \left(-lo{g}_2 p_i\right)={\displaystyle \sum }_{i=1}^n{p}_i lo{g}_2\left(1/p_i\right)$

The final formulation of Shannon entropy can be more helpful for intuitively understanding entropy as a kind of expected information content, sometimes also called expected surprise (Crupi et al., 2018). Shannon entropy can be measured in various units; for instance, the bit (an abbreviation of binary digit; Rényi, 1982, p. 19) is used for base 2 logarithms; the nat is used for base e logarithms. A constant multiple can convert from one base to another; for instance, one nat is log₂(e) ≈ 1.44 bits.

We have previously conducted studies that established that children have intuitions about the value of information, and that children can adapt question strategies to statistical properties of the environments in question (Nelson et al., 2014; Meder et al., 2019). Although probabilistic models of the value of information are based on the concept of entropy, a number of simple heuristic strategies could also have been used by children in our previous work to assess the value of questions. Many heuristic strategies may not require having intuitions about entropy per se.

In this paper we explore whether primary school students have the potential to intuitively understand the concept of entropy itself. We emphasize that in primary school we do not envision using technical terms such as entropy or probability at all; rather, the goal is to treat all of these concepts intuitively. Our hope is that intuitive early familiarization of concepts related to entropy, coding, information, and decoding may facilitate future formal learning of these concepts, when (hopefully in secondary school) informatics and mathematics curricula can start to explicitly treat concepts such as probability and expected value. A further point here is that one does not need to be a mathematician to be able to use the Entropy Mastermind game as an educational device in their primary or secondary school classroom.

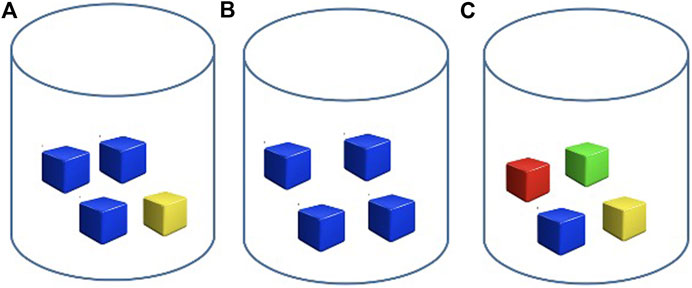
The learning environments we propose are based on enactive playing either with jars and colored cubes or with cards. As a concrete example consider a jar like the one illustrated in Figures 3A–C. Mathematically, the average information or entropy of the distribution of colors in the jar in Figure 3A is.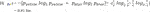If a jar contains only blue cubes, as in Figure 3B, then p_blue = 1 and the entropy of the distribution is defined as 0. The entropy is larger in a jar with many different colors, if those colors are similarly frequent, as in Figure 3C: Here the entropy of the distribution of the jar is $-4\left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.\log \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.\right)=-\log \left(\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$4$}\right.\right)=2$.

FIGURE 3

FIGURE 3. Three jars with three different distributions and corresponding entropies.

A theorem of information theory closely related to Laplace’s Principle (see Information and Entropy) states that maximal entropy is attained by uniform distribution. A key question is whether primary-school children can learn this implicitly, when it is presented in a meaningful gemified context.

Asking Useful Questions, Coding and Decoding

Jars with cubes of different colors make a good environment for guiding children to develop good strategies for asking questions. This can happen when the aim is to determine the color of a particular cube. A more sophisticated learning environment is also just based on jars with colored cubes where children are led to strategizing at a metacognitive level on how the distribution of colors in a jar relates to the difficulty in determining the composition of the jar. The concepts behind the two learning environments just described are information content and entropy. Both activities, asking good questions and assessing the difficulty determining the composition of a jar, are prototypical competencies in dealing with uncertainty.

As we mentioned at the beginning of the preceding section, the game “Guess Who?” is tightly connected to the concepts of information content and entropy. In that game, just as when guessing a number between 1 and 64 (see Information and Entropy) by means of posing yes-no questions, a good strategy is the split-half heuristic, which consists of formulating at each step yes-no questions whose answers systematically divide the remaining items in halves, or as close as possible to halves.

Consider the following arrangement of cards for playing the “Guess Who?” game in Figure 4:

FIGURE 4

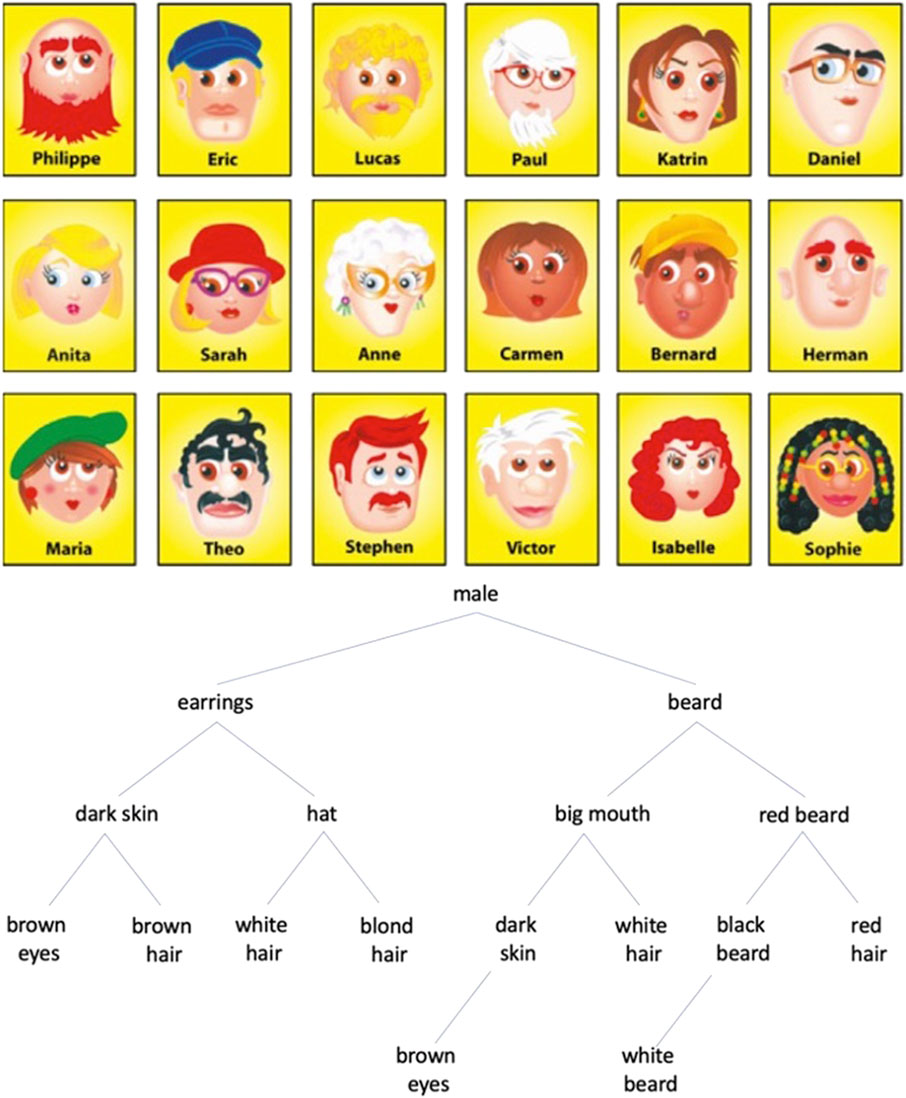
FIGURE 4. The grid of the Person Game used in the study reported in (Nelson et al., 2014); the stimuli are reprinted with permission of Hasbro. The optimal question strategy (from Nelson et al., 2014).

Which is the best sequential question strategy in this game? This can be solved mathematically: it is the one illustrated by the tree in Figure 4, where branches to the right correspond to the answer “yes”, while branches to the left correspond to the answer “no”:

We have previously investigated children's intuitions and behavior in connection with these fundamental games. Some studies investigated whether children in fourth grade are able to adapt their question strategies to the features of the environment (Nelson et al., 2014; Meder et al., 2019). Other studies investigated a variety of tasks, including number-guessing tasks and information-encoding tasks (Knauber et al., 2017; Knauber, 2018).

The Foundation of the Present Study: Asking Good Questions About the Composition of Jars Containing Cubes of Different Colors

The common feature of the study using the “Guess Who?” game and the study presented here is the investigation of question-asking strategies. We exemplify question-asking strategies analogous to those used in the Guess-Who game using jars filled with colored cubes. One of the cubes is drawn blindly, as in Figure 5, blindly and the goal of the question asker is to find out which cube it was. Importantly, only binary yes/no questions are allowed. Figure 5 shows a jar and its corresponding question-asking strategy, visualized as tree.

FIGURE 5

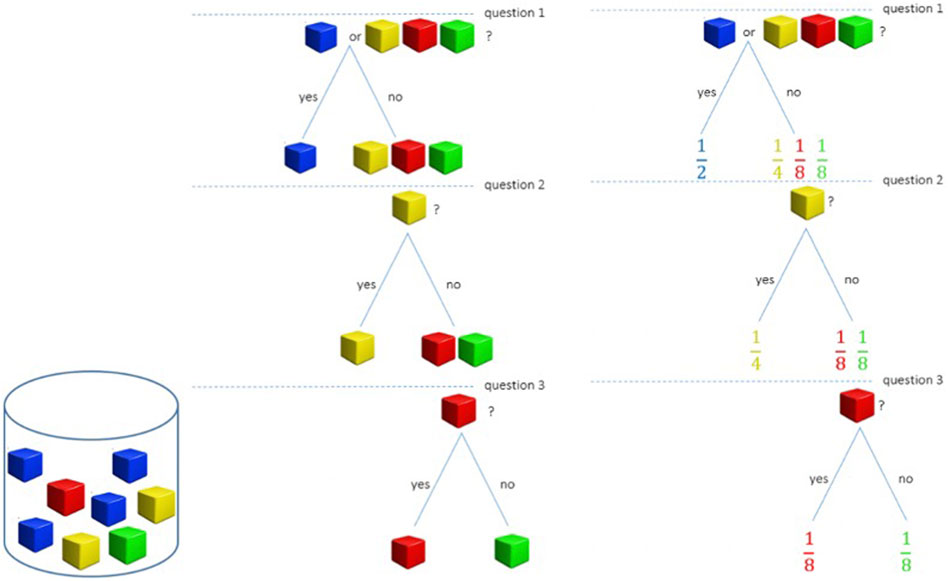
FIGURE 5. A jar filled with colored cubes and the corresponding illustration of a question asking strategy and the associated probabilities.

An Educational Unit Using Entropy Mastermind for Fostering Intuitions About Entropy

We now describe a novel game-based mathematics intervention for fostering children’s intuitions about entropy and probabilities using Entropy Mastermind. Entropy Mastermind (Schulz et al., 2019) is a code breaking game based on the classic game Mastermind. In Entropy Mastermind a secret code is generated from a probability distribution by random drawing and replacement. For example, the probability distribution can be a code jar filled with cubes of different colors. The cubes in the jar are mixed, an item drawn and its color noted. Then, the item is put back into the jar. The jar is mixed again, another item is drawn, its color noted and the item is put back into the jar. The procedure is repeated until the code (for example a three-item code) is guessed correctly. This code is the secret code the player, also referred to as code braker, has to guess. To guess the secret code, the code breaker can make queries. In each query, a specific code can be tested. For each tested code, the codebreaker receives feedback about the correctness of the guessed code. Depending on the context and version of the game, the feedback can be given by another player, the general game master or the teacher or, in the case of a digital version of the game, the software. The feedback consists of three different kinds of smileys: A happy smiley indicates a guessed item is correct in kind (in our example the color) and position (in our example position 1, 2 or 3) in the code; a neutral smiley indicates that a guessed item is the correct kind but not in the correct position; and a sad smiley indicates that a guessed item is incorrect in both kind and position. The feedback smileys are arranged in an array. Importantly, the order of smileys in the feedback array is always the same: happy smileys come first, then neutral and lastly sad smileys. Note that the position of smileys in the feedback array are not indicative of the positions of items in the code. For example, a smiley in position one of the feedback array could mean that position one, two or three of the guess is correct. To figure out which feedback item belongs to which code item is a crucial component of the problem-solving process players have to engage in when guessing the secret code.

But where does entropy come into play in Entropy Mastermind? Between rounds of the game (one round refers to a code being generated, the process of guessing until the correct code is guessed) code jars may differ in their composition. For example, in one round of the game the probability distribution may be 99 blue: 1 red and in another game it may be 50 blue: 50 red. Under the assumption that exactly two colors comprise the code jar, the entropy of the first code jar is minimal, whereas the entropy in the second code jar is maximal. Children experience different levels of entropy in the form of game difficulty. Empirical data from adult game play shows that in high entropy rounds of the game more queries are needed to guess the secret code than in the low entropy rounds (Schulz et al., 2019).

The research question guiding the present work is whether fourth grade students’ intuitions about the mathematical concept of entropy can be fostered by a classroom intervention using Entropy Mastermind. In the following section we present a road map for a pedagogical intervention on entropy and probabilities for fourth graders. In An Implementation of “Embodied Entropy Mastermind” in Fourth Grade we will then report first results on the effectiveness of Entropy Mastermind following precisely this road map from an intervention study.

The Entropy Mastermind intervention consists of two instruction units, each consisting of two regular hours of class. The first unit is designed to give children the opportunity to familiarize themselves with the rules of the game. The goal of this first unit is to convey the important properties of entropy via game play. Although these properties connect strongly to specific axioms in mathematical theories of entropy (Csiszár, 2008), technical terms are not explicitly used in the first unit. The jargon should be accessible and not intimidating for children at elementary school level. Students play the game first in the plenary session with the teacher and then in pairs. The main goal of the first unit is to convey to students an understanding of maximum entropy and minimum entropy. The associated questions students should be able to answer after game-play include:

• Given a number of different code jars (differing in entropy), with which jar is it hardest to play Entropy Mastermind?

• With which jar is it easiest to play Entropy Mastermind?

• Students also get the task to generate differently entropic code jars themselves by coloring black-white code jars themselves, so as to answer: Which color distribution would you choose to make Entropy Mastermind as easy/hard as possible?

The second unit is devoted to an in-depth discussion of the contents developed in the first unit. In addition, other aspects of the entropy concept are included in the discussion. For example, how do additional colors affect the entropy of the jar? What role does the distribution of colors play and what happens if the secret code contains more or less positions?

An important method to evaluate the effectiveness of interventions are a pre- and a post-test of the skills or knowledge intended to train in the intervention. In our first intervention using the Entropy Mastermind game the pre- and post-test were designed in the following way: In the pre-test we recorded to what extent the children already had a prior understanding of proportions and entropy. As entropy is based on proportions and children have not encountered the game yet (and thus may not be able to understand questions phrased in the context of Entropy Mastermind), testing children’s knowledge of proportions in the pretest sets a baseline for the assessment of learning progress through game-play.

In the post-test the actual understanding of entropy was assessed. The post-test allows for phrasing questions in the Entropy Mastermind context, where more detailed and targeted questions about entropy can be asked.

Again, the key goals are for children to learn how to maximize or minimize the entropy of a jar, how to identify the minimum and maximum entropy jar among a number of jars differing in proportions, how entropy is affected by changing the number or the relative proportions of colors in the jar, and that the entropy of a jar does not change if the color ratios remain the same but the colors are replaced by others. The data collected in the pre- and post-test were first evaluated to see whether the tasks were solved correctly or incorrectly. In addition, the children's responses were qualitatively analyzed in order to develop categories for classifying children’s answers. The aim of this analysis was to find out whether the given answers were indicative of a deeper understanding of entropy and which misconceptions arose. In addition, an analysis of the children's solutions was conducted, which was developed within the framework of the teaching units, in order to establish how the strategies for dealing with entropy had been developed during the unit.

Instruction Activity

Implementing Entropy Mastermind as an activity in the classroom can be done in at least two ways: by means of an “embodied approach” having children play with jars and cubes of different colors or with a more digital approach, in which they play with an Entropy Mastermind app. We describe here a roadmap for a classroom activity based on playing the “jar game”, which is a physically enactive version of Entropy Mastermind. The different steps of the intervention are presented as a possible road map for implementing the embodied Mastermind activity.

First Unit: Introducing Entropy Mastermind

The first step for the teacher following our roadmap is to introduce the modified Entropy Mastermind game by means of an example. The teacher uses a code jar, and several small plastic cubes of equal size and form, differing only in color. She asks a student to act as her assistant.

The teacher and (his/)her assistant demonstrate and explain the following activity:

The teacher (the coder) verifiably and exactly fills a 10 × 10 grid with 100 cubes of a specific color (green) and puts them into a fully transparent “code jar” so that the children can see the corresponding proportions. Then she fills the 10 × 10 grid again with 100 cubes of the same color and places them also into the jar. Finally she fills the 10 × 10 grid with cubes of another color (yellow). The teacher notes that it can sometimes be helpful to look at the code jar when all the cubes are inside, before they get mixed up. After the cubes have been put in the code jar, they get mixed up.

Drawing Cubes to Generate a Code

The teacher can work with a worksheet dedicated to codes and coding, which she/he projects on the whiteboard.

Guessing the Code:

The assistant, “the guesser”, determines the code by filling in each square on the worksheet in the “Guess 1” position (see Figure 6): For the first query, the guesser chooses yellow, yellow, yellow. The idea that guesses should be minimized is emphasized by having images of a 1 euro coin next to each guess; after a guess is made, the teacher crosses out the corresponding 1 euro coin. The aim of the game is to guess the code as quickly as possible using an efficient question strategy. The coder gives feedback consisting of one smiley face and two frowny faces (see Figure 6). The smiley face means that one of the squares, we don’t know which one, is exactly right: the right color and the right position. The two frowny faces mean that two items in the true code match neither the color nor the position in the guess. Now the guesser knows that the code contains exactly one yellow cube. Because the only other color is green, the code must also contain two green cubes. For the second query the guesser chooses yellow, green, green, as in Figure 6. The feedback for this guess is one smiley face and two neutral faces. Again, the order of the feedback smileys does not correspond to positions in the code; they only tell you how many positions in the guesses are exactly right (smiley face), partly right (neutral face) or completely wrong (frowny face). Explaining the feedback is a crucial point in the classroom. The teacher must ensure that the feedback terminology is understood. In guess 3 the guesser guesses the rightmost location of the yellow cube, and is correct, obtaining all smiley faces in the feedback. The guesser gets a score of 5, because he had to pay for each of the 3 guesses (include the guess when he had figured the right code out). There are 5 of 8 “Euros” left.

FIGURE 6

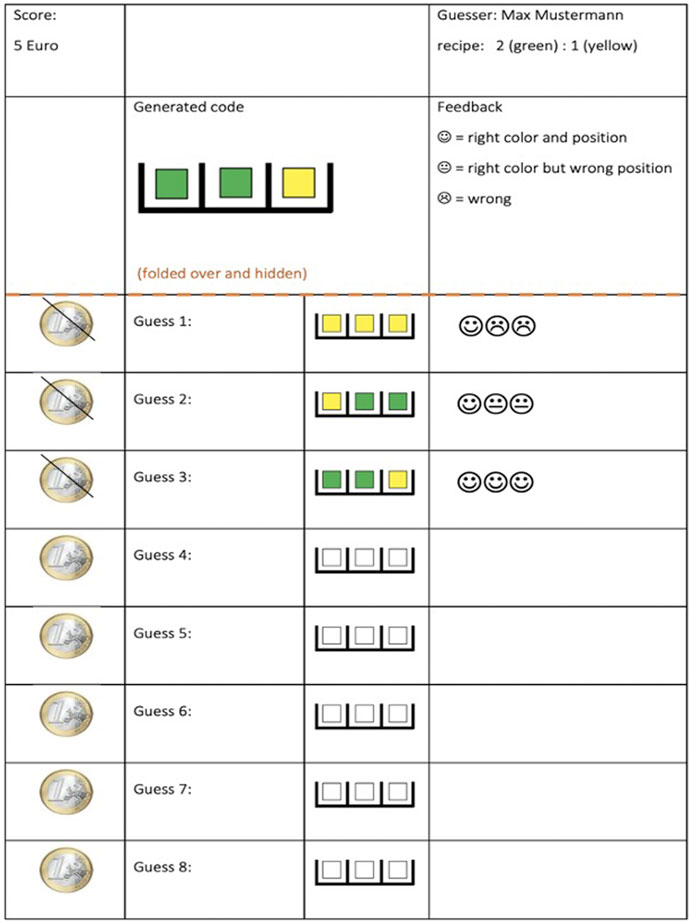
FIGURE 6. The Worksheet for playing Entropy Mastermind, completed following an example as illustrated in Guessing the Code.

This process is repeated with new code jars and recipes and corresponding worksheets projected on the whiteboard until the children understand the rules of the game.

Self-Guided Play: Entropy Mastermind in Pairs

The next step for the children is to play the game with small jars against each other. They are grouped in pairs. A coin toss decides which of the children in each pair is going to be the first guesser and who is going to be the first coder.

Filling the Code Jar and Getting the Worksheets

The teacher asks the coder to come to the front. A coin flip determines whether each pair starts with the 1:2 or 1:12 distribution. According to the distribution, the coder obtains a previously filled-and-labeled small jar or cup, for example with 20 yellow cubes and 40 green cubes. Furthermore, the coder picks up four corresponding worksheets, for the three-item-code-length game, that are already labeled with the corresponding recipe. The coder goes back to her place in order to play with her partner (guesser).

Verifying the Proportions

Each pair takes the cubes out of their code jar, verifies that the proportions are correct, puts the cubes back in, and mixes up the cubes in the code jar.

Blindly Generating and Guessing the Code

The coder and guesser switch roles and repeat the steps described in 4. They play the game twice more. Afterward the children turn in the code jars and the completed worksheets. The teacher adds up the scores (in euros) for all the children, who played the game with the 1:2 and the 1:12 code jars. She presents the scores for each of the two distributions and asks the children about the connection between the scores and the distributions. We describe this discussion in the following paragraph.

Discussion With the Children

The teacher leads the classroom discussion. The main topics/questions are: Which jar was ‘easier’ and which jar was ‘harder’ to play with? It should be clear that the scores are higher for the 1:12 jar than for the 1:2 jar, without using the word entropy. Furthermore, the teacher asks: Imagine you could code your own jar. You have two colors available. How would you choose the proportions to make the game as easy as possible (minimum entropy), and how would you choose the proportions to make the game as hard as possible (maximum entropy)? This discussion is a good opportunity to see whether children have figured out that the hardest jar (maximum entropy) in the case of two colors has a 50:50 distribution, and that the easiest (minimum entropy) jar in the case of two colors has all (or almost all--perhaps task pragmatics require having at least one jar of each color) cubes of the same color.

The following questions are intended to prepare students for the next intervention, while also encouraging them to intuitively think further about the concept of entropy intuitively:

• What would happen if there were more than two colors in the code jar?

• Would this make it easier or harder to guess the code?

• Would it depend on the proportions of each color?

• Would it be easier or harder to play if a code jar were made with small scoops or with large scoops, but using the same recipe?

• Would it be easier or harder or the same to guess the code if the jar contained blue and pink cubes, as opposed to green and yellow cubes?

• Would increasing the code length from three to four make the game easier or harder?

Summing up, the goal of the first intervention unit is to introduce the Entropy Mastermind game, to consolidate children’s understanding of proportions, and to highlight some principles of entropy that will apply irrespective of the number of different colors. In the following, we give an overview of the second unit.

Second Unit: Varying Code Lengths and Multiple Colors

The procedure of the second unit is similar to that of the first unit. However, the focus is on fostering children’s intuitions about how the code length and the number of colors impact on the difficulty of game play. For this unit, new jars are introduced. One code jar has three colors with the recipe (2:1:1). This could mean, for instance, that if four cubes are red, then two cubes are blue and two cubes are green. Another code jar has six colors with the recipe proportions of 35 cubes of one color and one cube each of the five other colors (35:1:1:1:1:1). During the independent self-guided group work, the teacher becomes an assistant to the pupils. Pupils have the opportunity to ask questions whenever something is unclear to them, thereby giving the teacher insight into the pupils’ strategies. Following the game play, the teacher conducts a discussion by asking questions testing students’ understanding of entropy, such as:

• How many colors are represented?

• What is the relative proportion of each color?

• If you could change the color of a cube in the 2:1:1 jar, to make it easier/harder, what would you do?

• Would you do the same thing if you could only use specific colors, or if you could use any color?

• If you had six available colors and wanted to make a code jar as easy/hard as possible, how would you do that?

The above procedure gives some guidelines for using these enactive activities and group discussion to foster intuitive understanding of Entropy. The teachers who implement these units can devise their own pre-tests and post-test to assess measures of success. In the next section we describe one such intervention that we have tested ourselves.

An Implementation of “Embodied Entropy Mastermind” in Fourth Grade

We now report here on a concrete implementation of Entropy Mastermind with jars and cubes in fourth grade in an empirical study based on intervention with N = 42 students (22 girls and 20 boys between the ages of 9 and 10, including 2 students with learning difficulties) from two fourth-grade classes in an elementary school.

In this intervention children were tested before and after the instruction units which were performed following the roadmap described above. Here we describe the contents of the pre- and post-test chosen in this particular case. The first author, who implemented the interventions, analyzed and evaluated the pre- and post-test. She also analyzed the children’s worksheets during the instruction unit. The aim of this analysis was to evaluate children’s strategies when dealing with entropy, and how they evolved during the unit.

Pre-Test: Building Blocks of Entropy

Because, prior to the Entropy Mastermind unit, children would not be in a position to answer questions about code jars being easier or harder for Entropy Mastermind, we decided to have a pre-test dedicated to the essential implicit competencies required for understanding entropy, namely dealing with proportions. For instance, a basic competency for both probability and entropy is that of being able to grasp whether 8 out of 11 is more than 23 out of 25. Thus, the tasks chosen for the pre-test (see Figure 7) allowed us to assess children's understanding of proportions prior to the intervention. The tasks used in the pre-test were inspired by tasks of the PISA Tests of 2003 (Prenzel and PISA Konsortium Deutschland, 2004), and also from the pre-test of a previous intervention study performed by two of the authors of this paper and (Knauber et al., 2017; Knauber, 2018). As an example of such tasks involving proportions, we present Task 1 in Figure 7A and we also present a proportion task with a text cover story (Task 3 in the pre-test) in Figure 7B:

FIGURE 7

FIGURE 7. (A) Task 1 of the Pre-test. (B) Task 3 of the Pre-test.

Children’s answers to the Pre-test were quantified and analyzed.

The Post-Test: Assessing Intuitions About Entropy

In the post-test, Entropy Mastermind-specific knowledge introduced in the teaching units could be taken into consideration for the design of the questions. Moreover, the rules introduced during the instruction unit made it possible to ask detailed and targeted questions. These questions were devoted to assessing the way children deal with entropy. It was possible to assess to what extent children understood how to maximize or minimize the entropy of a jar, whether they could design code jars according to predefined distributions, and how they dealt with comparing jars with different ratios and numbers of elements. They also made it possible to measure the extent to which children understood how entropy is affected by the number of colors in the code jar and that replacing colors without changing color ratios does not affect entropy. Some examples of the post-test tasks are given in Figure 8:

FIGURE 8

FIGURE 8. Selected tasks from the Post-test: 1, 3, 8, 10, 12.

Children’s answers to the post-test tasks were also quantified and analyzed.

We analyzed the results of the pre- and post-test, as well as of results of a detailed analysis of children’s answers during the instruction units. Data collected in the pre-test and post-test were first analyzed quantitatively to determine whether the tasks were solved correctly or incorrectly. Children’s' answers were then analyzed qualitatively by establishing categories and classifying answers accordingly. The aim of this categorization was to find features that show to what extent the answers given are actually based on a correct underlying theoretical understanding, and what difficulties arose in dealing with entropy.

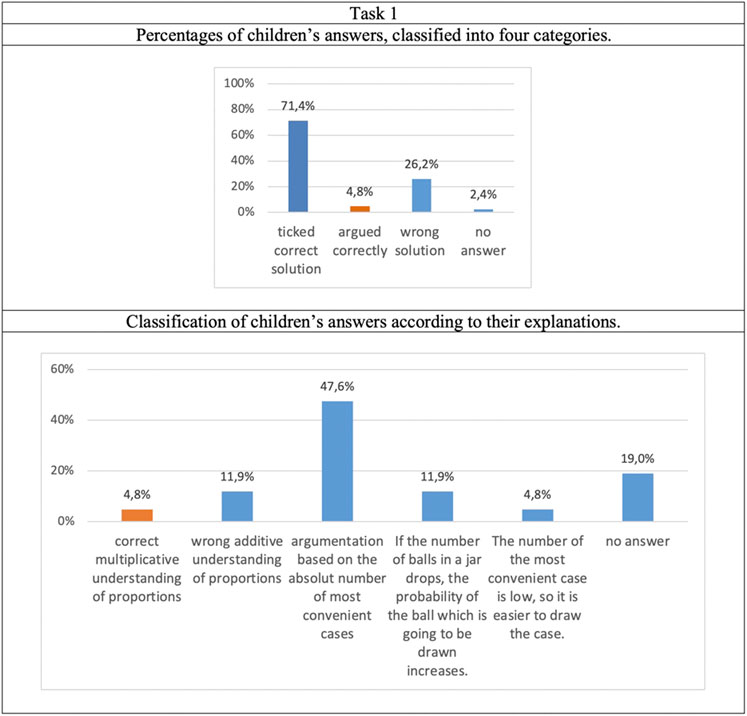
Results of the Pre-Test

71.4% of the students chose the correct answer in Task 1 (see Figure 9, top; here the orange bars represent correct argumentation). Because this percentage does not reveal features of children’s thinking and understanding while solving the task, a finer classification is also presented in the bottom panel of Figure 9. A closer look at reasons students gave for choosing this answer showed that only 2 children out of 42 related the task to proportional thinking. All the other 40 children argued in a way that suggests that proportional thinking did not take place and thus no intuitions about entropy in the jars; this is made clear by Figure 9. In particular, children tended to think that it is easier to draw a white marble in the jar with a smaller total number of marbles.

FIGURE 9

FIGURE 9. Percentages and classification of children’s answers on Task 1.

Some answers of the children according to the categories will be shown below:

Answer 1 in Figure 10 presents a child’s response who reasoned correctly. Here the distributions of the given jars were compared by multiplying the number of elements of the smaller jar so as to make it comparable to the number of the larger quantity.

FIGURE 10

FIGURE 10. Children’s answers according to the categories depicted in Figure 9.

Answer 2, 3 and 4 are examples of wrong reasoning. The child’s reasoning in answer 2 corresponds to the category of children who argued based on the total number of marbles in a jar: It is easier to draw a white marble out of a jar with less marbles than the other jar.

The third answer is an example of the following way of thinking: The less often a marble appears, the greater is the probability of drawing this ball.

About half of the children’s responses correspond to preferring a jar with the higher absolute number of convenient preferred-color marbles.

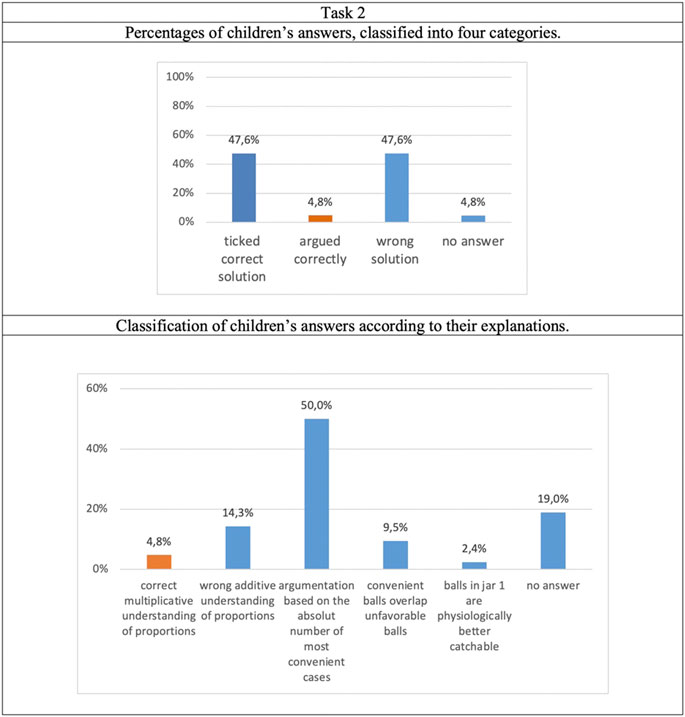
We show also the answers to Task 2, which was similar to Task 1 with 2 white and 3 black marbles in jar 1, and 6 white and 8 black marbles in jar 2. The rationales that the children gave mostly corresponded to those of Task 1.

Approximately half of all (47.6%) children chose the correct answer in Task 2 (see Figure 11). The dominant argument for Task 2 was, as in Task 1, based on the total number of marbles in the respective jars, not on the ratio. This shows that children in the pre-test had poor intuitions on proportions, which form a building block of the understanding of entropy.

FIGURE 11

FIGURE 11. Percentages and classification of children’s answers on task 2.

Because not all children’s responses could be assigned to the previously formed categories, the category system of Task 1 was expanded by one category. Statements that relate exclusively to the arrangement of the marbles in a jar, but do not consider probabilities, are assigned to this category.

As mentioned before, with the increased number of marbles in jar 2, additional naive arguments were added to the categorization system: Because there are more marbles in jar 2, it may happen that the convenient marbles are covered by the unfavorable marbles. Due to this fact, one has to reach deeper into the jar to get the desired marble. Proportions are not considered in this line of thinking.

Task 3 on lettuce, which explicitly tests proportional thinking, was correctly solved by 23 children (54.8% of the sample). 19% of the correctly chosen answers presented arguments by reference to proportions (see student example in Figure 12A); all other children gave answers which indicate that proportions were not considered (see Figure 12B).

FIGURE 12

FIGURE 12. (A). Explanation based on comparison. (B) A solution with no comparison of proportions of proportions.

All children’s responses for Task 3 could be assigned to the categories established for the children’s answers in the previous tasks. Figure 13 shows the distribution of the given answers:

FIGURE 13

FIGURE 13. Categories for the analysis of answers to Task 3 in the pre-test.

Results of the Posttest

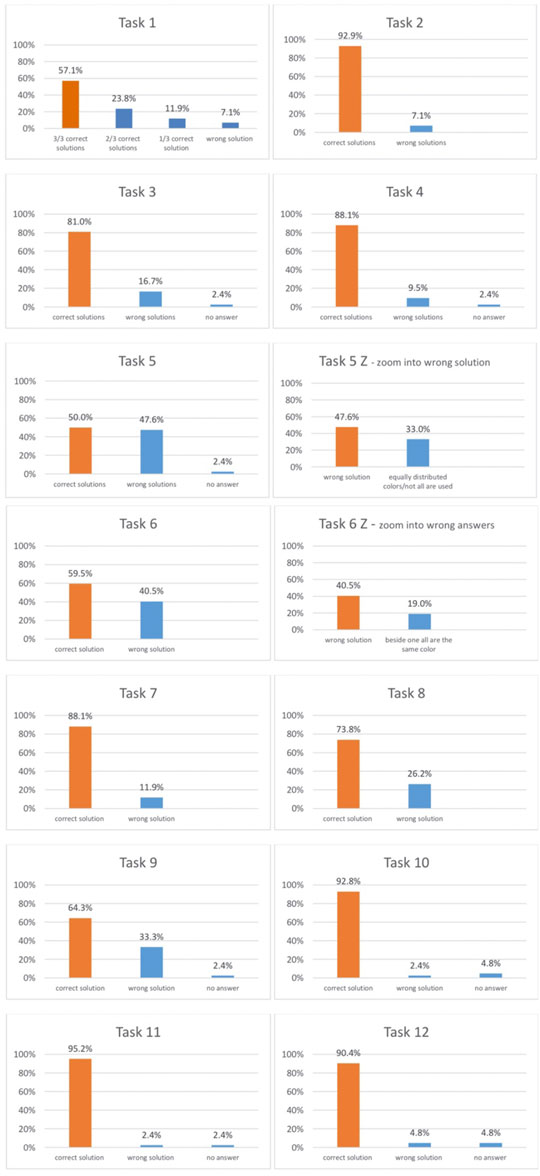
We give for each task in the posttest a short description and present the corresponding results. Task 1 requires an understanding of proportions. The children had to complete code jars by coloring squares as specified and according to given distributions. 57.1% of the children (24 children) fulfilled the requirements and painted all given jars correctly. 23.8% (10 children) completed two of three jars correctly, 11.9% (5 children) completed one jar correctly and 7.1% (3 children) colored the squares incorrectly (see task 1 in Figure 14).

FIGURE 14

FIGURE 14. Results of the post-test.

In Task 2, 3 and 4 the children had to identify the jar with the highest entropy (the “hardest”) out of the three. The jars in Task 2 are made up of cubes of two different colors, while in Task 3 and 4 the number of colors varies between two and five. These tasks required an understanding of how the level of entropy depends on the number of colors and their proportions. Task 2 was solved correctly by 92.9% of the children, task 3 by 81% and Task 4 by 88.1% (see Task 2, 3 and 4 in Figures 14).

In Task 5 and 8 the children had to complete jars by coloring squares according to a list of colors. They had to maximize entropy under given conditions. Only 50% of the children solved task 5 correctly. Nevertheless, 33% of the children who solved the task incorrectly, distributed their chosen colors equally, satisfying the requirement that entropy should be maximal. However, they did not use all the listed colors (see Tasks 5 and 5 Z in Figure 14).

Task 8 was correctly solved by 73.8% of the children (Figure 14).

In Task 6, 7 and 9 the children also had to complete jars by coloring in squares with listed colors. But this time they had to minimize the entropy under given conditions. These tasks also differ in the number of listed colors. Observe that Entropy Mastermind is easiest to play if the jar is coded with only one color. In this case the entropy is 0 bit. In task 6, four of the given twelve squares are colored orange and orange is among the listed colors. 59.5% of the children solved this task correctly by coloring in the remaining squares in orange as well. 40.5% of the children solved the task incorrectly: They reduced entropy by coloring all the squares orange except one. In this solution, entropy is very low, but not minimal (see Tasks 6 and 6 Z in Figure 14).

Task 7 was solved correctly by 88.1% of the children and Task 9 by 64.3% (see Task 7 and 9 in Figure 14).

Tasks 10 and 11 require an understanding of proportions. Two jars with different basic quantities and color distributions have to be compared. 92.8% of the children solved Task 10 correctly and 95.2% solved Task 11 correctly (Figure 14).

Task 12 shows two jars. Both of them have the same number of squares and the distributions of the colors are identical. They differ only in the choice of color. This task requires the understanding that the choice of color does not influence the entropy of a jar. 90.4% of all children solved this task correctly (Figure 14).

Comparison Between the Pre-Test and the Post-Test in Proportion Comparison

In summary, although an average of 57.9% of all tasks were correctly solved in the pre-test, the analysis of children's reasoning shows that only 9.5% of the answers were actually based on an intuitive understanding of proportion comparison. Many children showed misconceptions, such as the incorrect additive strategy in proportional thinking. Similarly, relationships between two basic sets were often not considered, and reasoning was mainly based on the absolute frequency of favorable or unfavorable marbles.

In the Post-test an average of 77.6% of the tasks were solved correctly. Nine of the 12 tasks had been designed with the goal that an understanding of proportion comparison on the one hand, and entropy on the other, was essential for correct answers. For the three other multiple-choice tasks, a correct answer by guessing cannot be excluded, but the solution rates for these tasks are not conspicuously higher than for the other tasks.

As we mentioned, the data collected in the pre-test and post-test were evaluated in order to determine whether the tasks were solved correctly or incorrectly. In addition, students' answers were analyzed qualitatively by establishing categories, to which the answers could be clearly and unambiguously assigned. As we already explained, the categories were based on similarities and differences between answers: the aim was to assess the extent to which the answers given were actually based on understanding. Another issue of interest was the type of difficulty that arose in dealing intuitively with the concept of entropy.

The most relevant aspect of our comparison was the following: while in the pre-test, children gave answers that indicate incorrect additive comparisons with regard to proportions, this seldom occurred in the post-test. Given that the pre- and post-test items were not exactly the same (because the pre-test could not contain Entropy-Mastermind-specific questions), some caution needs to be made in interpreting these results. However--especially given the much greater theoretical difficulty of the post-test items--we take the results as very positive evidence for the educational efficacy of the Entropy Mastermind unit.

Conclusion

Competence in the mathematics of uncertainty is key for everything from personal health and financial decisions to scientific reasoning; it is indispensable for a modern society. A fundamental idea here is the concept of probabilistic entropy. In fact, we see entropy both as “artificial” in the sense that it emerges from abstract considerations on structures imposed on uncertain situations, and as “natural” as suggested by our interaction with the environment around us. We propose that Entropy as a measure of uncertainty is fundamental in consideration of the physical order and symmetry of environmental structures around us (Bomashenko, 2020).

After having played Entropy Mastermind, the majority of fourth-grade students (77.6%) correctly assessed the color distribution of code jars in their responses. This can be interpreted as showing that children were able to develop an intuitive understanding of the mathematical concept of entropy. The analysis of the students’ written rationales for their answers gave further insight into how their strategies and intuitions developed during game-play. It seems that with increasing game experience children tended to regard Entropy-Mastermind as a strategy game, and not only as a game of chance. By developing strategies for gameplay, the children were able to increase the chance of cracking the code, despite the partly random nature of the game. Many strategies that were used are based on an understanding of the properties of entropy. It was impressive how the children engaged in gameplay and improved their strategies as they played the game. Although we did not include the post-test items in the pre-test, for the reasons explained above, and thus direct comparisons between the pre- and post-test are not straightforward, we infer that children’s high scores in the post-test are at least partly attributable to their experiences during the Entropy Mastermind unit.

Qualitatively, children reported that the game Entropy Mastermind was fun, and their verbal reports give evidence that the game fostered their intuitions about entropy: students repeatedly asked whether they could play the game again. This observation corroborates the finding in the literature that students enjoy gamified learning experiences (Bertram, 2020) and suggests that games can foster intuitive understanding of abstract concepts such as mathematical entropy. It is remarkable that we found this positive learning outcome in elementary school students, whose mathematical proficiency was far from understanding formulas as abstract as mathematical entropy at the time of data collection.

Building on the road map described here, we are extending the Entropy Mastermind unit to include a digital version of the game and additional questionnaires and test items in the pre- and post-test (Schulz et al., 2019; Bertram et al., 2020). We have developed a single-player app (internet-based) version in which children can play Entropy Mastermind with differently entropic code jars and varying code lengths. This makes the Entropy Mastermind App a malleable learning medium which can be adapted to children’s strengths and needs. A key issue in future work will be to identify how best to make the app-based version of Entropy Mastermind adapt to the characteristics of individual learners, to maximize desired learning and attitudinal outcomes. The digital Entropy Mastermind unit is well suited for digital learning in various learning contexts, for example for remote schooling during the Covid-19 pandemic. At the same time, the extended pre- and post-test, including psychological questionnaires and a variety of entropy-related questions, allows us to generate a better understanding of the psychology of game-based learning about entropy.

Summing up, using Entropy Mastermind as a case study, we showed that gamified learning of abstract mathematical concepts in the elementary school classroom is feasible and that learning outcomes are high. We are happy to consult with teachers who would like to introduce lesson plans based on Entropy Mastermind in their classrooms. Although our focus in this article is on Entropy Mastermind, we hope that our results will inspire work to develop gamified instructional units to convey a wide range of concepts in informatics and mathematics.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics Statement

The study was conducted with the approval and in accord with the ethical procedures of the Ludwigsburg University of Education and the Friedrich-Kammerer-Integrated School. Parents gave written consent for their children’s participation.

Author Contributions

JDN and EÖ designed the study; EÖ conducted the study as part of her Master's thesis under LM's supervision; JDN, EÖ, LB and LM contributed to the theoretical foundation, analysis and writing of the manuscript.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank the Deutsche Forschungsgemeinschaft MA 1544/12, part of the SPP 1516 “New Frameworks of Rationality” priority program (to L.M.) and the Ludwigsburg University of Education for support through the project “Mastermind”. We also thank Christoph Nau, the staff and the students of the Friedrich-Kammerer-Integrated School for support.

References

Attneave, F. (1959). Applications of Information Theory to Psychology: A Summary of Basic Concepts, Methods and Results. New York: Holt.

Bertram, L. (2020). Digital Learning Games for Mathematics and Computer Science Education: The Need for Preregistered RCTs, Standardized Methodology, and Advanced Technology. Front. Psychol. 11, 2127. doi:10.3389/fpsyg.2020.02127

PubMed Abstract | CrossRef Full Text | Google Scholar

Bertram, L., Schulz, E., Hofer, M., and Nelson, J. (2020). “The Psychology of Human Entropy Intuitions,” in 42nd Annual Meeting of the Cognitive Science Society (CogSci 2020): 5Developing a Mind: Learning in Humans, Animals, and Machines. Editors S. Denison, M. Mack, Y. Xu, and B. Armstrong (Red Hook, NY, USA: Curran), 1457–1463. doi:10.23668/psycharchives.3016

CrossRef Full Text | Google Scholar

Bomashenko, E. (2020). Entropy, Information, and Symmetry: Ordered Is Symmetrical. Entropy, 22, 11. doi:10.3390/e22010011

CrossRef Full Text | Google Scholar

Bruner, J. S. (1970). The Process of Education. Cambridge, MA: Harvard University Press.

Bruner, J. S. (1966). Toward a Theory of Instruction. Cambridge, MA: Harvard University Press.

Chamberlin, T. C. (1897). Studies for Students: The Method of Multiple Working Hypotheses. J. Geology 5, 837–848. doi:10.1086/607980

CrossRef Full Text | Google Scholar

Crupi, V., Nelson, J. D., Meder, B., Cevolani, G., and Tentori, K. (2018). Generalized Information Theory Meets Human Cognition: Introducing a Unified Framework to Model Uncertainty and Information Search. Cogn. Sci. 42 (5), 1410–1456. doi:10.1111/cogs.12613

PubMed Abstract | CrossRef Full Text | Google Scholar

Csiszár, I. (2008). Axiomatic Characterizations of Information Measures. Entropy 10, 261–273. doi:10.3390/e10030261

CrossRef Full Text | Google Scholar

Csiszár, I. (1975). Divergence Geometry of Probability Distributions and Minimization Problems. Ann. Probab. 3 (1), 146–158. doi:10.1214/aop/1176996454

CrossRef Full Text | Google Scholar

Devlin, K. (1991). Logic and Information. New York: Cambridge University Press.

Good, I. J. (1950). Probability and the Weighting of Evidence. New York: Charles Griffin.

Hertwig, R., Pachur, Th., and Pleskac, T. (2019). Taming Uncertainty. Cambridge: MIT Press. doi:10.7551/mitpress/11114.001.0001

CrossRef Full Text

Hirsh-Pasek, K., and Golinkoff, R. M. (2004). Einstein Never Used Flash Cards: How Our Children Really Learn - and Why They Need to Play More and Memorize Less. New York: Rodale.

Knauber, H. (2018). “Fostering Children’s Intuitions with Regard to Information and Information Search,”. Master Thesis (Ludwigsburg: Pädagogische Hochschule Ludwigsburg).

Google Scholar

Knauber, H., Nepper, H., Meder, B., Martignon, L., and Nelson, J. (2017). Informationssuche im Mathematikunterricht der Grundschule. MNU Heft 3, 13–15.

Google Scholar

Laplace, P. S. (1814). Théorie analytique des probabilités. Amazon: Facsimile Version.

Lindley, D. V. (1956). On a Measure of the Information provided by an Experiment. Ann. Math. Statist. 27 (4), 986–1005. doi:10.1214/aoms/1177728069

CrossRef Full Text | Google Scholar

Martignon, L., Deco, G., Laskey, K., Diamond, M., Freiwald, W., and Vaadia, E. (2000). Neural Coding: Higher-Order Temporal Patterns in the Neurostatistics of Cell. Assemblies. Neural Comput. 12, 2621–2653. doi:10.1162/089976600300014872

PubMed Abstract | CrossRef Full Text | Google Scholar

Martignon, L. (2015). “Information Theory,” in International Encyclopedia of the Social & Behavioral Sciences. Editor J. D. Wright 2nd edition (Oxford: Elsevier), Vol 12, 106–109. doi:10.1016/b978-0-08-097086-8.43047-3

CrossRef Full Text | Google Scholar

Martignon, L., and Krauss, S. (2009). Hands-on Activities for Fourth Graders: A Tool Box for Decision-Making and Reckoning with Risk. Int. Electron. J. Math. Edu. 4, 227–258.

Google Scholar

Meder, B., Nelson, J. D., Jones, M., and Ruggeri, A. (2019). Stepwise versus Globally Optimal Search in Children and Adults. Cognition 191, 103965. doi:10.1016/j.cognition.2019.05.002

PubMed Abstract | CrossRef Full Text | Google Scholar

Ministerium für KultusJugend und Sport (2016). Bildungsplan 2016. Gemeinsamer Bildungsplan der Sekundarstufe I. Avabilable at: http://www.bildungsplaene-bw.de/site/bildungsplan/get/documents/lsbw/export-pdf/depot-pdf/ALLG/BP2016BW_ALLG_SEK1_INF7.pdf (Accessed 04.05.2020).

Google Scholar

Nelson, J. D., Divjak, B., Gudmundsdottir, G., Martignon, L. F., and Meder, B. (2014). Children's Sequential Information Search Is Sensitive to Environmental Probabilities. Cognition 130 (1), 74–80. doi:10.1016/j.cognition.2013.09.007

PubMed Abstract | CrossRef Full Text | Google Scholar

Nelson, J. D. (2005). Finding Useful Questions: On Bayesian Diagnosticity, Probability, Impact, and Information Gain. Psychol. Rev. 112 (4), 979–999. doi:10.1037/0033-295x.112.4.979

PubMed Abstract | CrossRef Full Text | Google Scholar

Özel, E. (2019). “Grundschüler spielen Mastermind: Förderung erster Intuitionen zur mathematischen Entropie,”. Masterthesis (Ludwigsburg: Pädagogische Hochschule Ludwigsburg).

Google Scholar

Platt, J. R. (1964). Strong Inference: Certain Systematic Methods of Scientific Thinking May Produce Much More Rapid Progress Than Others. Science 146, 347–353. doi:10.1126/science.146.3642.347

PubMed Abstract | CrossRef Full Text | Google Scholar

Pólya, G. (1973). “As I Read Them,” in Developments in mathematical Education (Cambridge University Press), 77–78. doi:10.1017/cbo9781139013536.003

CrossRef Full Text | Google Scholar

Prenzel, M.PISA Konsortium Deutschland (2004). PISA 2003. Münster: Waxman Deutschland.

Rényi, A. (1982). Tagebuch der Informationstheorie. Basel u.a.: Birkhäuser.

Schulz, E., Bertram, L., Hofer, M., and Nelson, J. D. (2019). “Exploring the Space of Human Exploration Using Entropy Mastermind,” in Proceedings of the 41st Annual Meeting of the Cognitive Science Society. doi:10.1101/540666

Google Scholar

Shannon, C. E., and Weaver, W. (1949). The Mathematical Theory of Communication. Chicago, Illinois: University of Illinois Press.