Selecting Mathematical Tasks for Assessing Student’s Understanding: Pre-Service Teachers’ Sensitivity to and Adaptive Use of Diagnostic Task Potential in Simulated Diagnostic One-To-One Interviews

Introduction

Teachers’ pedagogical decisions are contingent on reliable assessments of students’ understanding (Van de Pol et al., 2010). Recently, teachers’ competences with regard to diagnosing student understanding have attracted increasing research focus, (e.g. Herppich et al., 2018; Leuders et al., 2018). Previous research has established a relationship between teachers’ judgment accuracy and student learning (Behrmann and Souvignier, 2013). The paradigm of judgment accuracy conceptualizes diagnostic competences as the match between teachers’ expectations of individual students’ test performance and the students’ actual test performance (Südkamp et al., 2012). The judgment accuracy paradigm has often been criticized for only considering diagnosis in the form of an estimated test score and for not investigating the diagnostic process itself (Südkamp & Praetorius, 2017; Herppich et al., 2018). Extending the concept of judgment accuracy has triggered more comprehensive approaches toward diagnostic competences (Praetorius et al., 2012; Aufschnaiter et al., 2015), which include a wider understanding of what constitutes a diagnosis, as well as the diagnostic process itself. While the first extension led to the inclusion of students’ (mis-)conceptions, understanding, and strategies for diagnosing (Herppich et al., 2018), the second extension targets how teachers actually collect information to form their diagnostic judgement. The current study focuses on the second extension, specifically the diagnostic process.

Heitzmann et al., (2019) define diagnosing as the goal-directed accumulation and integration of information to reduce uncertainty when making educational decisions. Generating diagnostic information about students’ understanding requires some form of teacher-student interaction (Klug et al., 2013), which may take place in very different situations (Karst et al., 2017). Diagnostic interviews with individual students about specific mathematical concepts have been highlighted as a prototypical example of such situations, (e.g. Wollring, 2004). While teachers may also diagnose “on the fly” during whole-group classroom discussions, or while supporting individual or small-group work, these situations allow for the detailed study of diagnostic processes and their disentanglement from subsequent pedagogical decisions (Kaiser et al., 2017).

Diagnosing requires that teachers have diagnostic competences, which are conceptualized as individual, cognitive, and context-sensitive dispositions (Koeppen et al., 2008; Ufer & Neumann, 2018) that become observable through the accuracy of the diagnostic processes and the subsequent diagnoses. Diagnostic competences, in this sense, enable “[…] people to apply their knowledge in diagnostic activities according to professional standards to collect and interpret data in order to make high-quality decisions” (Heitzmann et al., 2019). Tröbst et al., (2018) emphasize the importance of teachers’ professional knowledge to diagnostic competence. The lack of tools to investigate, measure, and foster (pre-service) teachers’ diagnostic competences (Südkamp et al., 2008; Praetorius et al., 2012) highlights the importance of simulations, which provide an authentic environment to investigate diagnostic competences under controlled conditions, as well as the possibility of improving participants’ skills based on the generated findings. Klug et al., (2013) point out that teachers mainly assess their students during face-to-face interaction in the classroom. Reconstructing such situations in simulations is discussed as a promising approach to apply newly learned knowledge in authentic situations, especially in the context of pre-service teacher education (Grossman et al., 2009).

As mentioned, prior works emphasize the need to understand the diagnostic process as the link between individual dispositions, such as professional knowledge, and the quality of diagnostic judgements and subsequent decisions (Heitzmann et al., 2019). This process includes diverse activities, such as the elicitation of diagnostic information from students, the observation and interpretation of the resulting student answers, and the integration of these interpretations into a diagnostic judgement that facilitates valid pedagogical decision making (Herppich et al., 2018; Heitzmann et al., 2019; Loibl et al., 2020). In this contribution, we focus on how teachers use tasks to elicit diagnostic information. We propose two constructs characterizing promising task selection during the diagnostic process: sensitivity to the diagnostic potential of tasks and adaptive use of diagnostic task potential. We introduce operationalizations of these constructs in an authentic diagnostic simulation and analyze the kinds of professional knowledge that underlie these aspects of task selection.

Process Models of Teachers’ Diagnoses

Existing models of the diagnostic process usually try to cover a wide range of diagnostic situations, for example, ranging from formal to informal assessment or from formative to summative assessment, or assessment based on verbal interaction vs. written documents (Philipp, 2018). The field has moved from generic models, for example, Klug, et al (2013) model, which closely resembles general self-regulation models, to more specific models that describe how diagnostic information is gathered and processed. For example, the NeDiKo model (Herppich et al., 2018) describes diagnostic processes in teachers’ professional practice as a sequence of prototypical decisions and subsequent diagnostic actions. It particularly focuses on accumulating diagnostic information by generating hypotheses and testing them with data collected from students. Similarly, the COSIMA model (Heitzmann et al., 2019) describes this process as an orchestration of eight diagnostic activities, including generating hypotheses, generating diagnostic evidence, evaluating diagnostic evidence, and drawing conclusions from this evidence. In contrast, the DiaKom model (Loibl et al., 2020) explicitly distinguishes observable situation characteristics from latent person characteristics and cognitive processes, and conceptualizes cognitive processes along the PID model (Blömeke et al., 2015) as perceiving features from a situation, interpreting them against professional knowledge, and making pedagogical decisions.

Except for the DiaKom model (which does not explicitly include observable actions), each model describes teacher actions that are intended to elicit diagnostically relevant information from students (evidence generation in the COSIMA model). The models are open to a wide range of possible evidence generation methods, such as administering a standardized test, making informal observations during class, and analyzing students’ work on exams or homework. In most of these cases, eliciting diagnostically relevant information involves assigning a student some kind of task (orally or in written form) and interpreting the student’s answers or responses. Studies based on the DiaKom model, (e.g. Ostermann et al., 2018) usually do not include such explicit evidence generation actions by teachers; rather, they provide participants with prepared diagnostic information. However, diagnosis in professional practice will, to a large extent, be initiated and coordinated by the teacher. Thus, it is a vital question how and based on what knowledge teachers select tasks to elicit and accumulate diagnostically relevant information about students’ understanding of particular concepts.

The Role of Professional Knowledge in Diagnosing

As described, professional knowledge is assumed to be a central individual resource underlying diagnostic competences, and is indeed part of most models of diagnostic competences. In the COSIMA model, it is listed as one of the central resources (Heitzmann et al., 2019); in the NeDiKo model (Herppich et al., 2018), it is subsumed under “dispositions”; and in the DiaKom model (Loibl et al., 2020), it is part of teachers’ person characteristics. In all of these models, the influence of teachers’ professional knowledge on their diagnoses, judgments, and decisions is mediated by the characteristics of the diagnostic process. Accordingly, how teachers apply their professional knowledge during a diagnostic situation is assumed to be the main link between their individual knowledge and the final diagnosis (cf. Blömeke et al., 2015).

While different conceptualizations of professional knowledge by knowledge type or content can be adopted (Förtsch et al., 2018), the categorization of Schulman (1987) is central in the context of teacher education. He proposes structuring teachers’ professional knowledge (among others) into content knowledge (CK), pedagogical content knowledge (PCK), and pedagogical knowledge (PK). CK describes knowledge about the subject matter, which, in our case, is mathematics. In a manner similar to the mathematical knowledge for teaching (MKT) measures (Ball et al., 2008) many studies have conceptualized CK as sound knowledge of school mathematics and its background (COACTIV: Baumert & Kunter 2013; TEDS-M: Blömeke et al., 2011; KiL: Kleickmann et al., 2014). PCK is necessary specifically for teaching a specific subject and usually consists of knowledge about student cognition, knowledge about instructional and diagnostic tasks, and knowledge about instructional approaches and strategies (Baumert and Kunter, 2013). PK refers to knowledge about teaching and learning in general, with no connection to a specific subject (Kleickmann et al., 2014).

Südkamp et al., (2012) indicates that CK and PCK do have an influence on teachers’ judgment accuracy. Beyond this, several studies have shown that components of teachers’ professional knowledge predict their diagnostic competence. For example, Van den Kieboom et al., (2013) investigated pre-service teachers’ questioning during one-to-one diagnostic interviews. They found that participants with low CK only affirmed students’ responses, without asking any probing questions. Participants with higher CK asked probing questions to investigate students’ understanding and try to help improve it.

Ostermann et al., (2018) investigated the influence of PCK on pre-service teachers’ estimates of task difficulty in an intervention study. Participants who received PCK instruction produced more accurate estimates of task difficulty than participants from a control group. However, Herppich et al., (2018) point out that previous research findings do not allow for final conclusions to be drawn about the relationship between a person’s professional knowledge and the given diagnosis.

Prior research is less clear about the role and interplay of the three components of professional knowledge and how these knowledge components are used in the diagnostic process. Herppich et al., (2018), for example, subsume all three components into teachers’ assessment competences but do not describe their specific roles. Tröbst et al., (2018) point out that it is not yet known how the different components of professional knowledge interact in the diagnostic process. Against this background, empirical evidence about the relationship between the components of teachers’ professional knowledge and the well-described characteristics of the diagnostic process is needed. To achieve this, we propose to study task selection as an important part of the diagnostic process, and analyze its connection to teachers’ professional knowledge.

Task Selection in the Diagnostic Process

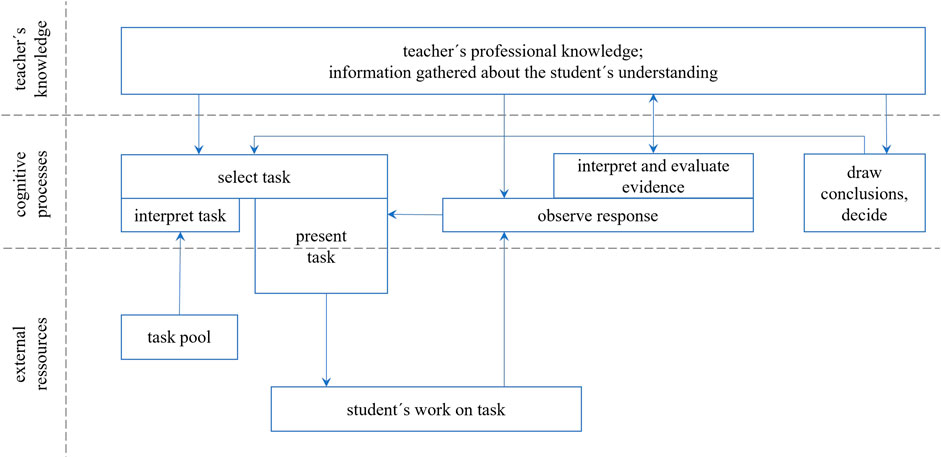
Neubrand et al., (2011) highlight the important role of tasks in mathematics instruction (Bromme, 1981) and further work has connected the quality of tasks (Baumert et al., 2010) and their implementation (Stein et al., 2008) with student learning. Black and Wiliam (2009) stress the use of learning tasks to elicit evidence of student understanding as a key strategy of formative assessment. Indeed, mathematical tasks not only play a role as learning opportunities for students, teachers also draw evidence about students’ mathematical understanding from their responses to tasks (Schack et al., 2013). How teachers select and use tasks for diagnostic purposes, however, has attracted little attention in past research. To frame our approach to filling this gap, we propose a process model of task-based diagnostic processes (Figure 1).

FIGURE 1

FIGURE 1. Model of task-based diagnostic processes.

The core of the model consists of a set of latent cognitive processes (the middle portion), that draw on teachers’ knowledge (the upper portion), as well as on external information and resources and visible actions (the lower portion). The arrows in the model indicate the flow of information between the (partially parallel) sub-processes and the other parts of the model. Regarding teachers’ knowledge, we differentiate professional knowledge, including CK, PCK, and PK as well as temporary information about a specific student’s mathematical understanding. This differentiation reflects claims from the literature that teachers’ professional knowledge is, at least to some degree, situation-specific, (e.g. Lin and Rowland, 2016). Diagnosing draws on professional knowledge and aims to accumulate information about students’ understanding. We assume an orchestration of three central cognitive processes to achieve this:

1) Drawing conclusions and deciding: Based on the available knowledge and accumulated information about the student’s understanding, this process continuously monitors whether sufficient information is available to draw certain conclusions and make reliable decisions. It has a regulatory function, as missing information (to make a decision or judgment) influences the second process, task selection.

2) Task selection relies on the teacher’s interpretation of the available tasks (as tools for evidence generation). Based on the accumulated information and evaluation in the previous process, it is vital to select tasks that will most likely add new evidence to the accumulated information. This process is strongly connected to the actual (observable) presentation of the task to the student, which usually triggers the student to show some kind of observable work on the task. Task presentation also includes asking follow-up questions based on student responses.

3) The third process is initially responsible for observing and attending to the student’s work. Since perception is a knowledge-based and knowledge-driven process, it draws on professional knowledge and accumulated information (Sherin and Star, 2011). Based on this observation, another sub-process is responsible for interpreting and evaluating the evidence, for example, weighing more or less reliable parts of the observed evidence or integrating them into the accumulated information about the student’s understanding.

Based on this perspective of task-based diagnosis, the selection of tasks becomes a crucial element of the diagnostic process. It has long been discussed that mathematical tasks can vary substantially regarding how much diagnostic information they can potentially unveil regarding, for example, a specific concept (Maier et al., 2010). A task that can be solved correctly with superficial strategies or even without understanding the concept has low potential to generate evidence about knowledge of this specific concept. For an example, the task of comparing the decimal fractions 0.417 and 0.3 has a low diagnostic potential regarding knowledge about decimal fractions, because even a student using superficial methods, (e.g. identifying 0.417 as the larger decimal fraction because 417 is larger than 3) could solve that task correctly. Without asking the student for further explanations, a teacher would not be able to generate reliable evidence as to whether the student can compare decimal fractions based on a proper understanding of place value principles. In the literature, the term “diagnostic potential of tasks” has been used, without an exact definition, to describe this dimension, and knowledge about the diagnostic potential of tasks has been repeatedly mentioned as part of mathematics teachers’ professional knowledge, (e.g. Moyer-Packenham & Milewicz, 2002; Maier et al., 2010; Baumert & Kunter, 2013). We define the diagnostic potential of a task as its ability to stimulate student responses, allowing for the generation of reliable evidence about students’ mathematical understanding. Asking a student to compare 0.354 to 0.55, for example, would have higher diagnostic potential than comparing 0.417 and 0.3 because the former task can only can be solved correctly when the student is capable of applying the underlying concept by comparing the values in each section. All known (systematic) superficial strategies of decimal comparison lead to incorrect decisions in this case.

The diagnostic potential of a mathematical task is primarily determined by the more or less elaborate mathematical strategies that can be used to solve the task. If only those strategies observed in typical student responses, which reflect at least some understanding of the underlying concepts, lead to a correct answer, this indicates high diagnostic potential. If the task can be solved correctly using one of the typically observed superficial strategies, which are not based on a reliable understanding of the underlying concepts, (e.g. treating the integer and the decimal part of the decimal number separately as if they were whole numbers), this implies low task potential.

In summary, we assume that the selection of tasks is an important part of diagnostic processes. It is reasonable to assume that task selection is not only influenced by teachers’ knowledge and cognition, as well as the characteristics of the available tasks, but also by the characteristics of the student. In view of this, we propose to distinguish between two facets of teachers’ selection of tasks during diagnosis: sensitivity to and adaptive use of diagnostic task potential.

Assuming that task selection is driven by information about the task and information about the student, we propose these two different facets of task selection. Sensitivity to the diagnostic task potential corresponds to the sub-processes “interpret task” and “select task”. It becomes visible in the diagnostic potential of the tasks presented during the interview and relies on the characteristics of the task. Adaptive use of the diagnostic task potential corresponds to the arrow from “draw conclusions, decide” to “select task”. It becomes visible in the extent to which a selected task can contribute new information about the student’s understanding, beyond what has been collected before/could have been collected based on prior observations. This facet thus relies on task and student characteristics.

Sensitivity to Diagnostic Task Potential

We conceptualize sensitivity to the diagnostic potential of tasks as a facet of diagnostic competence that is observable in the diagnostic processes. Being sensitive to the diagnostic potential of tasks means considering a task’s diagnostic potential to be an important factor during task selection. Participants’ sensitivity to the diagnostic potential of tasks would be reflected in a higher probability of selecting tasks with high potential in comparison to tasks with low potential.

In line with existing models and first evidence on the role of professional knowledge in diagnosis, we assume that sensitivity to diagnostic task potential is related to teachers’ professional knowledge (Baumert & Kunter, 2013). However, it is an open question as to which component of professional knowledge specifically underlies sensitivity to the diagnostic potential of tasks. Being able to select tasks with high potential requires that teachers be aware of and attend to relevant task characteristics in order to rate their diagnostic potential (e.g., Loibl et al., 2020). Baumert and Kunter (2013) conceptualize knowledge about the diagnostic potential of tasks as a part of PCK. However, other components may also play a role. For example, CK could be needed to identify the range of mathematical strategies that can be used to solve a task. PK might contribute to regulating the diagnostic process and, more specifically, to coordinating task selection in a superordinate manner.

Adaptive Use of Diagnostic Task Potential

A high level of importance may be attributed to selecting tasks with high diagnostic potential at the start of a diagnostic process when little or unreliable information about a student is available. However, once initial information has been gathered, this accumulated knowledge about learning characteristics should guide efficient diagnostic processes. Choosing an optimal task from a set of alternatives for a specific situation has been described under the term “adaptivity” in the past (Heinze & Verschaffel, 2009). We consider task selection adaptive (regarding the use of diagnostic potential) if the selected task can contribute evidence about facets of students’ understanding beyond what was inferred from prior observations. In this sense, if the selection of a specific task is adaptive, it does not only depend on the characteristics of the task itself, but also on existing information about the specific student. Selecting tasks adaptively requires teachers to take accumulated information about student’s mathematical understanding into account.

Adaptivity to the use of diagnostic task potential may lead to a different task selection than sensitivity to diagnostic potential alone. A task with low general diagnostic potential might offer additional information, as it may help to exclude a specific misconception that has not yet been considered. In contrast, a task with high general diagnostic potential might not offer additional information if it is redundant to what was visible in the tasks before. However, selecting tasks with high diagnostic potential (sensitivity) at the beginning of a diagnostic process might support the adaptive selection of diagnostic tasks later in the process, since more reliable information about students’ understanding is available.

Deciding, whether the selection of a specific task is adaptive in a specific diagnostic situation might be almost impossible for an external observer, since neither the “real” understanding of a real student nor the information accumulated by the teacher on this student is observable. To allow for an empirical investigation, we thus propose an approximation to adaptivity. Task selection is adaptive, if a selected task can, in principle, deliver additional information about the student that goes beyond what could possibly have been observed in preceding tasks.

Regarding the role of components of teachers’ professional knowledge for adaptivity regarding the use of diagnostic task potential, similar arguments can be made for sensitivity to diagnostic task potential. Adaptivity, however, puts a bigger demand on teachers’ representation of the current information about students’ understanding than just being sensitive to the diagnostic task potential. We can assume that stronger PCK, for example, about student cognition, may support teachers in organizing, retaining, and utilizing this information. Even though this argument may specifically explain the connection between PCK and adaptivity, relationships with CK and PK may be expected based on our theoretical conceptualization.

The Current Study

Although the concept is frequently mentioned in the literature on teachers’ professional knowledge and competences (Baumert & Kunter, 2013), it is not yet known how beginning and experienced teachers deal with the diagnostic potential of tasks when diagnosing students’ understanding. In particular, no reliable evidence pertaining to teachers’ actions in realistic situations is available. In the context of teacher education, it is crucial to understand how teachers can apply the knowledge, they acquired in university courses, to real-life situations. In this study, we investigate pre-service teachers’ task-selection in authentic role-play simulations of diagnostic one-to-one interviews about decimal fractions. Each participant took part in two simulation sessions. In each session, a trained actor played one out of four pre-defined student case profiles. Each simulation consisted of two phases: an initial phase in which teachers could select from a restricted set of screening tasks and a second phase in which a larger set of diagnostic tasks was additionally available. Overall, the simulation-based approach allows for the control of factors related to the student whose understanding is being diagnosed, and thus provides a reliable measurement.

The main goal of this study is to introduce the constructs of sensitivity to the diagnostic potential of tasks and the adaptive use of this potential, and provide initial results pertaining to these characteristics of the diagnostic process for pre-service teachers. Moreover, we investigate whether there are systematic inter-individual differences in these process characteristics and how they relate to components of pre-service teachers’ professional knowledge. To this end, the study focuses on the questions delineated in Sections Sensitive use of diagnostic task potential and Adaptive use of diagnostic task potential.

Sensitive Use of Diagnostic Task Potential

Our first goal was to obtain insights into whether pre-service teachers’ task selection is sensitive to the varying diagnostic potential of tasks.

RQ1.1 To what extent are pre-service teachers sensitive to the diagnostic potential of tasks? Is there systematic variation in pre-service teachers’ sensitivity to diagnostic potential?

Based on the fact that participants in our study had already participated in a lecture and tutorials on mathematics education in the area of numbers and operations (including decimal fractions), we expected that they would show some sensitivity to diagnostic potential, that is participants choose tasks with high diagnostic potential with a higher probability than tasks with low diagnostic potential. We controlled for the interview position (first vs. second simulation), but expected small differences, at most, between the two interviews. Moreover, we predicted no significant differences in pre-service teachers’ sensitivity over the four different student case profiles, but we expected systematic inter-individual variation between the participants in their tendency to prefer high-potential over low-potential tasks.

RQ1.2 To which extent is pre-service teachers’ sensitivity to the diagnostic potential of tasks related to different components of their professional knowledge (CK, PCK, PK)?

Based on the discussion emerging from prior research, we assumed that sensitivity to diagnostic potential would primarily be linked to the participants’ PCK. Thus, we expected that higher PCK would go along with higher odds of choosing high potential tasks (over low-potential tasks).

Adaptive Use of Diagnostic Task Potential

Second, adaptive use of diagnostic task potential was investigated. To study adaptive use, only the second phase of each interview was considered. Based on the prior definition, task selection was considered adaptive if the selected task could provide additional evidence about a student’s understanding beyond what could be observed in the initial (screening) phase of the interview; that is, the task has the diagnostic potential to yield information beyond what had already been gathered.

RQ2.1 To which extent is pre-service teachers’ task selection adaptive to evidence generated from prior tasks? Is there systematic variation in pre-service teachers’ adaptive use of diagnostic task potential?

Even though adaptive use of the diagnostic potential of tasks can be considered a more complex demand than sensitivity to this potential, we expected pre-service teachers to show a higher probability of making task selections coded as adaptive beforehand compared with those coded as non-adaptive. Again, we expected only small differences across the two interview positions (first vs. second interview) and the four student case profiles. Regarding systematic variation in pre-service teachers’ adaptive use of diagnostic task potential, we had no initial hypothesis, as research results on teachers’ adaptivity are scarce, and we were not able to find relevant results in prior empirical mathematics education research.

RQ2.2 To which extent is pre-service teachers’ adaptivity in the use of diagnostic task potential related to different components of their professional knowledge (CK, PCK, PK)?

Following the assumption of sensitivity to diagnostic task potential, we assumed that the adaptive use of diagnostic task potential would also be related to the participants’ PCK. Thus, we expected that higher PCK would go along with higher odds of making adaptive (vs. non-adaptive) task selections.

Methods

To investigate these questions, we used data from simulated diagnostic one-to-one interviews about decimal fractions. In these role-play simulations, pre-service teachers engaged in diagnostic interviews with one of the four types of simulated students. The simulated students were played by teaching assistants who had been trained to enact the four different student case profiles. Each participant worked on the simulation twice, each time with a different student case profile.

Participants

The simulation was embedded in regular courses in pre-service teacher education at a large university in Germany. Every course participant was asked to perform the simulation. Participation in the study, including the provision of data for analysis, was voluntary and based on explicit consent. Performance during the simulation had no influence on course grades. Participation in the study was remunerated. The ethics committee and the data protection officer approved the study in advance.

The sample consisted of 65 pre-service high school teachers (38 f, 26 m, 1 day; M_age$=23.9$, $SD=5.7$). Most participants were in their fifth or lower semester. Almost all participants had finished at least four university courses focusing on mathematics education in previous semesters. Based on these degree programs’ curricula, almost every participant should have completed one course focusing on the topic of decimal fractions before participating in the study. Two thirds of the participants reported, that they had taken at least one course specifically covering PCK on decimal fractions. Most participants had at least some experience teaching students from their practical studies; on average, they had held 9.15 lessons on their own ($SD=6.41$). They had 2.0 years of experience in private tutoring, on average ($SD=1.57$).

Procedure

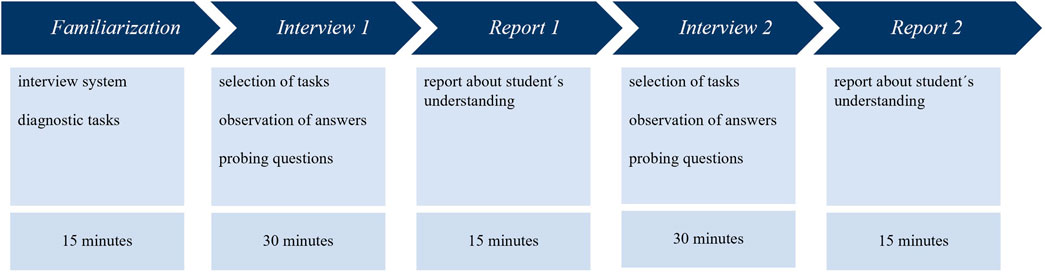
Each participant took part in one half-day session. The simulation was held in a face-to-face setting, supported by a web-based interview system that guided the participants through the simulation.

After a short introduction explaining the goals and procedures of the sessions, the participants had 15 min to acquaint themselves with the interview system and the diagnostic tasks embedded in the system. They then met a trained teaching assistant who played the role of the simulated student. The participants had up to 30 min to select diagnostic tasks and pose them to the simulated student. The simulated student answered according to the applicable student case profile; responses were provided verbally or in writing. After the participants completed the interview, they had 15 min to compose a report containing their diagnosis of the student’s understanding. Since the main focus of this contribution is the diagnostic process, the report phase will not be considered further. After the report on the first interview had been completed, the second interview started, following the same procedure as the first one (Figure 2).

FIGURE 2

FIGURE 2. Procedure of the simulation sessions.

After the participants had completed the two simulations, they were given a paper-and-pencil test (duration: 60 min) to assess their professional knowledge.

Design of the Role-Play-Based Live Simulation

The role-play-based live simulations were developed to investigate pre-service teachers’ diagnostic competences (Marczynski et al., in press). These role-plays simulate a diagnostic interview between a mathematics teacher and a sixth-grade student. All the participants had an opportunity to play the teacher’s role in the simulations. The implementation and design of the simulation received positive ratings from experts in a validation study (Stürmer et al., in press).

Based on prior research in mathematics education, the topic of decimal fractions was selected as the interview content because there is a substantial amount of research on students’ understanding and misconceptions in this field (Steinle, 2004; Heckmann, 2006; Padberg & Wartha, 2017). To structure the interview, we distinguished the three central fields of knowledge about decimal fractions:

(1) Number representation in the decimal place value system, including comparison of decimals

(2) Basic arithmetic operations of addition, subtraction, multiplication, and division, including flexible and adaptive use of calculation strategies for the four basic arithmetic operations

(3) Connections between arithmetic operations and their meaning in realistic situations and word problems

Based on this framework, four student case profiles were constructed. These represented different profiles of sound understanding and misconceptions over these three fields of knowledge. Each student case profile has strong misconceptions in one of the three fields, partial misconceptions in a second field, and quite sound understanding in the remaining field.

To pre-structure the diagnostic interview, participants were given a set of 16 clusters of diagnostic tasks. The first three task clusters, with ten tasks in total, were designed as initial tasks, focusing on different aspects of knowledge about decimal fractions. The 13 subsequent task clusters, with 35 tasks in total, were designed to provide additional information based on what could have been observed in the initial tasks. The interview itself was separated into two phases. In the first phase of the interview, only the initial tasks were available to the participants. The subsequent tasks were unlocked after at least one task from each of the three initial task clusters was selected. There were no limitations on the number of selected tasks. Additionally, participants were allowed to create their own tasks using blank task templates, but this opportunity was used only rarely (in 11 out of 130 simulations).

Familiarization Phase

Before the one-to-one interviews started, the participants were introduced to their assignment during the simulation. They were asked to imagine being in the position of a high school teacher who offers consultation meetings for students struggling with mathematics learning. In these meetings, they should try to get an impression of the student’s competences and misconceptions, in this case with regard to decimal fractions, by using a set of diagnostic tasks. They were informed that after the interview, they would be asked to write a report to the simulated student’s teacher containing a post-interview diagnosis. Before the first simulated student joined the setting, participants had 15 min to acquaint themselves with the interview system and the diagnostic tasks that they could use to conduct the diagnostic interview. They were instructed to analyze the tasks with respect to their usefulness for generating evidence about students’ mathematical understanding. The interview system offered a list of all available task clusters. Clicking on a cluster displayed a description and a list of the respective tasks. The participants were asked to make notes in the interview system during familiarization, and these notes were displayed during the interviews whenever the corresponding task was selected.

Interview Phase

After the familiarization phase, the simulated student joined the setting, and the first interview started. To diagnose the student’s mathematical understanding, participants could select from the provided tasks. Clicking on a task cluster displayed a list similar to the one that appeared on participants’ screen during familiarization together with the notes from the familiarization. The task itself was displayed on another screen, and the simulated student started to solve the task and write down the solution. The participants observed the student’s response and asked for further explanations if needed. The participants could also make notes during the interview. As described above, only the first three clusters with the initial tasks were displayed at the beginning of the interview. Participants were instructed that they should choose at least one task from each of the three clusters and to use up to half of the interview for this first phase. After they had gathered enough information about the student’s understanding or when the time limit was exceeded, they were moved on to the report phase.

Actor Training

The teaching assistants playing the students received standardized training spanning three half-day meetings. In the first meeting, they received theoretical background information about the content and aim of the study as well as their assignments during the simulations. For each of the four student case profiles, they received a detailed handout with background information about the relevant student’s mathematical understanding and a handout with the student’s handwritten solutions and verbal explanations for each task. The assistants were asked to familiarize themselves with the different student case profiles before the second meeting. In the second meeting, questions regarding the student case profiles were discussed, followed by a practical phase in which they were acquainted with the interview system. Subsequently, they worked on two simulations, once playing the student’s role and once playing the teacher’s role. Questions were discussed at the end of the meeting. In the final session, the assistants’ command of each student case profile was tested in single standardized interviews.

Structure of the Dataset and Analytic Approach

The data in this study have a three-level structure. On the person level, the dataset contains participants’ professional knowledge scores (person-parameters). Since each person worked on two simulations, data on the simulation level are nested within persons. At this level, the dataset contains the position of the simulation (first vs. second simulation) and which of the four student case profiles was used in the simulation. Finally, during each simulation, participants could decide whether to select each of the tasks from the diagnostic interview. These selections are nested in the simulations. The log files we extracted from the web-based interview system indicate whether a specific task was selected (or not) in a particular simulated interview.

Furthermore, we included two more variables, diagnostic potential and adaptivity, on the selection level. These were based on a priori coding of the tasks. Adaptivity was coded for each combination of task and student case profile. Diagnostic potential describes whether a task has high or low diagnostic potential and whether selecting a specific task in a specific simulation reflects sensitivity to diagnostic potential. Adaptivity describes whether selecting the task was considered to be an adaptive choice for the corresponding student case profile (only for tasks from the second phase of the interview). Sections Coding of diagnostic potential (sensitivity) and Coding of adaptivity of task selection for each student case profile provide a more detailed explanation of how sensitivity and adaptivity were coded.

We analyzed the data on the level of individual task selections, taking its nested structure into account. To achieve this, we estimated generalized linear mixed models (Bates et al., 2014) to predict the probability that a specific participant would select a specific task in a specific interview. The interview position (first vs. second interview) and its interaction with the other fixed factors were included in all models.

To investigate participants’ sensitivity to diagnostic task potential (RQ1.1, RQ1.2), we included the tasks’ diagnostic potential (low vs. high) as a fixed factor. The generalized linear mixed model (GLMM) estimators for this effect describe the logarithmized odds ratio for selecting a high-potential task vs. selecting a low-potential task.

To investigate the relationship between sensitivity and participants’ professional knowledge (RQ1.2), professional knowledge scores and their interaction effect with the diagnostic potential factor were additionally included as fixed effects. The GLMM estimate of the interaction term between diagnostic potential and professional knowledge scores describes how much the logarithmized odds ratio to select a high-potential task (compared to a low potential-task) changes if professional knowledge scores increase by one standard deviation.

For the questions about participants’ adaptive use of diagnostic potential (RQ2.1, RQ2.2), only task selections from the second phase were considered. We assumed that adaptivity builds on insights that could have been generated in prior observations during the first phase of the interview. In the corresponding GLMM, the adaptivity of task selection (non-adaptive vs. adaptive) was included as a fixed factor. The estimate corresponding to this factor describes the logarithmized odds ratio for making an adaptive vs. non-adaptive task selection.

The relationship with participants’ professional knowledge (RQ2.2) was again analyzed by including the professional knowledge scores and their interaction effect with the adaptivity.

Regarding the models’ random effects structure, random intercepts were included to account for differences between individual participants, the four student case profiles, and the different tasks. To investigate whether sensitivity to diagnostic potential or adaptive use of diagnostic potential varied systematically between persons (RQ1.1, RQ2.1), random slopes of diagnostic potential resp. adaptivity varying over individual participants were included. If the model with this random slope showed a better fit to the data than a model without it, this indicates that participants do indeed systematically vary in their preference for high-potential tasks over low-potential tasks (resp. in the adaptive use of task potential). Since participants’ sensitivity and adaptivity might depend on the student case profile, we also analyzed random slopes of diagnostic potential resp. adaptivity varying over student case profiles. Random slopes were removed from the models before the main analysis if they did not contribute significantly to model fit. Random effects with zero variance estimators were also removed from the models.

Model comparisons were performed with chi-square difference tests. Fixed effects were analyzed with Type-III Wald chi-square tests. Statistical analyses were computed using R and the package lme4 (Bates et al., 2014).¹

Instruments

Coding of Diagnostic Potential (Sensitivity)

To assess the participants’ sensitivity to the diagnostic potential of tasks, each task was coded as having low or high potential. The coding was performed by experienced mathematics education researchers, based on research on students’ understanding of decimal fractions, (e.g. Steinle, 2004). Within task clusters, the coding of potential also relied on the comparison of the tasks included in this specific cluster, with distinctions as to whether there was another task with a higher suitability for diagnosing competences or misconceptions in the field of decimal fractions. Two independent coders rated all the tasks. Discrepancies were resolved through discussion among the two coders and a third member of the research group. Four of the ten initial tasks and 16 of the 35 subsequent tasks were coded with high potential. The order of tasks was not linked to task potential.

Coding of Adaptivity of Task Selection for Each Student Case Profile

All tasks of the second phase of the interview were additionally coded as adaptive or non-adaptive independently for each student case profile. The concept of adaptivity takes into account whether a single task is appropriate for delivering further information. Consequently, the coding of adaptivity varies according to the different student case profiles. The coding of adaptivity was independent of the coding of sensitivity, but the method for coding adaptivity considered the indicated diagnostic possibility of a single task. This general suitability was then valued as to whether it could generate additional evidence based on what could have been observed in the screening tasks.

Adaptivity coding was performed by the same two coders independently from one another and separately for each student case profile. As previously mentioned, discrepancies were addressed through discussions among the two coders and a third member of the research group. From the 35 subsequent tasks, 16 were coded as adaptive for Student Case Profile 1 and 4, 12 for Student Case Profile 2, and 20 for Student Case Profile 3. The order of tasks was not linked to adaptivity coding.

Professional Knowledge

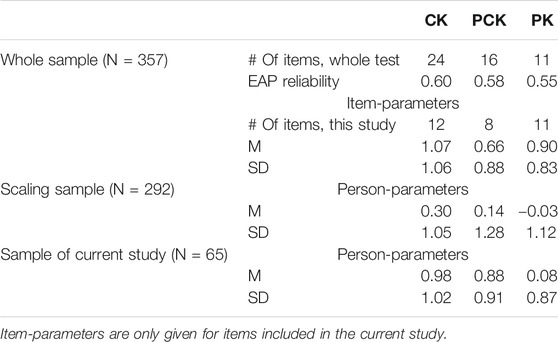
Participants’ professional knowledge was measured following the categorization of Schulman (1987). Twelve items were used for CK. The scale assessed mathematical knowledge of decimal fractions on a level that required substantial reflection on school mathematics. For example, participants had to justify (without using the usual calculation rules for decimal fractions), that 0.3 × 0.4 = 0.12 (Supplementary Figure S1 in the Supplementary Material). PCK was measured with eight items, focusing on the teaching and learning of decimal fractions. For example, participants were asked to describe a typical incorrect solution strategy for the division problem 4.8 : 2.2 = … (Supplementary Figure S2 in the supplementary material). For the CK and PCK items, single choice, multiple choice, and open-ended items were used. The scale for PK was adopted from the KiL project (Kleickmann et al., 2014). As this study focuses on diagnostic competences, only the items covering diagnostic-related knowledge were used. This amounts to 11 items pertaining to knowledge about assessment from a psychological point of view, for example, general judgment errors. All PK items had a multiple choice format.

Data from all the tests were made available for the participants of our study and an additional scaling sample of 292 pre-service mathematics high school teachers studying at the same university. For CK and PCK, the scaling sample covered a larger pool of items (24 CK items and 16 PCK items in total) in a multi-matrix design with four booklets. Individual knowledge scores² for each of the three components, as well as scaled characteristics, were calculated for both samples together (Table 1, for detailed information see Supplementary Table S1.1 in the supplementary material) using the one-dimensional one-parameter logistic Rasch model (Rasch, 1960); person-parameters are presented for each sample separately.

TABLE 1

TABLE 1. Item statistics.

Results

Descriptive Findings

On average, the participants’ first interview had a duration of 26.5 min ($SD=6.1$), and the second interview ended a bit earlier, on average, after 23.6 min ($SD=6.9$). The duration of the interviews did not differ remarkably across the different student case profiles. Participants, on average, selected 13.8 tasks for their first interview ($SD=5.7$) and 16.3 tasks ($SD=7.1$) for the second interview, with only small descriptive differences among the student case profiles. Even though the total duration of a single interview decreased from the first to the second interview, the number of selected tasks increased (Table 2).

TABLE 2

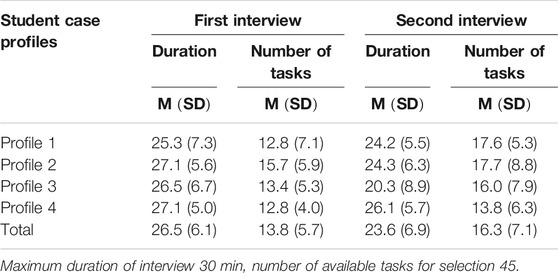
TABLE 2. Descriptive statistics for interviews: Mean values (M) and standard deviation (SD) of interview duration [in minutes] and number of selected tasks for each interview and student case profile.

An analysis of task selection across the different interview phases yielded almost no differences in the section of the initial tasks (Table 3). On average, participants selected 6.2 initial tasks for their first interview ($SD=1.5$) and 6.5 for their second interview ($SD=1.6$). From the 35 subsequent tasks, participants selected 7.6 tasks on average ($SD=5.3$) for the first interview and 9.8 tasks ($SD=6.6$) for the second interview. From first informal observations, we noticed that task selection in each task cluster seemed to be influenced by task order: participants often chose the first task in a task cluster first, followed by one or more subsequent tasks in the same task cluster.

TABLE 3

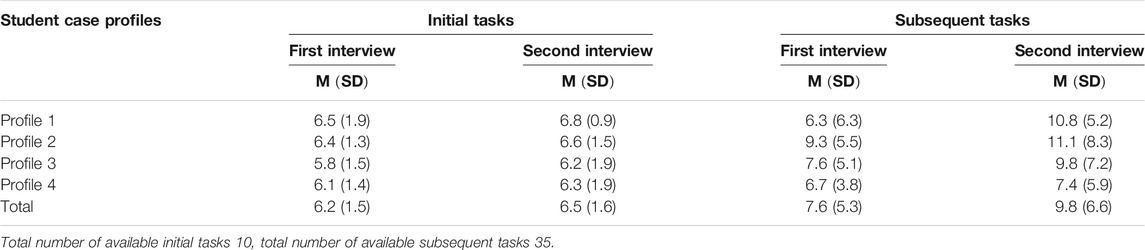
TABLE 3. Descriptive statistics for selection of tasks: Mean values (M) and standard deviation (SD) of number of selected tasks, differed by initial and subsequent tasks and student case profiles.

Sensitive Task Selection

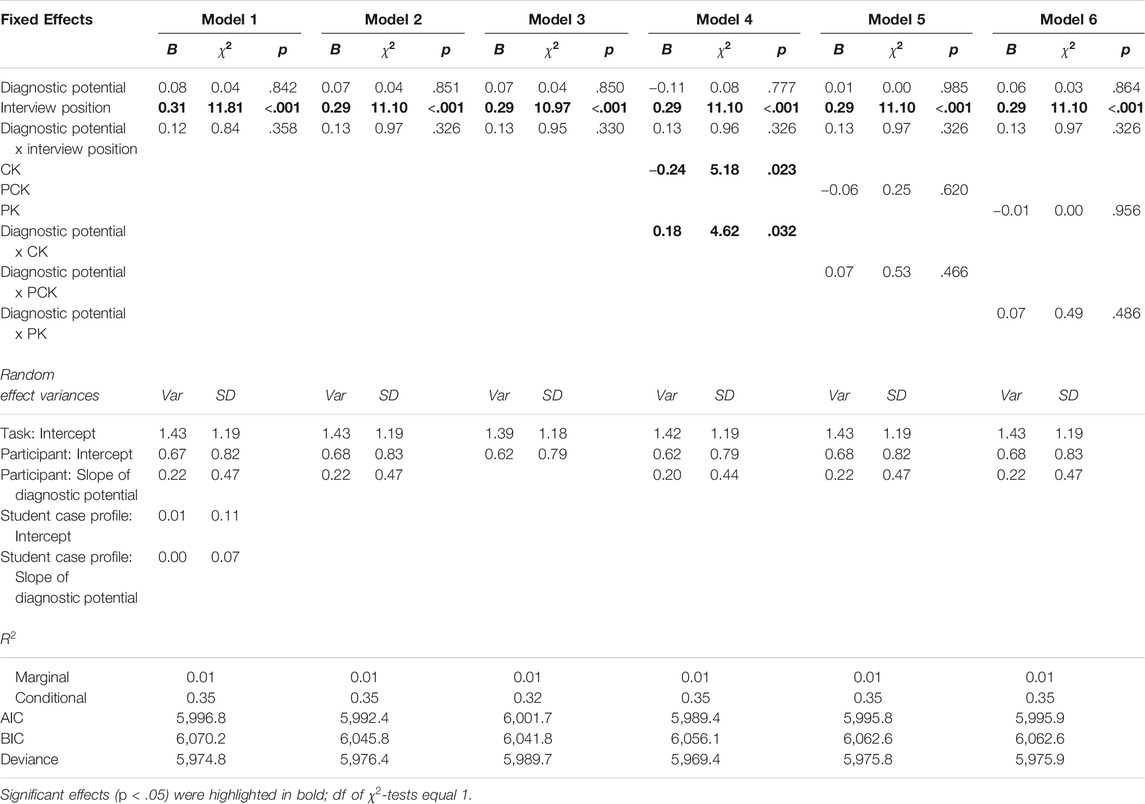
To investigate participants’ sensitivity to the diagnostic potential of tasks, we estimated GLMMs to predict selection (vs. non-selection) of a task based on its diagnostic potential (low vs. high), the interview position (first vs. second interview), and their interaction as fixed factors. In the initial model, we included random intercepts for each participant, each task, and each student case profile, as well as random slopes of the factor diagnostic potential varying over participants and student case profiles (Model 1, Table 4). Removing the random slope and intercept over student case profiles (Model 2) did not significantly affect model fit (${\chi }^2\left(3\right)=1.61; p=.658$). However, removing the random slope of diagnostic potential varying over participants (Model 3) would have significantly reduced model fit (${\chi }^2\left(2\right)=13.32; p=.001$), indicating that participants systematically varied in their tendency to prefer high-potential over low-potential tasks.

TABLE 4

TABLE 4. Different GLMM for analyzing the sensitivity to the diagnostic task potential.

Sensitivity to Diagnostic Potential (RQ1.1)

On average, participants selected 7.0 high-potential tasks ($SD=3.4$) and 8.0 low-potential tasks ($SD=3.9$). To study the overall sensitivity to diagnostic potential in the interviews, we analyzed the fixed effects in Model 2.

No significant effects of diagnostic potential (${\chi }^2\left(1\right)=0.04;p=.851$) occurred, indicating that the predicted probabilities for selecting a low- or a high-potential task did not differ significantly. The effect of interview position was significant (${\chi }^2\left(1\right)=11.10;p<.001$) indicating that during the second interview, the participants chose significantly more tasks than in the first interview. Finally, the interaction effect between diagnostic potential and interview position was not significant (${\chi }^2\left(1\right)=0.97;p=.326$), indicating that the selection of more tasks in the second interview was independent of the tasks’ diagnostic potential.

Professional Knowledge and Sensitivity to Diagnostic Potential (RQ1.2)

To investigate the role of professional knowledge in sensitivity to diagnostic potential, we included participants’ scores for each professional knowledge component (CK, PCK, PK) as well as interaction effects with diagnostic potential separately in Models 4 to 6.

For CK (Model 4), there was a significant main effect of the professional knowledge score (${\chi }^2\left(1\right)=5.18;p=.023$) and a significant interaction with diagnostic potential (${\chi }^2\left(1\right)=4.62;p=.032$). Trend analyses (Figure 3) showed that the selection of low-potential tasks was significantly negatively related to CK [B = −0.24, CI_95% (−0.45,−0.03)], while the selection of high-potential tasks was not significantly related to CK [B = −0.06, CI_95% (−0.28,0.16)]. The difference between the two (logistic) regression slopes was significant (B = 0.18, p = .030), indicating that when CK scores were one standard deviation higher, they were accompanied by approximately 19.3% higher odds of selecting a high-potential task, as opposed to a low-potential task (Figure 3).

For PCK (Model 5) and PK (Model 6), neither the main effects of the knowledge scores (PCK: χ²(1) = 0.25; p = .620; PK: χ²(1) = 0.00; p = .956) nor the corresponding interactions with diagnostic potential (PCK: χ²(1) = 0.53; p = .466; PK: χ²(1) = 0.49; p = .486) were significant.

FIGURE 3

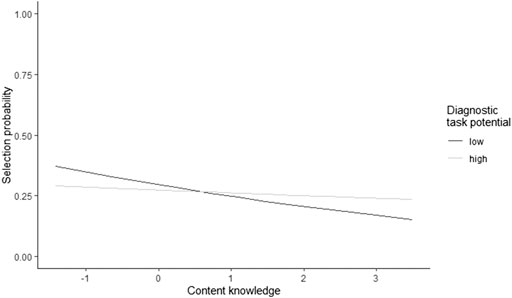
FIGURE 3. The relationship between CK and the selection probability of high-vs. low-potential tasks.

Adaptive Task Selection

In investigating the adaptive use of diagnostic task potential, only second-phase task selection was considered. In the second phase of the interview, participants had the opportunity to generate further evidence based on what they had observed during the first phase of the interview. The estimated GLMMs predict the selection (vs. non-selection) of a task based on its adaptivity to the related student case profile, the interview position (first vs. second interview), and their interaction as fixed factors. In the initial model, we included random intercepts for each participant, each task, and each student case profile, as well as random slopes of the factor adaptivity varying over participants and student case profiles (Model 1, Table 5). Removing the random slope and intercept over student case profiles (Model 2) did not significantly affect model fit (${\chi }^2\left(3\right)=2.36;p=.501$), as well as removing the random slope and intercept over participants (Model 3), indicating that participants did not systematically vary in their tendency to select tasks adaptively (${\chi }^2\left(2\right)=1.77;p=.413$).

TABLE 5

TABLE 5. Different GLMM for analyzing the adaptive use of diagnostic task potential.

Adaptive Use of Diagnostic Task Potential (RQ2.1)

To analyze the fixed effects in terms of the adaptive use of diagnostic task potential, Model 3 was investigated.

The effect of adaptivity was not significant (${\chi }^2\left(1\right)=0.06;p=\mathrm{.}811$), indicating that participants did not systematically take the characteristics of the student case profile into account when selecting tasks, at least not regarding adaptivity as operationalized above. The effect of the interview position was significant (${\chi }^2\left(1\right)=15.77;p<.001$), whereas the interaction of adaptivity and interview position had no effect (${\chi }^2\left(1\right)=0.00;p=.953$). Together, these results indicate that task selection changed from the first to the second interview, without being more adaptive to the student case profile.

Professional Knowledge and Adaptive Use of Diagnostic Task Potential (RQ2.2)

To investigate the role of professional knowledge in the adaptive use of diagnostic potential, we included participants’ scores separately for each professional knowledge component (CK, Model 4; PCK, Model 5; PK, Model 6) as well as interaction effects with adaptivity.

For none of the professional knowledge components significant effects occurred. Neither the main effects of the knowledge scores (CK: ${\chi }^2\left(1\right)=2.06;p=.151$; PCK: ${\chi }^2\left(1\right)=0.27;p=.602$; PK: ${\chi }^2\left(1\right)=0.28;p=.599$) nor the corresponding interactions with diagnostic potential (CK: ${\chi }^2\left(1\right)=0.70;p=.404$; PCK: ${\chi }^2\left(1\right)=0.12;p=.728$; PK: ${\chi }^2\left(1\right)=0.30;p=.585$) were significant.

Discussion

This article focuses on teachers’ task selection during diagnostic one-to-one simulations and investigates the study participants’ sensitivity to and adaptive use of the diagnostic potential of tasks when diagnosing students’ mathematical understanding. Live simulations of diagnostic one-to-one interviews were used to ensure authentic but comparable conditions. The importance of diagnostic competences (Herppich et al., 2018; Heitzmann et al., 2019; Loibl et al., 2020) and knowledge about the diagnostic potential of tasks have been put forward in the literature (Baumert & Kunter, 2013). The need for approaches to studying diagnostic processes under controlled but authentic settings has been raised as a desiderate (Grossman & McDonald, 2008). We propose and investigate an innovative perspective on the diagnostic process, focusing on the selection of diagnostic tasks. Differentiating between sensitivity to and the adaptive use of diagnostic task potential takes into account that a task can have more than just high or low diagnostic potential; that is, a task’s potential may be more or less useful depending on what is already known about a specific student’s mathematical understanding in a diagnostic process. In our study, we were able to investigate pre-service teachers’ sensitivity to and adaptive use of diagnostic task potential during authentic (though, of course, not real) diagnostic situations in a controlled setting. Even though the importance of diagnostic competences is undisputed (Behrmann & Souvignier, 2013) the constructs of sensitivity to and the adaptive use of diagnostic task potential during the diagnostic process have not been described in detail in the literature, and evidence from authentic diagnostic processes under controlled conditions is scarce. Our study provides results for the measurement of these characteristics, pre-service teachers’ sensitivity to and adaptive use of diagnostic task potential and the relationship with professional knowledge.

Measurement of the Proposed Process Characteristics

Knowledge and use of diagnostic task potential have been underlined as important aspects of teachers’ professional competences in the past (Baumert & Kunter, 2013), and their operationalization and measurement have been discussed repeatedly. For example, Herppich et al., (2018) call for a wider spectrum of criteria to assess diagnostic competence, including process-based measures. In response to this, the present study examined pre-service teachers’ sensitivity to and adaptive use of the diagnostic potential of tasks when diagnosing students’ mathematical understanding. Regarding participants’ sensitivity, our results partially met our expectations, as implied by prior research. However, there was no main effect of sensitivity, indicating that participants generally did not have a higher probability of selecting tasks with high diagnostic potential. The results reveal a systematic inter-individual variation between the participants in their tendency to prefer high-potential over low-potential tasks. The observed systematic variation indicates that the construct of sensitivity and its operationalization in our study might indeed reflect meaningful characteristics of the diagnostic process, which reflect the participants’ diagnostic competences.

The picture is different for the adaptive use of diagnostic potential, which we had already expected to be a more complex characteristic. First, the adaptive use of diagnostic potential requires complex cognitive processes, including the interpretation and integration of information from prior student answers, which may differ inter-individually. Second, the measurement of this construct is intricate, as participants’ prior information about the student cannot be accessed explicitly, but a proxy measure had to be used, assuming that participants had collected at least the basic information that could have been observed during the first phase of the interview based on the first three task clusters. In our study, we could not identify a significant direct effect of adaptivity or inter-individual variation in the adaptive use of task potential. This can be for different reasons. First, it might be that the demand for using tasks adaptively was just beyond what our participants could achieve, given that at the time of study, they were just mid-way through their university studies and had limited practical experience. In other words, the required cognitive processes might have been too complex for the participants. Second, it might be that our operationalization of the construct as a proxy measure was too coarse to capture the situation-specific adaptivity of teachers’ task selections. In this case, it remains an open question if and how more valid, but still efficient measures of adaptivity might be developed, for example, by explicitly asking participants about intermediate diagnoses or with more effort, by analyzing prior interactions in the interview qualitatively. Moreover, adaptive task selection might be influenced much more strongly by situation-specific factors than by individual dispositions, making finding systematic inter-individual variance impossible. In this case, the construct (possibly with improved operationalization) might even have additional predictive value for the final diagnosis in the sense of a situation-specific skill (Blömeke et al., 2015) beyond stable person characteristics. Based on our data, we cannot provide evidence for or against these assumptions. A good way to study this issue would be to investigate whether and how adaptivity (as measured in our study or with alternative operationalization) goes along with better, for example more accurate diagnoses.

Pre-Service Teachers’ Sensitivity to and Adaptive Use of Diagnostic Task Potential

Beyond establishing and measuring the construct, our study yields first evidence as to what degree pre-service teachers are indeed sensitive to the diagnostic potential of tasks. The results show that the odds of choosing high-potential tasks (over low-potential tasks) did not differ significantly. This indicates that on average, our participants did not prefer high-potential tasks, and that selecting tasks according to their diagnostic potential was not straightforward for our sample. Even though some participants seemed to systematically prefer high-potential tasks (significant systematic inter-individual differences), others did not. Thus, at least the latter participants, but also other pre-service teachers, might require further support in attending to task potential and developing their sensitivity. Prior studies have shown that dedicated training in the PCK component of professional knowledge can improve teachers’ ability to estimate task difficulty (Ostermann et al., 2018). Our study cannot provide evidence as to whether this is similar for sensitivity to tasks’ diagnostic potential of tasks. However, it can provide first insights into the role of all three components of professional knowledge (see below).

As for the adaptive use of diagnostic task potential, we did not find a significant effect on task selection or significant systematic inter-individual variation between participants. Thus, it appears that participants were generally not significantly more likely to make adaptive vs. non-adaptive task selections, implying that participants had difficulty with the adaptive use of diagnostic task potential. Since being sensitive to diagnostic task potential is a prerequisite to the adaptive use of task potential in our process model, it seems plausible that support would have to address strategies and knowledge pertaining to both to foster the ability to detect the diagnostic potential of a task and judge it against what is already known about a student.

Professional Knowledge

The measures used for professional knowledge only showed significant relationships with sensitivity to diagnostic task potential, but no relationship with the adaptive use of diagnostic task potential. However, as no significant systematic inter-individual variation could be observed for the adaptive use of diagnostic task potential, this came as no surprise given that professional knowledge is a person characteristic. Other factors, such as situation-specific motivational states (e.g., Herppich et al., 2018), might moderate these relationships and substantially reduce the bivariate correlations. Regarding sensitivity to diagnostic task potential, we primarily expected a relationship with participants’ PCK. This assumption was based on the fact that knowledge about the diagnostic potential of tasks is often discussed as a facet of PCK (Baumert & Kunter, 2013), and prior findings on the relationship of teachers’ PCK and their diagnostic competence (Ostermann et al., 2018). Moreover, although diagnostic potential is intrinsically a very content-related task characteristic, it is not only based on a task’s mathematical characteristics, but also on the strategies that can be applied to solve the task. However, in our study, only participants’ CK correlated with sensitivity to diagnostic task potential. This parallels the findings of Van den Kieboom et al., (2013) who noted that pre-service teachers’ CK was related to their questioning behavior in diagnostic interviews. It seems that for the participants in our sample, a preference for high-potential tasks relied more on their sound understanding of decimal fractions than on their knowledge about student cognition and instruction. In this context, it is an interesting result that higher CK scores did not significantly go along with higher odds of selecting high-potential tasks, but rather with lower odds of selecting low-potential tasks. CK thus appears to enable students to identify and discard low-potential tasks, but it is not sufficient to facilitate the identification and implementation of high-potential tasks. The relatively high impact of CK appears plausible, as superficial strategies, which lower the diagnostic potential of tasks, might be detected by two different methods: 1) recognition of well-known superficial strategies that students apply when dealing with decimals, which would be part of PCK, or 2) a mathematical analysis of as many strategies as possible to solve the task, which would theoretically rely primarily on CK. Our results indicate that our participants applied the second CK-based strategy to a larger extent. However, efficient selection of diagnostic tasks in everyday practice would plausibly be easier to achieve with the first strategy, as mathematical analysis can be expected to be more demanding and time consuming. Since prior studies have not identified a spontaneous transfer of learned CK to PCK tasks (Tröbst et al., 2019) changing to more efficient strategies might still rely on learning PCK. Training studies, but also analyzing diagnostic processes as used by practicing teachers, might provide first insights as to whether stronger or more enriched PCK might lead to different strategies. In this regard, specifically the distinction between personal PCK, (i.e. acquired knowledge related to the diagnostic situation) and enacted PCK, (i.e. knowledge actually used in diagnostic situations), following Carlson and Daehler (2019) refined consensus model, might be of high relevance. In particular, it is likely that our participants acquired the necessary PCK for the simulated diagnostic interview, but did not enact the required PCK for the situation, thus failing to put their theoretical knowledge into action.

Student Case Profiles

Differences between the four student case profiles were controlled in this study, mainly to avoid potential distortions of the results. However, it is interesting that the participants’ tendency to select high-potential tasks and make adaptive task selections did not vary systematically across the four student case profiles. For measurement purposes, this indicates that the four student case profiles can be used mostly interchangeably, as they do not show substantially different levels of difficulty regarding the two characteristics of the diagnostic process.

First vs. Second Interview

The results were mostly comparable for the first and the second interview, as far as participants’ tendency to select high-potential tasks and make adaptive task selections is concerned. In particular, we did not observe any short-term learning effects regarding either of the process measures. Beyond this, however, it seems that pre-service teacher’ task selection behavior and diagnostic processes did change from the first to the second interview. In particular, participants selected more (high- and low-potential and adaptive and non-adaptive) tasks in the second interview, but spent less time on these tasks, on average. Based on the data analyzed in this contribution, it has to remain an open question whether the reason for this is more efficient task presentation and diagnostic interpretation of students’ responses or whether it reflects more superficial work during the second simulation. Again, studying the relationship between pre-service teachers’ task selection, their diagnostic interpretations drawn from the task during the interview, and the accuracy of their final evaluation of the student’s understanding could provide a path to obtaining deeper insights into the mechanisms at work behind these differences. The observed differences themselves, however, point to the fact that investigating the effects of repeated engagement in simulations in pre-service teacher education should be carefully investigated in the future and may add interesting results regarding learning effects beyond single encounters with such situations.

The findings of this study show that without further support, pre-service teachers do not select tasks sensitively regarding their diagnostic potential or even adopt task selection in accordance with information that has already been gathered about the student’s understanding. From an informal perspective, it seems that the participants based their task selection more on aspects of task presentation (in particular, their order of presentation), than on task characteristics connected to diagnostic potential. The significant effect of CK points out that supporting pre-service teachers’ professional knowledge could be promising. The fact that the participants in our sample had already encountered all the necessary CK, PCK, and PK content for the simulations in lectures and small group tutorials points to the fact that simply acquiring the relevant knowledge (pPCK) might not be sufficient for enacting (ePCK) the knowledge in a diagnostic situation. Contrary to CK, which pre-service teachers have already encountered to some extent in their own school careers, the application of PCK and PK in particular might rely on sufficient learning opportunities in authentic situations, such as simulations (used as learning environments) and practical studies. Thus, the inclusion of authentic applications of acquired knowledge in university studies is of central interest, as well as how diagnostic processes, in particular, including task selection, can be supported in such settings. Investigating the effects of prompts (Berthold et al., 2007) and reflection phases (Mamede et al., 2012) could also provide differentiated insights about the role of professional knowledge. Assuming that the selection of tasks is a key part of the diagnostic process, fostering pre-service teachers’ sensitivity to and adaptive use of diagnostic task potential when selecting tasks (Moyer-Packenham & Milewicz, 2002) seems to be very promising.

Limitations

Of course, our study suffers from a number of limitations. Most importantly, the operationalization of the concept of adaptivity in the present study is quite limited. The construct of an adaptive use of diagnostic task potential builds on the insights that a participant gains at a specific point in a diagnostic interview. Thus, direct operationalization would need to build on individual information reconstructed by the participant, which cannot be systematically controlled. As described above, alternative approaches to measure adaptivity in diagnostic task selection, but also further analyses of the current operationalization might be promising for addressing the open issues connected to this construct.

Moreover, we introduce new process characteristics and investigate them in a very specific setting, spanning over four student case profiles, which, despite their differences, are all based on the same pool of diagnostic tasks from the content area decimal fractions. It thus remains an open question to what extent our results would transfer not only to different mathematical content, but also to different diagnostic situations and different populations of pre- and in-service teachers (Karst et al., 2017).

The chosen setting itself can be seen as valid for teachers, since diagnosing individual students’ understanding of a specific concept using mathematical tasks is part of teachers’ everyday practice. However, it must be taken into account that one-to-one interviews lasting about 30 min each are not feasible as everyday practice in many schools. On the other hand, this choice allowed us to generate a controlled yet sufficiently authentic setting to investigate our questions and gather a sufficient amount of data, which would not have been possible in less time. In particular, Grossman et al., (2009) propose the use of such approximations of practice as learning opportunities in pre-service teacher education, and Shavelson (2012) argues for their use as assessment tools. In this sense, the results are of interest for the development of such practice approximations, even though they are not broadly part of everyday teacher practice.

Due to the sample size of 65 participants, the insignificant or almost significant effects could be explained by restricted statistical power in our study. Investigating this approach based on a larger sample size could be promising. In addition, a comparison of pre- and in-service teachers’ task selection could lead to clearer contrasts between both groups and provide auspicious insights into how 1) pre-vs. in-service teachers shape their diagnostic processes and select tasks, and how 2) pre- and in-service teachers’ pPCK and ePCK are related to their sensitivity to and adaptive use of diagnostic task potential. These insights could be the basis for future professional development. Moreover, a replication with a larger, more representative sample, possibly also from different universities or countries, would help to support our findings about the absolute level of participants’ sensitivity. However, because inter-individual differences in performance are not systematically linked to a specific sample’s performance level, stronger generalizability can be assumed for these findings.

Finally, since only professional knowledge was considered as a participant prerequisite, investigating other trait prerequisites, such as interest or state variables like motivation, authenticity, or cognitive demand (Codreanu et al., 2020), would allow for more differentiated insights, for example, by considering the interplay of knowledge and motivation, and focusing on moderating effects that may obscure the effects of participants’ professional knowledge.

Conclusion

This study presents a role-play based live simulation that was used to assess mathematics pre-service teachers’ diagnostic competences in an authentic setting. Participants acted like real teachers, trying to diagnose students’ mathematical understanding. Since the students were played live by trained teaching assistants, the participants had a huge scope of action, (e.g. select tasks, interact with the student, pose follow-up questions), while still ensuring the comparability of the experiences within the simulation. The use of this authentic simulation thus enabled the investigation of a close approximation of the participants’ natural behavior. By focusing on the participants’ selection of tasks during diagnostic interviews, sensitivity to and adaptive use of diagnostic task potential were analyzed as well as the relationship with participants’ professional knowledge. Being sensitive to the diagnostic potential of tasks reflects that a task’s diagnostic potential is considered to be an important factor during task selection, whereas the construct of the adaptive use of diagnostic task potential additionally reflects the influence of previously collected information about the student’s understanding. The results show that sensitivity to diagnostic task potential seems to be related to participants’ CK.

This study provides insights into the repeatedly highlighted (Moyer-Packenham & Milewicz, 2002; Maier et al., 2010) yet quite under-investigated role of diagnostic task potential. Differentiating between sensitivity to and adaptive use of diagnostic task potential, this study focuses on the diagnostic process from an innovative perspective. The simulation-based approach in our study facilitated an investigation of the use of diagnostic task potential in task selection during diagnostic processes for the first time in an authentic empirical setting. The findings of this study underline the need for learning environments to foster pre-service teachers’ diagnostic competences as well as their underlying professional knowledge. In particular, a major focus should be on enabling them to apply their professional knowledge in appropriate authentic settings in order to develop sensitivity to tasks’ diagnostic potential, and make adaptive use of that potential, so that they are able to individually address their prospective students and create custom-tailored, effective diagnostic processes that will be beneficial to both, students and teachers. The findings of this study show that even basic aspects of diagnostic competence, such as the selection of diagnostic tasks, are related to the knowledge pre-service teachers acquire in their university courses. However, at the early stages of this development, it seems that it is not primarily PCK that plays a role in identifying tasks with high diagnostic potential, but CK is required to dismiss tasks with low diagnostic potential. A possible reason could be that students rely more on mathematical analysis of the tasks, rather than their knowledge about possible misconceptions. Accordingly, instructional approaches, like the use of simulations, should ensure that students activate and use their PCK, in addition to CK, to describe and improve their diagnostic actions.

Finally, the established simulation was designed to function as an assessment tool (as used in this study) and as a learning environment to foster pre-service teachers’ diagnostic competences. Future intervention studies will provide additional insights into how pre-service teachers can be supported effectively using this simulation to increase their diagnostic and assessment competences.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors, upon request without undue reservation.

Ethics Statement

The studies involving human participants were reviewed and approved by the ethics committee of the Faculty of Mathematics, Computer Science and Statistics, LMU Munich.

Author Contributions

SK participated in the design of the simulation, creation of the employed scales, collected the data, performed the main analyses, and wrote the manuscript. DS supported during the design of the simulation, the creation of the scales for professional knowledge, data analysis and revised the analysis scripts and the manuscript. MA supported during data collection and revised the manuscript. SU initiated the project and supported the design of the simulation, during data collection, and during data analysis. He revised the analyses and the manuscript.

Funding

The research presented in this contribution was funded by a grant of the DFG to Stefan Ufer, Kathleen Stürmer, Christof Wecker, and Matthias Siebeck (Grant numbers UF59/5-1 and UF59/5-2 as part of COSIMA, FOR2385).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2021.604568/full#supplementary-material.

Footnotes

¹Additional information about the instruments, the dataset, and the analysis of the data are available from the authors on request.

²The IRT knowledge scores can be interpreted in the following way: a person with knowledge score θ will, according to the Rasch model, solve an item with difficulty parameter δ with a probability of p = 1 (1+ exp (δ−θ)).

References

Aufschnaiter, C. v., Cappell, J., Dübbelde, G., Ennemoser, M., Mayer, J., Stiensmeier-Pelster, J., et al. (2015). Diagnostische Kompetenz. Theoretische Überlegungen zu einem zentralen Konstrukt der Lehrerbildung. 61 (5), 738–758.

CrossRef Full Text | Google Scholar

Ball, D. L., Thames, M. H., and Phelps, G. (2008). Content knowledge for teaching: what makes it special? J. Teach. Educ. 59, 389–407. doi:10.1177/0022487108324554

CrossRef Full Text | Google Scholar

Bates, D., Mächler, M., Bolker, B., and Walker, S. (2014). Fitting linear mixed-effects models using lme4. J. Stat. Soft. 67 1–103. doi:10.18637/jss.v067.i01

CrossRef Full Text | Google Scholar

Baumert, J., Kunter, M., Blum, W., Brunner, M., Voss, T., Jordan, A., et al. (2010). Teachers’ mathematical knowledge, cognitive activation in the classroom, and student progress. Am. Educ. Res. J. 47 (1), 133–180. doi:10.3102/0002831209345157

CrossRef Full Text | Google Scholar

Baumert, J., and Kunter, M. (2013). “The COACTIV model of teachers’ professional competence,” in Cognitive activation in the mathematics classroom and professional competence of teachers: results from the COACTIV project. Editors M. Kunter, J. Baumert, W. Blum, U. Klusmann, S. Krauss, and M. Neubrand (New York: Springer), 25–48.

CrossRef Full Text | Google Scholar

Behrmann, L., and Souvignier, E. (2013). The relation between teachers’ diagnostic sensitivity, their instructional activities, and their students' achievement gains in reading. Z. für Paedagogische Psychol. 27 (4), 283–293. doi:10.1024/1010-0652/a000112

CrossRef Full Text | Google Scholar

Berthold, K., Nückles, M., Renkl, A., and Instruction, (2007). Do learning protocols support learning strategies and outcomes? The role of cognitive and metacognitive prompts. Learn. InStruct. 17 (5), 564–577. doi:10.1016/j.learninstruc.2007.09.007

CrossRef Full Text | Google Scholar

Black, P., and Wiliam, D. (2009). Developing the theory of formative assessment. Educ. Assess. Eval. Account. 21 (1), 5. doi:10.1007/s11092-008-9068-5

CrossRef Full Text | Google Scholar

Blömeke, S., Gustafsson, J.-E., and Shavelson, R. J. (2015). Beyond dichotomies: viewing competence as a continuum. Z. für Psychol. 223, 3–13. doi:10.1027/2151-2604/a000194

CrossRef Full Text | Google Scholar

Blömeke, S., Kaiser, G., and Lehmann, R. (2011). “Messung professioneller Kompetenz angehender Lehrkräfte: “Mathematics Teaching in the 21st Century" und die IEA-Studie TEDS-M,” in Empirische Fundierung in den Fachdidaktiken. Editors H. Bayrhuber, U. Harms, B. Muszynski, B. Ralle, M. Rothgangel, L.-H. Schönet al. (Münster, Germany: Waxmann), 9–26.

CrossRef Full Text | Google Scholar

Bromme, R. (1981). Das Denken von Lehrern bei der Unterrichtsvorbereitung: eine empirische Untersuchung zu kognitiven Prozessen von Mathematiklehrern. Weinheim, Germany: Beltz.

CrossRef Full Text | Google Scholar

Carlson, J., and Daehler, K. (2019). “The refined consensus model of pedagogical content knowledge in science education,” in Repositioning pedagogical content knwoledge in Teachers´ knwoledge for teaching science. Editors A. Hume, R. Cooper, and A. Borowski (Singapore: Springer).

CrossRef Full Text | Google Scholar

Codreanu, E., Sommerhoff, D., Huber, S., Ufer, S., and Seidel, T. (2020). Between authenticity and cognitive demand: finding a balance in designing a video-based simulation in the context of mathematics teacher education. Teach. Teach. Educ. 95, 103146. doi:10.1016/j.tate.2020.103146

CrossRef Full Text | Google Scholar

Förtsch, C., Sommerhoff, D., Fischer, F., Fischer, M., Girwidz, R., Obersteiner, A., et al. (2018). Systematizing professional knowledge of medical doctors and teachers: development of an interdisciplinary framework in the context of diagnostic competences. Educ. Sci. 8 (4), 207. doi:10.3390/educsci8040207

CrossRef Full Text | Google Scholar

Grossman, P., Compton, C., Igra, D., Ronfeldt, M., Shahan, E., and Williamson, P. (2009). Teaching practice: a cross-professional perspective. Teach. Coll. Rec. 111 (9), 2055–2100.

CrossRef Full Text | Google Scholar

Grossman, P., and McDonald, M. (2008). Back to the future: directions for research in teaching and teacher education. Am. Educ. Res. J. 45 (1), 184–205. doi:10.3102/0002831207312906

CrossRef Full Text | Google Scholar

Heckmann, K. (2006). Zum Dezimalbruchverständnis von Schülerinnen und Schülern: theoretische Analyse und empirische Befunde. Berlin, Germany: Logos.

CrossRef Full Text | Google Scholar

Heinze, A., and Verschaffel, L. (2009). Flexible and adaptive use of strategies and representations in mathematics education. ZDM Mathematics Education 41, 535–540. doi:10.1007/s11858-009-0214-4

CrossRef Full Text | Google Scholar

Heitzmann, N., Seidel, T., Opitz, A., Hetmanek, C., Wecker, M. R., Fischer, S., et al. (2019). Facilitating diagnostic competences in simulations in higher education A framework and a research agenda. Flr 7, 1–24. doi:10.14786/flr.v7i4.384

CrossRef Full Text | Google Scholar

Herppich, S., Praetorius, A.-K., Förster, N., Glogger-Frey, I., Karst, K., Leutner, D., et al. (2018). Teachers’ assessment competence: integrating knowledge-, process-, and product-oriented approaches into a competence-oriented conceptual model. Teach. Teach. Educ. 76, 181–193. doi:10.1016/j.tate.2017.12.001

CrossRef Full Text | Google Scholar

Kaiser, J., Praetorius, A.-K., Südkamp, A., and Ufer, S. (2017). “Die enge Verwobenheit von diagnostischem und pädagogischem Handeln als Herausforderung bei der Erfassung diagnostischer Kompetenz,” in Diagnostische Kompetenz von Lehrkräften: theoretische und methodische Weiterentwicklungen. Editors A. Südkamp, and A.-K. Praetorius (Münster, Germany: Waxmann), 114–123.

CrossRef Full Text | Google Scholar

Karst, K., Klug, J., and Ufer, S. (2017). “Strukturierung diagnostischer Situationen im inner- und außerunterrichtlichen Handeln von Lehrkräften,” in Diagnostische Kompetenz von Lehrkräften: theoretische und methodische Weiterentwicklungen. Editors A. Südkamp, and A.-K. Praetorius (Münster, Germany: Waxmann), 95–113.

CrossRef Full Text | Google Scholar

Kleickmann, T., Großschedl, J., Harms, U., Heinze, A., Herzog, S., Hohenstein, F., et al. (2014). Professionswissen von Lehramtsstudierenden der mathematisch-naturwissenschaftlichen Fächer-Testentwicklung im Rahmen des Projekts KiL. Unterrichtswissenschaft 42 (3), 280–288.

Klug, J., Bruder, S., Kelava, A., Spiel, C., and Schmitz, B. (2013). Diagnostic competence of teachers: a process model that accounts for diagnosing learning behavior tested by means of a case scenario. Teach. Teach. Educ. 30, 38–46. doi:10.1016/j.tate.2012.10.004

CrossRef Full Text | Google Scholar

Koeppen, K., Hartig, J., Klieme, E., and Leutner, D. (2008). Current issues in competence modeling and assessment. Z. für Psychol./J. Psychol. 216 (2), 61–73. doi:10.1027/0044-3409.216.2.61

CrossRef Full Text | Google Scholar

Lin, F.-L., and Rowland, T. (2016). “Pre-service and in-service mathematics teachers’ knowledge and professional development,” in The second handbook of research on the psychology of mathematics education: the journey continues. Editors Á. Gutiérrez, G. C. Leder, and P. Boero (Rotterdam, Netherlands: Sense Publishers), 483–520.

CrossRef Full Text | Google Scholar

Loibl, K., Leuders, T., and Dörfler, T. (2020). A framework for explaining teachers' diagnostic judgements by cognitive modeling (DiaCoM). Teach. Teach. Educ. 91, 103059. doi:10.1016/j.tate.2020.103059

CrossRef Full Text | Google Scholar

Maier, U., Kleinknecht, M., and Metz, K. (2010). “Ein fächerübergreifendes Kategoriensystem zur Analyse und Konstruktion von Aufgaben,” in Lernaufgaben und Lernmaterialien im kompetenzorientierten Unterricht. Editors H. Kiper, W. Meints, S. Peters, S. Schlump, and S. Schmit (Stuttgart, Germany: Kohlhammer), 28–43.

CrossRef Full Text | Google Scholar

Mamede, S., van Gog, T., Moura, A. S., de Faria, R. M., Peixoto, J. M., Rikers, R. M., et al. (2012). Reflection as a strategy to foster medical students' acquisition of diagnostic competence. Med. Educ. 46 (5), 464–472. doi:10.1111/j.1365-2923.2012.04217

PubMed Abstract | CrossRef Full Text | Google Scholar

Marczynski, B., Kaltefleiter, L. J., Siebeck, M., Wecker, C., Stürmer, K., and Ufer, S. (in press). “Diagnosing 6th graders´ understanding of decimal fractions. Fostering mathematics pre-service teachers’ diagnostic competences with simulated one-to-one interviews,” in Learning to diagnose with simulations - examples from teacher education and medical education. Editors F. Fischer, and A. Opitz (Heidelberg, Germany: Springer).

CrossRef Full Text | Google Scholar

Moyer-Packenham, P., and Milewicz, E. (2002). Learning to question: categories of questioning used by preservice teachers during diagnostic mathematics interviews. J. Math. Teach. Educ. 5 (4), 293–315. doi:10.1023/A:1021251912775

CrossRef Full Text | Google Scholar

Neubrand, M., Jordan, A., Krauss, S., Blum, W., and Löwen, K. (2011). “Aufgaben im COACTIV-Projekt: Einblicke in das Potenzial für kognitive Aktivierung im Mathematikunterricht,” in Professionelle Kompetenz von Lehrkräften. Ergebnisse des Forschungsprogramms COACTIV. Editors M. Kunter, J. Baumert, W. Blum, U. Klusmann, S. Krauss, and M. Neubrand (Waxmann, Germany: Münster u.a.), 115–132.

CrossRef Full Text | Google Scholar

Ostermann, A., Leuders, T., and Nückles, M. (2018). Improving the judgment of task difficulties: prospective teachers’ diagnostic competence in the area of functions and graphs. J. Math. Teach. Educ. 21 (6), 579–605. doi:10.1007/s10857-017-9369-z

CrossRef Full Text | Google Scholar

Padberg, F., and Wartha, S. (2017). Didaktik der Bruchrechnung. Berlin, Germany: Springer Spektrum.

CrossRef Full Text | Google Scholar

Philipp, K. (2018). “Diagnostic competences of mathematics teachers with a view to processes and knowledge resources,” in Diagnostic competence of mathematics teachers: unpacking a complex construct in teacher education and teacher practice. Editors T. Leuders, J. Leuders, and K. Philipp (New York, NY: Springer), 109–127.

CrossRef Full Text | Google Scholar

Praetorius, A.-K., Lipowsky, F., and Karst, K. (2012). “Diagnostische Kompetenz von Lehrkräften. Aktueller Forschungsstand, unterrichtspraktische Umsetzbarkeit und Bedeutung für den Unterricht,” in Differenzierung im mathematisch-naturwissenschaftlichen Unterricht. Implikationen für Theorie und Praxis. Editors R. Lazarides, and A. Ittel (Bad Heilbrunn, Germany: Klinkhardt), 115–146.

CrossRef Full Text | Google Scholar

Rasch, G. (1960). Studies in mathematical psychology: I. Probabilistic models for some intelligence and attainment tests. Oxford, England: Nielsen & Lydiche.

CrossRef Full Text | Google Scholar

Schack, E. O., Fisher, M. H., Thomas, J. N., Eisenhardt, S., Tassell, J., and Yoder, M. (2013). Prospective elementary school teachers' professional noticing of children’s early numeracy. J. Math. Teach. Educ. 16 (5), 379–397. doi:10.1007/s10857-013-9240-9

CrossRef Full Text | Google Scholar

Schulman, L. S. (1987). Knowledge and teaching: foundations of the new reform. Harv. Educ. Rev. 57 (1), 1–23.

CrossRef Full Text | Google Scholar

Shavelson, R. J. (2012). Assessing business-planning competence using the Collegiate Learning Assessment as a prototype. Empirical Res Voc Ed Train 4 (1), 77–90. doi:10.1007/bf03546509

CrossRef Full Text | Google Scholar

Sherin, B., and Star, J. R. (2011). “Reflections on the study of teacher noticing,” in Mathematics teacher noticing: seeing throug teachers eyes. Editors M. Sherin, V. Jacobs, and R. Philipp (New York, NY: Routledge).

CrossRef Full Text | Google Scholar

Stein, M. K., Engle, R. A., Smith, M. S., and Hughes, E. K. (2008). Orchestrating productive mathematical discussions: five practices for helping teachers move beyond show and tell. Math. Think. Learn. 10, 313–340. doi:10.1080/10986060802229675

CrossRef Full Text | Google Scholar

Steinle, V. (2004). Changes with age in students’ misconceptions of decimal numbers. MS dissertation: University of Melbourne. Available at:http://hdl.handle.net/11343/39024.

CrossRef Full Text | Google Scholar

Stürmer, K., Marczynski, B., Wecker, C., Siebeck, M., and Ufer, S. (in press). “Praxisnahe Lerngelegenheiten in der Lehrerausbildung. Validierung der simulationsbasierten Lernumgebung DiMaL zur Förderung diagnostischer Kompetenz von angehenden Mathematiklehrpersonen.” in Vielfältig herausgefordert. Forschungs- und Entwicklungsfelder der Lehrerbildung auf dem Prüfstand. Editors N. Beck, T. Bohl, and S. Meissner. (Tübingen: Tübingen University Press).

CrossRef Full Text | Google Scholar

Südkamp, A., Kaiser, J., and Möller, J. (2012). Accuracy of teachers’ judgments of students’ academic achievement: a meta-analysis. J. Educ. Psychol. 104 (3), 743–762. doi:10.1037/a0027627

CrossRef Full Text | Google Scholar

Südkamp, A., Möller, J., and Pohlmann, B. (2008). Der simulierte Klassenraum. Eine experimentelle Untersuchung zur diagnostischen Kompetenz. Z. für Padagogische Psychol. 22 (34), 261–276. doi:10.1024/1010-0652.22.34.261

CrossRef Full Text | Google Scholar

Südkamp, A., and Praetorius, A.-K. (2017). “Eine Einführung in das Thema der diagnostischen Kompetenz von Lehrkräften,” in Diagnostische Kompetenz von Lehrkräften: theoretische und methodische Weiterentwicklungen. Editors A. Südkamp, and A.-K. Praetorius (Münster, Germany: Waxmann), 13–18.

CrossRef Full Text | Google Scholar

Leuders, T., Leuders, J., and Philipp, K. (Editors) (2018). Diagnostic Competence of Mathematics Teachers: Unpacking a Complex Construct in Teacher Education and Teacher Practice. New York: Springer.

CrossRef Full Text | Google Scholar

Tröbst, S., Kleickmann, T., Depaepe, F., Heinze, A., and Kunter, M. (2019). Transfer from instruction on pedagogical content knowledge about fractions in sixth-grade mathematics to content knowledge and pedagogical knowledge. Unterrichtswinssenschaft 47 (1), 79–97. doi:10.1007/s42010-019-00041-y

CrossRef Full Text | Google Scholar

Tröbst, S., Kleickmann, T., Heinze, A., Bernholt, A., Rink, R., and Kunter, M. (2018). Teacher knowledge experiment: testing mechanisms underlying the formation of preservice elementary school teachers' pedagogical content knowledge concerning fractions and fractional arithmetic. J. Educ. Psychol., 110, 1049. doi:10.1037/edu0000260

CrossRef Full Text | Google Scholar

Ufer, S., and Neumann, K. (2018). “Measuring competencies,” in International handbook of the learning sciences. Editors F. Fischer, C. E. Hmelo-Silver, S. R. Goldman, and P. Reimann (New York, NY: Routledge), 433–443.

CrossRef Full Text | Google Scholar

Van de Pol, J., Volman, M., and Beishuizen, J. (2010). Scaffolding in teacher-student interaction: a decade of research. Educ. Psychol. Rev. 22 (3), 271–296. doi:10.1007/s10648-010-9127-6

CrossRef Full Text | Google Scholar

Van den Kieboom, L. A., Magiera, M. T., and Moyer, J. C. (2013). Exploring the relationship between K-8 prospective teachers’ algebraic thinking proficiency and the questions they pose during diagnostic algebraic thinking interviews. J. Math. Teach. Educ., 17, 429. doi:10.1007/s10857-013-9264-1

CrossRef Full Text | Google Scholar

Wollring, B. (2004). Individualdiagnostik im Mathematikunterricht der Grundschule als Impulsgeber für Fördern, Unterrichten und Ausbildung. Teil 2: Handlungsleitende Diagnostik [Individual diagnosis as catalyst in the primary mathematics classroom. Part 2: Diagnostic for pedagogical decisions] Schulverwaltung. Ausgabe Hessen, Rheinland-Pfalz und Saarland, 8 (11), 297–298.

CrossRef Full Text | Google Scholar