A Diagnostic Framework for the Empirical Evaluation of Learning Maps

Learning progressions and learning map structures are increasingly being used as the basis for the design of large-scale assessments. Of critical importance to these designs is the validity of the map structure used to build the assessments. Most commonly, evidence for the validity of a map structure comes from procedural evidence gathered during the learning map creation process (e.g., research literature, external reviews). However, it is also important to provide support for the validity of the map structure with empirical evidence by using data gathered from the assessment. In this paper, we propose a framework for the empirical validation of learning maps and progressions using diagnostic classification models. Three methods are proposed within this framework that provide different levels of model assumptions and types of inferences. The framework is then applied to the Dynamic Learning Maps^® alternate assessment system to illustrate the utility and limitations of each method. Results show that each of the proposed methods have some limitations, but they are able to provide complementary information for the evaluation of the proposed structure of content standards (Essential Elements) in the Dynamic Learning Maps assessment.

A Diagnostic Framework for the Empirical Evaluation of Learning Maps

Learning progressions (LPs; also known as learning trajectories) are a model of pedagogical thinking to describe shifts between understanding new knowledge and more advanced targets as a sequence of possible transformations (Simon, 1995). LPs grew out of the Science Education for Public Understanding Program (Roberts et al., 1997) with “construct maps,” which are conceived of as “strategically developed cycles and sequences of instructional activities that guide learning pathways” (Duschl et al., 2011, p. 131). Thus, LPs are meant to describe the process of acquiring new knowledge over a given period of time or within a specific learning or content area (National Research Council, 2007).

LPs in science and mathematics education are currently seen as promising strategies for the redesign and reform of curriculum, instruction, and assessment in educational environments (Corcoran et al., 2009; Duschl et al., 2011). LPs mainly rely on cognitive science research on how students learn a particular concept to describe a path of skill acquisition (Alonzo and Steedle, 2009). The NRC volume, Knowing What Students Know (National Research Council, 2001), recommends the use of cognitive models take a central role in the assessment design process. Consistent with this idea, LPs can provide a framework for the development of both large-scale and classroom-based assessments to measure how student understanding develops in a given domain.

Validating the Structure of LPs

Of critical importance when considering the potential uses of LPs in practice is a validation of the hypothesized structure. If the structure is incorrect, then any inferences and instructional decisions that are made based on the structure are at risk of being incorrect as well. Traditionally, evidence supporting the structure of LPs has fallen into two categories. Procedural evidence is focused on the process of how the proposed structure of the LP was created. Empirical evidence is focused on statistical methods that can be used to validate the LP once data have been gathered to measure the proposed knowledge and skills and their connections. Both types of evidence are briefly described below, although the main focus of the remainder of the paper is on empirical evidence.

Procedural Evidence Approaches

Procedural evidence refers to the processes and procedures used to create the LPs. These processes typically involve an extensive research and literature review that is used to define the skills and how they are connected, external review of the LPs by outside experts, and various types of alignment checks and evaluations along the way. For example, the Science Education for Public Understanding Program (Roberts et al., 1997) created LPs with educator input and examples of student works along the progression. By following the increasing complexity of the associated materials, it is possible to also follow the logic of the LP organization. Similarly, the Teacher Analysis of Student Knowledge (Supovitz et al., 2013) developed a progression for teachers’ understanding of their students’ mathematics knowledge. This progression was then tied back to the Common Core State Standards, providing procedural evidence through the vertical articulation of the standards and its alignment to the LP. The Dynamic Learning Maps^® (DLM^®) alternate assessment project followed similar approaches when developing the learning map models for English language arts, mathematics, and science (Andersen and Swinburne Romine, 2019; Swinburne Romine and Schuster, 2019). For DLM assessments, the learning map models were first developed by content experts based on existing research literature. The draft maps underwent an external review process by educators and additional content experts and was then revised based on reviewer feedback.

Collecting procedural evidence is undoubtedly critical to the use of any developed LP. Without evidence-based research and expert input to support a conceptually sound structure, empirical evidence is unlikely to be sufficient to validate the structure of an LP. Indeed, having an entirely data-driven LP may result in a structure that is overfit to the collected data (i.e., too specific to the particular data that were collected) or conflicting with the wider research literature. However, procedural evidence is also insufficient in isolation. Although LPs can be developed using best procedural practices, there is always some level of uncertainty in the resulting structure. Thus, it is important to collect data and provide empirical evidence to corroborate the proposed structure.

Empirical Evidence Approaches

Empirical evidence involves collecting and analyzing data to evaluate the structure of an LP. There are many forms that this type of evidence could take. One example is analyzing examinee responses to items that align to specific levels within an LP. This was the approach taken by Briggs et al. (2006), who developed an assessment using ordered multiple-choice items to assess students’ level of achievement within an LP. In this assessment design, answer options are tied to specific levels in the progression, and the aggregated response patterns can provide evidence to support the structure (i.e., across all levels of assessment, a student’s selected responses should consistently correspond to a level in the progression).

Another possibility for empirical evidence is to relate the proposed LP to external outcomes. In the Length Measuring Learning Trajectory (Barrett et al., 2012), showed that use of their LPs in instruction was able to predict student growth within the targeted skills, and was associated with higher achievement in those areas during a final assessment. A similar approach was used by Jin et al. (2015) to develop LPs of science content. Using item response theory, Jin et al. (2015) first calibrated separate models for each level of the LP to show the distinctness of the progression. They then also showed that as teachers’ understanding of the LP increased, so did the performance of their students on the post-test. This approach of using external data for evidence was also employed by Supovitz et al. (2018) on the Teacher Analysis of Student Knowledge. In this project, teachers were asked to blindly rate student responses to items measuring different levels of a mathematics LP. Teachers were asked to place their students on the LP in the location that best represented their acquired knowledge. The student responses were then compared to the teacher placement in the LP. The findings showed that teachers were able to place students on the LP consistent with the students’ item responses.

Empirical evidence can also take the form of classical item statistics. Herrmann-Abell and DeBoer (2018) developed an LP to model the concept of energy in science. Items were written at three levels of complexity for each main idea within the energy concept (i.e., a three-attribute LP for each main idea). They then used Kendall’s $\tau$ correlation to evaluate the association between item difficulty and the progression complexity. The expectation was that a positive correlation would be observed. That is, as complexity increased within the progression, so too would item difficulty. Using the correlations, Herrmann-Abell and DeBoer (2018) were able to demonstrate that as the LPs became more complex, the items did get harder on average, thus supporting the overall structure. However, this method is limited when there is a small sample of items. For example, 20 items measuring each of the three levels would result in only 60 data points to use for the calculation of the correlation. This can lead to greater uncertainty in the estimated correlation if there is not a sufficient number of items.

A similar approach was taken by Clark et al. (2014) in an early evaluation of the DLM pilot administration. In the pilot study, students were administered test items at multiple levels of cognitive complexity, corresponding to different areas of the learning map structure. Clark et al. (2014) observed that for students with similar expressive communication skills and subject knowledge, the percentage of students providing a correct response decreased as the level of the testlet increased, thus providing preliminary evidence of the general ordering of the structure.

Taken together, empirical evidence has the ability to support or refute the proposed LP structure. However, the methods used to date for evaluating empirical evidence are all somewhat limited in that none use a model-based method that is consistent with the multidimensional nature of LPs. For example, when using multidimensional item response theory models, the different attributes of the LP can be modeled as separate, albeit related, latent abilities, but the structure of the LP cannot be fully enforced without applying a threshold to the latent trait to indicate presence or absence of each attribute in the LP (see Deng et al., 2017; Schwartz et al., 2017). Additionally, although the methods are useful for linear LPs, they may not generalize to a more complicated learning map structure, where multiple pathways can lead to the same knowledge acquisition. Thus, a flexible and generalizable framework of empirical validation is needed to fully evaluate these structures.

Map Validation With Diagnostic Classification Models

The purpose of this paper is to describe and illustrate, with examples, empirical approaches to learning map (and LP) validation using diagnostic classification models (DCMs). Specifically, three methods with varying levels of complexity and model assumptions are defined and then illustrated using the DLM alternate assessment. The methods are described in the context of the DLM assessment; however, these methods generalize to other learning map or LP models as well.

Diagnostic Classification Models

DCMs (also known as cognitive diagnostic models) are a class of multidimensional psychometric models that define a mastery profile on a predefined set of attributes (Rupp and Templin, 2008; Rupp et al., 2010). Given an attribute profile for an individual, the probability of providing a correct response to an item is determined by the attributes that are required by the item. Whereas traditional psychometric models (e.g., item response theory) model a single, continuous latent variable, DCMs model student mastery on multiple latent variables or skills of interest. Thus, a benefit of using DCMs for calibrating and scoring assessments is the ability to support instruction by providing fine-grained reporting at the skill level. Based on the collected item response data, the model determines the overall probability of students being classified into each latent class for each skill.

DCMs can also be used to test different learning map or LP structures. Given a number of attributes (e.g., nodes in a map, or stages/steps in an LP), there are $2^A$ possible attribute profiles, where A is the number of attributes. This represents all possible combinations of mastery and nonmastery across the attributes. Thus, by limiting the number of possible profiles, we can test different LP structures. For example, Templin and Bradshaw (2014) used a hierarchical DCM (HDCM) to test an attribute structure of skills related to English grammar, where some attributes had to be mastered for other attributes to be mastered. This hierarchical model adapts the log-linear cognitive diagnosis model (Henson et al., 2009), which is discussed next in more detail.

The Log-Linear Cognitive Diagnostic Model

The LCDM provides a generalized DCM that subsumes many of the other more restrictive DCMs. For example, the deterministic-input noisy-and-gate (de la Torre and Douglas, 2004) and deterministic-input noisy-or-gate (Templin and Henson, 2006) are both subsumed by the LCDM (Henson et al., 2009). In the LCDM, the item response function is expressed as a linear model with a logit link function. For example, the response function for an item, i, measuring two attributes, conditional on the respondent’s, r, attribute profile for these two attributes, ${\mathit{\alpha }}_r=\left[{\alpha }_{r1}, {\alpha }_{r2}\right]$, is given by:

$P\left(X_{ri}=1 \text{|}{\mathit{\alpha }}_r\right)= \frac{\exp \left({\lambda }_{i,0}+{\lambda }_{i,1,\left(1\right)}{\alpha }_{r1}+{\lambda }_{i,1,\left(2\right)}{\alpha }_{r2}+{\lambda }_{i,2,\left(\mathrm{1,2}\right)}{\alpha }_{r1}{\alpha }_{r2}\right)}{1+\exp \left({\lambda }_{i,0}+{\lambda }_{i,1,\left(1\right)}{\alpha }_{r1}+{\lambda }_{i,1,\left(2\right)}{\alpha }_{r2}+{\lambda }_{i,2,\left(\mathrm{1,2}\right)}{\alpha }_{r1}{\alpha }_{r2}\right)}(1)$

Where ${\alpha }_{ra}$ is a binary indicator for whether attribute a has been mastered by respondent r. For the estimated parameters, ${\lambda }_{i,0}$ represents the intercept, ${\lambda }_{i,1,\left(a\right)}$ is the simple main effect for attribute a on item i, and ${\lambda }_{i,2,(a,a\prime )}$ is the two-way interaction between attribute a and a′ on item i. Further interactions can be added as necessary for items that measure more than two attributes. This leads to the general of LCDM:

$P\left(X_{ri}=1 \text{|}{\mathit{\alpha }}_r={\mathit{\alpha }}_c\right)= \frac{\exp \left({\lambda }_{i,0}+{\mathit{\lambda }}_i^T\mathit{h}\left({\mathit{\alpha }}_r,{\mathit{q}}_i\right)\right)}{1+\text{exp}\left({\lambda }_{i,0}+{\mathit{\lambda }}_i^T\mathit{h}\left({\mathit{\alpha }}_r,{\mathit{q}}_i\right)\right)}(2)$

Where q_i is the vector of Q-matrix entries indicating whether attribute a is measured by item i, and ${\mathit{\lambda }}_i$ is vector of the item parameters for item i, not including the intercept. Finally, $\mathit{h}({\mathit{\alpha }}_r,{\mathit{q}}_i)$ is a vector function specifying whether a parameter is present, based on the attribute profile and Q-matrix entry. For example, if a test measured three attributes and a given item measured only attributes one and two, the main effect for attribute three would not be included. Thus, ${\mathit{\lambda }}_i^T\mathit{h}({\mathit{\alpha }}_r,{\mathit{q}}_i)$ can be expressed as:

${\mathit{\lambda }}_i^T\mathit{h}\left({\mathit{\alpha }}_r, {\mathit{q}}_i\right)={\displaystyle \sum _{a=1}^A{\lambda }_{i,1,\left(a\right)}}{\alpha }_{ra}+q_{ia}+{\displaystyle \sum _{a=1}^{A-1}{\displaystyle \sum _{b>a}{\lambda }_{i,2,\left(a,b\right)}}}{\alpha }_{ra}{\alpha }_{rb}{q}_{ia}{q}_{ib}+\dots (3)$

The LCDM specification has several advantages. First, the parameters are straightforward to interpret, as they are on the same log-odds scale as a standard logistic regression. Additionally, the parameters can be restricted to estimate other models for model comparison. For example, if all parameters except the intercept and highest-order interaction for each item are fixed at 0, the model is equivalent to the deterministic-input noisy-and-gate model. Thus, multiple models with different assumptions can be fit using the same framework and directly compared. Finally, as mentioned previously, the LCDM can be extended to test attribute hierarchies. Given these benefits, the LCDM framework is used for map validation for the DLM alternate assessment.

Extending the LCDM for Attribute Hierarchies

When attribute hierarchies are present not all attribute profiles are present. That is, if mastery of attribute one is a prerequisite for mastery of attribute two, then the attribute profile [0,1], should not be possible, as this profile represents mastery of attribute two only. In other words, the set of possible attribute profiles is reduced. The reduction in possible attribute profiles creates redundant profiles in the LCDM specification. Continuing the example, if profile [0,1] is not possible, then it follows the main effect for attribute two is a redundant parameter. That is, only a main effect for attribute one and the two-way interaction for attributes one and two are relevant for this example item. This leads to the HDCM specification described by Templin & Bradshaw (2014). For our example item, Eq. 1 can be re-expressed as:

$P\left(X_{ri}=1 \text{|}{\mathit{\alpha }}_r^{\mathit{*}}\right)= \frac{\exp \left({\lambda }_{i,0}+{\lambda }_{i,1,\left(1\right)}{\alpha }_{r1}+{\lambda }_{i,2,\left(2(1\right))}{\alpha }_{r1}{\alpha }_{r2}\right)}{1+\exp \left({\lambda }_{i,0}+{\lambda }_{i,1,\left(1\right)}{\alpha }_{r1}+{\lambda }_{i,2,\left(2(1\right))}{\alpha }_{r1}{\alpha }_{r2}\right)}(4)$

In Eq. 4, the item response function now includes only the item intercept, ${\lambda }_{i,0}$, the main effect for attribute one, ${\lambda }_{i,1,\left(1\right)}$, and the two-way interaction between attributes one and two, ${\lambda }_{i,2,(2\left(1\right))}$. The (2 (1)) notation in the two-way interaction term indicates that attribute two is nested within attribute one. Extending beyond two attributes, Eq. 3 can be re-expressed as:

${\mathit{\lambda }}_i^T\mathit{h}\left({\mathit{\alpha }}_r^{\ast }, {\mathit{q}}_i\right)={\lambda }_{i,1,\left(a\right)}{\alpha }_{ra}{q}_{ia}+{\lambda }_{i, 2,\left(b\left(a\right)\right)}{\alpha }_{ra}{\alpha }_{rb}{q}_{ia}{q}_{ib}+{\lambda }_{i,3,\left(c\left(b,a\right)\right)}{\alpha }_{ra}{\alpha }_{rb}{\alpha }_{rc}{q}_{ia}{q}_{ib}{q}_{ic}+\dots (5)$

Note that Eq. 5 assumes a linear hierarchy of the attributes, as is the case for the structures that will be explored in this paper. However, additional parameters may be included if the attribute hierarchy is not strictly linear.

The Dynamic Learning Maps Alternate Assessment

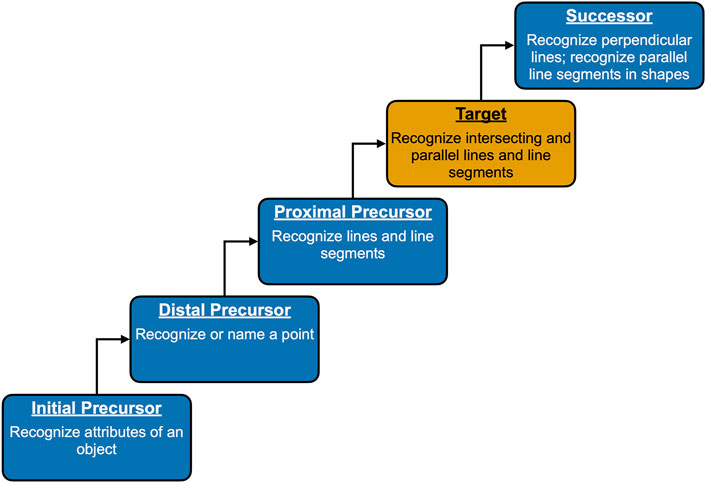
The DLM assessments are built based on learning map models, which are a type of cognitive model consisting of interconnected learning targets and other critical knowledge and skills (DLM Consortium, 2016). In the DLM assessment, the alternate content standards, or Essential Elements, are specific statements of knowledge and skills and are the learning targets for the assessment. To ensure that all students are able to access grade-level academic content, each Essential Element is associated with five levels, called “linkage levels,” that represent the content of the Essential Element at varying levels of complexity. For ELA and mathematics, there are five linkage levels within each Essential Element. The Target level is aligned to the Essential Element and represents the grade-level expectation for students taking the DLM assessments. Preceding the Target level are three precursor linkage levels that represent the Essential Element at varying levels of complexity to allow all students an entry point for accessing the assessment content and working toward grade-level expectations. The precursor linkage levels are Initial Precursor, Distal Precursor, and Proximal Precursor. There is also one linkage level, Successor, that extends beyond the Target grade-level expectation. The linkage levels are assumed to follow a hierarchical structure whereby higher linkage levels can only be mastered if the lower levels have also been mastered.

To evaluate the linkage level structure within a given Essential Element, student response data to items measuring adjacent linkage levels are needed. However, the DLM assessment administration is designed to align assessment content to each student’s unique level of knowledge, skills, and understandings. This means that students often test on only one linkage level that best matches their skill level for each Essential Element; however, teachers may choose to assess their students on additional linkage levels, depending on student performance and opportunity to learn additional content.¹ Additionally, DLM assessments follow a simple Q-matrix. That is, each item measures only one attribute—the linkage level the student is testing on.² Thus, the operational assessment offers insufficient opportunities to collect the cross-linkage-level data needed to fully evaluate the connections between linkage levels. Limited cross-linkage-level data have been collected through field testing, where students receive field test testlets at a different linkage level than what was assessed during the operational assessment.

To illustrate the DCM framework for map validation, a single Essential Element was selected that has sufficient cross-linkage-level data to support meaningful inferences from the estimated models. Specifically, we examined the mathematics Essential Element M.EE.4.G.1: Recognize parallel lines and intersecting lines. Figure 1 shows the hierarchical structure of the linkage levels for M.EE.4.G.1.

FIGURE 1

FIGURE 1. Hierarchical ordering of linkage levels for Essential Element M.EE.4.G.1.

Methods

Under the DCM framework of map validation, three methods are defined for testing a map structure: patterns of mastery profiles, patterns of mastery assignment, and patterns of attribute difficulty. To demonstrate the methods, analyses are focused on the assumption of the linear hierarchy of linkage levels depicted in Figure 1.

Method 1: Patterns of Mastery Profiles

The first method, patterns of mastery profiles, evaluates the ordering of the linkage levels within Essential Element M.EE.4.G.1 by comparing a full and constrained DCM. Specifically, a saturated LCDM (Henson et al., 2009) is estimated and compared to a constrained HDCM (Templin and Bradshaw, 2014) that matches the structure of the hypothesized linkage levels. By comparing a model with all possible profiles to a model with only hypothesized profiles, we can evaluate whether the nonhypothesized profiles significantly affect the model’s performance. If the hypothesized structure holds, we expect the models to have comparable fit to the observed data.

In the full LCDM, described above, there are $2^A$ possible mastery profiles, where A is the number of attributes, or in the case of DLM assessments, linkage levels. In the HDCM, only the profiles hypothesized by the map structure, the monotonically increasing profiles, are estimated. For Essential Element M.EE.4.G.1, there are five linkage levels, which are the attributes in the DCM. With five attributes, there are $2^5=32$ possible mastery profiles. However, under the hierarchical assumption of the linkage levels, not all of those profiles are possible. If the hierarchical structure is correct, only the monotonically increasing profiles should be possible. This is illustrated in Table 1.

TABLE 1

TABLE 1. Possible and hypothesized mastery profiles.

To test the presence of attribute hierarchies, Templin and Bradshaw (2014) suggest a likelihood ratio test between the full LCDM and HDCM models, with a simulation-derived p-value. However, using a fully Bayesian estimation process opens the door to more efficient methods of evaluating and comparing the LCDM and HDCM. Accordingly, both the LCDM and HDCM models were estimated using R version 3.6.1 (R Core Team, 2019) and the RStan package interface to the Stan probabilistic programming language (Carpenter et al., 2017; Stan Development Team, 2020). If the hierarchical structure holds, then it would be expected that the two models have comparable model fit. Because the full LCDM includes more parameters and possible mastery profiles, the full LCDM will always fit better than the constrained HDCM. However, if the HDCM shows comparable fit, then this indicates that removing those additional parameters and mastery profiles does not have an adverse effect on model performance. If the HDCM fits significantly worse than the LCDM, then this is evidence that the proposed structure is too restrictive. Absolute model fit is assessed through posterior predictive model checks. Relative fit is assessed through information criteria.

Absolute Fit

Absolute measures of model fit measure the extent to which the model actually fits the data. In the proposed method, absolute fit is assessed using posterior predictive model checks, which involves generating simulated replicated data sets, creating summary statistics for each replicated data set, and then comparing the distributions of the summary statistics to the value of each statistic in the observed data (for more details and examples, see Gelman, Carlin, et al., 2013; Levy and Mislevy, 2016; and McElreath, 2016). In a Bayesian estimation process, a posterior distribution is generated for each parameter in the model. The size of the posterior sample depends on the length of the Markov-Chain Monte Carlo chains. For the models described in this paper, four chains were estimated with 2,000 iterations each, and the first 1,000 were discarded for the warm-up period. This results in 4,000 retained draws (1,000 from each chain) that make up the posterior samples for each parameter. Thus, 4,000 replicated data sets can be created. Each data set is generated using the values of the parameters at a given iteration. This means that the uncertainty in the parameter estimates is incorporated into the simulation of the replicated data sets. Furthermore, these replicated data sets represent what the data would be expected to look like if the estimated model is correct. Thus, deviations in the observed data from the replicated data sets would indicate model misfit.

Once the replicated data sets have been generated, summary statistics can be calculated. In this study, we calculate an expected distribution of raw scores. For this summary, the number of students at each total raw score (sum score across items) is calculated, resulting in a distribution of the expected number of students at each total raw score. The observed number of students at each score point is then compared to these distributions using a 95% credible interval. For a global evaluation of model fit, this summary can be taken one step further. The mean of the distributions for each score point can be thought of as the expected number of students for that score point. These expected counts can be used to calculate a ${\chi }^2$ -like goodness-of-fit statistic. This is calculated in the same way as a traditional ${\chi }^2$ statistic but will not follow the distributional assumptions of the ${\chi }^2$. However, an empirical distribution can be estimated using the replicated data sets. For each replicated data set, the ${\chi }^2$ is calculated using the number of students observed at each score in that replication and the expected counts (the means of the distributions). Thus, a ${\chi }^2$ is estimated for each replication, creating a distribution of expected ${\chi }^2$ statistics. The ${\chi }^2$ from the observed data, ${\chi }_{obs}^2$, is then compared to this distribution, and a posterior predictive p-value (ppp) is calculated as the proportion of the empirical ${\chi }^2$ distribution that is greater than the observed ${\chi }_{obs}^2$. If the ppp is less than 0.05 (or another chosen threshold), then the model is rejected (i.e., the observed data are inconsistent with the replicated data sets, and therefore, the model fit is not sufficient).

Absolute model fit is crucial to the evaluation of any model, including DCMs. If the model does not fit the data sufficiently, then any inferences made from the model are prone to error. However, absolute fit indices are unable to adequately compare competing models. For example, if both the LCDM and HDCM demonstrate sufficient absolute fit, as would be expected if the hypothesized structure is correct, these indices are unable to differentiate which model fits better. For this comparison, relative fit indices are needed.

Relative Fit

Relative model fit indices directly compare two models to determine which provides a better overall fit to the data. These are common measures in many models outside of DCMs. For example, the Akaike information criterion (Akaike, 1974) and Bayesian information criterion (Schwarz, 1978) are widely used and recognized. Another relative fit comparison is cross validation. In cross validation, a portion of the data is withheld from the estimation process, and fit is assessed on this held-out portion. This is then repeated multiple times with different training and testing sets. The performance of the model across the held-out portions is then compared between models. Although cross validation can be computationally expensive, it can be approximated using predictive information criteria (Gelman, Hwang, et al., 2013). In the proposed method, an approximation of leave-one-out cross validation, known as Pareto-smoothed importance sampling leave-one-out cross validation (PSIS-LOO; Vehtari et al., 2017, 2019), is used. This method estimates the predictive density of the model, balancing predictive power with model complexity. This method is also readily available for models estimated with RStan using the loo package (Vehtari et al., 2020). When examining the PSIS-LOO of competing models, the magnitude of the difference in the expected log predictive density (the predictive power) of each model is compared to the standard error of the difference. If the magnitude of the difference is much larger than the standard error (e.g., 2.5 times as large; Bengio and Grandvalet, 2004), then one model is preferred over the other.

In addition, we can also compare models using model stacking (for an overview, see Hinne et al., 2020). These methods assign a weight to each model that corresponds to the weight that should be given to predictions from each model. Thus, these methods allow for more refined inferences (Vehtari and Ojanen, 2012) and are less prone to overfitting than methods based on information criteria (Piironen and Vehtari, 2017). For the models in this paper, we use the Bayesian stacking method described by Yao et al. (2018).

Although relative fit indices can provide information about which model may be preferred in a comparison, these values are not useful in isolation. An expected log predictive density from the PSIS-LOO is dependent on the size of the sample and the likelihood function and therefore not comparable across different types of models or data sets. Additionally, these methods do not tell you if the model fits the data. The comparisons are all relative to the other models. For example, the PSIS-LOO may indicate a preference for the reduced model over the saturated model; however, it could be that both models fit poorly, but the reduced model is less poor. Therefore, it is important that these methods be used in conjunction with absolute fit indices to ensure a comprehensive assessment of model fit.

Method 2: Patterns of Attribute Mastery

The second method reduces the model complexities that exist in Patterns of Profile Mastery method. For example, it does not rely on the use of cross-attribute data needed to estimate relationships between attributes. Thus, this method can be particularly useful in test designs where there is planned missingness at the attribute level, as in the DLM assessments. In this method, rather than estimating the LDCM with mastery profiles across all attributes, an independent LCDM with a dichotomous latent variable is estimated for each attribute. A polytomous attribute could be specified, but we use dichotomous attributes in this study to reflect the most common implementations of DCMs (Ma, 2021). This is similar to the approach taken by Jin et al. (2015), who used multiple independent unidimensional item response theory models to model each attribute. Thus, if there are five measured attributes in the learning map, five single-attribute LCDM models would be estimated. Each LCDM then has two possible classes: master and nonmaster of the given skill. With only two classes, this model is equivalent to a latent class analysis (see Bartholomew et al., 2011). These models are again estimated using RStan (Stan Development Team, 2020). After the estimation of the models, we calculated the probability of each student being a master of each skill. Thus, each student has a probability of mastery for each attribute that they tested on, calculated from the separate model estimations.

Patterns are then examined across the assessed attribute masteries. That is, across the attributes that were assessed, do the observed mastery patterns conform to the expected patterns? The patterns of the probabilities can be compared directly or dichotomized into 0/1 mastery decisions using a mastery threshold (e.g., 0.8). If the hierarchical structure holds, then it would be expected that the probability of attribute mastery would decrease as the learning map progressed to more complex levels. Similarly, if using a dichotomized mastery status, a student should not receive a master classification on an attribute unless all the lower-level attributes also received a master classification.

Method 3: Patterns of Attribute Difficulty

The third method represents another step down on the scale of model dependency. Whereas the first method (Patterns of Mastery Profiles) and the second method (Patterns of Mastery Assignment) both use some version of the LCDM, this third method does not depend on any specific DCM model. Similar to Herrmann-Abell and DeBoer (2018), this method involves the calculation of item difficulties for each attribute and then comparison of the pattern of difficulties across attributes within cohorts of students with similar skill levels. Within each student cohort, it is expected that the items should get harder as the attribute level increases.

For this method, we define the difficulty of the attribute as the average p-value of each linkage level for students in the cohort. The p-values for given structure or LP are estimated using a logistic regression. Students’ item scores are predicted by the students’ complexity band and the linkage level of the item. By using a logistic regression rather than calculating the p-values directly, we are able to estimate the marginal effect of linkage level on item difficulty (e.g., Searle et al., 1980; Lenth, 2021). Additionally, using a logistic regression allows for the direct calculation of a posterior distribution and credible intervals, rather than relying on asymptotic assumptions that may not be met in all situations using observed data (Shan and Wang, 2013). The model is estimated using the brms R package (Bürkner, 2017, 2018), which provides a Bayesian estimation of the logistic regression using Stan. The estimated model parameters can then be used to create a posterior distribution of the average p-value for each combination of complexity band and linkage level. The posterior distributions of the p-values can then be compared within cohorts, with the expectation that the average p-values should get lower as the attribute level increases (i.e., items get harder). By calculating the difference in the p-values along with effect sizes that incorporate the uncertainty in the posteriors, we can identify potential misspecifications in the map structure.

Data

To demonstrate this DCM framework of map validation in practice, all three methods were applied to data from DLM assessments from 2015–2016 to 2018–2019 for one example Essential Element, M.EE.4.G.1. This Essential Element was chosen based on the availability of cross-linkage-level data. Additionally, this Essential Element exhibits a potential misspecification in the defined structure, while still maintaining sufficient model fit (as described in the Results). Thus, this Essential Element provides an ideal use case for demonstrating the methods proposed in this paper. Following these analyses, this Essential Element was sent to the test development team for further review and potential revisions.

The full student sample for this Essential Element was filtered to only include students that tested on multiple linkage levels within this Essential Element. During the operational DLM assessment, cross-linkage-level data are primarily obtained by teachers choosing to assess a student on an Essential Element multiple times at different linkage levels.³ However, during the spring 2018 and spring 2019 assessments, a new field test design was used to assign students content at a linkage level adjacent to the level they were assessed in the operational assessment. Thus, additional cross-linkage-level data were collected to evaluate the structure of the Essential Elements. For the third method (Patterns of Attribute Difficulty), students were grouped into cohorts based on their complexity band, which is derived from educator responses to the First Contact survey and determines a student’s starting linkage level in the assessment.⁴ The questions on the First Contact survey assess a student’s subject matter knowledge as well as their expressive communication skills. There are four complexity bands: Foundational, Band 1, Band 2, and Band 3, where Foundational is the lowest and Band 3 is the highest.

In total, 1,101 students were assessed on Essential Element M.EE.4.G.1 at multiple linkage levels. Table 2 shows the demographic breakdown of the included students. The sample is majority male and white, which is also true for the full population of students who take the DLM assessments (Nash et al., 2015; Burnes & Clark, 2021).

TABLE 2

TABLE 2. Demographic subgroups for included sample of students.

Table 3 shows the number of students within each complexity band cohort who were assessed on each linkage level combination. As shown, data for the Band 1 cohort include 609 students. Of these, 410 students were assessed on the Initial Precursor and Distal Precursor linkage levels, 215 were assessed on the Distal Precursor and Proximal Precursor linkage levels, and 16 were assessed on more than two linkage levels. The columns may not sum to the total because of overlap in the counts (i.e., a student who tested on the Initial Precursor, Distal Precursor, and Proximal Precursor linkage levels would be counted in the IP/DP, DP/PP, and >2 Levels Tested columns). No students in the Band 3 cohort were assessed on multiple linkage levels for Essential Element M.EE.4.G.1.

TABLE 3

TABLE 3. Sample sizes for cross-linkage-level data, by complexity band.

Results

To demonstrate the DCM framework for learning map and LP validation in practice, the three methods were applied to the DLM assessment data for Essential Element M.EE.4.G.1. The results for each method are presented separately.

Method 1: Patterns of Mastery Profiles

The full LCDM and the constrained HDCM were fit to the observed data. Model convergence was evaluated using the $\widehat{R}$ statistic described by Vehtari, Gelman, et al. (2020), which should be below 1.01. The maximum $\widehat{R}$ values were 1.0030 and 1.0032 for the LCDM and HDCM, respectively. Additionally, Vehtari, Gelman, et al. (2020) recommend examining the effective sample size to ensure that the parameters adequately explored the sample space. The authors recommended that the effective sample size should be at least 100 per chain (i.e., 400 for the models estimated here). The minimum effective sample sizes for the LCDM and HDCM were 1,570 and 1,992, respectively. Thus, the estimation diagnostics indicate that both the LCDM and HDCM successfully converged, and the parameters adequately explored the sample space.

In addition to the estimation diagnostics, it is also important to examine the estimated items parameters. Because the DLM assessments use a simple Q-matrix design (i.e., each item measures only one linkage level), there are two parameters for each item. These are the intercept and the main effect, which represent the probability of providing a correct response when the respondent has not or has mastered the linkage level, respectively. Note that these parameters are on the log-odds scale. In the LCDM, the item intercepts ranged from −0.77 to 0.12, with a mean of −0.66 and a standard deviation of 0.24. The main effects ranged from 1.65 to 3.23 with a mean of 2.23 and a standard deviation of 0.72. The HDCM showed a similar pattern, with intercepts ranging from −0.92 to 0.42 with a mean of −0.41 and a standard deviation of 0.38 and main effects ranging from 1.51 to 3.17 with a mean of 2.26 and a standard deviation of 0.70. The relatively small intercepts and large main effects for both models indicate that the items are able to successfully discriminate between masters and non-masters.

Finally, we can examine the reliability of the attribute classifications. If the classifications are not reliable, then mastery patterns would be equally unreliable. In this study, reliability is assessed through classification consistency and classification accuracy, as described by Johnson & Sinharay (2018). These measures range from 0 to 1, where 1 represents perfect consistency or accuracy. Table 4 shows these two reliability indices for each of the LCDM, HDCM, and the separate attribute estimations (Method 2, detailed below). The classification consistency and classification accuracy were both uniformly higher for the HDCM compared to the LCDM. However, even the LCDM had adequate, if not ideal, consistency and accuracy (∼0.7 across all attributes). Thus, the classifications are sufficiently reliable to examine the mastery profile patterns.

TABLE 4

TABLE 4. Attribute reliability estimates for the LCDM and HDCM.

Absolute fit was assessed through the ${\chi }_{obs}^2$ statistic, calculated from the posterior predictive model checks (see Thompson, 2019). For this statistic, a ppp value of less than 0.05 generally indicates insufficient fit of the model to the observed data. Using this criterion, both the LCDM (${\chi }_{obs}^2$ = 31.0; ppp = 0.079) and the HDCM (${\chi }_{obs}^2$ = 37.7; ppp = 0.059) showed adequate model fit. That the HDCM showed adequate model fit indicates that the hierarchical structure of linkage levels is sufficient for describing the observed data.

Because both the LCDM and HDCM showed adequate absolute model fit, we can examine relative fit indices to determine if the additional complexity of the LCDM provides a significant improvement to predictive power of the model. The difference in PSIS-LOO between the LCDM and HDCM was –21,745.8, indicating a preference for the LCDM. The standard error of the difference was 200.5. Because the magnitude of the difference is much larger than the standard error (i.e., greater than 2.5 times as large; Bengio and Grandvalet, 2004), we can conclude that this is a meaningful difference. Additionally, the Bayesian stacking method proposed by Yao et al. (2018) strongly preferred the LCDM, giving >99% of the predictive weight to the LCDM, compared to only <1% for the HDCM. Thus, although the HDCM adequately represents the underlying data for the example mathematics Essential Element, the relative fit analyses indicate that the additional parameters of the LCDM do provide a significant improvement to the predictive capabilities of the model, even after accounting for model complexity.

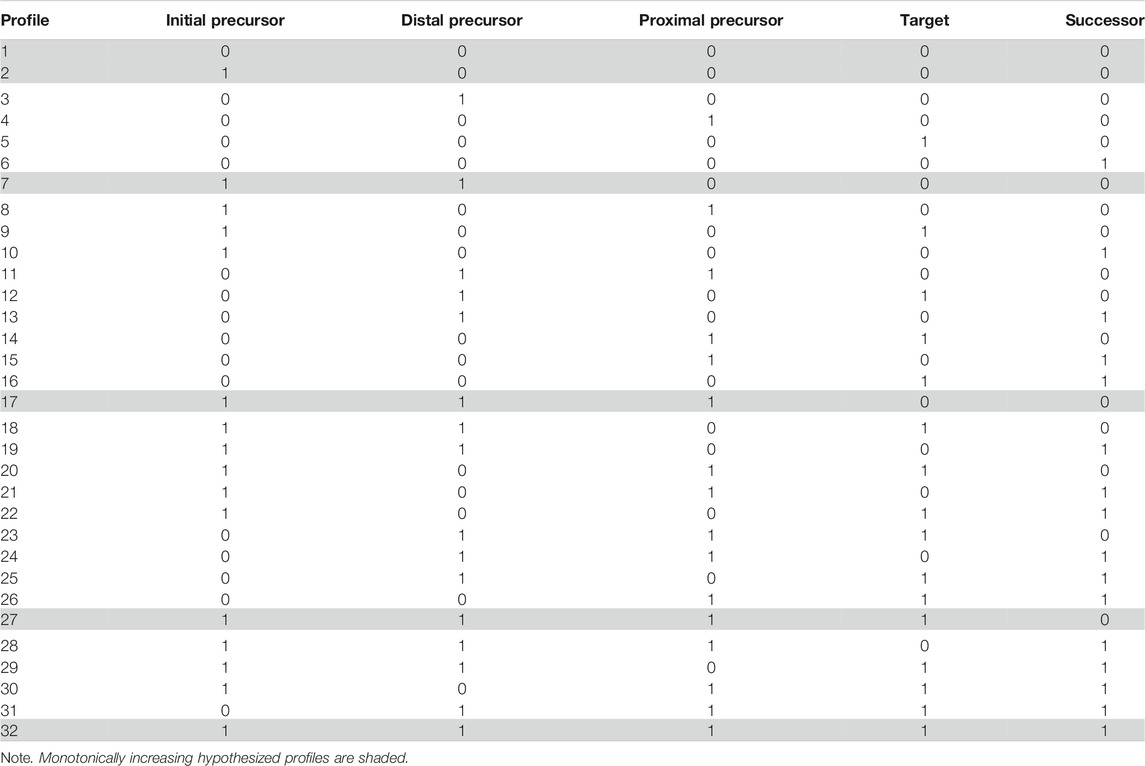
Figure 2 shows the percentage of students placed in each mastery profile for both the LCDM and HDCM. Overall, when using the LCDM, 17% of students were estimated to be in an unexpected class. Of these students estimated to belong to an unexpected mastery profile, 84% (15% of all students) were estimated to be in a profile where the reversal was between the Proximal Precursor and Target, or Target and Successor, linkage levels (e.g., [1,1,0,1,0], [1,1,1,0,1]). Thus, the improved predictive accuracy provided by the LCDM is likely due to the ability of the LCDM to discriminate additional, albeit unintended, mastery patterns across the higher linkage levels.

FIGURE 2

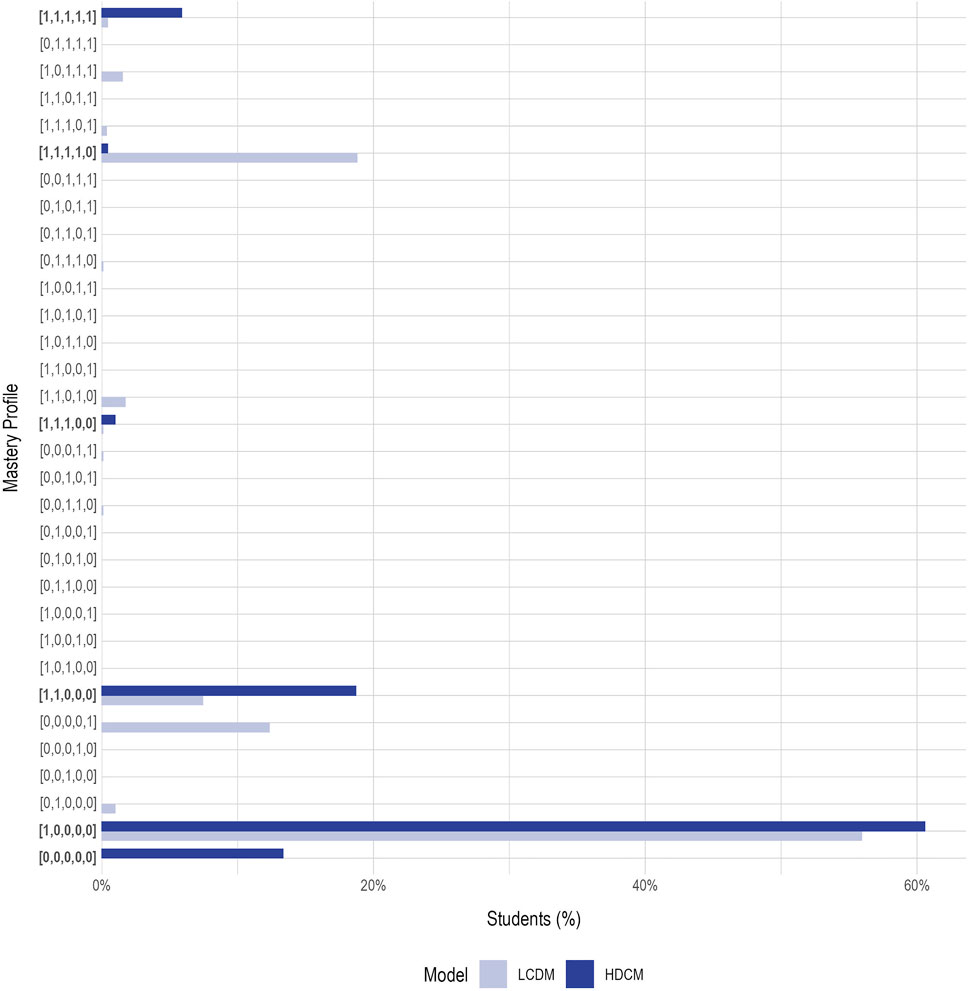
FIGURE 2. Student mastery profile classifications. Expected profiles estimated in the hierarchical diagnostic classification models (HDCM) are labeled in bold text. LCDM = linear cognitive diagnostic model.

Method 2: Patterns of Attribute Mastery

A single-attribute LCDM was estimated for each of the five linkage levels for Essential Element M.EE.4.G.1. Across all five models, the maximum $\widehat{R}$ was 1.0059, and the minimum effective sample size was 1,140. Thus, all five of the separate LCDM models successfully converged, and the parameters successfully explored the sample space. As was done with the full LCDM and HDCM, we also examined the item parameters and attribute reliability indices for the separate single attribute models. Across all five models, the item intercepts ranged from −1.27 to 0.32 with a mean of −0.47 and a standard deviation of 0.52. The main effects ranged from 1.46 to 3.15 with a mean of 2.32 and a standard deviation of 0.60. The reliability estimates for the separate models are included in Table 4. Overall, the classification consistency ranged from 0.683 to 0.999, and the classification accuracy ranged from 0.863 to 0.929. Together, the item parameters and reliability indices indicate that the classifications from the separate models are also adequately consistent and accurate.

Using the separate models, we then calculated students’ resulting posterior probability of mastering each assessed linkage level and dichotomized into master and nonmaster categories using a threshold of 0.8. A threshold of 0.8 was chosen because this is the threshold used for scoring the operational DLM assessments (see Chapter 5, DLM Consortium, 2016, for a complete description of assessment scoring). In total, 47 students (4%) showed a pattern of attribute mastery inconsistent with the proposed hierarchical structure of the linkage levels.

Figure 3 shows the percentage of students that were flagged for each of the linkage level combinations. The highest incidence of observed inconsistency was between the Proximal Precursor and Target linkage levels, where 20 (9%) of the 219 students who were assessed on these two linkage levels were estimated to be masters of the Target linkage level but not the Proximal Precursor linkage level. This may indicate that there is a possible misspecification in the linkage level structure or may be an artifact of the way test content is developed. In general, the content assessed at the higher linkage levels is much closer conceptually than the content assessed across the lower linkage levels. This is because the lower linkage levels often assess foundational skills, whereas the Successor linkage level generally assesses a skill just beyond the Target linkage level (DLM Consortium, 2016). For example, we can see the conceptual distance for this Essential Element in Figure 1. For this Essential Element, the skills assessed range from “Recognize attributes of an object” to “Recognize perpendicular lines; recognize parallel line segments in shapes.” Thus, it may be that the knowledge, skills, and understandings assessed at Proximal Precursor and Target linkage levels are very close conceptually and, therefore, could be reversed more easily.

FIGURE 3

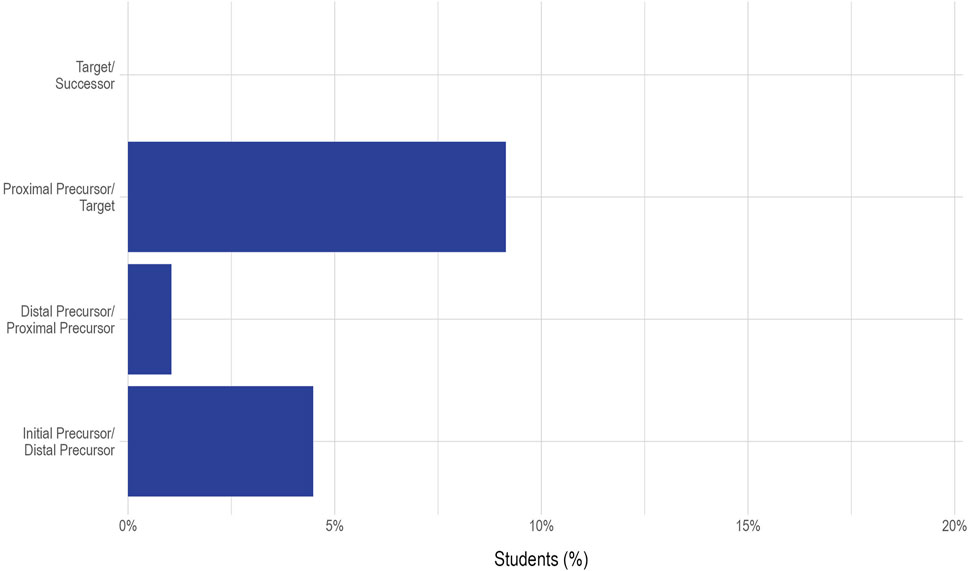
FIGURE 3. Percentage of students flagged for reversals at each linkage level combination for Essential Element M.EE.4.G.1.

Method 3: Patterns of Attribute Difficulty

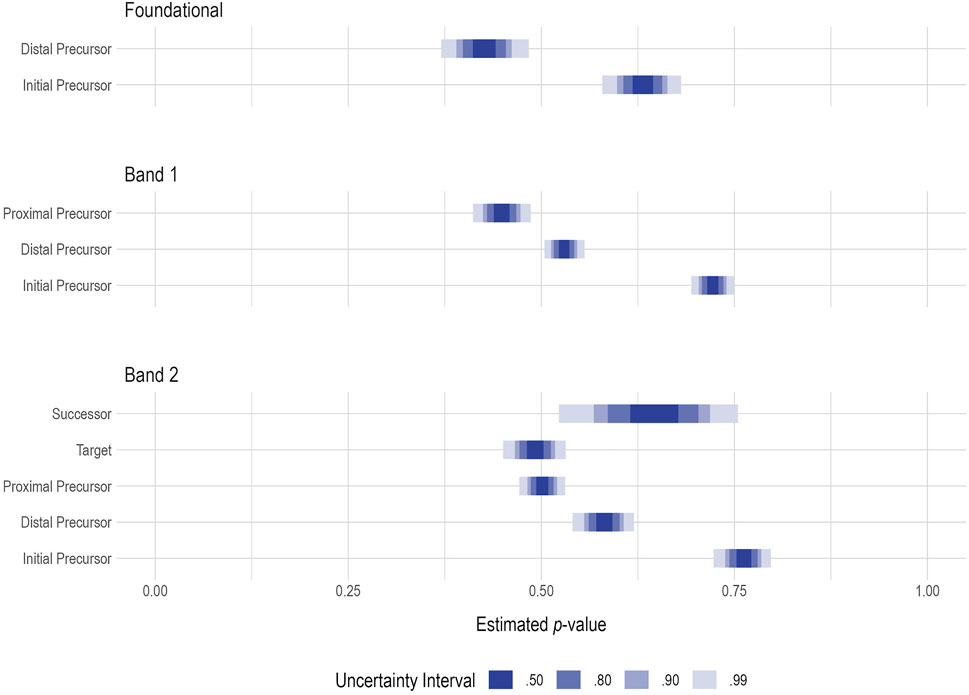
Student cohorts were based on the subject-specific complexity band, calculated from the First Contact survey, as described in Clark et al. (2014). Students were grouped into four cohorts based on expressive communication and academic skill levels as follows: Foundational, Band 1, Band 2, and Band 3. No students from Band 3 were included in this analysis because no students from this complexity band were assessed on multiple linkage levels for this Essential Element. Figure 4 shows the uncertainty intervals for the estimated average p-value for each complexity band and linkage level where students were assessed. Due to the missing data resulting from the DLM administration design (i.e., students are not intended to test on every linkage level), not all cohorts have data on all linkage levels. For example, students in the Foundational complexity band were only assessed on the Initial Precursor and Distal Precursor linkage levels. Overall, the average p-values follow the expected pattern, with lower linkage levels having higher p-values (i.e., easier) than the higher linkage levels, within each student cohort. The exception is the Successor linkage level for students in the Band 2 complexity band. The estimated p-value for this linkage level is higher than those estimated for the Target, Proximal Precursor, and Distal Precursor linkage levels. However, there is a large amount of uncertainty in this estimate, likely due to the relatively small sample size of Band 2 students testing at the Successor linkage level (n = 22; Table 3).

FIGURE 4

FIGURE 4. Credible intervals of the average p-value for each complexity band and linkage level.

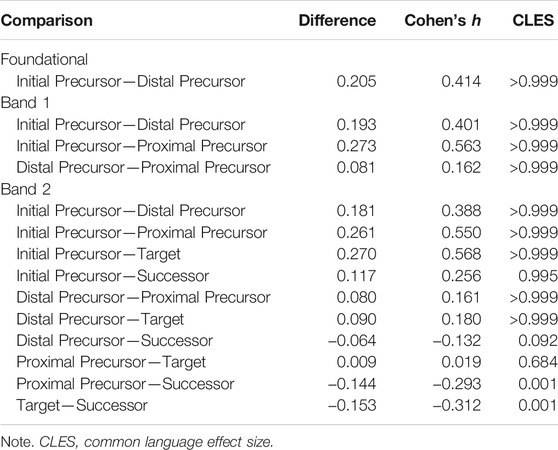
Table 5 reports the difference in average p-values for each linkage level combination observed in the data. Table 5 also includes two effect sizes. Cohen’s h (Cohen, 1988) is a standardized difference in proportions. Using cutoffs recommended by Sawilowsky (2009), the magnitude of Cohen’ h can be used to classify the observed effects as very small (0.01–0.2), small (0.2–0.5), medium (0.5–0.8), large (0.8–1.2), very large (1.2–2.0), and huge (≥2.0). The common language effect size (McGraw and Wong, 1992; Liu, 2015) is a measure of overlap in the distributions from each group. The common language effect size indicates the probability that a value sampled at random from the first group will be greater than a value randomly sampled from the second group. Thus, in Table 5, positive Cohen’s h values and common language effect sizes close to 1.0 indicate that the lower linkage level in the comparison is easier than the higher linkage level, as expected.

TABLE 5

TABLE 5. Difference in average linkage level p-values and effect sizes, by complexity band.

Almost all comparisons are in the expected direction. The only exceptions are the comparisons between the Successor linkage level and the Distal Precursor, Proximal Precursor, and Target linkage levels for students in the Band 2 cohort. The common language effect sizes for these comparisons indicate that there is very little overlap in the plausible ranges of theses p-values; however, the Cohen’s h values are all in the very small to small range. Additionally, although the difference is in the expected direction, the comparison for Band 2 students between the Proximal Precursor and Target linkage levels is near zero. Thus, as was also indicated from the results of the other two methods, it appears that there may be a misspecification in the structure of the higher linkage levels.

Discussion

In this paper, we present a framework for evaluating a proposed learning map structure using DCMs. Three methods were described with decreasing levels of model dependency. These methods were then applied to the hierarchical linear structure of linkage levels for an example Essential Element from the DLM mathematics assessment. The findings demonstrate the utility of the proposed framework for map validation using DCMs. By including methods with different levels of model dependency, the less model-dependent methods are still able to provide useful information when the highly model-dependent methods may not be feasible due to assessment design or data sparseness. Additionally, evidence of fit or misfit for the proposed structure from multiple methods provides a more comprehensive set of information from which final inferences can be made.

Framework for Map Validation

In the first method, Patterns of Mastery Profiles, the comparison of the full LCDM to the constrained HDCM provides the most robust evaluation of the attribute structure. This method presents a clear test of mastery profiles that are expected and unexpected, given the proposed attribute structure. Additionally, because the LCDM includes all possible profiles, this method offers a path forward for revising existing structures in cases in which the HDCM shows poor model fit. By examining the profile classifications in the LCDM, we can identify which unexpected profiles see the greatest numbers of students, informing future work to improve the proposed structures in consultation with subject matter experts.

The second method, Patterns of Attribute Mastery, can be used when the first method is not feasible due to sparse data. For example, if students do not test on all available attributes, the model may struggle to accurately estimate the relationships between attributes. To account for this, attributes can be estimated individually, with mastery classifications made for each attribute tested by the student. By estimating each attribute individually, the estimation of attribute-level relationships becomes moot. However, the trade-off is an assumption that mastery of any given attribute is independent of mastery of the other attributes. Thus, the Patterns of Attribute Mastery method offers additional flexibility in the modeling process but concedes the ability to directly test for the presence of unexpected profiles. However, it is possible to look at specific combinations of attributes to determine where a misspecification may be located.

Finally, the third method, Patterns of Attribute Difficulty, does not directly estimate any DCM. Rather, this method examines the average difficulty of items measuring each attribute for cohorts of students. Unlike the other two methods, this third method does not require estimated mastery classifications, even though these classifications could be incorporated. Although the applied example in this paper operationalized average difficulty as p-values, other measures of difficulty could be used. For example, Herrmann-Abel and DeBoer (2018) used the difficulty parameter from their Rasch model. In a diagnostic assessment using DCMs, one could examine the patterns of the probability providing a correct response to items measuring each attribute within a mastery profile. However, this would require the estimation of a DCM. A key benefit of this method is that the estimation of a latent variable model is not required. Accordingly, this method may be applicable to evaluating LPs or learning maps associated with assessments that are scaled with more traditional psychometric models (e.g., classical test theory or item response theory). Although this method doesn’t offer an explicit test of the proposed structured, evidence in support of or against the structure can be inferred by the posterior distributions of average difficulty for each attribute. That is, if one attribute is dependent on another, the former attribute should be more difficult, as the student would need to have mastered both skills to provide a correct response. Additionally, because this method allows additional groupings (e.g., student cohorts), it is possible to evaluate whether there are specific groups for whom the proposed attribute structure may not be appropriate.

These methods can be used as a comprehensive set of methods, or separately, for the evaluation of a proposed map structure. Together, these methods provide a well-rounded examination of the connections between attributes. The Patterns of Mastery Profiles method provides the most robust overall evaluation, as a fully model-based assessment of map structure. The Patterns of Attribute Mastery method, by not relying on the concurrently estimated mastery profile, is able to incorporate attribute-level scoring rules. The Patterns of Attribute Difficulty method goes beyond mastery classifications to incorporate additional information into the overall evaluation (i.e., attribute difficulty). Thus, even if the Patterns of Mastery Profiles does not support the structure, the other two methods can provide some level of support, as well as inform potential improvements to the map structure. For example, the Patterns of Attribute Mastery method can provide more fine-grained results that may be easier to interpret than the full mastery profile, and the Patterns of Attribute Difficulty method is able to indicate if particular groups of students may be less well represented by the proposed structure.

Additionally, the latter two methods can be used independently for map evaluation when the Patterns of Mastery Profiles method is not feasible (e.g., due to data sparseness). However, the latter two methods have not been as thoroughly developed and evaluated as the first method; additional research is needed to fully understand how effective the second and third methods are for detecting hierarchies under different data conditions. Although the evidence that can be provided by the other methods is not as strong as the evidence provided by Patterns of Mastery Profiles method, it may be sufficient depending on the intended uses of the map structure. In particular, the Patterns of Attribute Difficulty method requires only some measure of difficulty (p-values). Extreme data sparseness may result in exceptionally wide uncertainty intervals for this method, making inferences difficult; however, this is true of almost all methods when the sample size is small.

Application of the Framework

The applied example demonstrates the utility of this framework using a content standard expressed at different levels of complexity from the DLM alternate assessment system. Across all three methods, the example Essential Element showed compatibility with the hierarchical structure of linkage levels. In the Patterns of Mastery Profiles, the HDCM showed adequate model fit, indicating support for the linear structure of the DLM linkage levels. However, the relative fit indices indicated a preference for the LCDM, with 17% of student being placed in unexpected profiles. This suggests that although the HDCM fits, the model is significantly improved by the inclusion of the unexpected profiles. In the Patterns of Attribute Mastery, the results showed that almost all students exhibited an expected pattern of attribute mastery (only 4% of students demonstrated an unexpected profile). Of the students who did not have an expected pattern, most students showed a reversal at the higher linkage levels. Finally, the Patterns of Attribute Difficulty also showed that average linkage level p-values also follow expected patterns of difficulty within student cohorts. The exception was for students in the Band 2 complexity band who were assessed at the Successor and Target levels.

Thus, the totality of the evidence from this study supports the linear hierarchy for most linkage levels associated with the Essential Element. However, the results also indicate that although the hypothesized structure is supported; there are still opportunities for improvement among the higher linkage levels. Both the Patterns of Mastery Profiles and Patterns of Attribute Mastery methods indicated that reversals in the expected patterns were more common for the Target and Successor linkage levels. These results may be influenced by the missing data associated with the DLM administration design. For example, in the first method, of the 17% of students with an unexpected pattern, 71% (12% of all students) were estimated to have mastered only the highest linkage level (i.e., pattern [0,0,0,0,1] in Figure 2). However, no students who were assessed on the highest level were also assessed on the lowest level, and very few were assessed on both the highest and second lowest levels. In these cases, “non-mastery” of the lowest levels was a function of missing data, rather than students demonstrating non-mastery. Thus, the 17% of students with an unexpected pattern in the first method is likely inflated due to missing data patterns that are a result of the intended administration design of DLM assessments. Additionally, it should be noted that because the higher linkage levels are closer together conceptually, it may be easier to falsely identify a misspecification. For example, in the Patterns of Mastery Profiles, the constrained HDCM identified almost no students (n = 16; 1% of all students) in profiles [1,1,1,0,0] or [1,1,1,1,0]. That is, students tended to master either 0, 1, 2, or all 5 linkage levels (Figure 2). This indicates that the highest three linkage levels may not be completely distinct, making it easier for a student to show an unexpected pattern. This may also partially explain the discrepancy in the proportion of students with an unexpected pattern between the first and second methods (17 and 4%, respectively). When the attributes are forced to be independent, a decision must be made for each attribute individually, whereas correlating the attributes allows for the mastery of one attribute to influence another. If the attributes are not completely distinct, these approaches will result in different decisions, as was observed in this example. Overall, the ability to evaluate a proposed structure and assess potential areas for improvement highlight the benefits of using a multimethod approach to evaluating hypothesized map structures.

Learning maps or progressions can be used as instructional tools to foster students’ attainment of learning goals (Shepard, 2018). Providing teachers with a “roadmap” for instructional planning can support students’ learning needs on their way to meeting grade-level expectations. For example, the DLM score reports include a profile of all the linkage levels a student has mastered and which skills come next in the progression of each Essential Element (for example score reports, see Chapter 7 of DLM Consortium, 2016). However, for a learning map to be useful for instruction and learning, the proposed map structure must be supported by empirical data. This paper provides a proposed framework that can be used to support empirical evaluation of map structures, thereby increasing the potential benefit of using learning map structures in instruction and assessment.

Conclusion

Future work will continue to refine the methodology of the DCM framework for map validation and apply the methods to all DLM Essential Elements in mathematics, English language arts, and science as additional data are collected, as well as beyond the DLM assessments. In this paper, we considered only a linear hierarchy of attributes, which is utilized for DLM Essential Elements. However, other attribute structures may be appropriate for other contexts. Thus, nonlinear attribute structures could be examined in future applications of the proposed framework.

Methodologically, modifications can be made to the estimation process in the Patterns of Mastery Profiles, such as simplifying the parameterization of the structural model (e.g., Thompson, 2018), which could be used to improve model estimation with limited cross-attribute data. Furthermore, the Patterns of Attribute Mastery can be refined to develop a flagging criterion for what constitutes a meaningful discrepancy. That is, more work can be done to determine how many students can be placed in an unexpected pattern before the overall structure of the attributes comes into question. For example, in the applied example, 4% of students exhibited an unexpected pattern across tested linkage levels, but it is unclear what percentage (e.g., 5%, 10%) could be reasonably tolerated before the hierarchical assumption is threatened. Similarly, more research is needed to evaluate the power and precision of both the Patterns of Attribute Mastery and Patterns of Attribute Difficulty methods for detecting hierarchies, and potential violations of a proposed hierarchical structure.

In summary, the methods presented in this paper provide multiple approaches for evaluating the structure of an LP or learning map. Each method makes different assumptions and supports different types of evidence. Together, they provide a comprehensive and flexible framework to evaluate and improve hypothesized attribute structures. Further work in this area will both inform the literature on student learning processes and provide further guidance for the development of learning map and progression-based assessments.

Data Availability Statement

The datasets presented in this article are not readily available because data for this study comes from an operational K-12 educational assessment, and the data is owned by a consortium of state partners that use the assessment system. Requests to access the datasets should be directed to atlas-aai@ku.edu.

Ethics Statement

The studies involving human participants were reviewed and approved by the Human Research Protection Program (HRPP) at the University of Kansas. Written informed consent from the participants’ legal guardian/next of kin was not required to participate in this study in accordance with the national legislation and the institutional requirements.

Author Contributions

WT and BN contributed to the conception and design of the study. WT organized the data, executed the analyses, and wrote the first draft of the manuscript. WT and BN wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹For a description of instructionally embedded assessment, see Clark et al. (2019) and Swinburne Romine and Santamaria (2016).

²For a complete description of DLM assessments, including a discussion of the assessment blueprint and student populations, see (DLM Consortium, 2016).

³See Chapter 4 of the 2014–2015 Technical Manual—Integrated Model (DLM Consortium, 2016) for a complete description of how assessment content is assigned to students.

⁴For a complete description of the First Contact survey, see Chapter 4 of the 2014–2015 Technical Manual—Integrated Model (DLM Consortium, 2016) and the First Contact census report (Nash et al., 2015).

References

Akaike, H. (1974). A New Look at the Statistical Model Identification. IEEE Trans. Automat. Contr. 19 (6), 716–723. doi:10.1109/TAC.1974.1100705

CrossRef Full Text | Google Scholar

Alonzo, A. C., and Steedle, J. T. (2009). Developing and Assessing a Force and Motion Learning Progression. Sci. Ed. 93 (3), 389–421. doi:10.1002/sce.20303

CrossRef Full Text | Google Scholar

Andersen, L., and Swinburne Romine, R. (2019). “Iterative Design and Stakeholder Evaluation of Learning Map Models,” in Beyond Learning Progressions: Maps as Assessment Architecture. Symposium Conducted at the 2019 Annual Meeting of the National Council on Measurement in Education. Editor M. Karvonen (Toronto, Canada: moderator).

Google Scholar

Barrett, J. E., Sarama, J., Clements, D. H., Cullen, C., McCool, J., Witkowski-Rumsey, C., et al. (2012). Evaluating and Improving a Learning Trajectory for Linear Measurement in Elementary Grades 2 and 3: A Longitudinal Study. Math. Thinking Learn. 14 (1), 28–54. doi:10.1080/10986065.2012.625075

CrossRef Full Text | Google Scholar

Bengio, Y., and Grandvalet, Y. (2004). No Unbiased Estimator of the Variance of K-fold Cross-Validation. J. Mach. Learn. 5, 1089–1105. Available at: http://www.jmlr.org/papers/v5/grandvalet04a.html.

Google Scholar

Briggs, D., Alonzo, A., Schwab, C., and Wilson, M. (2006). Diagnostic Assessment with Ordered Multiple-Choice Items. Heda 11, 33–63. doi:10.1207/s15326977ea1101_2

CrossRef Full Text | Google Scholar

Bürkner, P.-C. (2018). Advanced Bayesian Multilevel Modeling with the R Package Brms. R. J. 10 (1), 395–411. doi:10.32614/RJ-2018-017

CrossRef Full Text | Google Scholar

Bürkner, P.-C. (2017). Brms: An R Package for Bayesian Multilevel Models Using Stan. J. Stat. Soft. 80 (1), 1–28. doi:10.18637/jss.v080.i01

CrossRef Full Text | Google Scholar

Burnes, J. J., and Clark, A. K. (2021). Characteristics of Students Who Take Dynamic Learning Maps Alternate Assessments: 2018–2019. Technical Report No. 20-01. Lawrence, KS: University of Kansas, Accessible Teaching, Learning, and Assessment Systems.

Google Scholar

Carpenter, B., Gelman, A., Hoffman, M. D., Lee, D., Goodrich, B., Betancourt, M., et al. (2017). Stan: A Probabilistic Programming Language. J. Stat. Soft. 76 (1), 1–32. doi:10.18637/jss.v076.i01

CrossRef Full Text | Google Scholar

Clark, A., Kingston, N., Templin, J., and Pardos, Z. (2014). Summary of Results from the Fall 2013 Pilot Administration of the Dynamic Learning Maps™ Alternate Assessment System. Technical Report No. 14-01. Lawrence, KS: University of Kansas, Center for Educational Testing and Evaluation.

Google Scholar

Clark, A. K. Thompson W. J., and Karvonen, M. (2019). Instructionally Embedded Assessment: Patterns of Use and Outcomes. Technical Report No. 19-01. Lawrence, KS: University of Kansas, Accessible Teaching, Learning, and Assessment Systems.

Google Scholar

Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences. 2nd ed.. New York: Routledge. doi:10.4324/9780203771587

CrossRef Full Text | Google Scholar

Corcoran T. Mosher, F.A., and Rogat, A. (2009). Learning Progressions in Science: An Evidence-Based Approach to ReformConsortium for Policy Research in Education Report #RR-63. Philadelphia, PA: Consortium for Policy Research in Education.

Google Scholar

D. Bartholomew, M. Knott, and I. Moustaki (Editors) (2011). “Latent Class Models,” Latent Variable Models and Factor Analysis: A Unified Approach. 3rd ed. (West Sussex, United Kingdom: Wiley), 157–189.

Google Scholar

de la Torre, J., and Douglas, J. A. (2004). Higher-Order Latent Trait Models for Cognitive Diagnosis. Psychometrika 69 (3), 333–353. doi:10.1007/BF02295640

CrossRef Full Text | Google Scholar

Deng, N., Roussos, L., and LaFond, L. (2017).Multidimensional Modeling of Learning Progression-Based Vertical Scales. In 2017 Annual Meeting of the National Council on Measurement in Education. [Paper Presentation]. San Antonio, TX, United States.

Google Scholar

Duschl, R., Maeng, S., and Sezen, A. (2011). Learning Progressions and Teaching Sequences: A Review and Analysis. Stud. Sci. Edu. 47, 123–182. doi:10.1080/03057267.2011.604476

CrossRef Full Text | Google Scholar

Dynamic Learning Maps Consortium (2016). 2014–2015 Technical Manual—Integrated Model. Lawrence, KS: University of Kansas, Center for Educational Testing and Evaluation.

Google Scholar

Gelman, A., Carlin, J. B., Stern, H. S., Dunson, D. B., Vehtari, A., and Rubin, D. B. (Editors) (2013). “Model Checking,” Bayesian Data Analysis. 3rd ed. (Boca Raton, FL: CRC Press), 141–164.

Google Scholar

Gelman, A., Hwang, J., and Vehtari, A. (2013). Understanding Predictive Information Criteria for Bayesian Models. Stat. Comput. 24, 997–1016. doi:10.1007/s11222-013-9416-2

CrossRef Full Text | Google Scholar

Henson, R. A., Templin, J. L., and Willse, J. T. (2009). Defining a Family of Cognitive Diagnosis Models Using Log-Linear Models with Latent Variables. Psychometrika 74 (2), 191–210. doi:10.1007/s11336-008-9089-5

CrossRef Full Text | Google Scholar

Herrmann-Abell, C. F., and DeBoer, G. E. (2018). Investigating a Learning Progression for Energy Ideas from Upper Elementary through High School. J. Res. Sci. Teach. 55 (1), 68–93. doi:10.1002/tea.21411

CrossRef Full Text | Google Scholar

Hinne, M., Gronau, Q. F., van den Bergh, D., and Wagenmakers, E.-J. (2020). A Conceptual Introduction to Bayesian Model Averaging. Adv. Methods Practices Psychol. Sci. 3, 200–215. doi:10.1177/2515245919898657

CrossRef Full Text | Google Scholar

Jin, H., Shin, H., Johnson, M. E., Kim, J., and Anderson, C. W. (2015). Developing Learning Progression-Based Teacher Knowledge Measures. J. Res. Sci. Teach. 52 (9), 1269–1295. doi:10.1002/tea.21243

CrossRef Full Text | Google Scholar

Johnson, M. S., and Sinharay, S. (2018). Measures of Agreement to Assess Attribute-Level Classification Accuracy and Consistency for Cognitive Diagnostic Assessments. J. Educ. Meas. 55 (4), 635–664. doi:10.1111/jedm.12196

CrossRef Full Text | Google Scholar

Lenth, R. V. (2021). Emmeans: Estimated Marginal Means, Aka Least-Square Means. R package version 1.6.0. Available at: https://cran.r-project.org/package=emmeans.

Google Scholar

Liu, X. S. (2015). Multivariate Common Language Effect Size. Ther. Innov. Regul. Sci. 49 (3), 126–131. doi:10.1177/2168479014542603

PubMed Abstract | CrossRef Full Text | Google Scholar

Ma, W. (2021). A Higher-Order Cognitive Diagnosis Model with Ordinal Attributes for Dichotomous Response Data. Multivariate Behav. Res., 1–22. doi:10.1080/00273171.2020.1860731

CrossRef Full Text | Google Scholar

McElreath, R. (2016). “Sampling the Imaginary,” in Statistical Rethinking: A Bayesian Course with Examples in R and Stan (Boca Raton, FL: CRC Press), 49–70.

Google Scholar

McGraw, K. O., and Wong, S. P. (1992). A Common Language Effect Size Statistic. Psychol. Bull. 111 (2), 361–365. doi:10.1037/0033-2909.111.2.361

CrossRef Full Text | Google Scholar

Nash, B., Clark, A., and Karvonen, M. (2015). First Contact: A Census Report on the Characteristics of Students Eligible to Take Alternate Assessments. Technical Report No. 16-01. Lawrence, KS: University of Kansas, Center for Educational Testing and Evaluation.

Google Scholar

National Research Council (2001). Knowing what Students Know: The Science and Design of Educational Assessment. Washington, DC: The National Academies Press.

Google Scholar

Piironen, J., and Vehtari, A. (2017). Comparison of Bayesian Predictive Methods for Model Selection. Stat. Comput. 27, 711–735. doi:10.1007/s11222-016-9649-y

CrossRef Full Text | Google Scholar

R Core Team (2019). R: A Language and Environment for Statistical Computing. Version 3.6.1. [Computer software]. R Foundation for Statistical Computing. Available at: https://www.R-project.org.

Google Scholar

National Research Council (2007).Taking Science to School: Learning and Teaching Science in Grades K–8. Editors R. A. Duschl, H. A. Schweingruber, and A. W. Shouse (Washington, DC: The National Academies Press).

Google Scholar

R. Levy, and R. J. Mislevy (Editors) (2016). “Model Evaluation,” Bayesian Psychometric Modeling (Boca Raton, FL: CRC Press), 231–252.

Google Scholar

Roberts L. Wilson, M., and Draney, K. (1997). The SEPUP Assessment System: An Overview. BEAR Report Series, SA-97-1. Berkeley: University of California.

Google Scholar

Rupp, A. A., Templin, J., and Henson, R. A. (2010). Diagnostic Measurement: Theory, Methods, and Applications. 1st ed.. New York: Guilford Press. Available at: https://www.guilford.com/books/Diagnostic-Measurement/Rupp-Templin-Henson/9781606235270.

Google Scholar

Rupp, A. A., and Templin, J. L. (2008). Unique Characteristics of Diagnostic Classification Models: A Comprehensive Review of the Current State-Of-The-Art. Meas. Interdiscip. Res. Perspective 6 (4), 219–262. doi:10.1080/15366360802490866

CrossRef Full Text | Google Scholar

Sawilowsky, S. S. (2009). New Effect Size Rules of Thumb. J. Mod. App. Stat. Meth. 8 (2), 597–599. doi:10.22237/jmasm/1257035100

CrossRef Full Text | Google Scholar

Schwartz, R., Ayers, E., and Wilson, M. (2017). Mapping a Data Modeling and Statistical Reasoning Learning Progression Using Unidimensional and Multidimensional Item Response Models. J. Appl. Meas. 18 (3), 268–298.

PubMed Abstract | Google Scholar

Schwarz, G. (1978). Estimating the Dimension of a Model. Ann. Statist. 6 (2), 461–464. doi:10.1214/aos/1176344136

CrossRef Full Text | Google Scholar

Searle, S. R., Speed, F. M., and Milliken, G. A. (1980). Population Marginal Means in the Linear Model: An Alternative to Least Squares Means. The Am. Statistician 34 (4), 216–221. doi:10.1080/00031305.1980.10483031

CrossRef Full Text | Google Scholar

Shan, G., and Wang, W. (2013). ExactCIDiff: An R Package for Computing Exact Confidence Intervals for the Difference of Two Proportions. R. J. 5 (2), 62–70. doi:10.32614/RJ-2013-026

CrossRef Full Text | Google Scholar

Shepard, L. A. (2018). Learning Progressions as Tools for Assessment and Learning. Appl. Meas. Edu. 31 (2), 165–174. doi:10.1080/08957347.2017.1408628

CrossRef Full Text | Google Scholar

Simon, M. (1995). Reconstructing Mathematics Pedagogy from a Constructivist Perspective. J. Res. Math. Educ. 26, 114–145.

CrossRef Full Text | Google Scholar

Stan Development Team (2020). RStan: The R Interface to Stan. Version 2.21.2. [Computer software]. Available at: https://mc-stan.org/rstan.

Google Scholar

Supovitz, J. A., Ebby, C. B., Remillard, J., and Nathenson, R. A. (2018).Experimental Impacts of the Ongoing Assessment Project on Teachers and Students. Research Report No. RR 2018–1 in Consortium for Policy Research in Education (Philadelphia, PA: University of Pennsylvania), 16. Available at: https://repository.upenn.edu/cpre_researchreports/107.

Google Scholar

Supovitz, J., Ebby, C. B., and Sirinides, P. (2013).Teacher Analysis of Student Knowledge: A Measure of Learning Trajectory-Oriented Formative Assessment. Synthesis Report in Consortium for Policy Research in Education (Philadelphia, PA: University of Pennsylvania), 28.

Google Scholar

Swinburne Romine, R., and Santamaria, L. (2016). Instructionally Embedded Assessment. Project Brief No. 16-01. Lawrence, KSand Assessment Systems: University of Kansas; Accessible Teaching, Learning.

Google Scholar

Swinburne Romine, R., and Schuster, J. (2019). “Learning Maps as Models of the Content Domain,” in Beyond Learning Progressions: Maps as Assessment Architecture. Symposium Conducted at the Annual Meeting of the National Council on Measurement in Education. Editors M. Karvonen, (Toronto, Canada.

Google Scholar

Templin, J., and Bradshaw, L. (2014). Hierarchical Diagnostic Classification Models: A Family of Models for Estimating and Testing Attribute Hierarchies. Psychometrika 79 (2), 317–339. doi:10.1007/s11336-013-9362-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Templin, J. L., and Henson, R. A. (2006). Measurement of Psychological Disorders Using Cognitive Diagnosis Models. Psychol. Methods 11 (3), 287–305. doi:10.1037/1082-989X.11.3.287

PubMed Abstract | CrossRef Full Text | Google Scholar

Thompson, W. J. (2019). Bayesian Psychometrics for Diagnostic Assessments: A Proof of Concept. Research Report No. 19-01. Lawrence, KS: University of Kansas, Accessible Teaching, Learning, and Assessment Systems. doi:10.35542/osf.io/jzqs8

CrossRef Full Text | Google Scholar

Thompson, W. J. (2018). Evaluating Model Estimation Processes for Diagnostic Classification Models. (Publication No. 10785604) [dissertation]. Lawrence, KS: University of Kansas. ProQuest Dissertations and Theses Global.

Google Scholar

Vehtari, A., Gabry, J., Magnusson, M., Yao, Y., Bürkner, P., Paananen, T., et al. (2020). Loo: Efficient Leave-One-Out Cross-Validation and WAIC for Bayesian Models. Version 2.3.1. [Computer software]. Available at: https://mc-stan.org/loo.

Google Scholar

Vehtari, A., Gelman, A., and Gabry, J. (2019). Pareto Smoothed Importance Sampling. arXiv. Available at: https://arxiv.org/abs/1507.02646.

Google Scholar

Vehtari, A., Gelman, A., and Gabry, J. (2017). Practical Bayesian Model Evaluation Using Leave-One-Out Cross-Validation and WAIC. Stat. Comput. 27 (5), 1413–1432. doi:10.1007/s11222-016-9696-4

CrossRef Full Text | Google Scholar

Vehtari, A., Gelman, A., Simpson, D., Carpenter, B., and Bürkner, P.-C. (2021). Rank-Normalization, Folding, and Localization: An Improved Rˆ for Assessing Convergence of MCMC (With Discussion). Bayesian Anal. 16 (2), 667–718. doi:10.1214/20-BA1221

CrossRef Full Text | Google Scholar

Vehtari, A., and Ojanen, J. (2012). A Survey of Bayesian Predictive Methods for Model Assessment, Selection, and Comparison. Stat. Surv. 6, 142–228. doi:10.1214/12-ss102

CrossRef Full Text | Google Scholar

Yao, Y., Vehtari, A., Simpson, D., and Gelman, A. (2018). Using Stacking to Average Bayesian Predictive Distributions (With Discussion). Bayesian Anal. 13, 917–1007. doi:10.1214/17-ba1091

CrossRef Full Text | Google Scholar