Equational reasoning: A systematic review of the Cuisenaire–Gattegno approach

1. Introduction

Educational policy changes have shifted the focus of early mathematics education research from arithmetic (computation with numbers) towards algebra (computation with types) (NCTM, 2000; Greenes and Rubenstein, 2008). In this paper we offer some technical vocabulary to elucidate this transition. We recover some of the intellectual history of early algebra research: the use of the Cuisenaire–Gattegno (Cui) curriculum. Section 2 introduces the historical context of research on introducing equational reasoning into the early years of school mathematics and the mixed results of employing manipulatives within contemporary curricula. In Section 3, we describe the distinctive characteristics of the Cui programme, an integrated approach to manipulatives and curriculum. We review William Brownell's post-test experiment with Cui on which we based our study design. We structure our meta-analysis of the literature on Cui effectiveness to test his hypothesis that it's not just using Cuisenaire rods that leads to the significant effects, but fidelity to Gattegno's curriculum and pedagogy. Section 4 reports the results of that analysis.

Section 5 discusses the contribution of this work and next steps. Two online appendices provide supplementary material. Appendix A documents the 37 studies from which the meta-analysis is drawn. Cui was developed by Gattegno in collaboration with the developmental psychologist Jean Piaget and with Jean Dieudonné, an author of the Bourbaki reforms to mathematics education. A similar initiative taken by Davydov and his colleagues in the Soviet Union is receiving renewed attention in the contemporary literature (Coles, 2021). Like Cui Davydov's curriculum “develops algebraic structure from the relationships between quantities such as length, area, volume, and weight. The arithmetic of the real numbers follows as a concrete application of these algebraic generalizations... In a study in which the entire 3-year elementary curriculum of Davydov was implemented in a US school setting, children using the curriculum developed the ability to solve algebraic problems normally not encountered until the secondary level in the US” (Schmittau and Morris, 2004, p 60). Gattegno goes further than Davydov. He advocates from the outset the study all four arithmetic operations and unit fractions as operators for small numbers. Appendix B discusses the relationship of Cui to Piaget's theories and Davydov's experiments.

2. Early algebra research, manipulatives, and the reform of school mathematics

Algebra encompasses the relationships between quantities, the use of notation, the modeling of phenomena, and the mathematical study of change. While the word algebra is not often heard in elementary school classrooms, the mathematical experiences and conversations of students in early grades frequently include elements of pattern recognition and related algebraic reasoning.

Much of the debate about the nature of algebra in secondary school mathematics ignores this pre-algebraic experience. It focusses instead on the problems students face with techniques of symbol manipulation when algebra is introduced after arithmetic. For example, in discussing seventh grade student difficulties (Herscovics and Linchevski, 1994, p. 76) notes that “the detachment of a number from the preceding minus sign had a high incidence and this indicates that evaluating strings of operations is not a trivial problem. These difficulties indicate that some of the problems in early algebra find their origin in the students' arithmetic background and warrant further investigation.”

Hewitt (2011) in his study of secondary mathematics with the virtual manipulative Grid Algebra notes that to achieve proficiency in algebraic reasoning students need to be able to switch between several levels of abstraction:

• Algebra as appearance of letters.

• Algebra as working with or on the unknown.

• Algebra as an expression of generality using actions, words and gestures.

• Algebra as seeing the general in the particular and the particular in the general, and after Gattegno.

• Algebra as an attribute of the mind. Here he argues that “students were working with operations in order to carry out these tasks and the awareness of equivalence of different sets of operations was certainly operating upon operations” (Hewitt, 2011, p 9).

In this paper we will be concerned with how and how well early algebra might serve as an enabler of arithmetic proficiency (accuracy) and arithmetic fluency (accuracy and response time) and as preparation for future learning of equational reasoning. We review the role that physical and virtual manipulatives play in supporting both conventional school mathematics, and the conceptually enriched curriculum of Cuisenaire–Gattegno (Cui). Equational reasoning is a particularly important activity in elementary algebra and in reasoning about the behavior of computer programs (O'Donnell et al., 2006; Sangwin, 2015). Equational reasoning, operating on equations, includes substituting equivalent expressions within part of an equation as well as other forms of reasoning such as operating on both sides of an equation or splitting a single equation into cases. Asserting that two expressions A and B are equivalent means that in certain circumstances A may be replaced by B and vice versa. Asserting that two equations A = 0 and B = 0 are equivalent is subtly but crucially different. It means that the solutions of A = 0 are precisely the solutions of B = 0 i.e., those particular values of the variables coincide.

Equational reasoning is important for several reasons. For example students might be asked to give an example of a quadratic equation whose roots are x = 3 and x = 5. (Sangwin, 2005, p. 441) reports that most of his first year undergraduate students tackled this without the slightest hesitation. Nevertheless some of his weaker students “(enough to notice a pattern) did not realize that the factored form of a quadratic would provide an almost immediate answer and instead wrote the quadratic as p(x) = ax² + bx + c” and attempted to solve the simultaneous equations that resulted from substituting in the two roots.

Reasoning by equivalence is a refinement of equational reasoning: a repetitive formal symbolic procedure where algebraic expressions, or terms within an expression, are replaced by an equivalent until a “solved” form is reached. The goal is to replace an expression or a sub-expression in a problem by an equivalent expression to provide a new problem having the same solutions.

In high school graduation examinations a third of examinable content is reasoning by equivalence (Rasila and Sangwin, 2016). Students typically do not pay attention to domains of definition or explicitly indicate which steps guarantee equivalence of adjacent lines and which do not. For example when undergraduate students are asked to solve equations such as (x + 5)/(x − 7) − 5 = (4x − 40)/(13 − x), they typically reason by equivalence working line by line. Most students need many lines of working, for this example typically about a dozen. This is problematic because “elementary algebra contains a number of subtle ‘traps’, including division by zero, or gaining/loosing solutions by squaring/square rooting both sides of an equation” (Rasila and Sangwin, 2016, p. 4).

Sangwin (2016) notes that equational reasoning is as important in undergraduate mathematics as it is in computer science since:

1. It exists at every level from solving linear equations onwards.

2. It is the start of proof & rigor (deductive geometry).

3. It contains logic and extended calculation.

4. It is a part of many methods, e.g., solving ordinary differential equations.

5. It is a key part of many pure mathematics proofs: the induction step, epsilon-delta proofs.

6. It enables reasoning about and verification of software.

The Massachusetts Comprehensive Assessment System (MCAS) is a high stakes standardized test that has been used as an efficient opportunity to gather data on early algebra interventions over time. Narrative reports of small scale quasi-experiments with early algebra suggest that even a limited exposure to equational reasoning can help children to out perform their peers when they take part in MCAS (Kaput and Blanton, 2000; Schliemann et al., 2007). A longitudinal intervention study in Boston has shown that introducing algebra as part of the early mathematics curriculum is highly feasible. Specific representational tools—manipulatives, tables, graphs, numerical and algebraic notation, and certain natural language structures—can be employed to help students express functional relations among numbers and quantities and solve algebra problems (Carraher et al., 2008).

The evidence that given an appropriate “mathematising situation” young learners are capable of sophisticated reasoning continues to mount. It accumulates in the developing market for customized apps and in the literature recounting small scale experiments with pattern making with physical manipulatives and structured drawings (Radford, 2014, 2018; Borthwick et al., 2021). It has led to a renewed attention to equational reasoning. Some of this activity builds explicitly on the pioneering work of Caleb Gattegno and his collaborators working with Cuisenaire rods in the 1950's (Mason, 2008; Benson, 2011; Goutard, 2017; Adom and Adu, 2020). Other researchers, working from first principles, have independently discovered many of Gattegno's findings especially those relating to the central importance of early algebra, pattern making, and mathematical equivalence (Davydov, 1962; Kaput, 1995a,b; Healy et al., 2002; Schmittau and Morris, 2004; Carraher et al., 2005; Schliemann et al., 2007; Baez, 2009; Mulligan and Mitchelmore, 2009; Blanton and Kaput, 2011; Cai and Knuth, 2011; Empson et al., 2011; McNeil et al., 2011; Rittle-Johnson et al., 2011; Kieran et al., 2016; Gadanidis et al., 2018; Kieran, 2018; Matthews and Fuchs, 2018; Simsek et al., 2021).

Gattegno was a working mathematician and educator, and an early collaborator on mathematics teaching reform with the influential developmental psychologist Jean Piaget (Piaget and Szeminska, 1952; Sfard, 1995). Piaget had a substantial influence on the school mathematics curriculum in the West. He identified human thought itself with logico-mathematical structures and held a rigorous view on how children would grow their understandings. Both he and Gattegno paid attention to integrating conceptual mathematics into their theories of mathematical cognition (Choquet, 1963; Piaget et al., 1992). Piagetian commentators “have almost universally accepted that his ‘mathematisation’ is at worst ‘ideosyncratic’ and left it alone, concentrating on his claim to have demonstrated the process of acquiring knowledge through the clinical method” (Seltman and Seltman, 1985, p. viii).

By contrast Gattegno brought together a Commission of mathematicians that included Evert Beth, inventor of the semantic tableau used in formal reasoning, Jean Dieudonné, a prime mover in the Nicolas Bourbaki group that reformed university mathematics after WWII and Gustave Choquet whose work on capacities and integral representations found many applications in analysis and probability. Choquet was founding Commission President. He studied the Cui experiments teaching young children with Cuisenaire rods and became both an adept at the approach and a skilled user of the rods. Choquet's “What is Modern Mathematics,” became the Commission's manifesto. In it he drew attention to some of the key tools of Bourbaki's axiomatic method: sets, functions, morphisms, categories, and functors.

We have adopted this conceptual mathematical definition of algebraic structure, in particular the notion of a type as found in mathematics and computer science, where amongst other things it names a property common to the elements of a set. Expressed in these terms Gattegno's definition of algebraic awareness may be regarded as an appreciation that the composition of two elements of the same type can result in a third element with the same property.

Choquet wrote “Since Bourbaki has such clear-cut concepts and is so intimately associated with the development of mathematics in our time, we can hope that a study of ‘his’ philosophical and mathematical work may lead us to the essence of modern trends in analysis. Such as study may serve to develop for all levels of education a teaching of mathematics better adapted to the needs of our time and the level of awareness of our generation” (Choquet, 1963, p. 3).

Manipulatives like the Cuisenaire, Stern, and Montessori materials have found a place in Western mathematics classrooms from the time of diagnostic testing with counters (a la Piaget), to contemporary bead strings, Numicon tiles and the Rekenrek abacus. Today they are often augmented by toys such as the Rubik cube, animations such as BBC Numberblocks and “virtual” manipulatives, delivered through the web, on a tablet or on a standalone computer.

For the most part physical manipulatives such as Dienes blocks and animations such as Numberblocks represent decimal numbers. The Cui approach is an exception in that the rods are not given prescribed number names, rather names are first encoded as letters and then resolved to values by measuring one rod with another (the unit). This emphasis on measurement as a basis for number is shared with Davydov's approach. He writes, “such introduction of whole numbers greatly facilitates the subsequent mastering of fractions—both simple and decimal—since the child understands from the very outset, first that abstract number as a relationship, and, second, the value being measured as a homogeneous object that may be measured with any degree of precision” (Davydov, 1962, p. 35).

In their definitive meta-analysis of physical manipulatives, Carbonneau et al. (2013) found that “simply incorporating manipulatives into mathematics instruction may not be enough to increase student achievement in mathematics.” They identified several factors that determined the size of effect: “instructional variables such as the perceptual richness of an object, level of guidance offered to students during the learning process, and the development status of the learner moderate the efficacy of manipulatives.” Jones et al. (2019) note that a major drawback in such quantitative research studies is that while many studies seek to measure conceptual understanding most observations assess only procedural or surface understanding. They have shown how to create more sophisticated metrics in their work of the efficacy of computer applications for learning algebra.

Gilmore et al. (2017) explored the procedural skill, conceptual understanding and working memory capacity of 75 children aged 5–6 years as well as their overall mathematical achievement. They found that, not only were all three capabilities independently associated with mathematics achievement, but there was also a significant interaction between them. In fact levels of conceptual understanding moderate the relationship between procedural skill and mathematics achievement. Fuchs et al. (2014) conducted a controlled experiment with fourth grade at risk students with interventions in fraction learning, emphasizing fluency and conceptual knowledge. Results revealed a significant aptitude-treatment interaction, in which students with very weak working memory learned better with conceptual activities but children with more adequate (but still low) working memory learned better with fluency activities.

Virtual manipulatives enable an even more customized interaction although “something may be being lost in the translation” (Nemirovsky and Sinclair, 2020, p. 107). Especially for young children, technology manipulatives may be more manageable and extensible. In one study, third graders working with technology manipulatives made statistically significant gains learning fraction concepts (Reimer and Moyer, 2005). Although most apps for young learners concentrate on handwriting training and drill and practice, some create direct manipulation situations in which the underlying mathematical structure can be accessed (Bakos and Pimm, 2020). For example for 3–5 year olds, Little Digits is an iOS app that uses fingers to work out all permutations and combinations (number bonds) for small numbers, one author's notHiding is a one or two player pelmanism game to develop strategies to map between colors and their letter codes and between upper and lower case letter forms and Dragon Box introduces linear equations (Benson, 2012; CowleyOwl, 2012; DragonBox, 2012). Thai et al. (2021) reports on a cluster randomized study of a digital game-based learning environment that provides personalized content and adaptive embedded assessments which shows that it can improve mathematics knowledge of transitional kindergarten and kindergarten students.

3. Methods

Our goal was to review through a systematic analysis the historical development of Gattegno's pioneering work and its reception, with the intention of subsequently abstracting, replicating and extending the most promising statistical findings. In Section 3.1, we describe the distinctive aspects of the Cuisenaire–Gattegno approach. One of the highest-fidelity studies was due to William Brownell who designed an unusual longitudinal experiment to investigate the efficacy of Cui. In Section 3.2, we explain how Brownell created a balanced quasi-experiment. We do this to highlight some important effects and to motivate both the meta-analysis and a subsequent study (forthcoming) which examines the long term transfer effects.

3.1. Cuisenaire–Gattegno: An integrated approach to manipulative and curriculum

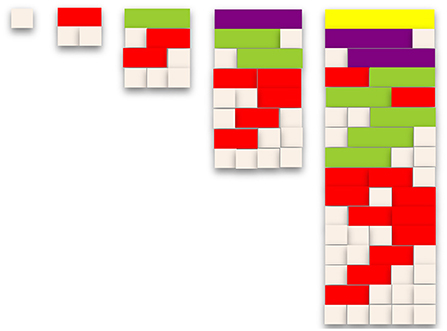
Cuisenaire rods are cuboids, the length of each a multiple of the length of the smallest—a 1 cm white cube. Rods of the same size have the same color. Each student has a box containing sufficient rods of different sizes to construct all the partitions of the smaller rods (Figure 1). In Cui physical and diagrammatic set combination and mathematical writing interacts with domain general reasoning aptitude as a preparation for arithmetic proficiency. Figure 2 shows how this educates learners' sensitivity to common patterns of mathematical relations by coordinating “vision, audition, haptic, sensorimotor and introspective modalities through constructions with color-coded rods of unit increments” (ATM, 1977, p. 185). Gattegno introduces the integers to teachers as the “numeral names for a sequence of diagrams constructed by partitioning” (Gattegno, 2010a, p. 80).

FIGURE 1

Figure 1. “Complete patterns” for small integers [1..5].

FIGURE 2

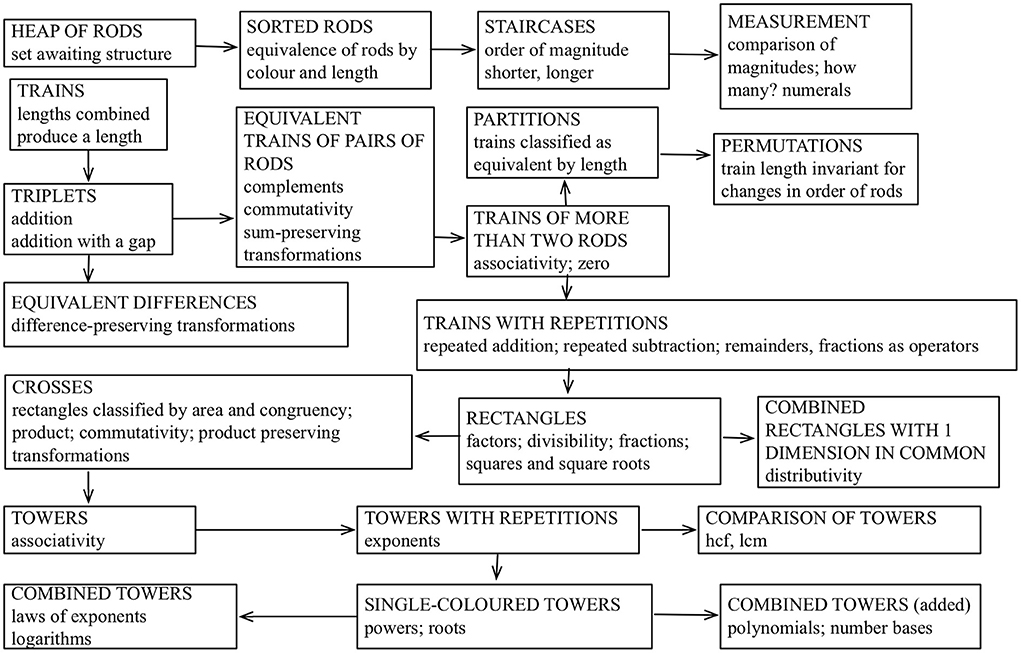
Figure 2. A flow chart for the Cui approach to coordinating vision, audition, haptic, sensorimotor and introspective modalities.

This experience of number is enhanced by the use of mathematical vocabulary, symbols and notation. From the outset Gattegno introduces the concept of “equivalence” as a generalization of “equivalent color” and “equivalent length.” Each “complete pattern” in the sequence of diagrams corresponds to an equivalence class of partitions of an integer (Figure 1). Other examples of equivalence are “equivalent expressions” (such as “w+r”, “r+w”) and equivalent equations. Figure 2 shows the conceptual coverage in the first 2 years of schooling. Concepts such a powers, roots, and logarithms go beyond the entitlements of the statutory UK National Curriculum. They prepare the way for the study of number systems of different bases: multi-digit numerals being formed by juxtaposing polynomial coefficients. This brings out the structure of the number system directly, in contrast with the conventional emphasis on the “place-value” reading of written numerals which takes up so much time in the early grades.

Color codes and expressions are at the same time named integer values, computed by measuring the length of one rod by another, and recipes for colored rod constructions: “+” for example being the action of placing two rods end to end to form a “train”. Gattegno generalizes the concepts of school algebra to encompass sensitivity to the dynamic that combines two objects of the same type (“w”,“r”) to form a third of that type (a named rod construction). He intended to make teachers and pupils aware of this dynamic which transforms rod constructions, diagrams, written expressions and equations into equivalent forms. He contrasted this “algebraic awareness” of the nature of number systems with traditional symbol manipulation in school algebra and with drill-based factual fluency (Gattegno, 1983). He summarized his philosophy in these terms, “the most important lesson that teachers can learn is that rather than teach mathematics we should strive to make people into mathematicians” (Gattegno, 2010a, p 82).

Gattegno uses operations with the rods—placing them end to end, side by side or stacked as towers—to model sets with structure such as the integer and rational number systems. In the Cui approach “all the operations with integers and fractions can be studied simultaneously (with colored rods); whole numbers being recognized as the equivalence class of their partitions and fractions as ordered pairs, one serving to measure the other, or as operators belonging to classes of equivalence which are the rational numbers involved in the operations” (Fedon, 1966, p. 201). He demonstrated that “Children of six or seven are thoroughly familiar with their tables, children of five conceive and compare fractions easily and accurately, children of eight solve simultaneous equations and at 10 they understand permutations and combinations which they themselves form and analyse” (Gattegno, 1956, p. 88).

The Cui programme has four distinctive characteristics.

Firstly, it consists of a suite of textbooks and teachers' guides with exercises with permutations of rods. These encourage the learner to pay attention to the relationship between quantities. They give rise to a substantial experience with integers and rational numbers (Cuisenaire and Gattegno, 1953, 1962; Gattegno, 1959, 2010a, 2011a; Benson, 2011; Goutard, 2017; Adom and Adu, 2020).

Secondly, the exercises are organized in a concept graph with 55 key mathematical concepts and their inter-dependencies. Gattegno calls this a map of elementary mathematics derived from tables of partitions. The map is drawn as a directed graph—a data structure studied in computer science. Nodes representing concepts are linked by a network of arrows. The graph introduces learners from the outset to concepts such as equivalence, set, function and domain. The arrows illustrate the dependencies between the concepts. The graph has four root nodes based on a study of subsets of the complete patterns of partitions. The hierarchy of conceptual dependencies is in places eight levels deep (Gattegno, 2010a; ATM, 2017; Cane, 2017). The technical vocabulary in the concept graph covers two sets of ideas: concepts that appear both in the graph and the textbooks are intended for learners, concepts that appear only in the graph are for teacher education. Coverage of the concepts means that teachers understand the graph in its totality. The idea that teachers need to know more than the statutory school curriculum in order to teach mathematics well is sometimes called “subject matter knowledge at the mathematical horizon” (Zazkis and Mamolo, 2011).

Thirdly, young children write expressions and equations in all four arithmetic operations and unit fractions as operators—initially for computation with types and subsequently for computation with small numbers. Gattegno called this sequence “algebra first” in contrast with conventional “counting first” school mathematics.

Fourthly, the “subordination of teaching to learning”: a theory of learning based on conscious (or unconscious) “awareness” as the unit of study (Gattegno, 1970, 1987, 2010c; ATM, 2018). Young and Messum (2011) have reviewed this model of human learning and shown how it can be applied both inside and outside the classroom. Griffin (2018) has described the questions teachers ask themselves when designing mathematical tasks in this approach:

• What might students (or teachers) be noticing (inside themselves) when engaged in the activity—what awarenesses might arise?

• How can I maximize the possibility that these awarenesses are available to the students (or teachers), that there is an awareness of these awarenesses so that it enables action—i.e., that the awareness can be educated.

• What is my role as the teacher in all this? When do I “step in” and when do I “step away” in order that the student is genuinely working with their own awareness but I am supporting that process and maybe helping it to be more efficient—how can my teaching be subordinated to the learning? and, when working with teachers:

• What activities and approaches enable teachers to be aware of this phenomenon themselves (that it is profitable for students to be aware of their own awareness) and consider how they might support this in their students—awareness of awareness of awareness.

3.2. Study design

Observational studies of early adopters of Cui were generally positive and in British Columbia a Royal Commission recommended a large-scale study with a view to integrating the method into elementary teacher training programmes (Howard, 1957; Ellis, 1964). Such findings encouraged researchers to compare the Cui vs. Conventional approach. Robinson cites 50 qualitative comparisons employing 15,000 students over several grade levels. He writes, “One could say that research reported to date has compared the effects of some 20,000 student years of Cuisenaire exposure to the effects of the equivalent amount of ‘traditional’ instruction” (Robinson, 1964).

Gattegno's work caught the attention of William Brownell, a pioneer of educational research and sometime president of the American Educational Research Association (Kilpatrick and Weaver, 1977). Brownell was open to Gattegno's intellectual ambition since he believed that “Children differ markedly in the ways in which they think of numbers and in the ways in which they learn number facts. No adequate measurement of degrees of development can be made, therefore, unless the measures of speed and accuracy are supplemented by a measure of the maturity of the processes employed in dealing with numbers” (Brownell, 1928, p. 201). As Dean Emeritus of the Berkeley School of Education Brownell undertook several large scale quantitative and qualitative studies of Cui (Brownell, 1967a,b).

Our study design drew on Brownell (1967b), an unusual design for this kind of evaluative research and one of the larger longitudinal studies. We will describe the study in some detail as it was the most comprehensive study to date. It was conducted in Scotland and California. Brownell administered pen and pencil tests to (n = 1,109) learners who remained in the program after 3 years of schooling—at the end of Scottish Primary III. It was a post-test-only control quasi-experiment classified as design type 6 by Campbell and Stanley (1963). Brownell recruited classrooms from 24 schools. Half of the classes had followed a pure Cuisenaire–Gattegno course of study, and half the traditional “counting first” curriculum. Teaching intensity averaged between 33 and 67 min per day. Accordingly Brownell divided his data into longer and shorter durations of study. Brownell assessed children's domain general cognitive skills that fall outside mathematics via a standardized verbal reasoning test, although he conceptualized this scholastic aptitude as “IQ” (sic) at the time. This test was administered at the end of the 3 years (Brownell, 1967b). Learners were selected at random from each group, matched by age, gender and verbal reasoning skills. High and Low scholastic aptitude subjects were determined by removing the middle 20% from the verbal reasoning distribution. This resulted in a smaller sample of 405 X and 453 C. The data was then divided into eight cells based on treatment (X, C), scholastic aptitude (Hi, Lo) and teaching intensity (high, low). Teaching in the range 31–34 min per day was classified as low intensity, and the range 47–64 min per day was taken as high intensity (Brownell, 1967b). From these eight cells, one cell would have been identified as having the smallest sample which in this case was 38. For statistical inference testing, it is desirable to have equal sample sizes in each cell. The reason why Brownell does this is to eliminate unwanted correlations between the additional variables e.g., scholastic aptitude and intensity of teaching. By doing this, he ended up mimicking a balanced experimental design which in an ideal world would have been achieved before the tests were administered. Obviously in this case it was not practical since children are allocated to schools by their parents and local authorities and not by Brownell. To achieve a balanced design Brownell removed samples from the other seven cells at random until he had 38 pupils in each cell. His final sample size was 304. This meant 1,003 of the original 1,337 population were excluded. By setting aside data in this way Brownell introduced a potential risk that the excluded pupils might have given different results.

He tested material covered in both courses of study (the Common test), and content covered in only one of them (the CUI and TRA tests). Brownell used an ANOVA test to confirm that the differences and interactions between effects were significant. High teaching intensity studies showed evidence of a treatment effect in all three tests. The interactions between treatment and scholastic aptitude in all three tests were statistically significant. Referring to the aptitude-treatment interaction Brownell wrote that “it is reasonable to suggest that children identified as low in intelligence and exposed to a relatively long period of instruction in arithmetic will gain more through involvement in the Cui program” (Brownell, 1967b). In the case of the CUI test it is children who scored highest on his scholastic aptitude task who gained the most.

3.3. Systematic review protocol

The goal of the meta-analysis was to evaluate the effectiveness of the Cuisenaire–Gattegno interventions on measures of mathematical performance. To find all studies that met our criteria, we conducted a literature search using the search terms Cuisenaire, Cuisenaire Gattegno, and Cuisenaire Gattegno quasi-experiment in the full text databases of ProQuest dissertations, theses and scholarly journals, ERIC, Google Scholar, JSTOR and Association of Teachers of Mathematics. We included the journals Educational Studies in Mathematics, Arithmetic Teacher, Mathematics Teacher, Review of Educational Research, For the Learning of Mathematics, Mathematical Gazette, Journal for Research in Mathematics Education and Zentralblatt für Didaktik der Mathematik. In the case of Masters and Doctoral dissertations we followed up bibliographic references. Where possible we consulted or obtained copies of the primary sources and repeated our enquiries on subsequent bibliographic references.

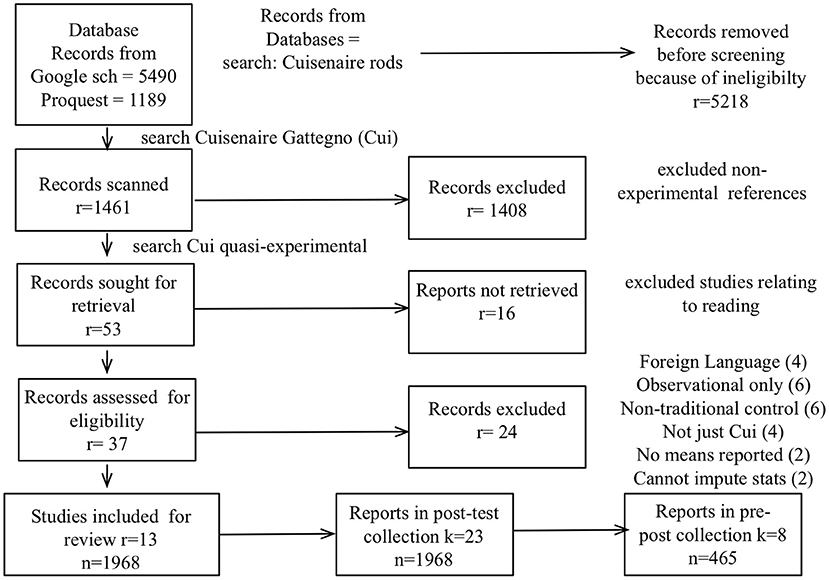
An initial search was conducted in Stanford libraries in 2005. It was last updated in March 2022. In total, the Cuisenaire searches returned 1,189 Proquest items and 5,490 Google Scholar items. Cuisenaire Gattegno returned 151 Proquest and 1,310 Google Scholar items. These abstracts were investigated for relevance to the topic. Relevant abstracts included general reviews of the use of manipulatives and references to experiments and quasi-experiments in elementary schools. This produced a long list of 37 quantitative studies for which abstracts were available (with full-text examination if necessary to determine inclusion). These are summarized in a table in Appendix A.

These 37 studies examined the impact of Cuisenaire rods on arithmetic development in children including those which reported a metric for arithmetic understanding. These tests quantify performance with arithmetic operations. They range from evaluating simple addition and subtraction expressions to missing number sentences to working with fractions. We looked for tests that could inform our research with the Woodcock-Johnson Mathematics Fluency subscale, a metric widely used in cognitive, educational and neuro-imaging studies (Woodcock et al., 2007). We excluded four foreign language dissertations that did not have an English translation, observational studies and studies where the control did not follow a traditional curriculum. Our analysis required reported means and standard deviation or sufficient statistical detail to allow us to impute these values. One dissertation was excluded as it did not report means.

These experiments can be distinguished by the experience of teachers with the Cui approach, type of intervention and control, the number of final sample subjects (n), grade level, duration, design [Experiment (EX), Quasi-experiment (QEX), Observational (OB)], availability of pre-test and post-test means and standard deviations, within and between subjects analysis and fidelity to the Cui approach. Unless otherwise reported, as in Brownell (1967a), a school year is taken as 180 days of teaching at five mathematics lessons of 50 min per week.The direction of the reported effect is shown as Cui = Control, Cui > Control, or Cui < Control. Peer reviewed findings were equally balanced between Cui and conventional teaching. Other studies were more favorable to Cui.

In preparation for the meta-analysis we excluded foreign language studies, du Bon Pasteur (1966), Bellemare (1967), Lin (2013) and Huang (2019) and all of which reported a direction for the effect of Cui > Control. We also excluded Brownell (1967a, 1968) which was a three way study in the relative conceptual development achieved by Cui, Tra (Traditional), and Dienes programs assessed using the techniques of observation and interview. We excluded observational studies in which there was no explicit control (Beard, 1964; Steencken, 2001; Bulgar, 2002; Marchese, 2009; Yankelewitz, 2009) or where the control didn't follow a conventional curriculum (Gell, 1963; Fedon, 1966; Sweeney, 1968; Lamon and Scott, 1970; Fennema, 1972; Keagle and Brummett, 1993). Rich (1972) was excluded as his experiment was not restricted to Cuisenaire. Rodman (1964), Rawlinson (1965) and Allen (1978) were excluded as they did not report means.

Whilst the remaining papers and dissertations recorded means and sample sizes, many were poor at recording the standard deviations. We included studies where a standard error of difference in the means, p-value, T or F statistic was included under the assumption that the coefficient of variation would be the same for experimental and control samples. This allowed us to impute the standard deviations for Nasca (1966) and Dairy (1969) although Dairy (1969) only reported means for her Kindergarten sample. Hollis (1964, 1965) reported means for three different pre-post tests. We excluded her evidence as we found no basis to estimate the relative coefficients of variation for the 3 different types of tests.

Haynes (1963) described two experimental (E1, E2) samples with a single control sample (C3). It was possible to explicitly derive 3 sample standard deviations using simultaneous equations and compare these with our imputation method. When we did this the largest error was 7%. Since the standard error of the difference between mean experimental and mean control was known for each pair, this allowed us to compute the pooled variance, PV, as follows (nX and nC being the size of the experimental and control samples):

$\begin{array}{l}PV=\frac{{Standard\text{\_}Error\text{\_}Diff}^2}{\frac{1}{nX}+\frac{1}{nC}}\end{array}$

Similarly pooled variance may be calculated as a weighted average of the sample variances where the weights are the sample degrees of freedom. Since the experimental and control sample sizes were identical we were able to derive each pooled variance as a straightforward average of the sample variances. Thus we ended up with 3 simultaneous equations

$\begin{array}{l}{V}_{E1}+V_{E2}=2*P{V}_{E1E2}\\ V_{E1}+V_{C3}=2*P{V}_{E1C3}\\ V_{E2}+V_{C3}=2*P{V}_{E2E2}\\ \end{array}$

Which were solved to derive the sample variances (V_S).

Robinson (1978) like Haynes (1963) reported two experimental classes matched with a single control. In both cases we amalgamated the two experiments by taking a weighted average of the means and calculating the combined standard deviation. Egan (1990) uses different measures for pre and post tests and is included only in the post-test analysis.

It was not possible to recover the standard deviations for Passy (1963a,b) as we could not discover the true sample sizes. The sample sizes given in the peer-reviewed article are much higher than implied by the degrees of freedom in an ANOVA table in his dissertation. This suggests some data has been removed but no explanation is given as to how and why the data was removed. Ellis (1964) doesn't mention p-values, T or F statistics or standard error of difference so we were not able to recover the standard deviation. Adom and Adu (2020) reported an effect size of 5 with a T2X standard deviation more or less the same as the T1X data. Since the standard deviation is normally proportional to the mean, and the mean doubled we would expect a doubling of the standard deviation. We therefore excluded it from the meta-analysis.

3.4. Meta-analysis

Meta-analysis was performed using the open-source statistical software package R, and employing the metafor package. Analyses were carried out using the standardized mean difference (effect size) as the outcome measure. A random-effects model was fitted to the data. The amount of heterogeneity (i.e., τ²), was estimated using the restricted maximum-likelihood estimator (Viechtbauer, 2005). In addition to the estimate of τ², the Q-test for heterogeneity (Cochran, 1954) and the I² statistic are reported (Higgins and Thompson, 2002). In case some amount of heterogeneity is detected (i.e., τ² > 0, regardless of the results of the Q-test), a prediction interval for the true outcomes is also provided and shown at the bottom of the forest plot. It is centered at the summary estimate, and its width accounts for the uncertainty of the summary estimate, the estimate of between study standard deviation in the true treatment effects (τ), and the uncertainty in the between study standard deviation estimate itself. It indicates the possible treatment effect in an individual setting (Riley et al., 2011). Studentized residuals and Cook's distances are used to examine whether studies may be outliers and/or influential in the context of the model (Viechtbauer and Cheung, 2010). Studies with a studentized residual larger than the 100 × (1−0.05/(2 × k))th percentile of a standard normal distribution are considered potential outliers (i.e., using a Bonferroni correction with two-sided α = 0.05 for k studies included in the meta-analysis). Studies with a Cook's distance larger than the median plus six times the interquartile range of the Cook's distances are considered to be influential. The rank correlation test (Begg and Mazumdar, 1994) and the regression test (Sterne and Eggar, 2005), using the standard error of the observed outcomes as predictor, are used to check for funnel plot asymmetry.

4. Results

After systematic application of these inclusion principles, 13 studies were deemed to pass all the above criteria. The process of selection of studies is summarized in Figure 3. These remaining studies gave rise to a collections of post test reports and pre-post test reports. To investigate the effect of fidelity to Cui we created a weighted ranking of the 13 studies, according to dimensions of fidelity suggested by Brownell. Several of these studies contained more than one comparison between control and treatment conditions appropriate for inclusion in the meta-analysis, such as when results were reported separately for males and females and by grade. In all this gave rise to k = 23 post-test contrasts at grade and gender level and k = 8 pre-post contrasts, each contrast representing an independent and distinct population of students. Where studies presented results from two or more independent samples (each with a control group) that received the same intervention they were coded as distinct assessments in our analysis. This gave a final assessment count of 23 (n = 1,968, nX = 1,096, nC = 928) for the post-test meta-analysis and 8 (n = 465, nX = 244, nC = 221) for the pre-post meta-analysis.

FIGURE 3

Figure 3. A Prisma flow chart for the selection of studies.

In each study we selected an outcome measure that best captured the construct of arithmetic fluency and best approximated the Woodcock-Johnson Mathematics Fluency subscale. Five studies reported the Metropolitan Readiness or Achievement Test, two studies the Science Research Associates Arithmetic test and other studies measured proficiency with fractions and missing number sentences (see Table 1). Brownell reported his raw data results at a test item level. We used the items below to construct a measure of arithmetic proficiency from his Common test missing number sentences that we could compare with the studies in our meta-analysis and we could use in our replication and extension study (forthcoming) (Brownell, 1967b, and Appendix):

$\begin{array}{c}2\times \square =12\\ 12-\square =7\\ 6+\square =14\\ 9-\square =0\\ \square +7=10\\ \square -5=7\\ \square ÷2=7\\ \square +8=8\\ \\ \end{array}$

TABLE 1

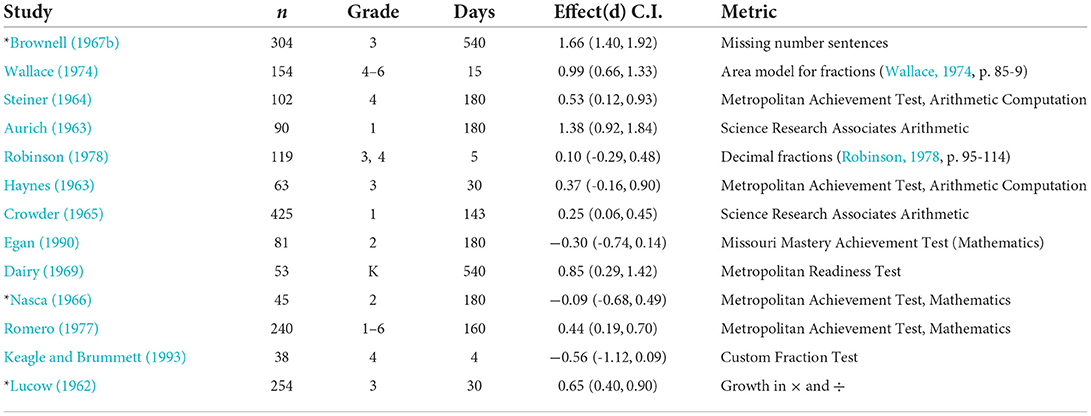
Table 1. Experiments included in the post-test meta-analysis ranked in order of fidelity (Peer reviewed findings are marked ^*).

Studies can be distinguished by the experience of teachers with the Cui approach, the number of final sample subjects (n), grade level, gender, frequency and duration of mathematics lessons, experiment design, control design, statistical tools and fidelity to the Cui approach.

Effect sizes were computed directly from the means and standard deviation values obtained from the manuscripts without regard for statistical significance reported in the source materials. For example, in one case (Haynes, 1963), a contrast originally reported as a null result appears in Table 1 as a small effect.

4.1. Quantifying fidelity to central Cui scholarship, curriculum, and pedagogy

The Cui approach was transmitted to the world through specific artifacts: an original curriculum and text books intended for children, scholarly books and papers, secondary literature that related Cui to main currents of mathematics education research and accounts of adoption. We explored an hypothesis that transmission became less effective the further a study drifted away from these benchmarks and that this might account for a significant element of the heterogeneity in the true effects/outcomes in the meta-analysis.

We quantified these aspects of the studies in four dimensions: the curriculum experienced by the learner (rank_learn), the teacher's experience with Cui (rank_teach), the teachers' Cui training (rank_train) and the preparation of the research team (rank_research). The 13 studies were compared by an independent adjudicator against one another in each dimension and ranked in order from most (1) to least (13) faithful. The adjudicator holds a PhD in applied mathematics. She was familiar with the overall literature, Cui classrooms and the criteria for ranking. The studies themselves were anonymized. In the event that all 13 studies were distinctive she ranked them from 1 to 13. In other dimensions were there were fewer distinctions some rankings were duplicated or not assigned.

The relative weights for these dimensions were chosen to reflect Brownell's account of his studies. He wrote “Dr. Gattegno stressed algebra more, and arithmetic less, than had M. Cuisenaire; and he formulated a system of instruction to which British teachers who follow the “Cui. program” adhere more or less scrupulously: Cuisenaire and Gattegno (1953), Gattegno (1957), Gattegno (2010b), Gattegno (2011b)” (Brownell, 1967a, p.14). We gave the highest weighting (4) to this curriculum and pedagogy as this is what the learners experience moment by moment. Then we weigh teacher experience (3) and preparation to deliver the curriculum with fidelity (2) and finally we weigh the evidence of researcher awareness of the debate on “number first” vs. “algebra first” progression (1). The overall metric for fidelity for a study was computed with the formula

$\begin{array}{l}fidelity=4*ran{k}_{learn}+3*ran{k}_{teach}+2*ran{k}_{train}+ran{k}_{research}\end{array}$

In the learn dimension the highest ranking was given to reports that exhibited evidence that they used Gattegno's curriculum in the classroom. Credit was given if the study reproduced a précis of the Cuisenaire–Gattegno approach and cited the seminal text-books for pupils (Gattegno, 1957, 1963). Brownell (1967a), for example, devoted seven pages to a description of “computation in the Cuisenaire program” written by the teacher who coordinated teacher training for his study. The lowest ranking studies have only a rudimentary account of Cui. They do not cite the seminal books.

In the teaching experience dimension the highest rankings were given to studies that reported more than 1 year's prior teaching experience with the approach.

In the teacher training dimension we looked for citations of Gattegno's seminal teacher training books and his writing on educational research. These influential works are listed in the bibliography below. This was taken to be evidence of the quality of teacher training.

In the research dimension we assessed the preparation of the research team by examining the extent to which the study's bibliography and Sections 5 covered the contemporary literature on early algebra and manipulatives.

Once the set of fidelities for the 13 studies had been computed it was mapped into an ordinal variable with values 1–8. This was calculated by dividing the difference between highest and lowest value into eight equal intervals, and assigning the resulting “fidelity rank” to each of the 13 studies. We did this because we wanted to design a moderator with a granularity that took account of the subjective nature of the classification. We didn't think that it was warranted to use the precision that the raw fidelity statistic implied.

These measures can only be informed by what the authors choose to report in their papers or dissertations. It could be that the authors did not mention something that was very significant within one or more of these dimensions. Nevertheless the literature as a whole conforms to Mason's observation that educational research tends to privilege novelty over coherence. He writes, “In the early 1980s I had the chance to attend a number of seminars led by Caleb Gattegno when he tried to re-vivify his science of education in the mathematics education community in England. ...I began to get a taste of what it is like when an experienced “gray-beard” assembles their to-them-coherent-and-comprehensive framework or theory. Whereas when the fragments were being worked on and described there is often considerable interest amongst colleagues, once the whole is assembled, people don't really want to know” (Mason, 2010, p. 5). Brownell's early attention to fidelity in study design, which was echoed by du Bon Pasteur (1966) and Bellemare (1967), is exceptional in the literature by the care taken to reflect the original Cui framework.

4.2. Results of the meta-analysis

The analysis was carried out using R (version 4.0.4) (R Core Team, 2020) and the metafor package (version 2.5.82) (Viechtbauer, 2010). Analysis was carried out using two different approaches: a random effects model for three analysis of arithmetic proficiency (k = 8, 13, 23), and a mixed effects model for the analysis of the fidelity rank as a moderator (k = 13). Several of the 13 studies in Table 1 presented results from two or more independent samples (each with a control group) that received the same intervention. They were coded as distinct assessments in our analysis, giving an assessment count of k = 23 (n = 1,968) for the post-test meta-analysis and k = 8 (n = 425) for the pre-post meta-analysis.

Metafor takes pooled standard deviation from the samples at T1 and T2. This assumes that the subjects are different at the two time points—which they are not in general. As a result the pooled standard deviation is an overestimate and the effect size is an underestimate.

In the first r = 13 analysis we used a single measure per study (i.e., k, the number of contrasts, was 13) as shown in Table 1. The weighted average effect size was d = 0.5 (95% C.I. 0.16, 0.84) with the majority of estimates being positive (77%). Therefore, the average outcome differed significantly from zero (z = 2.8969, p = 0.0038). Cohen suggested that d = 0.2 be considered a “small” effect size, 0.5 represents a “medium” effect size and 0.8 a “large” effect size (Cohen, 1988). That is, if two groups' means do not differ by 0.2 standard deviations or more, the difference is trivial, even if it is statistically significant. We analyzed sub-groups of studies according to the measure chosen. For the nine independent studies using the Metropolitan Achievement Test (n = 450) there was a small effect size of 0.34 (95% C.I. 0.10, 0.59) and for the 3 Science Research Associates arithmetic tests (n = 515) there was a large effect size 0.94 (95% C.I. 0.16, 1.72).

We calculated the prediction interval for the k = 13 analysis (−0.70, 1.71) with the metafor predict function. This indicates that the average effect does not tell us much about what happens in any particular study as there is a great deal of heterogeneity, that is between study variance. In Section 4.3, we explore how we might account for this variation. The r = 13 studies gave rise to k = 23 post-test reports, and k = 8pre-post reports.

The weighted effect size for the k = 23 post-test experiments was d = 0.55 (experimental sample size nX = 1,040, control sample nC = 928). The Confidence interval was (0.3, 0.8) and prediction interval (−0.56, 1.66).

The pre-post meta-analysis is shown in Table 2. These assessments used the same metrics as those in Table 1. The prediction interval was (−0.24, 1.47) with a weighted effect size of d = 0.61 (nX = 244, nC = 221).

TABLE 2

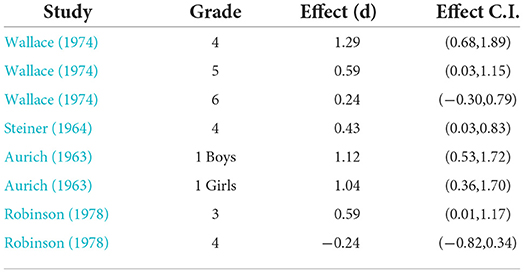
Table 2. Pre-post-test effect size (d), Confidence Intervals (C.I.) for the influence of Cui on arithmetic proficiency outcomes.

Figure 4 shows the observed outcome effects for the r = 13 studies in Table 1. The three random effects models confirm that our findings are broadly robust to treating each study as one observation rather than treating independent samples within each study as separate assessments.

FIGURE 4

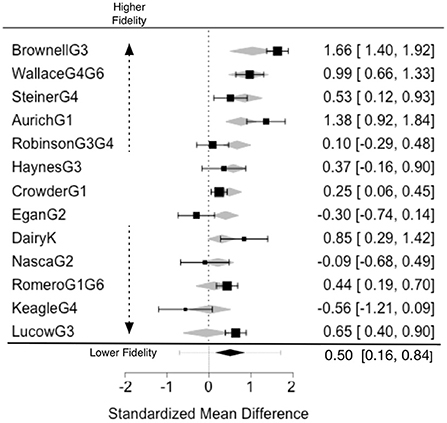
Figure 4. Post-test effect size (d) showing predicted (diamond) and observed (bar) proficiency outcome effect sizes by experiment in order of fidelity. Prediction interval and summary “diamond” for C.I. for estimate.

4.3. Assessing the effect of fidelity

We built a mixed effects model to study the extent to which arithmetic proficiency was influenced by fidelity to the Cui approach. The 13 experiments were ordered within each dimension by an external adjudicator. A weighted average ranking from 1 to 8 was calculated for each experiment and the results entered as a moderator in the meta-analysis.

Figure 4 shows the observed proficiency outcomes and a prediction based on the mixed effects model by experiment in order of fidelity. The gray diamonds show the predicted effects and their CI limits. The model shows that when fidelity changes by 1 on the 1 to 8 scale we used, the estimated effect size decreases by 0.19. The effect size for fidelity 1 was 1.2 which reduced to effect size −0.06 for fidelity 8. We checked to see if the effect of fidelity was non-linear but the model showed no sign of that and so our final model assumes the effect of fidelity is linear.

According to the Q-test, the true outcomes appear to be heterogeneous [Q₍₁₂₎ = 135.7691, p < 0.0001, τ² = 0.3461, I² = 91.8758%]. A 95% prediction interval for the true outcomes is given by −0.6990 to 1.7054. Hence, although the average outcome is estimated to be positive, in some studies the true outcome may in fact be negative.

An examination of the studentized residuals revealed that none of the studies had a value larger than ±2.8905 and hence there was no indication of outliers in the context of this model. According to the Cook's distances, none of the studies could be considered to be overly influential. Neither the rank correlation nor the regression test indicated any funnel plot asymmetry (p = 0.6754 and p = 0.1617, respectively).

A statistically significant relationship between treatment effect size and the rank order of fidelity to Gattegno's curriculum/pedagogy was revealed by a QM test of moderators [Q_M(df = 1) = 5.8416, p = 0.0157] (Viechtbauer, 2021). As evident in Figure 4 studies with the highest fidelity rankings produced effect sizes >1, while effects fell off systematically as evidence of fidelity to the original work waned. In fact, rank order of fidelity to the seminal work accounted for 32% of the heterogeneity of outcomes (R²).

5. Discussion

5.1. Findings

In this paper we have brought together two pieces of scholarship that interact and combine to form a new view of Cuisenaire–Gattegno. We have reappraised (Brownell, 1967b) one of the most rigorous previous studies and conducted a meta-analysis guided by Brownell's observations on the need for fidelity. In a forthcoming paper we report on a replication-extension of Brownell's experiment to investigate his hypothesis that the algebraic understanding gained by following the Cui approach will underpin later arithmetic and algebraic proficiency.

Brownell held that “one cannot “play around” with the Cui program.... expertness of the teachers is a prime requisite to success. Otherwise, classroom activities with the Cuisenaire rods may amount to no more than the haphazard manipulation of colored sticks” (Brownell, 1967a, p. 195). Our meta-analysis concurred that fidelity of transmission of the Cui equational reasoning approach is a moderator in arithmetic proficiency.

Attribute-treatment interactions such as the one reported by Brownell are increasingly studied in mathematics education research. This is because individual differences in children's cognitive resources are associated with mathematics learning, even when individual differences in elementary mathematics knowledge are statistically controlled. This indicates that mathematics intervention should be designed to help students with poor foundational mathematics skills compensate for limitations in the cognitive resources associated with poor learning.

5.2. Conclusions

Gattegno's work promoting Cuisenaire's invention and developing the Cui curriculum was seen by Brownell and his colleagues as a promising direction for mathematics education research. Their appraisal was endorsed by teachers' associations across the francophone and anglophone worlds. Our meta-analysis has highlighted that Cuisenaire rods can have a large effect on arithmetic proficiency and algebraic understanding if rigorous attention is given to the appropriate curriculum and pedagogy.

The meta-analysis showed that the average outcome is estimated to be of medium effect size, yet the efficacy of this approach is remarkably heterogeneous. Rather than attributable to noise, efficacy results appear to follow a pattern of diffusion, in which strong effects associated with the seminal curriculum materials and pedagogical practices dissipated as the teaching aides were adapted and the curriculum materials that inspired them were left behind. A high fidelity to the Cui approach was associated with a large effect size (1.2). This impact was reduced by 16% for each of eight levels of divergence from a benchmark we based on Brownell.

The policy implications are significant. As with all pedagogical interventions we have asked the key questions, who does it benefit? and, in what contexts? Our findings endorse Brownell's conclusions that learners falling below expected levels of academic performance may benefit most from gains in arithmetic fluency while leaners of all aptitudes will gain in algebraic reasoning. While his study can be readily adapted by researchers and teachers as a successful intervention in early years algebra through equational reasoning these results suggest that adoption of the Cuisenaire rods alone may be insufficient, and that careful consideration of how to effectively adopt the original curriculum and pedagogy is advisable.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

IB, NM, and BM contributed to conception and design of the meta-analysis and performed the statistical analysis. IB organized the dataset and wrote the first draft of the manuscript. NM and BM wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

The work has been part funded by a network of schools, the Ogden, Sutton and Shuttleworth Foundations, the Greg and Rosie Lock Charitable Foundation and Sociality Mathematics CIC. The UK government provided funding through the Maths Hubs of the Department of Education National Centre for Excellence in the Teaching of Mathematics and the Department's Primary Strategy Learning Networks. Funding also came from the UK Department of Trade and Industry Global Watch programme. The authors declare that this study received funding from Apple Inc. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article or the decision to submit it for publication.

Acknowledgments

Our thanks go to the senior leadership, teachers and learners in participating schools and to friends and colleagues for their hospitality at Stanford. Piers Messum, Anne Haworth, Greg Gomberg, and Steve Everhard helped devise and deliver professional development support. We are grateful for the assistance of library staff at the University of Laval, Quebec, Bibliotheque Nationale de France, the National Library of Australia, the Moore and University Libraries, Cambridge University and Cubberley Library, Stanford University. The authors acknowledge the valuable contributions of Jan Atkinson, Oliver Braddick, Colin Foster, Martin Hyland, and Anna Vignoles and the reviewers who commented on earlier drafts of this paper. We are grateful for an equipment grant and advice from John Couch and Janet Wozniak at Apple Inc and guidance on outreach project design from Bob Moses' Algebra Project and John Chowcat of Prospect, the UK union for school improvement consultants. The project forms part of the Tizard outreach initiative of Churchill College, Cambridge, 1967 mathematicians.

Conflict of interest

Author IB is the Director of a non-profit entity Sociality Mathematics CIC and Director of Ian Benson and Partners Ltd. He provides professional development services to a network of schools in the UK and US related to topics and findings reported in this manuscript. Author NM was employed by Marriott Statistical Consulting Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2022.902899/full#supplementary-material

References

Adom, G., and Adu, E. O. (2020). The use of Cuisenaire rods on learners' performance in fractions in grade 9 in Public High Schools in Chris Hani West District, South Africa. Int. J. Sci. Res. Publ. 10, 2250–3153. doi: 10.29322/IJSRP.10.06.2020.p10215

CrossRef Full Text | Google Scholar

Allen, H. R. (1978). The Use of Cuisenaire Rods to Improve Basic Skills (Addition-Subtraction) in Seventh Grade (Ph.D. thesis). New Brunswick, NJ: Rutgers, The State University of New Jersey.

Google Scholar

ATM (1977). Notes on Mathematics for Children. Association of Teachers of Mathematics.

Google Scholar

ATM (2017). Working with the Rods and Why. Association of Teachers of Mathematics.

Google Scholar

ATM (2018). On Teaching and Learning Mathematics with Awareness. Association of Teachers of Mathematics.

Google Scholar

Aurich, S. M. R. (1963). A comparative study to determine the effectiveness of the Cuisenaire method of arithmetic instruction with children at first grade level (master's thesis). Catholic University of America, Washington, DC, United States.

Google Scholar

Baez, J. (2009). Can Five-Year-Olds Compute Coproducts? n-Category Cafe. Available online at: http://golem.ph.utexas.edu/category/2009/12/can_fiveyearolds_compute_copro.html

Google Scholar

Bakos, S., and Pimm, D. (2020). Beginning to multiply (with) dynamic digits: fingers as physical-digital hybrids. Digit. Exp. Math. Educ. 6, 145–165. doi: 10.1007/s40751-020-00066-4

CrossRef Full Text | Google Scholar

Beard, D. K. (1964). An intensive study of the development of mathematical concepts through the Cuisenaire method in three year olds (master's thesis). Southern Connecticut State University, New Haven, CT, United States.

Google Scholar

Begg, C., and Mazumdar, M. (1994). Operating characteristics of a rank correlation test for publication bias. Biometrics 50, 1088–1101. doi: 10.2307/2533446

PubMed Abstract | CrossRef Full Text | Google Scholar

Bellemare, T. (1967). La Methode Cuisenaire-Gattegno et le development operatoire de la pensee (Ph.D. thesis). University Laval, Quebec, QC, Canada.

Google Scholar

Benson, I. (2012). notHiding iOS app. Available online at: https://apps.apple.com/us/app/nothiding/id521900115

Google Scholar

Benson, I. (2011). The Primary Mathematics: Lessons from the Gattegno School. Saarbrücken: Lambert Academic.

Google Scholar

Blanton, M. L., and Kaput, J. J. (2011). “Functional thinking as a route into algebra in the elementary grades,” in Early Algebraization: A Global Dialogue From Multiple Perspectives, eds J. Cai and E. Knuth (Springer). doi: 10.1007/978-3-642-17735-4_2

CrossRef Full Text | Google Scholar

Borthwick, A., Gifford, S., and Thouless, H. (2021). The Power of Pattern: Pattening in the Early Years. Association of Teachers of Mathematics.

Google Scholar

Brownell, W. (1968). Conceptual maturity in arithmetic under differing systems of instruction. Element. Schl. J. 69, 151–163. doi: 10.1086/460493

CrossRef Full Text | Google Scholar

Brownell, W. A. (1928). The Development of Children's Number Ideas in the Primary Grades. University of Chicago.

PubMed Abstract | Google Scholar

Brownell, W. A. (1967a). Arithmetical Abstractions: The Movement Towards Conceptual Maturity Under Differing Systems of Instruction. University of California, Berkeley, CA.

Google Scholar

Brownell, W. A. (1967b). Arithmetical Computation: Competence After Three Years of Learning Under Differering Instructional Programmes. Available onelin at: https://eric.ed.gov/?id=ED022703

Google Scholar

Bulgar, S. (2002). Through a teacher's lens: Children's constructions of division of fractions (Ph.D. thesis). New Brunswick, NJ: Rutgers.

Google Scholar

Cai, J., and Knuth, E. J. (2011). Early Algebraization. Heidelberg: Springer. doi: 10.1007/978-3-642-17735-4

CrossRef Full Text | Google Scholar

Campbell, D. T., and Stanley, J. (1963). “Experimental and quasi-experimental designs for research on teaching,” in Handbook of Research on Teaching, ed N. L. Gage (London: Rand McNally) 25–27.

Google Scholar

Cane, J. (2017). Mathematical journeys: our journey in colour with Cuisenaire rods. Math. Teach. 257, 7–11.

Google Scholar

Carbonneau, K. J., Marley, S. C., and Selig, J. P. (2013). A meta-analysis of the efficacy of teaching mathematics with concrete manipulatives. J. Educ. Psychol. 105, 380–400. doi: 10.1037/a0031084

CrossRef Full Text | Google Scholar

Carraher, D. W., Martinez, M. V., and Schliemann, A. D. (2008). Early algebra and mathematical generalization. ZDM Int. J. Math. Educ. 40, 3–22. doi: 10.1007/s11858-007-0067-7

CrossRef Full Text | Google Scholar

Carraher, D. W., Schliemann, A. D., and Brizuela, B. (2005). “Treating the operations of arithmetic as functions,” in Journal for Research in Mathematics Education, volume 13 of Monograph Medium and Meaning: Video Papers in Mathematics Education Research (Reston, VA: NCTM) 1–17. Available online at: https://www.jstor.org/stable/30037

Google Scholar

Choquet, G. (1963). What Is Modern Mathematics? Available online at: https://issuu.com/eswi/docs/1162_what-is-modern-mathematics

Google Scholar

Cochran, W. G. (1954). The combination of estimates from different experiments. Biometrics 10, 101–129. doi: 10.2307/3001666

CrossRef Full Text | Google Scholar

Cohen, J. (1988). Statistical Power Analysis for the Behavioral Sciences. Abingdon: Routledge.

PubMed Abstract | Google Scholar

Coles, A. (2021). Commentary on a special issue: Davydov's approach in the XXI century: views from multiple perspectives. Educ. Stud. Math. 106, 471–478. doi: 10.1007/s10649-020-10018-9

CrossRef Full Text | Google Scholar

CowleyOwl (2012). Little Digits app. Available online at: https://apps.apple.com/gb/app/little-digits/id511606843

Google Scholar

Crowder, A. B. (1965). A Comparative study of two methods of teaching arithmetic in the first grade (Ph.D. thesis). North Texas State University, Denton, TX, United States.

Google Scholar

Cuisenaire, G., and Gattegno, C. (1953). Numbers in Colour: A New Method of Teaching the Processes of Arithmetic to All Levels of the Primary School, 3rd Edn. London: Heinemann.

Google Scholar

Cuisenaire, G., and Gattegno, C. (1962). Initiation a la méthode, Les nombres en couleurs. Denges: Delachaux et Niestlé.

Google Scholar

Dairy, L. (1969). Does the Use of Cuisenaire Rods in Kindergarten, First and Second Grades Upgrade Arithmetic Achievement? Available online at: https://eric.ed.gov/?id=ED032128

Google Scholar

Davydov, V. V. (1962). An experiment in introducing elements of algebra in elementary school. Soviet Educ. 5, 27–37. doi: 10.2753/RES1060-9393050127

CrossRef Full Text | Google Scholar

DragonBox (2012). Dragon Box iOS App. Available online at: https://itunes.apple.com/gb/app/dragonbox-algebra-5/id522069155

Google Scholar

du Bon Pasteur, T. (1966). La méthode Cuisenaire et le développement opératoire de la pensée: recherche psychopédagogique sur l'efficacité de la méthode Cuisenaire (Ph.D. thesis). University Laval, Quebec, QC, Canada.

Google Scholar

Egan, D. L. (1990). The effects of using Cuisenaire rods on the math achievement of second grade students (master's thesis). Warrensburg, MI: Central Missouri State University.

Google Scholar

Ellis, E. N. (1964). The Use of Coloured Rods in Teaching Primary Number Work in Vancouver Public Schools. Available online at: http://www.eric.ed.gov/PDFS/ED028823.pdf

Google Scholar

Empson, S. B., Levi, L., and Carpenter, T. P. (2011). “The algebraic nature of fractions: developing relational thinking in elementary school,” in Early Algebraization: A Global Dialogue from Multiple Perspectives, eds J. Cai and E. Knuth (Berlin: Springer) 409–428. doi: 10.1007/978-3-642-17735-4_22

CrossRef Full Text | Google Scholar

Fedon, J. P. (1966). A study of the Cuisenaire-Gattegno method as opposed to an eclectic approach for promoting growth in operational technique and concept maturity with first grade children (master's thesis). Temple University, Philadelphia, PA, United States.

Google Scholar

Fennema, E. (1972). The relative effectiveness of a symbolic and a concrete model in learning a selected mathematical principle. J. Res. Math. Educ. 3, 233. doi: 10.2307/748490

CrossRef Full Text | Google Scholar

Fuchs, L. S., Schumacher, R. F., Sterba, S. K., Long, J., Namkung, J., Malone, A., et al. (2014). Does working memory moderate the effects of fraction intervention? An aptitude-treatment interaction. J. Educ. Psychol. 106, 499–514. doi: 10.1037/a0034341

CrossRef Full Text | Google Scholar

Gadanidis, G., Clements, E., and Yiu, C. (2018). Group theory, computational thinking, and young mathematicians. Math. Think. Learn. Int. J. 20, 1403542. doi: 10.1080/10986065.2018.1403542

CrossRef Full Text | Google Scholar

Gattegno, C. (1956). New developments in arithmetic teaching in Britain: introducing the concept of 'Set'. Arithmetic Teach. 3, 85–89. doi: 10.5951/AT.3.3.0085

CrossRef Full Text | Google Scholar

Gattegno, C. (1957). Arithmetic with Numbers in Colour. London: William Heinemann.

Google Scholar

Gattegno, C. (1959). Thinking afresh about arithmetic. Arithmetic Teach. 6, 30–32. doi: 10.5951/AT.6.1.0030

CrossRef Full Text | Google Scholar

Gattegno, C. (1963). Mathematics with Numbers in Colour: Numbers from 1 to 20, Vol. 1. Fishguard: Educational Explorers.

PubMed Abstract | Google Scholar

Gattegno, C. (1970). What We Owe Children: The Subordination of Teaching to Learning. New York, NY: Outerbridge and Dienstfrey.

Google Scholar

Gattegno, C. (1983). On algebra. Math. Teach. 105, 34–36.

Google Scholar

Gattegno, C. (1987). Science of Education: Part I Theoretical Considerations. New York, NY: Educational Solutions.

Google Scholar

Gattegno, C. (2010a). Common Sense of Teaching Mathematics. New York, NY: Educational Solutions.

Google Scholar

Gattegno, C. (2010b). Now Johnny Can Do Arithmetic: A Handbook on the Use of Coloured Rods. Fishguard: Educational Explorers.

Google Scholar

Gattegno, C. (2010c). Science of Education: Part 2B Awareness of Mathematisation. New York, NY: Educational Solutions.

Google Scholar

Gattegno, C. (2011a). Modern Mathematics with Numbers in Colour. Fishguard: Cuisenaire Company Ltd.

Google Scholar

Gattegno, C. (2011b). A Teacher's Introduction to the Cuisenaire-Gattegno Method of Teaching Arithmetic. New York, NY: Educational Solutions.

Google Scholar

Gell, J. A. (1963). An evaluation of the Cuisenaire method of teaching arithmetic (Master's thesis). Southern Connecticut State University, New Haven, CT, United States.

Google Scholar

Gilmore, C., Keeblea, S., Richardson, S., and Cragg, L. (2017). The interaction of procedural skill, conceptual understanding and working memory in early mathematics achievement. J. Num. Cogn. 3, 400–416. doi: 10.5964/jnc.v3i2.51

CrossRef Full Text | Google Scholar

Goutard, M. (2017). Mathematics and Children. Fishguard: Educational Explorers.

Google Scholar

Greenes, C. E., and Rubenstein, R., (eds.). (2008). Algebra and Algebraic Thinking in School Mathematics. Reston, VA: NCTM.

Google Scholar

Griffin, P. (2018). “A diary of a working group,” in On Teaching and Learning Mathematics With Awareness, eds D. Brown, A. Coles, and J. Ingram (Derby: Association of Teachers of Mathematics) 4–19.

Google Scholar

Haynes, J. O. (1963). Cuisenaire rods and the teaching of multiplication to third-grade children (Ph.D. thesis). Tallahassee, FL: Florida State University.

Google Scholar

Healy, L., Pozzi, S., and Sutherland, R. (2002). “Reflections on the role of the computer in the development of algebraic thinking,” in Perspectives on School Algebra, eds R. Sutherland, T. Rojano, A. Bell, and R. Lins (Dordrecht: Springer), 231–247. doi: 10.1007/0-306-47223-6_13

CrossRef Full Text | Google Scholar

Herscovics, N., and Linchevski, L. (1994). A cognitive gap between arithmetic and algebra. Educ. Stud. Math. 27, 59–78. doi: 10.1007/BF01284528

CrossRef Full Text | Google Scholar

Hewitt, D. (2011). “What is algebraic activity?” in Proceedings of the 7th Congress of the European Society for Research in Mathematics (CERME), eds M. Pytlak, T. Rowland, and E. Swoboda, (Rzeszñw).

Google Scholar

Higgins, J. P. T., and Thompson, S. G. (2002). Quantifying heterogeneity in a meta-analysis. Statistics in Medicine 21:1539–1558. doi: 10.1002/sim.1186

PubMed Abstract | CrossRef Full Text | Google Scholar

Hollis, L. Y. (1964). A study to compare the effects of teaching first and second grade mathematics by the Cuisenaire-Gattegno method with a traditional method (Ph.D. thesis). Texas Technological College, Lubbock, TX, United States. doi: 10.1111/j.1949-8594.1965.tb13550.x

CrossRef Full Text | Google Scholar

Hollis, L. Y. (1965). A study to compare the effects of teaching first and second grade mathematics by the Cuisenaire-Gattegno method with a traditional method. Schl. Sci. Math. 65, 683–687.

Google Scholar

Howard, C. F. (1957). British teachers' reactions to the Cuisenaire-Gattegno materials. Arithmetic Teach. 4, 191–195. doi: 10.5951/AT.4.5.0191

CrossRef Full Text | Google Scholar

Huang, Y. (2019). The effects of Cuisenaire rods on lower grade students' mathematical learning interests and learning achievements (master's thesis). Huafan University, New Taipei City, Taiwan.

Google Scholar

Jones, I., Bisson, M.-J., Gilmorea, C., and Inglisa, M. (2019). Measuring conceptual understanding in randomised controlled trials: Can comparative judgement help? Brit. Educ. Res. J. 45, 662–680. doi: 10.1002/berj.3519

CrossRef Full Text | Google Scholar

Kaput, J. J. (1995a). “Overcoming physicality and the eternal present: cybernetic manipulatives,” in Exploiting Mental Imagery with Computers in Mathematics Education, eds R. Sutherland and J. Mason (Berlin: Springer) 161–177. doi: 10.1007/978-3-642-57771-0_11

CrossRef Full Text | Google Scholar

Kaput, J. J., and Blanton, M. L. (2000). Algebraic Reasoning in the Context of Elementary Mathematics: Making It Implementable on a Massive Scale. Available online at: https://eric.ed.gov/?id=ED441663

Google Scholar

Kaput, J. J. (1995b). Transforming Algebra from an Engine of Inequity to an Engine of Mathematical Power by ”Algebrafying” the K-12 Curriculum. NCTM.

Google Scholar

Keagle, M. A., and Brummett, A. J. (1993). Manipulative versus traditional teaching for mathematics concepts: Instruction-testing match (Master's thesis). Ball State University, Muncie, IN, United States.

Google Scholar

Kieran, C., Pang, J. S., Schifter, D., and Ng, S. F. (2016). Early Algebra. Research into Its Nature, Its Learning, Its Teaching. Cham: Springer. doi: 10.1007/978-3-319-32258-2

CrossRef Full Text | Google Scholar

Kieran, C. (2018). “Conclusions and looking ahead,” in Teaching and Learning Algebraic Thinking with 5-to 12- Year-Olds, ICME-13 Monographs, eds C. Kieran (Cham: Springer), 427–438. doi: 10.1007/978-3-319-68351-5

CrossRef Full Text | Google Scholar

Kilpatrick, J., and Weaver, J. F. (1977). Place of William A. Brownell in mathematics education. J. Res. Math. Educ. 8, 382–384. doi: 10.5951/jresematheduc.8.5.0382

CrossRef Full Text | Google Scholar

Lamon, W. E., and Scott, L. F. (1970). An investigation of structure in elementary school mathematics: isomorphism. Educ. Stud. Math. 3, 95–110.

Google Scholar

Lin, H.-C. (2013). The study of relationship between concepts of place value and academic achievement of the first and second graders in elementary school in Taoyuan county (master's thesis). Chung Yuan University, Taoyuan City, Taiwan.

Google Scholar

Lucow, W. H. (1962). Cuisenaire method compared with the current methods of teaching multiplication and division. Winnepeg, MB: Manitoba Teachers Society.

Google Scholar

Marchese, C. (2009). Representation and generalization in algebra learning of 8th grade students (Ph.D. thesis). New Brunswick, NJ: Rutgers.

Google Scholar

Mason, J. (2008). “Making use of children's powers to produce algebraic thinking,” in Algebra in the Early Grades, eds J. J. Kaput, D. W. Carraher, and M. L. Blanton (Reston, VA: NCTM) 57–94.

Google Scholar

Mason, J. (2010). Mathematics education: theory, practice and memories over 50 years. Learn. Math. 30, 3–9.

Google Scholar

Matthews, P. G., and Fuchs, L. S. (2018). Keys to the gate? Equal sign knowledge at second grade predicts fourth-grade algebra competence. Child Dev. 91, e14–e28. doi: 10.1111/cdev.13144

PubMed Abstract | CrossRef Full Text | Google Scholar

McNeil, N. M., Fyfe, E. R., Petersen, L. A., Dunwiddie, A. E., and Brletic-Shipley, H. (2011). Benefits of practicing 4 = 2 + 2: nontraditional problem formats facilitate children's understanding of mathematical equivalence. Child Dev. 82, 620–1633. doi: 10.1111/j.1467-8624.2011.01622.x

PubMed Abstract | CrossRef Full Text | Google Scholar

Mulligan, J., and Mitchelmore, M. (2009). Awareness of pattern and structure in early mathematical development. Math. Educ. Res. J. 21, 33–49. doi: 10.1007/BF03217544

CrossRef Full Text | Google Scholar

Nasca, D. (1966). Comparative merits of a manipulative approach to second grade arithmetic. Arithmetic Teach. 13, 221–226. doi: 10.5951/AT.13.3.0221

CrossRef Full Text | Google Scholar

NCTM (2000). Principles and Standards for School Mathematics. National Council of Teachers of Mathematics.

Google Scholar

Nemirovsky, R., and Sinclair, N. (2020). On the intertwined contributions of physical and digital tools for the teaching and learning of mathematics. Digit. Exp. Math. Educ. 6, 107–108. doi: 10.1007/s40751-020-00075-3

CrossRef Full Text | Google Scholar

O'Donnell, J., Hall, C., and Page, R. (2006). Discrete Mathematics Using a Computer. London: Springer.

Google Scholar

Passy, R. A. (1963a). The effect of the Cuisenaire materials on reasoning and computation. Arithmetic Teach. 10, 439–440. doi: 10.5951/AT.10.7.0439

CrossRef Full Text | Google Scholar

Passy, R. A. (1963b). How do Cuisenaire materials in a modified elementary mathematics program affect the mathematical reasoning and computational skill of third-grade children? (Ph.D. thesis). New York University, New York, NY, United States.

Google Scholar

Piaget, J., Henriques, G., and Ascher, E. (1992). Morphisms and Categories: Comparing and Transforming. Hillsdale, NJ: Lawrence Erlbaum Associates.

Google Scholar

Piaget, J., and Szeminska, A. (1952). Genése du nombre chez l'enfant (The Child's Conception of Number). Transl. by C. Gattegno and F. M. Hodgson. Delachaux et Niestle (Abingdon: Routledge and Kegan Paul).

Google Scholar

R Core Team (2020). R: A language and environment for statistical computing. Vienna: R Foundation for Statistical Computing.

Google Scholar

Radford, L. (2014). Towards an embodied, cultural, and material conception of mathematics cognition. ZDM Math. Educ. 46, 349–361. doi: 10.1007/s11858-014-0591-1

CrossRef Full Text | Google Scholar

Radford, L. (2018). “The emergence of symbolic algebraic thinking in primary school,” in Teaching and Learning Algebraic Thinking with 5- to 12- Year-Olds, ed C. Kieran (Cham: Springer), 3–25. doi: 10.1007/978-3-319-68351-5_1

CrossRef Full Text | Google Scholar

Rasila, A., and Sangwin, C. (2016). “Development of stack assessments to underpin mastery learning,” in Proceedings of 13th International Congress on Mathematical Education (Hamburg).

Google Scholar

Rawlinson, R. W. (1965). An Assessment of the Cuisenaire-Gattegno Approach to the Teaching of Number in the First Year at School. Sydney, NSW: Australian Council for Educational Research.

Google Scholar

Reimer, K., and Moyer, P. S. (2005). Third-graders learn about fractions using virtual manipulatives: a classroom study. J. Comput. Math. Sci. Teach. 24, 5–25.

Google Scholar

Rich, L. W. (1972). The effects of a manipulative instructional mode in teaching mathematics to selected 7th grade inner city students (Ph.D. thesis). Temple University, Philadelphia, PA, United States.

Google Scholar

Riley, R. D., Higgins, J. P. T., and Deeks, J. J. (2011). Interpretation of random effects meta-analyses. Brit. Med. J. 342, 964–967. doi: 10.1136/bmj.d549

PubMed Abstract | CrossRef Full Text | Google Scholar

Rittle-Johnson, B., Matthews, P. G., Taylor, R. S., and McEldoon, K. L. (2011). Assessing knowledge of mathematical equivalence: a construct-modeling approach. J. Educ. Psychol. 103, 85–104. doi: 10.1037/a0021334

PubMed Abstract | CrossRef Full Text | Google Scholar

Robinson, E. B. (1978). The effects of a concrete manipulative on attitude toward mathematics and levels of achievement and retention of a mathematical concept among elementary students (Ph.D. thesis). East Texas State University, Commerce, TX, United States.

Google Scholar

Robinson, F. G. (1964). “A note on the quantity and quality of Canadian research on the Cuisenaire method,” in Canadian Experience with the Cuisenaire Method, eds F. G. Robinson (Ottawa, ON: Canadian Council for Research in Education), 181–2.

Google Scholar

Rodman, J. T. (1964). Equal time. Arithmetic Teach. 11, 342–343. doi: 10.5951/AT.11.5.0342

CrossRef Full Text | Google Scholar

Romero, R. C. (1977). Student achievement in a pilot Cureton reading, Cuisenaire mathematics program, and a bilingual program of an elementary school (Ph.D. thesis). Northern Arizona University, Flagstaff, AZ, United States.

Google Scholar

Sangwin, C. (2016). “How does CAS change mathematics?” in International Congress on Mathematics Education (Hamburg).

Google Scholar

Sangwin, C. J. (2005). On building polynomials. Math. Gazette 89, 441–450. doi: 10.1017/S0025557200178295

CrossRef Full Text | Google Scholar

Sangwin, C. J. (2015). An audited elementary algebra. Math. Gazette 99, 298–316. doi: 10.1017/mag.2015.38

CrossRef Full Text | Google Scholar

Schliemann, A., Carraher, D., and Brizuela, B. (2007). Bringing out the Algebraic Character of Arithmetic. New Jersey, NJ: Lawrence Erlbaum Associates. doi: 10.4324/9780203827192

CrossRef Full Text | Google Scholar

Schmittau, J., and Morris, A. (2004). The development of algebra in the elementary mathematics curriculum of V. V. Davydov. Math. Educ. 8, 60–87.

Google Scholar

Seltman, M., and Seltman, P. (1985). Piaget's Logic: A Critique of Genetic Epistemology. London: George Allen and Unwin.

Google Scholar

Sfard, A. (1995). The development of algebra: confronting historical and psychological perspectives. J. Math. Behav. 14, 15–39. doi: 10.1016/0732-3123(95)90022-5

CrossRef Full Text | Google Scholar

Simsek, E., Jones, I., Hunter, J., and Xenidou-Dervou, I. (2021). Mathematical equivalence assessment: measurement invariance across six countries. Stud. Educ. Eval. 70, 101046. doi: 10.1016/j.stueduc.2021.101046

CrossRef Full Text | Google Scholar

Steencken, E. P. (2001). Tracing the growth in understanding of fraction ideas: a fourth grade case study (Ph.D. thesis). New Brunswick, NJ: Rutgers.

Google Scholar

Steiner, K. E. (1964). A comparison of the Cuisenaire method of teaching arithmetic with a conventional method (Master's thesis). North Texas State University, Denton, TX, United States.

Google Scholar

Sterne, J. A. C., and Eggar, M. (2005). “Regression methods to detect publication and other bias in meta-analysis,” in Publication Bias in Meta-analysis: Prevention, Assessment and Adjustment, Chapter 6, eds Editors H. R. Rothstein, A. J. Sutton and M. Borenstein (Hoboken, NJ: Wiley), 99–110. doi: 10.1002/0470870168.ch6

PubMed Abstract | CrossRef Full Text | Google Scholar

Sweeney, J. (1968). A comparative study of the use of the Cuisenaire method and materials and a non-Cuisenaire approach and materials in a grade one mathematics program (master's thesis). University of Toronto, Toronto, ON, Canada.

Google Scholar

Thai, K.-P., Bang, H. J., and Li, L. (2021). Accelerating early math learning with research-based personalized learning games: a cluster randomized controlled trial. J. Res. Educ. Effect. 15, 1–24. doi: 10.1080/19345747.2021.1969710

CrossRef Full Text | Google Scholar

Viechtbauer W. (2010). Conducting meta-analyses in R with the metafor package, J. Stat. Softw. 36, 1–48.

Google Scholar

Viechtbauer, W. (2005). Bias and efficiency of meta-analytic variance estimators in the random-effects model. J. Educ. Behav. Stat. 30, 261–293. doi: 10.3102/10769986030003261

CrossRef Full Text | Google Scholar

Viechtbauer, W., and Cheung, M. W.-L. (2010). Outlier and influence diagnostics for meta-analysis. Res. Synthesis Methods 1, 112–125. doi: 10.1002/jrsm.11

PubMed Abstract | CrossRef Full Text | Google Scholar

Viechtbauer, W. (2021). “Model checking in meta-analysis,” in Handbook of Meta-Analysis, eds C. H. Schmid, T. Stijnen, and I. White (CRC Press) 219–254. doi: 10.1201/9781315119403-11

PubMed Abstract | CrossRef Full Text | Google Scholar

Wallace, P. (1974). An investigation of the relative effects of teaching a mathematical concept via multisensory models in elementary school mathematics (Ph.D. thesis). East Lancing, MI: Michigan State.

Google Scholar

Woodcock, R. W., McGrew, K. S., and Mather, N. (2007). Woodcock Johnson III Tests of Achievement. Itasca, IL: Riverside Publishing.

PubMed Abstract | Google Scholar

Yankelewitz, D. (2009). The development of mathematical reasoning in elementary school students' exploration of fraction ideas (Ph.D. thesis). New Brunswick, NJ: Rutgers.

Google Scholar

Young, R., and Messum, P. (2011). How We Learn and How We Should Be Taught: An Introduction to the Work of Caleb Gattegno. London: Duo Flumina.

Google Scholar

Zazkis, R., and Mamolo, A. (2011). Reconceptualizing knowledge at the Mathematical Horizon. Learn. Math. 31, 8–13.

Google Scholar