Rubric development for AI-enabled scoring of three-dimensional constructed-response assessment aligned to NGSS learning progression

Introduction: The Framework for K-12 Science Education (the Framework) and the Next- Generation Science Standards (NGSS) define three dimensions of science: disciplinary core ideas, scientific and engineering practices, and crosscutting concepts and emphasize the integration of the three dimensions (3D) to reflect deep science understanding. The Framework also emphasizes the importance of using learning progressions (LPs) as roadmaps to guide assessment development. These assessments capable of measuring the integration of NGSS dimensions should probe the ability to explain phenomena and solve problems. This calls for the development of constructed response (CR) or open-ended assessments despite being expensive to score. Artificial intelligence (AI) technology such as machine learning (ML)-based approaches have been utilized to score and provide feedback on open-ended NGSS assessments aligned to LPs. ML approaches can use classifications resulting from holistic and analytic coding schemes for scoring short CR assessments. Analytic rubrics have been shown to be easier to evaluate for the validity of ML-based scores with respect to LP levels. However, a possible drawback of using analytic rubrics for NGSS-aligned CR assessments is the potential for oversimplification of integrated ideas. Here we describe how to deconstruct a 3D holistic rubric for CR assessments probing the levels of an NGSS-aligned LP for high school physical sciences.

Methods: We deconstruct this rubric into seven analytic categories to preserve the 3D nature of the rubric and its result scores and provide subsequent combinations of categories to LP levels.

Results: The resulting analytic rubric had excellent human- human inter-rater reliability across seven categories (Cohen’s kappa range 0.82–0.97). We found overall scores of responses using the combination of analytic rubric very closely agreed with scores assigned using a holistic rubric (99% agreement), suggesting the 3D natures of the rubric and scores were maintained. We found differing levels of agreement between ML models using analytic rubric scores and human-assigned scores. ML models for categories with a low number of positive cases displayed the lowest level of agreement.

Discussion: We discuss these differences in bin performance and discuss the implications and further applications for this rubric deconstruction approach.

Introduction

Challenges of implementing Next-Generation Science Standards in practice: Fast scoring of Next-Generation Science Standards-aligned assessments

The Framework for K-12 science education (the Framework) and the Next-Generation Standards (NGSS) emphasize the importance of fostering the development of deep science understanding reflected in the ability to apply relevant content knowledge and skills to explain phenomena and solve problems in real life (National Research Council [NRC], 2012; Lead States, 2013). According to the Framework, in order to support students in developing deep science understanding, the educational process should focus on supporting them in integration of the three dimensions of science when explaining phenomena and solving real-life problems. The three dimensions include disciplinary core ideas (DCIs), scientific and engineering practices (SEPs), and crosscutting concepts (CCCs). According to the Framework, the ability to integrate the three dimensions in practice is indicative of deep conceptual understanding (also termed 3D understanding). For assessment, this means that NGSS-aligned assessments should measure student ability to integrate relevant DCIs, SEPs, and CCCs when explaining phenomena and solving real-life problems.

Further, the Framework suggests using learning progressions (LPs) as roadmaps for the development of curriculum, instruction, and assessment. Learning progressions are defined as “successfully more sophisticated ways of reasoning within a content domain” (Smith et al., 2006). The Framework and NGSS outline theoretical LPs for the three dimensions of science at each grade band and suggest building instruction, curriculum, and assessment following these LPs. For assessment, this means that NGSS-aligned assessments should measure the ability of students to integrate the three dimensions and probe their ability at various levels of sophistication in accordance with relevant LPs.

This leads to two important challenges to implementing the NGSS as related to assessment development. First, 3D understanding represents a complex type of understanding reflected in student ability to engage in authentic scientific practices, such as argumentation or modeling, and apply relevant DCIs and CCCs when explaining phenomena and solving problems. To accurately measure 3D understanding, assessments should allow students to demonstrate their ability to integrate all the relevant NGSS dimensions in a fashion discussed above. This ability to integrate the three dimensions is very hard to measure using a traditional recall-based assessment item format (Krajcik, 2021). Therefore, to accurately measure 3D understanding according to NGSS and the Framework, constructed-response (CR) assessments are needed (Kaldaras et al., 2021a; Krajcik, 2021). These assessments, however, are time-consuming and expensive to score and provide feedback for. Second, the Framework and NGSS call for aligning 3D assessments to relevant LPs in order to ensure targeted and effective feedback which is essential for productive learning (National Research Council [NRC], 1999). This adds another layer of complexity in scoring and providing feedback for the 3D assessments, since both the resulting score and the feedback should be aligned to a specific LP level. This feedback should guide the student and the teacher as to what additional support the student needs to help them move to higher LP levels.

Using artificial intelligence technology to score Next-Generation Science Standards-aligned assessments

Artificial intelligence (AI) technology, such as machine learning (ML) approaches have recently shown tremendous success in scoring short CR items in various STEM disciplines and student levels with reliability close to that of human scoring (Zhai et al., 2020). In pioneering work, Nehm et al. (2012) showed that ML text scoring could be used to identify key ideas in college students’ short, written evolutionary explanations. Jescovitch et al. (2020) compared different coding approaches and ML applications for assessment items aligned to a learning progression in undergraduate physiology. They showed that even items which were rich in disciplinary context and elicited complex student reasoning could be scored by ML with fairly good accuracy, although more complicated items proved to be more challenging for ML to score accurately. More recently, Maestrales et al. (2021) used ML to score several multidimensional assessment items designed for high school chemistry and physics. As part of the study, the researchers had to construct new coding rubrics to capture the multi-dimensional nature of student responses. Overall, the ML models showed good agreement with human scores, but the researchers found that student use of formal language in responses was a challenge for ML accuracy.

Several applications of ML-based text scoring have been used in assessment systems to provide automated guidance based on student responses (Tansomboon et al., 2017; Li et al., 2018; Lee et al., 2019). Importantly, ML-based scoring has been shown to be reliable and consistent with human scoring when measuring progression toward deeper understanding as reflected in learning progression-based assessments (Jescovitch et al., 2020; Wilson et al. in revision¹). ML-based scoring approaches therefore represent a promising tool in helping score and provide timely feedback for NGSS-aligned LP-based CR assessments. However, when designing ML-based scoring approaches to achieve this goal, it is important to ensure that the 3D nature of assessment items is reflected in the scoring process, the resultant scores, and the associated feedback (Maestrales et al., 2021). Otherwise, the resulting scores will lack alignment with NGSS and will not reflect the vision outlined in the Framework.

Challenges of using artificial intelligence technology to score Next-Generation Science Standards-aligned assessments

One of the main challenges in applying ML approaches to score NGSS-aligned LP-based assessments is developing rubrics that can both accurately capture the complex 3D nature of student understanding measured by the assessments and yield high inter-rater reliability (IRR) between human and machine scores. Generally, multi-level, holistic rubrics are used to assign a score to a given response, which in turn can be aligned to a specific LP level (Haudek et al., 2012; Kaldaras et al., 2021a). These holistic scores are meant to assess the overall quality of the student performance or response. For holistic rubrics aligned to NGSS LPs, each level in the rubric is designed to capture a distinctive set of DCIs, SEPs, and CCCs within the LP. In contrast, a number of automatic scoring applications rely on analytic rubrics for scoring student responses (Liu et al., 2014; Moharreri et al., 2014; Sieke et al., 2019). Analytic rubrics are a series of binary or dichotomous rubrics that identify the presence or absence of construct relevant ideas in student responses. Scores generated by both holistic (Anderson et al., 2018; Noyes et al., 2020) and analytic approaches (Sieke et al., 2019) have been used to develop functioning, predictive ML models for short, text-based CR items in science assessment.

A key study comparing analytic and holistic approaches to human coding for LP-aligned assessments found that training sets based on analytically coded responses showed equal or better ML model performance as compared to using holistic scores in training sets (Jescovitch et al., 2020; Wang et al., 2021). Another study deconstructed holistic rubrics into a series of analytic rubrics for middle school science assessment items, which were recombined into a single holistic score, which then was used to train the computer. The Spearman rank correlation for human-computer agreement showed moderate to high agreement levels (Mao et al., 2018). Additionally, in other work, it was shown that analytic scoring provides an easier way for evaluating the validity of ML-based scores with respect to LP levels (Kaldaras and Haudek, this issue).

In short, while holistic rubrics have traditionally been used more often for scoring LP-aligned assessments, and they could potentially be easier for presenting the 3D nature of the item at the scoring stage, analytic rubrics can potentially yield better machine-human agreements and contribute to improved validity of the resulting ML scores. Therefore, analytic scoring approaches could be more useful to scoring LP-aligned CR assessments. However, when developing and using analytic rubrics for scoring NGSS-aligned CR assessments, it is essential to ensure that the 3D nature of the items, and the emphasis on the integration of the three dimensions of NGSS (DCIs, SEPs, and CCCs) is properly reflected in the rubric. Currently, there is no research available on how to deconstruct an LP-aligned holistic rubric for scoring NGSS-aligned CR assessments into an analytic rubric suitable for ML scoring approaches while preserving the 3D nature of the rubric. Although previous reports have reported processes to deconstruct a holistic rubric to analytic rubrics in science assessments, these reports did not comment on the 3D nature of the rubrics nor how evidence from the item design process can be used to develop such rubrics (Jescovitch et al., 2019; Wang et al., 2021). Designing approaches for deconstructing LP-aligned holistic scoring rubrics for NGSS-aligned CR assessments focusing on preserving the 3D nature of the rubric and the assessment item is an important step toward designing AI-based automatic scoring systems for these assessments. If the 3D nature of the rubric is not preserved, the resulting AI-based scores will lack validity with respect to NGSS and the associated LP, which in turn will negate the efforts on designing AI-based scoring tools for quick and efficient scoring of NGSS-aligned CR items.

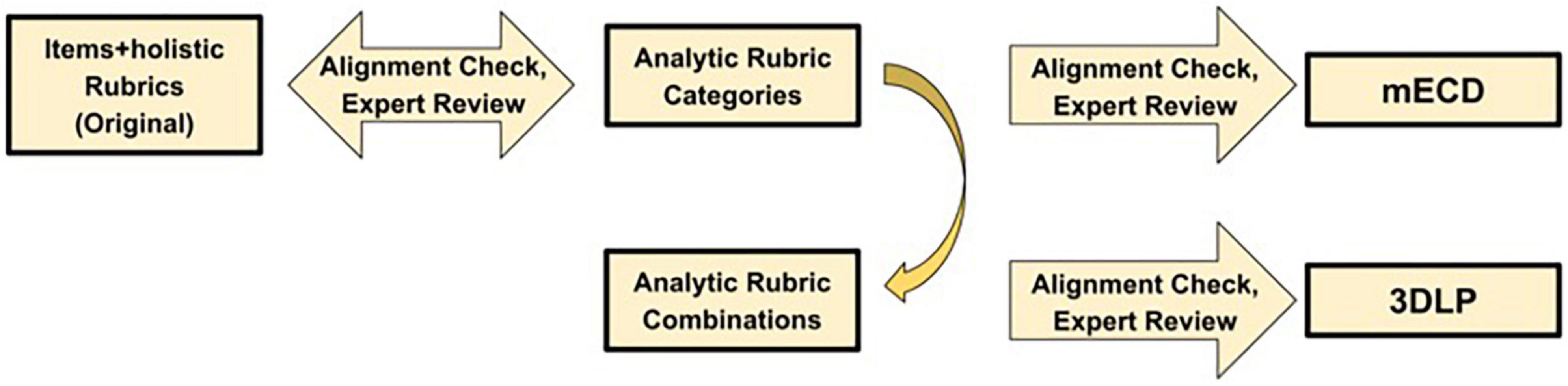
In this work, we will demonstrate a method for deconstructing a 3D holistic rubric for CR assessment probing the levels of previously validated NGSS-aligned LP for electrical interactions (Kaldaras, 2020; Kaldaras et al., 2021a). The overall process is shown in Figure 1. We will then report on using the resulting analytic rubric to develop an ML model to automatically score the assessment item. This study will address the following research question (RQ):

FIGURE 1

Figure 1. The process of analytic and holistic rubric development.

How can one deconstruct three dimensions holistic rubrics into three dimensions analytic rubrics to aid in developing machine learning-based scoring models for Next-Generation Science Standards-aligned three dimensions assessments?

The procedure demonstrated in this paper has a wide range of applications. For example, in the paper, we will show how ML-based scoring of student responses can be used to potentially provide automatic and LP-specific feedback to students regarding their performance. We will also discuss other important aspects, including challenges related to the automatic analysis of inaccurate ideas and how it can be approached in the context of LP-aligned assessments. We will also discuss how this procedure for AI-based scoring of NGSS-aligned assessments for LPs can help make the iterative nature of LP, rubric, and assessment development for NGSS more efficient.

Study setting

Prior work: Validated Next-Generation Science Standards-aligned three dimensions learning progressions

As part of prior work we developed and validated two NGSS-aligned LPs focusing on student ability to integrate the relevant NGSS dimensions (including DCIs, SEPs, and CCCs) when explaining phenomena involving electrical interactions. The LPs describe students’ increasing competency to develop causal models and explanations of phenomena involving electrical interactions focusing specifically on applying Coulomb’s law (Kaldaras et al., 2021a) and Energy (Kaldaras, 2020) to explain electrical interactions at the macroscopic and atomic molecular level. The two LPs are closely related and follow similar logic. They both start from level 0 reflecting no substantive evidence of using either Coulomb’s law (for LP on Coulomb’s law, Kaldaras et al., 2021a) or Energy (for LP of Energy, Kaldaras, 2020) to explain electrostatic phenomena. Further, level 1 reflects the ability to use Coulomb’s law (Kaldaras et al., 2021a) and Energy (Kaldaras, 2020) for developing partial causal models and explanations of electrostatic phenomena. Level 2 reflects the ability to use either Coulomb’s law (Kaldaras et al., 2021a) or Energy (Kaldaras, 2020) to explain electrostatic phenomena at the macroscopic level and partially at the atomic-molecular level. Finally, level 3 reflects the ability to use both Coulomb’s law and Energy ideas to explain electrostatic phenomena at the atomic molecular level. Table 1 shows a brief description of the levels for both LPs and reflects the features important for the current study. Both LPs focus on SEPs of Developing and Using Models and Constructing Explanations; the CCC of Cause and Effect and DCIs of Relationship between Energy and Forces and Types of Interactions.

TABLE 1

Table 1. NGSS LP for electrical interactions combining Coulomb’s law and energy ideas.

Both LPs were validated using the same procedure and context. Specifically, we developed CR 3D assessment items and aligned holistic rubrics probing the levels of each of the LPs following modified evidence-centered design process (mECD) (Harris et al., 2019). The items were administered as summative pre/post assessments in classrooms that were using NGSS-aligned curriculum targeting the same NGSS performance expectations (PEs) and NGSS dimensions (DCIs, SEPs, and CCCs) as the assessment instruments and the associated LPs. The student responses to the items were scored by a trained group of coders using holistic rubrics. The scores were then used to conduct measurement invariance (Kaldaras et al., 2021b) and item response theory analysis as part of the validation study which provided strong evidence for the validity of both LPs (Kaldaras, 2020; Kaldaras et al., 2021a).

The current work begins with a previously developed item and holistic rubric aligned to both LPs and probing all levels of the combined LP shown in Table 1. The item was administered to students as part of the pre/post summative assessments in curricular units. However, the item was not included as part of the previous validation studies. In the current work, we will demonstrate the deconstruction of the originally developed holistic rubric for the item into a series of analytic rubric categories, aiming to preserve the 3D nature of the item and rubrics.

Background of existing item and holistic rubric

The information used in the original mECD process for this CR is shown in Table 2. The item focused on probing student understanding when developing causal explanations for when two carts with similarly charged metal plates would stop and why. We used the mECD process to align the CR item with NGSS PEs and LP levels. Specifically, Table 2 provides information about each step of the mECD process of item development for this item and corresponding rubric. The process starts with identifying the target NGSS PE, follows the process of unpacking reflected in specifying the aspects of the PE that will be targeted by the assessment item, and results in the development of the claim and evidence statements. The claim described what students should be able to do with respect to the target NGSS PEs. The evidence specifies the information that should be reflected in student responses that would serve as evidence that students have met the requirement of the claim. The Carts item probes all three LP levels shown in Table 1. Specifically, the Carts item probes student ability to integrate ideas of Coulomb’s law and Energy when explaining phenomena involving electrical interactions. The original holistic rubric is shown in Table 2. Each level of the rubric aligns to the level of the LP shown in Table 1 and reflects the ideas that should be present in student answers corresponding to each LP level. The ideas reflected in the rubric are aligned to the LP through the mECD argument as shown in Table 2. Both the item and the rubric were reviewed by content and educational experts. Next, the item was piloted in the classrooms participating in the study. About 200 student responses were collected and evaluated by the first author of this study and other researchers to ensure that the item elicits the ideas reflected in the mECD argument and in the corresponding LP levels. This provided evidence consistent with response-process-based validity for the item (American Educational Research Association [AERA], 2018).

TABLE 2

Table 2. Modified evidence-centered design for carts item.

Materials and methods

Analytic rubric development

The holistic rubric was used as a basis for the development of analytic rubric as part of this study (see Figure 1) to employ ML-based automatic scoring of student responses. Table 3 shows the resulting seven categories in the analytic rubric based on the holistic rubric. Each of the categories reflects an important idea that is present in student responses and is aligned to evidence within the mECD argument or necessary to distinguish responses between LP levels. For example, an analytic category was developed to identify responses with many inaccuracies; this is not found in the mECD argument, but is necessary to distinguish responses between the final LP levels. Each category is dichotomously scored as present (score of 1 for that category) or absent (score of 0 for that category) in student responses. Briefly, category 1 requires students to state which direction the carts will move, category 2 requires students to explain why they think the carts will move in the stated direction, category 3 requires students to recognize that the carts will stop, categories 4 and 5 describe the explanation for when the carts will stop either using Coulomb’s law (category 4) or Energy (5). Category 6 reflects the integration of Coulomb’s law and Energy when explaining when the carts will stop and why. Category 7 aims to capture the presence of inaccuracies in the student response or the lack of evidence in the response for the student ability to integrate dimensions of NGSS.

TABLE 3

Table 3. Alignment between analytic rubric categories and the mECD argument for the carts item.

There were several strategies that we followed during analytic rubric development in order to ensure that the three-dimensionality of the rubric is preserved (see Figure 1). First, notice that all rubric categories were centered on ideas students used in responses, not defined by specific words or phrases. This ensured that the resulting scores for those categories go beyond simple presence or absence of words and capture ideas instead. Although in practice, coders noticed that some ideas were very frequently communicated by students using a limited number of words or phrases. Second, notice that the rubric categories focused on providing causal account (e.g., justification), such as categories 4–6, reflect the integration of relevant DCIs related to Energy or Coulomb’s Law respectively, SEP of constructing explanations and CCC of cause and effect as well as explicit connection to the phenomenon in question. These three categories are intended to capture the integration of the three dimensions of NGSS which is consistent with the vision of the Framework. This approach to analytic category design ensures that the dimensionality of the rubric is not reduced. After we had formed analytic categories, the categories were reviewed by two experts; one an assessment expert involved with the original LPs and the other an expert in ML text scoring of assessments. The goal of this review was two-fold. First, we wanted to ensure the analytic categories aligned with the original mECD statements and the quality of performances in student response captured by the holistic rubric. Second, we wanted feedback about the “grain-size” of the analytic categories for the future ML application and whether the analytic categories were focused on a singular component of a 3D performance.

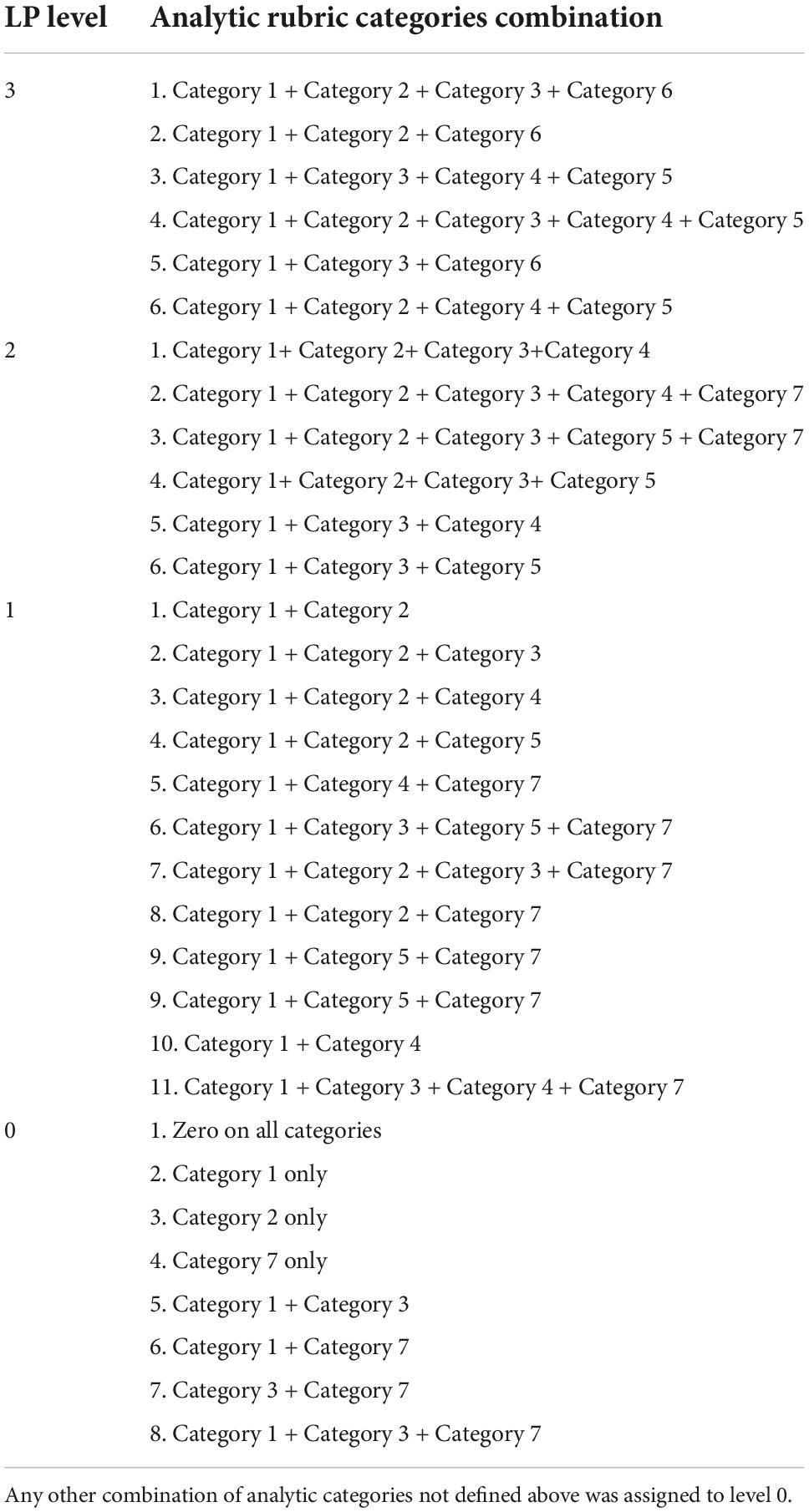
Further, in order for the analytic rubric categories to be used with the 3D LP, we needed a way to map specific combinations of the categories to individual levels in the LP (see Figure 1). That is, no single analytic category represents an LP level performance above the lowest level. Table 4 shows the alignment between specific combinations of the analytic rubric categories and the LP levels, by relying on the pieces of evidence within the mECD argument. The resulting combinations of analytic categories ensured that the student ability to use the three dimensions of NGSS together when answering the question is captured in the resulting final score. We then applied the analytic categories and the proposed combinations to a handful of student responses, to verify the categories targeted the critical ideas and that the proposed combinations resulted in proper LP-level alignment. Again, the combinations of analytic categories were reviewed by the same two experts. The goal of this review step was to ensure the resulting scores from the combinations would correctly place a response at a correct LP level, based on the performance of the response itself. We provide sample answers for each LP level using the combination of analytic rubric categories in the results section.

TABLE 4

Table 4. Alignment between combinations of analytic rubric categories and the LP levels.

Data sources

The Carts item was administered to 9th-grade students participating in the NGSS-aligned curriculum covering the ideas measured by the item. The ideas related to Coulomb’s law as related to electrical interactions were covered as part of Unit 1 of the curriculum while ideas related to Energy as related to interactions were part of Unit 2. Therefore, different types of ideas and sophistication of responses were expected from students upon completion of each unit. Specifically, upon completion of Unit 1 students were expected to be able to use ideas related to Coulomb’s law to construct causal explanations of phenomena, which is consistent with level 2 of the LP shown in Table 1. Upon completion of Unit 2 of the curriculum students were expected to also be able to use ideas related to Energy to construct causal explanations of phenomena (consistent with level 2 of the LP shown in Table 1) as well as integrate ideas of Energy and Coulomb’s Law when explaining phenomena (level 3 of the LP shown in Table 1). The Carts item was administered as part of the Unit 1 post test and Unit 2 post test and student responses from both time points were used for this study. The post test for both units was administered via the curriculum online portal. A total of 1252 student responses were collected from post Unit 1 and Unit 2 implementation. These responses were used to produce ML models in this study.

Data analysis

Analytic scoring and human inter-rater reliability

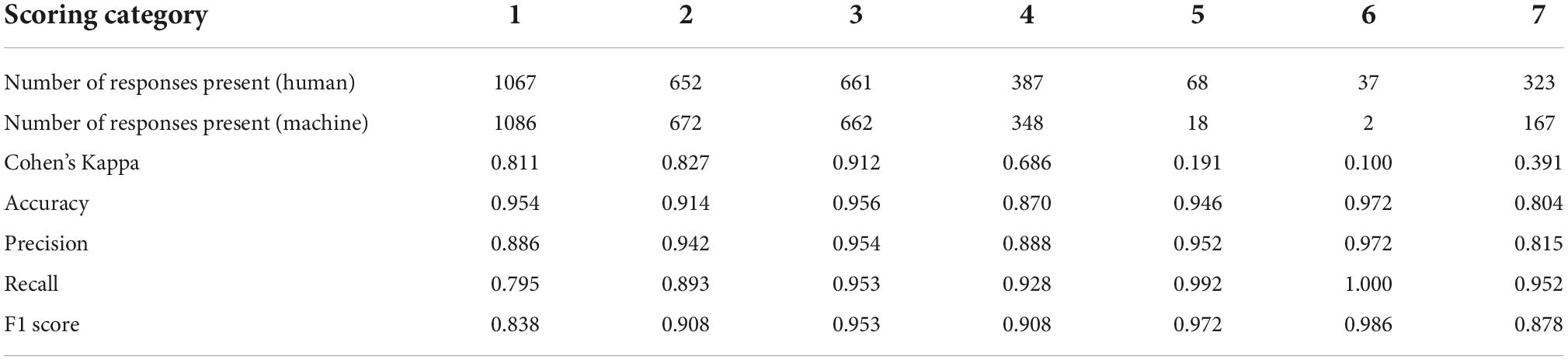
Student responses were coded by two independent coders utilizing the analytic rubric, after training together with the rubric. An experienced coder with the rubric (LK) discussed the rubric and example responses with a new coder (NY). Training was done with 1252 responses using the analytic rubric shown in Table 3. Training was done in subsets of 100 responses and coded independently by both coders. Results from independent coding on subsets were then checked for IRR for each analytic category utilizing Cohen’s Kappa statistic to account for chance agreements between raters (Cohen, 1960). We used a threshold of Cohen’s Kappa greater than 0.8 between human coders for each analytic category, as this indicates a strong level of agreement (McHugh, 2012). During coding, each response was read and analyzed for key ideas or phrases that demonstrated the presence of the concepts denoted in the analytic categories. Following independent coding, after training was complete, the coders reconvened with their scores and checked for human IRR. Categories that showed <0.8 Cohen’s kappa between coders were discussed by the two coders until agreed upon and the rubric was updated, when necessary, to improve the clarity of analytic categories and alignment with rubric goals and associated LP levels. The whole batch of responses was re-scored following the discussion. The final Cohen Kappas for all batches and all the scoring categories were no less than 0.8 and are shown in Table 5. This data set was used to train the ML model. Cohen’s Kappas values for each category are at least 0.82 with a majority of the categories >0.9, indicating strong to almost perfect human–human agreement (McHugh, 2012) using the analytic categories. This suggests the analytic categories had well defined criteria and examples.

TABLE 5

Table 5. Cohen’s Kappas for human–human analytic scoring.

Comparison of holistic and analytic scores

To examine whether developed combinations for the analytic categories led to the same LP level assignment as the original holistic rubrics, we compared scores assigned by human coders using these two coding approaches. From the entire data set, we selected 200 responses randomly by LP level to compare codes assigned via the original holistic rubric with codes assigned via the analytic categories and combination. Holistic scoring was conducted by an experienced coder (LK), who participated in the holistic rubric development. These responses were coded independently of the analytic scores. The agreement on the final score for each response between the two approaches was very high (Cohen’s kappa = 0.986). We also calculated Spearman’s rho (correlation) between final analytic and holistic scores and found r_s = 0.995, p < 0.01. In fact, we found only two responses out of 200 for which the final holistic score differed from the analytic score. The first response was assigned level 1 by analytic combination and level 2 by holistic scoring approaches. The response says: “When the wedges are removed, they will move the opposite way they’re facing. They move in that direction, because both the metal sheets are negatively charged. We know that like charges repel, so depending on how strong the negative charge is, is how far the carts will move away from each other.” In this response, the student does not explicitly state when the carts will stop, but rather implies that the carts will stop when the negative charges no longer interact, which depends on how strong they are. Therefore, the holistic score reflected level 2 on the LP. However, the analytic score reflected level 1 on the LP because a score of 1 was assigned to categories 1, 2, and 4. As you can see the analytic rubric makes it easy to diagnose the nature of misscores. The second misscore was assigned level 2 by analytic combination and level 3 by holistic scoring approach. The response says: “Since they’re alike charges, then when the wedges are removed the energy field will be strong because they’re close they will repel far enough away until they’re charges can’t interact. And when they lose KE.” In this response, students are using both the ideas on Coulomb’s law (bold), and the ideas of Energy (italics) to explain when the carts will stop. The analytic scores of 1 were assigned to categories 1–4. Since there was no score of 1 assigned to category 5, the resulting LP level assignment was lower than with the holistic score. This misscore between holistic and analytic LP level assignment might be due to the fact that the mention of the Energy came at the very end of the response, and scorers missed this idea, or didn’t understand that KE stands for “kinetic energy.” Just like in the previous example, you can see that the analytic rubric makes it relatively straightforward to diagnose the nature of the misscores.

Machine learning model development

Machine learning model development for text classification of student responses was performed using the Constructed Response Classifier tool (CRC; Jescovitch et al., 2020). In short, the CRC tool is based on RTextTools (Jurka et al., 2013) for text processing using a bag-of-words classification approach to natural language processing and allows some feature engineering. The extracted text features are then used as inputs for a series of eight ML classification algorithms. The CRC employs an ensemble model which combines outputs from multiple, individual classification algorithms to make a predicted classification for each response as present (i.e., positive) or absent (i.e., negative) for each analytic rubric category (Sieke et al., 2019). The machine-predicted scores (from the ensemble) are then compared to the human-assigned score in a 10-fold cross-validation approach for each rubric category to evaluate performance. For this study, we report results using the default feature extraction settings for text pre-processing from the CRC tool. These include using unigrams and bigrams as n-gram length, a limited set of stopwords (the, a, in, and) and removing numbers from the corpus. Because we used the results of a dichotomous, analytic rubric, we chose to use the CRC for an analytic/dichotomous output and apply an ensemble scheme utilizing a naive Bayes optimal classifier stacking routine (Mitchell, 1997). For evaluation of the ML-based automatic text scoring, we compare the human and machine assigned scores and report the model performance using overall accuracy, Cohen’s Kappa, F1 score, precision and recall measures for each category (Zhai et al., 2021). Both accuracy and Cohen’s kappa are measures of “agreement” between raters, in this case human and machine-assigned scores. Both precision and recall are measures of the ML ability to predict true positive cases in the data set. Since we are primarily interested in identifying when students include ideas in their responses, we report these measures but acknowledge there are a variety of metrics that can be used to evaluate ML model performance (Zhai et al., 2021). As such, we include the output confusion matrix for each category model in the Supplementary material.

Results

Analytic scoring and alignment to learning progression levels

Table 6 shows sample student responses for each LP level and the corresponding combinations of analytic scoring categories that led to the response being assigned to that level.

TABLE 6

Table 6. Sample combinations of analytic categories in student responses, the associated LP levels, and suggested feedback.

Automated text scoring

The ML-based automatic scoring was conducted using 1252 responses scored using the analytic rubric as described above. Table 7 shows the results of the model performance, including human-machine agreement (as Accuracy and Cohen’s Kappa) for each scoring category. The confusion matrix, which shows the full results of the ML predictions for each category is provided in the Supplementary material. As shown in Table 7, categories 1–4 exhibit good human–machine agreement as indicated by Kappa values of close to or above 0.7. These categories also contain a large number of student responses that were coded as present (or positive) by human coders. Although category 4 has the lowest Cohen’s Kappa value of these four categories, other ML performance metrics for this ML model are similar to the metrics for models for categories 1–3, with all four categories demonstrating high accuracy and good ML model performance as evidenced by high F1 scores. Although categories 5 and 6 appear to have acceptable model performance metrics based on accuracy and F1 score, these categories exhibit minimal human-machine agreement as indicated by Cohen’s Kappa values (<0.4). Because these categories have very few positive cases (<100) in the data set, the ML outputs show acceptable performance metrics by predicting nearly all responses as negative for these categories. We will further discuss these results and their implications.

TABLE 7

Table 7. Human and machine category frequency and evaluation metrics.

Discussion

Key challenge in developing artificial intelligence-enabled scoring system for learning progression-aligned three dimensions assessment: Preserving the three dimensions nature of understanding in designing the analytic rubric for artificial intelligence-enabled scoring

The key to successful implementation of NGSS in practice lies in designing high-quality assessments that measure student ability to integrate the three dimensions of NGSS (DCIs, SEPs, and CCCs) and track student progress along previously validated NGSS-based LPs. The ability to integrate the three dimensions reflects 3D understanding, which is complex and for which CR assessments are useful (Kaldaras et al., 2021a; Krajcik, 2021). AI technology, such as ML, has shown to be successful in providing accurate and reliable scores on CR assessments in various STEM disciplines. Therefore, using ML is a promising avenue for designing automatic scoring approaches for NGSS-based CR assessments aligned to previously validated LPs. A key challenge in employing such approaches lies in producing scores that reflect the 3D nature of student understanding and exhibit high human-machine agreement. The current work represents one example of such effort aimed at designing the methodology for deconstructing the NGSS-aligned holistic rubric into an analytic rubric to be used to produce accurate and reliable automatic scores for LP-aligned assessments. This process utilizes the 3D holistic rubrics and mECD arguments produced as part of the assessment development. We then evaluated the resulting analytic rubrics based on alignment to a 3D learning progression, human coder agreement, and results of automated text scoring.

Steps to preserve the three dimensions nature of understanding in designing the analytic rubric for artificial intelligence-enabled scoring

Using original assessment argument for developing analytic rubric

Using a principled approach to assessment development ensures alignment between the NGSS and the resulting assessment items and rubrics (Harris et al., 2019). This work leverages the mECD approach to design evidence statements and associated NGSS and LP-aligned assessment items. The original holistic rubric for the Carts item was produced to reflect specific ideas probed by the item with respect to LP levels and the corresponding NGSS standards. These ideas were specified in the original mECD argument (Table 2). The same mECD argument was then used in this study to guide the deconstruction process for developing the analytic rubric for AI scoring. Using mECD argument as a guiding tool for the deconstruction process ensures alignment between the two types of rubrics, the LP levels and the relevant NGSS dimensions. In this work we deconstructed the holistic scoring rubric into a series of seven analytic categories, based on evidence included from the mECD process, to use as a coding rubric. The number of analytic scoring categories could vary depending on the ideas being measured by the item, and the mECD argument can guide this process as illustrated in this study.

Breaking holistic rubric into analytic categories that reflect three dimensions of knowledge

Each analytic scoring category represents a much smaller piece of information required for classifying a response within a level than contained in a typical level within a holistic rubric. Therefore, special attention should be given to ensuring that each analytic category reflects the 3D nature of student understanding instead of a memorized fact. Examples of such categories in the current study are categories 4–6 and category 2 shown in Table 3. Note that each of those categories reflects the 3D nature of student understanding in different ways. For example, category 2 described a student’s ability to relate their observations (carts will repel) to the fundamental property of charges (similar charges repel), which is a component of a DCI, therefore resulting in a causal account of the phenomenon in question. The key in developing these analytic categories lies in identifying the smallest possible aspects of 3D knowledge that can be meaningfully described for a given category. For example, category 4 in Table 3 described different ways students can apply Coulomb’s law to explain the phenomenon in question: by using the idea of electric fields, electric forces, or electric charges and relating it to the distance between repelling cars. In short, notice that categories 4–6 which reflect higher level thinking consistent with the NGSS-aligned LP describe causal relationships combining relevant aspects of DCIs such as Coulomb’s law (category 4), Energy (category 5), or both (category 6) with the CCC of cause and effect and SEP of constructing explanations. This is reflected in the category descriptions that emphasize causal explanations that use relevant DCIs and connect to the phenomenon, not just the presence of ideas or words. For example, category 4 captures a causal statement: “The carts will stop moving when the distance is far enough away that electric forces are too weak to move the carts.” Similarly, all three of these categories emphasize the integration of the relevant DCIs, SEPs, and CCCs in their description rather than requiring only one of the dimensions to be present. This approach to preserve the 3D nature of the assessment item and rubric results in analytic rubric categories which can be subsequently combined to assign specific LP levels, tied to the 3D nature of the actual LP.

Breaking holistic rubric into analytic categories that reflect important aspects of the phenomenon in question that are not three dimensions

Apart from ensuring the 3D nature of the rubric is preserved, it is also important to ensure that all the important aspects of the phenomenon in question are reflected in the analytic rubric. For example, for the Carts item it is important to ensure that the two central aspects of the question are scored: (1) whether the carts will move away or toward each other and (2) when the carts will stop. These claims don’t reflect any 3D understanding per se. However, it is necessary to note the student predictions to produce accurate scores. To address this issue we created separate analytic rubric categories. Category 1 scores whether the student recognizes that the carts will move away from each other. Category 2 scores whether the student states in the question that the carts will stop at some point. These categories are also essential for ensuring that students have answered both aspects of the question. Even though the categories are not 3D, they will be used in combination with the 3D categories to produce the final LP score assignment, and therefore will not threaten the 3D nature of the final analytic score. In contexts other than the current study careful attention should be drawn to identifying the aspects of student responses that should be separated into this type of analytic category. This is usually achieved during analytic rubric review by research team members focusing on ensuring that all the relevant information is captured by the analytic rubric categories.

Capturing inaccuracies in student thinking using analytic rubric categories

Inaccuracies in student responses on LP-aligned assessments usually reflect lower LP level type of thinking. These are usually relatively easy to identify for a human scorer that uses a holistic rubric aligned to previously validated LP. However, it is much more difficult to train an AI algorithm to identify various inaccuracies in student thinking. There is no easy way of accounting for the various possible inaccuracies using automatic scoring approaches. In this study, we developed a separate analytic scoring category (category 7 in Table 3) that reflects various inaccuracies in student reasoning. However, as shown in this study there are certain challenges we observed when scoring responses in this category.

A significant challenge with producing valid and accurate automatic scores for LP-aligned 3D items is that there are numerous ways students can respond to a question using similar words but inaccurate or incomplete ideas. This impacts the automatic scoring of assessments in that some incorrect responses include words that are also present in correct responses, which are used differently, either in ways they are connected or in support of incorrect ideas. This can make it difficult for a trained ML model to distinguish both types of responses since the LP-level assignment for a response is based on the integration of ideas, and not simply on the presence of predetermined words. This is illustrated by category 7, which focuses on capturing responses that contain various inaccuracies when including ideas of Energy and Coulomb’s Law. This category was originally developed during the deconstruction process to reflect different types of inaccuracies and vagueness in student thinking. While this category helped in LP-level assignment (specifically, the highest level of the LP should not have any inaccuracies), there were certain drawbacks to adding this category in the analytic rubric. In particular, the category encompassed too many different types of inaccurate thinking (Liu et al., 2014). Such “inaccuracies” range from providing a totally wrong answer (level 0) to using vague thinking (for example, in a level 2 response “carts will stop when they no longer sense each other”). We note that category 4 had a similar number of responses (387) as category 7, but exhibited a much higher human-machine agreement (0.686 for category 4 compared to 0.391 for category 7). This suggests that the more likely reason for poor human-machine agreement for category 7 is the way the category is defined, or more precisely, the presence of significant heterogenous text used with inaccuracies. As a result, this category was likely not specific enough for the machine to score consistently. In the future, it might be useful to split this category into multiple categories, each reflecting a specific type of inaccurate or vague thinking. A drawback of this approach, however, might be that there won’t be enough representative cases among student responses to ensure effective training of the machine on all possible inaccuracies. The main takeaway from the current study is that designing analytic scoring categories reflecting inaccuracies in student thinking is a potentially useful approach for producing accurate AI-based scores, but more research is needed on effective ways of designing such categories to ensure good human-machine agreement.

Capturing heterogeneity in student phrasing using analytic rubric categories

The fact that some words are used differently based on the context of an individual student also poses a challenge to the automatic scoring of LP-aligned assessments. In some responses, some words are used to mean something that is different from its actual definition. For example, utilizing the phrase “The cars will repel until the negative charges aren’t strong enough to repel” is using the word “charge” as a term equivalent to force, rather than using its correct meaning by indicating that two negative charges repel by producing an electric force. In this example the word “charge” is used in a more colloquial manner as charge is usually associated with power from a battery and that as long as there is “charge” in the battery the object will move. This is a challenge because as a human scorer, it is possible to understand that a response might have correct ideas, but the words included were an incorrect application of the word’s definition or utilize the colloquial definitions of words. Therefore, considering LP-aligned assessments, these difficulties with automatic analysis of potentially incorrect ideas make it difficult to accurately score every possible incorrect idea using AI approaches. There is also a challenge to assess and produce scores automatically when analyzing responses that utilize colloquial definitions of words as one cannot be sure whether the colloquial definition was used or even what definition the student might be using. A possible solution to this problem in terms of analytic rubric development is to identify enough examples of this type of inaccurate reasoning to ensure that the algorithm can successfully capture them. Another possible approach is to prompt students to define potentially ambiguous words in their responses as they construct their explanations (Rector et al., 2013).

Aligning the final score with the learning progression levels through combining relevant analytic rubric categories

Once the analytic scoring rubric categories are developed, mECD along with the LP can be used to guide the process of combining the categories for each level of the LP as shown in Table 4. As demonstrated in this study, it is important to ensure that the final LP level assignment using AI-generated scores has high agreement with the LP levels assigned by human coders. This will also provide additional validity evidence toward the 3D nature of the resulting analytic rubric.

Implications

The procedure demonstrated in this work is the first example of successful decomposition of holistic rubric for LP-based NGSS-aligned CR assessment into a series of analytic rubric categories that preserve the 3D nature and therefore the NGSS alignment of the item. The procedure described here can be used by anybody interested in performing this type of work. The principles for analytic rubric development outlined above can also be used when directly developing LP-based NGSS-aligned analytic rubric for AI-enabled scoring of CR assessment. Therefore, the methods discussed here have the potential to be widely applicable for rubric development for AI applications to ensure the preservation of the 3D nature of the assessment rubric.

The implications of findings presented here are numerous. Specifically, one of the main advantages in automatic text scoring is the cost reduction of evaluating new sets of responses to open-ended assessments. While holistic rubrics have been traditionally used for automatic scoring of LP-aligned assessments, these rubrics make it challenging to evaluate the validity of the resulting machine-assigned scores with respect to the LP levels (Kaldaras and Haudek, this issue). Specifically, it is challenging to understand the nature of machine misscores, as the final holistic score often cannot be broken down into various elements in the same way as an analytic score (Kaldaras and Haudek, this issue). This represents a key tradeoff in the use of analytic rubrics in ML-based evaluation. Although the development of analytic rubrics from holistic rubrics takes additional time, and human coders necessarily assign more codes, the more-fine-grained category scores from analytic rubrics can be beneficial in diagnosing ML-based “misscores.” This may lead to fewer iterations of ML model development and overall, reduced time spent in ML model training and testing.

Further, lack of confidence in the validity of the resulting ML scores and the inability to effectively evaluate the degree of the final score validity can be a significant drawback in using holistic rubrics for ML-based scoring of LP-aligned assessments. However, in the context of NGSS-aligned LPs and the associated assessments, developing analytic rubrics remains a challenging task because it is imperative to preserve the 3D nature of the scoring rubric to ensure alignment between all the elements of the assessment system and compliance to the view of science learning foundational in NGSS. The work presented here outlines a process for decomposing a 3D holistic rubric for LP-aligned NGSS assessment into a series of analytic rubric categories that yielded good agreement on the final LP level assignment between holistic and analytic rubric, and critically, which also preserve the 3D nature or the targeted performance.

Limitations

This study has several limitations. First, we only used one item for deconstructing the NGSS-aligned holistic rubric into a series of analytic rubrics. In the future, it would be informative to conduct the same procedure for more items to see if similar results hold or what other challenges arise. Further, the item used in this study was an explanation item. It would be informative to conduct a similar holistic rubric deconstruction procedure for items measuring other NGSS practices. For example, items measuring modeling practice might require other specific approaches for deconstructing the rubric to ensure that the 3D nature of the item is preserved.

Future directions

In the future, the research will focus on collecting sufficient numbers of student responses at higher LP levels and across all categories to develop and validate ML models for automatically scoring higher level responses. This will allow researchers to examine student learning gains along the LP levels quickly and efficiently. Further, the approach outlined here provides a possible scaffold for individualized feedback to students based on their performances aiming to help them progress toward higher LP levels. For this, one can leverage both the evidence statements, LP levels and analytic combinations in order to produce feedback that can identify missing components or integration and provide fine-grained feedback. For example, for an explanation predicted to be at Level 2 of the LP and but missing the category 5 score, you could provide feedback like “Consider adding ideas related to energy to your explanation of when the carts will stop.” Such fine-grained feedback may better elicit student ideas for categories 5 and 6 and thus help students progress on the LP.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

LK designed the rubrics, conducted scoring, and did most of wrote the manuscript. NY conducted scoring and wrote parts of the manuscript. KH advised throughout the project, reviewed the rubrics, provided substantial feedback on the manuscript, and conducted statistical analysis for the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This material was based upon work supported by the National Science Foundation under Grants Nos. 1323162 and 1561159.

Acknowledgments

We would like to thank Joseph Krajcik for valuable feedback during the holistic and analytic rubric development process.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2022.983055/full#supplementary-material

Footnotes

1. ^ Wilson, C., Haudek, K. C., Osborne, J., Buck-Bracey, M., Cheuk, T., Donovan, B., et al. (in revision). Using automated analysis to assess middle school students’ competence with scientific argumentation. J. Res. Sci. Teach.

References

American Educational Research Association [AERA] (2018). Standards for educational and psychological testing. Washington, DC: American Educational Research Association.

Google Scholar

Anderson, C. W., de los Santos, E. X., Bodbyl, S., Covitt, B. A., Edwards, K. D., Hancock, J. B., et al. (2018). Designing educational systems to support enactment of the next generation science standards. J. Res. Sci. Teach. 55, 1026–1052. doi: 10.1002/tea.21484

PubMed Abstract | CrossRef Full Text | Google Scholar

Cohen, J. (1960). A coefficient of agreement for nominal scales. Educ. Psychol. Meas. 20, 37–46. doi: 10.1177/001316446002000104

CrossRef Full Text | Google Scholar

Harris, C. J., Krajcik, J. S., Pellegrino, J. W., and DeBarger, A. H. (2019). Designing knowledge-in-use assessments to promote deeper learning. Educ. Meas. Issues Pract. 38, 53–67. doi: 10.1111/emip.12253

CrossRef Full Text | Google Scholar

Haudek, K. C., Prevost, L. B., Moscarella, R. A., Merrill, J., and Urban-Lurain, M. (2012). What are they thinking? Automated analysis of student writing about acid–base chemistry in introductory biology. CBE—Life Sci. Educ. 11, 283–293. doi: 10.1187/cbe.11-08-0084

PubMed Abstract | CrossRef Full Text | Google Scholar

Jescovitch, L. N., Scott, E. E., Cerchiara, J. A., Doherty, J. H., Wenderoth, M. P., Merrill, J. E., et al. (2019). Deconstruction of holistic rubrics into analytic rubrics for large-scale assessments of students’ reasoning of complex science concepts. Pract. Assess. Res. Eval. 24, 1–13.

Google Scholar

Jescovitch, L. N., Scott, E. E., Cerchiara, J. A., Merrill, J., Urban-Lurain, M., Doherty, J. H., et al. (2020). Comparison of machine learning performance using analytic and holistic coding approaches across constructed response assessments aligned to a science learning progression. J. Sci. Educ. Technol. 30, 150–167. doi: 10.1007/s10956-020-09858-0

CrossRef Full Text | Google Scholar

Jurka, T. P., Collingwood, L., Boydstun, A. E., and Grossman, E. (2013). RTextTools: A supervised learning package for text classification. R J. 5, 6–12. doi: 10.32614/RJ-2013-001

CrossRef Full Text | Google Scholar

Kaldaras, L. (2020). Developing and validating NGSS-Aligned 3D learning progression for electrical interactions in the context of 9th grade physical science curriculum. East Lansing, MI: Michigan State University.

Google Scholar

Kaldaras, L., Akaeze, H., and Krajcik, J. (2021a). Developing and validating next generation science standards-aligned learning progression to track three-dimensional learning of electrical interactions in high school physical science. J. Res. Sci. Teach. 58, 589–618. doi: 10.1002/tea.21672

CrossRef Full Text | Google Scholar

Kaldaras, L., Akaeze, H., and Krajcik, J. (2021b). A methodology for determining and validating latent factor dimensionality of complex multi-factor science constructs measuring knowledge-in-use. Educ. Assess. 26, 241–263. doi: 10.1080/10627197.2021.1971966

CrossRef Full Text | Google Scholar

Kaldaras, L., and Haudek, K. (2022). Validation of automated scoring for learning progression-aligned next generation science standards performance assessments. Front. Educ. 896. doi: 10.3389/feduc.2022.968289

CrossRef Full Text | Google Scholar

Krajcik, J. S. (2021). Commentary—applying machine learning in science assessment: Opportunity and challenges. J. Sci. Educ. Technol. 30, 313–318. doi: 10.1007/s10956-021-09902-7

PubMed Abstract | CrossRef Full Text | Google Scholar

Lead States (2013). Next generation science standards: For states, by states. Washington, DC: The National Academies Press.

Google Scholar

Lee, H.-S., Pallant, A., Pryputniewicz, S., Lord, T., Mulholland, M., and Liu, O. L. (2019). Automated text scoring and real-time adjustable feedback: Supporting revision of scientific arguments involving uncertainty. Sci. Educ. 103, 590–622. doi: 10.1002/sce.21504

CrossRef Full Text | Google Scholar

Li, H., Gobert, J., Dickler, R., and Moussavi, R. (2018). “The impact of multiple real-time scaffolding experiences on science inquiry practices,” in Intelligent tutoring systems, eds R. Nkambou, R. Azevedo, and J. Vassileva (Cham: Springer International Publishing), 99–109. doi: 10.1007/978-3-319-91464-0_10

CrossRef Full Text | Google Scholar

Liu, O. L., Brew, C., Blackmore, J., Gerard, L., Madhok, J., and Linn, M. C. (2014). Automated scoring of constructed-response science items: Prospects and obstacles. Educ. Meas. Issues Pract. 33, 19–28. doi: 10.1111/emip.12028

CrossRef Full Text | Google Scholar

Maestrales, S., Zhai, X., Touitou, I., Baker, Q., Schneider, B., and Krajcik, J. (2021). Using machine learning to score multi-dimensional assessments of chemistry and physics. J. Sci. Educ. Technol. 30, 239–254. doi: 10.1007/s10956-020-09895-9

CrossRef Full Text | Google Scholar

Mao, L., Liu, O. L., Roohr, K., Belur, V., Mulholland, M., Lee, H. -S., et al. (2018). Validation of automated scoring for a formative assessment that employs scientific argumentation. Educ. Assess. 23, 121–138. doi: 10.1080/10627197.2018.1427570

CrossRef Full Text | Google Scholar

McHugh, M. L. (2012). Interrater reliability: The kappa statistic. Biochem. Med. 22, 276–282. doi: 10.11613/BM.2012.031

CrossRef Full Text | Google Scholar

Mitchell, T. M. (1997). Machine learning. Boston, MA: McGraw-Hill, 174–176.

Google Scholar

Moharreri, K., Ha, M., and Nehm, R. H. (2014). EvoGrader: An online formative assessment tool for automatically evaluating written evolutionary explanations. Evol. Educ. Outreach 7, 1–14. doi: 10.1186/s12052-014-0015-2

CrossRef Full Text | Google Scholar

National Research Council [NRC] (1999). How people learn: Bridging research and practice. Washington, DC: National Academies Press.

Google Scholar

National Research Council [NRC] (2012). A framework for K-12 science education: Practices, crosscutting concepts, and core ideas. Washington, DC: National Academies Press.

Google Scholar

Nehm, R. H., Ha, M., and Mayfield, E. (2012). Transforming biology assessment with machine learning: Automated scoring of written evolutionary explanations. J. Sci. Educ. Technol. 21, 183–196. doi: 10.1007/s10956-011-9300-9

CrossRef Full Text | Google Scholar

Noyes, K., McKay, R. L., Neumann, M., Haudek, K. C., and Cooper, M. M. (2020). Developing computer resources to automate analysis of students’ explanations of London dispersion forces. J. Chem. Educ. 97, 3923–3936. doi: 10.1021/acs.jchemed.0c00445

CrossRef Full Text | Google Scholar

Rector, M. A., Nehm, R. H., and Pearl, D. (2013). Learning the language of evolution: Lexical ambiguity and word meaning in student explanations. Res. Sci. Educ. 43, 1107–1133. doi: 10.1007/s11165-012-9296-z

CrossRef Full Text | Google Scholar

Sieke, S. A., McIntosh, B. B., Steele, M. M., and Knight, J. K. (2019). Characterizing students’ ideas about the effects of a mutation in a noncoding region of DNA. CBE—Life Sci. Educ. 18:ar18. doi: 10.1187/cbe.18-09-0173

PubMed Abstract | CrossRef Full Text | Google Scholar

Smith, C. L., Wiser, M., Anderson, C. W., and Krajcik, J. (2006). Implications of research on children’s learning for standards and assessment: A proposed learning progression for matter and the atomic-molecular theory. Meas. Interdiscip. Res. Perspect. 4, 1–98. doi: 10.1080/15366367.2006.9678570

CrossRef Full Text | Google Scholar

Tansomboon, C., Gerard, L. F., Vitale, J. M., and Linn, M. C. (2017). Designing automated guidance to promote productive revision of science explanations. Int. J. Artif. Intell. Educ. 27, 729–757. doi: 10.1007/s40593-017-0145-0

CrossRef Full Text | Google Scholar

Wang, C., Liu, X., Wang, L., Sun, Y., Zhang, H., et al. (2021). ‘Automated scoring of Chinese grades 7–9 students’ competence in interpreting and arguing from evidence’. J. Sci. Educ. Technol. 30, 269–282. doi: 10.1007/s10956-020-09859-z

CrossRef Full Text | Google Scholar

Zhai, X., Shi, L., and Nehm, R. H. (2021). A meta-analysis of machine learning-based science assessments: Factors impacting machine-human score agreements. J. Sci. Educ. Technol. 30, 361–379. doi: 10.1007/s10956-020-09875-z

CrossRef Full Text | Google Scholar

Zhai, X., Yin, Y., Pellegrino, J. W., Haudek, K. C., and Shi, L. (2020). Applying machine learning in science assessment: A systematic review. Stud. Sci. Educ. 56, 111–151. doi: 10.1080/03057267.2020.1735757

CrossRef Full Text | Google Scholar