- College of Education, University of Ha’il, Ha'il, Saudi Arabia
Introduction: The aim of this study was to investigate how enhancing topic-specific prior mathematical knowledge of students before introducing new topics impacts their outcomes in mathematics achievements.
Methods: A quasi-experimental design was applied to two groups: a control group [students who did not receive enhancement for their topic-specific prior mathematical knowledge (N = 37)] and an experimental group [students who received enhancement for their topic-specific prior mathematical knowledge (N = 36)].
Results: The results revealed that there were no significant differences between the students’ average scores in ‘conceptual knowledge’ in the immediate post-test for groups; however, the difference was significant in the delayed post-test in favor of the experimental group. The results also showed that there were significant differences between the students’ average scores in ‘procedural knowledge’ in both the immediate and delayed post-tests in favor of the experimental group.
Discussion: The results showed the importance of this strategy in improving students’ outcomes.
1. Introduction
Many studies have found that prior knowledge strongly influences new learning (Rothman and McMillan, 2003; Thompson and Zamboanga, 2003; Aubrey et al., 2006; Byrnes and Wasik, 2009; Fazio et al., 2016; Byrnes et al., 2018; Kosiol et al., 2019). For example, a longitudinal study by Aubrey et al. (2006) tracked primary school pupils during the first 5 years (from 6 to 11 years old). The study found that early numeracy skills were a good predictor for later mathematics achievement, while a low starting level of mathematical knowledge was predictive of failure to progress. Prior knowledge includes content, skills, and beliefs (Hattie and Yates, 2013). The scope of this research is limited to the content of prior mathematical knowledge that includes critical topic-specific information, which is a necessary foundation for learning that involves conceptual and procedural knowledge. Although much is known about the importance of prior knowledge for students’ achievement, little is known about the effect of manipulating prior knowledge on a student’s achievements. Such a study may give insight for instructional designers and teachers to use prior knowledge to improve students’ learning in mathematics as a highly interconnected discipline. It may also pave the way for further studies about manipulating prior knowledge for learning effectiveness.
This article begins with a discussion of prior knowledge and its relationship with cognitive load, followed by a review of how types of prior knowledge affect students’ subsequent learning. The experiment conducted here examined whether enhancing necessary topic-specific prior knowledge before introducing a new topic improves student outcomes in mathematics.
1.1. Prior knowledge and cognitive load
Studies have shown that students with different levels of prior knowledge or expertise perform differently in subsequent learning in several dimensions. Students with greater prior knowledge learn better (Yüksel, 2014; Fazio et al., 2016), demonstrate more positive attitudes (O'Donnell and Dansereau, 2000; Winters et al. 2008; Yüksel, 2014; Usman and Miranda, 2020), can control their learning better (Bernacki et al., 2012; Song et al., 2016; Mihalca and Mengelkamp, 2020; Alreshidi, 2021), and have stronger perseverance (Hattie and Yates, 2013; Riazy et al., 2020) than students with less prior knowledge. These differences can be explained through cognitive load theory.
According to constructivist and cognitivist perspectives on learning, learners construct new knowledge individually using their prior knowledge about ideas or objects that are connected to new information (Fosnot, 1996; Wilson, 1996; Loyens and Gijbels, 2008; Yew and Schmidt, 2009; Rach and Ufer, 2020). Existing knowledge, therefore, should be actively used through information processes to form connections between it and new information (Mayer, 1979). Activation of prior knowledge occurs when individuals retrieve relevant prior knowledge from their long-term memory to their working memory. When dealing with unfamiliar information (that is, new or novel information that lacks relevant prior knowledge stored in long-term memory), one’s working memory is tremendously restricted. Individuals are able to process and store only a few combinations of unfamiliar elements at any given time (Miller, 1956). However, individuals can store vast amounts of information in their long-term memory.
Cognitive load theorists have argued that working memory capacity can be vastly increased by accessing information stored in long-term memory (Ericsson and Kintsch, 1995; Paas et al., 2003; Sweller, 2003). Cognitive load can be divided into three dimensions—namely, intrinsic, extraneous and germane cognitive load. The intrinsic cognitive load is imposed by complex tasks; for example, a task that has more interactive elements imposes a higher intrinsic cognitive load compared with a task that has fewer interactive elements. However, when learners have more expertise (i.e., prior knowledge) in the task, their intrinsic load can be reduced because they combine some interactive elements together as a chunk (i.e., one element); this reduces the number of interactive elements, and consequently, it decreases the intrinsic load. The extraneous cognitive load is imposed by poor instructional design; for example, when students are taught using conventional problems, they apply the means-ends analysis technique, which imposes a higher extraneous load. Finally, the germane cognitive load is responsible for forming schemas. In other words, it refers to the resources that remain after the other two dimensions are accounted for which can be used to construct schemas. It is related to relevant learning; for example, when students learn the steps of problem solving form worked examples, they devote the germane load to constructing generalizing procedures to solve similar problems (for more details about cognitive load dimensions, see Jordan et al., 2020).
When learners are exposed to new information, they can draw on prior knowledge, reducing the cognitive load, particularly the intrinsic cognitive load (Kester et al., 2010). When the intrinsic load is overloaded, it leaves no place for the germane load to form schemas. The germane load relates to how information turns out to be stored in long-term memory (Jordan et al., 2020).
If prior knowledge is insufficient or inaccurate, the long-term memory cannot support new learning, leading to overload working memory. For example, if an individual would like to learn a new concept that is ‘addition’ but does not know what ‘number’ means or what ‘combining’ is, then the individual has to learn the meaning of those concepts alongside the new concept. This challenge will either overload the working memory because the individual has insufficient prior knowledge to learn the new concept, or it could result in surface learning (e.g., rote memorization). Surface learning could take place if students cannot connect the new knowledge to their prior knowledge base (Dochy et al., 1999; Donald, 2002). In addition to insufficient prior knowledge, inaccurate prior knowledge could, in fact, do more harm than good; learners could be conflict with they believe to be correct. Several studies found that the activation of inaccurate prior knowledge could hinder new learning (Lipson, 1982; Alvermann et al., 1985; Braasch and Goldman, 2010; Arbiyah et al., 2020). Therefore, integrating existing knowledge to new knowledge works well only if the existing knowledge can be extended by new ideas or concepts (Mihalca and Mengelkamp, 2020).
1.2. Types of prior knowledge and learning
It is important to distinguish between the effects of different types of prior knowledge. There are two key types of prior knowledge: conceptual knowledge and procedural knowledge (Alexander et al., 1991; De Jong and Ferguson-Hessler, 1996; Anderson and Krathwohl, 2001; Ningsih and Retnowati, 2020). Conceptual knowledge is the knowledge of facts and concepts, or knowing what, while procedural knowledge is knowing how and when to apply different procedures. Knowing facts does not necessitate knowing how and when to implement procedures, and vice versa. In other words, students can know concepts or facts but cannot know how and when to apply them (Clement, 1982). Likewise, students can execute procedural tasks, but they may not be able to show a clear understanding of what they are doing or why (Berry and Broadbent, 1988; Reber and Kotovsky, 1997; Sun et al., 2001). In mathematics, students might be able to use a formula to solve a certain problem; however, they may not be able to explain the principles underlying the solution. These students may possess sufficient procedural knowledge, which enables them to perform successfully in certain contexts, while lacking conceptual knowledge of the deep principles and features that would permit them to adapt to different situations. Research has found that procedural prior knowledge contributes to student achievement more than conceptual prior knowledge (Hailikari et al., 2007). However, this situation is quite complicated, as discussed in the following paragraphs.
Conceptual knowledge is a web of relationships of concepts (Miller and Hudson, 2007; Rittle-Johnson and Schneider, 2015) that develops between a previously learned concept and new one or between two early learned mathematical concepts (Rittle-Johnson et al., 2016). To develop conceptual knowledge, students should first learn the concepts and then learn the relationships between the concepts. If students lack the necessary prior concepts, then learning connections between the concepts would be unsuccessful. Similarly, procedural knowledge is visualized as the ability to follow steps in a sequence to reach a mathematical goal or solve mathematical problems (Canobi, 2009; Rittle-Johnson and Schneider, 2015), which can often be interrelated or rooted within other procedures (Baroody et al., 2007). Learning new procedures that have relationships with other procedures that students do not already learned would lead to overload memory. Differences arising between different students in prior knowledge strongly affect students’ learning processes (Smith et al., 1994; Ackerman and Cianciolo, 2000). The impact can extend beyond a single domain to affect both conceptual and procedural knowledge. Several studies have revealed that prior conceptual knowledge about the target content is among the most important factors of subsequent learning processes, including the gaining of new procedural knowledge (Hecht et al., 2003; Schneider et al., 2009). The research has shown that the lack of a conceptual understanding of mathematics critically impedes students’ ability to transfer and generalize mathematics (Richland et al., 2012). For example, when a learner needs to solve a new problem, prior conceptual knowledge should support the production of new procedures (Gelman and Williams, 1998). Other researchers have found that prior procedural knowledge also impact on a later conceptual understanding (Karmiloff-Smith, 1992). A study conducted by Canobi (2009) suggested that improving procedural knowledge can support improvements in conceptual knowledge. For example, before children understand most of the underlying concepts of counting, they learn counting procedures (Frye et al., 1989; LeFevre et al., 2006).
Recently, Rittle-Johnson et al. (2001) proposed that the causal relation between conceptual and procedural knowledge is bidirectional, with increases in one type of knowledge leading to subsequent increases in the other type of knowledge. In a study examining elementary school students’ knowledge of fractions in the fourth and fifth grades, Hecht and Vagi (2010) discovered that conceptual knowledge in fourth grade predicted procedural knowledge in fifth grade, while procedural knowledge in fourth grade predicted conceptual knowledge in fifth grade. These results illustrate that prior knowledge works as a moderator to support learning for both conceptual and procedural knowledge because its relationships with each other. Enhancing students’ prior knowledge, particularly necessary topic-specific prior knowledge, might contribute to students’ outcomes. This process might reduce the cognitive load, particularly the intrinsic load, and increase the germane load for supporting learning connections (i.e., scheme formation). However, enhancement would not be considered when teachers assume that teaching always leads to intended learning.
1.3. Present study
Students do not learn the necessary prior knowledge just because it was previously taught, so teachers cannot assume that students have sufficient and accurate prior knowledge to support subsequent learning. Therefore, enhancing students’ necessary prior knowledge, which includes addressing insufficient prior knowledge, addressing inaccurate prior knowledge and activating prior knowledge before introducing new topics, might be useful in helping students learn subsequent new knowledge.
Mathematics knowledge includes conceptual and procedural knowledge, as discussed in a previous section (i.e., Introduction section).
Although studies have shown that prior conceptual or procedural knowledge affects student’s cognitive load and contributes to outcomes in mathematics, no study has been conducted to assess how manipulating the necessary prior mathematical knowledge affects students’ outcomes.
In this study, a quasi-experimental design was used to assess the effectiveness of enhancing necessary topic-specific prior knowledge before introducing new topics affects student outcomes in mathematics. This study aimed to address the following questions:
1. What is the immediate and late effect of enhancing necessary topic-specific prior mathematical knowledge before introducing new topics on students’ mathematical knowledge?
2. What is the immediate and late effect of enhancing necessary topic-specific prior mathematical knowledge before introducing new topics on students’ mathematical conceptual knowledge?
3. What is the immediate and late effect of enhancing necessary topic-specific prior mathematical knowledge before introducing new topics on students’ mathematical procedural knowledge?
2. Method
2.1. Participants and design
The school selected for the study was located in an urban district in Ha’il, a major city in Saudi Arabia. It was chosen because the school administration and the teacher were willing to participate in the study. The participants consisted of 73 third-grade students in four classes in one Saudi primary school (age M = 8.9 years; SD = 0.23). A quasi-experimental design was applied with two groups. Two classes (n = 37) were randomly assigned as the ‘control group’, and the other two classes (n = 36) were assigned as the ‘experimental group’. The same mathematics teacher taught both groups. All participants and their parents gave their consent and agreed to take part in this study; they were informed that they could withdraw at any time without having to provide any reason for their decision to leave the study. Based on the statistical test induces: ANCOVA test (effect size, α err, sample size, numerator df and covariates), a post hoc power analysis was conducted using G*Power 3.1 to check whether the sample size was adequate. G*Power indicated a power level of 0.94. That is, the sample size was adequate for the study.
2.2. Materials
2.2.1. Topics
The study topic was ‘fractions’. The content was new to the students and included the concept of fractions, the representation of fractions, fractions as parts of a whole, fractions as parts of a group, equivalent fractions and comparing and ordering fractions. The instruction lasted for 2 weeks and took place during seven 45-min sessions. Four sessions were held per week, resulting in a total of 5.15 h for each group. Both groups were given the same amount of time.
2.2.2. Mathematics test
The mathematics test contained 15 questions: 8 conceptual questions (5 multiple choices, 2 short answer and 1 drawing test) and 7 procedural questions (4 multiple choices, 2 short answer and 1 drawing test). The same test was conducted three times: Time1, before the experiment took place (pre-test); Time 2, immediately after the intervention was completed (immediate post-test); and Time3, a week later (delayed post-test). The pre-test was conducted to ensure that no significant difference existed between groups in their prior knowledge related to the content. The immediate post-test was carried out to measure the differences between groups following the intervention. The delay post-test was intended to measure the difference between groups in retention. The mathematics items were adopted from released items of the Trends in International Mathematics and Science Study (TIMSS) 2003, 2007 and 2011 (Mullis et al., 2004, 2008, 2011). The selected TIMSS items exactly matched the objectives of the topics for conceptual knowledge and procedural knowledge. After the tests had been prepared, they were presented to five arbitrators for checking. The arbitrators gave feedback on the adequacy, clarity, relevance of the content and validity in terms of measuring the students’ abilities in conceptual and procedural knowledge. The arbitrators’ evaluations were considered during the preparation of the final versions of the tests. The reliability by test-retests was 0.93, and the internal consistency for the sub-scale of the tests was 0.91. For the examination marks, each item (multiple choice, short answer and drawing) was scored as either one or zero. Examples of the items are shown in Appendices 1 and 2.
2.3. Strategy for enhancing necessary topic-specific prior knowledge
Together, the authors and the teacher, as a team, identified the content of the necessary topic-specific prior conceptual and procedural knowledge for each topic intended to be taught. The design of the content of prior knowledge was conducted in three stages. First, the team identified the unit (i.e., fractions) and determined how many sessions it needed (eight sessions). Second, the team identified the conceptual and procedural knowledge necessary for learning each topic. Third, the team developed small problems to address the identified prior knowledge.
In typical classrooms, teachers might suppose that students learned equivalent fractions in the previous lesson simply because it was previously taught. The control group represented this normal classroom, where the teacher assumed that his students had already learned equivalent fractions. This assumption was not made for the experimental group. For example, when students need to learn the concept of comparing and ordering fractions, the lesson of equivalent fractions becomes necessary prior knowledge for comparing and ordering fractions. Both groups were taught equivalent fractions before teaching comparing and ordering fractions. However, when the teacher was about to teach comparing and ordering fractions to the experimental group, he began the lesson by enhancing the students’ conceptual knowledge (i.e., recognized equivalent fractions) and procedural knowledge (i.e., how to determine an equivalent fraction for a certain fraction) of equivalent fractions.
The strategy for enhancing necessary topic-specific prior knowledge includes three components: addressing insufficient prior knowledge, addressing inaccurate prior knowledge, and activating prior knowledge. This can be done by posing predetermined problems. These problems aimed to activate accurate and relevant prior knowledge and address inaccurate or inadequate prior mathematical knowledge and were provided only for the experimental group at the beginning of each topic through problem-solving formats. For instance, at the beginning of each topic, the prior knowledge of the experimental group was enhanced by posing small problems to be solved by students individually, such as ‘Draw a circle and express ¼’. The teacher then provided the students collectively with appropriate feedback. This strategy activates the necessary prior knowledge when students engage in problem-solving processes and addresses inaccurate or inadequate prior knowledge by providing appropriate feedback. The team determined that the feedback should not take more than half of the time allocated to the session (i.e., not more than 20 min). Both groups were taught using conventional teaching methods, which included the teacher explaining concepts to students and then the students doing exercises. The only difference between the groups was that the experimental group received enhancement at the beginning of each lesson, as discussed above.
Three experts in the field verified the validity of the prior knowledge content as being relevant, appropriate, and sufficient for the purpose of the study. Their feedback was taken into consideration.
2.4. Procedures
As detailed above, the school was chosen and permission was granted to implement the study in the school. All participants and their parents gave their consent and agreed to participate in the study. The author designed the content of the necessary topic-specific prior knowledge and checked for its validity. The mathematics test was adapted from TIMSS released items, and its validity and reliability were checked. The teacher was trained before the commencement of the intervention, and the teacher of the experimental group was provided with extensive training on how to conduct the experiment. The authors conducted 4 h of training on how to use the strategy for the teacher. The teacher performed appropriately before the intervention took place. The author attended all lessons (for both groups) to make sure that the experiment was going as planned.
Two groups were randomly selected (control and experimental groups). A pre-test was conducted for both groups. Both groups were taught the same content and given the same allocated time. For the experimental group, students’ necessary topic-specific prior knowledge was enhanced at the beginning of each topic. Both groups were taught using conventional teaching methods. After 2 weeks, the content was taught to both groups, and the post-test was administered to both groups. A week later, the delayed post-test was also administered to both groups (see Figure 1). The same mathematical tests were administered three times. Between the immediate post-test and late post-test (i.e., a 1 week interval), the same teacher taught both groups the same next topics using the same conventional methods with no enhancement. The collected data were analyzed using IBM SPSS v 22.
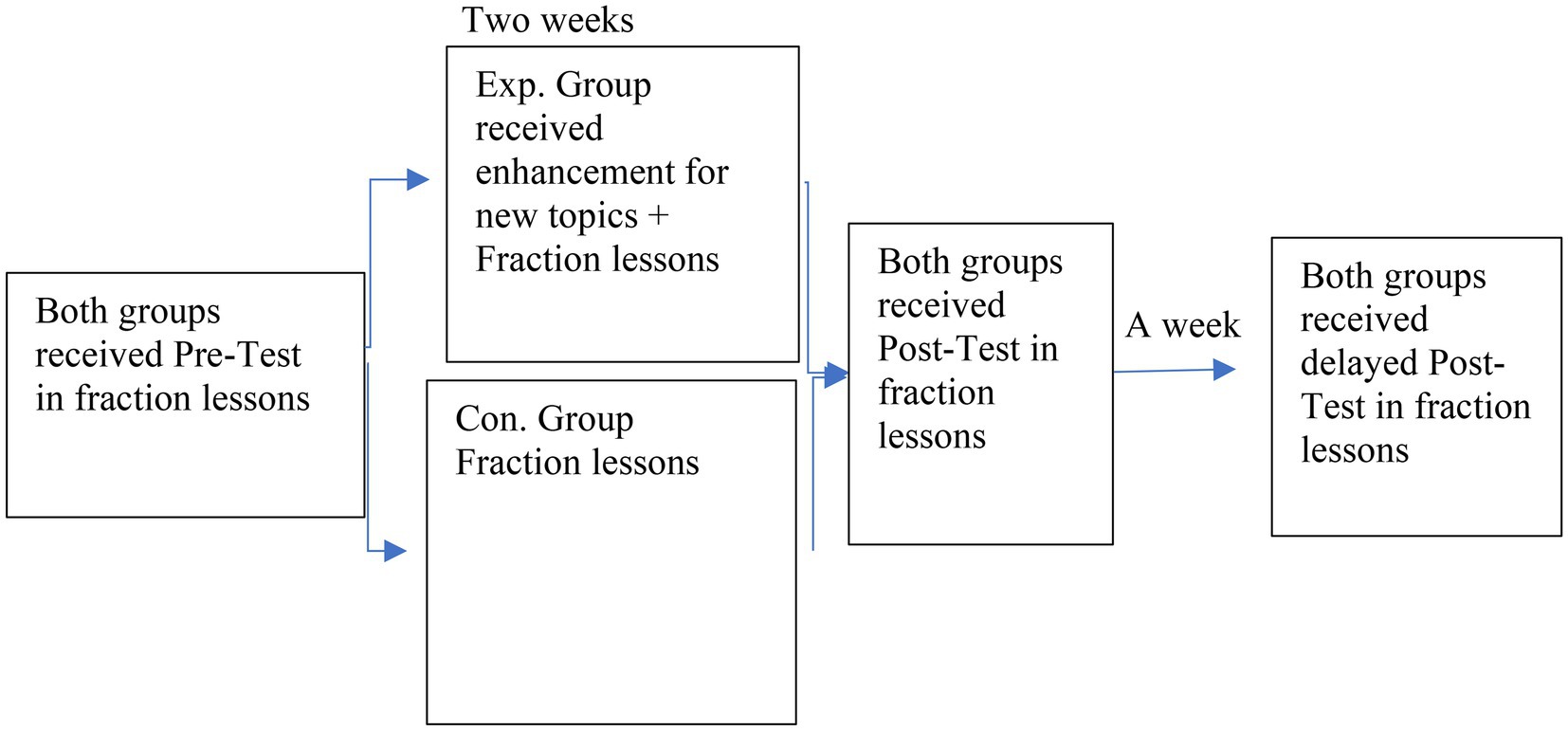
Figure 1. Design of the study. Enhancement includes three components: addressing insufficient prior knowledge, addressing inaccurate prior knowledge, and activating prior knowledge.
3. Results
The data were analyzed using the t-test and one-way ANCOVA. The main assumptions of these tests were included; normality and Levene’s test checks were performed, and the assumptions were met. The values of skewness and kurtosis were acceptable. According to Curran et al. (1996), data are considered normal when the skewness is between −2 and + 2 and the kurtosis is between −7 and + 7. In this study, the skewness values ranged from 0.096 to 0.923, whereas the kurtosis values ranged from −0.895 to 1.272. Therefore, the data for all dependent factors is considered to be normally distributed. The homogeneity of the results was also tested using Levene’s test, and the result of the test was (p > 0.05). This indicates that the data met the homogeneity conditions (see Field, 2013). The results are presented for each question as follows:
3.1. What is the immediate and late effect of enhancing necessary topic-specific prior mathematical knowledge before introducing new topics on students’ mathematical knowledge?
The t-test results indicated no significant difference in the pre-test scores for the control and experimental groups (t = 0.994).
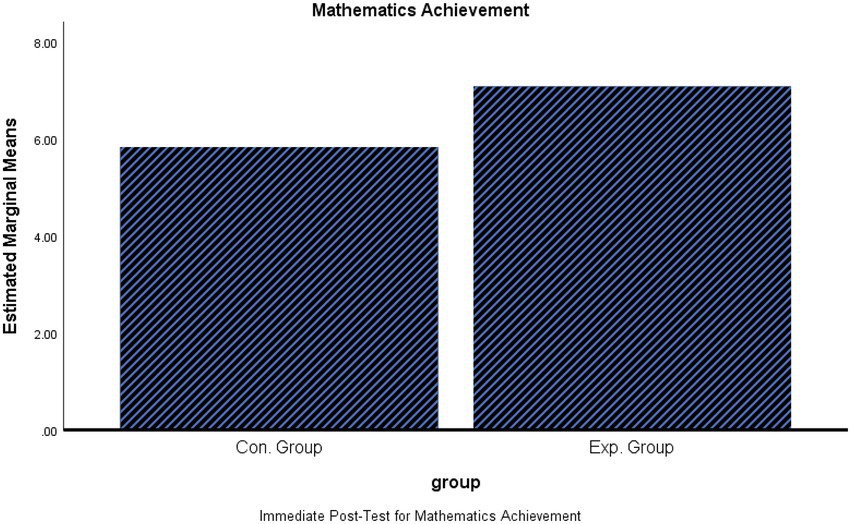
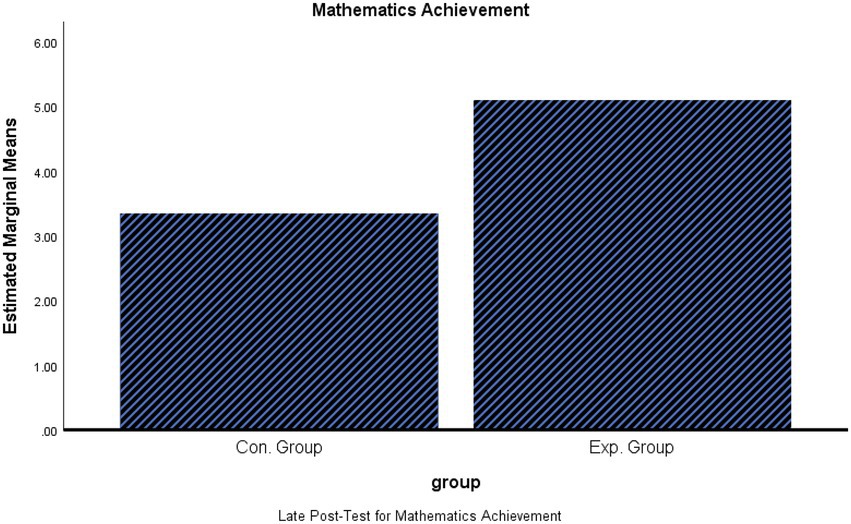
A one-way ANCOVA was conducted to compare the effectiveness of the strategy, controlling for prior knowledge. There was a significant difference in the post-test F (1,71) = 4.71, p < 0.05. Students in the experimental group had higher post-test scores (M = 7.22, SD = 3.12) than students in the control group (M = 5.70, SD = 2.17) with small effect size (0.063). The results also indicated that students in the experimental group had higher delay post-test scores (M = 5.25, SD = 2.76) than students in the control group (M = 3.22, SD = 2.07), F (1,71) = 12.08, p < 0.01, with small effect size (0.147; see Table 1; Figures 2, 3).
This result indicates that enhancing necessary mathematical prior knowledge before teaching a new topic significantly improves students’ achievement in immediate and delayed mathematics tests when compared to students who did not receive enhancement.
The test included knowledge (conceptual knowledge) and knowledge application (procedural knowledge). It was important to check which types of knowledge were more effective.
3.2. What is the immediate and late effect of enhancing necessary topic-specific prior mathematical knowledge before introducing new topics on students’ mathematical conceptual knowledge?
The t-test results indicated no significant difference in the pre-test scores for the experimental and control groups (t = 0.1.31).
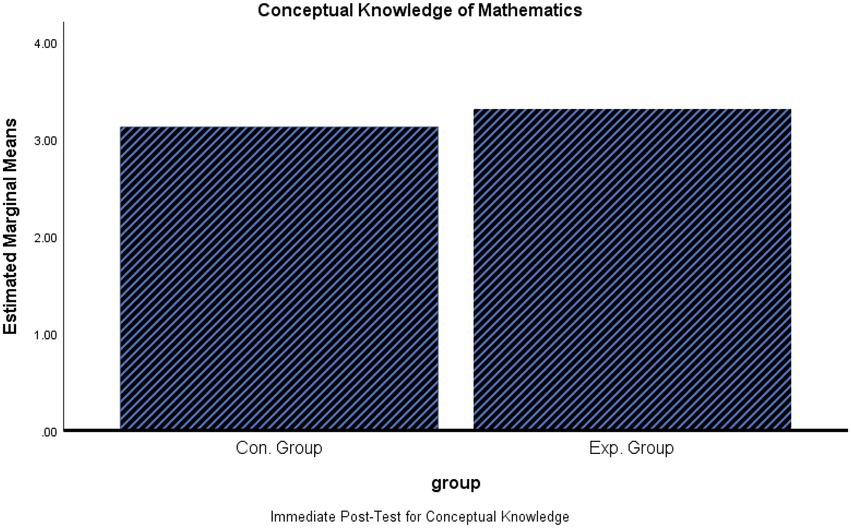
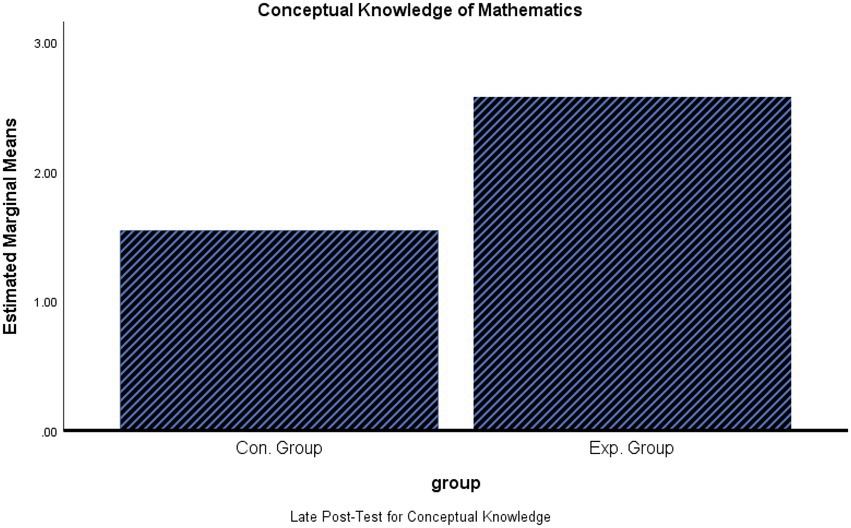
Table 2 and Figures 4, 5 show that there was no significant difference in the post-test F (1,71) = 2.99, p > 0.05. However, there was a significant difference in the delay post-test F (1,71) = 11.61, p < 0.01, it indicated that students in the experimental group had significantly higher average scores in conceptual knowledge (M = 2.64, SD = 1.44) than students in the control group (M = 1.49, SD = 1.22), with small effect size (0.142).
This result indicates that enhancing necessary mathematical prior knowledge before teaching a new topic significantly improves students’ achievement in only delayed conceptual mathematics tests when compared to students who did not receive enhancement.
3.3. What is the immediate and late effect of enhancing necessary topic-specific prior mathematical knowledge before introducing new topics on students’ mathematical procedural knowledge?
The t-test results indicated no significant difference in the pre-test scores for the control and experimental groups (t = 2.66).
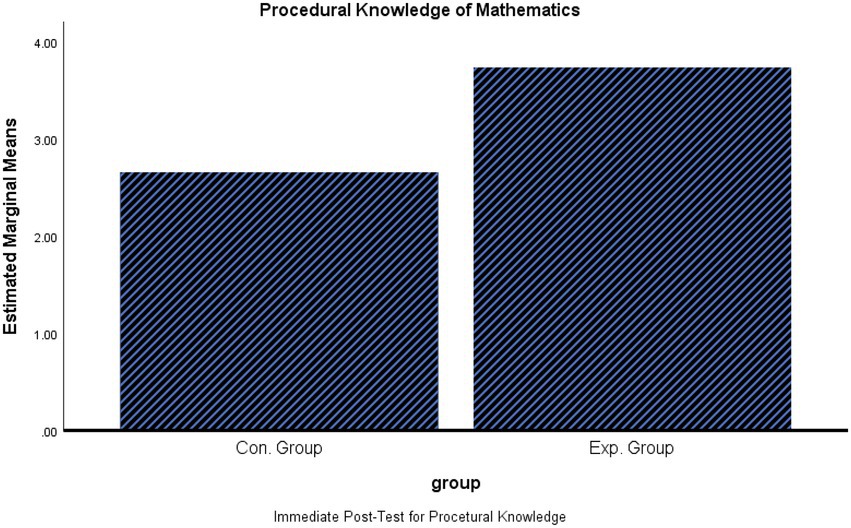
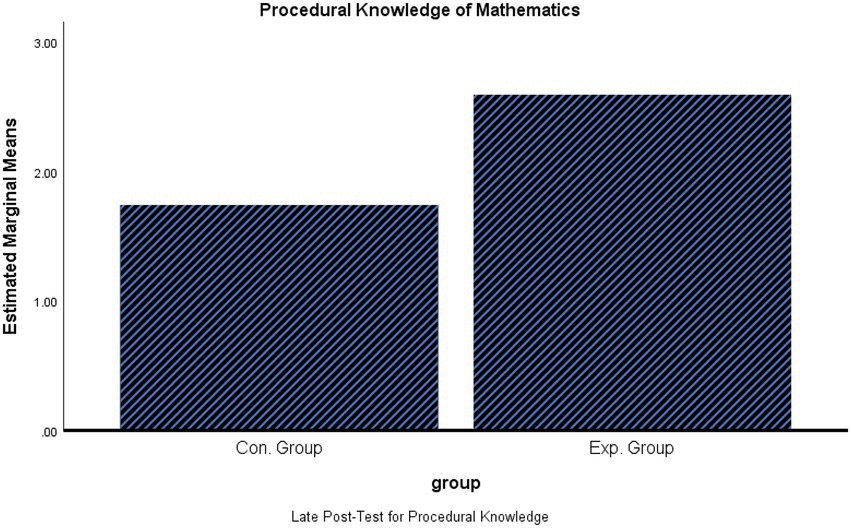
The one-way ANCOVA results indicated that there was a significant difference in the post-test F (1,71) = 9.08, p < 0.01. Students in the experimental group had higher post-test scores (M = 3.75, SD = 1.63) than students in the control group (M = 2.64, SD = 1.49), with small effect size (0.115). The results also showed that students in the experimental group had higher delay post-test scores (M = 2.61, SD = 1.73) than students in the control group (M = 1.73, SD = 1.30), F (1,71) = 6.24, p < 0.05, with small effect size (0.082; see Table 3; Figures 6, 7).
This result indicates that enhancing necessary mathematical prior knowledge before teaching a new topic significantly improves students’ achievement in immediate and delayed procedural mathematics tests when compared to students who did not receive enhancement.
4. Discussion
When the necessary topic-specific prior mathematical knowledge was enhanced for students before teaching new topics, students’ average scores in immediate and delayed mathematics tests improved in the intervention group when compared to the average scores of students who did not receive enhancement. More specifically, students who received enhancement improved in the immediate post-test for procedural knowledge and in the delayed post-test for conceptual and procedural knowledge with a small size effect.
Enhancement here targets the necessary topic-specific prior mathematical knowledge and includes three components: addressing insufficient prior knowledge, addressing inaccurate prior knowledge, and activating prior knowledge. This prior knowledge was selected to enhance by determining what is necessary for students in order to facilitate its integration into new information. For example, students cannot learn to compare or order fractions unless they have already learned equivalent fractions. Being able to recognize equivalent fractions works as a facilitator for new learning (i.e., comparing or ordering fractions). In other words, learning equivalent fractions is sufficient mathematical prior knowledge for learning to compare or order fractions. Sufficient prior knowledge supports working memory to increase its capacity. The capacity to utilize working memory can be vastly increased by the information stored in the long-term memory (Ericsson and Kintsch, 1995; Paas et al., 2003; Sweller, 2003). This can reduce the cognitive load, particularly the intrinsic cognitive load for working memory, by making working memory partially rely on the support of long-term memory, consequently increasing germane load capacity. The germane load is critical for learning, and it relates to how information turns out to be stored in long-term memory. When learners have sufficient prior knowledge to learn new materials, this can reduce the intrinsic load and augment the germane load, which leads to effective learning (Jordan et al., 2020). Therefore, when students hold sufficient prior knowledge, they can learn better than those who lack the necessary prior knowledge.
Another component of enhancement is addressing inaccurate prior knowledge. If there is a misconception in prior knowledge, the learning of new knowledge is probably resisted. For example, if the students hold misconceptions about ‘equivalent fractions’, the learning of ‘comparing or ordering fractions’ is likely to be resisted. Learners could conflict with what they believe to be correct (for more details, see; Lipson, 1982; Alvermann et al., 1985; Braasch and Goldman, 2010; Arbiyah et al., 2020). Therefore, addressing inaccurate prior knowledge could pave the way for new information to connect to existing knowledge.
The last component of enhancement is the activation of prior knowledge. Activating necessary prior knowledge is a key function for the integration of knowledge. Existing knowledge should be actively used through information processes to form connections between existing knowledge and new information (Mayer, 1979). Activation of prior knowledge is important as a foundation for new knowledge. When instruction ignores prior knowledge activation, learners will feel overwhelmed. Consequently, the learners will rely on memorizing the material presented. This is because a new knowledge structure cannot be done without its foundation (relevant prior knowledge; Merrill, 2002). Therefore, enhancing necessary prior knowledge can lay a solid foundation for facilitating connecting new information. Solidly relevant existing knowledge can help facilitate new learning (Ausubel, 1968; Dochy and Alexander, 1995; Bandura, 1997).
It is not surprising that the immediate post-test results revealed similar improvements in conceptual knowledge for both groups. The potential explanation is that this type of knowledge can be gained through low-level thinking, such as recalling facts. Both groups were able to demonstrate at least surface learning, even though students in the control group were not expected to link old knowledge to new knowledge as effectively as students in the experimental group. Surface learning may take place if students cannot connect the new knowledge to their prior knowledge base (Dochy et al., 1999; Donald, 2002). However, when students in the experimental group were tested later, their knowledge retention was significantly higher than that of control group. This finding could indicate that students made successful connections between existing knowledge and new information. When new knowledge is connected to past experiences, it becomes more memorable (Morris et al., 1981; National Research Council, 2000; Kole and Healy, 2007; Zambrano et al., 2019).
Furthermore, the experimental group students’ procedural knowledge was significantly improved in the immediate and delayed post-tests compared to the control group. Prior procedural knowledge contributes to student achievement more than prior conceptual knowledge (Hailikari et al., 2007). This type of knowledge requires students to know how and when to apply different procedures (Anderson and Krathwohl, 2001). Using procedural knowledge might also require students to have the relevant conceptual knowledge of the deep principles and features that would permit them to adapt to different situations. Research has shown that the lack of conceptual understanding of mathematics is critically impeding students’ ability to transfer and generalize mathematics (Richland et al., 2012). Students in the experimental group learned conceptual knowledge more deeply than others, as discussed above, which likely supported students’ abilities in procedural knowledge. Several studies have revealed that prior conceptual knowledge about the target content is among the most important factors of subsequent learning processes, including the gaining of new procedural knowledge (Hecht et al., 2003; Schneider et al., 2009). In addition, procedural knowledge can often be interrelated or rooted within other procedures (Baroody et al., 2007). Therefore, learning new procedures that have relationships with other procedures that students possess would contribute to learning connections.
5. Conclusion
A quasi-experimental design study investigated the effectiveness of enhancing necessary topic-specific prior knowledge at the beginning of topics on students’ conceptual knowledge and procedural knowledge. The results showed the importance of this strategy in improving students’ outcomes. Future research is needed to test similar approaches for older students (e.g., secondary school students).
6. Limitations
The limitations of this study are that the results can be generalized only to similar contexts. This study is limited to male students due to the gender segregation system that is operational in Saudi Arabia. The quasi-experimental approach can be a limitation due to its lack of random assignment. Further study should include larger sample sizes of school students from different education levels. It is important to note that the same test was used repeatedly during the three time points of data collection, which might potentially have a practice effect on students’ performance on this test. Further studies should consider controlling such factor for more accurateresults.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics statement
The studies involving human participants were reviewed and approved. Written informed consent to participate in this study was provided by the participants’ legal guardian/next of kin.
Author contributions
The author confirms being the sole contributor of this work.
Funding
This work was supported by the University of Ha’il [Project Number (BA-1515)].
Conflict of interest
The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2023.1050468/full#supplementary-material
References
Ackerman, P. L., and Cianciolo, A. T. (2000). Cognitive, perceptual speed, and psychomotor determinants of individual differences during skill acquisition. J. Exp. Psychol. Appl. 6, 259–290. doi: 10.1037/1076-898X.6.4.259
Alexander, P. A., Schallert, D. L., and Hare, V. C. (1991). Coming to terms: how researchers in learning and literacy talk about knowledge. Rev. Educ. Res. 61, 315–343. doi: 10.3102/00346543061003315
Alreshidi, N. A. K. (2021). The effect of enhancing prior knowledge on the learning behaviors of students and the teaching practices of mathematics teachers. J. Human Sci. 9, 271–284.
Alvermann, D. E., Smith, L. C., and Readence, J. E. (1985). Prior knowledge activation and the comprehension of compatible and incompatible text. Read. Res. Q. 20, 420–436. doi: 10.2307/747852
Anderson, L. W., and Krathwohl, D. R. (Eds.) (2001). A Taxonomy for Learning, Teaching and Assessing: A Revision of Bloom's Taxonomy of Educational Objectives: Complete Edition. New York, NY:Longman.
Arbiyah, N., Ardiningtyas, D., Widodo, M., Safitri, A., and Nurcahyati, N. (2020). The danger of hoax: the effect of inaccurate information on semantic memory. Makara Hum. Behav. Stud. Asia 24, 80–86. doi: 10.7454/hubs.asia.1020719
Aubrey, C., Godfrey, R., and Dahl, S. (2006). Early mathematics development and later achievement: further evidence. Math. Educ. Res. J. 18, 27–46. doi: 10.1007/BF03217428
Ausubel, D. P. (1968). The Psychology of Meaningful Learning; An Introduction to School Learning. New York, NY: Grune and Stratton.
Baroody, A. J., Feil, Y., and Johnson, A. R. (2007). An alternative reconceptualization of procedural and conceptual knowledge. J. Res. Math. Educ. 38, 115–131. doi: 10.2307/30034952
Bernacki, M. L., Byrnes, J. P., and Cromley, J. G. (2012). The effects of achievement goals and self-regulated learning behaviors on reading comprehension in technology-enhanced learning environments. Contemp. Educ. Psychol. 37, 148–161. doi: 10.1016/j.cedpsych.2011.12.001
Berry, D. C., and Broadbent, D. E. (1988). Interactive tasks and the implicit -explicit distinction. Br. J. Psychol. 79, 251–272. doi: 10.1111/j.2044-8295.1988.tb02286.x
Braasch, J. L., and Goldman, S. R. (2010). The role of prior knowledge in learning from analogies in science texts. Discourse Process. 47, 447–479. doi: 10.1080/01638530903420960
Byrnes, J. P., Miller-Cotto, D., and Wang, A. H. (2018). Children as mediators of their own cognitive development: the case of learning science in kindergarten and first grade. J. Cogn. Dev. 19, 248–277. doi: 10.1080/15248372.2018.1470975
Byrnes, J. P., and Wasik, B. A. (2009). Language and Literacy Development: What Educators Need to Know (Solving Problems in the Teaching of Literacy) New York, NY: Guilford Press.
Canobi, K. H. (2009). Concept-procedure interactions in children's addition and subtraction. J. Exp. Child Psychol. 102, 131–149. doi: 10.1016/j.jecp.2008.07.008
Clement, J. J. (1982). Students’ preconceptions in introductory mechanics. Am. J. Phys. 50, 66–71. doi: 10.1119/1.12989
Curran, P. J., West, S. G., and Finch, J. F. (1996). The robustness of test statistics to nonnormality and specification error in confirmatory factor analysis. Psychol. Methods 1, 16–29. doi: 10.1037/1082-989X.1.1.16
De Jong, T., and Ferguson-Hessler, M. G. (1996). Types and qualities of knowledge. Educ. Psychol. 31, 105–113. doi: 10.1207/s15326985ep3102_2
Dochy, F. J., and Alexander, P. A. (1995). Mapping prior knowledge: a framework for discussion among researchers. Eur. J. Psychol. Educ. 10, 225–242. doi: 10.1007/BF03172918
Dochy, F., Segers, M., and Buehl, M. M. (1999). The relation between assessment practices and outcomes of studies: the case of research on prior knowledge. Rev. Educ. Res. 69, 145–186. doi: 10.3102/00346543069002145
Donald, J. G. (2002). Learning to Think: Disciplinary Perspectives. The Jossey-bass Higher and Adult Education Series. Jossey-Bass, Inc.: San Francisco, CA 94103.
Ericsson, K. A., and Kintsch, W. (1995). Long-term working memory. Psychol. Rev. 102, 211–245. doi: 10.1037/0033-295X.102.2.211
Fazio, L. K., DeWolf, M., and Siegler, R. S. (2016). Strategy use and strategy choice in fraction magnitude comparison. J. Exp. Psychol. Learn. Mem. Cogn. 42, 1–16. doi: 10.1037/xlm0000153
Fosnot, C. T. (1996). Teachers construct constructivism: the center for constructivist teaching/teacher preparation project. Constructivism: theory, perspectives, and practice, 205-216. Fraction skills. J. Educ. Psychol. 102, 843–859. doi: 10.1037/a0019824
Frye, D., Braisby, N., Lowe, J., Maroudas, C., and Nicholls, J. (1989). Young children’s understanding of counting and cardinality. Child Dev. 60, 1158–1171. doi: 10.2307/1130790
Gelman, R., and Williams, E. M. (1998). “Enabling constraints for cognitive development and learning: domain specificity and epigenesis” in Handbook of Child Psychology: Vol. 2. Cognition, Perception, and Language. eds. D. Kuhn and R. S. Siegler. 5th ed (New York, NY: John Wiley & Sons, Inc), 575–630.
Hailikari, T., Nevgi, A., and Lindblom-Ylänne, S. (2007). Exploring alternative ways of assessing prior knowledge, its components and their relation to student achievement: a mathematics based case study. Stud. Educ. Eval. 33, 320–337. doi: 10.1016/j.stueduc.2007.07.007
Hattie, J., and Yates, G. C. (2013). Visible Learning and the Science of How We Learn. England: Routledge.
Hecht, S. A., Close, L., and Santisi, M. (2003). Sources of individual differences in fraction skills. J. Exp. Child Psychol. 86, 277–302. doi: 10.1016/j.jecp.2003.08.003
Hecht, S. A., and Vagi, K. J. (2010). Sources of group and individual differences in emerging fraction skills. J. Educ. Psychol. 102, 843–859. doi: 10.1037/a0019824
Jordan, J., Wagner, J., Manthey, D. E., Wolff, M., Santen, S., and Cico, S. J. (2020). Optimizing lectures from a cognitive load perspective. AEM Educ Train 4, 306–312. doi: 10.1002/aet2.10389
Karmiloff-Smith, A. (1992). Beyond Modularity: A Developmental Perspective on Cognitive Science. Cambridge, MA: MIT Press.
Kester, L., Paas, F., and Van Merriënboer, J. (2010). Instructional Control of Cognitive Load in the Design of Complex Learning Environments. eds. J. L. Plass, R. Moreno, and R. Brunken (Cambridge: Cambridge University Press), 109–130.
Kole, J. A., and Healy, A. F. (2007). Using prior knowledge to minimize interference when learning large amounts of information. Mem. Cogn. 35, 124–137. doi: 10.3758/BF03195949
Kosiol, T., Rach, S., and Ufer, S. (2019). (which) mathematics interest is important for a successful transition to a university study program? Int. J. Sci. Math. Educ. 17, 1359–1380. doi: 10.1007/s10763-018-9925-8
LeFevre, J.-A., Smith-Chant, B. L., Fast, L., Skwarchuk, S.-L., Sargla, E., Arnup, J. S., et al. (2006). What counts as knowing? The development of conceptual and procedural knowledge of counting from kindergarten through grade 2. J. Exp. Child Psychol. 93, 285–303. doi: 10.1016/j.jecp.2005.11.002
Lipson, M. Y. (1982). Learning new information from text: the role of prior knowledge and reading ability. J. Reading Behav. 14, 243–261. doi: 10.1080/10862968209547453
Loyens, S. M., and Gijbels, D. (2008). Understanding the effects of constructivist learning environments: introducing a multi-directional approach. Instr. Sci. 36, 351–357. doi: 10.1007/s11251-008-9059-4
Mayer, R. E. (1979). Twenty years of research on advance organizers: assimilation theory is still the best predictor of results. Instr. Sci. 8, 133–167. doi: 10.1007/BF00117008
Merrill, M. D. (2002). First principles of instruction. Educ. Technol. Res. Dev. 50, 43–59. doi: 10.1007/BF02505024
Mihalca, L., and Mengelkamp, C. (2020). Effects of induced levels of prior knowledge on monitoring accuracy and performance when learning from self-regulated problem solving. J. Educ. Psychol. 112, 795–810. doi: 10.1037/edu0000389
Miller, G. A. (1956). The magical number seven, plus or minus two: some limits on our capacity for processing information. Psychol. Rev. 63, 81–97. doi: 10.1037/h0043158
Miller, S. P., and Hudson, P. J. (2007). Using evidence-based practices to build mathematics competence related to conceptual, procedural, and declarative knowledge. Learn. Disabil. Res. Pract. 22, 47–57. doi: 10.1111/j.1540-5826.2007.00230.x
Morris, P. E., Gruneberg, M. M., Sykes, R. N., and Merrick, A. (1981). Football knowledge and the acquisition of new results. Br. J. Psychol. 72, 479–483. doi: 10.1111/j.2044-8295.1981.tb01777.x
Mullis, I. V. S., Martin, M. O., and Foy, P. (2008). TIMSS 2007 International Mathematics Report: Findings from IEA’s Trends in International Mathematics and Science Study for the Fourth and Eighth Grades. Chestnut Hill, MA: TIMSS and PIRLS International Study Center, Boston College.
Mullis, I. V., Martin, M. O., Gonzalez, E. J., and Chrostowski, S. J. (2004). TIMSS 2003 International Mathematics Report: Findings from IEA’s Trends in International Mathematics and Science Study at the Fourth and Eighth Grades. International Association for the Evaluation of Educational Achievement. Herengracht 487, Amsterdam, 1017 BT, The Netherlands.
Mullis, I. V., Martin, M. O., Foy, P., and Arora, A. (2011). International Results in Mathematics. Chenut Hill, MA: TIMMS & PIRLS Internasional study center, Boston College.
National Research Council. (2000). How People Learn: Brain, Mind, Experience, and School: Expanded Edition. Washington, DC: National Academies Press.
Ningsih, E. F., and Retnowati, E. (2020). “Prior knowledge in mathematics learning” in SEMANTIK Conference of Mathematics Education (SEMANTIK 2019) eds. S. A. Widodo, S. Maharani, E. F. Ningsih, Leonard and H. Nurdiyanto (Wiley: Atlantis Press. NY), 61–66.
O'Donnell, A. M., and Dansereau, D. F. (2000). Interactive effects of prior knowledge and material format on cooperative teaching. J. Exp. Educ. 68, 101–118. doi: 10.1080/00220970009598497
Paas, F., Renkl, A., and Sweller, J. (2003). Cognitive load theory and instructional design: recent developments. Educ. Psychol. 38, 1–4. doi: 10.1207/S15326985EP3801_1
Rach, S., and Ufer, S. (2020). Which prior mathematical knowledge is necessary for study success in the university study entrance phase? Results on a new model of knowledge levels based on a reanalysis of data from existing studies. Int. J. Res. Undergraduate Math. Educ. 6, 375–403. doi: 10.1007/s40753-020-00112-x
Reber, P. J., and Kotovsky, K. (1997). Implicit learning in problem solving: the role of working memory capacity. J. Exp. Psychol. 126, 178–203. doi: 10.1037/0096-3445.126.2.178
Riazy, S., Simbeck, K., Woestenfeld, R., and Traeger, M. (2020). “Prior knowledge as a predictor for persistence” in Proceedings of the 12th International Conference on Computer Supported Education. SCITEPRESS – Science and Technology Publications, 137–144.
Richland, L. E., Stigler, J. W., and Holyoak, K. J. (2012). Teaching the conceptual structure of mathematics. Educ. Psychol. 47, 189–203. doi: 10.1080/00461520.2012.667065
Rittle-Johnson, B., Fyfe, E., and Loehr, A. (2016). The content of instruction within a mathematics lesson: implications for conceptual and procedural knowledge development. Br. J. Educ. Psychol. 86, 576–591. doi: 10.1111/bjep.12124
Rittle-Johnson, B., and Schneider, M. (2015). “Developing conceptual and procedural knowledge of mathematics” in Oxford Handbook of Numerical Cognition. eds. R. C. Kadosh and A. Dowker (Oxford: Oxford University Press), 1118–1134.
Rittle-Johnson, B., Siegler, R. S., and Alibali, M. W. (2001). Developing conceptual understanding and procedural skill in mathematics: an iterative process. J. Educ. Psychol. 93, 346–362. doi: 10.1037//0022-0663.93.2.346
Rothman, S., and McMillan, J. (2003). Influences on Achievement in Literacy and Numeracy. LSAY Research Reports, 40. England: Routledge.
Schneider, M., Grabner, R. H., and Paetsch, J. (2009). Mental number line, number line estimation, and mathematical achievement: their interrelations in grades 5 and 6. J. Educ. Psychol. 101, 359–372. doi: 10.1037/a0013840
Smith, J. P., di Sessa, A. A., and Roschelle, J. (1994). Misconceptions reconceived: a constructivist analysis of knowledge in transition. J. Learn. Sci. 3, 115–163.
Song, H. S., Kalet, A. L., and Plass, J. L. (2016). Interplay of prior knowledge, self-regulation and motivation in complex multimedia learning environments. J. Comput. Assist. Learn. 32, 31–50. doi: 10.1111/jcal.12117
Sun, R., Merrill, E., and Peterson, T. (2001). From implicit skills to explicit knowledge: a bottom-up model of skill learning. Cogn. Sci. 25, 203–244. doi: 10.1207/s15516709cog2502_2
Sweller, J. (2003). Evolution of human cognitive architecture. Psychol. Learn. Motiv. 43, 216–266. doi: 10.1016/S0079-7421(03)01015-6
Thompson, R. A., and Zamboanga, B. L. (2003). Prior knowledge and its relevance to student achievement in introduction to psychology. Teach. Psychol. 30, 96–101. doi: 10.1207/S15328023TOP3002_02
Usman, O., and Miranda, V. (2020). The influence of learning motivation, cognitive strategy, prior knowledge on learning satisfaction. Available at SSRN: https://ssrn.com/abstract=3641269
Wilson, B. G. (1996). Constructivist Learning Environments: Case Studies in Instructional Design. Englewood Cliffs, NJ: Educational Technology.
Winters, F. I., Greene, J. A., and Costich, C. M. (2008). Self-regulation of learning within computer-based learning environments: a critical analysis. Educ. Psychol. Rev. 20, 429–444. doi: 10.1007/s10648-008-9080-9
Yew, E. H., and Schmidt, H. G. (2009). Evidence for constructive, self-regulatory, and collaborative processes in problem-based learning. Adv. Health Sci. Educ. 14, 251–273. doi: 10.1007/s10459-008-9105-7
Yüksel, I. (2014). Impact of activity-based mathematics instruction on students with different prior knowledge and reading abilities. Int. J. Sci. Math. Educ. 12, 1445–1468. doi: 10.1007/s10763-013-9474-0
Keywords: mathematics learning, prior knowledge, problem solving, conceptual knowledge, procedural knowledge
Citation: Alreshidi NAK (2023) Enhancing topic-specific prior knowledge of students impacts their outcomes in mathematics. Front. Educ. 8:1050468. doi: 10.3389/feduc.2023.1050468
Edited by:
Sheheryar Banuri, University of East Anglia, United KingdomReviewed by:
Katarzyna Anna Bobrowicz, University of Luxembourg, LuxembourgYing Wang, Georgia Institute of Technology, United States
Copyright © 2023 Alreshidi. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Nawaf Awadh Khallaf Alreshidi, ✉ bmF3d2FmMjAxMkBob3RtYWlsLmNvbQ==
 Nawaf Awadh Khallaf Alreshidi
Nawaf Awadh Khallaf Alreshidi