An application of Bayesian inference to examine student retention and attrition in the STEM classroom

1. Introduction

Over the last three decades, the development and emergence of artificial intelligence (AI) technology has revolutionized the classroom environment (McArthur et al., 2005; Roll and Wylie, 2016; Chen L. et al., 2020). Baker et al. (2019) define AI as “computers which perform cognitive tasks, usually associated with human minds, particularly learning, and problem-solving.” Adaptive pedagogical frameworks, early warning systems, and learning management systems (LMS) have been developed incorporating AI-driven capabilities to provide students, teachers, and educational administrators with a plethora of tools and data that can be leveraged to assess, track, and monitor student performance patterns (Wen and Lin, 2008; Vandenewaetere et al., 2011; Fernández-Caramés and Fraga-Lamas, 2019; Kabudi et al., 2021). In recent years, summative and formative assessments that provide instantaneous feedback to students using automated and explainable AI grading and response systems have personalized the classroom environment, giving instructors the ability to tailor curricula to the individual aptitude levels of students using these interfaces (Jokhan et al., 2019; Bañeres et al., 2020; Afzaal et al., 2021; Xu et al., 2021; Nawaz et al., 2022). Bolstered by the emergence of newer technological innovations such as virtual reality, augmented reality, and gamification in the classroom, digital tools continue to supplement traditional pedagogical strategies and have spurred the development of diverse and novel data sources (Huang et al., 2019; Sailer and Homner, 2020; Yang et al., 2021; Alam, 2022). Despite these advances, a major challenge that has emerged with the growth of classroom technology is how to meaningfully derive cognitive insights and inferences pertaining to student learning and performance from the plethora of data and knowledge created and contained within these systems (Van Camp et al., 2017; Chen X. et al., 2020; Musso et al., 2020; Yang et al., 2021; Kubsch et al., 2022).

Underpinning the analyses of these technological tools are a series of mathematical frameworks and statistical methodologies that have been applied to quantitatively assess the impact of various complex constructs, assessments, and remediation/intervention strategies on student cognition and learning. Machine learning (ML) serves as a critical tool in this endeavor due to its ability to leverage knowledge from large quantities of structured, unstructured, and semi-structured corpora to generate performance implications with a high degree of accuracy (Zhai et al., 2020a,b; Zhai, 2021; Zhai et al., 2021). The study and use of ML in education has spurred the growth of various subfields, including educational data mining (EDM) and predictive learning analytics (LA), to study, develop, and apply these techniques to different pedagogical settings (Baker, 2010; Romero and Ventura, 2020). To advance the fields of EDM and LA, researchers seek to refine existing statistical methodologies and ML techniques for analyzing large and diverse educational corpora (Brooks and Thompson, 2017; Bertolini, 2021).

Student retention and attrition in introductory science, technology, engineering, and mathematics (STEM) classes is one critical issue that continues to remain a paramount concern for academic stakeholders (Chen, 2013; Penprase, 2020). Identifying the factors associated with student performance and implementing pedagogical strategies to foster student success in STEM settings is an international priority in education research. (Chang et al., 2014; Lee et al., 2015; Ikuma et al., 2019; Kricorian et al., 2020; López Zambrano et al., 2021). Many studies have applied existing ML frameworks, or proposed their own novel methodologies, to make predictions of student success. Depending on the pedagogical environment, course context, and grade level (e.g., hybrid, remote, asynchronous, and in-person classroom settings), different types of academic and non-academic factors have been shown to impact student performance (Nouri et al., 2019; Xu et al., 2021; Bertolini et al., 2021a; Albreiki, 2022).

With ML becoming more mainstream and commonplace within the body of educational research, a major criticism of its usage is that model development and its subsequent output are often complex, esoteric, and at times uninterpretable (Conati et al., 2018; Liu and Tan, 2020). While the usage of these “black box” methodologies have led to the development of more accurate data-driven models for forecasting student performance (see Musso et al., 2013; Cascallar et al., 2014; Tsiakmaki et al., 2020 for examples), statistical and mathematical intricacies governing these tools and their outputs often hinder communication of these results to faculty and other educational stakeholders (Rudin, 2019). While various statistical frameworks have been developed and produced to make these “black box” algorithms more interpretable, it is difficult to precisely quantify the informative candidate features that were used in a ML algorithm to arrive at a certain outcome, making it difficult to communicate and formulate educational actions and interventions among stakeholders (Arrieta et al., 2020; Bertolini et al., 2021a).

In education, uncertainty in estimates for ML model parameters and mechanisms to assess the differential efficacy of competing prediction algorithms have predominately used frequentist statistical techniques, most notably null hypothesis significance testing. Bayesian inference and modeling, which account for the relationship between data and prespecified information about the distribution of model parameters, are methods of statistical inference that emerged due to the widespread availability of technological software, minimizing the need for researchers to rely on the usage of large-scale computing architectures (Brooks, 1998; Lunn et al., 2000; Plummer, 2003; Lambert et al., 2005; Kruschke, 2011a; Gelman et al., 2015; Van den Bergh et al., 2021). Bayesian approaches to modeling are commonly employed in many scientific disciplines including medicine (Spiegelhalter et al., 1999), ecology (McCarthy, 2007), and cosmology (Hobson et al., 2010), but have been sparsely incorporated into EDM and LA research to systematically compare performance variability in models of student classroom success based on the characteristics of input predictors. Homer (2016) remarks that the use of Bayesian methods and their application to forecast student performance and STEM attrition has the potential to revolutionize EDM and LA in the next decade.

In this study, a Bayesian framework is applied to model student success in an introductory baccalaureate biology course. We are interested in establishing the effectiveness of traditional data types (i.e., demographics, standardized aptitude tests, prior academic performance) and data from nascent AI-driven technological software and formative assessments (e.g., LMS, diagnostic concept inventory (CI) assessments) to identify factors that impact student performance. After introducing our research questions (Section 2), we provide a brief overview of the strengths of Bayesian analytics compared to traditional frequentist and ML frameworks (Section 3.1). This is followed by a brief literature review on their usage in STEM education research, and how Bayesian modeling aligns with four components of ML assessment proposed in the literature (Section 3.2). We then outline the methodologies used in this study (Section 4), our results (Section 5), and conclude with a discussion (Section 6) and future research directions (Section 7).

2. Research questions

Our study addressed the following research questions:

(RQ 1) How do various student- and course-specific data types impact the odds of student retention in a STEM classroom context?

(RQ 2) Given the ability to integrate prior knowledge into Bayesian models via prespecified probability distributions, does incorporating aggregated historical records of student performance data enhance model fit, compared to when uninformative priors are used?

3. Literature review

3.1. Overview of Bayesian methods

Bayesian inference uses probability to quantify uncertainty in the estimates of model parameters. Unlike frequentist statistical techniques, parameters are treated as random variables which take on an associated probability distribution, instead of fixed quantities (Ellison, 1996; Hobbs and Hooten, 2015; Muth et al., 2018; Hooten and Hefley, 2019). Table 1 depicts the major differences between Bayesian and frequentist methods commonly cited and summarized in the literature (Berger and Berry, 1988; Ellison, 1996; Stephens et al., 2007). Unlike frequentist methods, Bayesian methods are capable of “yield[ing] answers which are much easier to understand than standard statistical answers, and hence much less likely to be misinterpreted” (Berger and Berry, 1988).

TABLE 1

Table 1. Comparison of frequentist and Bayesian methods.

The strength of Bayesian techniques lies in the prespecification of probability distributions for analytical parameters. These prior distributions are explicit mathematical statements that either incorporate previous information from published studies (known as informative priors), or a plausible range of values that specific model parameters can take on (known as noninformative priors; McCarthy and Masters, 2005; Lemoine, 2019; Banner et al., 2020). As output, Bayesian techniques produce posterior outputs providing researchers with a quantitative distribution and range of final parameter estimates that explicitly account for uncertainty and variability in predictive efficacy (Neal, 2004). Bayesian inference is not a strictly separate type of ML model but is a probabilistic method of inference that can be incorporated into these existing algorithmic frameworks. ML algorithms generally use the raw data to generate inferences, while Bayesian methods use the raw data along with explicitly assigned probability distributions (i.e., priors) to estimate model parameters. In testing for statistical significance, one advantage of Bayesian methodologies is that the posterior distribution can be used to tabulate the probability that different hypotheses are true (e.g., both the null and alternative hypotheses), which is more intuitive compared to frequentist methods. Traditional null hypothesis significance testing only calculates a p-value, a long-run probability of obtaining a data set at least as extreme as the one observed (Fornacon-Wood et al., 2022).

When a plethora of candidate features are included in a model, Bayesian methods can minimize the impact of highly correlated variables by using regularization priors to shrink posterior estimates toward their parameter values to induce sparsity and perform variable selection (Komaki, 2006). Unlike frequentist methods, Bayesian shrinkage methods define a criterion for selecting values on the credible or high density intervals of posterior distributions rather than constraining the magnitude of coefficient estimates (Li and Pati, 2017). These regularization priors are generally mixture models that combine multiple statistical distributions together resulting in a high concentration point mass and a diffusive prior with a heavy tail (Van de Schoot et al., 2021). While Bayesian regularization priors do not produce unstable variance estimates for model parameters, a common criticism of frequentist methods, Bayesian regularization priors are more mathematically sophisticated compared to traditional uninformative and informative univariate prior distributions (Casella et al., 2010; Van Erp et al., 2019).

Bayesian methods can also be used to study different cohorts of a population nested within and between different factors. Such frameworks can yield more conservative parameter estimates, do not rely on asymptotics like frequentist methods, and are capable of handling heterogeneous and imbalanced corpora, the latter of which is commonly encountered in education (Fordyce et al., 2011; Gelman et al., 2012; van de Schoot et al., 2014). To summarize, Bayesian frameworks are a plausible alternative to frequentist techniques with some documented theoretical and pragmatic benefits (see Kruschke, 2011a,b; van de Schoot et al., 2014). In the next section, we highlight prior studies that have incorporated Bayesian methods to examine diverse student data types and how these techniques align with four ML assessment educational criteria.

3.2. Application to STEM educational settings and ML assessment

In previous STEM classroom studies examining student performance, emphasis has been placed on using conventional sources of university data for this endeavor, which traditionally encompass past student academic performance and achievement predictors such as high school grade point average and student demographics (Orr and Foster, 2013; Berens et al., 2019). There is increasing interest in examining how combining these traditional formative data types with course-specific data-driven tools and assessment data (e.g., LMS usage patterns, diagnostic tests) extracted from intelligent systems may differentially inform models suitable for course-level instructor actions in the STEM classroom. These novel assessment types, in conjunction with academic characteristics and personalized data records, have been shown to improve the overall performance of ML algorithms (Lee et al., 2015; Zabriskie et al., 2019; Yang et al., 2020; Zhai et al., 2020a,b; Bertolini et al., 2021a,b, 2022). However, frequentist and non-Bayesian methods have been the primary techniques utilized in these analyses to assess competing performance variability between different algorithms and to identify the significant features that drive overall ML model performance.

In many prior EDM and LA studies, researchers have employed a type of ML algorithm, known as Naïve Bayes, to forecast student performance in various STEM settings (see Shahiri and Husain, 2015; Ahmed et al., 2021; Perez and Perez, 2021 for examples). In recent systematic literature reviews, Shafiq et al. (2022), Peña-Ayala (2014), and Baashar et al. (2021), found that Naïve Bayes was used in 35%, 20%, and 14% of education studies surveyed, respectively. While this supervised ML algorithm has the word “bayes” in its name, it has not been traditionally classified as a Bayesian methodology because it assumes that all features included in the model are independent of one another (Hand and Yu, 2001; Russell, 2010). While having a firm theoretical basis, independence between student-specific factors do not typically hold in practice, as there are correlations and associations between them which impact performance outcomes. For example, if an educator or institutional researcher wanted to develop a model to predict student performance in a class using socioeconomic data factors and SAT scores, Naïve Bayes would treat these features as being independent of one another when rendering the final predictions. However, there are documented studies that have identified an association between socioeconomic status and student performance on the SAT (Zwick and Himelfarb, 2011; Higdem et al., 2016). In a survey of 100 EDM and LA studies over the last 5 years, Shafiq et al. (2022) found that only 5% of studies used a formal type of Bayesian methodology (i.e., did not assume independence between features).

The three most common applications of Bayesian inference in education have been their usage in unsupervised text mining, natural language processing, and in Bayesian knowledge tracing. Unsupervised methods (such as Latent Dirichlet Allocation) and natural language processing provide educators with the capability of synthesizing words, phrases, categories, and topics from student text corpora to extract data and inferences pertaining to student cognition, learning and concept retention, factors that impact student performance (Almond et al., 2015; Culbertson, 2016; Xiao et al., 2022). Moreover, many AI-driven educational tools have been developed using these techniques to automatically score open-ended and constructed response assessments using these methodologies, achieving a high degree of accuracy that was comparable with manual human scoring (Moharreri et al., 2014; Liu et al., 2016). However, these techniques have limited applications and use if text corpora are not being incorporated into ML models. In Bayesian knowledge tracing, hidden Markov models use probability to determine the likelihood of an outcome based on a sequence of prior events (Van de Sande, 2013). These techniques are used to scrutinize student learning dynamics to study concept retention and mastery by tracking the student learning process over time. Observed data from educational assessments and interventions (e.g., tutoring sessions, personalized learning technology) acquired at distinct longitudinal time points during the students’ academic tenure are used as input to these models (Corbett and Anderson, 1994; Mao et al., 2018; Cui et al., 2019).

Despite their limited use in AI education-based research, Bayesian inference techniques align with the four components of ML assessment proposed and outlined by Zhai (2021). The first criterion “allows assessment practices to target complex, diverse, and structural constructs, and thus better approach science learning goals.” This has been the primary focus and application of Bayesian methods in education thus far. Indeed, most studies employing Bayesian methods have used them to perform psychometric and factor analyses of novel assessment types (e.g., multi-skill itemized activities and question types) and surveys to study student comprehension, cognition, and attitudes toward learning (Desmarais and Gagnon, 2006; Pardos et al., 2008; Brassil and Couch, 2019; Martinez, 2021; Parkin and Wang, 2021; Vaziri et al., 2021; Wang et al., 2021). The insights obtained from these studies have led to the design, development, and deployment of more adaptive learning and student-focused knowledge assessment content, based on their aptitude levels, allowing educators to learn more about student comprehension and how individualized content can be tailored to students (Drigas et al., 2009).

The second and third criteria “extends the approaches used to elicit performance and evidence collection” and “provide a means to better interpret observations and use evidence” are the crux of Bayesian modeling, as described in Section 3.1. Within this statistical framework, the data models are defined explicitly using intuitive notions and knowledge about the relationships between different features and their distributions (Dienes, 2011; Kruschke, 2011b) via expert elicitation, knowledge, and experimental findings to inform priors for Bayesian statistical models (Choy et al., 2009).

The fourth criterion “supports immediate and complex decision-making and action-taking.” The Bayesian paradigm allows users to update knowledge via prior distributions without testing multiple hypotheses repeatedly, allowing researchers to reflect on the similarities and differences between model outputs, thereby placing decision making on the subjectivity of the recipients and consumers of the model results (Berger and Berry, 1988; Stephens et al., 2007). ML algorithms primarily rely on using aggregated training data where hyperparameters are tuned to enhance model efficacy and performance. In contrast, Bayesian inference methodologies incorporate probabilistic prior knowledge, beliefs, and findings from past studies into these models. Standard statistical assumptions that encompass many frequentist techniques, such as regression, do not need to be satisfied in Bayesian frameworks, allowing models to be developed with greater complexity that utilize asymmetric probability distributions, a current limitation of some frequentist approaches such as maximum likelihood estimation which does not explicitly assign probabilities and only provides a point estimate for model parameters (van de Schoot et al., 2014, 2021). Moreover, Bayesian methods have been shown to be computationally faster compared to default numerical integration techniques traditionally employed in frequentist mixed effects models (McArdle et al., 2009; van de Schoot et al., 2014).

Despite their alignment with these four ML assessment criteria, compared to the use of traditional statistical methodologies, Bayesian ML methods are an underrepresented and underutilized statistical methodology employed in education research (Subbiah et al., 2011; König and van de Schoot, 2018). A limited amount of work in the literature has used Bayesian techniques to understand the factors impacting student performance such as the grade point average (GPA) of college students (Hien and Haddawy, 2007), graduation rates (Crisp et al., 2018; Gebretekle and Goshu, 2019), and final examination performance (Ayers and Junker, 2006). Even less work has focused on quantitatively assessing the impact of different data types on student performance outcomes. In this study, we explore the use of a Bayesian framework to comparatively examine the differential impact that the amalgamation of traditional and AI-driven predictors has on overall model fit and performance.

4. Materials and methods

4.1. Course context

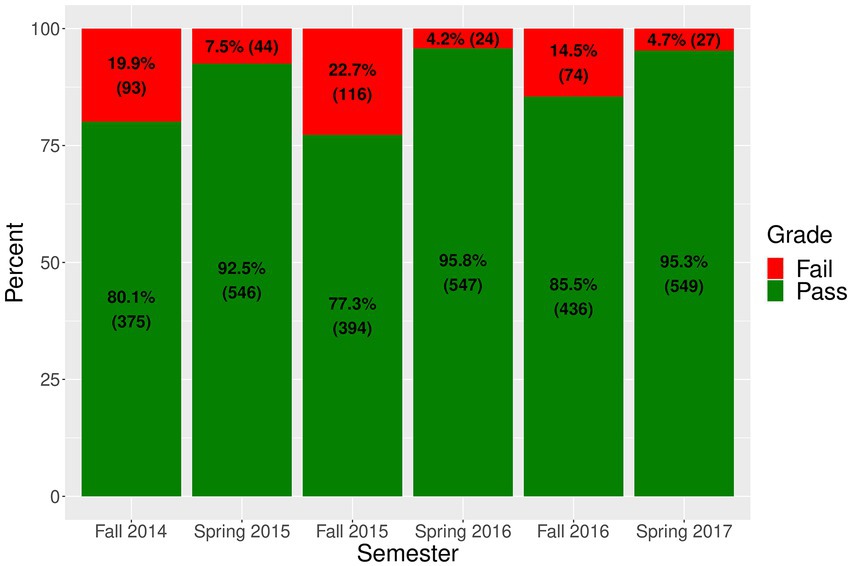
Our study focused on examining student performance in a baccalaureate, lecture-based, in-person biology course at a public higher educational research institution in the United States. A core topic in this course is evolution. In total, 3,225 students enrolled in the class over six academic semesters (fall 2014, spring 2015, fall 2015, spring 2016, fall 2016, and spring 2017) were examined in this observational study (Figure 1).

FIGURE 1

Figure 1. Course grade information by semester examined.

This analysis focused on the pass/fail status for each student, the dependent variable $Y_{i,j}$, which was modeled as Bernoulli-distributed (Equation 1):

$\begin{array}{ll}{\mathit{Y}}_{\mathit{i}\mathbf{,}\mathit{j}}\mathbf{~}\mathit{\text{Bernoulli}}\mathbf{\left(}{\mathit{\theta }}_{\mathit{i}\mathbf{,}\mathit{j}}\mathbf{\right)}& (1)\end{array}$

$Y_{i,j}$ takes on a value of ‘1’ with probability ${\theta }_{i,j}$ and a value of ‘0’ with probability 1 − ${\theta }_{i,j}$, where ${\theta }_{i,j}$ is the probability that student i passed the course when enrolled in term j. The tilde relation in Equation 1 “~” means “is distributed as” (Allenby and Rossi, 2006). A passing grade ($Y_{i,j}$ = 1) included the marks A, A−, B+, B, B−, C+, C, and C−, while a failing course grade (Y_i, j = 0) included the marks D+, D, F, I (incomplete), I/F (incomplete course mark which turned into an F), NC (no credit), and W (withdrawal). The biology class selected for this analysis was chosen because it is a gateway STEM course categorized by a relatively large disparity between retention and attrition rates at our institution. Across all six semesters, the overall failing rate was 11.7% (n = 378). Fall semester passing rates ranged between 77.3% and 85.5%, which was lower than spring passing rates ranging between 92.5% and 95.8%.

4.2. Data sources

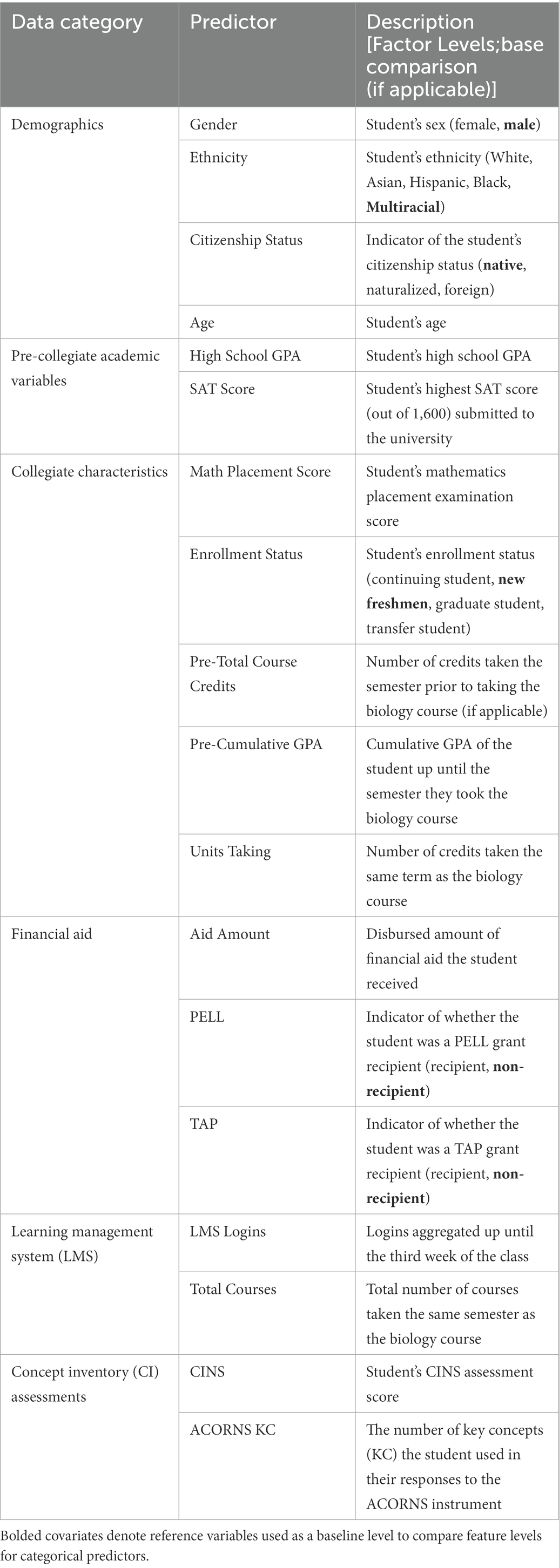
A diverse set of student academic and non-academic features were extracted from the institution’s data warehouse (Table 2). Traditional student-specific data features pertained to (1) demographics, (2) pre-collegiate characteristics, (3) collegiate characteristics, and (4) financial aid data. For technological systems and novel assessment types, student engagement with the LMS Blackboard, and performance on two concept inventory (CI) diagnostic assessments: the Assessing COntextual Reasoning about Natural Selection (ACORNS); Nehm et al. (2012) and the Conceptual Inventory of Natural Selection (CINS); Anderson et al. (2002) were incorporated into the Bayesian framework. CI assessments are widely used in the collegiate biology classroom to provide novel insights into student perceptions and attitudes toward biological concepts and theory and may employ automatic grading capabilities using ML and AI (Nehm, 2019). Detailed summary statistics for these variables can be found in Supplementary material. All predictors corresponded to variables acquired by the institution and instructor prior to the third week in the course, based on the findings of Lee et al. (2015), Xue (2018), and Bertolini (2021).

TABLE 2

Table 2. Description of predictor variables by data category.

During data preprocessing, categorical predictors were converted into indicator variables. Following the recommendation by Marshall et al. (2010), missing data were imputed using the predictive mean matching imputation technique in the ‘mice’ package for the R programming environment (Van Buuren and Groothuis-Oudshoorn, 2011). Prior to model fitting, covariates were standardized to have a zero mean and a standard deviation of one.

4.3. Bayesian statistical analysis

To answer RQ 1, we ran a multiple logistic regression model incorporating the effects of both traditional and course-specific predictors using a Bayesian framework:

$\begin{array}{ll}\mathit{\text{logit}}\left({\mathit{\theta }}_i\right)=={\mathit{\beta }}_0+{\mathit{\alpha }}_{\mathit{j}}+{\displaystyle \sum _{p=1}^{24}}{\mathit{\beta }}_{\mathit{p}}{\mathit{x}}_{\mathit{p}}& (2)\end{array}$

Since the coefficients in logistic regression models are either positive, negative or zero, broad uninformative normal distribution priors were used for these parameters in Equation 2. The normal distribution is a common statistical distribution that many institutional researchers and educators are familiar with and utilize (see Coughlin and Pagano, 1997; Van Zyl, 2015). These prior distributions can be written mathematically as $N\left(\mu ,\tau \right)$ where $N$ is a normal distribution centered at mean μ with precision $\tau =\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${\sigma }^2$}\right.$ (the inverse of the variance ${\sigma }^2$). In Equation 2, the covariate features were assigned uninformative priors with a mean of zero and small precision of 0.000001: ${\beta }_p~N\left(0,0.000001\right)$ where $p$ = 1,…,24. Table 3 maps the data features described in Table 2 with the parameters found in Equation 2. We also performed a prior predictive simulation to validate the suitability of these prior distribution choices by using synthetic data to confirm that the Bayesian logistic regression model could recover numerical values prescribed on the analytical parameters. Due to word count limitations, this analysis is detailed in Supplementary material.

TABLE 3

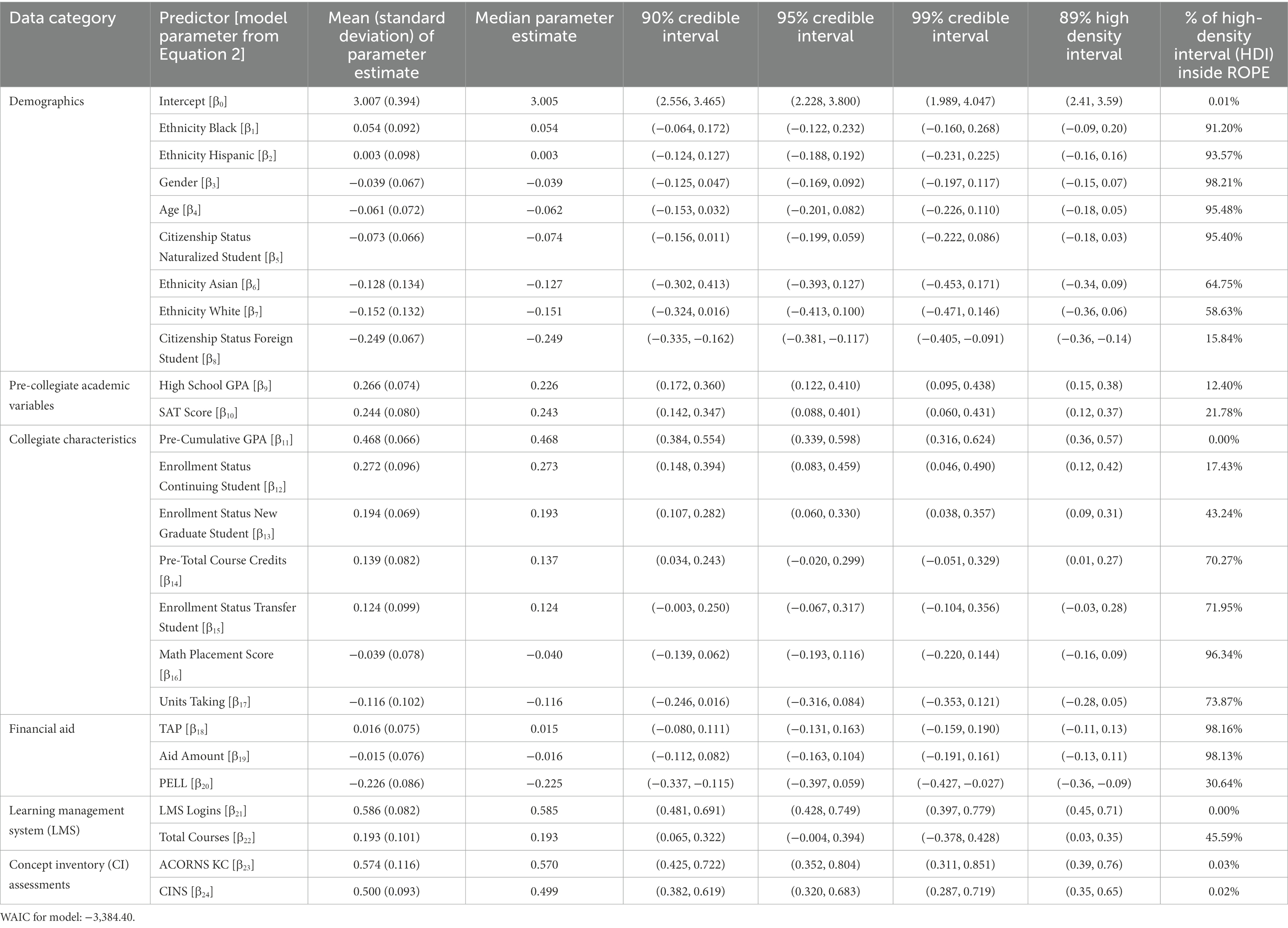
Table 3. Logistic regression parameter estimates, credible intervals, 89% high density interval, and ROPE overlap percentage estimates.

All students had the same estimated intercept ${\beta }_0~N\left(0,0.000001\right)$ and coefficient estimates (i.e., fixed effects). A semester-specific random effects term (${\alpha }_j$ where $j=1,\dots ,6$) was added to quantify variability in student performance across the different semesters. Since ${\alpha }_j$ is a random-effects term, a nested prior for this model parameter was used: ${\alpha }_j~N\left(0,{\tau }_{\alpha }\right)$. In this context, ${\alpha }_j$ is a normal distribution with a zero mean and precision denoted as ${\tau }_{\alpha }$, which follows another statistical distribution ${\tau }_{\alpha }~\mathit{\text{Gamma}}\left(0.001,0.001\right)$; a gamma distribution with a shape and scale parameter value of 0.001. The parameter ${\tau }_{\alpha }$ is called a hyperparameter and the distribution $\mathit{\text{Gamma}}\left(0.001,0.001\right)$ is known as a hyperprior distribution (Hobbs and Hooten, 2015). The gamma distribution is a continuous probability distribution that is traditionally used as a prior distribution for the variance when nested priors are used (Gelman, 2006). The nesting of priors resembles a hierarchical form of a Bayesian model, which considers data from multiple levels to compare similarities and differences between independent groups (McCarthy and Masters, 2005). In this research context, we are interested in discerning whether the term the student took the course (either fall or spring) impacted student performance (retention or attrition), due to differences in the composition of the student body between these semesters.

To identify the features that significantly impacted student retention and attrition in our STEM classroom context, the region of practical equivalence (ROPE) was calculated for each of the model parameters. ROPE corresponds to a statistical “null” hypothesis for the model parameter. The overlap percentage between each credible interval and ROPE region are used to ascertain statistical significance (Kruschke, 2011b). An overlap percentage closer to zero indicates that the feature is significant in the model, while a value closer to 100% indicates that the model parameter is not statistically significant. This differs from the frequentist way of identifying statistically significant features by determining whether their model parameter values differ significantly from zero. Based on the recommendations by Kruschke (2011b) and McElreath (2018), a specific type of credible interval based on probability density, known as the 89% high density interval, was used. Since a Bayesian logistic regression model was used in this study, per Kruschke and Liddell (2018), the ROPE range was prespecified between −0.18 and 0.18.

The Bayesian model was implemented in JAGS (Plummer, 2003) using the R2jags package (Plummer, 2013) found in the R programming environment. JAGS uses Markov chain Monte Carlo (MCMC) methods to obtain the posterior distribution for each regression parameter by sampling values from it, following an initial burn-in period, before the posterior distribution stabilizes (McCarthy and Masters, 2005).

Posterior distributions for the logistic regression coefficients were computed using two chains. The number of iterations run in the MCMC sampling was 50,000 with a burn-in number of 5,000. Thinning was not applied to the chains and all chains converged unambiguously. Convergence was assessed using the Gelman-Rubric statistic ($\widehat{R}<1.1$) for all regression parameters (Brooks and Gelman, 1998). This model was then used to ascertain the factors that were predictors of student performance in our collegiate biology course setting.

In RQ 2, an empirical Bayesian approach was taken to examine whether incorporating informative priors using knowledge from aggregated historical corpora (i.e., prior information of student performance from past semesters) enhanced model fit, compared to the use of traditional uninformative normal distribution priors. Data from two, three, four, and five past semesters of course data were used to assign values for the prior distributions of the regression coefficients. For this research question, the semester-specific random effect term was omitted. The Bayesian logistic regression model was run on a single subsequent semester of course data (Figure 2). Since passing and failing rates differed between fall and spring semesters, these terms were also examined separately (Figures 2E,F).

$\begin{array}{ll}\mathit{\text{logit}}\left({\mathit{\theta }}_{\mathit{i}}\right)={\mathit{\beta }}_0+{\displaystyle \sum _{\mathit{p}=1}^{24}}{\mathit{\beta }}_{\mathit{p}}{\mathit{x}}_{\mathit{p}}& (3)\end{array}$

FIGURE 2

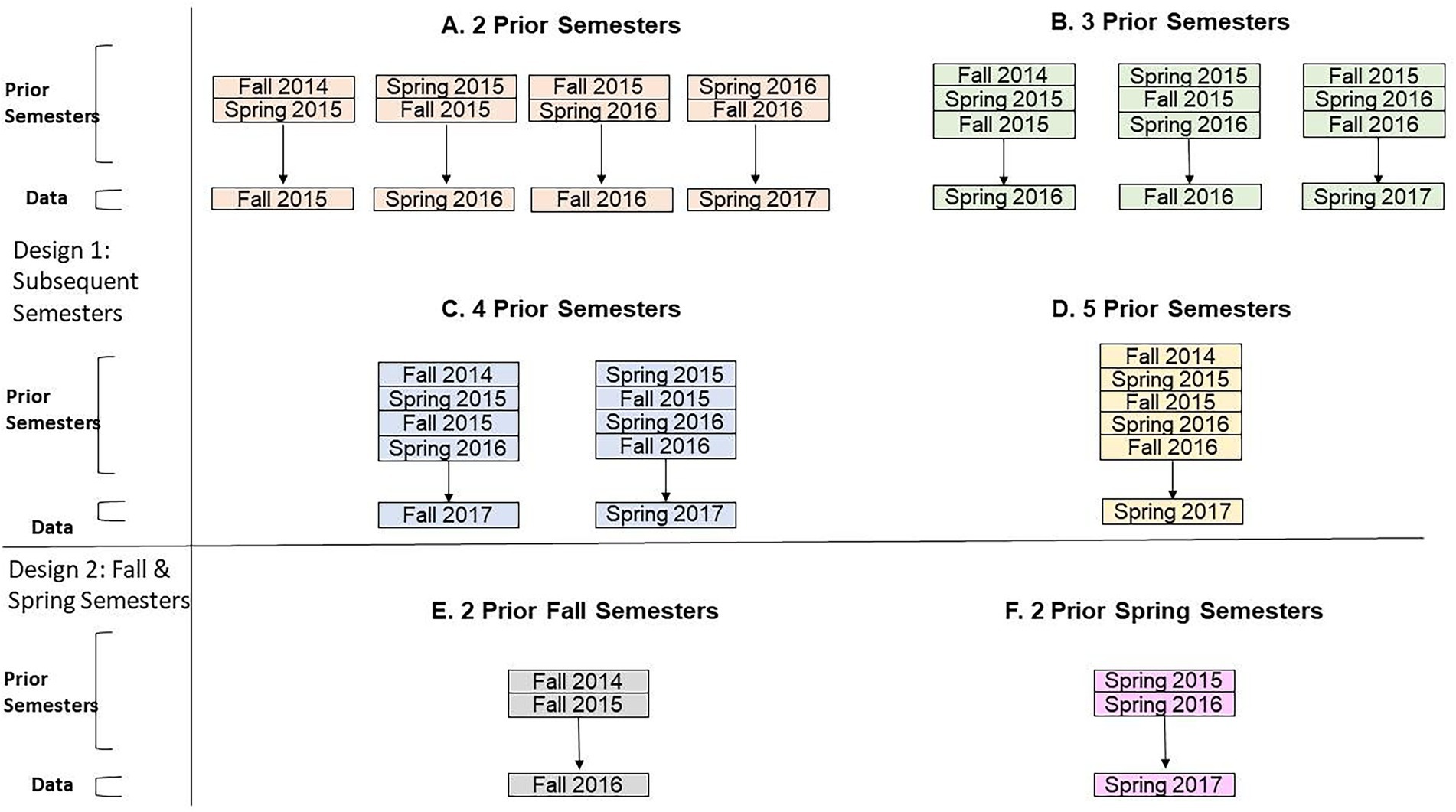
Figure 2. Empirical Bayesian methodology using aggregated semesters of prior data. The “Prior Semesters” are used to specify the mean and precision for the distribution of the model covariates. The “Data” terms are the single semesters of course data that the logistic regression models were run on.

In this modified setup for RQ 2, we used informative normal prior distributions estimated from aggregated past corpora records (Equation 3) where ${\beta }_p~N\left(b_p,{\tau }_p\right)$. $b_p$ and ${\tau }_p$ were estimates for the mean and precision of the covariate, which differed depending on whether the predictor was continuous or categorical. For continuous predictors, $b_p$ and ${\tau }_p$ corresponded to the mean and precision for the p^th covariate, tabulated from prior course records. For categorical predictors, $b_p$ was the proportion of entries from aggregated semesters, while ${\tau }_p$= 0.000001. For example, in Figure 2A, for the continuous covariate age using fall 2015 data, the value $b_p$ was the average age and ${\tau }_p$ was the precision of age for students who took the biology course in fall 2014 and spring 2015. For the categorical covariate pertaining to Asian ethnicity, $b_p$ was the proportion of Asian students enrolled in the biology course in fall 2014 and spring 2015, and ${\tau }_p$= 0.000001. All mean and precision values were calculated prior to data imputation. The values of $b_p$ and ${\tau }_p$ for all covariates can be found in Supplementary material. A broad uninformative prior was used for the intercept: ${\beta }_0~N\left(0,0.000001\right)$.

Unlike RQ 1, for RQ 2 we focused on comparing model fit, instead of studying differences in the model estimates for the Bayesian parameters between individual models. In this auxiliary analysis, posterior distributions were computed using two chains. The number of iterations run in the MCMC sampling was 200,000 with a burn-in number of 50,000. Thinning was not applied to these chains. Model performance using informative prior distributions was compared to when broad uninformative normal distributions priors replaced the informative prior distributions in Equation 3: ${\beta }_p~N\left(0,0.000001\right),p=0,\dots ,24$.

4.4. Widely applicable information criterion (WAIC) evaluation metric

For all models, performance was compared using the widely applicable information criterion (WAIC), also known as the Watanabe-Akaike information criterion. This is a generalized version of the Akaike information criterion (Akaike, 1973) which is a commonly employed evaluation metric in EDM and LA (Stamper et al., 2013). This metric is used to estimate out-of-sample performance for a model by computing a logarithmic pointwise posterior predictive density and correcting this estimate based on the number of parameters included in the model to prevent overfitting (Gelman et al., 2014). Smaller WAIC values are indicative of a better fitting model.

5. Results

5.1. (RQ 1): How do various student- and course-specific data types impact the odds of student retention in a STEM classroom context?

Standardized parameter estimates are shown in Table 3. Many traditional university-specific predictors were found to be associated with classroom success. A one standard deviation increase in the student’s cumulative collegiate GPA, high school GPA, and SAT score increased their odds of passing the course by 1.600 (60.0%), 1.305 (30.5%) and 1.277 (27.7%), respectively, controlling for all other factors. Compared to native students, international/foreign students were forecasted to perform worst (odds ratio = $e^{-0.249}$ = 0.780), along with students who received a PELL grant (odds ratio = $e^{-0.226}$ = 0.798). Relative to new freshmen, transfer students performed slightly, but not significantly better (odds ratio = $e^{0.124}$ = 1.132). Continuing students (i.e., students who are not taking the biology course during their first term at the institution) were most likely to pass the course (odds ratio = $e^{0.272}$ = 1.313).

The magnitude for the course-specific predictors was positive and the largest among all other variables incorporated into the model. LMS logins had the greatest association with student performance; a one standard deviation increase in the number of student logins increased the odds of passing the course by 1.800 (80.0%). While the effects of both CI assessments on student performance were comparable (ACORNS KC: ${\beta }_{23}$ = 0.574; CINS: ${\beta }_{24}$ = 0.500), higher scores on these assessments yielded a greater likelihood of passing (57% and 50% for the ACORNS and CINS assessments, respectively).

Weak semester-specific effects were also observed (${\sigma }_{\alpha }^2=\frac{1}{{\tau }_{\alpha }}=0.5$). The average modes of the Bayesian posterior densities for the deviations of individual semester effects were non-negative for spring semesters, compared to fall semesters (Figure 3).

FIGURE 3

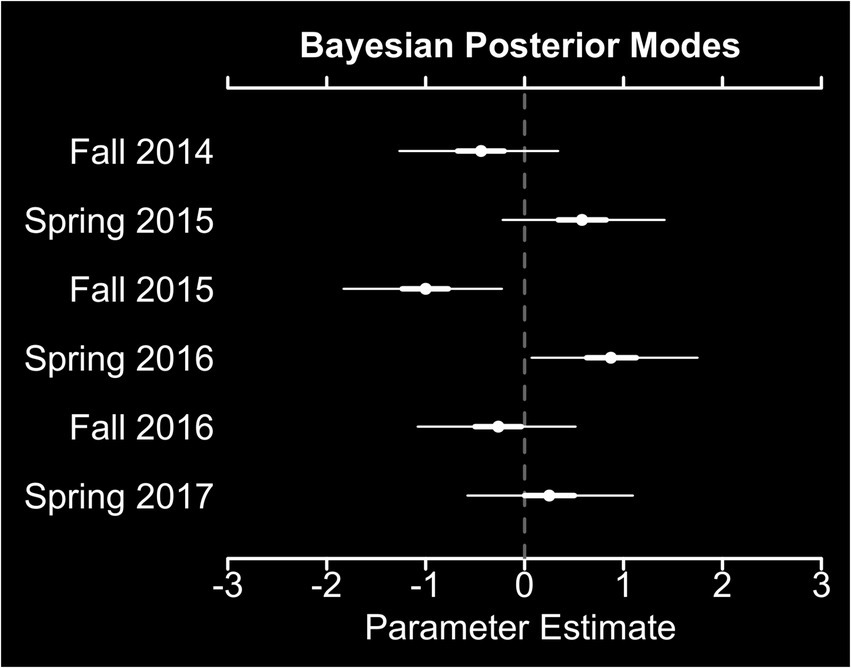
Figure 3. Bayesian posterior modes for semester-specific random effects. Thick white lines indicate 50% credible intervals, while thin white lines indicate 95% credible intervals.

5.2. (RQ 2): Given the ability to integrate prior knowledge into Bayesian models via prespecified probability distributions, does incorporating aggregated historical records of student performance data enhance model fit, compared to when uninformative priors are used?

Table 4 provides a comparative assessment of the differences between the WAIC values, ${\mathrm{\Delta }}_{WAIC}$, between the logistic regression models incorporating uninformative and informative normal distribution priors. Negative values for ${\mathrm{\Delta }}_{WAIC}$ indicate that the model performed better when uninformative priors were used. Positive values for ${\mathrm{\Delta }}_{WAIC}$ indicate that the model using informative priors performed better. Mixed results were observed pertaining to the superiority of the logistic regression model when informative prior values were used – for some semesters such as spring 2017, informative prior values enhanced model fit except when two semesters of historical data were used to prescribe the normal distribution priors (${\mathrm{\Delta }}_{WAIC}$ = −34.90). Except for the spring 2017 corpus, the magnitude of ${\mathrm{\Delta }}_{WAIC}$ increased as more historical data were considered. The best model performance was achieved when prior distribution parameters values were prescribed using data from two prior semesters of the same term (i.e., two fall and two spring semesters). For the fall 2016 and spring 2017 corpus, models incorporating uninformative prior values performed slightly better compared to the use of informative priors (${\mathrm{\Delta }}_{WAIC}$ = −1.30 for fall 2016 and ${\mathrm{\Delta }}_{WAIC}$ = −34.00 for spring 2017).

TABLE 4

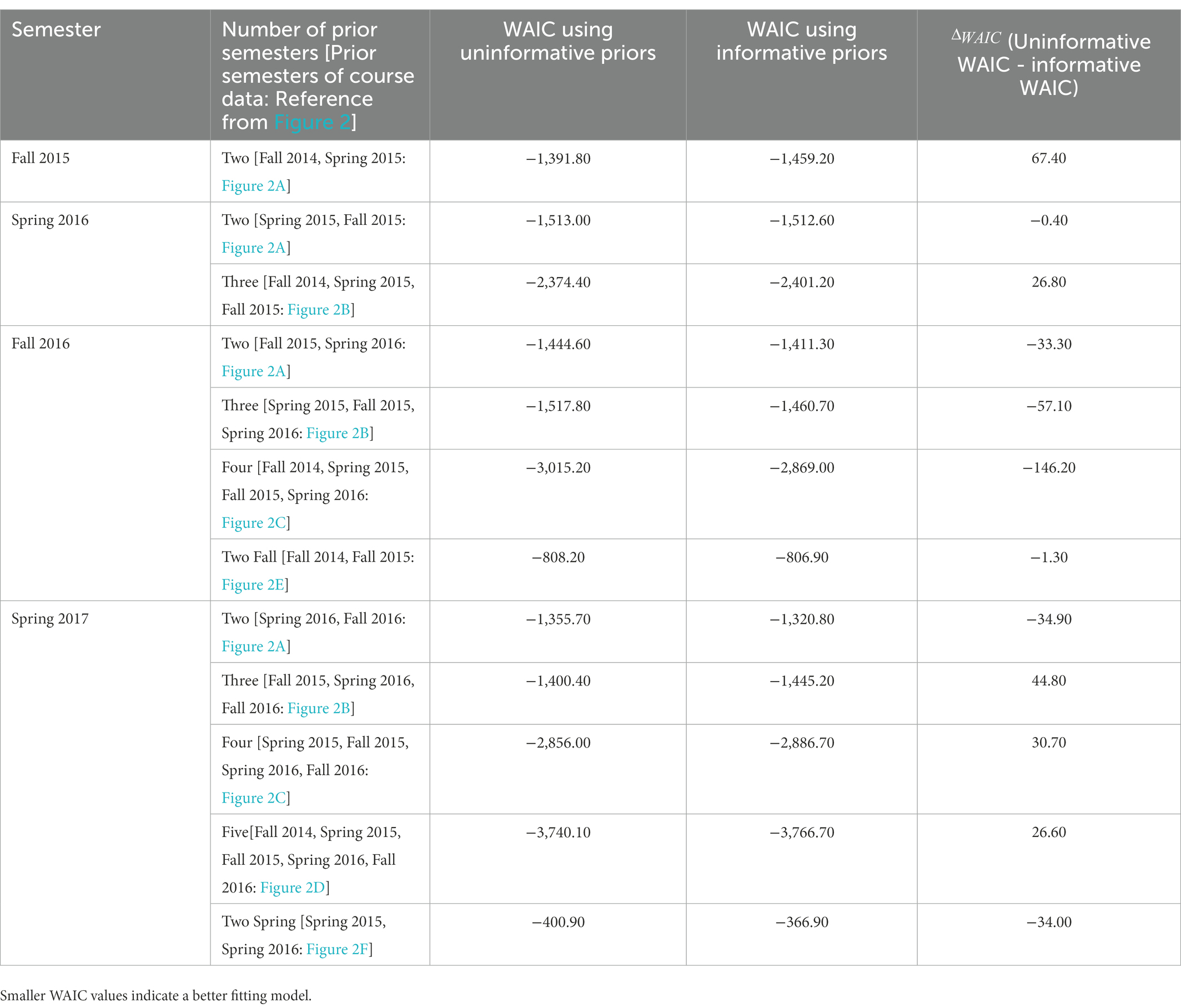
Table 4. WAIC results comparing Bayesian models using uninformative and informative model priors per the study design in Figure 2.

6. Discussion

Modeling student performance is not a new development in EDM and LA (see Chatti et al., 2012; Clow, 2013; Sin and Muthu, 2015; Lang et al., 2017). Although a plethora of studies have investigated different mathematical frameworks for modeling student outcomes in STEM settings using ML and frequentist methods, much less AI educational research has used Bayesian methods to explore the impact of different data types and sources on student performance.

The answer to RQ 1 is that course-specific data types provided the greatest insight into student performance patterns. A one standard deviation increase in LMS logins and CI scores significantly increased the odds of course retention. These findings are consistent with similar observations in other classroom contexts and STEM disciplines that utilized non-Bayesian methods, demonstrating the utility of these novel assessment types as being highly informative of student retention and attrition (Salehi et al., 2019; Simmons and Heckler, 2020; Bertolini, 2021; Chen and Zhang, 2021). While prior academic experiences were identified as factors that were significant predictors of course performance in our biology course setting, they were not as strong predictors as those derived from AI-driven technology; this finding supports calls for educators to embrace and incorporate these tools into the classroom environment since they can be used to provide valuable insights into student performance.

The inclusion of LMS data in EDM and LA models have been predominantly utilized in online, blended, or flipped classroom environments where they were deemed necessary tools for guiding administrative and pedagogical interventions (see Al-Shabandar et al., 2017; Wang, 2017; Lisitsyna and Oreshin, 2019; Shayan and van Zaanen, 2019; Louhab et al., 2020; Nieuwoudt, 2020). Our findings demonstrated that using technological resources with in-class instruction provided greater insights into student achievement. While not considered, the utility of other information extracted from (LMSs) (e.g., student access to course deliverables; see Chandler and Skallos, 2012) aside from student login data should be examined to further explore student comprehension, learning, and course interaction (Bertolini et al., 2021b).

Since instructors may be more confident in their ability to address student misconceptions of various course topics instead of developing models to forecast classroom success, CIs were incorporated since they are capable of diagnosing student learning barriers (Haudek et al., 2011; Nehm, 2019). It is important to note that there are some documented cases where incorporating multiple CI assessments on the same subject matter into the classroom environment may cloud intervention planning (Coletta et al., 2007; Lasry et al., 2011). While performance on the AI-scored ACORNS and traditionally scored CINS was positively correlated (ρ = 0.321) across all six semesters, we do not believe that studying both diminishes the impact of these CIs due to the nature of the two assessments. The ACORNS is a constructed-response assessment that requires a student to generate expository responses to explain evolutionary concepts (i.e., develop scientific explanations), while the CINS is a multiple-choice assessment that prompts students to recognize accurate information (i.e., select a statement). Our findings suggest that utilizing CI assessments with a diverse array of question types may provide differential and greater insight into student learning. While pre-and post-hoc analyses have examined student performance on these assessments before and after course completion, it is still an open question in biology education research whether the administration of these CI assessments at different time points in the course would be more effective in quantifying and forecasting student success (Wang, 2018; Nehm et al., 2022).

Demographic characteristics were not significant factors that impacted classroom performance, compared to student academic attributes in this classroom context. This finding is consistent with many non-Bayesian EDM and LA studies (Leppel, 2002; Thomas and Galambos, 2004; Hussain et al., 2018; Paquette et al., 2020; Bertolini et al., 2021a). Except for PELL recipients, financial aid data were not highly informative in quantifying the odds of passing this biology course. These data types were included since financial needs have a negative effect on student persistence in STEM (Johnson, 2012; Castleman et al., 2018). It is important to note that these data types should not be considered as proxies for individual or parental socioeconomic status since they group middle-income and low-income students together, as well as undercount the latter group (see Tebbs and Turner, 2005; Delisle, 2017). Further scrutiny of these features is needed given these limitations.

New freshmen students were less likely to pass the course compared to transfer students, even though there is substantial documentation that transfer students struggle academically after transitioning to a 4-year institution (Laanan, 2001; Duggan and Pickering, 2008; Shaw et al., 2019). There are several factors that may have contributed to this finding. While a significant portion of student attrition occurs in the student’s first term at an institution (Delen, 2011; Martin, 2017; Ortiz-Lozano et al., 2018), for new freshmen, academic performance is strongly associated with each student’s social interaction with the campus environment (Tinto, 1987; Virdyanawaty and Mansur, 2016; Thomas et al., 2018). Large introductory STEM courses have often been associated with student alienation (Brown and Fitzke, 2019). Furthermore, insufficient mastery of prerequisite material coupled with a decrease in morale may also be attributed to poorer freshmen performance in a course (McCarthy and Kuh, 2006). Further research should explore these factors in this and other collegiate STEM courses by educational stakeholders and institutional researchers at our university.

Minimal variability was observed between semester-specific effects, consistent with the findings of Bertolini et al. (2021a,b) who compared ML performance using frequentist statistical techniques. Differences between student enrollment characteristics were likely the reason for the disproportionate number of passing and failing students between the fall and spring course offerings. In addition to having a lower passing rate, the fall semesters enrolled students with lower high school GPAs (mean: 91.8 vs. 93.0) and more transfer students (8.7% vs. 4.7%), compared to spring semesters.

Although the current study focused on developing a Bayesian framework to examine retention and attrition, factors that impact student persistence, it is valuable to consider the ways in which the results could be applied to our classroom setting, given that these methodologies have received limited attention in the literature (Bertolini, 2021). By identifying student characteristics and features that impact student performance, instructors and academic stakeholders can work to develop educational interventions and psychosocial support structures to foster student success (see Bertolini et al., 2021b for a list of examples). Overall, while diverse data types have the potential to enhance the generality of student success predictions and guide instructor engagement and action, these findings suggest that educational interventions and psychosocial groups should be structured based on both the academic achievements and characteristics of students. For example, if the instructor chooses to place students into collaborative learning groups, these support structures should avoid homogeneous groups composed of students likely to fail the course (e.g., new freshmen and international students). At the institution level, educational stakeholders can work to provide greater support services for these students through tutoring, outreach, and mentoring services. While students on track to succeed can benefit from an intervention, timely identification of struggling students is critical to reduce attrition and high dropout STEM rates (Ortiz-Lozano et al., 2018; Bertolini et al., 2021b).

In RQ 2, using informative priors from aggregated past semesters of course corpora (i.e., more historical semesters) did not always enhance model fit. Some prior work in education found that utilizing information from larger data sets improves model performance (Epling et al., 2003; Boyd and Crawford, 2011; Liao et al., 2019). The purpose of presenting this empirical analysis was to mirror prior frequentist EDM, LA, and ML studies where researchers increased the amount of historical data used in their training corpora to see if this enhanced model efficacy (Bertolini, 2021). Since the use of Bayesian inference is nascent in education, incorporating subjective and elucidated priors are a documented concern for educators since it is difficult for them to precisely decide what the distributions for model parameters should be, and they fear that this specification of prior knowledge may allow researchers to deliberately bias posterior results (Kassler et al., 2019). It is imperative to note that the underlying mathematical frameworks of frequentist techniques also utilize implicit priors; however, they are rather nonsensical since underlying parameters are fixed and remain constant even during data resampling. Many education researchers are likely unaware of these priors governing traditional frequentist models, even though they have been adhered to and incorporated into a plethora of educational research contexts. Greater knowledge and instruction on the mathematical underpinnings of frequentist and Bayesian techniques are warranted and may provide educators with a new perspective and greater appreciation toward using informative prior distributions in Bayesian analytics, embracing them as a pragmatic alternative to frequentist statistical methodologies.

For these educational corpora examined in this research context, this empirical Bayesian design may not always be suitable for establishing informative normally distributed priors for covariates using historical data, as indicated by the large amount of variability in model performance and fit shown in Table 4. This differs from other educational studies which found that incorporating informative priors leads to more meaningful insights into student comprehension and learning (Johnson and Jenkins, 2004; Kubsch et al., 2021). Several plausible reasons that may account for our contrasting findings include (1) running models on a single semester of course data (either fall or spring), (2) variability of student engagement and heterogeneity in the students’ aptitude over different semesters, (3) more selective admissions criteria over different academic terms, and (4) choice of the normal prior distribution. The role of domain-specific knowledge and further scrutiny of these prior distributions and model parameters need to be the focus of future Bayesian educational studies going forward.

ML and its integration with AI technology has tremendous potential to enhance student learning activities, assessments, and scientific inquiries, while providing academic stakeholders with greater insight into student learning, cognition, and performance to address a plethora of STEM challenges (Zhai et al., 2020b; Zhai, 2021). Our study demonstrated that Bayesian methods are another tool that educators can utilize to quantify student retention and attrition, factors that impact student performance, in the science classroom. These techniques are a more intuitive approach to the rejection/acceptance criteria of frequentist methods, linking prior assumptions, and data together to provide a quantitative distribution of final model parameter estimates. Additional studies in the EDM and LA literature are needed to continue studying the effectiveness of these methods in alternative educational contexts, STEM settings, and AI/ML educational tools for informing data-driven pedagogical decisions.

7. Limitations and future directions

There are several limitations to this observational study. The results obtained are corpora dependent and may not generalize to other introductory STEM classes based on (1) institution type (e.g., public, private, for-profit), (2) class size, (3) course duration, and (4) course content coverage (Bertolini et al., 2021b). Given the centrality of evolution to the undergraduate biology curriculum (Brewer and Smith, 2011), we used scores from the ACORNS and CINS assessments. There are many additional published, validated, and commonly employed CI assessments that should be studied as alternative possible sources for modeling (Nehm, 2019). Furthermore, Bayesian methods should be applied to examine whether the findings in this manuscript generalize to other STEM subjects (e.g., physics, chemistry) and classroom contexts (e.g., smaller classes, summer, or winter sessions).

In this study, we focused on comparing model performance and fit using the WAIC metric. Other Bayesian evaluation metrics, such as Bayes factor, were not utilized in the study since this metric does not explicitly include a term quantifying model complexity; furthermore, the Bayes factor tends to be unstable and sensitive to the choice of the prior distribution (Kadane and Lazar, 2004; Ward, 2008). Moreover, we also did not employ the deviance information criterion since this metric is not a completely Bayesian evaluation metric (Richards, 2005; McCarthy, 2007; Spiegelhalter et al., 2014).

One premise of this study was to identify the features associated with biology classroom success. An analogous analysis can use these Bayesian logistic regression models to predict student success in subsequent semesters of the course offering. Moreover, alternative prior distributions, aside from a normal distribution, for the regression parameters should be considered in future studies, including regularization priors and variable selection methodologies.

Biology course performance was categorized as a dichotomous outcome. In future studies, the student’s raw course grade can be modeled using linear regression techniques. Individualized logistic regression models were not run in this study since they have been thoroughly explored in other EDM and LA studies (see Goldstein et al., 2007; Chowdry et al., 2013; Lee et al., 2015; Wang, 2018). Furthermore, we did not consider synergistic effects between different covariates in this analysis. A comprehensive study of these interactions would be a pragmatic next step.

In the future, this work can be extended to model student performance in online and hybrid classroom settings. Due to the recent and dramatic rise of remote instruction, leveraging diverse forms of information from other AI-enhanced learning tools, as well as phenotypic variables from video conferencing software, may provide greater insight into student learning and comprehension. Moreover, the inclusion of these data types has the potential to yield more accurate predictions of retention and attrition, factors that impact student performance, when aggregated with traditional university-specific corpora (Bertolini, 2021).

8. Conclusion

The special issue AI for Tackling STEM Education Challenges focuses on the technological, educational, and methodological advances devised by academic researchers in AI to address a multitude of STEM educational challenges. While ML algorithms have been widely used in the literature to discern insights into student performance patterns, our study has sought to advance this work by demonstrating that Bayesian inference techniques are a useful and pragmatic alternative for ascertaining the differential association between traditional and novel assessment data types on STEM retention and attrition. Features extracted from the LMS and CI assessments were found to be the most significant factors associated with student performance in a baccalaureate biology course setting, compared to traditional features such as demographics and prior course performance. These findings are a small, yet important step for leveraging the power of Bayesian modeling to examine educational outcomes and aid stakeholders in designing personalized content, interventions, and psychosocial structures to support student STEM success.

Data availability statement

The data analyzed in this study is subject to the following licenses/restrictions: The research grant supporting this study is still ongoing. Therefore, all data analyzed in this study will be available from the corresponding author on reasonable request after the grant end date of August 2023. Requests to access these datasets should be directed to roberto.bertolini@alumni.stonybrook.edu.

Ethics statement

The studies involving human participants were reviewed and approved by Stony Brook University. The patients/participants provided their written informed consent to participate in this study.

Author contributions

RB, SF, and RN conceptualized the study, reviewed and approved the final manuscript. RB performed all data analyses, prepared all tables and figures, and wrote the first draft of the manuscript. All authors contributed to the article and approved the submitted version.

Funding

The Howard Hughes Medical Institute Science Education Program provided funding (grant number 79545). The views in this contribution do not necessarily reflect those of the Howard Hughes Medical Institute.

Acknowledgments

The authors thank Heather J. Lynch for helpful suggestions and for providing feedback on an early draft of the methods section in this manuscript. We also acknowledge Yaqi Xue and Nora Galambos for assembling the data files analyzed in this study. The authors thank the Howard Hughes Medical Institute Science Education Program for providing funding. We also thank the guest editor and reviewers for their helpful comments and feedback on the manuscript.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2023.1073829/full#supplementary-material

Abbreviations

ACORNS, Assessing COntextual Reasoning about Natural Selection; AI, Artificial intelligence; CI, Concept inventory; CINS, Conceptual Inventory of Natural Selection; EDM, Educational data mining; GPA, Grade point average; KC, Key concepts; MCMC, Markov chain Monte Carlo; LA, Learning analytics; LMS, Learning management system; ML, Machine learning; ROPE, Region of practical equivalence; STEM, Science, technology, engineering, and mathematics; WAIC, Widely applicable information criterion.

References

Afzaal, M., Nouri, J., Zia, A., Papapetrou, P., Fors, U., Wu, Y., et al. (2021). Explainable AI for data-driven feedback and intelligent action recommendations to support students self-regulation. Front. Artif. Intell. 4:723447. doi: 10.3389/frai.2021.723447

PubMed Abstract | CrossRef Full Text | Google Scholar

Ahmed, D. M., Abdulazeez, A. M., Zeebaree, D. Q., and Ahmed, F. Y. (2021). “Predicting university’s students performance based on machine learning techniques,” in 2021 IEEE International Conference on Automatic Control & Intelligent Systems (I2CACIS). (Shah Alam, Malaysia: IEEE) 276–281.

Google Scholar

Akaike, H. (1973). “Information theory and an extension of the maximum likelihood principle” in 2nd International Symposium on Information Theory. eds. B. N. Petrov and F. Csáki (Tsahkadsor, Armenia, USSR. Budapest: Akadémiai Kiadó), 267–281.

Google Scholar

Alam, A. (2022). “Employing adaptive learning and intelligent tutoring robots for virtual classrooms and smart campuses: reforming education in the age of artificial intelligence” in Advanced computing and intelligent technologies (Singapore: Springer), 395–406.

Google Scholar

Albreiki, B. (2022). Framework for automatically suggesting remedial actions to help students at risk based on explainable ML and rule-based models. Int. J. Educ. Technol. High. Educ. 19, 1–26. doi: 10.1186/s41239-022-00354-6

CrossRef Full Text | Google Scholar

Allenby, G. M., and Rossi, P. E. (2006). “Hierarchical bayes models” in The Handbook of Marketing Research: Uses, Misuses, and Future Advances. Thousand Oaks, California, United States: SAGE Publications, Inc., 418–440.

Google Scholar

Almond, R. G., Mislevy, R. J., Steinberg, L. S., Yan, D., and Williamson, D. M. (2015). Bayesian Networks in Educational Assessment. New York, United States: Springer.

Google Scholar

Al-Shabandar, R., Hussain, A., Laws, A., Keight, R., Lunn, J., and Radi, N. (2017). “Machine learning approaches to predict learning outcomes in Massive open online courses” in 2017 International Joint Conference on Neural Networks (IJCNN) (IEEE). 713–71720.

Google Scholar

Anderson, D. L., Fisher, K. M., and Norman, G. J. (2002). Development and evaluation of the conceptual inventory of natural selection. J. Res. Sci. Teach. 39, 952–978. doi: 10.1002/tea.10053

PubMed Abstract | CrossRef Full Text | Google Scholar

Arrieta, A. B., Díaz-Rodríguez, N., Del Ser, J., Bennetot, A., Tabik, S., Barbado, A., et al. (2020). Explainable Artificial Intelligence (XAI): concepts, taxonomies, opportunities and challenges toward responsible AI. Inf. Fusion. 58, 82–115. doi: 10.1016/j.inffus.2019.12.012

CrossRef Full Text | Google Scholar

Ayers, E., and Junker, B. W. (2006). “Do skills combine additively to predict task difficulty in eighth grade mathematics” in Educational data mining: Papers from the AAAI Workshop (Washington D.C., United States: AAAI Press).

Google Scholar

Baashar, Y., Alkawsi, G., Ali, N. A., Alhussian, H., and Bahbouh, H. T. (2021). “Predicting student’s performance using machine learning methods: a systematic literature review” in 2021 International Conference on Computer & Information Sciences (ICCOINS) IEEE, 357–362.

Google Scholar

Baker, R. S. (2010). Data mining for education. Int. Encycl. Educ. 7, 112–118. doi: 10.1016/B978-0-08-044894-7.01318-X

CrossRef Full Text | Google Scholar

Baker, T., Smith, L., and Anissa, N. (2019). Educ-AI-Tion Rebooted? Exploring the Future of Artificial Intelligence in Schools and Colleges (London: Nesta). Available at: https://www.nesta.org.uk/report/education-rebooted (Accessed January 28, 2023).

Google Scholar

Bañeres, D., Rodríguez, M. E., Guerrero-Roldán, A. E., and Karadeniz, A. (2020). An early warning system to detect at-risk students in online higher education. Appl. Sci. 10:4427. doi: 10.3390/app10134427

CrossRef Full Text | Google Scholar

Banner, K. M., Irvine, K. M., and Rodhouse, T. J. (2020). The use of Bayesian priors in ecology: the good, the bad and the not great. Methods Ecol. Evol. 11, 882–889. doi: 10.1111/2041-210X.13407

CrossRef Full Text | Google Scholar

Berens, J., Schneider, K., Görtz, S., Oster, S., and Burghoff, J. (2019). Early detection of students at risk – predicting student dropouts using administrative student data and machine learning methods. J. Educ. Data Mining. 11, 1–41. doi: 10.5281/zenodo.3594771

CrossRef Full Text | Google Scholar

Berger, J. O., and Berry, D. A. (1988). Statistical analysis and the illusion of objectivity. Am. Sci. 76, 159–165.

Google Scholar

Bertolini, R. (2021). Evaluating performance variability of data pipelines for binary classification with applications to predictive learning analytics. [Dissertation]. Stony Brook (NY): Stony Brook University.

Google Scholar

Bertolini, R., Finch, S. J., and Nehm, R. H. (2021a). Enhancing data pipelines for forecasting student performance: integrating feature selection with cross-validation. Int. J. Educ. Technol. High. Educ. 18, 1–23. doi: 10.1186/s41239-021-00279-6

CrossRef Full Text | Google Scholar

Bertolini, R., Finch, S. J., and Nehm, R. H. (2021b). Testing the impact of novel assessment sources and machine learning methods on predictive outcome modeling in undergraduate biology. J. Sci. Educ. Technol. 30, 193–209. doi: 10.1007/s10956-020-09888-8

CrossRef Full Text | Google Scholar

Bertolini, R., Finch, S. J., and Nehm, R. H. (2022). Quantifying variability in predictions of student performance: examining the impact of bootstrap resampling in data pipelines. Comput. Educ. Artif. Intell. 3:100067. doi: 10.1016/j.caeai.2022.100067

CrossRef Full Text | Google Scholar

Boyd, D., and Crawford, K. (2011). “Six provocations for big data” in A decade in internet time: Symposium on the dynamics of the internet and society. Oxford, UK: Oxford Institute.

Google Scholar

Brassil, C. E., and Couch, B. A. (2019). Multiple-true-false questions reveal more thoroughly the complexity of student thinking than multiple-choice questions: a Bayesian item response model comparison. Int. J. STEM Educ. 6, 1–17. doi: 10.1186/s40594-019-0169-0

CrossRef Full Text | Google Scholar

Brewer, C. A., and Smith, D. (2011). Vision and change in undergraduate biology education: a call to action. American Association for the Advancement of Science, Washington, DC.

Google Scholar

Brooks, S. (1998). Markov chain Monte Carlo method and its application. J. R. Stat. Soc. Ser. D (The Statistician). 47, 69–100.

Google Scholar

Brooks, S. P., and Gelman, A. (1998). General methods for monitoring convergence of iterative simulations. J. Comput. Graph. Stat. 7, 434–455.

Google Scholar

Brooks, C., and Thompson, C. (2017). “Predictive modelling in teaching and learning” in Handbook of learning analytics, 61–68.

Google Scholar

Brown, M. A., and Fitzke, R. E. (2019). The importance of student engagement and experiential learning in undergraduate education. J. Undergrad. Res. 10:2. Available at https://par.nsf.gov/servlets/purl/10204919 (Accessed January 28, 2023).

Google Scholar

Cascallar, E., Musso, M., Kyndt, E., and Dochy, F. (2014). Modelling for understanding AND for prediction/classification--the power of neural networks in research. Frontline Learn. Res. 2, 67–81. doi: 10.14786/flr.v2i5.135

CrossRef Full Text | Google Scholar

Casella, G., Ghosh, M., Gill, J., and Kyung, M. (2010). Penalized regression, standard errors, and Bayesian lassos. Bayesian Anal. 5, 369–411. doi: 10.1214/10-BA607

CrossRef Full Text | Google Scholar

Castleman, B. L., Long, B. T., and Mabel, Z. (2018). Can financial aid help to address the growing need for STEM education? The effects of need-based grants on the completion of science, technology, engineering, and math courses and degrees. J. Policy Anal. Manage. 37, 136–166. doi: 10.1002/pam.22039

CrossRef Full Text | Google Scholar

Chandler, S. D., and Skallos, M. (2012). “Do Learning Management System Tools Help Students Learn?” in 23rd International Conference on College Teaching and Learning.

Google Scholar

Chang, M. J., Sharkness, J., Hurtado, S., and Newman, C. B. (2014). What matters in college for retaining aspiring scientists and engineers from underrepresented racial groups. J. Res. Sci. Teach. 51, 555–580. doi: 10.1002/tea.21146

CrossRef Full Text | Google Scholar

Chatti, M. A., Dyckhoff, A. L., Schroeder, U., and Thüs, H. (2012). A reference model for learning analytics. Int. J. Technol. Enhanced Learn. 4, 318–331. doi: 10.1504/IJTEL.2012.051815

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, X. (2013). STEM Attrition: College Students’ Paths into and out of STEM Fields. Statistical Analysis Report. NCES 2014-001. National Center for Education Statistics.

Google Scholar

Chen, L., Chen, P., and Lin, Z. (2020). Artificial intelligence in education: a review. IEEE Access. 8, 75264–75278. doi: 10.1109/ACCESS.2020.2988510

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, X., Xie, H., Zou, D., and Hwang, G. J. (2020). Application and theory gaps during the rise of artificial intelligence in education. Comput. Educ.: Artif. Intell. 1:100002. doi: 10.1016/j.caeai.2020.100002

CrossRef Full Text | Google Scholar

Chen, Z., and Zhang, T. (2021). Analyzing the Heterogeneous Impact of Remote Learning on Students’ Ability to Stay on Track During the Pandemic. arXiv [2108.00601]. Available at: https://arxiv.org/abs/2108.00601 (Accessed October 7, 2022).

Google Scholar

Chowdry, H., Crawford, C., Dearden, L., Goodman, A., and Vignoles, A. (2013). Widening participation in higher education: analysis using linked administrative data. J. R. Stat. Soc. A. Stat. Soc. 176, 431–457. doi: 10.1111/j.1467-985X.2012.01043.x

CrossRef Full Text | Google Scholar

Choy, S. L., O’Leary, R., and Mengersen, K. (2009). Elicitation by design in ecology: using expert opinion to inform priors for Bayesian statistical models. Ecology 90, 265–277. doi: 10.1890/07-1886.1

PubMed Abstract | CrossRef Full Text | Google Scholar

Clow, D. (2013). An overview of learning analytics. Teach. High. Educ. 18, 683–695. doi: 10.1080/13562517.2013.827653

PubMed Abstract | CrossRef Full Text | Google Scholar

Coletta, V. P., Phillips, J. A., and Steinert, J. J. (2007). Interpreting force concept inventory scores: normalized gain and SAT scores. Phys. Rev. Spec. Top. – Phys. Educ. Res. 3:010106. doi: 10.1103/PhysRevSTPER.3.010106

CrossRef Full Text | Google Scholar

Conati, C., Porayska-Pomsta, K., and Mavrikis, M. (2018). AI in Education needs interpretable machine learning: Lessons from Open Learner Modelling. arXiv [1807.00154]. Available at: https://arxiv.org/abs/1807.00154 (Accessed October 7, 2022).

Google Scholar

Corbett, A. T., and Anderson, J. R. (1994). Knowledge tracing: modeling the acquisition of procedural knowledge. User Model. User-Adap. Inter. 4, 253–278.

Google Scholar

Coughlin, M. A., and Pagano, M. (1997). Case study applications of statistics in institutional research: resources in institutional research, number ten. Association for Institutional Research, Florida State University, Tallahassee, FL.

Google Scholar

Crisp, G., Doran, E., and Salis Reyes, N. A. (2018). Predicting graduation rates at 4-year broad access institutions using a Bayesian modeling approach. Res. High. Educ. 59, 133–155. doi: 10.1007/s11162-017-9459-x

CrossRef Full Text | Google Scholar

Cui, Y., Chu, M. W., and Chen, F. (2019). Analyzing student process data in game-based assessment with Bayesian knowledge tracing and dynamic Bayesian networks. J. Educ. Data Mining. 11, 80–100. doi: 10.5281/zenodo.3554751

CrossRef Full Text | Google Scholar

Culbertson, M. J. (2016). Bayesian networks in educational assessment: the state of the field. Appl. Psychol. Meas. 40, 3–21. doi: 10.1177/0146621615590401

PubMed Abstract | CrossRef Full Text | Google Scholar

Delen, D. (2011). Predicting student attrition with data mining methods. J. College Stud. Retention: Res. Theory Pract. 13, 17–35. doi: 10.2190/CS.13.1.b

CrossRef Full Text | Google Scholar

Delisle, J. (2017). The Pell Grant proxy: a ubiquitous but flawed measure of low-income student enrollment. Evidence Speaks Rep. 2, 1–12. Available at https://www.brookings.edu/wp-content/uploads/2017/10/pell-grants-report.pdf (Accessed January 28, 2023).

Google Scholar

Desmarais, M. C., and Gagnon, M. (2006). “Bayesian student models based on item to item knowledge structures” in European Conference on Technology Enhanced Learning, Springer 111–124.

Google Scholar

Dienes, Z. (2011). Bayesian versus orthodox statistics: which side are you on? Perspect. Psychol. Sci. 6, 274–290. doi: 10.1177/1745691611406920

PubMed Abstract | CrossRef Full Text | Google Scholar

Drigas, A. S., Argyri, K., and Vrettaros, J. (2009). Decade review (1999-2009): progress of application of artificial intelligence tools in student diagnosis. Int. J. Social Humanistic Comput. 1, 175–191. doi: 10.1504/IJSHC.2009.031006

CrossRef Full Text | Google Scholar

Duggan, M. H., and Pickering, J. W. (2008). Barriers to transfer student academic success and retention. J. College Stud. Retention: Res. Theory Pract. 9, 437–459. doi: 10.2190/CS.9.4.c

PubMed Abstract | CrossRef Full Text | Google Scholar

Ellison, A. M. (1996). An introduction to Bayesian inference for ecological research and environmental decision-making. Ecol. Appl. 6, 1036–1046. doi: 10.2307/2269588

CrossRef Full Text | Google Scholar

Epling, M., Timmons, S., and Wharrad, H. (2003). An educational panopticon? New technology, nurse education and surveillance. Nurse Educ. Today 23, 412–418. doi: 10.1016/S0260-6917(03)00002-9

PubMed Abstract | CrossRef Full Text | Google Scholar

Fernández-Caramés, T. M., and Fraga-Lamas, P. (2019). Towards next generation teaching, learning, and context-aware applications for higher education: a review on blockchain, IoT, fog and edge computing enabled smart campuses and universities. Appl. Sci. 9:4479. doi: 10.3390/app9214479

CrossRef Full Text | Google Scholar

Fordyce, J. A., Gompert, Z., Forister, M. L., and Nice, C. C. (2011). A hierarchical Bayesian approach to ecological count data: a flexible tool for ecologists. PLoS One 6:e26785. doi: 10.1371/journal.pone.0026785

PubMed Abstract | CrossRef Full Text | Google Scholar

Fornacon-Wood, I., Mistry, H., Johnson-Hart, C., Faivre-Finn, C., O’Connor, J. P., and Price, G. J. (2022). Understanding the differences between Bayesian and frequentist statistics. Int. J. Radiat. Oncol. Biol. Phys. 112, 1076–1082. doi: 10.1016/j.ijrobp.2021.12.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Gebretekle, T. K., and Goshu, A. T. (2019). Bayesian analysis of retention and graduation of female students of higher education institution: the case of Hawassa University (HU), Ethiopia. Am. J. Theor. Appl. Stat. 8, 47–66. doi: 10.11648/j.ajtas.20190802.12

CrossRef Full Text | Google Scholar

Gelman, A. (2006). Prior distributions for variance parameters in hierarchical models. Bayesian Anal. 1, 515–534. doi: 10.1214/06-BA117A

CrossRef Full Text | Google Scholar

Gelman, A., Hill, J., and Yajima, M. (2012). Why we (usually) don’t have to worry about multiple comparisons. J. Res. Educ. Effect. 5, 189–211. doi: 10.1080/19345747.2011.618213

CrossRef Full Text | Google Scholar

Gelman, A., Hwang, J., and Vehtari, A. (2014). Understanding predictive information criteria for Bayesian models. Stat. Comput. 24, 997–1016. doi: 10.1007/s11222-013-9416-2

PubMed Abstract | CrossRef Full Text | Google Scholar

Gelman, A., Lee, D., and Guo, J. (2015). Stan: a probabilistic programming language for Bayesian inference and optimization. J. Educ. Behav. Stat. 40, 530–543. doi: 10.3102/1076998615606113

CrossRef Full Text | Google Scholar

Goldstein, H., Burgess, S., and McConnell, B. (2007). Modelling the effect of pupil mobility on school differences in educational achievement. J. R. Stat. Soc. A. Stat. Soc. 170, 941–954. doi: 10.1111/j.1467-985X.2007.00491.x

CrossRef Full Text | Google Scholar

Hand, D. J., and Yu, K. (2001). Idiot’s Bayes – not so stupid after all? Int. Stat. Rev. 69, 385–398. doi: 10.1111/j.1751-5823.2001.tb00465.x

CrossRef Full Text | Google Scholar

Haudek, K. C., Kaplan, J. J., Knight, J., Long, T., Merrill, J., Munn, A., et al. (2011). Harnessing technology to improve formative assessment of student conceptions in STEM: forging a national network. CBE–Life Sci. Educ. 10, 149–155. doi: 10.1187/cbe.11-03-0019

PubMed Abstract | CrossRef Full Text | Google Scholar

Hien, N. T. N., and Haddawy, P. (2007). “A decision support system for evaluating international student applications” in 2007 37th annual frontiers in education conference – global engineering: knowledge without borders, opportunities without passports (IEEE), F2A-1.

Google Scholar

Higdem, J. L., Kostal, J. W., Kuncel, N. R., Sackett, P. R., Shen, W., Beatty, A. S., et al. (2016). The role of socioeconomic status in SAT–freshman grade relationships across gender and racial subgroups. Educ. Meas. Issues Pract. 35, 21–28. doi: 10.1111/emip.12103

CrossRef Full Text | Google Scholar

Hobbs, N. T., and Hooten, M. B. (2015). Bayesian models. Princeton, New Jersey, United States: Princeton University Press.

Google Scholar

Hobson, M. P., Jaffe, A. H., Liddle, A. R., Mukherjee, P., and Parkinson, D. (2010). Bayesian methods in cosmology. Cambridge, England: Cambridge University Press.

Google Scholar

Homer, M. (2016). The future of quantitative educational research methods: Bigger, better and, perhaps, bayesian ? Available at: http://hpp.education.leeds.ac.uk/wp-content/uploads/sites/131/2016/02/HPP2016-3-Homer.pdf (Accessed January 28, 2023).

Google Scholar

Hooten, M. B., and Hefley, T. J. (2019). Bringing Bayesian models to life. Boca Raton, Florida: CRC Press.

Google Scholar

Huang, K. T., Ball, C., Francis, J., Ratan, R., Boumis, J., and Fordham, J. (2019). Augmented versus virtual reality in education: an exploratory study examining science knowledge retention when using augmented reality/virtual reality mobile applications. Cyberpsychol. Behav. Soc. Netw. 22, 105–110. doi: 10.1089/cyber.2018.0150

PubMed Abstract | CrossRef Full Text | Google Scholar

Hussain, S., Dahan, N. A., Ba-Alwib, F. M., and Ribata, N. (2018). Educational data mining and analysis of students’ academic performance using WEKA. Indones. J. Electr. Eng. Comput. Sci. 9, 447–459. doi: 10.11591/ijeecs.v9.i2.pp447-459

CrossRef Full Text | Google Scholar

Ikuma, L. H., Steele, A., Dann, S., Adio, O., and Waggenspack, W. N. Jr. (2019). Large-scale student programs increase persistence in STEM fields in a public university setting. J. Eng. Educ. 108, 57–81. doi: 10.1002/jee.20244

CrossRef Full Text | Google Scholar

Johnson, M. H. (2012). An analysis of retention factors in undergraduate degree programs in science, technology, engineering, and mathematics. [Dissertation]. (Missoula (MT): University of Montana.

Google Scholar

Johnson, M. S., and Jenkins, F. (2004). A Bayesian hierarchical model for large-scale educational surveys: an application to the National Assessment of Educational Progress. ETS Res. Rep. Ser. 2004, i–28. doi: 10.1002/j.2333-8504.2004.tb01965.x

CrossRef Full Text | Google Scholar

Jokhan, A., Sharma, B., and Singh, S. (2019). Early warning system as a predictor for student performance in higher education blended courses. Stud. High. Educ. 44, 1900–1911. doi: 10.1080/03075079.2018.1466872

CrossRef Full Text | Google Scholar

Kabudi, T., Pappas, I., and Olsen, D. H. (2021). AI-enabled adaptive learning systems: a systematic mapping of the literature. Comput. Educ.: Artif. Intell. 2:100017. doi: 10.1016/j.caeai.2021.100017

CrossRef Full Text | Google Scholar

Kadane, J. B., and Lazar, N. A. (2004). Methods and criteria for model selection. J. Am. Stat. Assoc. 99, 279–290. doi: 10.1198/016214504000000269

PubMed Abstract | CrossRef Full Text | Google Scholar

Kassler, D., Nichols-Barrer, I., and Finucane, M. (2019). Beyond “treatment versus control”: how Bayesian analysis makes factorial experiments feasible in educational research. Eval. Rev. 4, 238–261. doi: 10.1177/0193841X1881890

CrossRef Full Text | Google Scholar

Komaki, F. (2006). Shrinkage priors for Bayesian prediction. Ann. Stat. 34, 808–819. doi: 10.1214/009053606000000010

CrossRef Full Text | Google Scholar

König, C., and van de Schoot, R. (2018). Bayesian statistics in educational research: a look at the current state of affairs. Educ. Rev. 70, 486–509. doi: 10.1080/00131911.2017.1350636

CrossRef Full Text | Google Scholar

Kricorian, K., Seu, M., Lopez, D., Ureta, E., and Equils, O. (2020). Factors influencing participation of underrepresented students in STEM fields: matched mentors and mindsets. Int. J. STEM Educ. 7, 1–9. doi: 10.1186/s40594-020-00219-2

CrossRef Full Text | Google Scholar

Kruschke, J. K. (2011a). Bayesian assessment of null values via parameter estimation and model comparison. Perspect. Psychol. Sci. 6, 299–312. doi: 10.1177/1745691611406925

PubMed Abstract | CrossRef Full Text | Google Scholar

Kruschke, J. K. (2011b). Doing Bayesian data analysis: a tutorial with R and BUGS. London, United Kingdom: Academic Press.

Google Scholar

Kruschke, J. K., and Liddell, T. M. (2018). The Bayesian New Statistics: hypothesis testing, estimation, meta-analysis, and power analysis from a Bayesian perspective. Psychon. Bull. Rev. 25, 178–206. doi: 10.3758/s13423-016-1221-4

PubMed Abstract | CrossRef Full Text | Google Scholar

Kubsch, M., Czinczel, B., Lossjew, J., Wyrwich, T., Bednorz, D., Bernholt, S., et al. (2022). “Toward learning progression analytics—developing learning environments for the automated analysis of learning using evidence centered design” in Frontiers in education, vol. 605 (Lausanne, Switzerland: Frontiers)

Google Scholar

Kubsch, M., Stamer, I., Steiner, M., Neumann, K., and Parchmann, I. (2021). Beyond p-values: Using bayesian data analysis in science education research. Pract. Assess. Res. Eval. 26, 1–18. doi: 10.7275/vzpw-ng13

CrossRef Full Text | Google Scholar

Laanan, F. S. (2001). Transfer student adjustment. New Directions Community Colleges 2001, 5–13. doi: 10.1002/cc.16

PubMed Abstract | CrossRef Full Text | Google Scholar

Lambert, P. C., Sutton, A. J., Burton, P. R., Abrams, K. R., and Jones, D. R. (2005). How vague is vague? A simulation study of the impact of the use of vague prior distributions in MCMC using WinBUGS. Stat. Med. 24, 2401–2428. doi: 10.1002/sim.2112

PubMed Abstract | CrossRef Full Text | Google Scholar

Lang, C., Siemens, G., Wise, A., and Gašević, D. (2017). The handbook of learning analytics. Beaumont, Alberta, Canada: SOLAR, Society for Learning Analytics and Research.

Google Scholar

Lasry, N., Rosenfield, S., Dedic, H., Dahan, A., and Reshef, O. (2011). The puzzling reliability of the force concept inventory. Am. J. Phys. 79, 909–912. doi: 10.1119/1.3602073

CrossRef Full Text | Google Scholar

Lee, U. J., Sbeglia, G. C., Ha, M., Finch, S. J., and Nehm, R. H. (2015). Clicker score trajectories and concept inventory scores as predictors for early warning systems for large STEM classes. J. Sci. Educ. Technol. 24, 848–860. doi: 10.1007/s10956-015-9568-2

CrossRef Full Text | Google Scholar

Lemoine, N. P. (2019). Moving beyond noninformative priors: why and how to choose weakly informative priors in Bayesian analysis. Oikos 128, 912–928. doi: 10.1111/oik.05985

CrossRef Full Text | Google Scholar

Leppel, K. (2002). Similarities and differences in the college persistence of men and women. Rev. High. Educ. 25, 433–450. doi: 10.1353/rhe.2002.0021

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, H., and Pati, D. (2017). Variable selection using shrinkage priors. Comput. Stat. Data Anal. 107, 107–119. doi: 10.1016/j.csda.2016.10.008

PubMed Abstract | CrossRef Full Text | Google Scholar

Liao, S. N., Zingaro, D., Alvarado, C., Griswold, W. G., and Porter, L. (2019). “Exploring the value of different data sources for predicting student performance in multiple cs courses” in Proceedings of the 50th ACM technical symposium on computer science education.

Google Scholar

Lisitsyna, L., and Oreshin, S. A. (2019). “Machine learning approach of predicting learning outcomes of MOOCs to increase its performance” in Smart Education and e-Learning 2019 (New York, United States: Springer), 107–115.

Google Scholar

Liu, O. L., Rios, J. A., Heilman, M., Gerard, L., and Linn, M. C. (2016). Validation of automated scoring of science assessments. J. Res. Sci. Teach. 53, 215–233. doi: 10.1002/tea.21299

PubMed Abstract | CrossRef Full Text | Google Scholar

Liu, R., and Tan, A. (2020). Towards interpretable automated machine learning for STEM career prediction. J. Educ. Data Mining. 12, 19–32. doi: 10.1002/tea.21299

CrossRef Full Text | Google Scholar

López Zambrano, J., Lara Torralbo, J. A., and Romero Morales, C. (2021). Early prediction of student learning performance through data mining: a systematic review. Psicothema Oviedo. 33, 456–465. doi: 10.7334/psicothema2021.62

CrossRef Full Text | Google Scholar

Louhab, F. E., Bahnasse, A., Bensalah, F., Khiat, A., Khiat, Y., and Talea, M. (2020). Novel approach for adaptive flipped classroom based on learning management system. Educ. Inf. Technol. 25, 755–773. doi: 10.1007/s10639-019-09994-0

CrossRef Full Text | Google Scholar

Lunn, D. J., Thomas, A., Best, N., and Spiegelhalter, D. (2000). WinBUGS – a Bayesian modelling framework: concepts, structure, and extensibility. Stat. Comput. 10, 325–337. doi: 10.1023/A:1008929526011

CrossRef Full Text | Google Scholar

Mao, Y., Lin, C., and Chi, M. (2018). Deep Learning vs. Bayesian Knowledge Tracing: Student Models for Interventions. J. Educ. Data Mining 10, 28–54. doi: 10.5281/zenodo.3554691

CrossRef Full Text | Google Scholar

Marshall, A., Altman, D. G., and Holder, R. L. (2010). Comparison of imputation methods for handling missing covariate data when fitting a cox proportional hazards model: a resampling study. BMC Med. Res. Methodol. 10, 1–10. doi: 10.1186/1471-2288-10-112

CrossRef Full Text | Google Scholar

Martin, J. M. (2017). It just didn’t work out: Examining nonreturning students’ stories about their freshman experience. J. College Stud. Retention: Res. Theory Pract. 19, 176–198. doi: 10.1177/1521025115611670

CrossRef Full Text | Google Scholar

Martinez, A. J. (2021). Factor structure and measurement invariance of the academic time management and procrastination measure. J. Psychoeduc. Assess. 39, 891–901. doi: 10.1177/07342829211034252

CrossRef Full Text | Google Scholar

McArdle, J. J., Grimm, K. J., Hamagami, F., Bowles, R. P., and Meredith, W. (2009). Modeling life-span growth curves of cognition using longitudinal data with multiple samples and changing scales of measurement. Psychol. Methods 14, 126–149. doi: 10.1037/a0015857

PubMed Abstract | CrossRef Full Text | Google Scholar

McArthur, D., Lewis, M., and Bishary, M. (2005). The roles of artificial intelligence in education: current progress and future prospects. J. Educ. Technol. 1, 42–80. doi: 10.26634/jet.1.4.972

CrossRef Full Text | Google Scholar

McCarthy, M. A. (2007). Bayesian methods for ecology. Cambridge, England: Cambridge University Press.

Google Scholar

McCarthy, M., and Kuh, G. D. (2006). Are students ready for college? What student engagement data say. Phi Delta Kappan. 87, 664–669. doi: 10.1177/003172170608700909

CrossRef Full Text | Google Scholar

McCarthy, M. A., and Masters, P. I. (2005). Profiting from prior information in Bayesian analyses of ecological data. J. Appl. Ecol. 42, 1012–1019. doi: 10.1111/j.1365-2664.2005.01101.x

CrossRef Full Text | Google Scholar

McElreath, R. (2018). Statistical rethinking: a bayesian course with examples in R and stan. Chapman; Hall/CRC.

Google Scholar

Moharreri, K., Ha, M., and Nehm, R. H. (2014). EvoGrader: an online formative assessment tool for automatically evaluating written evolutionary explanations. Evol.: Educ. Outreach. 7, 1–14. doi: 10.1186/s12052-014-0015-2

CrossRef Full Text | Google Scholar

Musso, M. F., Hernández, C. F. R., and Cascallar, E. C. (2020). Predicting key educational outcomes in academic trajectories: a machine-learning approach. High. Educ. 80, 875–894. doi: 10.1007/s10734-020-00520-7

CrossRef Full Text | Google Scholar

Musso, M. F., Kyndt, E., Cascallar, E. C., and Dochy, F. (2013). Predicting general academic performance and identifying the differential contribution of participating variables using artificial neural networks. Frontline Learn. Res. 1, 42–71. doi: 10.14786/flr.v1i1.13

CrossRef Full Text | Google Scholar

Muth, C., Oravecz, Z., and Gabry, J. (2018). User-friendly Bayesian regression modeling: a tutorial with rstanarm and shinystan. Quant. Methods Psychol. 14, 99–119. doi: 10.20982/tqmp.14.2.p099

CrossRef Full Text | Google Scholar

Nawaz, R., Sun, Q., Shardlow, M., Kontonatsios, G., Aljohani, N. R., Visvizi, A., et al. (2022). Leveraging AI and machine learning for national student survey: actionable insights from textual feedback to enhance quality of teaching and learning in UK’s higher education. Appl. Sci. 12:514. doi: 10.3390/app12010514

CrossRef Full Text | Google Scholar

Neal, R. M. (2004). Bayesian methods for machine learning NIPS Tutorial. Available at: https://www.cs.toronto.edu/radford/ftp/bayes-tut.pdf (Accessed January 28, 2023).

Google Scholar

Nehm, R. H. (2019). Biology education research: building integrative frameworks for teaching and learning about living systems. Discip. Interdiscip. Sci. Educ. Res. 1, 1–18. doi: 10.1186/s43031-019-0017-6

CrossRef Full Text | Google Scholar

Nehm, R. H., Beggrow, E. P., Opfer, J. E., and Ha, M. (2012). Reasoning about natural selection: diagnosing contextual competency using the ACORNS instrument. Am. Biol. Teach. 74, 92–98. doi: 10.1525/abt.2012.74.2.6

CrossRef Full Text | Google Scholar

Nehm, R. H., Finch, S. J., and Sbeglia, G. C. (2022). Is active learning enough? The contributions of misconception-focused instruction and active-learning dosage on student learning of evolution. Bioscience 72, 1105–1117. doi: 10.1093/biosci/biac073

CrossRef Full Text | Google Scholar

Nieuwoudt, J. E. (2020). Investigating synchronous and asynchronous class attendance as predictors of academic success in online education. Australas. J. Educ. Technol. 36, 15–25. doi: 10.14742/ajet.5137

CrossRef Full Text | Google Scholar

Nouri, J., Saqr, M., and Fors, U. (2019). “Predicting performance of students in a flipped classroom using machine learning: towards automated data-driven formative feedback” in 10th International conference on education, training and informatics (ICETI 2019) 17, 17–21.

Google Scholar

Orr, R., and Foster, S. (2013). Increasing student success using online quizzing in introductory (majors) biology. CBE–Life Sci. Educ. 12, 509–514. doi: 10.1187/cbe.12-10-0183

PubMed Abstract | CrossRef Full Text | Google Scholar

Ortiz-Lozano, J. M., Rua-Vieites, A., Bilbao-Calabuig, P., and Casadesús-Fa, M. (2018). University student retention: Best time and data to identify undergraduate students at risk of dropout. Innov. Educ. Teach. Int. 57, 1–12. doi: 10.1080/14703297.2018.1502090

CrossRef Full Text | Google Scholar

Paquette, L., Ocumpaugh, J., Li, Z., Andres, A., and Baker, R. (2020). Who’s learning? Using demographics in EDM research. J. Educ. Data Mining. 12, 1–30. doi: 10.5281/zenodo.4143612

CrossRef Full Text | Google Scholar

Pardos, Z., Heffernan, N., Ruiz, C., and Beck, J. (2008). “The composite effect: Conjuntive or compensatory? An analysis of multi-skill math questions in ITS” in Proceedings of the 1st International Conference on Educational Data Mining. Montreal, Canada, 147–156.

Google Scholar

Parkin, J. R., and Wang, Z. (2021). Confirmatory factor analysis of the WIAT-III in a referral sample. Psychol. Sch. 58, 837–852. doi: 10.1002/pits.22474

CrossRef Full Text | Google Scholar

Peña-Ayala, A. (2014). Educational data mining: a survey and a data mining-based analysis of recent works. Expert Syst. Appl. 41, 1432–1462. doi: 10.1016/j.eswa.2013.08.042

CrossRef Full Text | Google Scholar

Penprase, B. E. (2020). “History of STEM in the USA” in STEM education for the 21st century. (New York, United States: Springer), 1–16.

Google Scholar

Perez, J. G., and Perez, E. S. (2021). Predicting student program completion using Naïve Bayes classification algorithm. Int. J. Modern Educ. Comput. Sci. 13, 57–67. doi: 10.5815/ijmecs.2021.03.05

CrossRef Full Text | Google Scholar

Plummer, M. (2003). “JAGS: A program for analysis of Bayesian graphical models using Gibbs sampling” in Proceedings of the 3rd International Workshop on Distributed Statistical Computing. 124, 1–10.

Google Scholar

Plummer, M. (2013). rjags: Bayesian graphical models using MCMC. Available at: https://CRAN.R-project.org/package=rjags (Accessed October 7, 2022).

Google Scholar

Richards, S. A. (2005). Testing ecological theory using the information-theoretic approach: examples and cautionary results. Ecology 86, 2805–2814. doi: 10.1890/05-0074

CrossRef Full Text | Google Scholar

Roll, I., and Wylie, R. (2016). Evolution and revolution in artificial intelligence in education. Int. J. Artif. Intell. Educ. 26, 582–599. doi: 10.1007/s40593-016-0110-3

PubMed Abstract | CrossRef Full Text | Google Scholar

Romero, C., and Ventura, S. (2020). Educational data mining and learning analytics: an updated survey. Wiley Interdiscip. Rev.: Data Min. Knowl. Discovery. 10:e1355. doi: 10.1002/9781118956588.ch16

CrossRef Full Text | Google Scholar

Rudin, C. (2019). Stop explaining black box machine learning models for high stakes decisions and use interpretable models instead. Nat. Mach. Intell. 1, 206–215. doi: 10.1038/s42256-019-0048-x

PubMed Abstract | CrossRef Full Text | Google Scholar

Russell, S. J. (2010). Artificial intelligence: a modern approach. Essex, England: Pearson Education, Inc.

Google Scholar

Sailer, M., and Homner, L. (2020). The gamification of learning: a meta-analysis. Educ. Psychol. Rev. 32, 77–112. doi: 10.1007/s10648-019-09498-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Salehi, S., Burkholder, E., Lepage, G. P., Pollock, S., and Wieman, C. (2019). Demographic gaps or preparation gaps?: The large impact of incoming preparation on performance of students in introductory physics. Phys. Rev. Phys. Educ. Res. 15:020114. doi: 10.1103/PhysRevPhysEducRes.15.020114

PubMed Abstract | CrossRef Full Text | Google Scholar

Shafiq, D. A., Marjani, M., Habeeb, R. A. A., and Asirvatham, D. (2022). Student retention using educational data mining and predictive analytics: a systematic literature review. IEEE Access. 10, 72480–72503. doi: 10.1109/ACCESS.2022.3188767

CrossRef Full Text | Google Scholar

Shahiri, A. M., and Husain, W. (2015). A review on predicting student’s performance using data mining techniques. Procedia Comput. Sci. 72, 414–422. doi: 10.1016/j.procs.2015.12.157

PubMed Abstract | CrossRef Full Text | Google Scholar

Shaw, S. T., Spink, K., and Chin-Newman, C. (2019). “Do I really belong here?”: The stigma of being a community college transfer student at a four-year university. Community Coll. J. Res. Pract. 43, 657–660. doi: 10.1080/10668926.2018.1528907

CrossRef Full Text | Google Scholar

Shayan, P., and van Zaanen, M. (2019). Predicting student performance from their behavior in learning management systems. Int. J. Inf. Educ. Technol. 9, 337–341. doi: 10.18178/ijiet.2019.9.5.1223

PubMed Abstract | CrossRef Full Text | Google Scholar

Simmons, A. B., and Heckler, A. F. (2020). Grades, grade component weighting, and demographic disparities in introductory physics. Phys. Rev. Phys. Educ. Res. 16:020125. doi: 10.1103/PhysRevPhysEducRes.16.020125

CrossRef Full Text | Google Scholar

Sin, K., and Muthu, L. (2015). Application of big data in educational data mining and learning analytics – a literature review. ICTACT J. Soft Comput. 5, 1035–1049. doi: 10.21917/ijsc.2015.0145

PubMed Abstract | CrossRef Full Text | Google Scholar

Spiegelhalter, D. J., Best, N. G., Carlin, B. P., and Van Der Linde, A. (2014). The deviance information criterion: 12 years on. J. R. Stat. Soc.: Ser. B (Statistical Methodology). 76, 485–493. doi: 10.1111/rssb.12062

PubMed Abstract | CrossRef Full Text | Google Scholar

Spiegelhalter, D. J., Myles, J. P., Jones, D. R., and Abrams, K. R. (1999). An introduction to Bayesian methods in health technology assessment. Br. Med. J. 319, 508–512. doi: 10.1136/bmj.319.7208.508

PubMed Abstract | CrossRef Full Text | Google Scholar

Stamper, J., Koedinger, K., and McLaughlin, E. (2013). “A comparison of model selection metrics in Datashop” in Proceedings of the 6th International Conference on Educational Data Mining.

Google Scholar

Stephens, P. A., Buskirk, S. W., and del Rio, C. M. (2007). Inference in ecology and evolution. Trends Ecol. Evol. 22, 192–197. doi: 10.1016/j.tree.2006.12.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Subbiah, M., Srinivasan, M. R., and Shanthi, S. (2011). Revisiting higher education data analysis: a Bayesian perspective. Int. J. Sci. Technol. Educ. Res. 2, 32–38. doi: 10.5897/IJSTER.9000027

CrossRef Full Text | Google Scholar

Tebbs, J., and Turner, S. (2005). Low-income students: a caution about using data on Pell grant recipients. Change Mag. Higher Learn. 37, 34–43. doi: 10.3200/CHNG.37.4.34-43

CrossRef Full Text | Google Scholar

Thomas, E. H., and Galambos, N. (2004). What satisfies students? Mining student-opinion data with regression and decision tree analysis. Res. High. Educ. 45, 251–269. doi: 10.1023/B:RIHE.0000019589.79439.6e

CrossRef Full Text | Google Scholar

Thomas, D. T., Walsh, E. T., Torr, B. M., Alvarez, A. S., and Malagon, M. C. (2018). Incorporating high-impact practices for retention: a learning community model for transfer students. J. College Stud. Retention: Res. Theory Pract. 23, 243–263. doi: 10.1177/1521025118813618

CrossRef Full Text | Google Scholar

Tinto, V. (1987). Leaving college: rethinking the causes and cures of student attrition. Chicago, Illinois, United States: The University of Chicago Press.

Google Scholar

Tsiakmaki, M., Kostopoulos, G., Kotsiantis, S., and Ragos, O. (2020). Transfer learning from deep neural networks for predicting student performance. Appl. Sci. 10:2145. doi: 10.3390/app10062145

PubMed Abstract | CrossRef Full Text | Google Scholar

Van Buuren, S., and Groothuis-Oudshoorn, K. (2011). mice: multivariate imputation by chained equations in R. J. Stat. Softw. 45, 1–67. doi: 10.18637/jss.v045.i03

CrossRef Full Text | Google Scholar

Van Camp, L. S. C., Sabbe, B. G. C., and Oldenburg, J. F. E. (2017). Cognitive insight; a systematic review. Clin. Psychol. Rev. 55, 12–24. doi: 10.1016/j.cpr.2017.04.011

PubMed Abstract | CrossRef Full Text | Google Scholar

Van de Sande, B. (2013). Properties of the Bayesian knowledge tracing model. J. Educ. Data Min. 5, 1–10. doi: 10.5281/zenodo.3554629

CrossRef Full Text | Google Scholar

Van de Schoot, R., Depaoli, S., King, R., Kramer, B., Märtens, K., Tadesse, M. G., et al. (2021). Bayesian statistics and modelling. Nat. Rev. Methods Primers 1, 1–26. doi: 10.1038/s43586-020-00001-2

CrossRef Full Text | Google Scholar

Van de Schoot, R., Kaplan, D., Denissen, J., Asendorpf, J. B., Neyer, F. J., and Van Aken, M. A. (2014). A gentle introduction to Bayesian analysis: applications to development research. Child Dev. 85, 842–860. doi: 10.1111/cdev.12169

PubMed Abstract | CrossRef Full Text | Google Scholar

Van den Bergh, D., Clyde, M. A., Gupta, A. R. K. N., de Jong, T., Gronau, Q. F., Marsman, M., et al. (2021). A tutorial on Bayesian multi-model linear regression with BAS and JASP. Behav. Res. Methods 53, 1–21. doi: 10.3758/s13428-021-01552-2

CrossRef Full Text | Google Scholar

Van Erp, S., Oberski, D. L., and Mulder, J. (2019). Shrinkage priors for Bayesian penalized regression. J. Math. Psychol. 89, 31–50. doi: 10.1016/j.jmp.2018.12.004

PubMed Abstract | CrossRef Full Text | Google Scholar

Van Zyl, D. (2015). Introduction to statistics for institutional research. Southern African Association for Institutional Research. Available at: https://www.saair-web.co.za/wp-content/uploads/2015/08/5-SAAIR-IR-Foundations-Intro-to-stats.pdf (Accessed October 7, 2022).

Google Scholar

Vandenewaetere, M., Desmet, P., and Clarebout, G. (2011). The contribution of learner characteristics in the development of computer-based adaptive learning environments. Comput. Hum. Behav. 27, 118–130. doi: 10.1016/j.chb.2010.07.038

CrossRef Full Text | Google Scholar

Vaziri, S., Vaziri, B., Novoa, L. J., and Torabi, E. (2021). Academic motivation in introductory business analytics courses: a Bayesian approach. INFORMS Trans. Educ. 22, 121–129. doi: 10.1287/ited.2021.0247

CrossRef Full Text | Google Scholar

Virdyanawaty, R. I., and Mansur, A. (2016). “Drop out estimation students based on the study period: comparison between naive bayes and support vector machines algorithm methods” in IOP conference series: materials science and engineering. Bristol, England: IOP Publishing. 15, 012039.

Google Scholar

Wang, F. H. (2017). An exploration of online behaviour engagement and achievement in flipped classroom supported by learning management system. Comput. Educ. 114, 79–91. doi: 10.1016/j.compedu.2017.06.012

CrossRef Full Text | Google Scholar

Wang, X. (2018). Longitudinal learning dynamics and the conceptual restructuring of evolutionary understanding [Dissertation]. Stony Brook (NY): Stony Brook, New York.

Google Scholar

Wang, Y., Wang, Y., Stein, D., Liu, Q., and Chen, W. (2021). The structure of Chinese beginning online instructors’ competencies: evidence from Bayesian factor analysis. J. Comput. Educ. 8, 411–440. doi: 10.1007/s40692-021-00186-9

CrossRef Full Text | Google Scholar

Ward, E. J. (2008). A review and comparison of four commonly used Bayesian and maximum likelihood model selection tools. Ecol. Model. 211, 1–10. doi: 10.1016/j.ecolmodel.2007.10.030

CrossRef Full Text | Google Scholar

Wen, D., and Lin, F. (2008). “Ways and means of employing AI technology in e-learning systems” in 2008 Eighth IEEE International Conference on Advanced Learning Technologies. (IEEE), 1005–1006.

Google Scholar

Xiao, W., Ji, P., and Hu, J. (2022). A survey on educational data mining methods used for predicting students’ performance. Eng. Rep. 4:e12482. doi: 10.1002/eng2.12482

PubMed Abstract | CrossRef Full Text | Google Scholar

Xu, W., Meng, J., Kanaga Suba Raja, S., Padma Priya, M., and Kiruthiga Devi, M. (2021). Artificial intelligence in constructing personalized and accurate feedback systems for students. Int. J. Model. Simul. Sci. Comput. :2341001. doi: 10.1142/S1793962323410015

CrossRef Full Text | Google Scholar

Xue, Y. (2018). Testing the differential efficacy of data mining techniques to predicting student outcomes in higher education [Dissertation]. Stony Brook, New York, Stony Brook (NY).

Google Scholar

Yang, J., DeVore, S., Hewagallage, D., Miller, P., Ryan, Q. X., and Stewart, J. (2020). Using machine learning to identify the most at-risk students in physics classes. Phys. Rev. Phys. Educ. Res. 16:020130. doi: 10.1103/PhysRevPhysEducRes.16.020130

CrossRef Full Text | Google Scholar

Yang, S. J., Ogata, H., Matsui, T., and Chen, N. S. (2021). Human-centered artificial intelligence in education: seeing the invisible through the visible. Comput. Educ.: Artif. Intell. 2:100008. doi: 10.1016/j.caeai.2021.100008

CrossRef Full Text | Google Scholar

Zabriskie, C., Yang, J., DeVore, S., and Stewart, J. (2019). Using machine learning to predict physics course outcomes. Phys. Rev. Phys. Educ. Res. 15:020120. doi: 10.1103/PhysRevPhysEducRes.15.020120

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhai, X. (2021). Practices and theories: how can machine learning assist in innovative assessment practices in science education. J. Sci. Educ. Technol. 30, 139–149. doi: 10.1007/s10956-021-09901-8

CrossRef Full Text | Google Scholar

Zhai, X., C Haudek, K., Shi, L., H Nehm, R., and Urban-Lurain, M. (2020a). From substitution to redefinition: a framework of machine learning-based science assessment. J. Res. Sci. Teach. 57, 1430–1459. doi: 10.1002/tea.21658

CrossRef Full Text | Google Scholar

Zhai, X., Shi, L., and Nehm, R. H. (2021). A meta-analysis of machine learning-based science assessments: factors impacting machine-human score agreements. J. Sci. Educ. Technol. 30, 361–379. doi: 10.1007/s10956-020-09875-z

CrossRef Full Text | Google Scholar

Zhai, X., Yin, Y., Pellegrino, J. W., Haudek, K. C., and Shi, L. (2020b). Applying machine learning in science assessments: a systematic review. Stud. Sci. Educ. 56, 111–151. doi: 10.1080/03057267.2020.1735757

CrossRef Full Text | Google Scholar

Zwick, R., and Himelfarb, I. (2011). The effect of high school socioeconomic status on the predictive validity of SAT scores and high school grade-point average. J. Educ. Meas. 48, 101–121. doi: 10.1111/j.1745-3984.2011.00136.x

CrossRef Full Text | Google Scholar