Exploring the potential of a game-based preschool assessment of mathematical competencies

1 Introduction

Early mathematical competencies are the basis for mastering more complex mathematical understanding (Fritz et al., 2018). Yet, despite the large amount of research on early mathematical competencies, there is not always consensus on the definition of these skills (Bakker et al., 2022). Most of the researchers seem to agree that apart from counting, early mathematical competencies include components such as the understanding of cardinality and the ability to compare magnitudes (Purpura and Lonigan, 2013; Purpura et al., 2017; Bakker et al., 2022). Children intuitively develop such concepts through personally meaningful activities that facilitate the learning process (Fisher et al., 2012). They seek meaning in what they do and actively construct their knowledge through exploration and discovery. Such activities are found in everyday situations, including play (Hirsh-Pasek et al., 2009; Fisher et al., 2012). For example, they estimate how many blocks they need to build the tallest skyscraper or translate the number on the dice in a board game and move that many spaces on the board (Ginsburg et al., 2001; Fisher et al., 2012).

Accordingly, different trajectories of mathematical competence begin to emerge before school entry (Stern, 2009). Research suggests that developmental trajectories of mathematical development are cumulative, meaning that individual differences in children’s math performance increase over time (Aunola et al., 2004). Therefore, children with low mathematical competencies in the kindergarten are most likely to have difficulties with mathematics in school. Difficulties with mathematics at school may include the developmental learning disorder with impairment in mathematics (dyscalculia). Dyscalculia is defined in ICD-11 as “an impairment in mathematical skills such as number sense, memorization of number facts, accurate calculation, fluent calculation, and accurate mathematic reasoning” (ICD-11, 6A03.2). Children with dyscalculia show mathematical performance well below that expected for their age and intellectual functioning (World Health Organization, 2019/2021). Similarly, dyscalculia is defined in DSM-V as the difficulties in processing numbers, acquiring arithmetic factual knowledge and performing arithmetic operations quickly and accurately (American Psychiatric Association, 2013). These impairments are manifested by more errors and longer solution times on mathematical tasks in comparison to people with no such disorder. They are also usually accompanied by reduced performance particularly in visual-spatial working memory and/or reduced performance in inhibitory control. Dyscalculia can be reliably diagnosed from the end of the second year of primary school, when math performance becomes more stable (Morgan et al., 2009). An earlier assessment of math competencies in kindergarten and the first year of primary school can identify a risk of developing dyscalculia (Deutsche Gesellschaft für Kinder- und Jugendpsychiatrie, Psychosomatik und Psychotherapie e.V, 2023).

In the recent years, a series of studies have highlighted the importance of early mathematical competencies as specific precursors of later mathematical performance during formal education (i.a., Krajewski and Schneider, 2006, 2009; Chu et al., 2018). Specifically, according to the study of Stern (2009) referring to mathematical development, even after controlling for intelligence at the ages 6, 8, 12, and 18, the correlations between mathematical reasoning at those ages and at the age of 23 remained statistically significant. The results of Krajewski and Schneider (2006) show that preschool quantity-numeracy skills could explain about 25% of the variance in primary school mathematics skills at the end of grades 1 and 4, while intelligence as a nonspecific cognitive predictor explained only up to 10% of the variance in basic numerical skills. Thus a lack of fostering of relevant skills during the preschool years (before enrollment in first elementary grade) and even an overestimation of individual skills at school entry can lead to persisting discrepancies in mathematical competencies during the school years (Krajewski and Schneider, 2006; Morgan et al., 2009; Stern, 2009; Anders et al., 2013). That being so, difficulties in mathematical understanding during the school years are not only due to school-related reasons (Wittmann, 2001).

Early mathematical competencies are highly heterogeneous among preschool children (Mähler et al., 2017; Cahoon et al., 2021; Bakker et al., 2022) but research shows that these competencies can be effectively promoted in kindergarten before school enrolment (Ehlert and Fritz, 2016; Moraske et al., 2018; Skillen et al., 2018a). The educational staff stimulates children’s interest in further engaging with new mathematical concepts in the daily kindergarten routine, and potential developmental risks can be examined more intensively (Ministerium für Kultus, Jugend und Sport Baden-Württemberg, 2022). Characteristics that seem to foster the success of preschool intervention studies are shown to be the promotion of support of the social environment, children being viewed as active, experiential learners, and educational staff adapting the curriculum to children’s individual needs (Hirsh-Pasek et al., 2009).

Playful approaches are a familiar, spontaneous, and engaging opportunity for learning math. Hirsh-Pasek et al. (2009) make a distinction between ordinary children’s play and guided play. The former is usually unstructured, whereas guided play is structured and guided by adults with a set of learning objectives in mind. Guided play allows educators to be goal oriented but also sensitive and responsive to children’s behavior. They can find out what children already know and build on their prior math knowledge. Developmentally appropriate and guided play can provide rich context for children’s learning by motivating children to participate (Hirsh-Pasek et al., 2009). The effectiveness of play-based methods using guided play, both at home and in the classroom, in promoting mathematical skills in preschool children has been well documented (Ramani et al., 2012; Jörns et al., 2013; Hauser et al., 2014; Vogt et al., 2018). In particular, the potential of linear board games has often been shown to be quite effective in fostering early mathematical competencies (Ramani et al., 2012; Laski and Siegler, 2014; Elofsson et al., 2016; Skillen et al., 2018b; Gasteiger and Moeller, 2021). Linear board games, such as the commercial board game Chutes and Ladders (Milton Bradley Company, 1978), have linearly arranged, consecutively numbered and equally sized spaces (Siegler and Ramani, 2009). The distinctive property of linear board games is that they support the mental linear number representation. Such games provide multiple cues that help understand more about the order and the magnitude of the displayed numbers (Siegler and Ramani, 2009; Laski and Siegler, 2014).

Effective assessment tools are needed to enable educational staff to assess children’s developmental status and identify their individual needs in order to adapt the fostering. Yet, since time and personnel resources of educators are limited in the kindergarten, there is a need for resource-saving approaches that can be integrated into everyday life (Textor, 2006; Jörns et al., 2013). Moreover, effective early identification of cases at risk is necessary in order to provide targeted support and attempt to close interindividual developmental gaps (Gerlach et al., 2013; Ricken et al., 2013). Screening tests are suitable for this purpose. They are economic, as they are simple, easy to carry out, time and cost-effective procedures (Moosbrugger and Kelava, 2020). Screening tests are used to look for the first signs of a disorder and provide a general statement about a child’s developmental status according to age as to whether there are any developmental abnormalities. If there are indications of developmental deviations, the screening result is to be objectified and differentiated by means of more comprehensive diagnostics. They thus, have a filtering function, as they aim to identify individuals at risk in a larger population. Apart from these characteristics, screenings must also fulfill the general quality criteria for tests (reliability, validity, and objectivity) (Tröster, 2009; Moosbrugger and Kelava, 2020). The current assessment of early mathematical competencies in German-speaking countries is mainly carried out with standardized preschool math tests like the Test mathematischer Basiskompetenzen im Kindergartenalter [Test of basic math skills at kindergarten age] (MBK 0; Krajewski, 2018b), the Würzburger Vorschultest [Würzburg preschool test] (WVT; Endlich et al., 2016) or the Mathematik- und Rechenkonzepte im Vorschulalter – Diagnose [Preschool mathematics and numeracy concepts – Diagnosis] (MARKO-D; Ricken et al., 2013). Nonetheless, these are all typical test procedures with interactive material but no game elements.

Despite much research on the potential of linear board games in promoting early mathematical competencies, so far comparatively few attempts have been made to develop and examine the potential of game-based approaches to assessing these competencies. Most research on game-based assessment concentrates on the digital gamification of assessment of cognitive tasks in research (Lumsden et al., 2016) or in education (e.g., Ninaus et al., 2017). Gamification in this context is the transformation of simple test tasks by enhancing them with game-like features such as competition, narrative, and other game elements (Lumsden et al., 2016). The results show that in-game measures can reliably and valid assess students math knowledge (Ninaus et al., 2017). This finding speaks in favor of the applicability of a game-based approach as a diagnostic and research tool. One non-digital game-based approach is the House of Numbers (HoN), a screening instrument which allows the assessment of early mathematical competencies (Skillen et al., 2023). The HoN has been developed in the form of a linear board game. There are several reasons for developing a game-based assessment in the form of an analog linear board game rather than a digital assessment. Although preschool children grow up in a media-influenced environment, the findings on young children’s exposure to digital media are controversial and recommendations suggest limited screen time (Linebarger et al., 2014; World Health Organization, 2019; Bochicchio et al., 2022; Deutsche Gesellschaft für Kinder- und Jugendmedizin e.V, 2022; Thorell et al., 2022; Paulus and Gerstner, 2023; Radesky et al., 2023). Whereas board games are fun to play, they offer an open space for creative expression and have an unpredictable course because it is not clear from the start who will win. They are a social activity, which can be easily integrated into everyday life. On top of that, children who may refrain from participating in a performance measurement, may be motivated to participate in a game-based evaluation (Ramani et al., 2012; Bayeck, 2020). Board games are also a familiar process, which adds to the content validity of the assessment. Children are usually familiar with the game process and the equipment used. In contrast, with unfamiliar tools, there is a risk that the respective mathematical competences are not tested, but the way in which the tools are used (Moser Opitz and Ramseier, 2012). Similarly, it could be argued that by digital tests, task presentation can be an impediment to content validity. In these tests, for example, the assessment of processing time depends on how the children use the keyboard or tablet. Finally, the board game format adds ecological validity to the assessment by ensuring that the tasks are related to reality and are not just hypothetical in nature (Moser Opitz and Ramseier, 2012).

The items of the HoN screening were developed in the manner of conventional assessment tools for preschool children (Ricken et al., 2013; Krajewski, 2018b) but are integrated in a linear board game. The screening HoN consists of a board depicting a house, probably a familiar motif for many preschool children. The house consists of five accelerating floors. There are 10 numbered doors on each floor. This alignment of numbers on each floor always progressing from left to right allows the representation of decades on the rows and units on the columns. Players use one token per person, two 10-sided dice with the Arabic numerals one to five evenly distributed on the 10 sides, task cards and further accompanying material such as colorful sticks. The screening HoN is used in a single setting with a child and a trained experimenter. Both players start at the entrance (“0”) and work their way up the floors to the finish (door number 50). During a game session, the experimenter provides standardized instructions on how to play the game, sets standardized test items and documents the child’s responses. Some items are set at specific points during the playing progress and others are masked by game tasks that must be solved when a task card is drawn (for item examples see Skillen et al., 2023). Although the game starts with easy items as “icebreakers,” the difficulty of the items varies throughout the whole game. This helps explore all levels according to the developmental model the screening is based on. At the same time, this arouses the interest of children at all levels of competence to participate and finish the game. The standardization of items and procedures for administering and scoring the screening contributes to the objectivity of the HoN.

Previous research on the applicability, the psychometric quality (reliability and validity) of the HoN screening and its successful identification of children with below average math performance in a sample of 275 4–6-year-old children has demonstrated promising results (Skillen et al., 2023). The game-based setting allows the implementation of items while playing the linear board game. Yet, after conducting a pilot study (Skillen et al., 2023), further validation aspects need to be examined. Moreover, the item characteristics ought to be further analyzed to decide whether they remain in the final test version and considerations on the theoretical model need to be controlled (Moosbrugger and Kelava, 2020). Therefore, this study focuses on the game-based approach HoN with the primary aim to further investigate its quality aspects.

The HoN examined in this study is a 24-item version based on the model for the development of numerical concepts of Ricken et al. (2013). This empirically confirmed model (Fritz et al., 2018) describes the development of mathematical competencies through five stages extending from the age of about 4–8 years. In the first level (count number), children are able to compare two quantities, to name number words in the correct order, and to count out small quantities. However, they are not yet able to associate number words to individual entities. At the second level (mental number line) children mentally construct a successive alignment of numbers. That is, they can understand that numbers have a definite position and that some numbers proceed other numbers, which means that some numbers are also smaller than others. At this level children are also able to perform simple addition and abstraction tasks in smaller number ranges. The next level (cardinality and decomposability) describes the cardinal understanding of numbers. The understanding that a word number represents a number of elements. Furthermore, children at this level can understand that numbers as cardinal entities are composed of smaller quantities. Level four (class inclusion and embeddedness) describes the concrete understanding of the relationship between the total quantity and its partial quantities. That is, after understanding that a given quantity is composed of a number of elements, the child can understand the connection between the partial quantities. Moreover, it can understand the fixed relationship between them. As a result, if two partial quantities are known, a third can be determined. For example, having understood that the number five as a total amount consists of five elements, the child can now understand that a five can also be the total of two plus three or even one plus four elements. This leads on to recognizing differences between quantities as well as part-whole relationships. Children at this level can solve tasks that ask for the final quantity, an exchange quantity or the initial quantity. At the fifth level of this model (relationality) children deepen their understanding of the part-whole concept as well of the relational number concept and can conduct calculations modeling the difference between two quantities. Nonetheless, this model does not describe the development of mathematical competencies as a linear process. Rather, mathematical development up to the early school years is described as a process of overlapping waves (Siegler, 1995), with no sharp boundaries between the stages, but rather transitions (Fritz and Ricken, 2008).

Finally, as one of the goals of developing the HoN is to create an innovative assessment tool for children’s competencies, one of its major features should be age-appropriateness. Previous research showed that the HoN can be reliably conducted with young children as young as 4 years of age (Skillen et al., 2023). However, further research is needed to investigate how children perceive this instrument and whether they find the game-based assessment of mathematical competencies an attractive procedure. To this end, children’s views should be taken into account.

2 Study goals

The purpose of the present study was to investigate the potential of a linear board game with mathematical tasks for the assessment of early mathematical competencies. To the best of our knowledge, there is no such game-based instrument other than the HoN. However, there is a need for such valid, resource-saving and innovative approaches. The properties of the HoN have not yet been extensively examined. Therefore, four questions were investigated.

(1) Do children perform equivalently on a game-based test as on a standard test? To investigate this question, we compared the results of the HoN with the results of an established math test. We expected that the game-based setting would not affect the children’s performance.

(2) Can the game-based approach be used to assess early mathematical competencies in a valid and reliable way? In particular, with regard to the construct validity of the HoN, we expected that younger children would score lower on the HoN than older children. We also expected the HoN to show convergent validity, that is, the performance on the HoN would correlate positively with other test scores of mathematical competence. Furthermore, we expected the items of the HoN to show good indices of model fit and reflect the levels of the theoretical model the HoN is based on. In terms of reliability, our expectation was that the HoN would show good item and person reliability.

The next question concerned the diagnostic validity of the HoN. More specifically, (3) can the game-based approach successfully identify children who show below-average performance in individual diagnostics and therefore children at risk of developing math difficulties? We evaluated the diagnostic performance and accuracy of the HoN as a screening tool by comparing its performance to an established diagnostic test. Previous research has shown good screening indices for the HoN, thus we expected to find equally good results for the 24-item version of the HoN.

(4) Is this game-based approach attractive for young children? The fourth aim of this study was to explore how children perceive and evaluate the game-based assessment setting and whether they prefer it to a standard procedure. To do so we explored children’s opinions about the HoN and a standard test for this age group separately and in comparison to one another.

3 Materials and methods

3.1 Participants

A sample of N = 147 preschoolers was recruited from 15 kindergartens in Germany. The age of children ranged from 5 years to 6 years and 8 months (M_age = 5 years 10 months, SD_age = 5 months). Girls (71) and boys (76) were represented in roughly equal numbers. Kindergartens had been contacted by telephone. Those agreeing to participate received further information material via e-mail. Participation was voluntary. Ethical committee approval was obtained prior to testing. Only children to whom parents had given written consent were allowed to participate, and only if these children had given their verbal consent. From these cases, all children attended the last year of kindergarten before formal schooling and could understand German as a spoken language. One hundred twenty-four of the distributed parent questionnaires were returned fully completed. Only 2.4% of these children were not born in Germany. A total of 80.6% of them speak only German at home, 16.9% speak German and another language and 2.4% speak no German at home. The mother of 17.7% of these children was born in a country other than Germany. The highest German school leaving certificate (Abitur) is held by 49.2% of the mothers and 54% of the fathers. In addition, a subsample of n = 47 children (M_age = 5 years 9 months, SD_age = 5 months; 18 girls and 29 boys) participated in a survey asking about their opinions of the instruments in which they had taken part.

3.2 Instruments

3.2.1 Assessment of early mathematical competencies

The linear board game HoN (Skillen et al., 2023) that allows assessment of early mathematical competencies was administered by trained experimenters to all participating children. The HoN was administered in a single session and lasted on average 21:32 min (SD_duration = 04:48 min; minimum_duration = 08:00 min; maximum_duration = 42:11 min). The version of the HoN used in this study consisted of 24 dichotomous items based on the model for the development of numerical concepts of Ricken et al. (2013). The experimenter documented one point for each correctly solved item. The result was a raw score out of a maximum of 24 points for each child. This raw score was then converted into a percentage score.

Early mathematical competencies of all participating children were also examined using the MARKO-D (Ricken et al., 2013). The MARKO-D is a standardized preschool mathematics test that consists of 55 dichotomous items based on the same model mentioned above (Ricken et al., 2013). As with the HoN, the MARKO-D takes place in a single setting with a trained experimenter and a child (Ricken et al., 2013). In this study, the MARKO-D took on average 27:23 min (SD_duration = 04:58 min; minimum_duration = 18:00 min, maximum_duration = 45:00 min) to complete. The item difficulty is varied throughout the test. To interpret the test results, a raw total score is obtained for each of the 55 items achieved and a percentage score can be calculated from the raw score. The excellent test quality characteristics of the MARKO-D and the common theoretical construct it shares with the HoN (Ricken et al., 2011, 2013) makes it a reasonable option for testing the HoNs quality characteristics. In this study person reliability of the MARKO-D was 0.92 and item reliability 0.98.

3.2.2 Assessment of the perception of the instruments used

The subsample (n = 47) was also surveyed individually by trained experimenters about their perceptions of the math instruments in which they had participated. A questionnaire consisting of five items was used for each of the two instruments. The first item was a dichotomous question about whether the instrument was a game or not. The next three items were in a four-point Likert scale format and asked how much fun the instrument was, whether the child would like to do it again and whether it is a pity that it is over. The fifth item was a preference question between the two instruments and was therefore only asked once after the child had participated in both instruments. The answering format of the first four items was based on the format of the picture scale Bildskala zur Erfassung von Lernfreude und Selbstkonzept in Mathematik und Schriftsprache bei Vorschulkindern [Picture scale for the assessment of learning enjoyment and self-concept in preschool mathematics and language abilities] (BLSL-MS; Roux et al., 2010). The BLSL-MS is a further development of the original picture scale of Harter and Pike (1984) and is used mainly in the self-concept research. The picture-based approach makes it easier for preschool children to respond on a multi-level scale. In this study, the experimenter presented a picture of two children for each item. While pointing to one child, the experimenter said, for example, that this child enjoyed the HoN. The experimenter would then point to the other child and say that this child did not enjoy the HoN. The child would then be asked to point to the child who was like them. Depending on which child was chosen, a further distinction was made between the two options no fun at all and somewhat fun or quite a lot of fun and a lot of fun by pointing to a smaller or larger circle under each child (four circles in total). For a better understanding see Figure 1. No scala was used for the fifth item, as the child was only asked about its preference. The interview took approximately 4 min to complete for each child.

FIGURE 1

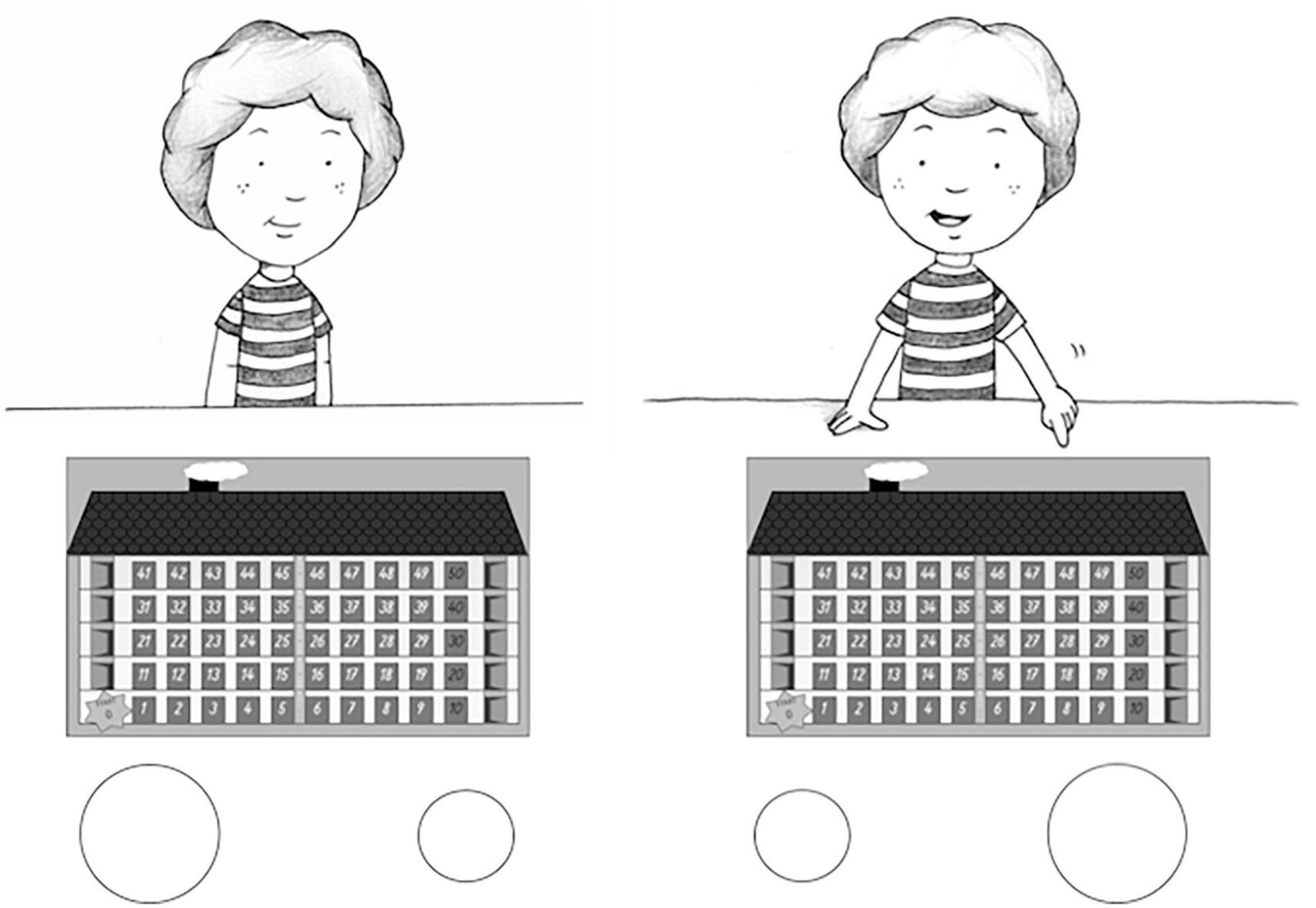
Figure 1. Example of the picture scale response format. Here is item number four about whether it is a pity that the HoN is over. The picture scale of this study was developed based on the scale of Roux et al. (2010). The original graphics were created by Caroline Reusch.

3.3 Design

This study uses a cross-sectional design. Data were collected as part of larger studies during three survey periods between March 2019 and June 2022. Each child was tested individually with the HoN and the MARKO-D in a quiet kindergarten room during a normal kindergarten day. For each math assessment there was one session on a different day. A random part of the sample was tested first with the HoN and the other part first with the MARKO-D. After participating in both instruments, the subsample was administered the survey on the perception of the assessment tools.

3.4 Analytic strategy

There were 1.99% of missing values for the MARKO-D and 0.2% of missing values for the HoN. All missing values were examined individually. Most missing values occurred due to performance-related reasons. The experimenter skipped one or more items because the child could not answer equivalent items correctly or could not answer related items correctly. For example, a child would be asked the same question in succession but with different numbers. In another example, a child would be asked which number his pawn is on. The next two items would ask the child to name the number before and the number after that number. The next item would then be the question “How many do you need to get to 10?” If the child could not answer the previous questions correctly, he or she will most likely not be able to answer this question. Missing values due to such performance-related problems were defined as “item not achieved” and 0 points were awarded for this item. Finally, we compared the results with and without imputed data. They remained the same.

Bayesian inference has the advantage over frequentist methods of being able to consider evidence for, as well as against the null hypothesis (van Doorn et al., 2021), and was therefore used for some analyses in this study. The Bayesian approach uses the Bayes factor (BF) to evaluate the degree of probability of one hypothesis over the other. When testing for hypotheses, the subscript of the BF indicates which hypothesis is being addressed. The BF₁₀ signifies the BF in favor of the alternative hypothesis (H₁) over the null hypothesis (H₀), whereas the BF₀₁ indicates the BF in favor of the H₀ over the H₁. A BF can range from 0 to ∞. According to van Doorn et al. (2021), a BF of 10 or larger (or 0.1% and smaller) indicates strong evidence for the respective hypothesis (i.e., in favor of the H₁ in case of a BF₁₀ and in favor of H₀ in case of a BF₀₁). Correspondingly, a BF between 3 and 10 (or between 0.1 and 0.33) indicates moderate evidence in favor of the respective hypothesis. A BF of 3 is typically used as a cut-off criterion to determine the existence (BF₁₀) or non-existence (BF₀₁) of an effect (Jeffreys, 1998; Dienes, 2014). Thus, BF ≥ 3 will also serve as the cut-off criterion of this study. As there was no basis for a more informed choice of prior, default priors (JASP Team, 2024) were used. Preliminary analyses of the math performance were conducted using the Bayesian approach to examine possible differences by period of assessment, kindergarten, experimenter, gender, or test taken first. Specifically, Bayesian analyses of variance and Bayesian independent samples t-tests were performed to examine the evidence against a difference, with the total sum of points achieved in MARKO-D as the dependent variable. All preliminary analyses resulted in BFs₀₁ ≥ 3, which indicates support for the H₀: δ = 0 against the one- or two sided H₁: δ > 0, H₁: δ < 0 or H₁: δ ≠ 0. Thus, indicating that it is more likely that there are no differences between the respective conditions given the data than that there are differences (van Doorn et al., 2021).

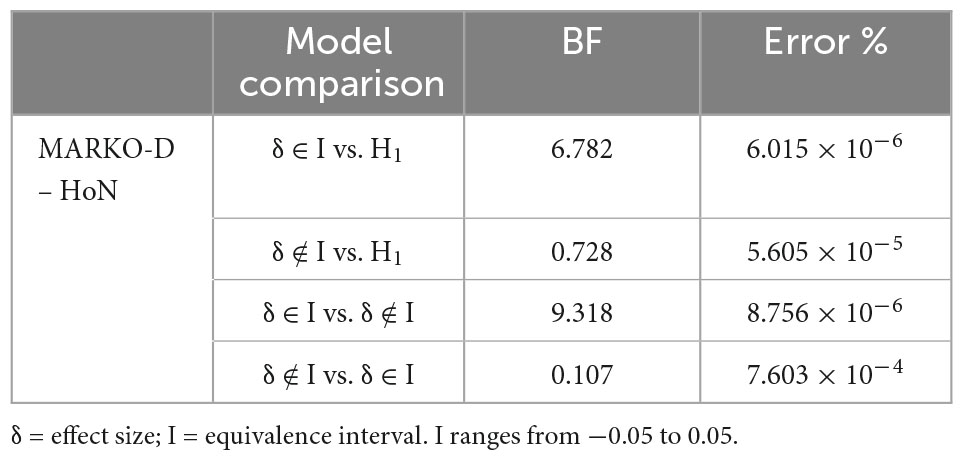
To examine the first research question and thus confirm the equivalence of the performance results in both tests, an equivalence Bayesian paired-samples t-test comparing the total percentage scores in both tests was performed. This BF approach to equivalence testing (Morey and Rouder, 2011) uses alternative BFs. According to this approach, the H₁ describes that the effect size (δ) is defined by an unrestricted prior distribution. Two restricted versions of the H₁ describe that the δ falls inside the equivalence interval (I) (H_∈), or that the δ falls outside the I (H_∉). The so-called overlapping hypotheses (OH) BF examines the probability of the H₁ against the two restricted H_∈ and H_∉. The non-overlapping hypotheses (NOH) BF shows the probability of the H_∈ against the H_∉.

Independent samples t-tests (Student and Mann–Whitney) were used to test whether both instruments were sensitive to age differences in total percentage performance. After checking for sources of bias, a correlation was performed to investigate convergent validity using Pearson’s correlation coefficient and Spearman’s rho between the total percentage scores on each instrument. Due to the limited sample size sensitivity power analyses were performed. These analyses were tested for the independent t-tests between the age groups and for the correlation analysis to determine the minimum effect sizes that the tests were sufficiently sensitive to detect in the context of this study (statistical power; Faul et al., 2007). The power of the 1 − β probability error was set at the 95% confidence level for both power analyses. Based on the item response theory, Rasch analysis to examine the model fit, the item characteristics and the internal consistency of the HoN was run (Boone, 2016).

To investigate the screening characteristics of the HoN, a receiver operating characteristic (ROC) analysis and a crosstabs procedure were carried out. According to Tröster (2009) the quality indices sensitivity (SEN) and specificity (SPE) should not be viewed as invariant quality screening characteristics because they also depend on the selection and basic quota. Therefore, the relative improvement over chance (RIOC) index (Marx, 1992) was also used.

To explore the children’s perception of the two instruments, the percentage frequencies of their responses were examined. Chi-square tests were calculated to check whether the children’s answers to the interview items differed between the established and the game-based method. Finally, sensitivity power analyses were calculated for the Chi-square tests.

These calculations were operated using SPSS 29.0.0 (IBM Corp, 2022), JASP 0.18.3.0 (JASP Team, 2024) and Winsteps 5.7.0 (Linacre, 2024a). Power analyses were performed using G*Power 3.1.9.7 (Faul et al., 2009). All programs used in this study were run with Windows 11 operating system.

4 Results

4.1 Effect of the setting

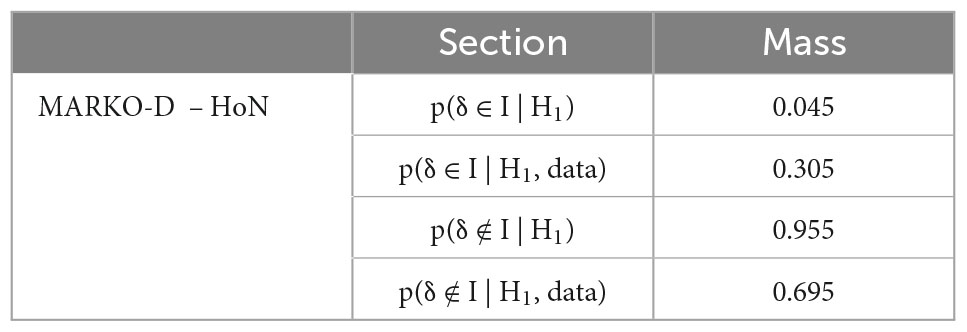
Descriptive statistics for the HoN and the MARKO-D are shown in Table 1. The total percentage scores both for the HoN and the MARKO-D appear to be approximately symmetric and platykurtic in distribution, suggesting that most of the children scored average, but in a flat distribution. The mean total percentage score for the MARKO-D was 59.85 (SD = 18.09) and for the HoN 61.96 (SD = 18.86). As the descriptive statistic show, the children scored slightly better in the game-based than in the standardized assessment. An equivalence Bayesian paired samples t-test was used to examine whether the total percentage scores of the two tests were equivalent. The OH BF in favor of the H_∈ was 6.782 (error 6.015 × 10^–6 %), and the NOH BF in favor of the H_∈ was 9.318 (error 8.756 × 10^–6 %) (see Tables 2, 3 for further results). Both BFs show moderate evidence that the δ falls in the I, and that the scores are not meaningfully different from each other. As Figure 2 also shows, the median of the resulting posterior distribution for the standardized effect size δ equals −0.08 with a central 95% CI [−0.237, 0.082]. According to the same figure, the mass inside the I has increased from prior to posterior, which also speaks in favor of a parameter estimate inside the I. That is, there is evidence to support the equivalence of the results.

TABLE 1

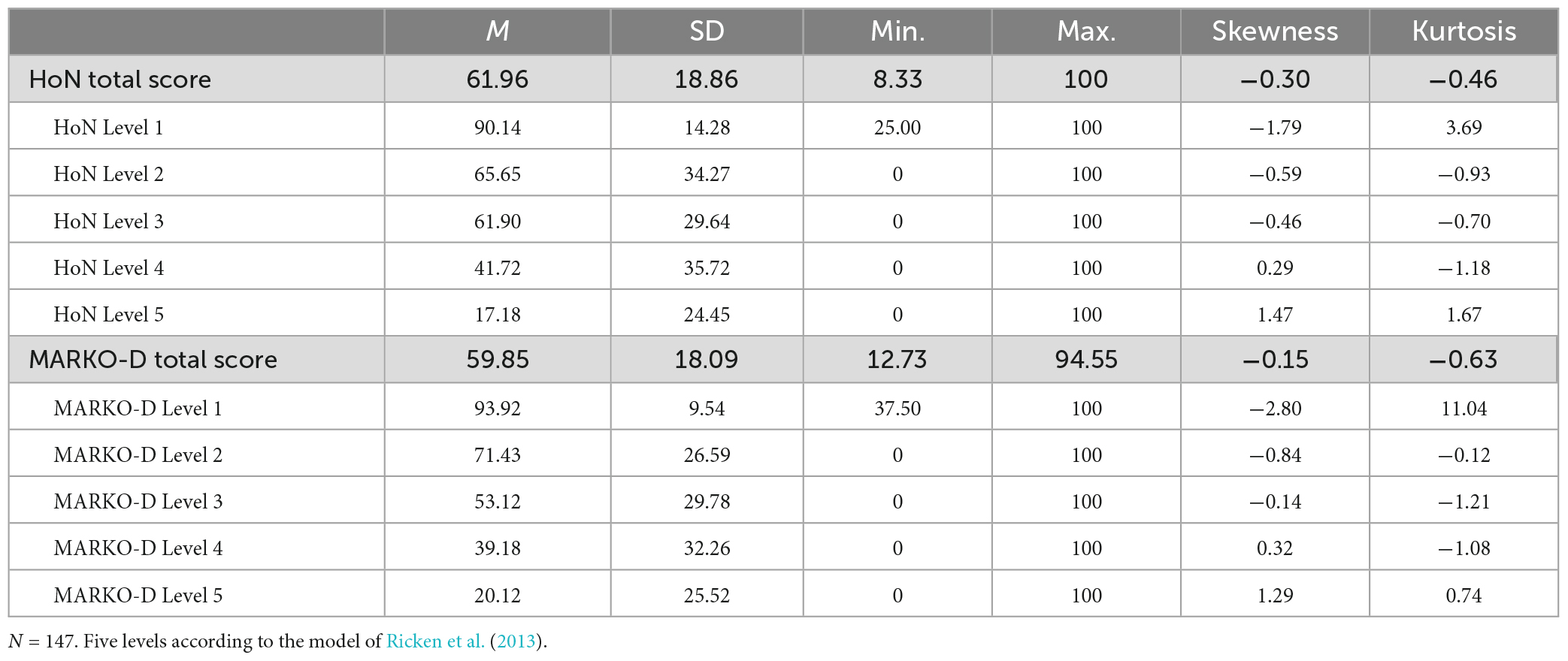
Table 1. Total percentage scores and percentage scores for each model level in both math instruments.

TABLE 2

Table 2. Equivalence Bayesian paired samples t-test.

TABLE 3

Table 3. Equivalence mass table.

FIGURE 2

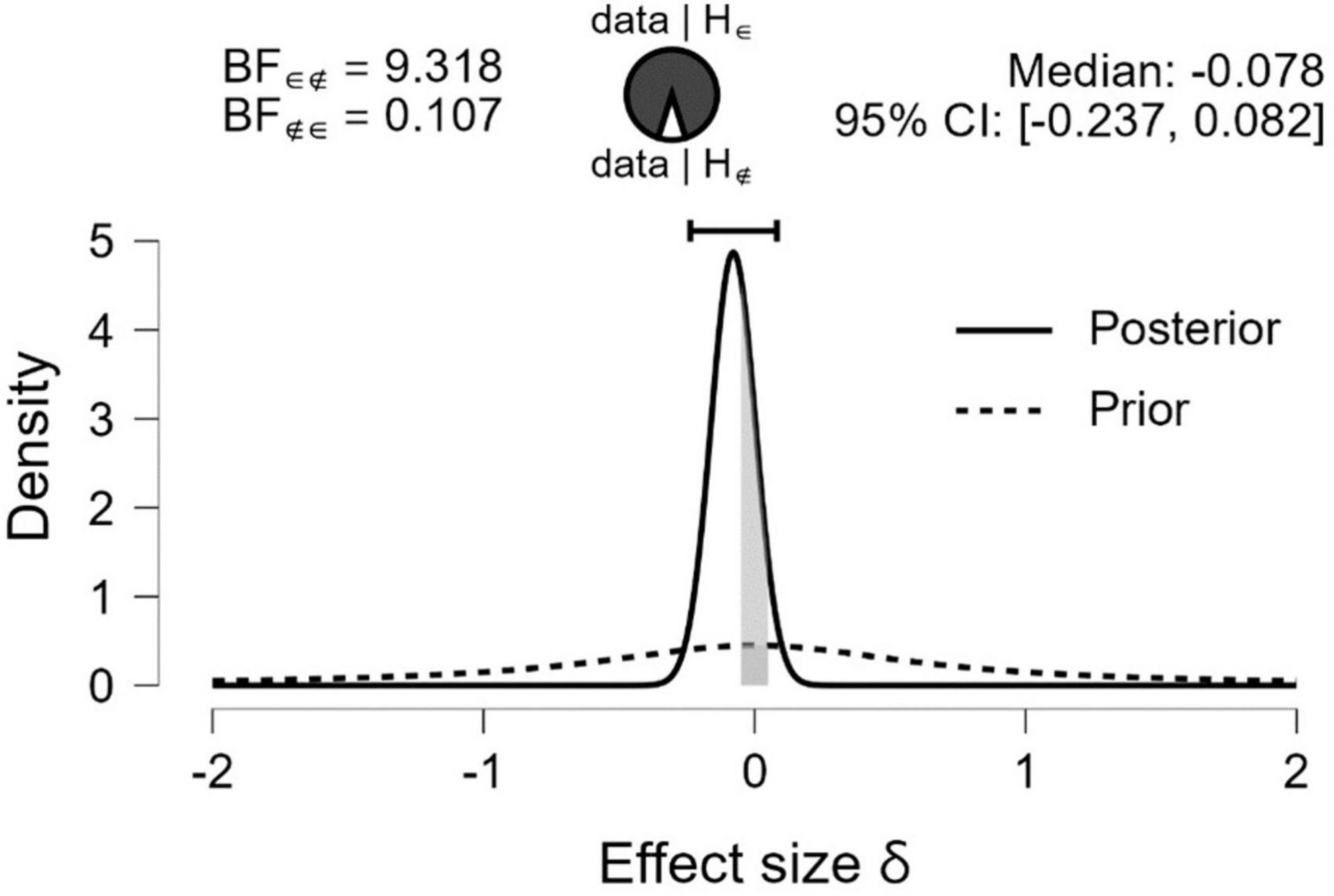
Figure 2. Prior and posterior plot. The dashed line represents the prior distribution. The solid line represents the posterior distribution. The gray area represents the specified equivalence region.

4.2 Reliability and validity

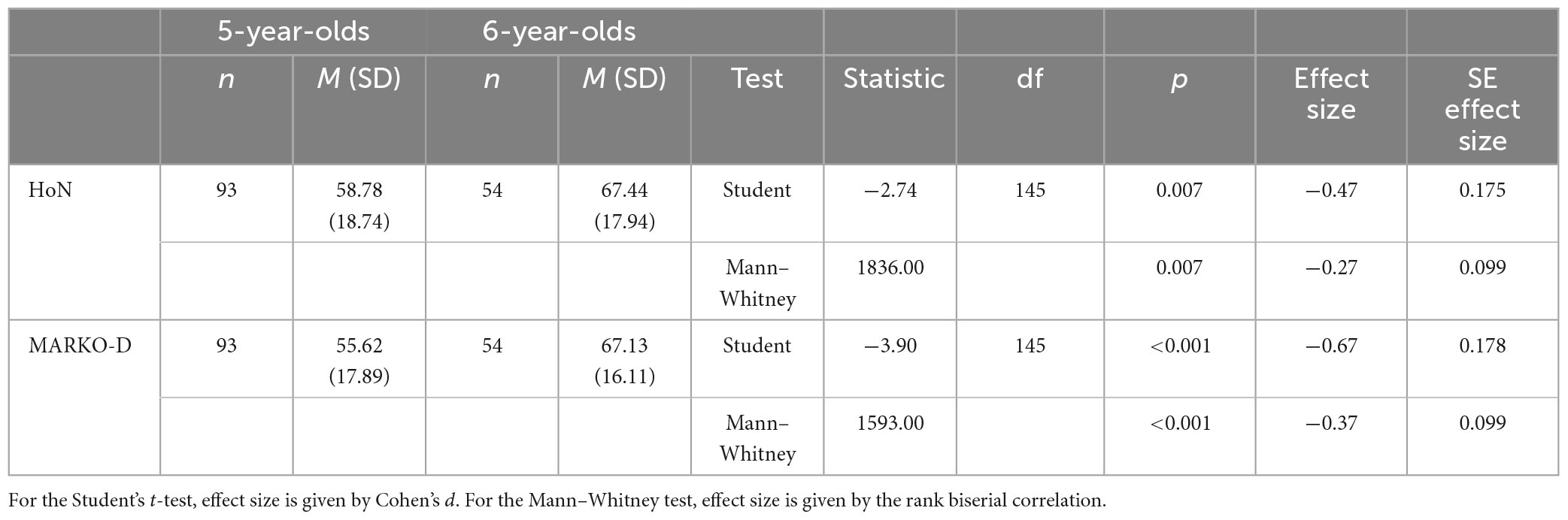
As far as construct validity is concerned, the 6-year-old children scored higher than the 5-year-old children in both instruments. The independent samples t-tests revealed significant math performance differences between the 5 and the 6-year-old children in both instruments (see Table 4). This suggests that both tests could detect age-related differences in performance. However, a sensitivity power analysis showed that the independent samples t-test with the given N could reliably detect effect sizes of d = 0.62 or larger. The limitation of the medium effect size d = −0.47 for the HoN must be considered in this case. To evaluate the convergent validity of the HoN, the degree of agreement between the total percentage scores of the MARKO-D and of the HoN was examined. There was a significant correlation between the two assessments r = 0.85, 95% CI [0.79, 0.89], p < 0.001. Non-parametric analysis showed the same result ρ = 0.84, 95% CI [0.88, 0.78], p < 0.001. The sensitivity analysis against the null hypothesis of a null correlation resulted in a correlation parameter of ρ = 0.29, 95% CI [−0.16, 0.16]. That is, the results of the high correlation between the two tests can be treated as a clear result.

TABLE 4

Table 4. Percentage math performance by age group in each test and comparison for each test.

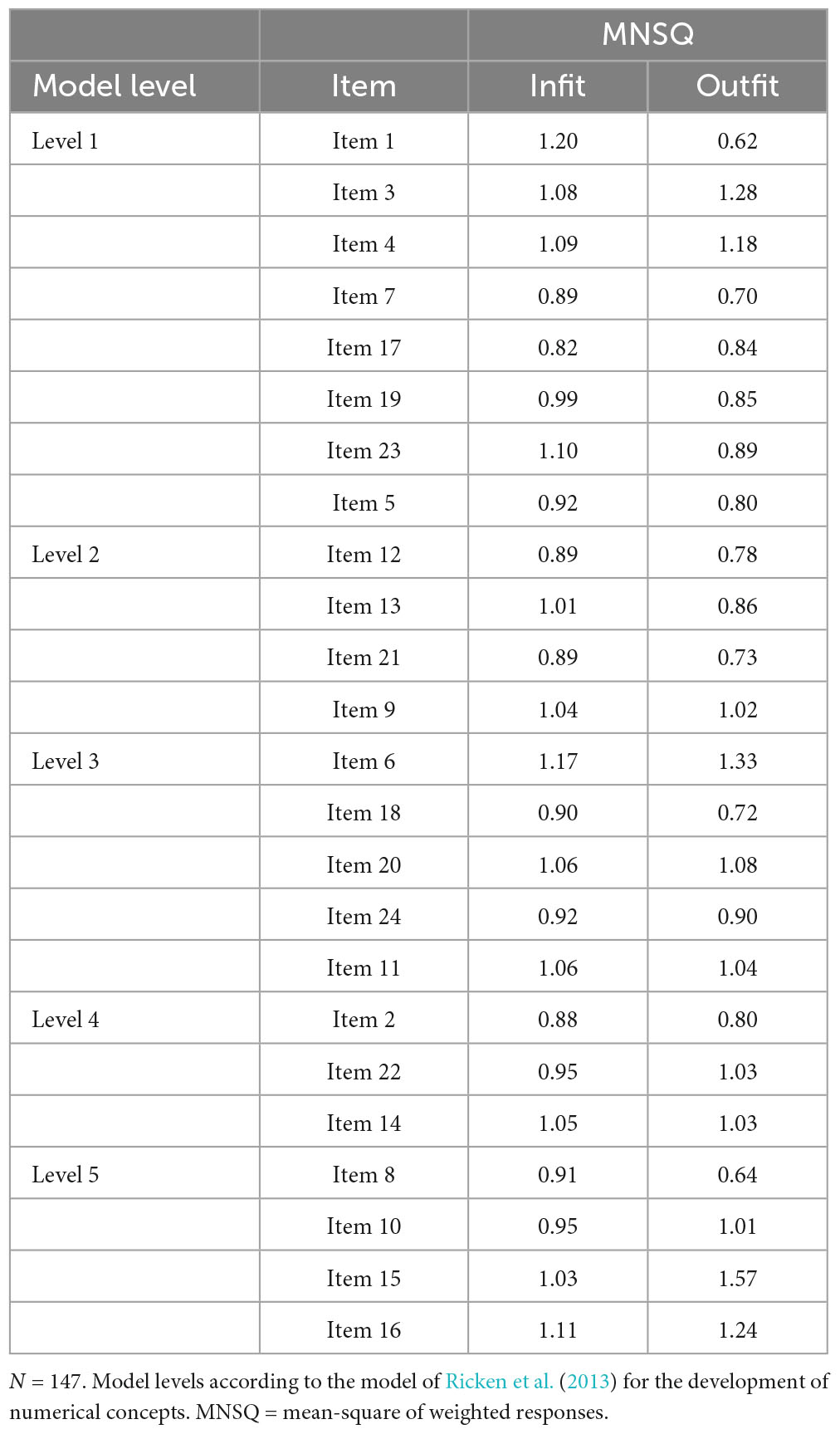
Regarding further aspects of construct validity and the internal consistency of the HoN, the results of the Rasch analysis provide information on the model fit and the reliability of the 24 items of the HoN. As shown in Table 5, the Rasch analysis indicated Mean-square (MNSQ) item Infit values of 1 ± 0.20 for all HoN items. The distribution of the HoN items on the logit measurement ruler of the Person-Item Map corresponds, with the exception of three items, to the five levels of the Ricken et al. (2013) model based on which these items were developed (see Figure 3). The HoN displayed a person reliability of 0.82, an item separation of 6.51 and an item reliability of 0.98. Person reliability is similar to reliability indices of the classical test theory (Linacre, 2024b). According to this, the test reliability of 0.82 is considered good, since values close to 1 suggest a more internally consistent instrument (Boone et al., 2014). The item reliability depends on the range of item measures and the size of the sample (Linacre, 2024b). According to Linacre (2024b) a low item separation (<3) and an item reliability <0.90 suggests that the sample size was inadequate to confirm the construct validity of the measure. In this study, the high item separation and reliability suggest that the sample was large enough to confirm the construct validity of the HoN.

TABLE 5

Table 5. HoN Rasch analysis item statistics.

FIGURE 3

Figure 3. HoN Person-Item Map. N = 147. On the left side of the logit span the participants are shown according to their performance (the higher the more items scored). On the right side the items are displayed according to their difficulty (the higher the more difficult the item). The five levels of the Ricken et al. (2013) model are marked on the distribution of items on the logit span.

4.3 Screening quality indices

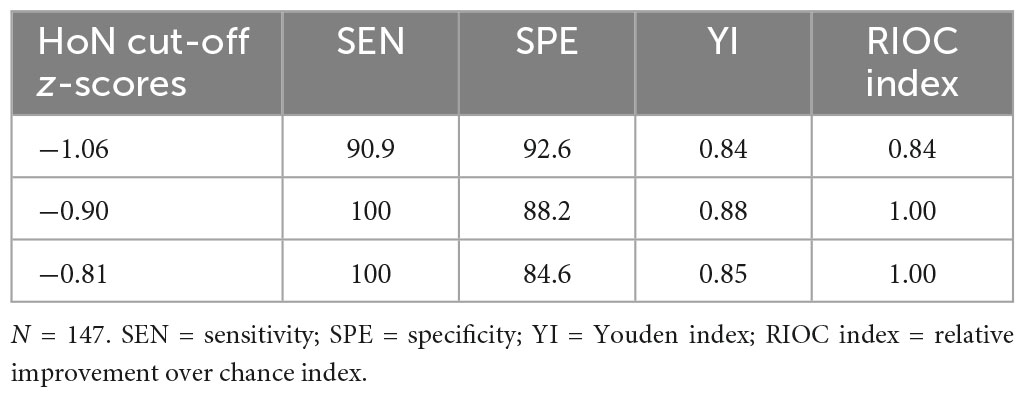
To examine the screening diagnostic quality characteristics of the HoN, a ROC analysis was performed using a MARKO-D t-value of <40 as the state variable. The results show an area under the curve (AUC) of 0.97, p < 0.001, SE = 0.01, 95% CI [0.94, 1.00]. Due to the splitting of the ROC curve in the upper left quadrant, there are three possible cut-off values, which can be seen in Figure 4. A comparison of the quality indices of the three possible cut-off scores can be seen in Table 6. The sample relevant cut-off z-score of −0.90 with the highest Youden Index (YI = SEN + SPE−1) was chosen. With this cut-off score the HoN demonstrated a SEN of 100% and a SPE of 88.2%. The RIOC index was 100%. See Table 7 for further results.

FIGURE 4

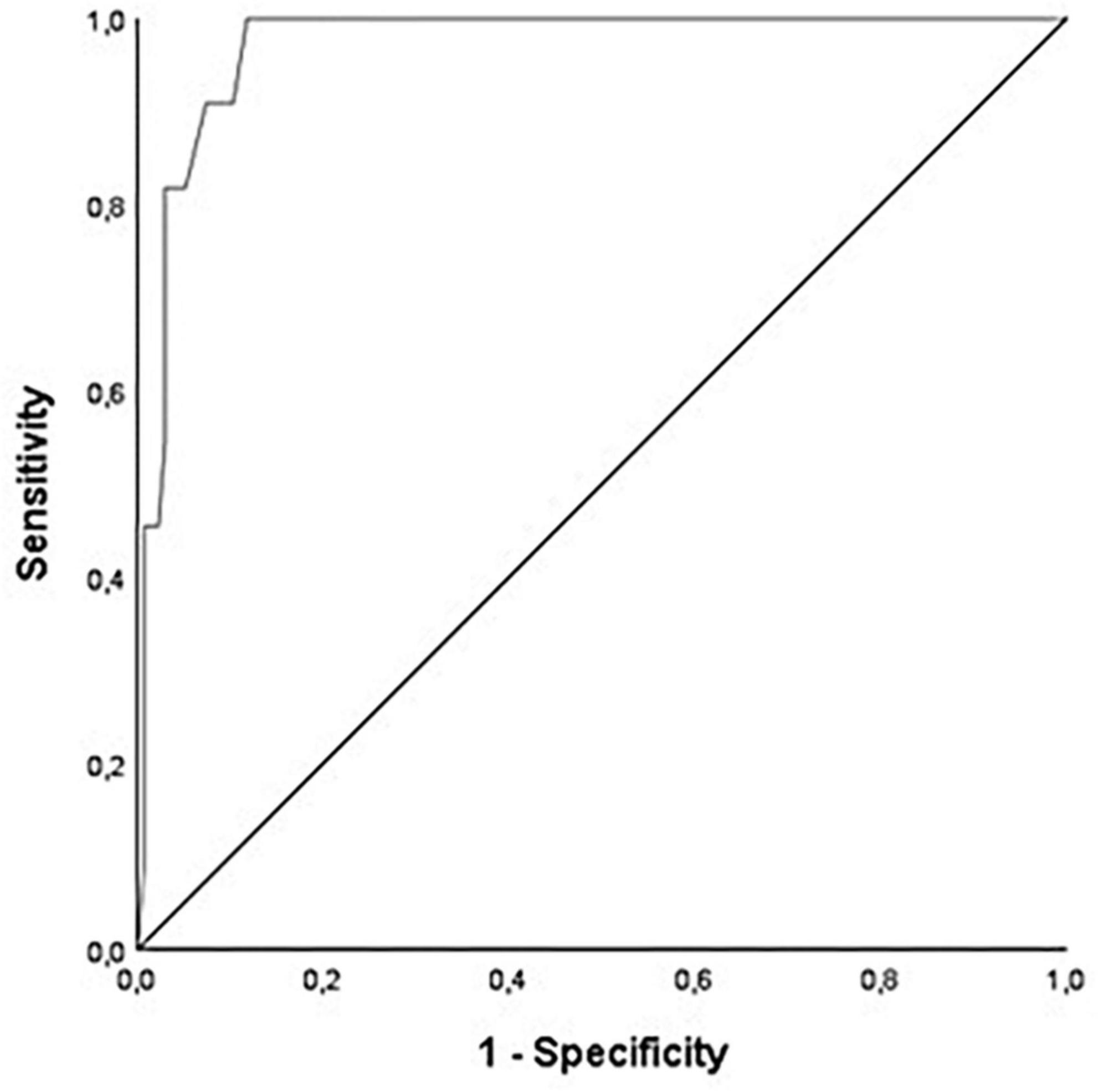
Figure 4. Receiver operating characteristic (ROC) curve of the HoN. N = 147. The diagonal line represents the case of random prediction. The ROC curve (on the left) represents the diagnostic performance of the test. The area under the ROC curve represents the predictive quality of the test.

TABLE 6

Table 6. Comparison of the quality indices of the potential cut-off values.

TABLE 7

Table 7. Crosstabs of children identified as low-achieving and therefore at risk by the two instruments.

4.4 Children’s perceptions of the assessment

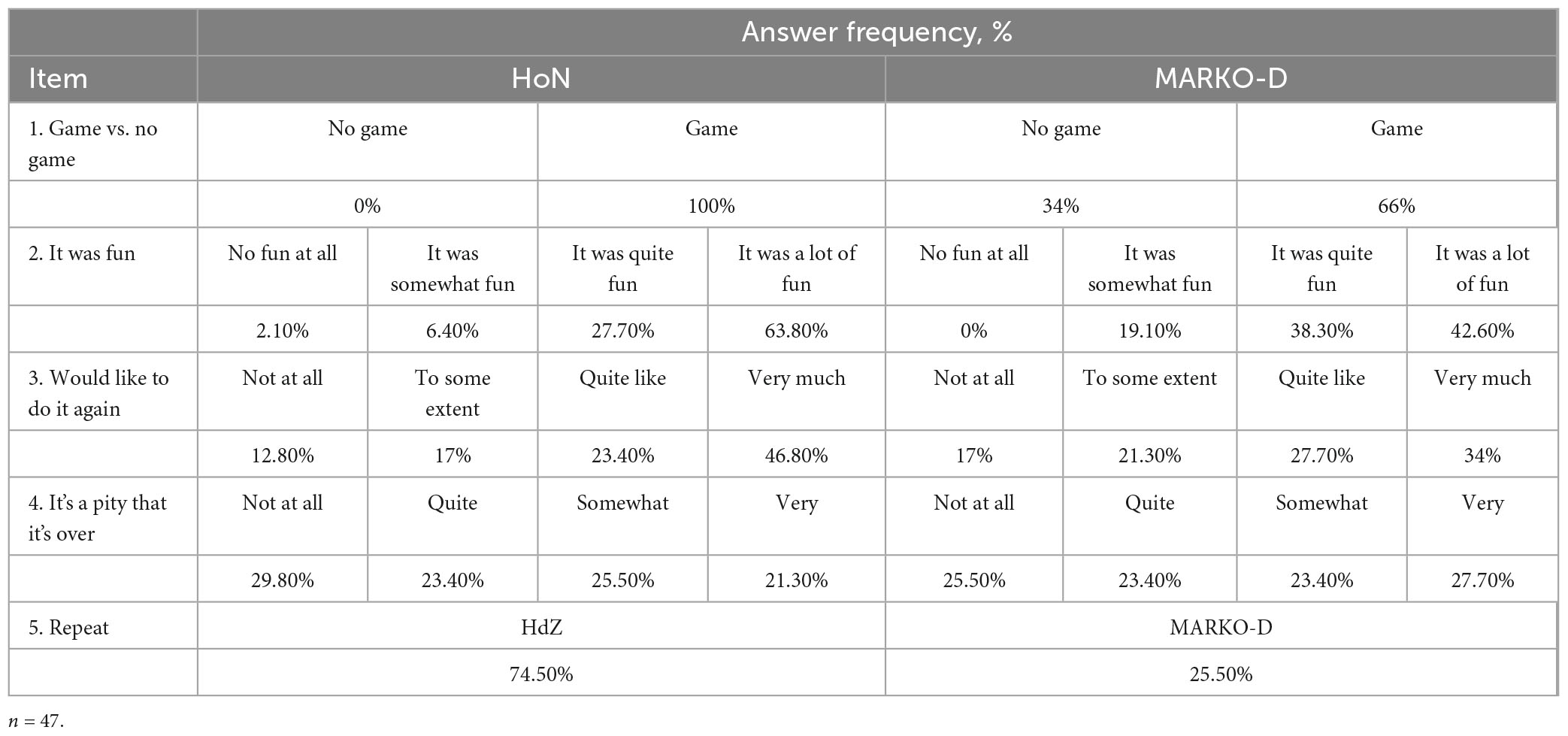
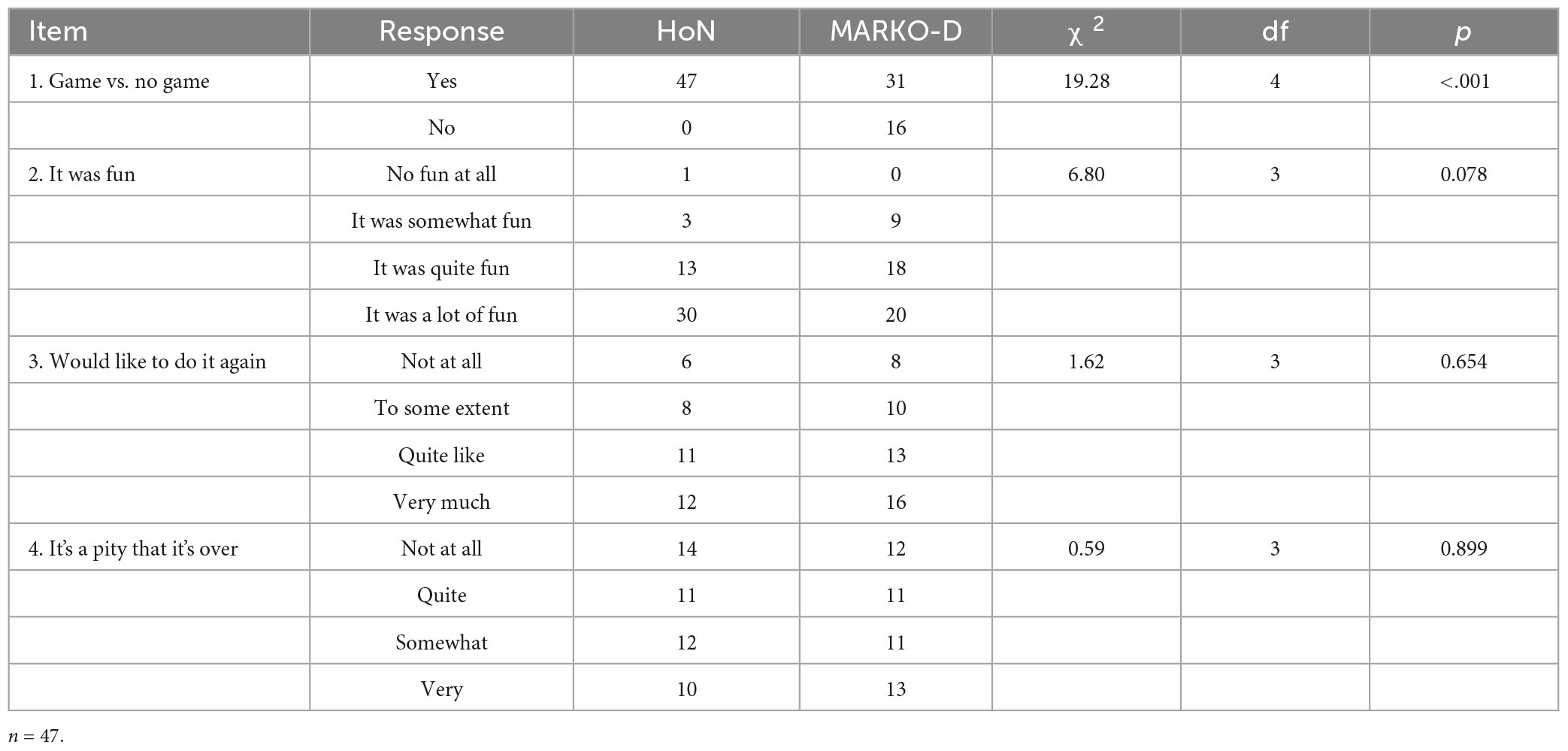
According to the results of the survey on children’s perception of the instruments used, and as can be seen from Table 8, 100% of the children in the subsample (n = 47) thought that the HoN was a game. By contrast, only 66% of the children also thought the MARKO-D to be a game. We further calculated a Chi-square test to see if there was a significant association between the instrument and whether or not it was perceived as a game. The result was significant χ² (4) = 19.28, p < 0.001 with a medium effect φ = −0.45 (p < 0.001). A sensitivity power analysis for df = 4 was calculated. The result showed that the Chi-square test with a 95% power (1 − β error probability) would be able to detect a critical χ² = 9.49. The majority of the children (63.80%) said that they had a lot of fun with the HoN. In contrast only 42.60% said they had a lot of fun doing the MARKO-D. Regarding the questions about repetition and whether it’s a pity that it’s over, the children gave similar answers in both instruments. Most of the children would very much like to do them again. As to whether it’s a pity that it’s over, the children gave evenly distributed answers at all levels of the Likert scale. Further Chi-square analyses were calculated for the three Likert scale items to test whether there was a relationship between the instrument and the child’s response on the Likert scale. None of them showed significant results (see Table 9 for more details). A sensitivity power analysis for df = 3, showed that the 95% power Chi-square test would be able to detect a critical χ² = 7.81. That is, the results of the Chi-square tests for the Likert scale items did not show efficient power to reliably detect effects smaller than the critical χ². Finally, 74.5% of the children said that they would rather do the HoN again than the MARKO-D.

TABLE 8

Table 8. Results of the children survey for the HoN and the MARKO-D.

TABLE 9

Table 9. Frequencies and Chi-square results for the first four items of the survey.

5 Discussion

Although a considerable amount of research has been carried out on the game-based promotion of early mathematical competencies with linear board games (Hauser et al., 2014; Skillen et al., 2018a; Gasteiger and Moeller, 2021; Lange et al., 2021), only few studies have examined their potential for the preschool assessment of these competencies (Skillen et al., 2023). Thus, the purpose of the present study was to examine the potential of the 24-item screening HoN for the assessment of early mathematical competencies.

The first question of this study was whether the game-setting would affect the children’s performance in a preschool math test. To investigate this question, we evaluated the equivalence in the performance outcomes between the newly developed game-based assessment HoN and the established standardized test for mathematical competencies in preschool MARKO-D. The MARKO-D is based on the same theoretical model on the development of mathematical competencies as the HoN (Ricken et al., 2013). We expected that the game-based setting would not affect children’s performance. The results show that children scored slightly higher in the HoN than in the MARKO-D. The small difference in the mean performance between the two assessments is in line with the findings of Skillen et al. (2023) and also with studies showing higher performance on cognitive tasks compared to the same cognitive tasks when gamification features have been added (Mekler et al., 2013; Ninaus et al., 2015). However, in this study, although there is a slight difference between the two scores, the results also suggest that the performance scores on the two tests are probably equivalent. In any case, the experimental treatment can be ruled out as a possible explanation as the children were randomly divided into two groups and preliminary analyses showed a probability of no differences depending on whether they attended the HoN or the MARKO-D appointment first. The task format of an assessment is crucial for the reliability of a preschool test. Non-mathematical requirements during the test, such as the strain on working memory due to exclusively verbal tasks or the motor demands of handling objects, must not interfere with the results (Gloor, 2023). It could be expected that the game material and the actions of the HoN might influence the reliability of the test, because they demand attention and processing capacity, or require greater involvement of the central executive, but this result is not given. Against the expectation that the game context might impose additional cognitive demands that could negatively affect performance, the performance in the HoN was higher than in the MARKO-D. This finding is particularly relevant with regard to comorbid attention deficits of dyscalculia. Children with learning deficits, among them dyscalculia, show an increased risk of developing attention/hyperactivity disorders (Schuchardt et al., 2015). Hence, the characteristics of the test approach may influence the performance. One further example of such a characteristic, is the duration of the test. The HoN took approximately 21:32 min to complete. This is an excellent duration for a test for 5–6-year-olds (Gloor, 2023). According to the recommendation of Wyschkon (2015), test duration for this population, even with interactive test procedures, should not exceed 60 min, because preschool children are not used to working for so long on a task determined by others and often have short attention spans. One plausible explanation of why children scored higher in the HoN than in the MARKO-D, could lie in the nature of the setting of the HoN. Mathematics assessment is often associated with preschoolers’ experiences of negative affect and worry (Lu et al., 2021). It is possible, that children who do not perceive the process of the HoN as a test performance process, may show better performance. On top of that, the exciting game-setting, which allows the engaging in social interaction and the use of interesting materials such as moving game tokens, rolling dice, and drawing task cards, may promote the motivation to participate, which in turn also may have a positive effect on the performance of the children. As Hirsh-Pasek et al. (2009) put it, playful children are motivated children. Similarly, Gelman (2006) observed that children as young as 2 years and 6 months could successfully perform tasks of prediction of items and counting when they were embedded in a play task, but not when they were bluntly asked to count in a count-only task. Further research is needed to investigate whether the small performance difference is due to the HoN setting characteristics or due to other unknown factors.

Regarding the second question of this study and according to our expectations, the results show that both instruments were able to reliably detect differences in performance between the groups of the 5- and the 6-year-olds. This finding is also consistent with the results of Skillen et al. (2023) who investigated whether mathematical performance in the game-based approach differed between the groups of 4-, 5-, and 6-year old children. Such age-related differences in performance are expected according to the developmental model, which posits that older children excel their skills and develop further competencies that allow them to deal with more complex mathematical understanding (Ricken et al., 2013). To determine the convergent validity of the HoN, the degree of agreement between the mean percentage scores of the HoN and the MARKO-D was examined. In line with our hypothesis, the positive correlation between the new and the established tool of 0.85 is high according to Cohen (1988) and it shows that probably both tools evaluate the same mathematical concepts. This result is also in accordance with the findings of earlier evaluation of the psychometric characteristics of the HoN (Skillen et al., 2023) and the findings of studies on gamification of cognitive testing (Lumsden et al., 2016). The latter found relatively good correlations between gamified assessments and their non-gamified counterparts, which provide evidence that cognitive tests can be gamified and remain useful research tools. Furthermore, as expected, in the results of the Rasch analysis all items showed a model fit between 0.82 and 1.20, which according to Wright and Linacre (1994) indicates a reasonable model fit. These MNSQ values suggest that there is neither too much unexplained variance in the data nor that the model overpredicts the data causing inflated reliability statistics (Boone et al., 2014). The plotting of the items on the logit range of the Person-Item Map confirmed with only three exceptions the levels of the model of Ricken et al. (2013). The three overlapping items can be assigned to the level two (mental number line) and three (cardinality and decomposability). In line with the overlapping theory (Siegler, 1995), skills acquired at level two are also required to solve tasks that address level three. This could be one possible interpretation of this overlap, which also appears in established tests (see MARKO-D; Ricken et al., 2013). Finally, the high values of item and person reliability for the HoN suggest that item parameters calculated from the current data are generalizable for similar person and item samples (Boone et al., 2014).

The third question in this study was whether the HoN can successfully predict later difficulties in math. To evaluate the diagnostic validity of the HoN screening, its performance in detecting potential “at risk” cases was compared with the performance of the MARKO-D. The sample of this study was randomly selected. A total of 7.5% of the children were identified by the MARKO-D as having below average math performance compared to the expected performance for their age and therefore at risk of developing dyscalculia. This finding reflects the prevalence rates of dyscalculia, which lie within approximately 2%–8%, making the sample representative (Wyschkon et al., 2009; Fischbach et al., 2013). According to our hypothesis, the results of the ROC analysis are overall promising. The high AUC of 0.97 manifests the ability of the HoN to successfully distinguish between children with age-appropriate expected math skills and children possibly at risk. A sample related cut-off value was defined. The resulting high rates of SEN and SPE indicate a high likelihood that the HoN will be able to detect a possible impairment in early mathematics and a good likelihood that the absence of an impairment will be also successfully detected by the HoN. In particular, the highest possible SEN is desirable for a screening test. A high proportion of false positives is accepted in view of the concept of a screening test as a coarse screening procedure, which should be followed by a fine diagnosis for all “at-risk” children (Marx and Lenhard, 2011). The RIOC index above 66%, according to Jansen et al. (2002), can be described as a very good classification. The high psychometric results of this study are similar to the high results of Skillen et al. (2023). Testing the 23-item version of the HoN based on the model of Ricken et al. (2013), they found a high AUC value of 0.86, p < 0.001, 95% CI [0.78, 0.93]. After defining two possible sample-relevant cut-off z-scores the same authors found good screening indices. In detail, using the z-scores of −0.63 (percentile rank 26%) and −0.24 (percentile rank 41%) as resulting cut-off scores, they found a SEN of 79% and 95%, a SPE of 76% and 65% and high RIOC indices of 71% and 91%, respectively.

The fourth question of this study was whether the game-based HoN is attractive for young children. The aim of this question was to shed light on how children perceive this newly developed instrument. To examine this question the preschool children’s perception of the HoN was investigated with a short survey. The explorative findings show that all surveyed children perceived the HoN as a game. In contrast, only 66% of the children also perceived the MARKO-D as a game. This result shows that the children perceived a difference between the HoN and the MARKO-D. In addition, 74.5% of the children chose the HoN over the standard assessment. This finding is also consistent with findings from gamification studies that have compared gamified and non-gamified tasks, showing that intrinsic motivation is enhanced by the use of the gamified tasks (Lumsden et al., 2016). The above results support further development of the game-based HoN as a tool with potential in the preschool population.

5.1 Implications

Additional research is required to examine further (validation) aspects of the screening HoN. For example, it would be interesting to evaluate the test-retest reliability of the HoN, the extent to which the HoN also overlaps with other competence tests for preschool mathematics, or with tests of other competence areas (divergent validity). In future studies, further information could also be obtained to better determine the influence of nonspecific cognitive or environmental predictors of later mathematical performance. Such predictors include intelligence, home numeracy environment and working memory. In addition, to further investigate the potential of the HoN screening, it could be applied to different populations. The focus of this study was the age group attending the last year of kindergarten (5–6-year-olds). In future studies, the test could also be administered to younger or older children (e.g., first graders) to evaluate whether the HoN still responds to expected developmental difficulties. Alternatively, it could be tested in different kinds of populations, such as primary school children who have already been diagnosed with dyscalculia. In this way, it could be demonstrated whether the HoN correctly identifies cases who show difficulties with mathematics. Another possibility would be to examine the HoN properties based on other theoretical models (e.g., Krajewski, 2018a).

Once multiple aspects of the screening have been thoroughly reviewed and all characteristics of the HoN have been clarified, the next step would be to collect sufficient data on performance in several age groups and to establish population-based reference scores for the HoN (norming). Our aim for the future is to develop the HoN as an instrument that can be used by (preschool) educators. Further research is therefore important to investigate how these educators would apply the HoN and what their specific needs are with regard to this instrument.

5.2 Limitations

An apparent limitation of this study is the small sample size. The limited sample size has an impact on the power of some of the statistical analyses in this study. The first reason for this limitation is the nature of this type of assessment. Data collection in kindergartens can be very time consuming. At the same time, many kindergartens in Germany are understaffed and overburdened. As a result, some kindergartens did not agree to participate. Furthermore, even among those that did participate, we often faced the problem of missing assessment sessions, because preschool children were often sick and stayed at home. In addition, the almost 2 years of the COVID-19 pandemic were a great loss of potential data, as external persons were not allowed access to educational institutions in Germany for longer periods of time. Even so, the fact that the HoN already shows good results despite the small sample size is very promising.

Another limitation of this study is that other variables, such as intelligence, were not measured for the whole sample and therefore could not be documented in this article. This limits the description of the sample and the comparison of various aspects of performance. Moreover, there were no fidelity controls other than comparing the average children math performance between experimenters for differences. However, all experimenters received training and had to obtain supervisor approval after demonstrating the testing procedure to be allowed to go into the field. In addition, a detailed documentation of the data, including the dates and start and end times of the testing for each measure can help to reconstruct the conditions of the procedure.

Lastly, as far as the children’s survey is concerned, and as the results of the Chi-square tests show, the Likert scale items were probably difficult for the young children to understand, despite the age-appropriate adapted format. This may also explain why the children responded similarly between the HoN and the MARKO-D to these items. In addition, the exploratory findings on children’s perception of the tools should be treated as tentative, as preschool children tend to exhibit a response bias when questioned by giving affirmative answers (Okanda and Itakura, 2010). Similarly, the children in this study may have given more positive responses. In future studies, the use of mixed methods with mainly open-ended question formats should be the preferred method of questioning in a preschool sample. Nevertheless, our aim in this study was achieved, as it was only a first attempt to describe in an exploratory way what children think about the HoN.

6 Conclusion

Overall, the results so far suggest that the game-based approach can be used to assess early mathematical competencies. Moreover, they suggest that the HoN is a game-based assessment, which can reliably and effectively evaluate early mathematical skills and detect possible cases at risk for developing math difficulties. The HoN represents an attractive option for preschool children in comparison to standard preschool testing procedures. It is an innovative screening tool that combines requirements of screening procedures with the positive characteristics of board games. Screening procedures provide identification of a possible risk, which is linked to a recommendation for support. According to the findings, the HoN screening could provide reliable support to early childhood professionals in a time and resource efficient, and also enjoyable naturalistic way. The HoN could be easily integrated into the work that preschool educators already do. By eliminating or reducing the deficits in the precursor skills successfully identified by the screening, the chances of at-risk children to later acquire mathematical competencies can be increased through selective prevention for those at risk.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics statement

This study involves human subjects and has been approved by the Ethics Committe of the Catholic University of Eichstätt-Ingolstadt – Faculty of Philosophy and Education: Prof. Dr. Marco Steinhauser (Chair), Dr Valérie Berner, Dr. Martin E. Maier, Jun.-Prof. Dr. Christina Pfeuffer, and Prof. Dr. Michael Zehetleitner. The studies were conducted in accordance with the local legislation and institutional requirements. Written informed consent for participation in this study was provided by the participants’ legal guardians.

Author contributions

M-AC: Conceptualization, Data curation, Formal analysis, Funding acquisition, Methodology, Project administration, Validation, Visualization, Writing – original draft, Writing – review & editing. JS: Conceptualization, Data curation, Methodology, Project administration, Writing – review & editing. GR: Writing – review & editing. KS-S: Conceptualization, Methodology, Resources, Supervision, Writing – review & editing.

Funding

The author(s) declare financial support was received for the research, authorship, and/or publication of this article. Funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) – Project number 512640851.

Acknowledgments

We would like to thank all children, parents, and early childhood professionals who participated in our studies. A special thank you goes to all students involved in our research, as well as to work colleagues and fellow researchers for their support and collegial advice.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

American Psychiatric Association (2013). Diagnostic and statistical manual of mental disorders, 5th Edn. Washington, DC: American Psychological Association.

Google Scholar

Anders, Y., Grosse, C., Rossbach, H., Ebert, S., and Weinert, S. (2013). Preschool and primary school influences on the development of children’s early numeracy skills between the ages of 3 and 7 years in Germany. Sch. Effect. Sch. Improv. 24, 195–211. doi: 10.1080/09243453.2012.749794

Crossref Full Text | Google Scholar

Aunola, K., Leskinen, E., Lerkkanen, M., and Nurmi, J. (2004). Developmental dynamics of math performance from preschool to grade 2. J. Educ. Psychol. 96, 699–713. doi: 10.1037/0022-0663.96.4.699

Crossref Full Text | Google Scholar

Bakker, M., Torbeyns, J., Verschaffel, L., and DeSmedt, B. (2022). Longitudinal pathways of numerical abilities in preschool: Cognitive and environmental correlates and relation to primary school mathematics achievement. Dev. Psychol. 59, 442–459. doi: 10.1037/dev0001491

PubMed Abstract | Crossref Full Text | Google Scholar

Bayeck, R. Y. (2020). Examining board gameplay and learning: A multidisciplinary review of recent research. Simul. Gam. 51, 411–431. doi: 10.1177/1046878119901286

Crossref Full Text | Google Scholar

Bochicchio, V., Keith, K., Montero, I., Scandurra, C., and Winsler, A. (2022). Digital media inhibit self-regulatory private speech use in preschool children: The “digital bubble effect”. Cogn. Dev. 62:101180. doi: 10.1016/j.cogdev.2022.101180

Crossref Full Text | Google Scholar

Boone, W. J. (2016). Rasch analysis for instrument development: Why, when, and how? CBE Life Sci. Educ. 15:rm4. doi: 10.1187/cbe.16-04-0148

PubMed Abstract | Crossref Full Text | Google Scholar

Boone, W. J., Staver, J. R., and Yale, M. S. (2014). Rasch analysis in the human sciences. Dordrecht: Springer Netherlands.

Google Scholar

Cahoon, A., Gilmore, C., and Simms, V. (2021). Developmental pathways of early numerical skills during the preschool to school transition. Learn. Instruct. 75:101484. doi: 10.1016/j.learninstruc.2021.101484

Crossref Full Text | Google Scholar

Chu, F. W., vanMarle, K., Rouder, J. N., and Geary, D. C. (2018). Children’s early understanding of number predicts their later problem-solving sophistication in addition. J. Exp. Child Psychol. 169, 73–92. doi: 10.1016/j.jecp.2017.12.010

PubMed Abstract | Crossref Full Text | Google Scholar

Cohen, J. (1988). Statistical power analysis for the behavioral sciences, 2nd Edn. Hillsdale, NJ: Routledge.

Google Scholar

Deutsche Gesellschaft für Kinder- und Jugendmedizin e.V (2022). Leitlinie zur Prävention dysregulierten Bildschirmmediengebrauchs in der Kindheit und Jugend [SK2-guideline: Guideline for the Prevention of dysregulated screen media use in childhood and adolescence]. Berlin: Deutsche Gesellschaft für Kinder- und Jugendmedizin e.V. Available online at: https://register.awmf.org/de/leitlinien/detail/027-075.

Google Scholar

Deutsche Gesellschaft für Kinder- und Jugendpsychiatrie, Psychosomatik und Psychotherapie e.V (2023). S3-Leitlinie: Diagnostik und behandlung der rechenstörung [S3-guideline: diagnosis and treatment of dyscalculia]. München: Deutsche Gesellschaft für Kinder- und Jugendpsychiatrie, Psychosomatik und Psychotherapie. Available online at: https://register.awmf.org/de/leitlinien/detail/028-046

Google Scholar

Dienes, Z. (2014). Using bayes to get the most out of non-significant results. Front. Psychol. 5:781. doi: 10.3389/fpsyg.2014.00781

PubMed Abstract | Crossref Full Text | Google Scholar

Ehlert, A., and Fritz, A. 2016. “MARKO-T” - Ein mathematisches Förderprogramm evaluiert an Kindern mit dem Förderschwerpunkt Lernen. [“MARKO-T” - a mathematical support programme evaluated on children with learning difficulties].” In Förderprogramme für Vor- und grundschule, eds M. Hasselhorn and W. Schneider (Göttingen: Hogrefe), 29–48.

Google Scholar

Elofsson, J., Gustafson, S., Samuelsson, J., and Träff, U. (2016). Playing number board games supports 5-year-old children’s early mathematical development. J. Math. Behav. 43, 134–147. doi: 10.1016/j.jmathb.2016.07.003

Crossref Full Text | Google Scholar

Endlich, D., Berger, N., Küspert, P., Lenhard, W., Marx, P., Schneider, W., et al. (2016). Würzburger Vorschultest: Erfassung schriftsprachlicher und mathematischer (Vorläufer-)Fertigkeiten und sprachlicher Kompetenzen im letzten Kindergartenjahr: [Würzburg preschool test: Assessment of written and mathematical (precursor) skills and language competencies in the last year of kindergarten]. Göttingen: Hogrefe.

Google Scholar

Faul, F., Erdfelder, E., Buchner, A., and Lang, A. (2009). Statistical power analyses using g*power 3.1: Tests for correlation and regression analyses. Behav. Res. Methods 41, 1149–1160. doi: 10.3758/BRM.41.4.1149

PubMed Abstract | Crossref Full Text | Google Scholar

Faul, F., Erdfelder, E., Lang, A., and Buchner, A. (2007). G*Power 3: A flexible statistical power analysis program for the social, behavioral, and biomedical sciences. Behav. Res. Methods 39, 175–191. doi: 10.3758/BF03193146

PubMed Abstract | Crossref Full Text | Google Scholar

Fischbach, A., Schuchardt, K., Brandenburg, J., Klesczewski, J., Balke-Melcher, C., Schmidt, C., et al. (2013). “Prävalenz von Lernschwächen und Lernstörungen: Zur Bedeutung der Diagnosekriterien.” [Prevalence of poor learners and children with learning disorders: Investigating the role of diagnostic criteria]. Lern. Lernstörungen 2, 65–76. doi: 10.1024/2235-0977/a000035

Crossref Full Text | Google Scholar

Fisher, K., Hirsh-Pasek, K., and Golinkoff, R. M. (2012). “Fostering mathematical thinking through playful learning,” in Contemporary debates in childhood education and development, eds S. Suggate and E. Reese (London: Routledge), 95–106.

Google Scholar

Fritz, A., and Ricken, G. (2008). Rechenschwäche [Dyscalculia], 1st Edn. München: Ernst Reinhardt Verlag.

Google Scholar

Fritz, A., Ehlert, A., and Leutner, D. (2018). Arithmetische Konzepte aus kognitiv-entwicklungspsychologischer Sicht [Arithmetic concepts from a cognitive-developmental psychological perspective]. J. Math. Didaktik 39, 7–41. doi: 10.1007/s13138-018-0131-6

Crossref Full Text | Google Scholar

Gasteiger, H., and Moeller, K. (2021). Fostering early numerical competencies by playing conventional board games. J. Exp. Child Psychol. 204:105060. doi: 10.1016/j.jecp.2020.105060

PubMed Abstract | Crossref Full Text | Google Scholar

Gelman, R. (2006). Young natural-number arithmeticians. Curr. Direct. Psychol. Sci. 15, 193–197. doi: 10.1111/j.1467-8721.2006.00434.x

Crossref Full Text | Google Scholar

Gerlach, M., Fritz, A., and Leutner, D. (2013). Mathematik- und Rechenkonzepte im Vor- und Grundschulalter-Training (MARKO-T) [Mathematics and numeracy concepts in pre-school and primary school age training (MARKO-T)], 1st Edn. Göttingen: Hogrefe.

Google Scholar

Ginsburg, H. P., Pappas, S., and Seo, K. H. (2001). “Everyday mathematical knowledge: Asking young children what is developmentally appropriate,” in Psychological perspectives on early childhood education: Reframing dilemmas in research and practice. The Rutgers invitational symposium on education series, ed. S. L. Golbeck (New Jersey, Lawrence Erlbaum Associates Inc), 181–219.

Google Scholar

Gloor, N. (2023). Erfassung von numerischen Kompetenzen im Kindergarten. [Assessment of numerical skills in kindergarten]. Lernen und Lernstörungen 12, 175–187. doi: 10.1024/2235-0977/a000409

Crossref Full Text | Google Scholar

Harter, S., and Pike, R. (1984). The pictorial scale of perceived competence and social acceptance for young children. Child Dev. 55, 1969–1982. doi: 10.2307/1129772

Crossref Full Text | Google Scholar

Hauser, B., Vogt, F., Stebler, R., and Rechsteiner, K. (2014). “Förderung früher mathematischer Kompetenzen: Spielintegriert oder trainingsbasiert.” [Promotion of early mathematical competences: Game-integrated or training-based]. Frühe Bild. 3, 139–145. doi: 10.1026/2191-9186/a000144

Crossref Full Text | Google Scholar

Hirsh-Pasek, K., Michnick, R., Berk, L. E., and Singer, D. G. (2009). A mandate for playful learning in preschool: Presenting the evidence. Oxford: Oxford University Press.

Google Scholar

IBM Corp (2022). IBM SPSS statistics. New York, NY: IBM Corp.

Google Scholar

Jansen, H., Mannhaupt, G., Marx, H., and Skowronek, H. (2002). Bielefelder Screening zur Früherkennung von Lese-Rechtschreibschwierigkeiten (BISC) [Bielefeld screening for the early detection of reading and spelling difficulties (BISC)], 2nd Edn. Göttingen: Hogrefe.

Google Scholar

JASP Team (2024). JASP. Amsterdam: J Team.

Google Scholar

Jeffreys, H. (1998). “The theory of probability,” in Oxford classic texts in the physical sciences, 3rd Edn. Oxford: Oxford University Press.

Google Scholar

Jörns, C., Schuchardt, K., Mähler, C., and Grube, D. (2013). “Alltagsintegrierte Förderung numerischer Kompetenzen im Kindergarten.” [Everyday integrated promotion of numerical competences in kindergarten]. Frühe Bild. 2, 84–91. doi: 10.1026/2191-9186/a000088

Crossref Full Text | Google Scholar

Krajewski, K. (2018a). Vorhersage von Rechenschwächen in der Grundschule. Studien zur Kindheits- und Jugendforschung 29 [Predicting dyscalculia in primary school]. 2nd Edn. Hamburg: Dr. Kovac.

Google Scholar

Krajewski, K. (2018b). MBK-0: Test mathematischer Basiskompetenzen im Kindergartenalter [MBK-0: Test of basic mathematical competencies at kindergarten age], 1st Edn. Göttingen: Hogrefe.

Google Scholar

Krajewski, K., and Schneider, W. (2006). “Mathematische Vorläuferfertigkeiten im Vorschulalter und ihre Vorhersagekraft für die Mathematikleistung bis zum Ende der Grundschulzeit.” [Preschool mathematical precursor skills and their predictive power for mathematics achievement by the end of the primary school years.]. Psychol. Erziehung Unterricht 53, 246–262.

Google Scholar

Krajewski, K., and Schneider, W. (2009). Early development of quantity to number-word linkage as a precursor of mathematical school achievement and mathematical difficulties: Findings from a four-year longitudinal study. Learn. Instruct. 19, 513–526. doi: 10.1016/j.learninstruc.2008.10.002

Crossref Full Text | Google Scholar

Lange, A. A., Brenneman, K., and Sareh, N. (2021). Using number games to support mathematical learning in preschool and home environments. Early Educ. Dev. 32, 459–479. doi: 10.1080/10409289.2020.1778386

Crossref Full Text | Google Scholar

Laski, E. V., and Siegler, R. S. (2014). Learning from number board games: You learn what you encode. Dev. Psychol. 50, 853–864. doi: 10.1037/a0034321

PubMed Abstract | Crossref Full Text | Google Scholar

Linacre, J. M. (2024a). Winsteps^® Rasch measurement computer program. Portland, OR: Winsteps.com. Available online at: https://www.winsteps.com/ (accessed on January 20, 2024).

Google Scholar

Linacre, J. M. (2024b). Winsteps^® Rasch Measurement Computer Program User’s Guide: Version 5.7.0. Portland, OR: Winsteps.com.

Google Scholar

Linebarger, D. L., Barr, R., Matthew, A., and Piotowski, J. (2014). Associations between parenting, media use, cumulative risk and children’s executive functioning. J. Dev. Behav. Pediatr. 35, 367–377. doi: 10.1097/DBP.0000000000000069

PubMed Abstract | Crossref Full Text | Google Scholar

Lu, Y., Li, Q., Patrick, H., and Mantzicopoulos, P. (2021). Math gives me a tummy ache!” Mathematics anxiety in kindergarten. J. Exp. Educ. 89, 362–378. doi: 10.1080/00220973.2019.1680518

Crossref Full Text | Google Scholar

Lumsden, J., Edwards, E. A., Lawrence, N. S., Coyle, D., and Munafò, M. R. (2016). Gamification of cognitive assessment and cognitive training: A systematic review of applications and efficacy. JMIR Ser. Games 4:e11. doi: 10.2196/games.5888

PubMed Abstract | Crossref Full Text | Google Scholar

Mähler, C., Grube, D., and Schuchardt, K. (2017). Interindividuelle Unterschiede kognitiver Kompetenzen als Herausforderung für die frühkindliche Bildung. [Inter-individual differences in cognitive competences as a challenge for early childhood education]. Pädagogische Rundschau 71, 349–366. doi: 10.3726/PR2017-3/4_349

Crossref Full Text | Google Scholar

Marx, H. (1992). “Methodische und inhaltliche Argumente für und wider eine frühe Identifikation und Prädiktion von Lese-Rechtschreibschwierigkeiten.” [Methodological and substantive arguments for and against early identification and prediction of reading and spelling difficulties]. Diagnostica 38, 249–268.

Google Scholar

Marx, P., and Lenhard, W. (2011). “Diagnostische Merkmale von Screening-Verfahren zur Früherkennung möglicher Probleme beim Schriftspracherwerb [Diagnostic features of screening procedures for the early detection of possible problems in the acquisition of written language],” in Frühprognose schulischer Kompetenzen, eds H. Marcus and W. Schneider (Göttingen: Hogrefe Verlag), 68–84.

Google Scholar

Mekler, E. D., Brühlmann, F., Opwis, K., and Tuch, A. N. (2013). “Do Points, levels and leaderboards harm intrinsic motivation?” in Gamification 2013: Proceedings of the 1st international conference on gameful design, research, and applications: October 2-4, 2013, Stratford, Ontario, Canada, eds H. Kevin, N. Randall, and L. E. Nacke (New York, NY: ACM), 66–73.

Google Scholar

Milton Bradley Company (1978). Chutes and ladders. Pawtucket, RI: Hasbro.

Google Scholar

Ministerium für Kultus, Jugend und Sport Baden-Württemberg (2022). ALLES ZÄHLT! Mathe im Kiga-Alltag: Begleitheft. Wissenschaftlicher Hintergrund für Fachkräfte, Multiplikatorinnen und Multiplikatoren im Kindheitspädagogischen Arbeitsfeld. [EVERYTHING COUNTS! Maths in everyday life at the kindergarten]. Stuttgart: Ministerium für Kultus, Jugend und Sport Baden-Württemberg.

Google Scholar

Moosbrugger, H., and Kelava, A. (2020). Testtheorie und Fragebogenkonstruktion. [Test theory and questionnaire construction]. Heidelberg: Springer.

Google Scholar

Moraske, S., Penrose, A., Wyschkon, A., Kohn, J., Rauscher, L., von Aster, M., et al. (2018). “Prävention von Rechenstörungen: Kurz- und mittelfristige Effekte einer Förderung der mathematischen Kompetenzen bei Risikokindern im Vorschulalter.” [Prevention of dyscalculia: Short– and medium-term effects of promoting mathematical competencies in at-risk preschool children]. Kindheit Entwicklung 27, 31–42. doi: 10.1026/0942-5403/a000242

Crossref Full Text | Google Scholar

Morey, R. D., and Rouder, J. N. (2011). Bayes factor approaches for testing interval null hypotheses. Psychol. Methods 16, 406–419. doi: 10.1037/a0024377

PubMed Abstract | Crossref Full Text | Google Scholar

Morgan, P., Farkas, G., and Qiong, W. (2009). Five-year growth trajectories of kindergarten children with learning difficulties in mathematics. J. Learn. Disabil. 42, 306–321. doi: 10.1177/0022219408331037

PubMed Abstract | Crossref Full Text | Google Scholar

Moser Opitz, E., and Ramseier, E. (2012). “Rechenschwach oder nicht Rechenschwach?” [Poor at maths or not poor at maths?]. Lern. Lernstörungen 1, 99–117. doi: 10.1024/2235-0977/a000013

Crossref Full Text | Google Scholar

Ninaus, M., Kiili, K., McMullen, J., and Moeller, K. (2017). Assessing fraction knowledge by a digital game. Comput. Hum. Behav. 70, 197–206. doi: 10.1016/j.chb.2017.01.004

Crossref Full Text | Google Scholar

Ninaus, M., Pereira, G., Stefitz, R., Prada, R., Paiva, A., Neuper, C., et al. (2015). Game elements improve performance in a working memory training task. IJSG 2:156. doi: 10.17083/ijsg.v2i1.60

Crossref Full Text | Google Scholar

Okanda, M., and Itakura, S. (2010). When do children exhibit a “Yes” bias? Child Dev. 81, 568–580. doi: 10.1111/j.1467-8624.2009.01416.x

PubMed Abstract | Crossref Full Text | Google Scholar

Paulus, F. W., and Gerstner, I. (2023). Vorschulkinder und digitale Medien in der zweiten Moderne.” [Preschool children and digital media in the second modern age]. Pädiatr. Pädol. 2, 99–102. doi: 10.1007/s00608-023-01111-2

Crossref Full Text | Google Scholar

Purpura, D. J., and Lonigan, C. J. (2013). Informal numeracy skills: The structure and relations among numbering, relations, and arithmetic operations in preschool. Am. Educ. Res. J. 50, 178–209. doi: 10.3102/0002831212465332

PubMed Abstract | Crossref Full Text | Google Scholar

Purpura, D. J., Day, E., Napoli, A. R., and Hart, S. A. (2017). Identifying domain-general and domain-specific predictors of low mathematics performance: A classification and regression tree analysis. J. Num. Cogn. 3, 365–399. doi: 10.5964/jnc.v3i2.53

PubMed Abstract | Crossref Full Text | Google Scholar

Radesky, J. S., Kaciroti, N., Weeks, H. M., Schaller, A., and Miller, A. L. (2023). Longitudinal associations between use of mobile devices for calming and emotional reactivity and executive functioning in children aged 3 to 5 years. JAMA Pediatr. 177, 62–70. doi: 10.1001/jamapediatrics.2022.4793

PubMed Abstract | Crossref Full Text | Google Scholar

Ramani, G. B., Siegler, R. S., and Hitti, A. (2012). Taking it to the classroom: Number board games as a small group learning activity. J. Educ. Psychol. 104, 661–672. doi: 10.1037/a0028995

Crossref Full Text | Google Scholar

Ricken, G., Fritz, A., and Balzer, L. (2011). Mathematik und Rechnen - Test zur Erfassung von Konzepten im Vorschulalter. Ein Beispiel für einen niveauorientierten Ansatz. [Mathematics and arithmetic –test for the acquisition of concepts in preschool age (MARKO-D). An example of a level-oriented approach]. Empirische Sonderpädagogik 3, 256–271. doi: 10.25656/01:9327

Crossref Full Text | Google Scholar

Ricken, G., Fritz, A., and Balzer, L. (2013). Mathematik- und Rechenkonzepte im Vorschulalter – Diagnose (MARKO-D) [Preschool mathematics and numeracy concepts - Diagnosis (MARKO-D)], 1st Edn. Göttingen: Hogrefe.

Google Scholar

Roux, S., Kammermeyer, G., Donie, C., and Kinnunen, M. (2010). Bildskala zur Erfassung von Lernfreude und Selbstkonzept in Mathematik und Schriftsprache bei Vorschulkindern (BSLS-MS) [Picture scale for the assessment of learning enjoyment and self-concept in preschool mathematics and language abilities]. Koblenz: University of Koblenz-Landau.

Google Scholar

Schuchardt, K., Fischbach, A., Balke-Melcher, C., and Mähler, C. (2015). “Die Komorbidität von Lernschwierigkeiten mit ADHS-Symptomen im Grundschulalter.” [The comorbidity of learning difficulties and ADHD symptoms in primary-school-age children]. Z. Kinder Jugendpsychiatr. Psychother. 43, 185–193. doi: 10.1024/1422-4917/a000352

PubMed Abstract | Crossref Full Text | Google Scholar

Siegler, R. S. (1995). How does change occur: A microgenetic study of number conservation. Cogn. Psychol. 28, 225–273. doi: 10.1006/cogp.1995.1006

PubMed Abstract | Crossref Full Text | Google Scholar

Siegler, R. S., and Ramani, G. B. (2009). “Playing linear number board games–but not circular ones–improves low-income preschoolers’ numerical understanding. J. Educ. Psychol. 101, 545–560. doi: 10.1037/a0014239

Crossref Full Text | Google Scholar

Skillen, J., Berner, V.-D., and Seitz-Stein, K. (2018b). The rule counts! Acquisition of mathematical competencies with a number board game. J. Educ. Res. 111, 554–563. doi: 10.1080/00220671.2017.1313187

Crossref Full Text | Google Scholar

Skillen, J., Berner, V.-D., Ricken, G., and Seitz-Stein, K. (2018a). Förderung basisnumerischer Kompetenzen mit einem regelbasierten Spiel im Einzel– und Gruppensetting.” [Promoting basic numerical skills with a rule-based game in individual and group settings]. Frühe Bild. 7, 144–151. doi: 10.1026/2191-9186/a000381

Crossref Full Text | Google Scholar

Skillen, J., Ricken, G., and Seitz-Stein, K. (2023). Game-based assessment of early mathematical competencies –a pilot study. Empirische Sonderpädagogik 1, 38–60. doi: 10.25656/01:27183

Crossref Full Text | Google Scholar

Stern, E. (2009). “The development of mathematical competencies: Sources of individual differences and their developmental trajectories,” in Human development from early childhood to early adulthood, eds S. Wolfgang and M. Bullock (Milton Park: Taylor and Francis), 221–237.

Google Scholar

Textor, M. R. (2006). Bildung im Kindergarten: Zur Förderung der kognitiven Entwicklung. [Education in the kindergarten: On promoting cognitive development]. Münster: Monsenstein und Vannerdat.

Google Scholar

Thorell, L. B., Burén, J., Wiman, J. S., Sandberg, D., and Nutley, S. B. (2022). Longitudinal associations between digital media use and ADHD symptoms in children and adolescents: A systematic literature review. Eur. Child Adolesc. Psychiatry doi: 10.1007/s00787-022-02130-3 [Epub ahead of print].

PubMed Abstract | Crossref Full Text | Google Scholar

Tröster, H. (2009). Früherkennung im Kindes- und Jugendalter: Strategien bei Entwicklungs-, Lern- und Verhaltensstörungen [Early diagnosis in childhood and adolescence: Strategies for developmental, learning and behavioural disorders], 1st Edn. Göttingen: Hogrefe.

Google Scholar

van Doorn, J., van den Bergh, D., Böhm, U., Dablander, F., Derks, K., Draws, T., et al. (2021). The JASP guidelines for conducting and reporting a Bayesian analysis. Psychon. Bull. Rev. 28, 813–826. doi: 10.3758/s13423-020-01798-5

PubMed Abstract | Crossref Full Text | Google Scholar

Vogt, F., Hauser, B., Stebler, R., Rechsteiner, K., and Urech, C. (2018). Learning through play – pedagogy and learning outcomes in early childhood mathematics. Eur. Early Child. Educ. Res. J. 26, 589–603. doi: 10.1080/1350293X.2018.1487160

Crossref Full Text | Google Scholar

Wittmann, E. C. (2001). “Ein alternativer ansatz zur förderung “rechenschwacher” Kinder, [An alternative approach to supporting “maths-deficient” children]” in Beiträge zum mathematikunterricht, ed. K. Gabriele (Berlin: Franzbecker), 660–663.

Google Scholar

World Health Organization (2019). Guidelines on physical activity, sedentary behaviour, and sleep for children under 5 years of age. Geneva: World Health Organization.

Google Scholar

World Health Organization (2019/2021). International classification of diseases, eleventh revision (ICD-11), 11th Edn. Geneva: World Health Organization.

Google Scholar

Wright, B. D., and Linacre, J. M. (1994). Reasonable mean-square fit values. Rasch Meas. Trans. 8:370.

Google Scholar

Wyschkon, A. (2015). “Erfassung und prognostische Bedeutung der nonverbalen Intelligenz im Vorschulalter: Analyse vorliegender Testverfahren und Kurzvorstellung des PIT-VA”. [Assessment and prognostic significance of non-verbal intelligence at pre-school age: analysis of existing test procedures and brief presentation of the PIT-VA], in Diagnostik im vorschulalter, eds E. Günter, M. Hasselhorn, and W. Schneider (Göttingen: Hogrefe), 1–11.

Google Scholar

Wyschkon, A., Kohn, J., Ballaschk, K., and Esser, G. (2009). Sind Rechenstörungen genau so häufig wie Lese-Rechtschreibstörungen?” [Is a specific disorder of arithmetic skills as common as reading/spelling disorder?]. Z. Kinder Jugendpsychiatr. Psychother. 37, 499–510. doi: 10.1024/1422-4917.37.6.499

PubMed Abstract | Crossref Full Text | Google Scholar