- Department of Mathematics, Science and Technology Education, Faculty of Education, University of Zululand, KwaDlangezwa, South Africa
Introduction: Mathematics achievement is the level of knowledge, proficiency or skill attained by undergraduates in mathematics, often explained by grade point average or cumulative grade point average. Many factors could either improve or deter this achievement. In this study, we assess the factors that predict the academic achievement of mathematics undergraduates through structural equation model (SEM).
Methods: A survey was conducted with a sample of 411 randomly selected undergraduates from the Department of Mathematics in public universities in Southwestern Nigeria who were studying mathematical science or mathematics education. An adapted questionnaire on a 5-point Likert scale hosted online through Google Forms was used for the survey. The data gathered was analyzed through SEM with the aid of SmartPLS 4.
Results: The factors examined, mathematics self-efficacy, attitude, motivation and study habits, collectively accounted for 59.4% of the observed variance in the academic achievement of mathematics undergraduates. Similarly, self-efficacy and study habits accounted for 47.7% of the observed variance in academic motivation, while study habits, motivation and self-efficacy accounted for 67.8% of the observed variance in academic attitudes.
Discussion: Among the predictors, study habit has the most predictive influence on academic achievement, followed by mathematics self-efficacy and academic motivation, while academic attitude has the least influence on academic achievement. Hence, academics and institutions should develop and implement various instructional interventions, such as mentoring, monitoring programs and feedback supports, to help students improve their study habits and build their mathematics self-efficacy.
Introduction
Mathematics is the foundational link connecting science and technology, enabling the innovation that drives a nation’s progress. A mathematical framework often makes every breakthrough in science and technology possible. Due to its multifaceted nature, mathematics is considered an essential discipline for any nation that relies on science and technology. For its richness, the discipline became a foundation upon which other science disciplines may stand. Mathematics is the bedrock of sciences and technology, and no nation can hope to achieve any measure of scientific and technological advancement without adequately exploring it (Asanre et al., 2024). It helps in the development of models used in science and technology. Despite the relevance of mathematics to the advancement of society, there has been a report of spatial and unimpressive enrolment rates in Nigerian universities (Salman et al., 2011) and dropout due to low academic achievement among mathematics undergraduates (Abah, 2018).
Undergraduate mathematics programs in Nigerian universities encompass both mathematical sciences and mathematics education, reflecting a varied and demanding academic situation. The mathematical sciences focus on pure and applied mathematics, equipping students with advanced problem-solving skills and analytical thinking essential for various fields. Core courses being exposed to include Calculus, Linear Algebra, Differential Equations, Abstract Algebra, Real Analysis, Probability and Statistics, Numerical Methods, and Mathematical Modeling. On the other hand, mathematics education programs emphasize pedagogical strategies, curriculum development, and educational psychology, preparing future educators to teach mathematics effectively at primary and secondary level of education. Key courses in addition to some of the mathematical science courses in this discipline often include Teaching Methods in Mathematics, Curriculum Development in Mathematics, Educational Psychology, Assessment and Evaluation in Mathematics, Technology in Mathematics Education, History of Mathematics, and contemporary issues in Mathematics Education. The curriculum in both programs is designed to foster critical thinking and practical application of mathematical concepts. As a result, these programs aim to produce graduates who are proficient in mathematics and capable of contributing to the improvement of mathematics education in Nigeria. What individual undergraduate achieve academically then could be explained by how they perform in the various courses being exposed to during their program.
Academic achievement explains how well an undergraduate does in school or how much they learn, reflected in their Grade Point Average (GPA) at the end of a semester or Cumulative Grade Point Average (CGPA) by the end of the session. However, studies have shown that this academic achievement has been unimpressive for many reasons, which are evident in the report published by the National Universities Commission (2019), which reflected that in the year reported, only 1.47% of undergraduates enrolled in mathematics (mathematics science or mathematics education) and from this number, 2.83% supposed to have graduated. While considering the graduation rate of the total enrolled students, Mathematics undergraduates made 1.18% of the output. Studies have identified factors that influence undergraduates’ achievement in mathematics, among which are self-efficacy (Zakariya, 2021), attitude (Almaraz-López et al., 2023), motivation (Lishchynska et al., 2023), study habit (Charles-Ogan and Alamina, 2014), self-concept (Arens et al., 2022), confidence (Ercikan et al., 2005) among others. There is no study that has investigated the combined influence of all the identified factors on undergraduate mathematics students’ academic achievement particularly through structural equation modeling. In this study, our focus is on self-efficacy, motivation, attitude, and study habits, seeking their influence on mathematics undergraduates’ academic achievement. Mathematic academic achievement, as used in this study, is the CGPA of the mathematics undergraduates. The reason for focusing on these factors is to addresses the gap in existing literature by specifically examining the combined and individual influences of self-efficacy, motivation, attitude, and study habits on the academic achievement (CGPA) of mathematics undergraduates, providing a comprehensive understanding of how these factors interact to influence student achievement in this discipline.
Mathematics self-efficacy is the undergraduates’ belief in their capabilities to succeed in mathematics courses. It has been observed that many mathematics undergraduates in some Nigerian universities initially were not willing to offer the course, and most often, students in this category appear to struggle with the course as they advance, lacking belief in themselves to navigate through with outstanding performance. Self-efficacy beliefs in one area may influence beliefs in another. Therefore, an increase in mathematics self-efficacy might function as a resilience element to reduce depressive-related issues that could affect students’ performance (Falebita and Olofin, 2020; Sachitra and Bandara, 2017; Schunk, 1989). Hence, academics could play a role in boosting or draining mathematics undergraduates’ self-efficacy, which Bandura (1986) suggested is more straightforward to achieve. However, self-efficacy has a way of influencing an individual’s attitude.
Attitude toward mathematics is the set of beliefs, feelings and behavioral intentions about mathematics. Attitude does not come alone; it is often shaped by the complex interplay of individual, educational, and sociological factors (Jansen et al., 2016). In other words, it is an interaction between an individual, the learning, and the environment. Undergraduates’ attitudes toward mathematics have been found to be sharpened by factors such as prior mathematical experiences, beliefs, teaching approach, and parental influence (Wiebe et al., 2018); thus, the attitude demonstrated toward mathematics could be negative or positive. Attitudes such as unwillingness to engage in learning or participating in instructional activities constitute negative attitudes, while willingness to be involved in learning activities, commitment to studying, and belief in achieving specific goals driven toward academic success make positive attitudes.
Mathematics study habits are the consistent actions, behaviors, and techniques students use to grasp., comprehend, and remember mathematics content. It is generally believed that students have to prepare before going for mathematics examination in order to pass. For mathematics, consistent efforts may be required to go through the content so that it can be retained for efficient usage. Developing good study habits will help in this regard. Studies have shown that good study habits promote good academic achievement (Capuno et al., 2019; Odiri, 2015; Sakirudeen and Sanni, 2017). However, the question that comes to mind is: can an unmotivated student develop good study habits or attain good academic achievement?
Mathematics motivation is the internal and external elements influencing a person’s behavior, energy, and orientation toward fulfilling a specific goal or activity in mathematics. Whether it be the urge to succeed, the will to learn, or the need to reach, it drives someone to act in relation to learning mathematics contents. Motivation may be extrinsic, which results from outside incentives, recognition, or pressure, or intrinsic, which comes from inside the person, from a genuine interest or a feeling of personal fulfillment (Herges et al., 2017; Jansen et al., 2016; Lishchynska et al., 2023). Knowing the function of motivation is essential in an academic environment, as it guides teaching plans, learning environments, and interventions meant to improve students’ engagement and learning outcomes, most especially academic achievement.
For educational researchers and policymakers, undergraduate students’ academic achievement, especially in mathematics, is of great concern. Therefore, providing support systems to improve student achievement depends on an awareness or understanding of the main factors influencing mathematical achievement at the undergraduate level. In this study, we used Structural Equation Modeling (SEM) to examine the effects of selected factors on academic achievement in undergraduate mathematics. These factors include students’ attitudes, self-efficacy, study habits, and motivation. SEM is a method well-known in educational research for investigating the intricate interactions among many predictive variables and academic achievement. This method allows researchers to examine the direct and indirect impacts of several factors concurrently, helping to provide a more complete knowledge of the fundamental processes influencing student achievement (McCoach, 2003).
Literature review and study framework
Theoretical framework
The Expectancy-Value Theory (EVT), initially theorized by Atkinson (1957) and later expanded by Eccles et al. (1983), posits that students’ beliefs about their abilities and the value they place on tasks significantly influence their motivation and academic achievement. This makes EVT an essential framework for examining the factors that affect mathematics undergraduates’ success. At the core of EVT are two key components: students’ anticipation of success and the subjective value they attach to tasks. These elements interact dynamically, shaping students’ engagement, effort, and perseverance in academic settings. According to Eccles and Wigfield (2002), for example, students who believe they can succeed (self-efficacy) and find a task meaningful (attitude) are more likely to produce better results. This paradigm provides a complete lens through which we might examine how attitude, study habits, motivation, and self-efficacy taken together affect academic achievement. Furthermore, attitude and motivation bring complexity into this conversation covering both intrinsic and extrinsic aspects of EVT’s value component. Students motivated by extrinsic goals like career aspirations as well as by intrinsic elements like a real passion in learning often show more involvement and endurance (Deci and Ryan, 1985; Wu and Fan, 2017). Positive attitudes toward learning further enhance both anticipation and value, creating a virtuous cycle that fosters improved academic success. Research by Pintrich and De Groot (1990) reinforces this notion, revealing that students with positive attitudes and strong motivation are more likely to excel academically, thus underscoring the critical role of EVT in educational contexts. Together, these characteristics reveals the multifaceted nature of EVT in explaining academic achievement and offer valuable insights for educators aiming to enhance student success.
Mathematics self-efficacy
The desire of undergraduates to study mathematics is mostly shaped by their beliefs in their capabilities, which may drive them toward excellence or sink them into deep self-doubt and underachievement. Studies have shown that a positive relationship exists between students’ academic self-efficacy and achievement in mathematics among undergraduates. The have been scanty literature on mathematics self-efficacy as most study considered academic self-efficacy. According to Turgut (2013), students’ academic self-efficacy beliefs were greatly influenced by their academic performance and grade level. Similarly, Palestro and Jameson (2020) reveal that mathematics self-efficacy mediates the relationship between mathematics anxiety and achievement. For Zakariya (2021), knowledge and self-efficacy contributed 30%, while for Negara et al. (2021), self-efficacy contributed 14.8% to the prediction of academic achievement in mathematics. These all point toward the direction that higher-achieving students had strong self-efficacy beliefs about their capabilities. Regarding self-efficacy as an influencer of attitude toward mathematics, there has also been a consistent demonstration of a significant relationship between self-efficacy and attitude toward mathematics. For example, Akin and Kurbanoglu (2011) and Laranang and Bondoc (2020) studies reveal that students’ self-efficacy positively correlates to their academic attitude toward mathematics. The positive correlation suggests that a student with a positive self-efficacy belief would have a positive attitude toward mathematics. Also, research consistently suggests a significant relationship between self-efficacy and academic motivation. Arık (2019), Demi̇R (2024), and Lishchynska et al. (2023) all found that students’ self-efficacy significantly influences their academic motivation. This suggests that fostering self-efficacy will enhance students’ academic motivation. These findings highlight self-efficacy’s significant contributions to students’ academic achievement, attitude, and motivation. However, this study focuses specifically on mathematics self-efficacy as against general academic self-efficacy commonly found in literature. Its contribution to predicting mathematics undergraduates’ academic achievement, attitude, and motivation, as well as the model developed were considered in this study. We therefore hypothesized that:
H1: Mathematics self-efficacy predicts undergraduate’s academic achievement.
H2: Mathematics self-efficacy predicts undergraduate’s attitude toward mathematics.
H3: Mathematics self-efficacy predicts undergraduate’s mathematics motivation.
Students’ mathematics study habit
As the patterns of behavior form the basis upon which students’ mathematics ability is built, the habits and routines they develop in their mathematics study can mean the difference between soaring high academically and depressing failure. Studies show a strong correlation between study habits and mathematics academic achievement among students. The mathematics achievement of students with good study habits, especially those who spend more time, solving problems and maintain a high concentration level, usually improves (Charles-Ogan and Alamina, 2014; Odiri, 2015). It is important to state here that most literature focus on general study habit without considering mathematics study habit. According to Alva (2017), study habits were clearly proven to be a major predictor of undergraduate students’ achievement in mathematics. Particularly in early phases, students must be helped to develop good study habits mostly by including the instruction of good study habits in the school curriculum, which, when maintained, will help such individual students throughout their academic endeavors (Charles-Ogan and Alamina, 2014). Also, Hashim et al. (2022) found a significant relationship between undergraduate students’ study habits and attitudes toward mathematics. This explains how good study habits tend to bring out positive attitudes in undergraduate students toward mathematics. In addition, according to Mahmudah et al. (2021), study habits were found to relate to students’ academic motivation positively. These findings have shown how study habits shape students’ academic achievement, attitude, and motivation. However, in this study the focus is mainly on mathematics study habit which is more specific to the general study habit being considered in previous studies from literature. To consider the interactive effects of the factors on academic achievement, we hypothesized that:
H4: Mathematics study habits predict undergraduate’s achievement.
H5: Mathematics study habits predict undergraduate’s attitude toward mathematics.
H6: Mathematics study habits predict undergraduate’s mathematics motivation.
Students’ mathematics motivation
Motivation often comes with enthusiasm, energy and willingness to get things done. A student’s search for mathematical mastery might be motivated by as many different factors as the discipline itself, including a complex interaction of various forms of motivation. Studies on motivation and mathematics achievement among undergraduates have revealed intricate interactions. Motivation according to Yarin et al. (2022), has been shown to have a small but significant link with academic achievement in mathematics, while intrinsic motivation was identified as the best predictor. Lishchynska et al. (2023) further stressed that motivation is a significant factor influencing performance. On the contrary, Schoeffel et al. (2017), revealed that motivation did not influence software engineering students’ mathematics achievement. These results draw attention to the complicated character of motivation in mathematics education. In addition, Oyedeji (2017) and da Mata et al. (2012) reveals how different motivating factors affect students’ attitudes toward mathematics. Students’ attitudes directly benefit from intrinsic motivation, family environment, and teacher assistance (Oyedeji, 2017). This study considered mathematics undergraduates’ motivation as it influences their achievement and attitude. We therefore hypothesized that:
H7: Mathematics motivation predicts undergraduate’s achievement.
H8: Mathematics motivation predicts undergraduate’s attitude toward mathematics.
Attitude toward mathematics
Whether positive or negative, one’s attitude toward mathematics may significantly affect the course of one’s academic and personal activities and cast an extended shadow over one’s potential for achievement. Studies have shown that undergraduates’ performance is significantly influenced by their attitude toward mathematics. While negative attitudes were linked to poor achievement, Subia et al. (2018) revealed a significant link between positive attitudes and better academic achievement. Mazana et al. (2018) found a weak, though positively significant, link between attitude and academic achievement. This demonstrates the predictive power of attitude in determining or fostering students’ academic achievement in mathematics. These studies also highlight how important attitude is to undergraduate mathematical achievements. Our focus in this study is to explain the predictive power of attitude as the determiner of undergraduates’ academic achievement, as hypothesized below;
H9: Attitude toward mathematics predicts undergraduate’s academic achievement.
Methodology
Design, sample and data collection procedure
Our investigation used a survey and ex-post-facto design. The survey collected data regarding the respondents’ self-efficacy, motivation, study habits, and attitudes toward mathematics. The ex-post-facto design was considered appropriate because the undergraduates’ academic achievement preexisted as measured by GPA.
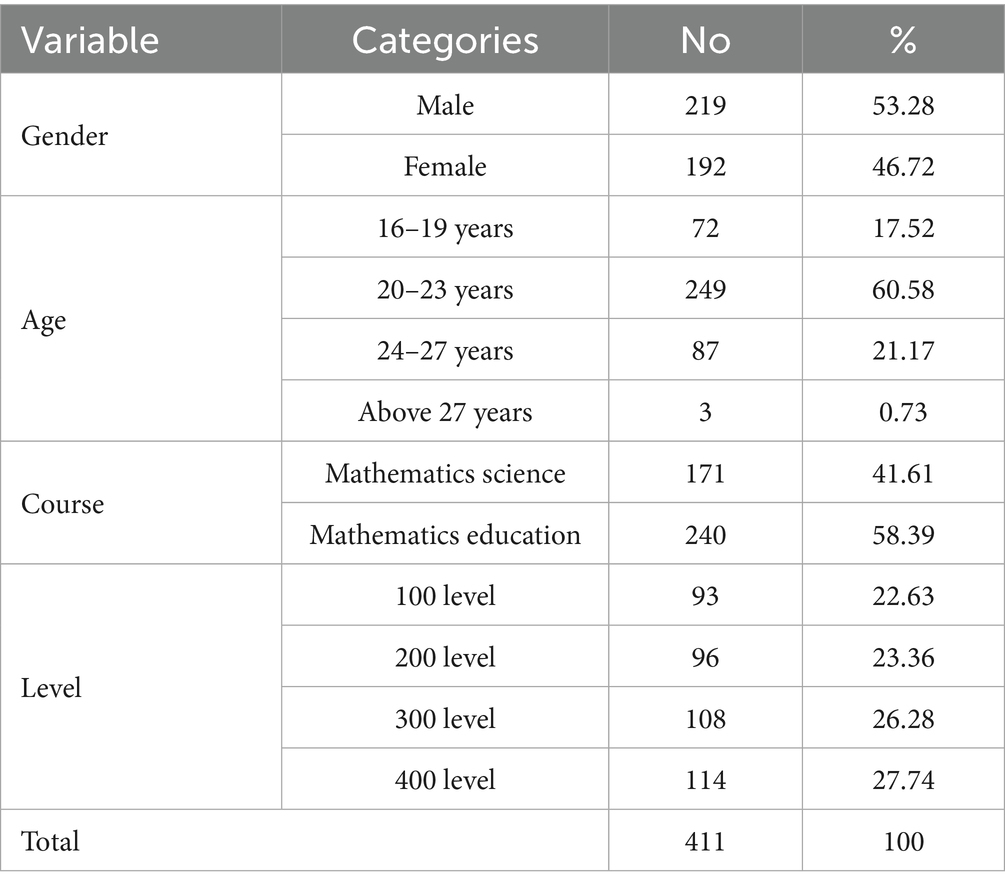
The study’s sample is 411 undergraduate students selected using simple random technique from the mathematics department of three public universities in southwestern Nigeria. They are either studying mathematical science or mathematics education. The sample size was determined by the Cochran’s method for determining sample size from a large or unknown population. For generalization at a 95% confidence level with 5% margin of error, at least around 385 participants are required (Ahmed, 2024). This study therefore opted for a sample of 411 university students, which is well above this required sample size, hence it addresses adequate statistical power and representativeness of the population under study. Simple random sampling also adds to the generalizability of findings of the study among the population. As revealed in Table 1, most of the undergraduates were male, representing 53.28%, and most of the respondents (60.58%) were aged 20–23. Also, most respondents (58.39%) were studying mathematics education, and 27.74%, which constitute the majority, were in their fourth year (400 level).
After obtaining ethical approval for the study from the Research Committee of the Faculty of Education, Federal University of Education, Oye-Ekiti, Nigeria, on February 20, 2024 (Ref No. FUOYE/FE/RCE/24-007), all participants provided informed consent, and confidentiality was ensured throughout the investigation. All data collected were handled in strict compliance with data protection regulations, ensuring participants’ personal information was anonymized, securely stored, and accessible only to the research team. We hosted the questionnaire used for data collection in the study online through Google Forms. In the first instance, we shared the link with the mathematics undergraduates, seeking their consent to participate in the study. They were encouraged to back out anytime they felt uncomfortable to continue. The matriculation number supplied by respondents was later used to collect their GPA. The confidentiality and anonymity were ensured by using matriculation numbers solely for the purpose of matching responses with academic records, after which all identifiable information was removed from the dataset, and access was restricted to the research team only.
Instrumentation
The instrument we used for data collection is a questionnaire adapted from different sources based on the constructs considered (see Supplementary Material). The questionnaire has four different constructs that seek to measure the self-efficacy, attitude, motivation, and study habits of mathematics undergraduates. Some of the items adapted were slightly modified to fit our research’s context. The items of the self-efficacy construct were adapted from Kranzler and Pajares (1997), attitude from Fennema and Sherman (1976), motivation from Vallerand et al. (1989), and study habits from Sharma (2018). We rated the questionnaire items on a 5-point Likert scale of “Strongly Agree” to “Strongly Disagree” to get the most accurate responses (Subedi, 2016).
Data analysis approach
We evaluated the constructs of the instrument for validity and reliability in the measurement model evaluation. We considered the item factor loadings (FL ≥ 0.70), construct reliability using Cronbach alpha (CA ≥ 0.70) and composite reliability (CR ≥ 0.70), convergent validity (average variance extracted: AVE ≥ 0.5), and discriminant validity (Fornell–Larcker criterion greater than the correlation coefficients among constructs) (Ayanwale and Ndlovu, 2024; Chibisa and Mutambara, 2022; Hair et al., 2019, 2021; Hair and Sarstedt, 2019; Ringle et al., 2024; Sarstedt et al., 2017). The models were then improved after removing items with factor loadings less than 0.70 and constructs with average variance extracted (AVE) less than 0.50. We used bootstrapping with 5,000 PLS subsamples to examine the correlations between the structural model constructs to evaluate the hypotheses put forward in our research. To determine which constructs in the structural model are more important in explaining others, we evaluated the direct effect size and statistical significance (Ayanwale et al., 2024; Hair et al., 2019; Ringle et al., 2024; Sarstedt et al., 2017). We validated the instrument’s psychometric properties prior to testing the substantive hypothetical connections outlined in its conceptual model. This analytical approach is considered best practice when conducting quantitative research using the latent variable approach (Hair et al., 2021).
Results
Measurement model, convergent validity and reliability
The result of the analysis is presented in this section. The measurement model explains the connection that exists between constructs and the indicators. Convergent and discriminant validity were used to evaluate the measurement model’s degree of goodness of fit (Chin, 1998). Convergent validity measures the degree to which a measure is positively correlated with other measures of the same construct, indicating that the measure truly captures the intended underlying concept (Hair et al., 2021). Discriminant validity measures the extent to which a measure is distinct from other measures, demonstrating that it is measuring a unique concept and not simply overlapping with other related constructs (Hair et al., 2019).
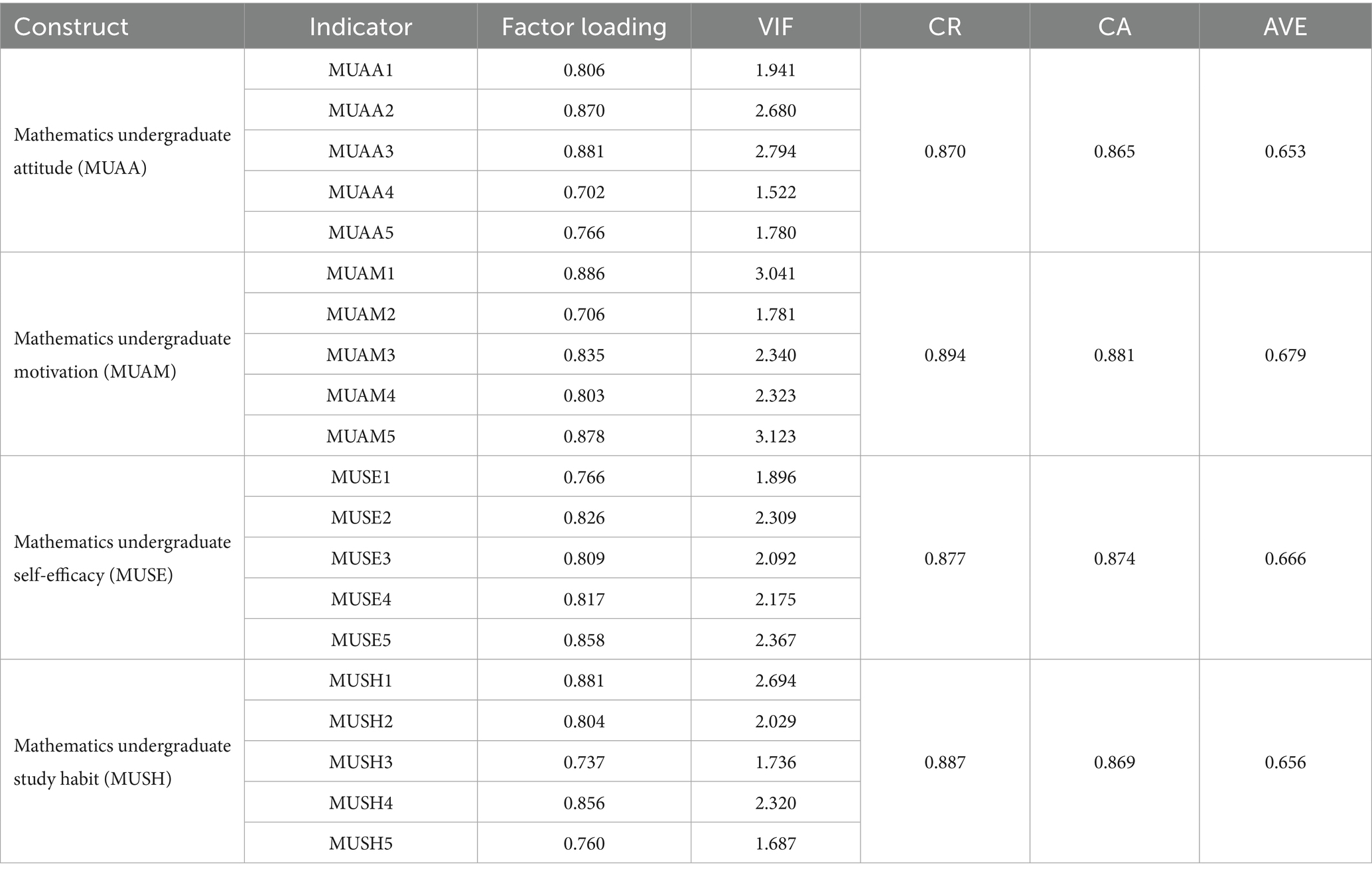
To determine whether or not convergent validity exists, we did a thorough examination of the average variance extracted (AVE), internal consistency, and indicator reliability of the constructs (Sarstedt et al., 2017). The AVE measures the amount of variance captured by a construct in relation to the amount of variance due to measurement error, assessing the convergent validity of a construct (Hair et al., 2014). When determining the reliability of an indicator, outer loadings were used, and as a general rule, the outer loadings should be greater than 0.7 (Sarstedt et al., 2017). The results in Table 2 demonstrate that all constructs had outer loadings greater than 0.7. These results suggest the reliability of accepted indicators.
We measure the items’ multicollinearity using the Variance Inflation Factor (VIF) approach. Table 2 shows that the VIF indices for all the items were below the acceptable value (<5), ranging from 1.687 to 3.123 (Hair et al., 2010). Similarly, the AVE values are 0.653, 0.679, 0.666, and 0.656 for the MUAA, MUAM, MUSE, and MUSH constructs, which were all above 0.5, indicating a strong convergent validity that is good for the model (Adelana et al., 2024; Chibisa et al., 2022; Fornell and Larcker, 1981). In a similar vein, it is indicated in Table 2 that the CA and CR, which measure the constructs’ reliability, indicate values above 0.70 for each construct establishing the reliability (internal and overall consistency) of the construct (Fornell and Larcker, 1981; Hair et al., 2014).
Discriminant validity
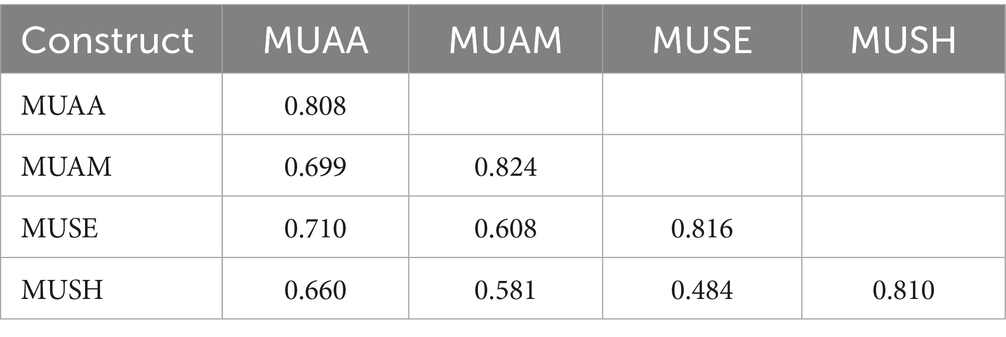
The Fornell–Larcker criterion approach was used to explain the discriminant validity of the instrument. The AVE square roots of the constructs, having a higher index when compared with the correlation coefficient of any of the constructs, establish its validity (Fornell and Larcker, 1981). Given that the construct exhibits less variation with its linked indicators than with other model constructs, this implies that the concept has discriminant validity (Sarstedt et al., 2017). Each construct’s square root of the AVE is larger than all of its correlations with every other construct (see Table 3). This implies that the latent variables are distinct from one another, hence bolstering the discriminant validity of the model. Overall, all constructs were shown to be valid and reliable. Consequently, an evaluation of the structural model was conducted.
The structural model
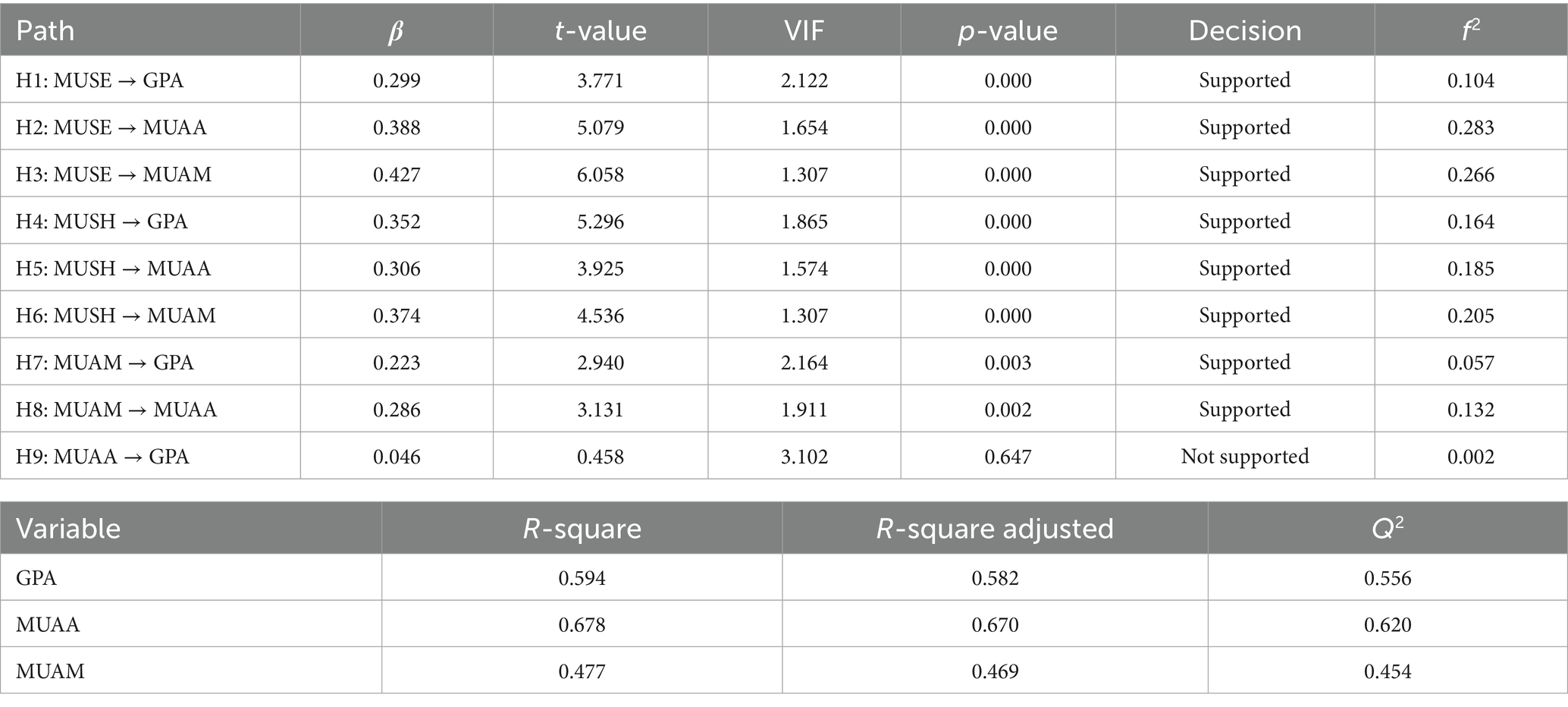
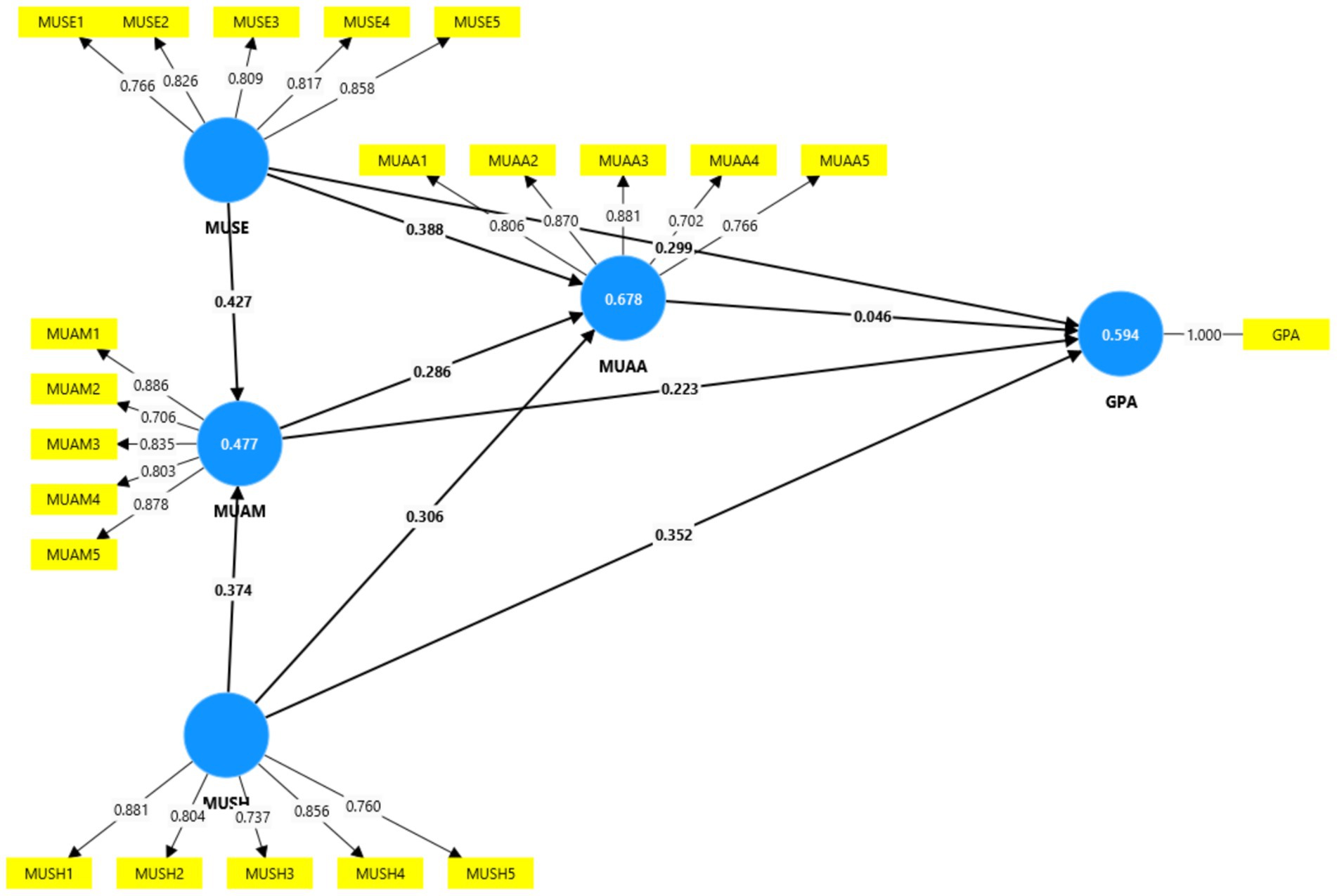
The results in Table 4 and Figure 1 summarize the structural model evaluation. We examine the structural model by considering some criteria: path coefficient size, t-test, and significance (β, t, and p); effect size (f2); structural model collinearity (VIF); R2 of endogenous variables; and predictive relevance (Q2). The result indicates that mathematics undergraduates’ academic achievement is significantly positively predicted by their mathematics self-efficacy (β = 0.299, t = 3.771, p < 0.05), which supports H1. It is discovered that mathematics undergraduates’ attitude toward mathematics is significantly positively predicted by their mathematics self-efficacy (β = 0.388, t = 5.079, p < 0.05), which also supports H2. Also, H3 is supported because mathematics undergraduates’ mathematics motivation is significantly positively predicted by their mathematics self-efficacy (β = 0.427, t = 6.058, p < 0.05). Mathematics study habits significantly positively predict mathematics undergraduates’ academic achievement (β = 0.352, t = 5.296, p < 0.05), and this supports H4. Mathematics undergraduates’ mathematics study habits significantly positively predict their attitudes toward mathematics (β = 0.306, t = 3.925, p < 0.05), which confirms support for H5. The result also shows that mathematics undergraduates’ mathematics motivation is significantly positively predicted by their mathematics study habits (β = 0.374, t = 4.536, p < 0.05), which supports H6. Mathematics undergraduate academic achievement is significantly positively predicted by mathematics motivation (β = 0.223, t = 2.940, p < 0.05), which supports H7. Additionally, H8 is supported because mathematics undergraduates’ mathematics motivation significantly positively predicts their attitude toward mathematics (β = 0.286, t = 3.131, p < 0.05). Finally, attitude toward mathematics does not significantly positively predict the academic achievement of mathematics undergraduates (β = 0.046, t = 0.458, p = 0.647), which does not support H9.
In assessing the model’s explanatory power using the effect size (f2) values and coefficient of determination (R2), we considered f2 ≥ 0.02 as small, f2 ≥ 0.15 as medium, and f2 ≥ 0.35 as large effect sizes (Cohen, 1988; Hair et al., 2021). This indicates that the paths MUSE → GPA, MUAM → GPA, and MUAA → GPA all had small effects, while MUSH → GPA, MUSE → MUAA, MUSH → MUAA, MUSE → MUAM, MUSH → MUAM, and MUAM → MUAA had medium effects.
For the coefficient of determination, R2 ≥ 0.19 is considered weak, R2 ≥ 0.33 is moderate, and R2 ≥ 0.67 is a strong level of accuracy in the prediction (Ayanwale and Molefi, 2024; Hair et al., 2021). The result shows that the independent variables moderately contribute to the prediction of the dependent variable. We use the explanatory power (adjusted R2) to assess the model, with possible values ranging from 0 to 1. Values close to 0.50 indicate moderate power, and those above 0.50 indicate high power (Adelana et al., 2024). The result shows that the explanatory power of the construct MUAM is at a moderate level while GPA and MUAA are at a high level. The GPA, MUAA, and MUAM have indices of 0.582, 0.670 and 0.469, respectively. The predictive relevance of the model (Q2) was examined; a value greater than zero is considered satisfactory in the predictive relevance (Chin, 1998; Mutambara and Chibisa, 2022). The endogenous variables’ GPA, MUAA, and MUAM Q2 values are 0.556, 0.620, and 0.454, respectively. Since these values are more significant than zero, it indicates that all the variables are related and relevant in the prediction of academic achievement of mathematics undergraduates.
Discussion
We used structural equation modeling (SEM) to assess the factors predicting the academic achievement of mathematics undergraduates. The factors considered in this study include mathematics self-efficacy, attitude toward mathematics, mathematics motivation, and mathematics study habits. This study’s novelty is its focus on university students studying mathematics and its examination of the four factors (mathematics attitude, mathematics self-efficacy, mathematics motivation and mathematics study habit) that could predict academic achievement, using SEM to examine these factors. Eight of the suggested hypotheses (H1 to H8) were confirmed to be supported by the study’s results, while only one (H9) was shown not to be supported. The constructs collectively accounted for 59.4% of the observed variance in the academic achievement of mathematics undergraduates. Similarly, the constructs MUSE and MUSH accounted for 47.7% of the observed variance in academic motivation, while MUSH, MUAM, and MUSE accounted for 67.8% of the observed variance in attitudes toward mathematics. Among the predictors, mathematics study habit has the most predictive influence on academic achievement, followed by mathematics self-efficacy and mathematics motivation, while attitude toward mathematics has the least influence on academic achievement. Also, mathematics self-efficacy has the most predictive influence on mathematics undergraduates’ attitudes toward mathematics, followed by mathematics study habits, while mathematics motivation has the least predictive influence. Similarly, mathematics self-efficacy is more influential than mathematics study habits in predicting mathematics undergraduate mathematics motivation. These findings agree with previous studies on attitude, self-efficacy, study habit and motivation, such as Negara et al. (2021), Zakariya (2021), Mahmudah et al. (2021), Hashim et al. (2022), Oyedeji (2017), Yarin et al. (2022), and Mazana et al. (2018).
The study’s findings show that mathematics undergraduates’ academic achievement is significantly positively predicted by their mathematics self-efficacy. A sense of belief in own capabilities has been found across the literature to be one of the key factors in predicting students’ academic achievement. The positive predictive influence established in this study conforms with the findings of Palestro and Jameson (2020), Zakariya (2021), and Negara et al. (2021), who all showed that self-efficacy contributed significantly to the prediction of academic achievement. Palestro and Jameson (2020) further emphasized that self-efficacy predicts and mediates achievement. The positive influence found means that students who are positive in their belief in their capabilities tend to have better achievement in mathematics, which further plays down the important role of self-efficacy. This study emphasizes the idea that fostering students’ confidence in their mathematical abilities can significantly improve their academic achievement, emphasizing the need for educational strategies that build self-efficacy in mathematics learning environments. It is discovered in this study that mathematics undergraduates’ attitude toward mathematics is significantly positively predicted by their mathematics self-efficacy. This, by implication, means that a sense of positive self-efficacy will lead to a positive attitude toward mathematics. In other words, this reveals that mathematics undergraduates who believe in their abilities are more likely to develop a positive attitude toward mathematics, showcasing the powerful interplay between self-efficacy and students’ perceptions of the subject. This aligns with Akin and Kurbanoglu (2011), who reveal the influential potential of self-efficacy on students’ attitudes. It further upholds Laranang and Bondoc (2020), who also stated that students with positive self-efficacy always have a positive attitude toward learning. Also, this study found that mathematics undergraduates’ mathematics motivation is significantly positively predicted by their self-efficacy. This study highlights that mathematics undergraduates with strong self-efficacy are not only more confident in their abilities but also more motivated to engage with mathematics, illustrating how belief in oneself fuels a passion for learning. Our finding conforms with Arık (2019), Demi̇R (2024), and Lishchynska et al. (2023), who all present self-efficacy as a key factor that influences students’ motivation. These findings stressed the importance of self-efficacy in academic achievement, attitude, and motivation. This implies that mathematics self-efficacy could be a kind of energy that could make undergraduate students devoid of academic apprehension, boosting their confidence in working toward academic excellence and making them positive about what they do. Many undergraduates are being deluded by the myth of mathematics being abstract in nature, causing damage to their belief about their abilities to comprehend what they are being taught. Therefore, boosting mathematics undergraduates’ mathematics self-efficacy would be critical to improved academic achievement, attitude, and motivation, which could be provided by well-structured interventions or therapy.
The result from our study also shows that mathematics study habits significantly positively predict mathematics undergraduates’ academic achievement. This reveals that effective mathematics study habits are a game-changer for mathematics undergraduates, significantly boosting their academic achievement and underscoring the importance of strategic learning practices in mastering the subject. Previous studies have affirmed that a consistent studying pattern influences students’ academic achievement. This was evident in the work of Alva (2017), when it was found that study habits were clearly proven to be a major predictor of undergraduate students’ achievement in mathematics. In addition, we found that mathematics undergraduates’ study habits significantly positively predict their academic attitudes. This suggest that strong mathematics study habits among mathematics undergraduates not only enhance their academic achievement but also foster a more positive attitude toward their studies, highlighting the critical link between effective learning strategies and student mindset. The finding agrees with the study of Hashim et al. (2022), where it was found that a significant relationship exists between undergraduate students’ study habits and attitudes toward mathematics. This suggests that undergraduate students with good study habits will have a positive attitude toward learning mathematics. Also, the finding of this study indicates that the mathematics undergraduates’ study habits significantly positively predict their academic motivation. This finding also conforms with Mahmudah et al. (2021), who showed that study habits positively affect students’ academic motivation. This, in some way, also suggests that mathematics undergraduate students with consistently good studying habits would demonstrate high motivation levels toward various mathematics activities. The outcomes of our research emphasized the significance of study habits to academic achievement, attitude, and motivation. This indicates that when mathematics undergraduates develop good study habits, which range from time management and organization to effort regulation directed toward studying and reading, academic achievement improvement follows the development pattern (Zimmerman et al., 2023). These students tend to retain what they study consistently over a long period, which boosts their preparation for examinations and their chances of performing well in such examinations. Students with good mathematics study habits are likely to demonstrate positive attitudes such as willingness and readiness to attend classes, write tests, do assignments and engage in group or collaborative work toward mathematics. Developing consistently good mathematics study habits starts with self-discipline and requires much commitment devoid of distractions. Hence, academics and institutions should create an environment that will help undergraduates cultivate good study habits, which, in the long run, influence their academic achievement, attitude and motivation.
Additionally, this study’s results indicate that mathematics motivation significantly and positively predicts undergraduate academic achievement in mathematics. This is in line with the findings from the work of Yarin et al. (2022), where intrinsic motivation was identified as the best predictor of academic achievement in mathematics. Also, Lishchynska et al. (2023) found that motivation significantly influences students’ achievement. In disagreement, Schoeffel et al. (2017) revealed that motivation did not influence students’ mathematics achievement. The students considered by the scholar are the software engineering students who might not take mathematics throughout their academic journey in the university compared to the mathematics undergraduates who were the major focus of our study whose courses cut across various aspects of mathematics and left with no option but to get themselves motivated to forge ahead in their academic journey. Hence, academic goals could be a major factor in undergraduates’ motivation. Also, we found that mathematics undergraduates’ mathematics motivation significantly positively predicts their academic attitude. This affirms the findings of Oyedeji (2017) and da Mata et al. (2012), who both reveal in their different studies that motivating factors influence students’ attitudes toward mathematics. Some of the motivating factors include family and school environments, the teacher and even peers. The teacher plays a significant role in motivating or demotivating the students through their attitudes and teaching approaches regarding the teaching and learning of mathematics (Pepkolaj et al., 2024). Above all, the results show that mathematics motivation is key to improved academic achievement and attitude. Hence, parents, mathematics academics, and institutions must provide resources and use various instructional approaches that motivate students to learn.
Conversely, the study’s results demonstrate that attitude toward mathematics does not significantly positively predict the academic achievement of mathematics undergraduates. The finding of this study is in contrast to Subia et al. (2018) who showed a significant path between positive attitudes and better academic achievement. Also, Mazana et al. (2018) revealed a weak, though positively significant, relationship between attitude and academic achievement. However, in this current study, the non-significance path, though a positive one between attitude and achievement, could be due to the population of the study or the course considered since mathematics is generally believed to come with its own uniqueness. The finding could mean that irrespective of the attitude undergraduates showcase toward mathematics, once they have good study habits, positive mathematics motivation, and strong mathematics self-efficacy, they are more likely to have a high academic achievement.
Implication for practice
Recognizing factors that predict undergraduates’ academic achievement in mathematics will greatly impact how policies and practices that support the teaching and learning of mathematics across various departments are developed or reviewed in universities. The study has implications for undergraduates, academics and institutions. Foremost, undergraduates should prioritize the development of their mathematics self-belief and confidence in their mathematical abilities. This could involve seeking out opportunities for mastery experiences, such as solving challenging problems with peers or participating in tutorial groups, to build a robust sense of mathematics self-efficacy. Additionally, undergraduates should proactively seek positive feedback and encouragement from their peers, tutors, and lecturers, as these mediated learning experiences can further bolster their self-confidence. Moreover, undergraduates should make a concerted effort to cultivate productive mathematics study habits, such as time management, organization, and the use of evidence-based learning techniques. By taking ownership of their learning process and developing self-regulatory behaviors, students can better position themselves for better or improved academic achievement.
Moreover, academics should develop and implement various instructional interventions, such as mentoring programs, and feedback supports, to help students build their mathematics self-efficacy. These activities should provide opportunities for engagement that boost students’ confidence in their mathematics abilities. In addition, academics should motivate students to learn by interacting with undergraduates based on their individual differences and not making the subject appear abstract. This will boost their confidence and help them crave learning and studying, which might also help their academic achievement in the long run.
In addition, institutions should prioritize helping students improve their study habits and abilities through various monitoring programs and policies. This might be done by offering specialized academic support services or by implementing study skills courses. Also, counseling units of the university, faculties, or departments should step up their activities to orientate, reorientate, and guide undergraduates in developing good study habits. By developing effective study habits, educational institutions may assist students in realizing their optimum academic potential.
Limitations and future research
Despite the insightful findings of this study, some limitations must be noted. The eligibility for participation in the study was restricted to students studying mathematical sciences and mathematics education from three public universities in southwestern Nigeria. Therefore, it is essential to consider students’ participation from other disciplines in the university system and other geographical areas to comprehensively understand the predictive factors of undergraduates’ academic achievement. Also, the findings may not be as broadly applicable due to the small sample size. Future studies must consider a larger sample size in a variety of settings. In addition, the amount of information we can get from students on the factors influencing achievement is limited when we just use a quantitative method. A mixed-method approach should be considered to accommodate other factors that may predict academic achievement and for triangulation purposes. Only four factors were considered as identified factors hence the relatively low (59.4%) explanatory power. Future studies may need to include more factors, such as interest in the subject, social norms, and so on.
Data availability statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Ethics statement
The studies involving humans were approved by Faculty of Education Ethics Committee. The studies were conducted in accordance with the local legislation and institutional requirements. The participants provided their written informed consent to participate in this study.
Author contributions
OF: Conceptualization, Data curation, Formal analysis, Methodology, Software, Validation, Writing – original draft, Writing – review & editing. AA: Conceptualization, Data curation, Investigation, Writing – original draft, Writing – review & editing. AC: Conceptualization, Data curation, Methodology, Software, Writing – original draft, Writing – review & editing.
Funding
The author(s) declare that no financial support was received for the research and/or publication of this article.
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Generative AI statement
The authors declare that no Gen AI was used in the creation of this manuscript.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary material
The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2025.1572840/full#supplementary-material
References
Abah, J. A. (2018). Low achievers and the quest for institutional standard in mathematics education: a phenomenology of subject matter experts’ opinions from Nigerian higher education. Int. J. Teach. Learn. Math. 1, 1–15. doi: 10.18860/ijtlm.v1i2.6338
Adelana, O. P., Ayanwale, M. A., and Sanusi, I. T. (2024). Exploring pre-service biology teachers’ intention to teach genetics using an AI intelligent tutoring—based system. Cogent Educ. 11:2310976. doi: 10.1080/2331186X.2024.2310976
Ahmed, S. K. (2024). How to choose a sampling technique and determine sample size for research: a simplified guide for researchers. Oral Oncol. Rep. 12:100662. doi: 10.1016/j.oor.2024.100662
Akin, A., and Kurbanoglu, I. N. (2011). The relationships between math anxiety, math attitudes, and self-efficacy: a structural equation model. Stud. Psychol. 53, 263–273.
Almaraz-López, C., Almaraz-Menéndez, F., and López-Esteban, C. (2023). Comparative study of the attitudes and perceptions of university students in business administration and management and in education toward artificial intelligence. Educ. Sci. 13:609. doi: 10.3390/educsci13060609
Alva, M. L. C. (2017). Self-esteem, study habits and academic performance in university students. Propós. Represent. 5, 101–127. doi: 10.20511/pyr2017.v5n1.145
Arens, A. K., Frenzel, A. C., and Goetz, T. (2022). Self-concept and self-efficacy in math: longitudinal interrelations and reciprocal linkages with achievement. J. Exp. Educ. 90, 615–633. doi: 10.1080/00220973.2020.1786347
Arık, S. (2019). The relations among university students’ academic self-efficacy, academic motivation, and self-control and self-management levels. Int. J. Educ. Literacy Stud. 7:23. doi: 10.7575/aiac.ijels.v.7n.4p.23
Asanre, A. A., Sondlo, A., and Oluwadayo, A. T. (2024). Impact of problem-based learning strategy on learning outcomes of senior secondary school student in mathematics. J. Adv. Sci. Math. Educ. 4, 15–23. doi: 10.58524/jasme.v4i1.370
Atkinson, J. W. (1957). Motivational determinants of risk-taking behaviour. Psychol. Rev. 64, 359–372. doi: 10.1037/h0043445
Ayanwale, M. A., Frimpong, E. K., Opesemowo, O. A. G., and Sanusi, I. T. (2024). Exploring factors that support pre-service teachers’ engagement in learning artificial intelligence. J. STEM Educ. Res. 8, 1–31. doi: 10.1007/s41979-024-00121-4
Ayanwale, M. A., and Molefi, R. R. (2024). Exploring intention of undergraduate students to embrace chatbots: from the vantage point of Lesotho. Int. J. Educ. Technol. High. Educ. 21:20. doi: 10.1186/s41239-024-00451-8
Ayanwale, M. A., and Ndlovu, M. (2024). Investigating factors of students’ behavioral intentions to adopt chatbot technologies in higher education: perspective from expanded diffusion theory of innovation. Comput. Hum. Behav. Rep. 14:100396. doi: 10.1016/j.chbr.2024.100396
Bandura, A. (1986). Social foundations of thought and action: a social cognitive theory. Englewood Cliffs, NJ: Prentice-Hall.
Capuno, R., Necesario, R., Etcuban, J. O., Espina, R., Padillo, G., and Manguilimotan, R. (2019). Attitudes, study habits, and academic performance of junior high school students in mathematics. Int. Electron. J. Math. Educ. 14, 547–561. doi: 10.29333/iejme/5768
Charles-Ogan, G., and Alamina, J. I. (2014). Differential students’ study habit and performance in mathematics. J. Educ. Pract. 5, 133–139.
Chibisa, A., and Mutambara, D. (2022). An exploration of STEM students’ and educators’ behavioural intention to use mobile learning. J. E-Learn. Knowl. Soc. 18, 166–176. doi: 10.20368/1971-8829/1135622
Chibisa, A., Sibaya, D. C., and Mutambara, D. (2022). Factors affecting pre-service teachers’ acceptance of online learning to promote social distancing. Progression 43, 1–20. doi: 10.25159/2663-5895/12229
Chin, W. W. (1998). “The partial least squares approach for structural equation modeling” in Modern methods for business research (Mahwah, NJ: Lawrence Erlbaum Associates Publishers), 295–336.
Cohen, J. (1988). Statistical power analysis for the behavioral sciences. Hillsdale, NJ: L. Erlbaum Associates.
da Mata, M. P. E. N., Monteiro, V., and Peixoto, F. (2012). Attitudes towards mathematics: effects of individual, motivational, and social support factors. Child Dev. Res. 2012, 1–10. doi: 10.1155/2012/876028
Deci, E. L., and Ryan, R. M. (1985). Intrinsic motivation and self-determination in human behaviour. New York: Springer.
Demi̇R, S. (2024). An examination of the relationship between academic self-efficacy and academic motivation. J. Hist. School LXIX, 1246–1266. doi: 10.29228/joh.70860
Eccles, J., Adler, T. F., Futterman, R., Goff, S. B., Kaczala, C. M., Meece, J., et al. (1983). Expectancies, values and academic behaviors. In J. T. Spence (ed.) Achievement and Achievement Motives, W. H. Freeman, San Francisco.
Eccles, J. S., and Wigfield, A. (2002). Motivational beliefs, values, and goals. Annual review of psychology, 53, 109–132.
Ercikan, K., McCreith, T., and Lapointe, V. (2005). Factors associated with mathematics achievement and participation in advanced mathematics courses: an examination of gender differences from an international perspective. Sch. Sci. Math. 105, 5–14. doi: 10.1111/j.1949-8594.2005.tb18031.x
Falebita, O. S., and Olofin, S. O. (2020). Impact of teachers’ instructional practices on students’ achievement and self-efficacy in mathematics. Commonwealth J. Acad. Res. 1, 1–14. doi: 10.5281/ZENODO.3879417
Fennema, E., and Sherman, J. A. (1976). Fennema-Sherman mathematics attitudes scales: instruments designed to measure attitudes toward the learning of mathematics by females and males. J. Res. Math. Educ. 7, 324–326. doi: 10.2307/748467
Fornell, C., and Larcker, D. F. (1981). Evaluating structural equation models with unobservable variables and measurement error. J. Mark. Res. 18, 39–50. doi: 10.1177/002224378101800104
Hair, J. F. Jr., Black, W. C., Babin, B. J., and Anderson, R. E. (2010). Multivariate data analysis. New York: Pearson, 785.
Hair, J. F., Hult, G. T. M., Ringle, C. M., Sarstedt, M., Danks, N. P., and Ray, S. (2021). “Evaluation of the structural model” in Partial least squares structural equation modeling (PLS-SEM) using R: a workbook (Cham: Springer), 115–138.
Hair, J. F., and Sarstedt, M. (2019). Factors versus composites: guidelines for choosing the right structural equation modeling method. Proj. Manag. J. 50, 619–624. doi: 10.1177/8756972819882132
Hair, J. F., Sarstedt, M., Hopkins, L., and Kuppelwieser, V. G. (2014). Partial least squares structural equation modeling (PLS-SEM): an emerging tool in business research. Eur. Bus. Rev. 26, 106–121. doi: 10.1108/EBR-10-2013-0128
Hair, J. F., Sarstedt, M., and Ringle, C. M. (2019). Rethinking some of the rethinking of partial least squares. Eur. J. Mark. 53, 566–584. doi: 10.1108/EJM-10-2018-0665
Hashim, M. M., Tlemsani, I., Mohamed Hashim, M. A., and Matthews, R. (2022). Higher education strategy in digital transformation. Educ. Inf. Technol. 27, 3171–3195. doi: 10.1007/s10639-021-10739-1
Herges, R. M., Duffield, S., Martin, W., and Wageman, J. (2017). Motivation and achievement of middle school mathematics students. Math. Educ. 26, 83–106.
Jansen, B. R. J., Schmitz, E. A., and van der Maas, H. L. J. (2016). Affective and motivational factors mediate the relation between math skills and use of math in everyday life. Front. Psychol. 7:513. doi: 10.3389/fpsyg.2016.00513
Kranzler, J. H., and Pajares, F. (1997). An exploratory factor analysis of the mathematics self-efficacy scale—revised (MSES-R). Meas. Eval. Couns. Dev. 29, 215–228. doi: 10.1080/07481756.1997.12068906
Laranang, J. A. I., and Bondoc, J. M. F. (2020). Attitudes and self-efficacy of students toward mathematics. Int. J. Engl. Lit. Soc. Sci. 5, 1392–1423. doi: 10.22161/ijels.55.11
Lishchynska, M., Palmer, C., Lacey, S., and O’Connor, D. (2023). Is motivation the key? Factors impacting performance in first year service mathematics modules. Eur. J. Sci. Math. Educ. 11, 146–166. doi: 10.30935/scimath/12529
Mahmudah, K., Pambudi, D. S., Oktavianingtyas, E., Lestari, N. D. S., and Murtikusuma, R. P. (2021). The relationship between study habits and learning motivation with mathematics learning achievement of junior high school students during online learning. Kadikma 12, 58–68. doi: 10.19184/kdma.v12i2.26345
Mazana, M. Y., Montero, C. S., and Casmir, R. O. (2018). Investigating students’ attitude towards learning mathematics. Int. Electron. J. Math. Educ. 14, 207–231. doi: 10.29333/iejme/3997
McCoach, D. B. (2003). SEM isn’t just the schoolwide enrichment model anymore: structural equation modeling (SEM) in gifted education. J. Educ. Gift. 27, 36–61. doi: 10.1177/016235320302700104
Mutambara, D., and Chibisa, A. (2022). Rural STEM preservice teachers’ acceptance of virtual learning. Int. J. Learn. Teach. Educ. Res. 21:155. doi: 10.26803/ijlter.21.2.9
National Universities Commission (2019). Nigerian university system statistical digest. Maitama: National Universities Commission.
Negara, H. R. P., Nurlaelah, E., Herman, T., and Tamur, M. (2021). Mathematics self efficacy and mathematics performance in online learning. J. Phys. Conf. Ser. 1882:012050. doi: 10.1088/1742-6596/1882/1/012050
Odiri, O. E. (2015). Relationship of study habits with mathematics achievement. J. Educ. Pract. 6, 168–170.
Oyedeji, S. O. (2017). A path analysis of the effects of students’ motivational factors on their attitudes toward mathematics. Int. J. Eval. Res. Educ. 6:277. doi: 10.11591/ijere.v6i4.10770
Palestro, J. J., and Jameson, M. M. (2020). Math self-efficacy, not emotional self-efficacy, mediates the math anxiety-performance relationship in undergraduate students. Cognit. Brain Behav. Interdiscip. J. 24, 379–394. doi: 10.24193/cbb.2020.24.20
Pepkolaj, L., Arnal-Palacián, M., Begué, N., and Prahmana, R. C. I. (2024). Demotivating factors in teaching mathematics: a study of Albanian teachers. Infinity J. 13, 27–44. doi: 10.22460/infinity.v13i1.p27-44
Pintrich, P. R., and De Groot, E. V. (1990). Motivational and self-regulated learning components of classroom academic performance. J. Educ. Psychol. 82, 33–40. doi: 10.1037/0022-0663.82.1.33
Sachitra, V., and Bandara, U. (2017). Measuring the academic self-efficacy of undergraduates: the role of gender and academic year experience. World Acad. Sci. Eng. Technol. Int. J. Educ. Pedagog. Sci. 11, 2608–2613. doi: 10.1080/10401334.2021.1877713
Sakirudeen, O., and Sanni, B. (2017). Study habits and academic performance of secondary school students in mathematic: a case study of selected secondary schools in Uyo local education council. Res. Pedag. 7, 283–297. doi: 10.17810/2015.65
Salman, M. F., Yahaya, L. A., and Adewara, A. A. (2011). Mathematics education in Nigeria. Int. J. Educ. Sci. 3, 15–20. doi: 10.1080/09751122.2011.11890004
Sarstedt, M., Ringle, C. M., and Hair, J. F. (2017). “Partial least squares structural equation modeling” in Handbook of market research. eds. C. Homburg, M. Klarmann, and A. Vomberg (Cham: Springer), 1–40.
Schoeffel, P., Wazlawick, R. S., and Ramos, V. (2017). Impact of pre-university factors on the motivation and performance of undergraduate students in software engineering. 2017 IEEE 30th Conference on Software Engineering Education and Training (CSEE&T). 266–275
Schunk, D. H. (1989). Self-efficacy and achievement behaviors. Educ. Psychol. Rev. 1, 173–208. doi: 10.1007/BF01320134
Sharma, D. (2018). Construction and validation of the study habits scale for the secondary school students. Int. J. Res. Soc. Sci. 8, 964–978.
Subedi, B. P. (2016). Using Likert type data in social science research: confusion, issues and challenges. Int. J. Contemp. Appl. Sci. 3, 36–49.
Subia, G. S., Salangsang, L. G., and Medrano, H. B. (2018). Attitude and performance in mathematics I of bachelor of elementary education students: a correlational analysis. Am. Sci. Res. J. Eng. Technol. Sci. 39, 206–213.
Turgut, M. (2013). Academic self-efficacy beliefs of undergraduate mathematics education students. Acta Didact. Napoc. 6, 33–40.
Vallerand, R. J., Pelletier, L. G., Blais, M. R., Brière, N. M., Senécal, C. B., and Vallières, É. F. (1989). Academic motivation scale (AMS-C 28) college version. Educ. Psychol. Meas. 52, 323–349.
Wiebe, E., Unfried, A., and Faber, M. (2018). The Relationship of STEM Attitudes and Career Interest. EURASIA Journal of Mathematics, Science and Technology Education, 14.
Wu, F., and Fan, W. (2017). Academic procrastination in linking motivation and achievement-related behaviours: a perspective of expectancy-value theory. Educ. Psychol. 37, 695–711. doi: 10.1080/01443410.2016.1202901
Yarin, A. J., Encalada, I. A., Elias, J. W., Surichaqui, A. A., Sulca, R. E., and Pozo, F. (2022). Relationship between motivation and academic performance in Peruvian undergraduate students in the subject mathematics. Educ. Res. Int. 2022, 1–11. doi: 10.1155/2022/3667076
Zakariya, Y. F. (2021). Self-efficacy between previous and current mathematics performance of undergraduate students: an instrumental variable approach to exposing a causal relationship. Front. Psychol. 11:556607. doi: 10.3389/fpsyg.2020.556607
Keywords: self-efficacy, attitude, motivation, study habits, mathematics undergraduates, structural equation model, academic achievement
Citation: Falebita OS, Asanre AA and Chibisa A (2025) A structural equation modeling of predictive factors of mathematics undergraduates academic achievement. Front. Educ. 10:1572840. doi: 10.3389/feduc.2025.1572840
Edited by:
Maruf Ahmed Tamal, Daffodil International University, BangladeshReviewed by:
Ali Rashash R. Alzahrani, Umm Al-Qura University, Saudi ArabiaVictor Eyo Essien, University of Maryland, College Park, United States
Maharunnasha Antora, Daffodil International University, Bangladesh
Copyright © 2025 Falebita, Asanre and Chibisa. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Oluwanife Segun Falebita, b2x1d2FuaWZlZmFsZWJpdGFAZ21haWwuY29t; RmFsZWJpdGFPQHVuaXp1bHUuYWMuemE=
†ORCID: Oluwanife Segun Falebita, orcid.org/0000-0002-8287-4005
Akorede A. Asanre, orcid.org/0000-0003-2787-2346
 Oluwanife Segun Falebita
Oluwanife Segun Falebita Akorede A. Asanre
Akorede A. Asanre Admire Chibisa
Admire Chibisa