A conceptual framework for multi-component summative assessment in an e-learning management system

The article presents a conceptual framework for the design, implementation, and analysis of multi-component summative assessment systems in an electronic educational environment. A universal model is proposed, based on a four-level hierarchy – meta-meta-model, meta-model, model, and actual assessment system. Various structures and assessment components are examined, including Bloom’s taxonomy, higher- and lower-order thinking skills, theory and practice, and the use of fuzzy logic and artificial intelligence. The processes of modeling, configuration, usage, and system analysis are described, along with the roles of the main participants—administrator, author and learner. The use of generative artificial intelligence for the automated creation of test questions is also explored. The system aims to enhance transparency, objectivity, and effectiveness of assessment in digital learning environments, offering practical solutions for modern higher education.

1 Introduction

In recent decades, significant changes have occurred in learners’ preferences and attitudes toward the educational process. During the modernist period, learners viewed high-quality education as a guarantee of success. Learners from Generation Z (born between 1996 and 2009) associate the learning process with the reception and processing of large volumes of information, which they receive daily through various channels, including social and professional networks. They believe that learning is a continuous process rather than just a stage in life, and as such, it should be engaging and enjoyable. A similar perspective is shared by the next generation – Generation Alpha (born after 2009). From an early age, individuals from this generation use robotic toys, smartphones, and tablets, and have access to a practically unlimited amount of information, much of which they cannot fully absorb. They are curious, but have their own opinions on what is useful and interesting, and they want to choose what and how they learn.

Undoubtedly, this presents a significant challenge for educators – on one hand, to teach knowledge and skills defined by national educational standards, which are not always of interest to learners and are often perceived as boring, irrelevant, or even unnecessary; and on the other hand, to find appropriate ways to assess the acquired theoretical knowledge and practical skills. In search of new teaching approaches and methodologies, instructors have started developing electronic learning materials hosted in e-learning environments, experimenting with tools for conducting electronic examinations, and engaging in synchronous communication with learners through video conferencing software applications. It is also worth noting the growing interest in using artificial intelligence technologies to optimize the learning process. One such application is utilizing intelligent agents integrated into Learning Management Systems (LMS), which enhance communication between instructors and learners (Nenkov et al., 2016).

The pursuit of more effective education has led to the use, adaptation, and modification of various models that differ in pedagogical approach, teaching forms and methods, organization and structuring of learning content, pedagogical interaction, and more. A widely used approach is blended learning, which combines elements of traditional classroom education and e-learning. In this model, students attending in-person courses also use corresponding e-learning courses hosted on an e-learning platform. These electronic courses include theoretical materials, practice exercises and (self-) assessment tools, orientation guidelines, support resources, and communication tools for interacting with teachers and peers (Gaftandzhieva et al., 2023). In traditional education, new knowledge that requires understanding and memorization is delivered in the classroom, while students are expected to work independently outside of class on tasks that demand Higher Order Thinking Skills (HOTS). An interesting opportunity is the implementation of interdisciplinary education through project-based learning, in which key competences are developed through teamwork (Kirilova, 2024). This presents new challenges for assessing learners’ competences across different subject areas (Kirilova, 2023).

Another model is the flipped classroom, in which learners independently study the course material before class, and during class, working individually or in teams under the teacher’s guidance, they solve more complex tasks requiring higher cognitive skills. This model is particularly suitable for teaching programming and engineering subjects (Hendrik and Hamzah, 2021).

Massive Open Online Courses (MOOCs) have proven effective for providing foundational theoretical education. They offer free access to learning materials to anyone interested in a given subject. Students can interact with one another and with instructors via dedicated forums, periodically assess their acquired knowledge and skills throughout the course, and – upon successfully passing a final exam – receive a certificate of completion. A major drawback of MOOCs is the lack of real-time interaction between instructors and learners, which can negatively affect the quality of learning (Minev and Koeva-Dimitrowa, 2019). One possible solution to this problem is the modeling of pedagogical patterns in e-courses and e-learning environments (Hristov et al., 2022). For now, MOOCs are widely used for off-campus training and sharing of educational resources (Kiryakova, 2019).

The need to adapt the educational process to learners’ needs and to provide more specialized professional knowledge and skills has motivated the emergence of a new concept: Small Private Online Courses (SPOCs). These support blended and flipped learning models by combining digital learning resources and activities with face-to-face interaction between instructors and learners (Kaplan and Haenlein, 2016). This enables instructors to organize the learning process in various ways by choosing which parts of the online course content to incorporate into in-person sessions and how to do so (e.g., through case studies, projects, video lectures, tests, group assignments, discussion forums, etc.). The use of SPOCs has shown a positive impact on learners’ attitudes and academic performance (Wen and Wu, 2022). The possibility of using various innovative technologies in the learning process also motivates learners and engages them more actively in their education (Velcheva and Peykova, 2024).

Learners, for their part, have different individual characteristics and preferences when it comes to adopting new technologies in the learning process. In general, learners with positive attitudes toward new technologies tend to achieve better learning outcomes and report higher levels of satisfaction with this mode of learning (You, 2019). Innovative approaches should be sought to explore their opinions on the conducted training, including in-depth interviews (Hristov and Krushkov, 2016).

Despite all the advantages of technology and new learning models, the absence of face-to-face classroom interaction often leads to several issues, including demotivation among both instructors and learners. On one hand, some learners neglect the learning process, study without genuine understanding, and use unauthorized aids during exams to obtain higher grades. On the other hand, building a digital learning environment is a continuous process that requires acquiring skills to work with various tools for developing and delivering educational content, as well as for testing and assessing knowledge. During this process, instructors take on additional responsibilities and face numerous challenges, including implementing methods to attract and maintain learners’ attention and ensuring fair and objective assessment of the acquired knowledge.

This article explores the challenges faced by instructors when conducting assessments in an electronic environment. Section 2 examines the main challenges of electronic assessment, such as fairness, objectivity, and fraud prevention. It presents a study of different models and characteristics of fair assessment, which enhance learners’ motivation to actively engage in the learning process. Technical and pedagogical solutions for minimizing cheating are described, including individualized tests, randomized questions, time limits, and more. Section 3 introduces a concept for modeling and implementing a multi-component assessment system that enables the creation, application, and analysis of a variety of specific assessment models and methods.

2 Conducting assessments in an electronic environment

Assessment has many aspects. One of the most popular assessment tools in an electronic environment is tests. Classical test theory (CTT) is one of the most significant concepts for test design and analysis. According to CTT, any observed test performance is viewed as the sum of two components – the true score and measurement error. The goal of CTT is to minimize errors and ensure that the test measures the learner’s actual knowledge or skills as accurately as possible. Research in this area emphasizes key indicators such as the reliability and validity of tests. Reliability measures the extent to which a test produces stable and consistent results when administered repeatedly or in different forms of the test, while validity reflects the extent to which the test measures what it claims to measure. Numerous empirical studies have shown that when tests are properly constructed by the CTT, high levels of reliability and validity can be achieved (Crocker and Algina, 2008; Allen and Yen, 2001). This accounts for the importance and popularity of the CTT in assessment, despite the development of more modern theories such as Item Response Theory (IRT).

A major challenge in the learning process is ensuring fairness in the classroom. The overall perception of fairness is shaped by three main factors: interactional, procedural, and outcome fairness (Whitley et al., 2000). Interactional fairness refers to the nature of the instructor’s interaction with learners and includes characteristics such as impartiality and equal treatment of all students; respect and politeness, even in the face of impolite behavior from learners; concern for students’ problems; integrity, demonstrated through clear communication of rules and their consistent and honest application; and maintaining professional conduct in front of students. Procedural fairness is defined by the rules governing assessment and classroom management. Important indicators of procedural fairness include a reasonable course workload; fair tests that cover the full scope of the material taught, are appropriately difficult for the course level, and present clear questions and answer options; timely feedback on assessments; and responsiveness to students’ questions. Outcome fairness relates to the perception of fairness in grading and is based on features such as: adherence to institutional practices that ensure consistent assessment mechanisms for the same subjects, even when taught by different instructors; use of accurate assessment tools that reliably reflect student performance; implementation of multiple types of assessments to evaluate different aspects of student knowledge; provision of clear information in advance about assessment criteria; and individual assessment based on an absolute scale rather than on comparative performance among peers.

Close (2009) describes three assessment models that define different purposes and functions of grading: grades are perceived either as rewards or punishments for mastering the course material; as the main goal of education; or as part of an informational process that accurately and objectively reflects the degree to which learners have acquired knowledge in the studied disciplines. In the first two models, final grades may be influenced by external factors such as personal impressions of the learner, comparisons between students, and the personal feelings of either the learner or the instructor. The third model, which presents assessment as a fair and impartial process, emphasizes principles such as objectivity and expert evaluation of students’ demonstrated knowledge. To achieve these principles, several conditions must be met: the grading criteria must be clearly stated at the beginning of the course; the assessment components must have precisely defined weights; each student must receive a grade for each component; and the components must allow for an accurate assessment of every learner.

Fair assessment has been the subject of numerous discussions and studies. Despite the variety of approaches used to define different types, methods, and forms of assessment, many scholars share a common understanding regarding the essential requirements for evaluation. An assessment should be objective and reflect actual performance; differentiated and comprehensive, capturing various aspects of a learner’s preparation – whether theoretical knowledge or practical skills – and adapted to the nature of the subject matter, as well as to the age and individual characteristics of the learners. It should be systematic, conducted regularly, well-justified, with clear reasoning behind each grade; it should offer variety in terms of assessment forms and methods; and it should not be used as a means of punishment (Ruskov and Ruskova, 2013).

Suskie defines seven steps for fair assessment that largely reflect the shared understanding among educational professionals. She outlines recommendations that include: formulated learning outcomes; aligning assessment with the course content; using multiple measures; helping students understand how to complete the assessment task; engaging and encouraging learners; appropriately interpreting assessment results; and evaluating the effectiveness of the assessment itself (Suskie, 2002).

All research related to assessment touches, to some extent, on the topic of objective evaluation. It is generally accepted that objective assessments possess the following characteristics: accurate results, reliability and validity, fairness, differentiation, comprehensiveness of the evaluation, and more (Schaughency et al., 2012).

Fair testing and assessment is a critical issues in electronic examinations, where the risk of exam cheating significantly increases. To address such problems, traditional monitoring techniques – such as enabling cameras and microphones, screen sharing, and others – are not always effective or appropriate. Their application often provokes negative emotions among learners, as it shifts the assessment model toward one based on “rewards and punishments” and implies a presumption of dishonest behavior by students. A current challenge is the development of intelligent software systems for comprehensive control and management of examination procedures, including plagiarism detection, minimization of cheating attempts (TeSLA Project, 2019), adaptability of assessments for people with disabilities or special needs, and more (Nacheva-Skopalik and Green, 2016). However, implementing such systems with a presumption of guilt may also undermine the understanding of assessment as an informational process.

Academic freedom in higher education institutions allows for the application and experimentation with various assessment methods, forms, and tools. Most learning management systems support a wide range of electronic assessment tools (Kiryakova, 2021). For example, one of the most popular e-learning platforms, Moodle, offers a plugin that identifies the student before granting access to tests and captures images every 30 s during the test session. Safe Exam Browser (SEB) is a specialized browser supported by Moodle that blocks access to external websites, chats, and even AI tools. Some plugins attempt to determine whether a given text was written by AI, though they should be used with appropriate critical judgment.

On the other hand, to ensure fair testing and assessment, instructors can adhere to standard task design principles used in traditional educational settings without relying on invasive monitoring practices. Instead, they can minimize opportunities for cheating – such as group completion of tests, the use of unauthorized resources when solving problems, or assistance in writing short-answer responses – by carefully designing the assessment process.

To achieve a balance between conducting fair assessments, minimizing dishonest behavior from learners, and avoiding intrusive monitoring techniques, certain rules can be formulated to promote a relatively normal distribution of grades and, in most cases, unique solutions to identical tasks. These rules include:

• Individual tests on theory and basic practical topics:

• A large number of multiple-choice questions, from which random questions with randomly ordered answer choices are automatically generated;

• Sequential navigation through test questions, without the ability to return to previous ones;

• No open-ended questions, which allow for quick lookups on the internet or in lecture materials;

• Simultaneous start time for all learners, with clearly defined start and end times;

• Optimized test duration, based on observations in a normal environment (in many cases, one minute per test question is sufficient).

• Practical tasks:

• A relatively large pool of similar tasks with comparable difficulty, from which one is randomly assigned to each learner;

• Reducing the complexity of the tasks;

• Reducing the time allocated for solving the tasks.

• Establishment of a grading system with different weights for different assessment components – increasing the weight of components with a lower likelihood of cheating, and decreasing the weight of those with a higher risk of dishonest practices.

A positive effect of using only multiple-choice questions is the ability to provide automatic and immediate feedback upon completion of the test. When forming the final grade, there is still the option to pose follow-up questions to the learner in a dialog format.

It should be noted here that the assessment process can be optimized with the help of Artificial Intelligence (AI) software tools. Popular in recent years is the use of artificial intelligence chatbots such as ChatGPT, Claude, Bert, etc. Numerous studies demonstrate the great potential of large language models (LLMs) for automated generation of assessment questions. Zhuge et al. propose the TwinStar architecture – a dual-LLM engine, which combines a question generation model and a cognitive-level assessment model. With it, they achieve significantly better relevance to knowledge compared to GPT-4 and Bard (Zhuge et al., 2025). Nikolovski et al. present a pioneering study on implementing LLM in the assessment of students in a university (Nikolovski et al., 2025). The proposed systematic framework with three agents – VectorRAG, VectorGraphRAG and fine-tuned LLM evaluated against a meta-evaluator, supervised by human experts, to assess alignment accuracy and explanation quality. The results show practical value in creating reliable and fair test items. Another study (Wang et al., 2024) analyzes prompts for generating educational questions and evaluates their effectiveness through expert (human) review. The results show that high-quality questions can be created that meet education standards and approach the quality of questions manually composed by teachers in certain aspects. The authors emphasize the possibility of joint work between artificial intelligence and teachers in the educational process. The use of LLM in education should be ethical and transparent. Critical use and expert validation of all AI-generated information is essential (Milano et al., 2023).

3 Modeling multi-component assessment

Numerous models for assessing learners’ knowledge and skills are described in the scientific literature. Various techniques for multi-criteria assessment have been studied by Mardani et al. (2015).

One approach to multi-component assessment, based on the revised Bloom’s taxonomy by Anderson and Krathwohl, is presented in Hadzhikoleva et al. (2019). In this approach, the components correspond to the different levels of the taxonomy, and the final grade is calculated as a linear function of these components. The grade $E$ is computed using the formula:

$E=\sum _{i=1}^n{a}_i{y}_i$

Where $y_i$ are the scores for each component categorized according to Bloom’s taxonomy, $a_i\ge 0$ are their respective weights, ${\sum }_{\mathrm{i}=1}^{\mathrm{n}}{\mathrm{a}}_{\mathrm{i}}=1$ , and $n$ is the number of components (which is 6 in Bloom’s taxonomy). The evaluator can choose from four main assessment models or their variations, each with its advantages and disadvantages: flat model – all weights are equal; progressive model – weights increase with higher Bloom levels; basic model – mid-level Bloom scores carry more weight, while extremely basic or overly complex skills carry less; regressive model – weights decrease with higher Bloom levels.

Models for multi-component fuzzy assessment have been proposed in Hadzhikolev et al. (2020). In these models, the final grade is formed step by step using linear functions and fuzzy logic, with component scores calculated hierarchically across successive levels. The use of historical data on instructor-assigned grades enables the application of artificial intelligence methods for the partial automation of the assessment process.

Based on the reviewed models for multi-component assessment, we propose a unified system for modeling multi-component evaluation, built upon an abstract assessment structure and a process for its concretization. The ultimate goal of this assessment system is to provide methods and tools for developing diverse assessment approaches tailored to the needs and requirements of different evaluators.

The main stages in the process of modeling an assessment system consist of four phases, corresponding to the creation of a Meta-meta-model, a Meta-model, a Model, and the actual Assessment System. Each stage defines different levels of abstraction or concretization of two core elements of the assessment system: the Assessment Model and the Assessment Methods.

The stages that follow the modeling process include the Use of the Assessment System through the administration of test tasks and the Analysis of the Assessment System.

The meta-meta-model is embedded within the software system, and users with different roles model, configure, and utilize the assessment models. The main roles in the system are: administrator, author, and learner. The administrator models and approves meta-models proposed by other users. The author creates assessment models and configures test tasks for them. The author can use their tasks or tasks created by other users when configuring tests, and can also perform additional analyses on completed tests. The learner completes the tests assigned to them.

3.1 Meta-meta-model of an assessment system

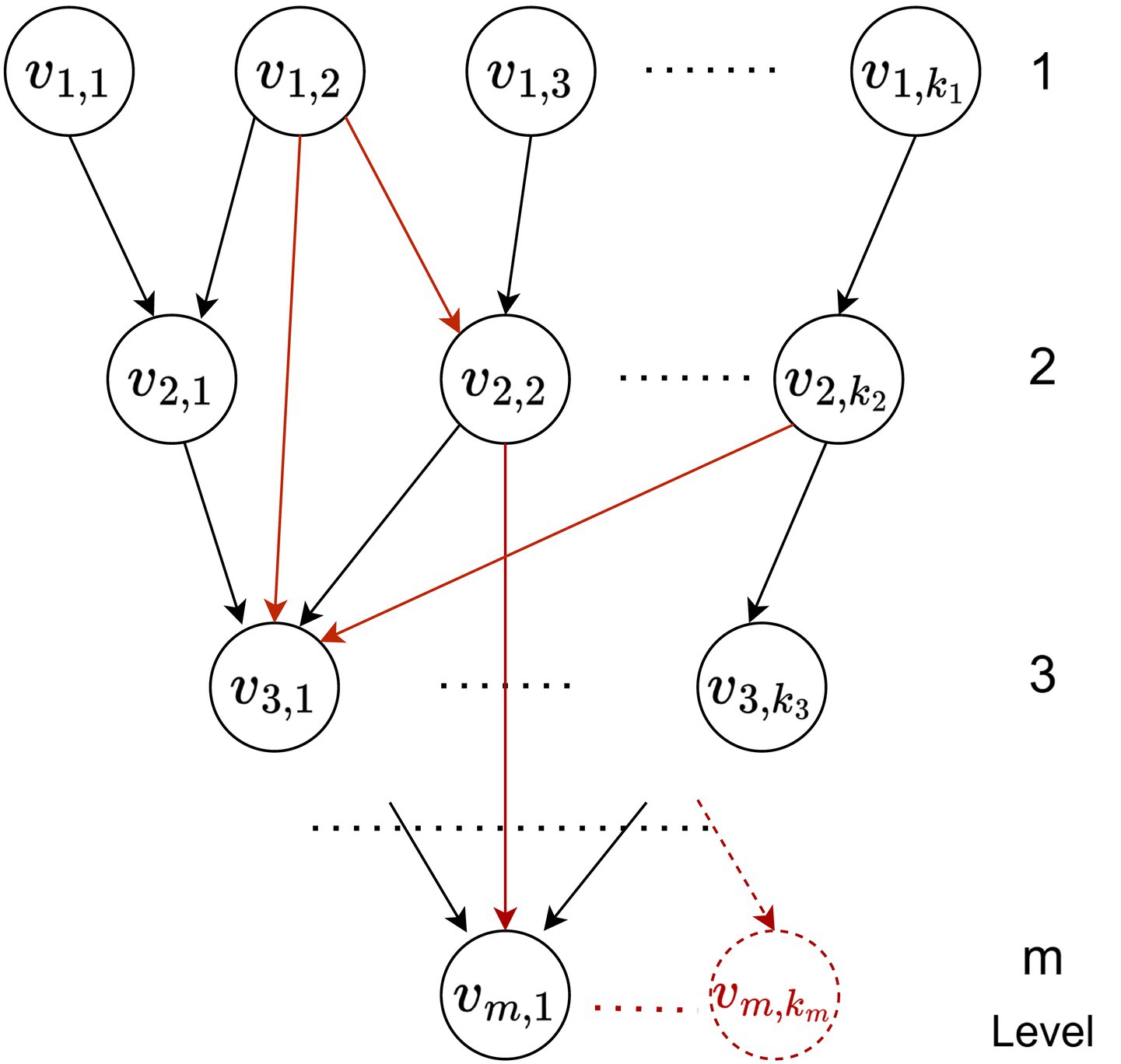
Figure 1 shows a general meta-meta-model for multi-component assessment, which serves as the foundation for building all specific models. It is represented as a directed graph, where the nodes are abstract assessment components (knowledge and skills), organized hierarchically by levels, and the edges indicate logical dependencies for composition and aggregation. These connections acquire specific meaning during the modeling of the assessment system by defining how the score of a given node depends on its input components. The nodes at the last level represent one or more final grades.

Figure 1

Figure 1. Meta-meta model of hierarchical graph organization of assessment components.

Mathematically, a graph G with $m$ levels and $k_m$ elements at each level can be described as an ordered pair nodes $V$ and edges $E$ : $G=(V,E)$ , where $V=\left\{v_{i,j}\right\},i=\mathrm{1..}m,j=\mathrm{1..}{k}_i\forall i,m\in N,k_i\in N$ , and $E\subseteq \left\{\right(v_{p,q},v_{r,s}\left)\right\},p=\mathrm{1..}(m-1),q=\mathrm{1..}{k}_p\forall p,r=(p+1)\mathrm{..}m\forall p,s=\mathrm{1..}{k}_r\forall r$ .

Although the model allows for networked dependencies, in practice, tree-like structures are more commonly used – an example of such a structure is shown in black in the figure.

3.2 Meta-model of an assessment system

Assessment meta-models provide a more concrete description compared to the general meta-meta-model. Each meta-model describes a whole class of assessment systems with a common structure – it defines the core assessment components, the relationships between them, and possible parameterized methods for calculating scores. The components in meta-models are typically based on established classifications of knowledge and skills.

A classic example is the theory–practice meta-model (Figure 2a), which consists of two main components – one for theoretical knowledge and one for practical skills. The final grade is calculated as a function of these two values. A linear function is commonly used, where individual scores are normalized to a common scale: $\mathit{\text{finalGrade}}=w_1\mathit{\text{theory}}+w_2\mathit{\text{practice}}$ , where $w_1>0$ and $w_2>0$ are the weights reflecting the significance of the theory and practice scores, and $w_1+w_2=1$ .

Figure 2

Figure 2. Example assessment meta-models: (a) theory–practice; (b) theory–practice over HOTS–LOTS; (c) HOTS–LOTS over theory–practice; (d) Bloom’s cognitive taxonomy; (e) HOTS–LOTS over Bloom’s cognitive taxonomy.

In the meta-model, specific weights in the assessment functions and the exact methods for calculating the scores of first-level components are not defined. These details are specified in the next stage of the modeling process.

Other assessment meta-models – including those focused on Lower Order Thinking Skills (LOTS) and Higher Order Thinking Skills (HOTS), as well as extensions of the theory–practice model – can be derived from our previous studies (Hadzhikolev et al., 2020). In these models, the main assessment components are: theory HOTS, theory LOTS, practice HOTS, and practice LOTS.

In the theory–practice over HOTS–LOTS meta-model (Figure 2b), the second-level components are theory and practice, obtained by aggregating the corresponding HOTS and LOTS elements. In the HOTS–LOTS over theory–practice meta-model (Figure 2c), the second level is divided into HOTS and LOTS, which aggregate theoretical and practical assessments based on the type of cognitive skills.

Bloom’s cognitive taxonomy provides rich opportunities for constructing assessment models (Figure 2d). Using such a meta-model requires users to have a solid understanding of Bloom’s taxonomy and the ability to properly and accurately create specific assessment items/questions distributed across the cognitive levels.

Incorporating HOTS–LOTS logic into the HOTS–LOTS over Bloom’s cognitive taxonomy meta-model (Figure 2e) offers evaluators the ability to develop a more flexible assessment methodology by assigning weights to the assessment components at a later stage.

The methods for calculating intermediate and final scores typically use linear functions with weights reflecting the importance of the parent components. However, more complex non-linear dependencies are also possible, including cross-level evaluations, transformations such as normalization to a common scale, rounding, and others. Assessment methods can be based on linear models, fuzzy logic, artificial intelligence, or combinations thereof. The choice of an appropriate approach depends on the specific educational discipline and the decisions made by the team responsible for the assessment.

3.3 Model of an assessment system

When creating and configuring assessment models, it is necessary to define how the scores of the first-level components will be calculated, as well as which assessment methods will be used. In educational environments, these components typically correspond to different activities such as Assignment, Test, etc., and the method of evaluation is determined by the instructor. Assessment methods can be viewed as functions whose variables take values from the results of the first-level components.

Examples of such models, based on the presented meta-models, are illustrated in Figure 3. In the models built around HOTS and LOTS (Figures 3a–c), the main first-level components include theoretical and practical HOTS and LOTS. These components can be evaluated using different types and numbers of questions, which are defined at a later stage during the construction of the assessment system. Various methods can be used to calculate intermediate and final scores – artificial neural networks, fuzzy logic, linear and nonlinear functions, and others. Training artificial intelligence-based methods for assessment purposes requires the prior collection of sufficient data, including scores for each component of the model.

Figure 3

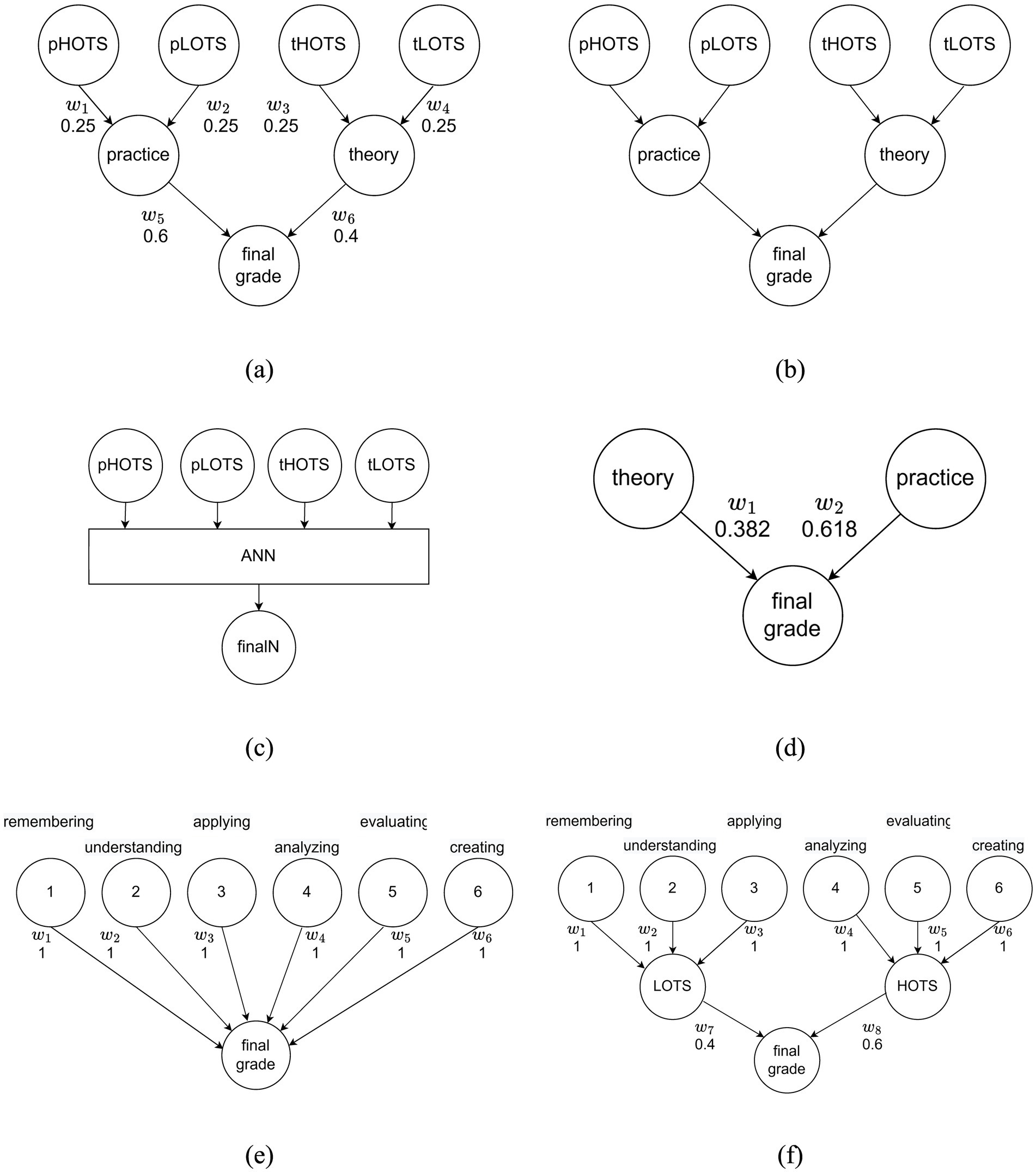
Figure 3. Example assessment models with component weights: (a) theory–practice over HOTS–LOTS; (b) HOTS–LOTS over theory–practice; (c) ANN over HOTS–LOTS; (d) theory–practice; (e) Bloom’s cognitive taxonomy; (f) HOTS–LOTS over Bloom’s cognitive taxonomy.

Assessment methods based on two main components – theory and practice (Figure 3d) – can be reduced to a formula for calculating the arithmetic mean, where the weights of the components are equal: $w_1=w_2=0.5$ . In the search for balance between theory and practice, and consideration of the risk of dishonest behavior by students during remote assessments, other weightings can be experimented with – for example, those based on the golden ratio: $w_1=0.618,w_2=0.382$ .

Assessment methods based on Bloom’s taxonomy can be reduced to assigning specific weights to the different components according to predefined models – flat, progressive, basic, regressive (Hadzhikoleva et al., 2019) – or other models defined by the user.

3.4 Assessment system

The specification of the questions used to calculate the scores for first-level components is carried out during the creation of the actual assessment system. Each component at this level contains multiple assessment elements – for example, test questions, each of which carries a specific value when answered correctly.

During the configuration stage of the system, various parameters are defined for each component, such as: a question bank; the method of question selection during the test (e.g., random or fixed); time limits for completion; overall difficulty, based on predefined difficulty levels for individual questions; the primary assessment method; and additional assessment methods used for more in-depth analysis of the results.

3.5 Use and analysis of the assessment system

The use of the assessment system involves generating an individual test for each learner and completing it. The score is calculated based on the selected primary assessment method.

During the analysis stage, the test author compares the results from different assessment methods in order to select the most appropriate and effective primary method for future assessments.

3.6 Generating test questions using generative artificial intelligence

Creating a diverse range of questions aligned with Bloom’s taxonomy represents a significant challenge for test authors. It requires a deep understanding of cognitive levels and knowledge categories, as well as the skills to formulate tasks that correspond to each of them. Questions developed using this methodology can be relatively easily grouped into the two broader categories – LOTS and HOTS.

Techniques for creating questions according to Bloom’s levels are presented in Bloom (1956), Anderson and Krathwohl (2001), and Crocker and Algina (2008). These include the use of specific key verbs and question words when formulating assignments, essays, questions, and other tasks appropriate for each level.

Approaches and sample questions for designing test tasks in the field of programming, based on Bloom’s taxonomy levels, are described in Omar et al. (2012) and Sobral (2021).

For the purposes of electronic and automated assessment, multiple-choice questions are the most suitable, as they can be easily evaluated automatically. However, this approach limits the ability to use more complex types of tasks that require open-ended responses or analytical reasoning.

Experiments with large language models (LLMs), such as ChatGPT, demonstrate effective capabilities for the automated generation and integration of questions into learning systems through LLM APIs (Hadzhikoleva et al., 2024). On the other hand, authors can also use standard LLM applications to generate questions without relying on additional automated tools. Of course, in both cases, the generated questions and answers must be verified and aligned with the learners’ knowledge level.

An example prompt for generating questions at different Bloom’s taxonomy levels for the course “Programming” is as follows:

Create a test for the course “Programming.” Generate 6 questions, one for each level of Bloom’s taxonomy (Remembering, Understanding, Applying, Analyzing, Evaluating, Creating).

Use various question types such as multiple-choice, short-answer, open-ended, code-writing, debugging, or design tasks. Make sure that the question for the “Creating” level requires the learner to produce or design something (for example, write a short piece of code or outline a program structure), rather than simply selecting a correct answer.

The results generated by ChatGPT-4o are presented in Table 1. Additional instructions in the prompt may relate to the programming language, difficulty level, and other factors. It is also important to note that questions can be generated based on user-provided materials, such as a text file containing a lecture.

Table 1

Table 1. Sample Bloom’s taxonomy-based test generated by ChatGPT-4o.

In the presented examples, Bloom’s Taxonomy was used to differentiate cognitive objectives. However, there are other taxonomies that could be used with equal success, such as the SOLO Taxonomy (Jaiswal, 2019), Fink’s Taxonomy (Fink, 2009), Webb’s Depth of Knowledge (Hess, 2013), and others.

3.7 Summary

Table 2 presents a summary of the stages involved in the modeling, use, and analysis of an assessment system.

Table 2

Table 2. Stages for modeling, using, and analyzing an assessment system.

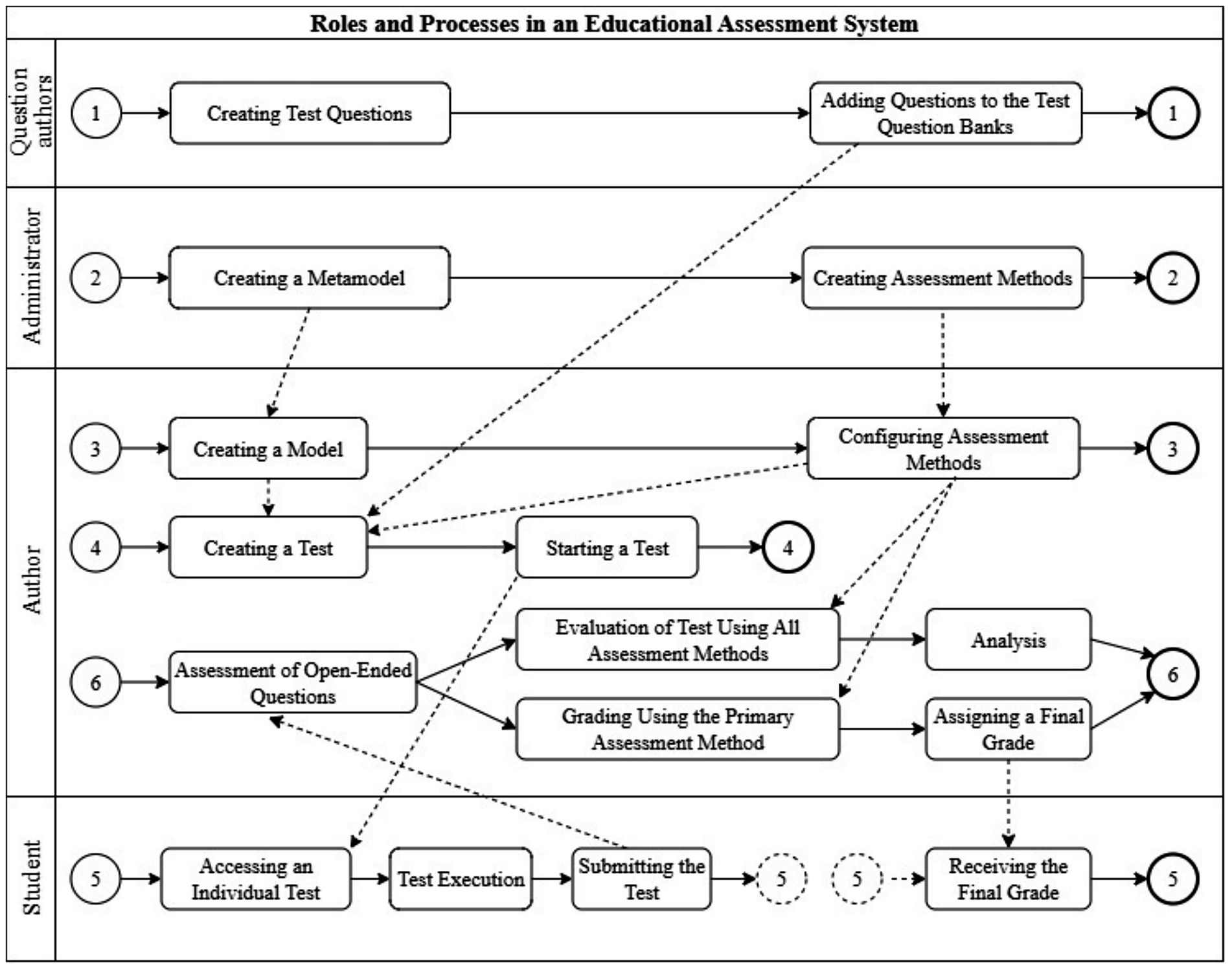
The main user roles and processes in an educational assessment system are presented in Figure 4.

Figure 4

Figure 4. Roles and processes in an educational assessment system.

Question authors create questions and store them in question banks (process 1), which can later be used by model and test authors. The administrator creates meta-models based on the system’s built-in meta-meta-model and adds possible assessment methods to them (process 2). The author creates an assessment model and selects and configures the corresponding assessment methods (process 3). Based on the created model and its assessment methods, the author can configure tests (process 4) by using the available question banks. After configuring a test, the author can launch it for a specific group of students.

Each student receives an individual test, completes it, and submits it (process 5), after which they can view their final grade.

Test evaluation (process 6) includes manual grading of open-ended questions by the author, automated scoring of all tests using the primary assessment method, and distribution of final grades to the respective students. Tests can also be evaluated using additional assessment methods, and the results can be analyzed to improve questions, choose a more suitable primary assessment method, and more.

4 Discussion

This paper aims to present a comprehensive theoretical model for multi-component assessment, focusing on the conceptual modeling and formalization of the main components, methods and relationships between them. It is focused on the modeling and architectural aspect of the system and aims to propose a unified framework that would unify different assessment paradigms – Bloom’s Taxonomy, LOTS/HOTS, theory/practice, fuzzy logic, AI, etc. The proposed models are inspired by empirical experiments on assessing higher-order thinking skills of university students (Hadzhikolev et al., 2021; Hadzhikolev et al., 2019). As future work, we have planned additional research dedicated to the validation and testing of the framework in a specific environment, which will be presented in other publications.

4.1 Configuring weights

Configuring the weights of the assessment components is essential for the purposes of assessment. The weights can be customized depending on the specifics of the academic discipline. For example, in disciplines with a high practical focus, a weight of w₁ = 0.4 for theory and w₂ = 0.6 for practice can be set, while in more theoretical disciplines, these values can be interchanged. Automated configuration of the weights can be performed using the following algorithm:

1. Entering the type of academic discipline (theoretical, practical, mixed).

2. Selecting a predefined profile (e.g., equal weights, golden ratio, teacher’s choice or other).

3. When selecting “teacher’s choice”:

3.1 Entering weights by the teacher—manually, via a graphical interface.

3.2 Check whether the sum of the entered weights is equal to 1.

4. Record the weights and apply them to the assessment model.

The modeling system allows the teacher to choose weights according to:

• The objectives of the training (e.g., emphasis on critical thinking or factual knowledge),

• The type of assessed activities (project, test, case study, etc.),

• The number and type of components in the model (LOTS, HOTS, theory, practice, etc.).

In this way, flexibility and adaptability are ensured, taking into account the specifics of the educational discipline and the individual teaching style.

4.2 Validation of AI-generated questions

Automatic question generation using generative artificial intelligence must necessarily be subject to verification by a qualified teacher (validation and filtering). In this context, a basic validation process is appropriate to include the following steps:

1. Setting criteria, e.g., Bloom’s level, question type, complexity level, language/syntax (in programming), etc.

2. Generating questions via LLM with a predefined prompt.

3. Automatic checking for duplicate or obviously wrong questions (e.g., with incorrect syntax).

4. Manual expert verification by a teacher:

4.1 Does the question correspond to the target cognitive level;

4.2 Is there a single correct answer (if the question is closed-ended);

4.3 Is the question relevant in the context of the learning content being studied.

5. Approval or editing of the question before including it in the question database.

A similar approach has been implemented and successfully experimented in Hadzhikoleva et al. (2024).

4.3 Applicability, scalability, and teacher training

One of the potential barriers to the implementation of the proposed framework is the need for institutional support and the availability of teacher expertise in areas such as Bloom’s Taxonomy and the use of specialized AI tools suitable for teaching. In order for the model to be applicable in a wider context, including in educational institutions with limited resources, it is necessary to foresee the possibility of flexible and phased implementation.

First, the framework can be adapted for simpler use by using open source platforms such as Moodle and free AI tools with minimal technical requirements. In the absence of automation, certain processes such as taxonomy classification or validation of test questions can be performed manually by teachers using templates and sample guides.

Second, the need for teacher training can be compensated for through internal training, online courses and the exchange of good practices within the academic community. It is recommended that the implementation of the framework be accompanied by a phased professional development aimed at building basic skills in pedagogical planning, task differentiation and the use of AI-based educational tools.

In this context, the proposed framework can serve not only as an assessment tool, but also as a strategic reference for institutions seeking a sustainable and technologically supported approach to measuring educational outcomes.

5 Conclusion

The present article introduces a comprehensive concept for modeling and implementing multi-component assessment systems. The proposed modeling approach, based on a single foundational meta-meta-model, enables the integration of various assessment strategies within a unified system – such as Bloom’s cognitive taxonomy, LOTS/HOTS, theory/practice, fuzzy logic, artificial intelligence, and others.

Through built-in analysis capabilities, instructors can improve the quality of their tests and assessments by enhancing objectivity and fairness in electronic examinations. This, in turn, may increase student motivation and trust in the assessment process.

The implementation of the proposed theoretical model in a LMS represents a significant challenge and is the subject of ongoing and future research and development.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

SH: Writing – original draft, Resources, Conceptualization, Methodology, Formal analysis; EH: Writing – original draft, Conceptualization, Methodology, Formal analysis, Visualization; SG: Writing – original draft, Investigation, Formal analysis, Project administration, Funding acquisition; GP: Writing – review & editing, Formal analysis, Validation.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The paper is funded by the European Union-Next GenerationEU, through the National Recovery and Resilience Plan of the Republic of Bulgaria, project no. BG-RRP-2.004-0001-C01. The first author also thanks the University of Plovdiv “Paisii Hilendarski”, project No MUPD25-FMI-015, for supporting this study.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Allen, M., and Yen, W. (2001). Introduction to measurement theory. Long Grove, USA: Waveland Pr Inc. 157766230X.

Google Scholar

Anderson, L. W., and Krathwohl, D. R. (2001). A taxonomy for learning, teaching, and assessing: a revision of Bloom's taxonomy of educational objectives: complete edition. New York, USA: Addison Wesley Longman, Inc.

Google Scholar

Bloom, B. (1956). “Taxonomy of educational objectives: The classification of educational goals” in Handbook I: Cognitive domain ed. B. S. Bloom (New York: David McKay Company).

Google Scholar

Close, D. (2009). Fair grades. Teach. Philos. 32, 361–398. doi: 10.5840/teachphil200932439

Crossref Full Text | Google Scholar

Crocker, L., and Algina, J. (2008). Introduction to classical and modern test theory. Mason, USA: Cengage Learning 0495395919.

Google Scholar

Fink, D. L. (2009) A self directed guide to designing course for significant learning, San Francisco: Jossey-Bass. Available online at: https://www.bu.edu/sph/files/2014/03/www.deefinkandassociates.com_GuidetoCourseDesignAug05.pdf

Google Scholar

Gaftandzhieva, S., Doneva, R., and Bliznakov, M. (2023). A comprehensive approach for monitoring student satisfaction in blended learning courses. Cybern. Inf. Technol. 23, 181–198. doi: 10.2478/cait-2023-0043

Crossref Full Text | Google Scholar

Hadzhikolev, E., Hadzhikoleva, S., Yotov, K., and Borisova, M. (2021). Automated assessment of lower and higher-order thinking skills using artificial intelligence methods. Commun. Comput. Inform. Sci. 1521, 13–25. doi: 10.1007/978-3-031-04206-5_2

Crossref Full Text | Google Scholar

Hadzhikolev, E., Hadzhikoleva, S., Yotov, K., and Orozova, D. (2020). Models for multicomponent fuzzy evaluation, with a focus on the assessment of higher-order thinking skills. TEM J. 9:1656. doi: 10.18421/TEM94-43

Crossref Full Text | Google Scholar

Hadzhikolev, E., Yotov, K., Trankov, M., and Hadzhikoleva, S.. (2019). Use of neural networks in assessing knowledge and skills of university students, Proceedings of ICERI2019 conference, 11th-13th November 2019, Seville, Spain, 7474–7484.

Google Scholar

Hadzhikoleva, S., Hadzhikolev, E., and Kasakliev, N. (2019). Using peer assessment to enhance higher order thinking skills. TEM J. 8, 242–247. doi: 10.18421/TEM81-34

Crossref Full Text | Google Scholar

Hadzhikoleva, S., Rachovski, T., Ivanov, I., Hadzhikolev, E., and Dimitrov, G. (2024). Automated test creation using large language models: a practical application. Appl. Sci. 14:9125. doi: 10.3390/app14199125

Crossref Full Text | Google Scholar

Hendrik, H., and Hamzah, A. (2021). Flipped classroom in programming course: a systematic literature review. Int. J. Emerg. Technol. Learn. 16, 220–236. doi: 10.3991/ijet.v16i02.15229

Crossref Full Text | Google Scholar

Hess, К. (2013). A guide for using Webb’s depth of knowledge with common Core state standards, 2013 common Core Institute. Available online at: https://www.paadultedresources.org/wp-content/uploads/2022/08/Webbs-DOK-Flip-Chart.pdf

Google Scholar

Hristov, H., and Krushkov, H. (2016). In-depth interview. Math. Inform. 59, 368–380.

Google Scholar

Hristov, H., Yonchev, E., and Tsvetkov, V. (2022). Modelling of pedagogical patterns through e-learning objects. Inf. Technol. Learn. Tools 89, 121–130. doi: 10.33407/itlt.v89i3.4859

Crossref Full Text | Google Scholar

Jaiswal, P. (2019). Using constructive alignment to foster teaching learning processes. Engl. Lang. Teach. 12, 10–23. doi: 10.5539/elt.v12n6p10

Crossref Full Text | Google Scholar

Kaplan, A. M., and Haenlein, M. (2016). Higher education and the digital revolution: about MOOCs, SPOCs, social media, and the cookie monster. Bus. Horiz. 59, 441–450. doi: 10.1016/j.bushor.2016.03.008

Crossref Full Text | Google Scholar

Kirilova, B. (2023). Assessment of the different subject areas in an interdisciplinary project. Proc. Int. Conf. Educ. New Dev. 2, 35–47. doi: 10.36315/2023v2end004

Crossref Full Text | Google Scholar

Kirilova, B. (2024). Addressing challenges in enhancing team collaboration and evaluating interdisciplinary projects. Pedagogika-Pedagogy 96, 655–670. doi: 10.53656/ped2024-5.05

Crossref Full Text | Google Scholar

Kiryakova, G. (2019). Massive open online courses–a modern form of distance education. Trakia J. Sci. 17, 909–913. doi: 10.15547/tjs.2019.s.01.150

Crossref Full Text | Google Scholar

Kiryakova, G. (2021). E-assessment-beyond the traditional assessment in digital environment. IOP Conf. Ser. Mater. Sci. Eng. 1031:12063. doi: 10.1088/1757-899X/1031/1/012063

Crossref Full Text | Google Scholar

Mardani, A., Jusoh, A., Nor, K., Khalifah, Z., Zakwan, N., and Valipour, A. (2015). Multiple criteria decision-making techniques and their applications–a review of the literature from 2000 to 2014. Econ. Res.-Ekon. Istraž. 28, 516–571. doi: 10.1080/1331677X.2015.1075139

Crossref Full Text | Google Scholar

Milano, S., McGrane, J. A., and Leonelli, S. (2023). Large language models challenge the future of higher education. Nat. Mach. Intell. 5, 333–334. doi: 10.1038/s42256-023-00644-2

Crossref Full Text | Google Scholar

Minev, M., and Koeva-Dimitrowa, L. (2019). Review of the development of massive open online courses (MOOCs) on international level and perspectives for their implication in Bulgarian higher education, Proceedings of the second Varna conference on e-learning and knowledge management, pp. 11–18

Google Scholar

Nacheva-Skopalik, L., and Green, S. (2016). Intelligent adaptable e-assessment for inclusive e-learning. Int. J. Web Learn. Teach. Technol. 11, 21–34. doi: 10.4018/IJWLTT.2016010102

Crossref Full Text | Google Scholar

Nenkov, N., Dimitrov, G., Dyachenko, Y., and Koeva, K.. (2016). Artificial intelligence technologies for personnel learning management systems. In 2016 IEEE 8th international conference on intelligent systems (IS) (pp. 189–195). IEEE.

Google Scholar

Nikolovski, V., Trajanov, D., and Chorbev, I. (2025). Advancing AI in higher education: a comparative study of large language model-based agents for exam question generation, improvement, and evaluation. Algorithms 18:144. doi: 10.3390/a18030144

Crossref Full Text | Google Scholar

Omar, N., Haris, S. S., Hassan, R., Arshad, H., Rahmat, M., Zainal, N. F. A., et al. (2012). Automated analysis of exam questions according to Bloom's taxonomy. Procedia Soc. Behav. Sci. 59, 297–303. doi: 10.1016/j.sbspro.2012.09.278

Crossref Full Text | Google Scholar

Ruskov, S., and Ruskova, Y. (2013). The problem of evaluation in higher education, XXI International Scientific-Technical Conference Trans & Motauto’ 13, vol. 3, 73–79 ISSN 1310-3946.

Google Scholar

Schaughency, E., Smith, J. K., van der Meer, J., and Berg, D. (2012). “Classical test theory and higher education: five questions” in Handbook on measurement, assessment, and evaluation in higher education. ed. J. K. Smith (Mason, USA: Routledge), 137–151.

Google Scholar

Sobral, S. R. (2021). Bloom's taxonomy to improve teaching-learning in introduction to programming. Int. J. Inf. Educ. Technol. 11, 148–153. doi: 10.18178/ijiet.2021.11.3.1504

Crossref Full Text | Google Scholar

Suskie, L. (2002). Fair assessment practices: giving students equitable opportunities to demonstrate learning. Adv. Assess. 14, 5–10.

Google Scholar

TeSLA Project. Trust-Based Authentication & Authorship—TeSLA Project (2019). Available online at: https://tesla-project.eu/ (Accessed May 11, 2025).

Google Scholar

Velcheva, I., and Peykova, D. (2024). Innovative practices in teachers’ and students’ trainings. Pedagogika-Pedagogy 96, 108–118. doi: 10.53656/ped2024-1.08

Crossref Full Text | Google Scholar

Wang, L., Song, R., Guo, W., and Yang, H. (2024). Exploring prompt pattern for generative artificial intelligence in automatic question generation. Interact. Learn. Environ. 33, 2559–2584. doi: 10.1080/10494820.2024.2412082

Crossref Full Text | Google Scholar

Wen, D., and Wu, X. (2022). Influence of SPOC classroom teaching on e-learning satisfaction. Int. J. Emerg. Technol. Learn. 17, 16–28. doi: 10.3991/ijet.v17i12.31761

Crossref Full Text | Google Scholar

Whitley, B. E., Perkins, D. V., Balogh, D. W., Keith-Speigel, P., and Wittig, A. F. (2000). Fairness in the classroom. APS Obs. 13, 24–27.

Google Scholar

You, H. (2019). Students’ perception about learning using MOOC. Int. J. Emerg. Technol. Learn. 14, 203–208. doi: 10.3991/ijet.v14i18.10802

Crossref Full Text | Google Scholar

Zhuge, Q., Wang, H., and Chen, X. (2025). TwinStar: a novel design for enhanced test question generation using dual-LLM engine. Appl. Sci. 15:3055. doi: 10.3390/app15063055

Crossref Full Text | Google Scholar