Psychometric evaluation of the abbreviated math anxiety scale in Russian university students

Math anxiety can hinder learning and deter students from pursuing STEM fields. The Abbreviated Math Anxiety Scale (AMAS) is a short measure of math anxiety, but its use among Russian university students has not been previously evaluated. We assessed the psychometric properties of the AMAS in a sample of 6,337 Russian first-year university students (mean age 18.6 ± 0.96; 64.4% female). Confirmatory factor analysis indicated that a bifactor model—with a general Math Anxiety factor and two specific factors (Learning Math Anxiety and Math Evaluation Anxiety)—fit the data best (CFI = 0.995, RMSEA = 0.048). The AMAS demonstrated good internal consistency (Cronbach’s α = 0.82–0.86; McDonald’s ω = 0.83–0.86) and convergent validity via moderate correlations with trait anxiety (r = 0.35–0.44, p < 0.001). Measurement invariance across gender and academic profile (STEM vs. non-STEM majors) was supported, suggesting that the scale functions equivalently across these groups. Overall, the Russian version of the AMAS exhibits strong psychometric properties in this population and can be confidently used to assess math anxiety among Russian university students.

1 Introduction

Math anxiety is characterized by an intensive feeling of fear, apprehension and tension during math-related activities, such as basic arithmetic calculations or solving differential equations (Richardson and Suinn, 1972). It is accompanied by a negative math self-concept (Kaskens et al., 2020), negative attitudes towards math (Hembree, 1990; Casanova et al., 2021), low math interest (Du et al., 2021), low math value (Wang et al., 2014), and math avoidance, resulting in reduced math competence and restricted career opportunities (Ashcraft, 2002). Although it often overlaps with general and test anxiety, math anxiety is considered a domain-specific construct tied to math contexts (e.g., calculations, exams). A number of studies have reported a negative link between math anxiety and math performance (see Zhang et al., 2019; Barroso et al., 2021 for a meta-analysis), which is likely bidirectional (Carey et al., 2015). On the one hand, individuals with initially low math abilities tend to exhibit higher math anxiety (Maloney et al., 2012; Ferguson et al., 2015). On the other hand, high math anxiety has a detrimental effect on math performance by disrupting cognitive processing and working memory (Ashcraft, 2002; Carey et al., 2015; Lau et al., 2024; Ramirez et al., 2018; Dowker et al., 2016; Foley et al., 2017).

Although the majority of studies on math anxiety concern schoolchildren, some studies have focused on college and university students (Betz, 1978; Bjälkebring, 2019; Cumhur and Tezer, 2019; Rossi et al., 2023; Zanabazar et al., 2023; Khasawneh et al., 2021). Like schoolchildren, students with high math anxiety show lower math achievement (Betz, 1978) and are prone to seek help from their peers to pass math courses (Bjälkebring, 2019).

The abbreviated math anxiety scale (AMAS), developed from the mathematics anxiety rating scale (MARS) by Hopko et al. (2003), is one of the most widespread tools for measuring math anxiety. The AMAS has been validated for a variety of cultural contexts and age groups, showing good fit with the data, as well as both gender and cultural invariance (Primi et al., 2020; Cohen and Limbers, 2022). The AMAS—a 9-item questionnaire with two subscales: Learning Math Anxiety (LMA) and Math Evaluation Anxiety (MEA). Items are rated on a 0–4 scale, and the tool has shown strong reliability, a robust two-factor or bifactor structure, and measurement invariance across gender and cultures. Recent studies also support its reliability among Russian schoolchildren (Marakshina et al., 2023, 2024).

Several studies have compared math anxiety prevalence across different cultures (Linna et al., 2024; Yuan et al., 2023).

Prevalence varies by measurement, but research consistently finds higher math anxiety in females and lower levels in STEM students. These group differences highlight the need for valid and unbiased assessment tools across gender and academic profiles. To our knowledge, no study has investigated the psychometric properties of the AMAS in a population of Russian students. This study addresses that gap by evaluating: Factor structure (via confirmatory factor analysis), Reliability of total and subscale scores, Construct validity (correlation with trait anxiety), and Measurement invariance across gender and academic profile (STEM vs. non-STEM).

Based on prior work, we expected strong reliability, a good-fitting bifactor model, and invariance across groups.

2 Method

2.1 Participants

The study involved 6,337 first-year university students (35.6% male, 64.4% female) aged 18–24 years (M = 18.58, SD = 0.96), recruited from 26 public universities across 19 regions of Russia, during scheduled online assessment sessions. Academic majors were categorized into STEM (science, technology, engineering, mathematics), and non-STEM (including humanities, social sciences, and life sciences), to facilitate comparisons by academic profile. Approximately 26% of the sample were enrolled in STEM majors, while the remaining 74% pursued non-STEM disciplines. Participation was voluntary, and responses were collected anonymously to minimize any response bias. Informed consent was obtained electronically. Ethical approval was granted by the Ethics Committee of the Psychological Institute of the Russian Academy of Education. The questionnaires were administered in a scheduled online session at the university under standardized conditions with staff supervision. Respondents with incomplete demographic or questionnaire data were excluded from analysis.

2.2 Measures

The Abbreviated Math Anxiety Scale was adapted from Hopko et al. (2003). The AMAS consists of 9 items, with 5 items comprising the learning math anxiety subscale (LMA) and 4 items comprising the math evaluation anxiety subscale (MEA). Translation and back-translation procedures ensured semantic equivalence. Each item presents a math-related situation, and the respondent is asked to assess the intensity of anxiety in that scenario on a 5-point Likert scale ranging from 0 (low anxiety) to 4 (high anxiety).

To evaluate convergent validity, participants also completed the Trait subscale of the State–Trait Anxiety Inventory (STAI-T; Spielberger et al., 1983), a 20-item measure of general anxiety propensity rated on a 4-point Likert scale. This instrument has demonstrated acceptable internal consistency (Cronbach’s α ≈ 0.76).

2.3 Statistical analysis

All analyses were conducted in R (v4.3.1) using psychometric packages. Descriptive statistics were computed for AMAS scores, followed by confirmatory factor analysis (CFA) to evaluate four competing models: one-factor, two-factor (correlated LMA and MEA), second-order (LMA and MEA as first-order factors under a higher-order factor), and bifactor (general factor plus orthogonal LMA and MEA). Given the ordinal nature of item responses, large sample size and potentially skewed distribution, estimation was performed using the robust weighted least squares estimator (WLSMV). Model fit was assessed using established cutoffs for CFI and TLI (≥ 0.95), and RMSEA and SRMR (≤ 0.08). Model comparisons were based on these indices and, when appropriate, chi-square difference tests.

Internal consistency was assessed via Cronbach’s alpha and McDonald’s omega coefficients for the total scale and subscales, with values between 0.70 and 0.90 considered satisfactory. Item-total correlations were examined to assess item discrimination. Convergent validity was evaluated by calculating Pearson correlations between AMAS scores and the STAI-T trait anxiety score, with a moderate positive association hypothesized. Statistical significance was evaluated at α = 0.05 (two-tailed).

Measurement invariance across gender and academic profile was tested using multi-group CFA. Three nested models were specified for each grouping variable: configural (unconstrained), metric (equal factor loadings), and scalar (equal loadings and intercepts). Invariance was assessed based on changes in fit indices, with ΔCFI ≤ 0.01 and ΔRMSEA ≤ 0.015 indicating invariance, consistent with recommendations by Cheung and Rensvold (2002) and Chen (2007). Given the large sample size, chi-square differences were interpreted with caution, and model fit indices were prioritized.

3 Results

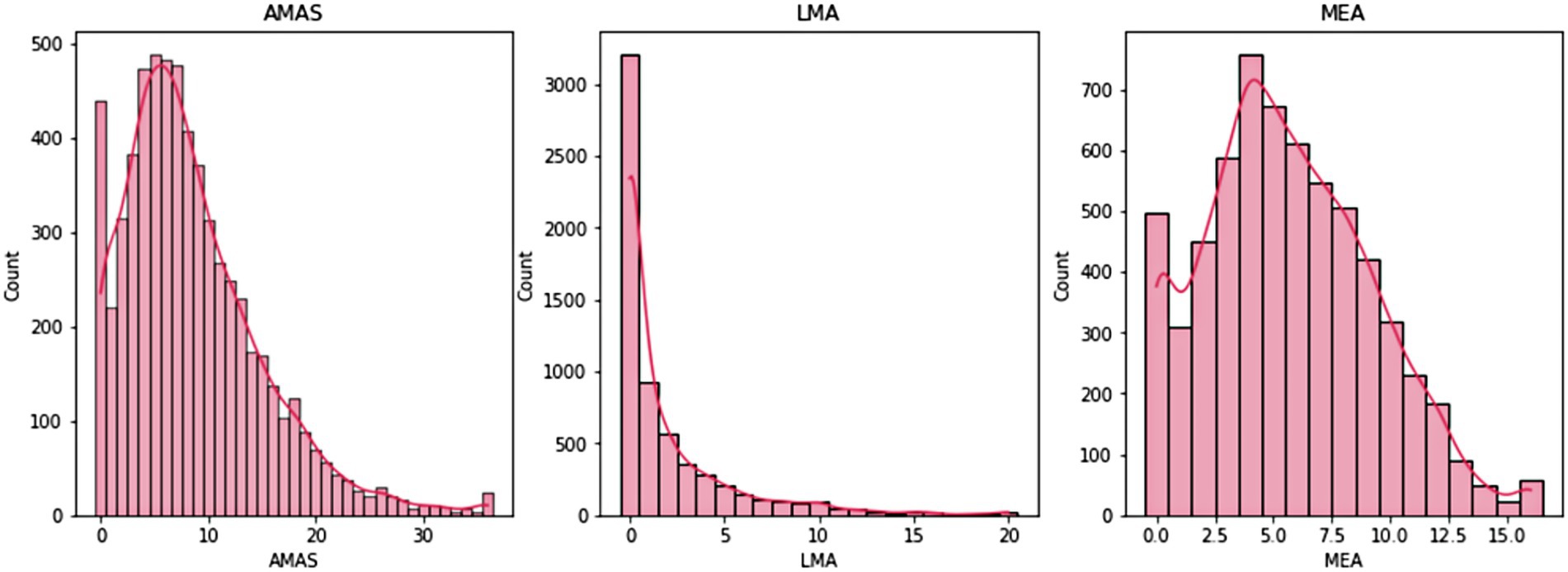
Table 1 presents descriptive statistics of the total AMAS scale as well as the LMA and MEA subscales. The distributions for all the scales are right skewed, especially the distribution of the LMA scores (see Figure 1). The Pearson correlation coefficient revealed a strong correlation between the LMA and MEA scores, with r = 0.61 (p < 0.001).

Table 1

Table 1. Descriptive statistics for the LMA, MEA, and total AMAS scores.

Figure 1

Figure 1. AMAS score distribution.

Confirmatory factor analyses (CFA) supported a bifactor structure for the AMAS as the best representation of the data (see Table 2). The one-factor model demonstrated poor fit (CFI = 0.914, RMSEA = 0.162), while both the two-factor and second-order models showed improved but still suboptimal fit (CFI = 0.977, RMSEA = 0.085). In contrast, the bifactor model achieved excellent fit indices (CFI = 0.995, RMSEA = 0.048) and was the only model with RMSEA < 0.05. Chi-square difference tests confirmed its superiority over all alternatives (p < 0.001), justifying its selection for further analyses.

Table 2

Table 2. Comparison of CFA models for the AMAS (N = 6,337).

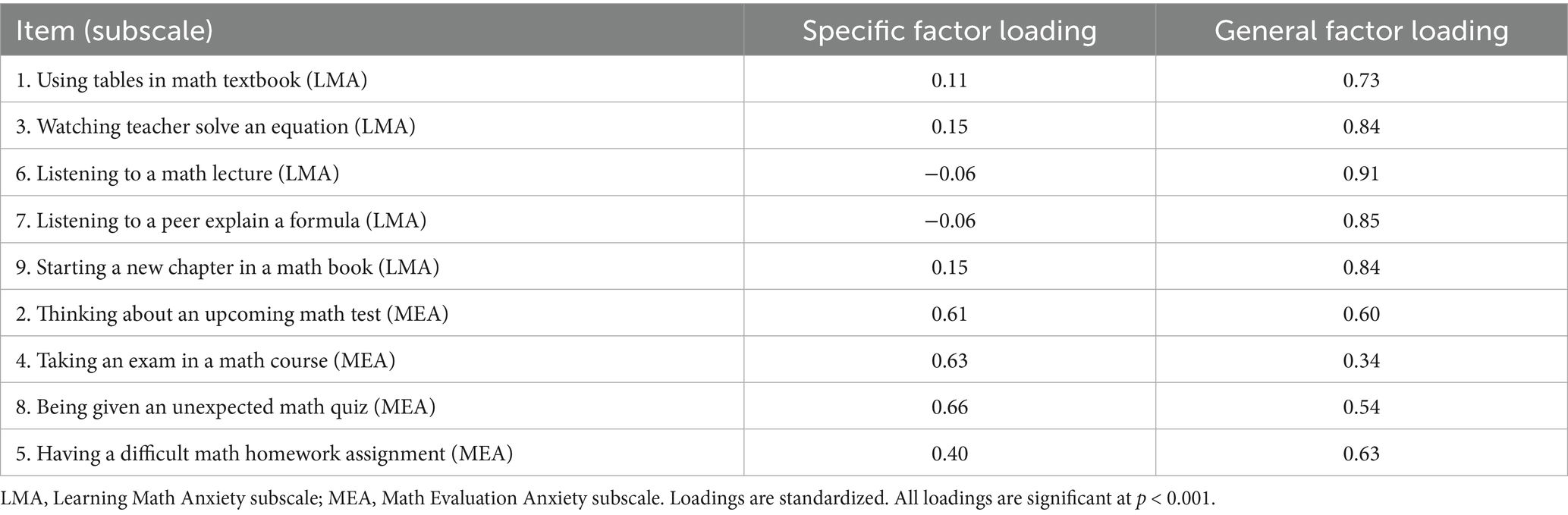
Factor loadings from the bifactor model indicated that all items loaded strongly on the general math anxiety factor (see Table 3). Loadings for Learning Math Anxiety (LMA) items ranged from 0.73 to 0.91, while Math Evaluation Anxiety (MEA) items ranged from 0.34 to 0.66. Specific-factor loadings were negligible for LMA items (−0.06 to 0.15), indicating near-complete overlap with the general factor. MEA items, however, retained moderate specific loadings (0.40 to 0.66), suggesting a distinct evaluative component in addition to the general anxiety factor. In our sample, the negligible loadings on the learning-specific factor indicate that math learning anxiety is largely subsumed by the general math anxiety factor, whereas evaluation-related anxiety retains distinctiveness.

Table 3

Table 3. Standardized factor loadings for the bifactor model of the AMAS.

The AMAS exhibited strong internal consistency (see Table 3), with Cronbach’s α values of 0.86 for the LMA subscale, 0.82 for MEA, and 0.86 for the total scale. McDonald’s ω coefficients were comparable (0.85–0.86), indicating minimal measurement error and confirming reliability across subscales. Corrected item-total correlations ranged from 0.48 to 0.70, supporting good item discrimination.

Construct validity was supported through moderate positive correlations with trait anxiety as measured by the STAI-T. The total AMAS score correlated at r = 0.44 (p < 0.001) with trait anxiety, while the LMA and MEA subscales correlated at r = 0.35 and r = 0.41, respectively (both p < 0.001). These associations align with theoretical expectations and prior research, indicating a meaningful but non-redundant relationship between math-specific and general anxiety constructs.

Multi-group CFA supported configural, metric, and scalar invariance of the AMAS across gender (see Table 3). The model demonstrated excellent fit in all invariance stages (CFI ≥ 0.985, RMSEA ≤ 0.042), with negligible changes in fit indices (ΔCFI ≤ 0.002, ΔRMSEA ≤ 0.002), and non-significant chi-square difference for scalar invariance (p = 0.49). These results indicate that the scale measures math anxiety equivalently in male and female students, allowing for meaningful group comparisons.

Invariance testing (see Supplementary Table 1) across academic profiles (STEM vs. non-STEM) also supported configural and metric invariance. Although chi-square difference tests for metric and scalar steps were significant (p < 0.001), changes in fit indices were minimal (total ΔCFI = 0.005; ΔRMSEA = 0.003), suggesting approximate scalar invariance. This indicates that while minor item-level differences may exist, the AMAS generally functions equivalently across academic domains.

4 Discussion

This study examined the psychometric properties of the Russian adaptation of the Abbreviated Math Anxiety Scale (AMAS) among a large cohort of university students. The findings support the AMAS as a reliable and valid measure of math anxiety in this population, aligning well with international evidence and extending prior research to the Russian higher education context.

The bifactor model provided the best fit to the data, outperforming alternative structures (one-factor, two-factor, and second-order). This aligns with prior work across diverse populations (e.g., Sadiković et al., 2018; Primi et al., 2020; Cohen and Limbers, 2022), which likewise reports a strong general math-anxiety factor accompanied by learning- and evaluation-specific facets. In our university sample, loadings on the learning-specific factor were negligible, whereas evaluation-specific loadings were moderate—indicating that learning-related anxiety is largely absorbed by the general factor, while evaluation-related anxiety retains distinctiveness. A plausible explanation is the performance-driven nature of higher education, in which evaluative settings pose a salient psychological challenge. Consistent with this interpretation, in our bifactor solution LMA items showed near-zero specific loadings (−0.06 to 0.15) but loaded strongly on the general factor (0.73–0.91), a pattern likely driven by item content that maps more closely to school-type study situations and by pronounced floor effects on LMA responses (≈90% “low/very low”). Although some authors caution that bifactor models can overfit for statistical reasons, in our case only the bifactor model met conventional fit thresholds, suggesting substantive rather than purely statistical superiority.

Notably, whereas Marakshina et al. (2023) found a second-order solution in Russian adolescents, our university sample exhibited a clearer bifactor structure. One parsimonious reading is developmental: by late adolescence/early adulthood, math anxiety behaves largely as a unidimensional construct, with evaluation experiences providing the primary differentiated trigger. Practically, AMAS scores in this context are best interpreted as reflecting a dominant general construct, with facet-level specificity most meaningful for evaluation and to be used cautiously for learning.

Measurement invariance across gender and academic profile was also supported at the configural, metric, and scalar levels. This indicates that the AMAS measures the underlying construct equivalently across male and female students and across STEM and non-STEM disciplines. While chi-square differences in profile-based comparisons were significant, minimal changes in CFI and RMSEA suggest that any non-invariance was negligible. These results align with prior findings of gender invariance (e.g., Marakshina et al., 2023) and extend the literature by demonstrating invariance across academic fields, which is rarely tested. Therefore, group differences observed in math anxiety scores likely reflect substantive differences rather than measurement bias, validating the AMAS for comparative research.

The scale demonstrated high internal consistency, with alpha and omega coefficients exceeding typical benchmarks and aligning with previous studies (Hopko et al., 2003; Primi et al., 2020). Item-total correlations confirmed that each item contributed meaningfully to the construct. Convergent validity was supported by moderate correlations between AMAS and trait anxiety scores, consistent with theoretical expectations and prior empirical work. This association affirms the conceptual link between math-specific anxiety and broader anxiety dispositions, while the moderate magnitude of the correlation confirms that math anxiety remains a distinct domain-specific phenomenon. These findings underscore the necessity of using tailored instruments like the AMAS rather than relying solely on general anxiety measures. Although the AMAS is a brief questionnaire and performed robustly in this study, it may not encompass all dimensions of math anxiety. In our sample, for instance, the learning-related anxiety items did not contribute much beyond the general anxiety factor, indicating a potential limitation in capturing that sub-dimension separately.

Nonetheless, several limitations merit consideration. The sample consisted exclusively of first-year students, limiting generalizability to more advanced or postgraduate populations. Future studies should examine whether the psychometric structure of the AMAS remains stable across educational stages. Additionally, while trait anxiety served as a useful convergent measure, future research could enhance construct validity evidence by including academic performance metrics or intervention outcomes.

5 Conclusion

In a large sample of Russian first-year students (N = 6,337), the Russian AMAS showed strong overall psychometric performance, with a dominant general factor and acceptable invariance across gender and academic profile (approximate scalar invariance). Prevalence estimates indicated that most students report low-to-moderate math anxiety, while a small subgroup (≈5%) exhibits high math anxiety. Practically, these results support the AMAS as a screening tool to identify students who may benefit from targeted support, particularly around evaluative contexts. Conceptually, the weak uniqueness of the learning-anxiety component suggests that, at the university level, math anxiety is largely unidimensional with evaluation-related experiences providing the main differentiated contribution. Future work should refine LMA item content for higher-education settings, incorporate additional validity evidence (e.g., academic outcomes), and examine institution-level factors not captured here.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Ethics statement

The studies involving humans were approved by Ethics Committee of the Psychological Institute of the Russian Academy of Education. The studies were conducted in accordance with the local legislation and institutional requirements. Written informed consent for participation in this study was provided by the participants’ legal guardians/next of kin.

Author contributions

SM: Conceptualization, Funding acquisition, Methodology, Supervision, Writing – review & editing. AP: Data curation, Formal analysis, Investigation, Writing – original draft. AM: Data curation, Investigation, Validation, Writing – original draft. TA: Data curation, Formal analysis, Investigation, Writing – review & editing. AT: Data curation, Formal analysis, Writing – review & editing. VI: Data curation, Investigation, Validation, Writing – review & editing. PK: Data curation, Investigation, Software, Writing – review & editing. TT: Data curation, Investigation, Project administration, Writing – review & editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This study was supported by a grant (No. 24-18-01102) from the Russian Science Foundation.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The authors declare that no Gen AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/feduc.2025.1669267/full#supplementary-material

References

Ashcraft, M. H. (2002). Math anxiety: personal, educational, and cognitive consequences. Curr. Dir. Psychol. Sci. 11, 181–185. doi: 10.1111/1467-8721.00196

Crossref Full Text | Google Scholar

Barroso, C., Ganley, C. M., McGraw, A. L., Geer, E. A., Hart, S. A., and Daucourt, M. C. (2021). A meta-analysis of the relation between math anxiety and math achievement. Psychol. Bull. 147, 134–168. doi: 10.1037/bul0000307

PubMed Abstract | Crossref Full Text | Google Scholar

Betz, N. E. (1978). Prevalence, distribution, and correlates of math anxiety in college students. J. Couns. Psychol. 25, 441–448. doi: 10.1037/0022-0167.25.5.441

Crossref Full Text | Google Scholar

Bjälkebring, P. (2019). Math anxiety at the university: what forms of teaching and learning statistics in higher education can help students with math anxiety? Front. Educ. 4:30. doi: 10.3389/feduc.2019.00030

Crossref Full Text | Google Scholar

Carey, E., Hill, F., Devine, A., and Szücs, D. (2015). The chicken or the egg? The direction of the relationship between mathematics anxiety and mathematics performance. Front. Psychol. 6:1987. doi: 10.3389/fpsyg.2015.01987

PubMed Abstract | Crossref Full Text | Google Scholar

Casanova, S., Vukovic, R. K., and Kieffer, M. J. (2021). Do girls pay an unequal price? Black and Latina girls’ math attitudes, math anxiety, and mathematics achievement. J. Appl. Dev. Psychol. 73:101256. doi: 10.1016/j.appdev.2021.101256

Crossref Full Text | Google Scholar

Chen, F.-F. (2007). Sensitivity of goodness of fit indexes to lack of measurement invariance. Struct. Equ. Model. 14, 464–504. doi: 10.1080/10705510701301834

Crossref Full Text | Google Scholar

Cheung, G. W., and Rensvold, R. B. (2002). Evaluating goodness-of-fit indexes for testing measurement invariance. Struct. Equ. Model. 9, 233–255. doi: 10.1207/S15328007SEM0902_5

Crossref Full Text | Google Scholar

Cohen, L. A., and Limbers, C. A. (2022). Factor structure and gender invariance of the abbreviated math anxiety scale (AMAS) in middle school students. Trends Psychol. 30, 788–807. doi: 10.1007/s43076-022-00167-6

PubMed Abstract | Crossref Full Text | Google Scholar

Cumhur, M., and Tezer, M. (2019). Anxiety about mathematics among university students: a multi-dimensional study in the 21st century. Cypriot J. Educ. Sci. 14, 222–231. doi: 10.18844/cjes.v14i2.4217

Crossref Full Text | Google Scholar

Dowker, A., Sarkar, A., and Looi, C. Y. (2016). Mathematics anxiety: what have we learned in 60 years? Front. Psychol. 7:508. doi: 10.3389/fpsyg.2016.00508

PubMed Abstract | Crossref Full Text | Google Scholar

Du, C., Qin, K., Wang, Y., and Xin, T. (2021). Mathematics interest, anxiety, self-efficacy and achievement: examining reciprocal relations. Learn. Individ. Differ. 91:102060. doi: 10.1016/j.lindif.2021.102060

Crossref Full Text | Google Scholar

Ferguson, A. M., Maloney, E. A., Fugelsang, J., and Risko, E. F. (2015). On the relation between math and spatial ability: the case of math anxiety. Learn. Individ. Diff. 39, 1–12. doi: 10.1016/j.lindif.2015.02.007

Crossref Full Text | Google Scholar

Foley, A. E., Herts, J. B., Borgonovi, F., Guerriero, S., Levine, S. C., and Beilock, S. L. (2017). The math anxiety–performance link: a global phenomenon. Curr. Dir. Psychol. Sci. 26, 52–58. doi: 10.1177/0963721416672463

Crossref Full Text | Google Scholar

Hembree, R. (1990). The nature, effects, and relief of mathematics anxiety. J. Res. Math. Educ. 21, 33–46. doi: 10.2307/749455

Crossref Full Text | Google Scholar

Hopko, D. R., Mahadevan, R., Bare, R. L., and Hunt, M. K. (2003). The abbreviated math anxiety scale (AMAS): construction, validity, and reliability. Assessment 10, 178–182. doi: 10.1177/1073191103010002008

PubMed Abstract | Crossref Full Text | Google Scholar

Kaskens, J., Segers, E., Goei, S. L., van Luit, J. E. H., and Verhoeven, L. (2020). Impact of children’s math self-concept, math self-efficacy, math anxiety, and teacher competencies on math development. Teach. Teach. Educ. 94:103096. doi: 10.1016/j.tate.2020.103096

Crossref Full Text | Google Scholar

Khasawneh, E., Gosling, C., and Williams, B. (2021). What impact does maths anxiety have on university students? BMC Psychol. 9:37. doi: 10.1186/s40359-021-00537-2

PubMed Abstract | Crossref Full Text | Google Scholar

Lau, N. T. T., Ansari, D., and Sokolowski, H. M. (2024). Unraveling the interplay between math anxiety and math achievement. Trends Cogn. Sci. 28, 937–947. doi: 10.1016/j.tics.2024.07.006

PubMed Abstract | Crossref Full Text | Google Scholar

Linna, D., Xinghua, W., Haiying, Y., Pavlova, A., Ismatullina, V., Malykh, A., et al. (2024). Psychometric properties of AMAS and math anxiety prevalence among Chinese and Russian schoolchildren: a comparative study. Front. Psychol. 15:1485753. doi: 10.3389/fpsyg.2024.1485753

Crossref Full Text | Google Scholar

Maloney, E. A., Waechter, S., Risko, E. F., and Fugelsang, J. A. (2012). Reducing the sex difference in math anxiety: the role of spatial processing ability. Learn. Individ. Differ. 22, 380–384. doi: 10.1016/j.lindif.2012.01.001

Crossref Full Text | Google Scholar

Marakshina, J., Pavlova, A., Ismatullina, V., Adamovich, T., Mironets, S., Sitnikova, M. A., et al. (2023). The Russian version of the abbreviated math anxiety scale: psychometric properties in adolescents aged 13–16 years. Front. Psychol. 14:1275212. doi: 10.3389/fpsyg.2023.1275212

PubMed Abstract | Crossref Full Text | Google Scholar

Marakshina, J. A., Pavlova, A. A., Ismatullina, V. I., Lobaskova, M. M., Adamovich, T. V., Mironets, S. A., et al. (2024). Psychometric properties of the abbreviated math anxiety scale in Russian high schoolers. Acta Biomed. Sci. 9, 151–160. doi: 10.29413/ABS.2024-9.1.16

Crossref Full Text | Google Scholar

Primi, C., Donati, M. A., Izzo, V. A., Guardabassi, V., O’Connor, P. A., Tomasetto, C., et al. (2020). The early elementary school abbreviated math anxiety scale (the EES-AMAS): a new adapted version of the AMAS. Front. Psychol. 11:1014. doi: 10.3389/fpsyg.2020.01014

Crossref Full Text | Google Scholar

Ramirez, G., Shaw, S. T., and Maloney, E. A. (2018). Math anxiety: past research, promising interventions, and a new interpretation framework. Educ. Psychol. 53, 145–164. doi: 10.1080/00461520.2018.1447384

Crossref Full Text | Google Scholar

Richardson, F. C., and Suinn, R. M. (1972). The mathematics anxiety rating scale: psychometric data. J. Couns. Psychol. 19, 551–554. doi: 10.1037/h0033456

Crossref Full Text | Google Scholar

Rossi, S., Xenidou-Dervou, I., and Cipora, K. (2023). Emotions and mathematics: anxiety profiles and their influence on arithmetic performance. R. Soc. Open Sci. 10:230861. doi: 10.1098/rsos.230861

Crossref Full Text | Google Scholar

Sadiković, S., Milovanović, I., and Oljača, M. (2018). Another psychometric proof of the abbreviated math anxiety scale usefulness: IRT analysis. Prim. Psihol. 11, 301–323. doi: 10.19090/pp.2018.3.301-323

Crossref Full Text | Google Scholar

Spielberger, C. D., Gorsuch, R. L., Lushene, R. E., Vagg, P. R., and Jacobs, G. A. (1983). Manual for the state-trait anxiety inventory. Palo Alto, CA: Consulting Psychologists Press.

Google Scholar

Wang, Z., Hart, S. A., Kovas, Y., Lukowski, S., Soden, B., Thompson, L. A., et al. (2014). Who is afraid of math? Two sources of genetic variance for mathematical anxiety. J. Child Psychol. Psychiatry 55, 1056–1064. doi: 10.1111/jcpp.12224

PubMed Abstract | Crossref Full Text | Google Scholar

Yuan, Z., Tan, J., and Ye, R. A. (2023). Cross-national study of mathematics anxiety. Asia-Pac. Educ. Res. 32, 295–306. doi: 10.1007/s40299-022-00652-7

Crossref Full Text | Google Scholar

Zanabazar, A., Deleg, A., and Ravdan, M. (2023). A study of factors causing math anxiety among undergraduate students. Int. J. Innov. Res. Sci. Stud. 6, 578–585. doi: 10.53894/ijirss.v6i3.1609

Crossref Full Text | Google Scholar

Zhang, J., Zhao, N., and Kong, Q. P. (2019). The relationship between math anxiety and math performance: a meta-analytic investigation. Front. Psychol. 10:1613. doi: 10.3389/fpsyg.2019.01613

PubMed Abstract | Crossref Full Text | Google Scholar