Empowering college students to select ideal advisors: a text-based recommendation model

College students often encounter numerous challenges throughout their academic journeys, making the guidance and support from educators indispensable. Recommendation systems can significantly reduce the difficulties students face when identifying suitable academic advisors. This paper proposes a AdVisor RecommenDation (AVRD) model based on textual data regarding college students' interests. AVRD first adopts Chinese Bidirectional Encoder Representations from Transformers (BERT) and unsupervised Simple Contrastive Learning of Sentence Embeddings (SimCSE) to train the corpus of advisors' records. The time decay factor is then introduced as the weight of the text record vectors, and the representation vectors of advisors are obtained using the weighted mean. Finally, the similarities between the advisor and student vectors are computed, and an advisor list is recommended to student according to the designed pooling and matching criteria. The questionnaire data from 170 college students are collected to evaluate the proposed model. Experimental results demonstrate the effectiveness of AVRD. The model outperforms other LLMs such as Qwen and DeepSeek by a significant margin, as well as the commonly used models like TF-IDF, LSA, and Word2Vec. Moreover, the ablation studies reveal that the SimCSE component of AVRD is crucial to the model's performance.

1 Introduction

College students face substantial societal expectations for cultivating multifaceted competencies, including academic excellence, personal development, and professional proficiency. In striving to achieve these goals, educators play an indispensable role in assisting students to overcome diverse challenges they may encounter by providing various forms of support (Goldberg et al., 2023; Christoforidou and Kyriakides, 2021). For instance, when students are engaging in high-level competitions like the Mathematical Contest in Modeling (MCM) and the Interdisciplinary Contest in Modeling (ICM), the invaluable guidance from experienced advisors can prove instrumental in maximizing students' success in these demanding competitions, particularly in enhancing their competition completion rate and award-winning opportunities (Wankat, 2005). As another illustration of the importance of an advisor, when students embark on their graduation projects, a proficient advisor can play a pivotal role in cultivating their academic interests and enhancing their academic performance, laying a solid foundation for their future academic research (Pargett, 2011).

For a university or school with a limited number of faculty members, students can rapidly identify an ideal advisor whose expertise and guidance closely align with their specific needs through online searches or peer recommendations. However, as the number of teachers increases, this process becomes increasingly challenging (Gordon and Steele, 2015). First, students might not have well-defined expectations regarding what they can expect from an advisor, making it challenging to identify an advisor who can meet their specific requirements. Second, there is a considerable and persistent information asymmetry between students and teachers. Typically, students often have limited access to in-depth details regarding potential advisors' specialized knowledge, instructional approaches, and research foci. Despite the fact that school websites usually offer comprehensive teacher profiles, students often lack the necessary experience and acumen to discern the subtle differences in various teachers' competencies and the specific support each can offer. This limitation significantly hinders their capacity to select the most appropriate advisor from a multitude of choices when in need of guidance. Third, students occasionally select advisors based on recommendations and experiences shared by familiar peers or teachers. While this practice can mitigate information asymmetry and broaden their options, it may also introduce bias into the selection process. This is because the recommended advisors might not always match the individual demands and preferences of the students seeking guidance. Finally, the search for an advisor can be a time-consuming endeavor, and students, burdened by their academic obligations, often have scarce time to devote to this crucial task. Given the reasons outlined above, helping students identify their ideal advisor in an efficient way is a task of importance and necessity.

To provide students with an advisor recommendation list for various competitions, paper writing, graduation projects, and other academic activities, this paper collects detailed data containing teacher profiles and students' actual needs for selecting advisors from a China's university and constructs an advisor recommendation model. The research objective is achieved by addressing the following four questions: (1) How to collect a validation set (matching records of text data between teachers and students) to evaluate model performance? (2) Which representation learning method works better in converting the texts of corpus into vectors? (3) How to properly integrate the teacher's text information, which contains different types and different periods, to generate the teacher representation vector? (4) How to use text similarity to recommend advisors with satisfactory accuracy?

To address these issues, we use text data, encompassing paper titles, course names, and teachers' research fields, as the corpus. In view of the fact that deep learning technology has demonstrated promising performance in the field of recommendation (Wu et al., 2023), we combine Chinese bidirectional encoder representations from Transformers (BERT) (Cui et al., 2021) with the unsupervised simple contrastive learning of sentence embeddings (SimCSE) (Gao et al., 2021) models to extract text features and train sentence vectors. For each teacher, we extract the representation vectors from the text records by using the time decay factor to handle the impact of research interests shift. By issuing questionnaires to students, we collected the short texts on students' demands for advisors and extracted the representation vectors of each student. Then, the cosine similarities between the vectors of teachers and students are calculated, and the pooling criterion and matching criterion are used to recommend an advisor list to each student. The validation set is the filtered questionnaire data filled out by the students, including students' demand-related short texts and their corresponding lists of ideal advisors. To enhance the accuracy of the ground truth, we employ the large language model (LLM) DeepSeek (DeepSeek-AI, 2024a) to generate teacher profiles. These profiles are then provided to questionnaire respondents for a second round of adjustments, with the goal of reducing biases resulting from information asymmetry.

This study has made the following major contributions:

(i) We propose an advisor recommendation model AVRD, which can assist students to identify advisors using demand-related short texts.

(ii) AVRD employs Chinese BERT and a contrastive learning model SimCSE to learn effective representations of texts. This approach of combing BERT with SimCSE can significantly enhance the performance of text similarity representation.

(iii) The time decay factor is adopted to learn the text record vectors of teachers, enabling the model to better capture the features of their recent achievements. Advisor recommendation criteria, i.e., the pooling and matching criteria, are designed for the advisor recommendation task. Both the time decay factor and recommendation criteria can effectively improve the recommendation effect.

2 Related work

2.1 Recommendations for education

In the field of education, information technology is increasingly being applied to help students, teachers, and administrators improve work efficiency, information construction has played a pivotal role in higher education improvement and teaching management (Yu, 2022; Lee, 2017). Information systems collect a large amount of campus data, including basic information and behavioral data of students and teachers. Based on these data, scientific researchers conduct research using data mining and machine learning theories and techniques to explore teaching suggestions and improve teaching quality.

Academic prediction and warning is one of the important research directions. (Cui et al. 2022) and (Yang et al. 2020) transformed behavior trajectory data of students and textural logs of records into learning images and trained images through convolutional neural network (CNN) variant to provide warnings of problems in the academic performances of students. (Imran et al. 2019) and (Zou et al. 2025) utilized machine learning approaches to predict student academic performance. (Oztas and Akcapinar 2025) predicted students' academic procrastination tendencies using online learning trajectories. Besides the prediction tasks, machine learning is more commonly used for recommendations, such as course recommendations, major recommendations, etc. Wang X. et al. (2022) and (Zhang et al. 2019) proposed massive open online course (MOOC) recommendation algorithms based on hyperedge-based graph neural networks and hierarchical reinforcement learning respectively. (Wang et al. 2020) proposed an attention-based CNN to predict user ratings and recommend top-ranked courses to users. Regarding major recommendation, (Obeid et al. 2022) collected the life trajectory information of graduates via questionnaires and then proposed a hybrid major recommendation system that incorporates knowledge base and collaborative filtering techniques. (Alghamdi et al. 2019) employed a fuzzy recommender system and random forest algorithm to facilitate personalized major recommendations for students.

The aforementioned studies contribute to enhancing students' learning effectiveness through various approaches, including grade prediction, resource recommendation, major recommendation, and more. Teacher recommendation is also very important for college students, when seeking guidance from teachers for graduation projects, professional competitions, or paper writing. In the field teacher recommendation, (Zhang et al. 2016) proposed a teacher recommendation model using the term frequency-inverse document frequency (TF-IDF) method, this model conducts recommendations by obtaining the social information between students and teachers within the school and calculating the connectivity, therefore, it is more suitable for recommending supervisors to the group of graduate students enrolled in undergraduate schools. (Zemaityte and Terzić 2019) designed a teacher recommendation tool for computer science students through calculating the TF-IDF scores to rank supervisors as well. Both studies assessed the recommendation performance of their models from the perspective of user satisfaction, which differs from the accuracy calculated based on the ground truth datasets, and they assume the mutual independence of words without considering their semantic meaning in the models. In our work, we construct a ground-truth dataset for advisor selection to evaluate the recommendation performance, and integrate the semantic meaning of words by leveraging the BERT model.

2.2 Recommender systems and algorithms

The recommender systems are software tools and techniques that provide suggestions for items that are most likely of interest to a particular user (Ricci et al., 2022), which are increasingly being applied in the field of education. Based on the online review data of MOOC users, (Nilashi et al. 2022) proposed a multi-criteria collaborative course recommender system through machine learning techniques. (Wu and Feng 2020) proposed an improved neural network-path sorting algorithm to improve the recommendation efficiency of online education resources. (Ma et al. 2017) applied course recommendations in the curriculum system by analyzing courses with similar semantics. The core algorithms of these recommender systems are information filtering approaches. At present, collaborative filtering and content-based filtering are two major approaches to constructing recommender systems. Collaborative filtering leverages the key source of user-item interaction data, whereas content enriched recommendation additionally utilizes the side information associated with users and items (Wu et al., 2023).

Content-based filtering extracts item features from users' usage records or item profiles and then recommends items based on similarity (Esmeli et al., 2020). (Zhang et al. 2016) used the modified TF-IDF algorithm and category tree to determine the direct similarity relationship between students and teachers. (Zemaityte and Terzić 2019) extracted two lists of keywords from the crawled text data of potential teachers and the demand text provided by students respectively, then ranked and matched the two keyword lists using TF-IDF algorithm as well. These two teacher recommendation approaches adopt content-based filtering, which extracts features of students and teachers through similarity calculation. Inspired by the remarkable achievements of deep learning, deep neural networks have demonstrated superior performance in text feature extraction and are widely employed in content-based filtering recommendation algorithms. For example, (Thierry et al. 2023) proposed a paper recommendation model using knowledge graph embedding and deep neural network, in which introduced an attention module to strengthen the semantic feature extraction and learns enhanced representations.

In addition to the field of education, there are also many researches in other recommendation fields based on deep learning. (Guo et al. 2017) interacted low-order and high-order features through deep learning and proposed the deep factorization machine (DeepFM) model to predict the click-through rate (CTR) of users in the recommendation system. (Fan et al. 2019) proposed the graph neural network framework GraphRec to predict recommendation item scores for users, the model captured the expression vectors of major user features and major item features through the attention mechanism. Wang Z. et al. (2022) proposed the PJFCANN model for job recommendation using recurrent neural network (RNN) to extract textual features from job applicants' resumes and recruiters' demands, while graph neural network (GNN) was used to extract features of recruiters in their historical experiences. These recommendation algorithms all need to train model parameters using a substantial amount of historical interaction data of users and items, whereas the commonly used recommendation models that perform text filtering based on semantic similarity such as those using TF-IDF and Latent Semantic Analysis (LSA) (Evangelopoulos et al., 2012) only extract the text features of paired records and don't need to train the model's parameters. Considering the demonstrated potential and efficacy of deep learning in the realm of recommendation systems, we employ a content-based filtering approach using deep neural network to facilitate advisor recommendation.

3 Methodology

The proposed AVRD model involves two key entities: universities and students. Universities provide updated teacher text data, which serves as the corpus for model processing. Students input their “demand-related short texts” into the model and offer feedback on the recommended teacher lists. The flowchart of advisor recommendation is shown in Figure 1.

Figure 1

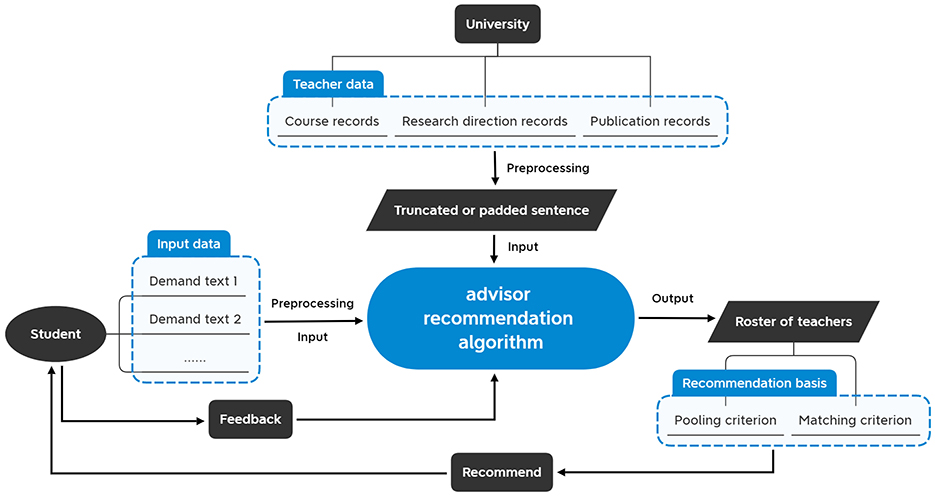
Figure 1. Flowchart of advisor recommendation. Students input short-text queries, and the advisor recommendation algorithm matches suitable teachers in the teacher database based on the pooling and matching criteria, and generates a list of recommended advisors.

Before the advisor recommendation algorithm can be deployed as an information system, the underlying recommendation model must be fully pre-trained. Although this pre-training process is computationally intensive and time-consuming, it ensures that once the system is operational, students can receive their personalized advisor recommendations instantaneously. However, due to the computational demands, pre-training cannot be performed frequently, as it would impose a substantial operational burden on system administrators.

3.1 Training process

The core of the training process is to train word texts to enable better semantic representation, thereby enhancing the performance of divisor recommendations. The semantic representation of a word can be modeled as a vector in high-dimensional Euclidean space, dense word vectors contain substantial information that can be harnessed to represent semantic relationships between words. Currently, scholars have proposed several methods of semantic representation. (Mikolov et al. 2013a) developed the Word2Vec model, which incorporates the continuous bag of words (CBOW) and skip-grams (SG) algorithms to represent word vectors. Additionally, they proposed negative sampling to simplify the solving process of the Word2Vec model (Mikolov et al., 2013b). (Devlin et al. 2019) proposed the BERT model, which employs a bidirectional encoder based on the Transformer architecture to represent word vectors while taking into account the contextual relationships among terms. The BERT model demonstrates an excellent performance in the text representation. Moreover, pre-trained LLMs [e.g. generative pre-trained transformer (GPT) (Ouyang et al., 2022), Qwen (Yang et al., 2024), Deepseek (DeepSeek-AI, 2024a) and BERT itself] can be fine-tuned for specific tasks, which can avoid the problems of training on a large corpus of text and long optimization time (Brown et al., 2020).

Pre-trained language models (PLMs) produce context-aware representations and have delivered impressive results across a wide spectrum of natural language processing (NLP) tasks. Notably, (Cui et al. 2021) developed Chinese pre-trained BERT models incorporating the whole word masking technique, which include closely related variants such as BERT-wwm-ext and RoBERTa-wwm-ext. In this section, we conduct a lightweight fine-tuning of the BERT model using teachers' textual records. This process aims to enable the PLM to generate more reliable word vectors that are better suited for advisor recommendation tasks. For the corpus of teachers' records, the fine-tuning is performed on Chinese RoBERTa-wwm-ext model (Cui et al., 2021). AVRD network architecture is illustrated in Figure 2.

Figure 2

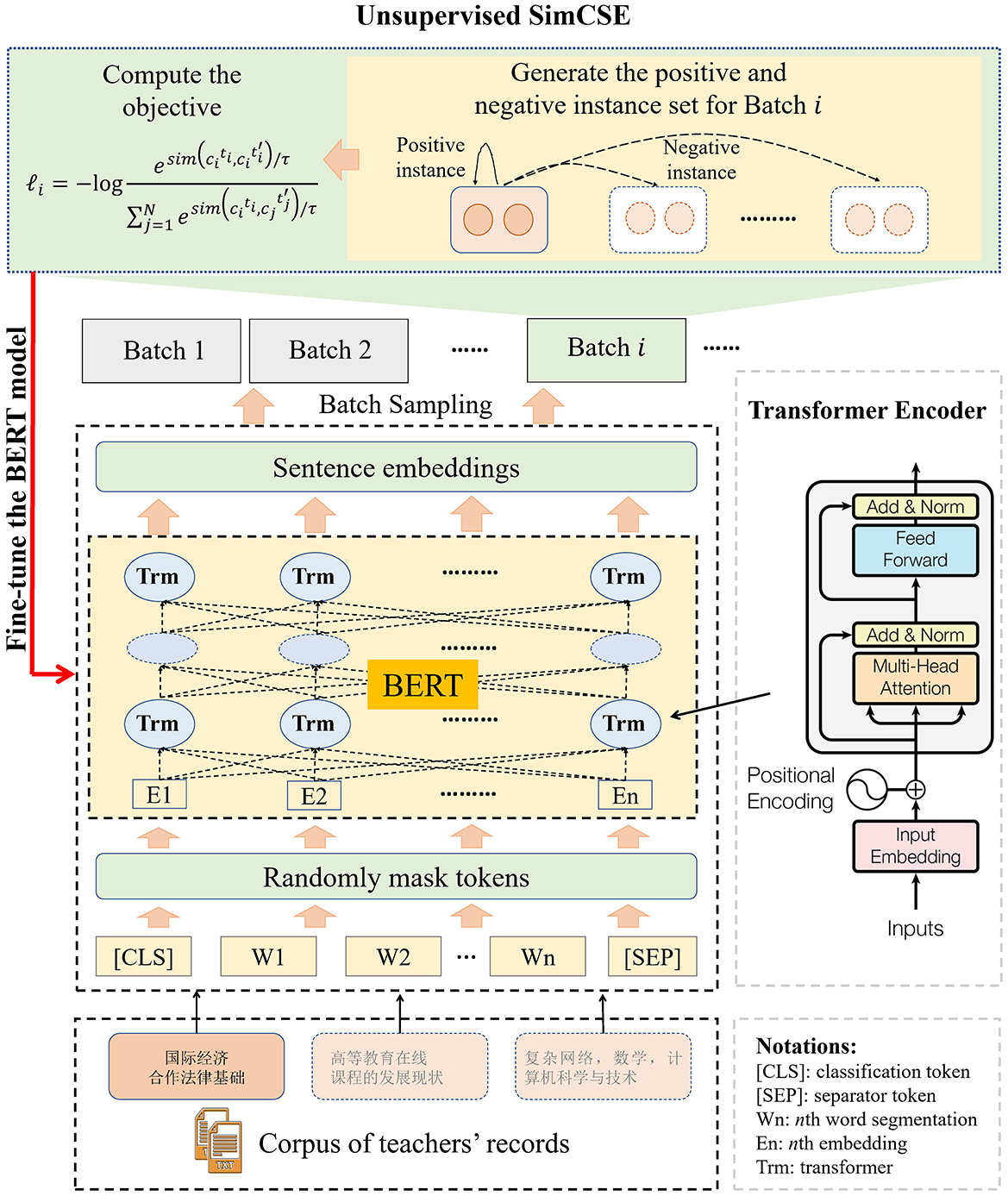
Figure 2. The network architecture of AVRD. This figure consists of two parts: BERT and SimCSE. During the training process, sentences are selected from the teacher corpus and fed into the BERT network to generate sentence embedding vectors. Subsequently, for each vector in the sampled batch extracted from the sentence embedding set, the vector is paired with itself to form a positive instance and with other vectors to form negative instances, followed by the generation of a corresponding batch-wise instance set. The BERT network is fine-tuned using the unsupervised SimCSE approach based on the constructed instance set, aiming to enhance the representational capacity of the sentence embeddings.

To further embed the sentence vectors derived from teacher text records, we conduct augmented training using the unsupervised SimCSE model proposed by (Gao et al. 2021). As illustrated in the upper part of Figure 2, the unsupervised SimCES model adheres to the contrastive learning framework and employs a cross-entropy objective with batch negatives (Equation 1). Let $\mathcal{S}$ denote the set of teachers' text records, $\mathcal{S}={\left\{t_i\right\}}_{i=1}^m$, m is the length of the teachers' text records. ${\mathcal{D}}^{+}={\left\{(t_i,t_i^{+})\right\}}_{i=1}^m$ and ${\mathcal{D}}^{-}={\left\{(t_i,t_i^{-})\right\}}_{i=1}^m$ denote the positive and negative instance sets respectively, which are generated from the set $\mathcal{S}$. Following the contrastive framework of unsupervised SimCSE, we set the positive instance $t_i^{+}=t_i$ and the negative instance $t_i^{-}=t_j$, i ≠ j.

Let ${\text{c}}_i^{t_i}$ and ${\text{c}}_i^{t_i^{\prime }}$denote the representations of t_i and $t_i^{\prime }$, where $t_i^{\prime }$ takes $t_i^{+}$ or $t_i^{-}$. The training objective with a mini-batch of N pairs is:

$\begin{array}{ll}{\ell }_i=-log\frac{e^{\text{sim}({\text{c}}_i^{t_i},{\text{c}}_i^{t_i^{\prime }})/\tau }}{{\displaystyle {\sum }_{j=1}^N}{e}^{\text{sim}({\text{c}}_i^{t_i},{\text{c}}_j^{t_j^{\prime }})/\tau }},& (1)\end{array}$

where τ is a hyperparameter and sim(c₁, c₂) is the cosine similarity:

$\begin{array}{ll}\text{sim}({\text{c}}_1,{\text{c}}_2)=\frac{{\text{c}}_1^{\top }{\text{c}}_2}{||{\text{c}}_1||·||{\text{c}}_2||}.& (2)\end{array}$

We denote the Chinese BERT output of the input sentence z_i as ${\text{c}}_i^{z_i}$, that is,

$\begin{array}{ll}{\text{c}}_i^{z_i}=f_{\theta }(z_i).& (3)\end{array}$

The training process is fundamental to the recommendation system and directly influences its accuracy. The core of achieving high accuracy lies in computing the similarity between vectors derived from students' short-text inquiries and teachers' text records. Therefore, the quality of the vector representations ultimately determines the effectiveness of the recommendations.

In practice, frequent retraining is unnecessary. For newly enrolled teachers, their vector representations can be computed using the well-trained model—unless their text records differ significantly from those of all existing teachers. To maintain efficiency, the model may be retrained and teachers' vector data updated annually or every few years.

3.2 Vector representation

In our work, teachers' text data contain three kinds of records, i.e., course records (T^C), research direction records (T^D), and paper publication records (T^P). Suppose that the total number of teachers is J, and the three types of text records of teacher j are denoted by $T_j^C$, $T_j^D$ and $T_j^P$ respectively, $j\in \mathcal{J}=\left\{1,2,\dots ,J\right\}$. Then the vectors ${\text{r}}_j^C$, ${\text{r}}_j^D$, and ${\text{r}}_j^P$ are extracted from the corresponding three records of teacher j. Therefore, the representation vector of teacher j is ${\text{r}}_j=\left[{\text{r}}_j^C,{\text{r}}_j^D,{\text{r}}_j^P\right]$, which is the concatenation of ${\text{r}}_j^C$, ${\text{r}}_j^D$, and ${\text{r}}_j^P$.

Take the paper publication records $T_j^P$ of teachers j for example, we introduce the calculation process of the vector ${\text{r}}_j^P$. Let $t_{ji}^P$ denotes the jth teacher's ith paper publication record, all the paper publication records of teacher j is denoted as follows:

$\begin{array}{ll}{T}_j^P=\{t_{j1}^P,\dots ,t_{ji}^P,\dots ,t_{j{m}_j^P}^P\},& (4)\end{array}$

where $m_j^P$ is the number of paper publication records of teacher j. According to Equation 3, the representation vector of record $t_{ji}^P$ is ${\text{c}}_i^{Pj}$, where $i=1,2,\dots ,m_j^P$.

Since the generated time of each paper publication record is different, we introduce the time decay factor ${\eta }^{{\lambda }_i}$ to emphasize the recent work of teachers, where η is a constant between 0 and 1, and ${\lambda }_i,i=1,2,\dots ,m_j^D$, is a positive integer related to the generated time of corresponding record. Taking the natural year as the interval, we set λ = 1 for records from the most recent year, λ = 2 for the second most recent year, and so on. At this time, the paper publication vector ${\text{r}}_j^P$ of teacher j is computed as the weighted average of the representation vector ${\text{c}}_i^{Dj}$ corresponding to each paper publication record, where the time decay factor ${\eta }^{{\lambda }_i}$ serves as the weighting coefficient. It can be expressed by the formula as follows:

$\begin{array}{ll}{\text{r}}_j^P=\frac{{\displaystyle {\sum }_{i=1}^{m_j^P}}{\eta }^{{\lambda }_i}{\text{c}}_i^{Pj}}{{\displaystyle {\sum }_{i=1}^{m_j^P}}{\eta }^{{\lambda }_i}}.& (5)\end{array}$

As the query texts for students in the advisor recommendation system are non-deterministic, we set three types of demand as the query texts, which are course names (Γ^C), research directions (Γ^D), and project keywords (Γ^P) related to the objectives of the activities or projects, this setting is analogous to the records used for teachers. After removing words that are not in the model corpus from these text records, we represent students using the same method as teacher vector representation. The representation vector of student e is defined as ${\text{u}}_e=\left[{\text{u}}_e^C,{\text{u}}_e^D,{\text{u}}_e^P\right]$.

3.3 Recommendation prediction

After the vector representation is obtained, some methods can be adopted to calculate the similarity between vectors, such as dot product, Euclidean distance, and cosine similarity (Manning et al., 2008). The values of dot product and Euclidean distance are susceptible to dimensional influence, with non-fixed ranges. However, even in the case of high dimensions, the cosine similarity still keeps the excellent property of “the same is 1, the orthogonal is 0, and the opposite is -1”. Hence, in the fields of information retrieval and text mining, cosine similarity is widely used to measure document similarity (Kirişci, 2023; Luo et al., 2018), as noted by Thongtan et al. (2019). Therefore, we adopt the cosine similarity s_{ue, rj} in Equation 2 as the metric between student vector u_e ($e\in \mathcal{E}=\left\{1,2,\dots ,L\right\}$) and teacher vector r_j ($j\in \mathcal{J}$).

Moreover, in the recommendation prediction module, we propose a pooling criterion and a matching criterion. A list of potential advisors is determined according to the pooling criterion firstly, which is then supplemented based on the matching criterion.

Three types of similarity can be computed based on ${\text{u}}_e^C,{\text{u}}_e^D,{\text{u}}_e^P$ between a student and a teacher. The pooling criterion selects the maximum output; specifically, the similarity score of the teacher record that best aligns with the student demand is adopted as the representative similarity between the teacher and the student. This approach filters out redundant similarity information and significantly reduces subsequent computations. Taking the input text ${\Gamma }_e^D$ of student e as an example, the similarity $s_{{\text{u}}_e^D,{\text{r}}_j}$ with teacher j is:

$\begin{array}{ll}{s}_{{\text{u}}_e^D,{\text{r}}_j}=\text{max}\{s_{{\text{u}}_e^D,{\text{r}}_j^C},s_{{\text{u}}_e^D,{\text{r}}_j^D},s_{{\text{u}}_e^D,{\text{r}}_j^P}\},& (6)\end{array}$

i.e., the maximum value of the similarity set between its representation vector ${\text{u}}_e^D$ and the teacher's three representation vectors ${\text{r}}_j^C$, ${\text{r}}_j^D$ and ${\text{r}}_j^P$. According to Equation 6, we obtain the similarity set $\{s_{{\text{u}}_e^D,{\text{r}}_1},\dots ,s_{{\text{u}}_e^D,{\text{r}}_j},\dots ,s_{{\text{u}}_e^D,{\text{r}}_k}\}$ between input text ${\Gamma }_e^D$ of user e and J teachers, and the same principle holds for ${\Gamma }_e^C$ and ${\Gamma }_e^P$. In this manner, the n maximum values are extracted from each of the three sets, each containing J similarity values, to form a new similarity set with a length of 3n. Subsequently, a list of recommended teachers is determined based on the frequency of teachers' occurrences and their similarity values in the new set.

The list of teachers with the highest similarity to students' demands can be generated based on the aforementioned pooling criterion. To tackle the problem of incomplete teacher selection when relying solely on similarity, we propose a matching criterion that first evaluates the text inclusion relationship and then recommends teachers based on similarity scores. However, the matching criterion may recommend teachers with similarity scores significantly lower than students' demands. Additionally, when the student's demand text contains an excessive number of words, no advisor may be recommended due to the absence of inclusion relations. Therefore, the teacher recommendation list generated by the matching criterion serves as a supplement to that derived from the pooling criterion. The matching criterion assesses whether the word sequences of teachers (i.e., $T_j^C,T_j^D$ and $T_j^P$) contain the word sequences of student e (i.e., ${\Gamma }_e^C,{\Gamma }_e^D$ and ${\Gamma }_e^P$), and selects the set T′ of all the teachers whose word sequences include any of student e's word sequences. Subsequently, the similarity between the teacher vector represented in T′ and the corresponding vector of student e is calculated. Advisors are then recommended based on both the frequency of their occurrence in the similarity sequence and their similarity scores.

Recommendation prediction is performed by applying a pre-trained AVRD model. This model is typically saved as a file that contains both the BERT-based network architecture and the associated parameter values, including weights and biases. To deploy a recommendation system using the pre-trained model, we can begin by computing vector representations for all teachers and storing them in a database. Upon receiving a student inquiry, the server uses the pre-trained model to generate a vector for the input text. It then produces a ranked list of recommended advisors by calculating and sorting the similarity scores between the inquiry vector and all pre-computed teacher vectors in the database. (Johnson et al. 2019) demonstrated in their experiment that retrieving the top-100 similarities from a dataset of 10,000 1024-dimensional vectors requires less than 10 ms. This experiment was performed on a system configured with two 2.8 GHz Intel Xeon E5-2680v2 CPUs, four Maxwell Titan X GPUs, and CUDA 8.0. Consequently, with proper server deployment, the advisor recommendation system can operate at a sufficiently fast and satisfactory speed.

4 Experimental results

Before being deployed as a recommendation system, recommendation algorithms are typically fully trained using large-scale datasets. The recommendation efficiency of the system depends entirely on the training performance. First and foremost, the quality of the dataset serves as the foundation, as all well-trained algorithms rely on high-quality ground truth. Meanwhile, a set of evaluation metrics is typically employed to compare the recommendation performance across classic algorithms.

This section starts with an introduction to the collection, processing, and testing of experimental data. Subsequently, it analyzes the recommendation results of the proposed model, baseline models, and ablation models on the validation dataset. Finally, t-distributed stochastic neighbor embedding (t-SNE) (Maaten and Hinton, 2008) is employed to transform the text representation vectors of teachers into two-dimensional scatter plots, which are then analyzed in depth based on different schools.

4.1 Datasets

In this paper, experimental data include information system-collected data and questionnaire survey data. Information system data are employed for text feature extraction and vectorized representation of teacher-related texts. Questionnaire survey data, meanwhile, include students' short texts describing their demands as well as the corresponding lists of target teachers. Based on the questionnaire survey data, we constructed the validation set for the advisor recommendation model and realized the vectorized representation of students' demands. The sources and processing methods of these two types of data are described in the following sections.

We collected 30,458 text records, including 4,067 course records, 1,970 research direction records, and 24,421 paper publication records in total. Following text length screening, we constructed a corpus consisting of 24,374 paper publication word sequences, 3,762 course word sequences, and 1,577 research direction word sequences; the length of remaining sentences uniformly aligned to 40. Subsequently, we used these 29,713 sentences to fine-tune the Chinese BERT (RoBERTa-wwm-ext) by applying the masked language model objective (Cui et al., 2021).

4.1.1 Teacher dataset

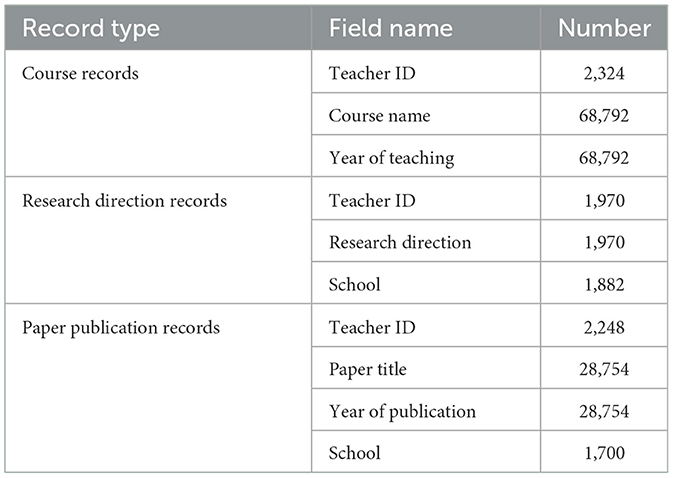
Teachers' text information is sourced from the Information Construction Department of a Chinese university, with abundant teacher data collected over the years. Specifically, academic research-related textual data primarily include course records, research direction records, and Chinese-language paper publication records. The research direction records comprise direction information uploaded by teachers and the names of corresponding primary and secondary disciplines, which clearly and systematically detail their research interests. The course records list all courses taught by individual teachers, reflecting their specialized competencies. The earliest course record dates back to 2004, with records covering the period up to 2021. The paper publication records include the titles of all papers authored by teachers, among which the most recent publication reflects their latest research endeavors. Although the earliest publication record traces back to 1970, the majority of documents were published between 1999 and 2021. A statistical summary of all three data types is presented in Table 1.

Table 1

Table 1. Teacher dataset.

Owing to the varying frequencies of textual records and differences in the number of teachers across data categories, significant disparities exist in the quantities of course records, research direction records, and paper publication records. For many teachers, course records tend to accumulate and recur as their teaching experience grows. Initially, there were 127,232 course records, covering 4,067 courses and 2,324 teachers. After removing annual duplicate course records for each teacher, 68,792 course records remained. The other two types of records were subsequently cleaned and organized. The research direction data include records for 1,970 teachers, while the publication data contain 28,754 records from 2,248 teachers, involving 24,421 papers. Finally, 1,921 teachers with course records from the past three years were selected as potential recommendable candidates, excluding those who had resigned or retired.

4.1.2 Student dataset

Students' demand data were collected via a questionnaire survey, with respondents being students from the same university whose teacher data are used for text vector representation learning. The questionnaires were distributed through the professional survey platform “Wenjuanxing” and disseminated online via communication tools such as WeChat and QQ. It comprises 3 multiple-choice questions and 11 open-ended questions, covering students' general information, course names related to their demands, research fields of interest, project keywords, and a list of preferred advisors. The list of intended advisors provided by students in the questionnaire serves as the ground truth for this study.

For the information asymmetry regarding students' knowledge of teachers' academic expertise, some intended advisors selected by students may not align with their demands, leading to low-quality ground truth. To enhance the accuracy of the ground truth, we conducted a second-round advisor adjustment by providing students with teacher profiles generated using DeekSeek. We generated teacher profiles (with a length of less than 250 words for each teacher) based on teaching records and demand profiles based on students' query texts by calling the DeepSeek interface. In the second round, we constructed a set of ten candidate teacher profiles for each student respondent to adjust advisor selection. The set of ten candidates include: (1) three teachers initially intended by the student in the first round; (2) three teachers with profile similarity to the intended teachers; (3) four teachers with text similarity between the student's demand profile and teacher profiles. The similarity is calculated using the last hidden layer vectors of profiles from deepseek-llm-7b-chat model (DeepSeek-AI, 2024b). After the second-round advisor selection, the final list of intended advisors is designated as the ground truth for our AVRD model.

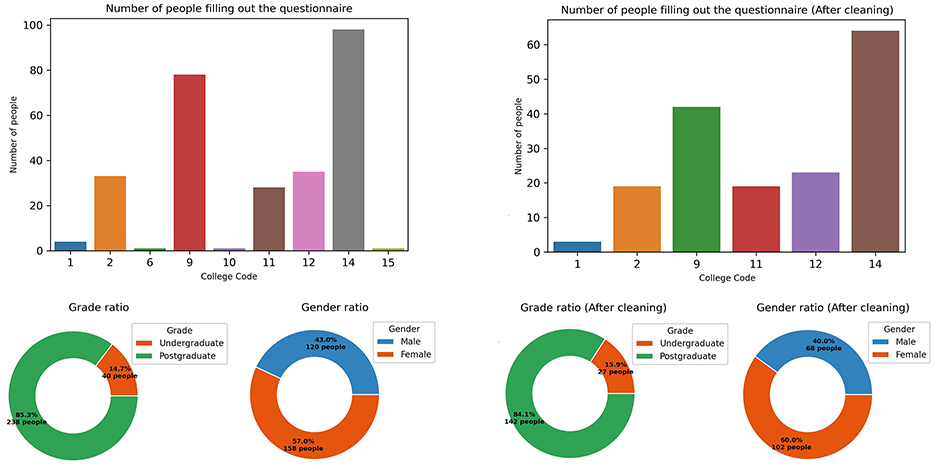
Finally, a total of 279 questionnaires are recovered online. Respondents are from 9 schools within the selected university. Distributions by school, gender, and grade are presented in Figure 3 (left). The number of respondents from School 14 and School 9 is 98 and 78, respectively. For School 12, School 2, and School 1, the corresponding number of respondents stands at 35, 33, and 28, respectively. The remaining four schools each has fewer than 5 respondents. The male-to-female ratio among respondents is approximately 1:1, and the postgraduate-to-undergraduate ratio is 5:2.

Figure 3

Figure 3. Data distribution before (left) and after (right) questionnaire processing.

The quality of questionnaire responses is assessed, and invalid questionnaires are excluded. Three evaluation criteria are employed to assess questionnaire quality: (1) the completeness and validity of teachers' names, which required no blanks, repetitions, or special characters; (2) the filling standards for course names, research fields, and paper keywords, with no blanks or special characters allowed; (3) the uniqueness requirement that course names, research fields, and paper keywords must not be identical. Finally, 170 questionnaires are retained. The distribution of respondents by school, as well as their gender and grade information, is presented in Figure 3 (right). Three schools with only 1 respondent are deleted and the remaining 6 schools are retained. Additionally, the school distributions, gender ratios, and grade proportions of respondents are basically consistent with those before screening. Therefore, although more than 1/3 of the questionnaires are deleted, the personnel distribution structure of the questionnaire is not damaged, indicating that the questionnaire screening is relatively reasonable.

4.2 Parameter settings

We utilize the base-level Chinese BERT model, characterized by its 12 transformer layers and a hidden dimension of 768. The following parameter settings are applied only during fine-tuning. Once the model is fully trained, the saved model architecture and learned weights are deployed in the recommendation system for inference.

During the fine-tuning of the Chinese BERT, the model is trained for 3 epochs with batches of 64 samples, using AdamW optimizer at a learning rate of 3e-5. Subsequently, the unsupervised SimCSE model is trained using this newly fine-tuned BERT model as the backbone. The SimCSE model is trained for 1 epoch with with a batch size of 64, adopting the AdamW optimizer (learning rate = 1e-5) and a dropout rate of 0.3.

For vector representation, each record is encoded as a vector using the [CLS] token from the last hidden state of BERT. With the time decay factor of η= 0.88, the teacher's representation vector is computed via the weighted average of records, as shown in Equation 5. Student representation vectors are derived from three types of questionnaire items: two items regarding preferred course names, three items about interested research fields, and three items related to project keywords. Ultimately, three 768-dimensional teacher vectors and three 768-dimensional student vectors are obtained.

We set the length of the recommendation list to 10 or 20, meaning that 10 or 20 teachers from 1,921 candidates are first recommended to each of the 170 students according to the pooling criterion. Subsequently, an additional 2 teachers are recommended to each student according to the matching criterion. In practice, when pooling and matching criteria are applied simultaneously, the length of the recommendation list may not exceed 10 or 20 due to potential overlaps among recommended advisors. When applying the pooling criterion, the top 15 maximum values are extracted from each of the three sets (each containing 1,921 similarity values) to form a new similarity set of length 45, which is then used to generate the final recommendation list. For the matching criterion, each text record is segmented using the Jieba word segmentation tool. Stopwords are selected from the Baidu Stopwords List and the Stopwords List of Harbin Institute of Technology.

4.3 Model performance

4.3.1 Evaluation metrics

For evaluation metrics of the recommendation system, (Liu et al. 2023) used the hit rate (HR) index to assess the system's performance, (Huang et al. 2021) adopted the HR index and NDCG (Normalized Discounted Cumulative Gain) index. The HR index (Deshpande and Karypis, 2004) calculates the recall rate of the entire recommendation system by averaging the recall rates of all users. The NDCG index (Zhang et al., 2023; Karthik and Ganapathy, 2021) is a measurement standard that considers user scores and recommendation order. (Gu et al. 2020) utilized recall rate, precision and F1 value. Additionally, mean reciprocal rank (MRR) and mean average precision (MAP) are frequently used metrics to measure item order in recommendation lists (Gu et al., 2022).

In this paper, we select the two commonly used metrics, MAP and HR, to evaluate the performance of our advisor recommendation model. MAP and HR can be regarded as the average probability of correctly recommending each advisor in the ground truth. To investigate the proportion of students whose demands are satisfied, we additionally propose two new metrics: I-REA and II-REA. I-REA is defined as the ratio of students for whom at least one advisor is successfully recommended, while II-REA is the ratio of students for whom at least two advisors are successfully recommended. In fact, the four selected metrics reflect two perspectives for evaluating recommendation performance.

The formulas for the evaluation metrics are defined as follows:

$\begin{array}{ll}HR@K=\frac{1}{L\left|T_e\right|}{\displaystyle \sum _{e=1}^L}|{ℝ}_e@K\cap T_e|& (7)\end{array}$

$\begin{array}{ll}MAP@K==\frac{1}{L}{\displaystyle \sum _{e=1}^L}|{ℝ}_e@K\cap T_e|\frac{|{ℝ}_e@K\cap T_e|}{\left|T_e\right|}& (8)\end{array}$

$\begin{array}{ll}\text{I-REA}@K=\frac{1}{L}\left|\left\{e\in E||{ℝ}_e@K\cap T_e|\ge 1\right\}\right|& (9)\end{array}$

$\begin{array}{ll}\text{II-REA}@K=\frac{1}{L}\left|\left\{e\in E||{ℝ}_e@K\cap T_e|\ge 2\right\}\right|.& (10)\end{array}$

@K denotes the length of recommendation list. ℝ_e@K represents the set of recommended teachers for student e, while T_e is the ground-truth set of student e. |·| denotes the cardinality (i.e., the number of elements) of a set.

4.3.2 Comparative evaluation on AVRD

We conducted experiments to evaluate the performance differences between the proposed advisor recommendation model (AVRD) and several baseline vector representation methods. The following four algorithms are commonly employed recommendation models that leverage vector similarity. A brief introduction to each is provided below:

• TF-IDF: TF-IDF is computed by multiplying a local component (term frequency) with a global component [inverse document frequency (Jones, 1972)], followed by normalizing the resulting document vectors to unit length.

• LSA: In LSA model (Deerwester et al., 1990), singular value decomposition (SVD) is applied to the term-document matrix, and the first 300 dimensions are retained as text vectors. In our experiment, we used SVD on the term-document matrix of the teacher corpus to capture the latent semantics of words, with the number of factors (latent dimensions) set to 480.

• LSA+TF-IDF: The word frequencies in the word-document matrix are replaced by the TF-IDF values of the words, and SVD is applied to the matrix (Li and Shen, 2017). In our experiment, the number of factors (latent dimensions) was set to 430.

• Word2Vec: We employed the Skip-Gram algorithm (Mikolov et al., 2013a) with hierarchial softmax output layer (Morin and Bengio, 2005) to represent each word as a 340-dimensional dense vector. During training, the minimum word occurrence frequency was set to 1, effectively preserving infrequent professional terms. Additionally, the window size for each movement is set to 7. We used the same text tokenization tool and stopwords list as those applied in the matching criteria. The corpus contained a total of 22,237 valid and non-repetitive terms.

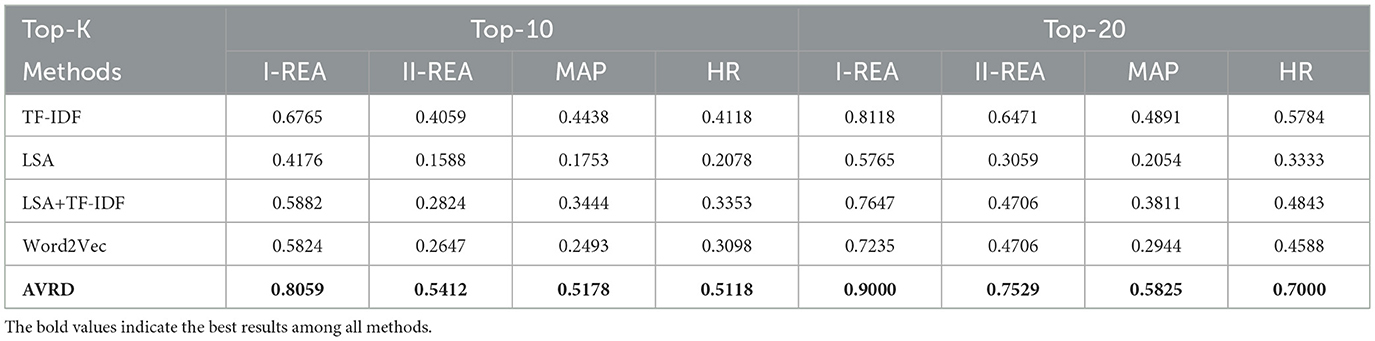
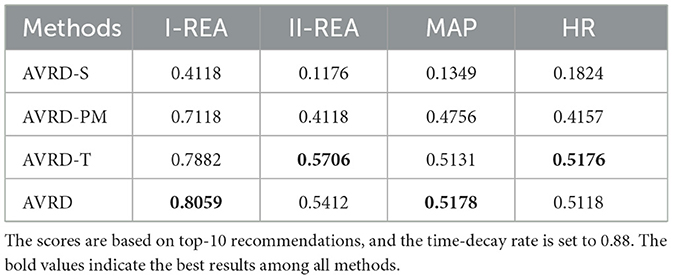
The performance of each model is presented in Table 2. Regarding all four evaluation metrics, our AVRD model outperforms the other four models. Specifically, the I-REA index based on the top-10 recommendations is 0.8059, indicating that the demands of more than 80% students (170 in all) can be met. When recommending 20 advisors, this rate increases to 90%. The II-REA index stands at 0.5412, indicating that over half of the students can receive at least two ideal recommendations. With an HR of 0.5118, our AVRD model, on average, can provide each student with at least one ideal advisor when generating a recommendation list of 10 advisors.

Table 2

Table 2. Performance of the AVRD model and baselines.

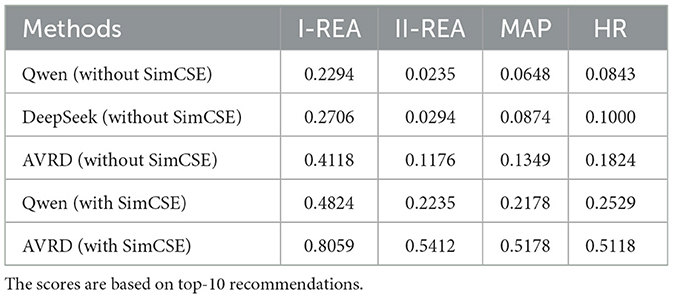
As discussed in Section 3, our AVRD model is essentially a fine-tuned BERT architecture. A natural follow-up question is: can other fine-tuned LLMs outperform fine-tuned BERT in the task of advisor recommendation? To further compare the performance of our AVRD model with that of other LLMs, we selected the Qwen2.5-7b (Qwen team, 2024) and DeepSeek-llm-7b-chat (DeepSeek-AI, 2024b) models for the advisor recommendation task. The results are shown in Table 3. “Without SimCSE” denotes recommendations made directly with the [CLS] representations of the three LLMs, without undergoing SimCSE training. For the Qwen(with SimCSE) model, we adopted an attention network to be the training model for SimCSE, using the [CLS] token of Qwen2.5-7b as the input to the attention network. Due to the high computational cost associated with full-parameter training of Qwen, we did not use Qwen2.5-7b as the training model for SimCSE. As shown in Table 3, the I-REA scores of Qwen, DeepSeek and AVRD without SimCSE are 0.2294, 0.2706 and 0.4118 respectively. In the advisor recommendation task, the sentence representation effect of the Chinese BERT model (RoBERTa-wwm-ext) outperforms that of Qwen and DeepSeek—this advantage is consistent with the II-REA, MAP, and HR metrics. The application of the SimCSE process leads to a substantial boost in recommendation performance. Specifically, the I-REA scores for Qwen and AVRD stand at 0.4824 and 0.8059, respectively. Notably, the improvements in II-REA, MAP, and HR are even more pronounced. The RoBERTa model removes the next sentence prediction objective and dynamically changes the masking pattern applied to the training data (Cui et al., 2021), therefore, it exhibits stronger sentence representation capabilities compared to models focused on text generation. In contrast, LLMs such as Qwen and DeepSeek place greater emphasis on long-text generation. For semantic textual similarity (STS) tasks such as advisor recommendation, the RoBERTa model shows superior performance, as shown in Table 3.

Table 3

Table 3. Comparison of performance among LLMs.

4.3.3 Ablation study

Ablation experiments are conducted to evaluate the effectiveness of each module in our AVRD model. Three variant models are defined as follows:

• AVRD-S: This variant of the AVRD model makes recommendations without considering the SimCSE training process.

• AVRD-PM: This variant utilizes all modules of the AVRD model except for the pooling and matching criterion. Recommendations are generated by computing the similarities between the combined vectors of student text representations and teacher record representations.

• AVRD-T: This variant utilizes all modules of the AVRD model without considering the time decay factor.

As shown in Table 4, the scores of the AVRD-S model are significantly lower than those of the AVRD-PM, AVRD-T, and AVRD models, which demonstrates the effectiveness of the SimCSE module. The pooling and matching criteria play important roles in the AVRD model. After implementing the pooling and matching criteria, the I-REA score increased from 0.7118 to 0.8058, representing a 13.2% enhancement. Simultaneously, improvements are also observed in the II-REA, MAP, and HR metrics. The time-decay rate demonstrates a slight improvement effect, yet it shows no impact on the II-REA, MAP, and HR metrics.This can be attributed to the fact that teachers' research interests and teaching courses do not change frequently, which limit the time-decay rate's impact on similarities.

Table 4

Table 4. Performance of variants of the AVRD model.

4.4 Visualization of representation vectors

As aforementioned, the quality of the vector representations ultimately determines the effectiveness of the recommendations. A high-quality vector representation enables similar texts to maintain small distances and dissimilar texts to maintain large distances in the vector space, thereby enhancing the accuracy of recommendations. To illustrate the vector representation performance of the AVRD model, we provide three low-dimensional diagrams in this section to facilitate visualization.

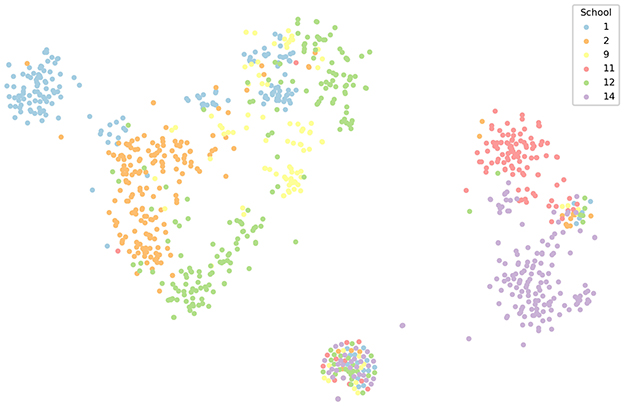
For visualizing sentence representations, representation vectors of teachers from six validation-set schools are plotted as 2D scatter plots. Inter-school dissimilarity is analyzed by comparing the distribution of teacher scatter points across schools. The distributions of teachers from 6 schools after dimensionality reduction of their research direction vectors are shown in Figure 4. Schools 2, 9 and 11 exhibit high intra-class compactness, whereas the other three schools show obvious intra-class dispersion. School 1 has a subcategory that tends to cluster with School 9. School 12 shows slight overlap with Schools 2 and 9. School 14 also has a subcategory biased towards School 11.

Figure 4

Figure 4. Visualization of research direction vectors.

As is well established, after dimensionality reduction via t-SNE, points that are closer together indicate higher similarity. Consequently, for Schools 2, 9, and 11, the research directions of teachers within each school are highly correlated. Furthermore, for Schools 1, 12, and 14, some teachers in each school share similarities in their research directions with those in other schools–which is corroborated by their proximity in the scatter plot.

The distributions of teachers from six schools after dimensionality reduction of their course vectors are shown in Figure 5. Compared with Figure 4, the course records of teachers across different schools exhibit clearer inter-school distinctions, and the overlap phenomenon is reduced. Additionally, the distribution of teachers across schools in Figure 5 is similar to that in Figure 4. For example, Schools 1 and 14 still contain small fractions of points that are biased toward Schools 9 and 11, respectively.

Figure 5

Figure 5. Visualization of course vectors.

The distributions of teachers from 6 schools after dimensionality reduction of their paper publication vectors are shown in Figure 6. It can also be observed that the school distributions in Figure 6 are similar to those in Figure 4. A key distinction, however, is that inter-school overlap is more pronounced. There is a minor overlap between School 14 and School 11, as well as among Schools 12, 1, 2 and 9.This overlapping phenomenon primarily stems from two factors: First, each teacher's paper publication records contain a more diverse range of terms, rather than being limited to fixed research direction vocabularies or course names. Second, when teachers from different schools have similar research direction records (as shown in Figure 4), shared terminology may appear in their publication records—contributing to slight overlap. Additionally, collaborative research and co-authored papers between teachers from different schools further exacerbate this overlap.

Figure 6

Figure 6. Visualization of paper publication vectors.

Based on the aforementioned analysis, the six schools can be categorized into two groups in Figure 6: School 11 and School 14 are located on the right, while Schools 1, 2, 9, and 12 are situated on the left. Data validation further confirms that the disciplinary orientations of the schools on the left and right are predominantly science-based and arts-based, respectively. Specifically, School 14 offers programs in literature, law, and art, whereas School 11 specializes in economics and management. Notably, in Figure 4, some teachers from School 14 are positioned closer to School 11—this is attributed to their expertise in commercial law, a field that shares close links with economic management. School 12 offers fundamental science disciplines, including mathematics, chemistry, and physics. Due to collaborative efforts between some of its teachers and those from other schools, an overlap between School 12 and other schools is observed in Figure 4. In addition, as shown in Figures 4–6, there are some subcategories comprising teachers from 6 schools. One possible explanation for this phenomenon is the existence of teachers with incomplete or missing information, whose representations appear in the central regions of Figures 4, 6. Another contributing factor is that some teachers are affiliated with school-wide courses (e.g., Career Planning Courses for College Students located in the center of Figure 5) or school-wide research directions (e.g., Research on University Teaching Exploration located in the right region of Figure 6). In summary, the vector representations of teachers generated by the AVRD model can effectively capture the underlying text information.

5 Conclusion

In this paper, we proposed an advisor recommendation model (AVRD), which employs BERT and unsupervised SimCSE to generate sentence vectors, to achieve recommendation based on students' short-text queries. To enhance the recommendation performance, a pooling and matching criterion and a time-decay rate are integrated into the model. Empirical studies on the ground truth demonstrated the superiority of our proposed AVRD model. Notably, this model showed a significant improvement in accuracy, outperforming other LLMs such as Qwen and DeepSeek, as well as the traditional recommendation models like TF-IDF, LSA, and Word2Vec. Although the model training process is time-consuming, often taking several hours, the inference process (i.e., providing recommendations for a student) is nearly instantaneous. Due to the challenges of collecting high-quality student datasets, we utilized a relatively small dataset. In future work, we will develop an advisor recommendation system based on our proposed model to support students in learning and innovative activities. As data accumulates, we will construct a larger dataset to further enhance recommendation accuracy.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found below: https://github.com/wxmwer/AVRD.

Ethics statement

Ethical approval was not required for the study involving humans in accordance with the local legislation and institutional requirements. Written informed consent to participate in this study was not required from the participants or the participants' legal guardians/next of kin in accordance with the national legislation and the institutional requirements.

Author contributions

XW: Conceptualization, Formal analysis, Writing – review & editing, Methodology, Validation, Data curation, Writing – original draft, Software. JZ: Methodology, Formal analysis, Data curation, Software, Conceptualization, Writing – original draft, Visualization. LJ: Funding acquisition, Conceptualization, Supervision, Resources, Validation, Project administration, Writing – review & editing. YY: Writing – review & editing, Software, Data curation, Investigation, Formal analysis. LL: Writing – review & editing, Resources, Data curation, Validation.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work was supported by the Laboratory Projects of “Institute for Digital Transformation” and “Institute for Energy System Intelligent Management and Policy Simulation” of China University of Petroleum, the Teaching Case Dataset Construction Project on Postgraduate Education of Shandong Province (Grant No. SDYAL2023030), the Teaching Research and Reform Project at China University of Petroleum (Grant No. CM2024050), and the Postgraduate Program Construction Project for Big Data Analytics at China University of Petroleum (Grant No. UPCYZH-2025-15).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Gen AI was used in the creation of this manuscript.

Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.

Publisher's note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alghamdi, S., Alzhrani, N., and Algethami, H. (2019). “Fuzzy-based recommendation system for university major selection,” in Proceedings of the 11th International Joint Conference on Computational Intelligence (Setúbal: Science and Technology Publications), 317–324. doi: 10.5220/0008071803170324

Crossref Full Text | Google Scholar

Brown, T. B., Mann, B., Ryder, N., Subbaih, M., Kalpan, J., Dhariwal, P., et al. (2020). “Language models are few-shot learners,” in Advances in Neural Information Processing Systems 33, 1877–1901. doi: 10.48550/arXiv.2005.14165

Crossref Full Text | Google Scholar

Christoforidou, M., and Kyriakides, L. (2021). Developing teacher assessment skills: the impact of the dynamic approach to teacher professional development. Stud. Educ. Eval. 70:101051. doi: 10.1016/j.stueduc.2021.101051

Crossref Full Text | Google Scholar

Cui, C., Zong, J., Ma, Y., Wang, X., Guo, L., Chen, M., et al. (2022). Tri-branch convolutional neural networks for Top-k focused academic performance prediction. IEEE Trans. Neural Netw. Learn. Syst. 35, 1–12. doi: 10.1109/TNNLS.2022.3175068

PubMed Abstract | Crossref Full Text | Google Scholar

Cui, Y., Che, W., Liu, T., Qin, B., and Yang, Z. (2021). Pre-training with whole word masking for Chinese BERT. IEEE/ACM Transactions on Audio, Speech, and Language Processing. 29, 3504–3514. doi: 10.1109/TASLP.2021.3124365

Crossref Full Text | Google Scholar

DeepSeek-AI (2024a). DeepSeek-V2: a strong, economical, and efficient mixture-of-experts language model. arXiv [preprint] arXiv:2405.04434. doi: 10.48550/arXiv.2405.04434

Crossref Full Text | Google Scholar

DeepSeek-AI (2024b). DeepSeek-LLM-7B-Chat [Computer software]. Hugging Face. Available online at: https://huggingface.co/deepseek-ai/deepseek-llm-7b-chat (Accessed September 22, 2025).

Google Scholar

Deerwester, S., Dumais, S. T., Furnas, G. W., Landauer, T., and Harshman, R. (1990). Indexing by latent semantic analysis. J. Am. Soc. Inform. Sci. 41, 391–407. doi: 10.1002/(sici)1097-4571(199009)41:6<391::aid-asi1>3.0.co;2-9

Crossref Full Text | Google Scholar

Deshpande, M., and Karypis, G. (2004). Item-based top-N recommendation algorithms. ACM Trans. Inform. Syst. 22, 143–177. doi: 10.1145/963770.963776

Crossref Full Text | Google Scholar

Devlin, J., Chang, M. W., Lee, K., and Toutanova, K. (2019). “BERT pre-training of deep bidirectional transformers for language understanding,” in Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics (Medford: Association for Computational Linguistics), 4171–4186. doi: 10.18653/v1/N19-1423

PubMed Abstract | Crossref Full Text | Google Scholar

Esmeli, R., Bader-El-Den, M., and Abdullahi, H. (2020). “Using Word2Vec recommendation for improved purchase prediction,” in Proceedings of the 2020 International Joint Conference on Neural Networks (IJCNN) (Glasgow, UK: IEEE), 1–8. doi: 10.1109/IJCNN48605.2020.9206871

Crossref Full Text | Google Scholar

Evangelopoulos, N., Zhang, X., and Prybutok, V. R. (2012). Latent semantic analysis: five methodological recommendations. Eur. J. Inform. Syst. 21, 70–86. doi: 10.1057/ejis.2010.61

Crossref Full Text | Google Scholar

Fan, W., Ma, Y., Li, Q., He, Y., Zhao, E., Tang, J., et al. (2019). “Graph neural networks for social recommendation,” in Proceedings of the WWW '19: The World Wide Web Conference (New York, NY: ACM), 417–426. doi: 10.48550/arXiv.1902.07243

Crossref Full Text | Google Scholar

Gao, T., Yao, X., and Chen, D. (2021). “SimCSE: simple contrastive learning of sentence embeddings,” in Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing. Dominican Republic (Medford: Association for Computational Linguistics (ACL)), 6894–6910. doi: 10.18653/v1/2021.emnlp-main.552

PubMed Abstract | Crossref Full Text | Google Scholar

Goldberg, P., Wagner, W., Seidel, T., and Stürmer, K. (2023). Why do students exhibit different attention-related behavior during instruction? investigating effects of individual and context-dependent determinants. Learn. Instruct. 83:101694. doi: 10.1016/j.learninstruc.2022.101694

Crossref Full Text | Google Scholar

Gordon, V. N., and Steele, G. E. (2015). The Undecided College Student: an Academic and Career Advising Challenge. Springfield, Illinois: Charles C. Thomas Publishers.

Google Scholar

Gu, J., Song, C., Jiang, W., Wang, X., and Liu, M. (2020). “Enhancing personalized trip recommendation with attractive routes,” in Proceedings of the AAAI Conference on Artificial Intelligence (Palo Alto, CA: AAAI Press), 662–669. doi: 10.1016/j.knosys.2025.113639

Crossref Full Text | Google Scholar

Gu, X., Zhao, L., and Jiang, L. (2022). Sequence neural network for recommendation with multi-feature fusion. Expert Syst. Appl. 210, 118459. doi: 10.1016/j.eswa.2022.118459

Crossref Full Text | Google Scholar

Guo, H., Tang, R., Ye, Y., Li, Z., and He, X. (2017). “DeepFM: a factorization-machine based neural network for CTR prediction,” in Proceedings of the 26th International Joint Conference on Artificial Intelligence (San Jose, CA: IJCAI Organization), 1725–1731. doi: 10.48550/arXiv.1703.04247

PubMed Abstract | Crossref Full Text | Google Scholar

Huang, L., Fu, M., Li, F., Qu, H., Liu, Y., and Chen, W. (2021). A deep reinforcement learning based long-term recommender system. Knowl.-Based Syst. 213:106706. doi: 10.1016/j.knosys.2020.106706

Crossref Full Text | Google Scholar

Imran, M., Latif, S., Mehmood, D., and Shah, M. S. (2019). Student academic performance prediction using supervised learning techniques. Int. J. Emerg. Technol. Learn. 14, 92–104. doi: 10.3991/ijet.v14i14.10310

Crossref Full Text | Google Scholar

Johnson, J., Douze, M., and Jégou, H. (2019). Billion-scale similarity search with GPUs. IEEE Trans. Big Data 7, 535–547. doi: 10.1109/TBDATA.2019.2921572

PubMed Abstract | Crossref Full Text | Google Scholar

Jones, K. S. A. (1972). statistical interpretation of term specificity and its application in retrieval. J. Document. 28, 11–21. doi: 10.1108/eb026526

Crossref Full Text | Google Scholar

Karthik, R. V., and Ganapathy, S. A. (2021). fuzzy recommendation system for predicting the customers interests using sentiment analysis and ontology in e-commerce. Appl. Soft Comp. 108:107396. doi: 10.1016/j.asoc.2021.107396

Crossref Full Text | Google Scholar

Kirişci, M. (2023). New cosine similarity and distance measures for Fermatean fuzzy sets and TOPSIS approach. Knowl Inf Syst. 65, 855–868. doi: 10.1007/s10115-022-01776-4

PubMed Abstract | Crossref Full Text | Google Scholar

Lee, K. (2017). Rethinking the accessibility of online higher education: a historical review. Intern. Higher Educ. 33, 15–23. doi: 10.1016/j.iheduc.2017.01.001

Crossref Full Text | Google Scholar

Li, Y., and Shen, B. (2017). “Research on sentiment analysis of microblogging based on LSA and TF-IDF,” in Proceedings of the 3rd IEEE International Conference on Computer and Communications (ICCC) (Danvers: IEEE), 2584–2588. doi: 10.1109/CompComm.2017.8323002

Crossref Full Text | Google Scholar

Liu, Y., Yang, S., Xu, Y., Miao, C., Wu, M., and Zhang, J. (2023). Contextualized graph attention network for recommendation with item knowledge graph. IEEE Trans. Knowl. Data Eng. 35, 181–195. doi: 10.1109/TKDE.2021.3082948

Crossref Full Text | Google Scholar

Luo, C., Zhan, J., Xue, X., Wang, L., Ren, R., and Yang, Q. (2018). “Cosine normalization: Using cosine similarity instead of dot product in neural networks,” in Proceedings of the International Conference on Artificial Neural Networks-ICANN (Cham: Springer), 382–391. doi: 10.48550/arXiv.1702.05870

Crossref Full Text | Google Scholar

Ma, H., Wang, X., Hou, J., and Lu, Y. (2017). “Course recommendation based on semantic similarity analysis,” in Proceedings of the 2017 3rd IEEE International Conference on Control Science and Systems Engineering (ICCSSE) (New York, NY: IEEE), 638–641. doi: 10.1109/CCSSE.2017.8088011

Crossref Full Text | Google Scholar

Maaten, L. v. d., and Hinton, G. E. (2008). Visualizing data using t-SNE. J. Mach. Learn. Res. 9, 2579–2605. Available online at: http://jmlr.org/papers/v9/vandermaaten08a.html

Google Scholar

Manning, C. D., Raghavan, P., and Schütze, H. (2008). Introduction to Information Retrieval. New York, USA: Cambridge university press.

Google Scholar

Mikolov, T., Chen, K., Corrado, G., and Dean, J. (2013a). “Efficient estimation of word representations in vector space,” in Proceedings of the 1st International Conference on Learning Representations (Brookline: Journal of Machine Learning Research). doi: 10.48550/arXiv.1301.3781

PubMed Abstract | Crossref Full Text | Google Scholar

Mikolov, T., Sutskever, I., Chen, K., Corrado, G., and Dean, J. (2013b). “Distributed representations of words and phrases and their compositionality,” in Proceedings of the NIPS'13: Neural Information Processing Systems (New Yok, NY: Curran Associates), 3111–3119. doi: 10.48550/arXiv.1310.4546

Crossref Full Text | Google Scholar

Morin, F., and Bengio, Y. (2005). “Hierarchical probabilistic neural network language model,” in Proceedings of the 10th International Workshop on Artificial Intelligence and Statistics (Brookline: Society for Artificial Intelligence and Statistics), 246–252. Available online at: https://proceedings.mlr.press/r5/morin05a/morin05a.pdf

Google Scholar

Nilashi, M., Minaei-Bidgoli, B., Alghamdi, A., Alrizq, M., Alghamdi, O., Nayer, F. K., et al. (2022). Knowledge discovery for course choice decision in Massive Open Online Courses using machine learning approaches. Expert Syst. Appl. 199:117092. doi: 10.1016/j.eswa.2022.117092

Crossref Full Text | Google Scholar

Obeid, C., Lahoud, C., El Khoury, K., and Champin, P. A. (2022). A novel hybrid recommender system approach for student academic advising named COHRS, supported by case-based reasoning and ontology. Comp. Sci. Inform. Syst. 19, 979–1005. doi: 10.2298/CSIS220215011O

Crossref Full Text | Google Scholar

Ouyang, L., Wu, J., Jiang, X., Almeida, D., Wainwirght, C., Mishkin, P., et al. (2022). Training language models to follow instructions with human feedback. arXiv [preprint] arXiv:220302155. doi: 10.48550/arXiv.2203.02155

Crossref Full Text | Google Scholar

Oztas, G. S., and Akcapinar, G. (2025). Predicting students' academic procrastination tendencies using online learning trajectories. Educ. Technol. Soc. 28, 77–93. doi: 10.30191/ETS.202504_28(2).RP05

Crossref Full Text | Google Scholar

Pargett, K. K. (2011). The Effects of Academic Advising on College Student Development in Higher Education (Educational Administration: Theses, Dissertations, and Student Research), 81. Available online at: https://digitalcommons.unl.edu/cehsedaddiss/81

Google Scholar

Qwen team (2024). Qwen2.5-7B [Computer software]. Hugging Face. Available online at: https://huggingface.co/Qwen/Qwen2.5-7B (Accessed September 22, 2025).

Google Scholar

Ricci, F., Rokach, L., and Shapira, B. (2022). Recommender Systems Handbook. New York, NY: Springer.

PubMed Abstract | Google Scholar

Thierry, N., Bao, B. K., Chatelain, I. B. C., Tan, Z., Ali, Z., and Kefalas, P. (2023). PRM-KGED: paper recommender model using knowledge graph embedding and deep neural network. Appl. Intellig. 53, 30535–30551. doi: 10.1007/s10489-023-05162-7

Crossref Full Text | Google Scholar

Thongtan, T., and Phienthrakul, T. (2019). “Sentiment classification using document embeddings trained with cosine similarity,” in Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics: Student Research Workshop (Medford: Association for Computational Linguistics (ACL)), 407–414. doi: 10.18653/v1/P19-2057

PubMed Abstract | Crossref Full Text | Google Scholar

Wang, J., Au, O. T. S., Wang, F. L., Xie, H., and Zou, D. (2020). “Attention-based CNN for personalized course recommendations for MOOC learners,” in Proceedings of the 2020 International Symposium on Educational Technology (ISET) (New York, NY: IEEE), 180–184. doi: 10.1109/ISET49818.2020.00047

Crossref Full Text | Google Scholar

Wang, X., Ma, W., Guo, L., Jiang, H., Liu, F., and Xu, C. (2022). HGNN: hyperedge-based graph neural network for MOOC course recommendation. Inform. Proc. Managem. 59:102938. doi: 10.1016/j.ipm.2022.102938

Crossref Full Text | Google Scholar

Wang, Z., Wei, W., Xu, C., Xu, J., and Mao, X. (2022). Person-job fit estimation from candidate profile and related recruitment history with co-attentionf neural networks. Neurocomputing. 501, 14–24. doi: 10.1016/j.neucom.2022.06.012

Crossref Full Text | Google Scholar

Wankat, P. C. (2005). Undergraduate student competitions. J. Eng. Educ. 94, 343–347. doi: 10.1002/j.2168-9830.2005.tb00860.x

Crossref Full Text | Google Scholar

Wu, J., and Feng, Q. (2020). Recommendation system design for college network education based on deep learning and fuzzy uncertainty. J. Intellig. Fuzzy Syst. 38, 7083–7094. doi: 10.3233/JIFS-179787

Crossref Full Text | Google Scholar

Wu, L., He, X., Wang, X., Zhang, K., and Wang, M. (2023). A survey on accuracy-oriented neural recommendation: from collaborative filtering to information-rich recommendation. IEEE Trans. Knowl. Data Eng. 35, 4425–4445. doi: 10.1109/TKDE.2022.3145690

Crossref Full Text | Google Scholar

Yang, A., Yang, B., Hui, B., Zheng, B., Yu, B., Zhou, C., et al. (2024). Qwen2 technical report. arXiv [preprint] arXiv:240710671. doi: 10.48550/arXiv.2407.10671

Crossref Full Text | Google Scholar

Yang, Z., Yang, J., Du, X., Rice, K., and Hung, J. L. (2020). Using convolutional neural network to recognize learning images for early warning of at-risk students. IEEE Trans. Learn. Technol. 13, 617–630. doi: 10.1109/TLT.2020.2988253

Crossref Full Text | Google Scholar

Yu, Q. (2022). Factors influencing online learning satisfaction. Front. Psychol. 13, 852360–852360. doi: 10.3389/fpsyg.2022.852360

PubMed Abstract | Crossref Full Text | Google Scholar

Zemaityte, G., and Terzić, K. (2019). “Supervisor recommendation tool for computer science projects,” in CEP'19: Proceedings of the 3rd Conference on Computing Education Practice (New York, NY: ACM), 1–4. doi: 10.1145/3294016.3294030

Crossref Full Text | Google Scholar

Zhang, C., Xue, S., Li, J., Wu, J., Du, B., Liu, D., et al. (2023). Multi-aspect enhanced graph neural networks for recommendation. Neural Netw. 157, 90–102. doi: 10.1016/j.neunet.2022.10.001

PubMed Abstract | Crossref Full Text | Google Scholar

Zhang, J., Hao, B., Chen, B., Li, C., Chen, H., and Sun, J. (2019). “Hierarchical reinforcement learning for course recommendation in MOOCs,” in Proceedings of the AAAI Conference on Artificial Intelligence (Palo Alto, CA: AAAI Press), 435–442. doi: 10.1609/aaai.v33i01.3301435

Crossref Full Text | Google Scholar

Zhang, M., Liu, Z., Sun, J., Ma, J., and Silva, T. (2016). A research analytics framework-supported recommendation approach for supervisor selection. Br. J. Educ. Technol. 47, 403–420. doi: 10.1111/bjet.12244

Crossref Full Text | Google Scholar

Zou, W., Zhong, W., Du, J., and Yuan, L. (2025). Prediction of student academic performance utilizing a multi-model fusion approach in the realm of machine learning. Appl. Sci-Basel. 17:3550. doi: 10.3390/app15073550

Crossref Full Text | Google Scholar