A Modified Theoretical Model to Accurately Account for Interfacial Roughness in Predicting the Interfacial Thermal Conductance

The acoustic mismatch model and the diffuse mismatch model (DMM) have been widely used to predict the thermal interface conductance. However, the acoustic mismatch model and the DMM are based on the hypothesis of a perfectly smooth interface and a completely disordered interface respectively. Here, we present a new modified model, named as the mixed mismatch model, which considers the roughness/bonding at the interface. By taking partially specular and partially diffuse transmission into account, the mixed mismatch model (MMM) can predict the thermal interface conductance with arbitrary roughness. The proportions of specular and diffuse transmission are determined by the interface roughness which is described by the interfacial density of states. We show that the predicted results of the MMM match well with the values of molecular dynamics simulation and experimental data.

Thermal transport across interfaces is an important issue for microelectronics, photonics, and thermoelectric devices, and has been studied both experimentally and theoretically recently (Swartz and Pohl, 1989; Zhu et al., 2010; Cahill et al., 2014; Wu et al., 2016; Zheng et al., 2016). Generally, the interfacial thermal conductance (ITC) is used to evaluate the physical properties of thermal transport in devices and materials (Yang et al., 2012), such as composites (Nan et al., 1997; Deng et al., 2017) superlattices (Dresselhaus et al., 2007), thin-film multilayers (Cahill et al., 2000), nanoscale devices (Goodson and Ju, 1999; Han et al., 2015), and nanocrystalline materials (Soyez et al., 2000). Therefore, a deep understanding and an accurate prediction of ITC are crucial to improve the design and performance of various devices and materials.

To date, two theoretical models, the acoustic mismatch model (AMM) and the diffuse mismatch model (DMM), have been widely used in predicting the ITC (Swartz and Pohl, 1989). The AMM makes an essential simplified assumption that phonons incident at an interface undergo specular transmission and are governed by continuum mechanics (Swartz and Pohl, 1989). Contrarily, the DMM assumes that the interface is completely disordered and phonons lose their memory after reaching the interface (Little, 1959; Swartz and Pohl, 1989). Although these two models have advanced the understanding of thermal transport across interface, both the AMM and DMM purely consider the bulk properties, and ignore the interfacial roughness (Tian et al., 2012; Merabia and Termentzidis, 2014; Ramiere et al., 2016; Shao et al., 2017), interfacial modes(Chalopin and Volz, 2013; Gong et al., 2013; Yang et al., 2015; Gordiz and Henry, 2016; Lee and Luo, 2017), electron-phonon coupling (Huang and Kaviany, 2008; Hohensee et al., 2015), and inelastic scattering at the interface (Xiong et al., 2018), which leads to the inaccuracy of the two models (Swartz and Pohl, 1989; Wu and Luo, 2014).

In the past decades, some works have improved the accuracy of the AMM and DMM, and sophisticated modifications to the original models that account for the inelastic scattering have been proposed. For example, the maximum transmission model (Dames and Chen, 2004), the higher harmonic inelastic model (Hopkins, 2009), the joint frequency DMM (Hopkins and Norris, 2007), the scattering-mediated acoustic mismatch model (Prasher and Phelan, 2001), and the anharmonic inelastic model (Hopkins et al., 2011). In addition, several literature studies have included the electron-phonon couplings at metal/non-metal interfaces (Majumdar and Reddy, 2004; Wang et al., 2012; Wu and Luo, 2015).

In 1960, Ziman analyzed the partially specular and partially diffuse reflection of phonons at surface (Ziman, 1960). Then Chen applied this idea to interface scattering model to predict the thermal conductivity of superlattice structures (Chen, 1997). The idea is worth to be applied in calculating the ITC. Besides, it is found that the phonon interface states which are localized close to the interfacial region and different from bulk states have a large effect on ITC (Shin et al., 2010; Liang et al., 2014; Murakami et al., 2014; Gordiz and Henry, 2015; Polanco et al., 2015). However, all of the existing theoretical models do not consider the interface states. Therefore, there is a great demand for a theoretical model that accounts for interface states in predicting the ITC.

In this letter, we developed a new model to predict the ITC, named as the mixed mismatch model (MMM). Based on partially specular and partially diffuse transmissions, by taking interface states into account, the MMM can predict the ITC with arbitrary roughness and overcomes the shortcomings of AMM and DMM. Here, we considered the interface states in obtaining the proportions of diffuse and specular transmission. To validate the accuracy of the MMM, we compared the ITC values of MMM to those by MD simulations and experimental measurements.

At the interface between material A and B, an incident phonon with frequency ω and mode j can either scatter back or transmit (Swartz and Pohl, 1989). According to the Landauer formalism (Chen, 2005), we can predict the ITC, G, as

$\begin{array}{r}G=\frac{1}{4}{\displaystyle \sum _j}{\displaystyle {\int }_0^{{\omega }_{A,j}^v}}{D}_{A,j}(\omega )\frac{\partial n(\omega ,T)}{\partial T}\hslash \omega v_{A,j}{\alpha }_{A\to B,j}(\omega )d\omega \end{array}$

where ω is the frequency, ω^v is the cutoff frequency, D is the phonon density of states, n(ω,T) is the Bose-Einstein distribution function, v is the phonon group velocity for the phonon mode of interest at frequency ω, and α is the phonon transmission coefficient. The subscript “j” refers to the phonon polarization.

In the AMM and DMM, the transmission coefficient can be calculated as (Swartz and Pohl, 1989; Cahill et al., 2000)

$\begin{array}{rcl}{\alpha }_{AMM,A\to B}& =& \frac{4{\rho }_A{v}_A{\rho }_B{v}_B}{{({\rho }_A{v}_A+{\rho }_B{v}_B)}^2}\end{array}$

$\begin{array}{rcl}{\alpha }_{DMM,A\to B}& =& \frac{{\displaystyle {\sum }_j}{D}_{B,j}{v}_{B,j}}{{\displaystyle {\sum }_j}{D}_{A,j}{v}_{A,j}+{\displaystyle {\sum }_j}{D}_{B,j}{v}_{B,j}}\end{array}$

where ρ is the mass density.

According to previous studies (Soffer, 1967; Chen, 1997; Chen and Neagu, 1997; Phelan, 1998; Bellis et al., 2000; Zhao and Freund, 2009), for solid-solid interfaces, both diffuse and specular transmissions are taking place at the interface. Hence, an assumed specular parameter, p, can be used to represent the proportion of phonons specularly transmitted across the interface (Soffer, 1967; Chen, 1997). Hence, in the MMM, we define the transmission coefficient by linearly combining AMM and DMM terms as

$\begin{array}{r}{\alpha }_{MMM,A\to B}=(1-p)·{\alpha }_{DMM,A\to B}+p·{\alpha }_{AMM,A\to B}\end{array}$

According to Ziman (Soffer, 1967), the p is related to the root mean square roughness (RMSR), η, and to phonon wavelength, λ. Ziman postulated the relationship as

$\begin{array}{r}p=exp\left(-\frac{16{\pi }^2{\eta }^2}{{\lambda }^2}\right)\end{array}$

Generally, for simplification the roughness is considered as a constant for a given surface. While the roughness of the surface is measured by the height of the asperities, and is a rather rapidly changing function at the point where the height and wavelength are about equal (Ziman, 1960). It means that constant value of η is too restrictive to be applied to real surfaces. The whole interface should be divided into many different small sampling areas whose size is relative to a few wavelengths in dimensions (Ziman, 1960). Regarding to different wavelength of phonons, the size of the sampling area is different. According to statistics from different sampling area, the roughness is different and depends on phonon frequency.

As we know, the η depends on the interfacial structure (e.g., the arrangement of atoms at the interface). Recently, it is found that the interfacial structure is related to interfacial density of states (IDOS), which may differ from that of the bulk materials (Yang et al., 2015; Gordiz and Henry, 2016). That is, the η depends on IDOS. For the specular interface corresponding to the AMM case, the interface is treated as a perfect plane and the η is zero (Swartz and Pohl, 1989). To make the interface as a perfect plane, the atoms close to interface stay at the equilibrium situation as in the bulk (D_bulk,A and D_bulk,B). Therefore, the atoms close to interface vibrate as the bulk and the IDOS should be the same as the DOS of the bulk. Generally, interface is consisting of two materials which have different force constant, they interact with each other and will definitely distort the interfacial structure. In this case, the specular plane does not exist in interface (Chalopin and Volz, 2013; Gordiz and Henry, 2016). On the contrary, for the completely diffuse interface corresponding to the DMM case, all the phonons are diffusely scattered and the acoustic correlations are completely destroyed (Swartz and Pohl, 1989). And the structure is similar to amorphous structures where each atom has a distinct local environment (Kaviany, 2014) and the acoustic correlations are completely destroyed. Thus, we speculate that the IDOS of a completely diffuse interface should also be similar to the DOS of an amorphous structure (D_amo,A and D_amo,B). Since both the real interface structure and its IDOS (D_int,A and D_int,B) are between the two extremities, there is a mapping between RMSR and IDOS. We choose to use a simple mapping function of RMSR on the density of states, expressed as:

$\begin{array}{l}\eta \left(\omega \right)=C·\frac{1}{2}·(\frac{D_{bulk,A}\left(\omega \right)-D_{int,A}\left(\omega \right)}{D_{int,A}\left(\omega \right)-D_{amo,A}\left(\omega \right)}\\ +\frac{D_{bulk,B}\left(\omega \right)-D_{int,B}\left(\omega \right)}{D_{int,B}\left(\omega \right)-D_{amo,B}\left(\omega \right)})\end{array}$

where C is a constant, which does not depend on the frequency. The D_bulk, D_amo are the DOS in the bulk and in amorphous structure, respectively. It is worth noting that here we obtain the value of C by MD simulations, but not limited to MD simulations, the value of C can be obtained by experiment or any other simulation methods.

According to Equations (5) and (6), the specular parameter, p, is obtained

$\begin{array}{l}p(\omega )=\exp (-\frac{4{\pi }^2{C}^2}{{\lambda }^2}·(\frac{D_{int,A}\left(\omega \right)-D_{bulk,A}\left(\omega \right)}{D_{int,A}\left(\omega \right)-D_{amo,A}\left(\omega \right)}\\ +{\frac{D_{int,B}\left(\omega \right)-D_{bulk,B}\left(\omega \right)}{D_{int,B}\left(\omega \right)-D_{amo,B}\left(\omega \right)})}^2)\end{array}$

This is the key equation of this letter. By substituting Equation (7) into Equation (4), we can get the transmission coefficient α, then the ITC can be figured out by Equation (1). It is shown that the interfacial structure or IDOS will greatly affect the phonon transport. As shown in Figure 3, for the perfectly smooth interface, the specular reflection does not change the energy and the momentum components along the direction of the temperature gradient (Chen, 1997), thus the IDOS should be the same as the DOS of the bulk. Contrarily, for the extremely rough interface, the IDOS is similar to the DOS of amorphous structures. For a partially specular and partially diffuse interface, the IDOS is in between the two extreme situations.

The MD simulation and green function are being widely used to predict the ITC (Landry and McGaughey, 2009; Ma et al., 2016). While there is no assumption on the phonon scattering in MD (Ma et al., 2016). To demonstrate the accuracy of the MMM, we calculated the ITC of interfaces with different roughness, and then compared the results of MMM with MD values. In our MD simulations (The MD simulation details are shown in Supporting information (Figure 1d and Figure SI), we create two Al/Si interface structures with different roughness, structure (a) and (b) (shown in Figure SI). The structures after relaxation are shown in Figures 1a,b. The interface roughness of structure (b) is larger than that of structure (a). And the IDOS of structure (a) and (b) is calculated as the average phonon modes of atoms at the interface. And the interface thickness is set as 0.815 nm. The phonon group velocity of each mode is calculated by sorting the phonon dispersion relationship. (as shown in Figure SII) We also simulate an amorphous (completely disordered) structure (shown in Figure 1c) to obtain the D_amo,Al and D_amo,Si in Equation (8).

FIGURE 1

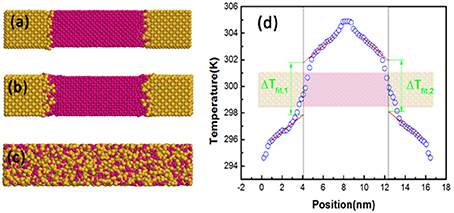
Figure 1. (a–c) are the side views of simulation cell. The red atoms are Al, and the yellow atoms are Si. The lattice constants of Al and Si are 0.407 and 0.543 nm, respectively. (a) Al 8 × 8 × 20 unit cells³/Si 6 × 6 × 15 unit cells³ is the small interface roughness structure. (b) Al 8 × 8 × 20 unit cells³/Si 6 × 6 × 15 unit cells³ is the large interface roughness structure. (c) This completely disordered structure is used to obtain the IDOS of DMM. (d) A typical time-averaged temperature profile of interface structure. The interface temperature difference is defined as average of the difference between the linearly extrapolated temperature at each side of the interface. Then, ΔT_fit = (ΔT_fit,1 + ΔT_fit,2)/2.

The main results are shown in Figure 2A. The ITC of AMM and DMM correspond to the ITC of the perfectly smooth interface and completely disordered interface, respectively. The interfaces of structure (a) and (b) are partially diffuse and partially specular. We calculated the ITC of the two interfacial structures [structure (a) with smaller roughness and structure (b) with larger roughness] by MD. We perform several simulations with different initial states for one structure, and the value shown here is the average value, where the error bar is the standard deviation. The results of MD show that both of them fall in AMM and DMM predictions, and the ITC of structure (b) is larger than that of structure (a). In the calculation of MMM, the value of C is unknown, but can be obtained by fitting to the MD data of structure (a), as 5.75 × 10⁻¹¹. Then we applied Equation (7) to predict ITC of structure (b) by MMM which matches well with the data of MD (Figure 2A). It declares the validity of MMM. It is worth noting that here we obtain the value of C by MD, but not limited to MD, the value of C can be get by experiment or any other simulation method.

FIGURE 2

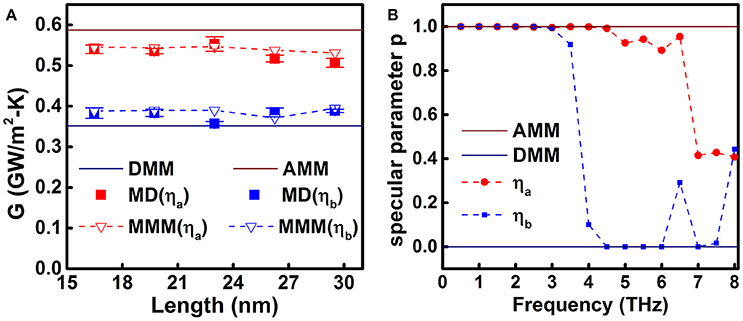
Figure 2. (A) The results of thermal interface conductance calculated by AMM, DMM, and MMM. MD means our MD calculation results of ITC. η_a and η_b denote different interface roughness, and the roughness of η_a is smaller than that of η_b; (B) The specular parameter p of structures with different interface roughness: η_a and η_b, which correspond with the structures in Figures 1a,b.

The specular parameter is the most important parameter in the MMM which presents the proportion of phonons specular transmitted across the interface. As shown in Figure 2B, the dependence of specular parameters on frequency for difference interface structures was calculated and compared. (The specular parameters of other structures are shown in Figure SV) There is an obvious decline in the p-curves of both structures (a) and (b). For lower frequency phonons in each p-curve, with longer wavelength, it shows that the values of p for both (a) and (b) are close to one. That is, the phonons with longer wavelength are not sensitive to the nanoscale interface roughness and transit across them similar to a specular interface. For higher frequency phonons, the shorter wavelength phonons transmit across the interface with more diffusive scatterings. Besides, the decline frequency of (a), ~6.5 THz, is higher than that of (b), ~3.5 THz, because the roughness of structure (a) is smaller than that of structure (b). As shown in Equation (5) the IDOS dominates the value of p, which makes the MMM consider the interfacial structure. To show the relationship between the IDOS and the interfacial structure, we calculated the IDOS of different interfacial structures. Figures 3A,B show the IDOS of a perfectly smooth interface in AMM and a completely disordered interface in DMM, corresponding to the DOS of bulk and amorphous structure [Figure S1 (f)], respectively. While Figures 3C,D show the IDOS of structures (a) and (b), respectively. (The IDOS of other structures are shown in Figures SIII, SIV) By comparing the difference of IDOS between Al and Si, we find that the IDOS of Al and Si become similar with each other as the interface roughness increases because the disorder structure at interface diminishes the bulk properties.

FIGURE 3

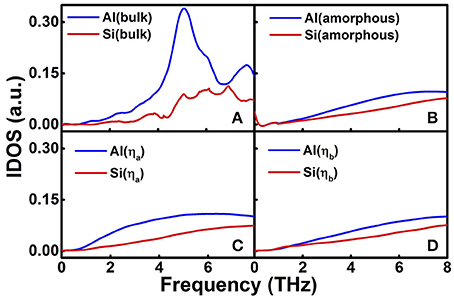
Figure 3. (A) DOS of Al and Si in bulk crystals; (B) DOS of amorphous Al and Si; (C) IDOS of the structure (A) with a system length as 16.473 nm; (D) IDOS of structure (B) with a system length as 16.473 nm.

To further validate the MMM, we compare the transmission coefficient calculated by the MMM with the experimental results (Hua et al., 2017). Minnich et al. obtained the results by interpreting data from TDTR experiment with ab initio phonon transport model. In Figure 4, it shows that the transmission coefficients of the MMM match well with the experimental values. Besides, we can see that the DMM underestimates the transmission coefficient of lower-frequency phonons because the phonons with longer wavelengths are less likely to be scattered. Contrarily, the AMM overestimates the transmission coefficient of high frequency phonons due to the phonons with shorter wavelengths are more likely to be scattered.

FIGURE 4

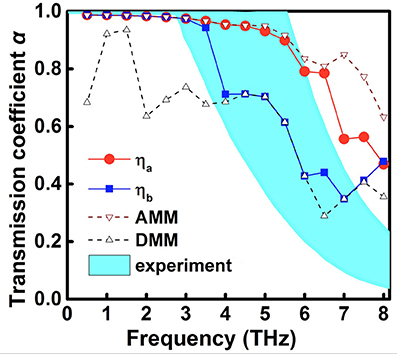
Figure 4. Comparison of the transmission coefficient α of our proposed MMM (specified symbols) with those obtained from the AMM (downward open triangles), DMM (upward open triangles), and experimental data (light blue region) (Hua et al., 2017).

It is worth noting that in experiments, the oxidation of interface is a very common issue (Hopkins et al., 2010, 2012; Lee et al., 2016), which will affect phonon transport. Generally, the native oxides will increase the interfacial roughness and induce more scattering, thus decrease the transmission coefficient (Hopkins et al., 2010; Mu et al., 2016). While if the oxidation strengthens the chemical bond of the interface, this effect will be much stronger than the induced roughness scattering, the transmission coefficient will increase, and the ITC will increase (Hopkins et al., 2012). In MMM, IDOS is used to describe the interfacial information, which includes the increasing of roughness and strengthening of bond caused by oxides. Therefore, the MMM is also valid to deal with interfaces which have oxidation.

In summary, we have developed a new theoretical model, named as the mixed mismatch model, which predicts the thermal interface conductance by considering the interfacial structure. The MMM takes into account partially specular and partially diffuse transmissions using the IDOS to determine the proportion of specular parameter. The value of specular parameter has an obvious dependence on the phonon wavelength and interfacial roughness. The MMM is validated by comparing its prediction with both MD results and measurements. Both ITC and the transmission coefficients calculated by the MMM agree well with those obtained from the direct MD simulation and from experiment.

Author Contributions

YyZ and DM contributed equally to proposing the new model in this manuscript, and YZ helped validate the data. XW contributed to revising the manuscript and replying to reviewers' comments. NY provided essential guidance to this work.

Conflict of Interest Statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

NY was sponsored by National Natural Science Foundation of China (No. 51576076 and No. 51711540031), Hubei Provincial Natural Science Foundation of China (2017CFA046) and Fundamental Research Funds for the Central Universities (2016YXZD006). XW was sponsored by the National Science Foundation through the University of Minnesota MRSEC (DMR-1420013) and the Legislative-Citizen Commission on Minnesota Resources. The authors are grateful to Hua Bao, and Xin Qian for useful discussions. Besides, the authors thank the National Supercomputing Center in Tianjin (NSCC-TJ) and China Scientific Computing Grid (ScGrid) for providing assistance in computations.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2018.00048/full#supplementary-material

References

Bellis, L. D., Phelan, P. E., and Prasher, R. S. (2000). Variations of acoustic and diffuse mismatch models in predicting thermal-boundary resistance. J. Thermophys. Heat Transf. 14, 144–150. doi: 10.2514/2.6525

CrossRef Full Text | Google Scholar

Cahill, D. G., Braun, P. V., Chen, G., Clarke, D. R., Fan, S., Goodson, K. E., et al. (2014). Nanoscale thermal transport. II. 2003–2012. Appl. Phys. Rev. 1:011305. doi: 10.1063/1.4832615

CrossRef Full Text | Google Scholar

Cahill, D. G., Bullen, A., and Seung-Min, L. (2000). Interface thermal conductance and the thermal conductivity of multilayer thin films. High. Temp. High. Press. 32, 135–142. doi: 10.1068/htwi9

CrossRef Full Text | Google Scholar

Chalopin, Y., and Volz, S. (2013). A microscopic formulation of the phonon transmission at the nanoscale. Appl. Phys. Lett. 103:051602. doi: 10.1063/1.4816738

CrossRef Full Text | Google Scholar

Chen, G. (1997). Size and interface effects on thermal conductivity of superlattices and periodic thin-film structures. J. Heat Transf. 119, 220–229. doi: 10.1115/1.2824212

CrossRef Full Text | Google Scholar

Chen, G. (2005). Nanoscale Energy Transport and Conversion: A Parallel Treatment of Electrons, Molecules, Phonons, and Photons. New York, NY: Oxford University Press.

Google Scholar

Chen, G., and Neagu, M. (1997). Thermal conductivity and heat transfer in superlattices. Appl. Phys. Lett. 71, 2761–2763. doi: 10.1063/1.120126

CrossRef Full Text | Google Scholar

Dames, C., and Chen, G. (2004). Theoretical phonon thermal conductivity of Si/Ge superlattice nanowires. J. Appl. Phys. 95, 682–693. doi: 10.1063/1.1631734

CrossRef Full Text | Google Scholar

Deng, C., Yu, X., Huang, X., and Yang, N. (2017). Enhancement of interfacial thermal conductance of SiC by overlapped carbon nanotubes and intertube atoms. J. Heat Transf. 139:054504. doi: 10.1115/1.4035998

CrossRef Full Text | Google Scholar

Dresselhaus, M. S., Chen, G., Tang, M. Y., Yang, R., Lee, H., Wang, D., et al. (2007). New directions for low-dimensional thermoelectric materials. Adv. Mat. 19, 1043–1053. doi: 10.1002/adma.200600527

CrossRef Full Text | Google Scholar

Gong, C., Zhang, H., Wang, W., Colombo, L., Wallace, R. M., and Cho, K. (2013). Band alignment of two-dimensional transition metal dichalcogenides: application in tunnel field effect transistors. Appl. Phys. Lett. 103:053513. doi: 10.1063/1.4817409

CrossRef Full Text | Google Scholar

Goodson, K. E., and Ju, Y. S. (1999). Heat conduction in novel electronic films. Annu. Rev. Mater. Sci. 29, 261–293. doi: 10.1146/annurev.matsci.29.1.261

CrossRef Full Text | Google Scholar

Gordiz, K., and Henry, A. (2015). Examining the effects of stiffness and mass difference on the thermal interface conductance between Lennard-Jones solids. Sci. Rep. 5:18361. doi: 10.1038/srep18361

PubMed Abstract | CrossRef Full Text | Google Scholar

Gordiz, K., and Henry, A. (2016). Phonon transport at crystalline Si/Ge interfaces: the role of interfacial modes of vibration. Sci. Rep. 6:23139. doi: 10.1038/srep23139

PubMed Abstract | CrossRef Full Text | Google Scholar

Han, H., Li, B., Volz, S., and Kosevich, Y. A. (2015). Ultracompact interference phonon nanocapacitor for storage and lasing of coherent terahertz lattice waves. Phys. Rev. Lett. 114:145501. doi: 10.1103/PhysRevLett.114.145501

PubMed Abstract | CrossRef Full Text | Google Scholar

Hohensee, G. T., Wilson, R. B., and Cahill, D. G. (2015). Thermal conductance of metal-diamond interfaces at high pressure. Nat. Commun. 6:6578. doi: 10.1038/ncomms7578

PubMed Abstract | CrossRef Full Text | Google Scholar

Hopkins, P. E. (2009). Multiple phonon processes contributing to inelastic scattering during thermal boundary conductance at solid interfaces. J. Appl. Phys. 106:013528. doi: 10.1063/1.3169515

CrossRef Full Text | Google Scholar

Hopkins, P. E., Baraket, M., Barnat, E. V., Beechem, T. E., Kearney, S. P., Duda, J. C., et al. (2012). Manipulating thermal conductance at metal–graphene contacts via chemical functionalization. Nano Lett. 12, 590–595. doi: 10.1021/nl203060j

PubMed Abstract | CrossRef Full Text | Google Scholar

Hopkins, P. E., Duda, J. C., and Norris, P. M. (2011). Anharmonic phonon interactions at interfaces and contributions to thermal boundary conductance. J. Heat Transf. 133:062401. doi: 10.1115/1.4003549

CrossRef Full Text | Google Scholar

Hopkins, P. E., and Norris, P. M. (2007). Effects of joint vibrational states on thermal boundary conductance. Nanosc. Microsc. Therm. 11, 247–257. doi: 10.1080/15567260701715297

CrossRef Full Text | Google Scholar

Hopkins, P. E., Phinney, L. M., Serrano, J. R., and Beechem, T. E. (2010). Effects of surface roughness and oxide layer on the thermal boundary conductance at aluminum/silicon interfaces. Phys. Rev. B 82:085307. doi: 10.1115/IHTC14-22268

CrossRef Full Text | Google Scholar

Hua, C., Chen, X., Ravichandran, N. K., and Minnich, A. J. (2017). Experimental metrology to obtain thermal phonon transmission coefficients at solid interfaces. Phys. Rev. B 95:205423. doi: 10.1103/PhysRevB.95.205423

CrossRef Full Text | Google Scholar

Huang, B.-L., and Kaviany, M. (2008). Ab initio and molecular dynamics predictions for electron and phonon transport in bismuth telluride. Phys. Rev. B 77:125209. doi: 10.1103/PhysRevB.77.125209

CrossRef Full Text | Google Scholar

Kaviany, M. (2014). Heat Transfer Physics. New York, NY: Cambridge University Press.

Google Scholar

Landry, E. S., and McGaughey, A. J. H. (2009). Thermal boundary resistance predictions from molecular dynamics simulations and theoretical calculations. Phys. Rev. B 80:165304. doi: 10.1103/PhysRevB.80.165304

CrossRef Full Text | Google Scholar

Lee, E., and Luo, T. (2017). The role of optical phonons in intermediate layer-mediated thermal transport across solid interfaces. Phys. Chem. Chem. Phys. 19, 18407–18415. doi: 10.1039/C7CP02982A

PubMed Abstract | CrossRef Full Text | Google Scholar

Lee, E., Zhang, T., Yoo, T., Guo, Z., and Luo, T. (2016). Nanostructures significantly enhance thermal transport across solid interfaces. ACS Appl. Mater. Inter. 8, 35505–35512. doi: 10.1021/acsami.6b12947

PubMed Abstract | CrossRef Full Text | Google Scholar

Liang, Z., Sasikumar, K., and Keblinski, P. (2014). Thermal transport across a substrate–thin-film interface: effects of film thickness and surface roughness. Phys. Rev. Lett. 113:065901. doi: 10.1103/PhysRevLett.113.065901

PubMed Abstract | CrossRef Full Text | Google Scholar

Little, W. A. (1959). The transport of heat between dissimilar solids at low temperatures. Can. J. Phys. 37, 334–373. doi: 10.1139/p59-037

CrossRef Full Text | Google Scholar

Ma, D., Ding, H., Meng, H., Feng, L., Wu, Y., Shiomi, J., et al. (2016). Nano-cross-junction effect on phonon transport in silicon nanowire cages. Phys. Rev. B 94:165434. doi: 10.1103/PhysRevB.94.165434

CrossRef Full Text | Google Scholar

Majumdar, A., and Reddy, P. (2004). Role of electron–phonon coupling in thermal conductance of metal–nonmetal interfaces. Appl. Phys. Lett. 84, 4768–4770. doi: 10.1063/1.1758301

CrossRef Full Text | Google Scholar

Merabia, S., and Termentzidis, K. (2014). Thermal boundary conductance across rough interfaces probed by molecular dynamics. Phys. Rev. B 89:054309. doi: 10.1103/PhysRevB.89.054309

CrossRef Full Text | Google Scholar

Mu, X., Song, Z., Wang, Y., Xu, Z., Go, D. B., and Luo, T. (2016). Thermal transport in oxidized polycrystalline graphene. Carbon 108, 318–326. doi: 10.1016/j.carbon.2016.07.023

CrossRef Full Text | Google Scholar

Murakami, T., Hori, T., Shiga, T., and Shiomi, J. (2014). Probing and tuning inelastic phonon conductance across finite-thickness interface. Appl. Phys. Exp. 7:121801. doi: 10.7567/APEX.7.121801

CrossRef Full Text | Google Scholar

Nan, C.-W., Birringer, R., Clarke, D. R., and Gleiter, H. (1997). Effective thermal conductivity of particulate composites with interfacial thermal resistance. J. Appl. Phys. 81, 6692–6699. doi: 10.1063/1.365209

CrossRef Full Text | Google Scholar

Phelan, P. E. (1998). Application of diffuse mismatch theory to the prediction of thermal boundary resistance in thin-film high-T_C superconductors. J. Heat Transf. 120, 37–43. doi: 10.1115/1.2830060

CrossRef Full Text | Google Scholar

Polanco, C. A., Rastgarkafshgarkolaei, R., Zhang, J., Le, N. Q., Norris, P. M., Hopkins, P. E., et al. (2015). Role of crystal structure and junction morphology on interface thermal conductance. Phys. Rev. B 92:144302. doi: 10.1103/PhysRevB.92.144302

CrossRef Full Text | Google Scholar

Prasher, R. S., and Phelan, P. E. (2001). A scattering-mediated acoustic mismatch model for the prediction of thermal boundary resistance. J. Heat Transf. 123, 105–112. doi: 10.1115/1.1338138

CrossRef Full Text | Google Scholar

Ramiere, A., Volz, S., and Amrit, J. (2016). Thermal resistance at a solid/superfluid helium interface. Nat Mater 15, 512–516. doi: 10.1038/nmat4574

PubMed Abstract | CrossRef Full Text | Google Scholar

Shao, C., Rong, Q., Hu, M., and Bao, H. (2017). Probing phonon–surface interaction by wave-packet simulation: effect of roughness and morphology. J. Appl. Phys. 122:155104. doi: 10.1063/1.5008367

CrossRef Full Text | Google Scholar

Shin, S., Kaviany, M., Desai, T., and Bonner, R. (2010). Roles of atomic restructuring in interfacial phonon transport. Phys. Rev. B 82:081302. doi: 10.1103/PhysRevB.82.081302

CrossRef Full Text | Google Scholar

Soffer, S. B. (1967). Statistical model for the size effect in electrical conduction. J. Appl. Phys. 38, 1710–1715. doi: 10.1063/1.1709746

CrossRef Full Text | Google Scholar

Soyez, G., Eastman, J. A., Thompson, L. J., Bai, G.-R., Baldo, P. M., McCormick, A. W., et al. (2000). Grain-size-dependent thermal conductivity of nanocrystalline yttria-stabilized zirconia films grown by metal-organic chemical vapor deposition. Appl. Phys. Lett. 77, 1155–1157. doi: 10.1063/1.1289803

CrossRef Full Text | Google Scholar

Swartz, E. T., and Pohl, R. O. (1989). Thermal-boundary resistance. Rev. Mod. Phys. 61, 605–668. doi: 10.1103/RevModPhys.61.605

CrossRef Full Text | Google Scholar

Tian, Z., Esfarjani, K., and Chen, G. (2012). Enhancing phonon transmission across a Si/Ge interface by atomic roughness: first-principles study with the Green's function method. Phys. Rev. B 86:235304. doi: 10.1103/PhysRevB.86.235304

CrossRef Full Text | Google Scholar

Wang, Y., Ruan, X., and Roy, A. K. (2012). Two-temperature nonequilibrium molecular dynamics simulation of thermal transport across metal-nonmetal interfaces. Phys. Rev. B 85:205311. doi: 10.1103/PhysRevB.85.205311

CrossRef Full Text | Google Scholar

Wu, X., and Luo, T. (2014). The importance of anharmonicity in thermal transport across solid-solid interfaces. J. Appl. Phys. 115:014901. doi: 10.1063/1.4859555

CrossRef Full Text | Google Scholar

Wu, X., and Luo, T. (2015). Effect of electron-phonon coupling on thermal transport across metal-nonmetal interface —A second look. Europhys. Lett. 110:67004. doi: 10.1209/0295-5075/110/67004

CrossRef Full Text | Google Scholar

Wu, X., Ni, Y., Zhu, J., Burrows, N. D., Murphy, C. J., Dumitrica, T., et al. (2016). Thermal transport across surfactant layers on gold nanorods in aqueous solution. ACS Appl. Mater. Inter. 8, 10581–10589. doi: 10.1021/acsami.5b12163

PubMed Abstract | CrossRef Full Text | Google Scholar

Xiong, G., Xing, Y., and Zhang, L. (2018). Interfacial thermal transport via one-dimensional atomic junction model. Front. Energy Res. 6:6. doi: 10.3389/fenrg.2018.00006

CrossRef Full Text | Google Scholar

Yang, N., Luo, T., Esfarjani, K., Henry, A., Tian, Z., Shiomi, J., et al. (2015). Thermal interface conductance between aluminum and silicon by molecular dynamics simulations. J. Compt. Theor. NanoSci. 12:168174. doi: 10.1166/jctn.2015.3710

CrossRef Full Text | Google Scholar

Yang, N., Xu, X., Zhang, G., and Li, B. (2012). Thermal transport in nanostructures. AIP Adv. 2:041410. doi: 10.1063/1.4773462

CrossRef Full Text | Google Scholar

Zhao, H., and Freund, J. B. (2009). Phonon scattering at a rough interface between two fcc lattices. J. Appl. Phys. 105:013515. doi: 10.1063/1.3054383

CrossRef Full Text | Google Scholar

Zheng, K., Sun, F., Zhu, J., Ma, Y., Li, X., Tang, D., et al. (2016). Enhancing the thermal conductance of polymer and sapphire interface via self-assembled monolayer. ACS Nano 10, 7792–7798. doi: 10.1021/acsnano.6b03381

PubMed Abstract | CrossRef Full Text | Google Scholar

Zhu, J., Tang, D., Wang, W., Liu, J., Holub, K. W., and Yang, R. (2010). Ultrafast thermoreflectance techniques for measuring thermal conductivity and interface thermal conductance of thin films. J. Appl. Phys. 108:094315. doi: 10.1063/1.3504213

CrossRef Full Text | Google Scholar

Ziman, J. M. (1960). Electrons and Phonons: The Theory of Transport Phenomena in Solids. Oxford: Oxford University Press.

Google Scholar