- 1Department of Statistics, Rice University, Houston, TX, United States
- 2The Center for Computational Finance and Economic Systems (CoFES), Rice University, Houston, TX, United States
This paper quantifies the rising global dynamic, interconnected relationship between energy and water commodities. Over the last decade, increased international concern has emerged about the water-energy nexus. However, recent research still lacks a quantified understanding of the role of water within a financial-economic view of the nexus. The complexity of commodity markets contributes to this lack of understanding. These markets consist of a wide variety of participants having different objectives, resulting in non-stationary time series. Wavelets are mathematical functions that detect common time-localized oscillations in non-stationary time series. The novelty of our analysis lies in applying wavelet techniques to better quantify the financial implications and understand opportunities of the dynamic relationship that exists in the water-energy nexus. Using daily water and energy commodity ETF price data from 2007 to 2017 we deconstruct each of the time series into different horizon components and evaluate their respective wavelet transforms. Comparing the wavelet squared coherence (WSC) and the windowed scalogram difference (WSD) allows us to specify nexus similarities and differences. We further analyze the wavelet local multiple correlations (WLMC) by including S&P500 ETF price data to conditionally eliminate market effects. Previous studies heavily focused on the qualitative relationships between water and energy. Whereas, the analysis in this paper, to the best of our knowledge, is the first to confirm the time-varying relationship in a quantitative manner. The most significant financial-economic result from our analysis is that water prices, at certain time horizons, lead energy prices during specific localized economic events.
1. Introduction
In trying to understand the extremely volatile price dynamics after the 2008 financial crisis, economic researchers introduced the concept of commodity financialization (Cheng and Xiong, 2013), giving rise to energy finance becoming a standalone stream of research. Recently, Zhang (2018) further clarified the concept of energy finance by discussing the fields interdisciplinary nature and emphasizing the need for analyzing linkages between energy commodity markets and other markets to better understand price dynamics. Vacha and Barunik (2012) pointed out that energy commodities affect a wide range of markets and that it is fundamentally important to study the statistical properties and interconnections of these markets. For more recent econometric literature focusing on the dynamic and statistical properties of these markets (see Creti et al., 2013; Abdelradi and Serra, 2015; Ahmadi et al., 2016; Reboredo et al., 2017).
Publications ranging from policy implications to the econometric quantification are supporting the increased need for evaluating the water-energy nexus. Studies that impact policy include the integrated risk analysis of the water-energy nexus with reasonable policy recommendations by Cai et al. (2019), evaluations of water-related impacts due to energy-related decisions by Wang et al. (2019), and a detailed review of existing methods and tools to analyze the water-energy nexus by Dai et al. (2018). Ozturk (2017) goes even further by evaluating the dynamic relationship between food-water-energy and agricultural sustainability in sub-Saharan countries, as well as in earlier work examining countries that make up BRICS (Ozturk, 2015).
For a thorough literature review on the dependency of energy type on water (see Tan and Zhi, 2016). Global studies encouraging the need for evaluating the link between energy and water include the quantitative assessment of the water-energy nexus in the Middle East and North Africa region (Siddiqi and Anadon, 2011), the quantification of the water-energy nexus in Greece (Ziogou and Zachariadis, 2017), studies showing the linkage analysis for the water-energy nexus of Beijing (Fang and Chen, 2017). Additionally, the research of Keulertz and Woertz (2015) looks at the financial challenges of the nexus in the Arab world, Hamiche et al. (2016) comprehensively reviews the links between water and electricity, and Gallegos et al. (2015) studies the potential environmental implications of hydraulic fracturing water use in the United States.
Rising uncertainty in global markets creates fluctuations that lead to increased interdependency between water and energy commodities. For example, a leading global drilling fluids market research report indicates that during the 2014 to 2015 global oil glut, aqueous drilling fluids were most prominent because of low cost and reduced environmental impact. However, this extensive use placed a tremendous amount of stress, globally, on water availability. The need for inclusion of water scarcity within energy planning is more important today than ever before. Costs related to energy and water play a crucial role in decision making at various levels of investing. Smajgl et al. (2016) points out that the integrated and dynamic relationship between these commodities impacts large scale development investments and Wichelns (2017) clearly emphasizes the importance of quantifying investments and integrating research policies needed for future sustainability. To the best of our knowledge our current research is first in quantifying the dynamic financial interaction between water and energy commodities.
Common behaviors or patterns in two jointly stationary time series can be quantified using standard time-domain techniques such as cross-correlation, cross-spectrum, and coherence. However, there are two main reasons for not using traditional financial time series methods in our analysis. First, commodity marketplaces are complex with a wide variety of participants having different objectives. Time series formed by these non-stationary processes consist of combinations of different components functioning at different frequencies making it difficult to analyze with traditional time series methods. Methodologies must address the fact that comovements between commodity markets are time-varying and horizon dependent. For example, Dajcman et al. (2012) provide a discussion on European stock market comovement dynamics comparing the DCC-GARCH and wavelet multiscale analysis, showing that stock market returns are time-varying and scale dependent. Secondly, in financial time series analysis, Fourier analysis is used to identify relationships between frequencies of different time series. The smooth transition of the cosine and sine basis functions in Fourier analysis, however, fails to capture abrupt changes in the stochastic behavior of the commodities time series. We address these issues by breaking individual series into their component pieces or horizons using a continuous wavelet transform and comparing similarity and differences at different scales/horizons and time components together rather than separately. Our analysis provides unique results that are difficult to obtain from only analyzing the aggregate long-run economic impact (Aguiar-Conraria et al., 2014). Davidson et al. (1997) were one of the first papers to introduce the use of wavelets to study commodity price behavior and Connor and Rossiter (2005) estimated price correlations of commodity markets by time series scale/horizon decomposition using discrete wavelets. In recent years, applied research on the comovement of commodities related to the dynamics of energy has increased significantly (Vacha and Barunik, 2012; Mensi et al., 2017). Bilgili et al. (2016) for instance took a wavelet coherence approach to evaluating the impact of biomass on carbon dioxide emissions.
Application of time-varying techniques to augment traditional portfolio management tools by distinguishing across multiple investment horizons or scales is becoming a growing field of interest (Ftiti et al., 2017; Kumar et al., 2017; Wang et al., 2017). Chaudhuri and Lo (2016) who coined the term spectral portfolio theory suggests that the flexibility of the wavelet transform could be used to overcome various difficulties of the Fourier transform for spectral portfolio analysis. For an expansive introduction to wavelet theory in finance (see In and Kim, 2012).
Market data such as indices are traditionally used to describe the underlying behavior of a commodity, and ETF's capitalize on these behaviors by tracking commodity indices. To understand the dynamic associations of water and energy commodities, we propose to explore their comovement using time-varying spectral representations. We illustrate the value of these techniques using the wavelet squared coherence (WSC) and the windowed scalogram difference (WSD). Using both the WSC and WSD we can capture, from two different perspectives, the degree of statistically significant similarity in time and scale/horizon for the commodity ETFs representing water and energy. We also introduce the analysis of wavelet local multiple correlations (WLMC), recently published by Fernández-Macho (2018).
Studying the comovement of multiple time series can traditionally be achieved using WSC. The WSD, complementary to the WSC, is a measure designed to compare non-stationary time series in time and scale/horizon for a fixed window (Bolós et al., 2017). Both these techniques evaluate the association between time series, but each of these methods highlights different aspects. The WSD gives greater flexibility in allowing the change of window size depending on which scale/horizon is of interest. The WSC does not have this flexibility. However, the WSC can easily define scale/horizon specific local linear correlations in regions of statistically significant comovement. For example, Pal and Mitra (2017) used WSC to address certain policy concerns of the food-energy nexus. We contribute to this type of analysis by not only looking at the WSC of the water-energy nexus but also the WSD allowing us to identify and confirm scale/horizon specific micro-interactions. Using both these wavelet tools we are able to identify and discuss characteristics not possible with traditional time series tools. Further, by using the recently introduced WLMC method we analyze the time-varying correlations of the S&P500 ETF with the water-energy nexus. We specifically use the WLMC to point out the conditional relationship between the water-energy nexus and the S&P500 by eliminating S&P500 market effects that individually impact the behaviors of the water and energy commodity indices.
The overall goal of this paper was to quantitatively show the time-varying behaviors of the water-energy nexus which could support practitioner in making more fact driven decision. Therefore, the structure of this paper is as follows. Section 2 describes the wavelet-based methods used in the analysis of the water-energy nexus. Section 3 presents a data description, visualization of results, and a discussion on the evaluation of the water-energy nexus after applying the wavelet-based methods from section 2. We conclude the paper with section 4 by examining the dynamic economic behavior between these commodities over the past 10 years and addressing certain policy implications and opportunities for cost reduction in energy production.
2. Methods
After a mathematical exposition of wavelets in sections 2.1, 2.2, 2.3, and 2.4 introduces statistical methods that extend the capabilities of wavelets to visualize structure in multidimensional data. See the Appendix for more details regarding a robustness check on methods.
2.1. Wavelets
Even though promising results in economics and finance have come from implementing wavelet analysis, many of these professionals are still developing their understanding of wavelet-based methods. Consequently, a more expansive and baseline introduction to the wavelet techniques are needed. In support of this development, this section describes in detail the wavelet functions we later implement to analyze the complex time-varying water-energy nexus.
Wavelets are mathematical, wave-like functions that are used to extract information from many different kinds of data. When applied to time series, wavelet transforms synthesize signals into different frequency components, decomposing the original time series into multiple time series. Each of these newly decomposed time series represents specific characteristics unique to a particular investment horizon. For example, an investment horizon of six months corresponds to a scale of 6 months. A better-known label for an investment horizon is a scale. We use the label scales in the mathematical exposition and then later we return to the label investment horizons as it is more appropriate for the application in this paper. We also intentionally refer to the decomposed time series as different frequency components because the relationship between frequency and scale is specifically determined by the center frequency of the wavelet. For the sake of simplicity, the relationship between frequency and scale is defined as, Fa = Fc/a, where Fc is the center frequency of the wavelet and Fa the frequency corresponding to scale a. Only when certain specifications related to wavelet frequency are met are scales inversely proportional to frequencies. Figure 1 demonstrates a simple example of this relationship. If the investment horizon increases (high-scale), the wavelet becomes more spread out, resulting in a lower frequency. An expansion of these relationships and the exact details on these specifications are discussed later in this section.
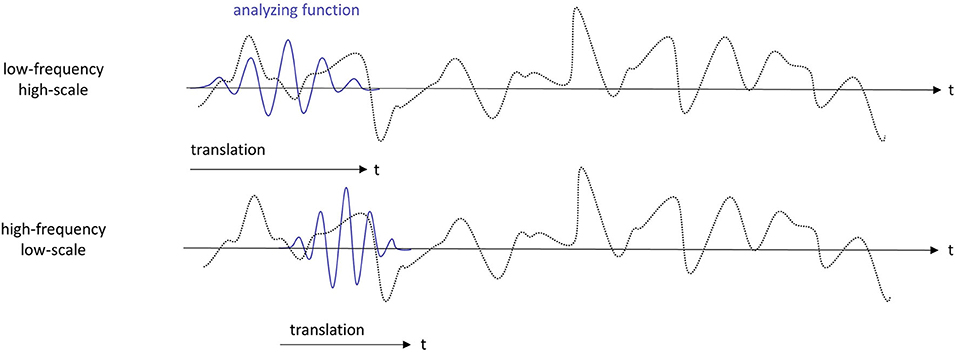
Figure 1. Example of the analyzing wavelet function scaling and shifting across the time series that is being transformed. Equation (1) is the mathematical exposition of what is visualized in this figure.
Given a time series x(t) ∈ L2(ℝ) and an analyzing wavelet function , the decomposition of time series x(t) into time-scale wavelet coefficients can be written as,
The transformation is formally referred to as the continuous wavelet transform (CWT) and * denotes the complex conjugate. The CWT can be seen as a set of continuous band-pass filters applied to a time series.
We define an analyzing wavelet as being derived from the scaling, where a > 0 defines the scale, and shifting, where b ∈ ℝ defines the shift, of a mother wavelet ψ(t) ∈ L2(ℝ) into daughter wavelets :
The wavelet power, , is visualized in the time-scale {b, a} half plane with a horizontal linear scale axis in time, b, and a vertical logarithmic scale axis in, a, see Figure 2 for an example for the power spectrum.
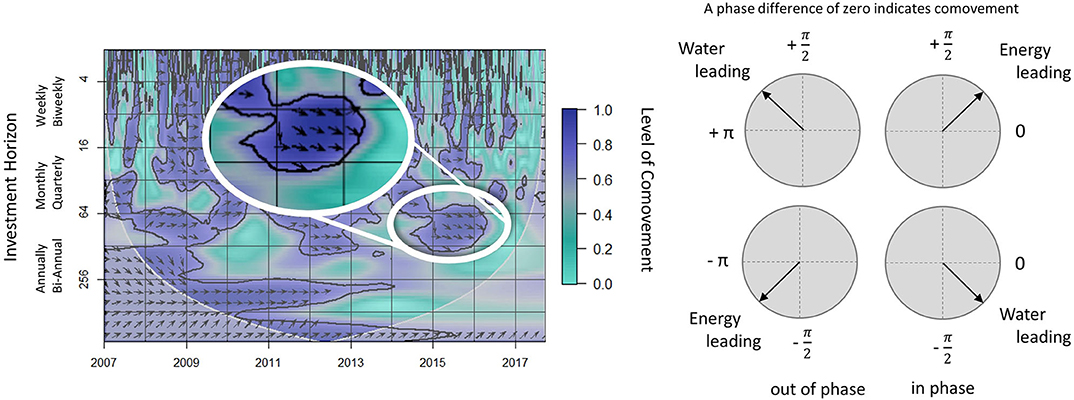
Figure 2. The WSC of prices for water and energy (left) and phase change descriptions (right). The vertical axis shows investment horizons in days and the horizontal axis shows time in years. The darker purple the regions are (areas with arrows), the higher the level of comovement. The regions that are lined with black are regions of statistical significance at the 5% level estimated using multiple Monte Carlo randomizations. The white overlay defines the cone of influence. The arrows are an indication of phase movement (leading-lagging relationship) described in section 2.2.3 and visualized on the right side of this figure. See Gouhier et al. (2016) for more details.
We can ensure reconstruction of a time series from its wavelet transform,
if the following conditions are met: (1) , (2) , and (3) the admissibility condition is satisfied. The constant (Cψ) is called the wavelet admissible constant and a wavelet whose admissible constant satisfies 0 < Cψ < ∞ is called an admissible wavelet. Mathematically Cψ is defined as, where is the Fourier transform of ψ(t) in the CWT.
The Morlet wavelet is the most commonly used mother wavelet in finance and economic research. This choice and the detailed specifications pointed out in Aguiar-Conraria et al. (2014) proves best when using wavelets to extract investment horizon specific characteristics, because the Morlet wavelet is reasonably localized in both time and scale. The Morlet wavelet is defined as:
where normalizes the wavelet, is a Gaussian envelope with standard deviation of one, and is the complex sinusoid. For the Morlet wavelet ω0 is the central frequency. The usual relation of Fourier frequency to scale is . As specified in Aguiar-Conraria et al. (2008) and Reboredo et al. (2017) we set ω0 = 6. We do so because when ω0 = 6, which provides better interpretability of scale and frequency. Even though the Morlet wavelet is commonly used in finance and economic practice there are various different sources describing different wavelets and their inherent characteristics. One of the more recent sources is Addison (2017).
We are dealing with finite time series in our application of quantifying the water-energy nexus and therefore need to address the issues of edge effects. This problem arises when filters are used for transformation. In dealing with these borders, we follow the methods of Grinsted et al. (2004) and ameliorate these effects by choosing the Morlet mother wavelet, as specified above (Torrence et al., 1998). We limit our interpretations to the areas within the cone of influence.
2.2. Details of the Wavelet Squared Coherence (WSC)
The wavelet squared coherence (WSC) is used in studying the comovement of two time series. Before we can define WSC, we first need to introduce the cross wavelet transform (XWT). Simply put, the wavelet cross spectrum is a measure of the power density and the WSC is a correlation measure between series. In Figure 2, we visualize these methods for the water-energy nexus using a time-scale {b, a} half plane with logarithmic scale a-axis (vertical) increasing downwards and a linear scale on time b-axis (horizontal).
2.2.1. Cross Wavelet Transform (XWT)
According to Torrence and Webster (1999) the XWT of two time series x(t) and y(t) is
where Wx(a, b) and Wy(a, b) are CWT's of x(t) and y(t) and again * indicates the complex conjugate. We further define |Wx, y(a, b)| as the XWT power. While each CWT preserves the energy of an individual time series, the XWT finds regions of high common power between time series across time for all frequencies. The scale or investment horizon in our application is the reciprocal of frequency. For more details on the theoretical distribution of the XWT power of two time series and how confidence levels are calculated (see Torrence et al., 1998).
2.2.2. WSC
By computing WSC we find regions in time-frequency space where the two time series co-vary. The idea is to measure the coherence of the XWT in these regions. The WSC is simple to interpret since it resembles the squared correlation coefficient in regression. The WSC is mathematically defined as
The symbol S(·) is the smoothing operator. Without smoothing, the WSC(a, b) is not in [0, 1]. See Torrence and Webster (1999) and Grinsted et al. (2004) for how convolution in both scale and time is used to smooth. These details can be adjusted depending on the application.
2.2.3. Wavelet Phase Difference and Interpretation
As defined in Grinsted et al. (2004) and Aguiar-Conraria et al. (2014) the local or instantaneous wavelet phase-angle or displacement of periodicity in the interval [-π, π] is,
where ℜ{Wx(a, b)} is the real part and ℑ{Wx(a, b)} is the imaginary part of the complex-valued Wx(a, b). For the XWT the phase difference of x over y (ϕx, y) localized in time b and scale a is:
A phase difference of zero indicates comovement. If the time series are in-phase with y leading x and if the time series are in-phase with x leading y. If the time series are anti-phase with y leading x and if the time series are anti-phase with x leading y.
See Figure 2 for visualization of these behaviors using arrows. Arrows pointing right (left) represent time series that are in-phase (anti-phase) and positively (negatively) correlated. Arrows representing point up and right, point down and right, point up and left, and point down and left.
2.3. Windowed Scalogram Difference (WSD)
The scalogram was designed to identify scales that are most representative in the time series. As a result time series with similar behavior have similar windowed scalograms (WS), resulting in values close to zero after a transformation. The transformation is primarily implemented to create a scale which is comparable with the WSC. Bolós et al. (2017) designed the WSD to measure the difference between the WS of time series x and y. The WSD of two time series centered at time t and log-scale k where k ∈ ℝ for the CWT with log-scale radius r and time radius τ, is defined as
where WSτ is the WS of time series x and is the WS of time series y. As the name states, the WS has the ability to determine the importance of different scales windowed around a specific time point. The WS is defined as,
Bolós et al. (2017) describes in detail the practicality of using base 2 power scales and the process of dealing with boundary conditions. Figures 7, 8 are visualizations of the WSD for the water-energy nexus.
2.4. Wavelet Local Multiple Correlation (WLMC)
Fernández-Macho (2018) recently introduced a new method for analyzing the dynamic comovement of various time series simultaneously. The aim of the proposed method is to produce a single set of correlations for each scale along time, instead of the standard pairwise wavelet correlation maps defined in sections 2.2 and 2.3.
Extracting from the details of Fernández-Macho (2018) we let Wjt be the scale specific, λj, wavelet coefficient for order j = 1, …, J. The maximal overlap discrete wavelet transform (MODWT) of order J is applied to each time series xi(t) in the multivariate time series X to obtain Wjt. The T × n matrix X is composed of the n real-valued time series, each of length T.
It follows that the wavelet local multiple correlation (WLMC) can be expressed as
where Pj, s is the weighted correlation matrix of Wjt = (w1jt, w2jt, …, wnjt).
The WLMC can further be simplified by realizing the square of the correlation between the fitted (ŵijt) and observed (wijt) values is the regression coefficient of determination, where ŵijt is the local regression of wijt on the rest of Wjt at scale λj. Then the WLMC can be simplified to
θ(·) is a given moving average weight function and s = 1, …, T is the shift we use for the weight function. In our application, we are using the Gaussian window weight function for the best comparison to the Morlet wavelet. In Fernández-Macho (2018), the authors follow with a theorem for the sampling distribution of the WLMC statistic from Equation (12). This allows the construction of confidence intervals for the wavelet multiple correlation coefficient displayed in Figure 9.
3. Results
3.1. Data Description and Visualization
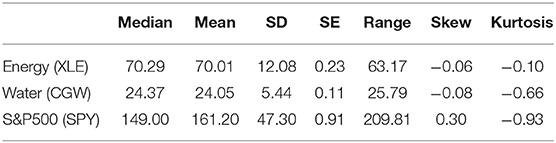
Figure 3 contains three ETF price series and Table 1 the descriptive statistics of each series. These ETF's are the Energy Select Sector SPDR Fund ETF (XLE), the Guggenheim S&P Global Water Index ETF (CGW), and the SPDR S&P500 Trust ETF (SPY). The XLE is the largest energy sector ETF and represents the energy sector of the S&P500 which includes companies in energy-related services and drilling as well as companies that produce and develop crude oil and natural gas. The CGW focuses on S&P500 companies important in the global water industry with the U.S. making up more than 50% of its holdings. The reason for choosing CGW compared to other water ETF's was because CGW was designed to expand as the demand for water companies, focusing on the issue of scarcity, increased. These two ETF time series are tracking companies that are representing mostly the U.S. markets from each side of the nexus that we are quantifying. Both the XLE and CGW pull their stocks from the S&P 500 rather than the total market. The addition of SPY is to explore the dynamic interaction of XLE and CGW or more specifically the water-energy nexus with respect to the S&P500 Index. We particularly point out two global economic events and identify behavioral differences between these series during these events. As indicated by Figure 3 these events are the 2008 financial crisis and the 2014–2016 global oil glut.
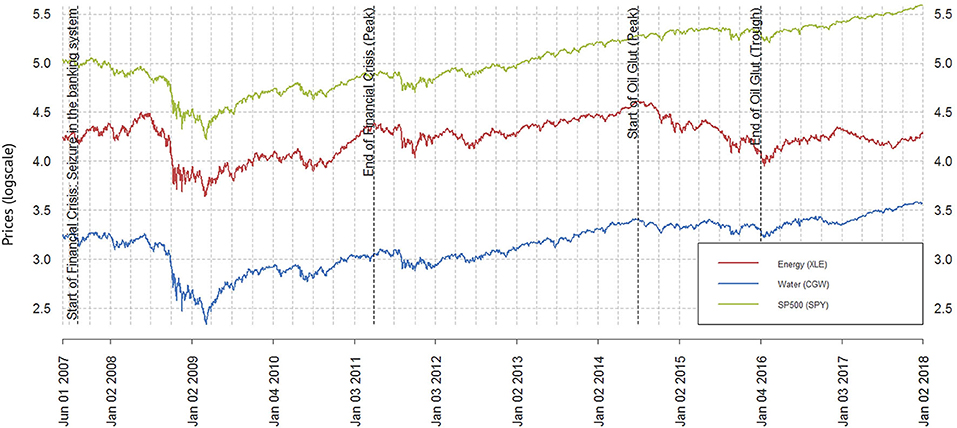
Figure 3. Logscale closing price chart of the ETF's: CGW, XLE, and SPY. Vertical lines are inserted to indicate the approximate (peak to peak) start and end dates of the 2008 financial crisis, two key events during the crisis, and the 2014–2016 global oil glut from peak to trough (Peterson and Carl, 2015).
The descriptive statistics in Table 1 indicate non-stationary behavior. To confirm that our series are non-stationary we analyze the behavior of each series using three different tests. The Augmented Dickey-Fuller (ADF) test for the null hypothesis that each series has a unit root, the Kwiatkowski-Phillips-Schmidt-Shin (KPSS) test for the null hypothesis that each series is level or trend stationary, and the Phillips-Perron test for the null hypothesis that the series has a unit root against a stationary alternative. All tests confirmed that each of these ETF price series are non-stationary. We also applied the Ljung-Box-Pierce test (Box) concluding there is autocorrelation present in each series.
The rest of this section visually explores and analyzes the statistical properties related to CGW, XLE, and the SPY by implementing all the wavelet techniques we introduced the CWT, WSC, WSD, and WLMC. Throughout the rest of the paper, we refer to XLE as energy, CGW as water, and SPY as S&P500. Figure 4 summarizes the information provided by each method in section 2.
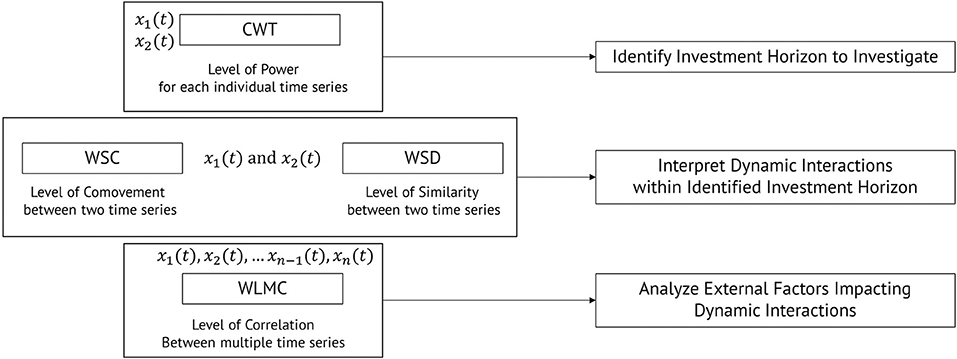
Figure 4. The visualization process of the water-energy nexus has three distinct steps. (1) Identifying the investment horizons to investigate using the CWT. (2) Interpreting the dynamic interactions within the water-energy nexus using the WSC and WSD. And (3) analyzing any external factors impacting the dynamic behavior of the water-energy nexus.
Note, the graphical summaries also provide inferential information, depicting significance and confidence bands where appropriate. Figure 5 depicts, the CWT power spectrum of the water and energy price series to identify the optimal investment horizons. Figure 6 depicts the WSC of the water-energy nexus as well as the WSC of energy and the S&P500 price series. These techniques are used to identify the level of comovement and visualize the dynamics of the leading-lagging relationships between these time series over time. The WSD, presented in Figure 7, evaluates the level of similarity within the water-energy nexus as well as the level of similarity between energy and the S&P500, specifically pointing out in Figure 8, the level of similarity during a specific time-localized event. The section ends with Figure 9 evaluation the wavelet local multiple correlations between the water-energy nexus and the S&P500.
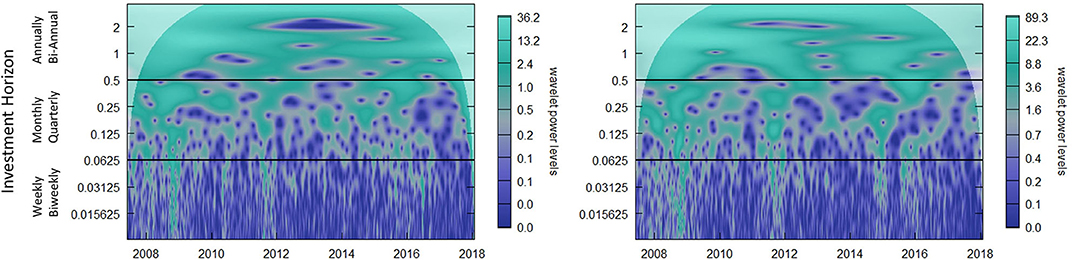
Figure 5. The continuous wavelet transform (CWT) power spectrum of water (CGW left) and energy (XLE right) commodity ETF prices. These two plots are visual representations of the power spectrum of each individual series. The investment horizons (vertical axis) are such that the value one represents 250 days (annual investment horizon) and 0.25 represents 64 days (quarterly investment horizon). The horizontal axis indicates the 10 years of data. These plots are divided into three sections with the goal of separating low (bottom), medium (middle), and high (top) power. These sections are categorized as regions which are representative of short (weekly, biweekly), medium (monthly, quarterly), and long (annually, bi-annual) run behavior, respectively. The white overlay defines the cone of influence. Figures were created by implementing minor modifications to Rösch and Schmidbauer (2014).
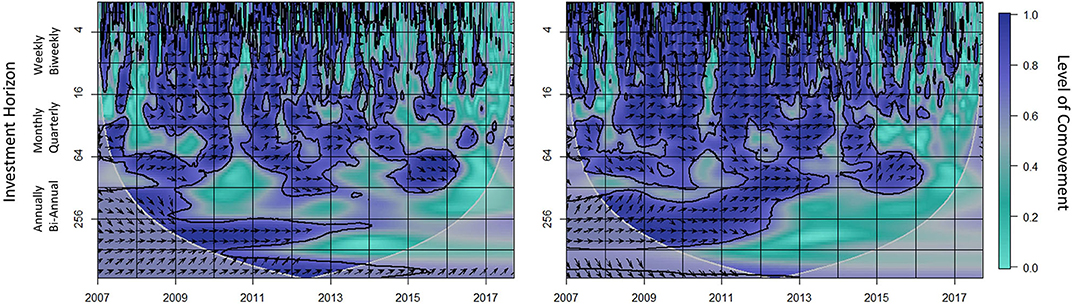
Figure 6. The WSC of the water-energy nexus (left) and energy and S&P500 (right). The vertical axis shows investment horizons in days and the horizontal axis shows time in years. The darker purple the regions are the higher the statistical significant level of comovement. The regions that are lined with black are regions of statistical significance at the 5% level estimated using Monte Carlo simulations. The white overlay defines the cone of influence. The arrows are an indication of phase movement (leading-lagging relationship) described in section 2.2.3.
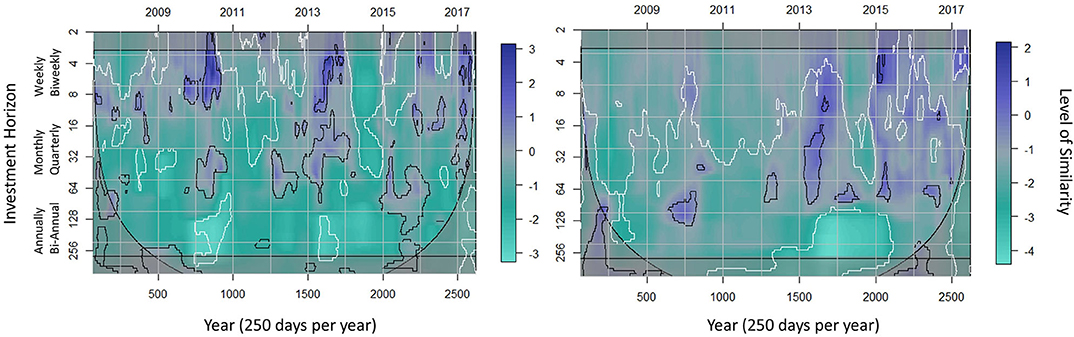
Figure 7. The WSD of the water-energy nexus (left) and energy and S&P500 (right). The more purple the color, the higher the similarity is between time series. The black-line regions are regions of statistical significance at the 5% level (high similarity) and the white-line regions are regions of statistical significance at the 95% level (low similarity) estimated using Monte Carlo simulations. The box and thin black region are the border effects and define the cone of influence, respectively. Here we are using a fixed time radius of 64 days and the investment horizon radius (window margins) is determined by the length of the series.
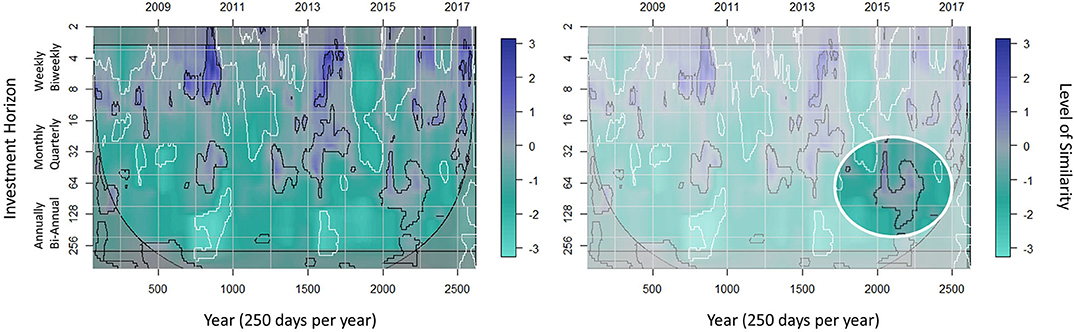
Figure 8. Magnification of the WSD of the water-energy nexus from Figure 7. The white circle emphasizes the WSD of the water-energy nexus during the quarterly investment horizon. The black-line regions are regions of statistical significance at the 5% level (high similarity). As we pointed out in section 2.3, the WSD is a difference equation so high similarity means values close to zero.
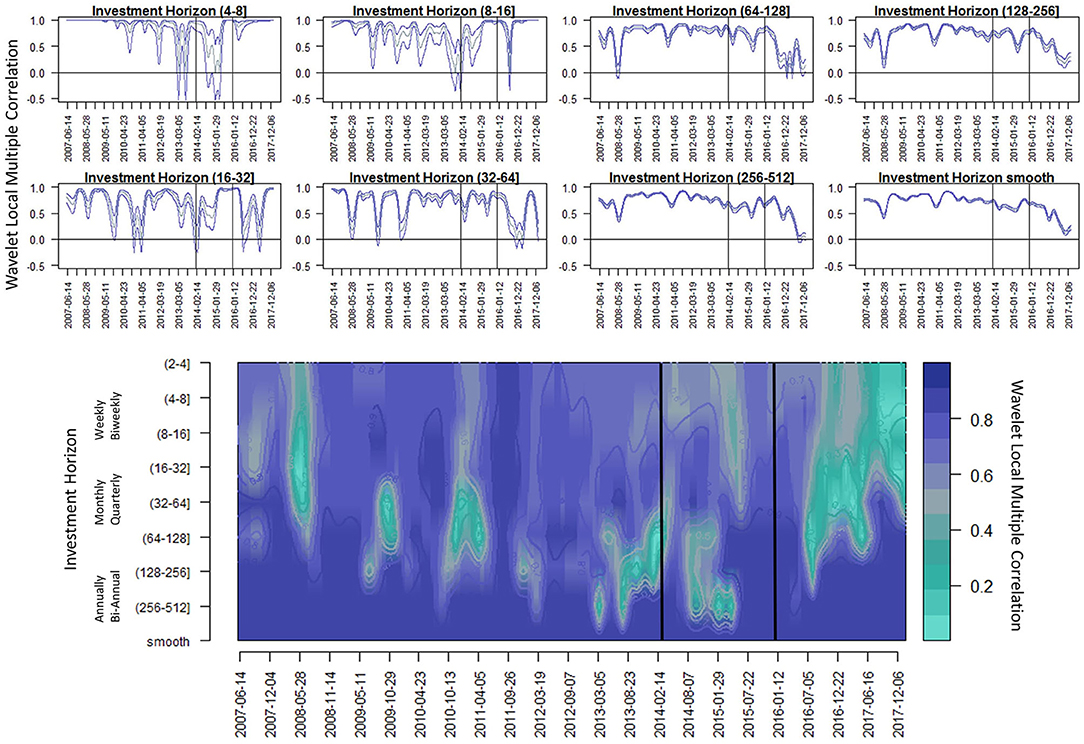
Figure 9. The WLMC of the water-energy nexus and the S&P500. At the top the purple lines correspond to the upper and lower bounds of the 95% confidence interval for the WLMC statistic at four different investment horizons. On the bottom the heat plot corresponds to the single set of correlations for all three time series (XLE, CGW, and SPY) for each scale across time, the contour lines correspond to the confidence intervals depicted for the investment horizons at the top.
We extract data using the R package quantmod (Ryan and Ulrich, 2017). We analyze ten years of daily price data from 2007-06-01 to 2018-01-16 to capture the changing mean behavior in addition to a range of investment horizons. Our data history starts in 2007 to not only study the decade since the 2008 financial crisis but also because CGW was one of the first water ETF's and before its inception in 2007 we were limited to single securities or themed investment trusts having no index that captures all the time-varying behaviors wavelets are best suited to capture.
3.1.1. Continuous Wavelet Transform (CWT)
In Figure 5, we decompose the water and energy price series into their respective component pieces each representing an investment horizon. Our evaluation and analysis must be focused on areas with medium to high power intensity (see section 2.1). These regions can be seen as the components that carry most of the behavioral weight. For an example on how to interpret Figure 5, consider the wavelet power levels across time for the quarterly investment horizon. This horizon is mostly medium intensity with regions of low intensity. As we point out in section 2.1, wavelet power is visualized in the time-scale half plane. The squared wavelet coefficient values represent the statistical significance of the behavior or better known as the power of a specific feature described at each of the time-scale locations.
Determining and translating scales to relevant time domain periods like investment horizons are useful in seeking future applications. These include finding the optimal investment horizon for each asset in a multi-asset portfolio or identifying the investment horizon that explains most of the behavior in the price series and adjusting risk management accordingly. The high power intensity range of Figure 5 is of particular interest, but caution should be taken when analyzing this range because it is impacted by the cone of influence and results can be skewed by border effects (discussion in section 2.1 and for further details see Grinsted et al., 2004). As mentioned in section 2.1, we limit our interpretations to the areas within the cone of influence.
3.1.2. Wavelet Squared Coherence (WSC)
The goal of the analysis in Figure 6 is primarily to study the development of correlation over the past 10 years for the water-energy nexus and to understand more about how these interactions change over time for different investment horizons.
We explore in detail these interactions in section 3.1.4 by pointing out specifically the dates of the two economic events referred to in Figure 3. The evaluation on the right analyzes the dynamic interactions of energy and the S&P500 to identify the statistically significant behavioral impact of the market. Figure 6 also depicts a leading-lagging relationship using the tools mentioned in section 2.2.3. Consider, for example, the quarterly investment horizon in Figure 6 on the left during the 2014–2016 global oil glut. An arrow pointing down and right (−45° or −π/4 angle) indicates that water (first series) is leading energy (second series) with statistically significant positive correlation, see the water-energy nexus on the left side of Figure 6 for magnification of these details. On the right side of Figure 6 at the annual investment horizon range during the 2008 financial crisis, an arrow pointing up and right (45° or π/4 angle) indicates that energy (first series) is being led by the S&P500 (second series) with statistically significant positive correlation and an arrow pointing only right indicates that these prices are comoving without any leading or lagging relationship.
3.1.3. Windowed Scalogram Difference (WSD)
The analysis performed using the WSD, as seen in Figure 7, is instrumental in distinguishing between behavior impacted by external factors vs. behaviors identified due to dynamic interactions. To further explore the similarity and differences between water and energy we analyze the WSD.
At the quarterly investment horizon in Figure 7, the water-energy nexus (left) shows dissimilarity during the 2008 financial crisis. The statistically significant increased similarity during the 2014–2016 global oil glut is identified by the magnified region in Figure 8. Figure 7 (right) demonstrates that there is not a major statistically significant similarity between energy and the S&P500 during the two economic events we are evaluating. This second analysis is useful in trying to eliminate the possibility that the market is significantly impacting the dynamic behavior of the water-energy nexus since we previously identified that the S&P500 is leading the dynamic behavior of energy in Figure 6. However, this market leading effect is still not clear and will be addressed in the next section.
3.1.4. Wavelet Local Multiple Correlation (WLMC)
Up to this point, the three different time series have increased levels of comovement and similarity depending on which investment horizon is being considered. However, there seems to be some significance in the water-energy nexus during the 2014–2016 global oil glut. Next, we will analyze the simultaneous correlation at a local level to see if we can identify a deviation in the similarity and comovement. The wavelet local multiple correlation (WLMC) (Fernández-Macho, 2018) allows us to extend wavelet methodology to handle comovement dynamics of multivariate time series. This statistical tool allows us to view the joint comovement of the water-energy nexus with the S&P500 (Figure 9). The analysis visualized in Figure 9 (top) shows statistically significant deviations in the high correlation between the water-energy nexus and the S&P500.
The deviations specifically indicative of the 2014–2016 global oil glut are pointed out again in these figures. This is most prominent during the quarterly investment horizon referencing the correlations shown in the (16–128) range. Our evaluation of these figures indicates that during the start of the global oil glut the correlation deviated significantly and by the end, the significant correlation picked back up. These results would be very difficult to obtain using time domain analysis (for example with DCC-GARCH) or even frequency only analysis (Fourier). The dynamics we identified are time-varying requiring simultaneous analysis in both time and at specific horizons to make sense of underlying behaviors or characteristics.
We have now stepped through all three of the visualization processes mentioned in Figure 4. In summary, each step was created to optimize the analysis process. The ability to identify the statistically significant dynamic interactions within the water-energy nexus for optimal investment horizons, during certain key economic events, aid in the discussions highlighted in the next section. An interesting result that we identified from our analysis is the potential that market behavior is currently impacted more heavily by energy than energy is impacted by the market behavior. There is very recent literature that supports these findings (Ferreira et al., 2019), however, to clearly recover these results requires expanding our application to include a longer history.
3.1.5. Evidence From Time-Varying Spectral Analysis
Understanding the investment horizon and interaction between commodities is important for practitioners to consider in the design of investment models. From the analysis of the CWT, we see a potential investment opportunity for quarterly investment horizons; from Figure 5 we analyzed that both time series' quarterly contribution to the overall behavior of the series has medium to high power intensity. Further Figure 6, clearly indicates a comoving relationship during the quarterly investment horizon, identified by Figure 5, as one of the dominant signals in the series. There is an interesting distinctive difference between the interactive behavior during the 2008 financial crisis and the 2014-2016 global oil glut which is also pointed out in Figure 6 by modeling the comparison between energy and the S&P500.
The WSC from Figure 6 allows us to examine the water-energy phase behaviors for these two events. During the first event at the quarterly investment horizon energy is leading water, however, for the annual investment horizon, these series are mostly comoving. This relationship can be confirmed by looking at the price series in Figure 3 and the analysis of Figure 7. This comovement is a result of the market impact seen in Figure 6 (right) where energy and the S&P500 series are mostly in-phase. At the quarterly investment horizon, energy is leading the S&P500, but at the annual investment horizon, the S&P500 is leading. In contrast, during the 2014–2016 global oil glut, there is a clear indication that water and energy are in-phase with water leading energy prices during this quarterly investment horizon.
Our results have the following U.S. policy implications. As fracking expands in the United States and oil prices stay relatively low, the use of aqueous-drilling fluids will increase due to low cost and limited environmental impact as required by the EPA [United States Environmental Protection Agency (EPA), 2000]. Between 2000 and 2014 the average amount of water used to drill a well has increased from 177,000 gallons to 5.1 million gallons per well (Gallegos et al., 2015). As newer technology becomes available to drill deeper into the ground the volume of water needed will place strain on the U.S. water supply. Even though the amount of water needed for fracking is less than that needed for farming and cooling it can still strain water supply in areas where water is limited. As water becomes an increasingly scarce commodity, discussions of the water-energy nexus policy reform need to be addressed alongside the food-energy nexus discussion (Pal and Mitra, 2017). We specifically used the CGW ETF in our analysis because it was initially designed to expand as the demand for water companies, focusing on the issue of scarcity, are added to the portfolio. We believe that the holdings of this ETF are representative of those companies primarily focused on providing water in areas where there exist limited resources. So the result of water leading energy during the 2014–2016 global oil glut indicates that there should be a higher value placed on these water scarcity focused companies.
During the past few years, there have been increased discussions in the Texas Permian Basin suggesting that the future of upstream-energy water management cost reduction is water commoditization or a water price index. The water management market makes up about $20 billion and most of this money is spent on water logistics (Barclays and Columbia Water Center, 2017). The creation of a marketplace for water would allow water services to be accurately priced based on the demand and supply of the market. However, creating this marketplace could potentially lead to various conflicts regarding rights to water resources. If this marketplace should exist or not is a matter of discussion, but as we have shown in this paper there is a quantifiable dynamic relationship between water and energy commodities. Understanding these dynamics and constantly evaluating the time-varying changes of these price behaviors could potentially reduce water management costs in the energy industry. This can be achieved by simply capitalizing on the ongoing leading-lagging relationship and potential investment horizon that is easily identified with the same analysis implemented in this paper.
4. Conclusion
We present method and visualization tools that quantify the time-varying relationship between water and energy prices while highlighting key investment-horizon behaviors. Our choice of wavelet-based methods results in strategies for quantified fact-driven decision making about the water-energy nexus. To the best of our knowledge, this paper is the first to confirm the water and energy relationship in a quantitative manner. Our intention, however, is to provide empirical observations and not to suggest an economic mechanism for this observed relationship. The latter perspective is beyond the scope of the paper.
The novelty of our approach lies in the exploration of the water-energy nexus using non-stationary financial instruments in the time-scale domain. We distinguish between the impacts of two economic events on water-energy price movement at different investment horizons. Incorporating the S&P500 into our time-varying study of the price behavior isolates the variation due to general market structure, and that due to the relationship between water and energy. Investment decisions based on the insights presented in this paper can be made under the umbrella of portfolio investment theory to determine the optimal risk-return trade-off between the two commodities. We specifically chose to analyze the water-energy nexus to demonstrate our ability to capture complex time-varying relationships using wavelet based tools.
The water-energy nexus represents complex structures with global impact. For example, the UN forecast for 2035 indicates that energy and water consumption will increase by 35 and 85%, respectively, and the withdrawal of water for energy use would increase by 20%. Correctly identifying the dynamic interactions of water and energy commodities not only creates a vehicle to improve upon current investment strategies within the United States but could also impact decisions and policy processes within countries that have high water stress. Our research speaks directly to this important global challenge of the next two decades by helping investment planners and risk managers, through informing their decisions with quantitative insight, on how to dynamically allocate water to maximize energy returns while preserving potable water sources (Barclays and Columbia Water Center, 2017).
Data Availability Statement
All datasets generated in this study are included in the article/supplementary material.
Author Contributions
KR significantly contributed to the conception of the work as well as the analysis and interpretations and was also responsible for drafting the work. KE was responsible for revising it critically for important intellectual content resulting in both authors contributing equally. All authors contributed to the article and approved the submitted version.
Funding
This material was based upon work supported by the Ken Kennedy Institute for Information Technology 2016/17 Shell Graduate Fellowship, the Rice Center for Computational Finance and Economic Systems, and the National Science Foundation Graduate Research Fellowship Program under Grant No. (DGE# 1842494). Any opinions, findings, and conclusions or recommendations expressed in this material are those of the authors and do not necessarily reflect the views of the National Science Foundation.
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
Abdelradi, F., and Serra, T. (2015). Food-energy nexus in Europe: Price volatility approach. Energy Econ. 48, 157–167. doi: 10.1016/j.eneco.2014.11.022
Addison, P. S. (2017). The Illustrated Wavelet Transform Handbook: Introductory Theory and Applications in Science, Engineering, Medicine and Finance, Second Edition. Irvine, CA: CRC Press.
Aguiar-Conraria, L., Azevedo, N., and Soares, M. J. (2008). Using wavelets to decompose the time-frequency effects of monetary policy. Phys. A 387, 2863–2878. doi: 10.1016/j.physa.2008.01.063
Aguiar-Conraria, L., Soares, M. J., and Aguiar-Conraria, L. (2014). The continuous wavelet transform: moving beyond uni- and bivariate analysis. J. Econ. Surv. 28, 344–375. doi: 10.1111/joes.12012
Ahmadi, M., Bashiri Behmiri, N., and Manera, M. (2016). How is volatility in commodity markets linked to oil price shocks? Energy Econ. 59, 11–23. doi: 10.1016/j.eneco.2016.07.006
Barclays and Columbia Water Center (2017). The Water Challenge: Preserving a Global Resource. Technical report, Barclays.
Bilgili, F., Öztürk, l., Koçak, E., Bulut, M., Pamuk, Y., Muğaloğlu, E., et al. (2016). The influence of biomass energy consumption on CO2 emissions: a wavelet coherence approach. Environ. Sci. Pollut. Res. 23, 19043–19061. doi: 10.1007/s11356-016-7094-2
Bolós, V. J., Benítez, R., Ferrer, R., and Jammazi, R. (2017). The windowed scalogram difference: a novel wavelet tool for comparing time series. Appl. Math. Comput. 312, 49–65. doi: 10.1016/j.amc.2017.05.046
Cai, Y., Cai, J., Xu, L., Tan, Q., and Xu, Q. (2019). Integrated risk analysis of water-energy nexus systems based on systems dynamics, orthogonal design and copula analysis. Renew. Sustain. Energy Rev. 99, 125–137. doi: 10.1016/j.rser.2018.10.001
Chaudhuri, S., and Lo, A. (2016). Spectral Portfolio Theory. Technical report, MIT Sloan School of Management.
Cheng, I.-H., and Xiong, W. (2013). The financialization of commodity markets. SSRN Elecron. J. 6:419–441. doi: 10.1146/annurev-financial-110613-034432
Connor, J., and Rossiter, R. (2005). Wavelet transforms and commodity prices. Stud. Nonlin. Dyn. Econ. 9, 1–22. doi: 10.2202/1558-3708.1170
Creti, A., Joëts, M., and Mignon, V. (2013). On the links between stock and commodity markets' volatility. Energy Econ. 37, 16–28. doi: 10.1016/j.eneco.2013.01.005
Dai, J., Wu, S., Han, G., Weinberg, J., Xie, X., Wu, X., et al. (2018). Water-energy nexus: a review of methods and tools for macro-assessment. Appl. Energy 210, 393–408. doi: 10.1016/j.apenergy.2017.08.243
Dajcman, S., Festic, M., and Kavkler, A. (2012). European stock market comovement dynamics during some major financial market turmoils in the period 1997 to 2010 - a comparative DCC-GARCH and wavelet correlation analysis. Appl. Econ. Lett. 19, 1249–1256. doi: 10.1080/13504851.2011.619481
Davidson, R., Labys, W. C., and Lesourd, J.-B. (1997). Walvelet analysis of commodity price behavior. Comput. Econ. 11, 103–128. doi: 10.1023/A:1008666428579
Fang, D., and Chen, B. (2017). Linkage analysis for the water-energy nexus of city. Appl. Energy 189, 770–779. doi: 10.1016/j.apenergy.2016.04.020
Fernández-Macho, J. (2018). Time-localized wavelet multiple regression and correlation. Phys. A 492, 1226–1238. doi: 10.1016/j.physa.2017.11.050
Ferreira, P., Pereira, E. J. d. A. L., Silva, M. F. d., and Pereira, H. B. (2019). Detrended correlation coefficients between oil and stock markets: The effect of the 2008 crisis. Phys. A 517, 86–96. doi: 10.1016/j.physa.2018.11.021
Ftiti, Z., Jawadi, F., and Louhichi, W. (2017). Modelling the relationship between future energy intraday volatility and trading volume with wavelet. Appl. Econ. 49, 1981–1993. doi: 10.1080/00036846.2016.1229453
Gallegos, T. J., Varela, B. A., Haines, S. S., and Engle, M. A. (2015). Hyraulic fracturing water use varibility in the United States and potential environmental implications. Water Resour. Res. 51, 5839–5845. doi: 10.1002/2015WR017278
Gouhier, T. C., Simko, V., and Grinsted, A. (2016). Biwavelet: Conduct univariate and bivariate wavelet analyses.
Grinsted, A., Moore, J. C., and Jevrejeva, S. (2004). Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlin. Process. Geophys. 11, 561–566. doi: 10.5194/npg-11-561-2004
Hamiche, A. M., Stambouli, A. B., and Flazi, S. (2016). A review of the water-energy nexus. Renew. Sustain. Energy Rev. 65, 319–331. doi: 10.1016/j.rser.2016.07.020
In, F., and Kim, S. (2012). An Introduction to Wavelet Theory in Finance : a Wavelet Multiscale Approach. World Scientific.
Keulertz, M., and Woertz, E. (2015). Financial challenges of the nexus: pathways for investment in water, energy and agriculture in the Arab world. Int. J. Water Resour. Dev. 31, 312–325. doi: 10.1080/07900627.2015.1019043
Kumar, S., Pathak, R., Tiwari, A. K., and Yoon, S.-M. (2017). Are exchange rates interdependent? Evidence using wavelet analysis. Appl. Econ. 49, 3231–3245. doi: 10.1080/00036846.2016.1257108
Mensi, W., Hkiri, B., Al-Yahyaee, K. H., and Kang, S. H. (2017). Analyzing time-frequency co-movements across gold and oil prices with BRICS stock markets: a VaR based on wavelet approach. Int. Rev. Econ. Fin. 54, 74–102. doi: 10.1016/j.iref.2017.07.032
Ozturk, I. (2015). Sustainability in the food-energy-water nexus: evidence from BRICS (Brazil, the Russian Federation, India, China, and South Africa) countries. Energy 93, 999–1010. doi: 10.1016/j.energy.2015.09.104
Ozturk, I. (2017). The dynamic relationship between agricultural sustainability and food-energy-water poverty in a panel of selected Sub-Saharan African Countries. Energy Policy 107, 289–299. doi: 10.1016/j.enpol.2017.04.048
Pal, D., and Mitra, S. K. (2017). Time-frequency contained co-movement of crude oil and world food prices: a wavelet-based analysis. Energy Econ. 62, 230–239. doi: 10.1016/j.eneco.2016.12.020
Peterson, B. G., and Carl, P. (2015). PerformanceAnalytics: econometric tools for performance and risk analysis.
Raath, K. C., Ensor, K. B., Scott, D. W., and Crivello, A. (2019). Denoising non-stationary signals by dynamic multivariate complex wavelet thresholding. SSRN Electron. J. doi: 10.2139/ssrn.3528714
Reboredo, J. C., Rivera-Castro, M. A., and Ugolini, A. (2017). Wavelet-based test of co-movement and causality between oil and renewable energy stock prices. Energy Econ. 61, 241–252. doi: 10.1016/j.eneco.2016.10.015
Siddiqi, A., and Anadon, L. D. (2011). The water-energy nexus in Middle East and North Africa. Energy Policy 39, 4529–4540. doi: 10.1016/j.enpol.2011.04.023
Smajgl, A., Ward, J., and Pluschke, L. (2016). The water-food-energy Nexus-Realising a new paradigm. J. Hydrol. 533, 533–540. doi: 10.1016/j.jhydrol.2015.12.033
Tan, C., and Zhi, Q. (2016). The energy-water nexus: a literature review of the dependence of energy on water. Energy Proc. 88, 277–284. doi: 10.1016/j.egypro.2016.06.154
Torrence, C., Compo, G. P., Torrence, C., and Compo, G. P. (1998). A practical guide to wavelet analysis. Bull. Am. Meteorol. Soc. 79, 61–78. doi: 10.1175/1520-0477(1998)079<0061:APGTWA>2.0.CO;2
Torrence, C., and Webster, P. J. (1999). Interdecadal changes in the ENSO-monsoon system. J. Clim. 12, 2679–2690. doi: 10.1175/1520-0442(1999)012<2679:ICITEM>2.0.CO;2
United States Environmental Protection Agency (EPA) (2000). EPA: A Development Document for Final Effluent Limitations Guidelines and Standards for Synthetic-Based Drilling Fluids and other Non-Aqueous Drilling Fluids in the Oil and Gas Extraction Point Source Category. Technical report, United States Environmental Protection Agency (EPA).
Vacha, L., and Barunik, J. (2012). Co-movement of energy commodities revisited: Evidence from wavelet coherence analysis. Energy Econ. 34, 241–247. doi: 10.1016/j.eneco.2011.10.007
Wang, G.-J., Xie, C., and Chen, S. (2017). Multiscale correlation networks analysis of the US stock market: a wavelet analysis. J. Econ. Interact. Coord. 12, 561–594. doi: 10.1007/s11403-016-0176-x
Wang, S., Fath, B., and Chen, B. (2019). Energy-water nexus under energy mix scenarios using input-output and ecological network analyses. Appl. Energy 233–234, 827–839. doi: 10.1016/j.apenergy.2018.10.056
Wichelns, D. (2017). The water-energy-food nexus: is the increasing attention warranted, from either a research or policy perspective? Environ. Sci. Policy 69, 113–123. doi: 10.1016/j.envsci.2016.12.018
Zhang, D. (2018). Energy finance: background, concept, and recent developments. Emerg. Markets Fin. Trade 54, 1687–1692. doi: 10.1080/1540496X.2018.1466524
Ziogou, I., and Zachariadis, T. (2017). Quantifying the water-energy nexus in Greece. Int. J. Sustain. Energy 36, 972–982. doi: 10.1080/14786451.2016.1138953
Appendix
A. Robustness
We demonstrate through simulation the robustness of the continuous wavelet transform and repeat our analysis on a subset of the data. For additional analysis (see Raath et al., 2019).
A.1. Robustness Check on Methods
All the methods used originally stem from the CWT as seen in Figure 4. In Figure A1, we test the robustness of the CWT power spectrum to analyze investment-horizon specific behaviors by simulating an additive noise model, with three stationary signals.
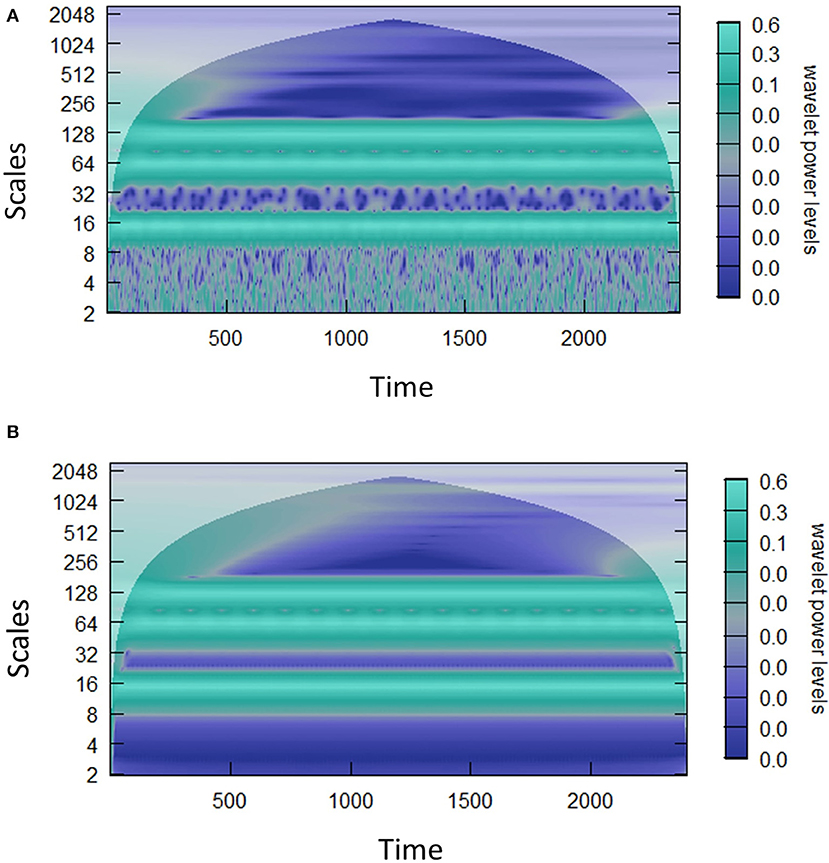
Figure A1. Additive noise Model. Pure signal. The CWT power spectrum (A) of a simple additive noise model with three stationary signals. Biweekly (15 days), quarterly (64 days), and biannually (125 days). Hence we have that where ϵ ~ N(0, 0.1) and t = (1, …, 2400). Also in this figure is the CWT power spectrum (B) which is the pure signal without noise.
A.2. Robustness Check on Data
Evaluating the robustness of the water-energy nexus relationship we eliminate 20% of the data and evaluate the same 64 day leading-lagging relationship analyzed in Figures 2, 6, 9. The robustness check still validates our conclusion.
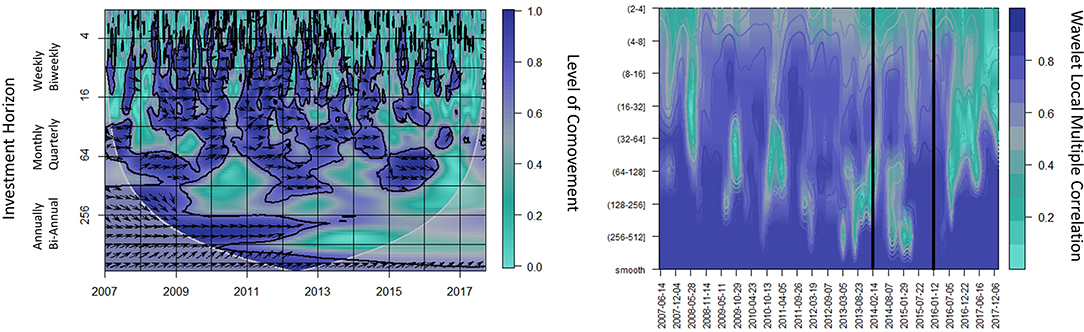
Figure A2. Eliminating 20% of the data we analyze the results of our analysis using the WSC of the water-energy nexus (left) and the WLMC of the water-energy nexus and the S&P500 (right). The vertical axis shows investment horizons in days and the horizontal axis shows time in years. The darker purple the regions are the higher the statistical significance.
Keywords: time-varying analysis, water-energy nexus, complex continuous wavelet transform, wavelet squared coherence, windowed scalogram difference, wavelet local multiple correlation
Citation: Raath KC and Ensor KB (2020) Time-Varying Wavelet-Based Applications for Evaluating the Water-Energy Nexus. Front. Energy Res. 8:118. doi: 10.3389/fenrg.2020.00118
Received: 19 January 2020; Accepted: 18 May 2020;
Published: 23 June 2020.
Edited by:
Dayong Zhang, Southwestern University of Finance and Economics, ChinaReviewed by:
Xiangyun Gao, China University of Geosciences, ChinaIlhan Ozturk, Çaǧ University, Turkey
Wang Tiantian, Nanjing Audit University, China
Copyright © 2020 Raath and Ensor. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Kim C. Raath, a2NyMkByaWNlLmVkdQ==
†Noah G. Harding Professor of Statistics and Director of CoFES
 Kim C. Raath
Kim C. Raath Katherine B. Ensor
Katherine B. Ensor