Dual Hydrogen- and Oxygen-Transport Membrane Reactor for Solar-Driven Syngas Production

A novel thermochemical dual-membrane reactor is considered with the goal of efficiently converting CO₂ to fuels using concentrated solar energy as the process heat source. In contrast to the temperature-swing redox cycle, in this isothermal system the thermolysis of H₂O at above 1,800 K is assisted by removal of O₂ across an oxygen-permeable membrane and of H₂ across a hydrogen-permeable membrane. The latter is consumed by a stream of CO₂ via the reverse water-gas shift reaction to re-form H₂O and continuously generate CO. The net reaction is the splitting of CO₂ to CO and $\frac{1}{2}$_O2. Because reactions at such high temperature are expected to be thermodynamically controlled, thermodynamic models are developed to calculate the equilibrium limits of the proposed dual-membrane configuration. For comparison, two reference configurations comprising either a single oxygen-permeable membrane or a single hydrogen-permeable membrane are analyzed. At 1,800 K, 1 bar total pressure, and (not applicable for the hydrogen-membrane reactor) 10 Pa O₂, the equilibrium mole fraction of fuel is 2% with a single oxygen membrane, 4% with a single hydrogen membrane, and 15% in the dual-membrane system. In all cases, total selectivity of CO₂ to CO and O₂ is obtained. Assuming thermodynamic equilibrium, the solar-to-fuel energy efficiency realistically attainable is 4% with a single oxygen membrane, 8% with a single hydrogen membrane, and 17% in the dual-membrane configuration at the aforementioned conditions. By increasing the pressure of the feed of steam to 100 bar, the dual-membrane model system could theoretically approach full mass conversion of CO₂ and reach up to 26% solar-to-fuel energy efficiency. However, developing appropriate and stable ceramic materials for such a system poses a significant challenge.

Introduction

Liquid hydrocarbon fuels are convenient energy carriers because of their high volumetric energy density, storability, and transportability with the existing global infrastructure. To that end, the formation of CO and H₂ (syngas) would be valuable as a feedstock for several established liquid fuel synthesis processes, such as Fischer-Tropsch or methanol synthesis. Research on various solar-driven approaches to convert CO₂ and H₂O to syngas has grown steadily as calls to reduce carbon emissions in the transportation and energy sector have intensified (Lewis, 2016). While solar photovoltaics combined with electrolysis offers one commercialized option for producing H₂ from H₂O, an economically competitive solar technology to liquid fuels production from H₂O and CO₂ is still missing (Tuller, 2015).

The solar thermochemical approach to dissociate CO₂ and H₂O is promising because it utilizes the entire solar spectrum in the form of high-temperature process heat and, thus, enables thermodynamically favorable reactions and the potential of reaching high energy conversion efficiencies (Romero and Steinfeld, 2012). Specifically, a thermochemical membrane reactor suggests a path to isothermal and continuous splitting of CO₂ and H₂O, reactions described by

$\mathrm{C}{\mathrm{O}}_2\leftrightarrow \mathrm{C}\mathrm{O}+\frac{\mathrm{1}}{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}(1)$

${\mathrm{H}}_{\mathrm{2}}\mathrm{O}\leftrightarrow {\mathrm{H}}_{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}{\mathrm{O}}_{\mathrm{2}}(2)$

In membrane-assisted thermolysis, one of the products is removed across a selective membrane to boost reaction conversion and prevent recombination. The idea to apply this concept to solar fuel production was pioneered by Fletcher and co-workers in the late 1970s (Fletcher and Moen, 1977; Noring et al., 1981). The first studies on solar thermal membrane reactors were theoretical in nature and focused on splitting H₂O (Fletcher and Moen, 1977; Noring et al., 1981; Kogan, 1997), and the vast majority of previous work has focused on oxygen-transport membranes (Franca et al., 2012; Muhich et al., 2013; Wang et al., 2015). This is because high-temperature oxygen-ion conducting materials are reasonably common, and their development has been propelled by applications in sensors, air separation (Sunarso et al., 2008; Geffroy et al., 2013), and solid-oxide fuel cells (Kharton et al., 2004; Garagounis et al., 2011). Recently, we have experimentally demonstrated the use of ceria-based oxygen-transport membranes in a solar cavity-receiver splitting CO₂ (Tou et al., 2017), and co-splitting CO₂ and H₂O simultaneously (Tou et al., 2019). However, the extent of H₂O and CO₂ thermolysis, even when enhanced by an oxygen-transport membrane, is impractically low at the required operating temperatures, typically in the range 1,500–2,000 K (Ermanoski et al., 2014; Li et al., 2019). For example, at a temperature of 2,000 K and a pressure of 1 bar, with oxygen extracted at a partial pressure of 3 × 10⁻⁵ bar, the thermodynamic limit for conversion of H₂O to H₂ is still only 5%.

The development of suitable hydrogen-permeable materials could improve the prospects of membrane reactor technology. In a 1981 study by Noring et al. (1981), a water-splitting reactor with two membranes, one each for oxygen and hydrogen removal was proposed. This combination significantly increases the driving force for thermolysis of H₂O and thus the theoretical fuel yield. Another benefit is the 100% purity of each product stream provided both membranes are perfectly selective. Nevertheless, the idea remained dormant for over three decades because the state-of-the-art could not supply stable materials at the temperatures required. Noring et al.’s concept applies uniquely to H₂O thermolysis because there has not been any research on CO-selective membranes that operate at and above 1,500 K to the knowledge of the authors. However, such a dual-membrane reactor (DMR) could still be useful for CO₂ splitting. The reactor system proposed by Noring et al. (1981) needs only a minor but nevertheless crucial modification: a feed of CO₂ introduced to the hydrogen chamber. Then, in addition to the thermolysis of H₂O in the steam chamber, CO₂ can react simultaneously with H₂ via the reverse water-gas shift (RWGS) reaction to produce CO:

${\mathrm{H}}_{\mathrm{2}}+\mathrm{C}{\mathrm{O}}_2\leftrightarrow \mathrm{C}\mathrm{O}+{\mathrm{H}}_{\mathrm{2}}\mathrm{O}(3)$

Both reactions in Eqs 2 and 3 are enhanced by the transfer of H₂ across the membrane, and, in turn, drive further transport as they proceed. The net reaction is CO₂ splitting, as given in Eq. 1. To the authors’ knowledge, such a membrane reactor concept is novel and could potentially become a breakthrough in this emerging field. Here we present a comparative thermodynamic analysis to understand how this DMR could work and to assess its performance potential. We also discuss the material challenges which researchers face to test this concept experimentally.

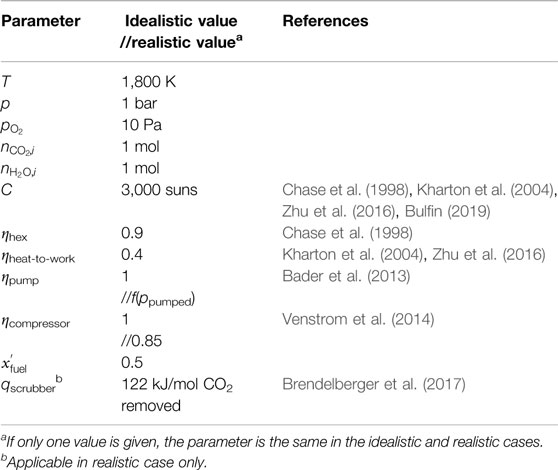
We select three representative configurations of a membrane reactor that could achieve the net reduction of CO₂: the DMR and two reference systems with a single membrane. For the sake of elucidating the key thermodynamics, the configurations are set up as three simple thought experiments as shown in Figure 1. In all cases, a closed volume is divided into chambers by semi-permeable boundaries—the membranes. Each chamber is filled with an initial amount of gases at set temperature T and pressure p. The system is then allowed to equilibrate at constant T and p. The walls are movable such that volumes can adjust freely as the number of molecules in each chamber changes (indicated by the spring symbol in Figure 1).

FIGURE 1

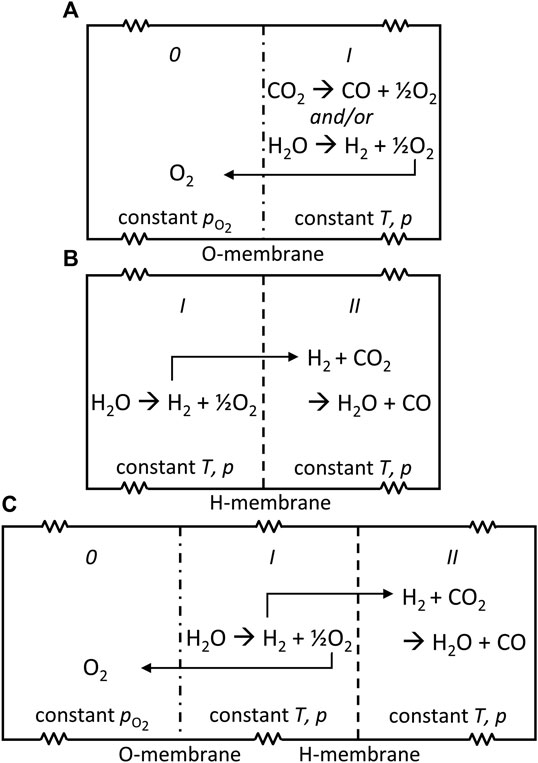
FIGURE 1. Schematics of three configurations for the net thermochemical splitting of CO₂ to CO and O₂: (A) oxygen-membrane reactor, (B) hydrogen-membrane reactor, and (C) dual-membrane reactor. A spring symbol is used to indicate the free adjustment of volume in each chamber to maintain constant p.

The first configuration is depicted in Figure 1A. Let’s call the system the oxygen-membrane reactor (OMR). The simplest configuration of the three to be analyzed, the OMR contains two chambers, 0 and I, separated by an oxygen-permeable membrane. In chamber 0 a constant low value of $p$_O2 is maintained. An initial feed of CO₂, H₂O, or a combination thereof, is charged in chamber I. Given T and p, the feed dissociates to some extent to reach an equilibrium composition mixture of CO and/or H₂ and O₂, each exerting a corresponding partial pressure on the walls of chamber I. Assuming $$_pO2,0 is set to a value less than $$_pO2,I, a difference in chemical potential forms between the chambers, causing O₂ to diffuse across the membrane until the partial pressures balance on each side. However, this chemical potential equilibration via the removal of O₂ shifts the reaction equilibrium in chamber I, which must reach a new equilibrium based on the changed gas composition. According to Le Chatelier’s principle, the reaction will proceed toward product formation. Any production of O₂ that results in $$_pO2,I exceeding $$_pO2,0 also diffuses out of chamber I. Thus, the process continues until both chemical and mechanical equilibrium are reached in the OMR system. In this way, the oxygen-permeable membrane provides a way to drive the thermolysis reaction by controlling $$_pO2. Note that the OMR is the closed-system analog of the oxygen-transport membrane reactor studied in other theoretical and experimental work (Evdou et al., 2008; Zhu et al., 2016; Tou et al., 2017; Tou et al., 2019).

The second configuration, shown in Figure 1B, follows the same principles as the first. Let’s call it the hydrogen-membrane reactor (HMR). The HMR consists of two chambers, I and II, separated by a hydrogen-permeable membrane. Initially, chamber I contains H₂O and chamber II contains CO₂. T and p are controlled in each chamber. At these conditions, H₂O undergoes thermolysis like in the OMR. In this case, the equilibrium is shifted by the removal of H₂ as it diffuses to chamber II. Unlike the OMR, $$_pH2 is not set directly, but rather depends on another reaction equilibrium in chamber II: the RWGS reaction which consumes H₂ and CO₂ to produce CO and re-form H₂O. Thus, the overall reaction in the HMR is also the splitting of CO₂. The more H₂ is transferred from chamber I to II, the greater the extent of H₂O thermolysis (via removal of product) and of RWGS (via addition of reactant). The final state is reached once reactions and $$_pH2 have all equilibrated in both chambers. Thus, with the right choice of reactants, a hydrogen-permeable membrane can also drive the thermochemical conversion of CO₂ to CO.

The third configuration combines the OMR and HMR concepts to harness a dual driving force. The DMR shown in Figure 1C has three chambers, 0, I, and II, demarcated by two membranes, one oxygen-selective and one hydrogen-selective. Each component behaves like its counterpart in the previous two configurations. However, now the thermolysis of H₂O in chamber I is enhanced by both the O₂ removal into chamber 0 and H₂ removal into chamber II, driven by differences in partial pressure of the respective species. The RWGS reaction consumes H₂ from chamber I to drive formation of CO in chamber II. At equilibrium, $$_pO2 must be equal in chambers 0 and I, and $$_pH2 must be equal in chambers I and II. Setting $$_pO2 in chamber 0 influences the extent of the RWGS reaction in chamber II by increasing the amount of H₂ available in chamber I. The DMR is the most complex of the three configurations, but may unlock higher reaction conversions and efficiencies in isothermal thermochemical processes. The next sections develop thermodynamic models and an efficiency analysis from these thought experiments to evaluate the DMR in comparison to the two single-membrane reference cases.

Thermodynamic Model

The thermodynamic limits of the membrane reactor are governed by mass conservation and equilibrium relations, which, in turn, are dependent on the initial feed, temperature, total chamber pressures, and partial pressures of the components. We assume:

• closed system

• constant and uniform temperature and pressure in each chamber

• ideal gases

• well-mixed reactor chambers

• perfectly selective membranes

• thermodynamic equilibrium

The system as a whole is closed and at constant temperature and pressure, so that equilibrium will be the state with minimum Gibbs free energy, subject to mass balance constraints which are set by the initial conditions and the allowed chemical reactions. The Gibbs free energy is given by G = ∑μ_in_i, where μ_i and n_i are the chemical potential and number of moles of species i. Because the system is isothermal and the species are modeled as ideal gases, we can use

${\mu }_i\left(T\right)={\mu }_i^{○}\left(T\right)+\mathrm{R}\mathrm{T}\ln \left(\frac{p_i}{p^{○}}\right),(4)$

where ${\mu }_i^{○}$ is the standard chemical potential at T, and the standard pressure $$_p○ is 1 bar. Therefore, we can conveniently switch to considering partial pressure differences across the membrane instead of chemical potentials, to check if species will favorably cross. By setting the Gibbs free energy of each expected reaction to zero (ΔG = 0), together with mass balance constraints, this results in a system of equations defining the equilibrium state. The thermodynamic data needed (e.g., standard Gibbs free energies $\Delta G_i^{○}$) are available from the NIST JANAF thermochemical tables (Chase et al., 1998). The system can be solved analytically for the equilibrium composition, but to track molar amounts of all species, including due to other potential side reactions, it becomes necessary to solve numerically.

Therefore, a second approach is implemented using thermodynamic software to account for all reactions possible starting from the initial composition. Cantera, a toolkit for chemical kinetics, thermodynamics, and transport problems, and its GRI-Mech 3.0 database (consisting of 53 species and 325 reactions detailing the natural gas combustion mechanism, including thermodynamic data for all species in the membrane reactor system) is called from Python and used for equilibrium composition calculations (Goodwin et al., 2009). To find the minimum Gibbs free energy we allow each chamber to go to chemical equilibrium separately, satisfying ΔG ≤ 0, and then check if there is a difference in chemical potential (partial pressure) of hydrogen across the hydrogen membrane and/or of oxygen across the oxygen membrane. If there is a difference, some of the membrane selective species Δn_i is transferred from higher to lower chemical potential so that ΔG = Δμ_iΔn_i ≤ 0, where Δμ_i is the drop in chemical potential of the hydrogen or oxygen across the membrane. Each chamber is again allowed to go to equilibrium separately, and the process is repeated iteratively. In this way, we can converge on equilibrium in a finite number of steps, all of which satisfy ΔG ≤ 0, so that the entire process can proceed spontaneously.

Because the OMR and HMR serve as references for the DMR, and to avoid repetition, the OMR and HMR models are described in Supplementary Figures S1,S2 and Supplementary Tables S1,S2 and only the DMR model is detailed here. The model inputs are T, p, $$_pO2, $$_nCO2,i, and $$_nH2O,i. The system of equations determining the equilibrium state without side reactions is summarized in Table 1. The Gibbs free energy relations for H₂O thermolysis and RWGS govern the composition of gases in chambers I and II, respectively. The hydrogen membrane links the thermodynamics of these chambers by enforcing a common $$_pH2. The oxygen membrane adds an additional constraint by fixing $$_pO2. Finally, the mole balances ensure that species are formed in stoichiometric amounts and account for mass transfer between chambers. The equations are formulated in terms of the fewest number of unknown variables by using the known stoichiometry of the reactions.

TABLE 1

TABLE 1. System of equations for the dual-membrane reactor.

Figure 2 depicts the DMR model flow. Because there are two membranes, two sets of nested iterations are needed to determine the equilibrium state for the entire system. First, the reaction conditions and the initial feed are defined. Chambers I and II are equilibrated and the resulting $$_pO2,I is compared to $$_pO2,0. Then, the value of $$_nO2,I is reset to get $$_pO2,0 (simulating the removal of O₂) and the gas mixture is equilibrated again. Next, $$_pH2,I is compared to $$_pH2,II. H₂ is transferred between chambers I and II to balance $$_pH2 and the new equilibrium state is calculated. This loop is repeated until $$_pH2,I converges to $$_pH2,II, at which point $$_pO2 is checked again. Iterations stop once both loops simultaneously converge within their respective tolerances.

FIGURE 2

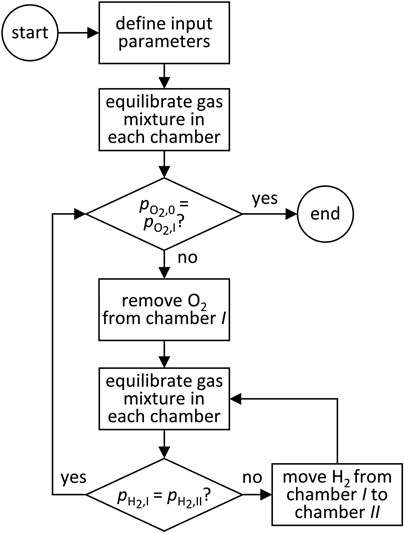
FIGURE 2. A flowsheet illustrating the logic applied in the dual-membrane reactor equilibrium model.

The model outputs are the equilibrium mole amounts of every species in each chamber, from which performance indicators can be calculated. The first is the mole fraction of fuel in the product mixture, which for the HMR and DMR is given by

$x_{\mathrm{f}\mathrm{u}\mathrm{e}\mathrm{l}}=\frac{n_{{\mathrm{H}}_{\mathrm{2}},II}+n_{\mathrm{C}\mathrm{O},II}}{N_{II}-n_{{\text{H}}_2\text{O,}II}}(5)$

For the HMR and DMR, x_fuel indicates the purity of the fuel produced, after condensation of the steam out of the syngas. For the OMR the fuel fraction is simply given by the mole fraction of CO or H₂, (e.g., $$_xfuel =_xCO). The second performance indicator is the fuel ratio in the product, H₂:CO, relevant only in cases where both H₂ and CO are produced. This quantity indicates which reaction is dominant at given conditions. Furthermore, its value is important for many downstream applications of syngas, and thus also indicates the amount of post-processing needed.

In the DMR, both H₂ and O₂ are removed from chamber I and conversion of H₂O could theoretically reach 100%. This implies that the number of moles in chamber I could approach zero. Because values close to zero cause numerical issues, a tolerance was set in the model to avoid infinite iteration. Another consequence of full conversion of H₂O is that it could limit the RWGS reaction in chamber II. That is, the equilibrium state has been reached for the given conditions and initial feed, but if there were additional H₂O relative to the CO₂ available, CO₂ would react further, and a different equilibrium composition would result. This means that there exists a minimum H₂O:CO₂ feed ratio to reach “unconstrained” equilibrium in the DMR. This dependence on H₂O:CO₂ is shown in Supplementary Figure S6.

Theoretical Energy Efficiency Analysis

Another critical performance indicator is the solar-to-fuel energy efficiency of the reactor, η_{solar-to-fuel}. Here, η_{solar-to-fuel} is defined as the heating value of the fuel produced divided by the total heat input,

${\eta }_{\mathrm{s}\mathrm{o}\mathrm{l}\mathrm{a}\mathrm{r}-\mathrm{t}\mathrm{o}-\mathrm{f}\mathrm{u}\mathrm{e}\mathrm{l}}=\frac{n_{\mathrm{f}\mathrm{u}\mathrm{e}\mathrm{l}}\mathrm{H}\mathrm{H}{\mathrm{V}}_{\mathrm{f}\mathrm{u}\mathrm{e}\mathrm{l}}}{Q_{\mathrm{i}\mathrm{n}}},(6)$

where the numerator is calculated using the appropriate higher heating value based on the amounts of CO and H₂ produced at equilibrium, and Q_in represents all heat and work heat-equivalents entering the solar reactor cavity. To define Q_in, a few assumptions must be made about the process, which is diagrammed with all possible process units in Figure 3. Thus, the solar-to-fuel energy efficiency is not a pure thermodynamic property. First, only solar radiation entering through the cavity’s aperture is accounted for. That is, heliostat field losses are not included. The solar cavity-receiver is assumed to be a perfectly insulated blackbody absorber. Re-radiation losses from the cavity are included, but conductive and convective losses are neglected. It is assumed that the membrane reactor is operated in continuous parallel-flow mode and heat recovery from the exiting gases pre-heats the incoming streams. Low $$_pO2 is achieved by vacuum pumping. As an aside, low $$_pO2 can also be reached using an inert sweep gas. However, various studies have shown that sweeping is less efficient than pumping (Tan and Li, 2007; Bulfin et al., 2015). Furthermore, the most effective sweep gas is in counter-flow, and the calculation of the minimum flow rate of sweep gas to maintain a certain $$_pO2 is not trivial. As recently pointed out by Bulfin (2019) and Li et al. (2019), it has previously been incorrectly determined, resulting in overly optimistic sweep gas requirements. Both Bulfin (2019) and Li et al. (2019) describe thermodynamic analyses applicable to countercurrent reactors. In case the pressure of the CO₂-containing chamber is below atmospheric, a vacuum pump is again used. In case the pressure of a CO₂-containing chamber is above atmospheric, a compressor is needed. If the purity of the product is below a certain threshold, some unreacted CO₂ is removed in a separation process. Thus, Q_in is defined to include

$Q_{\mathrm{i}\mathrm{n}}=\frac{1}{{\eta }_{\mathrm{a}\mathrm{b}\mathrm{s}}}\left(Q_{\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}+Q_{\mathrm{s}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{b}\mathrm{l}\mathrm{e}}+Q_{\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}}\right)+Q_{\mathrm{p}\mathrm{u}\mathrm{m}\mathrm{p},{\mathrm{O}}_{\mathrm{2}}}+Q_{\mathrm{p}\mathrm{u}\mathrm{m}\mathrm{p},\mathrm{C}{\mathrm{O}}_{\mathrm{2}}}+Q_{\mathrm{s}\mathrm{e}\mathrm{p}\mathrm{a}\mathrm{r}\mathrm{a}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}(7)$

FIGURE 3

FIGURE 3. Process diagram of the dual-membrane reactor including process units and heat inputs. Different subsets of these process units are applicable for different membrane configurations and operating conditions.

The cavity absorption efficiency, η_abs, is only applied on the inputs added to the system in the form of concentrated solar heat: reaction enthalpy, Q_reaction; sensible heating of gases, Q_sensible; and latent heat of vaporization of steam, Q_latent. The other inputs are work penalties converted to heat: heat equivalent to pump O₂ out of chamber 0, $$_Qpump,O2; heat equivalent to compress or pump a CO₂ chamber, $$_Qpump,CO2; and heat equivalent to separate CO₂ from product to ensure sufficient fuel purity, Q_separation. Note that not all the components of total heat input are applicable in every membrane configuration.

As a blackbody absorber, re-radiation from the solar cavity is characterized by (Steinfeld and Palumbo, 2001):

${\eta }_{\mathrm{a}\mathrm{b}\mathrm{s}}=1-\frac{\sigma T^4}{IC},(8)$

where σ is the Stefan-Boltzmann constant, I is the direct normal solar irradiation (DNI = 1 kW/m²), and C is the solar concentration ratio. The reaction enthalpy is calculated for each reaction as

$Q_{\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{i}\mathrm{o}\mathrm{n}}={\chi }_{\mathrm{f}\mathrm{e}\mathrm{e}\mathrm{d}}{n}_{\mathrm{f}\mathrm{e}\mathrm{e}\mathrm{d},i}{\displaystyle \sum _i{\nu }_i{h}_{f,i}\left(T\right)},(9)$

where χ_feed and n_feed are the conversion and the initial number of moles, respectively, ν_i is the stoichiometric coefficient of species i, and h_f,i is the molar heat of formation of species i at T. The feed species refers to CO₂ or H₂O, depending on the reaction. The sum of Q_reaction for each reaction in the system defines the total. Without heat recovery, heating is required to bring the feed species from ambient T₀ to reaction temperature T. The sensible portion is the total change in enthalpy less the latent heat of vaporization, if applicable:

$Q_{\mathrm{s}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{b}\mathrm{l}\mathrm{e}}=n_{\mathrm{f}\mathrm{e}\mathrm{e}\mathrm{d},i}\left(h_{\mathrm{f}\mathrm{e}\mathrm{e}\mathrm{d}}\left(T\right)-h_{\mathrm{f}\mathrm{e}\mathrm{e}\mathrm{d}}\left(T_0\right)-\Delta h_{\mathrm{v}\mathrm{a}\mathrm{p}}\right).(10)$

For H₂O streams, the latent heat requirement is then:

$Q_{\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t}}=n_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O},i}\Delta h_{\mathrm{v}\mathrm{a}\mathrm{p}}.(11)$

With heat recovery, some fraction of the heat available in the outlet streams preheats the inlet to T_x, as determined by the heat recovery efficiency (Bader et al., 2013; Ermanoski et al., 2014; Venstrom et al., 2014; Bulfin et al., 2015):

${\eta }_{\text{ΗΕX}}=\frac{n_{\mathrm{f}\mathrm{e}\mathrm{e}\mathrm{d},i}\left(h_{\mathrm{f}\mathrm{e}\mathrm{e}\mathrm{d}}\left(T_x\right)-h_{\mathrm{f}\mathrm{e}\mathrm{e}\mathrm{d}}\left(T_0\right)\right)}{\sum _{i\mathrm{i}\mathrm{n}\mathrm{o}\mathrm{u}\mathrm{t}\mathrm{l}\mathrm{e}\mathrm{t}}{n}_i\left(h_i\left(T\right)-h_i\left(T_0\right)\right)},(12)$

where the denominator sums the change in enthalpy of each species in the outlet stream. Then, the sensible heating requirement is reduced to

$Q_{\mathrm{s}\mathrm{e}\mathrm{n}\mathrm{s}\mathrm{i}\mathrm{b}\mathrm{l}\mathrm{e},\mathrm{H}\mathrm{E}\mathrm{X}}=n_{\mathrm{f}\mathrm{e}\mathrm{e}\mathrm{d},i}\left(h_{\mathrm{f}\mathrm{e}\mathrm{e}\mathrm{d}}\left(T\right)-h_{\mathrm{f}\mathrm{e}\mathrm{e}\mathrm{d}}\left(T_x\right)\right).(13)$

For an H₂O stream, we assume that the heat exchanger is used for latent heating first, and so this modification of Q_sensible only applies if $$_hH2O(_Tx)>Δ_hvap. Under that condition, the heat exchanger has the capacity to vaporize all of the H₂O, and Q_latent,HEX = 0. Otherwise, the latent heat requirement is

$Q_{\mathrm{l}\mathrm{a}\mathrm{t}\mathrm{e}\mathrm{n}\mathrm{t},\mathrm{H}\mathrm{E}\mathrm{X}}=n_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O},i}\left(\Delta h_{\mathrm{v}\mathrm{a}\mathrm{p}}-h_{{\mathrm{H}}_{\mathrm{2}}\mathrm{O}}\left(T_x\right)\right).(14)$

In general, a heat input may not be negative, it may only be reduced to zero. Because the DMR has two gas streams, there are two possible arrangements for the two heat exchangers. In one, each outlet stream preheats its own inlet, as shown in Figure 3. In the other, streams are crossed in the heat exchangers so that one outlet stream preheats the opposite inlet and vice versa. Depending on the operating conditions, one of the arrangements may be favorable to maximize the amount of recovered heat.

The magnitude of the energy penalties in Q_in depend strongly on the assumptions made respecting the efficiency of their processes. Therefore, two cases are presented: the ideal case marking the thermodynamic limit and the more realistic case considering real processes and empirically observed efficiencies.

For vacuum pumping of a chamber to vacuum pressures, as done to control $$_pO2 in chamber 0 or to reduce p in another chamber, the minimum heat equivalent is based on isothermal expansion:

$Q_{\text{pump,ideal}}=\frac{n_{\mathrm{p}\mathrm{u}\mathrm{m}\mathrm{p}\mathrm{e}\mathrm{d}}R{T}_0}{{\eta }_{\mathrm{h}\mathrm{e}\mathrm{a}\mathrm{t}-\mathrm{t}\mathrm{o}-\mathrm{w}\mathrm{o}\mathrm{r}\mathrm{k}}}\ln \left(\frac{p_{\mathrm{a}\mathrm{t}\mathrm{m}}}{p_{\mathrm{p}\mathrm{u}\mathrm{m}\mathrm{p}\mathrm{e}\mathrm{d}}}\right),(15)$

where n_pumped is the amount of gas pulled through the vacuum pump ($$_nO2,0 for O₂ pumping), η_heat-to-work is the heat-to-work conversion efficiency, p_atm is atmospheric pressure, and p_pumped is the desired pressure ($$_pO2,0 for O₂ pumping). The empirical efficiency of vacuum pumping systems decreases strongly with decreasing vacuum pressure. Therefore, a realistic estimate of the pump work heat-equivalent is

$Q_{\text{pump,real}}=\frac{Q_{\mathrm{p}\mathrm{u}\mathrm{m}\mathrm{p},\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{a}\mathrm{l}}}{{\eta }_{\mathrm{p}\mathrm{u}\mathrm{m}\mathrm{p}}},(16)$

where η_pump is determined by an envelope function fit to the empirical efficiency of vacuum pumps reported by Brendelberger et al. (2017). If CO₂ is fed at elevated pressure, the idealized heat equivalent for the pumping work is based on isentropic compression, because most compressors in industry are designed to run adiabatically (Campbell, 2014):

$Q_{{\text{pump,CO}}_2,\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{a}\mathrm{l}}=\frac{n_{\mathrm{C}{\mathrm{O}}_{\mathrm{2},i}}{C}_p{T}_0}{{\eta }_{\mathrm{h}\mathrm{e}\mathrm{a}\mathrm{t}-\mathrm{t}\mathrm{o}-\mathrm{w}\mathrm{o}\mathrm{r}\mathrm{k}}}\left({\left(\frac{p_{\mathrm{p}\mathrm{u}\mathrm{m}\mathrm{p}\mathrm{e}\mathrm{d}}}{p_{\mathrm{a}\mathrm{t}\mathrm{m}}}\right)}^{R/C_p}-1\right),(17)$

where C_p is the heat capacity of CO₂ and R is the ideal gas constant. $$_{Qpump,CO2,ideal} is scaled by a realistic compressor efficiency, η_compressor, to determine:

$Q_{{\text{pump,CO}}_2,\mathrm{r}\mathrm{e}\mathrm{a}\mathrm{l}}=\frac{Q_{\mathrm{p}\mathrm{u}\mathrm{m}\mathrm{p},\mathrm{C}{\mathrm{O}}_{\mathrm{2}},\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{a}\mathrm{l}}}{{\eta }_{\mathrm{c}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{s}\mathrm{s}\mathrm{o}\mathrm{r}}}.(18)$

Thermolysis reactions suffer from low molar conversions at insufficiently high T. Therefore, the gas mixture exiting the reactor may need purification. H₂O can be separated via condensation at low T and requires no additional work. CO₂ removal, on the other hand, requires an additional process. The minimum work to separate CO₂ from fuel in the product gas mixture is the difference in Gibbs free energy of mixing between the reactor outlet composition and the desired purity. Assuming any H₂O present in the product stream is previously removed, the gas mixture is treated as a binary mixture of fuel and CO₂:

$Q_{\text{separation,}\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{a}\mathrm{l}}=\frac{R{T}_0}{{\eta }_{\mathrm{h}\mathrm{e}\mathrm{a}\mathrm{t}-\mathrm{t}\mathrm{o}-\mathrm{w}\mathrm{o}\mathrm{r}\mathrm{k}}}\left[\frac{n_{\mathrm{f}\mathrm{u}\mathrm{e}\mathrm{l}}}{x_{\mathrm{f}\mathrm{u}\mathrm{e}\mathrm{l}}^{\prime }}\left(x_{\mathrm{f}\mathrm{u}\mathrm{e}\mathrm{l}}^{\prime }\ln x_{\mathrm{f}\mathrm{u}\mathrm{e}\mathrm{l}}^{\prime }+\left(1-x_{\mathrm{f}\mathrm{u}\mathrm{e}\mathrm{l}}^{\prime }\right)\ln \left(1-x_{\mathrm{f}\mathrm{u}\mathrm{e}\mathrm{l}}^{\prime }\right)\right)-N\left(x_{\mathrm{f}\mathrm{u}\mathrm{e}\mathrm{l}}\ln x_{\mathrm{f}\mathrm{u}\mathrm{e}\mathrm{l}}+\left(1-x_{\mathrm{f}\mathrm{u}\mathrm{e}\mathrm{l}}\right)\ln \left(1-x_{\mathrm{f}\mathrm{u}\mathrm{e}\mathrm{l}}\right)\right)\right],(19)$

where x_fuel and N are the mole fraction of fuel and total number of moles in the dehydrated product, respectively, and $x_{\mathrm{f}\mathrm{u}\mathrm{e}\mathrm{l}}^{\prime }$ and $$_nfuel/xfuel′ are the same quantities in the purified product. Determination of a realistic separation penalty is challenging, because there are few industrial examples of separating mixtures with comparable compositions. To approximate the magnitude of this quantity in this work, an amine-based adsorption process for the scrubbing of flue gases described by Rochelle et al. (2011) is taken as reference. Using the heat duty and work required for the scrubber, the separation heat equivalent is calculated to be approximated q_scrubber = 122 kJ/mol CO₂ removed. Thus,

$Q_{\text{separation,real}}=n_{\mathrm{C}{\mathrm{O}}_{\mathrm{2}},\mathrm{r}\mathrm{e}\mathrm{m}\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{d}}{q}_{\mathrm{s}\mathrm{c}\mathrm{r}\mathrm{u}\mathrm{b}\mathrm{b}\mathrm{e}\mathrm{r}}.(20)$

It is worth noting that the heating value of CO is 283 kJ/mol, which is the same order of magnitude as q_scrubber. Thus, Q_{separation,real} can already be anticipated to have a large impact on η_{solar-to-fuel}.

Results and Discussion

The thermodynamic equilibrium models and energy efficiency analysis form the basis of parametric studies to compare the DMR configuration to the single-membrane configurations and identify the operating conditions needed for best performance. The baseline values of the input parameters are summarized in Table 2, distinguishing between idealistic and realistic assumptions, where applicable. The chosen parameter sweep range is broad enough to demonstrate trends while simultaneously reflecting realistically attainable conditions. High T is needed to drive highly endothermic reactions, but the maximum T is limited by the solar concentration ratio (Steinfeld and Palumbo, 2001) and material stability considerations (Noring et al., 1981; Kalogirou, 2004). Therefore, here we focus on the range 1,500–2,000 K. For studies at constant T, 1800 K is used, considered the highest realistic operating T (Ermanoski et al., 2014; Marxer et al., 2017). Low $$_pO2 is favorable to drive O₂ removal, but the minimum is limited by the energy penalty of pumping at very low pressures (Brendelberger et al., 2017). Therefore, we consider the range 1–100 Pa O₂, and 10 Pa O₂ is used for studies at constant $$_pO2. (From this point forward, $$_pO2 refers to the partial pressure of O₂ set in chamber 0, i.e., $$_pO2,0, unless otherwise specified.) However, we also look at some edge cases, especially when investigating the effect of p in different chambers. Atmospheric pressure is taken as a base case for all reaction chambers. Gas compression does not pose severe energy penalties to the process, but there is a maximum pressure difference that the membranes can mechanically withstand. While the membranes could be designed to be more robust, there is a foreseen tradeoff with diffusion rates. Because of the novelty of this type of membrane reactor, realistic limits on p are uncertain, and, therefore, a large range is explored.

TABLE 2

TABLE 2. Baseline parameters used in thermodynamic efficiency analysis.

Both thermodynamic modeling approaches yielded equivalent results, indicating that neglecting side reactions was justified. Details of the comparison of the two approaches are given in the Supplementary Material and Supplementary Table S3. Figure 4 compares the OMR, HMR, and DMR on the basis of (A) x_fuel and (B) η_{solar-to-fuel} under realistic assumptions, as functions of T. Note that if H₂O is fed to the OMR, the net reaction is water splitting, not CO₂ splitting. All chambers containing a chemical reaction are set to 1 bar total pressure. For the OMR and DMR, $$_pO2 is set to 10 Pa. This is not a free variable for the HMR. There, only H₂O:CO₂ can be controlled, and it is set to the value which maximizes η_{solar-to-fuel} at each T considered. The same rationale is used for setting H₂O:CO₂ in the DMR.

FIGURE 4

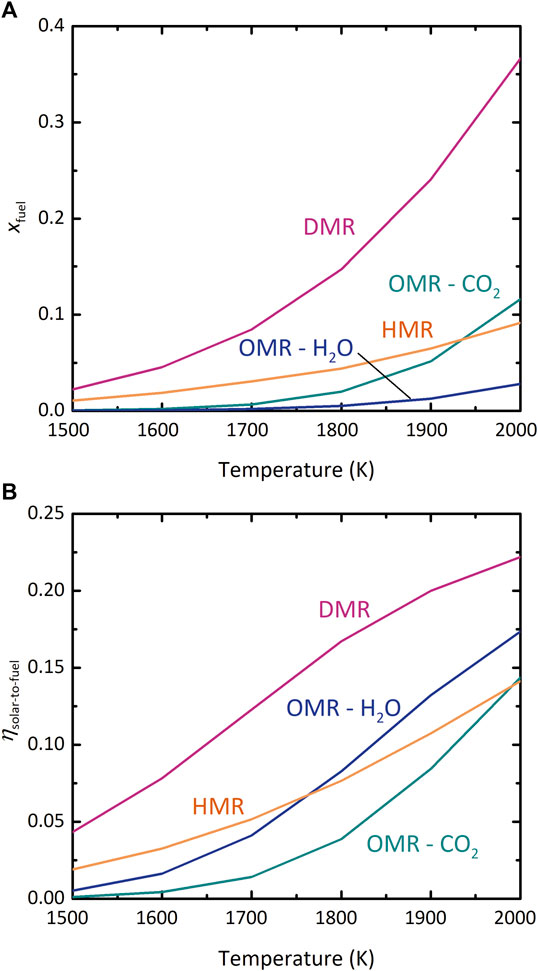
FIGURE 4. Comparison of the oxygen-membrane reactor (OMR), hydrogen-membrane reactor (HMR), and dual-membrane reactor (DMR) configurations. (A) x_fuel vs. T, (B) η_{solar-to-fuel} vs. T. p_I, p_II = 1 bar, where applicable. $$_pO2 = 10 Pa, where applicable. Where applicable, H₂O:CO₂ chosen to maximize η_{solar-to-fuel} at each point.

In Figure 4A, x_fuel in the DMR is higher than in the other configurations over the entire range of T. This result could be expected because the OMR and HMR each depend on a driving force across a single membrane, whereas the DMR benefits from the combined driving force of both membranes. Furthermore, effectiveness of each single membrane can be evaluated by comparing the “HMR” and “OMR–CO₂” curves. At most T, driving the CO₂-splitting reaction with $$_pH2 leads to higher x_fuel than using $$_pO2. This is partially because the amount of H₂ produced per mole of reaction exceeds O₂ by a factor of two, making it easier to create a large Δp across the membrane. In addition, the product stream in the HMR is a mixture of CO, H₂, CO₂, and H₂O, which is entropically favored over the mixture of CO and CO₂ in the OMR. However, reaction in the HMR is limited by the amount of H₂ able to cross the membrane at equilibrium, which depends on the thermolysis of H₂O. At high T, H₂O thermolysis is less favorable than CO₂ thermolysis, and the difference grows exponentially with T. Thus, x_fuel in the OMR overtakes that in the HMR above 1,900 K.

Figure 4B shows that the DMR also outperforms the OMR and HMR in terms of η_{solar-to-fuel}. Furthermore, in the OMR the realistic efficiency of H₂O splitting exceeds CO₂ splitting, a reversal from the results for x_fuel. Thermolysis of CO₂ is thermodynamically more favorable than of H₂O at these high temperatures, leading to higher x_fuel, but the greater energetic cost of separating unreacted CO₂ from the CO/CO₂ mixture relative to condensing steam out of the H₂/H₂O mixture counteracts this benefit, resulting in lower η_{solar-to-fuel}. This effect is also why a higher T is needed before the “OMR–CO₂” efficiency curve overtakes that of the HMR relative to Figure 4A. As expected, the DMR exhibits advantages over the single-membrane OMR and HMR designs. The rest of this work examines the behavior of the DMR more closely; results of the individual analyses of the OMR and HMR are available in the Supplementary Material and Supplementary Figures S1–S5.

Figure 5 shows the detailed contributions to Q_in at the maximum η_{solar-to-fuel} for four scenarios. In case 1, p_I and p_II are equal at 1 bar. In case 2, p_I is 10 bar and p_II is 0.1 bar. The “X” applied to each case designates the alternative heat exchanger arrangement described in the efficiency analysis. Both case 1 and 1X include a large contribution for Q_separation, more than one-third of the total heat required, because x_fuel is not high enough at these conditions. Case 2 and 2X do not incur any separation energy penalty, because x_fuel is greater than the minimum specified in Table 2. Due to the higher conversion in case 2, Q_reaction increases. The amount of O₂ removed is also higher, leading to a significantly higher proportion of heat input going to $$_Qpump,O2. Case 2 includes a contribution of heat to vacuum pumping of chamber II, $$_Qpump,CO2, which is unnecessary in case 1. In sum, when comparing these specific scenarios, investing in $$_Qpump,CO2 is worthwhile to avoid Q_separation in the DMR. Figure 5 further demonstrates that the choice of heat exchanger arrangement is not critical to the efficiency of the DMR. The sensible and latent heating of the gas streams only accounts for 10% or less of Q_in. Therefore, although arrangement “X” reduces the fraction of heat required for the gases (and eliminates it altogether in case 1X), the influence on overall efficiency is small.

FIGURE 5

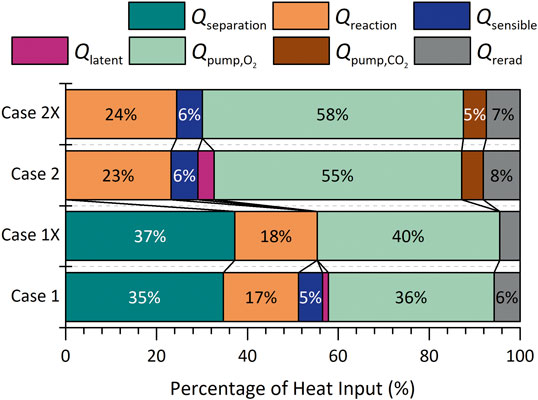
FIGURE 5. Distribution of the components of Q_in for the dual-membrane reactor. Case 1: p_I = p_II = 1 bar. Case 2: p_I = 10 bar, p_II = 0.1 bar. The suffix “X” denotes the cross-stream arrangement of heat exchangers, whereas in the standard arrangement the inlet and outlet of the same stream exchange heat. T = 1,800 K and $$_pO2 = 10 Pa.

Figure 6 shows the dependence in the DMR of x_fuel and η_{solar-to-fuel} on T at various $$_pO2.Here both p_I and p_II are constant at 1 bar. x_fuel increases monotonically with increasing T and decreasing $$_pO2, as expected from the equilibrium relationship of the reaction. At these conditions, η_{solar-to-fuel} also increases with T, but with decreasing slope because at some point a maximum will be reached due to re-radiation from the cavity. The effect of $$_pO2 on η_{solar-to-fuel} is not necessarily monotonic and changes with T. At the lowest T considered in Figure 6, 1,500 K, η_{solar-to-fuel} increases as $$_pO2 decreases, but at the highest T of 2,000 K, the trend is reversed and η_{solar-to-fuel} decreases as $$_pO2 decreases. Thus, the $$_pO2 that maximizes η_{solar-to-fuel} increases with T. While decreasing $$_pO2 increases the fuel output of the reactor, it also demands pump work input to the reactor. At low T, the improvement in fuel production justifies the additional work to reduce $$_pO2. However, as the amount of O₂ to be removed increases at higher T, there is a point where maintaining $$_pO2 requires more energy than is gained from the heating value of the fuel. For example, at a reference T of 1,800 K and a $$_pO2 of 1 Pa, x_fuel exceeds 20%, but η_{solar-to-fuel} is less than 10%. If at the same T the $$_pO2 were increased to 10 Pa, x_fuel would drop to 15%, but η_{solar-to-fuel} would almost double.

FIGURE 6

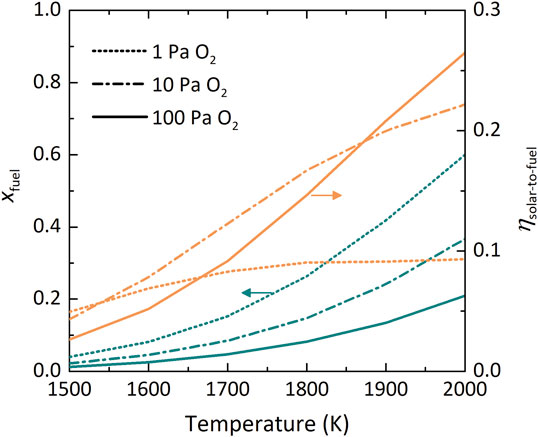
FIGURE 6. Dual-membrane reactor performance indicators x_fuel (teal) and η_{solar-to-fuel} (orange) as a function of T at various $$_pO2. p_I = p_II = 1 bar.

Figure 7 shows the effect of the ratio of pressures in chambers I and II on the three performance indicators: (A) x_fuel, (B) H₂:CO molar ratio, and (C) η_{solar-to-fuel}. T and $$_pO2 are constant at 1,800 K and 10 Pa, respectively. Results are grouped by the value of p_I. The plots show that, with the exception of η_{solar-to-fuel} at high p_I:p_II in Figure 7C, the absolute values of p_I and p_II do not matter, but only the ratio between them, because the data collapse onto a single curve. As p_I:p_II increases, x_fuel and H₂:CO shown in Figures 7A,B, respectively, also increase until CO₂ is fully consumed and then they level off. At these conditions the threshold is at a 200:1 p_I-to-p_II ratio. Manipulation of p_I:p_II seems to be effective to drive the reaction to completion, as x_fuel reaches a maximum value of 1 in Figure 7A. As seen in Figure 7B, control over p_I:p_II also allows a broad range of H₂:CO ratios from 0.04 to 26 to become accessible, including industrially relevant ratios around 2 (Schulz, 1999; Leckel, 2009). In Figure 7C, η_{solar-to-fuel} varies over a relatively smaller range than the other performance indicators, between 17 and 26%. η_{solar-to-fuel} reaches a maximum at the same threshold ratio as observed for x_fuel and H₂:CO. At lower values of p_I:p_II, the different values of p_I have similar efficiencies. However, it is already apparent that lower p_I leads to lower η_{solar-to-fuel}. At higher values of p_I:p_II, this trend becomes very clear, as the η_{solar-to-fuel} at lower p_I falls more steeply. This effect is a consequence of increasing pumping cost in chamber II as p_II decreases, which is the case when p_I decreases at constant p_I:p_II. Keeping p_I greater than p_II is always thermodynamically beneficial, therefore there is no reason to consider doing work to evacuate H₂O in chamber I below atmospheric pressure, or to compress CO₂ in chamber II above atmospheric pressure. Moreover, changing p_I above atmospheric pressure does not affect heat requirements, because the feed to chamber I is produced by vaporizing H₂O. Therefore, assuming it is feasible to withstand large Δp across the membrane, efficiency is maximized by increasing p_I and keeping p_II atmospheric.

FIGURE 7

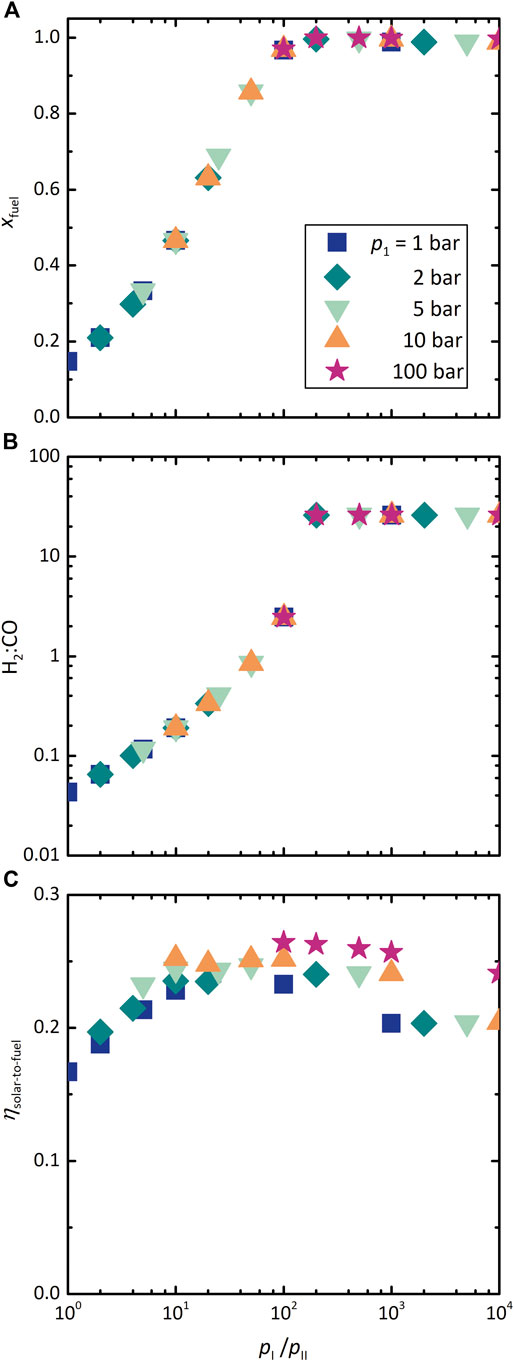
FIGURE 7. Effect of the dual-membrane reactor chamber pressure ratio, p_I:p_II, on (A) x_fuel, (B) H₂:CO molar ratio, and (C) η_{solar-to-fuel} at various values of p_I. T = 1,800 K and $$_pO2 = 10 Pa.

Materials Outlook

Although the values of process parameters used here were chosen to be as realistic as possible, there are nevertheless many idealistic assumptions in this theoretical analysis. The most optimistic assumption is that materials for such high-temperature, selective membranes exist. To test the actual capabilities and limitations of the membrane reactor, functional membranes are first necessary. Kinetics, material stability, and membrane selectivity will affect the performance of a physical system. Oxygen-conducting membranes based on nonstoichiometric ceria have been characterized and demonstrated for solar-driven thermolysis of CO₂ and H₂O (Tou et al., 2017; Tou et al., 2019). The analog for hydrogen at these operating conditions has not emerged, but some insight may be gained from neighboring fields.

Hydrogen-conducting membrane materials have been studied in the context of sensors, hydrogen fuel cells, electrolyzers, and (de)hydrogenation reactions (Liu et al., 2006). Dense metallic membranes show high conductivity and selectivity of H⁺, but are limited to operation below 1,000 K. Furthermore, they are often Pd-based, which is expensive and impractical at the industrial scale (Tao et al., 2015). Considering the small size of H₂, selective transport based on molecular sieving through micropores has also been suggested (Fletcher and Moen, 1977; Kogan, 1997; Tao et al., 2015). Here, controlling pore size and stability is a challenge, and perfect selectivity impossible (Kogan, 1998). Dense ceramics have also been shown to conduct H⁺, and are the only class of hydrogen-conductors stable at 1,800 K. Despite their own set of challenges, these mixed protonic-electronic conducting (MPEC) materials appear the most promising for hydrogen-conducting membranes.

Research has focused on perovskites, many of which are oxygen ion conductors. The compositions of perovskites that conduct hydrogen are limited, most often with Ba or Sr on the A site and Ce or Zr on the B site of the characteristic ABO₃ structure (Iwahara et al., 1982; Fabbri et al., 2010; Dong et al., 2011). Several studies identified BaCe_0.2Zr_0.7Y_0.1O₃ (BCZY27) to be a promising composition (Dippon et al., 2016). Ba-based perovskites have the highest proton conductivities, but their electron conductivity tends to limit the overall transfer of hydrogen (Fabbri et al., 2010). For better electron conductivity, the B site is often doped with a trivalent dopant such as Y (Dong et al., 2011). Due to tradeoffs in protonic and electronic mobility, the optimal temperature range for proton conduction in MPECs is about 673–873 K (Bonanos and Poulsen, 1999; Fabbri et al., 2010). Even then, the flux of hydrogen through these materials is considered impractically low and requires membrane thicknesses on the μm-scale (Phair and Badwal, 2006; Dong et al., 2011). Furthermore, studies have found that Ba-based perovskites also conduct O²⁻ at high temperatures, which is detrimental for our desired application in H₂O thermolysis (Fabbri et al., 2010).

To check the behavior of an MPEC material at temperature conditions needed for membrane-assisted thermolysis, we prepared tubular BCZY27 membranes and tested them in a set of simple permeation experiments (experimental details in the Supplementary Material). Figures 8A,B show a photograph and a scanning electron microscopic image of representative membranes. As shown in Figure 8C, BCZY27 indeed conducts O²⁻, and in fact the measured flux of O²⁻ is higher than H⁺ in the relevant range tested 1,073–1,773 K. Although the membrane thickness (∼800 μm) likely limited hydrogen diffusion, more importantly, these experiments revealed a critical lack of selectivity. In sum, the practicality of the DMR depends on the development of hydrogen-selective, high-temperature membranes, and more materials science research to this end is still necessary.

FIGURE 8

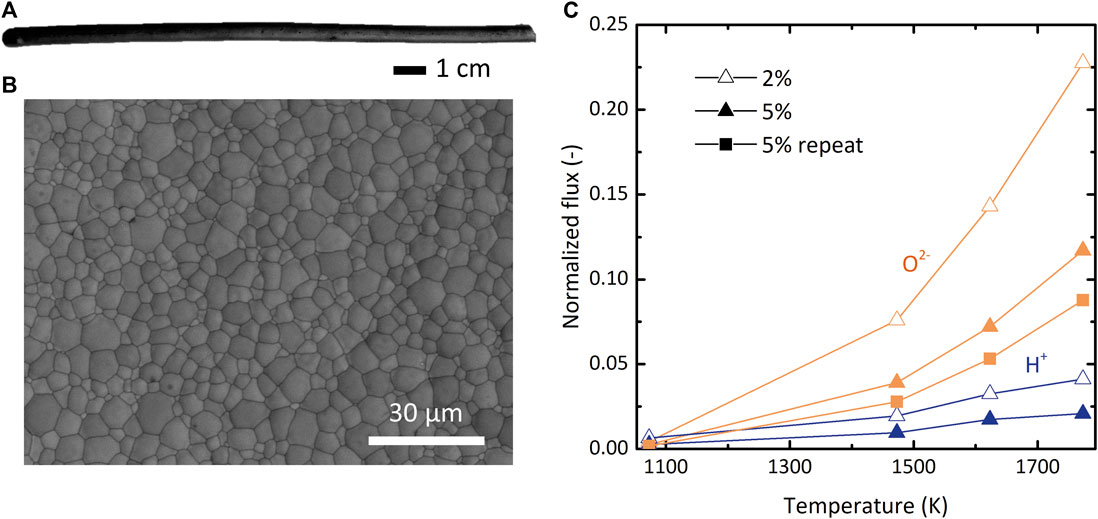
FIGURE 8. (A) Photograph of a representative BCZY27 membrane, which were tubular and closed on one end. (B) Scanning electron microscopic image of the inner surface of a BCZY27 membrane. (C) Normalized ionic flux of H⁺ (blue) and O²⁻ (orange) at the respective H₂ or O₂ feed gas concentrations of 2% (hollow) and 5% (solid) through a BCZY27 membrane as a function of T. A repetition of 5% O₂ feed with a different membrane is shown with square symbols.

Summary and Conclusions

We examined the concept of a thermochemical membrane reactor to split CO₂ and produce solar fuels from a thermodynamic perspective for three configurations: a single oxygen-permeable membrane (OMR), a single hydrogen-permeable membrane (HMR), and an oxygen-permeable and hydrogen-permeable dual-membrane (DMR) configuration. The theoretical solar-to-fuel energy efficiency calculations for all configurations assumed thermodynamic equilibrium and made realistic process assumptions to highlight process limitations. Low product purity in the OMR at all realistic operating conditions leads to low η_{solar-to-fuel} of CO₂ thermolysis. The performance of the HMR depends on the choice of feed ratio, H₂O:CO₂, and values of x_fuel and η_{solar-to-fuel} are expected to be below 15%. As expected, the DMR outperformed the OMR and HMR. The thermodynamic model identified non-unique operating conditions where $$_χCO2 and x_fuel in the DMR could exceed 90%. One example is at 1,800 K, 10 Pa O₂ in chamber 0, 100 bar total in chamber I, and 1 bar total in chamber II, where η_{solar-to-fuel} reaches 26%. The same efficiency was predicted at 2,000 K, 100 Pa O₂ in chamber 0, and 1 bar total in chambers I and II, where in this case x_fuel was 21%. The determination of the “best” operating conditions depends on physical feasibility. Reactor temperatures of 2,000 K like in the latter case are not currently possible. It also remains an open question whether membranes can be built that withstand extreme pressure differences like the one in the former case. More pressingly, suitable materials need to be developed, particularly for the hydrogen-permeable membrane.

Data Availability Statement

All datasets presented in this study are included in the article/supplementary material.

Author Contributions

MT wrote the manuscript, and developed the model together with her colleagues. She also performed the experimental work. AG did his master’s thesis with MT, working on the thermodynamic models discussed in the manuscript. ArS, performed experimental work on membranes and assisted with the modeling work. BB formulated the approach to the modeling together with MT, and assistant in writing the manuscript. AlS co-supervised the work and assisted in writing the manuscript. RM co-supervised the work and assisted in writing the manuscript.

Funding

This work was funded by the Swiss National Science Foundation (Ambizione Energy Grant No. 166883).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We thank Noah Oswald and Severin Kull for helping develop the experimental procedure.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2020.570884/full#supplementary-material

References

Bader, R., Venstrom, L. J., Davidson, J. H., and Lipiński, W. (2013). Thermodynamic analysis of isothermal redox cycling of ceria for solar fuel production. Energy Fuels 27 (9), 5533–5544. doi: 10.1021/ef400132d.

CrossRef Full Text | Google Scholar

Bonanos, N., and Poulsen, F. W. (1999). Considerations of defect equilibria in high temperature proton-conducting cerates. J. Mater. Chem. 9, 431–434. doi: 10.1039/a805150j.

CrossRef Full Text | Google Scholar

Brendelberger, S., von Storch, H., Bulfin, B., and Sattler, C. (2017). Vacuum pumping options for application in solar thermochemical redox cycles – assessment of mechanical-, jet- and thermochemical pumping systems. Solar Energy 141, 91–102. doi: 10.1016/j.solener.2016.11.023.

CrossRef Full Text | Google Scholar

Bulfin, B. (2019). Thermodynamic limits of countercurrent reactor systems, with examples in membrane reactors and the ceria redox cycle. Phys. Chem. Chem. Phys. 21, 2186–2195. doi: 10.1039/c8cp07077f.

CrossRef Full Text | Google Scholar

Bulfin, B., Call, F., Lange, M., Lübben, O., Sattler, C., Pitz-Paal, R., et al. (2015). Thermodynamics of CeO₂ thermochemical fuel production. Energy Fuels 29 (2), 1001–1009. doi: 10.1021/ef5019912.

CrossRef Full Text | Google Scholar

Campbell, J. M. (2014). Gas conditioning and processing: the equipment modules. 9th Edn. Editors R. Hubbard and K. Snow-McGregor (Norman, OK: Campbell Petroleum Series), Vol. 2.

Google Scholar

Chase, M. W., Davies, C. A., Downey, J. R., Frurip, D. J., McDonald, R. A., and Syverud, A. N. (1998). NIST-JANAF thermochemical tables: NIST standard reference database 13. Standard reference data program. National Institute of Standards and Technology.

Google Scholar

Dippon, M., Babiniec, S. M., Ding, H., Ricote, S., and Sullivan, N. P. (2016). Exploring electronic conduction through BaCe_xZr_0.9−xY_0.1O_3−d proton-conducting ceramics. Solid State Ion. 286, 117–121. doi: 10.1016/j.ssi.2016.01.029.

CrossRef Full Text | Google Scholar

Dong, X., Jin, W., Xu, N., and Li, K. (2011). Dense ceramic catalytic membranes and membrane reactors for energy and environmental applications. Chem. Commun. 47 (39), 10886–10902. doi: 10.1039/c1cc13001c.

CrossRef Full Text | Google Scholar

Ermanoski, I., Miller, J. E., and Allendorf, M. D. (2014). Efficiency maximization in solar-thermochemical fuel production: challenging the concept of isothermal water splitting. Phys. Chem. Chem. Phys. 16 (18), 8418–8427. doi: 10.1039/c4cp00978a.

CrossRef Full Text | Google Scholar

Evdou, A., Nalbandian, L., and Zaspalis, V. (2008). Perovskite membrane reactor for continuous and isothermal redox hydrogen production from the dissociation of water. J. Membr. Sci. 325 (2), 704–711. doi: 10.1016/j.memsci.2008.08.042.

CrossRef Full Text | Google Scholar

Fabbri, E., Pergolesi, D., and Traversa, E. (2010). Materials challenges toward proton-conducting oxide fuel cells: a critical review. Chem. Soc. Rev. 39 (11), 4355–4369. doi: 10.1039/b902343g.

CrossRef Full Text | Google Scholar

Fletcher, E. A., and Moen, R. L. (1977). Hydrogen and oxygen from water. Science 197 (4308), 1050–1056. doi: 10.1126/science.197.4308.1050

CrossRef Full Text | Google Scholar

Franca, R. V., Thursfield, A., and Metcalfe, I. S. (2012). La_0.6Sr_0.4Co_0.2Fe_0.8O_3−δ microtubular membranes for hydrogen production from water splitting. J. Membr. Sci. 389, 173–181. doi: 10.1016/j.memsci.2011.10.027.

CrossRef Full Text | Google Scholar

Garagounis, I., Kyriakou, V., Anagnostou, C., Bourganis, V., Papachristou, I., and Stoukides, M. (2011). Solid electrolytes: applications in heterogeneous catalysis and chemical cogeneration. Ind. Eng. Chem. Res. 50 (2), 431–472. doi: 10.1021/ie1001058.

CrossRef Full Text | Google Scholar

Geffroy, P.-M., Fouletier, J., Richet, N., and Chartier, T. (2013). Rational selection of MIEC materials in energy production processes. Chem. Eng. Sci. 87, 408–433. doi: 10.1016/j.ces.2012.10.027.

CrossRef Full Text | Google Scholar

Goodwin, D. G., Moffat, H. K., and Speth, R. L. (2009). Cantera: an object-oriented software toolkit for chemical kinetics, thermodynamics, and transport processes. Pasadena, CA: Caltech.

Google Scholar

Iwahara, H., Uchida, H., and Maeda, N. (1982). High temperature fuel and steam electrolysis cells using proton conductive solid electrolytes. J. Power Sources 7, 293–301. doi: 10.1016/0378-7753(82)80018-9.

CrossRef Full Text | Google Scholar

Kalogirou, S. A. (2004). Solar thermal collectors and applications. Prog. Energy Combust. Sci. 30 (3), 231–295. doi: 10.1016/j.pecs.2004.02.001.

CrossRef Full Text | Google Scholar

Kharton, V., Marques, F., and Atkinson, A. (2004). Transport properties of solid oxide electrolyte ceramics: a brief review. Solid State Ion. 174 (1–4), 135–149. doi: 10.1016/j.ssi.2004.06.015.

CrossRef Full Text | Google Scholar

Kogan, A. (1997). Direct solar thermal splitting of water and on site separation of the products – I. Theoretical evaluation of hydrogen yield. Int. J. Hydrogen Energy 22 (5), 481–486. doi: 10.1016/s0360-3199(96)00125-5.

CrossRef Full Text | Google Scholar

Kogan, A. (1998). Direct solar thermal splitting of water and on-site separation of the products – II. Experimental feasibility study. Int. J. Hydrogen Energy 23 (2), 89–98. doi: 10.1016/s0360-3199(97)00038-4.

CrossRef Full Text | Google Scholar

Leckel, D. (2009). Diesel production from Fischer-Tropsch: the past, the present, and new concepts. Energy Fuels 23, 2342–2358. doi: 10.1021/ef900064c.

CrossRef Full Text | Google Scholar

Lewis, N. S. (2016). Research opportunities to advance solar energy utilization. Science 351 (6271), aad1920. doi: 10.1126/science.aad1920.

CrossRef Full Text | Google Scholar

Li, S., Kreider, P. B., Wheeler, V. M., and Lipiński, W. (2019). Thermodynamic analyses of fuel production via solar-driven ceria-based nonstoichiometric redox cycling: a case study of the isothermal membrane reactor system. J. Sol. Energy Eng. 141 (2), 021012. doi: 10.1115/1.4042228.

CrossRef Full Text | Google Scholar

Liu, Y., Tan, X., and Li, K. (2006). Mixed conducting ceramics for catalytic membrane processing. Catal. Rev. 48 (2), 145–198. doi: 10.1080/01614940600631348.

CrossRef Full Text | Google Scholar

Marxer, D., Furler, P., Takacs, M., and Steinfeld, A. (2017). Solar thermochemical splitting of CO₂ into separate streams of CO and O₂ with high selectivity, stability, conversion, and efficiency. Energy Environ. Sci. 10 (5), 1142–1149. doi: 10.1039/c6ee03776c.

CrossRef Full Text | Google Scholar

Muhich, C. L., Evanko, B. W., Weston, K. C., Lichty, P., Liang, X., Martinek, J., et al. (2013). Efficient generation of H₂ by splitting water with an isothermal redox cycle. Science 341, 540–542. doi: 10.1126/science.1239454.

CrossRef Full Text | Google Scholar

Noring, J. E., Diver, R. B., and Fletcher, E. A. (1981). Hydrogen and oxygen from water – V. The ROC system. Energy 6, 109–121. doi: 10.1016/0360-5442(81)90131-6.

CrossRef Full Text | Google Scholar

Phair, J. W., and Badwal, S. P. S. (2006). Review of proton conductors for hydrogen separation. Ionics 12 (2), 103–115. doi: 10.1007/s11581-006-0016-4.

CrossRef Full Text | Google Scholar

Rochelle, G., Chen, E., Freeman, S., Van Wagener, D., Xu, Q., and Voice, A. (2011). Aqueous piperazine as the new standard for CO₂ capture technology. Chem. Eng. J. 171 (3), 725–733. doi: 10.1016/j.cej.2011.02.011.

CrossRef Full Text | Google Scholar

Romero, M., and Steinfeld, A. (2012). Concentrating solar thermal power and thermochemical fuels. Energy Environ. Sci. 5 (11), 9234–9245. doi: 10.1039/c2ee21275g.

CrossRef Full Text | Google Scholar

Schulz, H. (1999). Short history and present trends of Fischer–Tropsch synthesis. Appl. Catal. A Gen. 186 (1), 3–12. doi: 10.1016/s0926-860x(99)00160-x.

CrossRef Full Text | Google Scholar

Steinfeld, A., and Palumbo, R. (2001). “Solar thermochemical process technology,” in Encyclopedia of physical science and technology (Cambridge, MA: Academic Press), 237–256.

Google Scholar

Sunarso, J., Baumann, S., Serra, J. M., Meulenberg, W. A., Liu, S., Lin, Y. S., et al. (2008). Mixed ionic–electronic conducting (MIEC) ceramic-based membranes for oxygen separation. J. Membr. Sci. 320, 13–41. doi: 10.1016/j.memsci.2008.03.074.

CrossRef Full Text | Google Scholar

Tan, X., and Li, K. (2007). Oxygen production using dense ceramic hollow fiber membrane modules with different operating modes. AIChE J. 53 (4), 838–845. doi: 10.1002/aic.11116.

CrossRef Full Text | Google Scholar

Tao, Z., Yan, L., Qiao, J., Wang, B., Zhang, L., and Zhang, J. (2015). A review of advanced proton-conducting materials for hydrogen separation. Prog. Mater. Sci. 74, 1–50. doi: 10.1016/j.pmatsci.2015.04.002.

CrossRef Full Text | Google Scholar

Tou, M., Jin, J., Hao, Y., Steinfeld, A., and Michalsky, R. (2019). Solar-driven co-thermolysis of CO₂ and H₂O and in-situ oxygen removal across a non-stoichiometric ceria membrane. React. Chem. Eng. 4, 1431–1438. doi: 10.1039/C8RE00218E.

CrossRef Full Text | Google Scholar

Tou, M., Michalsky, R., and Steinfeld, A. (2017). Solar-driven thermochemical splitting of CO₂ and in situ separation of CO and O₂ across a ceria redox membrane reactor. Joule 1 (1), 146–154. doi: 10.1016/j.joule.2017.07.015.

CrossRef Full Text | Google Scholar

Tuller, H. L. (2015). Solar to fuels conversion technologies. An MIT Future of Solar Energy Study Working Paper, Massachusetts Institute of Technology.

Google Scholar

Venstrom, L. J., De Smith, R. M., Hao, Y., Haile, S. M., and Davidson, J. H. (2014). Efficient splitting of CO₂ in an isothermal redox cycle based on ceria. Energy Fuels 28 (4), 2732–2742. doi: 10.1021/ef402492e.

CrossRef Full Text | Google Scholar

Wang, H., Hao, Y., and Kong, H. (2015). Thermodynamic study on solar thermochemical fuel production with oxygen permeation membrane reactors. Int. J. Energy Res. 39 (13), 1790–1799. doi: 10.1002/er.3335.

CrossRef Full Text | Google Scholar

Zhu, L., Lu, Y., and Shen, S. (2016). Solar fuel production at high temperatures using ceria as a dense membrane. Energy 104, 53–63. doi: 10.1016/j.energy.2016.03.108.

CrossRef Full Text | Google Scholar