- 1Institute of Theoretical Chemistry, Ulm University, Ulm, Germany
- 2Helmholtz Institute Ulm (HIU) for Electrochemical Energy Storage, Ulm, Germany
Periodic density functional theory calculations have been performed to study the migration of various charge carriers in spinel‐type MgSc2Se4. This compound exhibits low barriers for Mg ion diffusion, making it a potential candidate for solid electrolytes in Mg-ion batteries. In order to elucidate the decisive factors for the ion mobility in spinel-type phases, the diffusion barriers of other mono- and multivalent ions (Li+, Na+, K+, Cs+, Zn2+, Ca2+, and Al3+) in the MgSc2Se4 framework have been determined as well. This allows for disentangling structural and chemical factors, showing that the ion mobility is not solely governed by size and charge of the diffusing ions. Finally, our results suggest that charge redistribution and rehybridization caused by the migration of the multivalent ions increase the resulting migration barriers.
Introduction
Due to the combination of potentially high capacity, increased safety and beneficial environmental aspects, batteries with multivalent charge carriers represent a promising alternative to lithium-ion technology. Through the pairing of metal anodes with high voltage cathodes, energy densities which exceed the current limits of lithium-ion batteries are likely to become possible (Elia et al., 2016; Canepa et al., 2017b). In addition, multivalent ion batteries appear to exhibit a low tendency for dendrite formation (Aurbach et al., 2001; Matsui, 2011; Jäckle et al., 2018; Stottmeister and Groß, 2020). Nevertheless, there are obstacles which need to be overcome for making multivalent batteries a viable alternative to the state of the art lithium-ion technology. One of the greatest challenges is the search for high voltage cathode materials which offer sufficient ion mobility. In fact, multivalent ions like Mg2+, Zn2+, and Ca2+ show very different ion mobility in structurally identical materials, which leads to identifying the charge carrier site preference as a criterion for good ion conductivity (Rong et al., 2015). Furthermore, the fact that compounds with high lithium-ion mobility tend to show poor multivalent ion mobility (Levi et al., 2009) complicates the search for suitable cathode materials. Spinel type phases are a class of materials which shows promising multivalent ion mobility (Rong et al., 2015). While showing good lithium-ion mobility, the spinel structure, moreover, offers a topology that is particularly well-suited for magnesium ion conduction.
Reversible intercalation of magnesium ions into oxide spinels could be verified (Kim et al., 2015; Yin et al., 2017) and several spinel phases were identified as suitable cathode materials (Liu et al., 2015; Bayliss et al., 2019). Interestingly, the ion conductivity of spinel materials can be further increased by moving towards sulfide (Emly and Van der Ven, 2015; Liu et al., 2016; Sun et al., 2016; Kulish et al., 2017) and selenide based (Canepa et al., 2017a; Wang et al., 2019; Koettgen et al., 2020) spinels. The volume per anion increases in the order of O2− < S2− < Se2− and is connected to a rising polarizability, which is beneficial for the cation mobility (Canepa et al., 2017a). Thus, materials like the MgSc2Se4 spinel phase could be identified, exhibiting excellent migration barriers for magnesium ions of less than 0.4 eV (Canepa et al., 2017a; Wang et al., 2019). It has to be noted that the increased ion mobility in sulfides and selenides comes at the expense of a significantly decreased insertion potential which consequently results in a lower energy density of the battery. Hence, many spinel chalcogenides are rather unsuited for the use as cathode materials, however, they are interesting candidates for solid ionic conductors to enable all-solid-state multivalent ion batteries. Spinel materials have been investigated as cathode materials for several different multivalent charge carriers (Liu et al., 2015; Rong et al., 2015; Liu et al., 2016; Kulish et al., 2017). However, the origin of the vastly different migration barriers is still not fully understood. While the size and charge of the migrating cation clearly play a role, these properties alone are not sufficient to explain the differences in the diffusion barriers. In this study, migration barriers for a series of selected charge carriers in the MgSc2Se4 spinel are determined using periodic density functional theory calculations, aiming to reveal the factors that determine the observed differences in the ion migration.
Computational Details
Periodic density functional theory (Hohenberg and Kohn, 1964; Kohn and Sham, 1965) calculations are well-suited to reveal microscopic details of structures and processes in battery materials (Hörmann et al., 2015; Groß, 2018). Here we have used them to study the ASc2Se4 (A = Li, Na, K, Cs, Mg, Ca, Zn, and Al) spinel structure with a particular focus on the migration of the respective charge carriers “A.” Exchange and correlation are considered within the generalized gradient approximation, employing the functional form as introduced by Perdew, Burke, and Ernzerhof (Perdew et al., 1996). The electron-core interactions are accounted for by the Projector Augmented Wave (Blöchl, 1994) method as implemented in the Vienna Ab Initio Simulation Package (Kresse and Hafner, 1993; Kresse and Furthmüller, 1996; Kresse and Joubert, 1999). The migration barriers of the charge carriers were determined using the climbing image Nudged Elastic Band (NEB) (Sheppard et al., 2008) method in the conventional 56 atom 1
Results and Discussion
Spinel compounds crystallize in space group
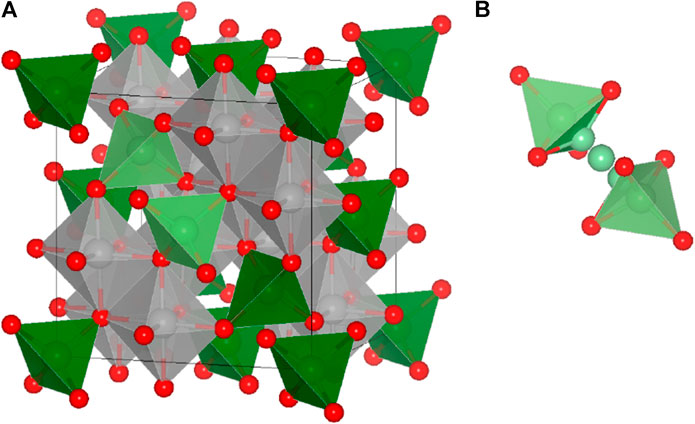
FIGURE 1. (A) The AB2X4 spinel structure. The “X” anions (red) form a face-centered cubic lattice, the “B” cations (gray) are octahedrally coordinated, and the “A” cations (green) occupy tetrahedrally coordinated sites and (B) the schematic representation of a diffusion path between two adjacent tetrahedral sites (tet-oct-tet). The migration path of an exemplary tet-oct-tet diffusion event is indicated by the light green atoms.
For this purpose, the relaxed cubic unit cell of the MgSc2Se4 spinel is taken as the starting point for a screening of selected charge carriers, namely Li+, Na+, K+, Cs+, Mg2+, Zn2+, Ca2+, and Al3+. To allow for direct comparison of the diffusion properties of the different charge carriers, a special set up has been chosen as a model system. While this model system can hardly be realized in experiment, it allows us to directly compare the results for the various charge carriers in the spinel structure. Thus we are able to derive trends in the migration barriers as a function of the properties of the migrating ion und thus to gain a deeper understanding of the factors underlying the ion mobility in the spinel structures. One Mg vacancy is introduced in the MgSc2Se4 supercell, and the structure is subsequently relaxed. Then, one of the neighboring Mg atoms is replaced by one of the charge carriers of interest, and a NEB calculation for a fixed host lattice is performed. Since the migration path topology, being of the form tetrahedral-octahedral-tetrahedral (tet-oct-tet), is symmetric, only the path from tetrahedral to octahedral coordination needs to be calculated. The corresponding minimum energy paths, as obtained by the NEB method, are shown in Figure 2. The energies are given relative to the charge carrier in the initial tetrahedral coordination environment and are mirrored with respect to the octahedral site in order to represent the full tet-oct-tet migration path. The site preference of the respective charge carrier can be readily deduced from the difference in energy of the octahedral and tetrahedral site.
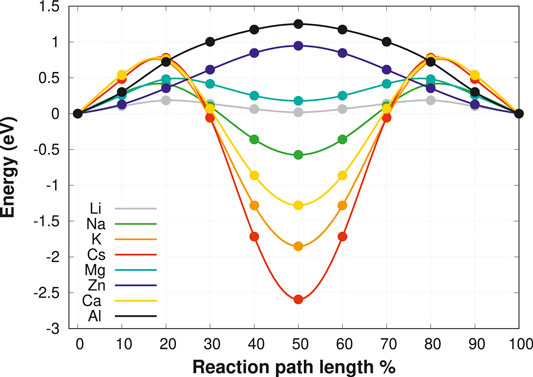
FIGURE 2. The tet-oct-tet migration of possible charge carriers in the fixed MgSc2Se4 spinel structure without ionic relaxation. The energies are taken relative to the energy of the charge carrier in the tetrahedral coordination.
These results indicate that Mg2+ and Li+ show good ionic mobility with barriers below 0.5 eV, while the other charge carriers exhibit significantly higher barriers. Nevertheless, it should be noted that these barriers are obtained for fixed geometry, which allows for accessing the interaction type and strength of the different charge carriers with the host structure. In an actual compound, the host structure can adapt to the ion’s movement, and consequently the barriers are likely to decrease. Interestingly, our results show significant differences in the activation barriers and site preferences of the different charge carriers. Notably, for most charge carriers the difference in energy between the tetrahedral and octahedral coordination, responsible for the respective site preference, contributes significantly to the overall migration barrier. In the following this contribution is referred to as the static part of the migration barrier. Furthermore, apart from the static barrier the transition state energy varies significantly for the various charge carriers which can be interpreted as the kinetic contribution to the overall barrier. Both contributions need to be taken into account to fully understand the ion migration. First, we will focus on the dominant static barriers described by the site preference of the respective ion. In fact, the ratio of the cation to the Se2− anion radii can be identified to exert a significant impact on the site preference. Large cations, such as Cs+, K+, and Ca2+, strongly favor octahedral coordination, whereas small ions like Zn2+ and Al3+ prefer a tetrahedral environment. On the other hand, Zn2+, Mg2+ and Li+ exhibit very similar ionic radii but Zn2+ favors the tetrahedral site significantly while Mg2+ only shows a slight tetrahedral site preference.
As already stated, the size of the charge carrier ions can be quantified by their ionic radii (Koettgen et al., 2020). However, these ionic radii are obtained by employing a set of assumptions, including independence of the structure type. Furthermore, an ionic radius can only be assigned correctly if the respective ion shows purely ionic interactions with its surrounding. Therefore, the standard values for ionic radii are not necessarily an ideal quantity to reflect the bonding situation for a certain ion in a particular structure. In order to get a better understanding of the true size of the charge carriers of interest in the spinel structure, the lattice constants for the full charge carrier spinels have been calculated. The obtained lattice constants and charge carrier selenium (A-Se) distances are given in Table 1. Indeed, the A-Se distances, which follow the same trend as the lattice constants, are in accordance with the site preference of the charge carriers observed in Figure 2. Here, the comparison between Mg2+ and Zn2+ is of particular interest. While the ionic radii are very similar for both ions, the actual A-Se distances are notably different. In fact, the Mg compound shows a significantly larger lattice constant and consequently larger A-Se distances. Furthermore, comparing the A-Se distances of Li+ and Mg2+ indicates that Li+ appears to be smaller and therefore an octahedral site preference for the Mg2+ ion should be expected. However, Mg2+ favors the tetrahedral site by about 0.2 eV. This points to the fact that apart from the dominating ion size, the charge and electronic structure additionally affect the site preference and therefore also the corresponding static contribution to the barriers. Nevertheless, if properly defined, the ion size strongly dominates the site preference and hence the resulting migration barriers. However, it has to be noted that all ASc2Se4 spinels, except for the Al and Zn spinel, show a certain degree of trigonal distortion that increases with the ion size. The trigonal distortion does not affect the coordination tetrahedron of the charge carrier “A” and only translates in a distortion of the coordination octahedron of the charge carrier “A” and the transition metal, respectively. This might have an influence on the lattice constant but leaves the A-Se distance essentially unaffected.
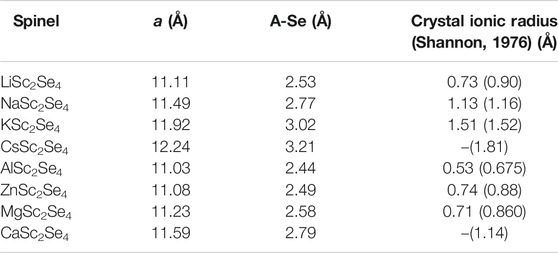
TABLE 1. Lattice constants a and charge carrier selenium distances A-Se of the ASc2Se4 spinel structures. Crystal ionic radii for the charge carriers in tetrahedral environment are listed (Cs and Ca are typically not observed in tetrahedral coordination). For comparison the values for octahedral environment are given in brackets.
As already mentioned, not only the cation size is a crucial parameter for the site preference and therefore for the static part of the migration barriers, but obviously also the charge of the respective ion plays a vital role. Indeed, ions of almost the same size but different charge, e.g., Li+ and Mg2+ or Na+ and Ca2+, differ significantly in their migration barrier. Higher charged ions show increased static contributions to the activation barriers for migration, which is mostly due to a significant energy difference between the tetrahedral and octahedral site. In order to understand the direct impact of the charge, it is necessary to obtain a better insight into the underlying interactions between the charge carriers and the surrounding anions. While most arguments are typically based on a fully ionic interaction between the charge carrier and the anion, many interactions actually have a considerable covalent component. To gain more insight into the chemistry of the A-X bonds, charge density difference plots have been created. The latter ones are obtained by subtracting both, the charge density of the isolated host structure and of the selected charge carrier from the charge density of the combined system. In order to illustrate the charge density differences, we have plotted isosurfaces for selected octahedral and tetrahedral environments in Figure 3. Moreover, Figure 4 depicts contour plots of the octahedrally coordinated sites, showing the plane connecting four atoms of the Se octahedron, as illustrated in panel A. Only the most stable sites at high charge carrier concentration are considered, i.e., the tetrahedral and octahedral sites. Areas of charge depletion are shown in blue, and areas of charge accumulation are shown in red. It should be noted that the appearance of the isosurface plots depends strongly on the selected isosurface level (see Supplementary Figure S1). To allow for comparison, the same isosurface value was chosen for all panels in Figure 3. The charge densities are slightly distorted and do not show the full octahedral symmetry. This is a consequence of the trigonal distortion of the MgSc2Se4 spinel which slightly displaces the Se atoms in front of and behind the plane depicted in Figure 4A. Li is known to show mostly ionic interaction in the spinel structure, as can be inferred from Figures 3A,B, 4B.
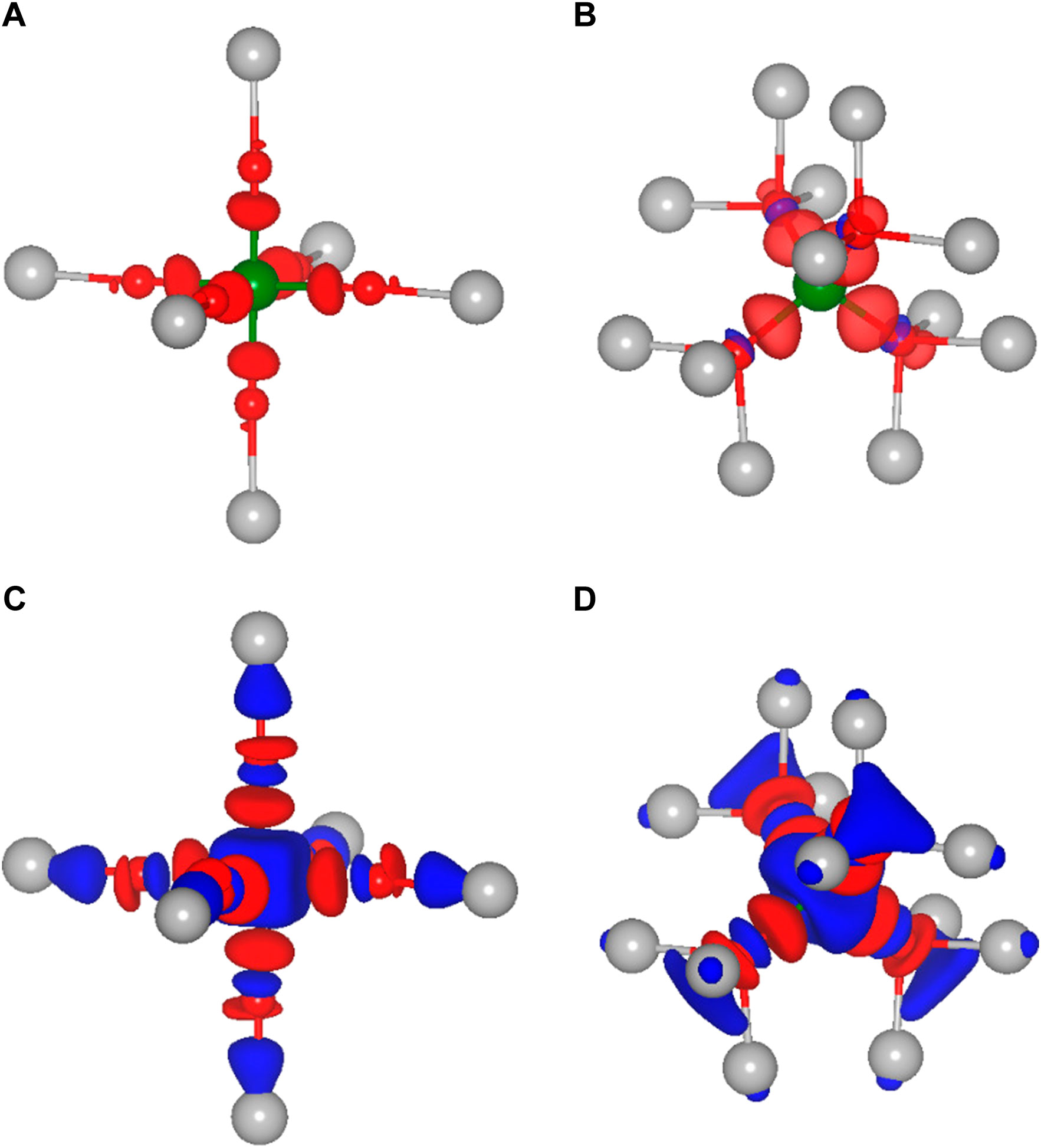
FIGURE 3. Isosurfaces of the charge density difference of MgSc2Se4 structures in side view with the charge carrier (A) Li, (C) Al in octahedral coordination and (B) Li, (D) Al in tetrahedral coordination. Areas of charge depletion are shown in blue and areas of charge accumulation are shown in red.
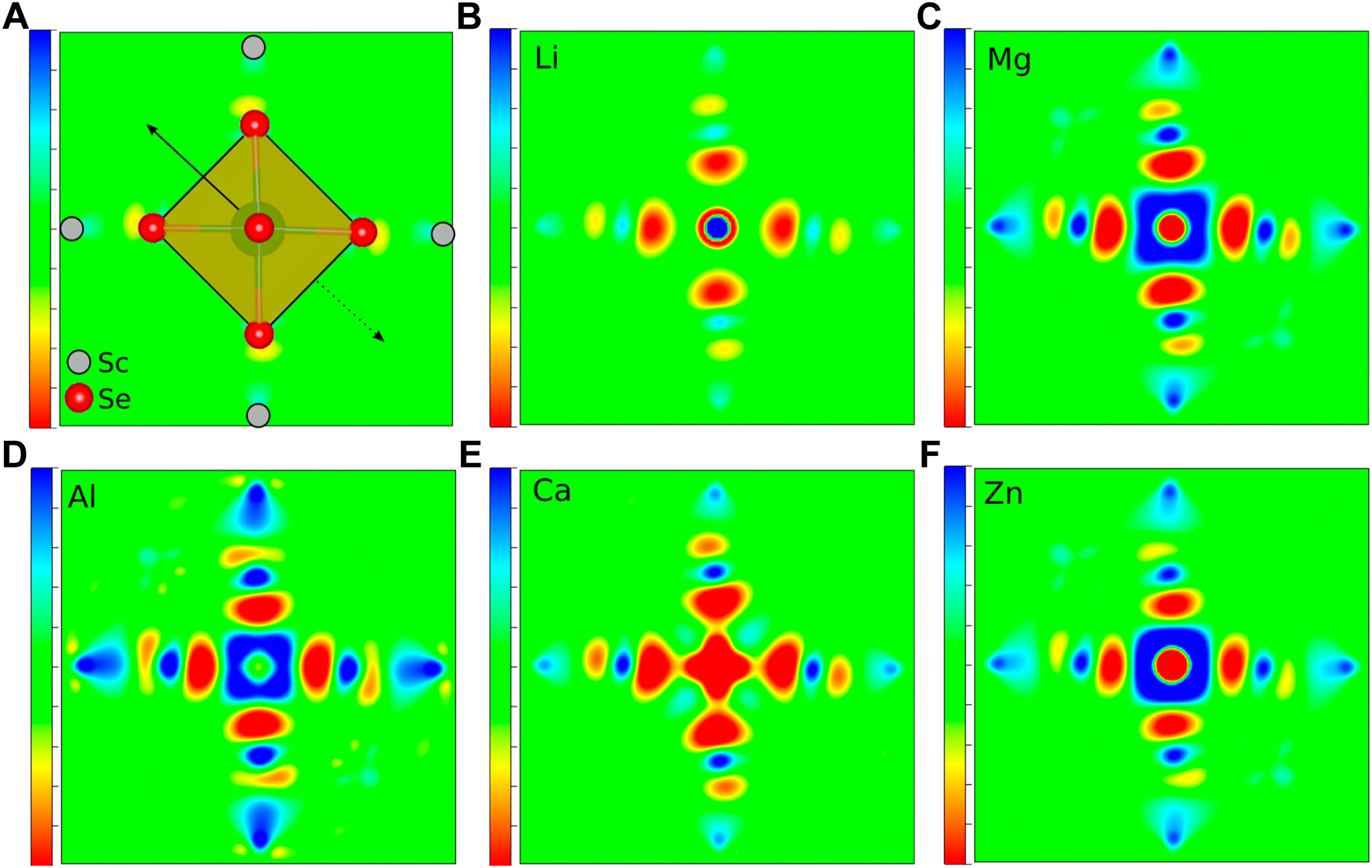
FIGURE 4. Charge density difference contour plots of MgSc2Se4 structures with (A) a schematic presentation, (B) Li, (C) Mg, (D) Al, (E) Ca, and (F) Zn atoms in octahedral coordination. Areas of charge depletion are shown in blue and areas of charge accumulation are shown in red. The solid arrow indicates the displacement of the upper Se atom, while the dashed arrow shows the opposing shift of the Se atom below the plane.
Furthermore, the other alkaline metals show charge density differences very similar to the one of Li (Supplementary Figures S2, S3), with the charge density difference for K being even further smeared out. These charge density difference plots show mostly ionic bonding for the alkaline metals at the octahedral site, however, with a possibly increasing covalent character for the larger and softer ions. These findings are essentially the same for the tetrahedral site, as shown for the case of Li in Figure 3B.
In the case of the divalent charge carriers Mg and Zn, the same slight distortion is visible, however, additional strong charge depletion is observed in the vicinity of the charge carriers, as depicted in Figures 4C, F. For Ca, the isosurfaces are qualitatively very similar to the other divalent ions (Supplementary Figure S4). However, the charge depletion areas are less pronounced in the plane depicted in the contour plot, such that only a slight charge depletion is visible inside the octahedron, shown in light blue in Figure 4E. For Al, even more pronounced charge depletion is present (see Figures 3C, D, 4D). The charge depletion in the vicinity of the octahedron center, as observed for the multivalent ions, may be associated with the formation of an ionic bond and a greater interaction strength with the host lattice. This results in an increased oxidation of the Se atoms of the coordination octahedron upon deintercalation of the charge carrier. Essentially the same trend in terms of charge depletion around the charge carrier position is seen for the tetrahedral site, meaning additional charge depletion in the tetrahedron center for multivalent ions.
Most importantly, for the charge carrier at the octahedral site, the multivalent ions cause a significant charge depletion in the vicinity of the Sc atom next to the octahedron corners, however, without changing the Sc oxidation state. At the same time, a corresponding charge accumulates close to the Se atoms of the coordination octahedron. Hence, this may be understood as a polarization of the charge density of the Sc-Se bond due to the presence of the charge carrier. In contrast to the multivalent charge carriers, the alkaline metals hardly polarize the charge distribution of the Sc-Se bond, and therefore, at the transition metal. This is best seen when comparing the 3D plots for Li and Al (see Figure 3). In the case of multivalent ions, the charge distribution at the transition metal is strongly changed when moving from octahedral to tetrahedral coordination (see Figures 3C, D), and the charge depletion distributes over the twelve Sc atoms neighboring the tetrahedral site. For Al, an additional charge depletion between each Se atom of the tetrahedron and its three neighboring Sc atoms is observed. In general, this means that for the multivalent ions a strong charge redistribution takes place when moving from tetrahedral to octahedral site. Indeed, this confirms the findings of Levi et al. (2009) and Emly and Van der Ven (2015), that the reduced multivalent ion mobility in the spinel structure is not only a consequence of the ionic interaction alone. Instead, the observed charge redistribution accompanied by rehybridization significantly increases the migration barriers.
Further understanding can be obtained from the partial density of states of the atoms divided into the respective s-, p- and d-components. The calculated density of states (DOS) for the investigated charge carriers on the octahedral and tetrahedral sites are shown in Figure 5. The filled valence band, which extends from −4 to 0 eV, is predominantly of Se-p character (red) with some contribution of Sc-d orbitals (blue). They represent the Sc-Se bonding states. The Sc-d states are located 1–4 eV above the valence band. The subfigures show the projected density of states for the migrating single-ion in the fixed framework. For the case of Li+, Figure 5A reveals a negligible contribution of the cation to the valence band, confirming the purely ionic character. The same is true for Na+ (see Supplementary Figure S5), whereas the other alkali metals show increasing contributions to the valence bands, confirming that the bonds become partially covalent. For instance, the DOS of K+ indeed reveals an increased covalency as already suggested by the charge density differences (see Figure 5B). The same trend is observed in the case of Cs+. Mg2+ on the other hand again shows only very small covalent contributions, while it increases for Ca2+, such that the covalent character seems to increase with the ion size. Interestingly, the DOS for K+ and Ca2+ show similar covalent contributions, while Na+ and Mg2+ are almost fully ionic, thus pointing to the impact of the chemical character for elements in the same row. A similar tendency is again observed for Al3+ and Zn2+ which are small in size and show almost no or only small covalent interaction, respectively. Furthermore, it is interesting to note that for Al3+ (Figure 5F) and Zn2+ (Figure 5E), the projected density of states of the migrating ion depends on the coordination number. The lower coordination number shifts the p-orbital contributions near the Fermi level downwards. This displacement of the states means that the tetrahedral sites show increased hybridization and stronger bonding compared to the octahedral sites. This electronic rearrangement contributes to the fact, that Zn2+ and Al3+ ions strongly favor tetrahedral coordination.
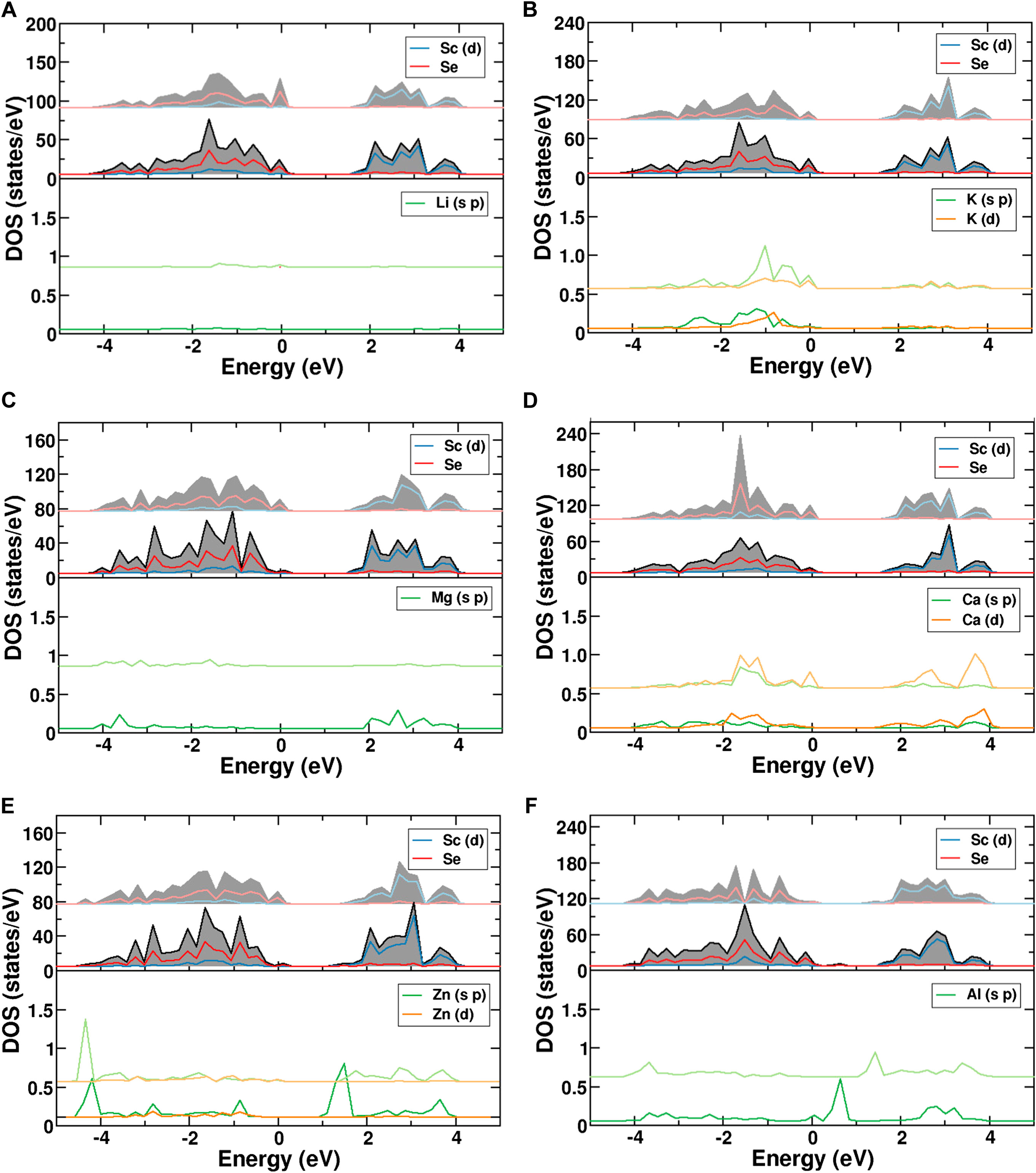
FIGURE 5. PDOS of MgSc2Se4 with (A) Li, (B) K, (C) Mg, (D) Ca, (E) Zn, and (F) Al atoms in octahedral and tetrahedral coordination. The DOS of the ion in tetrahedral coordination (light color) is shifted upwards relative to the DOS of the ion in octahedral coordination (dark color).
So far, we have focused on the site preference and the respective static barrier as the dominating part of the overall migration barrier. Yet, also the transition state dominated kinetic part contributes significantly to the overall migration barrier. As already mentioned earlier, the transition state constitutes a threefold coordination environment of the ion, making it the bottleneck of the migration. While readily describing the site preference, the ion size also shows a strong impact on the energy of the transition state. For the small ions Zn2+ and Al3+ the threefold coordination environment does not strongly influence the energetics of the ion migration and the difference between octahedral and tetrahedral site readily determines the overall barrier. The energy of the transition state of the other investigated charge carriers, with respect to the tetrahedral site energy, mostly increases with the size of the ion. However, further in‐depth examination of the transition state energy reveals that the charge and the electronic structure have a significant influence on the kinetic part of the migration barrier. Thus, relative to the tetrahedral site, Mg2+ and the much larger Na+ ions show similar transition state energies and so do Ca2+ and the much larger K+ and Cs+ ions.
In order to conclude our thorough study on the charge carrier mobility in the spinel structure, we compare our findings with the materials design rules for multivalent ion mobility developed by Rong et al. (2015). These guidelines state that high multivalent ion mobility is, in first order, determined by the site preference of the charge carrier. However, they conclude that the ion size described by the respective ionic radii is not a useful descriptor to estimate the ion mobility. Our findings strongly support the importance of the site preference for multivalent ion mobility, yet, show that a properly defined ion size actually is a good descriptor for the site preference. In addition, our findings indicate that multivalent ions show a certain degree of covalency, which causes rehybridization and charge redistribution along the migration path, resulting in increased overall migration barriers. Thus, the importance of the site preference remains undoubtful and is predominantly influenced by the ion size. Additionally, the ion size affects the transition state energy and thus small ions are favorable. At last the covalent character of the interactions increases the barriers and mostly ionic interaction is highly favorable. Comparing our results for the various charge carriers indicates that Zn2+ and Al3+ are of small size and only show very limited covalent character. Thus if the site preference of these charge carriers could be positively affected, e.g., by doping the Sc gate sites by other (transition) metals (Xiao et al., 2018), a high ion mobility for the Zn2+ ion seems possible.
Conclusion
In this work, we have investigated the migration barriers for various mono and multivalent ions (Li+, Na+, K+, Cs+, Zn2+, Ca2+, and Al3+) in the spinel‐type MgSc2Se4 phase. We find that both the size and the charge of the cations strongly influence the height of the migration barriers. However, our findings indicate that crystal ionic radii are not suitable to describe the ion size in the spinel structure, instead A-Se distances are suggested for a more accurate description. Using this descriptor, the ion size is found to determine the site preference of the ion and the resulting diffusion barrier in first order. However, the transition state energy is also influenced by the ion size, but here the impact of the charge and bonding characteristics appears to be more pronounced. Indeed, calculated charge density distributions and electronic densities of state reveal the essence of the bonding character which is necessary to be taken into account to fully understand the migration barriers. We find that Li+ and Na+ are purely ionic in this framework, while other ions show different degrees of partially covalent bonding. Our results indicate that the ion size, when properly defined, indeed can be applied to estimate the order of the migration barriers in the spinel structure. Nevertheless, an in‐depth understanding can only be obtained when the influence of the charge and the electronic structure are incorporated. Thus, the simple concept of purely ionic charge carriers only yields limited understanding of the multivalent ion migration in the spinel structure, additionally rehybridization and the charge density redistribution that modify the migration barriers need to be considered. Furthermore, our results indicate that tuning the site preference of Zn2+ could lead to superior ion mobility in the spinel structure. Specifically, we shed light on the role of the ionic size, the charge and the bonding character of the mobile ions. Therefore, our calculations identified factors that are applicable to fast ion migration in a broad range of energy storage techniques.
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.
Author Contributions
MD performed the bulk of the DFT calculations, additional calculations were performed by MS who was also instrumental in the analysis of the computational output. AG designed and together with HE supervised the project. MD, MS, and HE wrote the first version of the manuscript. All authors revised the manuscript, and read and approved the submitted version.
Funding
Computer time provided by the state of Baden-Württemberg through the bwHPC project and the German Research Foundation (DFG) through grant no INST 40/467-1 FUGG (JUSTUS cluster) is gratefully acknowledged. This work contributes to the research performed at Center for Electrochemical Energy Storage Ulm-Karlsruhe (CELEST) and was funded by the German Research Foundation (DFG) under Project ID 390874152 (POLiS Cluster of Excellence).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
MD thanks Sung Sakong and Mohnish Pandey for fruitful discussions.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2020.584654/full#supplementary-material
References
Aurbach, D., Cohen, Y., and Moshkovich, M. (2001). The study of reversible magnesium deposition by in situ scanning tunneling microscopy. Electrochem. Solid State Lett. 4, A113. doi:10.1149/1.1379828
Bayliss, R. D., Key, B., Sai Gautam, G., Canepa, P., Kwon, B. J., Lapidus, S. H., et al. (2019). Probing mg migration in spinel oxides. Chem. Mater. 32 (2), 663–670. doi:10.1021/acs.chemmater.9b02450
Blöchl, P. E. (1994). Projector augmented-wave method. Phys. Rev. B 50, 17953–17979. doi:10.1103/physrevb.50.17953
Canepa, P., Bo, S. H., Gautam, G. S., Key, B., Richards, W. D., Shi, T., et al. (2017a). High magnesium mobility in ternary spinel chalcogenides. Nat. Comm. 8, 1–8. doi:10.1038/s41467-017-01772-1
Canepa, P., Sai Gautam, G., Hannah, D. C., Malik, R., Liu, M., Gallagher, K. G., et al. (2017b). Odyssey of multivalent cathode materials: open questions and future challenges. Chem. Rev. 117, 4287–4341. doi:10.1021/acs.chemrev.6b00614
Elia, G. A., Marquardt, K., Hoeppner, K., Fantini, S., Lin, R., Knipping, E., et al. (2016). An overview and future perspectives of aluminum batteries. Adv. Mater. 28 (35), 7564–7579. doi:10.1002/adma.201601357
Emly, A., and Van der Ven, A. (2015). Mg intercalation in layered and spinel host crystal structures for mg batteries. Inorg. Chem. 54, 4394–4402. doi:10.1021/acs.inorgchem.5b00188
Euchner, H., Chang, J. H., and Groß, A. (2020). On stability and kinetics of Li-rich transition metal oxides and oxyfluorides. J. Mater. Chem. 8, 7956–7967. doi:10.1039/d0ta01054e
Groß, A. (2018). Fundamental challenges for modeling electrochemical energy storage systems at the atomic scale. Top. Curr. Chem. 376, 17. doi:10.1007/s41061-018-0194-3
Hohenberg, P., and Kohn, W. (1964). Inhomogeneous electron gas. Phys. Rev. 136, B864–B871. doi:10.1103/PhysRev.136.B864
Hörmann, N. G., Jäckle, M., Gossenberger, F., Roman, T., Forster-Tonigold, K., Naderian, M., et al. (2015). Some challenges in the first-principles modeling of structures and processes in electrochemical energy storage and transfer. J. Power Sources 275, 531–538. doi:10.1016/j.jpowsour.2014.10.198
Jäckle, M., Helmbrecht, K., Smits, M., Stottmeister, D., and Groß, A. (2018). Self-diffusion barriers: possible descriptors for dendrite growth in batteries?. Energy Environ. Sci. 11 (12), 3400–3407. doi:10.1039/C8EE01448E
Kim, C., Phillips, P. J., Key, B., Yi, T., Nordlund, D., Yu, Y.-S., et al. (2015). Direct observation of reversible magnesium ion intercalation into a spinel oxide host. Adv. Mater. 27, 3377–3384. doi:10.1002/adma.201500083
Koettgen, J., Bartel, C. J., and Ceder, G. (2020). Computational investigation of chalcogenide spinel conductors for all-solid-state mg batteries. Chem. Commun. 56, 1952–1955. doi:10.1039/c9cc09510a
Kohn, W., and Sham, L. J. (1965). Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, A1133–A1138. doi:10.1103/PhysRev.140.A1133
Kresse, G., and Furthmüller, J. (1996). Efficient iterative schemes forab initiototal-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186. doi:10.1103/PhysRevB.54.11169
Kresse, G., and Hafner, J. (1993). Ab initiomolecular dynamics for liquid metals. Phys. Rev. B 47, 558–561. doi:10.1103/PhysRevB.47.558
Kresse, G., and Joubert, D. (1999). From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775. doi:10.1103/PhysRevB.59.1758
Kulish, V. V., Koch, D., and Manzhos, S. Aluminium and magnesium insertion in sulfur-based spinels: a first-principles study (2017). Phys. Chem. Chem. Phys. 19, 6076–6081. doi:10.1039/c6cp08284j
Levi, E., Levi, M. D., Chasid, O., and Aurbach, D. A review on the problems of the solid state ions diffusion in cathodes for rechargeable Mg batteries (2009). J. Electroceram. 22, 13–19. doi:10.1007/s10832-007-9370-5.
Liu, M., Jain, A., Rong, Z., Qu, X., Canepa, P., Malik, R., et al. (2016). Evaluation of sulfur spinel compounds for multivalent battery cathode applications. Energy Environ. Sci. 9, 3201–3209. doi:10.1039/c6ee01731b
Liu, M., Rong, Z., Malik, R., Canepa, P., Jain, A., Ceder, G., et al. (2015). Spinel compounds as multivalent battery cathodes: a systematic evaluation based on ab initio calculations. Energy Environ. Sci. 8, 964–974. doi:10.1039/c4ee03389b
Matsui, M. (2011). Study on electrochemically deposited mg metal. J. Power Sources 196, 7048–7055. doi:10.1016/j.jpowsour.2010.11.141
Perdew, J. P., Burke, K., and Ernzerhof, M. (1996). Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868. doi:10.1103/PhysRevLett.77.3865.
Rong, Z., Malik, R., Canepa, P., Sai Gautam, G., Liu, M., Jain, A., et al. (2015). Materials design rules for multivalent ion mobility in intercalation structures. Chem. Mater. 27, 6016–6021. doi:10.1021/acs.chemmater.5b02342
Shannon, R. D. (1976). Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta. Cryst. A32, 751–767. doi:10.1107/s0567739476001551
Sheppard, D., Terrell, R., and Henkelman, G. (2008). Optimization methods for finding minimum energy paths. J. Chem. Phys. 128, 134106. doi:10.1063/1.2841941
Stottmeister, D., and Groß, A. (2020). Strain dependence of metal anode surface properties. ChemSusChem 13, 3147–3153. doi:10.1002/cssc.202000709
Sun, X., Bonnick, P., Duffort, V., Liu, M., Rong, Z., Persson, K. A., et al. (2016). A high capacity thiospinel cathode for mg batteries. Energy Environ. Sci. 9, 2273–2277. doi:10.1039/c6ee00724d
Wang, L. P., Zhao-Karger, Z., Klein, F., Chable, J., Braun, T., Schür, A. R., et al. (2019). MgSc 2 Se 4 -A magnesium solid ionic conductor for all-solid-state Mg batteries?. ChemSusChem 12, 2286–2293. doi:10.1002/cssc.201900225
Xiao, W., Xin, C., Li, S., Jie, J., Gu, Y., Zheng, J., et al. (2018). Insight into fast Li diffusion in Li-excess spinel lithium manganese oxide. J. Mater. Chem. 6, 9893–9898. doi:10.1039/c8ta01428k
Keywords: electrochemical energy storage, batteries, multivalent ions, ion mobility, ion radius, spinel, computational chemistry, density functional theory
Citation: Dillenz M, Sotoudeh M, Euchner H and Groß A (2020) Screening of Charge Carrier Migration in the MgSc2Se4 Spinel Structure. Front. Energy Res. 8:584654. doi:10.3389/fenrg.2020.584654
Received: 17 July 2020; Accepted: 15 September 2020;
Published: 22 October 2020.
Edited by:
Kai S. Exner, Sofia University, BulgariaReviewed by:
Syed Muhammad Alay-e-Abbas, Government College University Faisalabad, PakistanSang Kyu Kwak, Ulsan National Institute of Science and Technology, South Korea
Copyright © 2020 Gross, Dillenz, Sotoudeh and Euchner. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Axel Groß, YXhlbC5ncm9zc0B1bmktdWxtLmRl
 Manuel Dillenz
Manuel Dillenz Mohsen Sotoudeh
Mohsen Sotoudeh Holger Euchner
Holger Euchner Axel Groß
Axel Groß