Power Sharing in Island Microgrids

The growth of local renewable energy sources and heavy loads in power distribution networks, such as the increasing electric vehicles charging stations, causes several issues with a direct impact on the stability of the electrical grid. An attempt to overcome such issues is the microgrid concept, which has the grid structured into local sub-grids that manage their power and energy balancing. A microgrid may operate connected or disconnected from the main grid, being dynamically necessary to guarantee a power balancing between local loads and sources. Furthermore, as several power units are connected to the same microgrid, equity is also required in terms of power sharing. Current work explores a scenario of an island operation of a microgrid with multiple sources, including battery storage systems and sharing power with multiple loads, including electric vehicle chargers, a scenario appropriated to a city grid. A local control solution for a stable operation of the microgrid in terms of both power balancing and power sharing is presented and validated through numerical and experimental results.

1 Introduction

Nowadays, the energy market is experiencing disruption with an increase of distributed and local energy sources as well as with the emergence of local high demanding loads, e.g., electric vehicles (EV) chargers. In accordance with Eurostat (2020c), the energy industry is the sector with the higher net reduction of greenhouse gas emissions, with a reduction of around 500 million tons of ${\text{CO}}_2$, which corresponds to a $30\text{\%}$ reduction in 27 years. This achievement is due to the increase in the penetration of renewable energy sources in the European Union (EU). Specifically, the share of renewable energy almost doubled between 2004 and 2018, Eurostat (2020b).

Contrary to the energy sector, the transportation sector is still increasing its greenhouse emissions, and the increase is of around $30\text{\%}$. Nevertheless, the number of electric and hybrid electric cars registered in the EU is rising, with an exponential increase of around $600\text{\%}$ in 5 years Eurostat (2020a). Globally, this exponential growth trend is visible in the 2018 IEA global EV outlook, where the yearly growth between 2016 and 2017 is over $50\text{\%}$.

The growth of local renewable energy sources and heavy loads in power distribution networks, such as the increasing electric vehicles chargers, causes several issues with a direct impact on the stability of the electrical grid. The microgrid concept is one approach to overcome such issues. The main idea behind microgrids is to have the electrical grid divided into sub-grids, each of them with power and management systems (also known as nanogrids Burmester et al. (2017)). The microgrid should be able to operate in grid-connected or in island mode Hatziargyriou (2013), where the latter requires having an Energy Storage System (ESS). These systems comprise a primary storage unit (e.g., battery, fly-wheel, fuel cell, diesel-battery, etc.) and a bi-directional power converter. The capacity on such systems must allow the microgrid either to supply all loads or adopt demand flexibility, e.g., managing to take out of service non-important loads.

The paper addresses a control strategy to ensure proper power sharing among several bi-directional power converters that interface the power sources with the microgrid. In a microgrid, it is dynamically necessary to adapt the power flow toward equity in terms of power sharing to maximize the overall available power to fulfill the load power demand.

The power sharing issue has been addressed in the literature, as reviewed in Han et al. (2016); Rokrok et al. (2018). The methods are divided into two major classes: communication-based or distributed methods (droop based). In communication-based methods, high reliability and redundant communication links between all converters are required and also high-bandwidth control loops. The communication-based methods offer the advantages of tight current sharing, high power quality, fast transient response, and reduction of circulating currents. But it has the disadvantages of being hard to expand the microgrid, owing to the communications strategy the need to have a full overview of the electric network, and the physical communication link costs. The distributed methods, normally based on droop control, allow a fully distributed and redundant strategy that uses local measurements of the electric network state variables, with several advantages in terms of expandability, modularity, flexibility, and redundancy. Distributed control disadvantages include circulation currents between converters, frequency and amplitude deviations, and slow transient response. Additionally, as highlighted in Tayab et al. (2017), some disadvantages of the conventional droop method is also the poor sharing of harmonics caused by non-linear loads, line impedance mismatch between parallel converters (affects active and reactive power sharing), and poor performance of renewable energy resources (operation deviance from MPPT). Hence in the last years, there were several improvement suggestions to the conventional droop method to overcome some of the mentioned issues. The following literature revision includes different approaches toward load power sharing in islanded microgrids including droop control.

To overcome the power-sharing problem due to mixed line impedance (R and X), a transformation matrix was proposed in De Brabandere et al. (2007); Wu et al. (2016) to obtain a virtual power frame allowing decoupled power droop control. Though the presented method requires to know the line $X/R$ ratio. The authors also suggest adding a virtual impedance to turn the line impedance predominantly inductive or resistive, allowing an accurate and decoupled power sharing between parallel converters and simultaneously being able to add droop control to voltage harmonics. The suggested approach presents good results, though it requires previous knowledge of the line impedance ratio ($X/R$) for the correct power decoupling. On the other hand, virtual impedance can be majored to guarantee power decoupling under uncertain line impedance knowledge but will affect the local grid nominal voltage and frequency. The virtual impedance method is also explored in DC microgrids Gu et al. (2015) where the virtual impedance is adjusted to coordinate the power sharing between different nature power sources. The same author also explores the use of the common DC bus voltage to communicate with other connected units by regulating the DC bus voltage amplitude accordingly with the increase or decrease in power demand-C bus signaling (DBS) Gu et al. (2014).

Since conventional droop is based on the behavior of the synchronous generator, some authors explored the virtual synchronous generators Zhong (2016); Ma et al. (2017) (also known as synchronverter or virtual synchronous machine). The method consists of controlling the power converter to mimic the synchronous machine behavior, mostly due to the kinetic energy stored in the rotational mass. In this control technique, the virtual machine friction behaves as the $P-f$ droop coefficient therefore only reactive power droop needs to be added. Despite this, in D’Arco and Suul (2014); Renjit et al. (2016), it is shown that adding a low pass filter to the active power droop is equivalent to adding the virtual inertia of the synchronous generator, and droop curves coefficients can thus be tuned to perform similarly with the virtual synchronous generator and present the same advantages. The virtual synchronous generator operates as a voltage source, and the inverter output voltage (at $LCL$ or $LC$ capacitance) must therefore be regulated and synced with the microgrid voltage before the converter connection. In Zhong et al. (2014); Ramezani and Li (2018), techniques that allow the converters to pre-sync are explored, but it becomes clear that such approaches demand extra voltage sensors and additional control loops. On the other hand, current-controlled converters are by their principle of work synced with the grid, which simplifies the connection with the grid, though the grid must be already formed for its operation (do not present voltage forming capability). Another important aspect to highlight in the virtual synchronous generator operation is the fact that similarly with the droop only methods, a virtual inductance is required to be added in the control loop for proper power decoupling.

Since electric storage systems are needed, to add inertia to the microgrid system, some authors also explored modified (or adaptive) droop techniques that better fit with storage systems. In Zhang (2017), a capacity-based adaptive active power droop is proposed to increase the participation of storage units with higher energy flexibility ($SoC\approx 50\%$). To achieve this, the authors suggest adding an extra term to the droop curve that modifies the droop curve slope accordingly with a constant $k_{\text{cap}}$. This approach lacks information on how to determine the extra droop constant, and the results are limited to the method behavior during microgrid operation mode transition to island mode. In Urtasun et al. (2015) it is discussed two different approaches for modifying the conventional droop curve with the storage system $SoC$: slope shift or curve displacement, where the second is suggested as the best alternative since it allows a decoupled droop tuning. Furthermore, in Urtasun et al. (2015); Sun et al. (2017), the curve displacement method droop control is presented, allowing us to balance the $SoC$ of different storage systems connected in parallel. The authors also show that the method can successfully balance the $SoC$ and simultaneously share the active and reactive power. Despite this, what remains unclear are how we should properly set the $SoC$ droop gain ($k_{SoC}$) and what its impact on the $SoC$ balancing and power sharing dynamics is.

The solution proposed in this work is based on droop control with virtual inertia and AC bus signaling applied to electric storage systems connected to the grid. The solution considers a single converter operating in grid-forming (voltage-controlled) and “n” converters operating in grid-supporting (current-controlled). The grid-forming converter adjusts and regulates the microgrid voltage amplitude and frequency accordingly with an adaptive $P/SoC-V$ and $Q-\omega$ droop characteristic. The grid-supporting converters operate with the adaptive $V-P/SoC$ and $\omega -Q$ droops by adjusting their output power. The presented method allows to fulfill the load power demand with minimal transients and simultaneously to share that power with other parallel converters in steady state with minor AC bus voltage amplitude and frequency deviance (within EN 50438 limits). The adaptive $V-P/SoC$ droop presented in this paper also guarantees a steady state $SoC$ balancing of the different electric storage systems, maximizing the power availability of the parallel converters. Contrary to some other methods found in the state of the art, the presented method exploits the voltage change caused by the droop control, i.e., the droop is designed to ensure a certain maximum voltage amplitude and frequency variation, and no voltage restoration loop is desired. This way, any converter connected to the microgrid has information about the microgrid power needs through the voltage and frequency observation. This approach also allows a systematic design of the droop controllers, where droop gains are intrinsically set based on the converter power rating, battery capacity, and desired voltage variation.

The paper is structured into six sections. In Section 2 we present the theory supporting the approach, namely, discussing the power sharing and system inertia challenges. In Section 3 we identify the operation modes of power converters, focusing on control loops and droop curves characteristics either for the grid-forming and grid-supporting converters. In Section 4 we present the simulation and experimental results to validate the proposed solution along with the respective discussion. Conclusions are presented in the last section along with proposed future work.

2 Active and Reactive Power in Power Systems

The active and reactive power influence in the grid voltage can be demonstrated through the classic power flow between two voltage sources $V_m$ and $V_g$, and an impedance $R+j\omega L$Eq. 1 Rocabert et al. (2012); Moradi et al. (2016). For small power angles ($\cos \delta \approx 1$) and a pure inductive line, Eq. 1 is simplified into Eq. 2 or Eq. 3 when a pure resistive line is considered. Noteworthy that when considering the synchronous machine as one of the sources, the line accounts also with the magnetizing and leakage machine windings inductances, and the impedance nature is thus mostly inductive.

$\begin{array}{c}P=\frac{R{V}_i^2-R{V}_i{E}_g\cos \left(\delta \right)+X{V}_i{E}_g\sin \left(\delta \right)}{{\left|Z\right|}^2},\\ Q=\frac{-R{V}_i{E}_g\sin \left(\delta \right)+X{V}_i^2-X{V}_i{E}_g\cos \left(\delta \right)}{{\left|Z\right|}^2}.\end{array}(1)$

$\begin{array}{l}Z=X:\\ P=\frac{V_i{E}_g}{X}\delta ,\\ Q=\frac{V_i}{X}\left(V_i-E_g\right).\end{array}(2)$

$\begin{array}{l}Z=R:\\ P=\frac{V_i}{R}\left(V_i-E_g\right),\\ Q=-\frac{V_i{E}_g}{R}\delta .\end{array}(3)$

Eqs. 2, 3 show that there is a decoupled relationship between $P-\delta$, $Q-V$ for inductive lines and $P-V$, $Q-\delta$ for resistive lines. Taking into account that power angle change is caused by a speed variation (${\omega }_n-\omega$), the following droop curves are obtained Eqs. 4 5.

$\begin{array}{l}Z=X:\\ P_o=P-k_P\left({\omega }_n-\omega \right),\\ Q_o=Q-k_Q\left(V_i-E_g\right).\end{array}(4)$

$\begin{array}{l}Z=R:\\ P_o=P-k_P\left(V_i-E_g\right),\\ Q_o=Q+k_Q\left({\omega }_n-\omega \right).\end{array}(5)$

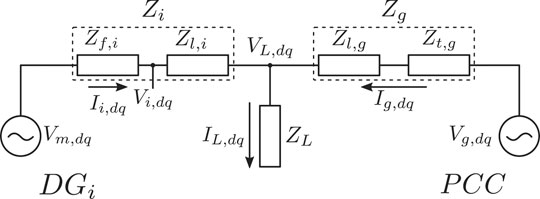
Following the previous analysis, it is important to highlight that the power decoupling is highly dependent on the impedance nature between both voltage sources. Taking Figure 1 as a reference, it is possible to highlight how to use the different power decouple equations in the same scenario. Assuming that the filter impedance of the distributed generation unit $D{G}_i$ and the respective line impedance present the following relationship, $\left(Z_{f,i}=X\right)\gg \left(Z_{l,i}=R\right)$ and $Z_g=0$, two scenarios can be considered:

1.Voltage controlled at $V_m$: in this case the resulting impedance $Z_i$ is dominated by $Z_{f,i}=X$, accounting for power flow respect Eq. 2 and droop curves Eq. 4;

2.Voltage controlled at $V_i$: the resulting impedance is $Z_{l,i}$ and the power flow Eq. 3 and droop curves Eq. 5 are applied.

FIGURE 1

FIGURE 1. Equivalent model of parallel converters.

In steady state, a synchronous machine (SM) without pole saliency can be represented by its Thevenin equivalent, i.e., a voltage source with a series inductance Kundur et al. (1994). The equivalent AC voltage source amplitude is controlled by the DC field generated by the exciter, while frequency follows the swing equation or rotational equation of motion Eq. 6 Zhang et al. (2019). In Eq. 6$P_m$ is the prime mover power, $P_e$ the electric power, J the moment of inertia, D the damping, δ the power angle, and ${\omega }_n$ and ${\omega }_m$ the nominal and prime mover frequencies. In the Thevenin equivalent, the series inductance represents the stator windings, where normally resistance is neglected. When the synchronous machine is connected to another voltage source (e.g., grid or microgrid) the power angle between both sources results in an active power flow between both sources (as earlier discussed). The source of energy that flows between the generator and the grid is provided by the kinetic energy stored in the rotating mass and the prime mover.

$\{\begin{array}{l}J\frac{\partial {\omega }_m}{\partial t}=\frac{P_m}{{\omega }_m}-\frac{P_e}{{\omega }_m}-D\left({\omega }_m-{\omega }_n\right),\\ \frac{\partial \delta }{\partial t}={\omega }_m-{\omega }_n.\end{array}(6)$

The power converter is normally a voltage-source converter (VSC), and it can therefore also be seen by its Thevenin equivalent circuit, which is similar to the SM (a voltage source with a series inductance). The inductance in the VSC is added to filter the current harmonics produced by the semi-conductor switching and thus also reduces the harmonics distortion introduced in the grid. The VSC voltage amplitude and frequency are both controlled by the converter modulation scheme (conventionally a sinusoidal PWM). There are therefore no constraints in the frequency rate of change imposed by the VSC hardware (it is an inertialess system). To introduce inertia and mimic the SG behavior, the VSC control loops must integrate the swing equation and reactive power droop (as in the SG case). The control loop adds inertia virtually but allows the manipulation of the virtual system in ways that cannot be accomplished in an SG, e.g., dynamically change the inertia of the system as suggested in Saxena et al. (2020). There are no rotating parts in the VSC hence, active power is supplied by the energy stored in the DC bus capacitance and interconnected sources.

In the scope of modern low voltage island microgrids, the intrinsic behavior of traditional power systems is not necessarily observed. The power converters interface with all sorts of sources (including rotational ones), and synchronous machines are therefore not directly connected to the grid. In this case, the active and reactive power sharing should be addressed considering the line impedance, converter dynamics, and the respective control loops.

2.1 Steady State Analysis of Parallel Sources

To understand the impact of load changes in the voltage and currents flowing in the local grid, Figure 1 is considered. In the Figure, a converter operating in grid-feeding ($D{G}_i$) and a voltage source forming the grid at $PCC$ (either the main grid or a converter) are illustrated. Furthermore, analysis is based on steady-state or slow transients since current derivatives are considered null.

Assuming that $I_{i,\text{d}q}$ is controlled (and constant in this analysis), it can be concluded that load changes are compensated by the $PCC$ source Eq. 7. The load voltage can be determined by the $PCC$ voltage and current Eq. 8, and load change therefore has a direct impact on load voltage: $\left|\Delta V_{L,dq}\right|\propto \left|\Delta I_{g,dq}\right|=\left|\Delta I_{L,dq}\right|$Eq. 9.

$\{\begin{array}{c}{I}_{L,dq}=I_{i,dq}+I_{g,dq},\\ \left|\Delta I_{L,dq}\right|=\left|\Delta I_{g,dq}\right|,\Delta I_{i,dq}=0.\end{array}(7)$

$\left[\begin{array}{c}{V}_{L,d}\\ V_{L,q}\end{array}\right]=\left[\begin{array}{c}{V}_{g,d}\\ V_{g,q}\end{array}\right]-\left[\begin{array}{cc}{R}_g& -X_g\\ X_g& R_g\end{array}\right]\left[\begin{array}{c}{I}_{g,d}\\ I_{g,q}\end{array}\right].(8)$

$\left[\begin{array}{c}{V}_{L,d}+\Delta V_{L,d}\\ V_{L,q}+\Delta V_{L,q}\end{array}\right]=\left[\begin{array}{c}{V}_{g,d}\\ V_{g,q}\end{array}\right]-\left[\begin{array}{cc}{R}_g& -X_g\\ X_g& R_g\end{array}\right]\left[\begin{array}{c}{I}_{g,d}+\Delta I_{L,d}\\ I_{g,q}+\Delta I_{L,q}\end{array}\right]\iff \left[\begin{array}{c}\Delta V_{L,d}\\ \Delta V_{L,q}\end{array}\right]=\left[\begin{array}{cc}{R}_g& -X_g\\ X_g& R_g\end{array}\right]\left[\begin{array}{c}\Delta I_{L,d}\\ \Delta I_{L,q}\end{array}\right],(9)$

The current flowing in the $D{G}_i$ branch is dependent in the modulation voltage of the converter $V_{m,\text{d}q}$ and the sensed output voltage $V_{i,\text{d}q}$, which is also dependent in the voltage drop across the line (constant due to constant $I_{i,\text{d}q}$) and the load voltage $V_{L,\text{d}q}$Eq. 10. When $V_{L,\text{d}q}$ changes with $\text{Δ}{I}_{g,\text{d}q}$, $V_{m,\text{d}q}$ and $V_{i,\text{d}q}$ thus also change in the same proportion. The converter can thus sense load voltage variations Eq. 11.

$\left[\begin{array}{c}{I}_{i,d}\\ I_{i,q}\end{array}\right]=\left[\begin{array}{cc}\frac{R_{f,i}}{Z_{f,i}^2}& \frac{X_{f,i}}{Z_{f,i}^2}\\ -\frac{X_{f,i}}{Z_{f,i}^2}& \frac{R_{f,i}}{Z_{f,i}^2}\end{array}\right]\left[\begin{array}{c}{V}_{m,d}-V_{i,d}\\ V_{m,q}-V_{i,q}\end{array}\right].(10)$

$\begin{array}{l}\left[\begin{array}{c}\text{Δ}{I}_{i,d}\\ \text{Δ}{I}_{i,q}\end{array}\right]=\left[\begin{array}{cc}\frac{R_{f,i}}{Z_{f,i}^2}& \frac{X_{f,i}}{Z_{f,i}^2}\\ -\frac{X_{f,i}}{Z_{f,i}^2}& \frac{R_{f,i}}{Z_{f,i}^2}\end{array}\right]\left[\begin{array}{c}\text{Δ}{V}_{m,d}-\text{Δ}{V}_{i,d}\\ \text{Δ}{V}_{m,q}-\text{Δ}{V}_{i,q}\end{array}\right]\iff \\ \iff \left[\begin{array}{c}\text{Δ}{I}_{i,d}\\ \text{Δ}{I}_{i,q}\end{array}\right]=0\iff \left[\begin{array}{c}\text{Δ}{V}_{m,d}\\ \text{Δ}{V}_{m,q}\end{array}\right]=\left[\begin{array}{c}\text{Δ}{V}_{i,d}\\ \text{Δ}{V}_{i,q}\end{array}\right]\left(=\left[\begin{array}{c}\text{Δ}{V}_{L,d}\\ \text{Δ}{V}_{L,q}\end{array}\right]\right).\end{array}(11)$

During load transients significantly faster than converter current control bandwidth, converter modulation voltage $V_{m,\text{d}q}$ becomes constant instead of the converter current $I_{i,\text{d}q}$. In this case, the load is still sensed by the converter Eq. 12, and it is partially compensated by the power converter.

$\left[\begin{array}{c}\Delta I_{i,d}\\ \Delta I_{i,q}\end{array}\right]=\left[\begin{array}{cc}\frac{R_i}{Z_i^2}& \frac{X_i}{Z_i^2}\\ -\frac{X_i}{Z_i^2}& \frac{R_i}{Z_i^2}\end{array}\right]\left[\begin{array}{c}-\Delta V_{L,d}\\ -\Delta V_{L,q}\end{array}\right].(12)$

Taking into account previous analysis and considering n converters connected at $V_{L,\text{d}q}$ node (neglecting line impedances), there are three important characteristics to highlight:

1. To share the load power it is necessary to know the PCC current;

2. Converter PLL does not allow us to track power angle change since each converter is synchronized with $V_{i,\text{d}q}$ ($V_{i,q}=0$) through a PLL, and changes in quadrature load voltage $V_{L,q}$ (considering PCC as the reference node) are consequently hardly discriminately sensed‐a change of $V_{L,q}$ in the steady state is sensed as a change in $V_{i,d}$ by the power converter;

3. Since load voltage is equally sensed by each converter, information about how many converters are connected would be required for proper load sharing.

To overcome the described issues, droop control is included in each converter control loop considering resistive line impedance, i.e., $P-V$ and $Q-\omega$. Hence voltage source at PCC regulates the output voltage amplitude and frequency depending on the active and reactive power measurements respectively. Such voltage regulation allows to qualitatively inform connected converters, operating as current sources (current-controlled), of the voltage source converter instantaneous power. The fact of using frequency as signaling for the instantaneous reactive power allows to overcome the issue in the power angle detection since the frequency is measurable by the PLL. In next Section 3 we describe the control loops for each converter.

3 Grid-Forming and Grid-Support Operation Modes

Addressing the problems discussed in previous sections, we present a power-sharing control strategy based on both droop and AC bus signaling. The strategy consists of a converter operating as grid-forming responsible for grid generation and n slave converters that participate in the grid stability (operating in grid-support). The method resembles the master-slave approach, where a single unit generates references to the slave units. Though in this case there are no communications evolved and instead droop curves are designed to transmit the microgrid power needs, i.e., through AC bus signaling.

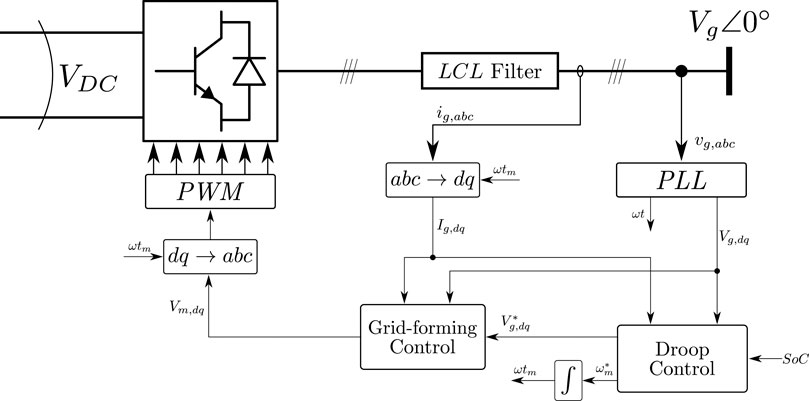
The grid-forming converter generates the microgrid voltage based on internal references ($V_n$ and ${\omega }_n$) and supplies the fast load’s transient power. The grid-forming converter, based on its instantaneous output active and reactive power, regulates the generated voltage and frequency following a droop curve $\left(P-V,Q-\omega \right)$. The change in microgrid voltage amplitude and frequency allows signaling the grid-support converters. The converters operating in grid-support, regulate its active and reactive power based on the measured grid voltage and frequency ($V-P,\omega -Q$ droops). The converters have regulated current/voltage at its output, and the adopted droop characteristic is therefore based on the low voltage line impedance Eq. 5, which is mainly resistive accordingly with cable impedance data available in ABB SACE (2004).

3.1 Grid-forming Converter

The grid-forming converter is presented in Figure 2, where reference voltage and current are measured at filter output (grid side). The modulation voltage $V_{m,dq}$ is generated based on the steady state voltage oriented control Eq. 8 rewritten to include the inverter modulation voltage $V_m$, output or microgrid voltage $V_g$ and filter impedance $R_f+j{X}_f$ (13). The current signal change is just to follow the power convention: positive power for loads and negative for generators. The measured voltage is transformed into the synchronous frame considering the detected phase angle $\omega t$ of the PLL, while the measured current is transformed considering the internally generated angle $\omega t_m$. In the Droop Control block, power is calculated Eq. 14, processed accordingly with the droop characteristic described later in this section, and filtered with a first-order LPF with ${\omega }_{0,V}$ and ${\omega }_{0,\omega }$ cut-off frequencies. The LPFs are added to increase system inertia and can therefore be adjusted accordingly, though for the sake of system stability and droop interaction between the parallel converters, they should always be included. The droop control block outputs are the reference output voltage $V_{g,\text{d}q}^{\ast }$ and frequency ${\omega }^{\text{*}}$. Grid-forming control generates the modulation voltage that results in the desired output voltage $V_{g,\text{d}q}^{\ast }$ at $V_g$.

$\left[\begin{array}{c}{V}_{m,d}\\ V_{m,q}\end{array}\right]=\left[\begin{array}{c}{V}_{g,d}\\ V_{g,q}\end{array}\right]-\left[\begin{array}{cc}{R}_f& -X_f\\ X_f& R_f\end{array}\right]\left[\begin{array}{c}{I}_{g,d}\\ I_{g,q}\end{array}\right].(13)$

$P=\frac{3}{2}{V}_{g,d}{I}_{g,d},(14)$

$Q=-\frac{3}{2}{V}_{g,d}{I}_{g,q}.$

FIGURE 2

FIGURE 2. Simplified scheme of the Grid-forming converter.

The Grid-forming controller mode of operation is based on typical workbench power supplies, and the respective block diagram is presented in Figure 3, where it can be noticed that the control scheme is based on three main blocks. The forward gain $V_{m,\text{d}q\left(f\right)}$ and decoupling $V_{m,\text{d}q\left(d\right)}$ are obtained based on Eq. 13. An Output Voltage PI controller is added to regulate the generated voltage with zero error at $V_g$$\left(V_{m,\text{d}q\left(v\right)}\right)$. A second control loop is added in parallel with the voltage controller to limit converter over-currents, i.e., when measured currents reach the converter limits, over-current detection (OCD) block generates a trigger that enables Current Controller PI and disables the Output Voltage PI. At this point, the converter starts operating in a current-controlled mode instead of voltage, and, consequently, a voltage sag occurs until load power demand, seen by the grid-forming converter, is reduced back to limits within the converter power range. To identify such reduction, $V_{m,d\left(i\right)}$ is observed, and when its signal changes (positive to negative during overload), it means that there is no need to regulate the current anymore. Consequently, voltage PI is enabled by the OCD trigger, current PI is disabled, and the generated voltage is restored within allowed normal operating limits. After the transition from over-current to normal operation, an LPF brings the accumulated error from the current PI to zero and reset controller state variables. To illustrate the described, the control block diagram of Figure 3 is presented.

FIGURE 3

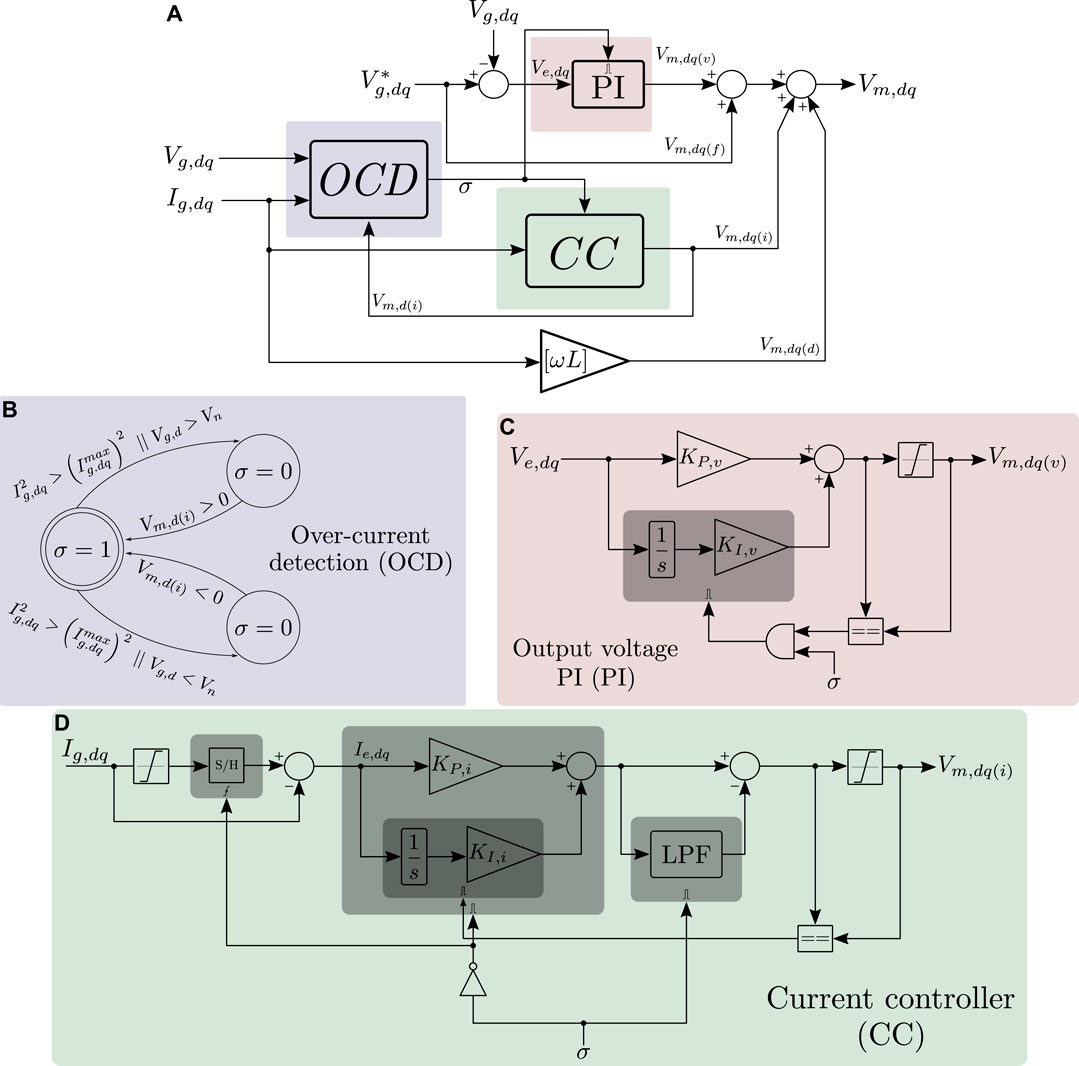
FIGURE 3. Grid-forming voltage and current control block diagram with over-current detection and regulator. (A) complete control loop, (B) over current detection state machine, (C) output voltage PI, and (D) current control loop.

The reference voltage $V_{g,\text{d}q}^{\ast }$ of Figure 2 is generated through internal references (grid nominal values) and changed with droops. Since the converter available power is supplied by an electric storage system and the line is considered mainly resistive, this work presents an active power droop $P/SoC-V$ that dynamically adjusts droop curve accordingly with the storage system $SoC$. The method consists in shifting the conventional droop curve accordingly with the measured $SoC$. The reactive power droop maintains the $Q-\omega$ relationship. The described droop control is synthesized as illustrated in Figure 4. Furthermore, the change in voltage and frequency introduced by the droop curves are within the limits recommended by the EN 50438 (2013), i.e.,$V\in \left[0.9V_n;1.1V_n\right]$ and $\omega \in \left[0.97{\omega }_n;1.03{\omega }_n\right]$.

FIGURE 4

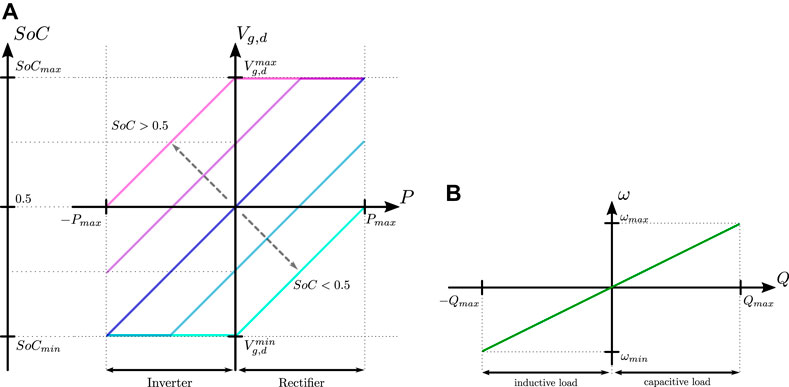
FIGURE 4. Representation of the grid-forming converter droop curves. (A) is the $P/SoC-V$ droop, (B) the $Q-\omega$ droop.

The presented droop curves generate the AC bus signaling of the grid-forming converter. For a given $SoC$ the output voltage is adjusted proportionally to the measured active power that mimics the voltage drop in the line. Additionally, it can be noticed that for lower battery $SoC$ voltage remains below nominal value while for higher $SoC$ remains above. The $SoC$ action can be seen as a change in the value of an equivalent virtual resistance. The voltage set-point indicates to other battery grid-support converters when should supply power (voltage below nominal) or absorb (voltage above nominal).

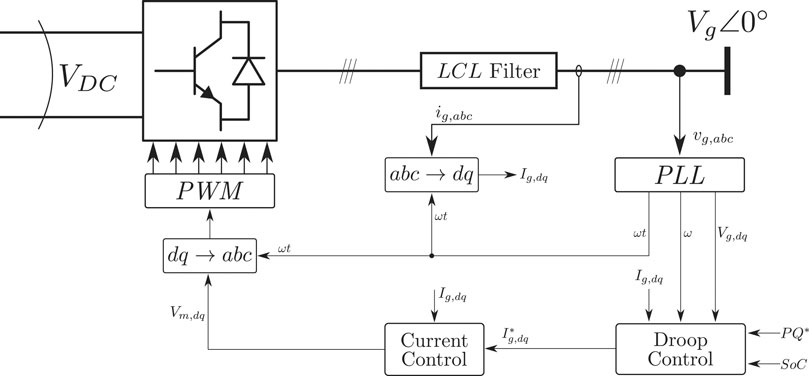
3.2 Grid-Support Converters

The grid-support converters considered in this work are bi-directional power sources that interface an energy storage system (e.g., electric vehicle on-board converter). The converter control scheme is illustrated in Figure 5. The control architecture consists of an inner current control loop based on the VOC Eq. 15 whose current references are obtained directly from the computation of power references (16).

$\left[\begin{array}{c}{V}_{m,d}\\ V_{m,q}\end{array}\right]=\left[\begin{array}{c}{V}_{g,d}\\ V_{g,q}\end{array}\right]-L_f\left[\begin{array}{c}{\dot{I}}_{g,d}\\ {\dot{I}}_{g,q}\end{array}\right]-\left[\begin{array}{cc}{R}_f& -X_f\\ X_f& R_f\end{array}\right]\left[\begin{array}{c}{I}_{g,d}\\ I_{g,q}\end{array}\right].(15)$

$I_d^{\ast }=\frac{2P^{\ast }}{3V_{g,d}},(16)$

$I_q^{\ast }=-\frac{2Q^{\ast }}{3V_{g,d}}.$

FIGURE 5

FIGURE 5. Simplified scheme of Grid-support converter.

The droop curves are similar to the grid-forming converter for a null external active power set-point as shown in Figure 6A. The droops are inverted, and converter power references are thus adjusted accordingly with the measured output voltage and frequency. As discussed before, the grid-forming converter thus lowers the microgrid voltage when its supplied power is increased. Such behavior signals the grid-support converters to increase their output power and consequently share the load power demand. The same logic is applied to the frequency and reactive power. Since active power curves are similar it should become obvious that for two units with the same $SoC$ and power rating, the power sharing in steady state will be equally distributed among them, unless significant differences in the line impedance are observed. In such a case, higher line impedance will result in a higher voltage drop, and the respective unit will contribute less. This behavior is desired since indicates that converters near the loads tend to contribute more. Additionally, when battery $SoC$ drops, the droop curve shifts toward positive active power (battery charging) while for higher $SoC$ the droop curve shifts toward negative active power (battery discharging). Droop is processed only during normal grid voltage level ($V_{g,d}^{\min }\le V_{g,d}\ge V_{g,d}^{\max }$) to minimize perturbations during over-current occurrence in the grid-forming converter.

FIGURE 6

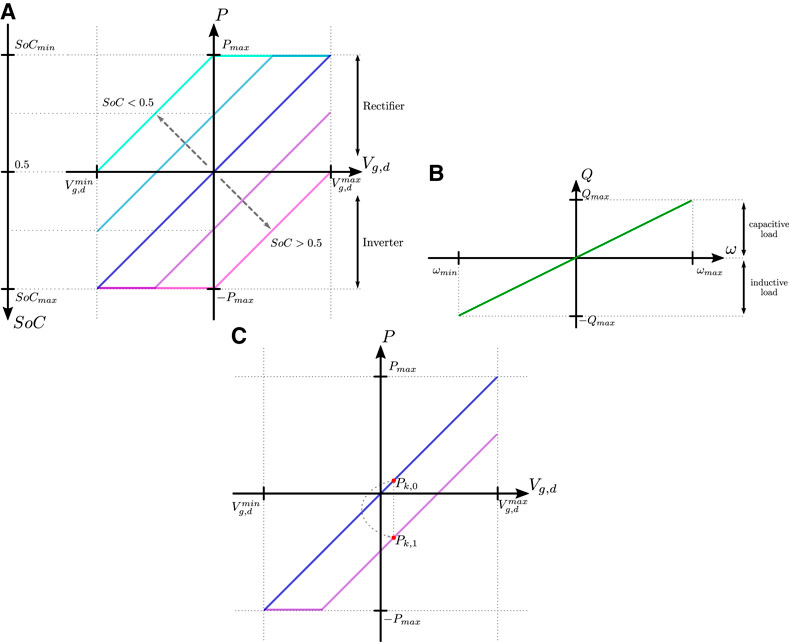
FIGURE 6. Representation of the grid-support converter droop curves. (A) is the $V-P/SoC$ droop, (B) the $\omega -Q$ droop and (C) example of an external power reference impact on the droop curve.

When the unit’s power set-point is externally changed in grid-supporting mode, the droop curve is shifted accordingly. The adjustment is equivalent to a change in the $SoC$, and this mode will therefore not be emphasized. The described behavior is illustrated in Figure 6C, i.e., when an external reference $P_{\text{ext}}$ changes from $P_{k,0}$ ($P_{\text{ext}}=0$) to $P_{k,1}$ ($P_{\text{ext}}=-0.5P_{\max }$). It is obvious that external power reference, in the given example, changes via the droop curve due to voltage measurement deviance from the rated value.

There are two characteristics to be highlighted when considering the grid-forming converter operating with $P/SoC-V$ and grid-supporting converters operating with $V-P/SoC$ (all with null external power references):

(1) Converter power sharing is proportional to the available energy and power rating;

(2) The system tends toward battery energy balancing among the connected units, and as long as some units have available energy, system blackout or re-connection with the main grid is prevented.

4 Results and Discussion

This section presents the relevant results obtained through a numerical simulation and experimental prototype alongside with the respective discussion.

4.1 Simulation Results

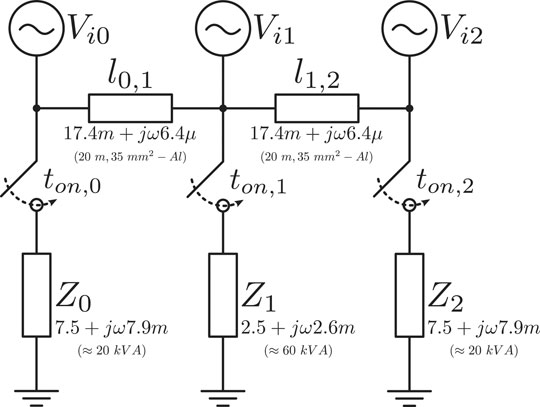
The previously described methods were initially implemented through co-simulation with Matlab (Simulink) and Ansys (Simplorer). For the sake of simplicity, a converter switching model was replaced by controllable voltage sources, i.e., generated modulation voltages directly control a voltage source instead of being compared with a carrier and generate the respective PWMs. All units are three-phase converters operating in the synchronous reference frame with ratings as shown in Table 1. Furthermore, phase synchronization is achieved through a FFDSOGI-PLL Hoepfner et al. (2019) and the output filter is a $LCL$ designed accordingly with Jayalath and Hanif (2017); Said-Romdhane et al. (2017). The controller gains are listed in Table 2.

TABLE 1

TABLE 1. Converters ratings and $LCL$ filters parameters.

TABLE 2

TABLE 2. converters controllers gains.

The considered testbed consists of three independent battery inverters with similar characteristics as described before. The converter ′$0$′ is the master converter and therefore operates in grid-forming. The converters ′$1$′ and ′$2$′ operate as slaves in grid-support mode. Figure 7 shows the testbed equivalent circuit, where $Z_x$ is the $RL$ load connected to the ′$x$′ node, and $l_{i,j}$ is the $RL$ impedance of the line between the node ′$i$′ and ′$j$′ accordingly with ABB SACE (2004). Table 3 presents the test conditions and the respective evaluation targets.

FIGURE 7

FIGURE 7. Island mode test bed.

TABLE 3

TABLE 3. Power sharing test conditions.

Exceptionally for test 3 and 4, we adopted a model based only on the droop curves characteristic, the respective low pass filters and an additional low pass filter to replace the PLL dynamics (ω and $V_{g,d}$ measurements). Additionally, the battery $SoC$ was modeled considering that each converter has a $10 \text{kWh}$ battery and a linear relationship between battery energy and $SoC$.

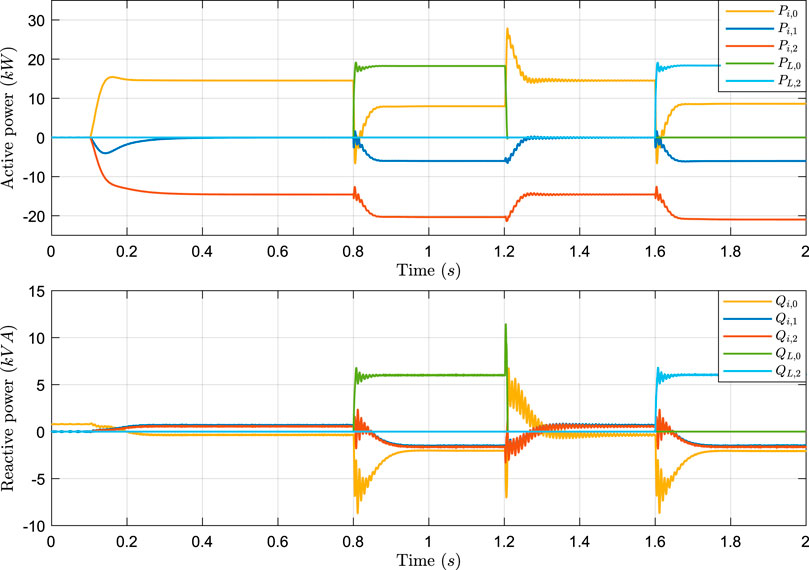
The results obtained for the test conditions described in Table 3 are shown in Figures 8–10.

FIGURE 8

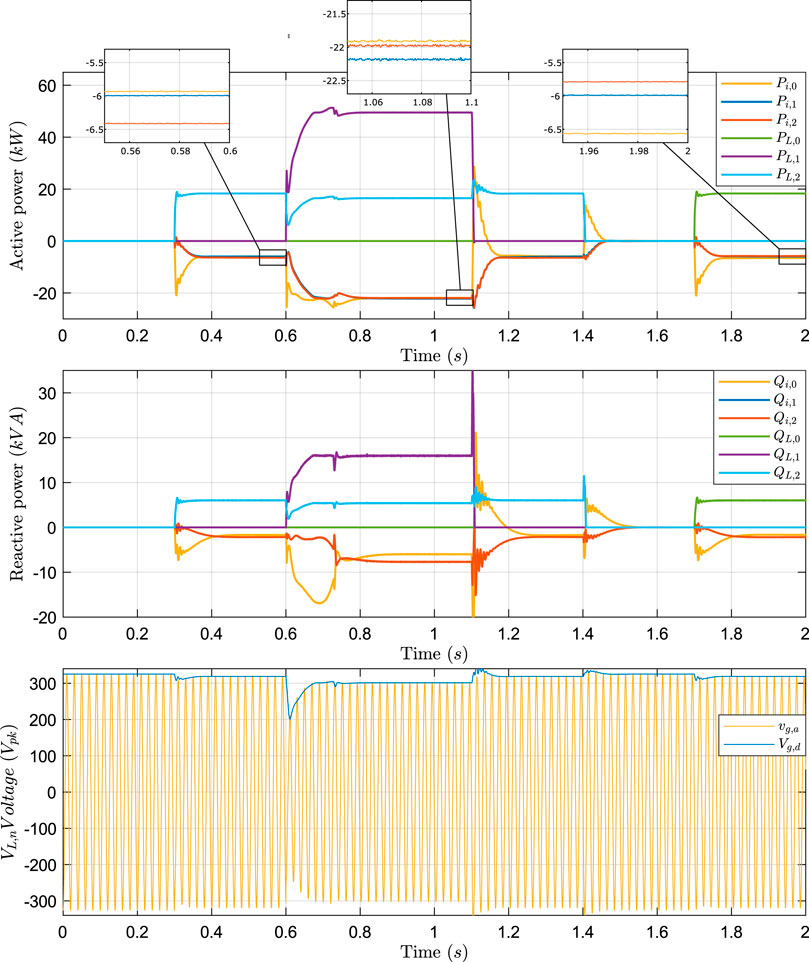
FIGURE 8. Test one simulation results. Active power, reactive power, and AC voltage of reference phase.

FIGURE 9

FIGURE 9. Test two simulation results. Active and reactive power. The $SoC$ of each unit is $So{C}_0=35\%$, $So{C}_1=50\%$ and $So{C}_2=65\%$.

FIGURE 10

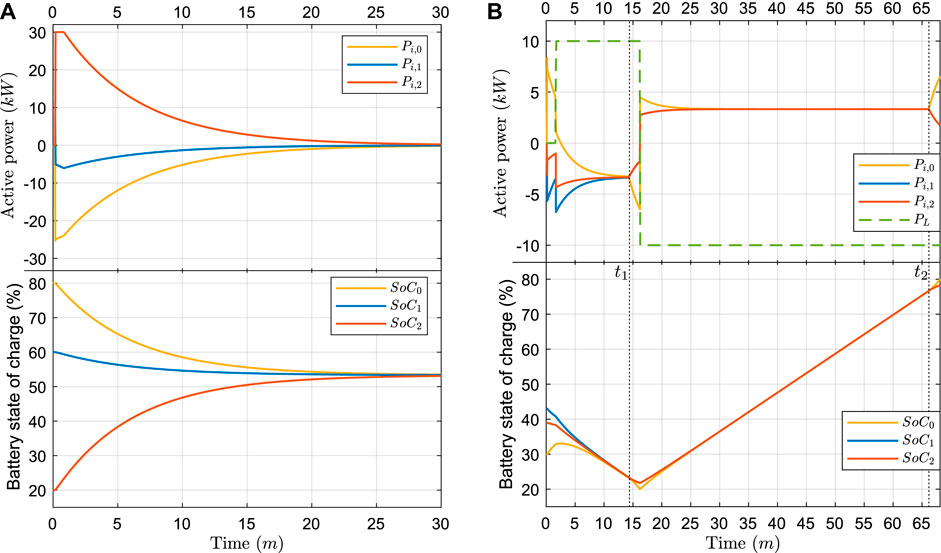
FIGURE 10. Active power and storage system $SoC$ for test three and 4. (A) test three results with no load and (B) test four results with load power.

In 8, we show the active and reactive power of each converter and load. In the same Figure, we also show the reference phase AC voltage and synchronous voltage at the grid-forming converter ($V_{g,0}$). There are three important aspects to highlight during this test: the fast response to supply load power demand, the over-current protection during heavy loads connection, and the steady state power sharing between the grid-forming and grid-support converters.

In the Figure, it is possible to verify the fast response of the master converter during load change at $t=0.3 s$ and $t=1.7 s$ by observing the load power ${\left(P,Q\right)}_{L,2}$, and ${\left(P,Q\right)}_{L,0}$, respectively. The grid-forming converter instantaneously supplies the demand load power due to the proposed control loop strategy. The load one change at $t=0.6 s$ represents an overload condition since the load power demand is above the power rating of the grid-forming converter, and the over-current protection control loop thus generates a voltage sag of approximately $35 \%$. The contribution of the grid-support converters in the power sharing of the heavy load allows the over-current recovery of the grid-forming converter and switch operation mode back to the voltage control mode at $t=0.75 s$, where a small transient is verified. Furthermore, a slight difference in the active power sharing among the connected converters is noticeable. While load two is fed, converter two contributes slightly more than one and 3. The same behavior is noticeable during load one connection, with converter one contributing more, and load 3 with converter 3. Such behavior, as discussed in the earlier section, is because the droop control strategy follows the line impedance nature, and the nearest converter to the load therefore contributes more than the remaining ones.

Figure 9 represents the power sharing when each converter unit presents a different $SoC$. All converters participate in load demand though with different magnitudes of power. In this specific case, converter 0 (grid-forming) fulfills the load power demand transients while charging its battery (in this test, grid-support converters present higher energy availability).

In test three of Figure 10A, we apply a condition with no load. There is therefore only the connection between the converters. As it can be seen by the proposed droop strategy, the droop will generate individual power references that tend to balance the different unit’s battery $SoC$. In the presented particular case, storage systems are balancing after 30 min with the given initial $SoC$.

In Figure 10B it is presented the results for test 4. In this test it can be noticed that the $SoC$ of the storage units tends to become balanced even when there is nonzero load power, i.e., during load ($t\approx \left[0;16\right]\text{m}$) or excess of generation ($t\approx \left[16;70\right]\text{m}$). It is important to highlight two important operation points at $t_1$ and $t_2$ (denoted by dashed lines). Both lines represent a particular condition where the shared load power demand is higher than the grid-support converter’s capability. In $t_0$, such happens because the droop curve shifting limits the maximum negative power accordingly with the $SoC$ of each unit, resulting in a limited power contribution. On another hand, the grid-forming converter power limit is independent of the droop curveinstead only the reference voltage amplitude is changed and limitedbut will always fulfill the power demand as far as it is within the limits imposed by the hardware. That is the reason why, at those particular points, a load power sharing divergence is observed (consequently also reflected in the respective SoC’s). The scenario repeats at $t_2$ when there is an excess of power injected in the microgrid.

The results obtained for the different tests allows to conclude that the grid forming converter would preferably be associated with the unit that presents higher energy storage availability. Additionally, it has to present enough power to fulfill the worst case load demand, which suggests some knowledge of the microgrid loads.

4.2 Experimental Results

The experimental setup consists of a downscale of the previous testbed of Figure 7, where only two units are used and the line impedance between them can be neglected. The experimental testbed can thus be considered a single node system. Additionally, there are no actual batteries in the system, and $SoC$ are therefore defined through software.

In the Figure 11A it is presented the steady state voltage and currents of reference phase “a” with the $SoC$ of both converters set at $50\text{\%}$. The voltage is measured at the common node, while currents are measured in the output of each converter $LCL$ filter. It can be noticed that load power is properly shared by both converters since the currents of each converter present a similar amplitude and phase. The dynamic behavior during a resistive load change is shown in Figure 11B. It can be visualized the fast transient behavior of the grid-forming converter (blue) and the slower compensation of the grid-support converter (magenta) that in the end shares the load power with the grid-forming converter. In 11C we present the same load conditions of Figure 11B but with the grid-forming converter presenting a $SoC=40\text{\%}$. In this case, it is noticeable that the grid-forming converter decreased its power share since it presented less energy availability. For $So{C}_0=40\text{\%}$ and $So{C}_1=50\text{\%}$ the theoretical power share should be of $\approx 30\text{\%}$ for the grid-forming converter and $\approx 60\text{\%}$ for grid-support, which is close to the obtained values of $28.6\text{\%}$ and $71.4\text{\%}$ respectively.

FIGURE 11

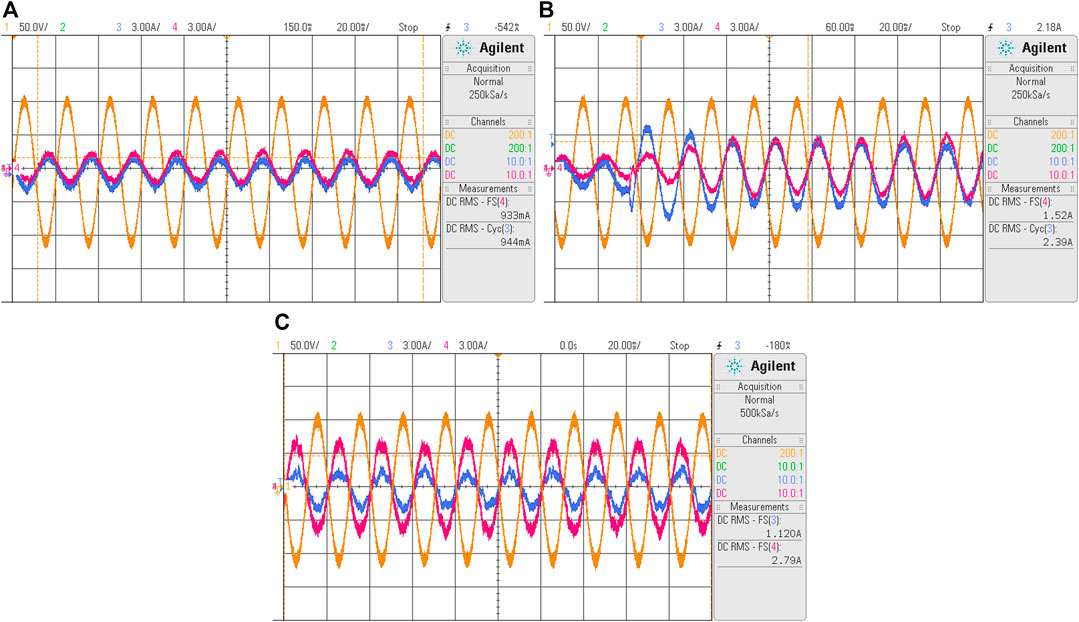
FIGURE 11. Steady-state condition. Line-neutral voltage at reference phase (yellow), reference phase current of grid-forming converter (blue), and reference phase current of grid-support converter (magenta). (A) initial steady state, (B) resistive load change with $So{C}_0=So{C}_1=0.5$, and (C) steady state with resistive load with grid forming $So{C}_0=0.45$ and grid support $So{C}_1=0.5$.

Figure 12A presents the over-current protection results, which were obtained during an induction motor startup. The grid-forming maximum current was set at $\left|I_{\max }\right|=7.7 A_{\text{rms}}$. It is noticeable that the voltage sag (yellow) is caused by the maximum current limitation (blue). Additionally, the grid-support converter increases the output current (magenta) to maintain the reference power (droop is on halt when voltage sag is detected). Once the induction motor reaches a certain speed the respective electromotive force increases and the over-current protection is turned off, as can be seen in Figure 12B.

FIGURE 12

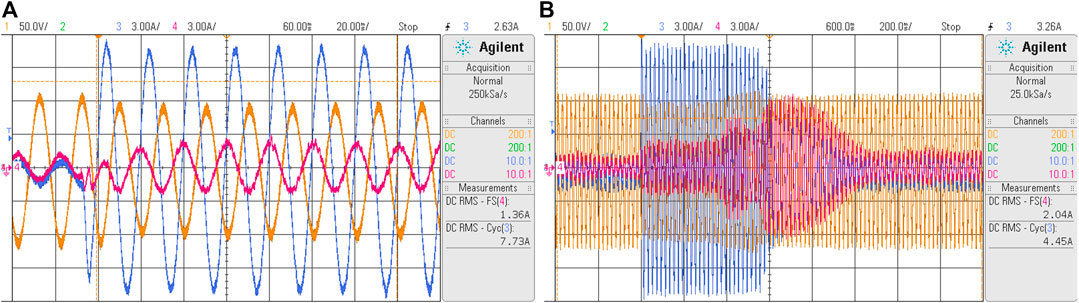
FIGURE 12. Transient during heavy load change-induction motor startup. Line-neutral voltage at reference phase (yellow), reference phase current of grid-forming converter (blue), and reference phase current of grid-support converter (magenta). (A) initial transient, and (B) total transient.

5 Conclusion

In this work, we present a new method that ensures proper power sharing and balancing between local loads and parallel converters in microgrids operating in island mode. The method also adds system inertia, which allows for seamless fulfillment of load power demands. The presented adaptive droop changes the active power droop gain accordingly with the battery $SoC$, ensuring that the load is compensated mostly by the storage system with higher energy availability while charging the storage system with less energy. This approach allows to balance the $SoC$ of the connected battery units maximizing the power capability of the system.

The proposed system can be applied in charging stations with renewable energy resources and storage systems, allowing for islanding without compromising the vehicle charging. Additionally, the method can be also implemented in a vehicle-to-grid approach, allowing multiple cars to generate a local grid in off-grid areas. Another example is the application in a vehicle-to-vehicle charging, where several vehicles may share the available energy and balance their batteries $SoC$.

Future works should extend the method to handle unbalanced phases by implementing a virtual impedance to the zero and negative sequence as proposed in Najafi et al. (2018). Furthermore, the grid-forming method should be improved during an over-current detection operation to allow the continuous operation of the droop control of the grid-support converters. As an extension of the current work, the authors also suggest further study of the $P-SoC$-adaptive droop performance considering different power/energy ratios of the storage systems of each unit. Additionally, we suggest enhancing it to allow for the full use of the grid-support storage system energy before blackout or re-connection with the main grid. Furthermore, it is also suggested to study the method scalability, i.e., considering multiple grid-forming converters operating in parallel.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author Contributions

All authors have made a substantial, direct, and intellectual contribution to the work and approved it for publication.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2020.609218/full#supplementary-material.

References

ABB SACE (2004). Electrical installation handbook. Bergamo, Italy: ABB SACE Vol. 2

Google Scholar

Burmester, D., Rayudu, R., Seah, W., and Akinyele, D. (2017). A review of nanogrid topologies and technologies. Renew. Sustain. Energy Rev. 67, 760–775. doi:10.1016/j.rser.2016.09.073

CrossRef Full Text | Google Scholar

De Brabandere, K., Bolsens, B., Van den Keybus, J., Woyte, A., Driesen, J., Belmans, R., et al. (2007). “A voltage and frequency droop control method for parallel inverters,” in 2004 IEEE 35th Annual Power Electronics Specialists Conference IEEE Cat. No.04CH37551, Aachen, Germany, June 20–25, 2004 (IEEE) 4, 2501–2507. doi:10.1109/PESC.2004.1355222

CrossRef Full Text | Google Scholar

D’Arco, S., and Suul, J. A. (2014). Equivalence of virtual synchronous machines and frequency-droops for converter-based MicroGrids. IEEE Transactions on Smart Grid. 5, 394–395. doi:10.1109/TSG.2013.2288000

CrossRef Full Text | Google Scholar

Eurostat, (2020a). Number of electric cars is on the rise, [Dataset]

Google Scholar

Eurostat, (2020b). Share of renewable energy almost doubled between 2004 and 2018, [Dataset]

Google Scholar

Eurostat, (2020c). Total emissions, main breakdowns by source and general drivers, [Dataset]

Google Scholar

Gu, Y., Li, W., and He, X. (2015). Frequency-coordinating virtual impedance for autonomous power management of DC microgrid. IEEE Trans. Power Electron. 30, 2328–2337. doi:10.1109/TPEL.2014.2325856

CrossRef Full Text | Google Scholar

Gu, Y., Xiang, X., Li, W., and He, X. (2014). Mode-adaptive decentralized control for renewable DC microgrid with enhanced reliability and flexibility. IEEE Trans. Power Electron. 29, 5072–5080. doi:10.1109/TPEL.2013.2294204

CrossRef Full Text | Google Scholar

Han, H., Hou, X., Yang, J., Wu, J., Su, M., and Guerrero, J. M. (2016). Review of power sharing control strategies for islanding operation of AC microgrids. IEEE Transactions on Smart Grid. 7, 200–215. doi:10.1109/TSG.2015.2434849

CrossRef Full Text | Google Scholar

Hatziargyriou, N. (2013). Microgrids: architectures and control. Hoboken, NJ: Wiley-IEEE (Wiley)

Google Scholar

Hoepfner, B., Vick, R., and Magdeburg, O.-V.-G.-U. (2019). “Symmetrical components detection with FFDSOGI-PLL under distorted grid conditions,” in 2019 international conference on smart energy systems and technologies (SEST), Porto, Portugal, September 11, 2019 (IEEE) 2, 1–6

Google Scholar

Jayalath, S., and Hanif, M. (2017). Generalized LCL-filter design algorithm for grid-connected voltage-source inverter. IEEE Trans. Ind. Electron. 64, 1905–1915. doi:10.1109/TIE.2016.2619660

CrossRef Full Text | Google Scholar

Kundur, P., Balu, N. J., and Lauby, M. G. (1994). Power system stability and control., Vol. 7. New York, NY: McGraw-Hill

Google Scholar

Ma, Y., Cao, W., Yang, L., Wang, F. F., and Tolbert, L. M. (2017). Virtual synchronous generator control of full converter wind turbines with short-term energy storage. IEEE Trans. Ind. Electron. 64, 8821–8831. doi:10.1109/TIE.2017.2694347

CrossRef Full Text | Google Scholar

Moradi, M. H., Eskandari, M., and Hosseinian, S. M. (2016). Cooperative control strategy of energy storage systems and micro sources for stabilizing microgrids in different operation modes. Int. J. Electr. Power Energy Syst. 78, 390–400. doi:10.1016/j.ijepes.2015.12.002

CrossRef Full Text | Google Scholar

Najafi, F., Hamzeh, M., and Fripp, M. (2018). Unbalanced current sharing control in islanded low voltage microgrids. Energies. 11, 2776. doi:10.3390/en11102776

CrossRef Full Text | Google Scholar

Ramezani, M., and Li, S. (2018). “Simple and effective synchronization technique for synchronous generator emulating VSCs,” in IEEE Power and Energy Society General Meeting, Atlanta, GA, August 5–9, 2018 (IEEE) doi:10.1109/PESGM.2018.8586161

CrossRef Full Text | Google Scholar

Renjit, A. A., Guo, F., and Sharma, R. (2016). “An analytical framework to design a Dynamic Frequency Control scheme for microgrids using energy storage,” in 2016 IEEE applied power electronics conference and exposition (APEC), Long Beach, CA, March 24, 2016 (IEEE). doi:10.1109/APEC.2016.7468093

CrossRef Full Text | Google Scholar

Rocabert, J., Luna, A., Blaabjerg, F., and Rodríguez, P. (2012). Control of power converters in AC microgrids. IEEE Trans. Power Electron. 27, 4734–4749. doi:10.1109/TPEL.2012.2199334

CrossRef Full Text | Google Scholar

Rokrok, E., Shafie-khah, M., and Catalão, J. P. (2018). Review of primary voltage and frequency control methods for inverter-based islanded microgrids with distributed generation. Renew. Sustain. Energy Rev. 82, 3225–3235. doi:10.1016/j.rser.2017.10.022

CrossRef Full Text | Google Scholar

Said-Romdhane, M., Naouar, M., Belkhodja, I., and Monmasson, E. (2017). An improved LCL filter design in order to ensure stability without damping and despite large grid impedance variations. Energies. 10, 336. doi:10.3390/en10030336

CrossRef Full Text | Google Scholar

Saxena, P., Singh, N., and Pandey, A. K. (2020). Enhancing the dynamic performance of microgrid using derivative controlled solar and energy storage based virtual inertia system. Journal of Energy Storage. 31, 101613. doi:10.1016/j.est.2020.101613

CrossRef Full Text | Google Scholar

Sun, X., Hao, Y., Wu, Q., Guo, X., and Wang, B. (2017). A multifunctional and wireless droop control for distributed energy storage units in islanded AC microgrid applications. IEEE Trans. Power Electron. 32, 736–751. doi:10.1109/TPEL.2016.2531379

CrossRef Full Text | Google Scholar

Tayab, U. B., Roslan, M. A. B., Hwai, L. J., and Kashif, M. (2017). A review of droop control techniques for microgrid. Renew. Sustain. Energy Rev. 76, 717–727. doi:10.1016/j.rser.2017.03.028

CrossRef Full Text | Google Scholar

Urtasun, A., Sanchis, P., and Marroyo, L. (2015). State-of-charge-based droop control for stand-alone AC supply systems with distributed energy storage. Energy Convers. Manag. 106, 709–720. doi:10.1016/j.enconman.2015.10.010

CrossRef Full Text | Google Scholar

Wu, T., Liu, Z., Liu, J., Wang, S., and You, Z. (2016). A unified virtual power decoupling method for droop-controlled parallel inverters in microgrids. IEEE Trans. Power Electron. 31, 5587–5603. doi:10.1109/TPEL.2015.2497972

CrossRef Full Text | Google Scholar

Zhang, H., Zhang, R., Sun, K., and Feng, W. (2019). Performance improvement strategy for parallel-operated virtual synchronous generators in microgrids. Journal of Power Electronics. 19, 580–590. doi:10.6113/JPE.2019.19.2.580

CrossRef Full Text | Google Scholar

Zhang, Y. (2017). Battery energy storage operation with adaptive droop control. In 2017 IEEE Conference on Control Technology and Applications (CCTA) (IEEE), 2017-Janua, 793–798. doi:10.1109/CCTA.2017.8062557

CrossRef Full Text | Google Scholar

Zhong, Q.-C. (2016). Virtual Synchronous Machines: a unified interface for grid integration. IEEE Power Electronics Magazine. 3, 18–27. doi:10.1109/MPEL.2016.2614906

CrossRef Full Text | Google Scholar

Zhong, Q.-C., Nguyen, P.-L., Ma, Z., and Sheng, W. (2014). Self-synchronized synchronverters: inverters without a dedicated synchronization unit. IEEE Trans. Power Electron. 29, 617–630. doi:10.1109/TPEL.2013.2258684

CrossRef Full Text | Google Scholar