Environmental Benefit and Investment Value of Hydrogen-Based Wind-Energy Storage System

Alongside the rapid expansion of wind power installation in China, wind curtailment is also mounting rapidly due to China’s energy endowment imbalance. The hydrogen-based wind-energy storage system becomes an alternative to solve the puzzle of wind power surplus. This article introduced China’s energy storage industry development and summarized the advantages of hydrogen-based wind-energy storage systems. From the perspective of resource conservation, it estimated the environmental benefits of hydrogen-based wind-energy storages. This research also builds a valuation model based on the Real Options Theory to capture the distinctive flexible charging and discharging features of the hydrogen-based wind-energy storage systems. Based on the model, simulation results, including the investment value and operation decision of the hydrogen energy storage system with different electricity prices, system parameters, and different levels of subsidies, are presented. The results show that the hydrogen storage system fed with the surplus wind power can annually save approximately 2.19–3.29 million tons of standard coal consumption. It will reduce 3.31–4.97 million tons of CO₂, SO₂, NO_x, and PM, saving as much as 286.6–429.8 million yuan of environmental cost annually on average. The hydrogen-based wind-energy storage system’s value depends on the construction investment and operating costs and is also affected by the mean-reverting nature and jumps or spikes in electricity prices. The market-oriented reform of China’s power sector is conducive to improve hydrogen-based wind-energy storage systems’ profitability. At present, subsidies are still essential to reduce initial investment and attract enterprises to participate in hydrogen energy storage projects.

Introduction

In China, with the rapid development of renewable energy power, installed wind power capacity is increasing year by year. However, wind power generation has a high-frequency power curtailment phenomenon, making the renewable energy consumption problem more serious. The resulting contradictions between the on-grid load and the excess wind power generation become increasingly prominent. According to the statistics of the National Energy Administration of China, from 2011 to 2018, China’s cumulative wind power curtailed totaled 215.1 billion kWh, suffering an economic loss of 116.5 billion yuan, and the average annual wind surplus ratio is as high as 12.89%. If energy storage systems are connected to the wind farms to shave the peak load, the electricity operators can better ensure the wind power output stability and improve the power output quality (Apostolou and Enevoldsen 2019). The hydrogen-based energy storage system (HESS) provides a reasonable solution for wind power generation flaws—excess wind power can render the energy storage system. It will be used to electrolyze water to produce hydrogen. The hydrogen either returns to the grid through methods such as fuel cells or is used as energy carrier ending up in industrial or commercial application (Chen et al., 2009; Ipsakis et al., 2009; Bakke et al., 2016; Javed et al., 2020; Mayyas et al., 2020). According to the Global Energy Storage Database of the Department of Energy of the United States, as of June 2018, the world's total installed capacity of energy storage systems had reached 195.74 GW, and 1747 projects are running in operation. The number of hydrogen storage projects totals 14 with an installed capacity of 0.02 GW.

Chinese government has explicitly supported the development of the hydrogen energy industry since 2014. The State Council has issued policies to upscale developing the hydrogen fuel-cell motor vehicle (HFEV) industry. Subsidies compensate the whole industrial chain from hydrogen production and vehicle sales to hydrogenation station construction (see the Supplementary Material). As for the research and development of HESS, the government and the industry have carried out three demonstration projects of HESS in China. The first one is the “Technology Research and Demonstration Test Project of Direct Hydrogen Production by Wind Power and Fuel-Cell Power Generation System,” which is put into practice by China Energy Conservation and Environmental Protection Group Corporation since April 2014. The project was projected with a hydrogen production power of 100 kW and a fuel cell electric power of 30 kW. The second is the demonstration project of a wind-power HESS operated by Sino-German cooperation since April 2015. Its hydrogen generation power reaches 200 MW, and the production capacity reaches 17.52 million standard cubic meters per year. The third one is a wind-power HESS invested by Goldwind Technology Company in Jilin Province. Its total installed capacity of wind power generation reaches 100 MW, and the maximum energy storage capacity is 10 MW.

However, the research and development of critical technologies for wind-power HESS in China are still in its infancy. The technical bottlenecks lie in critical technologies such as the efficient conversion of power to hydrogen, large-scale and low-cost hydrogen storage, and comprehensive energy utilization. Besides, unlike developed countries such as the United States and Japan, China has not yet regarded energy storage as an independent industry, it lacks the top-down design of energy storage payment mechanism, and the hydrogen energy storage industry has not yet achieved commercial development. However, it is essential to evaluate the resource value, environmental value, and investment value of the wind-power HESS from the perspective of sustainable development of wind power and large-scale hydrogen energy commercialization.

Some researchers adopted the cost-benefit analysis and discounted cash flow approach to evaluate the value of energy storage. The report published by American Electric Power Research Institute and Sandia Laboratories discussed the potential costs and benefits of energy storage applied to power generation, transmission, and distribution (Eckroad, 2003). Schoenung (2011) analyzed both the short-term and long-term applications of energy storage systems, including load balancing, peak load shaving, and power quality improvement. They analyzed the influence of various operating parameters such as time response, capital cost, efficiency, operating cost, and renewal cost on the energy storage system's application effects. Many scholars compared the economics of different energy storage technologies from a broader range of technical features, including service life, energy efficiency, power density, and degree of technology maturation (Harrison et al., 2009; Steward et al., 2009; Schoenung, 2011). With a deep understanding of energy storage technology, researchers introduced uncertainties in the economic evaluation of energy storage systems (Denholm and Sioshansi, 2009; Loisel et al., 2015; Parra et al., 2019). Yu and Foggo (2017) pointed out that the lack of understanding of investment risks related to energy storage is an obstacle to its application and popularization. They established a stochastic valuation model of energy storage in the large-scale electricity market. Bakke et al. (2016) suggested considering the uncertainty of electricity price fluctuation when conducting power storage investment evaluations. The spot price of electricity generally shows strong seasonality, mean recovery, high volatility, clustering effect, and extreme price changes. This high-frequency electricity market price fluctuation provides flexibility in operation of the energy storage system.

Foreign countries attach great importance to the economic research of hydrogen energy storage technology and wind-power HESS and have begun to develop the evaluation simulation software of wind-power HESS, including the following three software platforms: first, HOMER, a power system optimization platform developed by the Renewable Energy Laboratory of the United States Department of Energy, is mainly used to evaluate the effect of grid-connected power generation system and can effectively assess and analyze the economy and sensitivity of the integrated system of wind power and fuel cells hydrogen production (Bansal et al., 2020; Hassani et al., 2020). Second, TRNSYS, a system dynamic behavior simulation software platform designed and released by the New Energy Power Laboratory of the University of Wisconsin-Madison, United States, effectively quantifies and evaluates the operation effect of power system through simulation, and its standard database is composed by nearly 150 calculation models, including the simulation calculation models of hydrogen production system by wind power and fuel cell generation models (Bakić Vukman et al., 2012; Buonomano et al., 2018). Third, URHYS, a renewable energy grid-connected systems optimization platform, is mainly used for economic evaluation and decision-making optimization of wind-power HESS (Twaha and Ramli, 2018). All these models provide implications for the research and development of a comprehensive wind-power HESS appraisal model in China. Nevertheless, both the model and parameters should be adjusted to fit for the reality of Chinese wind-power HESS industry.

Overall, previous literature mostly used cost-benefit analysis and the traditional NPV method for energy storage evaluation. However, considering the uncertainties during the energy storage system's operation, static cost-benefit analysis and net present value calculation may underestimate the flexibility value of energy storage projects. The real options method can improve the accuracy and effectiveness of elastic valuation. Besides, most of the current research focused on the mature mechanical energy storage technology, quite few on the comprehensive evaluation of wind-power HESS. As a frontier energy storage alternative, HESS provides an alternative pathway that not only helps to integrate wind power generation, but also enables the decarbonization of the transportation and natural-gas sectors. A comprehensive appraisal of the wind-power HESS has particular theoretical and practical significance to unlock its environmental and investing potentials in China.

Structure and Characteristics of Wind-Power Hydrogen-Based Energy Storage System

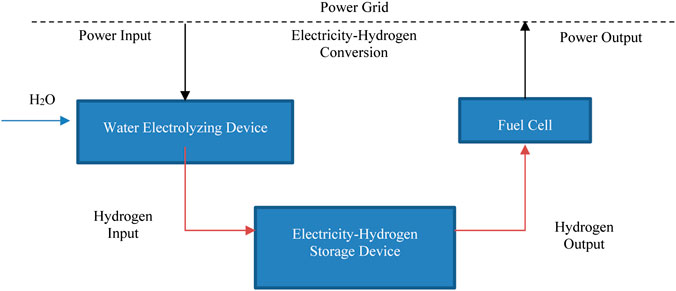
Wind-power HESS usually includes wind power input, water electrolysis device, hydrogen storage device, fuel cell, and other power generation devices connected to the grid. The operation started from inputting excess wind power into HESS, electrolyzing water to produce hydrogen, and inputting hydrogen into the energy storage device. The system further increases the storage density by means such as high-pressure compression. Finally, hydrogen energy can be returned to the grid through the fuel cell at an appropriate time, thus improving the utilization of grid-connected wind power and ensuring the stable output of power system (see Figure 1).

FIGURE 1

FIGURE 1. System configuration of wind-power HESS.

In the wind power storage industry, traditional electrolyzers make difficult to maintain a stable hydrogen production because of the intermittence and fluctuation of power input. It is necessary to equip high-performance electrolyzers to ensure the HESS’s hydrogen energy input safety. Under the current technical conditions, the proton exchange membrane (PEM) electrolyzer can meet the technical requirements of hydrogen production in the wind-power HESS. PEM electrolyzer can keep the hydrogen production rate stable under high intermittent and high fluctuation of electricity input. It can resist high voltage and digest a strong current density (Patrício et al., 2012).

The hydrogen storage device is the most critical component of the wind power-hydrogen storage system, and it can replace the traditional energy storage technology. Hydrogen can be compressed into a gaseous state, liquid state (such as metal hydride and carbon material), or solid state (such as methanol and ammonia) for storage. At present, compressed gaseous hydrogen is widely used in large-scale hydrogen energy storage systems because of low energy leakage (lower than 0.00033%·d⁻¹) and high conversion efficiency (higher than 90%). High energy efficiency can adequately compensate for the long time-consuming disadvantage of hydrogen production by water electrolysis (Bergen et al., 2009).

As the hydrogen-based wind-energy storage system's back-end, the fuel cell is responsible for power output and grid-connected sales. There are two alternatives: high-temperature fuel cells and low-temperature fuel cells. Generally speaking, low-temperature fuel cells are more suitable for the power generation of hydrogen energy storage system because of its flexible working hours and the ability to start and stop at any time (Andrijanovits and Beldjajev, 2012).

Resources and Environmental Benefits of Wind-Power Hydrogen-Based Energy Storage System

As a backup facility of wind farms, the wind-power HESS plays the role as energy buffer. Its powerful resources and environmental benefits will bring a revolution to the energy storage industry.

Energy-Saving Effect

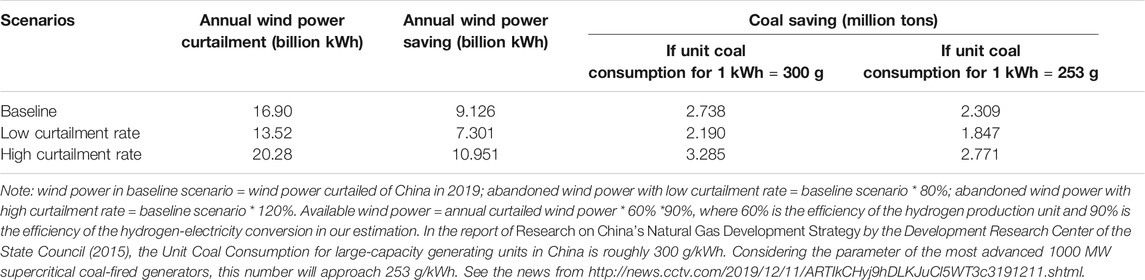
According to the National Energy Administration of China, the energy loss of wind power curtailment in China was 16.9 billion kWh in 2019. The curtailment rate was 4%, which was the lowest level for the past decade. Take the year 2019 as the benchmark year, considering the increasing installed capacity of wind power, the improvement of grid-connected rate, and the further improvement of clean power incentive policies in the future. In that case, the average annual wind power curtailed may fluctuate by 20% based on the benchmark scenario. In the ideal situation, the wind power-hydrogen energy storage device would absorb all the surplus wind power.

This article takes the base-load coal-fired power as the reference to estimate the energy-saving effect of the wind-power HESS. The coal-fired power plants in China apply the 600-MW or 1000-MW ultrasupercritical units with an average standard coal consumption of 300 g/kWh. Suppose the efficiency of the hydrogen production unit is 60% and the efficiency of the hydrogen-electricity conversion is 90%, the energy storage system can save as much as 2.190–3.285 million tons of standard coal consumption. The calculation results are shown in Table 1.

TABLE 1

TABLE 1. Coal consumption savings of wind-power HESS.

The 1000 MW supercritical generators are the most advanced coal-fired power plants globally, highlighting high-efficiency and ultra-low emission. The generators' power efficiency is 47.82%, and the standard coal consumption for power generation is 253 g/kWh. If taking the 1000 MW supercritical generators as a reference, the total saving of standard coal consumption by the HESS will be as high as 1.847–2.771 million tons/year (see Table 1).

Emission Reduction Effect

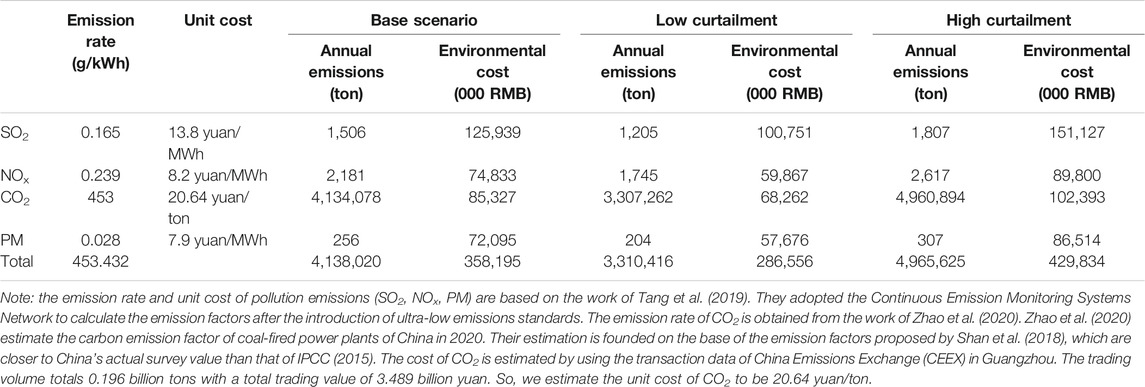
Wind power generation has outstanding environmental protection advantages because it has no emission of dust (PM_2.5), SO₂, NO_x, CO₂, or other toxic gases, which is also the highlight feature of the wind-power HESS. Here, we take the base-load coal-fired power generation as the reference and calculate the hydrogen energy storage system’s emission reduction effect. In fact, substantial emission has been reduced from Chinese power plants after the introduction of ultra-low emissions standards (Tang et al., 2019). Suppose the coal-fired power plants apply the current mainstream ultrasupercritical generators, which emit about 453 g of CO₂ per kilowatt/hour (Zhao et al., 2020). The SO₂, NO_x, and PM emission rates are 0.165 g/kWh, 0.239 g/kWh, 0.028 g/kWh, respectively (Tang et al., 2019). Table 2 summarizes conventional coal-fired power plants' pollutant emission rates and unit environmental costs.

TABLE 2

TABLE 2. Environmental benefits of the wind-power HESS.

The annual emission of pollutants is calculated by multiplying the annual wind power saving in Table 1 by the pollutant emission rate. The environmental cost, which is the external environmental benefit of the wind-power HESS, can be obtained by multiplying the annual emission by the unit environmental cost. Based on the above parameter assumptions, the wind-power HESS can reduce the CO₂ emissions by 3.307–4.961 million tons and the pollutant emissions by 3,154–4,731 tons per year.

People pay lots of attention to the air pollution problem in China, and the air pollution emission standards are increasingly strict. China has implemented the new emission standard for air pollutants in thermal power plants (GB 13223–2011) since July 1, 2014, and the new National Ambient Air Quality Standard (GB 3095–2012) since January 1, 2016, with the emission limit of PM_2.5 being raised. The wind-power HESS will undoubtedly play a positive role in improving wind power utilization and reducing pollutants and greenhouse gas emissions from coal-fired power plants. However, no matter how much resource and environmental benefits the new storage system brings, it is the investment value that decides the commercialization and market prospects of the wind-power HESS.

Investment Value of Wind-Power Hydrogen-Based Energy Storage System

Nature of Real Options

The critical advantage of wind power-hydrogen storage technology is its operational flexibility. The wind power plant operators can select different operation modes according to the price change in the power market, thus creating a time difference between wind power generation and on-grid sales. Therefore, wind-power HESS’s maximum economic value is closely related to the operational decision. Operators can adopt reasonable charging and discharging strategies to earn maximum profits. As electricity price increases, the system releases hydrogen energy and convert it into electricity through fuel cells for on-grid sales to earn profits. As electricity price decreases, the system electrolyzes water to produce hydrogen, converts electric energy into hydrogen energy, replenishes the workload of the wind-power HESS, and sells it when the electricity price reverts to its high level. Operational flexibility is a kind of Compound Real Option since operators face many choices to delay charging and discharging decisions; thus, they can wait for more information and favorable prices to make better-informed decisions. It is necessary to set up a suitable valuation model to cover the Compound Real Options features of the wind-power HESS.

In the process of energy storage, a considerable volume of curtailed wind power is fed to the wind-power HESS, and this part of electric energy can be directly stored by electrolyzing water to produce hydrogen without purchase cost. Therefore, the fluctuation of input wind power will have a particular impact on the profit of the wind-power HESS, and, at the same time, it will affect the actual operating power of the energy storage system (the system is limited by rated capacity). Therefore, the wind-power HESS evaluation model needs to simulate this part of free wind input to quantify the system’s economy accurately.

Valuation Model Construction

Cost-Benefit Analysis

For a wind-power HESS directly connected to the wind farms, its cost consists of fixed cost and variable cost. The fixed cost includes the depreciation and amortization of initial investment and the fixed operating and management expenses. The variable cost includes the unit operating cost of energy storage or release. It varies directly to the energy storage system's operating power and the input/output power. The operating income comes from the sales of on-grid electricity discharged from the wind-power HESS.

Assume that at time t, the working capacity of the hydrogen storage system is I(t), I(t)$\in$[0, I_max], where I_max indicates the maximum working capacity (kWh) of the hydrogen storage system. u(t) indicates the control variable of the hydrogen storage system, that is, the power of storing or releasing hydrogen energy, which satisfies u_min≤u(t)≤u_max. u_max> 0 indicates the maximum discharge power, and u_min < 0 indicates the maximum hydrogen storage power.

There is no purchase cost for the surplus wind power digested by the wind-power HESS. We use the mean-reverting model established by Kelouwani et al. (2005) to simulate the change in excess wind power input to the hydrogen storage system, as shown in Eq. 1 follows:

$Ei\left(t\right)=a+bsin\left[2\pi \left(t-t_0\right)\right]+{\alpha }_1\left[E{i}_0-Ei\left(t-1\right)\right]dt+{\sigma }_{1}Ei(t-1)dZ,(1)$

where Ei(t) represents the input power of the surplus wind into the hydrogen energy storage system; a and b are two periodic variation parameters of excess wind power’s input power; $t_0$ is the time of maximum input power in 1 year; ${\alpha }_1$ is the average recovery rate; ${\sigma }_1$ is volatility; dZ is a standard Wiener process. The actual operating power after removing excess wind power’s input power should satisfy u_min - Ei(t) ≤ u(t) ≤ u_max.

The energy storage capacity volatility is mainly determined by the power of charge and discharge energy and electrohydrogen conversion efficiency. Considering the uncertain consumption of excess wind power’s input power, the change of energy storage working capacity is shown in .

$\frac{dI}{dt}=[-u\left(t\right)+Ei\left(t\right)]a\left(u\right),(2)$

where I represents the energy storage capacity of the wind-power HESS and a(u) indicates the efficiency of electrohydrogen conversion when hydrogen is input or output, a(u)≥0.

We focus on the annual total cost during the operational stage, so set the time when the energy storage system is officially put into operation as t₀. Calculate the equivalent annual cost of the initial construction investment to allocate initial capital expenditure evenly among operational stage. Then discount the operating costs, subsidies, and the equivalent annual cost of the initial construction to t₀. The formula of the total cost is as follows:

$C_D\left(t\right)=\{ \begin{array}{c}c\left[-u\left(t\right)+Ei\left(t\right)\right]a\left(u\right), u\left(t\right)<0\\ cu\left(t\right)a\left(u\right), u\left(t\right)\ge 0\end{array},$

$\underset{0}{\overset{T}{{\displaystyle \int }}}{e}^{-r\tau }{C}_{s}d\tau =\underset{-t_1}{\overset{0}{{\displaystyle \int }}}{e}^{-r\tau }(I_S-Sub)d\tau ,$

$C_S=\frac{e^{-r{t}_1}-1}{1-e^{-rT}}(I_S-Sub),$

$C\left(t\right)=C_0+C_D\left(t\right)+\frac{e^{-r{t}_1}-1}{1-e^{-rT}}(I_S-Sub),$

$C\left(t\right)=\{ \begin{array}{c}{C}_0+c\left[-u\left(t\right)+Ei\left(t\right)\right]a\left(u\right)+\frac{e^{-r{t}_1}-1}{1-e^{-rT}}\left(I_S-Sub\right), u\left(t\right)<0\\ C_0+cu\left(t\right)a\left(u\right)+\frac{e^{-r{t}_1}-1}{1-e^{-rT}}\left(I_S-Sub\right), u\left(t\right)\ge 0\end{array},(3)$

where t₁ indicates the investment period of the project and T is the total operation period. C(t) represents the operating cost of the system per unit time, including (1) C_S(t), the net cost during the investment stage offset by subsidies; (2) C₀, the energy storage cost per unit time; and (3) C_D(t), the charge and discharge cost per unit time, which is directly proportional to the unit cost c and the real-time charge and discharge power. I_C represents the one-time initial investment cost, Sub means subsidies on the equipment purchase expense, and r represents the discount rate.

Fluctuations in Electricity Price

At present, China is deepening its power industry reform, gradually liberalizing the power sector from the government's macro-control. One of the reform’s objectives is to abolish the fixed electricity prices into marketized electricity prices. Therefore, this research assumes that electricity price is a liberalized market price.

The electricity price in a liberalized market shows robust seasonal features and peaks and jumps in its movement. Soaring and jumping ups in price are related to supply interruption and abnormal incremental demand due to extreme weather. The severe dives in price are related to uncertain external factors, such as the excess power generated by the wind farms’ failure of “shut down”. This kind of price surge or plunge is usually short lived. Once the supply and demand interruptions are alleviated, the price will quickly return to its original level. The seasonal fluctuation of electricity prices is related to the demand, price rising in the period of high demand and falling in the period of low demand. To sum up, for most market-oriented electricity markets in the world, the characteristics of electricity prices are periodicity, seasonality, high volatility, mean reversion, and peak-jumping.

To establish a multifactor electricity price model, we modified the multifactor electricity price model of Borovkova and Schmeck (2017) to adapt to the Chinese power sector. The complex multifactor electricity price model of Borovkova and Schmeck (2017) is as follows:

$Y_t=A_t+M_t^c+M_t^d$

$A_t=e^{-\theta T(t)}+\mu \left(1-e^{-\theta T(t)}\right)-\theta \underset{0}{\overset{t}{{\displaystyle \int }}}\underset{0}{\overset{u}{{\displaystyle \int }}}{e}^{\theta T\left(s\right)}\sigma \sqrt{\tau \left(s\right)}dB\left(s\right)e^{-\theta T\left(u\right)}\tau \left(u\right)du+\underset{0}{\overset{t}{{\displaystyle \int }}}\underset{R}{{\displaystyle \int }}xv\left(dx,du\right)-\theta \underset{0}{\overset{t}{{\displaystyle \int }}}\underset{0}{\overset{u}{{\displaystyle \int }}}\underset{R}{{\displaystyle \int }}{e}^{\theta T\left(s\right)}xN\left(dx,ds\right)e^{-\theta T\left(u\right)}\tau \left(u\right)du$

$s\left(t\right)=a_1\sin \left(\frac{a_2+2\pi t}{T}\right)+a_3$

$M_t^c=\sigma \underset{0}{\overset{t}{{\displaystyle \int }}}\sqrt{\tau \left(u\right)}dB\left(u\right)$

$M_t^d=\underset{0}{\overset{t}{{\displaystyle \int }}}\underset{R}{{\displaystyle \int }}x(N-v)\left(dx,du\right),(4)$

$Y_t$ is a spot price considering mean-reverting effect, seasonality, random volatility, jumping, and correlation of different random movements. $A_t$ describes the random walk trend considering mean reversibility, s(t) describes periodic seasonal fluctuation, and $M_t^c$ and $M_t^d$ describe the fluctuation and jumping, respectively.

As China’s power sector’s marketization is still in its infant stage, Borovkova and Schmeck’s (2017) model can be simplified. We can directly add the seasonal effect term to the reverting mean and reflect the random fluctuation and peak jumps with two parameters. Thus, the power market price model is established as follows:

$dP={\alpha }_2\left[K\left(t\right)-P\right]dt+{\sigma }_{2}PdB+\gamma Pd{Z}_1,(5)$

$K\left(t\right)=K_0+\beta sin\left[2\pi (t-t_{SA})\right],(6)$

where P stands for electricity market price, K(t) for long-term equilibrium price under seasonal effect, K₀ for long-term equilibrium price without seasonal effect, ${\alpha }_2$ for average price recovery rate, ${\sigma }_2$ for price fluctuation, γ for the jumping parameter of electricity price, and dB for standard Wiener process increment ($dB=\epsilon \sqrt{dt}$,$\epsilon \sim N\left(\mathrm{0,1}\right)$.$d{Z}_1$ represents the increment of the Poisson process ($d{Z}_1=\lambda dt$), β represents the seasonal parameter of electricity price, and $t_{SA}$ indicates the time when the seasonal electricity price is the highest.

Due to the surge in demand for heating in winter and cooling in summer, the power price reaches its peak then. So K(t) in Eq. 6, which reflects the seasonal fluctuation of equilibrium price in the electricity market, is a periodic function for a half year.

Valuation Model

Operators of the wind-power HESS can maximize the economic value by optimizing charge and discharge decisions. The operator's objective is as follows:

$ma{x}_{u}E\left\{\underset{0}{\overset{T}{{\displaystyle \int }}}{e}^{-rt}[u\left(t\right)a\left(u\right)P\left(t\right)-C\left(t\right)]dt\right\},(7)$

where $u\in [u_{min}\left(t\right)-Ei\left(t\right),u_{max}\left(t\right)]$, and E represents operators’ expected profit.

We define V(P,t) as the economic value of the wind-power HESS. That is, the value of the wind-power HESS is a function that depends on the price and time variation of the electricity market.

$V\left(P,t\right)=ma{x}_{u}E\left\{\underset{0}{\overset{T}{{\displaystyle \int }}}{e}^{-rt}[u\left(t\right)a\left(u\right)P\left(t\right)-C\left(t\right)]dt\right\},(8)$

To make the model intuitive, we establish a standard Bellman equation, which separates the energy storage system’s value from t to t + dt and t + dt to T and then simplify the value formula with the rectangle method. See the detailed derivation process:

$V\left(P,t\right)={\text{max}}_{u}E\left\{\underset{t}{\overset{t+dt}{{\displaystyle \int }}}{e}^{-r\left(\tau -t\right)}\left[u\left(\tau \right)a\left(u\right)P\left(\tau \right)-C\left(\tau \right)\right]d\tau +\underset{t+dt}{\overset{T}{{\displaystyle \int }}}{e}^{-r(\tau -t)}\left[u\left(\tau \right)a\left(u\right)P\left(\tau \right)-C\left(\tau \right)\right]d\tau \right\},$

$V\left(P,t\right)=ma{x}_{u}E\{{{\displaystyle \int }}^{\text{}}\{\left[u\left(t\right)a\left(u\right)P\left(t\right)-C\left(t\right)\right]dt+e^{-rdt}V\left(P+dP,t+dt\right)\}\},$

Bring the cost (Eq. 3) into the above formula, and carry out Taylor's expansion. According to Ito's Lemma, we can get

$V(P,t)=ma{x}_{u}E\{{{\displaystyle \int }}^{\text{}}\{\left[u\left(t\right)a\left(u\right)P\left(t\right)-C_0-C_D\left(t\right)-C_S\right]dt+\left(1-rdt\right)[V+\alpha \left(K_0+\beta sin\left(2\pi \left(t-t_{SA}\right)\right)-P\right)\frac{\partial V}{\partial P}dt+\frac{1}{2}{\sigma }^2\frac{{\partial }^{2}V}{{\partial }^{2}P}dt+\sigma \frac{\partial V}{\partial P}dB+\frac{\partial V}{\partial P}dZ+\frac{\partial V}{\partial t}dt]\}\},$

Finally, take the expectation of the above equation and divide the value at dt.

$\frac{\partial V}{\partial t}+\frac{1}{2}{\sigma }^2\frac{{\partial }^{2}V}{{\partial }^{2}P}+\alpha \left(K_0+\beta sin\left(2\pi \left(t-t_{SA}\right)\right)-P\right)\frac{\partial V}{\partial P}-rV-C_0$

$-C_S+ma{x}_{u}E[u\left(t\right)a\left(u\right)P\left(t\right)-C_D\left(t\right)]=0.(9)$

The last part of the above formula contains the variable u(t). To realize the optimal economic value of the wind-power HESS, the actual operating power, u(t), which is also the buying and selling power, should meet the following requirements:

$\{\begin{array}{c}ma{x}_{u}E\left\{u\left(t\right)a\left(u\right)\left[P\left(t\right)-c\right]\right\}, u\left(t\right)\ge 0\\ ma{x}_{u}E\left\{u\left(t\right)a\left(u\right)\left[P\left(t\right)-c\right]-cEi\left(t\right)a\left(u\right)\right\}, u\left(t\right)-Ei\left(t\right)<0\end{array},$

where $u\in [u_{min}\left(t\right)+Ei\left(t\right),u_{max}\left(t\right)]$, $a\left(u\right)=\{\begin{array}{c}{a}_1, u\ge 0\\ a_2, u-Ei\left(t\right)<0\end{array}$.

Therefore, when u(t) meets the optimal operation condition (u*), the wind-power HESS will satisfy

$\frac{\partial V}{\partial t}+\frac{1}{2}{\sigma }^2\frac{{\partial }^{2}V}{{\partial }^{2}P}+\alpha \left(K_0+\beta sin\left(2\pi \left(t-t_{SA}\right)\right)-P\right)\frac{\partial V}{\partial P}-rV-C_0-C_S+u\left(t\right)a\left(u\right)P\left(t\right)-C_D\left(t\right)=0.(10)$

Now the question comes to find the optimal control variable, u*.

Boundary Conditions

Assume that the energy storage system will stop working at the end of the project life, and then the system's real-time value will be zero.

$v\left(P,t\right)=0,t=T.$

When the market price of electricity is high, the optimal choice is to maximize the output power for grid-connected sales. When the market price of electricity is low, the optimal choice is to purchase power for energy storage for subsequent operation. However, if the market price stays still, the real-time value v of the system will not change, so the optimal choice at this time will be no additional buying or selling. To sum up, the boundaries for the value of the wind-power HESS are defined as follows:

$\{ \begin{array}{c}{V}_{PP}\to 0, P large\\ V_{PP}\to 0, P\to 0\end{array},$

Next, let us define the difference term's restrictions in the valuation model. Set $V_j^i$ as the value when the energy storage system operates at the time i and the electricity market price P is at its jth node, where i = 1, 2,..., N while j is a continuous variable with 0 as the lowest value. Therefore, take the discretized first-order difference of the value function with time t and price P. The results are shown in Eqs. 11, 12.

$\frac{\partial V_j^i}{\partial t}=\frac{V_j^{i+1}-V_j^i}{\delta t},(11)$

$\{ \begin{array}{c}\frac{\partial V_j^i}{\partial P}=\frac{V_{j+1}^i-V_j^i}{\delta P}, if \alpha >0\\ \frac{\partial V_j^i}{\partial P}=\frac{V_j^i-V_{j-1}^i}{\delta P}, if \alpha \le 0.\end{array}(12)$

Then, take the discretized second-order partial difference in the value function with price P.

$\frac{{\partial }^2{V}_j^i}{\partial P^2}=\frac{V_{j+1,}^i-2V_j^i+V_{j-1}^i}{{\left(\delta P\right)}^2}.(13)$

When the market price of electricity is zero or reaches its peak value, the second-order difference in the wind-power HESS’s value is zero. Hence, the following boundary conditions determine the second-order difference term in Eq. 13.

$\frac{{\partial }^2{V}_0^i}{\partial P^2}=0,$

$\frac{{\partial }^2{V}_N^i}{\partial P^2}=0.$

The constraints include the energy storage capacity, I, and its first-order derivative. The specific boundary conditions are defined as follows:

$\{\begin{array}{c}u\left(t\right)a\left(u\right)>0, I=I_{max} \\ [u\left(t\right)-Ei\left(t\right)]a\left(u\right)\le 0, I=0\end{array}.$

The above formula indicates that the input power is zero when the wind-power HESS works at its maximum capacity. That is, operators should adopt the strategy of discharge or no operation. When the working capacity of the system is zero, there is no power output. That is, operators should adopt the strategy of charge or no operation. Based on the above objections and restrictions, the optimal control variable, u*, can be solved with Monte Carlo simulations.

Simulation of the Investment Value

Simulation Assumptions

The operation and settlement cycle of the wind-power HESS is generally 1 year, so this resaerch studies the value and operation decision of the wind-power HESS within 1 year. According to the existing hydrogen storage technology specifications, we set the maximum energy storage capacity to be 100 MWh, maximum released power to be 6 MW, and maximum stored power of the wind-power HESS to be 10 MW. For the direct transmission power model of excessive wind power consumption, assume that the periodic parameters a and b are 2000 and −5,000, respectively, the peak time t₀ = 0, the average stored power Ei₀ is 5,000 kW, the average recovery rate ${\alpha }_1$ is 0.5, and the volatility at ${\sigma }_1$ is 0.2. The long-term average electricity price, K₀, is based on the benchmark on-grid price of onshore wind power in the four resource zones (see Table 3) and set as 0.5 yuan/kWh. t is in hours.

TABLE 3

TABLE 3. Wind power benchmarking price of four resource zones in China (yuan/kWh).

We assume that the average recovery rate ${\alpha }_2$ is 0.5, the volatility ${\sigma }_2$ is 0.05, the jumping parameter $\gamma$ is 0.05, and the seasonal parameter $\beta$ is 0.1. The simulation results of the electricity price are shown in Figure 2.

FIGURE 2

FIGURE 2. Single simulation of electricity prices (for 1 year).

Assuming unlimited operating time, the construction period (t₁) lasts for 4 years, = 1 (Yuan/kW), C₀ = 10⁴ (Yuan), and the annual discount rate during the construction period is 10%, $\text{a}\left(\text{u}\right)=\{\begin{array}{c}1/0.6\mathrm{}if u<0\\ 0.9\mathrm{} if u\ge 0\end{array}$.

Assume that the unit construction cost is 0.35 yuan/kWh and the total investment is 350 million yuan, that is, IC = 350 million yuan. For the convenience of calculation, assume that the subsidy is equal to the investment, that is, Sub = 350 million yuan, then Ic − Sub = 0. Suppose the initial hydrogen energy storage system is at full working capacity, I₀ = 10⁵ kWh.

Simulation Results

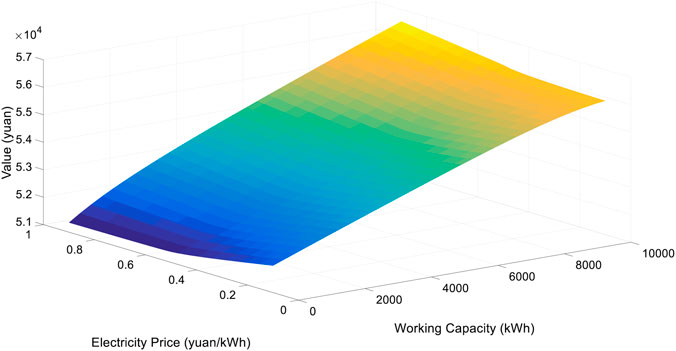
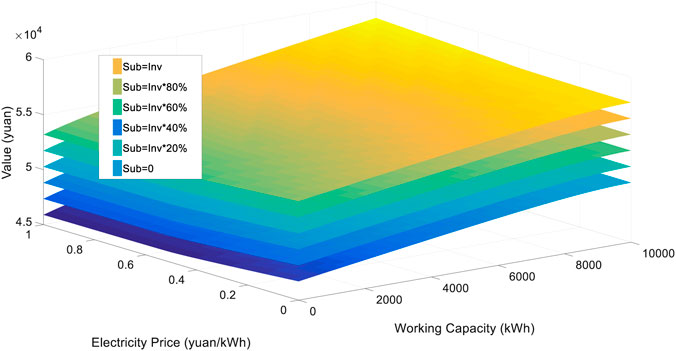
Figure 3 shows the value of the wind-power HESS under different electricity market prices and working capacities. When the electricity market price is high and the HESS reaches full load, the value of the wind-power HESS reaches its maximum. When the electricity market price is the highest and the HESS's working capacity is zero, then the value of the wind-power HESS reaches the minimum. This result can be understood as when the electricity price is very high, or the HESS is running at full capacity, the decision-makers always choose to produce hydrogen energy as soon as possible to obtain the maximum profit. When the HESS’s working capacity is zero, no matter how high the electricity price is, the decision-maker has no available stored hydrogen energy for power generation output. In that case, it is not worth buying extra electricity for sale because of the high purchasing price. Besides the above two extreme cases, the decision-makers will choose to purchase electricity from the spot market and convert it into hydrogen energy for storage if the electricity price is relatively low and the HESS still has vacant working capacity. In this way, they can convert hydrogen to output electricity through fuel cells after the electricity price rises. Therefore, when the system's working capacity is high, the wind power-HESS is equivalent to a call option of the electricity market price. When the system’s working capacity is low, it is equivalent to a put option. When the working capacity is between zero and its maximum, the wind power-HESS is equivalent to a saddle option (a compound option with calls and puts) of the electricity market price.

FIGURE 3

FIGURE 3. Wind-power HESS value surface.

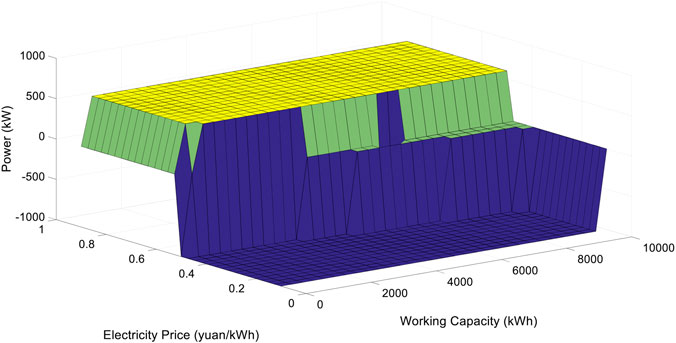
Figure 4 shows the optimal generating, storing, and discharging strategies of the HESS under various power prices and system capacities. The joint distribution of power price and working capacity decides the operator’s optimal generating, storing, and discharging decision. When the power price is low, the operator will be willing to purchase extra electricity from the spot market for storage after completing the overabundant wind power storage as long as the system has not fully loaded. When the electricity price increases to a threshold, the optimal choice changes to convert stored hydrogen into electric energy and sell it for profit. The boundary area in Figure 4 shows that when the working capacity of the wind-power HESS is zero, even if the electricity price is high, it is still impossible to convert hydrogen energy for on-grid sales. Similarly, when the wind-power HESS works at full load, the decision-maker will not purchase low-cost electricity for storage, even if the electricity market price is meager.

FIGURE 4

FIGURE 4. Control surface of wind-power HESS.

Besides, when the electricity price fluctuates to its long-term average level, the decision-maker may not buy additional power to charge the energy storage system if its working capacity is already high. It depends on the power price trend and the variable cost of producing and storing hydrogen energy.

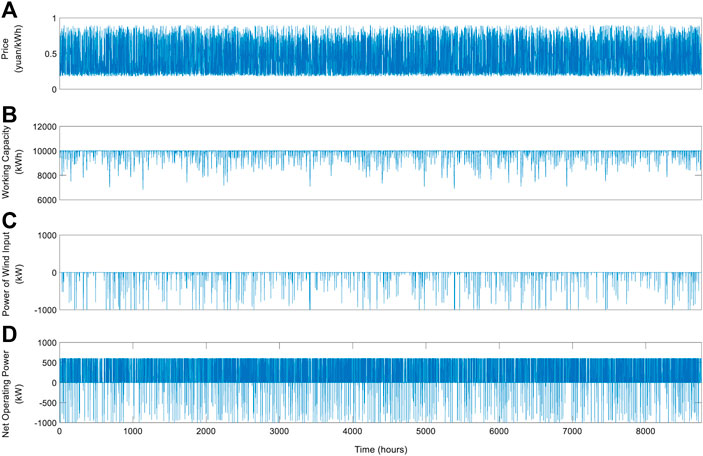
Figure 5 shows the changes in power price and the working capacity with time and the corresponding operation strategies.

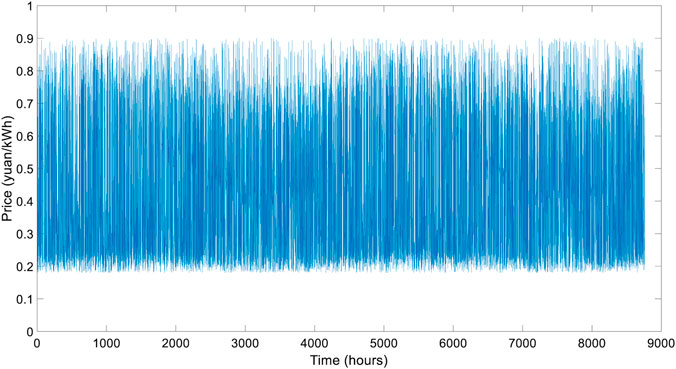
Price Volatility. We assume that the wind-power HESS was working at full load initially. The simulation results have captured the electricity price fluctuation during different hours. The seasonal effect is much smaller than the intraday fluctuation, although we set the electricity price to repeat the first rising then falling twice a year. The trend of electricity price is shown in Figure 5A.

Change of Working Capacity. Figure 5B describes the changes in working capacity during the operation. Within a day, as the electricity price rises high enough for the on-grid sales to compensate for the operating cost, the operator will always convert hydrogen energy to output electric power for sales. During that time, the energy storage system's working capacity keeps declining. Starting from the intraday peak, the price of electricity begins to decrease. When it drops to a certain level, the operator begins to purchase additional electricity to input the system and transform it into hydrogen to store. During this period, the operator waits until the power price rises for on-grid sales. However, when the electricity price falls to the bottom, it’s difficult to recover the operating cost of on-grid sales. When the electricity price reaches the peak, it is too expensive to buy additional electricity to produce hydrogen for subsequent discharging. In the above two states of nature, the system will only take in the zero-cost wind power and slowly reach saturation. Figure 5B shows that the system maintains more than 60% of energy at work and it reaches the full load frequently, which implies that the charging frequency is higher than the discharging frequency or energy storage speed is quicker than the discharging speed. This difference is mainly because the wind‐power HESS must first absorb surplus wind power during the storage phase, which is the system's principal primary function. Surplus wind power carries no procurement cost. As long as the unit energy storage cost is lower than the output electricity price, the storage system will always consume electric energy and transform it into hydrogen energy. When the wind‐power HESS starts to discharge continuously, the discharged power is the absolute operating power. To sum up, when the system starts storing energy, the excess wind power consumed is superimposed, increasing the energy storage velocity and the working capacity rapidly. Thus the wind‐power HESS can quickly reach the full load.

Energy Storage and Discharge Strategies. Figure 5C shows the system's operating power of wind absorbing, while Figure 5D describes the net operating power without surplus wind power. Comparing these two figures, we find that the HSEE system can timely digest surplus wind power to reduce capacitance loss from discharging. The operating strategy in Figures 5C,D varies consistently with the change of capacity in Figure 5B. The operator repeats a loop of releasing energy for sale (being bullish on electricity price), no operation (maintaining value), energy storage (being bearish on electricity price), and waiting for appreciation. The circulatory strategy accords with those above-mentioned three real options.

FIGURE 5

FIGURE 5. Working capacity and operational strategy changing with electricity prices.

Sensitivity Analysis

Seasonal Parameter of Electricity Price, β

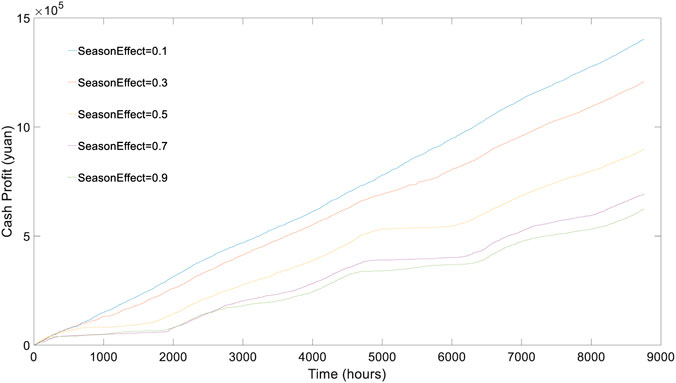
There is no seasonal effect when the seasonal fluctuation rate of electricity price, β, equals 0. As β increases, the seasonal fluctuation of the electricity price will increase gradually. We assume that the values of β are equal to 0.1 (which is the base scenario), 0.3, 0.5, 0.7, and 0.9, respectively; repeat the simulation procedures and summarize the results in Figure 6.

FIGURE 6

FIGURE 6. Total cash flows with different seasonal factors of electricity price (for one year).

As shown in Figure 6, with the seasonal fluctuation of electricity market price increases, the accumulated cash flow of the wind-power HESS gradually decreases so that operators’ profit decreases. Under different β values, the overall upward trend of the system’s accumulated cash flows is approximately the same.

When β = 0.9, the seasonal fluctuation of the electricity price is the strongest among the five scenarios, which means it takes the longest time for the price to return to its long-term average because the intraday fluctuations are superimposed with a large seasonal deviation. Therefore, operators have to face a lot of time to idle the system and wait for the price to fluctuate to the other side of the long-term average. A shorter operational window period leaves less room for the wind-power HESS to earn profits across time. Therefore, the accrued cash flow is the least when β = 0.9. Nevertheless, considering zero-cost excess wind power consumption, the annual accumulated cash flow is still positive in this case. As β decreases, the mean-reverting speed of electricity price rises gradually, and the real-time value of the wind-power HESS increases accordingly. It’s the intraday volatility instead of β that decides the opportunity to exercise the real options. The power sector’s marketization reform is conducive to improve the value of wind-power HESS and promote the industrialization of hydrogen energy storages. Marketization reform will increase the ultra-short-term price jumps or spikes in electricity prices and iron out the seasonal effects using electricity derivatives such as futures, options, and swaps.

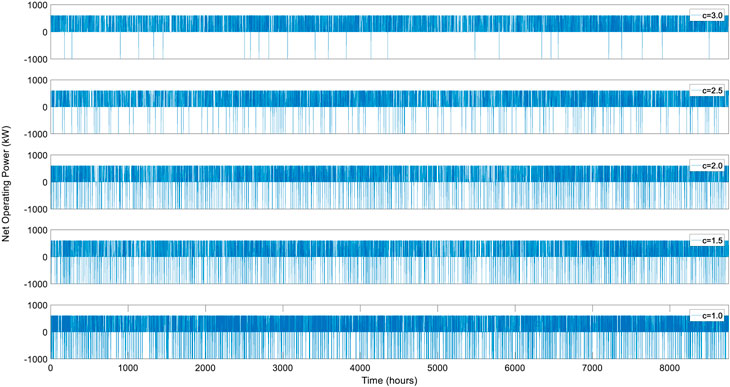
Unit Operating Cost of the System, c.

Figure 7 shows the simulation results of net operating power without surplus wind power when c is equal to 1.0 (which is the base scenario), 1.5, 2.0, 2.5, and 3.0, respectively. The time of zero operating power (u = 0) will be prolonged as c increases because the increasing operating cost reduces profit margin, leaving little space for operators to exercise options. That is, the time for operators not to execute storage operation is prolonged. It implies that technological breakthroughs are essential to reduce the system’s operating cost and further stimulate operators' enthusiasm for the system.

FIGURE 7

FIGURE 7. The impact of the operation costs on decision‐making in wind‐power HESS..

Subsidies, Sub

Figure 8 shows the change in the value of wind-power HESS when the subsidy parameter, Sub, is equal to 0, 20%, 40%, 60%, 80%, and 100% of investment (which is the base scenario). Subsidies can significantly improve the economy of energy storage systems. In the absence of subsidy (Sub = 0), which is the worst case and severe crackdown on operators' investment enthusiasm, the value of wind-power HESS will be 87% of that when initial investment is 100% subsidized. Therefore, it is still necessary for the government to subsidize enterprises to promote investment in energy storage system projects until notable technological innovations come.

FIGURE 8

FIGURE 8. The impact of the subsidy changes on value surface.

Conclusion

This article comprehensively evaluates the investment value of the wind-power HESS from three aspects: resource utilization, emission reduction, and economic value.

First of all, the intermittence and fluctuation of wind power generation decrease the power system's stability, causing great losses due to wind power casted away off-grid. Since the wind-power HESS can dynamically absorb the excess power and convert it into hydrogen energy for storage and timely release on-grid, it effectively makes up for the instability of wind power generation. According to our scenario hypothesis, China’s curtailed wind power is as high as 16.9 billion kWh per year. The installment of the wind-power HESS can absorb the surplus wind power and equivalently save 21.9–32.85 million tons of standard coal consumption per year. The coal consumption saving can reduce pollutant emissions (such as CO₂, SO₂, NO_x, and PM) by 3.31–4.97 million tons per year and save the environmental cost by 286.6–429.8 million yuan annually.

Secondly, operational flexibilities will increase the economic value of the wind-power HESS. We established a real option valuation model to capture the value of flexibilities and discuss the influence of factors (including price fluctuation, investment cost, unit operation cost, operation efficiency, and subsidies) on the project's value with a dynamic programming method. Specifically, the wind-power HESS can be regarded as a call option, put option, and saddle option according to the electricity price and storage workload. To maximize the system's value, operators need to make reasonable operational strategies according to the power price and the storage system's workload. Overall, operators should store energy when the electricity market price is low and discharge energy when the electricity market price climbs high.

Finally, the sensitivity analysis of the valuation model's critical parameters shows that (1) the less significant the seasonal fluctuation of electricity price, the better the HESS's economy. To some extent, the marketization of electricity industry will enhance energy storage’s potential benefits and further promote its industrialization. (2) The lower the unit operating cost is, the more frequent charging and discharging operators perform. Therefore, it is necessary to encourage investment in the technological breakthroughs of wind-power HESS to reduce the system’s operating cost. (3) The subsidy level has a meaningful influence on the value of wind-power HESS. The development of energy storage technology also relies on incentive policies (such as subsidies and tax incentives).

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author Contributions

QX participated in methodology, writing-reviewing, and editing. ZW performed conceptualization, establishing the framework, and supervision. YZ conducted simulation and writing original draft preparation. All authors contributed to the article and approved the submitted version.

Funding

This research was supported by the National Natural Science Foundation of China (grant no. 71904111), the Humanities and Social Sciences Program of Chinese Ministry of Education (grant nos. 19YJCZH106 and 20YJCZH201), and the Research Startup Fund of China University of Petroleum Beijing (grant no. ZX20200110).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary Material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2021.629136/full#supplementary-material.

References

Andrijanovits, A., and Beldjajev, V. (2012) “Techno-economic analysis of hydrogen buffers for distributed energy systems,” in Proceedings of 2012 international symposium on power electronics, electrical drives Sorrento, Italy, June 20-22, 2012 (Sorrento, Italy: Automation and Motion), 1401–1406.

Google Scholar

Apostolou, D., and Enevoldsen, P. (2019). The past, present and potential of hydrogen as a multifunctional storage application for wind power. Renew. Sustainable Energ. Rev. 112, 917–929. doi:10.1016/j.rser.2019.06.049

CrossRef Full Text | Google Scholar

Bakić Vukman, V., Pezo Milada, L., Jovanović Marina, P., and Turanjanin Valentina, M., Vučićević Biljana, S. (2012). Technical analysis of photovoltaic/wind systems with hydrogen storage. Thermal Sci. 16 (3), 865–875. doi:10.2298/TSCI120306132B

CrossRef Full Text | Google Scholar

Bakke, I., Fleten, S.-E., Hagfors, L. I., Hagspiel, V., and Norheim, B. (2016). Investment in mutually exclusive transmission projects under policy uncertainty. J. Commodity Markets. 3 (1), 54–69. doi:10.1016/j.jcomm.2016.08.002

CrossRef Full Text | Google Scholar

Bansal, S., Zong, Y., You, S., Mihet-Popa, L., and Xiao, J. S. (2020). Technical and economic analysis of one-stop charging stations for battery and fuel cell EV with renewable energy sources. Energies 13 (11), 15. doi:10.3390/en13112855

CrossRef Full Text | Google Scholar

Bergen, A., Pitt, L., Rowe, A., Wild, P., and Djilali, N. (2009). Transient electrolyser response in a renewable-regenerative energy system. Int. J. Hydrogen Energ. 34 (1), 64–70. doi:10.1016/j.ijhydene.2008.10.007

CrossRef Full Text | Google Scholar

Borovkova, S., and Schmeck, M. D. (2017). Electricity price modeling with stochastic time change. Energ. Econ. 63, 51–65. doi:10.1016/j.eneco.2017.01.002

CrossRef Full Text | Google Scholar

Buonomano, A., Calise, F., d’Accadia, M. D., and Vicidomini, M. (2018). A hybrid renewable system based on wind and solar energy coupled with an electrical storage: dynamic simulation and economic assessment. Energy 155, 174–189. doi:10.1016/j.energy.2018.05.006

CrossRef Full Text | Google Scholar

Chen, H., Cong, T. N., Yang, W., Tan, C., Li, Y., and Ding, Y. (2009). Progress in electrical energy storage system: a critical review. Prog. Nat. Sci. 19 (3), 291–312. doi:10.1016/j.pnsc.2008.07.014

CrossRef Full Text | Google Scholar

Denholm, P., and Sioshansi, R. (2009). The value of compressed air energy storage with wind in transmission-constrained electric power systems. Energy Policy. 37 (8), 3149–3158. doi:10.1016/j.enpol.2009.04.002

CrossRef Full Text | Google Scholar

Eckroad, S. (2003). EPRI-DOE handbook of energy storage for transmission and distribution applications. EPRI, Palo Alto, CA, and the US DOE, Washington, DC. Available at: https://www.researchgate.net/publication/267971650_EPRI-DOE_Handbook_of_Energy_Storage_for_Transmission_and_Distribution_Applications (Accessed November 12, 2020).

Google Scholar

Harrison, K. W., Martin, G. D., Ramsden, T. G., Kramer, W. E., and Novachek, F. J. (2009). Wind-to-hydrogen project: operational experience, performance testing, and systems integration, report, March 1, 2009; Golden, Colorado. Available at: https://digital.library.unt.edu/ark:/67531/metadc931214/ (Accessed November 12, 2020).

CrossRef Full Text | Google Scholar

Hassani, H., Zaouche, F., Rekioua, D., Belaid, S., Rekioua, T., and Bacha, S. (2020). Feasibility of a standalone photovoltaic/battery system with hydrogen production. J. Energ. Storage. 31, 6039. doi:10.1016/j.est.2020.101644

CrossRef Full Text | Google Scholar

Ipsakis, D., Voutetakis, S., Seferlis, P., Stergiopoulos, F., and Elmasides, C. (2009). Power management strategies for a stand-alone power system using renewable energy sources and hydrogen storage. Int. J. Hydrogen Energ. 34 (16), 7081–7095. doi:10.1016/j.ijhydene.2008.06.051

CrossRef Full Text | Google Scholar

Javed, M. S., Ma, T., Jurasz, J., and Amin, M. Y. (2020). Solar and wind power generation systems with pumped hydro storage: review and future perspectives. Renew. Energ. 148, 176–192. doi:10.1016/j.renene.2019.11.157

CrossRef Full Text | Google Scholar

Kelouwani, S., Agbossou, K., and Chahine, R. (2005). Model for energy conversion in renewable energy system with hydrogen storage. J. Power Sourc. 140 (2), 392–399. doi:10.1016/j.jpowsour.2004.08.019

CrossRef Full Text | Google Scholar

Loisel, R., Baranger, L., Chemouri, N., Spinu, S., and Pardo, S. (2015). Economic evaluation of hybrid off-shore wind power and hydrogen storage system. Int. J. Hydrogen Energ. 40 (21), 6727–6739. doi:10.1016/j.ijhydene.2015.03.117

CrossRef Full Text | Google Scholar

Mayyas, A., Wei, M., and Levis, G. (2020). Hydrogen as a long-term, large-scale energy storage solution when coupled with renewable energy sources or grids with dynamic electricity pricing schemes. Int. J. Hydrogen Energ. 45 (33), 16311–16325. doi:10.1016/j.ijhydene.2020.04.163

CrossRef Full Text | Google Scholar

Parra, D., Valverde, L., Pino, F. J., and Patel, M. K. (2019). A review on the role, cost and value of hydrogen energy systems for deep decarbonisation. Renew. Sustainable Energ. Rev. 101, 279–294. doi:10.1016/j.rser.2018.11.010

CrossRef Full Text | Google Scholar

Patrício, R. A., Sales, A. D., Sacramento, E. M., de Lima, L. C., and Veziroglu, T. N. (2012). Wind hydrogen energy system and the gradual replacement of natural gas in the State of Ceará – Brazil. Int. J. Hydrogen Energ. 37 (9), 7355–7364. doi:10.1016/j.ijhydene.2012.01.146

CrossRef Full Text | Google Scholar

Schoenung, S. (2011). Energy storage systems cost update: a study for the DOE energy storage systems program. Available at: https://prod-ng.sandia.gov/techlib-noauth/access-control.cgi/2011/112730.pdf (Accessed October 3, 2020).

CrossRef Full Text | Google Scholar

Shan, Y. L., Guan, D. B., Zheng, H. R., Ou, J. M., Li, Y., Meng, J., et al. (2018). China CO2 emission accounts 1997-2015. Sci.Data 5, 170201. doi:10.1038/sdata.2017.201

PubMed Abstract | CrossRef Full Text | Google Scholar

Steward, D., Saur, G., Penev, M., and Ramsden, T. (2009) Lifecycle cost analysis of hydrogen versus other technologies for electrical energy storage. United States. Available at: https://www.osti.gov/servlets/purl/968186 (Accessed September 3, 2020).

CrossRef Full Text | Google Scholar

Tang, L., Qu, J., Mi, Z., Bo, X., Chang, X., Anadon, L., et al. (2019). Substantial emission reductions from Chinese power plants after the introduction of ultra-low emissions standards. Nat. Energ. 4 (11), 929–938. doi:10.1038/s41560-019-0468-1

CrossRef Full Text | Google Scholar

Twaha, S., and Ramli, M. A. M. (2018). A review of optimization approaches for hybrid distributed energy generation systems: off-grid and grid-connected systems. Sustainable Cities Soc. 41, 320–331. doi:10.1016/j.scs.2018.05.027

CrossRef Full Text | Google Scholar

Yu, N., and Foggo, B. (2017). Stochastic valuation of energy storage in wholesale power markets. Energ. Econ. 64, 177–185. doi:10.1016/j.eneco.2017.03.010

CrossRef Full Text | Google Scholar

Zhao, Y., Cao, Y., Shi, X., Li, H., Shi, Q., and Zhang, Z. (2020). How China's electricity generation sector can achieve its carbon intensity reduction targets?. Sci. Total Environ. 706, 135689. doi:10.1016/j.scitotenv.2019.135689

PubMed Abstract | CrossRef Full Text | Google Scholar