- 1School of Electrical Engineering, Zhengzhou University, Zhengzhou, China
- 2CAS Key Laboratory of Human-Machine Intelligence-Synergy Systems, Shenzhen Institutes of Advanced Technology, Shenzhen, China
- 3Guangdong Provincial Key Lab of Robotics and Intelligent System, Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen, China
- 4Ultrasonic Nondestructive Engineering Technology Research Center of Guangdong, Shenzhen, China
- 5Shenzhen Institutes of Advanced Technology, Chinese Academy of Sciences, Shenzhen, China
- 6University of Chinese Academy of Sciences, Beijing, China
With the development of society, the demand for energy keeps increasing. Solar energy has received widespread concern for its renewable and environmentally friendly advantages. As one of the most efficient solar energy devices, the output power of photovoltaic (PV) cells is easily affected by the external environment. In order to solve the problem of the maximum power output of PV cells, this paper proposed a maximum power point tracking (MPPT) method. Based on the online particle swarm optimization (PSO) variable step length algorithm, the pulse width modulation (PWM) control module parameters are set according to the parameters of the PV cells’ output voltage. By dynamically adjusting the output voltage step of the PV cells online, the output of the PV cells is stabilized near the maximum power point (MPP). The simulation results concluded that the method and model could accurately adjust the output voltage according to the external environment changes in real time and reduce the voltage fluctuation at the MPP, providing a new idea to solve the problem of MPPT of PV cells.
1 Introduction
The energy demand increases with society’s development, yet the increasing depletion of fossil fuels cannot meet long-term growth. Moreover, fossil fuels’ application will also bring serious adverse effects, such as the greenhouse effect and environmental pollution (Bavarinos et al., 2021). Therefore, renewable energy has slowly broken traditional energy status with an enhanced eco-friendly philosophy (Zeeshan Tariq et al., 2021). One of the more essential energy sources is PV systems in nature. Over the last decades, governments worldwide are growing the share of PV technology to deal with energy demands competitively. With the advent of modern technology for PV cells, it has been one of the most promising solutions to address growing electricity needs (Pathak and Yadav, 2019). PV cells are a specialized semiconductor diode electronic device that converts light energy into electrical energy using various chemical and physical phenomena. The voltage output of PV cells is affected by their characteristics, external temperature, and irradiation. What’s more, PV cells have only one maximum power output point. Since physical factors such as solar radiation and temperature affect PV cells’ performance characteristics, the maximum power point (MPP) of PV cells may be different (Nguyen et al., 2020). The research on MPP of PV cells has become a hot topic.
Currently, the main methods of PV cells maximum power point tracking (MPPT) technology can divide into three categories: 1) mathematical models; 2) self-optimizing control algorithms; 3) intelligent algorithms (Ishaque and Salam, 2013). In (Desai and Patel, 2007), constant voltage tracking (CVT) and constant current tracking (CIT) based on PV cells’ mathematical models are applied to predict the voltage or current at the MPP of PV cells under different external conditions such as light intensity and temperature. MPP prediction only needs to detect the parameters such as the light intensity and radiation intensity in the actual operation of PV cells, which can be obtained with the look-up table method and interpolation calculation. In (Serrano-Guerrero et al., 2016), fixed voltage and fixed current methods have the advantages of low computational complexity and fast-tracking of maximum power, yet they have apparent shortcomings. It is challenging to keep PV cells’ characteristics unchanged after a long operation as the maximum power is an approximate value, causing error accumulation. In (Liu et al., 2018), an MPPT algorithm is proposed that combines an improved constant voltage algorithm with an enhanced variable step-length incremental conductance algorithm. The self-adaptive topology is designed to make the system get a better working condition. The results show that the mothed could improve the efficiency of PV power generation. On the other hand, the self-optimizing control algorithms’ main application is the open-circuit voltage proportional coefficient method (Kumar et al., 2019), the perturb and observe (P and O) method (Alik and Jusoh, 2018), and the conductance increment method (Jeong et al., 2012). The method is mainly realized by self-optimizing maximum power optimization based on PV cells’ equivalent and external characteristics while combining control theory (Hossain et al., 2016). In (Zhou et al., 2010), this article pointed out the voltage step is fixed, which will not stop the judgment after finding MPP but will continue to move with the originally fixed-step. If the step size is not selected correctly, large power fluctuations will occur near MPP, causing unnecessary loss of output power. If the step size chosen is short, the power oscillation at MPP will slow down to a certain extent, and the tracking speed will significantly reduce to a certain extent. On the other hand, many intelligent optimization algorithms have been applied to MPPT of PV cells. In (Mansoor et al., 2020), a grass hopper optimization (GHO) algorithm was proposed to solve the problem of MPPT of PV cells in complex environments. The article compared several traditional methods under different conditions and points out the shortcomings of the prior techniques in dealing with complex partial shading conditions. The analysis results show that the GHO algorithm has good robustness, high tracking efficiency, can reduce oscillation, and the tracking effect is within an acceptable range. Hassan et al. (2020) pointed out that PV cells as a renewable energy source have received more and more attention, but due to changes in the external environment, there are uncertainties in the modeling and MPPT of PV cells. In order to solve this problem, this article proposed an isolated PV system using a push pull converter with the fuzzy logic-based MPPT algorithm. The method achieved smooth tracking of output power near the MPP. A fuzzy logic closed loop controller was introduced to improve the power quality of the AC voltage through a current fed push pull boost converter circuit with a higher conversion ratio. The experimental results show that the method can track the MPP well and reduce the circuit loss. In (Danandeh and Mousavi, 2018), compared with the traditional P and O method, the fuzzy logic control algorithm improves the tracking efficiency, and it also has advantages in robustness and environmental adaptability. The above methods have achieved significant results in MPPT of PV cells. However, the fuzzy control method also have apparent shortcomings, which relies too much on selecting fuzzy rules and rich experience. In (Javed et al., 2019), the article gives a detailed introduction to the single diode, double diode, and PV components system. Then tests the output characteristics of PV cells under the uniform irradiance condition (UIC) and partial shading condition (PSC) conditions. The control circuit commonly used in tracking the PV cells’ MPP is explained. The author points out that there are many existing methods for solving the MPPT issue, including the factional short circuit current (FSCC) (Feroz Mirza et al., 2019), hill climbing (HC) (Alajmi et al., 2010) method, incremental conductance (Inc.) (Radjai et al., 2014) technique, and intelligent algorithms and so on. The article focuses on explaining the basic principles of each method, giving many alternative technologies for using intelligent algorithms to solve the MPPT problem. Finally, the paper proves the method through simulation experiments and compared them with each other. The realization of intelligent algorithms such as neural network method and ant colony optimization algorithm often requires a long operation cycle and hardware platform with good performance, which hinders their application in control systems to a certain extent.
In order to better solve the problem of MPPT of PV cells, this paper proposed a PWM variable carrier PV cells power optimization control method based on the online PSO variable step length. The optimal power control strategy based on a real-time change of the voltage step size is adopted, and the optimal voltage value at MPP of each operation is searched online. The voltage step obtained is more accurate, stable than CVT and CIT. Compared to the fixed step method, the step-length of the voltage value optimized with the above control strategy is not static but based on actual conditions. If the output power is far away from MPP, the voltage step-length will change considerably, and the output power closes to MPP, the voltage step-length will vary slightly, which makes the output power value update online in real-time. Finally, realize real-time control power, reduce output fluctuation, and improve tracking accuracy and efficiency. The control method adjusts the carrier module in PWM for different PV cells parameters to generate a better duty cycle signal that controls the switching device to turn on-off and further optimizes the MPPT problem.
The main contributions of this paper are as follows:
1) A novel technique for MPPT of PV cells is proposed, which can effectively reduce output fluctuations and increase the speed of convergence.
2) The output of PV cells under different external conditions was tested.
3) The comprehensive experiment is used to compare the method with the traditional MPPT method.
The organization of the rest is arranged as follows. Section 2 describes PV cells’ mathematical models and simulates in Matlab. The optimization method of MPP is introduced in Section 3. The results and analysis in Section 4. Section 5 presents the conclusions.
2 The Mathematical Model of PV Cells
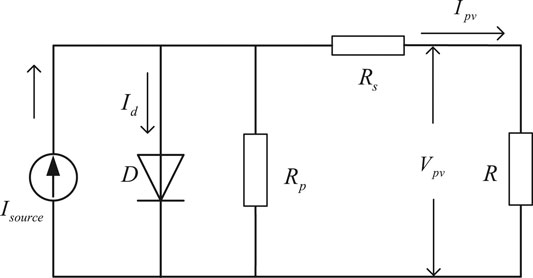
The photoelectric phenomenon is PN junction of PV cells through certain materials. They can transfer the energy of sunlight photons to electrical power. PV cells are a more effective way to directly use solar energy—the typical equivalent circuit shown in Figure 1 (Alghamdi et al., 2021). Kirchhoff’s current law (KCL) is applied to the equivalent circuit of solar cells in Figure 1, and the output equation of the PV cells can be obtained as shown in Eq. 1.
Where Iph is the photocurrent (A), Isat represents the diode saturation current (A), and η is the diode ideal factor. Vt (Vt = kT/q) is the thermal voltage (V), k is the Boltzmann constant (1.38 × 10−23J/K), T is the surface temperature of the PV panel (K), and q represents the electron charge (1.6 × 1019C). Some PV cells’ parameters are treated approximately to meet actual engineering and research needs. The basic equations describing the I − V characteristic are given in the following equations (Humada et al., 2020).
Where Ipv is PV cells output current (A), Isc represents PV cells short circuit current (A), Im is PV cells maximum power point current (A). Vpv denotes PV cells output voltage (V), Vm is PV cells maximum power point voltage (V), Voc represents PV cells open circuit voltage (V).
When PV cells work under the nominal condition (temperature T = 25°C, irradiation S = 1000W/m2), the manufacturer datasheet can provide the short-circuit current, the maximum power point current, the open-circuit voltage, and the maximum power point voltage. The values of C1 and C2 can be calculated by Eqs 3, 4 and then substituting Eq. 2 to describe the I − V curve of PV cells. But in the real environment, it is difficult for PV cells to work in the reference conditions, and environment temperature T and irradiation S will change with time. In this case, PV cells’ parameters are calculated as follows (Deveci and Kasnakoğlu, 2016).
Where, T and S are the nominal temperature and the nominal irradiation. α, β, γ are battery parameters and coefficients under standard conditions.
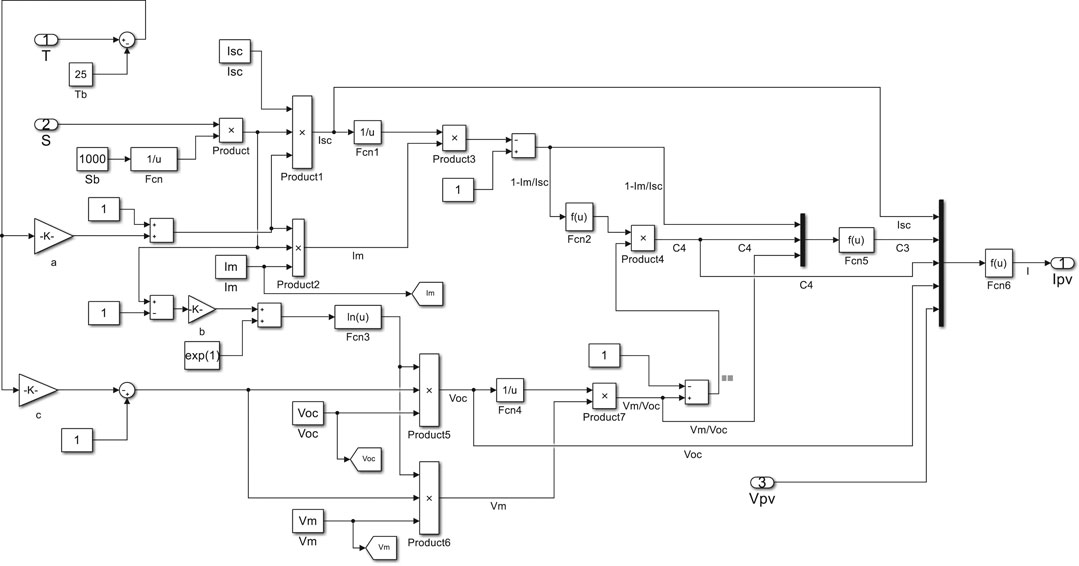
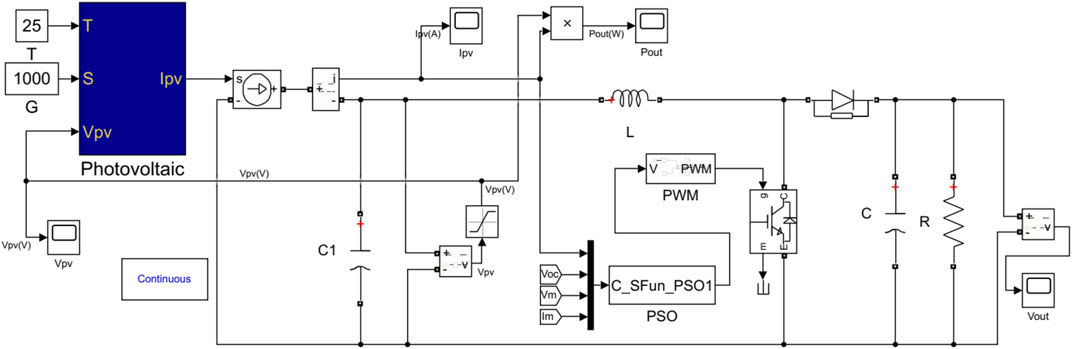
According to Eq. 2 ∼ Eq. 10, the model of PV cells can be established by using Matlab/Simulink (Xiao et al., 2012). The internal structure is shown in Figure 2. The battery contains some parameters: Tref, Sref, Isc′, Im′, Voc′, Vm′, and α, β, γ, which given by manufacturer datasheet. The external input parameters are the temperature T, the irradiation S, the input voltage Vpv in the current environment, and the output current Ipv.
3 MPPT of PV Cells
3.1 The Application of the Boost Circuit in MPPT
Under certain temperatures and light conditions, the output curve of the PV cells is always changing. When PV cells work at the MPP, the output power Pout = Pm to go along with Vpv = Vm and Ipv = Im. However, PV cells can work at MPP depends on the load because the external environmental factors usually can’t be changed artificially. During the working process of PV cells, the temperature and irradiation are constantly changing, so the output characteristics of PV cells and MPP will change accordingly. In order to find MPP quickly and make PV cells work at MPP, it is necessary to change the external load by controlling the terminal voltage of PV cells.
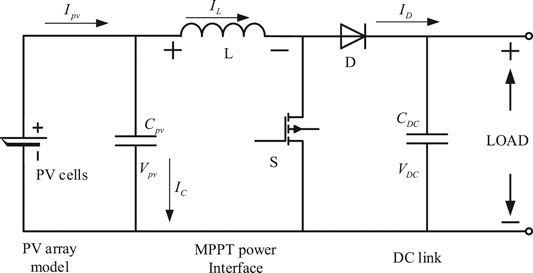
With the development of electronic technology, MPPT control of PV cells is completed generally with a DC-DC conversion circuit. In this paper, the Boost circuit is used as the DC-DC conversion circuit in the PV cells system (Amir et al., 2018), which can be stabilized the system output voltage via adjusting the terminal voltage and output the circuit’s voltage for later use. The boost circuit diagram structure is shown in Figure 3.
In DC-DC circuit, the impedance relationship is as follows.
Where, Rin is the input impedance of the converter. R represents the load impedance of the converter. D denotes the duty cycle of the switching device itself, regardless of the power loss of the Boost circuit itself. It can see from Eq. 11 that when the load impedance of the Boost circuit remains unchanged, the bigger the duty cycle D, the smaller the input impedance of the Boost circuit, and the smaller the duty cycle D, the larger the input impedance of the Boost circuit (Pires et al., 2016). The equivalent impedance Rm of PV cells can be changed by adjusting the duty cycle D of the switching device. The circuit knowledge knows that when the external circuit’s load impedance is equal to PV cells’ equivalent impedance, the system has the maximum power output (HA et al., 2016). Therefore, it is necessary to keep the equivalent resistance of the DC-DC conversion circuit always equal to the PV cell’s internal resistance and achieve MPPT of PV cells to meet the maximum output.
3.2 Online Variable Step-Length PSO in MPPT
3.2.1 Introduction to the Particle Swarm Optimization
The particle swarm optimization (PSO) algorithm is a swarm intelligence algorithm developed by Kennedy and Eberhardt in 1995 and inspired by the social behavior of flocking birds and schooling fishes (Kennedy and Russell, 1995; del Valle et al., 2008). Compared with other random methods such as a genetic algorithm, particle swarm optimization can quickly get higher-quality solutions, and these solutions have convergence characteristics (Femia et al., 2004). The mathematical description of PSO could be known. Suppose a population of m individuals in an N-dimensional search space
Where, i = 1, 2, … , n and n is the size of the population. d is the dimension of the search space. k represents the iteration number. c1 is the individual optimal coefficient, c2 is the individual global coefficient. ω represents the weight of inertia. r1 and r2 are random numbers which are uniformly distributed in (0,1). p1 represents the local optimum and pg represents the best individual among all the particles at every generation.
3.2.2 Initialization in MPPT System
Considering the system model and the power optimization problem, the number of particle groups can set to 20, and each particle’s iteration number is 100. The choice of individual optimal coefficient, global optimal coefficient, and inertia weight is significant to the algorithm’s calculation process. The c1 and c2 should have a strong self-cognition ability and maintain the information interaction ability between various particles. The choice of inertia weight ω should make the algorithm have excellent searchability. Therefore, considering comprehensively, define the particle individual optimal coefficient c1 = 0.5, the optimal global coefficient c2 = 0.5, and the inertia weight ω = 0.8. The particle represents the output voltage of PV cells, which is initialized randomly at first. The initial position and next position of particles need to be restricted considering the actual situation. The output voltage value of PV cells is specified in (0,V) to make it change within a reasonable range, which is (0, 35.4). Each particle movement’s velocity is limited to (−1, 1) to ensure particle search effectiveness.
After the particles’ initialization is completed, the system needs to select an appropriate objective function. In MPPT of PV cells, the output current Ipv of the circuit can be calculated according to Eq. 2 ∼ Eq. 10, and the fitness function can determine as Eq. 14.
3.2.3 Online PSO Variable Step-Length Control
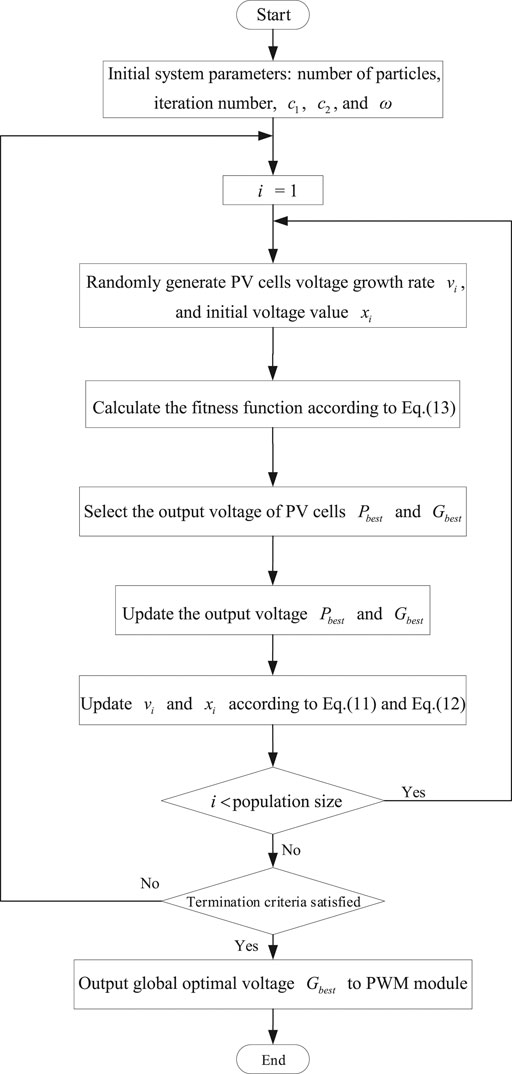
Through the previous analysis, the PV cell’s output current Ipv is connected as an input of the PSO module, brought into the fitness function to calculate. The PSO is used to perform online random initialization of the particle position, that is, to complete the random value of PV cells voltage online in real-time. Then, calculate the fitness function based on the input current value of PV cells. The optimal voltage value after each particle movement is regarded as the PSO module’s output. The PSO module’s optimal voltage output value is then used as the input of the PWM module. The processes mentioned above are all completed online in real-time to achieve real-time online control of PV cells’ output power.
In the PWM module, the voltage step-length is updated online instead of constant since the voltage input will change relative to the last voltage every time. Then, setting corresponding carrier parameters and combining the real-time input voltage value, the switching device’s duty ratio signal is synthesized to realize the switching device’s conduction and turn-off functions in the circuit. When Ipv = Im and Vpv = Vm, the output power Pout = Pm. Meanwhile, if Vpv < Vm, the power Pout will increase with the increase of the voltage. At this time, the PSO module needs to increase the voltage output. That is, increasing the step-length of the voltage. If Vpv > Vm, the power Pout will decrease as the voltage increases. It is necessary to reduce the voltage output through the PSO module, that is, reducing the voltage step-length. Finally, it is converted into the signal’s duty cycle for controlling the switching device in the PWM module. Among them, the output current Ipv of PV cells is sampled in real-time in each period, and the voltage of PV cells is randomly selected by PSO and real-time online update in each optimization. The output voltage will also affect the output current so that PSO is used to adjust the optimization step until the output current Ipv and output voltage Vpv corresponding to the maximum power Pm are found. The MPPT control method using online PSO to change the voltage step-length is shown in Figure 4.
3.3 Variable Carrier PWM in MPPT
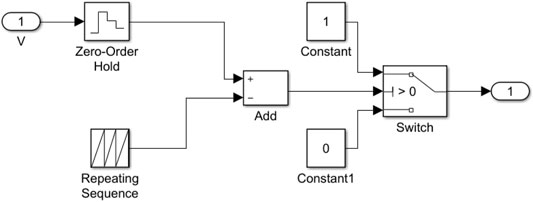
In order to obtain a better control effect and stabilize the output power of PV cells near the maximum power point, it is necessary to control the duty cycle signal generated by the PWM module. The PWM module’s working principle is to sample the optimal voltage value output by PSO, and this voltage value is the input signal of the PWM module. When this voltage signal is input, it is converted into the duty cycle signal controlling the switching device to turn off or turn on through the zero-order holder and other corresponding links.
When the voltage signal is available, it is combined with the set carrier signal. Then the corresponding conversion is carried out through the following links to generate the corresponding duty cycle signal. Since the signal is collected and changed in real-time, the PSO module’s voltage signal output will not be constant but will constantly be updated and changed in real-time. So, the voltage value input to the PWM module is also continually changing. Completes the maximum power control of PV cells using variable step PSO and realizes the change of the output voltage step-length. For battery modules with different parameters or PV cells with variable parameters, if a constant carrier wave is used to generate the duty cycle signal for controlling the switching device, the maximum power point tracking effect is relatively low. Therefore, the relationship between the carrier signal and the corresponding parameters of PV cells are searched. Through a lot of experiments and observations, it is found that the relationship between the PWM carrier module and the voltage of PV cells at MPP has a relationship as Eq. 15.
Where: A is the amplitude of the carrier wave in the PWM module, and Vm is the maximum power point voltage of PV cells.
4 MPPT Simulation Analysis of PV Cells
4.1 System Simulation Model and Parameters
The above analysis and the system’s simulation model are established in the Matlab/Simulink based on the mathematical model, as shown in Figure 5. In the simulation, the parameters of PV cells under standard conditions and Boost current parameters are illustrated in Table 1. The module structure diagram of PWM wave generation is shown in Figure 6. The parameters of the PWM module are: the sampling period of the zero-order holder is 0.0005.
4.2 Results When the Temperature Changes
Figure 7 shows the variation curve of PV cells’ online output current Ipv, voltage Vpv, power Pout, Boost circuit output voltage Vout when the temperature changes. In the simulation model, the temperature parameter PV cells reduces from 50°C to 25°C in 0.3 s and to 15°C in 0.7 s. It can be known from Figure 7. In different temperature conditions, the output of PV cells can stabilize in real-time, and MPP can be well tracked. The change of temperature has little effect on the output of PV cells. When the temperature drops and PV cells achieve MPPT, the output current and voltage both increase slightly, the maximum output power is also increased slightly. The output voltage of the Boost circuit increased. For detailed data, please refer to the Supplementary Material.
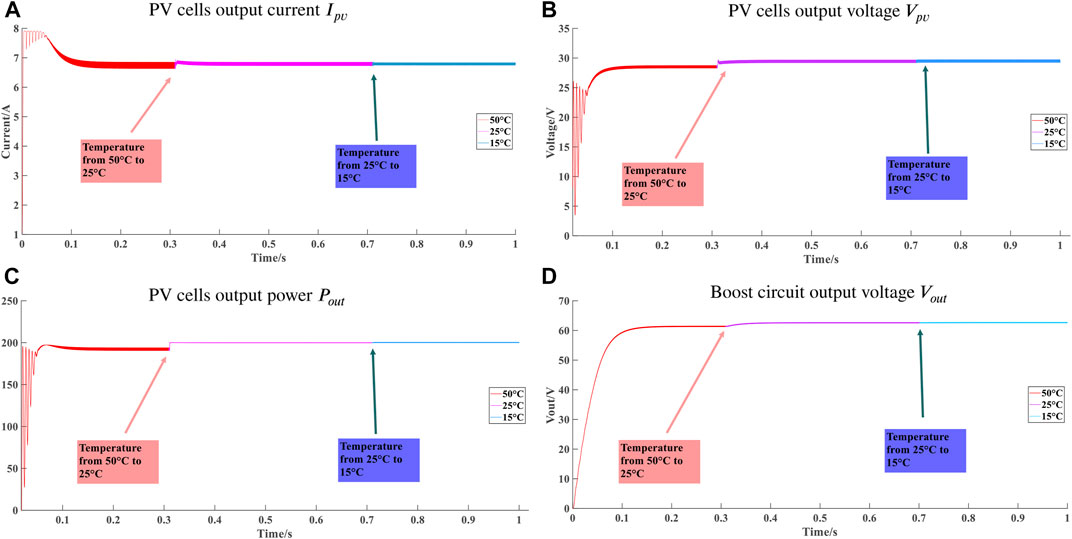
FIGURE 7. The output waveform of PV cells when the temperature changes\enleadertwodots. (A) PV cells output current Ipv. (B) PV cells output voltage Vpv. (C) PV cells output power Pout. (D) Boost circuit output voltage Vout.
4.3 Results When the Irradiation Changes
Figure 8 shows the variation curve of the output current Ipv, voltage Vpv, PV cells’ output power Pout, and the Boost circuit output voltage Vout under the change of irradiation. In the simulation model, the irradiation parameter of PV cells reduced from 1200 W/m2 to 1000 W/m2 at 0.3 s and to 800 W/m2 at 0.7 s. The output of PV cells can stabilize in real-time with the irradiation changes, and MPP can be well tracked. The irradiation has a more significant impact on the output of PV cells. When light intensity dropping and PV cells tracking MPP, the output of current and voltage all decrease to some extent, and the maximum output power decrease significantly. The output voltage of the Boost circuit significantly reduces. For detailed data, please refer to the Supplementary Material.
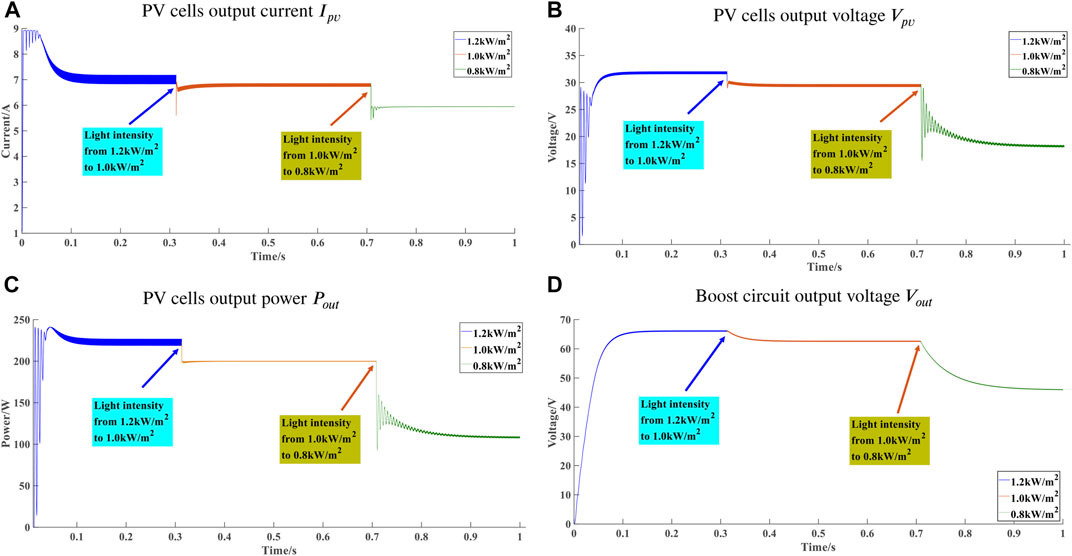
FIGURE 8. The output waveform of PV cells when the irradiation changes. (A) PV cells output current Ipv. (B) PV cells output voltage Vpv. (C) PV cells output power Pout. (D) Boost circuit output voltage Vout.
4.4 Analysis of Comparative Results
The above analysis results are consistent with the analysis of the characteristics of PV cells. In addition, to further illustrate the role of the method used for MPPT, Table 2 lists the maximum (MAX)/minimum (Min) fluctuations and rates of change between the PV cells output at MPP and the given parameters under the standard conditions. When the method proposed in this paper is used to MPPT of PV cells under standard conditions, the maximum and minimum fluctuations of output current Ipv, output voltage Vpv and output power Ppv obtained are all within a controllable range. Compared with the rated values, the relative error between them is small, and the error accounts for a considerable proportion of the rated values, which can meet the actual demand.
In order to illustrate the effect of the proposed method to reduce the fluctuation in the process of MPPT. Compared with the traditional P and O method, the results are shown in Figure 9. As can be seen from the figure, when the system is tracking MPP, the online PSO method can reduce the fluctuation at the beginning of the system, and reach MPP at a faster convergence. When the system reaches MPP, the online PSO method can reduce the output fluctuation of the system and has a more stable output waveform than the traditional P and O method. The stability of Ipv, Vpv, Pout, Vout has a smaller fluctuation range. The method adopted in this paper has shorter adjustment time, higher tracking accuracy, faster response speed, better real-time, and better control effects when the process of MPPT.
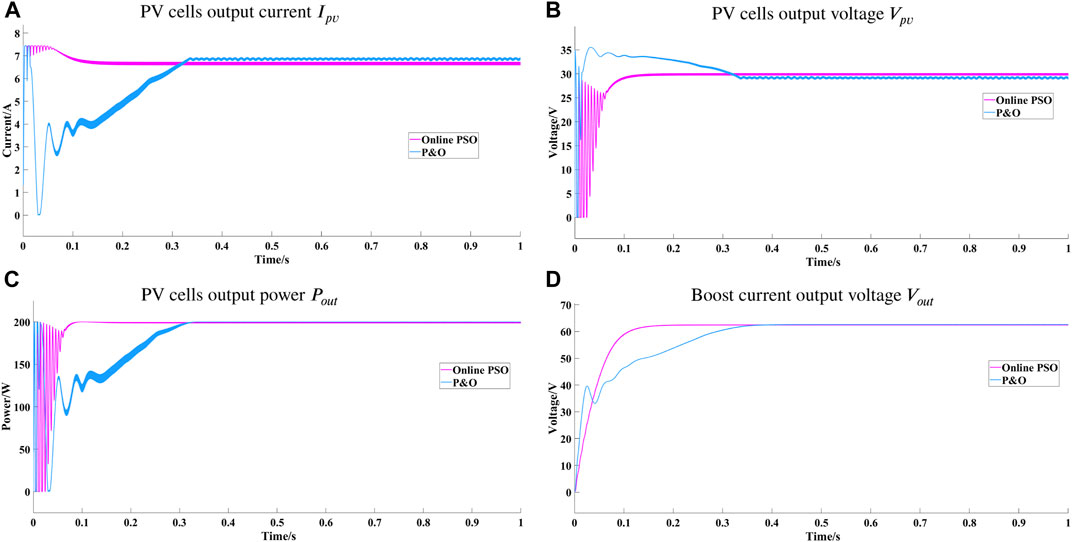
FIGURE 9. Comparison of online PSO and P and O results under the standard conditions. (A) PV cells output current Ipv. (B) PV cells output voltage Vpv. (C) PV cells output power Pout. (D) Boost current output voltage Vout
5 Conclusion
This paper proposed a PWM variable carrier power optimization control scheme based on the online PSO variable step size. A general model of PV cells was established through the analysis of the PV cells model and practical mathematical expressions, and the model was simulated and analyzed. Online PSO varible step length was used to change the step length of the output voltage. Real-time online optimization control of the PV cells’ MPP is realized by controlling the Boost circuit switching device’s duty cycle. Analyzed the specific realization principle and gave the realization process, and got a better control effect at MPP. The product was compared with the traditional P and O method. The results illustrate that the control strategy and the optimization module can judge MPP in real-time, find the optimal voltage value online, and change the step length of the output voltage. Finally, the PV cells’ output power can be stabilized at MPP. The output voltage of the Boost circuit can change with the change of the external environment to achieve an excellent real-time online tracking effect.
Data Availability Statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding authors.
Author Contributions
JZ: Methodology, Investigation, Writing-review and editing. YZ: Investigation, Conceptualization. SZ: Methodology, Investigation. YG: Software, Validation. ZY: Software, Funding acquisition, Writing-review and editing. WF: Investigation, Funding acquisition.
Funding
The authors are grateful for the financial support from the Guangdong-Hong Kong-Macao Joint Laboratory of Human-Machine Intelligence-Synergy Systems (#2019B121205007), the Science and Technology Innovation Commission of Shenzhen (No.ZDSYS20190902093209795), National Natural Science Foundation of China (No.U1813222), Shenzhen Science and technology project (JSGG20191118115801739), Guangdong Frontier and Key Technological Innovation (No. 2017B090910013), the Science and Technology Innovation Commission of Shenzhen (No.JCYJ20170818153048647 and No. JCYJ20180507182239617, JCYJ2018050718 223961).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2021.685415/full#supplementary-material
References
Alajmi, B. N., Ahmed, K. H., Finney, S. J., and Williams, B. W. (2010). Fuzzy-logic-control Approach of a Modified hill-climbing Method for Maximum Power point in Microgrid Standalone Photovoltaic System. IEEE Trans. Power Electron. 26 (4), 1022–1030. doi:10.1109/TPEL.2010.2090903
Alghamdi, M. A., Nadeem Khan, M. F., Ahmed, Khalil., Khan, Irfan., Ahmed, Ali., Tariq Kiani, A., et al. (2021). Pv Model Parameter Estimation Using Modified Fpa with Dynamic Switch Probability and Step Size Function. IEEE Access 9, 42027–42044.
Alik, R., and Jusoh, A. (2018). An Enhanced P&O Checking Algorithm MPPT for High Tracking Efficiency of Partially Shaded PV Module. Solar Energy 163, 570–580. doi:10.1016/j.solener.2017.12.050
Amir, A., Che, H. S., Amir, A., El Khateb, A., and Rahim, N. A. (2018). Transformerless High Gain Boost and Buck-Boost Dc-Dc Converters Based on Extendable Switched Capacitor (Sc) Cell for Stand-Alone Photovoltaic System. Solar Energy 171, 212–222. doi:10.1016/j.solener.2018.06.078
Bavarinos, K., Dounis, A., and Kofinas, P. (2021). Maximum Power point Tracking Based on Reinforcement Learning Using Evolutionary Optimization Algorithms. Energies 14 (2), 335. doi:10.3390/en14020335
Bechouat, M., Soufi, Y., Sedraoui, M., and Kahla, S. (2015). Energy Storage Based on Maximum Power point Tracking in Photovoltaic Systems: a Comparison between Gas and Pso Approaches. Int. J. Hydrogen Energ. 40 (39), 13737–13748. doi:10.1016/j.ijhydene.2015.05.008
Danandeh, M. A., and Mousavi, S. M. (2018). A New Architecture of Inc-Fuzzy Hybrid Method for Tracking Maximum Power point in Pv Cells. Solar Energy 171, 692–703. doi:10.1016/j.solener.2018.06.098
del Valle, Y., Venayagamoorthy, G. K., Mohagheghi, S., Hernandez, J.-C., and Harley, R. G. (2008). Particle Swarm Optimization: Basic Concepts, Variants and Applications in Power Systems. IEEE Trans. Evol. Computat. 12 (2), 171–195. doi:10.1109/tevc.2007.896686
Desai, H. P., and Patel, H. K. (2007). “Maximum Power point Algorithm in Pv Generation: An Overview,” in 2007 7th International Conference on Power Electronics and Drive Systems (IEEE), 624–630. doi:10.1109/peds.2007.4487766
Deveci, O., and Kasnakoğlu, C. (2016). Performance Improvement of a Photovoltaic System Using a Controller Redesign Based on Numerical Modeling. Int. J. Hydrogen Energ. 41 (29), 12634–12649. doi:10.1016/j.ijhydene.2016.05.149
Femia, N., Petrone, G., Spagnuolo, G., and Vitelli, M. (2004). “Optimizing Duty-Cycle Perturbation of P&o Mppt Technique,” in IEEE 35th Annual Power Electronics Specialists Conference (IEEE Cat. No. 04CH37551) (IEEE), Vol. 3, 1939–1944.
Feroz Mirza, A., Ling, Q., Yaqoob Javed, M., and Mansoor, M. (2019). Novel Mppt Techniques for Photovoltaic Systems under Uniform Irradiance and Partial Shading. Solar Energy 184, 628–648.
Ha, M., Ha, K., Mobarka, A., and Morsy, G. A. (2016). “Design, Control and Performance Analysis of Dc-Dc Boost Converter for Stand-Alone Pv System,” in 2016 Eighteenth International Middle East Power Systems Conference (MEPCON) (IEEE), 101–106. doi:10.1109/mepcon.2016.7836878
Hassan, T-l., Abbassi, R., Jerbi, H., Mehmood, K., Faizan Tahir, M., Mehmood Cheema, K., et al. (2020). A Novel Algorithm for Mppt of an Isolated Pv System Using Push Pull Converter with Fuzzy Logic Controller. Energies 13 (15), 4007.
Hossain, M. J., Tiwari, B., and Bhattacharya, I. l. (2016). “An Adaptive Step Size Incremental Conductance Method for Faster Maximum Power point Tracking,” in 2016 IEEE 43rd Photovoltaic Specialists Conference (PVSC) (IEEE), 3230–3233. doi:10.1109/pvsc.2016.7750262
Humada, A. M., Darweesh, S. Y., Mohammed, K. G., Kamil, M., Mohammed, S. F., Kasim, N. K., et al. (2020). Modeling of Pv System and Parameter Extraction Based on Experimental Data: Review and Investigation. Solar Energy 199, 742–760. doi:10.1016/j.solener.2020.02.068
Ishaque, K., and Salam, Z. (2013). A Review of Maximum Power point Tracking Techniques of Pv System for Uniform Insolation and Partial Shading Condition. Renew. Sustain. Energ. Rev. 19, 475–488. doi:10.1016/j.rser.2012.11.032
Javed, M. Y., Mirza, A. F., Hasan, A., Rizvi, S. T. H., Ling, Q., Gulzar, M. M., et al. (2019). A Comprehensive Review on a Pv Based System to Harvest Maximum Power. Electronics 8 (12), 1480. doi:10.3390/electronics8121480
Jeong, D-E., Ko, J-S., Lee, J-G., and Chung, D-H. (2012). “Mppt Control of Photovoltaic System Using Optimization Voltage with Temperature,” in 2012 12th International Conference on Control, Automation and Systems (IEEE), 1139–1143.
Kennedy, J., and Russell, E. (1995). “Particle Swarm Optimization,” in Proceedings of ICNN’95-international conference on neural networks (IEEE), Vol. 4, 1942–1948.
Kumar, R., Khandelwal, S., Upadhyay, P., and Subrahmanyam, P. (2019). Global Maximum Power point Tracking Using Variable Sampling Time and Pv Curve Region Shifting Technique along with Incremental Conductance for Partially Shaded Photovoltaic Systems. Solar Energy 189, 151–178.
Liu, Y., Gong, M., Liang, L., Liu, Q., and Gao, Y. (2018). Research and Design of Low-Power Grid-Connected Pv Power Generation System Based on Automatic Solar Tracking. Syst. Sci. Control. Eng. 6 (3), 278–288. doi:10.1080/21642583.2018.1553692
Mansoor, Majad., Adeel Feroz Mirza, , Ling, Qiang., and Yaqoob Javed, M. (2020). Novel Grass Hopper Optimization Based Mppt of Pv Systems for Complex Partial Shading Conditions. Solar Energy 198, 499–518.
Nguyen, B. N., Nguyen, V. T., Duong, M. Q., Hung Le, K., Nguyen, H. H., and Doan, A. T. (2020). Propose a Mppt Algorithm Based on Thevenin Equivalent Circuit for Improving Photovoltaic System Operation. Front. Energ. Res. 8 (14). doi:10.3389/fenrg.2020.00014
Pathak, P. K., and Yadav, A. K. (2019). Design of Battery Charging Circuit through Intelligent Mppt Using Spv System. Solar Energy 178, 79–89. doi:10.1016/j.solener.2018.12.018
Pires, V. Fernão., Foito, Daniel., Baptista, F. R. B., and Silva, J. Fernando. (2016). A Photovoltaic Generator System with a Dc/dc Converter Based on an Integrated Boost-Ćuk Topology. Solar Energy 136 (1–9). doi:10.1016/j.solener.2016.06.063
Radjai, T., Rahmani, L., Mekhilef, S., and Gaubert, J. P. (2014). Implementation of a Modified Incremental Conductance Mppt Algorithm with Direct Control Based on a Fuzzy Duty Cycle Change Estimator Using Dspace. Solar Energy 110, 325–337. doi:10.1016/j.solener.2014.09.014
Serrano-Guerrero, X., González-Romero, J., Cárdenas-Carangui, X., and Escrivá-Escrivá, G. (2016). “Improved Variable Step Size P&o Mppt Algorithm for Pv Systems,” in 2016 51st International Universities Power Engineering Conference (UPEC) (IEEE), 1–6. doi:10.1109/upec.2016.8114046
Xiao, W., Fongang Edwin, F., Spagnuolo, G., and Jatskevich, J. (2012). Efficient Approaches for Modeling and Simulating Photovoltaic Power Systems. IEEE J. photovoltaics 3 (1), 500–508.
Zeeshan Tariq, M., Rahman, S., Khan, I. A., and Khan, F. N. (2021). “Pv Fed Battery and Ultra-capacitor Based Hybrid Energy Storage for Powering marine Loads,” in International Conference on Digital Futures and Transformative Technologies (ICoDT2) (IEEE), 1–6. doi:10.1109/icodt252288.2021.94414792021
Zhou, X., Song, D., Ma, Y., and Cheng, D. (2010). “The Simulation and Design for Mppt of Pv System Based on Incremental Conductance Method,” in 2010 WASE international conference on information engineering (IEEE), Vol. 2 314–317.
Nomenclature
A carrier wave amplitude
CIV constant current tracking
CVT constant voltage tracking
D switching device duty cycle
F objective function
Im PV cells maximum power point current
Ipv PV cells output current
Isc PV cells short circuit current
Isource photocurrent
Max maximum
Min minimum
MPP miximum power point
MPPT miximum power point tracking
Pm maximum power point power
Pout PV cells output power
PSO particle swarm optimization
P and O perturb and observe method
PV photovoltaic
PWM pulse width modulation
R converter load impedance
rand random numbers in (0,1)
Rin converter input impedance
Rm PV cells equivalent impedance
S irradiation
T temperature
Vm PV cells maximum power point voltage
Voc PV cells open circuit voltage
Vout Boost circuit output voltage
Vpv PV cells output voltage
Vt thermal voltage
α battery parameters
β battery parameters
γ battery coefficients
Keywords: photovoltaic cell, particle swarm optimization, maximum power point tracking, variable step size, variable carrier
Citation: Zhou J, Zhang Y, Zhang S, Guo Y, Yang Z, Feng W and Zhang Y (2021) A Novel Maximum Power Point Tracking Strategy Based on Enhanced Real-Time Adaptive Step-Size Modified Control for Photovoltaic Systems. Front. Energy Res. 9:685415. doi: 10.3389/fenrg.2021.685415
Received: 25 March 2021; Accepted: 30 July 2021;
Published: 17 August 2021.
Edited by:
Ghulam Abbas, University of Lahore, PakistanReviewed by:
Raseswari Pradhan, Veer Surendra Sai University of Technology, IndiaIrfan Khan, Texas A and M University, United States
Muhammad Majid Gulzar, University of Central Punjab, Pakistan
Copyright © 2021 Zhou, Zhang, Zhang, Guo, Yang, Feng and Zhang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Wei Feng, d2VpLmZlbmdAc2lhdC5hYy5jbg==; Yanhui Zhang, emhhbmd5aEBzaWF0LmFjLmNu
 Junfeng Zhou
Junfeng Zhou Yubo Zhang1
Yubo Zhang1 Yanhui Zhang
Yanhui Zhang