A Hybrid Forecasting Model Based on CNN and Informer for Short-Term Wind Power

Wind power prediction reduces the uncertainty of an entire energy system, which is very important for balancing energy supply and demand. To improve the prediction accuracy, an average wind power prediction method based on a convolutional neural network and a model named Informer is proposed. The original data features comprise only one time scale, which has a minimal amount of time information and trends. A 2-D convolutional neural network was employed to extract additional time features and trend information. To improve the accuracy of long sequence input prediction, Informer is applied to predict the average wind power. The proposed model was trained and tested based on a dataset of a real wind farm in a region of China. The evaluation metrics included MAE, MSE, RMSE, and MAPE. Many experimental results show that the proposed methods achieve good performance and effectively improve the average wind power prediction accuracy.

Introduction

With the rapid development of the global economy, people’s living standards and the global energy demand are continuously increasing, while fossil-fuel energy sources have declined (Chakraborty et al., 2018; Tu et al., 2019). Wind power generation, which has the advantages of being clean, low-cost and in ample supply, is an indispensable aspect of developing new global energy (Chen and Yu, 2014; Hu et al., 2021; Oh and Son, 2020). The installed capacity of wind generation worldwide has reached 644.5 GW in 2018, which is 17.4% higher than that in the past year (Zhang et al., 2020). The Global Wind Energy Development Report 2019 shows that the newly installed capacity of global wind turbines in 2019 was 60.4 GW. The instability of wind power is the main problem faced by the grid-connected, operation technology of wind power (Chai et al., 2015; Jiang et al., 2019; Li et al., 2019; Hu et al., 2020). With an increasing number of large-capacity wind farms, when their power grid surpasses a certain limit, the stability of the power system will be seriously affected, even threatening the safety of the whole power grid due to the randomness and low energy density of wind energy. (Chang, 2014; Hazari et al., 2018). Therefore, the effective operation of the whole mechanism can be guaranteed, and the stability of the whole system can be enhanced only by more accurate forecasting of wind power generation (Hong and Rioflorido, 2019; Zhang et al., 2019).

Currently, the main wind power forecasting methods include physical methods, statistical methods, and artificial intelligence methods. The physical forecasting method is the first method applied in wind power forecasting. The physical forecasting method mainly includes three technical links: the introduction of numerical weather prediction (NWP) data, the acquisition of wind speed and direction at the height of a wind turbine hub, and wind speed-power conversion (Feng et al., 2010). Men Z (Men et al., 2016) used the Gauss hybrid model to construct the mapping relationship between measured wind speed and NWP data and employed this model to modify NWP wind speed. The corrected NWP data and power prediction accuracy were greatly improved. Cassola (Cassola and Burlando, 2012) used the Kalman filter algorithm to filter the NWP output line, which effectively reduced the systematic error of weather forecasting and significantly improved the accuracy of the NWP model. Because of the low forecast accuracy of physical methods, the accuracy of physical prediction models that directly use the NWP often cannot meet the application requirements. On the other hand, because of the low updating frequency of NWP data, it is difficult to meet the requirements of 0–3 h forecasting. The statistical method does not require the introduction of historical wind information from wind farms. This method can be employed to extrapolate and predict the output of wind power of wind farms at a particular time in the future based on historical sequence characteristics (such as autocorrelation, partial correlation, standard deviation, etc.) of the power generated by wind farms. Erdem (Erdem and Shi, 2011) decomposed the wind speed into horizontal and vertical components according to the direction of the wind and constructed an ARMA model to separately predict the wind speed, which improved the prediction results. Pan (Pan et al., 2008) combined the time series analysis method with the Kalman filter and dynamically corrected the prediction model system and improved the prediction accuracy at the next moment. Dong (Dong et al., 2008) utilized the phase space theory of chaotic time series to construct a wind power neural network prediction model.

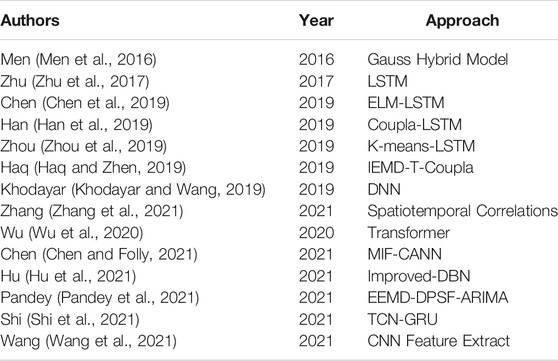
The artificial intelligence (AI) method mainly uses one or more AI algorithms to train historical power data and then predict future wind power. Kariniotakis (Kariniotakis et al., 1996) proposed ultrashort-term wind power prediction using an ANN. Shukur and Lee (Shukur and Lee, 2015) proposed a Kalman filter (KF)-(ANN) system to predict the wind speed sequences of Malaysia and Iraq. Chen (Chen and Folly, 2021) proposed a mixed input features-based cascade-connected artificial neural network (MIF-CANN). The method is employed to train input features from many neighbouring stations without encountering overfitting issues caused by many input features. Multiple ANNs train different combinations of input features in the first layer of the MIF-CANN model to produce preliminary results and then cascade into the second phase of the MIF-CANN model as inputs. Hu (Hu et al., 2014) applied Bayes theory to optimize the traditional SVM loss function and established a v-SVM model, which improved the accuracy of short-term wind speed prediction. With the development of big data technology, AI prediction methods have gradually developed from machine learning algorithms to deep learning algorithms (Wang et al., 2017). Haq (Haq and Zhen, 2019) proposed the improved empirical mode decomposition (IEMD) to decompose the load demand time series and selected T-Copula to incorporate the effect of exogenous variables by performing correlation analysis. Recently, many advanced models based on deep learning have also been reported (Wu et al., 2019). Khodayar (Khodayar and Wang, 2019) presented an algorithm for deep neural networks (DNNs). Zhu (Zhu et al., 2017) used long short-term memory (LSTM) to model multivariable time series to achieve wind power prediction. Chen (Chen et al., 2019) conducted correlation research on wind speed prediction based on extreme learning machines (ELMs), Elman neural networks, and LSTM networks. Han (Han et al., 2019) proposed a model based on the copula function and LSTM, which achieved better prediction results. Zhou (Zhou et al., 2019) proposed a K-means-long short-term memory (K-means-LSTM) neural network to classify wind power factors and establish a sub-prediction model. Peng (Peng et al., 2021) proposed a new neural-network prediction model named encoder attention BiLSTM-quantile regression (EALSTM-QR), which was developed for wind-power prediction considering the input of NWP and the deep-learning method. The combination inputs contain historical wind-power data and features extracted and obtained from the NWP through the encoder and attention levels. The bidirectional LSTM was utilized to generate wind-power time-series probability prediction results. The QR method and confidence interval limits were applied to obtain the final prediction intervals. Hu (Hu et al., 2021) proposed an improved deep belief network forecasting method for wind power, which employed a Gaussian-Bernoulli, restricted Boltzmann machine. Wang (Wang et al., 2021) applied a convolutional neural network for feature reconfiguration with temporal information, which increased the proportion of valid data, reduced the influence of outliers, and helped the neural network capture features and regularities from the historical dataset. Zhang (Zhang et al., 2021) proposed power prediction of a wind farm cluster based on spatiotemporal correlations. Pandey (Pandey et al., 2021) proposed two hybrid models for water demand forecasting. The first approach is based on the hybridization of ensemble empirical mode decomposition (EEMD) and difference pattern sequence forecasting (DPSF), and the second approach is based on the hybridization of EEMD with DPSF and autoregressive integrated moving average (ARIMA). The EEMD-DPSF approach provides better results, whereas the EEMD-DPSF-ARIMA approach requires shorter computational times. Shi (Shi et al., 2021) proposed a hybrid neural network, short-term, load forecasting model based on a temporal convolutional network (TCN) and gated recurrent unit (GRU) and utilized the state-of-the-art AdaBelief optimizer and attention mechanism were to enhance the prediction accuracy and efficiency. Dong (Dong et al., 2021) proposed a regional wind power probabilistic forecasting model comprising an improved kernel density estimation (IKDE), regular vine copulas, and ensemble learning. Wu (Wu et al., 2020) utilized a transformer to predict time series data. This method applied the self-attention mechanism to learn complex patterns and dynamics from time series data. However, some problems, such as high spatiotemporal complexity and limited input and output sequences, were still encountered. Zhou (Zhou et al., 2021) proposed Informer, a more effective time series prediction model than Transformer (Vaswani et al., 2017). Some hybrid models of wind power prediction are summarized in Table 1 for reference.

TABLE 1

TABLE 1. Recent studies for wind power forecasting based on hybrid models.

To sum up, most of the latest research progress of wind power prediction is based on machine learning (ML), artificial neural network (ANN), convolutional neural network (CNN) and recurrent neural network (RNN). These methods can effectively predict wind power. However, when the amount of input data becomes larger and the length of output data is long, the effect of these models is not particularly ideal. Nowadays, a large amount of data has been used in practical applications. How to forecast wind power more accurately in the environment of large data is a problem that needs to be solved.

This paper presents a method based on CNN-Informer for short-term, average wind power prediction. The average wind power can reflect the overall trend of wind power for a certain period, and the total wind power generation for a certain period can be obtained by determining the average power for a certain period in the future. To overcome the insufficiency of time series information contained in the historical power generation of a wind generator set at a single time scale, a convolution neural network is used to divide the original data into time series data at different time scales, and then the sub-sequences are input in the Informer model for training. The results are fused to obtain the final wind power prediction results.

The main contributions of this paper are presented as follows:

The prediction of wind power belongs to the problem of long-time series prediction. Therefore, to solve the problem of long-term series input, Informer is used to predict wind power in this paper.

To fully obtain the time-series features contained in the wind power data, this paper proposes a convolutional neural network to extract the features of the original wind power data to solve the problem that the time scale of the original wind power is single.

This paper is organized as follows: Methdology of Wind Power Prediction Section describes convolution, Informer, and the structure of the proposed CNN-Informer model. Experiment of Wind Power Prediction Section describes the datasets of wind power and illustrates the results of the experiment in this paper. The conclusions are summarized in Conclusion Section.

Methdology of Wind Power Prediction

This paper proposes a hybrid network model based on a convolutional neural network and Informer to forecast wind power.

The convolutional neural network can extract sufficient features from time series data, and Informer can more accurately predict long sequence inputs. The proposed model can effectively combine the advantages of these deep learning networks.

This chapter introduces the convolutional neural network, Informer, and proposed model.

Description of Convolutional Layers

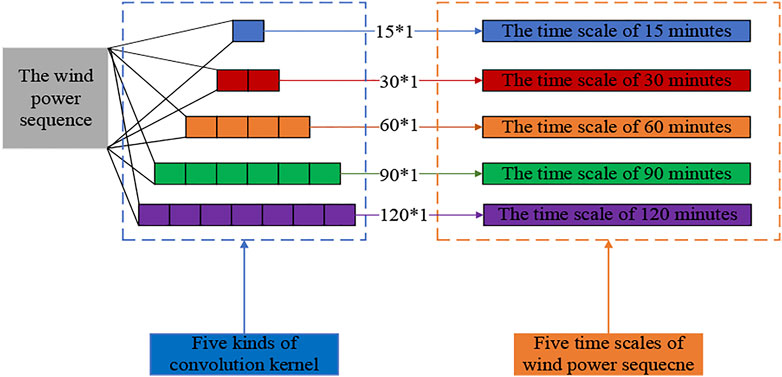
Single time-scale, historical wind power data contain a minimal amount of time information and cannot fully reflect the time sequence information and trend. Therefore, more time sequence features need to be extracted from the original wind power data. Convolutional neural networks can effectively extract some useful features. Therefore, this paper adopts a convolutional neural network to extract different time sequence features from original wind power data. The original wind power sequence is convoluted into a wind power sequence at different scales by two-dimensional convolution as follows:

$X_{i-en}=\mathit{Conv}2d\left(X_{input}\right)(1)$

$X_{i-en}$ represents the sequence of wind power generated by convolution at different time scales, and $X_{input}$ represents the original historical sequence of wind power. The network structure diagram of this part is shown in Figure 1.

FIGURE 1

FIGURE 1. Structure of convolution layers.

Two-dimensional convolutions with convolution kernel sizes of 15*1, 30*1, 60*1, 90*1, and 120*1 are employed to extract features of different time scales. Five convolution kernels are selected to divide the original wind power sequence into five sub-sequences with time scales of 15, 30, 60, 90, and 120 min.

Description of Informer

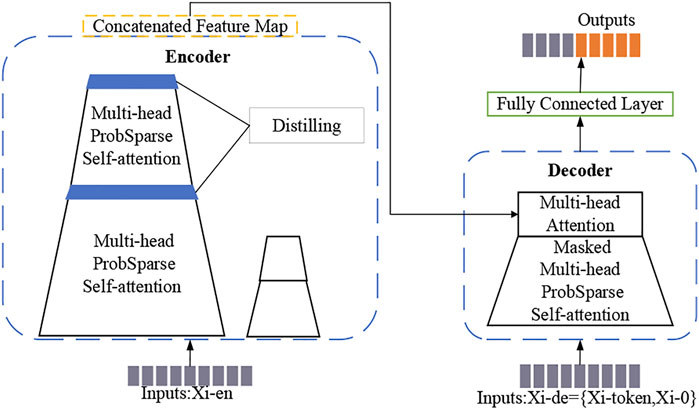
Informer (Zhou et al., 2021) is a network structure that is based on an attention mechanism that improves the square computational complexity of the self-attention mechanism, multilayer network stacking, and step-by-step decoding method. Informer mainly solves the prediction problem of long series data; its overall architecture is shown in Figure 2.

FIGURE 2

FIGURE 2. Architecture of informer.

In the encoder part of the model, ProbSparse self-attention (Zhou et al., 2021) is used to replace canonical self-attention, and self-attention distilling is used to reduce the size of the network. The decoder receives the long sequence of inputs, sets the target element to zero, and immediately predicts the outputs in a generative inference method.

ProbSparse Self-attention: The $i$-th query’s attention on all the keys is defined as probability $p\left(k_j|q_i\right)$, and the output is its composition with values $v$ in this model (Zhou et al., 2021). The likeness between $p\left(k_j|q_i\right)$ and the uniform distribution $q\left(k_j|q_i\right)=\frac{1}{L_k}$ is calculated by a method similar to Kullback–Leibler divergence.

$\overline{M}\left(q_i,K\right)=\underset{j}{\max }\left\{\frac{q_i{k}_j^T}{\sqrt{d}}\right\}-\frac{1}{L_K}{\displaystyle \sum _{j=1}^{L_k}\frac{q_i{k}_j^T}{\sqrt{d}}}(2)$

If the $i$-th query gains a larger $\overline{M}\left(q_i,K\right)$, its attention probability $p$ is more “diverse” and has a high chance of containing the dominant dot-product pairs in the header field of the long tail self-attention distribution (Zhou et al., 2021). According to this measurement, Informer only focuses on top-$u$ dominant queries for each $k$ value:

$A\left(Q,K,V\right)=\mathit{Soft}\max \left(\frac{\overline{Q}{K}^T}{\sqrt{d}}\right)V(3)$

$q_i$ is $Q$’s value in the $i$-th row, $k_j$ is $K$’s value in the $j$-th row, and $d$ is the input dimension. $\overline{Q}$ is a sparse matrix that contains only $u$ queries.

Self-attention distilling: The model uses the distilling operation to privilege the superior features with dominating features and to construct a focused, self-attention feature map in the next layer (Zhou et al., 2021). This distilling procedure forwards from the $j$-th layer to the $(j+1)$-th layer as:

$X_{j+1}^t=\mathit{MaxPooling}\left(\mathit{ELU}\left(\mathit{Conv}1\mathit{d}\left({\left[X_j^t\right]}_{att}\right)\right)\right)(4)$

where ${[·]}_{att}$ represents the attention block. After each convolutional layer, the distilling adds a max-pooling layer with stride 2 and downsamples $X_j^t$ to its half slice. The whole memory usage can be reduced to $O\left(\left(2-\lambda \right)L\log L\right)$, where $\lambda$ is a small number.

Generative Inference: The model feeds the decoder with the following vectors:

$X_{i-de}^t=\mathit{Concat}\left(X_{i-token}^t,X_{i-0}^t\right)\in {ℝ}^{\left(L_{i-token}+L_{i-y}\right)\times d_{\mathrm{mod}el}}(5)$

where $X_{i-de}^t$ is the $i$-th input sequence of the decoder, $X_{i-token}^t$ is the start token of the $i$-th sequence and $X_{i-0}^t$ is a placeholder for the target sequence of the $i$-th sequence, which are set to a scalar such as 0. This model uses a generative way to decode; its decoder predicts output by one forwards procedure.

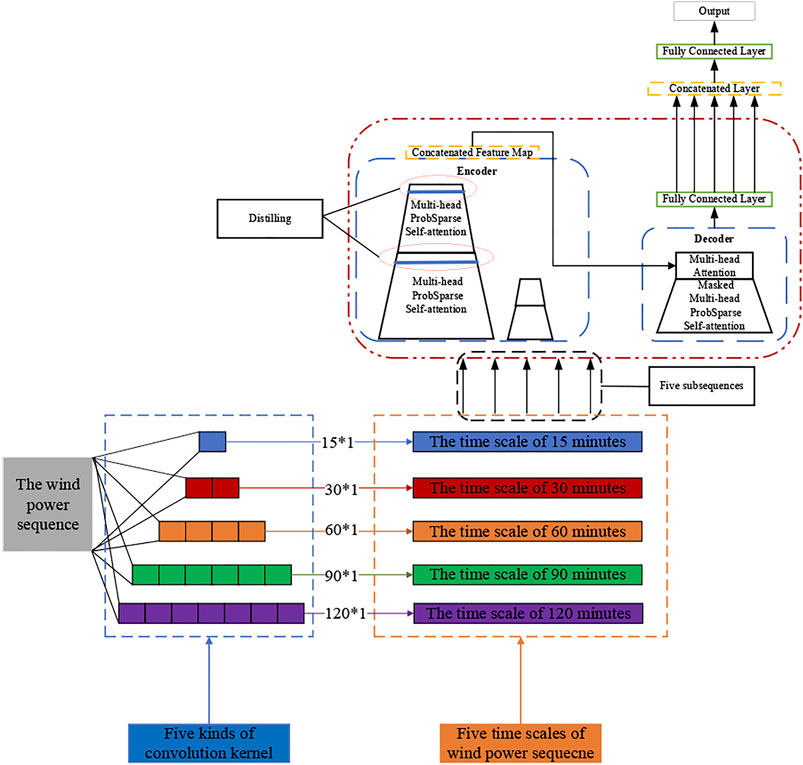
Proposed Model

In the proposed model, the original wind power series is scaled by a convolutional neural network, from which the features of different time scales are extracted. The sub-sequences of different time scales after convolution are taken as the inputs of the Informer network, and the Informer generates five outputs. These outputs are inputted to the concatenated layer for feature fusion, and the final forecast result is outputted through a fully connected layer. The overall framework of the proposed model is shown in Figure 3.

FIGURE 3

FIGURE 3. Overall framework of the proposed model.

Experiment of Wind Power Prediction

Description of Wind Power Datasets

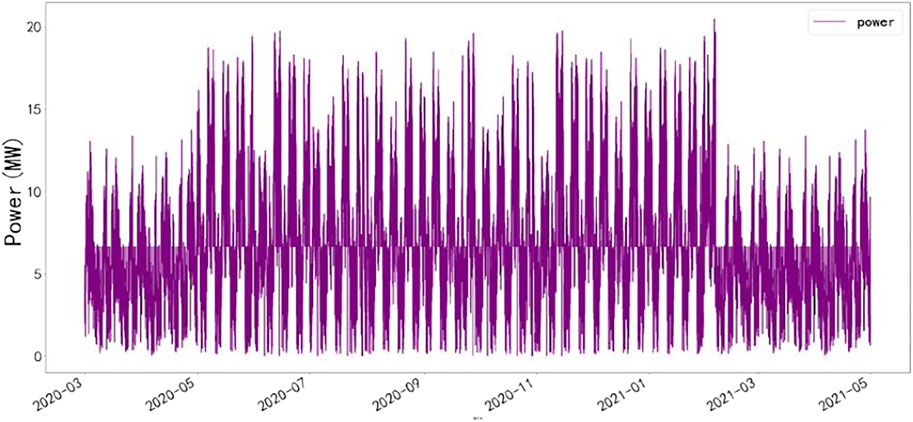
In this study, historical wind power datasets of a region in China from March 1, 2020, to April 30, 2020, are employed, and the interval of datasets is 1 minute. The dataset is collected by SCADA. Figure 4 shows the historical wind power curve of the region. The fluctuation range of the wind power data is 0–21 MW, and the wind power strongly fluctuates.

FIGURE 4

FIGURE 4. Historical wind power.

Table 2 gives descriptive statistics, including measured values: minimum, mean, maximum and median are selected to describe the characteristics of the distribution. The minimum value, mean value, maximum value and median of the dataset are 0.03717, 6.68971, 20.4642, and 6.32673 MW. Table 2 shows that the mean and median of the dataset are similar.

TABLE 2

TABLE 2. Statistical elements of the historical wind power.

Average Wind Power Prediction

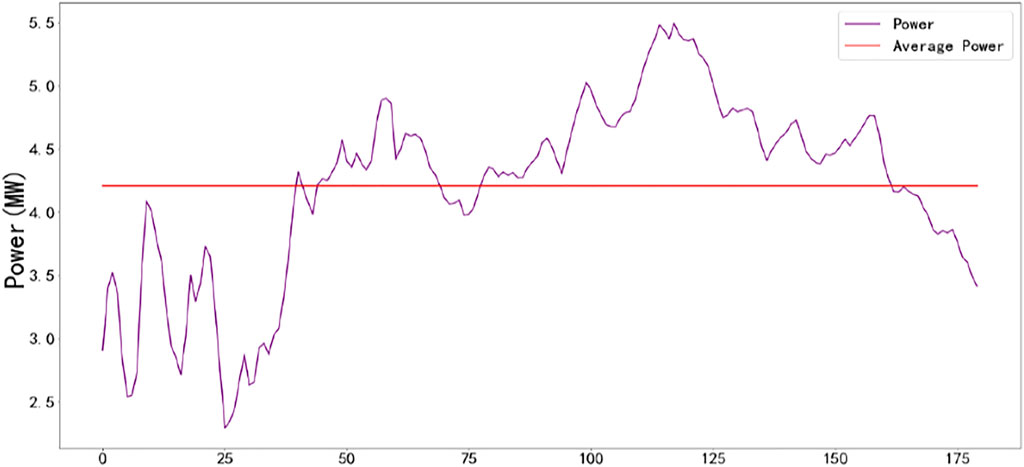
The average value of real wind power data can better reflect the centralized trend of wind power over this period, and the general trend of wind power over a certain period can be employed to assess the generation status of wind power. Therefore, this paper uses the method of the mean prediction of wind power to forecast the centralized trend of generation power over the next 3 hours. The power curve for 3 hours is shown in Figure 5. The fluctuation range of the wind power data is 2–5.5 MW. The mean value of the wind power of 3 hours is 4. 2421MW.

FIGURE 5

FIGURE 5. Three-hour wind power and mean.

Data Standardization and Missing Value Processing

Due to the fluctuation of actual wind power data, extensive data will cause numerical problems. To accelerate the speed of gradient descent to obtain the optimal solution, this paper standardizes the original power data before constructing the model, as shown in Equation 6, and converts the predictive results to the final predictive results, as shown in Equation 7.

$\mathrm{x}\prime =\frac{x-x_{mean}}{x_{std}}(6)$

$x=\mathrm{x}\prime \ast {\mathrm{x}}_{std}+x_{mean}(7)$

$x\prime$ is the normalized variable, $x$ is the original variable, $x_{mean}$ is the mean of the variable, and $x_{std}$ is the standard deviation of the variable. For missing values of wind power datasets, this paper uses mean interpolation to process missing values.

Division of Datasets

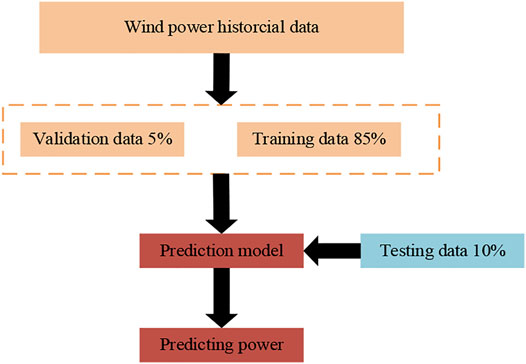
The partitioning of datasets is an important step and a prerequisite for training wind power data. To obtain reasonable forecasting results, wind power datasets are divided into training sets, testing sets, and validation sets at a ratio of 8.5:1:0.5. As shown in Figure 6, the training set and validation set are employed to train the model. We then input the testing set into the trained model for prediction.

FIGURE 6

FIGURE 6. Partition of wind power datasets.

Evaluation Metrics

The forecasting of the average wind power uses 6 hours of wind power to forecast the average wind power over the next 3 hours.

To evaluate the predictive performance of the model, this paper uses four evaluation metrics to evaluate the performance of the model. Four evaluation metrics are the mean absolute error (MAE), mean square error (MSE), root mean square error (RMSE) and mean absolute percent error (MAPE). The MAE is the average of the sum of the absolute difference between the true value and the predicted value. The MSE is the mean of the sum of the squares of the errors between the true value and the predicted value. The RMSE is the square root of the MSE. The MAPE is the percentage of the MAE. The four error evaluation indices are shown in Eqs 8–11.

$\mathit{MAE}=\frac{1}{n}{\displaystyle \sum _{i=1}^n|{\widehat{y}}_i-y_i|}(8)$

$\mathit{MSE}=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\left({\widehat{y}}_i-y_i\right)}^2}(9)$

$\mathit{RMSE}=\sqrt{\frac{1}{n}{\displaystyle \sum _{i=1}^n{\left({\widehat{y}}_i-y_i\right)}^2}}(10)$

$\mathit{MAPE}=\frac{100}{n}{\displaystyle \sum _{i=1}^n\left|\frac{{\widehat{y}}_i-y_i}{y_i}\right|}(11)$

where $n$ represents the number of predicted points, ${\widehat{y}}_i$ represents the predicted value, and $y_i$ represents the real value.

Experimental Environment and Strategies

In this paper, the experimental code is Python 3.7; the deep learning framework is PyTorch 1.8; and the experiment is implemented on a PC (Windows 10 operating system, Intel (R) core (TM) I7-9750 h CPU 2.6 GHz, 16 Gbyte RAM, and NVIDIA GeForce RTX 3070 GPU).

This paper adopts the cross-validation (Bokde et al., 2020) training strategy. In the experiments of out study, we divide the training data into training set and validation set and perform 100 iterations on each epoch. We take the average loss value over 100 iterations as the final loss value of each epoch. We test the model on the testing set and achieve the final forecasting results. The Gelu activation function is utilized as the activation function of the model; MSE is employed as the loss function of the model; and Adam is applied as the optimizer of the model. The Adam algorithm has no smoothing requirements for the objective function, and its loss function changes with time, so it can better handle noise samples. In the experiment, the batch size was 16, and the methods of early stopping and reducing the learning rate were adopted to prevent overfitting.

The forecasting time horizons of all the simulation results presented in this study were 3-h ahead forecasting. This paper uses 6 h of historical wind power data to predict the average wind power in the next 3 hours.

Comparison of the Proposed Model

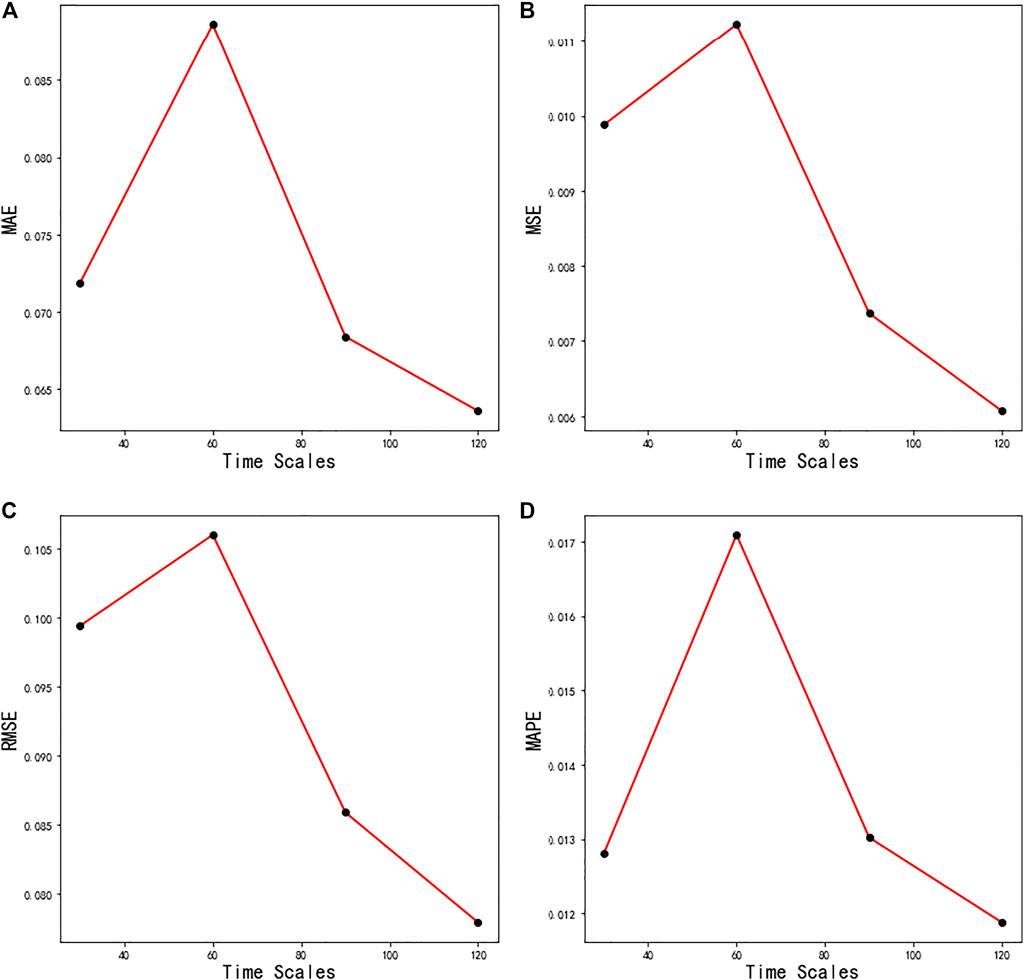
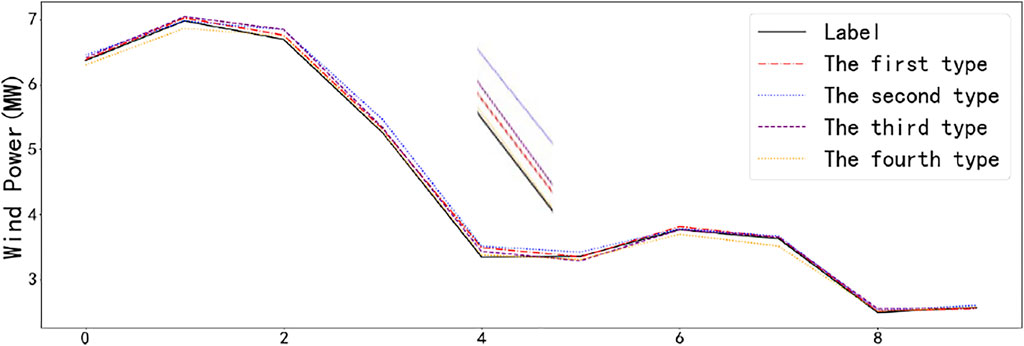
To achieve the best predictive performance, this paper compares CNN-Informer models with different time scales. To achieve the best predictive performance, this paper divides the original wind power data into four types of time scales. The first type is 15 and 30 min; the second type is 15, 30, and 60 min; the third type is 15, 30, 60, 90 min; and the fourth type is 15, 30, 60, 90, and 120 min. As shown in Figure 7, the error metrics reached the highest error metrics, while the time scales were 15, 30, and 60 min. The fourth type had the lowest error metrics.

FIGURE 7

FIGURE 7. Metrics of the proposed models: (A), MAE, (B), MSE, (C), RMSE, and (D), MAPE.

As shown in Figure 8, the performance of CNN + Informer models is similar, while the fourth type has less fluctuation and a forecast closer to the true value than other types. Furthermore, the convergence speed of the model slows with an increase in the number of convolution kernels, and the performance of the model with more convolution kernels show minimal improvement. Therefore, this paper selects the fourth type—15, 30, 60, 90, and 120 minutes—as the proposed model.

FIGURE 8

FIGURE 8. Predictive results of CNN-Informer models.

Comparison of the Previous Model

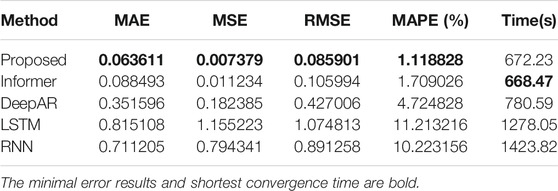
To verify the comprehensive performance of the proposed CNN-Informer model, five algorithms are selected and developed for comparison, including the proposed model, Informer, Long-Short Term Memory (LSTM), DeepAR, and Recurrent Neural Network (RNN). The hyperparameters and neural network topology of all comparison models have been optimized and summarized in Table 3.

TABLE 3

TABLE 3. Hyperparameters of these methods.

Six hours of historical wind power data are used to predict the mean value of wind power in the next 3 hours, as shown in Figure 9, which is the prediction diagram of the experimental results of the proposed CNN-Informer, Informer, DeepAR, LSTM and RNN models. The performance of the proposed model is the best, slightly higher than that of Informer, while the performance of RNN and LSTM is poor, which is far from the performance of the proposed model CNN-Informer, Informer and DeepAR.

FIGURE 9

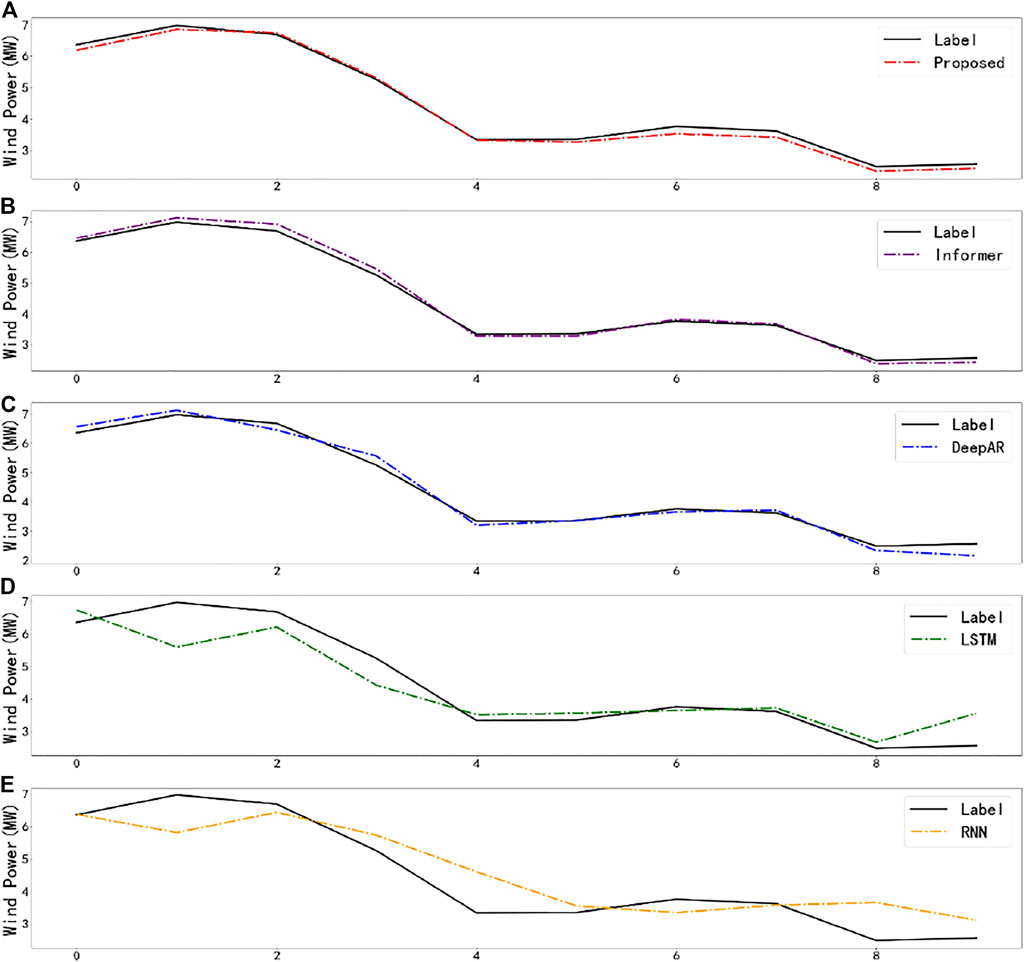
FIGURE 9. Curve of the forecast results: (A), Proposed model, (B), Informer, (C), DeepAR, (D), LSTM, and (E), RNN.

The experimental error results and convergence time of the proposed model, Informer, LSTM, RNN and DeepAR are shown in Table 4. Among the five models mentioned in Table 4, the minimal error results and shortest convergence time are bold. As shown in Table 4, for the proposed model, the MAE, MSE, RMSE, MAPE, and convergence time are 0.063611, 0.007379, 0.085901, 1.118828%, and 672.23 s. For the Informer, the MAE, MSE, RMSE, MAPE, and convergence time are 0.088493, 0.011234, 0.105994, 1.709026%, and 668.47s. Although the convergence time of the proposed model is higher than that of Informer, the performance of the proposed model is improved compared with that of Informer. Compared with the traditional model, the proposed method significantly improves the prediction performance and the convergence time.

TABLE 4

TABLE 4. Metrics of five models.

In conclusion, convolution of the original wind power series to a certain extent can improve the predictive performance of the model. The prediction performance of the model can obtain better performance when the original wind power sequence is convoluted to time scales of 15, 30, 60, 90, and 120 min.

Conclusion

Due to the instability and intermittency of wind power generation in a complex environment and to better obtain the historical wind power data, this paper proposes a composite network that is composed of a convolutional neural network and Informer and that uses this model to improve the prediction accuracy of wind power. The historical wind power data of a wind farm in China are employed for verification and compared with Informer, LSTM, RNN, and DeepAR. The detailed contributions of this paper are listed as follows:

The original historical wind power data are divided into multiple time scales by using a convolution neural network, and more time series features are extracted. This method can make better use of historical wind power data.

Based on the Informer network, this paper establishes a wind power prediction model that can input a long time series and predict the average power in the next 3 hours. Compared with Informer, LSTM, RNN, and DeepAR, the proposed CNN-Informer model can more accurately predict wind power.

Several limitations deserve further study. The model parameters proposed in this paper are large. In future research, we intend to propose a lightweight network. For the method of temporal feature extraction, in follow-up research, we hope to establish a more effective method to extract temporal features. In the task of short-term wind power prediction, the model has high requirements for convergence speed and accuracy that require the algorithm to balance time cost and accuracy. How to optimize the model to achieve this balance is worthy of further research.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Materials, further inquiries can be directed to the corresponding author.

Author Contributions

H-KW contributed to conception and design of the study. KS organized the database, performed the statistical analysis, and wrote the first draft of the manuscript. YC wrote sections of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This study was supported by the Scientific and Technological Research Program of Chongqing Municipal Education Commission (KJQN202001142), the Chongqing Research Program of Basic Research and Frontier Technology (Grant No. cstc2020jcyj-msxmX0352), the fellowship of China Postdoctoral Science Foundation (2021M700616), and the Chongqing University of Technology (2019ZD118).

Conflict of Interest

HW was employed by the Company Chongqing Industrial Big Data Innovation Center Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, orclaim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bokde, N. D., Yaseen, Z. M., and Andersen, G. B. (2020). ForecastTB-An R Package as a Test-Bench for Time Series Forecasting-Application of Wind Speed and Solar Radiation Modeling. Energies 13, 2578. doi:10.3390/en13102578

CrossRef Full Text | Google Scholar

Cassola, F., and Burlando, M. (2012). Wind Speed and Wind Energy Forecast through Kalman Filtering of Numerical Weather Prediction Model Output. Appl. Energ. 99, 154–166. doi:10.1016/j.apenergy.2012.03.054

CrossRef Full Text | Google Scholar

Chai, S., Xu, Z., Lai, L. L., and Wong, K. P. (2015). “An Overview on Wind Power Forecasting Methods,” in Proceedings of the 2015 International Conference on Machine Learning and Cybernetics (ICMLC), Guangzhou, China, July 2015 (IEEE), 765–770. doi:10.1109/ICMLC.2015.7340651

CrossRef Full Text | Google Scholar

Chakraborty, T., Watson, D., and Rodgers, M. (2018). Automatic Generation Control Using an Energy Storage System in a Wind Park. IEEE Trans. Power Syst. 33, 198–205. doi:10.1109/tpwrs.2017.2702102

CrossRef Full Text | Google Scholar

Chang, W.-Y. (2014). A Literature Review of Wind Forecasting Methods. J. Power Energ. Eng. 02, 161–168. doi:10.4236/jpee.2014.24023

CrossRef Full Text | Google Scholar

Chen, K., and Yu, J. (2014). Short-term Wind Speed Prediction Using an Unscented Kalman Filter Based State-Space Support Vector Regression Approach. Appl. Energ. 113, 690–705. doi:10.1016/j.apenergy.2013.08.025

CrossRef Full Text | Google Scholar

Chen, M.-R., Zeng, G.-Q., Lu, K.-D., and Weng, J. (2019). A Two-Layer Nonlinear Combination Method for Short-Term Wind Speed Prediction Based on ELM, ENN, and LSTM. IEEE Internet Things J. 6, 6997–7010. doi:10.1109/JIOT.2019.2913176

CrossRef Full Text | Google Scholar

Chen, Q., and Folly, K. A. (2021). Short-Term Wind Power Forecasting Using Mixed Input Feature-Based Cascade-connected Artificial Neural Networks. Front. Energ. Res. 9, 1–12. doi:10.3389/fenrg.2021.634639

CrossRef Full Text | Google Scholar

Dong, L., Wang, L., Gao, S., and Liao, X. (2008). Power Prediction Modeling and Research of Large Wind Farms Based on Chaotic Time Se. J. Electr. Technol. 23, 125–129. doi:10.3321/j.issn:1000-6753.2008.12.020

CrossRef Full Text | Google Scholar

Dong, W., Sun, H., Tan, J., Li, Z., Zhang, J., and Yang, H. (2022). Regional Wind Power Probabilistic Forecasting Based on an Improved Kernel Density Estimation, Regular Vine Copulas, and Ensemble Learning. Energy 238, 122045. doi:10.1016/j.energy.2021.122045

CrossRef Full Text | Google Scholar

Erdem, E., and Shi, J. (2011). ARMA Based Approaches for Forecasting the Tuple of Wind Speed and Direction. Appl. Energ. 88, 1405–1414. doi:10.1016/j.apenergy.2010.10.031

CrossRef Full Text | Google Scholar

Feng, S., Wang, W., Liu, C., and Dai, H. (2010). Research on Physical Methods of Wind Farm Power Prediction. J. China Electra. Eng. 30, 1–6. doi:10.13334/j.0258-8013.pcsee

CrossRef Full Text | Google Scholar

Han, S., Qiao, Y.-h., Yan, J., Liu, Y.-q., Li, L., and Wang, Z. (2019). Mid-to-long Term Wind and Photovoltaic Power Generation Prediction Based on Copula Function and Long Short Term Memory Network. Appl. Energ. 239, 181–191. doi:10.1016/j.apenergy.2019.01.193

CrossRef Full Text | Google Scholar

Haq, M. R., and Ni, Z. (2019). A New Hybrid Model for Short-Term Electricity Load Forecasting. IEEE. Access 7, 125413–125423. doi:10.1109/ACCESS.2019.2937222

CrossRef Full Text | Google Scholar

Hazari, M., Mannan, M., Muyeen, S., Umemura, A., Takahashi, R., and Tamura, J. (2018). Stability Augmentation of a Grid-Connected Wind Farm by Fuzzy-Logic-Controlled DFIG-Based Wind Turbines. Appl. Sci. 8, 20. doi:10.3390/app8010020

CrossRef Full Text | Google Scholar

Hong, Y.-Y., and Rioflorido, C. L. P. P. (2019). A Hybrid Deep Learning-Based Neural Network for 24-h Ahead Wind Power Forecasting. Appl. Energ. 250, 530–539. doi:10.1016/j.apenergy.2019.05.044

CrossRef Full Text | Google Scholar

Hu, Q., Zhang, S., Xie, Z., Mi, J., and Wan, J. (2014). Noise Model Based ν-support Vector Regression with its Application to Short-Term Wind Speed Forecasting. Neural Networks 57, 1–11. doi:10.1016/j.neunet.2014.05.003

PubMed Abstract | CrossRef Full Text | Google Scholar

Hu, T., Wu, W., Guo, Q., Sun, H., and Shi, L. (2020). Very Short-Term Spatial and Temporal Wind Power Forecasting: A Deep Learning Approach. CSEE J. Power Energ. Syst. 6, 434–443. doi:10.17775/CSEEJPES.2018.00010

CrossRef Full Text | Google Scholar

Hu, S., Xiang, Y., Huo, D., Jawad, S., and Liu, J. (2021). An Improved Deep Belief Network Based Hybrid Forecasting Method for Wind Power. Energy 224, 120185. doi:10.1016/j.energy.2021.120185

CrossRef Full Text | Google Scholar

Jiang, P., Yang, H., and Heng, J. (2019). A Hybrid Forecasting System Based on Fuzzy Time Series and Multi-Objective Optimization for Wind Speed Forecasting. Appl. Energ. 235, 786–801. doi:10.1016/j.apenergy.2018.11.012

CrossRef Full Text | Google Scholar

Kariniotakis, G. N., Stavrakakis, G. S., and Nogaret, E. F. (1996). Wind Power Forecasting Using Advanced Neural Networks Models. IEEE Trans. Energy Convers. 11, 762–767. doi:10.1109/60.556376

CrossRef Full Text | Google Scholar

Khodayar, M., and Wang, J. (2019). Spatio-Temporal Graph Deep Neural Network for Short-Term Wind Speed Forecasting. IEEE Trans. Sustain. Energ. 10, 670–681. doi:10.1109/TSTE.2018.2844102

CrossRef Full Text | Google Scholar

Li, C., Tang, G., Xue, X., Saeed, A., and Hu, X. (2019). Short-term Wind Speed Interval Prediction Based on Ensemble GRU Model. IEEE Trans. Sustain. Energ. 11, 1370–1380. doi:10.1109/TSTE.2019.2926147

CrossRef Full Text | Google Scholar

Men, Z., Yee, E., Lien, F.-S., Wen, D., and Chen, Y. (2016). Short-term Wind Speed and Power Forecasting Using an Ensemble of Mixture Density Neural Networks. Renew. Energ. 87, 203–211. doi:10.1016/j.renene.2015.10.014

CrossRef Full Text | Google Scholar

Oh, E., and Son, S.-Y. (2020). Theoretical Energy Storage System Sizing Method and Performance Analysis for Wind Power Forecast Uncertainty Management. Renew. Energ. 155, 1060–1069. doi:10.1016/j.renene.2020.03.170

CrossRef Full Text | Google Scholar

Pan, D., Liu, H., and Li, Y. (2008). A Wind Speed Forecasting Optimization Model for Wind Farms Based on Time Series Analysis and Kalman Filter Algorithm. Power Sys. Technol. 32, 82–86. doi:10.13335/j.1000-3673.pst.2008.07.012

CrossRef Full Text | Google Scholar

Pandey, P., Bokde, N. D., Dongre, S., and Gupta, R. (2021). Hybrid Models for Water Demand Forecasting. Water Resour. Plann. Manage. 147 (2), 0733–9496. doi:10.1061/(asce)wr.1943-5452.0001331

CrossRef Full Text | Google Scholar

Peng, X., Wang, H., Lang, J., Li, W., Xu, Q., Zhang, Z., et al. (2021). EALSTM-QR: Interval Wind-Power Prediction Model Based on Numerical Weather Prediction and Deep Learning. Energy 220, 119692. doi:10.1016/j.energy.2020.119692

CrossRef Full Text | Google Scholar

Shi, H., Wang, L., Scherer, R., Wozniak, M., Zhang, P., and Wei, W. (2021). Short-Term Load Forecasting Based on Adabelief Optimized Temporal Convolutional Network and Gated Recurrent Unit Hybrid Neural Network. IEEE Access 9, 66965–66981. doi:10.1109/ACCESS.2021.3076313

CrossRef Full Text | Google Scholar

Shukur, O. B., and Lee, M. H. (2015). Daily Wind Speed Forecasting through Hybrid KF-ANN Model Based on ARIMA. Renew. Energ. 76, 637–647. doi:10.1016/j.renene.2014.11.084

CrossRef Full Text | Google Scholar

Tu, Q., Betz, R., Mo, J., Fan, Y., and Liu, Y. (2019). Achieving Grid Parity of Wind Power in China - Present Levelized Cost of Electricity and Future Evolution. Appl. Energ. 250, 1053–1064. doi:10.1016/j.apenergy.2019.05.039

CrossRef Full Text | Google Scholar

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones, L., Gomez, A. N., et al. (2017). Attention Is All You Need. arXiv:1706.03762.

Google Scholar

Wang, H.-z., Li, G.-q., Wang, G.-b., Peng, J.-c., Jiang, H., and Liu, Y.-t. (2017). Deep Learning Based Ensemble Approach for Probabilistic Wind Power Forecasting. Appl. Energ. 188, 56–70. doi:10.1016/j.apenergy.2016.11.111

CrossRef Full Text | Google Scholar

Wang, S., Li, B., Li, G., Yao, B., and Wu, J. (2021). Short-Term Wind Power Prediction Based on Multidimensional Data Cleaning and Feature Reconfiguration. Appl. Energ. 292, 116851. doi:10.1016/j.apenergy.2021.116851

CrossRef Full Text | Google Scholar

Wu, Y. X., Wu, Q. B., and Zhu, J. Q. (2019). Data-driven Wind Speed Forecasting Using Deep Feature Extraction and LSTM. IET Renew. Power Generation 13, 2062–2069. doi:10.1049/iet-rpg.2018.5917

CrossRef Full Text | Google Scholar

Wu, N., Green, B., Xue, B., and O'Banion, S. (2020). Deep Transformer Models for Time Series Forecasting: The Influenza Prevalence Case. arXiv:2001.08317v1.

Google Scholar

Zhang, J., Yang, J., and Tong, Z. (2019). Research on the Impact of Large-Scale Wind Power Integration on Power Quality. Henan Sci. Technol. 678, 143–144. doi:10.3969/j.issn.1003-5168.2019.16.051

CrossRef Full Text | Google Scholar

Zhang, H., Liu, Y., Yan, J., Han, S., Li, L., and Long, Q. (2020). Improved Deep Mixture Density Network for Regional Wind Power Probabilistic Forecasting. IEEE Trans. Power Syst. 35, 2549–2560. doi:10.1109/TPWRS.2020.2971607

CrossRef Full Text | Google Scholar

Zhang, J., Liu, D., Li, Z., Han, X., Liu, H., Dong, C., et al. (2021). Power Prediction of a Wind Farm Cluster Based on Spatiotemporal Correlations. Appl. Energ. 302, 117568. doi:10.1016/j.apenergy.2021.117568

CrossRef Full Text | Google Scholar

Zhou, B., Ma, X., Luo, Y., and Yang, D. (2019). Wind Power Prediction Based on LSTM Networks and Nonparametric Kernel Density Estimation. IEEE Access 7, 165279–165292. doi:10.1109/access.2019.2952555

CrossRef Full Text | Google Scholar

Zhou, H., Zhang, S., Peng, J., Zhang, S., Li, J., Xiong, H., et al. (2021). Informer: Beyond Efficient Transformer for Long Sequence Time-Series Forecasting. arXiv:2012.07436v3.

Google Scholar

Zhu, Q., Li, H., Wang, Z., Chen, J., and Wang, B. (2017). Ultra-short Term Prediction of Wind Farm Power Generation Based on Long-Short Term Memory Network. Grid Technol. 41, 3797–3802. doi:10.13335/j.1000-3673.pst.2017.1657

CrossRef Full Text | Google Scholar