- North China Electric Power University, School of Nuclear Science and Engineering, Beijing, China
The advanced reactor design needs an accurate cross-section generation code. In this study, a new nuclear data processing code AXSP is developed, and the method and performance of which are described. Compared with the NJOY program, the precision of the unresolved resonance processing module UnresXS has been significantly improved due to the adoption of a more accurate solution method and the consideration of in-sequence overlap integrals. The time consumption of PUnresXS has been decreased significantly due to an optimized sorting algorithm. At the same time, other modules of AXSP are relatively comprehensive. The function of resolved resonance cross-section reconstruction and linearization is the ReconXS module. The Doppler broadening module is BroadXS by using Gauss–Hermite quadrature and Gauss–Legendre quadrature from 0 K temperature pointwise cross section to any temperature which is defined by the user. The shielding factor in the unresolved resonance energy region is calculated by the UnresXS or the PUnresXS module, which are developed based on the Bondarenko method and the probability table method, respectively. The ACE formatted cross sections for the Monte Carlo code is processed by the ACEXS module, and the multigroup cross sections are generated by the GroupXS module. The cross sections processed by different modules were verified by the NJOY2016 code, and the multigroup cross sections were also verified by using the critical benchmarks. The multiplication factor difference between AXSP and NJOY2016 is less than 20 pcm. In addition to this, the ZPR6/7 fast reactor is used for ACE format library verification. The results show that the criticality calculated by AXSP has a good agreement with that of NJOY2016.
Introduction
A total of six advanced reactor concepts have been selected for Generation IV reactor and are being investigated to meet the challenging goals of effective resource utilization and waste minimization. The cross section is one of the most fundamental quantities for the reactor design. The evaluated nuclear data files have been updated over the years with reflecting progress on nuclear modeling, new nuclear experiment measurement, and a lot of feedback from the benchmark analysis. The cross-sections’ data library of neutronics calculation codes is generated by processing the evaluated nuclear data files when it is updated. Therefore, the nuclear data processing code is very important for connecting the evaluated nuclear data file and the reactor analysis and design codes. The motivation for the development of the advanced cross-section process (AXSP) code is to establish a platform to research some new methods of nuclear processing to satisfy the demands on accurate cross sections for the advanced reactor design. For example, in the design of a mixed-spectrum reactor, it is necessary to consider not only the anisotropic scattering in the high-energy region but also the influence of the broad resonances and the upper scattering problems in the low-energy region. The problem of generating a high-precision multigroup cross section cannot be well resolved. Because if we want to better solve the problem of the hybrid spectrum reactor, we need to consider not only the anisotropic scattering in the high-energy region but also the solution of the moderation equation in the all-energy region. There are still many works to be carried out.
Currently, NJOY (Abou Jaoude, 2017), PREPRO (Cullen, 2017), and AMPX (Wiarda et al., 2016) are well-known nuclear data processing codes in the world. There are also some newly developed nuclear data processing codes. For example, RXSP (Jian-kai et al., 2013) (Li and WangKan, 2017) (Liu et al., 2020) (Li, 2012) (Yu, 2015) of Tsinghua University and FRENDY (Tada et al., 2017) of the Japan Atomic Energy Agency (JAEA) have developed to produce an ACE format library for the Monte Carlo code. Ruller (Liu et al., 2016) of the China Institute of Atomic Energy and NECP-Atlas (Zu et al., 2019) of Xi’an Jiao Tong University have been developed to provide a multigroup library. At the same time, EXUS-F of South Korea was developed for a faster reactor multigroup cross-section generation by direct processing of the evaluated nuclear data file.
For the nuclear data processing, the open source nuclear data processing system NJOY is still not perfectly processing the evaluated nuclear data for the advanced nuclear reactor analysis when it is used to calculate the KERMA factors and DPA cross sections (Konno et al., 2016) (Wen et al., 2020) because of some bugs.
Recently, the nuclear data format has been considered to change from the traditional ENDF-6 format to the generalized nuclear data (GND) format (Mattoon et al., 2012) by utilizing the Extensible Markup Language. Since the GND format is completely different from the current ENDF-6 format, which was defined several decades ago, the NJOY code cannot treat such a new format without extensive modification. To solve this problem, several nuclear data processing systems, such as NJOY21 (Conlin, 2015), FUDGE (Beck and Mattoon, 2014), and AMPX-2000, are under development in a few countries.
In this study, the outline of the development, method, and capability of AXSP are described in the Theory and processing method section. In Numerical calculation results section, the verification of each module of AXSP is investigated, and the results of AXSP are compared with those of NJOY 2016. The critical benchmarks from the ICSBEP handbook are applied to demonstrate the accuracy of the multigroup cross section with the Bondarenko method, and ZPR6/7 was used to verify the ACE format library generated by the ACEXS module. The last section is conclusion.
Theory and processing method
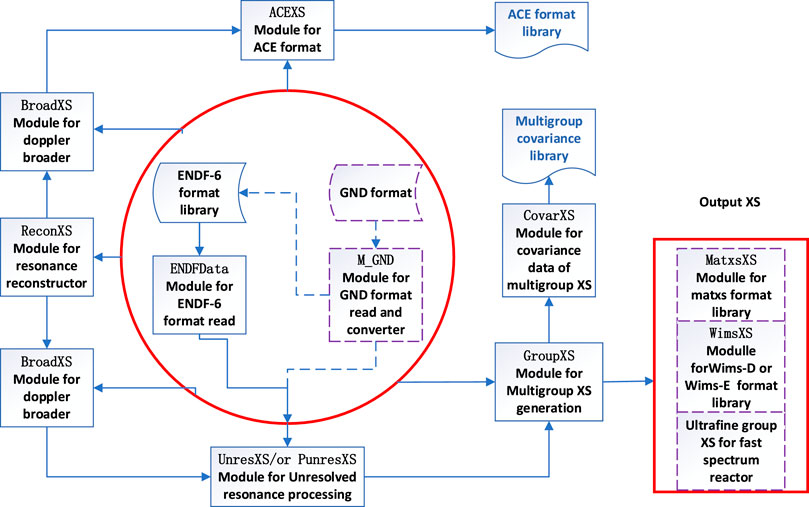
AXSP is developed to solve the problems of the current nuclear data processing systems and satisfy the demands on accurate cross sections (XS) for the advanced reactor. Therefore, modern programming techniques are utilized to make the code more maintainable, modularized, portable, and flexible; it was written in Fortran 2003 by using the object-oriented programming techniques and allocatable memory techniques. Each module has its own class, and the modification of the class does not affect the other classes. The ENDF data class can be easily reused in other modules. The schematic diagram of the AXSP structure is shown in Figure 1. The solid lined modules have already been implemented, while the dotted lined modules are still in development. The GND format is not finalized. Now, the GroupXS module is still based on the Bondarenko method, and on the other hand, the ultrafine group method and hyperfine group method for the fast reactor design will be developed in the future.
The ReconXS module is used to reconstruct resonance cross sections from resonance parameters and to reconstruct cross sections from ENDF nonlinear interpolation schemes by using a traditional inverted-stack method. The BroadXS module generates Doppler-broadened cross sections in the PENDF format from piecewise linear cross sections in the PENDF format from 0 K temperature. To improve the calculation efficiency and maintain the calculation accuracy at the same time, the Gauss–Hermite quadrature has been used in some energy regions, and two points of Gauss–Legendre quadrature are used in other energy ranges (Li, 2012).
The UnresXS module is used to produce effective self-shielded cross sections for resonance reactions in the unresolved energy range. In the unresolved energy range, it is not possible to define precise values for the cross sections of the resonance reactions
and
where
The background cross section
and
where
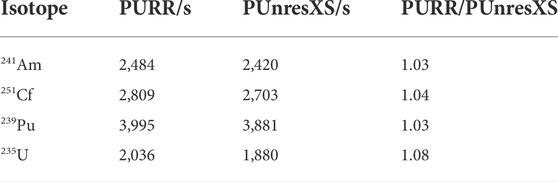
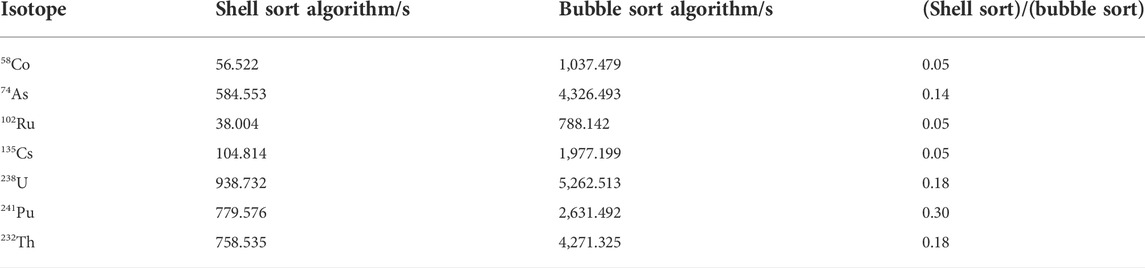
The unresolved self-shielding data generated by UnresXS are suitable for multigroup methods after processing by GroupXS based on the Bondarenko method. However, the Bondarenko method is not suitable for continuous-energy Monte Carlo codes like MCNP and RMC. Therefore, the PUnresXS module is developed by the ladder-sampling method to generate the probability table for the Monte Carlo code. On the other hand, the PUnresXS module can generate the effective self-shielded cross section which can be used for the multigroup cross-section generation. The disadvantage of PUnresXS is time consumption. To solve this problem, we have optimized the sorting method in the program, which greatly saves the calculation time while ensuring the accuracy. Previous research (Yu, 2015) has shown that the time consumption of the PURR module is mainly related to the sorting algorithm used, and the bubble sort algorithm has been applied in the PURR module. If the bubble sort algorithm was also used in the PUnresXS module of AXSP, the time consumption for the unresolved resonance processing with different codes is shown in Table 1. As shown in Table 1, the time consumption of the PUnresXS module is almost the same as the PURR module of NJOY if the same bubble sort algorithm is used. We also compared the impact of selection sort, quicksort, heap sort, and shell sort on time; the shell sort algorithm was selected and applied in the PUnresXS module because of the better calculation speed. The time consumption with the shell sort algorithm and bubble sort algorithm in PUnresXS for different isotopes is shown in Table 2. As shown in Table 2, for most isotopes, the computation time using the shell sort algorithm is 18% of the computation time of the bubble sort, or less. After using the shell sort algorithm, the calculation time is significantly reduced, and the calculation speed is significantly improved.
Multigroup constants are normally used by computer codes that calculate the distribution of neutrons and/ or photons in space and energy, and these compute various responses to these distributions. The GroupXS module in AXSP was developed to calculate the multigroup constants. The GroupXS module computes not only group average cross sections but also the group-to-group scattering matrix. The average cross sections and group-to-group scattering matrix can be represented as
where i, x, and g are the indices for isotopes, reaction type, and multigroup number, respectively.
where the integrals over the resolved resonance interval are evaluated in Eq. 7. When the integrals over the unresolved interval are evaluated, the self-shielding factor generated by the UnresXS or PUnresXS module should be used to be taken into account the self-shielding effects. The GroupXS module calculates the scattering matrix for neutron-induced scattering reactions such as elastic scattering, discrete inelastic scattering, and continuum inelastic scattering. The scattering matrix is also calculated for (n, 2n) and (n, 3n) reactions, including anisotropy by using the ENDF-formatted nuclear data library. The scattering matrix for the
where
For the multigroup constant generation, it is important to select the continuum energy neutron flux and flux moment
where
Numerical calculation results
Cross-section comparison
The ReconXS module was verified by comparing the cross sections which were generated with AXSP with that of NJOY 2016. Almost all the isotopes in ENDF/B-VII.1 (Chadwicka et al., 2011), ENDF/B-VIII.0 (Brown et al., 2018), and CENDL-3.2 (Ge et al., 2020) are used for testing. The results show that the cross sections generated by AXSP are in good agreement with those of NJOY2016. The cross sections of 235U for total, fission, elastic, and capture are shown in Figure 2 and Figure 3. As shown in the figures, the relative error between AXSP and NJOY2016 is all less than 0.5%, which is the maximum relative error setting for the cross-section reconstruction.
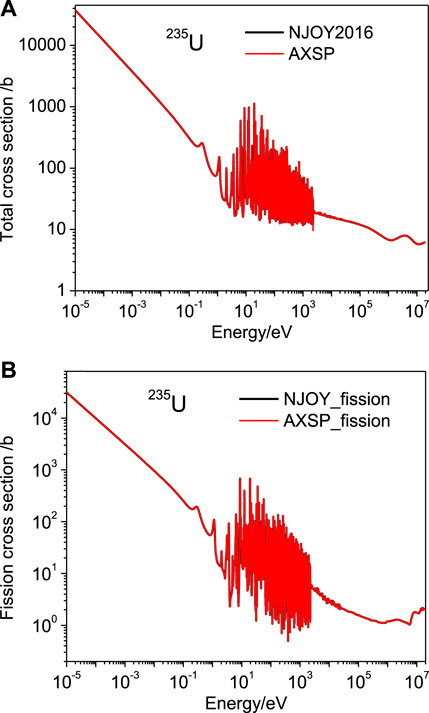
FIGURE 2. Comparison of total (A) and fission (B) cross sections of 235U produced by NJOY2016 and AXSP, respectively.
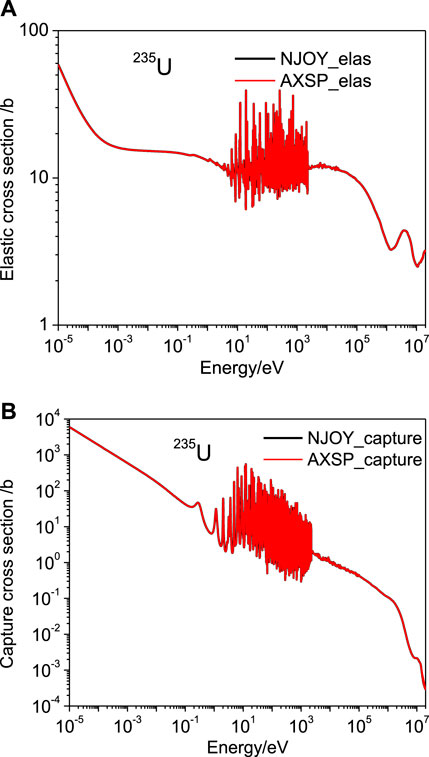
FIGURE 3. Comparison of elastic (A) and capture (B) cross sections of 235U produced by NJOY2016 and AXSP.
The BroadXS module was tested by using BROADR of NJOY. The Doppler-broadened cross sections of 235U for the total and elastic cross sections at 300 K are shown in Figure 4, and the relative errors of the cross sections between AXSP and NJOY2016 are all less than 0.25% in all energy ranges. Therefore, the Doppler-broadened cross section calculated by AXSP is in good agreement with the calculation results of NJOY2016.
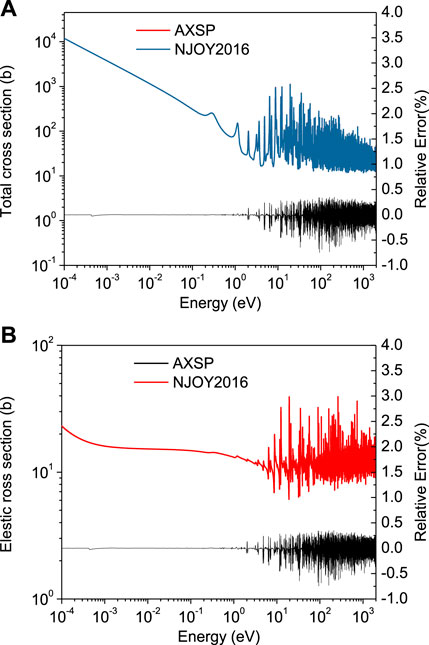
FIGURE 4. Comparison of broaden total (A) and elastic (B) cross sections of 235U produced by NJOY2016 and AXSP.
The UnresXS module has been developed to calculate the shielding factor for the multigroup cross-section generation. To verify the UnresXS module, first, the UnresXS has been developed by the same calculation method as the UNRESR of NJOY 2016; the UNRESR module of NJOY2016 has been used to perform the comparison. The self-shielding cross section of 235U and 241Am at its unresolved energy range at 293.6 K is shown in Figure 5. As shown in Figure 5, the absolute relative error between AXSP and NJOY2016 for all the energy points is less than 0.04%. The probability table for the Monte Carlo calculation has been calculated by the PUnresXS module of AXSP, and the probability table of 235U and 239Pu at energy 2.5 KeV and temperature at 293.6 K is shown in Figure 6. The probability table calculated by AXSP is also in good agreement with PURR of NJOY2016, and the absolute relative errors are less than 0.4%. Second, we improved the UnresXS module to make it to take into account the in-sequence overlap integrals, as shown in Equation 5. The in-sequence overlap integral effects have been shown in Figure 7. In the study, the PURR module calculation results have been set as the reference results, and the relative errors with in-sequence overlap integrals and without in-sequence overlap integrals for 235U and 239Pu have been obtained. As shown in Figure 7, when the background cross section is very large, there is almost no improvement by consideration of the overlap integrals. However, the improvement is more pronounced when the background cross section is relatively small and the self-shielding effects are strong.
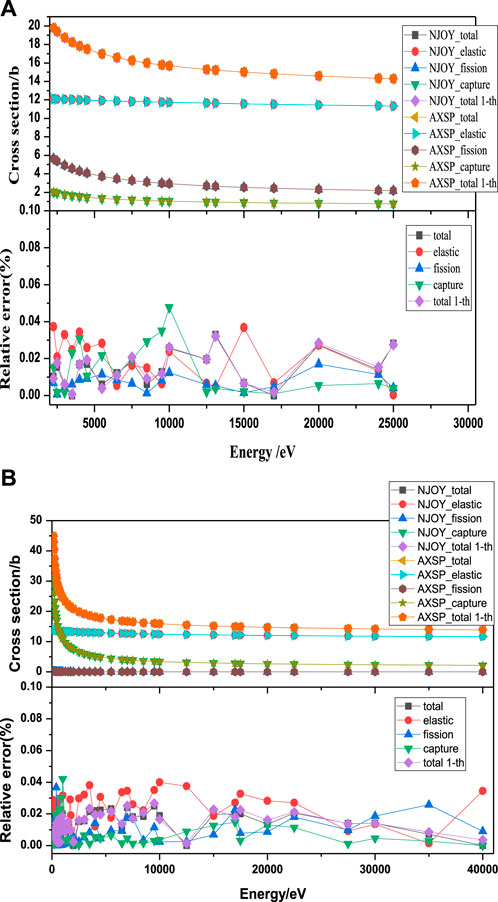
FIGURE 5. Self-shielding cross section of 235U (A) and 241Am (B) at unresolved energy range at 293.6 K and the self-shielding cross section relative error between NJOY2016 and AXSP.
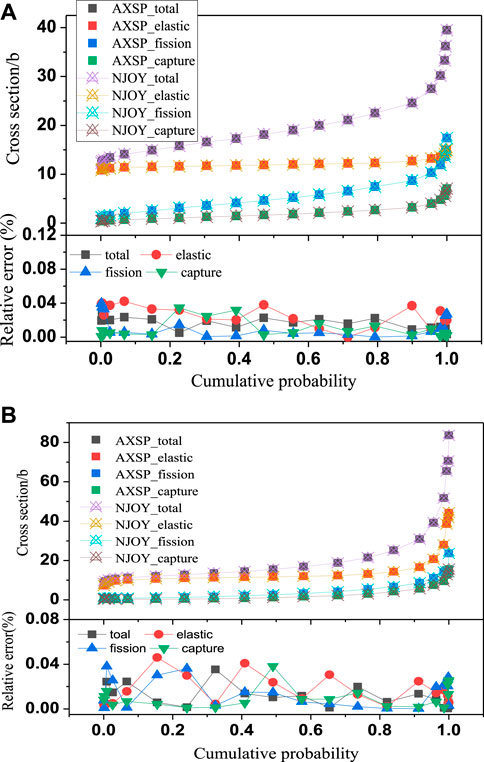
FIGURE 6. Probability table of 235U (A) and 239Pu (B) at energy 2.5 keV at 293.6 K and the relative error between NJOY2016 and AXSP.

FIGURE 7. In-sequence overlap integral effects to the self-shielding total cross sections of 235U and 239Pu with different background cross sections (the temperature is set as 293.6 K).
The calculation accuracy of the reactor physics is directly related to the calculation accuracy of the multigroup cross section. To verify the accuracy of the multigroup cross section generated by the GroupXS module and to facilitate the comparison with the calculation results of the NJOY2016 results, the ANL-230 energy group structures and the Bondarenko method were used to calculate the multigroup cross section and group-to-group matrix. The self-shielding cross section with different background cross sections was calculated. Currently, the GroupXS module can process the average cross sections and scattering matrices of all reaction channels in the Evaluated Nuclear Data File with the ENDF-6 format. These Evaluated Nuclear Data Files mainly include ENDF/B-VII.1, ENDF/B-VIII.0, and CENDL-3.2. Taking ENDF/B-VII.1 as an example, the number of materials in ENDF/B-VII.1 for specific file 5 formats for total fission, first-chance neutron-induced fission, and (n, 2n) reactions are shown in Table 3. A total of 261 materials were given in the format of file 5, in which the number of materials given by the (n, 2n) reaction in the file 5 format is 176, and among these 176 materials, 158 of which are given in the data format of LF = 1, and the rest are given in the data format of LF = 9. Different LF numbers represent different energy distribution laws. The LF = 1 law is the arbitrary tabulated function, and the LF = 9 law is the evaporation spectrum.

TABLE 3. Number of materials in ENDF/B-VII.1 for specific File 5 formats for total fission, first-chance neutron-induced fission, and (n, 2n) reactions.
The average cross sections calculated by GroupXS (Hu et al., 2022) and GROUPR for different isotopes and different reaction types are shown in Figure 8 ∼ Figure 12. The average total cross sections of 235U, 238U, and 239Pu with the background cross section
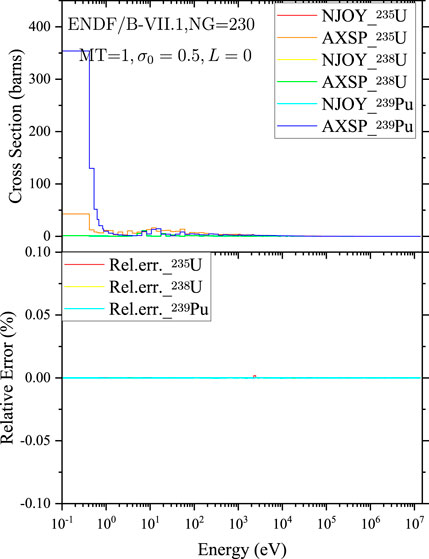
FIGURE 8. Comparison of the average total cross sections of 235U, 238U, and 239Pu calculated by NJOY2016 and AXSP.
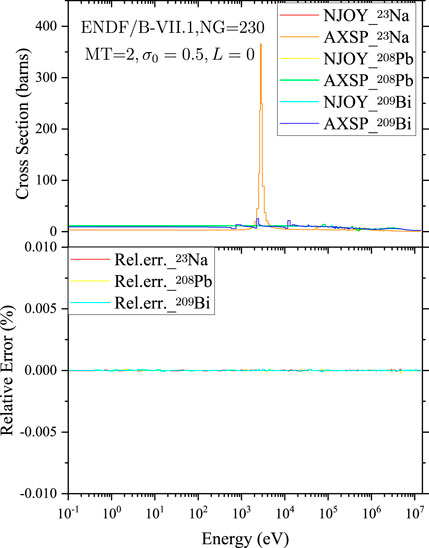
FIGURE 9. Comparison of the average elastic cross sections of 23Na, 208Pb, and 209Bi calculated by NJOY2016 and AXSP.
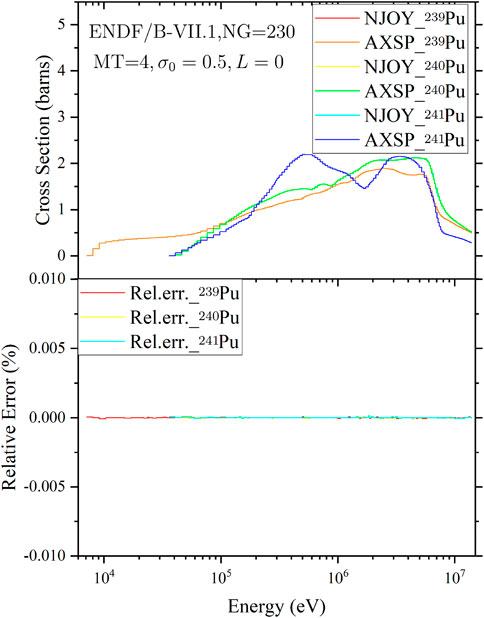
FIGURE 10. Comparison of the average inelastic cross sections of 239Pu, 240Pu, and 241Pu calculated by NJOY2016 and AXSP.
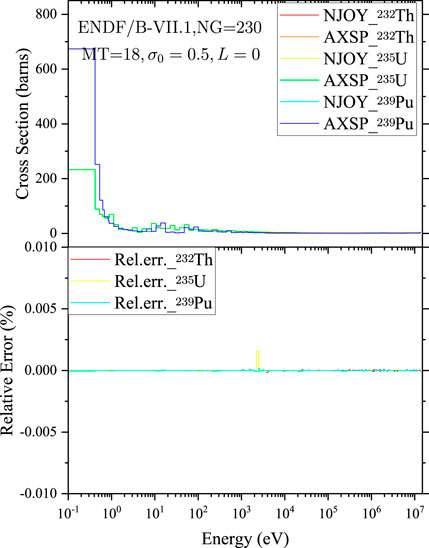
FIGURE 11. Comparison of the average fission cross sections of 232Th, 235U, and 239Pu calculated by NJOY2016 and AXSP.
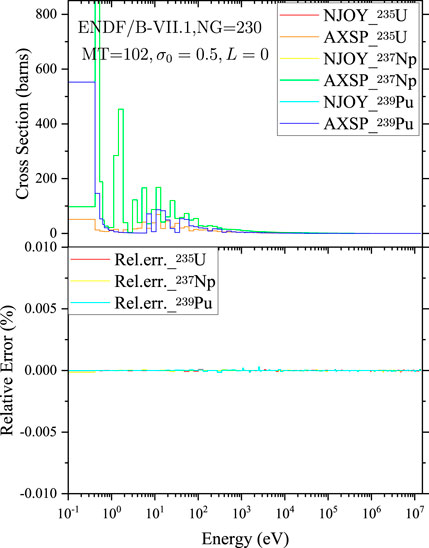
FIGURE 12. Comparison of the average capture cross sections of 235U, 237Np, and 239Pu calculated by NJOY2016 and AXSP.
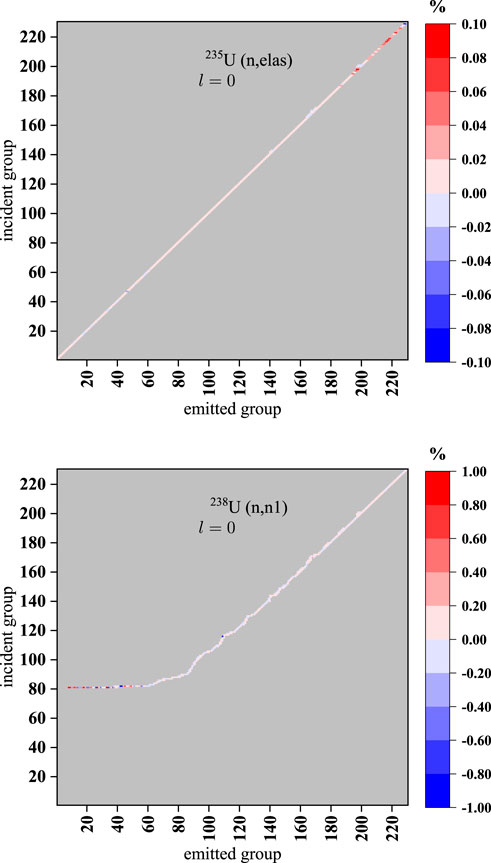
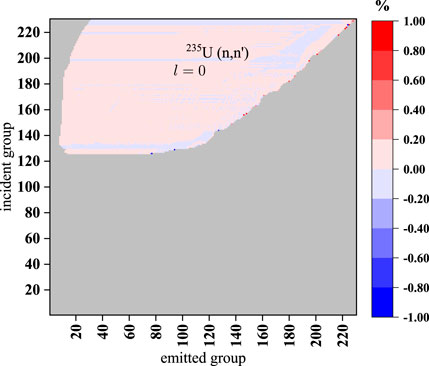
FIGURE 13. Relative error distribution of the elastic scattering matrix of 235U and (n, n1) scattering matrix of 238U between NJOY2016 and AXSP.
Critical benchmark verification
To verify the accuracy of the multigroup cross sections generated by AXSP, the criticality benchmarks from the International Criticality Safety Benchmark Evaluation Project (ICSBEP) are used. The reason why these critical benchmarks are selected to verify the accuracy of multigroup cross sections is that the energy spectrum of these critical devices is mostly hard, and the neutrons are mostly concentrated in the middle- and high-energy regions. In these energy regions, the cross sections generated by the Bondarenko method, which is used in AXSP and NJOY, have higher accuracy.
The effective multiplication factor
ACE format library generation
To verify the ability of the ACEXS module to generate the ACE format section library, ZPR6/7 was selected because of its fast neutron spectrum. The loading of ZPR-6 Assembly 7 (Smith et al., 2003) began in July 1970, and experiments on this assembly continued through October 1971. The particular configuration judged most suitable for a criticality safety benchmark was Loading 12 with a fissile loading of 15.4 kg 235U and 1118.1 kg 239Pu + 241Pu. The specifications of this experiment are provided in the “International Handbook of Evaluated Reactor Physics Benchmark Experiments” under the name “ZPR-LMFR-EXP-001” in the liquid metal fast reactor chapter. The homogeneous R-Z model and associated dimension are shown in Smith et al. (2003).
The ACE format nuclear library was generated based on the ENDF/B-VII.1 evaluated nuclear data file by using NJOY2016 and AXSP. In this calculation, the ACEXS module of AXSP was used to generate the library. However, the resonance reconstruction and the other module of NJOY2016 were applied. The reactor Monte Carlo RMC, which was developed by Tsinghua University, was used to calculate the ZPR6/7 benchmark.
The
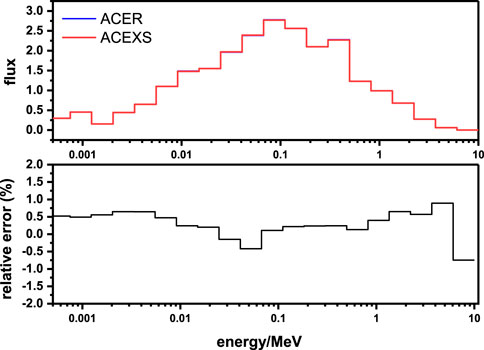
FIGURE 15. Neutron flux of the inner core for the ZPR6/7 benchmark with a different nuclear library.
Conclusion
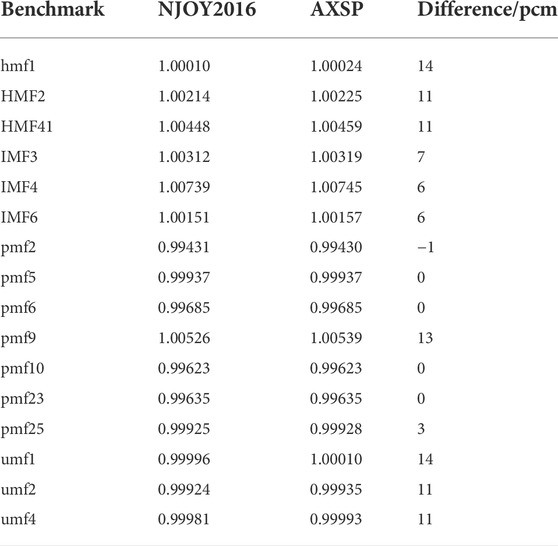
In this study, a new nuclear process code AXSP was developed, and the basic function of the process-evaluated nuclear data file has been verified by using NJOY2016. The critical benchmarks from the ICSBEP handbook were used to verify the multigroup cross section, and the effective multiplication factor maximum difference between AXSP and NJOY2016 is 14 pcm. The ZPR6/7 benchmark was used to verify the ACE format library generation for the Monte Carlo code, and the
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.
Author contributions
KH: GroupXS module development and data analysis. XbM: supervision, conceptualization, methodology, and software. XaM: ACEXS module development and data analysis. YH: data analysis and check. CZ: UnresXS module development and data analysis. YC: supervision and conceptualization.
Funding
This study was supported by the National Natural Science Foundation of China (No. 11875128).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Abou Jaoude, A. (2017). “Design of a mixed-spectrum long-lived reactor with improved proliferation resistance,” PHD thesis (Georgia Institute of Technology).
Beck, R. B., and Mattoon, M. C. (2014). FUDGE: a toolkit for nuclear data management and processing. Livermore, USA: Lawrence Livermore National Laboratory. LLNL-PROC-648476).
Brown, D. A., Chadwick, M. B., Capote, R., Kahler, A., Trkov, A., Herman, M., et al. (2018). ENDF/B-VIII.0: The 8 th major release of the nuclear reaction data library with CIELO-project cross sections, new standards and thermal scattering data. Nucl. Data Sheets 148, 1–142. doi:10.1016/j.nds.2018.02.001
Chadwicka, M. B., Hermanb, M., and Obložinský, P. (2011). ENDF/B-VII.1 nuclear data for science and Technology: Cross sections, covariances, fission product yields and decay data. Nucl. Data Sheets 112 (12), 2887–2996. doi:10.1016/j.nds.2011.11.002
Conlin, L. J. (2015). Modernization of NJOY: creating NJOY21. Los Alamos, USA: Los Alamos National Laboratory. LA-UR-15-24644.
Cullen, D. E. (2017). PREPRO 2017 2017 ENDF/B Pre-processing codes. Vienna, Austria: International Atomic Energy Agency. IAEA-NDS-39.
Ge, Z., Ge, Z., and Xu, R. (2020). CENDL-3.2: The new version of Chinese general purpose evaluated nuclear data library. EPJ Web Conf. 239, 09001. doi:10.1051/epjconf/202023909001
Henryson, H., Toppel, B. J., and Stenberg, C. G. (1976). MC2-2: A code to calculate fast neutron spectra and multigroup cross sections. Argonne Natl. Lab. Rep. ANL-8144 (ENDF-239). doi:10.2172/7143331
Hu, K., Ma, X., and Ma, X. (2022). “Development and verification of multigroup cross section generation module,” in GroupXS in AXSP, 29th International Conference on Nuclear Engineering, ICONE29, Shenzhen, China, August 8-12.
Jian-kai, Y., Song-yang, L., and Wang, K. (2013). Development and validation of nuclear cross section processing code for reactor analysis – RXSP. Nucl. Power Eng. 34. doi:10.1115/ICONE21-15442
Konno, C., Sato, S., Ohta, M., Kwon, S., and Ochiai, K. (2016). New remarks on KERMA factors and DPA cross section data in ACE files. Fusion Eng. Des. 109–111, 1649–1652. doi:10.1016/j.fusengdes.2015.10.038
Leszczynski, F., NRSC: Neutron resonance spectrum calculation system version 2001.0, user's manual, 2001.
Li, W., and WangKan, Y. G. (2017). Thermal scattering data processing and development of Thermc module. High Power laser Part. Beams 29 (3). doi:10.11884/HPLPB201729.160326
Li, S. (2012). “Research on the methods of online Doppler broadening and nuclear cross section processing,” PHD thesis (Tsinghua University).
Lim, C., Han, G., Won, S., and Yang, W. S. (2018). Development of a fast reactor multigroup cross section generation code EXUS-F capable of direct processing of evaluated nuclear data files. Nucl. Eng. Technol. 50, 340–355. doi:10.1016/j.net.2018.01.013
Liu, P., Wu, X., and Ge, Z. (2016). “Progress on China nuclear data processing code system,” in Proceedings of the ND2016, Bruges, Bergium, 2016 Sep 11–16.
Liu, S., Wang, K., and Chen, Y. (2020). Research on on-the-fly Doppler broading based on modified gauss-hermite method. Atomic Energy Sci. Technol. 54. doi:10.7538/yzk.2019.youxian.0466
Ma, X., Ma, X., and Huang, Y. (2022). Development and verification of continuous point section processing module ACEXS based on evaluated nuclear database. Nucl. Sci. Technol. 10 (3), 152–164. doi:10.12677/nst.2022.103016
Mattoon, M. C., Beck, R. B., Patel, R. N., Summers, N., Hedstrom, G., and Brown, D. (2012). Generalized nuclear data: a new structure (with supporting infrastructure) for handling nuclear data. Nucl. Data Sheets 113, 3145–3171. doi:10.1016/j.nds.2012.11.008
Smith, M. A., Lell, R. M., and Pedro, M. (2003). ZPR-6 assembly 7: A cylindrical assembly with mixed (Pu,U)-Oxide fuel and sodium with A thick depleted-uranium reflector. Nea/nsc/ doc(95)03/vi, mix-comp-fast-001.
Tada, K., Nagaya, Y., Kuieda, S., Suyama, K., and Fukahori, T. (2017). Development and verification of a new nuclear data processing system FRENDY. J. Nucl. Sci. Technol. 54, 806–817. doi:10.1080/00223131.2017.1309306
Wen, Y., Zu, T., Cao, L., and Wu, H. (2020). Development and verification of heat production and radiation damage energy production cross section module in the nuclear data processing code NECP-Atlas. Ann. Nucl. Energy 144, 107544. doi:10.1016/j.anucene.2020.107544
Wiarda, D., Dunn, M. E., Greene, N. M., Williams, M. L., Celik, C., and Petrie, L. M. (2016). AMPX-6: A modular code system for processing ENDF/B. USA: Oak Ridge National Laboratory. ORNL/TM-2016/43.
Williams, M. L., and Hollenbach, D. F., (2011). CENTRM: A one-dimensional neutron transport code for computing pointwise energy spectra, ORNL/TM-2005/39.
Yu, J. (2015). “Research on the key method s of evaluation, processing and application of important nuclear data for reactor and code development,” PHD thesis (Tsinghua University).
Keywords: nuclear data processing code, NJOY data processing, AXSP, ENDF format, advanced reactor design
Citation: Hu K, Ma X, Ma X, Huang Y, Zhang C and Chen Y (2022) Development and verification of a new nuclear data processing code AXSP. Front. Energy Res. 10:1009515. doi: 10.3389/fenrg.2022.1009515
Received: 02 August 2022; Accepted: 17 August 2022;
Published: 13 September 2022.
Edited by:
Jiankai Yu, The University of Tennessee, United StatesReviewed by:
Zhaoyuan Liu, Qilu University of Technology (Shandong Academy of Sciences), ChinaMohammad Alrwashdeh, Khalifa University, United Arab Emirates
Copyright © 2022 Hu, Ma, Ma, Huang, Zhang and Chen. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Xubo Ma, bWF4YkBuY2VwdS5lZHUuY24=
 Kui Hu
Kui Hu Xubo Ma
Xubo Ma