Multi-Step Ahead Prediction of Reheat Steam Temperature of a 660 MW Coal-Fired Utility Boiler Using Long Short-Term Memory

With increases in the penetration of renewables in grids, there is an increasing demand for coal-fired power plants to operate flexibly. Regulation of reheat steam temperature is of great importance for the safe and efficient operation of coal-fired power plants. However, the difficulty of reheat steam temperature regulation increases largely during flexible operation due to the large delay and nonlinear properties, especially those units designed to shoulder base load and with limited regulating strategy. A multistep prediction model on the reheat steam temperature of a 660-MW coal-fired utility boiler was developed based on long short-term memory. The results show that the multistep prediction model performs well. The average root mean square error and mean absolute percentage error values of the five-step prediction results are less than 0.52°C and 0.07%, respectively. The correlation coefficients of the five-step predictions are all greater than 0.95. With a sample interval of 30 s, the model provides an accurate prediction of reheat steam temperature within 2.5 min, which could supply an important reference for the reheat steam temperature regulation.

Introduction

As the largest contributor to global greenhouse gas emissions, the energy supply sector needs to make great changes to mitigate the climate change, for example, from traditional fossil fuel-based energy system to renewable energy-based energy system (Kang et al., 2020). The renewable energy generation capacity has increased rapidly in recent years (Verzijlbergh et al., 2016; Meysam et al., 2017; Shahbaz et al., 2020; Wang et al., 2020a; Zheng et al., 2021). However, renewables, such as solar and wind, are variable and intermittent, making them difficult to meet the stable and sustainable energy demand. Dispatchable and flexible power is urgent to balance the electrical supplies and demands (Wang et al., 2018; Zhao et al., 2018). Given the technological limitation of large-scale energy storage, conventional thermal power plants must compensate for the demand in the grid. In China, the large-scale existing coal-fired power plants have become an important pillar in balancing the demand and supply in grids. Traditionally, large coal-fired units were designed to operate at 6,000 to 8,000 full-load hours per year based on the designed conditions. Frequent load transients represent significant challenges to the operation of coal-fired plants with regard to safe operation and efficiency improvement (Zeng et al., 2019; Wang et al., 2020b).

The reheat steam temperature is an important factor that affects the safe, efficient, and economical operation of coal-fired unit (Zhu et al., 2019). Low reheat steam temperatures lead to decreases in the thermal efficiency and the operation safety of the unit because of the increase in humidity at the end of steam turbines. High reheat steam temperatures impact the strength of the metal tube, making it less safe. Frequent changes in load have a significant influence on the stability of reheat steam temperature (Fan et al., 2021; Wang et al., 2020c; Wang et al., 2020c; Fan et al., 2021). The reheat steam temperature has the characteristics of large delay and large inertia and is affected by many factors, such as unit load, coal quality, desuperheating water flow, fouling and slagging, coal-air distribution, and excess air coefficient. The reheat steam temperature object exhibits nonlinear and time-varying characteristics under various disturbances, making it difficult to control (Li et al., 2019).

To improve the regulation of steam temperature, scholars have carried out extensive researches. Sanchez-Lopez et al. designed a model-based controller (dynamic matrix control), and an intelligent controller (fuzzy logic control) has been and implemented for steam temperature regulation of a 300-MW thermal power plant (Sanchez-Lopez et al., 2004). The results indicated that the fuzzy logic controller had a better performance. The overshoot was reduced, and the regulation of the steam temperatures was tighter. Hýl and Wagnerová (2016) presented standard cascade control with two PI controllers and added feed forward control for disturbance measurement, compensation of level change in steam production, and compensation of valve nonlinearity. Ma et al. (2012) presented a predictive optimization control method based on improved mixed-structure recurrent neural network (RNN) model and a simpler Particle Swarm Optimization algorithm for superheated steam temperature control. Muhammad et al. (2012) presented a model predictive control (MPC) to implement at plant steam distillation pot with induction heating system and found MPC is able to control the steam temperature in more efficient way using a first-order ARX model. Lee et al. (2009) develop an Inverse Dynamic Neuro-Controller (IDNC) by utilizing the inverse dynamic relationship of the superheater system for a large-scale ultra-supercritical boiler unit and found the convergence speed of the IDNC is faster than the conventional cascaded PID control scheme. Best control result can be acquired by the IDNC together with a simple PID feedback compensator. Wang (2014) proposed a fuzzy-PID control scheme for main steam temperature control. Sun et al. (2017) upgraded the outer-loop PI controller to active disturbance rejection controller (ADRC) to eliminate the sluggish response to the external load disturbances and introduced multiobjective optimization to improve the superheater steam temperature control performance and thus to enable the load being quickly adjusted in a wider range. Wu et al. (2019) proposed a modified ADRC is to enhance the control performance of superheated steam temperature in a 300-MW circulating fluidized bed. Wang et al. (2020c) proposed a modified reheat steam control that takes the change of heat storage in metal and the deviation of reheat steam temperature into account, which is helpful to stabilize the steam temperature in the transient process. Although the regulation of primary steam temperature has attracted a lot of concerns, studies on reheat steam temperature is still lacking.

Owing to the complex combustion and heat transfer in coal-fired boilers, it is challenging to develop a full-scale dynamic model of coal-fired boilers based on the first principles of energy, mass, and momentum conservations. Fortunately, machine learning techniques, which are powerful in complex process modeling (Wu et al., 2020), offer an alternative approach. The novel methods extract the interrelationships among operational variables and target variables from historical operational data without the need to solve complicated conservation equations. With the rapid development of computer science and machine learning, application of intelligent algorithm in industrial process is possible. Meanwhile, large-scale power plants have abundant measuring points; a lot of operation data are recorded in distributed control system and supervisory information system (SIS). Therefore, data-driven modeling and predictive control with high requirements for data volume and computing power are increasingly applied to the improvement of control systems in coal-fired power plants. The data-driven methods have been widely applied in combustion prediction and optimization (Li et al., 2014; Li and Niu, 2016; Cheng et al., 2018), NOx emission prediction and reduction (Smrekar et al., 2013; Song et al., 2016; Yang et al., 2016; Tan et al., 2019; Xie et al., 2020; Kang et al., 2021), wall temperature prediction (Dhanuskodi et al., 2015; Xie et al., 2020), estimation of exhaust steam properties (Guo et al., 2016; Laubscher, 2019), boiler–turbine coordinated control (Wu et al., 2013; Wu et al., 2014a; Wu et al., 2014b), and so on. However, the application of machine learning on steam temperature prediction is rare. The essential problem in steam temperature regulation is the large and variable time delay. A multistep ahead prediction model may serve as a feedforward signal to improve the steam temperature regulation in flexible operations.

In this study, the long short-term memory (LSTM) (Hochreiter and Schmidhuber, 1997), which has a good performance on modeling dynamical systems (Zarzycki and Ławryńczuk, 2021), was introduced to carry out the multistep prediction modeling of reheat steam temperature with actual operation data of a 660-MW subcritical tangential pulverized coal-fired utility power plant.

Brief Introduction on LSTM Algorithm

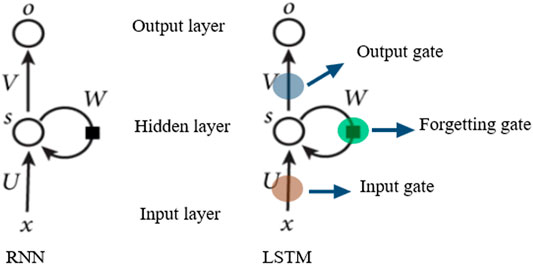
RNN is a class of artificial neural networks where connections between nodes form a directed or undirected graph along a temporal sequence as shown Figure 1. This allows it to represent temporal dynamic behavior. LSTM is an important variant of traditional RNN. It is augmented by adding recurrent gates called “forget gates” as shown in Figure 1, where information can be selectively remembered or forgotten, making it effectively solve problems with long-time dependence (Li et al., 2019). It is observed as the most effective RNN in industrial applications. The specific formula of LSTM is listed as follows:

FIGURE 1

FIGURE 1. Structure of RNN and LSTM.

Forgetting gate:

$f_t=\sigma \left(W_f\cdot \left[h_{t-1},x_t\right]+b_f\right)(1)$

Input gate:

$i_t=\sigma \left(W_i\cdot \left[h_{t-1},x_t\right]+b_i\right)(2)$

State updating:

$g_t=tanh\left(W_c\cdot \left[h_{t-1},x_t\right]+b_c\right)(3)$

$C_t=f_t\text{*}{C}_{t-1}+i_t\text{*}{g}_t(4)$

Output gate:

$o_t=\sigma \left(W_o\cdot \left[h_{t-1},x_t\right]+b_o\right)(5)$

$h_t=o_t\text{*}tanh\left(C_t\right)(6)$

where f, i, C, and o are the forget gate, input gate, cell state, and output gate activation vectors, respectively; W represents the connection matrix; x_t is the input vector at moment t; h_t-1 is the output of the hidden layer at moments t-1; b is the bias vector; and * represents element-wise multiplication. $\sigma$ and tanh are activation functions.

The function of “gate” is to filter information, which solves the information redundancy problem by strengthening the weight of the main information and weakening the weight of irrelevant information. The “gate” prevents LSTM from gradient vanishing or exploding.

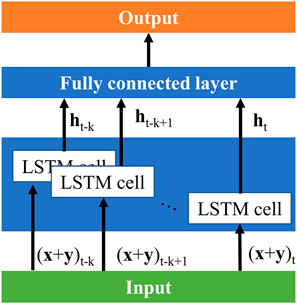
The prediction model in this work needs to add a full connection layer on the basis of the single-layer LSTM. To increase the number of LSTM layers, only the LSTM layer needs to be added before the fully connection layer. Figure 2 is a single-layer LSTM model for multistep prediction of reheat steam temperature.

FIGURE 2

FIGURE 2. Schematic diagram of single-layer LSTM model for multistep prediction model.

Modeling Reheat Steam Temperature With LSTM

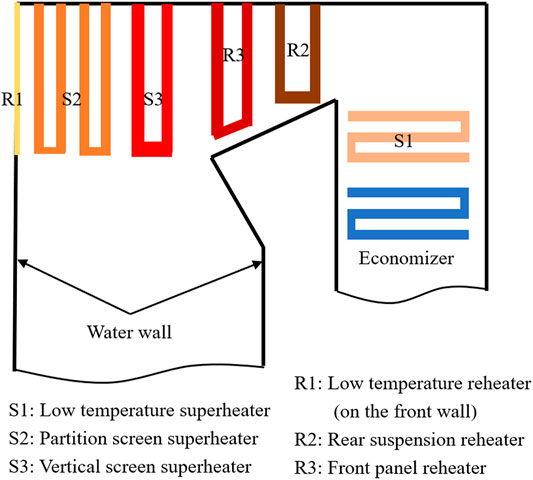
The studied object of this work is a 660-MW subcritical tangential pulverized coal-fired utility boiler. The continuous rating is 2,100 t/h. The rated reheat steam temperature is 542.7°C, and the allowable deviation from the rated value during operation ranges from −10°C to +8°C. The arrangement of heat exchangers is illustrated in Figure 3. It should be noted that the low-temperature reheater, marked as R1 in Figure 3, is arranged on the front wall above the elevation of furnace arch. It is radiative heat exchanger. The steam flows to the rear suspension reheater after leaving the low-temperature reheater and then flows to the front panel reheater. In the back flue, the low-temperature superheater and economizer are arranged successively. As the boiler was designed to undertake the base load, the reheated steam temperature adjusting measures is limited. Adjusting the elevation of the high-temperature zone in the furnace is the primary measure on the combustion side, specifically including adjustment of burner tilt position, excess air coefficient, and the distribution of secondary air. Desuperheating water is the only adjusting measure on the steam side.

FIGURE 3

FIGURE 3. Schematic diagram of the arrangement of heat exchangers.

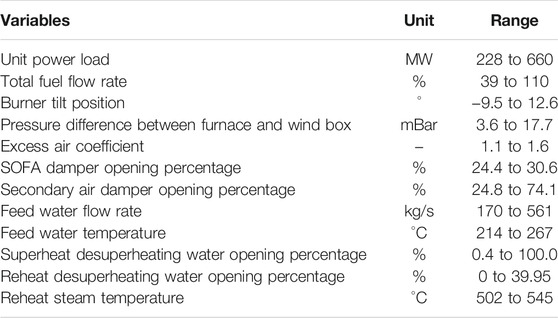
The reheat steam temperature in a coal-fired boiler is affected by many variables, which could be primarily divided into fire side and water and steam side. According to the basic knowledge of the coal-fired boiler and the engineers’ suggestions, a total of 11 variables are used as the input of the multistep prediction model. These variables include total fuel flow rate, burner tilt position, pressure difference between furnace and wind box, excess air coefficient, SOFA damper opening percentage, secondary air damper opening percentage, feed water flow rate, feed water temperature, superheat desuperheating water opening percentage, reheat desuperheating water opening percentage, and reheat steam temperature. Among these variables, furnace pressure difference represents the furnace wind speed, secondary air damper opening percentage represents the furnace wind flow rate, and the excess air coefficient is calculated by the oxygen content. Unit power load is a very important variable. However, the load is given for coal-fired units and is correlated with other variables. The unit power load is not taken as the input variable in this work. Because the output of the model is the predicted value at the future moment, rather than the regression value at the current moment, the output value at the past moment can also be regarded as input variables. Thus, the input of the multistep prediction model is $\left\{{[X Y]}_{t-(K-1)},{[X Y]}_{t-(K-2)}\dots {[X Y]}_t\right\}$, the output is $\left\{Y_{t+1},Y_{t+2}\dots Y_{t+5}\right\}$, and the time step of output is five. Unit and range of each variable are shown in Table 1.

TABLE 1

TABLE 1. Unit and range of each parameter.

In total, 360,000 sets of data, obtained from the SIS at a sampling frequency of 1 Hz, were used for modeling. The first 70% were set as the training set for the model training process, whereas the remaining 30% were set as the test set for the validation of the model. The test data were kept away from the model training process. In order to ensure that the two datasets have different distribution, the two sets were collected from two different operation periods.

Before modeling, data preprocessing was required. First, manual examinations of noise and outliers were conducted to improve the quality of the dataset. Second, variables that remain unchanged throughout the sampling period were removed, and variables with multiple measurement points were averaged.

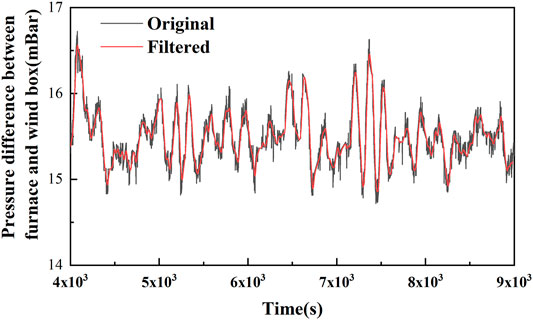
As the actual operating environment of the power plant is relatively harsh, electromagnetic interference and measurement fluctuation are inevitable. Noise or spike usually exists in the original data, which affect the modeling performance. Data filtering is necessary to further remove data noise. As boiler operation data are a deterministic signal, the finite impulse response (FIR) digital filter (Neuvo et al., 1984) was used. In the filtering process, Hanning window was applied with cutoff frequency of 0.02 to 0.03 Hz. The filter order was set as 50, and single filter data segment length was 4,000. The original and filtered pressure differences between furnace and wind box are illustrated in Figure 4. As seen, the filtered data keep the primary dynamics but filter out minor fluctuations, demonstrating that the filtering process is necessary and effective. Considering the time scale of reheat steam temperature is minute level. Occasionally, the response time could even be up to 10 min. In order to capture the dynamic characteristics of reheat steam temperature, resampling was carried out after filtering. Resampling process with intervals of 10 s, 30 and 60 s were conducted comparatively. Both 10- and 30 s resampling intervals can follow the primary dynamics of the reheat steam temperature, whereas the 60-s resampling interval may lose some small fluctuations. After a comprehensive consideration of the model complexity and the effectiveness for reheat steam temperature regulation, 30 s was finally used. After filtering and resampling, min–max normalization was used to decrease the effect of the magnitude differences of input variables on the model performance, and the variables was scaled to [0, 1].

FIGURE 4

FIGURE 4. Curves before and after FIR filtering.

The Keras library (Chollet, 2015) with a TensorFlow (Abadi et al., 2016) backend was used to build the LSTM-based multistep ahead steam temperature prediction framework in this study. EarlyStopping (Prechelt, 1998) and Dropout (Srivastava et al., 2014) are used in the model to prevent overfitting. EarlyStopping is used to monitor the training process of model. When the change amplitude of loss of training set is small enough, the training will be stopped in advance, which can effectively reduce the model training time and prevent from overfitting caused by the continuous training of model. The role of Dropout is to randomly set a part of the unit to 0 when the model training is updated to prevent the model from relying on individual units. When increasing the number of LSTM layers, Dropout is used for each layer. The model uses Adam training method, the learning rate is 0.001, and the learning target is mean square error. Three evaluation criteria, for example, root mean square error (RMSE), mean absolute percentage error (MAPE), and correlation coefficient (r), were introduced. Their formulas are as follows:

$\mathit{RMSE}=\sqrt{\frac{1}{n}{\displaystyle \sum }_{i=1}^n{\left(\widehat{y_i}-y_i\right)}^2}(7)$

$\mathit{MAPE}=\frac{1}{n}{\displaystyle \sum }_{i=1}^n\left|\frac{\widehat{y_i}-y_i}{y_i}\right|(8)$

$r=\frac{\mathit{Cov}\left(\widehat{Y},Y\right)}{\sqrt{\mathit{Var}\left[\widehat{Y}\right]\mathit{Var}\left[Y\right]}}(9)$

where $\widehat{y_i}$ represents the predicted value, and $y_i$ represents the actual value. Cov and Var are the covariance and the standard deviation, respectively.

In order to reduce the impact of parameter magnitude on model performance, it is necessary to optimize model parameters. As the five outputs of the model are predictive values of reheat steam temperature at different time steps, the RMSE of the output is in the same standard, and its mean value is significant. The RMSE value can better represent the model performance than the correlation coefficient (r) value, so the mean value of RMSE is used as the evaluation standard for the parameter adjustment of the multistep prediction model. For parameter calculation, the Dropout parameter is 0.3, and the length of the data set is 6,000. The first 70% is used as the training set, and the remaining 30% is used as the test set. After adjusting the model parameters and structure, the cutoff time step is selected to be 390 s; the number of LSTM hidden layer nodes is 256, and the number of LSTM layers is 1.

Results and Discussion

Model Development

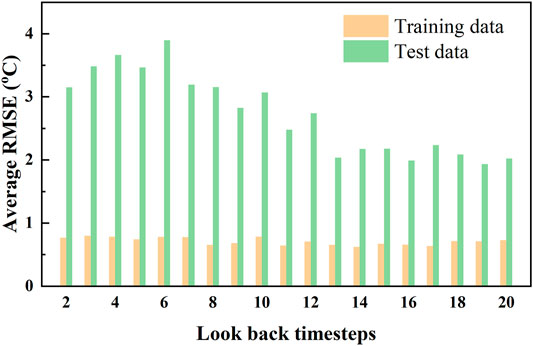
The performance of a data-driven primarily depends on the quality of data and the hyperparameter of the used model. As for the LSTM, the principal hyperparameters include the look-back time step, the number of LSTM layers, and the number of nodes in each layer. The look-back time step limits the depth of LSTM unfolding over time and determines the maximum length of the input data. It should be noted that the look-back time step in LSTM is different from the delay time order in conventional time-series forecasts. Theoretically, LSTM can automatically determine the delay time order through the gate structure in the memory cell if the preset time step is big enough. However, an elaborately determined look-back time step can prevent from underfitting or overfitting, reduce the difficulty of the training process, and speed up convergence. In this study, 19 trials of look-back time step, for example, 2, 3, … , 20, were conducted to obtain the optimal look-back time step while studying the effect of look-back time step on the performance of reheat steam temperature. As the weight matrices of LSTM are randomly initialized and the primary weight matrices have nonnegligible influences on the final prediction performance, five experiments were conducted for each look-back time step, and the average RMSE values of the five experiments were compared. As seen from Figure 5, the average RMSEs of training data change little with different look-back time steps, which indicates the LSTM model has an excellent representation ability upon the dynamics of reheat steam temperature. The average RMSEs of test data are much bigger those of training data, and the changes of average RMSEs with different look-back time steps are significant. This indicates that the look-back time step has an important influence on the generalization capacity of the model. Generally, the average RMSE decreases initially and then stabilizes as the look-back time step increases. In consideration of model complexity and computational cost, the look-back time step was set as 13.

FIGURE 5

FIGURE 5. Average RMSEs with different look-back time steps.

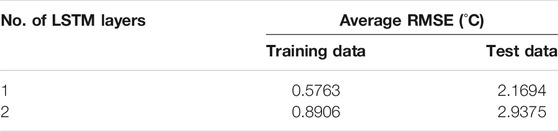
The number of LSTM layers is an important hyperparameter that determines the structure of the neural network. Generally, the representation capacity increases with the increase in the layers of neural networks. However, the training difficulty increases exponentially. Besides, too many hidden layers may lead to overfitting. Thus, the best choice of hidden layers is different for a specific problem. In this study, two trials with one and two LSTM layers were conducted to obtain the best neural network structure. Similarly, five repeated experiments were conducted for each trial to improve the reliability. The results are summarized in Table 2. Obviously, the network with one LSTM layer performed better than that with two LSTM layers upon both the average RMSEs of training data and test data. Therefore, one LSTM layer was finally selected.

TABLE 2

TABLE 2. Average RMSEs with different number of LSTM layers.

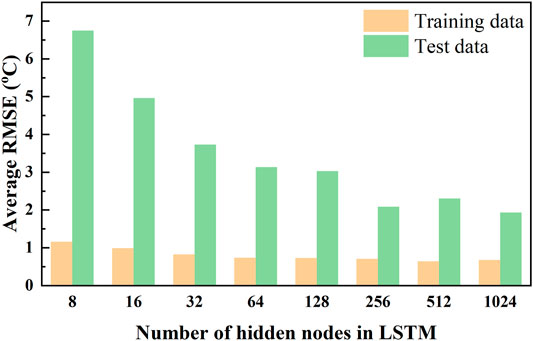
The number of LSTM nodes is another important hyperparameter for the LSTM. Eight trials on the number of nodes in LSTM layer, for example, 8, 16, 32, 64, 128, 128, 256, 512, and 1,024, were conducted with the previously determined look-back time step and number of LSTM layers. Five trials were conducted for each experiment. As seen from Figure 6, the average RMSE decreases initially and then slightly increases with the increase in the number of LSTM nodes. The average RMSE is smallest when the number of LSTM nodes is 256. Thus, 256 LSTM nodes were used in the final reheat steam temperature prediction model.

FIGURE 6

FIGURE 6. Average RMSEs with different number of hidden nodes.

Through optimizing the hyperparameter and structure, the LSTM-based multistep ahead prediction model of reheat steam temperature was finally established. Thirteen look-back time steps and one LSTM layer with 256 hidden nodes were used eventually. The number of predicted steps was 5.

LSTM Modeling Performance

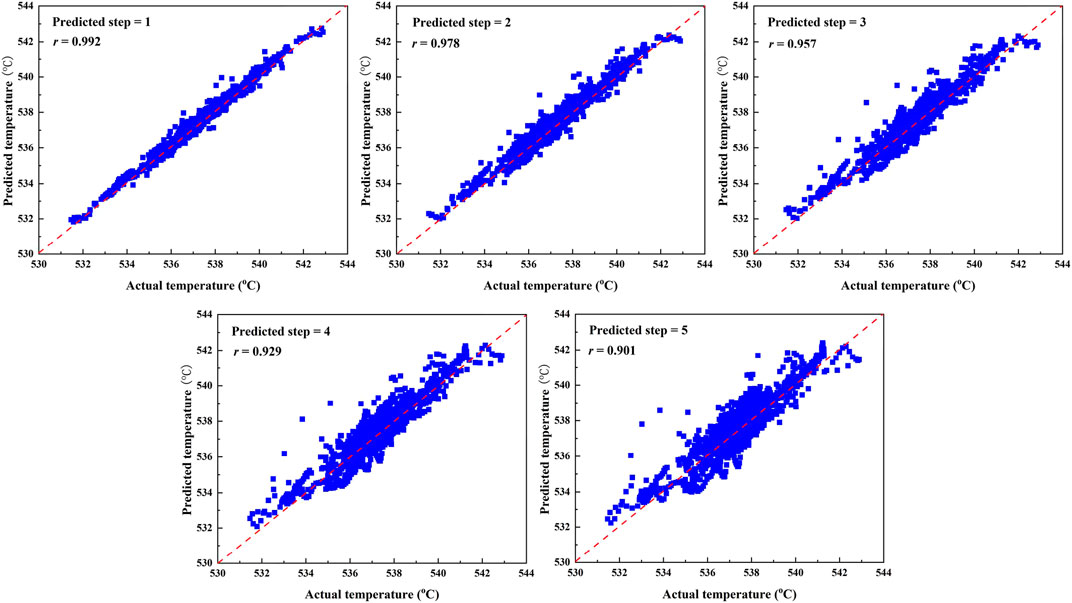
The predicted reheat steam temperatures versus the measured temperatures from the test data are illustrated in Figure 7. The red dashed line in the figure is the prefect line, on which the predicted results are equivalent to the measured values without error. The blue points, which correspond to the measured data, represent the predicted value. The five plots present results of different predicted steps, for example, from steps 1 to 5. As seen, most points in the five plots are closely distributed near the red dashed line, which implies that the developed model possesses a good capability of reheat steam temperature prediction. The performance deteriorates from t+1-step prediction to t+5-step prediction. This is reasonable and expectable as the later the prediction moment is, the more difficult it is to predict.

FIGURE 7

FIGURE 7. Results of predicted temperatures versus measured temperatures from test data.

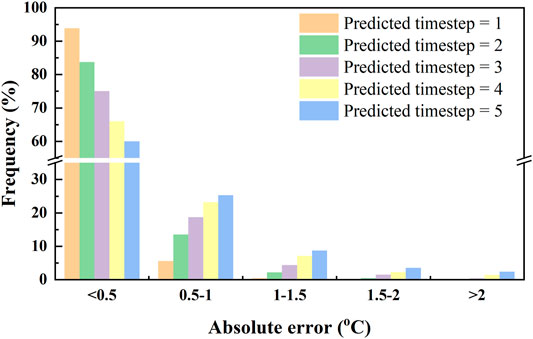
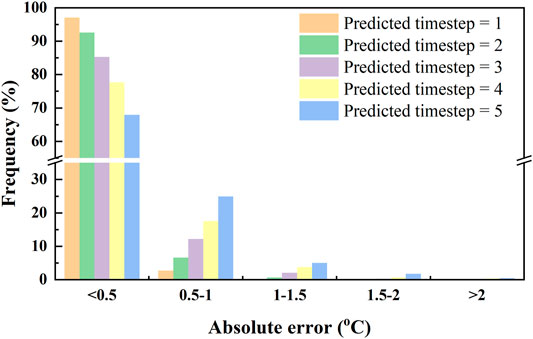
The absolute error distributions of the training data and test data are further illustrated in Figures 8, 9, respectively. For the training data, the absolute errors of 93.9% cases on t+1-step prediction are within 0.5°C. The ratios on t+2-, t+3-, t+4-, and t+5-step predictions are 83.7%, 75.0%, 66.0%, and 60.0%, respectively. The absolute errors of all cases are within 2°C when the predicted time step is 1. The numbers of cases, of which absolute errors are greater than 2°C, are 5, 30, 99, and 167 on t+2-, t+3-, t+4-, and t+5-step predictions, accounting for 0.07%, 0.43%, 1.42%, and 2.36%, respectively. The maximum absolute error appears on t+5-step prediction and is 4.55°C. As for the test data, the absolute errors of 97.1%, 92.5%, 85.3%, 77.7%, and 67.9% cases on t+1-, t+2-, t+3-, t+4-, and t+5-step predictions are within 0.5°C. The ratios of cases to absolute errors over 2°C are 0.00%, 0.03%, 0.20%, 0.37%, and 0.47%, respectively. The maximum absolute error appears on t+5-step prediction and is 4.78°C.

FIGURE 8

FIGURE 8. Distribution of the absolute errors on training data.

FIGURE 9

FIGURE 9. Distribution of the absolute errors on test data.

Quantitative evaluation of the developed multistep ahead reheat steam temperature prediction model is further conducted, and the results are summarized in Table 3. The RMSEs of both the training data and the test data on t+1-time-step prediction are less than 0.27°C, and the MAPEs are less than 0.035%. The RMSEs of both the training data and the test data at t+5 are within 075°C, and the MAPEs are less than 0.101%. The correlation coefficients of measured temperatures and predicted temperatures, denoted as r, are 0.962 and 0.901, respectively. In general, the multistep prediction model of reheat steam temperature performs well. In terms of training and test data, the average RMSE, MAPE, and r of the five-step prediction results are all within 0.52°C, 0.07%, and greater than 0.95, respectively. The good prediction performance on training data and test data demonstrates that the developed model has excellent accuracy and strong generalizability.

TABLE 3

TABLE 3. Performance of multistep prediction model based on LSTM.

Comparative Study

The performance of LSTM and the widely used support vector machine (SVM) was further compared in this work. Multi-output SVM from scikit-learn framework (Pedregosa et al., 2011) was used. The radial basis function was selected as the kernel function. Fivefold cross-validation coupled with grid search was introduced to determine the kernel parameter g and the plenty factor C. A total of 208 pairs of exponentially growing sequences (g, C) were attempted, that is, g = 2⁻⁹, 2^−8, … , 2⁰, … , 2³; C = 2⁻², 2⁻², 2⁰, … , 2¹³. The delay time order was set as 13, being consistent with LSTM.

The optimal (g, C) pairs were found to be (2¹⁰, 2⁻²) according to grid search. The average RMSEs of the training data and test data are 0.087°C and 1.680°C, respectively. The corresponding MAPEs are 0.014°C and 0.256%, and the R values are 0.999 and 0.951. Detailed results are demonstrated in Table 4. As seen, the performance of the SVM-based model on the training data is better than that of the LSTM-based model. However, the performance on the test data obviously deteriorated. This indicates the generalizability of is not good enough, and the SVM-based model may suffer from overfitting. Comparing the prediction performance of the two models developed in this study, the LSTM-based model outperforms the SVM-based model. LSTM exhibits a stronger capacity to make a multistep ahead reheat steam temperature prediction in the studied coal-fired boiler than SVM.

TABLE 4

TABLE 4. Performance of multistep prediction model based on SVM.

Conclusion

This study proposed a multistep prediction model on reheat steam temperature of a 660-MW coal-fired utility boiler with LSTM. There were 360,000 sets of actual operation data obtained from the SIS used to develop the model. The FIR digital filter was used to filter the noise and spikes in the operation data. The hyperparameters, for example, the look-back time step, and the model structure, including the number of LSTM layers and the number of nodes in each layer, were adjusted and optimized. The five-step prediction model performs pretty good. The average RMSE, MAPE, and R values of the five-step prediction results are less than 0.52°C, less than 0.07%, and greater than 0.95, respectively. The model can accurately predict the change of reheat steam temperature within 2.5 min. The model may serve as an important feedforward signal for the reheat steam temperature regulation.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

PT, CZ, QF, and GC contributed to conception and design of the study. ZH processed data. HZ and ZJ performed the statistical analysis. PT and HZ wrote the first draft of the manuscript. All authors contributed to manuscript revision, read, and approved the submitted version.

Funding

This work was supported by the National Natural Science Foundation of China (Grant No.52106011).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abadi, M. I. N., Agarwal, A., Barham, P., Brevdo, E., Chen, Z., Citro, C., et al. (2016). Tensorflow: Large-Scale Machine Learning on Heterogeneous Distributed Systems. arXiv preprint arXiv:1603.04467.

Google Scholar

Cheng, Y., Huang, Y., Pang, B., and Zhang, W. (2018). ThermalNet: A Deep Reinforcement Learning-Based Combustion Optimization System for Coal-Fired Boiler. Eng. Appl. Artif. Intelligence 74, 303–311. doi:10.1016/j.engappai.2018.07.003

CrossRef Full Text | Google Scholar

Chollet, F. (2015). Keras: Deep Learning Library for Theano and Tensorflow.

Google Scholar

Dhanuskodi, R., Kaliappan, R., Suresh, S., Anantharaman, N., Arunagiri, A., and Krishnaiah, J. (2015). Artificial Neural Networks Model for Predicting wall Temperature of Supercritical Boilers. Appl. Therm. Eng. 90, 749–753. doi:10.1016/j.applthermaleng.2015.07.036

CrossRef Full Text | Google Scholar

Fan, H., Xu, W., Zhang, J., and Zhang, Z. (2021). Steam Temperature Regulation Characteristics in a Flexible Ultra-supercritical Boiler with a Double Reheat Cycle Based on a Cell Model. ENERGY 229, 120701. doi:10.1016/j.energy.2021.120701

CrossRef Full Text | Google Scholar

Guo, S., Liu, P., and Li, Z. (2016). Estimation of Exhaust Steam Enthalpy and Steam Wetness Fraction for Steam Turbines Based on Data Reconciliation with Characteristic Constraints. Comput. Chem. Eng. 93, 25–35. doi:10.1016/j.compchemeng.2016.05.019

CrossRef Full Text | Google Scholar

Hochreiter, S., and Schmidhuber, J. (1997). Long Short-Term Memory. Neural Comput. 9, 1735–1780. doi:10.1162/neco.1997.9.8.1735

PubMed Abstract | CrossRef Full Text | Google Scholar

Hýl, R., and Wagnerová, R. (2016). Design and Implementation of cascade Control Structure for Superheated Steam Temperature Control, 253–258.

Google Scholar

Kang, J.-N., Wei, Y.-M., Liu, L.-C., Han, R., Yu, B.-Y., and Wang, J.-W. (2020). Energy Systems for Climate Change Mitigation: A Systematic Review. Appl. Energ. 263, 114602. doi:10.1016/j.apenergy.2020.114602

CrossRef Full Text | Google Scholar

Kang, J., Niu, Y., Hu, B., Li, H., and Zhou, Z. (2021). Dynamic Modeling of SCR Denitration Systems in Coal-Fired Power Plants Based on a Bi-directional Long Short-Term Memory Method. Process Saf. Environ. Prot. 148, 867–878. doi:10.1016/j.psep.2021.02.009

CrossRef Full Text | Google Scholar

Laubscher, R. (2019). Time-series Forecasting of Coal-Fired Power Plant Reheater Metal Temperatures Using Encoder-Decoder Recurrent Neural Networks. ENERGY 189, 116187. doi:10.1016/j.energy.2019.116187

CrossRef Full Text | Google Scholar

Lee, K. Y., Ma, L., Boo, C. J., Jung, W.-H., and Kim, S.-H. (2009). Inverse Dynamic Neuro-Controller for Superheater Steam Temperature Control of a Large-Scale Ultra-supercritical (USC) Boiler Unit. IFAC Proc. Volumes 42, 107–112. doi:10.3182/20090705-4-sf-2005.00021

CrossRef Full Text | Google Scholar

Li, G., and Niu, P. (2016). Combustion Optimization of a Coal-Fired Boiler with Double Linear Fast Learning Network. SOFT COMPUT. 20, 149–156. doi:10.1007/s00500-014-1486-3

CrossRef Full Text | Google Scholar

Li, G., Niu, P., Wang, H., and Liu, Y. (2014). Least Square Fast Learning Network for Modeling the Combustion Efficiency of a 300WM Coal-Fired Boiler. NEURAL NETWORKS 51, 57–66. doi:10.1016/j.neunet.2013.12.006

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, X., Liu, J., Wang, K., Wang, F., and Li, Y. (2019). Performance Analysis of Reheat Steam Temperature Control System of Thermal Power Unit Based on Constrained Predictive Control. COMPLEXITY 2019, 1–12. doi:10.1155/2019/9361723

CrossRef Full Text | Google Scholar

Ma, L. Y., Ge, Y. P., and Cao, X. (2012). Superheated Steam Temperature Control Based on Improved Recurrent Neural Network and Simplified PSO Algorithm. Applied Mechanics and Materials, 1065–1069.

Google Scholar

Meysam, Q., Hossein, A., Goran, S., and Nicholas, J. (2017). Efficacy of Options to Address Balancing Challenges: Integrated Gas and Electricity Perspectives. APPL. ENERG 190, 181–190. doi:10.1016/j.apenergy.2016.11.119

CrossRef Full Text | Google Scholar

Muhammad, Z., Yusoff, Z. M., Rahiman, M. H. F., and Taib, M. N. (2012). Steam Temperature Control for Steam Distillation Pot Using Model Predictive Control, 474–479.

Google Scholar

Neuvo, Y., Dong Cheng-Yu, D., and Mitra, S. (1984). Interpolated Finite Impulse Response Filters. IEEE Trans. Acoust. Speech, Signal. Process. 32, 563–570. doi:10.1109/tassp.1984.1164348

CrossRef Full Text | Google Scholar

Pedregosa, F., Varoquaux, G. E. L., Gramfort, A., Michel, V., Thirion, B., Grisel, O., et al. (2011). Scikit-learn: Machine Learning in Python. J. MACH LEARN. RES. 12, 2825–2830.

Google Scholar

Prechelt, L. (1998). Automatic Early Stopping Using Cross Validation: Quantifying the Criteria. NEURAL NETWORKS 11, 761–767. doi:10.1016/s0893-6080(98)00010-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Sanchez-Lopez, A., Arroyo-Figueroa, G., and Villavicencio-Ramirez, A. (2004). Advanced Control Algorithms for Steam Temperature Regulation of thermal Power Plants. Int. J. Electr. Power Energ. Syst. 26, 779–785. doi:10.1016/j.ijepes.2004.08.003

CrossRef Full Text | Google Scholar

Shahbaz, M., Raghutla, C., Chittedi, K. R., Jiao, Z., and Vo, X. V. (2020). The Effect of Renewable Energy Consumption on Economic Growth: Evidence from the Renewable Energy Country Attractive index. ENERGY 207, 118162. doi:10.1016/j.energy.2020.118162

CrossRef Full Text | Google Scholar

Smrekar, J., Potočnik, P., and Senegačnik, A. (2013). Multistep-ahead Prediction of NOx Emissions for a Coal-Based Boiler. Appl. Energ. 106, 89–99. doi:10.1016/j.apenergy.2012.10.056

CrossRef Full Text | Google Scholar

Song, J., Romero, C. E., Yao, Z., and He, B. (2016). Improved Artificial Bee colony-based Optimization of Boiler Combustion Considering NO Emissions, Heat Rate and Fly Ash Recycling for On-Line Applications. FUEL 172, 20–28. doi:10.1016/j.fuel.2015.12.065

CrossRef Full Text | Google Scholar

Srivastava, N., Hinton, G., Krizhevsky, A., Sutskever, I., and Salakhutdinov, R. (2014). Dropout: a Simple Way to Prevent Neural Networks from Overfitting. J. machine Learn. Res. 15, 1929–1958.

Google Scholar

Sun, L., Hua, Q., Shen, J., Xue, Y., Li, D., and Lee, K. Y. (2017). Multi-objective Optimization for Advanced Superheater Steam Temperature Control in a 300 MW Power Plant. Appl. Energ. 208, 592–606. doi:10.1016/j.apenergy.2017.09.095

CrossRef Full Text | Google Scholar

Tan, P., He, B., Zhang, C., Rao, D., Li, S., Fang, Q., et al. (2019). Dynamic Modeling of NOX Emission in a 660 MW Coal-Fired Boiler with Long Short-Term Memory. ENERGY 176, 429–436. doi:10.1016/j.energy.2019.04.020

CrossRef Full Text | Google Scholar

Verzijlbergh, R. A., Jdv, L., Pjd, G., and Mh, P. (2016). Institutional Challenges Caused by the Integration of Renewable Energy Sources in the European Electricity Sector. Renew. Sust. Energ. Rev. 75, 660–667. doi:10.1016/j.rser.2016.11.039

CrossRef Full Text | Google Scholar

Wang, C., Qiao, Y., Liu, M., Zhao, Y., and Yan, J. (2020). Enhancing Peak Shaving Capability by Optimizing Reheat-Steam Temperature Control of a Double-Reheat Boiler. Appl. Energ. 260, 114341. doi:10.1016/j.apenergy.2019.114341

CrossRef Full Text | Google Scholar

Wang, C., Zhao, Y., Liu, M., Qiao, Y., Chong, D., and Yan, J. (2018). Peak Shaving Operational Optimization of Supercritical Coal-Fired Power Plants by Revising Control Strategy for Water-Fuel Ratio. Appl. Energ. 216, 212–223. doi:10.1016/j.apenergy.2018.02.039

CrossRef Full Text | Google Scholar

Wang, H. (2014). Main Steam Temperature Control System Based on Fuzzy Control Scheme, 93–95.

Google Scholar

Wang, W., Chen, P., Zeng, D., and Liu, J. (2020). Electric Vehicle Fleet Integration in a Virtual Power Plant with Large-Scale Wind Power. IEEE Trans. Ind. Applicat. 56, 5924–5931. doi:10.1109/tia.2020.2993529

CrossRef Full Text | Google Scholar

Wang, W., Liu, J., Zeng, D., Fang, F., and Niu, Y. (2020). Modeling and Flexible Load Control of Combined Heat and Power Units. Appl. Therm. Eng. 166, 114624. doi:10.1016/j.applthermaleng.2019.114624

CrossRef Full Text | Google Scholar

Wu, X., Shen, J., Li, Y., and Lee, K. Y. (2013). Data-Driven Modeling and Predictive Control for Boiler-Turbine Unit. IEEE Trans. Energ. Convers. 28, 470–481. doi:10.1109/tec.2013.2260341

CrossRef Full Text | Google Scholar

Wu, X., Shen, J., Li, Y., and Lee, K. Y. (2014). Data-driven Modeling and Predictive Control for Boiler-Turbine Unit Using Fuzzy Clustering and Subspace Methods. ISA Trans. 53, 699–708. doi:10.1016/j.isatra.2013.12.033

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, X., Shen, J., Li, Y., and Lee, K. Y. (2014). Fuzzy Modeling and Stable Model Predictive Tracking Control of Large-Scale Power Plants. J. Process Control. 24, 1609–1626. doi:10.1016/j.jprocont.2014.08.007

CrossRef Full Text | Google Scholar

Wu, X., Shen, J., Wang, M., and Lee, K. Y. (2020). Intelligent Predictive Control of Large-Scale Solvent-Based CO2 Capture Plant Using Artificial Neural Network and Particle Swarm Optimization. ENERGY 196, 117070. doi:10.1016/j.energy.2020.117070

CrossRef Full Text | Google Scholar

Wu, Z., He, T., Li, D., Xue, Y., Sun, L., and Sun, L. (2019). Superheated Steam Temperature Control Based on Modified Active Disturbance Rejection Control. Control. Eng. Pract. 83, 83–97. doi:10.1016/j.conengprac.2018.09.027

CrossRef Full Text | Google Scholar

Xie, P., Gao, M., Zhang, H., Niu, Y., and Wang, X. (2020). Dynamic Modeling for NOx Emission Sequence Prediction of SCR System Outlet Based on Sequence to Sequence Long Short-Term Memory Network. ENERGY 190, 116482. doi:10.1016/j.energy.2019.116482

CrossRef Full Text | Google Scholar

Yang, T., Cui, C., Shen, Y., and Lv, Y. (2016). A Novel Denitration Cost Optimization System for Power Unit Boilers. Appl. Therm. Eng. 96, 400–410. doi:10.1016/j.applthermaleng.2015.11.111

CrossRef Full Text | Google Scholar

Zarzycki, K., and Ławryńczuk, M. (2021). LSTM and GRU Neural Networks as Models of Dynamical Processes Used in Predictive Control: A Comparison of Models Developed for Two Chemical Reactors. Sensors 21, 5625. doi:10.3390/s21165625

PubMed Abstract | CrossRef Full Text | Google Scholar

Zeng, D., Gao, Y., Hu, Y., and Liu, J. (2019). Optimization Control for the Coordinated System of an Ultra-supercritical Unit Based on Stair-like Predictive Control Algorithm. Control. Eng. Pract. 82, 185–200. doi:10.1016/j.conengprac.2018.10.001

CrossRef Full Text | Google Scholar

Zhao, Y., Wang, C., Liu, M., Chong, D., and Yan, J. (2018). Improving Operational Flexibility by Regulating Extraction Steam of High-Pressure Heaters on a 660 MW Supercritical Coal-Fired Power Plant: A Dynamic Simulation. Appl. Energ. 212, 1295–1309. doi:10.1016/j.apenergy.2018.01.017

CrossRef Full Text | Google Scholar

Zheng, H., Song, M., and Shen, Z. (2021). The Evolution of Renewable Energy and its Impact on Carbon Reduction in China. ENERGY 237, 121639. doi:10.1016/j.energy.2021.121639

CrossRef Full Text | Google Scholar

Zhu, H., Che, D., Liu, M., He, W., Yi, G., and Yan, J. (2019). Performance Evaluation of a Novel Double-Reheat Boiler with Triple-Rear Passes. Appl. Therm. Eng. 159, 113801. doi:10.1016/j.applthermaleng.2019.113801

CrossRef Full Text | Google Scholar