- Key Laboratory of Thermo-Fluid Science and Engineering of MOE, School of Energy and Power Engineering, Xi’an Jiaotong University, Xi’an, China
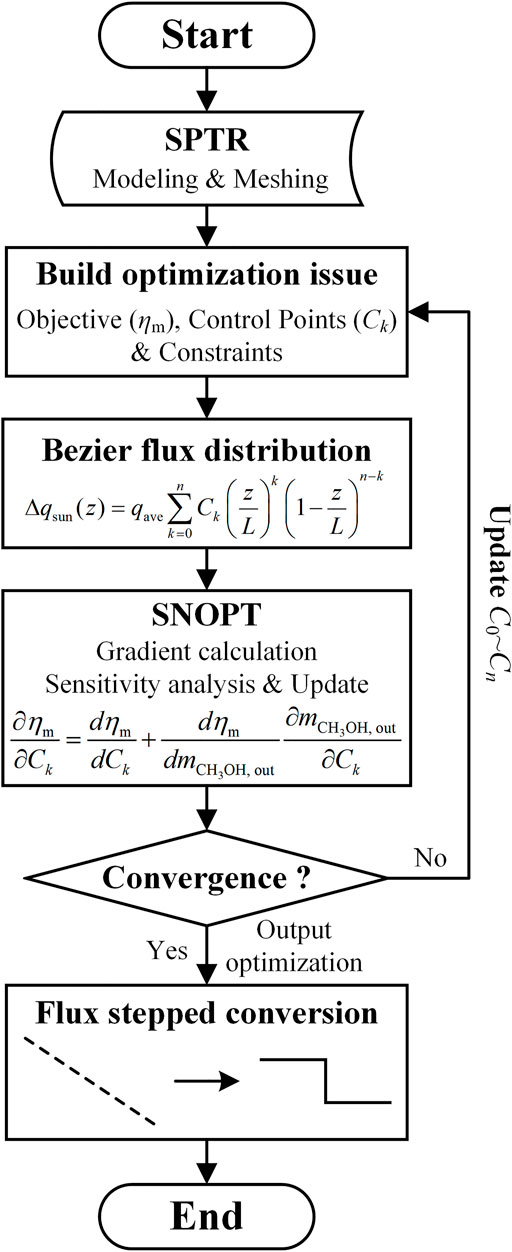
In this work, an inverse design method that couples the multi-physics model for a solar trough thermochemical reactor (SPTR) and shape optimization model is proposed to find out optimal solar flux distribution for maximizing overall reactor performance. The gradient-based segmentation method is applied to convert the continuous solar flux into step-like flux to guide the concentrator system design. Performance comparisons among uniform flux, linear decreasing flux, and the optimized non-linear flux are also conducted to discuss the reliability of SPTR performance improvement. The results show that the optimized non-linear solar flux can improve the methanol conversion, solar thermochemical conversion, and hydrogen yield of SPTR by 2.5, 3.3, and 2.4%, respectively, compared with the uniform flux. This is attributed to the fact that the optimized non-uniform flux distribution enhances the synergy between temperature and reaction fields, and achieves a better match between spatial solar flux supply and local energy demand by reactions. Also, it is shown that the optimized step-like flux, achieved by regressing the optimized non-linear flux, can perfectly maintain SPTR performance and is effective in boosting SPTR performance under different operating conditions.
1 Introduction
The increase in the proportion of solar energy utilization in the energy system will significantly reduce the consumption of fossil fuels, thus protecting the environment and promoting the energy economy (Brockway et al., 2019; Luz and Moura, 2019; He et al., 2020; Mahmoudan et al., 2022). Currently, solar energy utilization technologies include solar thermal power generation (Gilani et al., 2022), photovoltaic (Shakouri et al., 2022), and desalination (Sohani et al., 2022). Among them, solar thermochemical technology to convert solar energy into fuel has the advantages of high energy density, long storage time, and easy transportation (Tang et al., 2022). As an equally clean and high calorific fuel, hydrogen is one of the most desirable energy carriers for future energy systems (Abdalla et al., 2018; Razi and Dincer, 2020). The conversion of solar energy to hydrogen fuel for storing solar energy and hydrogen production can combine the advantages of solar and hydrogen energy, which has already become a focus for scientific research and engineering development (Hosseini and Wahid, 2020).
Currently, hydrogen production by thermochemical conversion driven by solar energy attracts more and more attention (Yadav and Banerjee, 2016; Liu et al., 2019; Zhang et al., 2022). Solar energy can be converted into thermal energy to provide the chemical reaction energy for catalytic hydrogen production such as reforming and pyrolysis of methane and methanol (Ma et al., 2018; Boretti, 2021a, 2021b). Usually, the pyrolysis process and methane reforming require a high temperature of over 800 K, leading to extra structural and cost burden (Wang F. et al., 2014). In contrast, methanol–steam reforming reaction (MSRR) with medium- to low-temperature operation (i.e., 423–573 K) is safer, more stable, and more economical (Kang et al., 2021). Moreover, methanol is a liquid hydrogen carrier that is easy to store and transport, has a high H/C ratio of 4:1, and can produce high-purity hydrogen when needed (Garcia et al., 2021). MSRR shows its significant virtues of high hydrogen selectivity, low carbon monoxide selectivity, and high conversion efficiency (Liu et al., 2016; Garcia et al., 2021), making it a convenient and effective method for hydrogen production in small-scale systems.
Generally, the MSRR system can be applied to parabolic trough collectors (PTC), which are also called solar parabolic trough reactors (SPTR) (Cheng et al., 2019c; Ma et al., 2020; Gharat et al., 2021). Although promising, there are still problems and challenges within the SPTR caused by the non-stationary solar input and non-uniform solar flux distribution, which degrades the reactor performance (He et al., 2019; Ma et al., 2021). There are already some studies on mitigating the effects of non-stationary energy input through active and passive control methods (Saade et al., 2014; Ma et al., 2018; Cheng et al., 2020; Tang et al., 2022). Meanwhile, there are also some studies on enhancing the performance in terms of optic, flow, and heat transfer for boosting SPTR performance (Bellos and Tzivanidis, 2019; Manikandan et al., 2019). For example, Cheng et al. (2019b, 2019a) proposed two kinds of SPTR internal structures to adjust the flow behavior of the reactant mixture inside the SPTR to improve the reactor performance. One is to install a Kenics static mixer inside the reactor tube, which enhances the fluid mixing, reduces the maximum temperature of the reaction bed, and thus increases the methanol conversion (Cheng et al., 2019b). The other one is a catalytic bed with decreasing porosity distribution from top to bottom (Cheng et al., 2019a), which also enhances the reactor’s performance. Similarly, Liu et al. (2018) optimized the porosity distribution of the catalytic bed based on the variational method to increase the methanol conversion in a reactor for methanol decomposition.
As for the optical aspect, Gong et al. (2020) proposed a secondary compound parabolic concentrator with enhanced surface flux uniformity, leading to a thermal efficiency improvement of 4.9%. Furthermore, Tang et al. (2021) proposed a broken-line–type secondary concentrator design method based on the flux compensation concept. The newly designed secondary concentrators can achieve over 90% circumferential solar flux uniformity for two kinds of conventional PTCs. Similarly, the secondary uniform reflector proposed by Wang et al. (2014) reduces the circumferential temperature difference. Instead of varying the circumferential solar flux, Wang et al. (2017) also proposed a concentrator structure with a linear variation of the aperture along the axial direction to vary the axial solar flux distribution to improve the reactor’s performance. Kulahli et al. (2019) proposed a new parabolic reflector with varying focal lengths along the length direction of the absorber, which improved the thermal efficiency and net efficiency by 0.21 and 0.63%, respectively.
The aforementioned literature shows that the SPTR performance can be improved to different degrees with different approaches. However, less research has been done to improve the SPTR performance by designing the solar flux spatial distribution of the reactor compared to flow-heat transfer and concentration uniformity improvement (Bellos and Tzivanidis, 2019; He et al., 2020, 2019). There is still a lack of understanding of how surface solar flux distribution affects the performance of SPTR and how to achieve an optimal and reasonable concentrator design. Motivated by these, in this work, we coupled the multi-physics SPTR model with a shape optimization model for solar flux optimization. With the model, the optimal solar flux distribution along the tube with fixed total energy input can be achieved. The gradient-based segmentation method is adopted to convert continuous non-linear solar flux into step-like solar flux distribution, which can be used to guide the design of the concentrator. Finally, the performance enhancement of SPTR by optimized step-like flux is verified under different operating conditions. A summary figure of the entire study to aid understanding can be found in Supplementary Figure S1.
2 Mathematical Model and Optimization Method
2.1 Model Description
As shown in Figure 1, the solar parabolic trough methanol steam reforming reactor (SPTR) in this study mainly comprises three parts: the concentrator system for sunlight collector, the vacuum absorber for solar-to-thermal energy conversion, and the reaction tube for thermal-to-chemical energy conversion, respectively. Our previous work (Tang et al., 2021) showed that a well-designed secondary reflector for PTC can nearly achieve a circumferentially uniform distribution of solar flux on the absorber’s surface. As a result, it is reliable and easy to build a 2-D axisymmetric SPTR model, as shown in Figure 1B by considering uniform circumferential solar flux distribution. In the SPTR, methanol and steam enter through the inlet, absorb solar heat and react on the reaction particle bed consisting of Cu/ZnO/Al2O3 catalyst (Peppley et al., 1999), and finally produce fuel products with solar energy stored. The relevant structural and physical parameters of SPTR are listed in Table 1, and a detailed description of the concentrator structure can be found elsewhere (Tang et al., 2021). It should be mentioned that the axial solar flux is not necessarily uniform to boost the reactor performance, which will be optimized in this study.
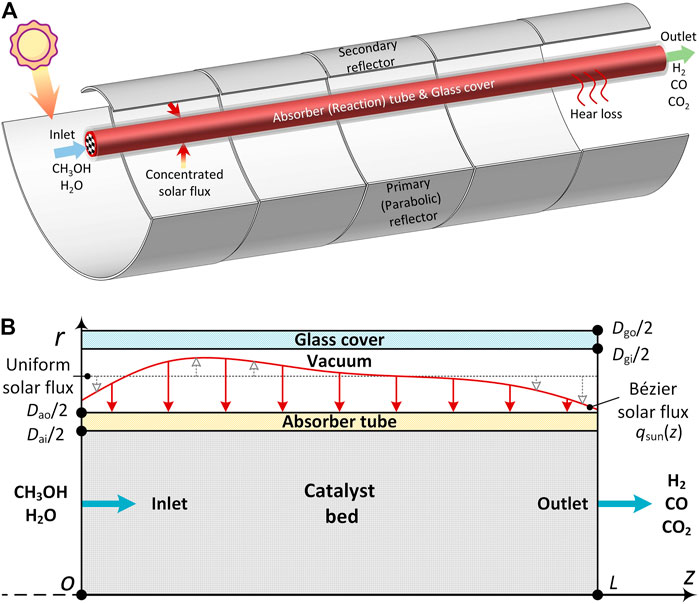
FIGURE 1. Schematic diagram of (A) 3-D and (B) 2-D axisymmetric of the solar methanol steam reforming reactor.

TABLE 1. Relevant structural and physical parameters of SPTR (Ma et al., 2018).
To build the multi-physics model for SPTR, it is useful and necessary to introduce reasonable assumptions in order to save computational resources while ensuring sufficient realism. The present 2-D multi-physics SPTR model is developed based on the following assumptions: 1) the catalytic reaction bed is an isotropic homogeneous porous medium, 2) the gas mixture flows in a steady laminar flow, 3) the heat loss is only for radiation and convection with the atmosphere, and 4) the local thermal equilibrium assumption in the porous reaction bed is valid (Liu et al., 2016). In the following, we briefly present the governing equations for simulating the mass/species transfer, fluid flow, heat transfer, and chemical reactions of the gas mixture.
2.1.1 Mass Conservation
The mass conservation equation for a gas mixture in the porous reaction bed is:
where
where p and
2.1.2 Momentum Conservation
The momentum conservation equation for fluid flow in the porous reaction bed can be expressed as:
where
where xi, μi, and Mi refer to the molar fraction, viscosity, and molecular weight of species i, respectively. The species i denotes one of the reaction gases, such as CH3OH, H2O, H2, CO, and CO2.
The resistance term
where dp is the average porous media pore size, which is related to the porosity εp:
2.1.3 Energy Conservation
Considering the assumption of local thermal equilibrium, there is no temperature difference between porous media and gas mixture at the same position. The energy conservation equation for the reaction bed region can be given by:
where Cp,m is the specific heat capacity of the gas mixture, λeff,p is the effective thermal conductivity of the porous reaction bed, and Schem denotes the chemical reaction source term.
The effective parameters of the porous media domain can be expressed by the volume averaging method as (Elbahjaoui and El Qarnia, 2019):
where the effective parameters of the gas mixture are expressed by Poling et al. (2001) as:
where the correlation properties of pure species i are defined as temperature-related Eqs 13–15, and the correlation coefficients are listed in Supplementary Tables S1–2 (Gordon and McBride, 1972).
2.1.4 Species Conservation
The concentration of each species in the reaction system is represented by the mass transfer equation:
where ci is the concentration of species i, Di is the mass diffusion coefficient of species i, and Ri denotes the chemical reaction source term of species i.
2.1.5 Reaction Kinetics
The MSRR reaction system with three reactions is present in SPTR, and the reaction kinetics (Peppley et al., 1999) are shown below:
1) Methanol steam reforming (MSR)
2) Methanol decomposition (MD)
3) Water–gas shift (WGS)
where the relevant kinetic parameters are listed in Supplementary Table S3, and the detailed definitions are described in Peppley et al. (1999).
Combined with the reaction kinetics, the reaction source term in the energy equation and the species equations can be expressed as:
where ni,r is the stoichiometric number and Rr is the reaction rate expressions shown in Eqs 18, 20, 22.
2.1.6 Boundary Conditions
In the computational domain of Figure 1B, the corresponding boundary conditions are listed in Table 2.
The surface-to-surface radiation exists between the absorber tube and the glass cover, and the diffuse surface flux is expressed as:
where G is the irradiation and εe is the emissivity of the diffuse surface. The surface emissivity is set to 0.9 for the glass cover and to
The radiation from the glass cover to the ambient is calculated by Stefan–Boltzmann’s law. Besides, there are natural convection losses with the ambient, and the heat transfer coefficient is calculated by the horizontal cylinder formula in Bergman et al. (2011), expressed as:
where Tamb is the ambient temperature and the air parameters in Eq. 26 come from the COMSOL material library.
2.2 Solar Flux Optimization Method
The solar flux distribution is optimized to get high-quality energy conversion and improve the overall SPTR performance by achieving a better match between the energy field and the reaction field. The primary performance evaluation parameters of SPTR are the methanol conversion efficiency ηm and the solar thermochemical conversion efficiency ηs, given below:
where
where Qchem and Qsun denote the thermochemical reaction energy and the total solar input energy, respectively.
Typically, one of the most important SPTR performances is the methanol conversion efficiency ηm, and other evaluation parameters are directly or indirectly related to the conversion rate, such as the hydrogen yield
For solar flux distribution, it is described by the Bezier curve. This curve is a way that can describe various types of shapes with mathematical expressions, and it has been widely used in scenarios such as airfoil optimization (Wei et al., 2020) and robot motion control (Song et al., 2021). Furthermore, the curve has the property of high-order derivability, which is well suited for the gradient-based optimization algorithm in this study. The corresponding nth-order Bernstein basis function representing the deviation Δqsun(z) of solar flux relative to the uniform flux qave is expressed as:
where Ck is the control point of the curve and is also the control variable.
Since the sintering temperature of the Cu/ZnO/Al2O3 catalyst is at 573.15 K (Yong et al., 2013), a maximum temperature constraint is required. Furthermore, a point-by-point constraint of constant surface solar flux greater than 0 is set to prevent unreasonable negative flux values. Also, in order to accelerate the optimization, an advance constraint of greater than 0 at the control points at both ends, that is, C0, Cn ≥ −1 is imposed. To sum up, for a certain total solar input, the optimization problem can be concluded as:
The optimization process of the solar flux distribution is solved by the Sparse Nonlinear Optimizer (SNOPT) based on Sequential Quadratic Programming, an algorithm suitable for solving large-scale constrained optimization problems with smooth non-linear functions in the objective and constraints (Gill et al., 2005). The overall process of SNOPT-based optimization of SPTR solar flux distribution is shown in Figure 2B.
COMSOL is a powerful numerical analysis software for multi-physics fields based on the finite element method, covering various fields such as mechanics, fluids, electromagnetism, heat transfer, chemicals, electrochemistry, and acoustics. It is especially suitable for developing models involving multiple physical fields (Fu et al., 2022; Tang et al., 2022). Calculations were performed on a computer with an 8-core 3.6 GHz CPU and 32 GB RAM, and the entire SPTR multi-physics model was solved iteratively by the full-coupling method in COMSOL (about 10 min), and the solar flux distribution is optimally solved by SNOPT (about 133 min). The convergence criterion for the above two solution processes was determined to be 10–5 by the tolerance test.
2.3 Model Validation
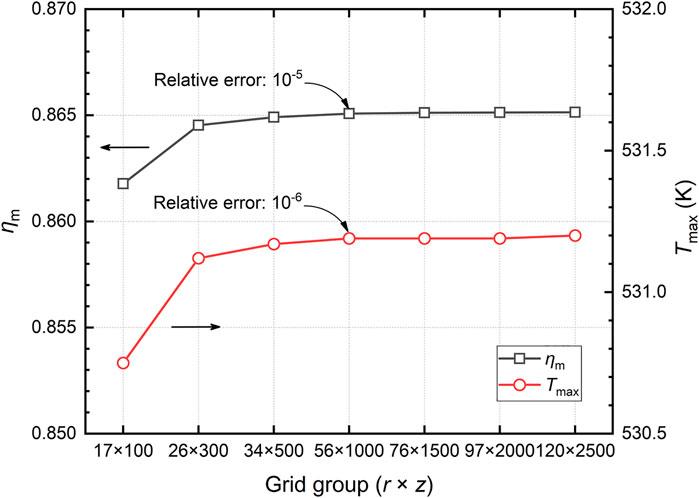
For grid types, structured grids have the advantages of fast generation, good quality, low memory consumption, and are suitable for regular and simple computational domains (e.g., Figure 1B). Thus, custom meshing in COMSOL is used to generate structured grids of different sizes for comparison, and the comparison results are shown in Figure 3. The grid group of 56 × 1,000 has only a relative error of 10–5 compared to the group of 76 × 1,500, which can be considered since the grid system of 56 × 1,000 is accurate enough for this study.
To verify the accuracy of the current multi-physics field model, the flow-heat exchange-radiation component is validated with the experimental results of Dudley et al. (1994). As shown in Table 3, the results obtained using the present model under different conditions show great agreement with the experimental results.

TABLE 3. Comparative verification of the flow-heat exchange-radiation component with experimental results (Dudley et al., 1994).
For chemical validation, the present model was compared with the experimental study by Peppley et al. (1999) and the simulation study by Cheng et al. (2019c). As shown in Figure 4, the methanol conversion of the present model matches each other with the results in Cheng et al. (2019c) and Peppley et al. (1999), which especially agrees well with the results of Cheng et al. (2019c). The aforementioned validation shows the reliability of the model.
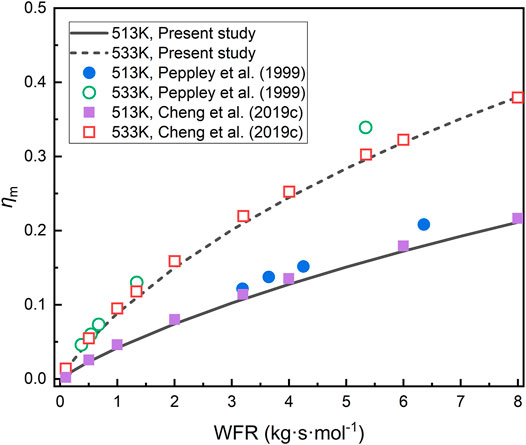
FIGURE 4. Comparative verification of the chemical part with the experimental results (Peppley et al., 1999) and simulation results (Cheng et al., 2019c).
3 Results and Discussion
3.1 Optimization Results of Solar Flux Distribution
To obtain the optimal concentrator combination for improving the SPTR performance, this section first optimized the axial distribution of solar flux on the SPTR at an inlet reaction gas mass flow rate of 0.012 kg s−1, an inlet steam methanol ratio of 1.1, and an average surface solar flux input of 13,000 W m−2. In the optimization process, two types of solar flux distributions are considered, which are linear and non-linear. The linear distribution corresponds to the 1st-order Bezier function, that is, n equals 1 in Eq. 30, while the non-linear distribution is set to the 5th-order Bezier function, corresponding to n equals 5.
Figure 5 shows the hydrogen generation rate field in SPTR for uniform solar flux distribution and two optimized distributions, where the relevant control parameters of Bernstein basis functions corresponding to the optimized distributions are listed in Table 4. For the distribution characteristics, the final optimization result of the linear flux distribution is decreasing from inlet to outlet, and this result validates each other with the conclusion of Wang et al. (2017), showing the feasibility of the optimization model. However, the optimal non-linear distribution shows an arch-shaped distribution with the solar flux converging in the middle and less on the sides, as in Figure 5C. For the hydrogen generation rate, both optimized solar flux distributions produce a higher hydrogen reaction zone (rH2>60 mol m−3 m−1) compared to the relatively low uniform generation rate (rH2<60 mol m−3 m−1) under the uniform distribution, while it shifts with the location of the energy concentration. Intuitively, the non-linear optimization has a higher and larger high reaction zone, indicating stronger reaction dynamics.
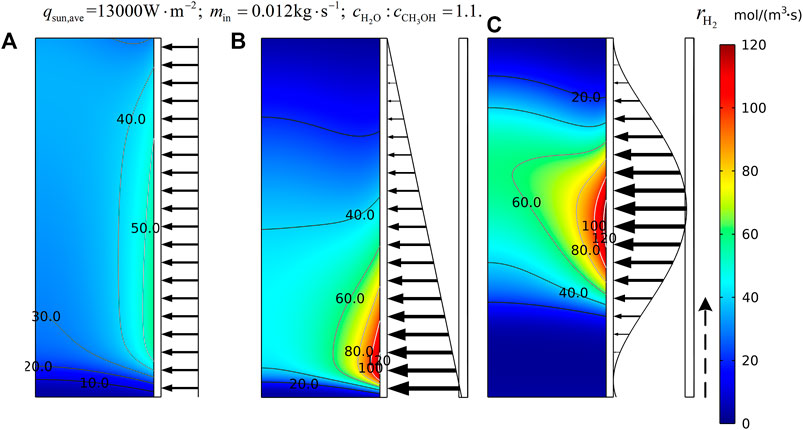
FIGURE 5. Comparison of hydrogen generation rate field within the SPTR before and after solar flux distribution optimization. (A) Uniform flux, (B) non-uniform linear flux, and (C) non-uniform non-linear flux.
To clearly observe the changes in comprehensive performance before and after flux optimization, Figure 6 synthesizes the comparative results of SPTR performance under different solar flux distributions. Apparently, both non-uniform optimized solar flux distributions exhibit better SPTR performance than uniform distributions, as reflected by higher methanol conversion, solar thermochemical efficiency, and hydrogen yield. Particularly, the enhancement reaches the maximum under the non-linear flux distribution as shown in Figure 5C, where the methanol conversion, solar thermochemical efficiency, and hydrogen yield are enhanced by 2.5, 3.3, and 2.4%, respectively, relative to the uniform flux. Although there is a relative increase of 19.0% in CO yield, the slow methanol decomposition reaction rate and the CO consumption of the water–gas shift reaction result in a CO yield of only about 1/10 of the H2 yield. Thus, the discussion later focuses on the primary target product H2 rather than the by-product CO. Moreover, the maximum catalytic bed temperatures are all below the catalyst sintering temperature of 573 K, which implies a long catalyst life and good stability of SPTR performance (Yong et al., 2013).
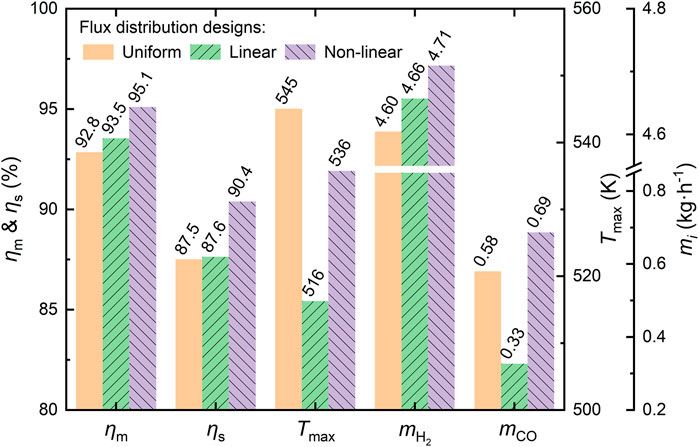
FIGURE 6. Comparison of SPTR comprehensive performance before and after solar flux distribution optimization.
To clarify the reason for the performance improvement, Figure 7 shows the average temperature, average hydrogen generation rate, and average methanol concentration distribution along the flow direction for the three solar flux distributions. To facilitate the analysis, the catalytic bed is divided into three zones (Z1–Z3) using the intersection of hydrogen generation rates as the boundary, as shown in the dashed line in Figure 7. As seen in Figure 7B, both optimized flux distributions have more concentrated fast reaction rate zones due to the concentrated solar energy distribution, which correspondingly appear in the Z1 and Z2 zone. With the linearly optimal solar flux distribution, more energy is invested in the front zone (Z1), which raises the reaction temperature more rapidly and reaches the higher fast reaction zone faster compared to the uniform distribution. However, in the Z3 zone, as seen in Figure 7A, only a small amount of reactants are present, where more energy will be used to heat the fluid (e.g., the uniform case in Figure 7A) apart from making the reaction complete. Clearly, neither the linear nor the non-linear optimized distribution allocates much energy input in Z3. Under the non-linear optimal solar flux distribution, more energy is distributed in the intermediate zone (Z2). Simultaneous temperature increases with progressively increasing solar input in Z1 at non-linear flux, at which the temperature level of Z2 (480–526 K) surpasses the 423–498 K of the optimal reaction zone Z1 at linear flux. Further, 80% of the reactant molar fraction remained when the best reaction zone Z2 reached under non-linear flux, thus being sufficient to show higher reaction performance in terms of temperature and reactant-dominated reaction kinetics.
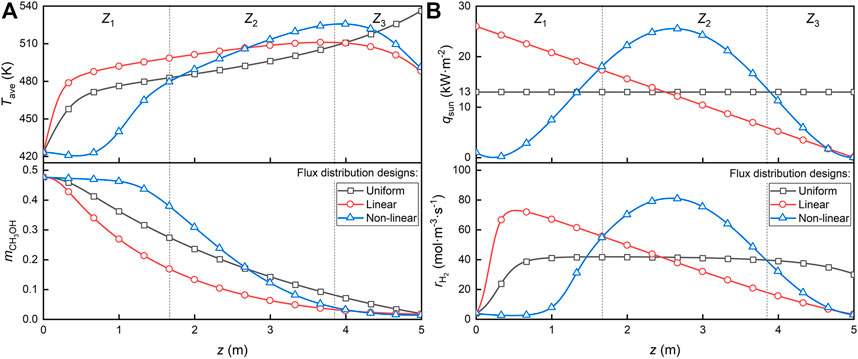
FIGURE 7. Distribution of the average values of the variables along the flow direction. (A) Temperature and methanol molar fraction and (B) solar flux and hydrogen generation rate.
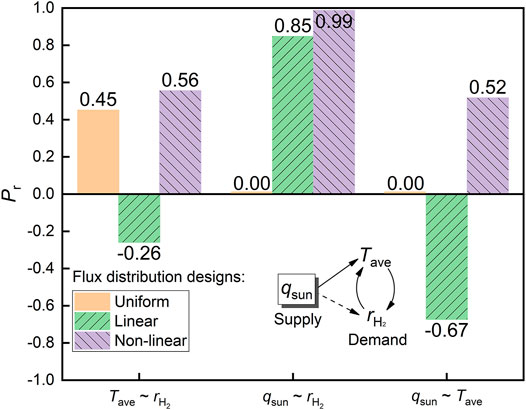
The relationship between the variable distributions in Figure 7 shows that there is a degree of similarity under the non-linear case, so Figure 8 compares the synergy between the fields by the correlation index described by the Pearson correlation coefficient Pr of Eq. 32:
where x and y denote the two discrete variables for comparison, n is the number of discrete variables, and ‾ represents the average of the corresponding variables.
Usually, the closer Pr is to 1, the higher the positive correlation is, especially when the sample of variables is constant, Pr is 0 (e.g., the solar flux in the uniform case in Figure 8 is constant). As seen in Figure 8, the correlations under the non-uniform optimal distribution are all the highest, showing the strongest synergistic effect to enhance the SPTR performance. Here, the solar flux as an external variable directly affects the temperature change, while the temperature and the reaction rate interact with each other, which ultimately manifests as the effect of the solar flux and the reaction rate, that is, the relationship between the solar energy supply and the reaction energy demand. It should be noted that due to the dominant role of MSR in the SPTR reaction system, the hydrogen reaction rate was found to almost represent the reaction heat consumption in this study.
Overall, the rational distribution of non-linear optimization achieves hysteresis matching of temperature distribution, which in turn achieves energy flow matching of energy input and consumption (i.e., reaction rate) through the synergistic relationship between reaction rate and temperature with Pr up to 0.99.
3.2 Regression of Real Concentrator
Considering the engineering reality, the current PTC cannot achieve continuous concentrated solar flux, so it is necessary to convert the continuous solar flux distribution into a step-like one in order to get a concentrator group with different apertures and finally get the design guidance of concentrator in SPTR. Since the step-like distribution can be viewed as having an infinite gradient at each junction, the gradient-based segmentation method is used in this study to segment the continuous solar flux distribution to ensure that the features of the distribution are fully preserved.
After comparative consideration, 100 and 75% of the maximum gradient are selected as the splitting points to split the non-linear flux into a step-like flux, as in Figure 9A.
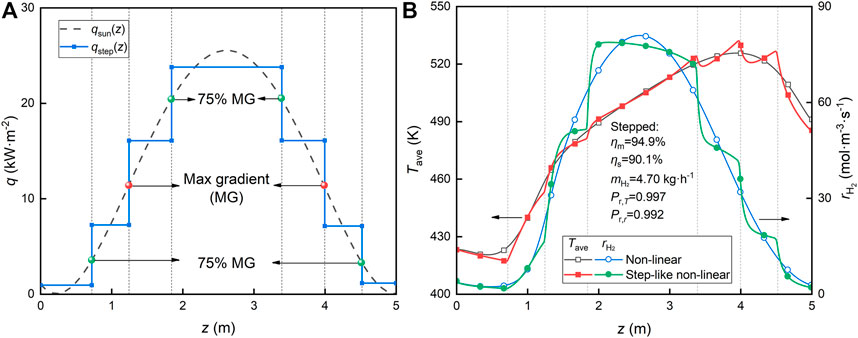
FIGURE 9. Step-like flux regression results for non-linear flux distribution. (A) Non-linear flux distribution regression and (B) field variable distribution.
Figure 9B summarizes the corresponding field variable changes and performance diagrams of SPTR under the step-like solar flux distribution. The characteristic of variable change can be observed, where after each flux change, the temperature and reaction rate first have a large rate of change and then gradually level off. In Figure 9B, there is an extremely high correlation of over 0.99 for the results of variable changes between the corresponding step-like and continuous type flux. Also, the SPTR performance is only slightly degraded by about 0.2% due to the loss of some continuous curve properties by the step-like shape, which also shows the effectiveness of the gradient-based segmentation method in this study.
3.3 Comparison of Performance Enhancement Under Different Conditions
To check the performance effect of the optimized solar flux distribution form (i.e., the step-like solar flux) under different conditions, this section explores the SPTR performance at different reactant mass flow rates and DNIs, which map the demand side and supply side in SPTR, respectively. Different DNIs correspond to different solar average fluxes, where DNI = 1 kW m−2 corresponds to a solar average flux of 13 kW m−2, implying an average concentration ratio of 13. Here, the solar average flux of 4–14 kW m−2 and the reactant mass flow rate of 0.012 kg s−1 are applied.
The performance comparison for different solar average fluxes is shown in Figure 10, where the methanol conversion ηm, hydrogen generation rate mH2, and maximum catalytic bed temperature Tmax all increase with increasing input solar energy, due to the increased total input allowing more chemical and thermal energy conversion. However, the solar thermochemical conversion efficiency ηs decreases as the input energy increases when it reaches a high conversion efficiency ηm, mainly because the chemical energy that can be converted reaches the limit. Furthermore, at different solar flux, the optimized flux all have better performance improvement compared to uniform flux, with the increase ratio (relative percentage improvement of corresponding performance indicator in present figure) increasing as the solar flux decreases. Together with the temperature variation in Figure 10B, where the reaction is weak when the energy input is small, the central concentration feature of the optimized solar flux distribution results in a higher temperature level and thus a more significant performance improvement. However, when the energy input is sufficient, the reaction proceeds completely and the energy input at the end flows to the thermal energy; thus, the optimized solar flux with less end distribution allows more energy to be used in the high reaction zone and reduces the temperature level.
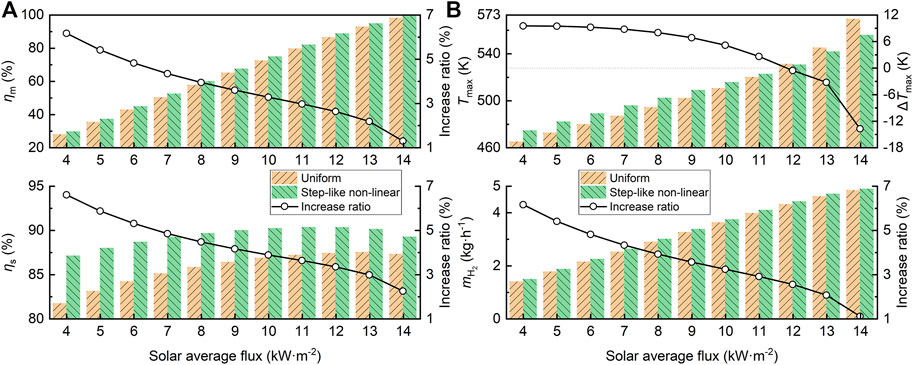
FIGURE 10. SPTR performance comparison for different solar average fluxes. (A) ηm and ηs, (B) Tmax and mH2.
For different mass flow rates, which represent the energy consumed on the demand side, 0.009–0.016 kg s−1 are chosen for the analysis, with a solar average flux of 10 kW m−2. The performance comparison summarized in Figure 11 shows that as the reactant mass flow rate increases, ηm and Tmax decrease due to the increase in the flow rate and the decrease in the reaction residence time. However, mH2 and ηs are essentially stable because the energy input determines the hydrogen production when the total amount of reactants is greater than the energy input. Similarly, the optimized solar flux is enhanced at different flow rates, and the increase ratio increases with increasing flow rate.
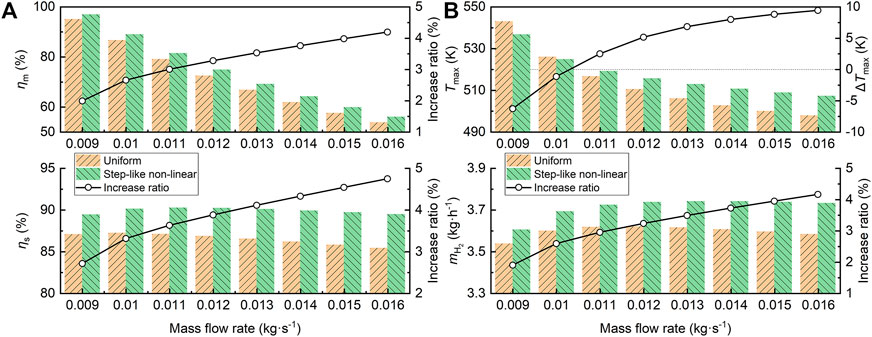
FIGURE 11. SPTR performance comparison for different reactant mass flow rates. (A) ηm and ηs, (B) Tmax and mH2.
Overall, the aforementioned results indicate that the form of optimal solar flux distribution with spatial energy supply and demand matching can improve SPTR performance regardless of the relationship between solar input and total reactants, and thus the present study is considered valid and general.
4 Conclusion
The primary purpose of this study is to propose an inverse design method for solar flux distribution to achieve optimal SPTR performance enhancement. First, a 2-D axisymmetric model of SPTR was coupled with an optimized solar flux distribution model, which applied the SNOPT algorithm to optimize the axial solar flux distribution described by Bezier curves to achieve better SPTR performance. Further, the energy matching and performance enhancement mechanism of SPTR were analyzed. Then, the continuous solar flux was regressed to a step-like flux with maintained performance to provide design guidance for the concentrator. Finally, the performance enhancement of the step-like flux distribution form with different solar energy input and different reactant flow rates was investigated. The particular conclusions were as follows:
(1) Optimized linear and non-linear solar flux distributions achieve higher and larger fast reaction zone compared to uniform flux, resulting in significantly improved SPTR performance. Especially at non-uniform flux, the methanol conversion, solar thermochemical conversion, and hydrogen yield are, respectively, enhanced by 2.5, 3.3, and 2.4% relative to the uniform flux. Furthermore, the optimized non-uniform flux enhances the synergy between the temperature field and the reaction field in SPTR, ultimately achieving a spatial correlation of 0.99 between solar energy supply and reaction demand, resulting in energy matching.
(2) To effectively guide the design of the concentrating system, the step-like solar flux distribution based on the gradient-based segmentation method is obtained. The simulation results between the step-like distribution and the continuous distribution have a high correlation of 0.99 and only about 0.2% performance loss, which maximally maintains the performance-enhancing capability of the original distribution shape. The feasibility of the segmentation method and design has also been verified.
(3) Optimized step-like solar flux distribution forms are always effective and suitable for improving SPTR performance under different solar inputs versus total reactants (e.g., different solar flux inputs and reactant mass flow rates). The performance improvement is especially significant when the total solar energy supply is insufficient.
Thus, the method of this study is instructive and informative for the optimal solar flux distribution and concentrator design that enhance the performance of concentrated solar energy utilization systems. Furthermore, in the future, we will consider experiments to further refine and validate the design method of this study.
Data Availability Statement
The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.
Author Contributions
XT: Conceptualization, methodology, validation, software, writing—original draft, formal analysis, writing—review and editing, and visualization. WY: Conceptualization, formal analysis, funding acquisition, writing—review and editing, and supervision. ZD: Investigation and writing—review and editing. YY: Visualization and writing—original draft.
Funding
This work was financially sponsored by the National Natural Science Foundation of China (No. 52090063).
Conflict of Interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s Note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2022.881822/full#supplementary-material
References
Abdalla, A. M., Hossain, S., Nisfindy, O. B., Azad, A. T., Dawood, M., and Azad, A. K. (2018). Hydrogen Production, Storage, Transportation and Key Challenges with Applications: A Review. Energy Convers. Manag. 165, 602–627. doi:10.1016/j.enconman.2018.03.088
Bellos, E., and Tzivanidis, C. (2019). Alternative Designs of Parabolic Trough Solar Collectors. Prog. Energy Combust. Sci. 71, 81–117. doi:10.1016/j.pecs.2018.11.001
Bergman, T. L., Incropera, F. P., DeWitt, D. P., and Lavine, A. S. (2011). Fundamentals of Heat and Mass Transfer. New York, United States: John Wiley & Sons.
Boretti, A. (2021b). A Perspective on the Production of Hydrogen from Solar-Driven Thermal Decomposition of Methane. Int. J. Hydrogen Energy 46, 34509–34514. doi:10.1016/j.ijhydene.2021.07.234
Boretti, A. (2021a). There Are Hydrogen Production Pathways with Better Than Green Hydrogen Economic and Environmental Costs. Int. J. Hydrogen Energy 46, 23988–23995. doi:10.1016/j.ijhydene.2021.04.182
Brockway, P. E., Owen, A., Brand-Correa, L. I., and Hardt, L. (2019). Estimation of Global Final-Stage Energy-Return-On-Investment for Fossil Fuels with Comparison to Renewable Energy Sources. Nat. Energy 4, 612–621. doi:10.1038/s41560-019-0425-z
Cheng, Z.-D., Leng, Y.-K., Men, J.-J., and He, Y.-L. (2020). Numerical Study on a Novel Parabolic Trough Solar Receiver-Reactor and a New Control Strategy for Continuous and Efficient Hydrogen Production. Appl. Energy 261, 114444. doi:10.1016/j.apenergy.2019.114444
Cheng, Z.-D., Men, J.-J., He, Y.-L., Tao, Y.-B., and Ma, Z. (2019a). Comprehensive Study on Novel Parabolic Trough Solar Receiver-Reactors of Gradually-Varied Porosity Catalyst Beds for Hydrogen Production. Renew. Energy 143, 1766–1781. doi:10.1016/j.renene.2019.05.137
Cheng, Z.-D., Men, J.-J., Liu, S.-C., and He, Y.-L. (2019b). Three-dimensional Numerical Study on a Novel Parabolic Trough Solar Receiver-Reactor of a Locally-Installed Kenics Static Mixer for Efficient Hydrogen Production. Appl. Energy 250, 131–146. doi:10.1016/j.apenergy.2019.04.179
Cheng, Z.-D., Men, J.-J., Zhao, X.-R., He, Y.-L., and Tao, Y.-B. (2019c). A Comprehensive Study on Parabolic Trough Solar Receiver-Reactors of Methanol-Steam Reforming Reaction for Hydrogen Production. Energy Convers. Manag. 186, 278–292. doi:10.1016/j.enconman.2019.02.068
Dudley, V. E., Kolb, G. J., Sloan, M., and Kearney, D. (1994). SEGS LS2 Solar Collector-Test Results. USA: Report of Sandia National Laboratories. SANDIA94-1884.
Elbahjaoui, R., and El Qarnia, H. (2019). Performance Evaluation of a Solar Thermal Energy Storage System Using Nanoparticle-Enhanced Phase Change Material. Int. J. Hydrogen Energy 44, 2013–2028. doi:10.1016/j.ijhydene.2018.11.116
Fu, W., Yan, X., Gurumukhi, Y., Garimella, V. S., King, W. P., and Miljkovic, N. (2022). High Power and Energy Density Dynamic Phase Change Materials Using Pressure-Enhanced Close Contact Melting. Nat. Energy 7, 270–280. doi:10.1038/s41560-022-00986-y
Garcia, G., Arriola, E., Chen, W.-H., and De Luna, M. D. (2021). A Comprehensive Review of Hydrogen Production from Methanol Thermochemical Conversion for Sustainability. Energy 217, 119384. doi:10.1016/j.energy.2020.119384
Gharat, P. V., Bhalekar, S. S., Dalvi, V. H., Panse, S. V., Deshmukh, S. P., and Joshi, J. B. (2021). Chronological Development of Innovations in Reflector Systems of Parabolic Trough Solar Collector (PTC) - A Review. Renew. Sustain. Energy Rev. 145, 111002. doi:10.1016/j.rser.2021.111002
Gilani, H. A., Hoseinzadeh, S., Esmaeilion, F., Memon, S., Garcia, D. A., and Assad, M. E. H. (2022). A Solar Thermal Driven ORC-VFR System Employed in Subtropical Mediterranean Climatic Building. Energy 250, 123819. doi:10.1016/j.energy.2022.123819
Gill, P. E., Murray, W., and Saunders, M. A. (2005). SNOPT: An SQP Algorithm for Large-Scale Constrained Optimization. SIAM Rev. 47, 99–131. doi:10.1137/S0036144504446096
Gong, J.-h., Wang, J., Lund, P. D., Hu, E.-y., Xu, Z.-c., Liu, G.-p., et al. (2020). Improving the Performance of a 2-stage Large Aperture Parabolic Trough Solar Concentrator Using a Secondary Reflector Designed by Adaptive Method. Renew. Energy 152, 23–33. doi:10.1016/j.renene.2020.01.019
Gordon, S., and McBride, B. J. (1972). Computer Program for Calculation of Complex Chemical Equilibrium Compositions.
He, Y.-L., Qiu, Y., Wang, K., Yuan, F., Wang, W.-Q., Li, M.-J., et al. (2020). Perspective of Concentrating Solar Power. Energy 198, 117373. doi:10.1016/j.energy.2020.117373
He, Y.-L., Wang, K., Qiu, Y., Du, B.-C., Liang, Q., and Du, S. (2019). Review of the Solar Flux Distribution in Concentrated Solar Power: Non-uniform Features, Challenges, and Solutions. Appl. Therm. Eng. 149, 448–474. doi:10.1016/j.applthermaleng.2018.12.006
Hosseini, S. E., and Wahid, M. A. (2020). Hydrogen from Solar Energy, a Clean Energy Carrier from a Sustainable Source of Energy. Int. J. Energy Res. 44, 4110–4131. doi:10.1002/er.4930
Kang, J., Song, Y., Kim, T., and Kim, S. (2022). Recent Trends in the Development of Reactor Systems for Hydrogen Production via Methanol Steam Reforming. Int. J. Hydrogen Energy 47, 3587–3610. doi:10.1016/j.ijhydene.2021.11.041
Kulahli, M. C., Akbulut Özen, S., and Etemoglu, A. B. (2019). Numerical Simulation of a Parabolic Trough Collector Containing a Novel Parabolic Reflector with Varying Focal Length. Appl. Therm. Eng. 161, 114210. doi:10.1016/j.applthermaleng.2019.114210
Liu, Q., Wang, Y., Lei, J., and Jin, H. (2016). Numerical Investigation of the Thermophysical Characteristics of the Mid-and-low Temperature Solar Receiver/reactor for Hydrogen Production. Int. J. Heat Mass Transf. 97, 379–390. doi:10.1016/j.ijheatmasstransfer.2016.02.012
Liu, T., Liu, Q., Lei, J., and Sui, J. (2019). A New Solar Hybrid Clean Fuel-Fired Distributed Energy System with Solar Thermochemical Conversion. J. Clean. Prod. 213, 1011–1023. doi:10.1016/j.jclepro.2018.12.193
Liu, Y., Chen, Q., Hu, K., and Hao, J.-H. (2018). Porosity Distribution Optimization Catalyst for Methanol Decomposition in Solar Parabolic Trough Receiver-Reactors by the Variational Method. Appl. Therm. Eng. 129, 1563–1572. doi:10.1016/j.applthermaleng.2017.10.151
Luz, T., and Moura, P. (2019). 100% Renewable Energy Planning with Complementarity and Flexibility Based on a Multi-Objective Assessment. Appl. Energy 255, 113819. doi:10.1016/j.apenergy.2019.113819
Ma, Z., Li, M.-J., He, Y.-L., and Max Zhang, K. (2020). Performance Analysis and Optimization of Solar Thermochemical Reactor by Diluting Catalyst with Encapsulated Phase Change Material. Appl. Energy 266, 114862. doi:10.1016/j.apenergy.2020.114862
Ma, Z., Li, M.-J., He, Y.-L., and Zhang, K. M. (2021). Effects of Partly-Filled Encapsulated Phase Change Material on the Performance Enhancement of Solar Thermochemical Reactor. J. Clean. Prod. 279, 123169. doi:10.1016/j.jclepro.2020.123169
Ma, Z., Yang, W.-W., Li, M.-J., and He, Y.-L. (2018). High Efficient Solar Parabolic Trough Receiver Reactors Combined with Phase Change Material for Thermochemical Reactions. Appl. Energy 230, 769–783. doi:10.1016/j.apenergy.2018.08.119
Mahmoudan, A., Esmaeilion, F., Hoseinzadeh, S., Soltani, M., Ahmadi, P., and Rosen, M. (2022). A Geothermal and Solar-Based Multigeneration System Integrated with a TEG Unit: Development, 3E Analyses, and Multi-Objective Optimization. Appl. Energy 308, 118399. doi:10.1016/j.apenergy.2021.118399
Manikandan, G. K., Iniyan, S., and Goic, R. (2019). Enhancing the Optical and Thermal Efficiency of a Parabolic Trough Collector - A Review. Appl. Energy 235, 1524–1540. doi:10.1016/j.apenergy.2018.11.048
Peppley, B. A., Amphlett, J. C., Kearns, L. M., and Mann, R. F. (1999). Methanol-steam Reforming on Cu/ZnO/Al2O3 Catalysts. Part 2. A Comprehensive Kinetic Model. Appl. Catal. A General 179, 31–49. doi:10.1016/S0926-860X(98)00299-3
Poling, B. E., Prausnitz, J. M., and O’Connell, J. P. (2001). Properties of Gases and Liquids. Fifth Edition. McGraw-Hill Education.
Razi, F., and Dincer, I. (2020). A Critical Evaluation of Potential Routes of Solar Hydrogen Production for Sustainable Development. J. Clean. Prod. 264, 121582. doi:10.1016/j.jclepro.2020.121582
Saade, E., Clough, D. E., and Weimer, A. W. (2014). Model Predictive Control of a Solar-Thermal Reactor. Sol. Energy 102, 31–44. doi:10.1016/j.solener.2013.12.029
Shakouri, M., Ghadamian, H., Hoseinzadeh, S., and Sohani, A. (2022). Multi-objective 4E Analysis for a Building Integrated Photovoltaic Thermal Double Skin Façade System. Sol. Energy 233, 408–420. doi:10.1016/j.solener.2022.01.036
Sohani, A., Delfani, F., Fassadi Chimeh, A., Hoseinzadeh, S., and Panchal, H. (2022). A Conceptual Optimum Design for a High-Efficiency Solar-Assisted Desalination System Based on Economic, Exergy, Energy, and Environmental (4E) Criteria. Sustain. Energy Technol. Assessments 52, 102053. doi:10.1016/j.seta.2022.102053
Song, B., Wang, Z., and Zou, L. (2021). An Improved PSO Algorithm for Smooth Path Planning of Mobile Robots Using Continuous High-Degree Bezier Curve. Appl. Soft Comput. 100, 106960. doi:10.1016/j.asoc.2020.106960
Tang, X.-Y., Dou, P.-Y., Dai, Z.-Q., and Yang, W.-W. (2022). Structural Design and Analysis of a Solar Thermochemical Reactor Partially Filled with Phase Change Material Based on Shape Optimization. Sol. Energy 236, 613–625. doi:10.1016/j.solener.2022.03.041
Tang, X. Y., Yang, W. W., Yang, Y., Jiao, Y. H., and Zhang, T. (2021). A Design Method for Optimizing the Secondary Reflector of a Parabolic Trough Solar Concentrator to Achieve Uniform Heat Flux Distribution. Energy 229, 120749. doi:10.1016/j.energy.2021.120749
Wang, F., Tan, J., Shuai, Y., Gong, L., and Tan, H. (2014a). Numerical Analysis of Hydrogen Production via Methane Steam Reforming in Porous Media Solar Thermochemical Reactor Using Concentrated Solar Irradiation as Heat Source. Energy Convers. Manag. 87, 956–964. doi:10.1016/j.enconman.2014.08.003
Wang, K., He, Y., and Cheng, Z. (2014b). A Design Method and Numerical Study for a New Type Parabolic Trough Solar Collector with Uniform Solar Flux Distribution. Sci. China Technol. Sci. 57, 531–540. doi:10.1007/s11431-013-5452-6
Wang, Y., Liu, Q., Sun, J., Lei, J., Ju, Y., and Jin, H. (2017). A New Solar Receiver/reactor Structure for Hydrogen Production. Energy Convers. Manag. 133, 118–126. doi:10.1016/j.enconman.2016.11.058
Wei, X., Wang, X., and Chen, S. (2020). Research on Parameterization and Optimization Procedure of low-Reynolds-number Airfoils Based on Genetic Algorithm and Bezier Curve. Adv. Eng. Softw. 149, 102864. doi:10.1016/j.advengsoft.2020.102864
Wilke, C. R. (1950). A Viscosity Equation for Gas Mixtures. J. Chem. Phys. 18, 517–519. doi:10.1063/1.1747673
Yadav, D., and Banerjee, R. (2016). A Review of Solar Thermochemical Processes. Renew. Sustain. Energy Rev. 54, 497–532. doi:10.1016/j.rser.2015.10.026
Yong, S. T., Ooi, C. W., Chai, S. P., and Wu, X. S. (2013). Review of Methanol Reforming-Cu-Based Catalysts, Surface Reaction Mechanisms, and Reaction Schemes. Int. J. Hydrogen Energy 38, 9541–9552. doi:10.1016/j.ijhydene.2013.03.023
Zhang, H., Shuai, Y., Lougou, B. G., Jiang, B., Yang, D., Pan, Q., et al. (2022). Effects of Foam Structure on Thermochemical Characteristics of Porous-Filled Solar Reactor. Energy 239, 122219. doi:10.1016/j.energy.2021.122219
Nomenclature
Abbreviations
DNI direct normal irradiance
MSRR methanol steam reforming reaction
SNOPT Sparse Nonlinear Optimizer
SPTR solar trough thermochemical reactor
WFR ratio of catalyst weight to methanol inlet molar flow rate
Nomenclature
c concentration (mol·m−3)
Cp specific heat (J kg−1 K−1)
dp mean catalyst particle size (m)
Dai inner diameter of absorber tube (m)
Dao outer diameter of absorber tube (m)
Dgi inner diameter of glass cover (m)
Dgo outer diameter of glass cover (m)
Di mass diffusion coefficient of species i (m2 s−1)
h heat transfer coefficient (W m−2 K−1)
hi molar enthalpy of species i (J mol−1)
ΔHr enthalpy change of the rth reaction (J mol−1)
L length of reactor (m)
mi mass flow rate of species i (kg h−1)
M molar weight (kg mol−1)
ni,r stoichiometric number of species i in the rth reaction
p pressure (Pa)
pi partial pressure of species i (bar)
q energy flux (W m−2)
Q power (W)
R chemical reaction rate (mol m−3 s−1)
Rg universal gas constant (J mol−1 K−1)
Rr chemical reaction rate of the rth reaction (mol m−3 s−1)
Schem chemical reaction source (W m−3)
T temperature (K)
r, z axisymmetric coordinates (m)
Greek symbols
εe emissivity of the diffuse surface
εp porosity of catalytic bed
ηm methanol conversion efficiency
ηs solar thermochemical conversion efficiency
λ thermal conductivity (W m−1 K−1)
μ dynamic viscosity (Pa s)
ρ density (kg m−3)
σ Stefan–Boltzmann constant (W m−2 K−4)
Subscripts
amb ambient
ave average value
eff effective value
i species (CH3OH, H2O, H2, CO, CO2)
in inlet
m mixed reaction gas
max maximum value
out outlet
p particle catalytic bed
Keywords: methanol steam reforming reaction, solar flux distribution, solar thermochemical reactor, shape optimization, multi-physics model
Citation: Tang X, Yang W, Dai Z and Yang Y (2022) Inverse Design of Local Solar Flux Distribution for a Solar Methanol Reforming Reactor Based on Shape Optimization. Front. Energy Res. 10:881822. doi: 10.3389/fenrg.2022.881822
Received: 23 February 2022; Accepted: 16 May 2022;
Published: 27 June 2022.
Edited by:
Cheng Xu, North China Electric Power University, ChinaReviewed by:
Siamak Hoseinzadeh, Sapienza University of Rome, ItalySrirat Chuayboon, King Mongkut’s Institute of Technology Ladkrabang, Thailand
Copyright © 2022 Tang, Yang, Dai and Yang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Weiwei Yang, eWFuZ3d3QG1haWwueGp0dS5lZHUuY24=
 Xinyuan Tang
Xinyuan Tang Weiwei Yang
Weiwei Yang Zhouqiao Dai
Zhouqiao Dai