A novel forward operator-based Bayesian recurrent neural network-based short-term net load demand forecasting considering demand-side renewable energy

Currently, traditional electricity consumers are now shifting to a new role of prosumers since more integration of renewable energy to demand side. Accurate short-term load demand forecasting is significant to safe, stable, and reliable operation of a renewable energy-dominated power system. In this paper, a short-term load forecasting model based on a bidirectional long short-term memory network (Bi-LSTM) using kernel transfer operator is proposed to achieve short-term load demand forecasting. To consider the influence of seasonality, holiday effects and weather on load demand forecasting, and simultaneously to improve the accuracy and performance of the forecasting model, this paper implements the dimensionality reduction of the input data by introducing an improved kernel transfer operator based on the Perron-Frobenius method. On this basis, a Bayesian Bi-LSTM for short-term load demand forecasting is formulated to obtain the probability prediction interval of load demand. To verify the validity of the proposed method, the actual historical load demand in a certain region in China was used for model training and verification. The forecasting results are compared with several conventional load demand methods using probability prediction technics. Simulation analysis shows that the proposed method can effectively reflect the short-term uncertainty of load demand, and is superior to the conventional methods in terms of forecasting accuracy and computational performance.

1 Introduction

To date, a large amount of renewable energy has been integrated to the demand side of power system. Due to the essential stochastic nature of load demand plus the drastic uncertainties of renewable energy connecting to the demand side, it has become a difficult task to obtain accurate net load demand forecasting results (Kaur et al., 2016). In order to cope with the severe challenges brought by the increasing uncertainty of the demand side and ensure the safe, reliable and stable operation of power systems, it is still urgent to further improve the short-term forecasting accuracy of net load demand under the premise of comprehensively considering the influencing factors (Lu et al., 2019).

Currently, the mainstream methods of short-term net load demand forecasting can be divided into mathematical-statistical methods and machine learning-based forecasting methods (Zhu et al., 2021).

Mathematical-statistical methods are generally simple and efficient in calculation, but it is difficult to meet the application requirements of short-term load demand forecasting when considering strong uncertainty and nonlinearity. Those forecasting methods based on machine learning can deal with nonlinear relationships and feature extraction of different factors on load demand, effectively improving the accuracy of forecasting results and overcoming the weakness of conventional mathematical-statistical methods (Hahn et al., 2009).

In reference, short-term net load demand forecasting methods using machine learning can be divided into deterministic forecasting and probabilistic forecasting. Deterministic forecasting usually adopts methods such as Recurrent Neural Network (RNN) (Kong et al., 2019), Support Vector Machine (SVM) (Pai and Hong, 2005), and Extreme Gradient Booster (XGBoost) (Zheng et al., 2017). Zhao et al. (2022) introduced temporal convolutional network (TCN) into short-term load forecasting. The TSCN-based forecasting model can extract features from very large samples of time series and provide an effective solution to degradation issues of deep neural networks. Sudheer and Suseelatha (2015) proposed a hybrid method based on wavelet transform, Triple Exponential Smoothing (TES) model and weighted nearest neighbor (WNN) model for STLF. This method uses Haar wavelet to convert the load demand series into deterministic and fluctuation series filters, which are fitted by the TES model and WNN model, respectively. Mei et al. (2019) implemented the phase space reconstruction of the net load time series data via C-C method and then established a deep neural network-based ultrashort-term forecasting model using the reconstructed data. Tan et al. (2020) constructed combined forecasting model of electricity, heat, cooling and gas loads based on the multi-task learning and least square SVM. However, forecasting results of deterministic forecasting are definite values, and it is difficult to fully characterize the uncertainties of load demand (Liu et al., 2020).

Probabilistic forecasting commonly uses methods such as quantile regression and Bayesian method, which generally reflect the uncertainty characteristics of load demand better than deterministic forecasting. Li D. et al. (2021) combined the long short-term memory neural network (LSTM) with quantile regression and added multiple quantile results of the generated forecasting results into the forecasting model to achieve probabilistic forecasting of load demand. Xu et al. (2020) introduced a quantile regression lightweight gradient boosting machine based on convolutional neural network (CNN) to obtain the probability distribution of load demand. Feng et al. (2019) proposed a two-layer short-term load forecasting model based on Q-learning, which outputs both deterministic forecasting and probabilistic forecasting results. Wang et al. (2019) used the constrained quantile regression averaging (CQRA) method to establish the probabilistic load demand forecasting model where the parameter estimation problem of the CQRA method is formulated as a linear program with the objective of minimizing the pinball loss. To consider the uncertainties in weather forecasts and abnormal peak load, Xu et al. (2019) created a probabilistic load demand forecasting model for building, including a probabilistic normal load forecasting model based on the artificial neural network (ANN) and the probabilistic temperature forecasts, and a probabilistic abnormal peak load forecasting model to quantify the probabilistic occurrence and magnitude of the peak abnormal differential load. In order to prevent local optimization in the training process, Liu et al. (2021) proposes a hybrid CNN model by integrating genetic algorithm (GA) and a particle swarm optimization (PSO) to collaboratively optimize the network hyperparameters and weights. A data-driven load probability density forecasting method is developed based on Orthogonal Maximum Correlation Coefficient feature selection and Convolutional Gated Recurrent Unit (CGRU) quantile regression to deal with the uncertainties of wind power and load demand (Liu et al., 2022). Brusaferri et al. (2022) proposed a probabilistic load forecasting framework using Bayesian Mixture Density Networks to enhance the mapping capabilities of neural networks and developed an end-to-end training method to discover the latent functional relation to conditioning variables and characterize the inherent load stochasticity and parameters uncertainty.

The major contribution of this paper is that a novel load demand forecasting structure is proposed by combining the modified forward operator and the Bayesian bidirectional long short-term memory network (Bi-LSTM), where Bayesian Bi-LSTM is a widely used method of RNN that can effectively handle time series forecasting, and the modified forward operator is introduced to improve the accuracy and performance of short-term net load demand forecasting.

The structure of this paper is organized as follows: Section 2 provides the definition of net load demand. Section 3 presents the proposed load demand forecasting method. Section 4 conducts a study case to verify the effectiveness of the proposed method. Finally, Section 5 concludes the paper.

2 Definition of net load demand

Since nowadays more renewable generation has been integrated with the demand side, the characteristics of load profile are fully changed. In order to obtain accurate load demand forecasting considering such circumstances, we need to take uncertainties of renewable energy into consideration.

First, we need to define the concept of the net load demand. The net load demand is generally a term that can reflect the influences of both load demand and renewable energy, which can be formulated as the sum of load demand minus renewable energy power output, that is

$P_{NL,t}=P_{LD,t}-P_{RE,t}(1)$

where P_NL,t, P_LD,t, and P_RE,t denote the net load demand, total load demand and renewable energy power output at time t, respectively.

3 Proposed net load demand forecasting method

3.1 Kernel transfer operator

For short-term load demand forecasting, it is generally difficult to obtain an accurate and comprehensive probability distribution because the forecasting results are affected by multiple complex factors. To solve this issue, the method of training a generative model can be used to approximate the true distribution by obtaining a suitable parameter distribution. One of the commonly used generative models is variational autoencoder (VAE). Assume that the true distribution p(X) of the input sample X is unknown while the distribution p(Z) of the latent variable Z in the generative model is given. Accordingly, we can have a mapping between X and Z, namely $f:Z\to X$. Thus, the distribution p_f(Z) of f can be approximated by learning approach p(X). Based on this conception, VAE can use a deep neural network to minimize the deviation distance between p(Z) and p_f(Z) by using maximum likelihood estimation. The operator used to optimize the deviation distance of the two distributions during the training process is called forward operator.

Determining forward operators during training often relies on the empirical performance of generative models. In order to determine the forward operator, VAE generally adopts an approximate posterior distribution, which may lead to a situation that does not completely match the prior distribution, thereby reducing the forecasting accuracy.

To solve this problem, this paper introduces the Kernel Transfer Operator (KTO) based on the Perron-Frobenius method proposed in Huang et al. (2021), and adapts it to the application scenario of short-term load demand forecasting.

Let ξ be a one-dimensional convolutional autoencoder and the training data samples are represented as $X=\left(x_{\mathit{1}},x_{\mathit{2}},...,x_n\right)$. The pseudocode of the modified KTO is presented as:

Step 1Calculate the encoded representation of the data X, i.e.,:

$X_e=\left(\xi \left(x_1\right),\xi \left(x_2\right),...,\xi \left(x_n\right)\right)(2)$

Step 2$\forall i,j=1,...,n$, calculate $K_{i,j}=k\left(X_{ei},X_{ej}\right)$, The k kernel function can be expressed as:

$k\left(x,y\right)=e^{-\frac{\Vert x-y\Vert }{2}}(3)$

Step 3Independently sample z from the n-dimensional standard Gaussian distribution Z, and $\forall i,j=\mathit{1},...,n$, calculate $L_{i,j}=k\left(z_i,z_j\right)$;

Step 4Calculate$K^{\prime }={\left(K-nI\right)}^{-\mathit{1}}$, where I is a unit matrix of order n;

Step 5Independently sample w from an n-dimensional standard Gaussian distribution Ω;

Step 6Calculate $s=L\cdot K^{\prime }\cdot V$, where, $\forall i,j=\mathit{1},...,n$, each element of V can be expressed as $V_{i,j}=k\left(z_i,w_j\right)$;

Step 7. Sort s in ascending order, and extract the original corresponding serial number H according to this order;

Step 8. $\forall h\in H$, calculate the new sample $x^{*}$ according to Eq. 4.

$x^{*}\left(h\right)=\frac{X_e\left(h\right)\cdot s\left(h\right)}{{\Vert s\left(h\right)\Vert }_1}(4)$

3.2 General long short-term memory model

By introducing the gating mechanism, LSTM, which is based on recurrent neural network (RNN), can effectively solve the gradient explosion and gradient disappearance problems brought by traditional RNNs (Li et al., 2022). Figure 1 shows the schematic diagram of the basic principle of LSTM.

FIGURE 1

FIGURE 1. Basic structure of LSTM (Bengio et al., 1994).

The forget gate can be expressed as

$f_t=\sigma \left(w_{f,x}{x}_t+w_{f,h}{h}_{t-\mathit{1}}+b_f\right)(5)$

The candidate state and the input gate are expressed as

${\stackrel{\sim }{C}}_t=\sigma \left(w_{\stackrel{\sim }{C},x}{x}_t+w_{\stackrel{\sim }{C},h}{h}_{t-\mathit{1}}+b_{\stackrel{\sim }{C}}\right)(6)$

$i_t=\sigma \left(w_{i,x}{x}_t+w_{i,h}{h}_{t-\mathit{1}}+b_i\right)(7)$

The output gate is expressed as

$o_t=\sigma \left(w_{o,x}{x}_t+w_{o,h}{h}_{t-\mathit{1}}+b_o\right)(8)$

According to i_t and f_t and the state value of the memory cell at time t-1, the state value of the memory cell at time t can be updated as

$c_t=f_t^{°}{c}_{t-\mathit{1}}+i_t°{\stackrel{\sim }{C}}_t(9)$

The hidden layer output value can be updated as

$h_t=o_t\circ \tanh \left(c_t\right)(10)$

where, x_t, c_t, and h_t are the input value, memory cell state value, and hidden layer output value at time t, respectively; w is the corresponding weight, b is the bias term; σ$\left(\cdot \right)$represents the Sigmoid function, tanh $\left(\cdot \right)$ represents the hyperbolic tangent function; $\circ$ represents the Hadamard product.

3.3 Bidirectional long short-term memory model

According to Figure 1, the standard LSTM model can only process the historical information of time series sequence. In order to consider the future information to increase the forecasting accuracy, the standard LSTM is extended by adding a backward layer to realize the preservation of historical and future information, thus forming a bidirectional LSTM (Bi-LSTM). The basic structure of Bi-LSTM is shown in Figure 2.

FIGURE 2

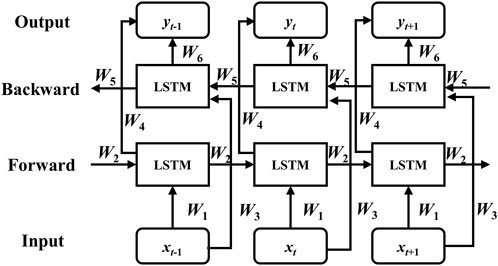
FIGURE 2. Basic structure of Bi-LSTM (Hochreiter and Schmidhuber, 1997).

The input-output relationship of each layer of bidirectional LSTM can be expressed as Eqs 11–13.

${\overrightarrow{h}}_t=\mathit{{\rm H}}\left(W_{\mathit{1}}{x}_t+W_{\mathit{2}}{\overrightarrow{h}}_{t-\mathit{1}}+\overrightarrow{b}\right)(11)$

${\stackrel{⃖}{h}}_t=\mathit{{\rm H}}\left(W_{\mathit{3}}{x}_t+W_{\mathit{4}}{\stackrel{⃖}{h}}_{t-\mathit{1}}+\stackrel{⃖}{b}\right)(12)$

$y_t=W_{\mathit{4}}{\overrightarrow{h}}_t+W_{\mathit{6}}{\stackrel{⃖}{h}}_t+b_y(13)$

where, ${\overrightarrow{h}}_t$, ${\stackrel{⃖}{h}}_t$, and $y_t$ represent the output values of the forward, backward, and output layers at time t, respectively; H represents a single LSTM calculation model; W and b represent the weight and bias terms, respectively.

3.4 Back propagation Bayesian

Back propagation Bayes (BBP) is a variational reasoning method used to learn the posterior distribution of neural network weights (Fortunato et al., 2019). Due to page limitation, this paper does not expand the specific principle of BBP, but only discusses its application to Bi-LSTM.

Generally, sample ε according to the distribution $\epsilon \sim N\left(\mathit{0},I\right)$ and let $w=\mu +\epsilon \cdot \sigma$. To speed up the training process and the proc(ess of handling long sequences, mini-batch methods and truncated sequences are hence introduced. The gradient g of w is calculated by forward and backward propagation. Then, calculate the gradients ${\mathrm{g}}_w^{\prime }$, ${\mathrm{g}}_{\mu }^{\prime }$, and ${\mathrm{g}}_{\sigma }^{\prime }$ corresponding to w, μ and σ in $\log {\rm N}\left(w|\mu ,{\sigma }^{\mathit{2}}\right)-\log p\left(w\right)$. Finally, update step μ and σ using Eqs 14, 15 until the variational free energy of the bi-LSTM is minimized.

$\mu :=\frac{g+g_w^{\prime }/N}{M}+\frac{g_{\mu }^{\prime }}{MN}(14)$

$\sigma :=\frac{g+g_w^{\prime }/N}{M}\epsilon +\frac{g_{\sigma }^{\prime }}{MN}(15)$

where, M is the total number of mini-batches, and N is the total number of truncated sequences.

3.5 Kernel transfer operator-based bidirectional long short-term memory forecasting method

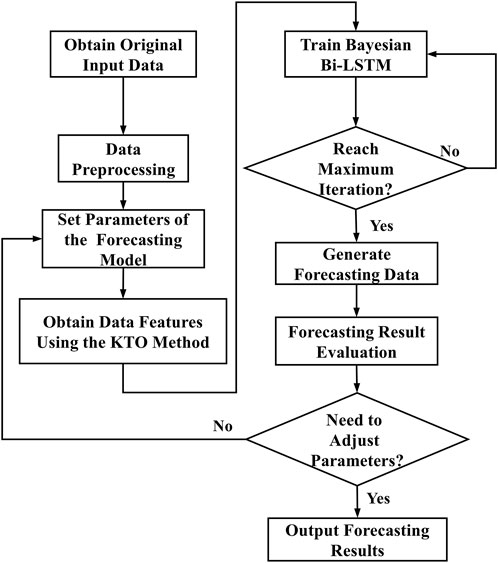
By combining the KTO and Bayesian Bi-LSTM models, we propose a short-term load forecasting method based on the KTO-based Bi-LSTM. The flowchart of the proposed method is shown in Figure 3. The major steps of the proposed method can be summarized as:

FIGURE 3

FIGURE 3. Flowchart of the proposed method.

Step 1Raw Data Collection. Collect historical data, such as load profile, temperature, relative humidity, precipitation, etc. as input samples, and the data sampling interval is set to be 1 h;

Step 2. Data Pre-processing. Perform data cleaning on the input sample data and normalized the input data after eliminating bad data;

Step 3. Set the model parameters for the proposed method;

Step 4. Data Feature Extraction. After passing the input sample data through a one-dimensional convolutional autoencoder (including convolutional layer and pooling layer), the proposed KTO method is used to obtain the representation of the latent variable, and the results are used as the inputs to the lower layer;

Step 5. Load Forecasting. Train the Bayesian Bi-LSTM forecasting model. Output approximate posterior distribution parameters after the maximum iterations are reached, and accordingly, calculate the load forecasting results;

Step 6. Forecasting Result Evaluation. Calculate the quantitative evaluation indices of the forecasting results: if evaluation indices are not satisfied, return to step 3 to adjust the forecasting model according to the evaluation results to improve the forecasting accuracy; or output the forecasting results.

3.6 Data Preprocessing

Due to the existence of different units in input data samples, it is necessary to normalize them in the common scale to accelerate the convergence of the proposed method, which can be formulated as:

$d^{\prime }=\frac{d-d_{\min }}{d_{\max }-d_{\min }}(16)$

where, d is the original input data samples; d_max and d_min are the maximum and minimum values of the original data, respectively; $d^{\prime }$ is the normalized input data samples.

For historical data such as load profile, temperature, wind speed, etc., data loss or data distortion may occur. For single-point-missed data, the average value of the two sampling points before and after the missing sampling point can be used as a supplement data point; for continuous multi-point-missed data, the average values of the two measurement periods before and after the missing sampling points are used to create supplement data points; for data distortion, it is recommended to directly eliminate the distorted data, and use the two approaches mentioned above to create supplement data points.

In addition, for parameters that are hard to quantify, such as seasons and holidays, we use the digital coding technic to label and distinguish them (Li Y. et al., 2021).

3.7 Evaluation indices

To verify the effectiveness of the proposed method, this paper uses two indices, namely Average Coverage Deviation (ACE) and Prediction Interval Average Width (PIAW), the details of which can be found in Pang et al. (2022).

Let the significance level be α, then the confidence level is $\left(\mathit{1}-\alpha \right)\times \mathit{100}\%$, and the upper and lower bounds of the prediction interval can be expressed as:

$\{\begin{array}{c}{\overline{y}}_t={\mu }_y+Z{\sigma }_y\\ {\underset{¯}{y}}_t={\mu }_y-Z{\sigma }_y\end{array}(17)$

where, Z is the Z-score.

ACE can be calculated according to Eq 18:

$\mathrm{A}\mathrm{C}\mathrm{E}=\left(\frac{{\displaystyle \sum }_{t=\mathit{1}}^T{\epsilon }_t}{T}-\mathrm{1}+\alpha \right)\times \mathit{100}\%(18)$

where, ε_t is a binary variable, ${\epsilon }_t\in \left[{\underset{¯}{y}}_t,{\overline{y}}_t\right]$ takes the value 1, otherwise it is 0. If ACE is less than 0, it means that the forecasting result is less reliable.

PIAW can be calculated according to Eq 19:

$\mathrm{P}\mathrm{I}\mathrm{A}\mathrm{W}=\frac{{\displaystyle \sum }_{t=\mathrm{1}}^T\left({\overline{y}}_t-{\underset{¯}{y}}_t\right)}{T}(19)$

4 Case study

4.1 Data description

This paper uses the historical load profile and renewable energy generation data from 1 January 2017 to 31 December 2021 in a certain area in Guangdong, China, to perform load forecasting, with the sampling interval of 1 h. The data from 2017 to 2019 are used as the training data set, the data of 2020 is used as the validation data set, and the data of 2021 is used as the test data set.

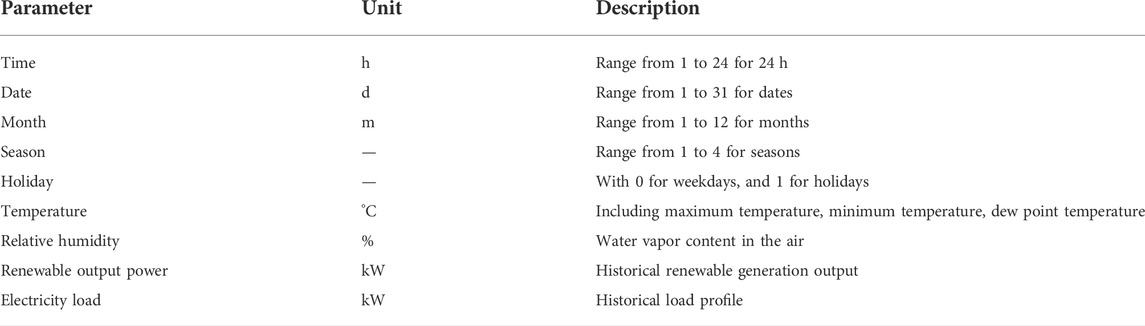
The basic parameters affecting net load demand considered in this paper include date (including months, holidays, working days and seasons), relative humidity, precipitation, temperature (including maximum temperature and minimum temperature), as shown in Table 1.

TABLE 1

TABLE 1. Parameter set for load demand forecasting.

4.2 Model parameter selection

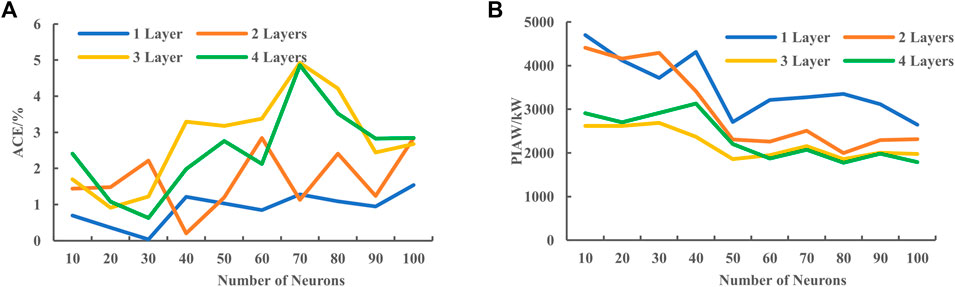
The number of network layers as well as the number of neurons in the Bayesian Bi-LSTM has a great influence on forecasting accuracy of the proposed model. To identify the suitable model parameters, we choose the number of network layers ranging from 1 to 4, and the number of neurons ranging from 10 to 100 at an interval of 10, separately, to compare the ACE and PIAW of the forecasting results, which are shown in Figure 4 and Figure 5.

FIGURE 4

FIGURE 4. Impact of parameters on (A) ACE and (B) PIAW.

FIGURE 5

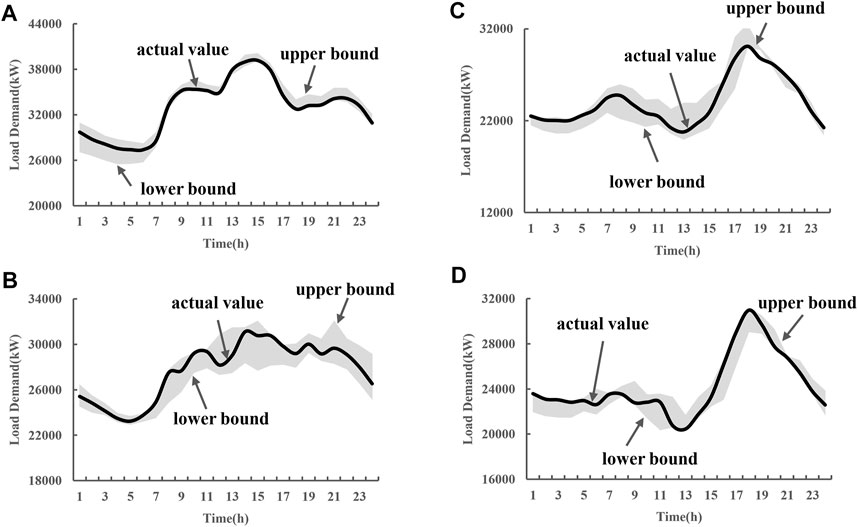
FIGURE 5. Load demand forecasting results of (A) typical weekday in summer, (B) typical weekend in summer. (C) Typical weekday in winter and (D) typical weekend in winter.

If the number of neurons is fixed, and the number of network layers is selected as one to two, the forecasting results have lower ACE values and larger PIAW deviations, indicating poor forecasting performance. The cases with the layer number of 3 or 4 exhibit nearly the same the forecasting performance. If we fix the number of network layers, as the number of neurons increases, the ACE value is effectively improved, and the PIAW deviation is gradually reduced. In general, the forecasting performance is better when the number of neurons is more than 50. In summary, this paper, making the trade-off between the computational efficiency and forecasting accuracy, set the number of network layer to 3 and the number of neurons to 50.

4.3 Result analysis

To evaluate the effectiveness of the proposed method, the confidence level $\left(\mathit{1}-\alpha \right)\%$ is set to 95%, and the proposed KTO-based Bi-LSTM forecasting method is used to forecast the load profile in 2020. For the convenience of presentation, the load demand forecasting results of typical working days and holidays in summer and winter and the evaluation of the forecasting results are selected respectively, as shown in Figures 5A–D.

Observed from the forecasting results of summer and winter, the actual values of load demand are between the upper and lower bounds of the forecasting interval whether it is a working day or a holiday, indicating that the method proposed in this paper can better obtain the load demand characteristics regarding seasonality and holidays. Hence, the forecasting results can effectively reflect the real situation of the load profile.

4.4 Performance comparison

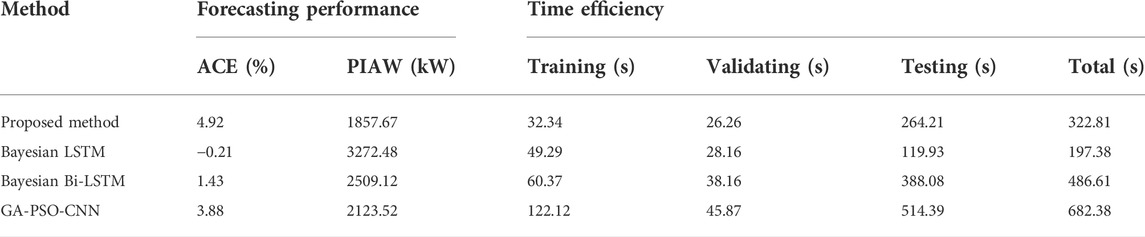
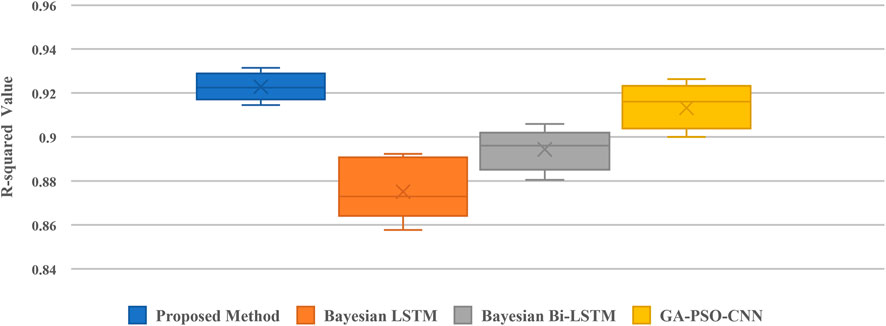
To further evaluate the validity and performance of the proposed method, we evaluate the same study case using the proposed method, the conventional Bayesian LSTM, Bayesian Bi-LSTM and GA-PSO-CNN (Liu et al., 2021) methods. The confidence level is set to 95%. The comparison results are shown in Table 2 and Figures 5, 6.

TABLE 2

TABLE 2. Performance comparison of different forecasting methods.

FIGURE 6

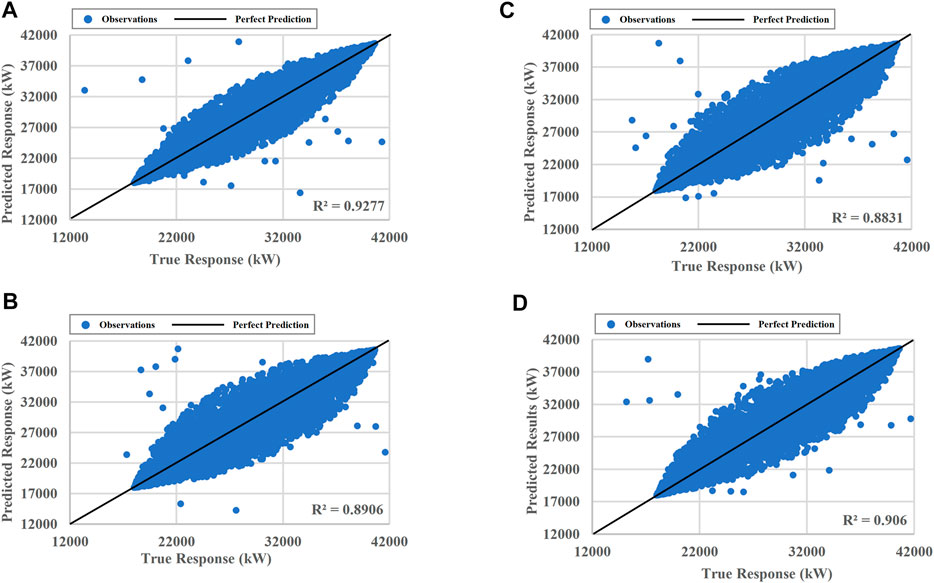
FIGURE 6. R-squared plots of (A) proposed method, (B) Bayesian LSTM. (C) Bayesian Bi-LSTM and (D) GA-PSO-CNN.

From Table 2, in terms of ACE, the proposed method and the Bayesian Bi-LSTM method have positive values of ACE, which implies that the forecasting results are more reliable. Additionally, the ACE value of the proposed method is greater than the ones of the Bayesian Bi-LSTM method and the GA-PSO-CNN method, which means that the forecasting results of the proposed method is closer to the actual values. However, the ACE value of the Bayesian LSTM method forecasting result is negative, indicating low reliability of its forecasting results.

In terms of PIAW, the proposed method has the lowest value of PIAW among the four methods, indicating that the intervals between the upper and lower forecasting bound are smaller. Hence, the proposed method can better reflect the uncertainty of load profile variation.

From Figure 6, we can see that the scatter points derived by the proposed method centre more tightly around the perfect prediction line than the other methods and the proposed method has the highest R-squared value (0.9277), which also demonstrates that the forecasting results of the proposed method can better track the true response. Additionally, we conducted 100 sampling experiments to investigate the stability of the forecasting results of each method, as shown in Figure 7. The quantile range of the proposed method is much smaller than the other methods, indicating the better stability of its forecasting results. The forecasting results of Bayesian Bi-LSTM method and the GA-PSO-CNN method present similar stability performance while the Bayesian LSTM method has mediocre performance to generate stable forecasting results.

FIGURE 7

FIGURE 7. Boxplots of R-squared values of each forecasting methods with 100 sampling experiments.

When it comes to running time, with the introduction of the Perron-Frobenius-based KTO, the training and validating process of the proposed method has been reduced compared with the Bayesian LSTM method and the Bayesian Bi-LSTM method. Regarding the testing process as well as the total running time, the Bayesian LSTM method has the fastest computing speed among the four methods due to its simpler RNN structure. The GA-PSO-CNN method consumes more time to generate forecasting results since it requires extra time to use the GA and PSO algorithms to fine-tune the network parameters.

To sum up, the proposed method has better performance than the conventional Bayesian LSTM method, the Bayesian Bi-LSTM method as well as the GA-PSO-CNN method, and its forecasting results demonstrate that it can effectively and stably reflect load profile uncertainties.

5 Conclusion

In this paper, a short-term net load demand forecasting method using KTO-based Bi-LSTM is proposed. We introduced the KTO based on the Perron-Frobenius method to the Bayesian Bi-LSTM, and compared the proposed method with the Bayesian LSTM, Bi-LSTM and GA-PSO-CNN methods to verify the performance of the proposed method. The conclusions are stated as follows:

• From the experimental results, the method proposed in this paper can comprehensively consider the parameters such as date, temperature, and humidity that affect load profiles, and properly reflect the characteristics of load profile variation according to seasonality and holiday effects.

• From the performance comparison, the proposed method has higher ACE and lower PIAW with fine computational performance, which indicates that the proposed method outdoes the three conventional forecasting methods.

In the future, the proposed forecasting method can be modified to serve renewable generation forecasting and the correlation and interactivity of variables associated with power outputs of renewable energy need to be investigated to further enhance the accuracy and stability of the forecasting results.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

JW: conceptualization, writing-original draft, and formal analysis; ZX: supervision, writing-review, and editing; KC: formal analysis and software; WL: project administration and resources.

Funding

This work was supported by Science and Technology Project of Foshan Power Supply Bureau (030600QQ00210002).

Conflict of interest

Authors JW and ZX were employed by Guangdong Power Grid Co., Ltd. Authors KC and WL were employed by Foshan Electric Power Design Institute Co., Ltd.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Bengio, Y., Simard, P., and Frasconi, P. (1994). Learning long-term dependencies with gradient descent is difficult. IEEE Trans. Neural Netw. 5 (2), 157–166. doi:10.1109/72.279181

PubMed Abstract | CrossRef Full Text | Google Scholar

Brusaferri, A., Matteucci, M., Spinelli, S., and Vitali, A. (2022). Probabilistic electric load forecasting through bayesian mixture density networks. Appl. Energy 309, 118341. doi:10.1016/j.apenergy.2021.118341

CrossRef Full Text | Google Scholar

Feng, C., Sun, M., and Zhang, J. (2019). Reinforced deterministic and probabilistic load forecasting via $Q$ -learning dynamic model selection. IEEE Trans. Smart Grid 11 (02), 1377–1386. doi:10.1109/TSG.2019.2937338

CrossRef Full Text | Google Scholar

Fortunato, M., Blundell, C., and Vinyals, O. (2019). Bayesian recurrent neural networks. Available at: https://arxiv.org/abs/1704.02798. doi:10.48550/arXiv.1704.02798

CrossRef Full Text | Google Scholar

Hahn, H., Meyer-Nieberg, S., and Pickl, S. (2009). Electric load forecasting methods: Tools for decision making. Eur. J. Operational Res. 199 (3), 902–907. doi:10.1016/j.ejor.2009.01.062

CrossRef Full Text | Google Scholar

Hochreiter, S., and Schmidhuber, J. (1997). Long short-term memory. Neural Comput. 9 (8), 1735–1780. doi:10.1162/neco.1997.9.8.1735

PubMed Abstract | CrossRef Full Text | Google Scholar

Huang, Z., Chakraborty, R., and Singh, V. (2021). Forward operator estimation in generative models with kernel transfer operators. Available at: https://arxiv.org/abs/2112.00305#:∼:text=Forward%20Operator%20Estimation%20in%20Generative%20Models%20with%20Kernel%20Transfer%20Operators,-Zhichun%20Huang%2C%20Rudrasis&text=Abstract%3A%20Generative%20models%20which%20use,to%20the%20unknown%20input%20distribution. doi:10.48550/arXiv.2112.00305

CrossRef Full Text | Google Scholar

Kaur, A., Nonnenmacher, L., and Coimbra, C. F. M. (2016). Net load forecasting for high renewable energy penetration Grids. Energy 114, 1073–1084. doi:10.1016/j.energy.2016.08.067

CrossRef Full Text | Google Scholar

Kong, W., Dong, Z., Jia, Y., Hill, D., Xu, Y., and Zhang, Y. (2019). Short-term residential load forecasting based on LSTM recurrent neural network. IEEE Trans. Smart Grid 10 (1), 841–851. doi:10.1109/TSG.2017.2753802

CrossRef Full Text | Google Scholar

Li, D., Yang, Y., Yang, B., and Wang, Q. (2021). Short time power load probabilistic forecasting based on constrained parallel-LSTM neural network quantile regression mode. Power Syst. Technol. 45 (04), 1356–1364. doi:10.13335/j.1000-3673.pst.2020.1124

CrossRef Full Text | Google Scholar

Li, H., Ge, H., Yang, H., Yan, J., and Sang, Y. (2022). An abnormal traffic detection model combined BiIndRNN with global attention. IEEE Access 43 (03), 30899–30912. doi:10.1109/ACCESS.2022.3159550

CrossRef Full Text | Google Scholar

Li, Y., Liu, X., Xing, F., Wen, G., Lu, L., He, H., et al. (2021). Daily peak load prediction based on correlation analysis and Bi-directional long short-term memory network. Power Syst. Technol. 45 (07), 2719–2730. doi:10.13335/j.1000-3673.pst.2020.1390

CrossRef Full Text | Google Scholar

Liu, B., Qin, C., Ju, P., Zhao, J., Chen, C., and Zhao, J. (2020). Short-term bus load forecasting based on xgboost and stacking model fusion. Electr. Power Autom. Equip. 40 (03), 147–153. doi:10.16081/j.epae.202002024

CrossRef Full Text | Google Scholar

Liu, J., Shi, Q., Han, R., and Yang, J. (2021). A hybrid GA-PSO-CNN model for ultra-short-term wind power forecasting. Energies 14 (20), 6500. doi:10.3390/en14206500

CrossRef Full Text | Google Scholar

Liu, R., Chen, T., Sun, G., Muyeen, S. M., Lin, S., and Mi, Y. (2022). Short-term probabilistic building load forecasting based on feature integrated artificial intelligent approach. Electr. Power Syst. Res. 206, 107802. doi:10.1016/j.epsr.2022.107802

CrossRef Full Text | Google Scholar

Lu, J., Zhang, Q., Yang, Z., Tu, M., Lu, J., and Peng, H. (2019). Short-term load forecasting method based on CNN-LSTM hybrid neural network model. Automation Electr. Power Syst. 43 (08), 131–137. doi:10.7500/AEPS20181012004

CrossRef Full Text | Google Scholar

Mei, F., Wu, Q., Shi, T., Lu, J., Pan, Y., and Zheng, J. (2019). An ultrashort-term net load forecasting model based on phase space reconstruction and deep neural network. Appl. Sci. (Basel). 9 (7), 1487. doi:10.3390/app9071487

CrossRef Full Text | Google Scholar

Pai, P., and Hong, W. (2005). Forecasting regional electricity load based on recurrent Support vector machines with genetic algorithms. Electr. Power Syst. Res. 74 (3), 417–425. doi:10.1016/j.epsr.2005.01.006

CrossRef Full Text | Google Scholar

Pang, C., Shang, X., Zhang, B., and Yu, J. (2022). Short-term wind power probability prediction based on improved gradient boosting machine algorithm. Automation Electr. Power Syst. Available at: http://kns.cnki.net/kcms/detail/32.1180.TP.20220301.1036.002.html (Accessed May 17, 2022.

Google Scholar

Sudheer, G., and Suseelatha, A. (2015). Short term load forecasting using wavelet transform combined with holt-winters and weighted nearest neighbor models. Int. J. Electr. Power & Energy Syst. 64, 340–346. doi:10.1016/j.ijepes.2014.07.043

CrossRef Full Text | Google Scholar

Tan, Z., De, G., Li, M., Lin, H., Yang, S., Huang, L., et al. (2020). Combined electricity-heat-cooling-gas load forecasting model for integrated energy system based on multi-task learning and least square Support vector machine. J. Clean. Prod. 248, 119252–119315. doi:10.1016/j.jclepro.2019.119252

CrossRef Full Text | Google Scholar

Wang, Y., Zhang, N., Tan, Y., Hong, T., Kirschen, D., and Kang, C. (2019). Combining probabilistic load forecasts. IEEE Trans. Smart Grid 10 (4), 3664–3674. doi:10.1109/TSG.2018.2833869

CrossRef Full Text | Google Scholar

Xu, J., Wang, X., and Yang, J. (2020). Short-term load density prediction based on CNN-qrlightgbm. Power Syst. Technol. 44 (09), 3409–3416. doi:10.13335/j.1000-3673.pst.2019.2243

CrossRef Full Text | Google Scholar

Xu, L., Wang, S., and Tang, R. (2019). Probabilistic load forecasting for buildings considering weather forecasting uncertainty and uncertain peak load. Appl. Energy 237, 180–195. doi:10.1016/j.apenergy.2019.01.022

CrossRef Full Text | Google Scholar

Zhao, Y., Wang, H., Kang, L., and Zhang, Z. (2022). Temporal convolution network-based short-term electrical load forecasting. Trans. China Electrotech. Soc. 37 (05), 1242–1251. doi:10.19595/j.cnki.1000-6753.tces.210223

CrossRef Full Text | Google Scholar

Zheng, H., Yuan, J., and Chen, L. (2017). Short-term load forecasting using EMD-LSTM neural networks with a xgboost algorithm for feature importance evaluation. Energies 10 (8), 1168. doi:10.3390/en10081168

CrossRef Full Text | Google Scholar

Zhu, L., Xun, Z., Wang, Y., Cui, Q., Chen, W., and Lou, J. (2021). Short-term power load forecasting based on CNN-BiLSTM. Power Syst. Technol. 45 (11), 4532–4539. doi:10.13335/j.1000-3673.pst.2021.0470

CrossRef Full Text | Google Scholar