Frequency support strategy for single-Stage grid-Connected photovoltaic generation with active power reserves

Large-scale photovoltaic (PV) generation grid connection causes lack of inertia and insufficient frequency regulation capacity of power system. To solve this problem, this study proposed the active power-frequency droop control (APFDC) and virtual inertia control (VIC) for single-stage PV generation. PV generation is able to participate in the grid frequency regulation by improving the control system of voltage source converter (VSC). The effect of control parameters on the inertia characteristic of PV generation is analyzed. On this basis, the distribution mechanism of unbalanced active power among PV generators with inertia control strategy is revealed. The simulation results indicated that PV generation can be controlled by setting the control strategy of the voltage source converter (VSC) to reduce or increase the active power; it also takes part in the frequency regulation of the system. The inertia provided by PV generation is controllable and frequency-dependent, increases with the increase in control gain, the decrease in the time constant of VIC, and the decrease in phase-locked loop (PLL) control bandwidth.

Introduction

The development of photovoltaic (PV) generation is an important means to deal with the current severe environmental problems and global energy transformation. At the end of 2020, the installed capacity of grid-connected PV generation in China has reached 253 million kW, indicating a year-on-year increase of 24.1%. It is estimated that by the end of 2030 and 2050, this value will reach 1,500 million and 2,700 million kW, respectively.

PV generation unit is connected to the power grid through power electronic converters. Large-scale PV generation grid connection weakens the system inertia, reduces the system ability of frequency regulation, and seriously endangers system frequency security and stability (Pedro et al., 2016; Jesus et al., 2017; Fang et al., 2019). Some countries and regions have issued requirements and technical guidelines, which require PV plants to have the ability to respond to system frequency changes (Datta et al., 2011; Liu et al., 2014; Jibji-bukar and Anaya-lara, 2019). Field test on PV generation participating in primary frequency control was conducted by the State Grid Corporation of China (Xiaoqiang et al., 2017; Xiaoqiang et al., 2018).

A novel power point track method was proposed by Pappu et al. (2010), which is used for frequency stabilization and active power reserves. In the frequency dynamic process, the reloading algorithm is activated by the control sign; the algorithm uses a modified fractional open-circuit voltage (Mohammad et al., 2017). A power point tracking method based on Lagrange quadratic interpolation method was proposed by Yun et al. (2012) and Huanhai et al. (2013), according to the relationship of the maximum output power and output demand of PV array, related to the relationship between the maximum output power and output PV array demand, PV generation can choose between two modes (constant power output mode and MPPT mode) automatically. Zarina et al. (2014) proposed a frequency regulation method by improving the DC voltage control loop of the inverter. The method illustrates frequency regulation by establishing the proportional integral relationship between the grid frequency deviation Δf and the output DC voltage deviation ΔU_dc. Nevertheless, how to establish the proportional integral relationship between Δf and ΔU_dc is still unanswered.

In the research from “A control strategy for photovoltaic generation system based on quadratic interpolation method.” (Yun et al., 2012) and “A new frequency regulation strategy for photovoltaic systems without energy storage” (Huanhai et al., 2013) and “Exploring frequency control capability of a PV system in a hybrid PV-rotating machine-without storage system.” (Zarina et al., 2014), the DC voltage controller of VSC plays one of the key roles of actualizing participation in the grid frequency modulation of PV generation. The reference value of the DC capacitor voltage can be adjusted using the grid frequency deviation Δf so PV generation can participate in frequency regulation. However, it is not easy to set initial reference of the DC capacitor voltage because of the randomness of illumination and the nonlinear relationship between the DC capacitor voltage and PV array output active power. PV generation participating in frequency modulation is strictly limited by the aforementioned relationship between Δf and ΔU_dc. Furthermore, how to evaluate the inertia characteristics of PV generation is rarely studied.

In the study of the frequency characteristics of system with PV generation, the relationship between the output active power of PV generation and grid frequency has gained a considerable amount of attention. Therefore, a model that accurately describes the characteristics of PV generation electromechanical transient serves as the basis for on-grid analysis. At present, America’s WECC and China’s GB/T 32,826–2016 “Guide for modeling photovoltaic power system” have proposed a general PV generation model for electromechanical transient analysis (WECC Renewable Energy Modeling Task Force, 2012; Lei et al., 2015; SPC, 2016). (Linan et al., 2018) combined with the measured data for the manual short-circuit test of a PV power station in Northwest China, effectively verified the proposed model is “verified the electromechanical transient model of PV generation.” Unlike the electromagnetic transient model, the electromechanical transient model ignores numerous processes, such as PWM modulation and coordinate transformation, and replaces its DC voltage controller with active power controller (Nanou and Papathanassiou, 2014). Because of the differences between the two model control systems, there is discrepancy in designed control strategies (Sangwongwanich et al., 2017; Lyu et al., 2018).

This study proposed the virtual inertia control (VIC) strategy and the active power-frequency droop control strategy (APFDC) based on the single-stage PV generation electromechanical transient model, evaluating the inertia characteristics of PV generation. The contributions of this study are as follows:

1) The control system of VSC was improved so that PV generation actively participates in the system frequency regulation.

2) According to the relationship between unbalanced active power from the system and phase output of internal voltage, the effect of the PLL control bandwidth, control gain, and time constant on the PV generation inertia characteristics is discussed, and the effect of the PV generation inertia on frequency dynamics is analyzed.

3) The dynamic power distribution mechanism of PV generation units with VIC is revealed.

The structure of this article is arranged as follows: the configuration of single-stage grid-connected PV generation is investigated in Section 2. The electromechanical transient model of VSC is proposed in Section 3. In Section 4, the frequency regulation control strategies, including APFDC and VIC, are presented. Section 5 discusses the inertia characteristics of PV generation. The simulation results are presented in Section 6 and the conclusions in Section 7.

Configuration of single-stage grid-connected photovoltaic power generation

The structure of grid-connected single-stage PV generation is presented in Figure 1. The figure shows the main parts of the system, including the PV array, voltage source converter (VSC), and AC grid. The output active power of the PV array can be delivered to the grid side through the VSC (Yu et al., 2018). C is the DC filter capacitor, U_dc is the DC-side voltage of the PV array, L_f is the filter inductance, U_t is the voltage of point of common coupling (PCC), L_g is the inductance, R_g is the resistance of the transmission line, P_load is the load, and U_g is the grid side voltage.

FIGURE 1

FIGURE 1. Configuration of single-stage grid-connected photovoltaic (PV) generation.

PV array

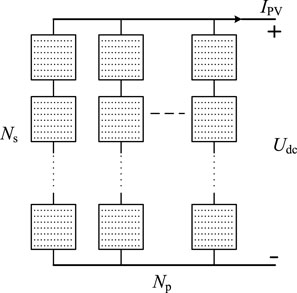
The configuration of the PV array is presented in Figure 2, in which N_s and N_p represent the number of series and parallel connected cells. The U_dc-I_PV characteristic of a PV array from manufacturer is shown in (1).

${\mathit{I}}_{\mathrm{PV}}={\mathit{N}}_{\mathrm{p}}{\mathit{I}}_{\mathrm{sc}}\left[1-{\mathit{C}}_1\left({\mathit{e}}^{\frac{{\mathrm{U}}_{\mathrm{dc}}}{{\mathrm{C}}_{\mathrm{2}}{\mathrm{N}}_{\mathrm{s}}{\mathrm{U}}_{\mathrm{oc}}}}-1\right)\right](1)$

FIGURE 2

FIGURE 2. PV array model.

Here, I_PV is the DC current, I_sc and U_oc are the short-circuit current and open-circuit voltage, respectively; C₁ and C₂ are coefficients obtained in (2).

$\{\begin{array}{l}{\mathit{C}}_1=\left(1-\frac{{\mathit{I}}_{\mathrm{m}}}{{\mathit{I}}_{\mathrm{sc}}}\right){\mathit{e}}^{-\frac{{\mathit{U}}_{\mathrm{m}}}{{\mathit{C}}_2{\mathit{U}}_{\mathrm{oc}}}}\\ {\mathit{C}}_2=\left(\frac{{\mathit{U}}_{\mathrm{m}}}{{\mathit{U}}_{\mathrm{oc}}}-1\right)/\ln \left(1-\frac{{\mathrm{I}}_{\mathrm{m}}}{{\mathrm{I}}_{\mathrm{sc}}}\right)\end{array}(2)$

Here, I_m and U_m represent the maximum current and voltage, respectively, when the PV array operates at the maximum power point.

The relationship of P_PV and U_dc is obtained in (3) based on (1).

${\mathit{P}}_{\mathrm{PV}}={\mathit{N}}_{\mathit{p}}{\mathit{I}}_{\mathrm{sc}}\left[1-{\mathit{C}}_1\left({\mathit{e}}^{\frac{{\mathit{U}}_{\mathrm{dc}}}{{\mathit{C}}_2{\mathit{N}}_s{\mathit{U}}_{\mathrm{oc}}}}-1\right)\right]\cdot {\mathit{U}}_{\mathrm{dc}}(3)$

Simplified model of the PV array

The transcendental equation in (3) adds many difficulties to the modeling of PV array. Thus, Lei et al. (2015) proposed a simplified output active power model of PV array, which is expressed in (4).

${\mathit{P}}_{\mathrm{PV}}={\mathit{N}}_{\mathit{p}}\cdot {\mathit{N}}_{\mathrm{s}}\cdot {\mathit{U}}_{\mathrm{m}}\cdot {\mathit{I}}_{\mathrm{m}}\cdot \frac{\mathit{S}}{{\mathit{S}}_{\mathrm{ref}}}\left[1+\frac{\mathit{b}}{\mathrm{e}}\left(\mathit{S}-{\mathit{S}}_{\mathrm{ref}}\right)\right](4)$

where S_ref is the rating irradiance, b is the constant associated with the material of battery (typical reference value b = 0.0005 m²/W), and e is the Euler number.

The active power reserves ΔP of PV generation if operating in the limited power mode (σ% is the active power reserve ratio) is expressed in (5).

$\mathrm{\Delta }\mathit{P}=\mathit{\sigma }\mathrm{\%}\cdot {\mathit{N}}_{\mathit{p}}\cdot {\mathit{N}}_{\mathrm{s}}\cdot {\mathit{U}}_{\mathrm{m}}\cdot {\mathit{I}}_{\mathrm{m}}\cdot \frac{\mathit{S}}{{\mathit{S}}_{\mathrm{ref}}}\left[1+\frac{\mathrm{b}}{\mathrm{e}}\left(\mathit{S}-{\mathit{S}}_{\mathrm{ref}}\right)\right](5)$

The electromechanical transient model of voltage source converter

The electromagnetic transient model of VSC is shown in Supplementary Figure SA1 of Supplementary Appendix SA, and a typical vector control strategy is shown in Supplementary Figure SA2 of Supplementary Appendix SA. In the electromagnetic transient control system of VSC, it contains the current controllers, PWM modulation, etc. However, the response speed of these modules is in millisecond, and the dynamic process of rapid response can be neglected while analyzing the electromechanical transient problems.

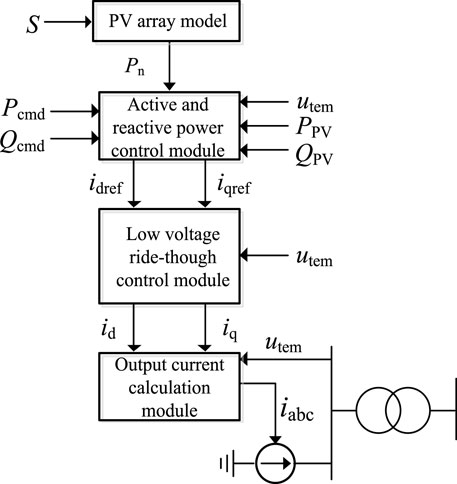
To accurately describe the electromechanical transient characteristics of VSC, Linan et al. (2018) established an electromechanical transient model of VSC. Figure 3 shows the VSC equivalent model, where S is the illumination; P_n is the maximum active power of PV array under the current illumination; P_cmd and Q_cmd represent the reference of active and reactive powers, respectively; P_PV and Q_PV represent the actual values of active and reactive power; and u_tem is the PCC voltage.

FIGURE 3

FIGURE 3. Electromechanical transient model of voltage source converter (VSC).

Supplementary Figure SA3 of Supplementary Appendix SA shows the specific control structure of active and reactive power control modules. Compared with the electromagnetic transient control system of VSC, the active power control replaces the DC voltage control in the electromechanical transient control system of VSC; however, this part will not be described in detail. The PV generation frequency support control strategy will pay more attention to the electromechanical transient model of VSC and its control system in the next part (Varma et al., 2015; Batzelis et al., 2017).

Additional requirements

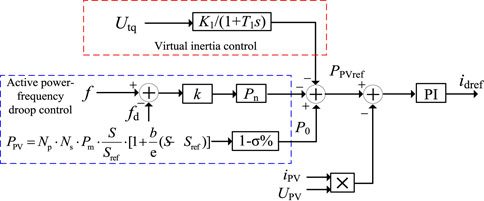
APFDC strategy

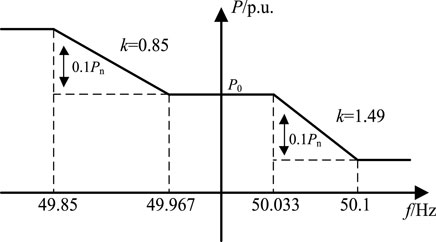
In this section, the active power-frequency droop characteristic curve of PV generation is presented in Figure 4 and the corresponding mathematical expression in (6).

$\mathit{P}={\mathit{P}}_{\text{0}}-\mathit{k}\cdot \left(\mathit{f}-{\mathit{f}}_{\mathrm{d}}\right)\cdot {\mathit{P}}_{\mathrm{n}}(6)$

where f_d is the system frequency response value of VSC, P_n is the maximum active power output of PV generation under the current illumination, k is the frequency adjustment coefficient in 1/Hz, and P₀ is the initial output active power of PV generation.

FIGURE 4

FIGURE 4. The droop characteristic curve of PV generation.

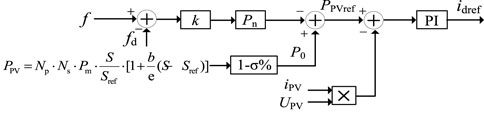
Figure 5 shows the modified control system of VSC, where PV generation is operated under limited power mode. The output active power of PV generation (P₀) when the grid frequency f is stable is P_PV*(1-σ%). When power disturbance occurs in the system, f is sent to the droop control loop and generates the output active power reference P_PVref (Firdaus and Mishra, 2019). The d-axis current reference value i_dref of VSC is generated by comparing the differences between P_PVref and P in active power controller.

FIGURE 5

FIGURE 5. The modified control strategy of VSC.

VIC strategy

As can be seen from Supplementary Figure SA2 of Supplementary Appendix SA, the function of the phase-locked loop (PLL) is to align the d-axis frame with the PCC voltage U_t. Supplementary Figure SA4 of Supplementary Appendix SA shows the control system of the PLL (Panda et al., 2019).

According to the control strategy of the PLL, the relationship of f and the PLL is shown in (7); (8) obtains the active power increment ΔP_PV of VIC, which makes VIC based on the dynamics of PLL achieved.

$\mathit{f}=\frac{{\mathit{U}}_{\mathrm{tq}}}{2\mathit{\pi }}\cdot \left({\mathit{k}}_{\mathrm{p}4}+{\displaystyle \int {\mathit{k}}_{\mathrm{i}4}\mathit{dt}}\right)(7)$

$\mathrm{\Delta }{\mathit{P}}_{\mathrm{PV}}=2{\mathit{H}}_{\mathrm{PV}}\frac{\mathit{df}}{\mathit{dt}}=2{\mathit{H}}_{\mathrm{PV}}\cdot \frac{{\mathit{U}}_{\mathrm{tq}}\cdot {\mathit{k}}_{\mathrm{i}4}}{2\mathit{\pi }}(8)$

where U_tq is the PCC voltage in the q-axis, k_p4 and k_i4 are the PLL parameters, and H_PV is the time constant of VIC.

Figure 6 presents the relationship of ΔP_PV, H_PV, and U_tq with the fixed integral coefficient of PLL. Figure 6 demonstrates that as the H_PV and U_tq increase, the PV will generate more active power.

FIGURE 6

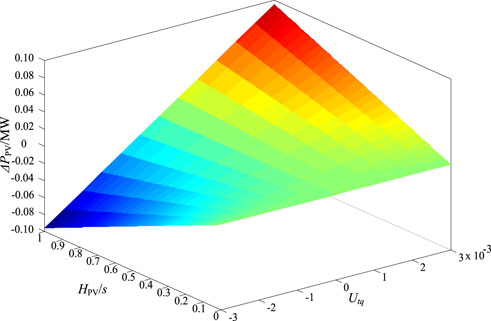
FIGURE 6. The relationship of ΔP_PV, H_PV, and U_tq with the fixed integral coefficient of PLL (k_i4 = 100)

In general, APFDC and VIC are combined to participate in frequency regulation; the control strategies are shown in Figure 7. When active power disturbances occur in the system, the grid frequency disturbance f is delivered to the VIC link (a low-pass filter is introduced to the inertia control link; K₁ and T₁ are the control gain and the filter time constant, respectively), and the APFDC link can generate the power reference value because of the detection by the PLL (Anderson and Mirheydar, 1990; Ma et al., 2021a).

FIGURE 7

FIGURE 7. The frequency support strategy for PV generation.

The inertia characteristics of photovoltaic generation

The unbalanced active power excitation–phase output response of the voltage source converter

Based on the relationship of VSC (Kakimoto et al., 2009; Fazeli et al., 2014), the inertia characteristics of PV generation with different control parameters will be further analyzed (Moradi-shahrbabak et al., 2018; Wu et al., 2018; Ma et al., 2021b). The linearization relationship of the unbalanced active power excitation–phase output response of the VSC is shown in Figure 8A (the influence of reactive power control on active power control is ignored). In Figure 8A, ΔP_in is the PV array output power disturbance, ΔP_PV is the VSC output power disturbance, Δθ_t is the PCC voltage phase disturbance, Δθ_pll is the PLL output phase disturbance, Δθ is the internal phase disturbance in VSC, and E₀ and U_t0 are the initial of the internal voltage of VSC and the initial of PCC voltage, respectively (Yuan et al., 2017; Ma et al., 2021c).

FIGURE 8

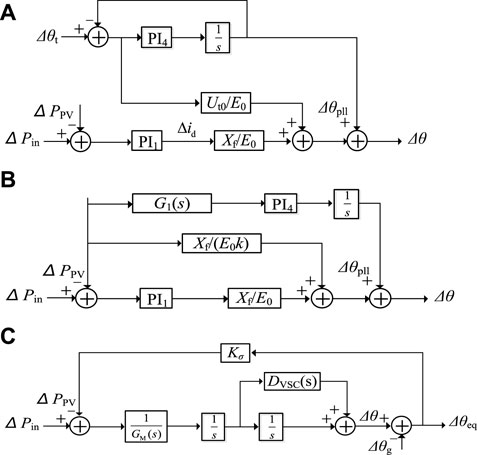
FIGURE 8. The unbalanced active power excitation–phase output response of VSC. (A) Block diagram of PV generation inner electric potential phase dynamic. (B) Block diagram of replaced PV generation voltage phase. (C) Block diagram of PV generation including equivalent inertia and damping coefficient.

The expression of PV generation output power and internal potential as well as the PCC voltage are presented in (9); replacing the Δθ_t in Figure 8A with the linearization result of (9). The relationship between the unbalanced active power excitation and the phase output response of VSC can be further simplified as in Figures 8B, C, where G₁(s) is expressed in (10).

$\{\begin{array}{l}{\mathit{P}}_{\mathrm{PV}}=\frac{\mathit{E}\cdot {\mathit{U}}_{\mathrm{t}}}{{\mathit{X}}_{\mathrm{f}}}\sin \left(\mathit{\theta }-{\mathit{\theta }}_{\mathrm{t}}\right)\\ {\mathit{Q}}_{\mathrm{PV}}=\frac{{\mathit{E}}^2}{{\mathit{X}}_{\mathrm{f}}}-\frac{\mathit{E}\cdot {\mathit{U}}_{\mathrm{t}}}{{\mathit{X}}_{\mathrm{f}}}\cos \left(\mathit{\theta }-{\mathit{\theta }}_{\mathrm{t}}\right)\end{array}(9)$

${\mathit{G}}_1\left(\mathit{s}\right)=\frac{{\mathit{X}}_{\mathrm{f}}}{\mathit{k}}\cdot \left({\mathit{k}}_{\mathrm{p}1}+\frac{{\mathit{k}}_{\mathrm{i}1}}{\mathit{s}}\right)+\frac{{\mathit{X}}_{\mathrm{f}}}{{\mathit{U}}_{\mathrm{t}0}\cdot \mathit{k}}(10)$

In Figure 8C, G_M(s) is the equivalent inertia of PV generation, and D_VSC(s) is the equivalent damping coefficient. G_M(s) and D_VSC(s) are related to system structure parameters and operating conditions; their expressions are presented in Supplementary Appendix SA. Furthermore, the unbalanced active power excitation–phase output response relationship indicates how power disturbance influences the movements of E by the inertia and damping coefficient (Ma et al., 2021d) and also how coefficients are determined by the operating points and control parameters of PV generation.

Considering the relationship between the rate of range of frequency (ROCOF) and U_tq, the linearization result is shown in (11). When the VIC strategy is adopted in PV generation, its unbalanced active power excitation–phase output response is shown in Figure 9A and further simplified in Figures 9B, C, D.

$\frac{\mathrm{d\Delta }\mathit{f}}{\mathrm{d}\mathit{t}}=\frac{\mathrm{\Delta }{\mathit{U}}_{\mathrm{tq}}\cdot {\mathit{k}}_{\mathrm{i}4}}{2\mathrm{\pi }}(11)$

FIGURE 9

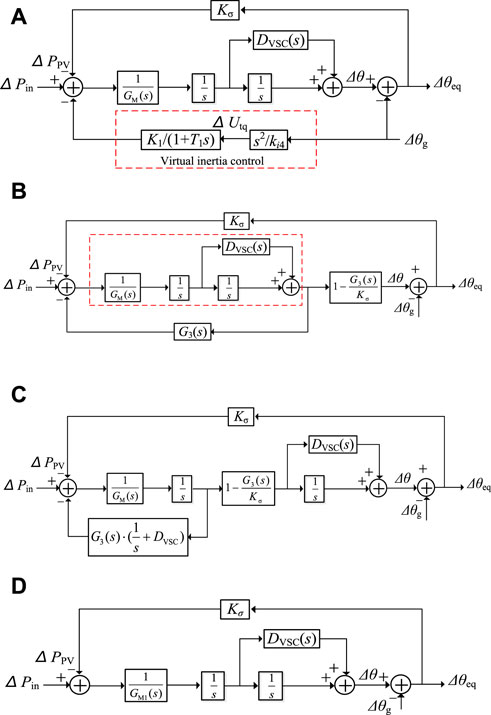
FIGURE 9. The unbalanced active power excitation–phase output response of VSC based on the virtual inertia control strategy. (A) Block diagram of PV generation inner electric potential phase dynamic. (B) Organized block diagram of PV generation inner electric potential phase dynamic. (C) Block diagram of input active power-output inner electric potential phase. (D) Block diagram of PV generation including equivalent inertia and damping coefficient.

In Figure 9D, its equivalent inertia G_M1(s) is shown in (12). Based on (12), Figure 10 shows the Bode diagrams of G_M1(s), which are obtained under different control gain coefficients K₁, different time constants T₁, and different PLL control bandwidths (Sangwongwanich et al., 2018). Figure 10shows that 1) the equivalent inertia of PV generation is frequency-dependent and controllable, different from the constant inertia of SG, and 2) with the increase in the control gain coefficient K₁ (1–30), decrease in the time constant T₁ (30–1), or decrease in the control bandwidth (9.99–3.65 Hz) of PLL, a larger inertia can be provided by PV generation in the dynamic process of grid frequency.

${\mathit{G}}_{\mathrm{M}1}\left(\mathit{s}\right)=\frac{{\mathit{G}}_{\mathrm{M}}\left(\mathit{s}\right)+{\mathit{G}}_3\left(\mathit{s}\right)\cdot \frac{1}{\mathit{s}}\cdot \left(\frac{1}{\mathit{s}}+{\mathit{D}}_{\mathrm{VSC}}\right)}{1-\frac{{\mathit{G}}_3\left(\mathit{s}\right)}{{\mathit{K}}_{\mathit{\sigma }}}}(12)$

FIGURE 10

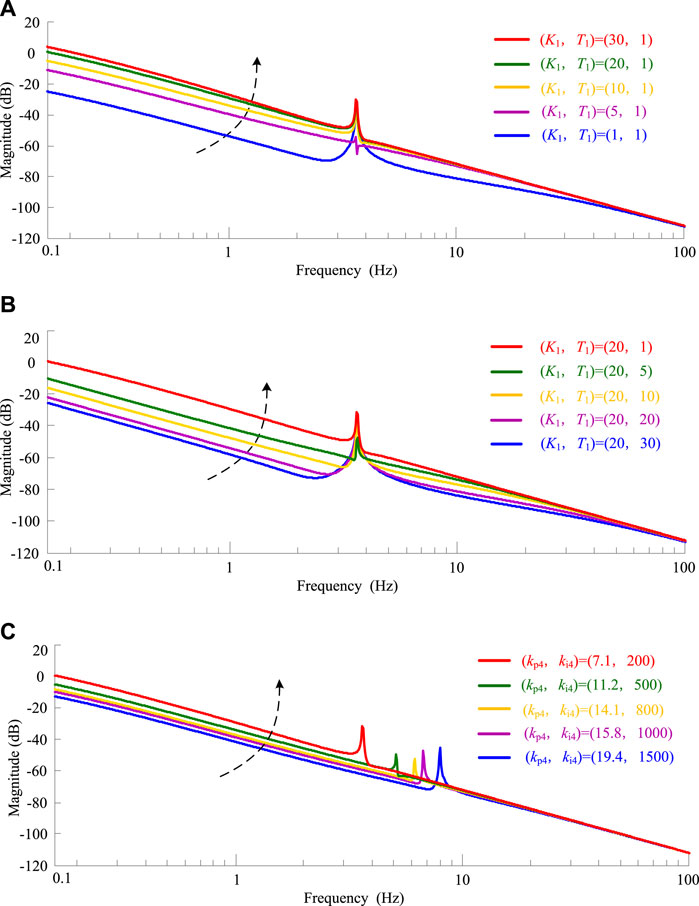
FIGURE 10. The inertia characteristics of PV generation. (A) Control gain coefficient variation. (B) Time constant variation. (C) PLL control bandwidths variation.

Dynamic response analysis of grid frequency

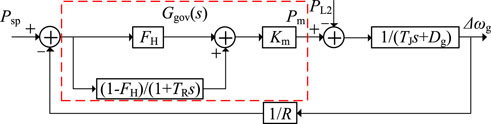
Figure 11 shows the synchronous frequency regulation (SFR) model of SG (Linan et al., 2018). In Figure 11, T_J is the inertia time constant of SG, D_g is the equivalent damping coefficient of SG, R is the adjustment coefficient of speed regulator, T_R is the prime mover reheat time constant, F_H is the fraction of total power generated by the HP turbine, K_m is the mechanical power gain factor, P_sp is the incremental power set point, P_L2 is the load power, and Δω_g is the inner frequency of the internal voltage of SG.

FIGURE 11

FIGURE 11. The synchronous frequency regulation (SFR) model of synchronous generator.

Based on the unbalanced power excitation–phase output relation in Figure 9 and the SFR model of SG in Figure 11, it can be observed that

$\mathrm{\Delta }{\mathit{P}}_{\mathrm{in}}-\mathrm{\Delta }{\mathit{P}}_{\mathrm{L}1}=\mathit{s}\cdot \mathrm{\Delta }{\mathit{\omega }}_{\mathrm{PV}}\cdot {\mathit{G}}_{\mathrm{M}1}\left(\mathit{s}\right)(13)$

where Δω_PV is the inner frequency of PV generation of internal voltage.

${\mathit{G}}_{\mathrm{gov}}\left(\mathit{s}\right)={\mathit{K}}_{\mathrm{m}}\cdot \left({\mathit{F}}_{\mathrm{H}}+\frac{1-{\mathit{F}}_{\mathrm{H}}}{1+{\mathit{T}}_{\mathrm{R}}\mathit{s}}\right)(14)$

$\left[\left(\mathrm{\Delta }{\mathit{P}}_{\mathrm{sp}}-\frac{1}{\mathit{R}}\cdot \mathrm{\Delta }{\mathit{\omega }}_{\mathrm{g}}\right)\cdot {\mathit{G}}_{\mathrm{gov}}\left(\mathit{s}\right)-\mathrm{\Delta }{\mathit{P}}_{\mathrm{L}2}\right]\cdot \frac{1}{{\mathit{T}}_{\mathrm{J}}\mathit{s}+{\mathit{D}}_{\mathrm{g}}}=\mathrm{\Delta }{\mathit{\omega }}_{\mathrm{g}}(15)$

If Δω_g = Δω_PV, by combining (13) and (15), Δω_g can be expressed as follows:

$\{\begin{array}{l}-\mathrm{\Delta }{\mathit{P}}_{\mathrm{L}}=\left[\frac{1}{\mathit{R}}\cdot {\mathit{G}}_{\mathrm{gov}}\left(\mathit{s}\right)+\left({\mathit{T}}_{\mathrm{J}}\mathit{s}+{\mathit{D}}_{\mathrm{g}}\right)+\mathit{s}\cdot {\mathit{G}}_{\mathrm{M}1}\left(\mathit{s}\right)\right]\cdot \mathrm{\Delta }{\mathit{\omega }}_{\mathrm{g}}\\ \mathrm{\Delta }{\mathit{P}}_{\mathrm{L}}=\mathrm{\Delta }{\mathit{P}}_{\mathrm{L}1}+\mathrm{\Delta }{\mathit{P}}_{\mathrm{L}2}\end{array}(16)$

In this method, we give a considerable amount of attention to ΔP_L in the form of a step function, ΔP_L = ΔP_s/s. Thus,

$\mathrm{\Delta }{\mathit{\omega }}_{\mathrm{g}}=-\frac{\frac{\mathrm{\Delta }{\mathit{P}}_{\mathrm{s}}}{\mathit{s}}}{\left[\frac{1}{\mathit{R}}\cdot {\mathit{G}}_{\mathrm{gov}}\left(\mathit{s}\right)+\left({\mathit{T}}_{\mathrm{J}}\mathit{s}+{\mathit{D}}_{\mathrm{g}}\right)+\mathit{s}\cdot {\mathit{G}}_{\mathrm{M}1}\left(\mathit{s}\right)\right]}(17)$

According to the final value theorem, we can obtain the initial ROCOF and steady-state frequency error of the system as follows:

${\frac{\mathrm{d\Delta }{\mathit{\omega }}_{\mathrm{g}}}{\mathrm{d}\mathit{t}}|}_{t\to 0}=\underset{s\to \infty }{{\displaystyle \lim }}\left({\mathit{s}}^2\cdot \mathrm{\Delta }{\mathit{\omega }}_{\mathrm{g}}\right)=-\frac{\mathrm{\Delta }{\mathit{P}}_{\mathrm{s}}}{{\mathit{T}}_{\mathrm{J}}}(18)$

${\mathrm{\Delta }{\mathit{\omega }}_{\mathrm{g}}|}_{\mathit{t}\to \mathrm{\infty }}=\underset{\mathit{s}\to \text{0}}{{\displaystyle \lim }}\left(\mathit{s}\cdot \mathrm{\Delta }{\mathit{\omega }}_{\mathrm{g}}\right)=-\frac{\mathit{R}\cdot \mathrm{\Delta }{\mathit{P}}_{\mathrm{s}}}{{\mathit{K}}_{\mathrm{m}}+\mathit{R}\cdot {\mathit{D}}_{\mathrm{g}}}(19)$

It can be seen from (17), (18), and (19) that PV generation with VIC does not affect the initial rate of change and steady-state deviation of the grid frequency (Yazdani et al., 2011; Sangwongwanich et al., 2018). However, during the dynamic of grid frequency means the dynamic characteristics of the grid frequency, PV generation plays a vital role, depending on its inertia. It can effectively restrain the drop of the lowest frequency point (or the rise of the highest frequency point) and the ROCOF under different control parameters.

The dynamic power distribution mechanism of photovoltaic generation units with the inertia control strategy

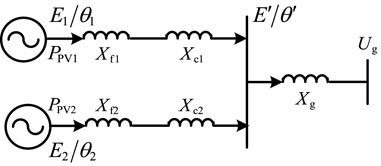
When PV generation units adopt the VIC, the dynamic power distribution mechanism of PV units is further discussed based on the unbalanced active power excitation–phase output response of VSC (Hydro Quebec TransÉnergie, 2009; Khazaei et al., 2020). The structure of two paralleled PV units is shown in Figure 12. In Figure 12, E₁ and E₂ are the magnitudes of the internal voltage vector; θ₁ and θ₂ are the phases of the internal voltage vector; E′ and θ’ are the magnitude and the phase of the PCC voltage vector, respectively; X_f1 and X_f2 are the output filter reactance; X_c1 and X_c2 are the reactance of each PV generation to the interconnection point; and X_g is the transmission line reactance.

FIGURE 12

FIGURE 12. The structure of two paralleled PV generation units.

The output power of each PV generation is shown in (20), linearizing (20) (neglect the effect of voltage magnitude disturbance), and the phase θ’ of the PCC voltage vector can be obtained using (21).

$\{\begin{array}{l}{\mathit{P}}_{\mathrm{PV}1}=\frac{{\mathit{E}}_1\cdot \mathit{E}\prime }{\mathit{X}}\sin \left({\mathit{\theta }}_1-\mathit{\theta }\prime \right)\\ {\mathit{P}}_{\mathrm{PV}2}=\frac{{\mathit{E}}_2\cdot \mathit{E}\prime }{\mathit{X}}\sin \left({\mathit{\theta }}_2-\mathit{\theta }\prime \right)\end{array}(20)$

$\{\begin{array}{l}\mathrm{\Delta }\mathit{\theta }\prime =\mathrm{\Delta }{\mathit{\theta }}_1-\frac{\mathit{X}}{{\mathit{E}}_1\cdot \mathit{E}\prime }\cdot \mathrm{\Delta }{\mathit{P}}_{\mathrm{PV}1}\\ \mathrm{\Delta }\mathit{\theta }\prime =\mathrm{\Delta }{\mathit{\theta }}_2-\frac{\mathit{X}}{{\mathit{E}}_2\cdot \mathit{E}\prime }\cdot \mathrm{\Delta }{\mathit{P}}_{\mathrm{PV}2}\end{array}(21)$

where X is the total reactance.

Combining (21) and Figure 9D, the unbalanced active power excitation–phase output response of two paralleled PV generation units with the inertia control strategy is shown in Figure 13A and the simplified relationship in Figure 13B, where the derivation and expression of G₁₁(s) and G₁₂(s) are given in Supplementary Appendix SB; D₁₁(s) and D₁₂(s) are the power distribution coefficients.

FIGURE 13

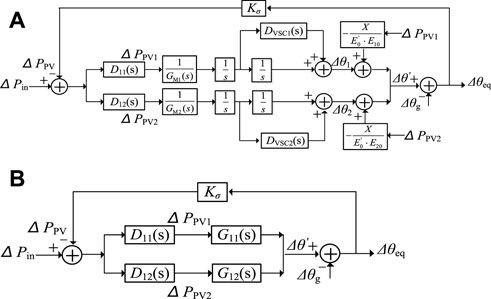
FIGURE 13. The unbalanced active power excitation–phase output response of two paralleled PV generation units based on the virtual inertia control strategy. (A) Block diagram of two parallel PV generation units. (B) Simplified block diagram of two parallel PV generation units.

According to Figure 13B, the phase θ’ of the PCC voltage vector is also shown in (22), and the dynamic power distribution coefficients D₁₁(s) and D₁₂(s) are shown in (23) and (24).

$\{\begin{array}{l}\mathrm{\Delta }\mathit{\theta }\prime ={\mathit{D}}_{11}\left(\mathit{s}\right)\cdot {\mathit{G}}_{11}\left(\mathit{s}\right)\cdot \mathrm{\Delta }{\mathit{P}}_{\mathrm{PV}}\\ \mathrm{\Delta }\mathit{\theta }\prime ={\mathit{D}}_{12}\left(\mathit{s}\right)\cdot {\mathit{G}}_{12}\left(\mathit{s}\right)\cdot \mathrm{\Delta }{\mathit{P}}_{\mathrm{PV}}\end{array}(22)$

$\{\begin{array}{l}{\mathit{D}}_{\mathrm{11}}\left(\mathit{s}\right)=\frac{\frac{1}{{\mathit{G}}_{11}\left(\mathit{s}\right)}}{\frac{1}{{\mathit{G}}_{11}\left(\mathit{s}\right)}+\frac{1}{{\mathit{G}}_{12}\left(\mathit{s}\right)}}\\ {\mathit{D}}_{\mathrm{12}}\left(\mathit{s}\right)=\frac{\frac{1}{{\mathit{G}}_{12}\left(\mathit{s}\right)}}{\frac{1}{{\mathit{G}}_{11}\left(\mathit{s}\right)}+\frac{1}{{\mathit{G}}_{12}\left(\mathit{s}\right)}}\end{array}(23)$

$\{\begin{array}{l}{\mathit{D}}_{\mathrm{11}}\left(\mathit{s}\right)=\frac{{\mathit{G}}_{\mathrm{M}1}\left(\mathit{s}\right)}{{\mathit{G}}_{\mathrm{M}1}\left(\mathit{s}\right)+{\mathit{G}}_{\mathrm{M2}}\left(\mathit{s}\right)}\\ {\mathit{D}}_{\mathrm{12}}\left(\mathit{s}\right)=\frac{{\mathit{G}}_{\mathrm{M2}}\left(\mathit{s}\right)}{{\mathit{G}}_{\mathrm{M}1}\left(\mathit{s}\right)+{\mathit{G}}_{\mathrm{M2}}\left(\mathit{s}\right)}\end{array}(24)$

From (24), it can be seen that the dynamic power distribution coefficients depend on the inertia characteristics of PV generation units. Therefore, the dynamic power distribution mechanisms are similar to those of conventional synchronous generators (ENTSO -E, 2013), which is helpful in understanding the dynamic process of PV generation units with inertia control strategy.

Figure 14 presents the Bode diagrams of D₁₁(s) and D₁₂(s) with different control parameters. We can see from Figure 14 that with the increase in control gain, decrease in the time constant of VIC, and decrease in the PLL control bandwidth, the power distribution coefficient of PV generation in the low-frequency band will also increase, indicating that PV generation provided a more active power during active power disturbance.

FIGURE 14

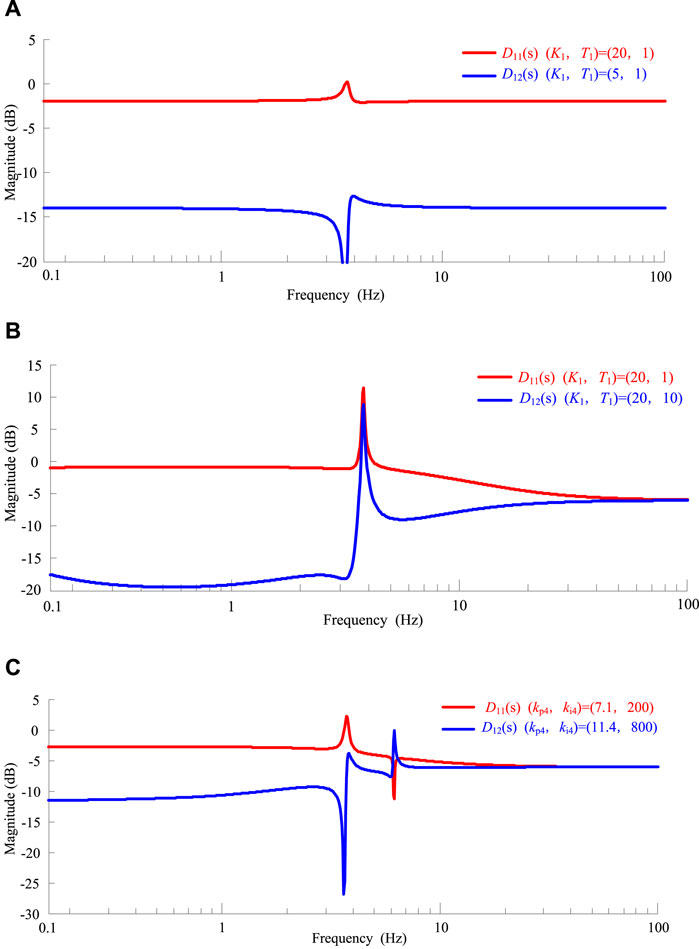
FIGURE 14. The Bode diagrams of D₁₁(s) and D₁₂(s) with different control parameters. (A) Control gain coefficient variation. (B) Time constant variation. (C) PLL control bandwidths variation.

Simulation validations

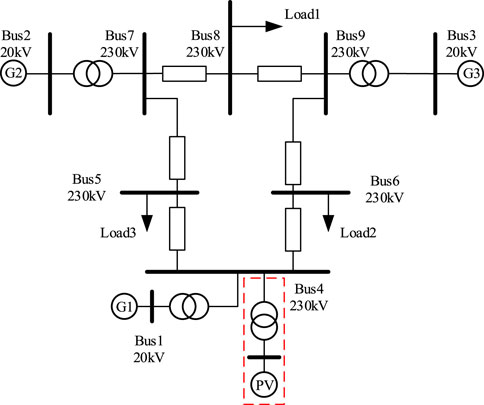
A simulation model was built in PSCAD/EMTDC to verify the above theory analysis, as shown in Figure 15. Table 1 presents the main parameters of the single-stage PV system; the PV power plant is represented by a single equivalent model in the following simulations.

FIGURE 15

FIGURE 15. Simulation model systems.

TABLE 1

TABLE 1. Main parameters of photovoltaic (PV) generation.

Photovoltaic generation responses to grid frequency disturbance simulation results

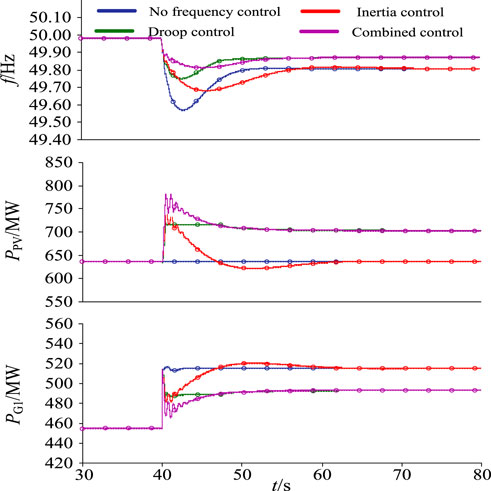
The background of the simulation is as follows: output active power of PV generation P_PV = 600 MW (σ% = 20%), system load P_L = 2000MW, and a load increased by 200-MW disturbance occurs at t = 40s. Figure 16 reflects the output power of synchronous unit 1 responses (P_G1), the output power of PV generation responses (P_PV) under different controls, and the grid frequency responses (f) during the disturbance.

FIGURE 16

FIGURE 16. System operation curve with different control strategies.

The simulation results in Figure 16 indicated the following: 1) If PV units do not participate in the system frequency regulation, the system frequency will drop below 49.6 Hz; the ROCOF of the system is large. 2) If VIC is activated, the PV units will increase the active power by 100 MW immediately to contain the drop of frequency. However, when the system frequency tends to be stable, the PV output active power has the same value as in the first case, which means that VIC does not affect the steady-state frequency after the disturbance, only the transient-state process of system frequency. 3) If the APFDC is activated, the active power of the PV array is controlled by the VSC according to the active power-frequency droop curve shown in Figure 4. As a result, an 80-MW extra active power is added to inhibit the drop of frequency. After a dynamic process of about 20 s, the steady-state frequency of the system is about 49.85 Hz, which is higher than those in the former cases. 4) If both droop control and VIC are activated, PV generation will obviously improve the dynamic process characteristic by adding more active power. It not only increases the equivalent inertia of the system, which can constrain the ROCOF, but also reduces the frequency deviation.

The simulation results of photovoltaic generation with inertia control under different control parameters

The background of the simulation is as follows: output active power of PV generation P_PV = 600 MW (σ% = 20%), system load P_L = 2000 MW, and a load increased by 200-MW disturbance occurs at t = 40 s. When the low-pass filter controlled by the virtual inertia is constant (T₁ = 1 s), the control gain of the low-pass filter is increased from 5 to 20. Figure 17A indicates that with the increase in control gain, the virtual inertia of PV generation gradually increases, the ROCOF of the system during the active power disturbance decreases, and the maximum frequency deviation decreases.

FIGURE 17

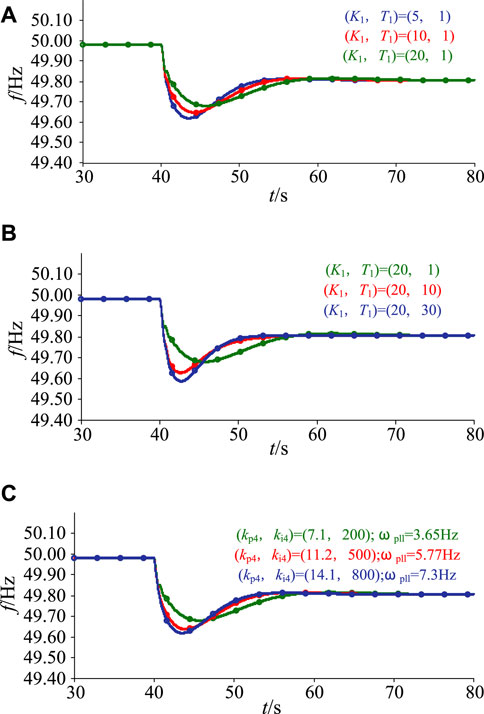
FIGURE 17. System operation curve with various control parameters. (A) control gain coefficient variation. (B) Time constant variation. (C) PLL control bandwidths variation.

When the control gain of the low-pass filter controlled by the virtual inertia is constant (K₁ = 20), T₁ is increased from 1 to 30. Figure 17B indicates that with the increase in time constant, the virtual inertia of PV generation gradually decreases, the ROCOF of the system during the active power disturbance increases, and the maximum frequency deviation increases.

Figure 17C shows the grid frequency responses at different PLL control parameters of the VSC. According to Figure 17C, with the increase in the PLL bandwidth (ω_PLL = 3.65–7.3 Hz), the equivalent inertia of PV generation decreases, the ROCOF of the system during the active power disturbance increases, and the maximum frequency deviation increases.

Taken together, with the increase in control gain, more output active power can be produced in the PV generation, the ROCOF becomes smaller, and the maximum frequency deviation decreases.

Simulation result of photovoltaic power generation with inertia control under different control parameters

The PV power station consist of two PV generation units, as shown in Figure 18, the rated active output power of each PV generation unit is 400 MW (=10%), the load of the system is 2000 MW, a disturbance with 200 MW load increase occurred at t = 40 s. Figure 18 shows the active power of PV array responses (P_in1 and P_in2) and the output power of PV generation unit responses (P_PV1 and P_PV2) under different control parameters.

FIGURE 18

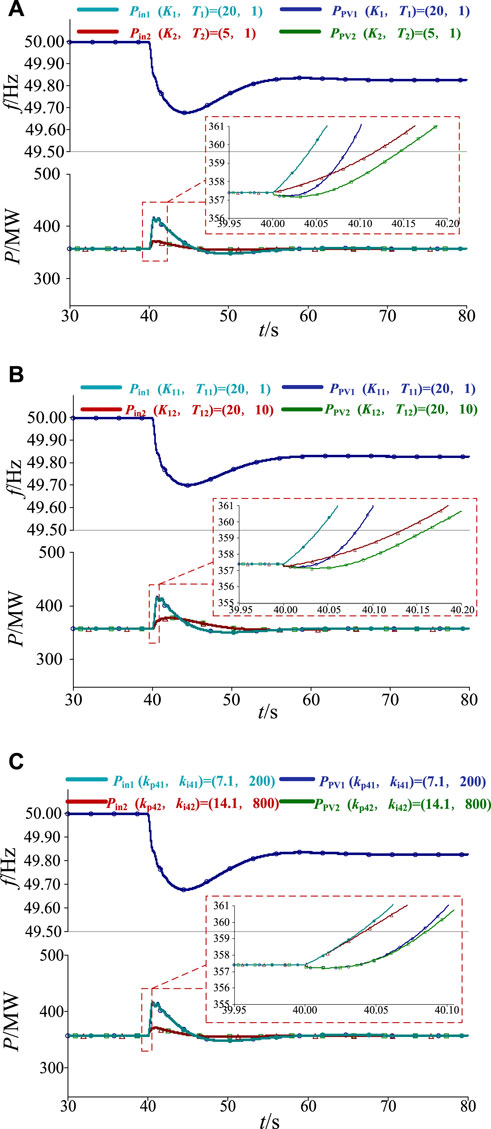
FIGURE 18. The system responses for PV generation units under different control parameters. (A) control gain coefficient variation. (B) Time constant variation. (C) PLL control bandwidths variation.

The difference between the input and output active powers of the PV array represents the unbalanced power borne by the PV generation unit. Figure 18 shows that when the control gain K₁ of PV generation unit 1 is greater than K₂ of PV generation unit 2, the time constant T₁ is smaller than the time constant T₂, or the control bandwidth ω_PLL1 of the PLL is smaller than ω_PLL2, the equivalent inertia G_M1(s) of PV generation unit 1 is greater than G_M2(s) of PV generation unit 2, the corresponding unbalanced power distribution coefficient D₁₁(s) is greater than D₁₂(s), and the unbalanced power borne by PV generation unit 1 is greater than the unbalanced power borne by PV generation unit 2 during the dynamic of grid frequency.

The simulation results of grid frequency under the variable load or irradiance

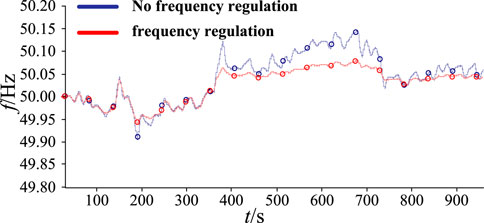
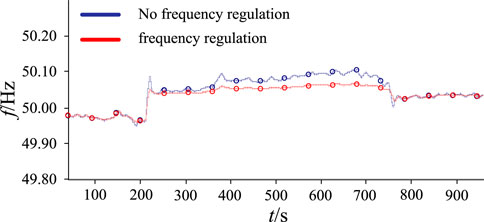
In the actual grid operation scenarios, the proposed PV generation frequency regulation strategy has proven effective. The simulation was performed under the condition of variable irradiance and load. Figure 19 presents the grid frequency responses under the variable load, and Figure 20 shows the normal distribution of grid frequency. Figure 21 presents the grid frequency responses under variable irradiance, and Figure 22 shows the normal distribution of grid frequency. We can see from Figures 19–22, we can conclude that when PV generation participates the frequency regulation, under this condition, the frequency fluctuation is inhibited as well as enhances the grid frequency stability based on the pre-set APFDC strategy and VIC strategy.

FIGURE 19

FIGURE 19. Grid frequency under the variable load.

FIGURE 20

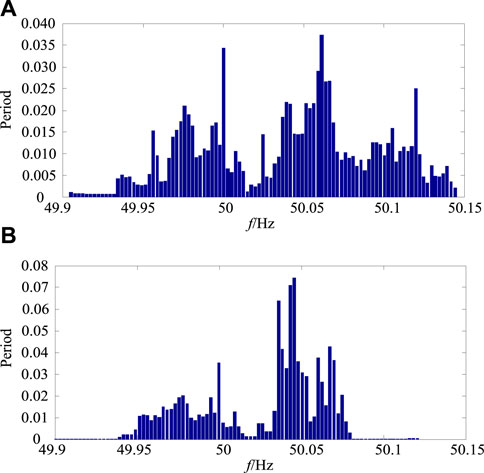
FIGURE 20. Normal distribution of grid frequency: (A) no frequency regulation, (B) frequency regulation.

FIGURE 21

FIGURE 21. Grid frequency under variable illumination.

FIGURE 22

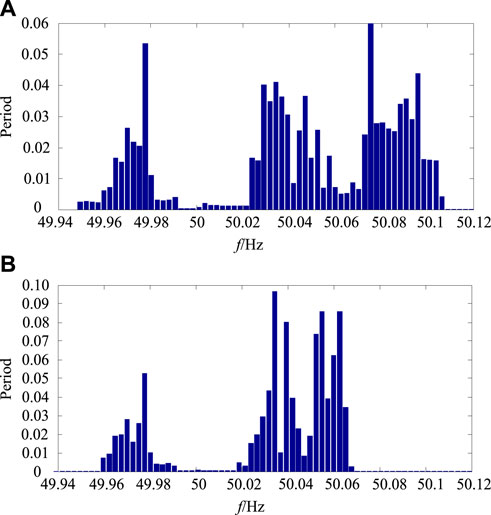
FIGURE 22. Normal distribution of grid frequency: (A) no frequency regulation, (B) frequency regulation.

Conclusion

In this study, the single-stage PV generation frequency regulation strategies are proposed, including VIC and droop control, based on the electromechanical transient model. The method proposed in this study is to realize that the control strategies modify the VSC control system. The effect of the control parameters on the inertia characteristics is analyzed. Furthermore, the dynamic power distribution mechanism of PV generation units with the inertia control strategy is revealed, and the following conclusions were drawn:

1) The PV generation can decrease or increase the output active power controlled by VSC based on the PV generation frequency regulation strategies, thus improving the frequency stability of the system. PV generation can increase (or decrease) the output active power to respond to the changes in the system frequency when active power disturbances occur in the system according to the pre-set droop curve.

2) Different from the synchronous unit (SG), the inertia provided by PV generation with VIC is controllable and depends on the grid frequency. With the increase in the gain, decrease in the time constant of the VIC, and decrease in the control bandwidth of PLL, more inertia will be provided by PV generation.

3) The dynamic power distribution mechanisms of PV generation units with the VIC strategy are similar to those of conventional synchronous generators, which depend on the inertia characteristics of PV generation units. With the increase in the gain, decrease in the time constant of the VIC, and decrease in the control bandwidth of PLL, the active power distribution coefficient of PV generation in the low-frequency band will also increase, and thus, more active power can be provided to constrain the changes in the grid frequency.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

XF: research paper writing, research paper structure design, simulation model design. XW: research paper writing, literature review. QJ: simulation model design. HW: research paper writing.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2022.964485/full#supplementary-material

References

Anderson, P., M., and Mirheydar, M. (1990). A low-order system frequency response model. IEEE Trans. Power Syst. 5 (3), 720–729. doi:10.1109/59.65898

CrossRef Full Text | Google Scholar

Batzelis, E. I., Kampitsis, G. E., Papathanassiou, S. A., and Member, S. (2017). Power reserves control for PV systems with real-time MPP estimation via curve fitting. IEEE Trans. Sustain. Energy 8 (3), 1269–1280. doi:10.1109/tste.2017.2674693

CrossRef Full Text | Google Scholar

Datta, M., Member, S., Senjyu, T., Member, S., and Yona, A. (2011). A frequency-control approach by photovoltaic generator in a PV – diesel hybrid power system. IEEE Trans. Energy Convers. 26 (2), 559–571. doi:10.1109/tec.2010.2089688

CrossRef Full Text | Google Scholar

ENTSO-E (2013). ENTSO-E: Network code for requirements for grid connection applicable to all generators (nc rfg). Brussels: Entsoe.

Google Scholar

Fang, J., Li, H., Tang, Y., and Blaabjerg, F. (2019). On the inertia of future more-electronics power systems. IEEE J. Emerg. Sel. Top. Power Electron. 7 (4), 2130–2146. doi:10.1109/jestpe.2018.2877766

CrossRef Full Text | Google Scholar

Fazeli, M., Ekanayake, J. B., Member, S., and Holland, P. M. (2014). Exploiting PV inverters to support local voltage. A Small-Signal Model 29 (2), 453–462. doi:10.1109/TEC.2014.2300012

CrossRef Full Text | Google Scholar

Firdaus, A., and Mishra, S. (2019). Auxiliary signal-assisted droop-based secondary frequency control of inverter- based PV microgrids for improvement in power sharing and system stability. IET Renew. Power Gener. 13, 2328. doi:10.1049/iet-rpg.2018.6171

CrossRef Full Text | Google Scholar

Huanhai, X., Yun, L., Zhen, W., Gan, D., and Yang, T. (2013). A new frequency regulation strategy for photovoltaic systems without energy storage. IEEE Trans. Sustain. Energy 4 (4), 985–993. doi:10.1109/tste.2013.2261567

CrossRef Full Text | Google Scholar

Hydro Quebec TransÉnergie (2009). Transmission provider technical requirements for the connection of power plants to the hydro-Québec transmission system. Canada: Hydro Quebec TransÉnergie, Montréal, QC.

Google Scholar

Jesus, C., H., Pedro, G., B., and Francisco, S. (2017). Enhanced utility-scale photovoltaic units with frequency support functions and dynamic grid support for transmission systems. IET Renew. Power Gener. 11 (3), 361–372. doi:10.1049/iet-rpg.2016.0714

CrossRef Full Text | Google Scholar

Jibji-bukar, F., and Anaya-lara, O. (2019). Frequency support from photovoltaic power plants using offline maximum power point tracking and variable droop control. IET Renew. Power Gener. 13, 2278. doi:10.1049/iet-rpg.2019.0211

CrossRef Full Text | Google Scholar

Kakimoto, N., Takayama, S., Satoh, H., and Nakamura, K. (2009). Power modulation of photovoltaic generator for frequency control of power system. IEEE Trans. Energy Convers. 24 (4), 943–949. doi:10.1109/tec.2009.2026616

CrossRef Full Text | Google Scholar

Khazaei, J., Tu, Z., Member, S., Liu, W., and Member, S. (2020). Small-Signal modeling and analysis of virtual inertia-based PV systems. IEEE Trans. Energy Convers. 35 (2), 1129–1138. doi:10.1109/TEC.2020.2973102

CrossRef Full Text | Google Scholar

Lei, Z., Lingzhi, Z., Ning, C., Zhao, D., and Qu, L. (2015). Review on generic model for renewable energy generation. Automation Electr. Power Syst. 39 (24), 129–138. doi:10.7500/AEPS20150629010

CrossRef Full Text | Google Scholar

Linan, Q., Luming, G., Lingzhi, Z., Shuanbao, N., Shuang, Z., and Sijia, B. (2018). Transient modeling of photovoltaic power plant and its test validation. Automation Electr. Power Syst. 42 (10), 170–175.

Google Scholar

Liu, Y., Xin, H., Wang, Z., and Yang, T. (2014). Power control strategy for photovoltaic system based on the Newton quadratic interpolation. IET Renew. Power Gener. 8, 611–620. doi:10.1049/iet-rpg.2013.0067

CrossRef Full Text | Google Scholar

Lyu, X., Xu, Z., Zhao, J., and Wong, K. P. (2018). Advanced frequency support strategy of photovoltaic system considering changing working conditions. IET Gener. Transm. &amp. Distrib. 12, 363–370. doi:10.1049/iet-gtd.2017.0700

CrossRef Full Text | Google Scholar

Ma, L., Wang, X., Wang, X., Wang, L., Shi, L., Huang, M., et al. (2021a). TCDA: Truthful combinatorial double auctions for mobile edge computing in industrial internet of things. IEEE Trans. Mob. Comput., 1. doi:10.1109/TMC.2021.3064314

CrossRef Full Text | Google Scholar

Ma, L., Huang, M., Yang, S., Wang, R., and Wang, X. (2021c). An adaptive localized decision variable analysis approach to large-scale multiobjective and many-objective optimization. IEEE Trans. Cybern. PP(99), 1–13. doi:10.1109/TCYB.2020.3041212

CrossRef Full Text | Google Scholar

Ma, Lianbo., Cheng, Shi, and Shi, Yuhui (2021b). Enhancing learning efficiency of brain storm optimization via orthogonal learning design. IEEE Trans. Syst. Man. Cybern. Syst. 51 (11), 6723–6742, Nov. doi:10.1109/tsmc.2020.2963943

CrossRef Full Text | Google Scholar

Ma, Lianbo, Li, Nan, Guo, Yinan, Huang, Min, Yang, Shengxiang, Wang, Xingwei, et al. (2021d). Learning to optimize: Reference vector reinforcement learning adaption to constrained many-objective optimization of industrial copper burdening system. IEEE Trans. Cybern., 1–14. doi:10.1109/TCYB.2021.3086501

CrossRef Full Text | Google Scholar

Mohammad, D., Mokhlis, H., and Saad, M. (2017). Inertia response and frequency control techniques for renewable energy sources: A review. Renew. Sustain. Energy Rev. 69, 144–155. doi:10.1016/j.rser.2016.11.170

CrossRef Full Text | Google Scholar

Moradi-shahrbabak, Z., Member, S., and Tabesh, A. (2018). Effects of front-end converter and DC-link of a utility-scale PV energy system on dynamic stability of a power system. IEEE Trans. Ind. Electron. 65 (1), 403–411. doi:10.1109/tie.2017.2721902

CrossRef Full Text | Google Scholar

Nanou, S. I., and Papathanassiou, S. A. (2014). Modeling of a PV system with grid code compatibility. Electr. Power Syst. Res. 116, 301–310. doi:10.1016/j.epsr.2014.06.021

CrossRef Full Text | Google Scholar

Panda, R. K., Mohapatra, A., and Srivastava, S. C. (2019). Enhancing inertia of solar photovoltaic-based microgrid through notch filter-based PLL in SRF control. IET Renew. Power Gener. 14, 379. doi:10.1049/iet-gtd.2018.7058

CrossRef Full Text | Google Scholar

Pappu, V., Chowdhury, B., and Bhatt, R. (2010). “Implementing frequency regulation capability in a solar photovoltaic power plant,” in Proceeding of North American Power Symposium Conference, Arlington, TX, USA, 26-28 September 2010 (NAPS), 1–6.

CrossRef Full Text | Google Scholar

Pedro, G., B., Jesus, C., H., and Francisco, J., R. (2016). Stability assessment for transmission systems with large utility-scale photovoltaic units. IET Renew. Power Gener. 10 (5), 584–597. doi:10.1049/iet-rpg.2015.0331

CrossRef Full Text | Google Scholar

Sangwongwanich, A., Yang, Y., Blaabjerg, F., and Sera, D. (2017). Delta power control strategy for MultistringGrid-connected PV inverters. IEEE Trans. Industry Appl. 53 (4), 3862–3870. doi:10.1109/TIA.2017.2681044[

CrossRef Full Text | Google Scholar

Sangwongwanich, A., Member, S., and Yang, Y. (2018). Benchmarking of constant power generation strategies for single-phase grid-connected photovoltaic systems. IEEE Trans. Industry Appl. 54 (1), 447–457. doi:10.1109/TIA.2017.2740380

CrossRef Full Text | Google Scholar

SPC (2016). Guide for modeling photovoltaic power system: GB/T 32826-2016. Beijing: Standards Press of China.

Google Scholar

Varma, R. K., Member, S., Rahman, S. A., and Vanderheide, T. (2015). New control of PV solar farm as STATCOM (PV-STATCOM) for increasing grid power transmission limits during night and day. IEEE Trans. Power Deliv. 30 (2), 755–763. doi:10.1109/tpwrd.2014.2375216

CrossRef Full Text | Google Scholar

WECC Renewable Energy Modeling Task Force (2012). Generic solar photovoltaic system dynamic simulation model specification.

Google Scholar

Wu, Z., Gao, W., Gao, T., Yan, W., Zhang, H., Yan, S., et al. (2018). State-of-the-art review on frequency response of wind power plants in power systems. J. Mod. Power Syst. Clean. Energy 6 (1), 1–16. doi:10.1007/s40565-017-0315-y

CrossRef Full Text | Google Scholar

Xiaoqiang, S., Song, C., Xin, L., Naixin, D., Yunlong, C., and Hua, L. (2018). Test method for frequency characteristics of Northwest sending-end power grid. Power Syst. Technol. 42 (2), 148–153.

Google Scholar

Xiaoqiang, S., Min, G., Xin, L., Song, C., Naixin, D., Yunlong, C., et al. (2017). Actual measurement and analysis of fast frequency response capability of PV-inverters in Northwest power grid. Power Syst. Technol. 41 (9), 2792–2798.

Google Scholar

Yazdani, A., Di Fazio, A. R., Ghoddami, H., Russo, M., and Kazerani, M. (2011). Modeling guidelines and a benchmark for power system simulation studies of three-phase single-stage photovoltaic systems. IEEE Trans. Power Deliv. 26 (2), 1247–1264. doi:10.1109/TPWRD.2010.2084599

CrossRef Full Text | Google Scholar

Yu, G., Wang, Y., Li, Z., Shi, X., Song, P., Yang, W., et al. (2018). Photovoltaic virtual synchronous generator engineering application effects analysis and optimization. Power Syst. Technol. 42 (9), 1–8.

Google Scholar

Yuan, H., Xiaoming, Y., and Jiabing, H. (2017). Modeling of grid-connected VSCs for power system small-signal stability analysis in DC-link voltage control timescale. IEEE Trans. Power Syst. 32 (5), 3981–3991. doi:10.1109/tpwrs.2017.2653939

CrossRef Full Text | Google Scholar

Yun, L., Ying, K., Huanhai, X., Lu, Z., and Gan, D. (2012). A control strategy for photovoltaic generation system based on quadratic interpolation method. Automation Electr. Power Syst. 36 (21), 29–35. doi:10.3969/j.issn.1000-1026.2012.21.006

CrossRef Full Text | Google Scholar

Zarina, P., P., Mishra, S., and Sekhar, P., C. (2014). Exploring frequency control capability of a PV system in a hybrid PV-rotating machine-without storage system. Int. J. Electr. Power & Energy Syst. 60, 258–267. doi:10.1016/j.ijepes.2014.02.033

CrossRef Full Text | Google Scholar