Design optimization of district heating systems: A review

District heating systems offer the possibility of lowering emissions and support the goal of reaching a carbon-neutral energy system by integrating renewable heat sources. Therefore, this work provided a systematic literature review to identify potential research gaps and show the literature distribution over the relevant topics. The focus is on the design optimization with (non-)linear programming of district heating systems in the context of decarbonization. Furthermore, crucial energy balance equations were extracted from the literature for a potential optimization problem. The systematic literature review limited its search to two databases, 10 years timespan, a quality measure, and uses keywords regarding topic and method. Categories were derived based on the subject and literature to cluster the found publications and identify potential research gaps. The results showed potential research gaps in the depiction of different stakeholder decisions, reduction of computational efforts, and their resulting uncertainties. Additionally, they identified gaps in the integration of low-grade heat sources, thermal storage facilities, and energy converters, especially geothermal energy, large-scale heat pumps, and seasonal storages.

Introduction

Since the millennium, global climate change has shown devastating outcomes due to natural disasters. The integration of renewables in the energy system is essential to limit the enhancement of global climate change. District heating systems (DHS) would offer the possibility to enhance the integration of renewables if the system’s design was optimized. In addition to global climate change, the independency of fossil fuels is more crucial than ever to European countries due to rising gas prices caused by the Ukrainian conflict (Global Conflict Tracker, 2022). Natural gas is an essential heat carrier in Europe, with a share of 36% gross heat generationin 2019 (DG Energy, 2020; European Commission, 2021b). Figure 1 illustrates the high dependency on fossil fuels in DHS in relation to net heat production. 66% of the net heat production was generated from less than 15% renewables¹. Because of the increasing demand for the independency of natural gas and other fossil fuels, most countries will face a decarbonization process in the upcoming years. The heat supply in countries like Germany is at a temperature of 80–130°C. High temperatures further complicate the decarbonization process due to higher losses and decreasing efficiencies for renewable heat sources (Paardekooper et al., 2018; EnBW Company, 2021). Mathematical optimization is a commonly applied method to support planners and operators in transforming their DHS (Sameti and Haghighat, 2017). The optimization tries to find a mathematical minimum of a cost function designing energy converters, storages, pipes, or other components.

FIGURE 1

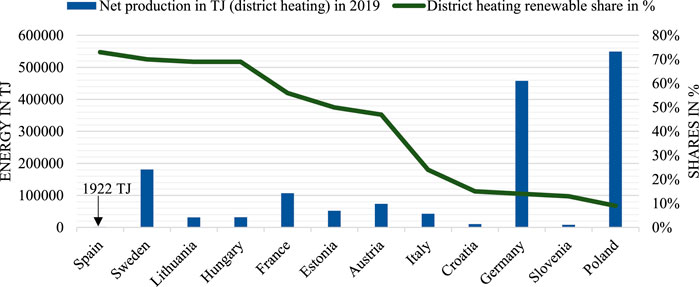
FIGURE 1. Renewable share and net heat production in DHS in dependency of some European countries in the year 2019 (European Commission, 2021a; Corscadden et al., 2021, p. 34, p. 34).

The field of optimization in DHS was reviewed by several researchers in the literature. The focus of those publications can be summarized as follows:

• Sameti and Haghighat (2017) discussed mathematical approaches on optimizing district heating and cooling systems in detail. The review described possible modeling techniques for energy conversion technologies or thermal storages and objective functions. The objectives minimized costs or CO₂ emissions. It gave a broad overview of optimization approaches in the literature, describing the method, the objective, and the type of installation (centralized, decentralized). The research was conducted in 2017. Therefore, our review focused on new topics with relevance, like the integration of renewable heat sources. In addition, we concluded the relevance or irrelevance of mathematical formulations for the grid.

• Lake et al. (2017) reviewed case studies of district heating and cooling systems to identify the advantages and drawbacks of different energy sources. Furthermore, the publication reviewed energy policies to determine their influence on designing such systems. Additionally to Lake et al. (2017), we provided a literature distribution on the different technology solutions.

• Li et al. (2017) examined smart grids, energy storages, and the integration of renewable energy sources in optimizing district heating and cooling systems. The publication highlighted the conversion of energy, its distribution, heat transfer stations, terminal users, and approaches in the literature. In addition to Li et al. (2017), we contributed with a strong focus on DHS‘ design optimization.

• Mazhar et al. (2018) reviewed DHS’s progress, focusing on technical configurations, regulations, and policies. The review identified an urgent need to expand DHS to accelerate the transformation process in the heating sector. Our work extended Mazhar et al.’s (2018) review by examining mathematical approaches with a strong focus on the grid.

• Olsthoorn et al. (2016) reviewed modeling and optimization approaches for integrating storage and renewable energy. Energy sources were classified depending on their sustainability and complexity of integration. The paper reviewed modeling approaches regarding computational time, detail level, and results certainty. In addition to Olsthoorn et al. (2016), we provided knowledge on equations for DHS.

• Paiho and Reda (2016) reviewed DHS in Finland and how they can possibly be transformed into a sustainable system. The review’s focus was an overview of promising innovative and realistic technologies for integration into DHS. In addition, we identified research gaps in the literature for the design optimization of DHS.

• Sarbu et al. (2017) reviewed different optimization techniques for DHS and proposed a detailed optimization model focusing on the network’s hydraulics. In addition, the authors presented the economics of DHS. We expanded Sarbu et al.’s (2017) work with different temperature models for the network based on the necessary level of detail.

• Sarbu et al. (2019) reviewed optimization and modeling techniques in DHS, discussing deterministic and heuristic optimization. Furthermore, they highlighted the numerical description of DHS and their components. The state-of-the-art was also categorized. We added a literature distribution over relevant technologies for the decarbonization process to Sarbu et al.’s (2019) work.

• Sarbu et al. (2020) provided an overview of DHS’s optimization, focusing on heuristic methods. In addition, an optimization problem (single-objective and multi-objective) was formulated, and the criteria for optimizing DHS was described. Again, we complemented this work with a literature distribution over relevant technologies for the decarbonization process.

The literature reviews provided valuable knowledge in the field of optimizing DHS. In addition to the state-of-the-art, we conducted a systematic literature review (SLR) based on a generic and reproducible method. Our review was driven by the question if the current optimization methods at hand can calculate a sustainable re-design of DHS facing a decarbonization process? In conclusion, our contribution was a SLR on DHS’s optimization focusing on their transformation process and identifying research gaps on the topic. Our scope is not only on the general design of DHS but on the method of linear programming. The SLR was explained in detail in the method section, and categories were derived for structuring the results. The result section followed, giving an overview of the found literature sorted into the categories. In the discussion section, major research gaps were identified. In the conclusion, the SLR’s main findings were described to give an outlook for upcoming research.

Methods

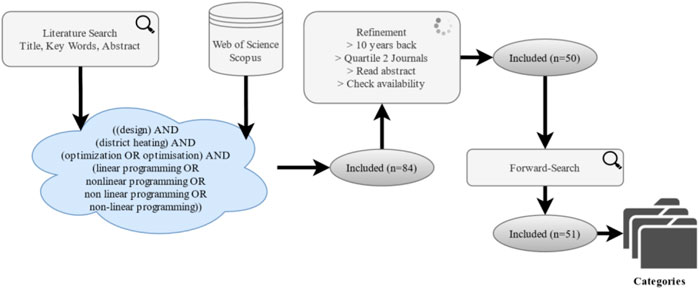
The SLR was based on Webster and Watson (2002) and Jan vom Brocke et al. (2009). The scope of the literature review was a sequential search of bibliographic databases using a comprehensive set of techniques such as keyword, backward search, and forward search (vom Brocke et al., 2015). This method ensured transparency and reproducibility of the results. The methodology was divided into five steps: selecting the databases, creating the search string, searching (forward/backward), refining the results, and deriving categories. In Figure 2, the applied methodology was visualized.

FIGURE 2

FIGURE 2. Summary of the methodology for the systematic literature review.

The search was conducted on Scopus and Web of Science as they are one of the largest scientific databases, and they allowed the implementation of search strings in contrast to Google Scholar (Paperpile, 2012). The search string consisted of the field, the problem, and the method. The main research question focused on DHS; therefore, the field was identified as district heating. The problem was the DHS’s design optimization to reach a carbon-neutral supply system. The literature usually formulated its problems as linear or nonlinear (Sameti and Haghighat, 2017). To conclude, the search string read (district heating) AND (optimization OR optimisation) AND (linear programming OR nonlinear programming OR non linear programming OR non-linear programming). The search resulted in 83 publications on the 22^cd of February 2022. This method does not exclude any regions or researchers. If a publication was not selected, it would have been excluded by the chosen key words, the refinement, or it would not be available on the searched databases.

A quality measure refined the 83 publications quartile one and two in the year 2020—excluding 12 journals: mathematical problems in engineering, Computer aided chemical engineering, Journal of energy engineering, Journal of physics conference series, Chemical engineering transactions, WIT Transactions on ecology and environment, Chemical Product and Process, Environmental and Climate Technologies, Yingyong Kexue Xuebao/Journal of Applied Sciences, Nippon Kikai Gakkai Ronbunshu, C Hen/Transactions of the Japan Society of Mechanical Engineers, Part C, Nihon Enerugi Gakkaishi/Journal of the Japan Institute of Energy (SCImago, 2007).

Additionally, all publications published before 2012 were excluded to create comparability due to significant developments in computational time (Sameti and Haghighat, 2017). On top of that, ten publications² were excluded because the topic did not match the DHS’s design optimization. Through the forward search, Krug et al. (2020) were included in the literature review due to their detailed model of the DHS in an optimization problem. In conclusion, 51 publications were selected to be reviewed in this article.

The categories clustered the 51 publications and enhanced a fast overview of the topic regarding the research question. In addition, it shows possible research gaps in the state-of-the-art. The categories were divided into nine supercategories: system, objective, method, solver, computational time, the validity of results, consumer, grid, and supply structure. Each of those supercategories consisted of subcategories to further describe the content of the literature. The arrangement and meaning of each category were explained in the results section, supported by figures illustrating the literature’s distribution concerning the DHS’s (re-)design optimization.

Results

The results section consisted of three subsections: District Heating System, Optimization, Modeling of District Heating Systems in Optimization, and Significant Findings of the Literature. In those subsections, the subcategories were derived, and the literature’s distribution was displayed. In addition, standard approaches to the topic were explained. The considered literature was documented in Table 1. Figure 3 is an overview of the literature distribution based on the categories for method, unit type, technology, system, computational time, and objective. Due to the applied method, all publications provided knowledge on those supercategories except for measures of lowering computational time. The graphic showed that most publications dealt with small scale-systems using a mix of renewable and nonrenewable heat sources or energy converters that are centrally installed. Usually, the mathematical model was linear and optimized towards a single objective. In 40 publications, computational methods were applied to decrease the calculation time. The following sections provide a more profound knowledge of the categories and the publication’s content.

TABLE 1

TABLE 1. Publications from the SLR for the literature distribution.

FIGURE 3

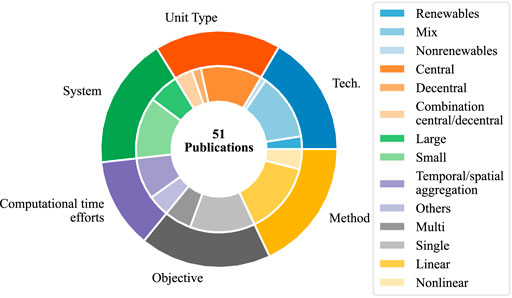
FIGURE 3. Overview of the literature distribution over the system’s size, the unit type, the technologies, the method, the objective function, and efforts for lowering computational time.

District heating system

DHS transport heat through pipes to consumers. Usually, DHS have a forward-flow transporting heat from the production units to the consumers and a backward-flow transporting the fluid back to the production unit. Some DHS operate on temperatures over 90°C, while the 4th Generation of DHS operates below 60°C (Lund et al., 2021). If the forward-temperature is below 60°C, the warm water must be heated decentrally to prevent legionella. The 5th generation of DHS enables parallel cooling and heating. Consumers can extract or inject energy into the grid. In that case, consumers become prosumers (Wirtz et al., 2020). Therefore, the three subcategories of the system were high temperature > 90°C, medium temperature 60–90°C, and low temperature < 60°C.

The DHS’s size influences the model complexity due to the need for spatial discretization (Sameti and Haghighat, 2017). Some DHS supply small districts, while others supply cities (Biedermann and Kolb, 2014). Therefore, large-scale and small-scale system were subcategories of the supercategory system. A system was considered small-scale if the problem was not spatially discretized or the optimization was performed over a few nodes. Furthermore, this work differentiated between real case studies and synthetic case studies.

About 70% of the literature used real case studies to support their model inputs. In Figure 3, most systems were small-scale: Bornand et al. (2020) derived an investment planning methodology and implemented it for a hospital site. This problem was categorized as small-scale due to the low number of nodes. The same category was set for Wirtz et al. (2021a) because the problem was not spatially discretized. In general, the temperature level was not always clearly identified; therefore, some methods can be applied to high- and medium-temperature systems. The vast majority of systems (∼85%) covered by the literature are small-scale systems with temperatures over 60°C.

Optimization

Mathematical optimization is a tool to support decision-making processes, e. g. designing and operating energy systems (Sameti and Haghighat, 2017). Mathematically, “optimization” means the determination of the maximum or minimum of a function f. In the literature, the function inherited economic, technical (exergy), social, or ecologic factors and was defined on a (restricted) domain S or state space. Classic optimization theory deals with cases where S is coherent, and the function f is optimized and continuous. The function f was also called the objective function in the optimization environment. The pending decisions (e.g., investments or dimensions of energy converters) were linked to the degrees of freedom of the problem. In an optimization model, variables represented degrees of freedom (e.g., the storage volume). The optimization algorithm assigned values to the variables resulting in the objective function’s optima reflecting the consequences of the decisions.

$\mathrm{Min}\left\{f\left(x,y\right)|\begin{array}{c}h\left(x,y\right)=0\\ g\left(x,y\right)\ge 0\end{array},\begin{array}{c}x\in \mathbb{R}\\ y\in \mathbb{R}\end{array}\right\}(1)$

is a generic objective function with $h\left(x,y\right)$ representing the equality and $g\left(x,y\right)$ the inequality constraints. Various factors influenced the objective value in the literature, e. g. subsidies for CO₂ lowering measures. The design optimization was usually performed over a given time period $\tau$, optimizing the variables at every timestep $t$ (Delubac et al., 2020). The objective function usually consisted of capital expenditures (CAPEX) and operational expenditures (OPEX). For example, the CAPEX could depend on the installed capacity for production units or the installed length of a pipe. The OPEX was often divided into fixed and variable costs. The variable costs usually depend on the operation power multiplied by specific costs, e.g., gas price for a gas boiler. The fixed OPEX depended on the nominal heat and the device, usually including costs for controlling devices, maintenance, and repair. Further information concerning costs for components in a DHS can be found in VDI 2067 or Steinbach et al. (2020). (Kallrath, 2013, pp. 1–2; Khatibi et al., 2019; Steinbach et al., 2020)

The depiction of different objectives in mathematical optimization was achieved via three methods. The first one was the introduction of a boundary for a variable, e.g., for CO₂ emissions. Nevertheless, introducing a boundary constraint is not a multi-objective problem (Gurobi, 2018). Bornand et al. (2020) used the supplementary $\epsilon$-constraint with a key performance indicator (here CO₂-emissions) to generate $n$ different solutions for Eq. 1 with

$\left\{KPI\le {\epsilon }_i|{\epsilon }_i={KPI}_{\min }+i\frac{{KPI}_{\max }-{KPI}_{\min }}{n-1}fori\in \left[0,n-1\right]\right\},(2)$

where the parametric boundary ${\epsilon }_i$ is gradually increased.

The second method formulated two separate objective functions, e.g., for costs and CO₂ emissions (Fazlollahi et al., 2015). The solver then forms a Pareto front of the optimal solutions depending on the objective functions. The Pareto front is the border between feasible and infeasible solutions. All solutions on the Pareto front are optimal. Figure 4 illustrates the solution space of two objective functions. The point of intersection is the minimum for both functions. The optima considering both functions’ objectives is the solution (dashed line in Figure 4) with the shortest distance to the point of intersection.

FIGURE 4

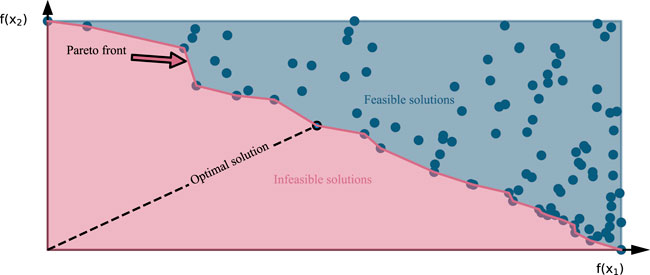
FIGURE 4. Qualitative graph of a Pareto front for a multi-objective optimization with two objective functions, f (x₁) and f (x₂).

The third method used a weighted-sum function, e. g. including CO₂ costs in the objective function (Sameti and Haghighat, 2017). Based on the influential factors for the objective and the possibility of multi-objective optimization, the subcategories ecologic, technical, economic, social, subsidies, and multi-objective were derived for the objective.

Figure 5 shows the distribution over the subcategories for objective. Schütz et al. (2018) considered subsidies for combined heat and power plants (CHP) to exploit total nominal power for CHP plants until a nominal limit is reached. Only two publications in total considered subsidies. Technology subsidies are often regionally limited; therefore, their publication does not significantly impact the international community. The influence of social factors on the objective had not been viewed at all.

FIGURE 5

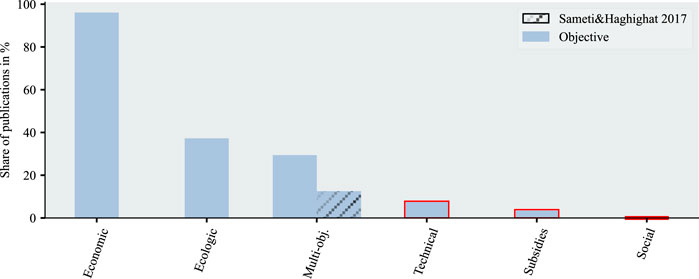
FIGURE 5. Literature distribution for the supercategory objective with a comparison of multi-objective with (Sameti and Haghighat, 2017); low numbers of publications are marked red as an indication of a potential research gap.

Most publications (>95%) used a cost function as their objective. Some publications (∼40%) combined the cost function with ecologic factors, e.g., limitation of CO₂ emissions (Walter et al., 2020) or multi-objective optimization (Mavromatidis and Petkov, 2021). The application of multi-objective optimization doubled (12.5% vs. 29.4%) relative to the samples taken by Sameti and Haghighat (2017).

As explained and shown in Figure 4, the constraints define the solution space for the objective function. The constraints can be formulated linearly and continuously (referred to as linear programming–LP), linearly and non-continuously (referred to as mixed-integer linear programming–MILP). Nonlinear problems can be formulated nonlinearly and continuously (referred to as nonlinear programming–NLP), or nonlinearly and non continuously (referred to as mixed-integer nonlinear programming–MINLP) (Kallrath, 2013). The decision to formulate the optimization depends on the task and the time at hand. In general, nonlinear problems can depict physical systems more in detail–e.g., modeling temperature gradients along a pipe segment (Krug et al., 2020)—but require higher computational time. Mixed-integer variables were often used for control strategies in energy systems (on/off) or designing components (Elsido et al., 2017). The introduction of those variables causes increased computational time as well. Mixed-integer variables were commonly used to design DHS (Sameti and Haghighat, 2017); therefore, the category method only consisted of the subcategories linear and nonlinear.

Besides the problem formulation, the solver can also influence the computational time. It can be distinguished between classic optimization (mathematical programming) and soft computing (heuristics and metaheuristics). However, this work focused on classic optimization because most energy system optimizations applied this method (Sameti and Haghighat, 2017). Therefore, most publications used global solvers such as cplex, gurobi, or ipopt (open-source) (Sameti and Haghighat, 2017). Nevertheless, some publications solved problems with heuristic solvers such as NSGA-II (van der Heijde et al., 2019).

The significant difference is that a heuristic solver can quickly find a solution; however, might be a local minimum and not a global one (Silveira et al., 2021). Silveira et al. (2021) suggested that heuristic solvers were better suited for large-scale systems. The category solver contained global and heuristic as subcategories.

Some problems required too much computational effort independent of the solving method. If that was the case, measures were considered to reduce the problem. The aggregation of space and time was one of those measures, e.g., one year is represented by a few days (van der Heijde et al., 2019), or two buildings were aggregated to one. Another measure decomposed the problem into several stages (Mavromatidis and Petkov, 2021). Based on the efforts to reduce computational time, the category computational time consisted of time aggregation, spatial aggregation, staged process/decomposition, and others.

Applying measures to reduce the computational time, simplifying the mathematical formulation of the physical system, or having uncertainties in the input data always caused errors. The technical validity of the results can be ensured by performing a detailed simulation after the optimization (Quaggiotto et al., 2021). Dealing with uncertainties in the input data can be done with a sensitivity analysis to examine the influence of inputs on the results. A more sophisticated approach would be a Monte Carlo method; however, that requires additional knowledge of the inputs and enormous computational power (Kausche, 2018, pp. 71–77). Therefore, the category validity of results consisted of simulation, sensitivity analysis/scenarios, and uncertainties.

Figure 6 shows the literature distribution for the mentioned supercategories. The figure compares Sameti and Haghighat’s (2017) results for the method and the solver. The results indicate that the optimizations of nonlinear problems using heuristic solvers had declined; however, this SLR was applied from 2012 until 2022. In addition, the search string included linear and nonlinear programming that might have excluded publications using heuristic solvers.

FIGURE 6

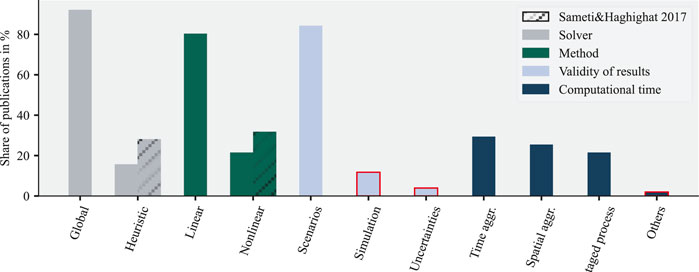
FIGURE 6. Literature distribution over the supercategories method, solver, computational time, and validity of results with comparison to (Sameti and Haghighat, 2017); low numbers of publications (<15%) are marked red as an indication of a potential research gap.

Most publications (∼80%) formulated a linear programming model and solved it with a global solver (∼90%). Computational efforts were mostly (∼30%) reduced by time series aggregation. Elsido et al. (2017) used a two-stage process to solve a MINLP problem. Other methods were the relaxation of constraints. This method was applied by Krug et al. (2020), resulting in decreased computational time. Most of the viewed literature (∼80%) validated their results with different scenarios or a sensitivity analysis. The technical validation of results with a detailed simulation or an uncertainty analysis for the input data was rarely performed in the literature.

Modeling of district heating systems in optimization

Equations

A DHS consists of consumers, production units, and the grid transports the heat, as shown in Figure 7. The modeling of DHS was divided into several energy balances for consumers (marked lilac), production units (marked red), pipes, and nodes (marked grey and blue). For a better understanding, equations for these energy balances were explained (see Table 2 for symbols). All equations used in the literature assumed incompressibility with a constant density over space and time and constant velocity over space (Krug et al., 2020). Furthermore, the following equations assumed that the flow directions are known. Krug et al. (2020) derived an approach to solving the problem of unknown flow directions. The constraints were initialized through a node set with $V=\left[1,\dots ,8\right]$ and a pipe set with $\gamma =\left[\mathrm{12,23,34,41,56,67,78,85}\right]$ (Krug et al., 2020). The following equations excluded boundary constraints.

FIGURE 7

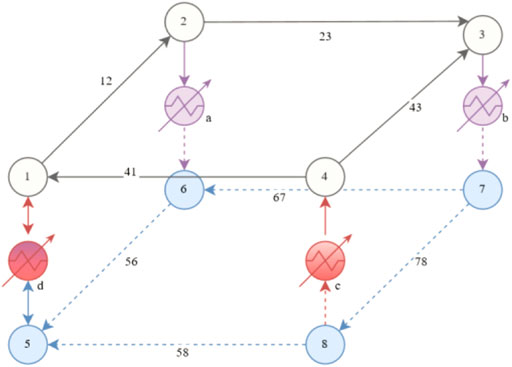
FIGURE 7. Exemplary DHS with two consumers–node 2 and 3—one production unit–node 4—one prosumer–node 1 (Krug et al., 2020).

TABLE 2

TABLE 2. Declarations of symbols with variables in the top and parameters in the bottom.

The consumer balance can be modeled temperature-dependent (Krug et al., 2020) or independent with (Schütz et al., 2018)

$\frac{{\dot{Q}}_{i,t}}{\mu }={\dot{Q}}_{i,t}^{\mathrm{i}\mathrm{n}}-{\dot{Q}}_{i,t}^{\mathrm{o}\mathrm{u}\mathrm{t}}={\dot{m}}_{i,t}{c}_{\mathrm{p}}\left(T_{i,t}^{\mathrm{i}\mathrm{n}}-T_{i,t}^{\mathrm{o}\mathrm{u}\mathrm{t}}\right)fort\in \tau ,i\in \left[a,b,d\right],(3)$

where for the independent case ${\dot{Q}}_{i,t}^{\mathrm{i}\mathrm{n}}$ flowed from the forward-flow node into the consumer $i$ and ${\dot{Q}}_{i,t}^{\mathrm{o}\mathrm{u}\mathrm{t}}$ flows from the consumer $i$ into the backward-flow node. The right part of the equal sign was temperature-dependent, and models ${\dot{m}}_{i,t}$, $T_{i,t}^{\mathrm{i}\mathrm{n}}$ and $T_{i,t}^{\mathrm{o}\mathrm{u}\mathrm{t}}$ as variables resulting in a nonlinear constraint. $\mu$ represents the efficiency of the transfer station. With the development of new DHS in the 5th generation, prosumers were modeled in the literature for an efficient design. In Figure 7, at node 1, a prosumer was depicted, which can consume or convert energy. The left-hand side of Eq. 3 would transform to $\frac{{\dot{Q}}_{i,t}^{\mathrm{c}\mathrm{o}\mathrm{n}}}{\mu }-{\dot{Q}}_{i,t}^{\mathrm{p}\mathrm{r}\mathrm{o}}\mu$ with ${\dot{Q}}_{i,t}^{\mathrm{p}\mathrm{r}\mathrm{o}}$ representing the converted energy at the prosumer (Wirtz et al., 2020). The concept of prosumers was a subcategory for the supply system as decentral.

The mass balance in the nodes was given by (Baehr and Kabelac, 2006, p. 85, p. 85)

${\displaystyle \sum }_{i\in {\delta }^{\mathrm{i}\mathrm{n}}\left(u\right)}{\dot{m}}_{i,t}={\displaystyle \sum }_{i\in {\delta }^{\mathrm{o}\mathrm{u}\mathrm{t}}\left(u\right)}{\dot{m}}_{i,t}fort\in \tau ,u\in V,(4)$

where ${\delta }^{\mathrm{i}\mathrm{n}}\left(u\right)$ was a set describing pipes, consumers, or production units entering the node $u$.

The fluid left the node with a mixing temperature $T_{u,t}^{\mathrm{m}\mathrm{i}\mathrm{x}}$ (Krug et al., 2020) given by

$T_{i\in {\delta }^{\mathrm{o}\mathrm{u}\mathrm{t}}\left(u\right),t}^{\mathrm{i}\mathrm{n}}=T_{u,t}^{\mathrm{m}\mathrm{i}\mathrm{x}}=\frac{{\displaystyle \sum }_{i\in {\delta }^{\mathrm{i}\mathrm{n}}\left(u\right)}{\dot{m}}_{i,t}{T}_{i,t}^{\mathrm{o}\mathrm{u}\mathrm{t}}}{{\displaystyle \sum }_{i\in {\delta }^{\mathrm{i}\mathrm{n}}\left(u\right)}{\dot{m}}_{i,t}}fort\in \tau ,u\in V,(5)$

where $T_{i\in {\delta }^{\mathrm{o}\mathrm{u}\mathrm{t}}\left(u\right),t}^{\mathrm{i}\mathrm{n}}$ refers to the temperature entering pipe $i$ and leaving node $u$. If temperatures were neglected, Eq. 5 would be irrelevant. The energy balance in the nodes was given by (Baehr and Kabelac, 2006, p. 85, p. 85)

${\displaystyle \sum }_{i\in {\delta }^{\mathrm{i}\mathrm{n}}\left(u\right)}{\dot{Q}}_{i,t}^{\mathrm{o}\mathrm{u}\mathrm{t}}={\displaystyle \sum }_{i\in {\delta }^{\mathrm{o}\mathrm{u}\mathrm{t}}\left(u\right)}{\dot{Q}}_{i,t}^{\mathrm{i}\mathrm{n}}fort\in \tau ,u\in V,(6)$

where ${\dot{Q}}_{i,t}^{\mathrm{o}\mathrm{u}\mathrm{t}}$ left the pipe $i$ and entered node $u$.

The thermal energy balance at production units was modeled analogously to Eq. 3 (Krug et al., 2020), with

${\dot{Q}}_{i,t}\mu ={\dot{Q}}_{i,t}^{\mathrm{o}\mathrm{u}\mathrm{t}}-{\dot{Q}}_{i,t}^{\mathrm{i}\mathrm{n}}={\dot{m}}_{i,t}{c}_{\mathrm{p}}\left(T_{i,t}^{\mathrm{o}\mathrm{u}\mathrm{t}}-T_{i,t}^{\mathrm{i}\mathrm{n}}\right)fort\in \tau ,i\in \left[c\right],(7)$

where ${\dot{Q}}_{i,t}^{\mathrm{i}\mathrm{n}}$ flowed from the backward-flow node 4 into the production unit and ${\dot{Q}}_{i,t}^{\mathrm{o}\mathrm{u}\mathrm{t}}$ flowed from the production unit into the forward-flow. The equations for the optimization were formulated positively; therefore, the signs changed (Wirtz et al., 2019). ${\dot{Q}}_{i,t}$ can calculate the operation of the production unit at node 4. Further information on thermal storage equations can be found in van der Heijde et al. (2019).

In the design optimization of DHS, the capacity of production units was a crucial variable to be optimized due to high investments (Steinbach et al., 2020). The investment curve for technologies usually behaved nonlinearly. A solution to model nonlinear functions in a MILP or LP problem is Special Ordered Set 2 (SOS2) (Williams, 2013). For the investment curve of a technology $i,$ a table with $N$ points for nominal power ${\dot{Q}}_{i,j}^{\mathrm{n}\mathrm{o}\mathrm{m}}$ and investment $C_{i,j}^{\mathrm{p}\mathrm{o}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{s}}$ needed to be given. Assuming (Wirtz et al., 2019)

${\dot{Q}}_i^{\mathrm{n}\mathrm{o}\mathrm{m}}\ge {\dot{Q}}_{i,t}fort\in \tau ,i\in \left[c\right],(8)$

where ${\dot{Q}}_i^{\mathrm{n}\mathrm{o}\mathrm{m}}$ was the variable for the nominal heat flow. Auxiliary variables were introduced to calculate the correct investments for the technology with (Wirtz et al., 2019)

$b_i{\dot{Q}}_i^{\mathrm{n}\mathrm{o}\mathrm{m},\min }\le {\dot{Q}}_i^{\mathrm{n}\mathrm{o}\mathrm{m}}-\left(1-b_i\right){\dot{Q}}_i^{\mathrm{n}\mathrm{o}\mathrm{m},\max }\le {\displaystyle \sum }_{j\in N}{\dot{Q}}_{i,j}^{\mathrm{n}\mathrm{o}\mathrm{m}}{\omega }_{i,j},i\in \left[c\right],(9)$

where ${\dot{Q}}_i^{\mathrm{n}\mathrm{o}\mathrm{m},\min /\max }$ represented the upper and lower boundary for the production unit and $b_i$ its buying decision. Eq. 9 calculated the auxiliary variables with the condition $b_{i\in \left[c\right]}={\displaystyle \sum }_{j\in N}{\omega }_{i\in \left[c\right],j}$ passed into

$C_{i\in \left[c\right]}={\displaystyle \sum }_{j\in N}{C}_{i,j}^{\mathrm{p}\mathrm{o}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{s}}{\omega }_{i,j}.(10)$

${\sum }_{i\in \left[c\right]}{C}_i$ was implemented in the objective function for the CAPEX of all production units. SOS2 was applied so that two neighboring auxiliary variables can be two at most (Williams, 2013). This methodology can be used to design other components of the DHS. (Wirtz et al., 2019)

The thermal energy balance of the pipes can be modeled with different degrees of freedom. The first degree was only to model the heat flow with (Weinand et al., 2019)

${\dot{Q}}_{i,t}^{\mathrm{i}\mathrm{n}}-{\dot{Q}}_{i,t}^{\mathrm{o}\mathrm{u}\mathrm{t}}-{\dot{Q}}_{i,t}^{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}=0fort\in \tau ,i\in \gamma ,(11)$

where ${\dot{Q}}_{i,t}^{\mathrm{i}\mathrm{n}}$ was the heat flow entering pipes, ${\dot{Q}}_{i,t}^{\mathrm{o}\mathrm{u}\mathrm{t}}$ leaving the pipes and ${\dot{Q}}_{i,t}^{\mathrm{l}\mathrm{o}\mathrm{s}\mathrm{s}}$ were the losses of the pipes. Another approach was to model losses in dependency on the temperature inside the pipe and the soil temperature with (Quaggiotto et al., 2021)

$c_{\mathrm{p}}{m}_i\frac{T_{i,t-1}^{\mathrm{o}\mathrm{u}\mathrm{t}}-T_{i,t}^{\mathrm{o}\mathrm{u}\mathrm{t}}}{∆t}+{\dot{Q}}_{i,t}^{\mathrm{i}\mathrm{n}}-{\dot{Q}}_{i,t}^{\mathrm{o}\mathrm{u}\mathrm{t}}-U_i{A}_i^{\mathrm{m}}\left(T_{i,t}^{\mathrm{o}\mathrm{u}\mathrm{t}}-T_t^{\mathrm{s}\mathrm{o}\mathrm{i}\mathrm{l}}\right)=0fort\in \tau ,i\in \gamma .(12)$

The first term of the equation described the storage capacity of the grid. The last term represented the thermal losses influenced by the pipe’s surface $A_i^{\mathrm{m}}$, the soil temperature $T_t^{\mathrm{s}\mathrm{o}\mathrm{i}\mathrm{l}}$, and the heat transfer coefficient $U_i$. The heat transfer coefficient was estimated based on the material and diameter of pipe and insulation (Nussbaumer et al., 2018). Some publications based their thermal losses on empirical calculations (Wirtz et al., 2021b). Eq. 12 can be rewritten by applying the first law of thermodynamics such as (Krug et al., 2020)

$c_{\mathrm{p}}{m}_i\frac{T_{i,t-1}^{\mathrm{o}\mathrm{u}\mathrm{t}}-T_{i,t}^{\mathrm{o}\mathrm{u}\mathrm{t}}}{∆t}+m_{i,t}{c}_{\mathrm{p}}\left(T_{i,t-1}^{\mathrm{i}\mathrm{n}}-T_{i,t}^{\mathrm{o}\mathrm{u}\mathrm{t}}\right)-U_i{A}_i^{\mathrm{m}}\left(T_{i,t}^{\mathrm{o}\mathrm{u}\mathrm{t}}-T_t^{\mathrm{s}\mathrm{o}\mathrm{i}\mathrm{l}}\right)=0fort\in \tau ,i\in \gamma .(13)$

Eq. 13 increased the degree of freedom for the optimizer, and the optimization problem became nonlinear. This additional degree of freedom allowed the calculation of the mass flow ${\dot{m}}_{i,t}$ inside the pipe and the entering temperature $T_{i,t}^{\mathrm{i}\mathrm{n}}$. To cluster the literature based on their temperature model, Eq. 11 represented the category heat flow, Eq. 12 the category simple temperature model, and Eq. 13 the category detailed temperature model.

The heat transport along a pipe was realized by generating pressure at the production units. In the literature, the modeling of hydraulics in a pipe differed from completely neglecting them (Szypowski et al., 2019) to pressure models based on the 1d momentum equation with the simplification of $\frac{d\rho }{dt}=\frac{d\rho }{dx}=\frac{dv}{dx}=0$ (Krug et al., 2020)

$∆p_{i,t}=L_i\rho \frac{v_{i,t}-v_{i,t-1}}{∆t}+g\rho h_i+L_i{\lambda }_i\frac{v_{i,t}{v}_{i,t}\rho }{2D_i}fort\in \tau ,i\in \gamma ,(14)$

where the first term on the right-hand side represented the pressure loss due to the velocity differences between timesteps t and $t-1$, and the second term represented the pressure delta due to height differences between the end and start of the pipe segment. The third term mathematically described the pressure losses due to friction. The pressure losses over a consumer can be attributed to the mass flow.

The hydraulic balance in the network can be described by Kirchhoff’s circuit laws given by (Serway, 2004)

${\displaystyle \sum }_{i\in \gamma }∆p_{i,t}+{\displaystyle \sum }_{i\in \left[a,b,d\right]}∆p_{i,t}={\displaystyle \sum }_{i\in \left[c\right]}∆p_{i,t}fort\in \tau ,(15)$

where $∆p_{i,t}$ had to be realized with (Krug et al., 2020)

$P_{i,t}^{\mathrm{p}\mathrm{u}\mathrm{m}\mathrm{p}}\mu =\frac{∆p_{i,t}{\dot{m}}_{i,t}}{\rho }fort\in \tau ,i\in \left[c\right].(16)$

Eq. 14, Eq. 15, and Eq. 16 represented the subcategory pressure model. The velocity along the pipe can be limited in dependency of a max. pressure loss along the pipe, avoiding nonlinearities (∼200 Pa m⁻¹ (Nussbaumer et al., 2018, p. 13). The subcategory–hydraulic boundaries–represented the fixed pressure loss.

Literature distribution

Modeling of DHS in optimization was divided into the supercategories consumer, grid, and supply structure. High demanding temperatures by consumers challenge the decarbonization process (Biedermann and Kolb, 2014). Therefore, temperature and refurbishment were subcategories of consumer. The demand was identified as the most crucial parameter in the design optimization of DHS; consequently, it was used in every publication of the SLR. The temperature is considered for half of the publications. Currently, refurbishment is an underrepresented topic, with only one publication.

Efficient transport of heat technically and economically³ depends on the design of the grid. Therefore, the supercategory grid had design, change of temperature level, combination of grids, and deconstruction as subcategories for the output. Paardekooper et al. (2018) projected an increasing share of district heating in buildings from 12% in 2015 to 50% in 2050. Besides infrastructural changes, the temperature level is an influential factor in the decarbonization of DHS. This influence is caused by the high-temperature dependency of heat pumps and their limit of a potential temperature lift which is given by the Carnot efficiency (Arpagaus et al., 2018):

${\mu }^{\mathrm{C}\mathrm{a}\mathrm{r}\mathrm{n}\mathrm{o}\mathrm{t}}=\frac{T^{\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{y}}-T^{\mathrm{s}\mathrm{o}\mathrm{u}\mathrm{r}\mathrm{c}\mathrm{e}}}{T^{\mathrm{s}\mathrm{u}\mathrm{p}\mathrm{p}\mathrm{l}\mathrm{y}}}\to COP=\frac{1}{{\mu }^{\mathrm{C}\mathrm{a}\mathrm{r}\mathrm{n}\mathrm{o}\mathrm{t}}}.(17)$

Heat pumps were projected to integrate environmental heat sources (Paardekooper et al., 2018, p. 12). The complexity and mathematical formulation of the grid modeling varied in the literature depending on the research question, as shown in the equation section. The grid can be modeled as one node with a given efficiency (Wirtz et al., 2019) or with nodes and edges spatially discretized, as shown in Figure 7 (Krug et al., 2020).

For larger systems, geoinformation systems (GIS) can be a helpful tool to support planers in the design process of DHS (Bill, 2010; Weinand et al., 2019). In general, GIS are information systems that support the analysis, caption, editing, organization, and presentation of spatial data (Bill, 2010). Another important modeling element is the grid’s water inertia (or storage capacity) (Wirtz et al., 2021b). Some publications modeled the forward-flow (grey lines in Figure 7) and the backward-flow (blue dashed lines in Figure 7) (Krug et al., 2020), while others neglected the backward-flow of the grid (Weinand et al., 2019).

Figure 8 shows that in the grid modeling, some subcategories were underrepresented (>12%) in the literature: GIS, storage capacity, detailed temperature modeling, and pressure modeling. A spatial dimension was used in 60% of the publications, and the forward-flow was modeled in every publication. Some publications focused on the hydraulics of the DHS causing the neglection of the heat flow in the grid (Li and Svendsen, 2013). The design of DHS was considered in half of the publications. The change of temperature level was viewed three times, and the combination of grids or infrastructural deconstruction was never content of the published work.

FIGURE 8

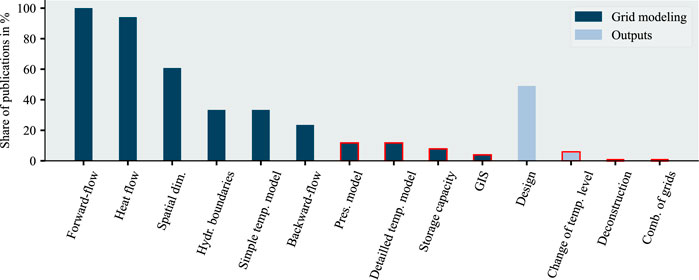
FIGURE 8. Literature distribution for the supercategory grid and the sublevels grid modeling and output; low numbers of publications (<15%) are marked red as an indication of a potential research gap.

Besides the grid, the supply structure is crucial in the decarbonization process for DHS. Paardekooper et al. (2018) suggested a combination of DHS and individual heat pumps as decentral solutions for more minor dense. Therefore, this work differentiated between central and decentral units (Sameti and Haghighat, 2017). In general, the heat roadmap Europe projected a more versatile system for DHS in the future. A potential system would consist of geo- and solar-thermal heat, Power-to-Heat (PtH) technologies, large-scale heat pumps, biomass boiler, CHP, and excess heat. Furthermore, it was shown that CHP and large-scale heat pumps would cover 45–65% of the demand. Boilers were projected to cover peak demands up to 10% over the year. The storage capacities further increased the system’s flexibility to react to the electricity market. It was differentiated between short-term storages and long-term or seasonal storages in the subcategories (Paardekooper et al., 2018, pp. 10–13).

Due to the high dependency on fossil fuels in Europe, with 40.1% in 2020 (Corscadden et al., 2021, p. 34), fossil boiler was another subcategory of the supercategory supply structure. Furthermore, the connection to the electricity market is given by sector-coupling technologies such as mainly CHP and heat pumps. The combination of photovoltaic cells (PV) and PtH technologies further increased the efficiency of the system. In addition, fuel cells were considered a subcategory for the SLR because they are sold for household solutions by companies like Viessmann (Rosenkranz, 2020). Regarding the modeling of storage and energy converters, heat flow and temperature dependency were subcategories of the supply structure. The output of the supply structure was represented by the design, deconstruction, operation, and location.

Figure 9 illustrates the literature distribution over technology types, installations, and output. The literature focused more on central units than on decentral units. Individual heat pumps (∼40%), fossil boilers (∼60%), CHP (∼60%), and short-term storages (∼65%) can be identified as one of the essential solutions in the literature. Solar thermal (∼20%), PtH (∼20%), biomass boilers (∼20%), excess heat (∼20%), and PV (∼27%) were in the mid-range. In contrast, geothermal energy (∼10%), large-scale heat pumps (∼4%), fuel cells (0%), and long-term storages (∼1%) were underrepresented. The operation of production units was in 92% part of the research, while the design decision was in 75% of the publications part of the undergone research. The location of the production units was optimized in about 20% of the literature, and deconstruction was never part of the optimization.

FIGURE 9

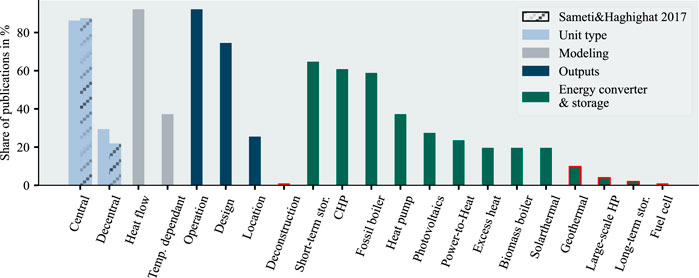
FIGURE 9. Literature distribution over the supercategory supply structure and the subcategories unit type, energy supply, modeling, outputs, and a comparison regarding the unit type with (Sameti and Haghighat, 2017); low numbers of publications (<15%) are marked red as an indication of a potential research gap.

Significant findings of the literature

This section gathers crucial findings and results of the discussed literature. The findings divide into technical findings regarding technologies and methodologies. The citation frequency has been used to filter literature with the most significant impact on the scientific community.

The grid extension is crucial for grid operators and planners because infrastructural changes are connected to high costs. Bordin et al. (2016) developed a planning tool to address grid expansion changes. They assumed static conditions for the hydraulics, and the decision to connect a new consumer to the grid was dependent on the length and diameter of the pipe. The objective is to maximize the net profit consisting of investments for grid expansion and the cash flow. The computational time rised with the increase of potential users. For the biggest test case—1,000 potential users and 500 existing users–the model was solved in 29 s. While for 100 potential and 100 existing users, the solution was reached in less than a second.

Figure 10 illustrates the connection rate depending on the ratio of potential and existing users. The connection rate was generally high, between 60% and 80%. If the number of potential users were assumed to be twice as high as the existing users, the connection rate would decrease. Bordin et al. (2016)focused on grid expansion setting general rules for the physical description of the system. The focus was less on the technology selection and sizing but on infrastructural decisions providing a valuable expansion algorithm.

FIGURE 10

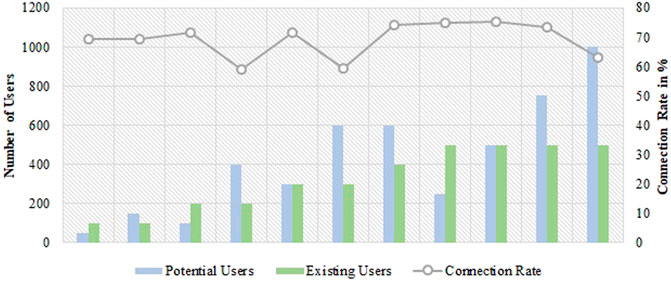
FIGURE 10. Sample of the distribution for connecting to the grid in dependency of the ratio potential vs. existing users; the capacity for the supplying plant was assumed as very high (Bordin et al., 2016).

Compared to Bordin et al. (2016), Morvaj et al. (2016) also considered decisions for designing energy converters and storages besides the expansion of the grid. Consumers could either supply themselves or connect to the DHS. The viewed technologies were gas boilers, PV, CHP, and thermal storages. The examined system is relatively small, allowing for a more detailed approach. Binary decision variables were used for infrastructural decisions, design decisions, and controlling CHP plants. The optimization runs were divided into different scenarios with different carbon emissions limitations. The buildings were operated as prosumers, and the greenfield scenario’s connection rate was exceptionally high. They were able to decrease carbon emissions by 33%, and the greenfield scenario–all technologies were available–resulted in the best case for carbon emissions and costs.

Furthermore, it was highlighted that the electric grid modeling was neglected. This neglection might cause instability if consuming or producing technologies are connected to the electric grid without representation. With an increase in carbon emissions, the connection rate and the use of PV decreased. These results showed that for decarbonizing DHS.

• modeling the grid combined with the supply system affects the design of the grid,

• decentralized units gain more importance with a higher share of renewables,

• thermal grid-connected energy becomes crucial for decarbonized thermal systems,

• sector-coupled DHS requires a representation of the electric grid.

Bracco et al. (2013) optimized a four-node system consisting of a residential complex, a swimming pool, a school, and a city hall. The objective was the optimal connection between the nodes and the design and operation of gas engines, boilers, and turbines. The mathematical model is based on energy balances between the buildings and the grid. They reduced the primary energy consumption and emissions by 43% and the costs by 47%. The system was gas-based, and the gas turbine was used as a base load while the gas boilers were utilized during peak demands.

Compared to Bracco et al. (2013), Wirtz et al. (2020) vastly increased the technology variety and optimized a bidirectional low-temperature network. The network could supply heating and cooling energy to the connected consumers. The energy was provided in an energy hub, and the mathematical model describes the system with energy balances. The residential building also provided decentral units. The technologies in the energy hub were gas boiler, CHP unit, electric boiler, compression chiller, absorbtion chiller, cooling tower, and PV. The technologies in the buildiing were heat pump, electric boiler, compression chiller, direct cooler, and a cooling tower. Figure 11 illustrates the results for the technologies’ capacities in Wirtz et al. (2020). Most publications before 2017 based their energy supply on gas being quite the contrary in Figure 11.

FIGURE 11

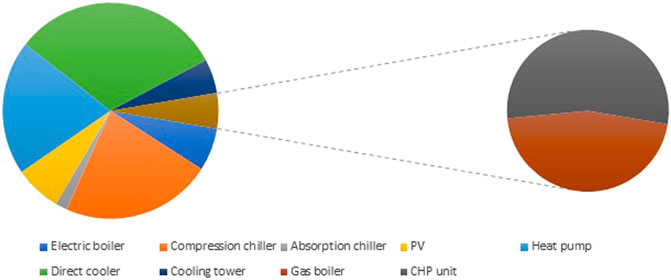
FIGURE 11. Distribution of the total capacity across the dimensioned technologies with separat focus on gas-based technologies from Wirtz et al. (2020).

Discussion and identification of research gaps and potential developments

The results already showed potential research gaps in the literature, and the comparison with Sameti and Haghighat (2017) identified potential trends and developments in the design optimization of DHS. One major trend was using multi-objective optimization with economic and ecologic factors. Social factors did not influence the optimization outcome in the viewed literature and can be identified as a potential research gap. In addition, economic decisions by end-consumers were never part of the optimization, even though multi-objective optimization would give the possibility to depict several decisions. One scenario could be the decision for a consumer to connect its building to the grid for a given heat price vs. an individual solution as one objective and the cost-efficient design and operation of the DHS as the second objective for the grid operator. The depiction of this conflict of interest could be of high relevance for designing the grid.

With the increasing demand for multi-objective optimization, the demand for faster computing is increasing simultaneously. Methods like time series aggregation were gaining more importance, and difficulties were identified regarding seasonal storages (van der Heijde et al., 2019). Aggregating input data temporal or spatial might result in errors and predicting the input data itself. However, sophisticated uncertainty analyses of input data were only done twice in the SLR and can be identified as a research gap. In addition, the need for optimizing DHS supplying cities that require decarbonization strategies in the following years is rising; therefore, the demand for decreased computational time is high. The computational time depends not only on the system’s size but also on the model complexity. In general, the model complexity should always fit the research question. Suppose the research question focused on the thermal design of grid or production units. A detailed pressure model seems unnecessary because the CAPEX for energy converters and storages determine the design optimization (A. Rieder et al., 2013). However, boundaries for the flow in the pipes dependent on the diameter should be considered. Most publications can solve their design optimization with a MILP or LP model with reduced complexity regarding hydraulic equations (see Eq. 14, Eq. 15, and Eq. 16).

Besides model complexity, computational time, and multi-objectivity, the supply system is the key to transforming the DHS. Fuel cells had never been viewed in the literature; however, their significance seems relatively low regarding the results of the heat roadmap Europe. Nevertheless, excess heat from electrolyzes could be a coupling option for DHS. Considering the rising connection to the electric market due to sector-coupling technologies, the importance of storage capacities becomes significant. The total storage capacity in the grid can only be exploited by modeling the forward-flow and the backward-flow–a potential research gap. The design of the DHS’s components was a well-known subject, but their deconstruction in the optimization model had not been done yet.

In addition to the deconstruction of components, the integration of low-grade heat sources is highly relevant for decarbonization favored by a low system temperature. Lowering the system’s temperature can be identified as a research gap in the literature. Wirtz et al. (2019) examined different temperature levels for the DHS to find the optimal operation point for a large-scale heat pump. The heat pump’s efficiency–also called the coefficient of performance (COP)—heavily depends on the sink and source temperature. Usually, the COP is calculated a priori with a model from the literature, e. g. in Jesper et al. (2021). Wirtz et al. (2019) performed a parameter study to calculate different resulting costs in dependency on the forward-flow temperature of the grid. However, the grid was not spatially discretized and worked as one consumer in the optimization. Methods to lower the demanding temperature were combining central and decentralized units, which had only been done for a few publications (see Figure 12), or refurbishment inside the optimization. Both methods are potential research gaps. Besides lowering the system’s temperature, integrating solar thermal energy and PV supports the transformation process. PV and solar thermal energy were represented in the midrange of the literature, but both technologies require space and are competing technologies. This problem was not addressed in the literature for large-scale systems and is a potential research gap. Additionally, geothermal energy and long-term storages are potential research gaps of high significance because they were identified by the heat roadmap Europe as one of the technologies in a future supply system of a DHS.

FIGURE 12

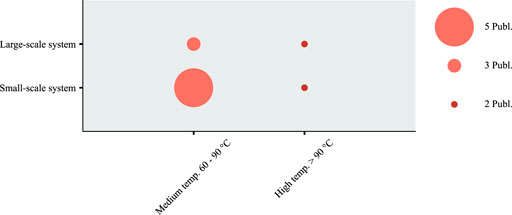
FIGURE 12. Combination of decentral and central units in dependency of system’s size and temperature.

In Section 3.2, four significant publications were analyzed concerning the design decisions of the grid and its supply system. The increased computational power allows the calculation of complex systems, including infrastructural and supply system choices. Utilizing mathematical optimization to support decision-making processes decreases costs and emissions, as shown in the literature. Morvaj et al. (2016) showed that the grid’s design is influenced not only by the consumers but also by the design of the supply system. Optimization algorithms depict these dependencies; however, the analyzed systems are often relatively small. To reduce the computational effort, the grid’s and the supply system’s design are often separated, e. g. in Wirtz et al. (2020). The decarbonization and electrification of the heating sector increase the complexity of the optimization. Optimizing larger systems with design decisions for the grid, a great variety of different technologies, and sector-coupling dependencies is a key challenge for the upcoming years.

Limitations

The major limitation of the SLR came with its advantage; publications with relevance to the topic might have been excluded due to the performed method. The exclusion can occur due to the limitation of databases, keywords, years, or quality measures. In addition, the derived categories might have excluded crucial topic information. The presented equations in Section 3.1.3 were representative, and the mathematical model can significantly vary from publication to publication. The mathematical description should always fit the problem at hand. Nevertheless, Section 3.1.3 showed the most critical energy balances for a problem dealing with designing a DHS thermally.

Conclusion

This work’s main findings were identifying model complexity to answer the research question of design optimization for decarbonized DHS and potential research gaps in the literature. The literature did not yet provide the results to design and transform a large-scale high-temperature DHS into a sustainable system.

Most publications used linear programming models solved with a global solver like Gurobi. If a large-scale system was optimized, a heuristic solver might result in a more efficient solution. Hydraulic equations were primarily neglected in the design optimization of a thermal supply system or grid. Some publications used hydraulic boundaries for the flow velocity, ensuring max. pressure loss in the pipe is not reached. The mathematical description of a DHS is divided into energy balances for pipes, nodes, consumers, and production units. Mostly, the objective was to find a cost-efficient design of the supply system and the grid. Sometimes ecologic factors were integrated, which led to multi-objective optimization. Multi-objective optimization can be performed with two different functions, a weighted sum function, or to run several optimizations with different boundaries for a KPI, e. g. CO₂ emissions. The optimization chose technologies like CHPs, boilers, individual heat pumps, and short-term storages. Most optimization problems concentrated on the central installation of the supply system. In conclusion, this work identified four major research fields:

• depiction of different stakeholder decisions in the DHS regarding the design;

• performance improvement of computational efforts through methods like spatial and temporal aggregation, especially regarding the problem of designing seasonal storages;

• uncertainty analysis for input data and the results;

• structure of a sustainable supply system, including measures for lowering the demanding temperature, integrating energy converters and heat sources like geothermal energy, large-scale heat pumps, seasonal storages, and other low-grade heat sources.

The depiction of different stakeholder decisions is often not the case. The optimizer usually finds a global minimum. However, this minimum might select the decisions of building owners they would never choose. Therefore, the depiction of those decisions, e. g. the connection to DHS, could be interesting for further investigation. Additionally, reducing computational time is always one of the key challenges in optimization. Some researchers apply spatial and temporal aggregation methods causing difficulties in designing seasonal storages due to the shift of time dependencies.

Furthermore, most optimization models base their results on one demand curve per consumer. This curve implies perfect foresight and might result in an energy system not being capable of supplying its consumers if the perfect foresight fails. One solution is the calculation of several scenarios. Then the output data can be analyzed to design a robust energy system. Other solutions often include methods like Monte Carlo simulations resulting in high computational times. Therefore, the analysis of uncertainties is also an important research field. Finally, all questions concerning the design of the grid and the supply system are key challenges in the optimization of DHS.

Besides the research gaps in the existing literature, several trends can be seen in the results. Generally, a carbon-free system benefits from grid-based energy resulting in high connection rates for potential consumers. The supply system’s design shifted from a gas-based supply to an electric-based design. The decarbonization of DHS leads to increased complexity in handling central and decentral units, thermal and electric energy flows and more restrictive boundary conditions due to the limited availability of renewable energies. Mathematical optimization can handle this complexity and increase the efficiency of those systems with cost reduction between 30 and 40%. However, increased complexity often requires higher computational effort. Handling this increased complexity efficiently will be a significant challenge in the optimization community.

Author contributions

MS conducted the research and wrote the manuscript. MiR reviewed the manuscript and supported the graphical design. MaR acquired the financial resources to support the research and reviewed the manuscript.

Funding

The Fraunhofer IEG funded the study with the project ODH@Jülich.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Footnotes

¹Not all European countries are included due to the lack of data.

²Excluded publications: Ryohei Yokoyama et al. (2016); Mojica et al. (2017); Wu et al. (2018); Sameti and Haghighat (2019); Alghool et al. (2020); Scolan et al. (2020); Campos et al. (2021); Halmschlager and Hofmann (2021); Liu et al. (2021); Neri et al. (2022).

³The specific investments for a grid can typically be approximated with 700 €/m (year 2020 in Germany) Steinbach et al. (2020).

References

Alghool, D. M., Elmekkawy, T. Y., Haouari, M., and Elomri, A. (2020). Optimization of design and operation of solar assisted district cooling systems. Energy Convers. Manag. X 6, 100028. doi:10.1016/j.ecmx.2019.100028

CrossRef Full Text | Google Scholar

Arpagaus, C., Bless, F., Uhlmann, M., Schiffmann, J., and Bertsch, S. S. (2018). High temperature heat pumps: Market overview, state of the art, research status, refrigerants, and application potentials. Energy 152, 985–1010. doi:10.1016/j.energy.2018.03.166

CrossRef Full Text | Google Scholar

Baehr, H. D., and Kabelac, S. (2006). Thermodynamik: Grundlagen und technische Anwendungen mit zahlreichen Tabellen. Berlin, Germany: Springer-Verlag Berlin Heidelberg.

Google Scholar

Bartolini, A., Carducci, F., Giovannelli, A., and Comodi, G. (2018). “Optimal planning of low carbon microgrids using primary energy savings as a constraining factor: The case of an industrial retrofit,” in International Conference on Environment and Electrical Engineering and 2018 IEEE industrial and commercial Power Systems Europe New York, USA.

CrossRef Full Text | Google Scholar

Best, R. E., Rezazadeh Kalehbasti, P., and Lepech, M. D. (2020). A novel approach to district heating and cooling network design based on life cycle cost optimization. Energy 194, 116837. doi:10.1016/j.energy.2019.116837

CrossRef Full Text | Google Scholar

Biedermann, F., and Kolb, M. (2014). Nah-/ fernwärme, fact sheet on behalf of the working association of chamber of commerce and industry (HIHK). Munich, Germany.

Google Scholar

Bill, R. (2010). Grundlagen der Geo-informationssysteme. Berlin, Offenbach: Wichmann, 804.

Google Scholar

Blommaert, M., Wack, Y., and Baelmans, M. (2020). An adjoint optimization approach for the topological design of large-scale district heating networks based on nonlinear models. Appl. Energy 280, 116025. doi:10.1016/j.apenergy.2020.116025

CrossRef Full Text | Google Scholar

Bordin, C., Gordini, A., and Vigo, D. (2016). An optimization approach for district heating strategic network design. Eur. J. Operational Res. 252 (1), 296–307. doi:10.1016/j.ejor.2015.12.049

CrossRef Full Text | Google Scholar

Bornand, B., Girardin, L., Belfiore, F., Robineau, J.-L., Bottallo, S., and Maréchal, F. (2020). Investment planning methodology for complex urban energy systems applied to a hospital site. Front. Energy Res. 8. doi:10.3389/fenrg.2020.537973

CrossRef Full Text | Google Scholar

Bracco, S., Dentici, G., and Siri, S. (2013). Economic and environmental optimization model for the design and the operation of a combined heat and power distributed generation system in an urban area. Energy 55, 1014–1024. doi:10.1016/j.energy.2013.04.004

CrossRef Full Text | Google Scholar

Buoro, D., Casisi, M., de Nardi, A., Pinamonti, P., and Reini, M. (2013). Multicriteria optimization of a distributed energy supply system for an industrial area. Energy 58, 128–137. doi:10.1016/j.energy.2012.12.003

CrossRef Full Text | Google Scholar

Campos, G., Liu, Y., Schmidt, D., Yonkoski, J., Colvin, D., Trombly, D. M., et al. (2021). Optimal real-time dispatching of chillers and thermal storage tank in a University campus central plant. Appl. Energy 300, 117389. doi:10.1016/j.apenergy.2021.117389

CrossRef Full Text | Google Scholar

Casisi, M., Buoro, D., Pinamonti, P., and Reini, M. (2019). A comparison of different district integration for a distributed generation system for heating and cooling in an urban area. Appl. Sci. 9 (17), 3521. doi:10.3390/app9173521

CrossRef Full Text | Google Scholar

Corscadden, J., Möhring, P., and Krasatsenka, A. (2021). Transformation of existing urban district heating and cooling systems from fossil to renewable energy sources.

Google Scholar

Dancker, J., Götze, J., Schulz, F., Könneke, N., Beyrau, F., and Wolter, M. (2019). Optimal design and operation of a CHP based district heating system including a heat storage and electrode boiler to increase self-consumption in 2019 IEEE PES Conference on Innovative Smart Grid Technologies, ISGT Latin America.

CrossRef Full Text | Google Scholar

Delubac, R., Serra, S., Sochard, S., and Reneaume, J.-M. (2021). A dynamic optimization tool to size and operate solar thermal district heating networks production plants. Energies 14 (23), 8003. doi:10.3390/en14238003

CrossRef Full Text | Google Scholar

Delubac, R., Serra, S., Sochard, S., and Reneaume, J.-M. (2020). “A multi-period tool to optimize solar thermal integration in district heating networks,” in ECOS 2020 - Proceedings of the 33rd International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems.

Google Scholar

DG Energy (2020). Quarterly report energy on European gas markets: With focus on the impact of global LNG markets on EU gas imports.

Google Scholar

Elsido, C., Bischi, A., Silva, P., and Martelli, E. (2017). Two-stage MINLP algorithm for the optimal synthesis and design of networks of CHP units. Energy 121, 403–426. doi:10.1016/j.energy.2017.01.014

CrossRef Full Text | Google Scholar

EnBW Company (2021). District heating: Energy with a future. Available at https://www.enbw.com/company/the-group/energy-production/district-heating/#:∼:text=With%20an%20average%20annual%20district,district%20heating%20companies%20in%20Germany.&text=In%20such%20transport%20pipes%20with,80%20and%20130%C2%B0C (Accessed June 1, 2022).

Google Scholar

European Commission (2021a). Fernwärmenetze - kapazitäten, Erzeugung und Verluste nach Netztyp und Anlagentyp. Available at https://appsso.eurostat.ec.europa.eu/nui/show.do?dataset=nrg_dhdc_cpl&lang=de (Accessed June 1, 2022).

Google Scholar

European Commission (2021b). Gross derived heat generation by fuel, EU, 2000-2019 (GWh). Available at https://ec.europa.eu/eurostat/statistics-explained/index.php?title=File:Gross_derived_heat_generation_by_fuel,_EU,_2000-2019_(GWh)_T4.png (Accessed June 1, 2022).

Google Scholar

Fazlollahi, S., Becker, G., Ashouri, A., and Maréchal, F. (2015). Multi-objective, multi-period optimization of district energy systems: IV – a case study. Energy 84, 365–381. doi:10.1016/j.energy.2015.03.003

CrossRef Full Text | Google Scholar

Fazlollahi, S., Becker, G., and Maréchal, F. (2014). Multi-objectives, multi-period optimization of district energy systems: II—daily thermal storage. Comput. Chem. Eng. 71, 648–662. doi:10.1016/j.compchemeng.2013.10.016

CrossRef Full Text | Google Scholar

Fitó, J., Hodencq, S., Ramousse, J., Wurtz, F., Stutz, B., Debray, F., et al. (2020). Energy- and exergy-based optimal designs of a low-temperature industrial waste heat recovery system in district heating. Energy Convers. Manag. 211, 112753. doi:10.1016/j.enconman.2020.112753

CrossRef Full Text | Google Scholar

Global Conflict Tracker (2022). Conflict in Ukraine. Available at https://www.cfr.org/global-conflict-tracker/conflict/conflict-ukraine (Accessed June 1, 2022).

Google Scholar

Gurobi, J. (2018). Working with multiple objectives. Available at https://www.gurobi.com/documentation/9.5/refman/working_with_multiple_obje.html (Accessed April 7, 2022).

Google Scholar

Haikarainen, C., Pettersson, F., and Saxén, H. (2016). A decomposition procedure for solving two-dimensional distributed energy system design problems. Appl. Therm. Eng. 100, 30–38. doi:10.1016/j.applthermaleng.2016.02.012

CrossRef Full Text | Google Scholar

Halmschlager, V., Birkelbach, F., and Hofmann, R. (2021). Optimizing the utilization of excess heat for district heating in a chipboard production plant. Case Stud. Therm. Eng. 25, 100900. doi:10.1016/j.csite.2021.100900

CrossRef Full Text | Google Scholar

Halmschlager, V., and Hofmann, R. (2021). Assessing the potential of combined production and energy management in Industrial Energy Hubs – analysis of a chipboard production plant. Energy 226, 120415. doi:10.1016/j.energy.2021.120415

CrossRef Full Text | Google Scholar

Hirsch, P., Duzinkiewicz, K., Grochowski, M., and Piotrowski, R. (2016). Two-phase optimizing approach to design assessments of long distance heat transportation for CHP systems. Appl. Energy 182, 164–176. doi:10.1016/j.apenergy.2016.08.107

CrossRef Full Text | Google Scholar

Jesper, M., Schlosser, F., Pag, F., Walmsley, T. G., Schmitt, B., and Vajen, K. (2021). Large-scale heat pumps: Uptake and performance modelling of market-available devices. Renew. Sustain. Energy Rev. 137, 110646. doi:10.1016/j.rser.2020.110646

CrossRef Full Text | Google Scholar

Kallrath, J. (2013). Gemischt-ganzzahlige Optimierung: Modellierung in der Praxis; mit Fallstudien aus Chemie, Energiewirtschaft, Papierindustrie, Metallgewerbe, Produktion und Logistik. Wiesbaden, Germany: Springer Spektrum, 381p.

Google Scholar

Kausche, M. (2018). Wirtschaftlichkeit schwimmender offshore windenergieanlagen: Wiesbaden. Springer Fachmedien Wiesbaden.

Google Scholar

Khatibi, M., Bendtsen, J. D., Stoustrup, J., and Tougaard, J. (2019). Local heating concepts for upgrading district heating networks, a real world case study in ECOS 2019 - Proceedings of the 32nd International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems, 2019-June.

Google Scholar

Krug, R., Mehrmann, V., and Schmidt, M. (2020). Nonlinear optimization of district heating networks. Optim. Eng. 19 (1), 783–819. doi:10.1007/s11081-020-09549-0

CrossRef Full Text | Google Scholar

Lake, A., Rezaie, B., and Beyerlein, S. (2017). Review of district heating and cooling systems for a sustainable future. Renew. Sustain. Energy Rev. 67, 417–425. doi:10.1016/j.rser.2016.09.061

CrossRef Full Text | Google Scholar

Li, H., and Svendsen, S. (2013). District heating network design and configuration optimization with genetic algorithm. J. Sustain. Dev. energy water Environ. Syst. 1 (4), 291–303. doi:10.13044/j.sdewes.2013.01.0022

CrossRef Full Text | Google Scholar

Li, L., Mu, H., Li, N., and Li, M. (2016). Economic and environmental optimization for distributed energy resource systems coupled with district energy networks. Energy 109, 947–960. doi:10.1016/j.energy.2016.05.026

CrossRef Full Text | Google Scholar

Li, Y., Rezgui, Y., and Zhu, H. (2017). District heating and cooling optimization and enhancement - towards integration of renewables, storage and smart grid. Renew. Sustain. Energy Rev. 72, 281–294. doi:10.1016/j.rser.2017.01.061

CrossRef Full Text | Google Scholar

Liu, B., Bissuel, C., Courtot, F., Gicquel, C., and Quadri, D. (2021). “A hierarchical decomposition approach for the optimal design of a district cooling system,” in Proceedings of the 10th International Conference on Operations Research and Enterprise Systems, 317–328.

CrossRef Full Text | Google Scholar

Lund, H., Østergaard, P. A., Nielsen, T. B., Werner, S., Thorsen, J. E., Gudmundsson, O., et al. (2021). Perspectives on fourth and fifth generation district heating. Energy 227, 120520. doi:10.1016/j.energy.2021.120520

CrossRef Full Text | Google Scholar

Marguerite, C., Bourges, B., and Lacarriere, B. (2013). Application of a district heating network (DHN) model for an ex-ante evaluation to support a multi-sources DH. 80–87.

Google Scholar

Marquant, J. F., Evins, R., Bollinger, L. A., and Carmeliet, J. (2017). A holarchic approach for multi-scale distributed energy system optimisation. Appl. Energy 208, 935–953. doi:10.1016/j.apenergy.2017.09.057

CrossRef Full Text | Google Scholar

Mavromatidis, G., and Petkov, I. (2021). Mango: A novel optimization model for the long-term, multi-stage planning of decentralized multi-energy systems. Appl. Energy 288, 116585. doi:10.1016/j.apenergy.2021.116585

CrossRef Full Text | Google Scholar

Mazhar, A. R., Liu, S., and Shukla, A. (2018). A state of art review on the district heating systems. Renew. Sustain. Energy Rev. 96, 420–439. doi:10.1016/j.rser.2018.08.005

CrossRef Full Text | Google Scholar

Mertz, T., Serra, S., Henon, A., and Reneaume, J.-M. (2016). A MINLP optimization of the configuration and the design of a district heating network: Academic study cases. Energy 117, 450–464. doi:10.1016/j.energy.2016.07.106

CrossRef Full Text | Google Scholar

Mertz, T., Serra, S., Henon, A., and Reneaume, J. M. (2017). A MINLP optimization of the configuration and the design of a district heating network: Study case on an existing site. Energy Procedia 116, 236–248. doi:10.1016/j.egypro.2017.05.071

CrossRef Full Text | Google Scholar

Mojica, J. L., Petersen, D., Hansen, B., Powell, K. M., and Hedengren, J. D. (2017). Optimal combined long-term facility design and short-term operational strategy for CHP capacity investments. Energy 118, 97–115. doi:10.1016/j.energy.2016.12.009

CrossRef Full Text | Google Scholar

Morvaj, B., Evins, R., and Carmeliet, J. (2016). Optimising urban energy systems: Simultaneous system sizing, operation and district heating network layout. Energy 116, 619–636. doi:10.1016/j.energy.2016.09.139

CrossRef Full Text | Google Scholar

Neri, M., Guelpa, E., and Verda, V. (2022). Design and connection optimization of a district cooling network: Mixed integer programming and heuristic approach. Appl. Energy 306, 117994. doi:10.1016/j.apenergy.2021.117994

CrossRef Full Text | Google Scholar

Nussbaumer, T., Thalmann, S., Ardens, A. J., and Ködel, J. (2018). Planungshandbuch fernwärme, study on behalf of EnergieSchweiz. Switzerland: Ittigen.

Google Scholar

Olsthoorn, D., Haghighat, F., and Mirzaei, P. A. (2016). Integration of storage and renewable energy into district heating systems: A review of modelling and optimization. Sol. Energy 136, 49–64. doi:10.1016/j.solener.2016.06.054

CrossRef Full Text | Google Scholar

Ommen, T., Markussen, W. B., and Elmegaard, B. (2016). Lowering district heating temperatures - impact to system performance in current and future Danish energy scenarios. Energy 94, 273–291. doi:10.1016/j.energy.2015.10.063

CrossRef Full Text | Google Scholar

Paardekooper, S., Lund, R. S., Mathiesen, B. V., Chang, M., Petersen, U. R., Grundahl, L., et al. (2018). Heat roadmap Europe 4: Quantifying the impact of low-carbon heating and cooling roadmaps.

Google Scholar

Paiho, S., and Reda, F. (2016). Towards next generation district heating in Finland. Renew. Sustain. Energy Rev. 65, 915–924. doi:10.1016/j.rser.2016.07.049

CrossRef Full Text | Google Scholar

Pantaleo, A. M., Giarola, S., Bauen, A., and Shah, N. (2014a). Integration of biomass into urban energy systems for heat and power. Part I: An MILP based spatial optimization methodology. Energy Convers. Manag. 83, 347–361. doi:10.1016/j.enconman.2014.03.050

CrossRef Full Text | Google Scholar

Pantaleo, A. M., Giarola, S., Bauen, A., and Shah, N. (2014b). Integration of biomass into urban energy systems for heat and power. Part II: Sensitivity assessment of main techno-economic factors. Energy Convers. Manag. 83, 362–376. doi:10.1016/j.enconman.2014.03.051

CrossRef Full Text | Google Scholar

Paperpile, L. L. C. (2012). The top list of academic research databases. Available at https://paperpile.com/g/academic-research-databases/ (Accessed April 6, 2022).

Google Scholar

Quaggiotto, D., Vivian, J., and Zarrella, A. (2021). Management of a district heating network using model predictive control with and without thermal storage. Optim. Eng. 22 (3), 1897–1919. doi:10.1007/s11081-021-09644-w

CrossRef Full Text | Google Scholar

Renaldi, R., Kiprakis, A., and Friedrich, D. (2017). An optimisation framework for thermal energy storage integration in a residential heat pump heating system. Appl. Energy 186, 520–529. doi:10.1016/j.apenergy.2016.02.067

CrossRef Full Text | Google Scholar

Rieder, A., Christidis, A., and Tsatsaronis, G. (2013). “Multi criteria dynamic design optimization of a distributed energy system,” in Proceedings of the 26th International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems.

Google Scholar

Rieder, A., Christidis, A., and Tsatsaronis, G. (2014). Multi criteria dynamic design optimization of a small scale distributed energy system. Energy 74, 230–239. doi:10.1016/j.energy.2014.06.007

CrossRef Full Text | Google Scholar

Röder, J., Meyer, B., Krien, U., Zimmermann, J., Stührmann, T., and Zondervan, E. (2021). Optimal design of district heating networks with distributed thermal energy storages – method and case study. Int. J. Sustain. Energy Plan. Manag. 31, 5–22.

Google Scholar

Rosenkranz, A. (2020). Brennstoffzellenheizung: Kosten, Funktion und Effizienz. Available at https://heizung.de/brennstoffzellenheizung/ (Accessed May 9, 2022).

Google Scholar

Sameti, M., and Haghighat, F. (2019). Hybrid solar and heat-driven district cooling system: Optimal integration and control strategy. Sol. Energy 183, 260–275. doi:10.1016/j.solener.2019.03.034

CrossRef Full Text | Google Scholar

Sameti, M., and Haghighat, F. (2017). Optimization approaches in district heating and cooling thermal network. Energy Build. 140, 121–130. doi:10.1016/j.enbuild.2017.01.062

CrossRef Full Text | Google Scholar

Sarbu, I., Mirza, M., and Crasmareanu, E. (2019). A review of modelling and optimisation techniques for district heating systems. Int. J. Energy Res. 43 (13), 4600–6598. doi:10.1002/er.4600

CrossRef Full Text | Google Scholar

Sarbu, I., Mirza, M., and Crasmareanu, E. (2017). Comprehensive review on modelling and optimisation of district heating systems. Int. Multidiscip. Sci. GeoConference Surv. Geol. Min. Ecol. Manag. SGEM 17–42.

CrossRef Full Text | Google Scholar

Sarbu, I., Mirza, M., and Crasmareanu, E. (2020). Optimisation of district heating systems using heuristic methods: A review. Proc. romanian Acad. Ser. a-mathematics Phys. Tech. Sci. Inf. Sci. 21 (4), 319–328.

Google Scholar

Schütz, T., Remy, S., Fuchs, M., and Müller, D. (2018). “Optimal design of local energy systems considering governmental subsidies: A German case study,” in ECOS 2018 - Proceedings of the 31st International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems.

Google Scholar

Scimago, (2007). Scimago journal & country rank. Available at https://www.scimagojr.com/ (Accessed April 6, 2022).

Google Scholar

Scolan, S., Serra, S., Sochard, S., Delmas, P., and Reneaume, J.-M. (2020). Dynamic optimization of the operation of a solar thermal plant. Sol. Energy 198, 643–657. doi:10.1016/j.solener.2020.01.076

CrossRef Full Text | Google Scholar

Serway, R. A. (2004). Physics for scientist and egineers: United States. Thomson/Brooks/Cole.

Google Scholar

Silveira, C. L. B., Tabares, A., Faria, L. T., and Franco, J. F. (2021). Mathematical optimization versus metaheuristic techniques: A performance comparison for reconfiguration of distribution systems. Electr. Power Syst. Res. 196, 107272. doi:10.1016/j.epsr.2021.107272

CrossRef Full Text | Google Scholar

Stange, P., Matthees, A., and Sander, T. (2018). Operational optimization of energy systems, 25 years – established and promising use cases. Energy Procedia 149, 15–24. doi:10.1016/j.egypro.2018.08.165

CrossRef Full Text | Google Scholar

Steinbach, J., Popovski, E., Henrich, J., Christ, C., Ortner, S., Pehnt, M., et al. (2020). Umfassende Bewertung des Potenzials für eine effiziente Wärme- und Kältenutzung für Deutschland.

Google Scholar

Szypowski, M., Siewierski, T., and Wedzik, A. (2019). Optimization of energy-supply structure in residential premises using mixed-integer linear programming. IEEE Trans. Ind. Electron. 66 (2), 1368–1378. doi:10.1109/tie.2018.2793276

CrossRef Full Text | Google Scholar

Unternährer, J., Moret, S., Joost, S., and Maréchal, F. (2017). Spatial clustering for district heating integration in urban energy systems: Application to geothermal energy. Appl. Energy 190, 749–763. doi:10.1016/j.apenergy.2016.12.136

CrossRef Full Text | Google Scholar

van der Heijde, B., Vandermeulen, A., Salenbien, R., and Helsen, L. (2019). Representative days selection for district energy system optimisation: A solar district heating system with seasonal storage. Appl. Energy 248, 79–94. doi:10.1016/j.apenergy.2019.04.030

CrossRef Full Text | Google Scholar

Vian, A., Bignucolo, F., and Cagnano, A. (2020). “Effects of environmental conditions on the optimal sizing and operation of an energy hub,” in 2020 IEEE International Conference on Environment and Electrical Engineering and 2020 IEEE Industrial and Commercial Power Systems Europe (EEEIC / I CPS Europe), 1–6.

CrossRef Full Text | Google Scholar

vom Brocke, J., Simons, A., Niehaves, B., Riemer, K., Plattfaut, R., and Cleven, A. (2009). in Ecis. Reconstructing the giant: On the importance of rigour in documenting the literature search process.

Google Scholar

vom Brocke, J., Simons, A., Riemer, K., Niehaves, B., Plattfaut, R., and Cleven, A. (2015). Standing on the shoulders of giants: Challenges and recommendations of literature search in information systems research. Commun. Assoc. Inf. Syst. 37.

CrossRef Full Text | Google Scholar

Walter, O., Tremel, A., Prenzel, M., Becker, S., and Schaefer, J. (2020). Techno-economic analysis of hybrid energy storage concepts via flowsheet simulations, cost modeling and energy system design. Energy Convers. Manag. 218, 112955. doi:10.1016/j.enconman.2020.112955

CrossRef Full Text | Google Scholar

Wang, D., Li, X., Marquant, J., Carmeliet, J., and Orehounig, K. (2021a). Advancing the thermal network representation for the optimal design of distributed multi-energy systems. Front. Energy Res. 9. doi:10.3389/fenrg.2021.668124

CrossRef Full Text | Google Scholar

Wang, X., Bie, Z., Liu, F., and Kou, Y. (2021b). Co-optimization planning of integrated electricity and district heating systems based on improved quadratic convex relaxation. Appl. Energy 285, 116439. doi:10.1016/j.apenergy.2021.116439

CrossRef Full Text | Google Scholar

Webster, J., and Watson, R. (2002). Analyzing the past to prepare for the future: Writing a literature review. MIS Q. 26.

Google Scholar

Weinand, J. M., Kleinebrahm, M., McKenna, R., Mainzer, K., and Fichtner, W. (2019). Developing a combinatorial optimisation approach to design district heating networks based on deep geothermal energy. Appl. Energy. 251.

CrossRef Full Text | Google Scholar

Williams, H. P. (2013). Model building in mathematical programming. Chichester: WILEY, 411.

Google Scholar

Wirtz, M., Hahn, M., Schreiber, T., and Müller, D. (2021a). Design optimization of multi-energy systems using mixed-integer linear programming: Which model complexity and level of detail is sufficient? Energy Convers. Manag. 240, 114249. doi:10.1016/j.enconman.2021.114249

CrossRef Full Text | Google Scholar

Wirtz, M., Kivilip, L., Remmen, P., and Müller, D. (2020). 5th generation district heating: A novel design approach based on mathematical optimization. Appl. Energy 260, 114158. doi:10.1016/j.apenergy.2019.114158

CrossRef Full Text | Google Scholar

Wirtz, M., Kivilip, L., Remmen, P., and Müller, D. (2019). “Optimal design and operation of large-scale heat pumps in district heating and cooling systems,” in ECOS 2019 - Proceedings of the 32nd International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems.

Google Scholar

Wirtz, M., Neumaier, L., Remmen, P., and Müller, D. (2021b). Temperature control in 5th generation district heating and cooling networks: An MILP-based operation optimization. Appl. Energy 288, 116608. doi:10.1016/j.apenergy.2021.116608

CrossRef Full Text | Google Scholar

Wu, C., Gu, W., Xu, Y., Jiang, P., Lu, S., and Zhao, B. (2018). Bi-level optimization model for integrated energy system considering the thermal comfort of heat customers. Appl. Energy 232, 607–616. doi:10.1016/j.apenergy.2018.09.212,

CrossRef Full Text | Google Scholar

Yılmaz Balaman, Ş., and Selim, H. (2016). Sustainable design of renewable energy supply chains integrated with district heating systems: A fuzzy optimization approach. J. Clean. Prod. 133, 863–885. doi:10.1016/j.jclepro.2016.06.001

CrossRef Full Text | Google Scholar

Yokoyama, Ryohei, Nakamura, Ryo, Wakui, Tetsuya, and Shinano, Yuji (2016). “Evaluation of performance robustness of a gas turbine cogeneration plant based on a mixed-integer linear model,” in ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, 1–9.

CrossRef Full Text | Google Scholar

Zhang, L., Wang, Y., and Feng, X. (2021). A framework for design and operation optimization for utilizing low-grade industrial waste heat in district heating and cooling. Energies (Basel). 14 (8), 2190. doi:10.3390/en14082190

CrossRef Full Text | Google Scholar