State estimation for dynamic systems with higher-order autoregressive moving average non-Gaussian noise

The classical Kalman filter is a very important state estimation approach, which has been widely used in many engineering applications. The Kalman filter is optimal for linear dynamic systems with independent Gaussian noises. However, the independence and Gaussian assumptions may not be satisfied in practice. On the one hand, modeling physical systems usually results in discrete-time state-space models with correlated process and measurement noises. On the other hand, the noise is non-Gaussian when the system is disturbed by heavy-tailed noise. In this case, the performance of the Kalman filter will deteriorate, or even diverge. This paper is devoted to addressing the state estimation problem of linear dynamic systems with high-order autoregressive moving average (ARMA) non-Gaussian noise. First, a triplet Markov model is introduced to model the system with high-order ARMA noise, since this model relaxes the independence assumption of the hidden Markov model. Then, a new filter is derived based on correntropy, instead of the commonly used minimum mean square error (MMSE), to deal with non-Gaussian noise. Unlike the MMSE, which uses only second-order statistics of error, correntropy can capture second-order and higher-order statistics. Finally, simulation results verify the effectiveness of the proposed algorithm.

1 Introduction

State estimation is a very important problem in many engineering applications, such as energy internet, system control, tracking, and so on [Zandavi and Chung (2019); Zhang et al. (2022)]. These engineering applications are essentially a dynamic system, which is usually described as a state-space model. The hidden Markov model (HMM) is the one of the most commonly used state-space models (Zhang et al. (2018)). For linear case, the state estimation problem is generally solved by the well-known Kalman filter(KF) (Kalman (1960)), which is an optimal filter in the minimum mean square error (MMSE) sense. MMSE is one of the most commonly used cost function in the case of Gaussian noise, and MMSE approach is an estimator which minimizes the mean square error. In addition, a large number of nonlinear filters have been proposed to solve nonlinear estimation problems, such as extended Kalman filter, unscented Kalman filter, cubature Kalman filter, particle filter, to name but a few (Anderson and Moore (2012)).

Although the KF in general performs well, it has rigorous requirements, that is, the process and measurement noises of dynamic systems are independent and Gaussian. However, the independence and Gaussian assumptions do not always hold in practice (Zhang G. et al. (2021)). On one hand, in fact, the noise of most dynamic systems is correlated. Research has shown that modeling physical systems usually results in discrete-time state-space models with correlated process and measurement noises, and some practical applications are explained in (Saha and Gustafsson (2012)). In addition, the dynamic and measurement noise may even high-order (i.e., multi-step) correlated in some severe environments (Zhang D. et al. (2021)). On the other hand, the main reason for using the Gaussian assumption is that it is mathematically simple, but in fact, dynamic systems are usually disturbed by some heavy-tailed impulse noise (Roth et al. (2013)). When the independence and Gaussian assumptions are not satisfied, the KF may fail to output reliable estimation results.

To deal with correlated noise, the traditional method is to reconstruct an HMM by prewhitening processing, and then the classical KF can be used to estimate the state (Bar-Shalom et al. (2001)). Another solution is to characterize dynamic systems with correlated noise through more flexible state-space models, such as the pairwise Markov model (PMM) (Pieczynski and Desbouvries (2003)) and the triplet Markov model (TMM) (Ait-El-Fquih and Desbouvries (2006)). In the PMM, the state and measurement as a whole are regarded as a Markov process, which improves the modeling ability of complex dynamic systems. In the TMM, an auxiliary variable is introduced to completely describe the dynamic systems. This auxiliary variable can play a very significant role in some engineering applications. For example, it can characterize the uncertainty of parameters, non-stationarity and error sources. It has been proved that the TMM is more general than the HMM and the PMM, and it structural advantages make it more preferable in addressing some real-world applications, such as image segmentation (Derrode and Pieczynski (2004)), speech processing (Ait El Fquih and Desbouvries (2005)), target tracking (Zhang et al. (2017); Lehmann and Pieczynski (2020, 2021)), and so on.

For non-Gaussian noise, several approaches have been proposed, which are mainly divided into three categories (Izanloo et al. (2016)). The first is to replace the Gaussian distribution with a more extensive heavy-tailed distribution (Huang et al. (2017)). For example, the Student’s t distribution is one of the most commonly used heavy-tailed distribution. The main disadvantage of heavy-tailed distributions is that they are usually analytically difficult, which brings about that related estimation approaches have no closed form solution. The second is the multiple model technique. In this approach, non-Gaussian noise is represented as a finite sum of Gaussian distribution (Shan et al. (2021)). The main difficulty of this approach is how to design the model set reasonably, and the disadvantage is that the amount of calculation will increase sharply with the increase of the number of models. The third is the Monte Carlo approach, in which a set of weighted random particles are employed to characterize the state (Liu et al. (2018)). Generally, sampling-based algorithms can be categorized into deterministic sampling method and random sampling method. Particularly, in the random sampling method, enough particles can approximate the real state with arbitrary precision, at the cost of expensive computation.

In the past few years, the correntropy-based filtering technology has become an important orientation to solve the state estimation of dynamic systems with non-Gaussian noise (Kulikova (2017); Chen et al. (2017)). In information theory, correntropy is a significant mathematical tool to measure the similarity of two random variables. Unlike the commonly utilized MMSE cost function, which uses only second-order statistic of error, the correntropy captures second-order and higher-order information, and is more suitable for non-Gaussian noise, such as heavy-tailed impulsive noise. Several filtering algorithms based on correntropy have been designed in the framework of HMMs, and they are more robust to non-Gaussian noise than the KF and its variants.

In this paper, we are devoted to addressing the state estimation problem of linear dynamic systems with high-order autoregressive moving average (ARMA) non-Gaussian noise. A new Kalman-like filter is developed in the framework of the TMM based on correntropy. First, we resort to a linear TMM to describe dynamic systems with high-order ARMA noise, since the TMM is more general than the HMM. Second, based on the model, a new Kalman-like filter is derived by using correntropy cost function, instead of the commonly used MMSE cost function. Because correntropy can capture not only second-order but also higher-order statistics of error, the proposed algorithm is more robust to non-Gaussian noise than the traditional filter. Finally, simulation results show the effectiveness of the proposed algorithm.

The rest of the paper is organized as follows. Section 2 is the modeling of linear dynamic systems with high-order ARMA noise. Section 3 derives a new Kalman filter by using correntropy cost function in the framework of the TMM. In Section 4, we validate the proposed algorithm via simulations. Finally, conclusion is provided in Section 5.

2 Modeling of linear dynamic systems with high-order ARMA noise

2.1 Linear hidden markov model

Consider the following linear dynamic system

$\left\{\begin{array}{c}\hfill x_{k+1}=F_k{x}_k+G_k{w}_k\hfill \\ \hfill z_k=H_k{x}_k+v_k\hfill \end{array}\right.(1)$

where k is the time index, $x_k\in {\mathbb{R}}^{n_x}$ is the state vector of dimension n_x, F_k the transition matrix, G_k is the process noise matrix, $w_k\sim \mathcal{N}\left(0,Q_k\right)$ is the process noise, $z_k\in {\mathbb{R}}^{n_z}$ is the measurement vector of dimension n_z, H_k is the measurement matrix, and $v_k\sim \mathcal{N}\left(0,R_k\right)$ is the measurement noise. $\mathcal{N}\left(m,P\right)$ denotes a Gaussian distribution with mean vector m and covariance matrix P.

In general, noise sequences $w={\left\{w_k\right\}}_{k\in \text{IN}}$ and $v={\left\{v_k\right\}}_{k\in \text{IN}}$ are assumed independent, jointly independent and independent of the initial state $x_0\sim \mathcal{N}\left({\widehat{x}}_0,P_0\right)$. Then the state estimate can be obtained by the classical KF, which is an optimal filter in the MMSE sense. However, the independence and Gaussian assumptions that are typically assumed in the HMM do not always hold in practice, such as dynamic systems with high-order ARMA non-Gaussian noise. In this case, the KF may not output reliable estimation results.

2.2 Linear triplet markov model for dynamic systems with high-order ARMA noise

2.2.1 Linear triplet markov chain model

We resort to a linear TMM to describe a linear HMM with correlated noise. Let $x_k\in {\mathbb{R}}^{n_x}$ is the state vector, $z_k\in {\mathbb{R}}^{n_z}$ is the measurement vector, $r_k\in {\mathbb{R}}^{n_r}$ is an auxiliary variable, and ${\zeta }_k={\left[x_k^{\text{T}},r_k^{\text{T}},z_{k-1}^{\text{T}}\right]}^{\text{T}}$. If $\zeta ={\left\{{\zeta }_k\right\}}_{k\in \text{IN}}$ is a Markov process, the following system is called a linear TMM (Ait-El-Fquih and Desbouvries (2006)):

$\underset{{\zeta }_{k+1}}{\underbrace{\left[\begin{array}{c}\hfill x_{k+1}\hfill \\ \hfill r_{k+1}\hfill \\ \hfill z_k\hfill \end{array}\right]}}=\underset{{\mathcal{F}}_k}{\underbrace{\left[\begin{array}{ccc}\hfill {\mathcal{F}}_k^{xx}\hfill & \hfill {\mathcal{F}}_k^{xr}\hfill & \hfill {\mathcal{F}}_k^{xz}\hfill \\ \hfill {\mathcal{F}}_k^{rx}\hfill & \hfill {\mathcal{F}}_k^{rr}\hfill & \hfill {\mathcal{F}}_k^{rz}\hfill \\ \hfill {\mathcal{F}}_k^{zx}\hfill & \hfill {\mathcal{F}}_k^{zr}\hfill & \hfill {\mathcal{F}}_k^{zz}\hfill \end{array}\right]}}\left[\begin{array}{c}\hfill x_k\hfill \\ \hfill r_k\hfill \\ \hfill z_{k-1}\hfill \end{array}\right]+\underset{{\xi }_k}{\underbrace{\left[\begin{array}{c}\hfill {\xi }_k^x\hfill \\ \hfill {\xi }_k^r\hfill \\ \hfill {\xi }_k^z\hfill \end{array}\right]}}(2)$

where $\xi ={\left\{{\xi }_k\right\}}_{k\in \text{IN}}$ is zero mean white noise and independent of the initial state ζ₀.

2.2.2 Modeling high-order ARMA noise using TMM

In this section, we utilize a linear TMM to model dynamic systems with high-order ARMA noise (Zhang D. et al. (2021)). The TMM provides a general framework for these typical stochastic systems.

(1) High-Order ARMA Process Noise.

For high-order ARMA process noise, it can usually be written in the form of the following difference equation:

$w_k=-\sum _{i=1}^{p^w}{\alpha }_i^w{w}_{k-i}+\sum _{i=0}^{q^w}{\beta }_i^w{\xi }_{k-i}^w(3)$

where ${\xi }_k^w$ is white noise. Model (3) is a typical high-order ARMA model, in which p^w is the autoregressive order, q^w is the moving average order, and coefficient parameters ${\alpha }_i^w$ and ${\beta }_i^w$ are determined by the spectral factor $H_k^w\left(z\right)$ of the power spectral density ${\mathrm{\Phi }}_k^w\left(z\right)$ of the process noise w_k.

Suppose ${\mathrm{\Phi }}_k^w\left(z\right)$ is a rational spectrum. According to the spectral decomposition theorem, there is a spectral factor satisfying

${\mathrm{\Phi }}_k^w\left(z\right)=H_k^w\left(z\right)H_k^w{\left(z\right)}^{\ast }(4)$

where ${\left(\cdot \right)}^{\ast }$ represents complex conjugate transpose operation, and $H_k^w\left(z\right)$ can be written by

$H_k^w\left(z\right)=C_k^w{\left(zI-A_k^w\right)}^{-1}{B}_k^w+D_k^w(5)$

Then, high-order ARMA process noise can be formulated by

$\left\{\begin{array}{c}\hfill x_{k+1}^w=A_k^w{x}_k^w+B_k^w{\xi }_k^w\hfill \\ \hfill w_k=C_k^w{x}_k^w+D_k^w{\xi }_k^w\hfill \end{array}\right.(6)$

If the process noise in model 1) is high-order ARMA noise, it can be described by model (6). In this case, $\left\{x_k\right\}$ is no longer a Markov process, but $\left\{\left(x_k,x_k^w\right)\right\}$ is a Markov process. Let ${\zeta }_k=\left(x_k,r_k=x_k^w,z_{k-1}\right)$. Model 1) with (6) can be written in the form of linear TMM (2), i.e.,

$\left[\begin{array}{c}\hfill x_{k+1}\hfill \\ \hfill x_{k+1}^w\hfill \\ \hfill z_k\hfill \end{array}\right]=\left[\begin{array}{ccc}\hfill F_k\hfill & \hfill G_k{C}_k^w\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill A_k^w\hfill & \hfill 0\hfill \\ \hfill H_k\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right]\left[\begin{array}{c}\hfill x_k\hfill \\ \hfill x_k^w\hfill \\ \hfill z_{k-1}\hfill \end{array}\right]+\left[\begin{array}{c}\hfill G_k{D}_k^w{\xi }_k^w\hfill \\ \hfill B_k^w{\xi }_k^w\hfill \\ \hfill v_k\hfill \end{array}\right](7)$

Assuming white noise ${\xi }_k^w\sim \mathcal{N}\left(0,Q_k\right)$, the noise covariance matrix of model 7) is

${\mathcal{Q}}_k=\left[\begin{array}{ccc}\hfill G_k{D}_k^w{Q}_k{\left(D_k^w\right)}^{\text{T}}{G}_k^{\text{T}}\hfill & \hfill G_k{D}_k^w{Q}_k{\left(B_k^w\right)}^{\text{T}}\hfill & \hfill 0\hfill \\ \hfill B_k^w{Q}_k{\left(D_k^w\right)}^{\text{T}}{G}_k^{\text{T}}\hfill & \hfill B_k^w{Q}_k{\left(B_k^w\right)}^{\text{T}}\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill R_k\hfill \end{array}\right](8)$

(2) High-order ARMA Measurement Noise.

For high-order ARMA measurement noise, it can also be written in the following form of difference equation

$v_k=-\sum _{i=1}^{p^v}{a}_i^v{v}_{k-i}+\sum _{i=0}^{q^v}{b}_i^v{\xi }_{k-i}^v(9)$

where ${\xi }_k^v$ is white noise, p^v and q^v are autoregressive order and moving average order, respectively. If the spectral density of high-order ARMA measurement noise is ${\mathrm{\Phi }}_k^v\left(z\right)$ and the corresponding spectral factor is $H_k^v\left(z\right)$, similar to model (6), v_k can be modeled as follows

$\left\{\begin{array}{c}{x}_{k+1}^v=A_k^v{x}_k^v+B_k^v{\xi }_k^v\hfill \\ v_k=C_k^v{x}_k^v+D_k^v{\xi }_k^v\hfill \end{array}\right.(10)$

If the measurement noise in model 1) is high-order ARMA noise, it can be described by model (10). Let ${\zeta }_k=\left(x_k,r_k=x_k^v,z_{k-1}\right)$. Model 1) with (10) can be written in the form of linear TMM (2), i.e.,

$\left[\begin{array}{c}\hfill x_{k+1}\hfill \\ \hfill x_{k+1}^v\hfill \\ \hfill z_k\hfill \end{array}\right]=\left[\begin{array}{ccc}\hfill F_k\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill A_k^v\hfill & \hfill 0\hfill \\ \hfill H_k\hfill & \hfill C_k^v\hfill & \hfill 0\hfill \end{array}\right]\left[\begin{array}{c}\hfill x_k\hfill \\ \hfill x_k^v\hfill \\ \hfill z_{k-1}\hfill \end{array}\right]+\left[\begin{array}{c}\hfill G_k{w}_k\hfill \\ \hfill B_k^v{\xi }_k^v\hfill \\ \hfill D_k^v{\xi }_k^v\hfill \end{array}\right](11)$

Assuming white noise ${\xi }_k^v\sim \mathcal{N}\left(0,R_k\right)$, the noise covariance matrix of model 11) is

${\mathcal{Q}}_k=\left[\begin{array}{ccc}\hfill G_k{Q}_k{G}_k^{\text{T}}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill B_k^v{R}_k{\left(B_k^v\right)}^{\text{T}}\hfill & \hfill B_k^v{R}_k{\left(D_k^v\right)}^{\text{T}}\hfill \\ \hfill 0\hfill & \hfill D_k^v{R}_k{\left(B_k^v\right)}^{\text{T}}\hfill & \hfill D_k^v{R}_k{\left(D_k^v\right)}^{\text{T}}\hfill \end{array}\right](12)$

(3) High-Order ARMA Process and Measurement Noises.

If the process noise and measurement noise are high-order ARMA noises, they can be described by model 6) and model (10), respectively. Let ${\zeta }_k=\left(x_k,r_k=\left(x_k^w,x_k^v\right),z_{k-1}\right)$. Model 1) with (6) and (10) can be written in the form of linear TMM (2), i.e.,

$\left[\begin{array}{c}\hfill x_{k+1}\hfill \\ \hfill \begin{array}{cc}\hfill & x_{k+1}^w\hfill \\ \hfill & x_{k+1}^v\hfill \end{array}\hfill \\ \hfill z_k\hfill \end{array}\right]=\left[\begin{array}{cccc}\hfill F_k\hfill & \hfill G_k{C}_k^w\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill A_k^w\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill A_k^v\hfill & \hfill 0\hfill \\ \hfill H_k\hfill & \hfill 0\hfill & \hfill C_k^v\hfill & \hfill 0\hfill \end{array}\right]\left[\begin{array}{c}\hfill x_k\hfill \\ \hfill \begin{array}{cc}\hfill & x_k^w\hfill \\ \hfill & x_k^v\hfill \end{array}\hfill \\ \hfill z_{k-1}\hfill \end{array}\right]+\left[\begin{array}{c}\hfill G_k{D}_k^w{\xi }_k^w\hfill \\ \hfill B_k^w{\xi }_k^w\hfill \\ \hfill B_k^v{\xi }_k^v\hfill \\ \hfill D_k^v{\xi }_k^v\hfill \end{array}\right](13)$

Assuming white noises ${\xi }_k^w\sim \mathcal{N}\left(0,Q_k\right)$ and ${\xi }_k^v\sim \mathcal{N}\left(0,R_k\right)$, the noise covariance matrix of model 13) is

${\mathcal{Q}}_k=\left[\begin{array}{cccc}\hfill G_k{D}_k^w{Q}_k{\left(D_k^w\right)}^{\text{T}}{G}_k^{\text{T}}\hfill & \hfill G_k{D}_k^w{Q}_k{\left(B_k^w\right)}^{\text{T}}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill B_k^w{Q}_k{\left(D_k^w\right)}^{\text{T}}{G}_k^{\text{T}}\hfill & \hfill B_k^w{Q}_k{\left(B_k^w\right)}^{\text{T}}\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill B_k^v{R}_k{\left(B_k^v\right)}^{\text{T}}\hfill & \hfill B_k^v{R}_k{\left(D_k^v\right)}^{\text{T}}\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill D_k^v{R}_k{\left(B_k^v\right)}^{\text{T}}\hfill & \hfill D_k^v{R}_k{\left(D_k^v\right)}^{\text{T}}\hfill \end{array}\right](14)$

2.3 Restoration algorithm

Let $x_k^{*}=\left(x_k,r_k\right)$. Then model 2) can be written as

$\left[\begin{array}{c}\hfill x_{k+1}^{\ast }\hfill \\ \hfill z_k\hfill \end{array}\right]=\left[\begin{array}{cc}\hfill {\mathcal{F}}_k^{x^{\ast }{x}^{\ast }}\hfill & \hfill {\mathcal{F}}_k^{x^{\ast }z}\hfill \\ \hfill {\mathcal{F}}_k^{z{x}^{\ast }}\hfill & \hfill {\mathcal{F}}_k^{zz}\hfill \end{array}\right]\left[\begin{array}{c}\hfill x_k^{\ast }\hfill \\ \hfill z_{k-1}\hfill \end{array}\right]+\left[\begin{array}{c}\hfill {\xi }_k^{x^{\ast }}\hfill \\ \hfill {\xi }_k^z\hfill \end{array}\right](15)$

where the initial state $x_0^{*}$ and noise ξ_k are

$x_0^{\ast }\sim \mathcal{N}\left({\widehat{x}}_0^{\ast },P_0^{\ast }\right),{\xi }_k\sim \mathcal{N}\left(0,\underset{{\mathcal{Q}}_k}{\underbrace{\left[\begin{array}{cc}\hfill {\mathcal{Q}}_k^{x^{\ast }{x}^{\ast }}\hfill & \hfill {\mathcal{Q}}_k^{x^{\ast }z}\hfill \\ \hfill {\mathcal{Q}}_k^{z{x}^{\ast }}\hfill & \hfill {\mathcal{Q}}_k^{zz}\hfill \end{array}\right]}}\right)(16)$

For model 15) with (16), a Kalman-like filter, called triplet Kalman filter (TKF), has been derived to estimate the state $x_k^{*}$. For convenience, the recursive equations are summarized as follows (Ait-El-Fquih and Desbouvries (2006)).

Initialization:

${\widehat{x}}_{0|0}^{\ast }={\widehat{x}}_0^{\ast },P_{0|0}=P_0^{\ast }(17)$

${\widehat{\mathcal{F}}}_k^{x^{\ast }{x}^{\ast }}={\mathcal{F}}_k^{x^{\ast }{x}^{\ast }}-{\mathcal{Q}}_k^{x^{\ast }z}{\left({\mathcal{Q}}_k^{zz}\right)}^{-1}{\mathcal{F}}_k^{z{x}^{\ast }}(18)$

${\widehat{\mathcal{F}}}_k^{x^{\ast }z}={\mathcal{F}}_k^{x^{\ast }z}-{\mathcal{Q}}_k^{x^{\ast }z}{\left({\mathcal{Q}}_k^{zz}\right)}^{-1}{\mathcal{F}}_k^{zz}(19)$

${\widehat{\mathcal{Q}}}_k^{x^{\ast }{x}^{\ast }}={\mathcal{Q}}_k^{x^{\ast }{x}^{\ast }}-{\mathcal{Q}}_k^{x^{\ast }z}{\left({\mathcal{Q}}_k^{zz}\right)}^{-1}{\mathcal{Q}}_k^{z{x}^{\ast }}(20)$

Prediction:

${\widehat{x}}_{k|k-1}^{\ast }={\widehat{\mathcal{F}}}_{k-1}^{x^{\ast }{x}^{\ast }}{\widehat{x}}_{k-1|k-1}^{\ast }+{\mathcal{Q}}_{k-1}^{x^{\ast }z}{\left({\mathcal{Q}}_{k-1}^{zz}\right)}^{-1}{z}_{k-1}+{\widehat{\mathcal{F}}}_{k-1}^{x^{\ast }z}{z}_{k-2}(21)$

$P_{k|k-1}^{\ast }={\widehat{\mathcal{F}}}_{k-1}^{x^{\ast }{x}^{\ast }}{P}_{k-1|k-1}^{\ast }{\left({\widehat{\mathcal{F}}}_{k-1}^{x^{\ast }{x}^{\ast }}\right)}^{\text{T}}+{\widehat{\mathcal{Q}}}_{k-1}^{x^{\ast }{x}^{\ast }}(22)$

Update:

$e_k=z_k-{\mathcal{F}}_{k-1}^{z{x}^{\ast }}{\widehat{x}}_{k|k-1}^{\ast }-{\mathcal{F}}_{k-1}^{zz}{z}_{k-1}(23)$

$R_{e,k}={\mathcal{F}}_{k-1}^{z{x}^{\ast }}{P}_{k|k-1}^{\ast }{\left({\mathcal{F}}_{k-1}^{z{x}^{\ast }}\right)}^{\text{T}}+{\mathcal{Q}}_{k-1}^{zz}(24)$

$K_k=P_{k|k-1}^{\ast }{\left({\mathcal{F}}_{k-1}^{z{x}^{\ast }}\right)}^{\text{T}}{R}_{e,k}^{-1}(25)$

${\widehat{x}}_{k|k}^{\ast }={\widehat{x}}_{k|k-1}^{\ast }+K_k{e}_k(26)$

$P_{k|k}^{\ast }=\left(I-K_k{\mathcal{F}}_k^{z{x}^{\ast }}\right)P_{k|k-1}^{\ast }(27)$

The TKF is also an optimal filter in the MMSE sense. It in general performs well in Gaussian noise. However, it performance will deteriorate or even diverge when applied to non-Gaussian systems, since the TKF is derived under MMSE criterion, which only uses second-order statistics of error. To solve this problem, in the next section, a new filter is developed by using correntropy cost function, which utilizes not only second-order but also higher-order statistics information.

3 Correntropy-based triplet kalman filter

3.1 Correntropy

Correntropy is a very useful metric tool to measure the similarity of two random variables in information theory (Chen et al. (2017)). For variables X and Y, the correntropy is defined by

$C\left(X,Y\right)=\mathrm{E}\left[\kappa \left(X,Y\right)\right]=\int \kappa \left(x,y\right)d{f}_{XY}\left(x,y\right)(28)$

where $\mathrm{E}\left[\cdot \right]$ is an expectation operator, $\kappa \left(\cdot ,\cdot \right)$ is a kernel function, and $f_{XY}\left(x,y\right)$ is the joint probability density function of X and Y. Generally, $f_{XY}\left(x,y\right)$ is unknown, and only a limited amount of data is provided. Thus, the correntropy can be computed by

$\widehat{C}\left(X,Y\right)=\frac{1}{N}\sum _{i=1}^N\kappa \left(x,y\right).(29)$

There are many options for kernel function. In this paper, we choose the Gaussian kernel function

$\kappa \left(x,y\right)={\mathrm{G}}_{\sigma }\left(x_i-y_i\right),(30)$

where σ is the kernel size, and ${\mathrm{G}}_{\sigma }\left(x_i-y_i\right)=\exp \left(-\frac{{‖x_i-y_i‖}^2}{2{\sigma }^2}\right)$. The Gaussian kernel function is positive definite and bounded. When X = Y, it takes the maximum value.

For the Gaussian kernel function, its Taylor series expansion can be written as

$C\left(X,Y\right)=\sum _{n=0}^{\infty }\frac{{\left(-1\right)}^n}{2^n{\sigma }^{2n}n!}\mathrm{E}\left[{\left(X-Y\right)}^{2n}\right].(31)$

It can be seen that the correntropy is in essence the weighted sum of all even-order moments of error. Compared with the MMSE, which uses only the second-order statistics of error, correntropy captures the second-order and higher-order statistics.

3.2 Main results

In this section, a new filter, called correntropy-based TKF (CTKF), is derived by using correntropy under TMM. For clarity, we first provide the main results, and then give the mathematical derivation.

The initialization and prediction steps of the CTKF are the same as those of the TKF, and its update step is summarized as follows:

$e_k=z_k-{\mathcal{F}}_{k-1}^{z{x}^{\ast }}{\widehat{x}}_{k|k-1}^{\ast }-{\mathcal{F}}_{k-1}^{zz}{z}_{k-1}(32)$

${\lambda }_k={\mathrm{G}}_{\sigma }\left({‖e_k‖}_{{\left(Q_k^{zz}\right)}^{-1}}\right)(33)$

$R_{e,k}={\mathcal{F}}_{k-1}^{z{x}^{\ast }}{P}_{k|k-1}^{\ast }{\left({\mathcal{F}}_{k-1}^{z{x}^{\ast }}\right)}^{\text{T}}+{\mathcal{Q}}_{k-1}^{zz}(34)$

$K_k^{\lambda }={\lambda }_k{P}_{k|k-1}^{\ast }{\left({\mathcal{F}}_{k-1}^{z{x}^{\ast }}\right)}^{\text{T}}{R}_{e,k}^{-1}(35)$

${\widehat{x}}_{k|k}^{\ast }={\widehat{x}}_{k|k-1}^{\ast }+K_k^{\lambda }{e}_k(36)$

$P_{k|k}^{\ast }=\left(I-K_k^{\lambda }{\mathcal{F}}_k^{z{x}^{\ast }}\right)P_{k|k-1}^{\ast }(37)$

Proof. For the linear TMM (2), we have

$\left[\begin{array}{c}\hfill {\widehat{x}}_{k|k-1}^{\ast }\hfill \\ \hfill z_k\hfill \end{array}\right]=\left[\begin{array}{c}\hfill I\hfill \\ \hfill {\mathcal{F}}_k^{z{x}^{\ast }}\hfill \end{array}\right]x_k^{\ast }+\left[\begin{array}{c}\hfill 0\hfill \\ \hfill {\mathcal{F}}_k^{zz}\hfill \end{array}\right]z_{k-1}+{\eta }_k(38)$

where I and 0 are identity and zeros matrices, and

${\eta }_k=\left[\begin{array}{c}\hfill -\left(x_k^{\ast }-{\widehat{x}}_{k|k-1}^{\ast }\right)\hfill \\ \hfill w_k^z\hfill \end{array}\right]\text{with}\mathrm{E}\left[{\eta }_k{\eta }_k^{\text{T}}\right]=\left[\begin{array}{cc}\hfill P_{k|k-1}^{\ast }\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill {\mathcal{Q}}_k^{zz}\hfill \end{array}\right](39)$

To address non-Gaussian noise, we use correntropy instead of MMSE to derive update equations. The cost function based on correntropy is established by

$\begin{array}{ll}\hfill J\left(x_k^{\ast }\right)& ={\mathrm{G}}_{\sigma }\left({‖z_k-{\mathcal{F}}_k^{z{x}^{\ast }}{x}_k^{\ast }-{\mathcal{F}}_k^{zz}{z}_{k-1}‖}_{{\left(Q_k^{zz}\right)}^{-1}}\right)\hfill \\ \hfill & +{\mathrm{G}}_{\sigma }\left({‖x_k^{\ast }-{\widehat{x}}_{k|k-1}^{\ast }‖}_{{\left(P_{k|k-1}^{\ast }\right)}^{-1}}\right)\hfill \end{array}(40)$

Then the optimal estimation of $x_k^{\ast }$ is ${\widehat{x}}_k^{\ast }=\arg \underset{x_k^{\ast }}{\max }J\left(x_k^{\ast }\right)$, which can be obtained by

$\begin{array}{cc}\hfill \frac{\partial J\left(x_k^{\ast }\right)}{\partial x_k^{\ast }}& =\frac{1}{{\sigma }^2}{\mathrm{G}}_{\sigma }\left({‖z_k-{\mathcal{F}}_k^{z{x}^{\ast }}{x}_k^{\ast }-{\mathcal{F}}_k^{zz}{z}_{k-1}‖}_{{\left(Q_k^{zz}\right)}^{-1}}\right)\hfill \\ \hfill & {\left({\mathcal{F}}_k^{z{x}^{\ast }}\right)}^{\text{T}}{\left(Q_k^{zz}\right)}^{-1}\left(z_k-{\mathcal{F}}_k^{z{x}^{\ast }}{x}_k^{\ast }-{\mathcal{F}}_k^{zz}{z}_{k-1}\right)\hfill \\ \hfill & -\frac{1}{{\sigma }^2}{\mathrm{G}}_{\sigma }\left({‖x_k-{\widehat{x}}_{k|k-1}^{\ast }‖}_{{\left(P_{k|k-1}^{\ast }\right)}^{-1}}\right){\left(P_{k|k-1}^{\ast }\right)}^{-1}\hfill \\ \hfill & \left(x_k-{\widehat{x}}_{k|k-1}^{\ast }\right)\hfill \\ \hfill & =0.\hfill \end{array}(41)$

Equation 41 can be written by

$\begin{array}{ll}\hfill {\Psi }_k{x}_k^{\ast }& ={\left(P_{k|k-1}^{\ast }\right)}^{-1}{\widehat{x}}_{k|k-1}^{\ast }+{\lambda }_k{\left({\mathcal{F}}_k^{z{x}^{\ast }}\right)}^{\text{T}}{\left(Q_k^{zz}\right)}^{-1}\hfill \\ \hfill & \left(z_k-{\mathcal{F}}_k^{zz}{z}_{k-1}\right)\hfill \end{array}(42)$

where

${\Psi }_k={\left(P_{k|k-1}^{\ast }\right)}^{-1}+{\lambda }_k{\left({\mathcal{F}}_k^{z{x}^{\ast }}\right)}^{\text{T}}{\left(Q_k^{zz}\right)}^{-1}{\mathcal{F}}_k^{z{x}^{\ast }},(43)$

${\lambda }_k=\frac{{\mathrm{G}}_{\sigma }\left({‖z_k-{\mathcal{F}}_k^{z{x}^{\ast }}{x}_k^{\ast }-{\mathcal{F}}_k^{zz}{z}_{k-1}‖}_{{\left(Q_k^{zz}\right)}^{-1}}\right)}{{\mathrm{G}}_{\sigma }\left({‖x_k^{\ast }-{\widehat{x}}_{k|k-1}^{\ast }‖}_{{\left(P_{k|k-1}^{\ast }\right)}^{-1}}\right)}.(44)$

Adding and subtracting a term ${\lambda }_k{\left({\mathcal{F}}_k^{z{x}^{\ast }}\right)}^{\text{T}}{\left(Q_k^{zz}\right)}^{-1}{\mathcal{F}}_k^{z{x}^{\ast }}{\widehat{x}}_{k|k-1}^{\ast }$ on the right-hand side of (42), we have

$\begin{array}{ll}\hfill {\Psi }_k{x}_k^{\ast }& ={\Psi }_k{\widehat{x}}_{k|k-1}^{\ast }+{\lambda }_k{\left({\mathcal{F}}_k^{z{x}^{\ast }}\right)}^{\text{T}}{\left(Q_k^{zz}\right)}^{-1}\hfill \\ \hfill & \left(z_k-{\mathcal{F}}_k^{z{x}^{\ast }}{\widehat{x}}_{k|k-1}^{\ast }-{\mathcal{F}}_k^{zz}{z}_{k-1}\right).\hfill \end{array}(45)$

Thus, the estimation of $x_k^{\ast }$ can be computed by

${\widehat{x}}_{k|k}^{\ast }={\widehat{x}}_{k|k-1}^{\ast }+K_k^{\lambda }\left(z_k-{\mathcal{F}}_k^{z{x}^{\ast }}{\widehat{x}}_{k|k-1}^{\ast }-{\mathcal{F}}_k^{zz}{z}_{k-1}\right)(46)$

where

$K_k^{\lambda }={\Psi }_k^{-1}{\lambda }_k{\left({\mathcal{F}}_k^{z{x}^{\ast }}\right)}^{\text{T}}{\left(Q_k^{zz}\right)}^{-1}(47)$

Note that the parameter λ_k is function of $x_k^{\ast }$. For simplicity, let $x_k^{\ast }\approx {\widehat{x}}_{k|k-1}^{\ast }$ in (44), and λ_k can be obtained by

${\lambda }_k={\mathrm{G}}_{\sigma }\left({‖z_k-{\mathcal{F}}_k^{z{x}^{\ast }}{\widehat{x}}_{k|k-1}^{\ast }-{\mathcal{F}}_k^{zz}{z}_{k-1}‖}_{{\left(Q_k^{zz}\right)}^{-1}}\right)(48)$

In addition, parameter σ plays an important role in correntropy-based filters. Inspired by (Kulikova (2017)), this paper adopts an adaptive method to choose σ, i.e.,

$\sigma ={‖z_k-{\mathcal{F}}_k^{z{x}^{\ast }}{\widehat{x}}_{k|k-1}^{\ast }-{\mathcal{F}}_k^{zz}{z}_{k-1}‖}_{{\left(Q_k^{zz}\right)}^{-1}}(49)$

In this section, a CTKF is developed to address the estimation problem of dynamic systems with high-order ARMA non-Gaussian noise. Instead of the commonly used MMSE criterion, which uses only second-order statistics of error, correntropy is employed to derive the filter, since it can captures second-order and higher-order statistics of error. It can be seen that the structure of CTKF is similar to that of TKF, except that an extra scale parameter λ_k is involved. The scale parameter is computed according to correntropy criterion to control the gain matrix $K_k^{\lambda }$, which results in that the CTKF in general performs well for non-Gaussian noise. In addition, the CTKF has a simple form, which facilitates its practical application.

4 Numerical simulations

In this section, two scenarios, i.e., dynamic system with high-order ARMA Gaussian and non-Gaussian noise, are taken into account to verify the effectiveness of the TMM and CTKF. In model (1), the state is $x_k={\left[p_{x,k},v_{x,k},p_{y,k},v_{y,k}\right]}^{\text{T}}$, and relevant matrices are

$\begin{array}{ll}\hfill & F_k=\left[\begin{array}{cccc}\hfill 1\hfill & \hfill T\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill T\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill \end{array}\right],G_k=\left[\begin{array}{cc}\hfill \frac{T^2}{2}\hfill & \hfill 0\hfill \\ \hfill T\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill \frac{T^2}{2}\hfill \\ \hfill 0\hfill & \hfill T\hfill \end{array}\right],\hfill \\ \hfill & H_k=\left[\begin{array}{cccc}\hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill 0\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \end{array}\right]\hfill \end{array}(50)$

where T = 1 is the sampling period. The spectral factors of process and measurement noises are

$H^w\left(z\right)=\frac{z^4-0.4z^3+0.9z^2-0.1z-0.3}{z^4-z^3+0.5z^2+0.2z-0.4}(51)$

$H^v\left(z\right)=\frac{z^6+0.6z^5+0.4z^4+0.3z^3-0.08z^2+0.05z+0.01}{z^6+0.8z^5+0.6z^4+0.2z^3-0.09z^2-0.08z+0.01}(52)$

Case 1: ${\xi }_k^w\sim \mathcal{N}\left(0,Q_k\right)$ and ${\xi }_k^v\sim \mathcal{N}\left(0,R_k\right)$ are Gaussian noises, where $Q_k=\text{diag}\left({0.01}^2,{0.01}^2\right)$ and $R_k=\text{diag}\left({0.1}^2,{0.1}^2\right)$. For comparison, the standard Kalman filter (KF), the traditional state augmented Kalman filter (SAKF) (Bar-Shalom et al. (2001)), and the triplet Kalman filter (TKF) are tested. Besides, the root mean square error (RMSE) is used to evaluate estimation performance, which is computed by

$\text{RMSE}=\sqrt{\frac{1}{M}\sum _{i=1}^M\left({\left(x_k^i-{\widehat{x}}_k^i\right)}^2+{\left(y_k^i-{\widehat{y}}_k^i\right)}^2\right)}(53)$

where $x_k^i$ and $y_k^i$ are the true values at time k in the ith Monte Carlo trail, and ${\widehat{x}}_k^i$ and ${\widehat{y}}_k^i$ are the corresponding estimation values. The number of Monte Carlo trails is M = 200.

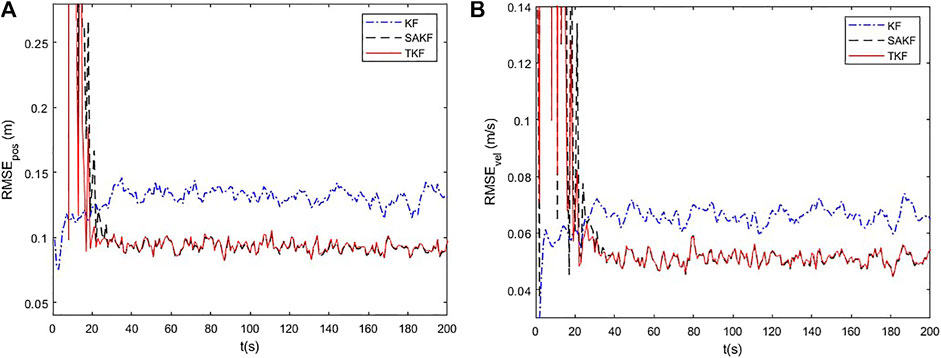
Position and velocity RMSE results are provided in Figure 1. It can be seen that the TKF and SAKF have similar estimation performance, and are better than the standard KF. High-order ARMA process and measurement noises do not meet the independence assumption, resulting in poor estimation performance of the KF. The TKF and SAKF are essentially equivalent, and they are optimal in the MMSE sense. The former models dynamic system with high-order ARMA noise through TMM, and the latter deals with high-order ARMA noise through prewhitening technique. Simulation results show that TMM can accurately model dynamic systems with high-order ARMA noise.

FIGURE 1

FIGURE 1. RMSE results for different filters. (A) Position RMSE. (B) Velocity RMSE.

Case 2: ${\xi }_k^w\sim \mathcal{N}\left(0,Q_k\right)$ and ${\xi }_k^v\sim \mathcal{N}\left(0,R_k\right)$ are Gaussian noise disturbed by shot noise with probability of 0.2, where Q_k and R_k are the same as those in case 1, and the shot noise is generated by 0.1 ×randi([5, 10]). Symbol randi([a, b]) denotes that an integer is returned from the uniform distribution of [a, b].

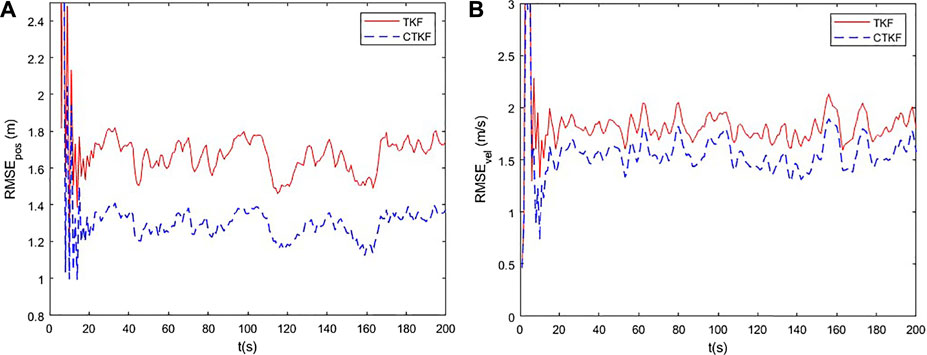
For comparison, the TKF and the proposed CTKF are tested. Position and velocity RMSE results are provided in Figure 2. It can be seen that the CTKF performs better than the TKF. Non-Gaussian noise results in the poor estimation performance of the TKF, since it adopts the MMSE criterion, which uses only second-order statistic of error. The CTKF shows stronger robustness to non-Gaussian noise, because the adopted correntropy cost function can capture second-order and higher-order statistics of error. Simulation results show that the CTKF is an effective state estimation method for dynamic systems with high-order ARMA non-Gaussian noise.

FIGURE 2

FIGURE 2. RMSE results for different filters. (A) Position RMSE. (B) Velocity RMSE.

5 Conclusion

In this paper, a new filter is designed to solve the state estimation problem of dynamic systems with high-order ARMA non-Gaussian noise. In this filter, high-order ARMA process and measurement noises are modeled in the TMM framework, and then the recursive algorithm is derived by using corretropy cost function. On the one hand, the TMM is more general than the HMM, and it can directly model dynamic systems with high-order ARMA noise. On the other hand, correntropy can capture second-order and higher-order statistics of error, and is more suitable for non-Gaussian noise than the MMSE cost function, which uses only second-order statistics of error. In addition, the CTKF has a simple form, which facilitates its practical application.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

GZ provided the idea of the work and organized the manuscript, LZ performed the experiment, FL provided revisions to this paper, XL designed experimental scenarios, and NF and SD conducted data analysis.

Funding

This work is supported by National Natural Science Foundation of China under Grants 62103318 and 62173266.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2022.990267/full#supplementary-material

References

Ait El Fquih, B., and Desbouvries, F. (2005). “Kalman filtering for triplet Markov chains : Applications and extensions,” in IEEE International Conference on Acoustics, Speech and Signal Processing, ICASSP, Philadelphia, PA, USA, 685–688. vol. IV. doi:10.1109/ICASSP.2005.1416101

CrossRef Full Text | Google Scholar

Ait-El-Fquih, B., and Desbouvries, F. (2006). Kalman filtering in triplet Markov chains. IEEE Trans. Signal Process. 54, 2957–2963. doi:10.1109/TSP.2006.877651

CrossRef Full Text | Google Scholar

Anderson, B. D., and Moore, J. B. (2012). Optimal filtering. New York: Courier Corporation.

Google Scholar

Bar-Shalom, Y., Li, X. R., and Kirubarajan, T. (2001). Estimation with applications to tracking and navigation: Theory, algorthims and software. New York: Wiley.

Google Scholar

Chen, B., Liu, X., Zhao, H., and Principe, J. C. (2017). Maximum correntropy kalman filter. Automatica 76, 70–77. doi:10.1016/j.automatica.2016.10.004

CrossRef Full Text | Google Scholar

Derrode, S., and Pieczynski, W. (2004). Signal and image segmentation using pairwise Markov chains. IEEE Trans. Signal Process. 52, 2477–2489. doi:10.1109/TSP.2004.832015

CrossRef Full Text | Google Scholar

Huang, Y., Zhang, Y., Li, N., Wu, Z., and Chambers, J. A. (2017). A novel robust Student’s t-based kalman filter. IEEE Trans. Aerosp. Electron. Syst. 53, 1545–1554. doi:10.1109/TAES.2017.2651684

CrossRef Full Text | Google Scholar

Izanloo, R., Fakoorian, S. A., Yazdi, H. S., and Simon, D. (2016). “Kalman filtering based on the maximum correntropy criterion in the presence of non-Gaussian noise,” in 2016 Annual Conference on Information Science and Systems, CISS, Princeton, NJ, USA, 500–505. doi:10.1109/CISS.2016.7460553

CrossRef Full Text | Google Scholar

Kalman, R. E. (1960). A new approach to linear filtering and prediction problems. J. Basic Eng. 82, 35–45. doi:10.1115/1.3662552

CrossRef Full Text | Google Scholar

Kulikova, M. V. (2017). Square-root algorithms for maximum correntropy estimation of linear discrete-time systems in presence of non-Gaussian noise. Syst. Control Lett. 108, 8–15. doi:10.1016/j.sysconle.2017.07.016

CrossRef Full Text | Google Scholar

Lehmann, F., and Pieczynski, W. (2021). Reduced-dimension filtering in triplet markov models. IEEE Trans. Autom. Contr. 67, 605–617. doi:10.1109/TAC.2021.3050721

CrossRef Full Text | Google Scholar

Lehmann, F., and Pieczynski, W. (2020). Suboptimal kalman filtering in triplet markov models using model order reduction. IEEE Signal Process. Lett. 27, 1100–1104. doi:10.1109/LSP.2020.3002420

CrossRef Full Text | Google Scholar

Liu, X., Qu, H., Zhao, J., and Yue, P. (2018). Maximum correntropy square-root cubature kalman filter with application to SINS/GPS integrated systems. ISA Trans. 80, 195–202. doi:10.1016/j.isatra.2018.05.001

PubMed Abstract | CrossRef Full Text | Google Scholar

Pieczynski, W., and Desbouvries, F. (2003). “Kalman filtering using pairwise Gaussian models,” in IEEE International Conference on Acoustics, Speech, and Signal Processing, ICASSP 2003, Hong Kong, China, 57–60. doi:10.1109/ICASSP.2003.1201617

CrossRef Full Text | Google Scholar

Roth, M., özkan, E., and Gustafsson, F. (2013). “A Student’s t filter for heavy tailed process and measurement noise,” in IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 5770–5774. doi:10.1109/ICASSP.2013.6638770

CrossRef Full Text | Google Scholar

Saha, S., and Gustafsson, F. (2012). Particle filtering with dependent noise processes. IEEE Trans. Signal Process. 60, 4497–4508. doi:10.1109/TSP.2012.2202653

CrossRef Full Text | Google Scholar

Shan, C., Zhou, W., Jiang, Z., and Shan, H. (2021). A new Gaussian approximate filter with colored non-stationary heavy-tailed measurement noise. Digit. Signal Process. 122, 103358. doi:10.1016/j.dsp.2021.103358

CrossRef Full Text | Google Scholar

Zandavi, S. M., and Chung, V. (2019). State estimation of nonlinear dynamic system using novel heuristic filter based on genetic algorithm. Soft Comput. 23, 5559–5570. doi:10.1007/s00500-018-3213-y

CrossRef Full Text | Google Scholar

Zhang, D., Duan, Z., Wang, P., and Zhang, Y. (2021a). “Spacecraft state estimation with multichannel higher-order ARMA colored noises,” in 2021 International Conference on Control, Automation and Information Sciences (ICCAIS) (Xi'an, China: IEEE), 602–607. doi:10.1109/ICCAIS52680.2021.9624490

CrossRef Full Text | Google Scholar

Zhang, G. H., Han, C. Z., Lian, F., and Zeng, L. H. (2017). Cardinality balanced multi-target multi-Bernoulli filter for pairwise markov model. Acta Autom. Sin. 43, 2100–2108. doi:10.16383/j.aas.2017.c160430

CrossRef Full Text | Google Scholar

Zhang, G., Lan, J., Zhang, L., He, F., and Li, S. (2021b). Filtering in pairwise markov model with Student’s t non-stationary noise with application to target tracking. IEEE Trans. Signal Process. 69, 1627–1641. doi:10.1109/TSP.2021.3062170

CrossRef Full Text | Google Scholar

Zhang, G., Lian, F., Han, C., Chen, H., and Fu, N. (2018). Two novel sensor control schemes for multi-target tracking via delta generalised labelled multi-Bernoulli filtering. IET signal Process. 12, 1131–1139. doi:10.1049/iet-spr.2018.5124

CrossRef Full Text | Google Scholar

Zhang, X., Liang, H., Feng, J., and Tan, H. (2022). Kalman filter based high precision temperature data processing method. Front. Energy Res. 10, 832346. doi:10.3389/fenrg.2022.832346

CrossRef Full Text | Google Scholar