- 1The First Sub-Institute, Nuclear Power Institute of China, Chengdu, China
- 2School of Materials Science and Engineering, Xi’an University of Technology, Xi’an, China
- 3School of Material Science and Engineering, Northwestern Polytechnical University, Xi’an, China
Due to the superior thermal conductivity and high uranium density, U3Si2 is an excellent candidate for conventional UO2 nuclear fuel and shows great potential application in accident-tolerant fuel (ATF) assembly of light water reactors (LWRs). Currently, the behavior of Xe bubbles with internal or applied stress is rarely investigated, restricting further understanding of swelling in U3Si2. The mesoscopic phase-field method has been developed in this work to study the spatial and temporal Xe bubble evolution in U3Si2. The results show that the bubble density and its average size increase as the fission rate increases. Applied stress accelerates the nucleation and growth of gas bubbles, reshaping the bubbles’ morphology from spherical in a stress-free state into elongated along the applied direction in a stressed state. The gas bubbles in a local dislocation stress field nucleate preferentially at stress-concentrated sites and spread over the whole system in succession, and the bubble coarsening is controlled by the stress overlap of the dislocation pair. The results show a practical phase-field method for Xe bubble evolution study in U3Si2, which can be expanded into swelling behavior investigation in other fuels and lay a solid foundation for the development of ATF assembly.
1 Introduction
U3Si2 has been considered a promising accident-tolerant fuel (ATF) to take the place of the UO2 pellets clad in Zircaloy used in light water reactors (LWRs) since the Fukushima-Daiichi accident (Bischoff, 2014). The reasons ascribed to the U3Si2 show higher thermal conductivity and uranium density than UO2 (White et al., 2015) though it has a lower melting temperature than UO2 (Miao et al., 2018). Owing to the extremely low solubility in the nuclear fuel, the fission gas atoms produced during the nuclear reaction process tend to accumulate in voids or grain boundaries. The voids or grain boundaries filled with gases form gas bubbles, leading to fuel pellets’ volume swelling and cracking, affecting fuel performance and the reactors’ safety. Hence, predicting and understanding gas bubble evolution is crucial for the scientific design of U3Si2 nuclear fuel, optimizing fuel operation, and reducing uncertainty in operational and safety margins. We know that the swelling of dispersion U3Si2 fuel is a significant issue in research reactors (Finlay et al., 2004); however, the swelling mechanism remains unclear when U3Si2 fuel is used in the typical temperature and fission rate of commercial LWRs.
Up to now, we lack available experimental data in light water reactors due to the oxidation of the U3Si2 samples at a specific temperature and fission rate. Therefore, researchers are considering using computer simulation to study the performance of U3Si2 fuel. On the other hand, gas bubble evolution in U3Si2 nuclear fuel is a highly complex process that involves tremendous time and length scales from the scale of femtoseconds and nanometers to the scale of years and meters; thus, it is popular to study U3Si2 using a multiscale simulation method. The phase-field simulation is a mesoscopic method based on the Ginzburg–Landau phase transition theory. It can deal with large length and time-scale issues such as the evolution of voids and bubbles under irradiation. Other approaches with comparable length and time-scales to the phase-field are kinetic Monte Carlo methods (KMC) (Soneda et al., 2003; Caturla et al., 2006; Torre et al., 2006), object kinetic Monte Carlo (OKMC) (Domain et al., 2004; Surh et al., 2004), cluster dynamics (Xu et al., 2012a; Xu et al., 2012b), and rate theory (Veshchunov, 2000; Surh et al., 2005; Bonilla et al., 2006; Veshchunov et al., 2006; Ortiz et al., 2007; Veshchunov et al., 2007). These studies have been used to study nuclear materials and provide us with helpful knowledge. The phase-field method is advantageous in taking into account the local microstructure inhomogeneity and long-range elastic interactions, making it capable of modeling the evolution of the microstructure and properties in U3Si2 and bridging atomistic and macroscopic simulations.
The evolution of gas bubbles is affected by two main factors: fuel fabrication conditions, such as stress and grain size, and operation conditions of reactors, such as temperature and fission rate. Due to the initial stage of different types of bubbles being considered to be similar that start as isolated fission gas atoms inside grains, understanding the mechanism of the nucleation and growth of intragranular bubbles plays a critical role. Some typical phase-field models have been proposed to study the evolution of bubbles in irradiated materials (Stan et al., 2007; Hu et al., 2009; Hu et al., 2010; Millett et al., 2011; Millett and Tonks, 2011; Millett et al., 2012a; Millett et al., 2012b; Li et al., 2013; Hu et al., 2015; Hu et al., 2016; Xiao et al., 2020). Few phase-field models can reproduce the stable intragranular gas bubble morphological changes upon irradiation. These models consider factors such as initial bubble density and the contact angle. However, they do not sufficiently consider the fuel fabrication conditions, such as stress and operating conditions of reactors in service, especially related to the extremely important ATF fuel U3Si2. Aagesen et al. (2020) developed a model for U3Si2 intergranular fission gas bubble behavior in LWRs. This phase-field model studied the growth, interconnection, and venting of intergranular fission gas bubbles, as well as determined fractional grain boundary coverage at gas saturation. Larry revealed the behaviors of intergranular fission gas bubbles but did not refer to intragranular gas bubbles in U3Si2 under different operating conditions. Wang et al. (2022) employed a phase-field model to describe the evolution of intragranular gas bubbles in tungsten under external loading. They found that intragranular fission gas bubbles vary with the direction and magnitude of external loading, and bubbles growth is accelerated along the loading direction. All the aforementioned studies provide us with a knowledgeable understanding of bubbles. It is well known that microstructures inhomogeneous are pretty common in materials in service.
The microstructures’ inhomogeneity will cause local elastic energy or interface energy, which will not only affect the spatial distribution of the vacancy and gas atom but also their combination in the crystal, further affecting the formation of bubbles. The influence of internal microstructures on bubble formation is scarcely mentioned. The stress, irradiation, and microstructures’ inhomogeneous effect on gas bubble formation wait to be revealed. Our current work provides a more comprehensive phase-field model of gas bubble evolution, a better understanding of intragranular Xe bubble evolution, and a solid foundation for the future study of the nucleation and growth of intergranular Xe bubble in U3Si2 fuel.
In this work, we mainly control three variables, the fission rate, applied stress, and dislocation stress field, to study their influence on intragranular Xe bubble evolution. The work is organized as follows. Section 2 presents the functional free energy and equation of motion to illustrate the model construction procedure. Section 3 demonstrates the Xe bubble evolution diagram for various fission rates (Section 3.1), bubbles upon applied stress (Section 3.2), and bubbles in a dislocation dipole stress field (Section 3.3). Section 4 draws the main conclusions.
2 Phase-field model formulation and parametrization
In this section, we develop a two-dimensional phase-field model with the assumption that the dominant defect species are U vacancies and fission gas atoms on U lattice sites. The insoluble fission gas atoms are described as Xe on U sites due to Xe production occurring at a rate nearly ten times that of Kr (Olander, 1976). Moreover, the phase-field model describes the evolution of intragranular Xe bubbles in U3Si2 fuels under irradiation conditions. The irradiated interstitials diffuse several orders of magnitude faster than vacancies; they either recombine quickly with vacancies or become trapped by dislocations and grain boundaries, leaving abundant vacancies and fission gas atoms interior. Hence, only gas atoms and vacancies are considered in formulating the functional free energy. In general, the total free energy F of the system is written as a function of phase-field variables cgas (for gaseous atoms) and cvac (for vacancies).
The total free energy F is a volume integral of free energy density, which consists of chemical energy, gradient energy, and elastic interaction energy. F(cgas, cvac) is the chemical energy. κgas and κvac are gradient coefficients associated with the gradient energy of gas bubbles, Felastic is the elastic energy associated with the stress field, and cgas(r,t) and cvac(r,t) represent the gas atom concentration and vacancy concentration at site r and time t.
2.1 Chemical energy
The evolution of Xe bubbles in the phase-field model is driven by the minimization of the total free energy of the system. Chemical energy is a crucial part of the total free energy of the system, and it is usually difficult to calculate the chemical free energy of U3Si2 fuel when defects and irradiation-induced phases are considered. Based on the simulation observations of gas bubbles (Hu et al., 2009), we give the form of chemical energy as
where fvac, fgas, fbind, b0, b1, b2, and b3 are constants, and constant fbind is associated with the binding energy between vacancy and gas atom. Here, fgas, fvac, b0, b1, b2, and b3 are affected by the equilibrium properties, and
2.2 Elastic energy
The fuels suffer mechanical or thermal stress upon processing or heat treatment, and they may also be subjected to complicated applied stress in service. In addition to that, various inner inhomogeneous microstructures, such as dislocations or defect clusters, will also inevitably introduce local distortion. These applied or internal stresses cause gas atoms or vacancies to diffuse directionally, reshaping the bubbles’ morphology (Braski et al., 1979; Suzuki et al., 1990; Wang et al., 2022). It is necessary to consider the elastic effects in the bubbles model for U3Si2. In this study, both the applied stress and dislocation stress field were considered in the elastic term, and the elastic energy Felastic is given by
where
The formula ensures elastic constants are zero in voids where cvac = 1 and cgas = 0. In gas bubbles where cvac equals 1, the elastic constants depend on the gas concentration cgas. The effect of dislocation on the Xe bubble is introduced through a pair of stable dislocation configurations into the elastic term of the free energy density. Then, the intrinsic strain is composed of three parts, which can be written as
where
Here,
In this work, a pair of dislocation dipoles (consisting of two edge dislocations) is introduced on the (110) slip plane. We choose the crystal direction [
2.3 Evolution equations and parametrization
The movement of vacancy and gas atoms is described by the Cahn–Hilliard equations (Cahn, 1961).
where Mgas and Mvac are the mobility of gas atoms and vacancies, respectively. Here, F is the total free energy given by Eq. 1, and
The generation rates of gas atoms and vacancies terms are given by
where
The Xe production rate is written as
where
To improve solution efficiency and ensure all quantities are of order unity, the governing equations Eqs 8, 9 were non-dimensionalized, using the characteristic length r0 = 0.1 μm, and the shear modulus of the matrix can be seen in Chattaraj and Majumder (2018).
where C44 is the shear modulus of the matrix and
3 Results and discussion
3.1 Xe bubble evolution under different fission rates
First, a comparative study of the intragranular Xe bubbles at typical fission rate conditions in LWRs is checked, and the fission rates’ effect on bubble morphology is explored. The stress effects are not considered to clarify the fission rate’s contribution. The simulations were implemented at a typical temperature of 1200K in LWRs, with a mesh grid of 128 and ∆l = 0.2 nm, using the implicit Fourier transformation method. To improve evolution efficiency and enhance the simulation effect, we introduce ξg = 0.0025 and ξv = 0.0025 as the thermal fluctuations of gas atoms and vacancies, respectively. The simulation evolution results of the intragranular Xe bubbles under different fission rates and statistical analysis are shown in Figure 1 and Figure 2, respectively.
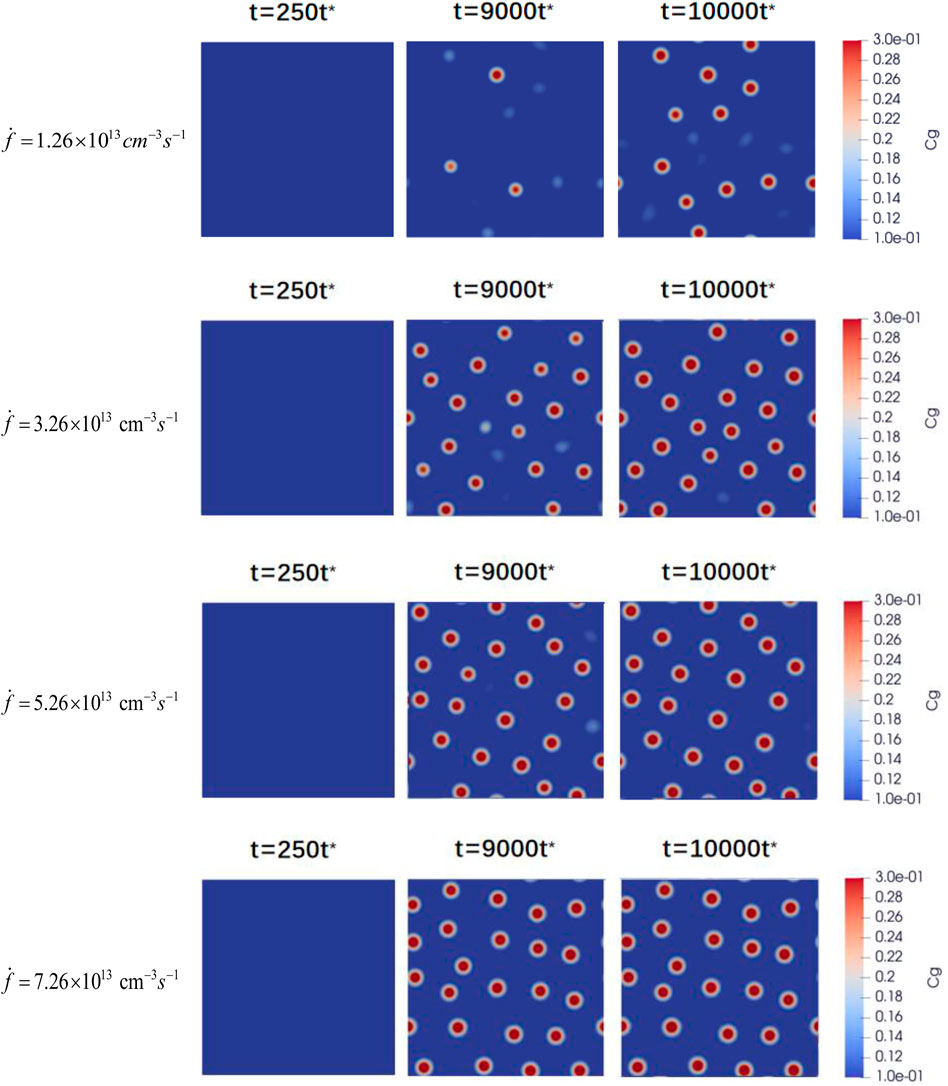
FIGURE 1. Two-dimension evolution diagram of the Xe bubbles at time t = 250t*, 9000t*, and 10000t* under fission rates of 1.26×1013 cm-3s-1, 3.26×1013 cm-3s-1, 5.26×1013 cm-3s-1, and 7.26×1013 cm-3s-1.
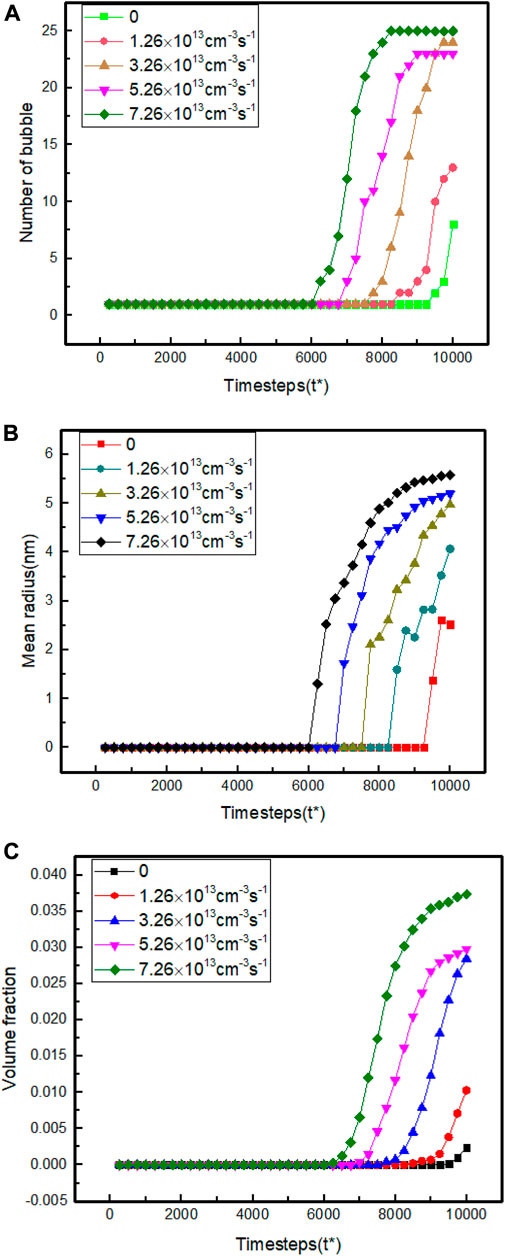
FIGURE 2. Comparison of the (A) number, (B) mean radius, and (C) volume fraction of Xe bubbles at different fission rates.
The predicted effect of the fission rate on the intragranular Xe bubble evolution in fuel U3Si2 is displayed in Figure 1 and Figure 2. Five typical fission rate conditions of 0, 1.26×1013 cm-3s-1, 3.26×1013 cm-3s-1, 5.26×1013 cm-3s-1, and 7.26×1013 cm-3s-1 are investigated in the simulations. The concentrated vacancies generated upon irradiation segregate and form vacancies clusters at the beginning. The limited solubility of fission gases in the U3Si2 matrix drives the gases to fill into these clusters through short-range diffusion steps. The void nucleation and gas filling co-occur, and gases swelling and void shrinkage effect attains equilibrium at the gas concentration approaches roughly 0.3 in a void. The voids persistently grow and coarsen by absorbing both vacancies and gases in such an equilibrium state for an extended period. With the increased fission rate, the incubation period of Xe bubbles is generally advanced, and the final bubble number, the average radius, and the volume fraction are enhanced. The volume fraction of Xe bubbles is highest for the enormous fission rate. As presented in Eqs 7, 9, the defect production rate is proportional to the fission rate; the point defects then rises with an increased fission rate. Although the defects annihilate simultaneously, numerous defects accumulation are generally found with enhanced fission rate, and the defects are condensed in high fission rate conditions. The condensed vacancies and gases in higher fission rate conditions accelerate the incubation process, and Xe bubbles appear significantly advanced. Compared to the drastically reduced incubation period and enlarged volume fraction of bubbles upon enhanced fission rate, the average size is not severely coarsened.
3.2 Xe bubble evolution under applied stress
The fuels are suffering stress originating from the processing process, in-service environments, or inhomogeneous microstructures, which makes the bubbles in a stress state different from those in the stress-free state, as previously described. To clarify the Xe bubble evolution in U3Si2 in a stress state, we consider the external stress and elastic inhomogeneity in the mathematic model in Eq. 3, based on the linear elasticity assumption caused by those stress. The conditions under the fission rates of 1.26×1013 cm-3s-1 and 7.26×1013 cm-3s-1 with applied stress were performed, and we obtained the evolution results and statistical analysis as exhibited in Figure 3 and Figure 4, respectively.
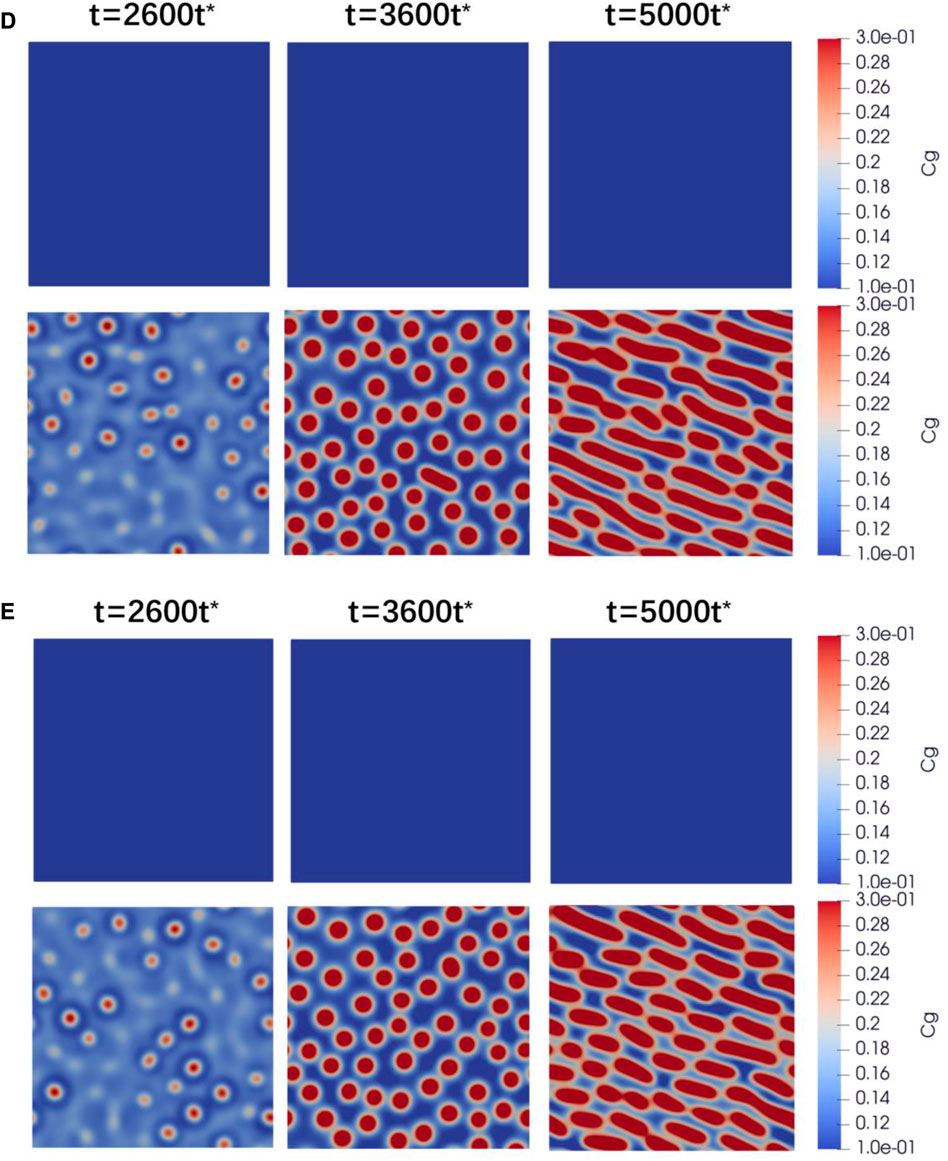
FIGURE 3. Xe bubble evolution with applied stress under different fission rates (D) 1.26×1013 cm-3s-1 and (E) 7.26×1013 cm-3s-1.
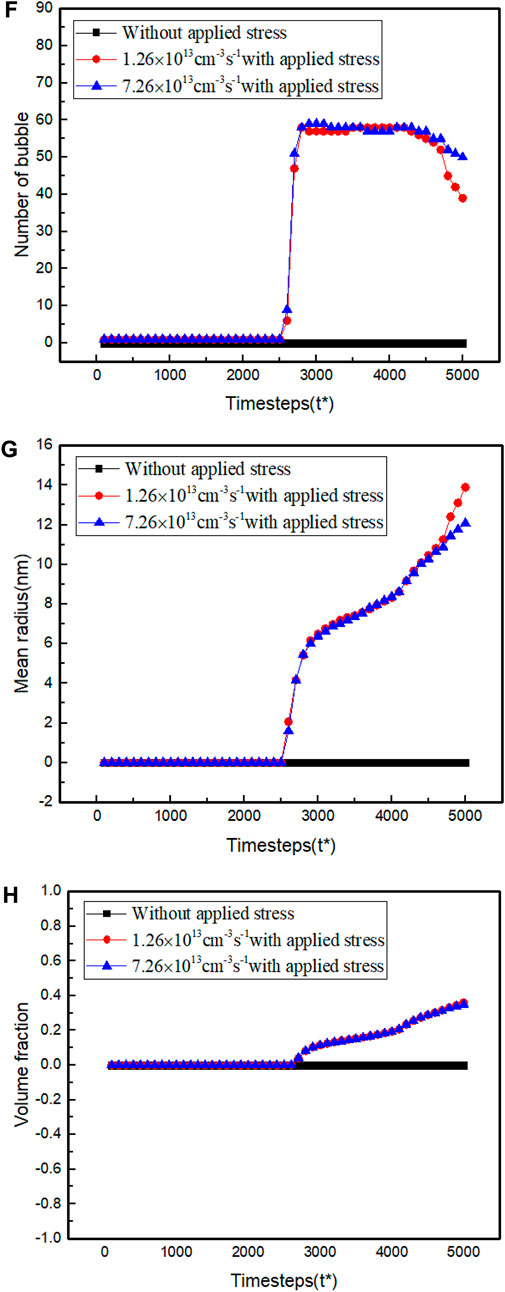
FIGURE 4. Comparison of the (F) number, (G) mean radius, and (H) volume fraction of Xe bubbles at 1.26×1013 cm-3s-1 and 7.26×1013 cm-3s-1.
As shown in Figure 3, the predicted bubble pattern under applied stress is quite different from that in a stress-free state. The applied stress induces bubbles’ nucleation and accelerates the growth and coarsening. After 5000 steps of time evolution, the stress-free bubbles are still incubating; however, coalescence and Ostwald ripening occur in the stress-assisted bubbles. The stress state of a system is metastable, and void or bubble formation occurs as a consequence of stress relaxation. Voids or bubbles formation is accomplished through the interior gases and vacancies diffusion guided by the stress. With continuous production of point defects and gas atoms, the bubbles grow faster in the direction parallel to the applied stress, and the cross-sectional shape of bubbles with applied stress becomes stripped eventually. According to our analysis, the applied stress can significantly promote the growth rate of the bubble along with the applied stress and can help gases and vacancies overcome the energy barrier of bubble nucleation. To quantitatively evaluate the applied stress effect on the evolution feature of the Xe bubble, the number, mean radius, and volume fraction of bubbles are statistically displayed in Figure 4. By comparing the curves of bubbles evolution in Figure 4, the applied stress boosts the increment of the number, mean radius, and volume fraction of bubbles, manifesting severe irradiation damage.
3.3 Xe bubble evolution under dislocation stress field
Intrinsic line defects, such as edge/screw dislocations or dislocation loops, widely existed in irradiation samples. U3Si2 fuel that suffers severe irradiation will produce massive defects, causing dislocation boosts. The high dislocation densities inevitably reshape the Xe bubble arrangement or morphology. A typical experimentally observed dislocation configuration consisting of a pair of dislocations with opposite signs is considered to investigate the dislocation-induced bubble formation. Based on the linear elasticity assumption and inclusion theory, the strain caused by the dislocation pairs is taken as inclusion; the strain is thus given by Eqs 5 and 6. The Xe bubble nucleation effect can be studied by adding an elastic energy term caused by the dislocation pair through the generalized Hooke law. At the fission rates of 1.26×1013 cm-3s-1 and 7.26×1013 cm-3s-1, we obtain the evolution results and statistical analysis that are displayed in Figure 5 and Figure 6, respectively.
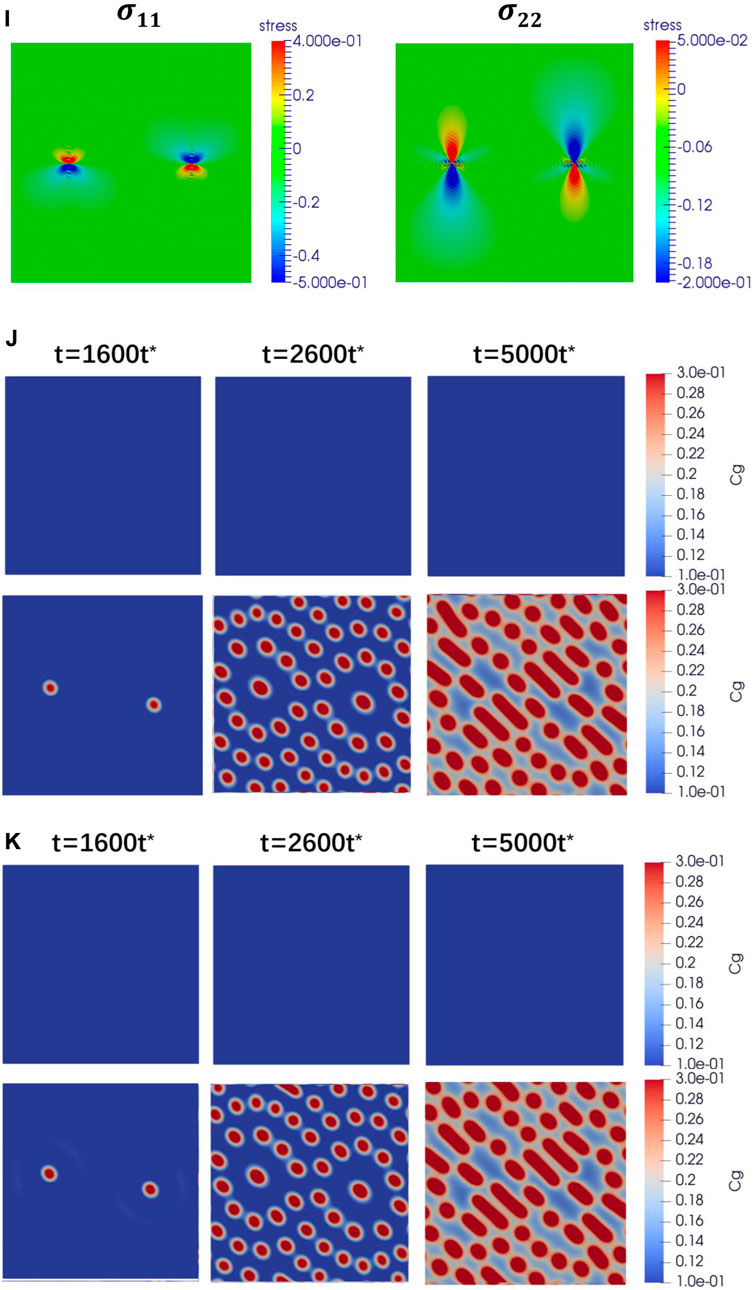
FIGURE 5. Dislocation dipole distribution model (I) and Xe bubble evolution with dislocation stress field under (J) 1.26×1013 cm-3s-1 and (K) 7.26×1013 cm-3s-1.
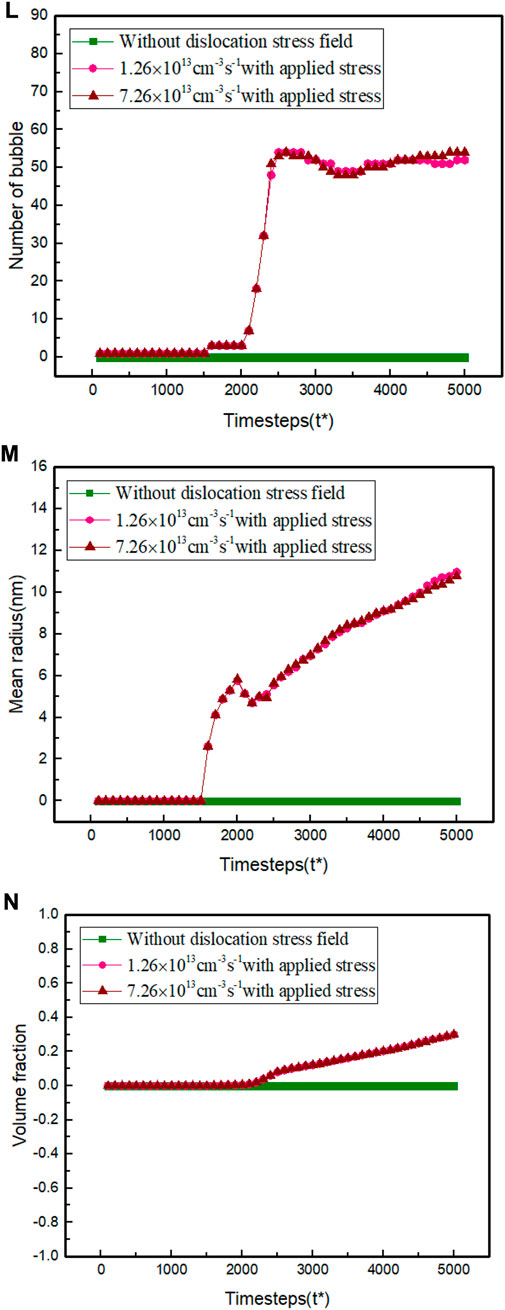
FIGURE 6. Comparison of the (L) number, (M) mean radius, and (N) volume fraction of Xe bubbles at 1.26×1013 cm-3s-1 and 7.26×1013 cm-3s-1.
In this case, the dislocation dipole set in the investigated system causes local elastic inhomogeneous. According to the analysis of Section 3.2, this inhomogeneous local stress will induce bubbles formation. As shown in Figures 5J and K, two bubbles form first near the dislocation dipole. The local stress concentrates nearby the line core, attracting vacancies and gases to relax the severe dislocation stress nearby. The segregation of vacancies and gases leads to microstructure instability, forming two bubbles at the most stress-concentrated sites. The local inhomogeneous stress breaks the homogenous nucleation of bubbles for the primary Xe bubbles to deplete the surrounding vacancies and gases, and then the rest nucleate in succession a little far away from the primary ones. These secondary Xe bubbles form at the periphery of the primary ones, arranged in dot-like layers roughly in two. With prolonged time, these bubbles coarsen in the dislocation stress at a different pace; some are elongated, and some are still spherical. These multiple morphologies of the bubbles are believed to be related to the stress overlap of the two dislocation pair, and it leads to the stress being reinforced in some regions while stress is offset in others. Bubbles nearby the stress-reinforced region coarsen faster than those in the stress-offsetted region. Eventually, these bubbles evolve into different cross-sectional shapes.
For a better prediction of the dislocation stress field on the evolution of Xe bubbles, the number, mean radius, and volume fraction of bubbles are statistically shown in Figure 6. Based on the analysis of Figure 6, the dislocation stress field encourages the nucleation and growth rate of bubbles around this pair of dislocations. In view of this phenomenon, it is believed that the elastic energy introduced by the dislocation pair drives gas atoms and vacancies to overcome the energy barrier of nucleation, providing heterogeneous nucleation sites. The inhomogeneous interior microstructures and local stress concentration caused by these microstructures are essential factors that contribute to bubble swelling.
4 Conclusion
In this work, typical irradiation and fabricated conditions for U3Si2 fuel are used in the simulations; i.e., the fission rates are 1.26×1013 cm-3s-1, 3.26×1013 cm-3s-1, 5.26×1013 cm-3s-1, and 7.26×1013 cm-3s-1, and the temperature is 1200K. Within our framework of the phase-field model, we systematically investigate the nucleation and growth of irradiation-induced intragranular Xe bubbles in U3Si2 fuel under different fission rates, applied stress, and dislocation stress field. From the simulated results, the following conclusions are summarized:
1) The intragranular Xe bubbles are sensitive to the fission rates. With increased fission rate, the bubble incubation periods are advanced, and the bubbles’ final number and average radius rise but are not severely coarsened.
2) The Xe bubbles, from their evolution process and their morphologies, are significantly affected by the applied stress. The stress induces the nucleation process, generating more bubble nucleus in a shorter time than those in the stress-free system. The stress-guided vacancies and gas diffusion reshapes the bubbles’ morphology, cause directional growth and coarsening along the load direction, and form elongated and strip bubble arrangement.
3) The Xe bubbles will preferentially nucleate nearby the stress-concentrated sites of the dislocation pair. The primary Xe bubbles deplete the surrounding vacancies and gases, leading to the non-random nucleation of roughly two-layers of secondary bubbles aligned at the periphery of the primary ones. The subsequent coarsening is influenced by the overlapped stress of the dislocation pair, forming elongated shapes in stress-reinforced regions and spherical ones in stress offset regions.
Our simulations demonstrate that the phase-field method is a promising and predictable computational tool for quantitatively studying and predicting microstructure evolution in U3Si2 fuel. Moreover, our study shows that the fuel fabrication and irradiation conditions may be used to control the bubble-induced swelling in U3Si2 fuel. Undoubtedly, the evolution of intergranular Xe bubbles can also be affected by different fission rates, applied stress, and dislocation stress field. Hence, future studies should be extended to consider the nucleation and evolution of intergranular Xe bubbles under fuel fabrication and irradiation conditions.
Data availability statement
The original contributions presented in the study are included in the article/supplementary materials; further inquiries can be directed to the corresponding authors.
Author contributions
CM: model development, data analysis, and writing original draft. CL: investigation, validation, and writing original draft. MZ: data analysis and checking. TX: conceptualization and methodology. LW: conceptualization, supervision, and funding acquisition. RP: methodology and data analysis. JQ: software, methodology, and data analysis. JZ: methodology, software, and supervision.
Funding
This work was supported by the National Key R&D Program of China (Grant No. 2018YFE0207400) and National Natural Science Foundation of China (Grant No. U2167217).
Conflict of interest
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
References
Aagesen, L. K., Andersson, D., Beeler, B. W., Cooper, M. W., Gamble, K. A., Miao, Y., et al. (2020). Phase-field simulations of intergranular fission gas bubble behavior in U3Si2 nuclear fuel. J. Nucl. Mater. 541, 152415. doi:10.1016/j.jnucmat.2020.152415
Agency, I. A. E. (2017). Chain fission yields. Available at: https://www-nds.iaea.org/sgnucdat/c1.htm (accessed Apr 13, 2017).
Bischoff, J. (2014). Development of fuels with enhanced accident tolerance, accident tolerant fuel concepts for light water reactors. IAEA Tecdoc 1797, 22–29.
Bonilla, L. L., Carpio, A., Neu, J., and Wolfer, W. (2006). Kinetics of helium bubble formation in nuclear materials. Phys. D. 222, 131–140. doi:10.1016/j.physd.2006.07.029
Braski, D. N., Schroeder, H., and Ullmaier, H. (1979). The effect of tensile stress on the growth of helium bubbles in an austenitic stainless steel. J. Nucl. Mater. 83, 265–277. doi:10.1016/0022-3115(79)90611-1
Cahn, J. W. (1961). On spinodal decomposition. Acta Metall. Mater. 9, 795–801. doi:10.1016/0001-6160(61)90182-1
Caturla, M. J., Soneda, N., Diaz de la Rubia, T., and Fluss, M. (2006). Kinetic Monte Carlo simulations applied to irradiated materials: The effect of cascade damage in defect nucleation and growth. J. Nucl. Mater. 351, 78–87. doi:10.1016/j.jnucmat.2006.02.019
Chattaraj, D., and Majumder, C. (2018). Structural, electronic, elastic, vibrational and thermodynamic properties of U3Si2: A comprehensive study using dft [J]. J.All.And Comp. 732, 160–166. doi:10.1016/j.jallcom.2017.10.174
Domain, C., Becquart, C., and Malerba, L. (2004). Simulation of radiation damage in Fe alloys: An object kinetic Monte Carlo approach. J. Nucl. Mater. 335, 121–145. doi:10.1016/j.jnucmat.2004.07.037
Finlay, M. R., Hofman, G., and Snelgrove, J. (2004). Irradiation behaviour of uranium silicide compounds. J. Nucl. Mater. 325, 118–128. doi:10.1016/j.jnucmat.2003.11.009
Hu, S., Burkes, D. E., Lavender, C. A., Senor, D. J., Setyawan, W., and Xu, Z. (2016). Formation mechanism of gas bubble superlattice in UMo metal fuels: Phase-field modeling investigation. J. Nucl.Mater. 479, 202–215. doi:10.1016/j.jnucmat.2016.07.012
Hu, S., Casella, A. M., Lavender, C. A., Senor, D. J., and Burkes, D. E. (2015). Assessment of effective thermal conductivity in U-Mo metallic fuels with distributed gas bubbles. J. Nucl. Mater. 462, 64–76. doi:10.1016/j.jnucmat.2015.03.039
Hu, S., Henager, C. H., Heinisch, H. L., Stan, M., Baskes, M. I., and Valone, S. M. (2009). Phase-field modeling of gas bubbles and thermal conductivity evolution in nuclear fuels. J. Nucl. Mater. 392, 292–300. doi:10.1016/j.jnucmat.2009.03.017
Hu, S., Li, Y., Sun, X., Gao, F., Devanathan, R., Henager, C. H., et al. (2010). Application of the phase-field method in predicting gas bubble microstructure evolution in nuclear fuels. J.Mater. Res. 101, 515–522. doi:10.3139/146.110304
Li, Y., Hu, S., Montgomery, R., Gao, F., and Sun, X. (2013). Phase-field simulations of intragranular fission gas bubble evolution in UO2 under post-irradiation thermal annealing. Nucl. Instrum. Methods Phys. Res. B 303, 62–67. doi:10.1016/j.nimb.2012.11.028
Miao, Y. B., Gamble, K. A., Andersson, D., Mei, Z. G., and Yacout, A. M. (2018). Rate theory scenarios study on fission gas behavior of U3Si2 under LOCA conditions in LWRs. Nucl. Eng. Des. 326, 371–382. doi:10.1016/j.nucengdes.2017.11.034
Millett, P. C., El-Azab, A., and Wolf, D. (2011). Phase-field simulation of irradiated metals Part II: Gas bubble kinetics. Comput. Mater. Sci. 50, 960–970. doi:10.1016/j.commatsci.2010.10.032
Millett, P. C., Tonks, M., and Biner, S. B. (2012). Mesoscale modeling of intergranular bubble percolation in nuclear fuels. J. Appl. Phys. 111, 083511. doi:10.1063/1.3702872
Millett, P. C., and Tonks, M. (2011). Phase-field simulations of gas density within bubbles in metals under irradiation. Comput. Mater. Sci. 50, 2044–2050. doi:10.1016/j.commatsci.2011.02.006
Millett, P. C., Tonks, M. R., Biner, S., Zhang, L., Chockalingam, K., and Zhang, Y. (2012). Phase-field simulation of intergranular bubble growth and percolation in bicrystals. J. Nucl.Mater. 425, 130–135. doi:10.1016/j.jnucmat.2011.07.034
Olander, D. R. (1976). Fundamental aspects of nuclear reactor fuel elements (California Univ., Berkeley, CA: Technical Information Center, Energy Research and Development Administration.
Ortiz, C. J., Caturla, M. J., Fu, C. C., and Willaime, F. (2007). He diffusion in irradiatedα−Fe: Anab-initio-based rate theory model. Phys. Rev. B 75, 100102. doi:10.1103/physrevb.75.100102
Soneda, N., Ishino, S., Takahashi, A., and Dohi, K. (2003). Modeling the microstructural evolution in bcc-Fe during irradiation using kinetic Monte Carlo computer simulation. J. Nucl. Mater. 323, 169–180. doi:10.1016/j.jnucmat.2003.08.021
Stan, M., Ramirez, J., Cristea, P., Hu, S., Deo, C., Uberuaga, B., et al. (2007). Models and simulations of nuclear fuel materials properties. J.Alloy. Compd. 444, 415–423. doi:10.1016/j.jallcom.2007.01.102
Surh, M. P., Sturgeon, J., and Wolfer, W. (2004). Master equation and Fokker-Planck methods for void nucleation and growth in irradiation swelling. J. Nucl. Mater. 325, 44–52. doi:10.1016/j.jnucmat.2003.10.013
Surh, M. P., Sturgeon, J., and Wolfer, W. (2005). Radiation swelling behavior and its dependence on temperature, dose rate and dislocation structure evolution. J. Nucl. Mater. 341, 235–236. Erratum to: ‘Master equation and Fokker–Planck methods for void nucleation and growth in irradiation swelling’ [J. Nucl. Mater. 325 (2004) 44], ‘Vacancy cluster evolution and swelling in irradiated 316 stainless steel’ [J. Nucl. Mater. 328 (2004) 107] and. doi:10.1016/j.jnucmat.2005.03.002
Suzuki, T., Yano, T., Iseki, T., and Mori, T. (1990). Effects of external stress on defect annihilation and bubble swelling during annealing of neutron-irradiated silicon carbide. J. Am. Ceram. Soc. 73, 2435–2440. doi:10.1111/j.1151-2916.1990.tb07609.x
Torre, J. D., Fu, C. C., Willaime, F., Barbu, A., and Bocquet, J. L. (2006). Resistivity recovery simulations of electron-irradiated iron: Kinetic Monte Carlo versus cluster dynamics. J. Nucl. Mater. 352, 42–49. doi:10.1016/j.jnucmat.2006.02.040
Veshchunov, M. S., Dubourg, R., Ozrin, V., Shestak, V., and Tarasov, V. (2007). Mechanistic modelling of urania fuel evolution and fission product migration during irradiation and heating. J. Nucl.Mater. 362, 327–335. doi:10.1016/j.jnucmat.2007.01.081
Veshchunov, M. S. (2000). On the theory of fission gas bubble evolution in irradiated UO2 fuel. J. Nucl. Mater. 277, 67–81. doi:10.1016/s0022-3115(99)00136-1
Veshchunov, M. S., Ozrin, V., Shestak, V., Tarasov, V., Dubourg, R., and Nicaise, G. (2006). Development of the mechanistic code MFPR for modelling fission-product release from irradiated UO2 fuel. Nucl. Eng. Des. 236, 179–200. doi:10.1016/j.nucengdes.2005.08.006
Wang, Y., Zhao, J., Ding, J., and Zhao, J. (2022). Modeling irradiation-induced intragranular gas bubble in tungsten under external tensile loading. Int. J.Refract.Met.Hard Mater. 105, 105824. doi:10.1016/j.ijrmhm.2022.105824
White, J. T., Nelson, A., Dunwoody, J., Byler, D., Safarik, D., and McClellan, K. (2015). Thermophysical properties of U3Si2 to 1773 K. J. Nucl. Mater. 464, 275–280. doi:10.1016/j.jnucmat.2015.04.031
Xiao, Z., Wang, Y., Hu, S., Li, Y., and Shi, S. Q. (2020). A quantitative phase-field model of gas bubble evolution in UO2. Comput. Mater. Sci. 184, 109867. doi:10.1016/j.commatsci.2020.109867
Xu, D. H., Wirth, B. D., Li, M., and Kirk, M. A. (2012). Combining in situ transmission electron microscopy irradiation experiments with cluster dynamics modeling to study nanoscale defect agglomeration in structural metals. Acta Mater 60, 4286–4302. doi:10.1016/j.actamat.2012.03.055
Xu, D. H., Wirth, B. D., Li, M., and Kirk, M. A. (2012). Defect microstructural evolution in ion irradiated metallic nanofoils: Kinetic Monte Carlo simulation versus cluster dynamics modeling and in situ transmission electron microscopy experiments. Appl. Phys. Lett. 101, 101905. doi:10.1063/1.4748980
Keywords: U3Si2 fuel, phase-field simulation, Xe bubble evolution, fission rate, applied stress, dislocation stress field
Citation: Ma C, Liu C, Zhao M, Xin T, Wu L, Pan R, Qin J and Zhang J (2023) Phase-field study of the effect of stress field and fission rate on intragranular Xe bubble evolution in U3Si2 nuclear fuel. Front. Energy Res. 11:1092433. doi: 10.3389/fenrg.2023.1092433
Received: 08 November 2022; Accepted: 07 March 2023;
Published: 17 March 2023.
Edited by:
Shichang Liu, North China Electric Power University, ChinaReviewed by:
Rong Liu, South China University of Technology, ChinaYuexia Wang, Fudan University, China
Copyright © 2023 Ma, Liu, Zhao, Xin, Wu, Pan, Qin and Zhang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Lu Wu, d3VsdTEwMDJAcXEuY29t; Jing Zhang, SmluZ3poYW5nQG53cHUuZWR1LmNu
 Cong Ma
Cong Ma Caiyan Liu2
Caiyan Liu2 Rongjian Pan
Rongjian Pan Jiantao Qin
Jiantao Qin