FSAR: Full neutron spectrum code for advanced reactor simulation

The full neutron spectrum code for advanced reactor simulation named FSAR has recently been developed at Nuclear Power Institute of China in order to meet the requirements of advanced reactor with large neutron energy range. Based on the two-step calculation scheme, FSAR consists of two-dimensional lattice calculation code and core calculation code. In two-dimensional lattice calculation, the subgroup method with ultrafine energy groups was implemented in the two-dimensional resonance self-shielding by incorporating the MOC to get the accurate self-shielded cross-section. For better consideration of the strong space coupling in different geometric sizes due to different mean free path of neutrons, the super-homogenization method and the leakage model were applied. In the core calculation, the discrete-ordinate method and micro burnup calculation method were used to simulate the core neutron transport and depletion. Preliminary calculation results showed that for the problems with wide spectrum, the self-shielded cross-sections have a good agreement with the Monte Carlo solution. The results shown in this paper indicate that FSAR has good performances of the cross-section generation in full neutron spectrum problem simulation.

1 Introduction

The research and development of advanced reactors has been pushed globally in recent decade (Wu, 2016) and promotes the development of reactor physics codes (Lee and Yang, 2017; Zhang and Yang, 2020). The neutron spectrum is complicate for some new reactors, especially for the special-use ones. In order to meet the requirements of the advanced reactors, it is necessary to develop the reactor analysis code with full neutron spectrum adapt ability.

At present, there are two main kinds of calculation methods for the reactor core simulation. First is the one-step calculation method (Rachamin and Kliem, 2017), which is used to simulate the core directly with as few approximations as possible. The other one is the two-step calculation method which is based on the homogenization techniques (Zhang et al., 2016). For the whole core physics simulation, the computational cost of one-step calculation with fully detailed description is too expensive using either stochastic (Wang et al., 2015) or deterministic method (Downar et al., 2016) even with the currently most advanced computing powers. So even though one-step calculation method has a lot of advantages, the dominant method for fast core simulation is the two-step scheme.

In the two-step scheme, deterministic procedures are currently the most widely used simulation methods. Compared to the traditional PWR codes, the fast reactor codes are easier to be extended for more complicated reactor design benefiting from their features of ultrafine group cross-sections, full core transport calculation, etc. However, there are several limits of the current fast reactor codes when they are applied in the full neutron spectrum cases. The first one is the accurate heterogeneity effect estimation in complex geometries coming with wider spectral range. The long mean free path of neutrons makes the local heterogeneity effect of typical fast reactors less important, thus the equivalent homogeneous models and one-dimensional models are accurate enough for the conventional fast reactor subassemblies (Allen et al., 2011). What’s more, the highly heterogeneous design has been considered as a breakthrough in the special-use advanced reactors, such as the axially heterogeneous fuel assembly design of the sodium fast reactor prototype ASTRID CFV concept (Faure et al., 2018). The homogeneous models of the conventional two-step approach are no longer applicable.

The resonance self-shielding effect is another important element. In reactor lattice analysis, the aim of resonance self-shielding calculation is to estimate the group-averaged cross-sections for solution of the core multi-group transport equation. The accuracy of the group parameters determines the precision of the core calculation. In the fast reactor analysis code, the method proposed by T. Tone (Tone, 1975) is a popular method to evaluate the self-shielded cross-sections with a set of group collision probability matrixes based on the isotope-dependent background cross-sections. Due to the calculation burden of CP matrixes, Tone’s method implemented in the one-dimensional geometry shows nearly equivalent precision for the effective multiplication factor and reaction rate calculation compared to the subgroup method (Mao and Zmijarevic, 2017). However, in order to meet the needs of resonance self-shielding treatment of assemblies with more complex geometries and more larger energy range, the resonance self-shielding treatment model incorporated with the two-dimensional transport calculation method should be researched for better geometric adaptability and higher efficiency.

In this paper, an overview of the Full neutron Spectrum code for Advanced Reactor simulation named FSAR is provided which is developed by Nuclear Power Institute of China (NPIC), China National Nuclear Corporation (CNNC). The important modules and their models contained in FSAR are introduced in Section 2. Section 3 gives the preliminary calculation results of the problems with different spectrum. Section 4 summarizes this paper.

2 Models in FSAR code

The deterministic two-step calculation strategy based on the homogenization theory is utilized in FSAR to perform the reactor core neutronics analysis. Firstly, the two-dimensional lattice calculation is performed. The two-dimensional method of characteristics (Song et al., 2020a) solver in hexagonal geometry for neutron transport calculation and the subgroup method with ultrafine groups for self-shielding calculation are utilized. For the typical assemblies, ultrafine-group cross-sections and neutron flux will be determined and the few-group homogenized micro cross-sections will be collapsed based on the flux-volume weight method and the principle of conservation of reaction rate.

The second step is the core simulation, which is to simulate core neutron behaviors based on the neutron transport solvers and micro burnup calculation. The discrete-ordinate method is utilized to carry out the neutron transport calculation, and the Chebyshev rational approximation method is used to compute the exponential of the burnup matrix.

2.1 Lattice calculation

In two-dimensional lattice calculation, the subgroup method with ultrafine groups was implemented in the two-dimensional resonance self-shielding by incorporating MOC to get the accurate self-shielded cross-sections. In FSAR, the number of the ultrafine energy group is 2164 and that of subgroups is determined according to the change amplitude of the cross section (maximum is three groups). For the heterogeneous system, the neutron source term is assumed to be isotropic and the steady Boltzmann transport equation shows as follows:

$\begin{array}{l}\overrightarrow{\mathrm{\Omega }}\cdot \nabla \varphi \left(\overrightarrow{r},E\right)+{\mathrm{\Sigma }}_t\left(\overrightarrow{r},E\right)\varphi \left(\overrightarrow{r},E\right)=Q\left(\overrightarrow{r},E\right)\end{array}(1)$

where Q is the neutron source. Based on the treatments of the neutron source, the subgroup method can be divided into the statistical model and the fixed source model (Takeda et al., 1991).

In the statistical model, the probability that the neutron source in group g lies in the subgroup sg is equal to the subgroup probability of sg. The corresponding subgroup transport equation is simplified as follow:

$\begin{array}{l}\overrightarrow{\mathrm{\Omega }}\cdot \nabla {\varphi }_{sg,g}\left(\overrightarrow{r}\right)+{\mathrm{\Sigma }}_{t,sg,g}\left(\overrightarrow{r}\right){\varphi }_{sg,g}\left(\overrightarrow{r}\right)=Q_{sg,g}\left(\overrightarrow{r}\right)=p_{sg,g}{Q}_g\left(\overrightarrow{r}\right)\end{array}(2)$

where p_sg,g is the subgroup probability of sg. The neutron source term Q includes scattering source and fission source and the detail flux spectrum is required for the calculation of the scattering source and the fission source. In this way, the resonance calculation and the transport calculation are coupled together in the statistical model and completed in one time.

In the fixed source model, the narrow resonance approximation is implemented, the corresponding subgroup transport is simplified as below:

$\begin{array}{l}\overrightarrow{\mathrm{\Omega }}\cdot \nabla {\varphi }_{sg,g}\left(\overrightarrow{r}\right)+{\mathrm{\Sigma }}_{t,sg,g}\left(\overrightarrow{r}\right){\varphi }_{sg,g}\left(\overrightarrow{r}\right)=\frac{{\mathrm{\Sigma }}_p\left(\overrightarrow{r}\right)}{4\pi }\end{array}(3)$

where Σ_p is the macroscopic potential cross section.

Compared to the statistical model, the fixed source model has better parallel performance. The subgroup flux of different subgroups in the entire energy range is coupled with each other, and can be calculated together. The self-shielding cross section is collapsed as:

$\begin{array}{l}{\sigma }_{x,g}\left(\overrightarrow{r}\right)=\frac{{\sum }_{sg\in g}{p}_{sg,g}{\sigma }_{x,sg,g}{\varphi }_{sg,g}\left(\overrightarrow{r}\right)}{{\sum }_{sg\in g}{p}_{sg,g}{\varphi }_{sg,g}\left(\overrightarrow{r}\right)}\end{array}(4)$

Comparing the above two models, it can be noticed that the statistical model needs iterations, while the fixed source model does not. It means that the latter requires fewer fixed source iterations. In the lattice calculation, the bondarenko iteration (Stamm’ler and Abbate, 1983) is used to deal with the resonance interference effect. When one isotope is treated as a resonance isotope, the other isotopes are treated as non-resonant isotopes, and the subgroup total cross section is written as follows:

$\begin{array}{l}{\mathrm{\Sigma }}_{t,sg,g}\left(\overrightarrow{r}\right)=N_r\left(\overrightarrow{r}\right){\sigma }_{t,sg,g}+{\displaystyle \sum }_{k\ne r}{N}_k\left(\overrightarrow{r}\right){\sigma }_{t,g,k}\left(\overrightarrow{r}\right)\end{array}(5)$

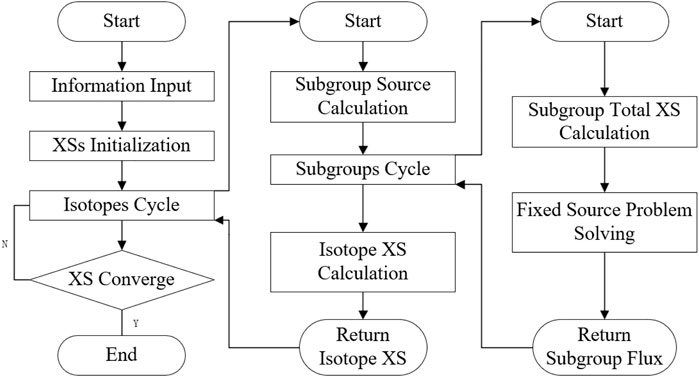
The subgroup flux is then calculated by Eq. 3. The new self-shielding cross section of isotope r is updated by Eq. 4. The flow chart of the resonance calculation is shown in Figure 1.

FIGURE 1

FIGURE 1. Resonance calculation flow chart.

The single assembly problems with reflective boundary condition are used to determine the homogenized cross-sections of fuel material. For better consideration of the strong space coupling in different geometric sizes due to different mean free path of neutrons, the super homogenization method (Zhang et al., 2016) is optional to be used as the homogenization technique. For the structural materials and other non-fuel materials, the super cell or assembly models are used to determine the SPH factors and the cross-sections. The cross-sections are modified as follows:

$\begin{array}{l}{\stackrel{\sim }{\mathrm{\Sigma }}}_{i,g}^{\mathit{hom}}={\mu }_{i,g}{\mathrm{\Sigma }}_{i,g}^{\mathit{hom}}\end{array}(6)$

2.2 Core simulation

Based on the multi-group cross-sections generated by the lattice calculation, the three-dimensional whole core calculation is carried out by the core simulator. The S_N method with triangular grid is applied as the solver of the transport equations. The three-dimensional multi-group neutron transport equation within the triangular prism grid can be written as follows, which assumes that the fission source is isotropic and scattering sources is anisotropic in the derivation.

$\begin{array}{l}{\mu }^m\frac{\partial {\mathrm{\Psi }}_g^m\left(x,y,z\right)}{\partial x}+{\eta }^m\frac{\partial {\mathrm{\Psi }}_g^m\left(x,y,z\right)}{\partial y}+\frac{{\xi }^m}{h_z}\frac{\partial {\mathrm{\Psi }}_g^m\left(x,y,z\right)}{\partial z}+{\mathrm{\Sigma }}_{\mathrm{t}}^g{\mathrm{\Psi }}_g^m\left(x,y,z\right)\\ ={\widehat{Q}}_g\left(x,y,z\right)\end{array}(7)$

where m represents a certain angular direction, ${\mu }^m,{\eta }^m,{\xi }^m$ is the component of the angular direction m on the coordinate axis (x, y, z), ${\mathrm{\Psi }}_g^m\left(x,y,z\right)$ is the angular flux of the g-th group.

For the reactor system without outer neutron source, the source ${\widehat{Q}}_g$ includes fission source and scattering source. The fission source is usually assumed to be isotropic, while the scattering source is anisotropic in reactor system. The assumption that the scattering source is isotropic limits the application of the triangular discrete ordinate nodal method in practical problems. The isotropic scattering source written as follows is considered in FSAR:

$Q_s\left(\mathit{r},E,\mathit{\Omega }\right)={\int }_0^{\infty }{\int }_{4\pi }{\mathrm{\Sigma }}_{\mathrm{s}}\left(\mathit{r},E^{\prime }\right)f\left(\mathit{r},E^{\prime }\to E,{\mathit{\Omega }}^{\prime }\to \mathit{\Omega }\right)\psi \left(\mathit{r},E^{\prime },{\mathit{\Omega }}^{\prime }\right)d{\mathit{\Omega }}^{\prime }d{E}^{\prime }(8)$

where f represents the scattering function.

The micro-depletion scheme is applied to simulate the core burn up and the Chebyshev Rational Approximation Method is used to solve the depletion equation. In FSAR, the depletion chains containing 21 heavy isotopes and 49 fission products is provided for the advanced reactor core system.

3 Numerical results

To verify the effectiveness of the method used in this paper, we test different spectrum and different scale problems. The ultrafine group library used in this section is made by the NJOY program (Macfarlane et al., 2016) based on ENDF/B-VII.0 library. The reference solutions are provided by the Monte Carlo code OpenMC (Romano et al., 2015).

In this section, the serval pin cell problems with different spectrum characteristics are selected as the verification problems. The results for the eigenvalue k_eff and for the absorption cross-sections of ²³⁸U and ²³⁹Pu are compared to the reference results.

3.1 Thermal spectrum problem

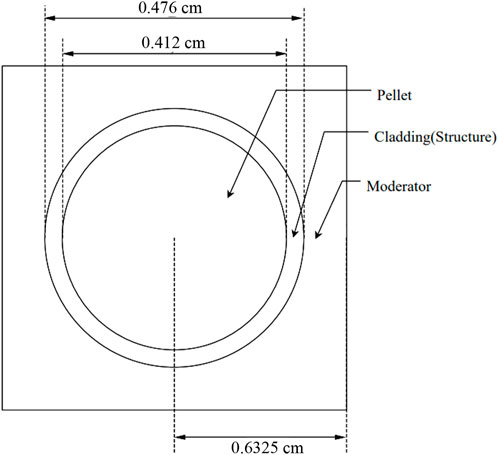
UO₂ and MOX pin cell problems from JAEA benchmark (Yamamoto et al., 2002) are utilized for the thermal spectrum and the geometry is shown in Figure 2. The two problems have the same mesh division. In the radial direction, the fuel, clad and moderator are divided into three and one and two equal-volume rings respectively. Each ring is divided into 8 equal-volume sectors. The MOC parameters are set to be three polar angles and 16 angles per octant, and 0.01 cm ray spacing. The multigroup transport equation with P₀ scattering was solved with the pure MOC calculation without any accelerations. In the calculations, the inter-molecular thermal scattering effect is not considered.

FIGURE 2

FIGURE 2. Geometry of thermal spectrum problem.

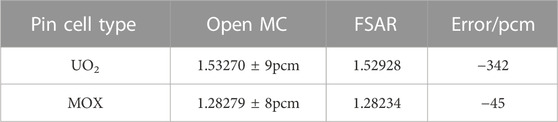
For the thermal spectrum problems, the results of eigenvalue are presented in Table 1, and the self-shielding cross section errors are shown in Figures 3, 4, 5. In the table, the errors of eigenvalue are calculated as follows:

$\begin{array}{l}Er{r}_k=\left(k_{MOC}-k_{ref}\right)\ast {10}^5\end{array}(9)$

TABLE 1

TABLE 1. JAEA pin cell eigenvalue.

FIGURE 3

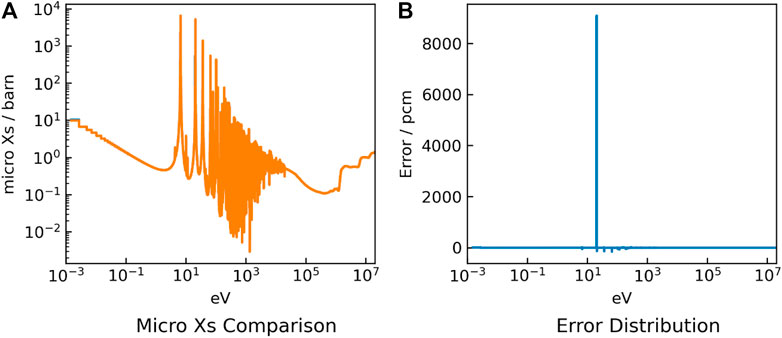
FIGURE 3. ²³⁸U absorption cross section results (A) and errors (B) for the UO₂ problem with thermal spectrum.

FIGURE 4

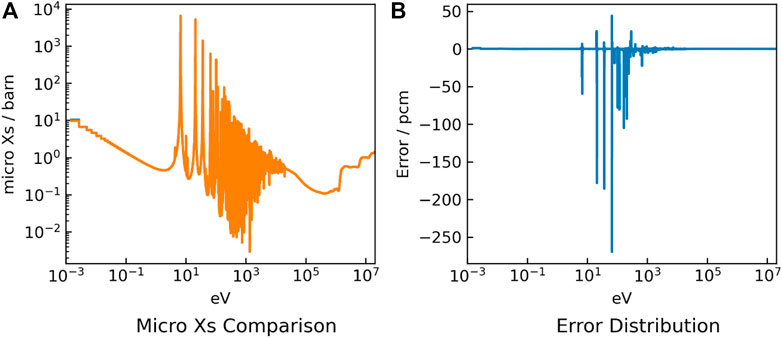
FIGURE 4. ²³⁸U absorption cross section results (A) and errors (B) for the MOX problem with thermal spectrum.

FIGURE 5

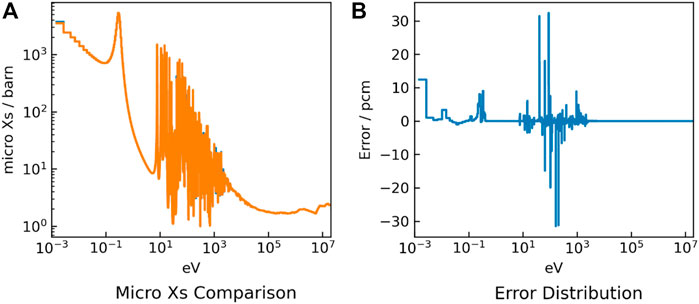
FIGURE 5. ²³⁹Pu absorption cross section results (A) and errors (B) for the MOX problem with thermal spectrum.

In the figures, the errors of cross section are calculated as follows:

$\begin{array}{l}Er{r}_{xs}=\frac{\left({\sigma }_{g,MOC}-{\sigma }_{g,ref}\right)\ast {\varphi }_{g,ref}}{{\sum }_{g\in G}{\sigma }_{g,ref}{\varphi }_{g,ref}}*{10}^5\end{array}(\mathrm{7b})$

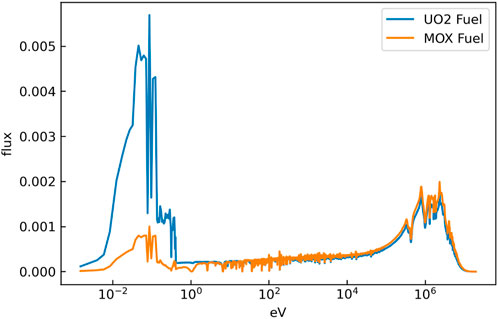
It can be found that the cross-sections have high accuracy for most groups. However, in the UO₂ problem, the absorption cross section of ²³⁸U has a large deviation at 20 eV energy. While the absorption cross section error of ²³⁸U at 20 eV energy of the MOX problem is smaller. This is because the MOX fuel including serval Pu isotopes hardens the neutron flux spectrum, as shown in Figure 6. Furthermore, affected by the harder flux spectrum, there is no significant increase in the errors of eigenvalue for the MOX fuel problem, even the obvious differences of the cross-sections appear in the energy range between 10 and 100 eV.

FIGURE 6

FIGURE 6. Flux comparison in fuel region.

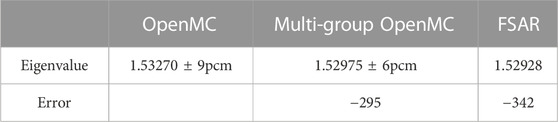
In order to determine the error source of the eigenvalue, the cross-sections tallied from OpenMC are used to get the macroscopic cross-sections. The multi-group model in OpenMC is used to perform the transport calculation. The results are shown in Table 2. It can be found that the result of FSAR and multi-group OpenMC is close and the anisotropic scattering effect would be the main error source.

TABLE 2

TABLE 2. UO₂ pin cell eigenvalue error.

3.2 Intermediate spectrum problem

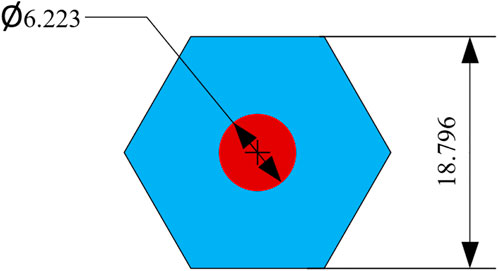
The hexagonal UO₂ cell with high enrichment (Lee, 2014) is utilized as the intermediate spectrum problem. The graphite is used as the moderator. The geometry is shown in Figure 7. Both fuel and moderator are divided into one ring. Each ring is divided into 6 equal-volume sectors.

FIGURE 7

FIGURE 7. Geometry of intermediate spectrum problem (unit: mm).

For the intermediate spectrum problem, the reference eigenvalue obtained by OpenMC is 1.28829 ± 8 pcm and the value of FSAR is 1.28465. The results of cross-sections are shown in Figure 8. The error results are similar to that of the UO₂ problem. There is also a significant deviation at 20 eV energy and small deviations at other positions. It can be explained by the invalidation of narrow approximation around 20 eV.

FIGURE 8

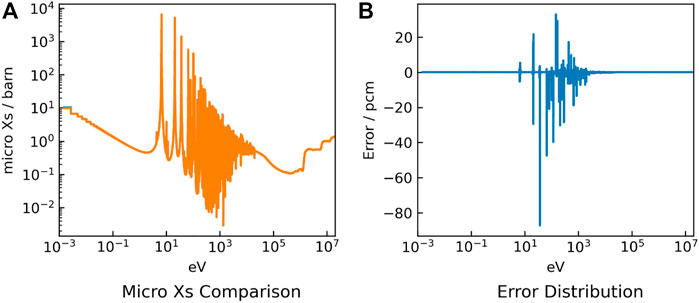
FIGURE 8. ²³⁸U absorption cross section results (A) and errors (B) for the intermediate spectrum problem.

3.3 Fast spectrum problem

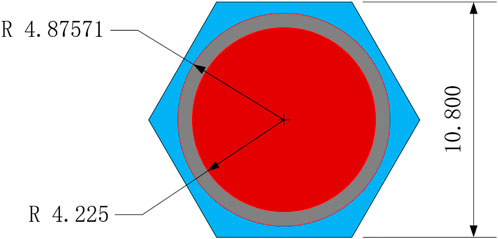
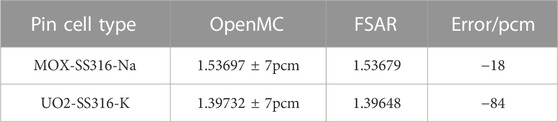
In order to test the performance of FSAR in the fast reactor, the calculations of UO₂ cell with high enrichment and MOX cell are carried out. The same hexagonal geometry of the two problems is shown in Figure 9. The clad material is SS 316 alloy, and two conventional coolants in fast reactors, sodium and potassium, are selected in this section. The compositions of the materials are obtained from the reference (Li et al., 2017). Finally, two fast spectrum problems are formed, expressed as MOX-SS316-Na and UO₂-SS316-K respectively.

FIGURE 9

FIGURE 9. Geometry of fast spectrum problem (unit: mm).

The eigenvalue results are shown in Table 3. The errors of cross-sections are shown in Figures 10, 11, 12. The numerical results indicate that the calculation in fast spectrum problems has higher accuracy than that of other problems. This is because the resonance peak is narrower in the high energy range and the resonance effect treatment is more applicable.

TABLE 3

TABLE 3. Fast spectrum problem eigenvalue.

FIGURE 10

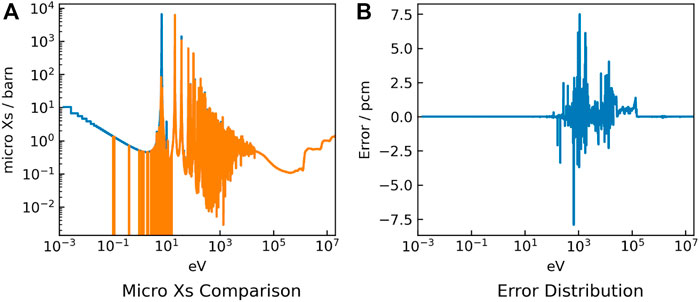
FIGURE 10. ²³⁸U absorption cross section results (A) and errors (B) for the MOX problem with fast spectrum.

FIGURE 11

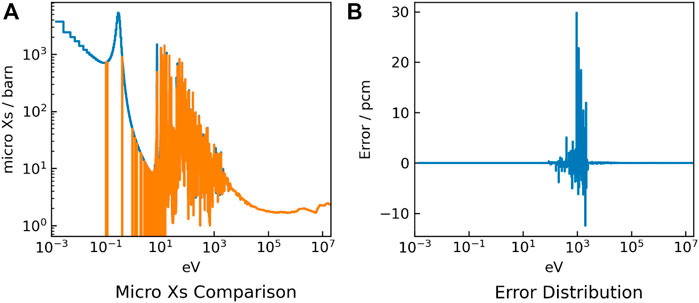
FIGURE 11. ²³⁹Pu absorption cross section results (A) and errors (B) for the MOX problem with fast spectrum.

FIGURE 12

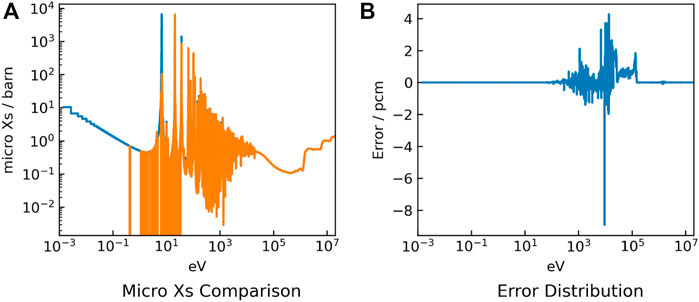
FIGURE 12. ²³⁸U absorption cross section results (A) and errors (B) for the UO₂ problem with fast spectrum.

4 Conclusion

The full neutron spectrum code for advanced reactor simulation named FSAR developed by NPIC, CNNC is introduced in this paper. The deterministic two-step calculation strategy based on the homogenization theory is utilized in FSAR. In the lattice calculation, the MOC method is used to determine the neutron flux, and the subgroup method with ultrafine energy groups was implemented to get the accurate self-shielded cross-section. In the core calculation, the discrete-ordinate method and micro burnup calculation method were used to simulate the core neutron transport and depletion. The preliminary verifications have been carried out, and the results indicated that FSAR has good performances in dealing with the resonance self-shielding effect of the full-range spectrum problems. In the near future, the verification of each module and the whole code system will be carried out. What’s more, other calculation functions such as thermal feedback module are being developed.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

LW: Methodology, Software, Investigation, Numerical Analysis, Writing—Original Draft; BZ: Methodology, Numerical Analysis; DL: Numerical Analysis; CZ: Methodology; JL: Writing—Original Draft.

Funding

This research is supported by the National Natural Science Foundation of China (Approved number Nos.12075228 and Nos.12205283). All the authors would like to thank Zhejiang University for the help with resonance self-shielding treatment model.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Allen, K., Knight, T., and Bays, S. (2011). Benchmark of advanced burner test reactor model using MCNPX 2.6.0 and ERANOS 2.1. Prog. Nucl. Energy 53 (6), 633–644. doi:10.1016/j.pnucene.2011.01.007

CrossRef Full Text | Google Scholar

Downar, T., Kochunas, B., and Collins, B. (2016). Validation and verification of the MPACT code[C]. United states: American Nuclear Society, 2961–2978.

Google Scholar

Faure, B., Archier, P., Vidal, J.-F., Palau, J. M., and Buiron, L. (2018). Neutronic calculation of an axially heterogeneous ASTRID fuel assembly with APOLLO3: Analysis of biases and foreseen improvements. Ann. Nucl. Energy. 115, 88–104. doi:10.1016/j.anucene.2017.12.035

CrossRef Full Text | Google Scholar

Lee, C. (2014). Development of a generalized cross section library applicable to various reactor types[C]. Japan: PHYSOR2014.

Google Scholar

Lee, C. H., and Yang, W. S. (2017). MC2 -3: Multigroup cross section generation code for fast reactor analysis. Nucl. Sci. Eng. 187, 268–290. doi:10.1080/00295639.2017.1320893

CrossRef Full Text | Google Scholar

Li, M., Zmijarevic, I., and Sanchez, R. (2017). Resonance self-shielding methods for fast reactor calculations—comparison of a new Tone’s method with the subgroup method in APOLLO3^Ⓡ. Nucl. Sci. Eng. 188 (1), 15–32. doi:10.1080/00295639.2017.1332890

CrossRef Full Text | Google Scholar

Macfarlane, R., Muir, D. W., Boicourt, R. M., Kahler, A. C., and Conlin, J. L. (2016). The NJOY nuclear data processing system, version 2016. USA: Los Alamos National Laboratory, 17–22.

Google Scholar

Mao, L., and Zmijarevic, I. (2017). “A new Tone’s method in APOLLO3 and its application to ZPPR benchmarks,” in Proc. M&C 2017 (Jeju, Korea: APOLLO).

Google Scholar

Rachamin, R., and Kliem, S. (2017). Validation of the dyn3d-serpent code system for SFR cores using selected BFS experiments. Part I: Serpent calculations. Ann. Nucl. Energy 102, 158–167. doi:10.1016/j.anucene.2016.12.023

CrossRef Full Text | Google Scholar

Romano, P. K., Horelik, N. E., Herman, B. R., Nelson, A. G., Forget, B., and Smith, K. (2015). OpenMC: A state-of-the-art Monte Carlo code for research and development. Ann. Nucl. Energy 82, 90–97. doi:10.1016/j.anucene.2014.07.048

CrossRef Full Text | Google Scholar

Song, P., Zhang, Z., Zhang, Q., Liang, L., and Zhao, Q. (2020a). Implementation of the CPU/GPU hybrid parallel method of characteristics neutron transport calculation using the heterogeneous cluster with dynamic workload assignment. Ann. Nucl. Energy 135, 106957. doi:10.1016/j.anucene.2019.106957

CrossRef Full Text | Google Scholar

Stamm'ler, R. J., and Abbate, M. J. (1983). Methods of steady-state reactor physics in nuclear design [M]. London: Academic Press, 286–355.

Google Scholar

Takeda, T., Fujimoto, H., and Sengoku, K. (1991). Application of multi-band method to KUCA tight–pinch lattice code. J. Nucl. Sci. Technol. 28, 836–869.

CrossRef Full Text | Google Scholar

Tone, T. (1975). A numerical study of heterogeneity effects in fast reactor critical assemblies. J. Nucl. Sci. Technol. 12 (8), 467–481. doi:10.1080/18811248.1975.9733139

CrossRef Full Text | Google Scholar

Wang, K., Li, Z. G., She, D., Liang, J., Xu, Q., Qiu, Y., et al. (2015). Rmc – a Monte Carlo code for reactor core analysis. Ann. Nucl. Eng. 82, 121–129. doi:10.1016/j.anucene.2014.08.048

CrossRef Full Text | Google Scholar

Wu, Y. C. (2016). Design and R&D progress of China lead-based reactor for ads research facility. Engineering 2 (1), 124–131. doi:10.1016/j.eng.2016.01.023

CrossRef Full Text | Google Scholar

Yamamoto, A., Ikehara, T., Ito, T., and Saji, E. (2002). Benchmark problem suite for reactor physics study of LWR next generation fuels. J. Nucl. Sci. Technol. 39 (8), 900–912. doi:10.1080/18811248.2002.9715275

CrossRef Full Text | Google Scholar

Zhang, B., Li, Y. Z., Wu, H. C., Cao, L., and Shen, W. (2016). Evaluation of pin-cell homogenization techniques for PWR pin-by-pin calculation. Nucl. Sci. Eng. 186 (2), 134–146. doi:10.1080/00295639.2016.1273018

CrossRef Full Text | Google Scholar

Zhang, G., and Yang, W. S. (2020). Quadratic axial expansion function with sub-plane acceleration scheme for the high-fidelity transport code PROTEUS-MOC. Ann. Nucl. Energy. 148, 107713. doi:10.1016/j.anucene.2020.107713

CrossRef Full Text | Google Scholar