Optimal power distributed control of the DC microgrid in meshed configuration

This paper proposes a Lyapunov-based power sharing control scheme and a fixed-time-based distributed optimization algorithm to achieve optimal power sharing of sources in a DC microgrid. The Lyapunov-based controller is designed based on so-called ratio consensus protocol, where it drives the sources to a desired proportional power sharing by regulating the voltage profile of the DC microgrid. The distributed optimization optimizer is established by integrating a finite-time weighted consensus algorithm with an iterative algebraic operation, where it calculates the optimal power dispatch on the target of minimizing the generation cost. The optimizer receives the current output power of the controlled DC microgrid and sends the obtained power dispatch to the power sharing controller as the proportionality coefficients. Both the controller and optimizer are carried out in a fully distributed way. Under the framework of the Lyapunov method, stability analysis of the DC microgrid with the proposed control scheme, as well as convergence and optimality analysis of the distributed optimization algorithm, is provided. However, the influence of the time delay of the controller on the system remains to be further investigated in future work.

1 Introduction

The smart grid has been attracting much attention in recent years, where it integrates the traditional power grid, renewable distributed resources, and advanced control and optimization methods on the bridge of cyber-physical techniques (Liu et al., 2021; Hou et al., 2022). With the increasing penetration of renewable energy sources (RESs) and distributed generators (DGs), traditional power systems are transforming into the form of a distributed autonomous power system, namely, the microgrid (Hatziargyriou et al., 2007). In recent years, a lot of research on the DC microgrid has been emerging since it avoids the reactive power regulation and the harmonic compensation compared with the traditional AC microgrid (Olivares et al., 2014; Papadimitriou et al., 2015; Meng et al., 2017; Wang et al., 2023).

Power sharing control is one of the important control targets of microgrids (Simpson-Porco et al., 2013; Morstyn et al., 2016a; Morstyn et al., 2016b). Under the framework of the hierarchical control (Guerrero et al., 2011; Bidram and Davoudi, 2012), the current sharing problem of parallel DC microgrids has been solved by decentralized methods (Guerrero et al., 2011; Khorsandi et al., 2014; Hamzeh et al., 2015) and distributed methods (Anand et al., 2013; Lu et al., 2014; Wang et al., 2016a), respectively. Indeed, the decentralized controller has been wildly used for the practical AC/DC microgrids (Hou et al., 2019). Recently, the distributed controller for the DC microgrid has been developed and attracts much attention (Liu et al., 2023b; Liu et al., 2023a). The decentralized methods require transmitting the voltage of a common bus to each converter, whereas the distributed methods merely require the current or voltage information on neighbors via an information network. Similarly, distributed control schemes have also been developed in the current sharing problem of the DC microgrid with meshed topology (Nasirian et al., 2014). However, current sharing guarantees the power sharing of loads but not that of sources. In addition, the existing current sharing controllers are not applicable to accurate energy management at the source side.

When considering the generation cost of power sources, achieving optimal power sharing becomes a crucial problem that can be solved through an economic dispatch model (Ahmed et al., 2023). Distributed economic dispatch optimization algorithms have been developed, taking advantage of consensus algorithms in multi-agent systems, including the ϵ-based consensus algorithm (Yang et al., 2013), distributed bisection method (Xing et al., 2015), distributed projected gradient algorithm (Guo et al., 2016), subgradient-based consensus algorithm (Wang et al., 2016b), event-triggered consensus algorithm (Li et al., 2016), and consensus-based energy management algorithm (Zhao et al., 2016). However, most existing algorithms for economic dispatch neglect the transmission loss of power lines, despite some literature studies discussing it [e.g., Kron’s loss formula models in Loia and Vaccaro (2014)]. It is noted that Kron’s loss formula models transmission loss, but obtaining the loss coefficients B in practice is difficult. Optimal power sharing controllers have been designed by integrating the physical system and economic dispatch model in several studies, including Hamad et al. (2016), Li et al. (2017), Moayedi and Davoudi (2017), and Hu et al. (2018). It is noted that Li et al. (2017) formulated an optimization problem but regard the power flow as a constraint, and they then used the optimized parameters in the decentralized primary controller. However, this optimization problem was solved by a centralized heuristic algorithm, which requires global information, and may become computationally expensive once the number of sources increases. As an alternative, power sharing control schemes with distributed optimization algorithms have been widely developed by interacting with neighboring sources (Hamad et al., 2016; Moayedi and Davoudi, 2017; Hu et al., 2018).

The proposed distributed method in Moayedi and Davoudi (2017) can simultaneously optimize the power sharing of sources and regulate the voltage profile, where the generation limits of sources are also guaranteed by their incremental cost consensus protocol. The method in Hu et al. (2018) is a discrete-time control protocol using the current imbalance information, where the economical regulator generates a reference current signal for each converter to achieve the optimal power sharing of sources. Supervisory control has been designed on the basis of the sensitivity analysis, where it successfully solves the equal power sharing problem (Hamad et al., 2016). Then, the distributed equal incremental cost (DEIC) algorithm is proposed to achieve the optimal power dispatch. Optimal power sharing control has been investigated in Chang et al. (2023) for a hybrid AC/DC microgrid, but it mainly focuses on the power dispatch between the AC and DC sides while ignoring the optimal power sharing of the sources at the DC side. Optimal energy consumption has been analyzed in Xiao et al. (2022) for a practical shipboard DC microgrid, where the analysis is based on the transfer function with a linear dynamic part. However, in the aforementioned literature, the stability criteria are hard to be verified because all the poles of the transfer functions or all the eigenvalues of a big matrix should be calculated and checked to ensure them within the open left-hand plane or within the unit circle at the origin. In addition, the parameter design may fail to work if the Laplacian matrix of the communication topology or the conductance matrix of the DC microgrid is unknown.

In this paper, a distributed Lyapunov-based proportional power sharing control and a distributed initial value restoration (distributed optimization) optimization algorithm are designed to achieve the optimal power sharing of sources in a meshed DC microgrid. The Lyapunov-based controller is a consensus-like scheme based on the power information on neighbors. The proposed distributed optimization algorithm consists of a finite-time weighted consensus protocol and an algebraic operation on initial value restoration. In the process of optimization operation, the optimizer receives the real-time output power information and calculates the optimal power dispatch, and then sends back the optimized power dispatch to the controller as the proportionality coefficients. Additionally, a rigorous analysis of stability, convergence, and optimality is given. Compared with existing methods, the key contributions of this paper are summarized as follows:

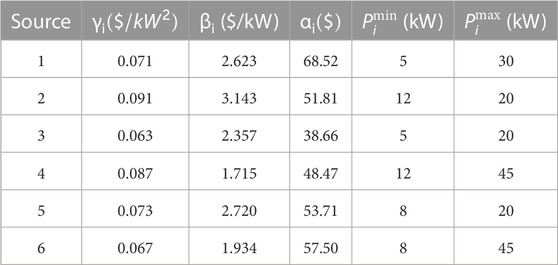
1. The Lyapunov-based proportional power sharing controller for a DC microgrid is designed, which does not require to know the Laplacian matrix of the communication topology and the conductance matrix of the DC microgrid, as needed in existing approaches (Hamad et al., 2016; Moayedi and Davoudi, 2017; Hu et al., 2018).

2. The proposed distributed optimization algorithm is a fully distributed algorithm. Compared with Moayedi and Davoudi (2017), our optimization method avoids transforming the information topology once a generation reaches its limits, where the change of topology may lead to the redesign of parameters. Compared with Hu et al. (2018) and Hamad et al. (2016), our optimization method can work without knowing the exact number of sources.

3. Optimal sharing control has been investigated in Dou et al. (2022), however, on the DC microgrid with the single-bus configuration. Moreover, the consensus-based secondary control is designed using the power on the load rather than the output power of the distributed generation unit (DGU). In this paper, we focus on the DC microgrid with meshed configuration and the optimal power sharing of the DGU.

4. Optimal control of the DC microgrid is discussed in Huang et al. (2022) with a rigorous theoretical analysis and considering balance of the charge state. However, the paper focuses on the optimal voltage control rather than on the power sharing control of the DC microgrid.

The organization of the remaining part is as follows. The preliminaries and problem statement are given in Section 2. The distributed Lyapunov-based proportional power sharing control is presented in Section 3, where stability analysis is given. The distributed optimization algorithm and the convergence proof are given in Section 4. The simulation test is given in Section 5, and the conclusion is drawn in Section 6.

2 Preliminaries

Consider a DC microgrid with N bus nodes, denoted as ${\mathcal{I}}_G=\{\mathrm{1,2},\dots ,N\}$. Define G_ij as the conductance of the transmission line connecting with nodes i and j, where G_ij > 0 if the i-th node and j-th node are connected via a power line, and otherwise, G_ij = 0 if they are not connected. G_ii is the shunt conductance of the local load. Then, the conductance matrix $Y=[Y_{ij}]\in {\mathbb{R}}^{N\times N}$ with Y_ij = −G_ij if i ≠ j; otherwise, $Y_{ij}={\sum }_{j=1}^N{G}_{ij}$. Before describing the optimal power sharing control problem of the DC microgrid, a brief introduction of information flow is given. Denote $\mathcal{G}=\left({\mathcal{I}}_G,\mathcal{E},\mathcal{A}\right)$ as the information flow of sources. The graph $\mathcal{G}$ is described with a set of nodes ${\mathcal{I}}_G$, a set of edges $\mathcal{E}\in {\mathcal{I}}_G\times {\mathcal{I}}_G$, and a weighted adjacency matrix $\mathcal{A}={(a_{ij})}_{N\times N}$ with non-negative adjacency elements. The node i represents the ith source. Note that a_ij > 0 if and only if the ith source can obtain information from the jth source. Define N_i = {j|a_ij > 0}, which is the set that contains the neighbors of the node i. The Laplacian matrix $\mathcal{L}={(l_{ij})}_{N\times N}$ of the graph $\mathcal{G}$ is defined as l_ij = −a_ij if i ≠ j; otherwise, $l_{ij}={\sum }_{k=1,k\ne i}^N{a}_{ik}$.

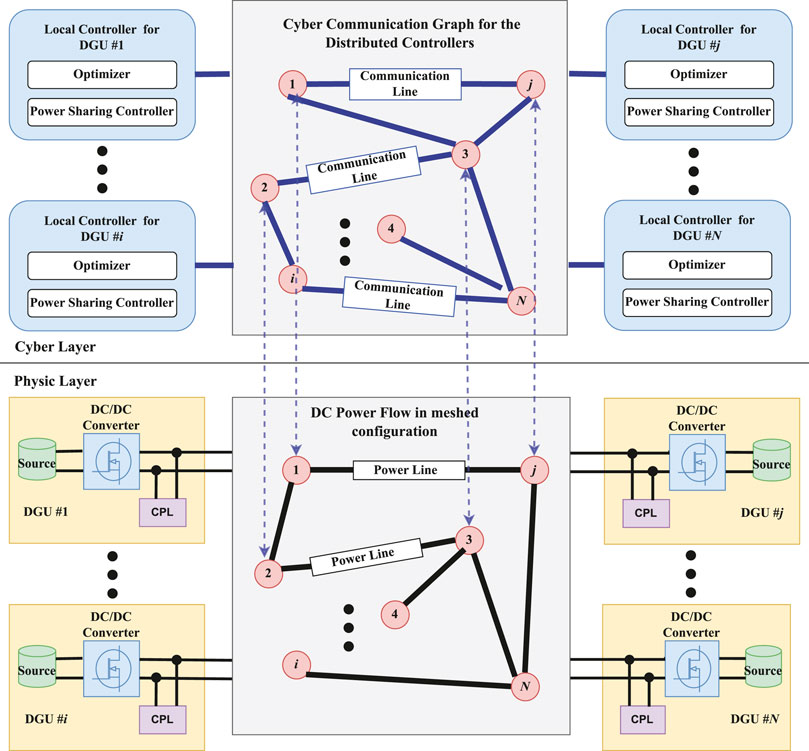
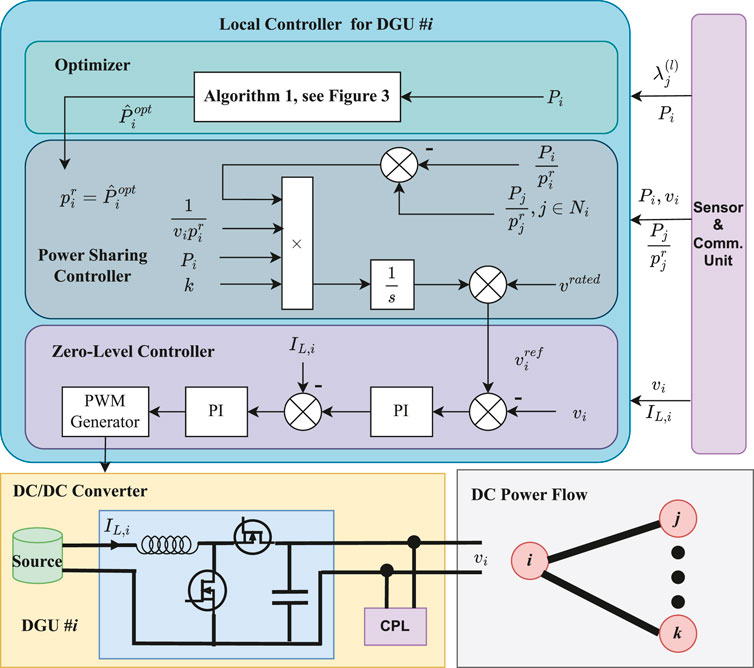
The cost of each generation unit is denoted as C_i(P_i), where P_i is the power generation of the i-th DG. As illustrated in Figure 1, the control and optimization framework of a DC microgrid is, in fact, a cyber-physical system which consists of a cyber system layer and a physical system layer. The physical layer is a real-time system including loads, sources, DC–DC converters, and zero-level controllers. The cyber layer is a management system that takes charge of control and optimization for the microgrid in a distributed manner through a communication network and local calculation units. In our framework, there are a power sharing controller and a generation optimizer in each source. They cooperatively calculate the reference voltages for the zero-level controllers, which directly regulate the output voltages of buses.

FIGURE 1

FIGURE 1. Cyber-physical framework of a DC microgrid in meshed configuration.

For the generation optimizer, it aims to calculate the optimal power dispatch of sources by solving an economic dispatch problem, which can be described as the following optimization formulations:

$\underset{{\widehat{P}}_i,i\in I_G}{\min }\sum _{i=1}^N{C}_i\left({\widehat{P}}_i\right),(1)$

$\text{s.t.}\sum _{i=1}^N{\widehat{P}}_i=P_{\mathit{Demand}},(2)$

$P_i^{\min }\le {\widehat{P}}_i\le P_i^{\max },i\in I_G(3)$

where C_i(⋅) is the generation cost function, ${\widehat{P}}_i$ is the optimization variable denoted as the ith power generation, P_Demand is the total power demand, and $P_i^{\min }$ and $P_i^{\max }$ are the lower bound and the upper bound of the output power, respectively. The optimization result ${\widehat{P}}_i^{\mathit{opt}}$ will be further sent to the power sharing controller as a reference.

For the power sharing controller, it aims to design the reference voltage of buses $V_i^{\mathit{ref}}$ for the zero-level controller such that the real-time output power could track on the optimized output power,

$P_i={\widehat{P}}_i^{\mathit{opt}},fori\in {\mathcal{I}}_G,(4)$

where P_i is the real-time output power and ${\widehat{P}}_i^{\mathit{opt}}$ is the optimal output power dispatch generated by the generation optimizer.

Under the framework in Figure 1, the objective of optimal power sharing control is to minimize the total generation cost of the microgrid by regulating the output voltage of buses while meeting the demand and power generator constraints. To solve the optimal power sharing control of the DC microgrid, a proportional power sharing controller and a distributed optimization algorithm are designed.

3 Proportional power sharing scheme

In this section, a proportional power sharing scheme is presented to achieve the desired proportional power dispatch of sources, i.e.,

$\frac{P_i}{p_i^r}=\frac{P_j}{p_j^r},for\forall i,j\in {\mathcal{I}}_G,(5)$

where P_i is the output power and $p_i^r$ is the proportionality coefficient.

3.1 Power sharing scheme

The power sharing control scheme for the ith source in the DC microgrid is designed as

$v_i^{ref}=v^{rated}+{\delta }_i,(\mathrm{6a})$

${\dot{\delta }}_i=\frac{k{P}_i}{v_i{p}_i^r}\sum _{j\in N_i}{a}_{ij}\left(\frac{P_j}{p_j^r}-\frac{P_i}{p_i^r}\right),(\mathrm{6b})$

where k is a positive control parameter, v^rated is the nominal voltage of microgrids, and P_i is the real-time output power of the ith source. The power sharing of sources in the DC microgrid can be achieved using the active power information on neighbors, as illustrated in Figure 2. Because the dynamics of the converter is evolving in a fast time-scale, the output voltage of the source could rapidly track on the reference voltage $v_i^{\mathit{ref}}$ by the zero-level controller, as shown in Figure 2. Under this circumstance, it could be assumed that $v_i=v_i^{\mathit{ref}}$. The following subsection gives the stability analysis of the DC microgrid under the proportional power sharing controller.

FIGURE 2

FIGURE 2. Distributed controller for each DC–DC converter.

3.2 Stability analysis

Let V = col(v₁, v₂…, v_N), δ = col(δ₁, δ₂…, δ_N), and P = col(P₁, P₂…, P_N). Define the notation $\text{diag}({[b_1,\dots ,b_N]}^T)$ as the diagonal matrix with diagonal elements b₁, …, b_N; then, the compact form of the sources’ dynamics is given by

$\begin{array}{cc}\hfill V& =V^{\mathit{rated}}+\delta ,\hfill \\ \hfill \dot{\delta }& =-k{D}^{-1}\tilde{P}{\tilde{V}}^{-1}L{D}^{-1}P,\hfill \end{array}$

where V^rated = 1_Nv^rated, $D=\text{diag}({[p_1^r,p_2^r,\dots ,p_N^r]}^T)$, $\tilde{P}=\text{diag}(P)$, and $\tilde{V}=\text{diag}(V)$. The dynamics of sources subject to the power flow equations

$P=P_D+\tilde{V}YV,(7)$

where $P_D=\text{col}(P_1^d,P_2^d\dots ,P_N^d)$ and $P_i^d$ is the demand power of local loads at bus i. Hence, the closed-loop system can be obtained as

$\dot{V}=-k{D}^{-1}\tilde{P}{\tilde{V}}^{-1}L{D}^{-1}P,(\mathrm{8a})$

$P=P_D+\tilde{V}YV.(\mathrm{8b})$

Indeed, taking the derivation of both sides of Eq. 6a and substituting Eq. 6b yields Eq. 8a and Eq. 8b, which is the DC power flow for the meshed configuration of the DC microgrid. Note that Eq. 8a is a differential equation and Eq. 8b is an algebraic equation. Before giving the stability analysis of the closed-loop system, denote the equilibrium of (8) as E = (P^⋆, V^⋆), which satisfies the following equations:

$\begin{array}{cc}\hfill & 0=-k{D}^{-1}{\tilde{P}}^{\star }{\tilde{V}}^{\star }{}^{-1}LD^{-1}{P}^{\star },\hfill \\ \hfill & P^{\star }=P_D+{\tilde{V}}^{\star }Y{V}^{\star }.\hfill \\ \hfill & \hfill & \hfill \end{array}$

Theorem 1. Suppose that the communication graph is connected. Consider the closed-loop system (8). The proposed distributed controller (6) ensures the following statements:i) the solution of (8) approaches the equilibrium E andii) the power sharing (5) is guaranteed.Proof: Define the Lyapunov functional candidate as

$\mathcal{W}=\frac{1}{2}{V}^{T}V.$

Taking the derivative of the Lyapunov function along (8), one has

$\begin{array}{cc}\hfill \dot{\mathcal{W}}& =V^T\dot{V}\hfill \\ \hfill & =-k{V}^T\tilde{P}{\tilde{V}}^{-1}{D}^{-1}L{D}^{-1}P\hfill \\ \hfill & =-k{P}^T{D}^{-1}L{D}^{-1}P\hfill \\ \hfill & \le 0.\hfill \end{array}$

It is noted that D⁻¹LD⁻¹ is a symmetric matrix with non-negative eigenvalues because the communication graph is connected.By LaSalle’s invariant principle, the solution of (8) will approach the largest invariant set of

$\mathcal{M}=\left\{\left(P,V\right)|\dot{\mathcal{W}}=0\right\}\text{as}t\to +\infty .$

Indeed, the solution is also subject to the algebraic flow equation $P=P_D+\tilde{V}YV$. Hence, it will approach the set ${\mathcal{M}}_s=\{(P,V)|\dot{\mathcal{W}}=0\text{and}P=P_D+\tilde{V}YV\}$. It is easy to find that $\text{E}={\mathcal{M}}_s$, which means the solution of (8) will approach the equilibrium E.Note that $\dot{\mathcal{W}}=0$ indicates P^TD⁻¹LD⁻¹p = 0, where it implies LD⁻¹p = 0. L is the Laplacian matrix, of which the row sum equals to zero. Therefore, the null space of the matrix LD⁻¹ is ${[p_1^r,p_2^r,\dots ,p_N^r]}^T$, which indicates there exists a positive constant p* such that $P=p^{*}{[p_1^r,p_2^r,\dots ,p_N^r]}^T$. Obviously, it guarantees

$\underset{t\to +\infty }{\lim }\left(\frac{P_i}{p_i^r}-\frac{P_j}{p_j^r}\right)=0,\text{for}\forall i,j\in {\mathcal{I}}_G.$

This completes the proof of Theorem 1.

Remark 1. Set$p_i^r={\mathcal{P}}_i$, where${\mathcal{P}}_i$is the desired output power of theith source satisfying${\sum }_i{\mathcal{P}}_i={\sum }_i{P}_i^d+P_{\mathit{loss}}$with$P_{\mathit{loss}}=\frac{1}{2}{\sum }_i{\sum }_j{Y}_{ij}{(V_i^{\star }-V_j^{\star })}^2=1_N{\tilde{V}}^{\star }Y{V}^{\star }$, denoted as the power loss on lines. The proportional power sharing controller ensures$\frac{P_i}{{\mathcal{P}}_i}=\chi$, whereχis a positive constant. By the power flow Eq. 8b), one has${\sum }_i{P}_i={\sum }_i{P}_i^d+P_{\mathit{loss}}$, which indicates that${\sum }_i{P}_i={\sum }_i{\mathcal{P}}_i$andχ = 1. In this way, it achieves the desired power output of sources.

Remark 2. Based on the Lyapunov stability analysis, the parameter design of the power sharing controller is quite simple, where it only requiresk > 0. Note that the selection ofkis independent of the Laplacian matrixLand the conductance matrixY. Moreover, the parameterkdetermines the speed of the convergence.

4 Optimal economic dispatch

This section aims to obtain the optimal power dispatch by solving the economic dispatch problem (Eqs 1–3).

4.1 Solution to the economic dispatch problem

Similar to the classic economic dispatch problem formulation in AC microgrids, the cost functions of dispatchable sources can be approximated as a quadratic function (Wood and Wollenberg, 2012),

$C_i\left({\widehat{P}}_i\right)={\gamma }_i{\widehat{P}}_i^2+{\beta }_i{\widehat{P}}_i+{\alpha }_i,(9)$

where ${\widehat{P}}_i$ is the output of the ith power generator, and α_i, β_i, and γ_i are the corresponded parameters.

Define the Lagrangian operator $L({\widehat{P}}_1,\dots ,{\widehat{P}}_N)$ such that

$L\left({\widehat{P}}_1,\dots ,{\widehat{P}}_N\right)=\sum _{i=1}^N{C}_i\left({\widehat{P}}_i\right)+\lambda \left(P_D-\sum _{i=1}^N{\widehat{P}}_i\right),(10)$

where λ is the Lagrange multiplier and P_D is the sum of the real-time output power transmitted from the controller. P_D includes both the load demand P_Demand and the transmission loss P_loss. For the EDP with power generation constraints, the optimal incremental cost λ* can be obtained by verifying [Eq. (3.7) in (Wood and Wollenberg, 2012)]

$\left\{\begin{array}{c}2{\gamma }_i{\widehat{P}}_i+{\beta }_i={\lambda }^{*},\text{for}{P}_i^{\min }<{\widehat{P}}_i<P_i^{\max },\hfill \\ 2{\gamma }_i{\widehat{P}}_i+{\beta }_i<{\lambda }^{*},\text{for}{\widehat{P}}_i=P_i^{\max },\hfill \\ 2{\gamma }_i{\widehat{P}}_i+{\beta }_i>{\lambda }^{*},\text{for}{\widehat{P}}_i=P_i^{\min }.\hfill \end{array}\right.(11)$

4.2 Distributed optimization algorithm

This subsection presents a discrete-time multi-agent system that employs the local variable λ_i(t), where $i\in {\mathcal{I}}_G$, to collaboratively estimate the optimal λ* in Eq. 11. Prior to introducing the distributed optimization algorithm, it is necessary to define a projection operator that maps from $\mathbb{R}\times \mathrm{\Omega }$ to Ω

$\text{Proj}\left(x,\mathrm{\Omega }\right)=\text{arg\hspace{0.17em}}\underset{\nu \in \mathrm{\Omega }}{\min }\Vert \upsilon -x\Vert ,(12)$

where $\mathrm{\Omega }\subseteq \mathbb{R}$ is a closed convex set, and λ_i locates within an accessible set ${\mathrm{\Omega }}_i^{\lambda }=\{{\lambda }_i\in \mathbb{R}|{\lambda }_i^{\min }\le {\lambda }_i\le {\lambda }_i^{\max }\}$, where ${\lambda }_i^{\min }=2{\gamma }_i{P}_i^{\min }+{\beta }_i$ and ${\lambda }_i^{\max }=2{\gamma }_i{P}_i^{\max }+{\beta }_i$. In light of Liu et al. (2020), a two-step distributed optimization algorithm is designed based on the projection operator, taking into account the power generation constraints.

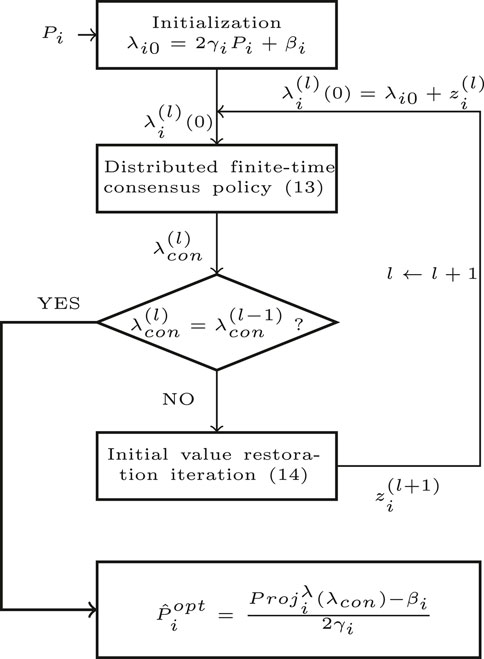
4.2.1 bfAlgorithm 1: two-step distributed optimization algorithm

Step 1. Distributed finite-time consensus policy.

$\left\{\begin{array}{c}{\lambda }_i^{\left(l\right)}\left(t+1\right)={\lambda }_i^{\left(l\right)}\left(t\right)-\mu \left(t\right){\gamma }_i\sum _{j\in N_i}{a}_{ij}\left[\left({\lambda }_i^{\left(l\right)}\left(t\right)-{\lambda }_j^{\left(l\right)}\left(t\right)\right)\right],\hfill \\ {\lambda }_i^{\left(l\right)}\left(0\right)={\lambda }_{i0}+z_i^{\left(l\right)}.\hfill \end{array}\right.(13)$

Step 2. Initial value restoration operation.

$z_i^{\left(l+1\right)}={\lambda }_{\mathit{con}}^{\left(l\right)}-{\text{Proj}}_i^{\lambda }\left({\lambda }_{\mathit{con}}^{\left(l\right)}\right),(14)$

where $\mu (t)=\frac{1}{{\lambda }_{\mathcal{L},t}}$ is a time-dependent gain with ${\lambda }_{\mathcal{L},t}$ being the t-th eigenvalue of the Laplacian matrix $\mathcal{L}$. λ_i0 = 2γ_iP_i + β_i, P_i is the output power, ${\text{Proj}}_i^{\lambda }(\cdot )$ represents $\text{Proj}(\cdot ,{\mathrm{\Omega }}_i^{\lambda })$z_i is called as the restoration variable, and ${\lambda }_{\mathit{con}}^{(l)}$ is the consensus value to be calculated in Step 1 at each iteration.A major difference to Liu et al. (2020) is that we apply a fixed-time consensus algorithm via the discrete-time multi-agent system. The distributed optimization algorithm involves two steps for each source. In Step 1, a fixed-time discrete-time consensus algorithm is employed to drive λ_i to converge to consensus within N steps. In Step 2, we carry out the projection to operate and restore the initial value of λ_i according to the consensus value calculated in Step 1. These two steps are run alternately until ${\lambda }_{\mathit{con}}^{(l)}$ converges. The flowchart of the distributed optimization algorithm is depicted in detail in Figure 3.

FIGURE 3

FIGURE 3. Flowchart of the distributed optimization algorithm.

Remark 3. Like the optimization algorithms in Hu et al. (2018) and Hamad et al. (2016), the proposed distributed optimization algorithm utilizes the increment cost of neighbors, i.e.,λ_j, j ∈ N_i. However, our algorithm still works without requirements on the total number of the sourcesNand the number of other neighbors|N_j|, j ∈ N_i.

4.3 Interactive operation of the controller and optimizer

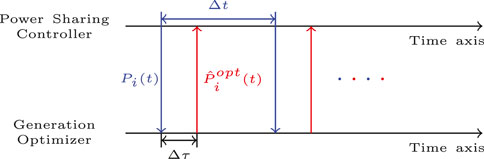
In the aforementioned sections, the proposed controller and optimizer separately achieve the desired proportional power sharing of sources and optimal power dispatch of sources. However, when the power sharing controller regulates the voltage profile, the transmission loss of lines changes accordingly such that the sum of real-time output power is no longer equal to the sum of optimized power, and to solve this problem, an interactive operation of the proposed controller and optimizer is presented, as shown in Figure 4.

FIGURE 4

FIGURE 4. Interactive operation of the controller and the optimizer in the ith source.

In Figure 4, Δτ is the duration of optimization at each time and Δt is the time interval between two optimizations. During the period Δt, the power sharing controller sends the real-time output power to its generation optimizer. Subsequently, the optimizer calculates the optimal power dispatch and sends back the obtained dispatch to the controller as the proportionality coefficients. Then, the power sharing controller calculates the reference voltage for the zero-level controller, and the zero-level controller drives the DC microgrid to its steady state. Additionally, the controller will resend the current real-time output power to the generation optimizer for the next optimization. Specifically, the operation in the DC microgrid follows four steps:

1) The output power P_i of each bus at the physical system will be sent to its generation optimizer.

2) The optimal power dispatch ${\widehat{P}}_i^{\mathit{opt}}$ under the current circumstance (i.e., the current output power P_i) is calculated and sent back to the power-sharing controller.

3) The power-sharing controller works with the proportionality coefficient $p_i^r={\widehat{P}}_i^{\mathit{opt}}$ until the DC microgrid reaches its steady state.

4) Repeat steps 1–3 until the optimal power dispatch ${\widehat{P}}_i^{\mathit{opt}}$ is convergent.

5 Simulation test

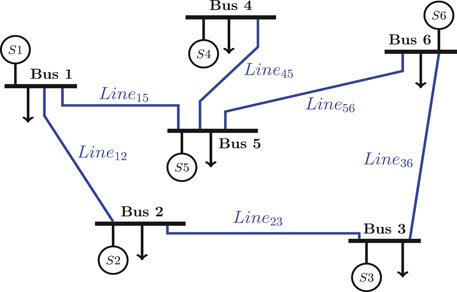
The simulation test is carried out based on MATLAB/Simulink to demonstrate the effectiveness of the proposed methods. Consider a meshed DC microgrid with six buses including six sources and six local loads, as shown in Figure 5. The rated voltage of the microgrid is selected at 380 V.

FIGURE 5

FIGURE 5. Microgrid tested with six buses.

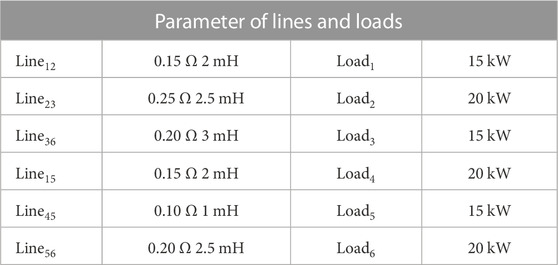
The line parameters and the load parameters are listed in Table 1. The parameters of generation cost are shown in Table 2. Each source is driven by a boost DC–DC converter with both current-loop and voltage-loop PI controllers, as shown in Figure 2, where v_s = 220 V, L = 2 mH, and C = 470 μF. In the proposed control method, the parameter k is designed as 4,000. The constant power load is modeled via a DC/DC buck converter with a constant impedance load.

TABLE 1

TABLE 1. Parameters of lines and loads.

TABLE 2

TABLE 2. Generation cost parameters.

5.1 Proportional power sharing

Before t = 5 s, it is supposed to achieve the average power sharing, which means each source provides 16.67% of the total power demand. After t = 5 s, it is supposed to achieve a desired proportional power sharing, where six sources provide 15%, 15%, 15%, 20%, 15%, and 20% of the total power demand. In this case, $p_i^r$ and $i\in {\mathcal{I}}_G$ are first set as 17,500, then $p_1^r$, $p_2^r$, $p_3^r$, and$p_5^r$ will be reset as 15,750 and $p_4^r$ and $p_6^r$ are reset as 21,000 at t = 5 s. As seen in Figure 6A, the output power of six sources is converging to 17.5 kW at the first 5 s. During the last 5 s, the desired power sharing is achieved, where the output power of sources 1, 2, 3, and 5 converges to 15.75 kW and the output power of sources 4 and 6 converges to 21.0 kW as well. Moreover, voltage shifts of six buses are shown in Figure 6B. By the proposed control method, the proportional power sharing of sources can be achieved.

FIGURE 6

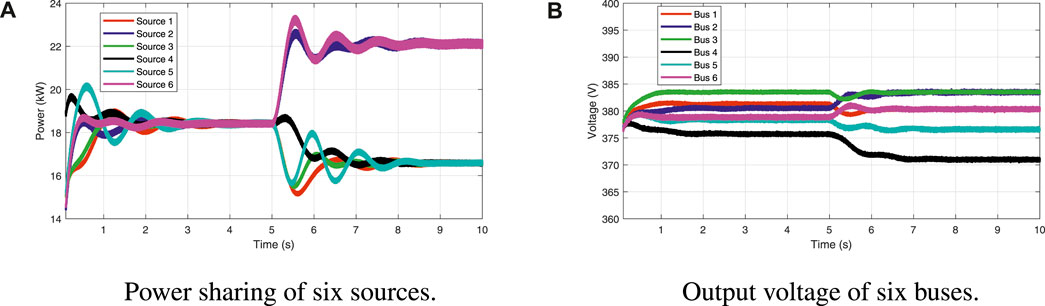
FIGURE 6. Performance of the proportional power sharing test: (A) output power of six sources and (B) voltage of six buses.

5.2 Load step test

The controller performance of the load step test is shown in Figure 7, where two 5-kW loads are added at t = 5 s and removed at t = 10 s on buses 3 and 5, respectively. Figure 7A shows the proportional power sharing of six sources could still be maintained during the period of the test. Figure 7B shows the voltage shifts of six buses.

FIGURE 7

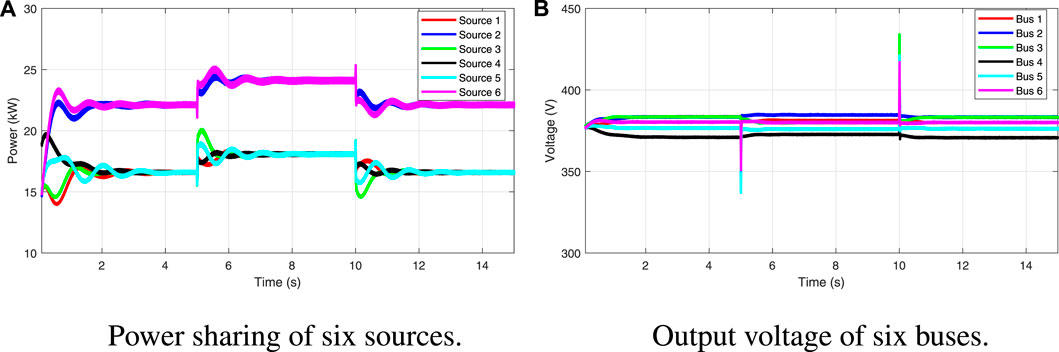
FIGURE 7. Performance of the load step test: (A) output power of six sources and (B) voltage of six buses.

5.3 Power sharing with time delay

In this subsection, we have tested our power sharing algorithm with time delay, where two 2-kW loads are added at t = 5 s and removed at t = 10 s on buses 3 and 5, respectively. We have tested on different time delays, say, 50 ms and 100 ms, as shown in Figures 8A–D. It can be observed that power sharing is failed when the time delay is 100 ms, but power sharing can be achieved if the time delay is 50 ms.

FIGURE 8

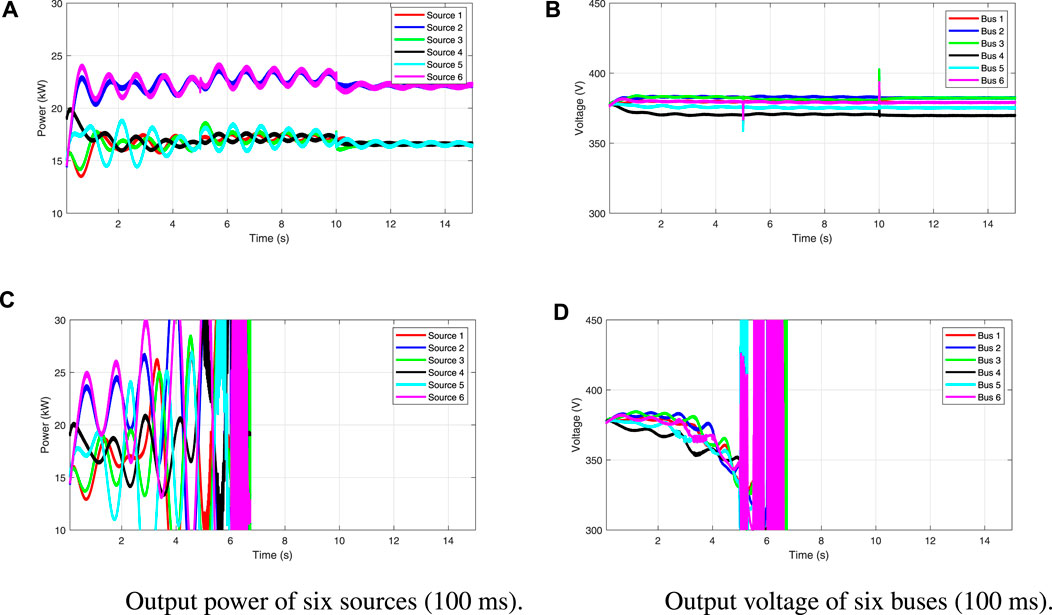
FIGURE 8. Performance of the time delay test: (A) output power of six sources (50 ms), (B) voltage of six buses (50 ms), (C) output power of six sources (100 ms), and (D) output voltage of six buses (100 ms).

5.4 Optimal power sharing

In this test, the optimizer starts to work at t = 5 s. The distributed optimization algorithm is employed with the setting μ = 3. Within 10 iterations, it obtains the optimal power dispatch: $P_1^{\mathit{opt}}=16.65$ kW, $P_2^{\mathit{opt}}=12$ kW, $P_3^{\mathit{opt}}=20$ kW, $P_4^{\mathit{opt}}=18.80$ kW, $P_5^{\mathit{opt}}=15.52$ kW, and $P_6^{\mathit{opt}}=22.78$ kW. The evolution of λ_con and cost C are shown in Figures 9A, B . It observes that λ_con keeps decreasing and finally converges to 4.986. The cost of sources decreases as well and converges to a steady state within several iterations. The optimal power sharing of sources is achieved, as seen in Figure 10A. It is worth noting that the output power of source 2 reaches its lower bound, while the output power of source 3 reaches its upper bound. Moreover, voltage shifts of six buses are shown in Figure 10B.

FIGURE 9

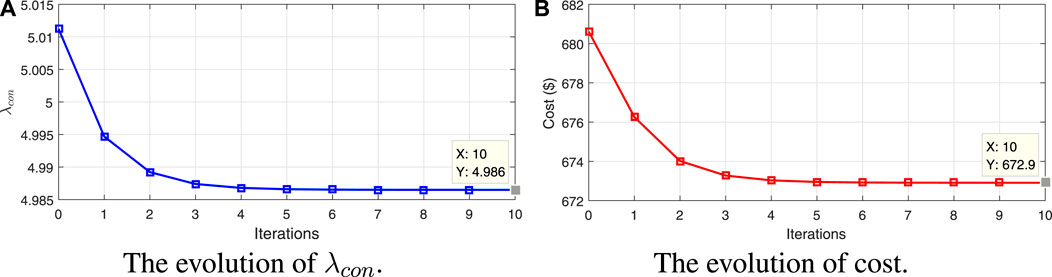
FIGURE 9. Simulation results of the distributed optimization algorithm: (A) evolution of λ_con and (B) evolution of the cost.

FIGURE 10

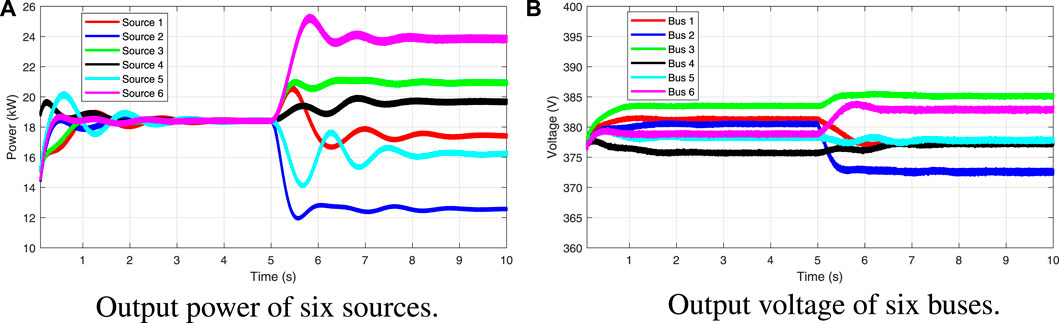
FIGURE 10. Performance of the optimal power sharing test: (A) output power of six sources and (B) voltage of six buses.

6 Conclusion

This paper presents a solution to the optimal power sharing problem in a DC microgrid using a combination of the proportional power sharing control algorithm and the DIVR algorithm. Theproportional power sharing control algorithm, designed based on the Lyapunov method, is used to regulate the voltage profile of the microgrid. The fixed-time based distributed optimization algorithm, which uses a weighted finite-time consensus protocol and an initial value restoration algebraic operation, optimizes power sharing among the sources in the microgrid. Both algorithms are fully distributed and implemented at the cyber system layer. The algorithms work together to calculate the reference voltage for the zero-level controller to track, resulting in optimal power sharing among the sources. The effectiveness of the proposed method is demonstrated through simulation on a six-bus DC microgrid. Future work may focus on giving a theoretical bound for the time delay of the distributed optimal power-sharing controller and considering the constraint of the bus voltage during the control process.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material; further inquiries can be directed to the corresponding author.

Author contributions

ZY contributed to the conception and design of the framework. FY organized the overall paper. JC wrote sections of the manuscript. All authors contributed to the article and approved the submitted version.

Funding

This work was supported by the science and technology project (52153222001H) of the State Grid Hubei Electric Power Research Institute.

Acknowledgments

The authors would like to appropriate the editor and reviewers for their valuable suggestions and comments.

Conflict of interest

ZY, FY, and JC were employed by the State Grid Hubei Electric Power Co., Ltd. The authors declare that this study received funding from State Grid Hubei Electric Power Research Institute.The funder had the following involvement in the study: design, data collection and analysis, decision to publish, or preparation of the manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Ahmed, M. A., Abbas, G., Jumani, T. A., Rashid, N., Bhutto, A. A., and Eldin, S. M. (2023). Techno-economic optimal planning of an industrial microgrid considering integrated energy resources. Front. Energy Res.11, 148. doi:10.3389/fenrg.2023.1145888

CrossRef Full Text | Google Scholar

Anand, S., Fernandes, B. G., and Guerrero, J. (2013). Distributed control to ensure proportional load sharing and improve voltage regulation in low-voltage dc microgrids. IEEE Trans. Power Electron.28, 1900–1913. doi:10.1109/TPEL.2012.2215055

CrossRef Full Text | Google Scholar

Bidram, A., and Davoudi, A. (2012). Hierarchical structure of microgrids control system. IEEE Trans. Smart Grid3, 1963–1976. doi:10.1109/TSG.2012.2197425

CrossRef Full Text | Google Scholar

Chang, J.-W., Chae, S., and Lee, G.-S. (2023). Distributed optimal power sharing strategy in an islanded hybrid ac/dc microgrid to improve efficiency. IEEE Trans. Power Deliv.38, 724–737. doi:10.1109/TPWRD.2022.3197434

CrossRef Full Text | Google Scholar

Dou, Y., Chi, M., Liu, Z.-W., Wen, G., and Sun, Q. (2022). Distributed secondary control for voltage regulation and optimal power sharing in dc microgrids. IEEE Trans. Control Syst. Technol.30, 2561–2572. doi:10.1109/TCST.2022.3156391

CrossRef Full Text | Google Scholar

Guerrero, J. M., Vasquez, J. C., Matas, J., de Vicuna, L. G., and Castilla, M. (2011). Hierarchical control of droop-controlled ac and dc microgrids—A general approach toward standardization. IEEE Trans. Industrial Electron.58, 158–172. doi:10.1109/TIE.2010.2066534

CrossRef Full Text | Google Scholar

Guo, F., Wen, C., Mao, J., and Song, Y. D. (2016). Distributed economic dispatch for smart grids with random wind power. IEEE Trans. Smart Grid7, 1572–1583. doi:10.1109/TSG.2015.2434831

CrossRef Full Text | Google Scholar

Hamad, A. A., Azzouz, M. A., and El-Saadany, E. F. (2016). Multiagent supervisory control for power management in dc microgrids. IEEE Trans. Smart Grid7, 1–1068. doi:10.1109/TSG.2015.2452191

CrossRef Full Text | Google Scholar

Hamzeh, M., Ghazanfari, A., Mohamed, Y. A. R. I., and Karimi, Y. (2015). Modeling and design of an oscillatory current-sharing control strategy in dc microgrids. IEEE Trans. Industrial Electron.62, 6647–6657. doi:10.1109/TIE.2015.2435703

CrossRef Full Text | Google Scholar

Hatziargyriou, N., Asano, H., Iravani, R., and Marnay, C. (2007). Microgrids. IEEE Power Energy Mag.5, 78–94. doi:10.1109/MPAE.2007.376583

CrossRef Full Text | Google Scholar

Hou, X., Sun, K., Zhang, X., Sun, Y., and Lu, J. (2022). A hybrid voltage/current control scheme with low-communication burden for grid-connected series-type inverters in decentralized manner. IEEE Trans. Power Electron.37, 920–931. doi:10.1109/TPEL.2021.3093080

CrossRef Full Text | Google Scholar

Hou, X., Sun, Y., Zhang, X., Zhang, G., Lu, J., and Blaabjerg, F. (2019). A self-synchronized decentralized control for series-connected h-bridge rectifiers. IEEE Trans. Power Electron.34, 7136–7142. doi:10.1109/TPEL.2019.2896150

CrossRef Full Text | Google Scholar

Hu, J., Duan, J., Ma, H., and Chow, M.-Y. (2018). Distributed adaptive droop control for optimal power dispatch in dc microgrid. IEEE Trans. Industrial Electron.65, 778–789. doi:10.1109/TIE.2017.2698425

CrossRef Full Text | Google Scholar

Huang, B., Zheng, S., Wang, R., Wang, H., Xiao, J., and Wang, P. (2022). Distributed optimal control of dc microgrid considering balance of charge state. IEEE Trans. Energy Convers.37, 1–2174. doi:10.1109/TEC.2022.3169462

CrossRef Full Text | Google Scholar

Khorsandi, A., Ashourloo, M., and Mokhtari, H. (2014). A decentralized control method for a low-voltage dc microgrid. IEEE Trans. Energy Convers.29, 793–801. doi:10.1109/TEC.2014.2329236

CrossRef Full Text | Google Scholar

Li, C., de Bosio, F., Chen, F., Chaudhary, S. K., Vasquez, J. C., and Guerrero, J. M. (2017). Economic dispatch for operating cost minimization under real-time pricing in droop-controlled dc microgrid. IEEE J. Emerg. Sel. Top. Power Electron.5, 587–595. doi:10.1109/JESTPE.2016.2634026

CrossRef Full Text | Google Scholar

Li, C., Yu, X., Yu, W., Huang, T., and Liu, Z. W. (2016). Distributed event-triggered scheme for economic dispatch in smart grids. IEEE Trans. Industrial Inf.12, 1775–1785. doi:10.1109/TII.2015.2479558

CrossRef Full Text | Google Scholar

Liu, X.-K., Wang, S.-Q., Chi, M., Liu, Z.-W., and Wang, Y.-W. (2023a). Resilient secondary control and stability analysis for dc microgrids under mixed cyber attacks. IEEE Trans. Industrial Electron.2023, 1–10. In press. doi:10.1109/TIE.2023.3262893

CrossRef Full Text | Google Scholar

Liu, X.-K., Wen, C., Xu, Q., and Wang, Y.-W. (2021). Resilient control and analysis for dc microgrid system under DoS and impulsive FDI attacks. IEEE Trans. Smart Grid12, 3742–3754. doi:10.1109/TSG.2021.3072218

CrossRef Full Text | Google Scholar

Liu, X.-K., Yan, J., Xing, L., and Wen, C. (2020). Constrained consensus-based iterative algorithm for economic dispatch in power systems. IECON 2020 46th Annu. Conf. IEEE Industrial Electron. Soc.2020, 3537–3542. doi:10.1109/IECON43393.2020.9255216

CrossRef Full Text | Google Scholar

Liu, Z., Li, J., Su, M., Liu, X., Yuan, L., Xie, K., et al. (2023b). Evaluation of myopia-associated genes in a Han Chinese population with high myopia. IEEE Trans. Power Syst.2023, 1–5. In press. doi:10.1080/13816810.2023.2191709

CrossRef Full Text | Google Scholar

Loia, V., and Vaccaro, A. (2014). Decentralized economic dispatch in smart grids by self-organizing dynamic agents. IEEE Trans. Syst. Man, Cybern. Syst.44, 397–408. doi:10.1109/TSMC.2013.2258909

CrossRef Full Text | Google Scholar

Lu, X., Guerrero, J. M., Sun, K., and Vasquez, J. C. (2014). An improved droop control method for dc microgrids based on low bandwidth communication with dc bus voltage restoration and enhanced current sharing accuracy. IEEE Trans. Power Electron.29, 1800–1812. doi:10.1109/TPEL.2013.2266419

CrossRef Full Text | Google Scholar

Meng, L., Shafiee, Q., Trecate, G. F., Karimi, H., Fulwani, D., Lu, X., et al. (2017). Review on control of dc microgrids and multiple microgrid clusters. IEEE J. Emerg. Sel. Top. Power Electron.5, 928–948. doi:10.1109/JESTPE.2017.2690219

CrossRef Full Text | Google Scholar

Moayedi, S., and Davoudi, A. (2017). Unifying distributed dynamic optimization and control of islanded dc microgrids. IEEE Trans. Power Electron.32, 2329–2346. doi:10.1109/TPEL.2016.2565517

CrossRef Full Text | Google Scholar

Morstyn, T., Hredzak, B., and Agelidis, V. G. (2016a). Cooperative multi-agent control of heterogeneous storage devices distributed in a dc microgrid. IEEE Trans. Power Syst.31, 2974–2986. doi:10.1109/TPWRS.2015.2469725

CrossRef Full Text | Google Scholar

Morstyn, T., Hredzak, B., Demetriades, G. D., and Agelidis, V. G. (2016b). Unified distributed control for dc microgrid operating modes. IEEE Trans. Power Syst.31, 802–812. doi:10.1109/TPWRS.2015.2406871

CrossRef Full Text | Google Scholar

Nasirian, V., Davoudi, A., Lewis, F. L., and Guerrero, J. M. (2014). Distributed adaptive droop control for dc distribution systems. IEEE Trans. Energy Convers.29, 944–956. doi:10.1109/TEC.2014.2350458

CrossRef Full Text | Google Scholar

Olivares, D. E., Mehrizi-Sani, A., Etemadi, A. H., Canizares, C. A., Iravani, R., Kazerani, M., et al. (2014). Trends in microgrid control. IEEE Trans. Smart Grid5, 1905–1919. doi:10.1109/TSG.2013.2295514

CrossRef Full Text | Google Scholar

Papadimitriou, C., Zountouridou, E., and Hatziargyriou, N. (2015). Review of hierarchical control in dc microgrids. Electr. Power Syst. Res.122, 159–167. doi:10.1016/j.epsr.2015.01.006

CrossRef Full Text | Google Scholar

Simpson-Porco, J. W., Dorfler, F., and Bullo, F. (2013). Synchronization and power sharing for droop-controlled inverters in islanded microgrids. Automatica49, 2603–2611. doi:10.1016/j.automatica.2013.05.018

CrossRef Full Text | Google Scholar

Wang, L., Li, T., Cheng, Z., Hu, X., Li, Z., Liu, Z., et al. (2023). A unified droop control of ac microgrids under different line impedances: Revisiting droop control and virtual impedance method. Front. Energy Res.11, 282–283. doi:10.1038/s41563-023-01487-3

CrossRef Full Text | Google Scholar

Wang, P., Lu, X., Yang, X., Wang, W., and Xu, D. (2016a). An improved distributed secondary control method for dc microgrids with enhanced dynamic current sharing performance. IEEE Trans. Power Electron.31, 6658–6673. doi:10.1109/TPEL.2015.2499310

CrossRef Full Text | Google Scholar

Wang, Z., Wu, W., and Zhang, B. (2016b). A fully distributed power dispatch method for fast frequency recovery and minimal generation cost in autonomous microgrids. IEEE Trans. Smart Grid7, 19–31. doi:10.1109/TSG.2015.2493638

CrossRef Full Text | Google Scholar

Wood, A. J., and Wollenberg, B. F. (2012). Power generation, operation, and control. United States: John Wiley & Sons.

Google Scholar

Xiao, Z.-X., Guan, Y.-Z., Fang, H.-W., Terriche, Y., and Guerrero, J. M. (2022). Dynamic and steady-state power-sharing control of high-efficiency dc shipboard microgrid supplied by diesel generators. IEEE Syst. J.16, 4595–4606. doi:10.1109/JSYST.2021.3111685

CrossRef Full Text | Google Scholar

Xing, H., Mou, Y., Fu, M., and Lin, Z. (2015). Distributed bisection method for economic power dispatch in smart grid. IEEE Trans. Power Syst.30, 3024–3035. doi:10.1109/TPWRS.2014.2376935

CrossRef Full Text | Google Scholar

Yang, S., Tan, S., and Xu, J. X. (2013). Consensus based approach for economic dispatch problem in a smart grid. IEEE Trans. Power Syst.28, 4416–4426. doi:10.1109/TPWRS.2013.2271640

CrossRef Full Text | Google Scholar

Zhao, C., He, J., Cheng, P., and Chen, J. (2016). Consensus-based energy management in smart grid with transmission losses and directed communication. IEEE Trans. smart grid8, 2049–2061. doi:10.1109/tsg.2015.2513772

CrossRef Full Text | Google Scholar