Based on the difference of Newton’s method integrated energy system distributed collaborative optimization

With the integration of renewable energy into the grid, the traditional power system stability faced by huge challenges, and the development of integrated energy system, it is of essence to improve the coupling of multiple integrated energy systems of different types, management in the integrated energy system and reduce the pressure of communication and computing, in this paper, we construct a distributed Newton algorithm based on Newton’s method to accelerate the solving speed, which decreases the times of iterations to reduce the pressure of communication and calculation, saving the cost of operation. Besides, privacy protection is particularly important for a distributed control system, under the premise that calculation speed is guaranteed, meanwhile, privacy protection of all agents in an integrated energy system is also critical. This study uses annular directed distributed algorithm to enhance the privacy of integrated distributed energy systems in the intelligent body, so as to fully ensure the privacy safety of all agents in the system. Moreover, the forementioned difference Newton algorithm in this study avoid the behavior of Zeno, greatly accelerating the speed of iteration and finding the best energy market price,. At the same time, the privacy safety of all agentsin the distributed energy system are ensured. Finally, a distributed integrated energy system based on the algorithm proposed by this study has went through theoretical proof and simulation experiment, whose result shows the validity of the algorithm.

1 Introduction

Recent years have seen the need to bring a major shift of energy source from coal to and electricity in an attempt to ensure power supply Therefore, renewable energy is connected to the power system, which can ensure sustainable and reliable power supply. Despite unprecedented challenge and change, the traditional power system gradually transformed into new power system generating clean energy. However, as the new energy power systemincreasing in scale, it still faces numerous challenges, such as new balance system and complex security mechanism. The introduction of the integrated energy system can meet the regional energy demand and the multi-source strategy development is of great significance, that said, the key still lies in safeguarding regional energy safety and stable operation of energy system.

For the traditional electric power system, renewable energy is introduced into too little, therefore, most of the scholars at home and abroad research contains only a single power network (YANG and WANG, 2021), and for the centralized algorithm. These algorithms included multi-objective optimization scheduling (Zhang et al., 2020), mixed nonlinear programming (Marty et al., 2017), (Hemamalini and Simon, 2009) Newton method, and traditional iterative methods (Lin and Viviani, 1984) (Hemamalini and Simon, 2009) to solve the non-convex participant energy management problem in centralized energy systems. The literature suggests that centralized algorithms can more accurately obtain optimal values (Hemamalini and Simon, 2009), and are fast and easy to design. However, using centralized algorithms requires significant computational resources and communication costs, and damage to the central agent can be difficult to recover, such as (Yin et al., 2018). To address the aforementioned challenges, a distributed algorithm has been proposed by relevant scholars, which effectively overcomes the issue of handling large volumes of data and prevents problems such as information processing. The distributed algorithm encompasses the following aspects: Chow initially proposed a numerical method for consistency that was utilized by foreign scholars to solve the problem of distributed energy scheduling (Zhang and Chow, 2012). For a single distribution power grid, the primary consideration is the impact of electricity prices on power consumption (Xie et al., 2022a). Moreover, the robustness and control of the micro grid must be taken into account (Xie et al., 2022b), while optimization of parallel distribution in weak power grids is achieved through the application of the method of group economical ICA and the NSGA-II (Nie et al., 2023), (Zhong et al., 2022), which aims to identify the optimal operating point for the micro grid. The optimization of the micro grid mainly includes approaches such as neural network-based methods (Zhang et al., 2023), alternating direction multiplier methods (Gao et al., 2022) (Zhu et al., 2022), and dynamic programming (Yang and Yang, 2022). Scholars, such as Yang Ping, have proposed the GPS model in light of the relationship between information flow and energy flow, and have also developed optimal control strategies to explore the micro grid (Yang and Yang, 2022). The aforementioned research effectively addresses the challenges associated with communication and computing stress in traditional micro grid control centers. In addition, due to the use of distributed methods, the absence of a control center ensures that local damage has minimal impact on the entire system. However, the research only focuses on electricity and does not consider other forms of energy. With the constant improvement of the proportion of new energy power system, balance system, the security mechanism of the new type of power system problems such as challenged, in this case, the collaborative optimization of a variety of energy for the stability and security of the power system is obviously much better than a single grid. In this context, some scholars have proposed the concept of an integrated energy system that differs from single energy networks. Considering multiple energy networks together can enhance the effect of energy optimization, but it also increases the complexity of the transformation mechanisms across various forms of energy, such as electricity, gas, and heat, in both time and space scales (Lv, 2022). Consequently, the comprehensive optimization of an integrated energy system is more challenging than optimizing a single grid (Schfer et al., 2018). To address these issues, scholars have developed distributed computing methods for finding optimal values in integrated energy systems. Many studies by domestic and foreign scholars have proposed distributed non-iterative algorithms for multi-agent coordination optimization problems (Tan et al., 2019; Tan et al., 2021). For instance, one study (Munshi and Mohamed, 2019) proposed an unsupervised algorithm that uses electric meter data to determine electrical load parameters, while another study (Zhang et al., 2017) introduced the mixed alternating direction multiplier method to solve the coupling relationship between various forms of energy in the integrated energy system. Scholars such as Zhang have applied the integrated energy unit and alternating direction multiplier method to address the multivariate coupling between electric and heat energy systems and solve coordination problems between the energy networks (Zhang et al., 2017). On the basis of previous research, scholars both at home and abroad have mainly focused on the optimization of distributed optimization methods in integrated energy systems with regards to convergence speed. This has been done by addressing issues such as information attacks (Zhao et al., 2016; Duan and Chow, 2019), non-convexity of energy systems (Chen and Zhao, 2019; Huang et al., 2019; Li et al., 2019), and so on.

Although about the optimal management of traditional integrated energy system research have been studied from many aspects, can meet the balance between supply and demand, energy scheduling and achievements, but the traditional studies in distributed energy system, between the iterative speed and privacy protection problems still exist, Literature (Zhang et al., 2017; Li et al., 2020) has shown that when the iteration speed is slow, it is possible to ignore the kink behavior, which can lead to a loss in wireless loop. The traditional energy management approach is thus faced with the challenge of being too slow for a long period of time, resulting in delayed energy supply during emergencies and inevitable loss. Pressure is too large and integrated energy systems of communication, iterative speed too slow, resulting in the high cost problem. Based on the above analysis, this paper combined with the ring to algorithm design difference Newton’s method, Newton method and greatly accelerate the iteration speed, reduce the number of iterations, delay to solve energy, reduce communication and computing pressure, privacy protection and integrated energy systems between adjacent agent. The main contributions of this paper are as follows.

1) The difference Newton’s method is proposed based on the Newton’s method. In comparison with the traditional approach, this method is characterized by a faster rate of iteration and a reduced number of iterations. Consequently, in the context of an integrated energy system, it can significantly reduce communication and computational overhead and mitigate energy latency.

2) The ring-based distributed algorithm is employed in the integrated energy system to ensure privacy protection among its participants. Conventional algorithms rely on participants to protect their privacy, but they require the exchange of adjacent information such as energy input/output power and energy price. In this regard, the use of the ring-based distributed algorithm effectively addresses this issue by providing complete privacy protection for all participants.

3) To avoid the divergence of Newton’s method during the downhill, a kino line may occur where the algorithm iterates indefinitely within a limited time, leading to an infinite loop. To prevent this behavior, the proposed algorithm in this paper is designed to avoid kino behavior.

The paper is structured as follows: In the first section, the integrated energy system established in this study is introduced, along with the function and constraint conditions for each participant’s cost in the system. The second section describes the Difference Newton’s method employed in this paper (DNEA) and how it addresses the energy coupling issue. The third section provides a proof of DNEA’s speed, convergence, optimality, and avoidance of kino behavior. The fourth section presents a simulation validation of the proposed DNEA algorithm in the established integrated energy system. Finally, the fifth section offers concluding remarks.

2 Models of IES

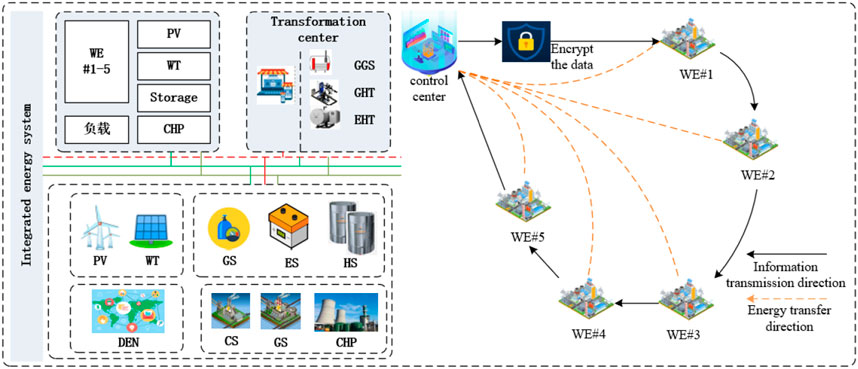
The composition of body, specifically its internal structure, comprises various energy devices that serve distinct functions. 1)The power generation device includes distributed coal-fired generators, gas generators, solar generators, wind turbines, and energy storage systems. 2) The heating device comprises distributed coal-fired heat production devices, distributed combustion gas heat production equipment, photovoltaic production engines, and distributed storage devices. 3) The thermal electric power plant machine. 4) The distributed gas suppliers constitute the remaining energy equipment. Each of these energy bodies accommodates three energy types, namely, electricity, gas, and heat, which need to be considered while accounting for electricity price fluctuations, load-side random scheduling, and demand response for electricity, gas, and heat. Because in traditional power system load is not adjustable, so you need to increase the “adjustable load”, such as: conversion of electricity and heat, electricity and hydrogen between mutual conversion, energy storage device, etc.,. This paper is suitable for small energy network connected to the electricity grid if there are toning, can from the grid to compensate.

The figure illustrates the encryption of data to safeguard the privacy of each pluripotent micro power grid in the integrated energy system. During each iteration process, the control center establishes encrypted data to ensure secure communication.

2.1 Models of renewable energy devices

This article considers five energy bodies and takes into account the changing demands and environmental factors affecting the energy efficiency of each equipment within these bodies. Based on this, the following constraints have been established.

1) Distributed energy physical quantity balance constraints

$P_{i,T}^{ex}=\left\{\begin{array}{c}{\displaystyle \sum }_{i\in {\mathrm{{\rm K}}}_i^{pg}}{P}_{ij,T}^g+{\displaystyle \sum }_{i\in {\mathrm{{\rm K}}}_i^{pc}}{P}_{ij,T}^c+{\displaystyle \sum }_{i\in {\mathrm{{\rm K}}}_i^{pes}}{P}_{ij,T}^{es}+{\displaystyle \sum }_{i\in {\mathrm{{\rm K}}}_i^{pchp}}{P}_{ij,T}^{chp}+{\displaystyle \sum }_{i\in {\mathrm{{\rm K}}}_i^{pp}}{P}_{ij,T}^p\\ +{\displaystyle \sum }_{i\in {\mathrm{{\rm K}}}_i^{pw}}{P}_{ij,T}^w-{\displaystyle \sum }_{i\in {\mathrm{{\rm K}}}_i^{\mathrm{\Lambda }}}\left(\mathrm{\Lambda }{P}_{ij,T}^r\right.+\mathrm{\Lambda }{P}_{ij,T}^{cl})\end{array}\right\}(1)$

Type: $P_{i,T}^{ex}$ for the ith a total electricity energy body; ${\displaystyle \sum }_{i\in {\mathrm{{\rm K}}}_i^{pg}}{P}_{ijT}^g$ for gas supplier by air to turn electric power. ${\displaystyle \sum }_{i\in {\mathrm{{\rm K}}}_i^{pc}}{P}_{ij,T}^c$ as the coal to produce electricity, ${\displaystyle \sum }_{i\in {\mathrm{{\rm K}}}_i^{pes}}{P}_{ij,T}^{es}$ as the energy storage equipment to produce electricity. ${\displaystyle \sum }_{i\in {\mathrm{{\rm K}}}_i^{pchp}}{P}_{ij,T}^{chp}$ for cogeneration plant producing; ${\displaystyle \sum }_{i\in {\mathrm{{\rm K}}}_i^{pp}}{P}_{ij,T}^p$ for photovoltaic generation; ${\displaystyle \sum }_{i\in {\mathrm{{\rm K}}}_i^{pw}}{P}_{ij,T}^w$ for wind power generation; $\mathrm{\Lambda }{P}_{ij,T}^r$ for the necessary power to the load side, $\mathrm{\Lambda }{P}_{ij,T}^{cl}$ for electric power loss when converted into heat. This paper only considers the electric load that is converted to heat load, and not the heat load converted to electricity load case. ${\mathrm{{\rm K}}}_i^{pg}$, ${\mathrm{{\rm K}}}_i^{pc}$, ${\mathrm{{\rm K}}}_i^{pes}$, ${\mathrm{{\rm K}}}_i^{pchp}$, ${\mathrm{{\rm K}}}_i^{pp}$, ${\mathrm{{\rm K}}}_i^{pw}$, ${\mathrm{{\rm K}}}_i^{\mathrm{\Lambda }}$ respectively represent the ith coal-fired generator set, energy storage device, gas supplier collection, cogeneration unit set, pv electricity production device set, load, and fan electricity production device under given energy body scenarios.

$H_{i,T}^{ex}=\left\{\begin{array}{c}{\displaystyle \sum }_{i\in {\mathrm{{\rm K}}}_i^{pg}}{H}_{ij,T}^g+{\displaystyle \sum }_{i\in {\mathrm{{\rm K}}}_i^{pc}}{H}_{ij,T}^c+{\displaystyle \sum }_{i\in {\mathrm{{\rm K}}}_i^{pes}}{H}_{ij,T}^{es}\\ +{\displaystyle \sum }_{i\in {\mathrm{{\rm K}}}_i^{pchp}}{H}_{ij,T}^{chp}+{\displaystyle \sum }_{i\in {\mathrm{{\rm K}}}_i^{pp}}{H}_{ij,T}^p-{\displaystyle \sum }_{i\in {\mathrm{{\rm K}}}_i^{\mathrm{\Lambda }}}\left(\mathrm{\Lambda }{H}_{ij,T}^r\right.+\mathrm{\Lambda }{H}_{ij,T}^{cl})\end{array}\right\}(2)$

$G_{i,T}^{ex}={\displaystyle \sum }_{i\in {\mathrm{{\rm K}}}_i^{gas}}{G}_{ij,T}^{gas}-{\displaystyle \sum }_{i\in {\mathrm{{\rm K}}}_i^{\mathrm{\Lambda }}}\left(H_{ij,T}^g\right.+P_{ij,T}^g+\mathrm{\Lambda }{G}_{ij,T}^{cl})(3)$

For each CLP energy body, the production amount of equipment for gas and heat must remain equal to the difference between the total load and the exchange of energy on the load side during operation. In addition, the exchange of distributed energy should satisfy the following constraints:

Regarding the heat transfer in type 2) variables, the concrete form of electricity exchange is as follows: the same redundancy avoidance applies, and it is not presented here. 3), $G_{i,T}^{ex}$ indicates the remaining gas amount for the ith energy body; $G_{ij,T}^{gas}$ represents the gas quantity supplied by gas suppliers; $\mathrm{\Lambda }{G}_{ij,T}^{cl}$ denotes the gas volume lost when converted into other energy forms. In this article, $P_{i,T}^{ex}$ and $H_{i,T}^{ex}$ are regulated as the timing for discharge or exothermic processes, while negative values indicate electricity or heat absorption. $P_{ij,T}^{es}$ and $H_{ij,T}^{es}$ represent timing for energy storage devices to emit or absorb electric heat; negative values indicate electricity and heat energy storage devices’ absorption.

2) Considering the randomness, volatility, and renewable energy output fluctuation value limit conditions, the following expressions apply:

$P_{ij,T}^{p,\min }\le P_{ij,T}^p\le P_{ij,T}^{p,\max }(4)$

$P_{ij,T}^{w,\min }\le P_{ij,T}^w\le P_{ij,T}^{w,\max }(5)$

$H_{ij,T}^{p,\min }\le H_{ij,T}^p\le H_{ij,T}^{p,\max }(6)$

Type: $P_{ij,T}^{p,\min }$, $P_{ij,T}^{w,\min }$, $H_{ij,T}^{p,\min }$ for renewable energy to produce power and thermal power limit, $P_{ij,T}^{p,\max }$, $P_{ij,T}^{w,\max }$, $H_{ij,T}^{p,\max }$ for renewable energy to produce power and thermal power limit. Renewable energy constraints are designed with consideration for the renewable energy capacity confidence interval and prediction error, expressing the randomness and volatility of renewable energy (Zhang et al., 2017).

As a renewable energy source, solar electricity is widely utilized currently; however, its volatility and randomness necessitate the inclusion of photovoltaic (pv) motor and solar heating into the following functions:

$C\left(P_{ij,T}^p\right)={\alpha }_{ij,T}^{p,p}{P}_{ij,T}^p+{\beta }_{ij,T}^{p,p}\exp \left({\epsilon }_{ij,T}^{p,p}\frac{P_{ij,T}^{p,\max }-P_{ij,T}^p}{P_{ij,T}^{p,\max }-P_{ij,T}^{p,\min }}\right)+{\kappa }_{ij,T}^{p,p}(7)$

$C\left(H_{ij,T}^p\right)={\alpha }_{ij,T}^{h,p}{H}_{ij,T}^p+{\beta }_{ij,T}^{h,p}\exp \left({\epsilon }_{ij,T}^{h,p}\frac{H_{ij,T}^{p,\max }-H_{ij,T}^p}{H_{ij,T}^{p,\max }-H_{ij,T}^{p,\min }}\right)+{\kappa }_{ij,T}^{h,p}(8)$

Type: ${\alpha }_{ij,T}^{p,p}$, ${\beta }_{ij,T}^{p,p}$, ${\epsilon }_{ij,T}^{p,p}$, ${\kappa }_{ij,T}^{p,p}$, ${\alpha }_{ij,T}^{h,p}$, ${\beta }_{ij,T}^{h,p}$, ${\epsilon }_{ij,T}^{h,p}$, and ${\kappa }_{ij,T}^{h,p}$ are the cost coefficients.

Fan electricity production cost function:

$C\left(P_{ij,T}^w\right)={\alpha }_{ij,T}^{p,w}{P}_{ij,T}^w+{\beta }_{ij,T}^{p,w}\exp \left({\epsilon }_{ij,T}^{p,w}\frac{P_{ij,T}^{w,\max }-P_{ij,T}^w}{P_{ij,T}^{w,\max }-P_{ij,T}^{w,\min }}\right)+{\kappa }_{ij,T}^{p,w}(9)$

Type: ${\alpha }_{ij,T}^{p,w}$、 ${\beta }_{ij,T}^{p,w}$、 ${\epsilon }_{ij,T}^{p,w}$、 ${\kappa }_{ij,T}^{p,w}$ of cost coefficient.

Note: this article does not consider the relationships between kW and heat, electricity, and gas; therefore, the comprehensive energy kW should be applied to all energy units involved.

3) Considering coal heating device, coal thermal power plant and cogeneration plant output fluctuation value limit condition are:

$P_{ij,T}^{c,\min }\le P_{ij,T}^c\le P_{ij,T}^{c,\max }(10)$

$H_{ij,T}^{c,\min }\le H_{ij,T}^c\le H_{ij,T}^{c,\max }(11)$

$P_{ij,T}^{chp,\min }\le P_{ij,T}^{chp}\le P_{ij,T}^{chp,\max }(12)$

$H_{ij,T}^{chp,\min }\le H_{ij,T}^{chp}\le H_{ij,T}^{chp,\max }(13)$

Type: $P_{ij,T}^{c,\min }$, $H_{ij,T}^{c,\min }$, $P_{ij,T}^{chp,\min }$, and $H_{ij,T}^{chp,\min }$ represent the lower limits for the power supply of T moment coal-fired thermal power equipment, coal heating equipment, and cogeneration plant heating power, respectively; $P_{ij,T}^{c,\max }$, $H_{ij,T}^{c,\max }$, $P_{ij,T}^{chp,\max }$, and $H_{ij,T}^{chp,\max }$ respectively denote the upper limits for the power supply of T moment coal-fired thermal power equipment, coal heating equipment, and cogeneration plant heating power, respectively.

4) Coal-fired thermal power equipment, coal heating equipment, and combined heat and power output ramping restrictions are as follows:

$-P_{ij,T}^{c,ccl}\le P_{ij,T}^c-P_{ij,T-1}^c\le P_{ij,T}^{c,ccl}(14)$

$-H_{ij,T}^{c,ccl}\le H_{ij,T}^c-H_{ij,T-1}^c\le H_{ij,T}^{c,ccl}(15)$

$-P_{ij,T}^{chp,ccl}\le P_{ij,T}^{chp}-P_{ij,T-1}^{chp}\le P_{ij,T}^{chp,ccl}(16)$

$-H_{ij,T}^{chp,ccl}\le H_{ij,T}^{chp}-H_{ij,T-1}^{chp}\le H_{ij,T}^{chp,ccl}(17)$

Type: $H_{ij,T}^{c,ccl}$, $P_{ij,T}^{chp,ccl}$, and $H_{ij,T}^{chp,ccl}$ represent the maximum change in T moment coal-fired thermal power equipment compared to T-1 h, the maximum change in T moment coal-fired heat production equipment compared to T-1 h, and the maximum change in T moment cogeneration equipment compared to T-1 h for electricity and heat production, respectively. $P_{ij,T-1}^c$, $H_{ij,T-1}^c$, $P_{ij,T-1}^{chp}$, and $H_{ij,T-1}^{chp}$ denote the initial production of T-1 coal-fired thermal power equipment, T-1 coal-fired heat production equipment, and T-1 cogeneration plant for electricity and heat, respectively.

Coal is commonly used in energy bodies to produce electricity and heat, and its consumption characteristics are determined by the energy size produced at time T. Although its stability is reliable, it causes a certain level of environmental pollution and is subject to ramping constraints. The cost functions for coal-fired generators and heat production engines are as follows:

$C\left(P_{ij,T}^c\right)={\alpha }_{ij,T}^{p,c}{\left(P_{ij,T}^c\right)}^2+{\beta }_{ij,T}^{p,c}{P}_{ij,T}^c+{\epsilon }_{ij,T}^{p,c}{\mathrm{e}}^{{\kappa }_{ij,T}^{p,c}{P}_{ij,T}^c}+{\lambda }_{ij,T}^{p,c}(18)$

$C\left(H_{ij,T}^c\right)={\alpha }_{ij,T}^{h,c}{\left(H_{ij,T}^c\right)}^2+{\beta }_{ij,T}^{h,c}{H}_{ij,T}^c+{\epsilon }_{ij,T}^{h,c}{\mathrm{e}}^{{\kappa }_{ij,T}^{h,c}{H}_{ij,T}^c}+{\lambda }_{ij,T}^{h,c}(19)$

Type: ${\alpha }_{ij,T}^{p,c}$, ${\beta }_{ij,T}^{p,c}$, ${\epsilon }_{ij,T}^{p,c}$, ${\kappa }_{ij,T}^{p,c}$, ${\lambda }_{ij,T}^{p,c}$, ${\alpha }_{ij,T}^{h,c}$, ${\beta }_{ij,T}^{h,c}$, ${\epsilon }_{ij,T}^{h,c}$, ${\kappa }_{ij,T}^{h,c}$, ${\lambda }_{ij,T}^{h,c}$ are cost coefficients, with R being positive.

As an energy body, the CLP cogeneration unit exhibits a thermal coupling relationship with its main equipment. The cost function is determined by the simultaneous production of electric and thermal energy, and its output falls within a specific range. The cogeneration unit cost function is as follows:

$C\left(P_{ij,T}^{chp},H_{ij,T}^{chp}\right)={\alpha }_{ij,T}^{p,chp}{\left(P_{ij,T}^{chp}\right)}^2+{\beta }_{ij,T}^{p,chp}{P}_{ij,T}^{chp}+{\epsilon }_{ij,T}^{h,chp}{\left(H_{ij,T}^{chp}\right)}^2+{\lambda }_{ij,T}^{h,chp}{H}_{ij,T}^{chp}+{\eta }_{ij,T}^{chp}(20)$

Type: ${\alpha }_{ij,T}^{p,chp}$, ${\beta }_{ij,T}^{p,chp}$, ${\epsilon }_{ij,T}^{h,chp}$, ${\lambda }_{ij,T}^{h,chp}$, ${\eta }_{ij,T}^{chp}$ represent the cost coefficients.

5) Distributed gas supplier supply constraints are given by the following expression:

$0\le G_{ij,T}^{gas}\le G_{ij,T}^{gas,\max }(21)$

Type: $G_{ij,T}^{gas,\max }$ represents the maximum gas supply provided by gas suppliers at time T. Gas, gas electricity production, and gas used as fuel for electricity and heat production exhibit similar characteristics to coal-fired capacity. The size of energy produced at time T determines the real-time fuel consumption amount, with combustion gas suppliers supplying gas within a specific range.

6) Resistance and energy storage restrictions for energy storage devices and heat values are as follows:

$P_{ij,T}^{es,\min }\le P_{ij,T-1}^{es,n}-\left|P_{ij,T}^{es}\right|\le P_{ij,T}^{es,\max }(22)$

$H_{ij,T}^{es,\min }\le H_{ij,T-1}^{es,n}-\left|H_{ij,T}^{es}\right|\le H_{ij,T}^{es,\max }(23)$

$G_{ij,T}^{es,\min }\le G_{ij,T-1}^{es,n}-\left|G_{ij,T}^{es}\right|\le G_{ij,T}^{es,\max }(24)$

Type: $P_{ij,T}^{es,\min }$, $H_{ij,T}^{es,\min }$, $G_{ij,T}^{es,\min }$ represent the lower limits of T moment heat storage equipment, storage equipment, and gas storage capacity, respectively. $P_{ij,T}^{es,\mathrm{n}}$, $H_{ij,T}^{es,\mathrm{n}}$, $G_{ij,T}^{es,\mathrm{n}}$ denote the storage of heat, electricity, and gas for T-1 h heat storage, storage equipment, and gas equipment, respectively. $P_{ij,T}^{es,\max }$, $H_{ij,T}^{es,\max }$, $G_{ij,T}^{es,\max }$ represent the upper limits of storage capacity for electricity, heat, and gas at time T.

7) Electricity, heat, and energy storage device discharge and power change constraints are as follows:

$P_{ij,T}^{es,\min }\le \left|P_{ij,T}^{es}\right|\le P_{ij,T}^{es,\max }(25)$

$H_{ij,T}^{es,\min }\le \left|H_{ij,T}^{es}\right|\le H_{ij,T}^{es,\max }(26)$

$G_{ij,T}^{es,\min }\le \left|G_{ij,T}^{es}\right|\le G_{ij,T}^{es,\max }(27)$

Type: $P_{ij,T}^{es,\min }$, $H_{ij,T}^{es,\min }$, $G_{ij,T}^{es,\min }$ represent the lower limits for discharge and energy absorption of storage, heat storage, and gas storage equipment, respectively. $P_{ij,T}^{es,\max }$, $H_{ij,T}^{es,\max }$, $G_{ij,T}^{es,\max }$ denote the upper limits for discharge and energy absorption of storage, heat storage, and gas storage equipment, respectively.

Energy storage devices store energy when electricity prices are low and release energy when prices are high, playing a regulatory role. Consequently, they are essential equipment within energy bodies. Due to varying factors across different types of energy storage devices, a unified storage device cost function is established as follows:

$C\left(P_{ij,T}^{es}\right)={\alpha }_{ij,T}^{p,es}{\left(P_{ij,T}^{es}+{\beta }_{ij,T}^{p,es}\right)}^2+{\lambda }_{ij,T}^{p,es}(28)$

$C\left(H_{ij,T}^{es}\right)={\alpha }_{ij,T}^{p,es}{\left(H_{ij,T}^{es}+{\beta }_{ij,T}^{p,es}\right)}^2+{\lambda }_{ij,T}^{p,es}(29)$

Type: ${\alpha }_{ij,T}^{p,es}$, ${\beta }_{ij,T}^{p,es}$, ${\lambda }_{ij,T}^{p,es}$, ${\alpha }_{ij,T}^{p,es}$, ${\beta }_{ij,T}^{p,es}$, ${\lambda }_{ij,T}^{p,es}$ represent cost coefficients.

8) Gas-to-electricity transfer and thermal conversion rates are as follows:

$P_{ij,T}^{es}=\alpha G_{ij,T}^{pes}(30)$

$H_{ij,T}^{es}=\beta G_{ij,T}^{hes}(31)$

Type: a and b represent the gas-to-electricity and heat conversion rates, respectively. $G_{ij,T}^{pes}$ and $G_{ij,T}^{hes}$ denote the capacity for electricity and heat conversion, respectively.

9) Lateral load consumption of electricity and heat cost functions are as follows:

$C\left(P_{ij,T}^{lp}\right)={\alpha }_{ij,T}^{p,lp}{\left(P_{ij,T}^{lp}\right)}^2+{\lambda }_{ij,T}^{p,lp}{P}_{ij,T}^{lp}+{\epsilon }_{ij,T}^{p,lp}(32)$

$C\left(H_{ij,T}^{lh}\right)={\alpha }_{ij,T}^{h,lh}{\left(P_{ij,T}^{lh}\right)}^2+{\lambda }_{ij,T}^{h,lh}{P}_{ij,T}^{lh}+{\epsilon }_{ij,T}^{h,lh}(33)$

Type: $P_{ij,T}^{lp}$, $H_{ij,T}^{lh}$ represent load side electricity and heat consumption, respectively. ${\alpha }_{ij,T}^{p,lp}$, ${\lambda }_{ij,T}^{p,lp}$, ${\epsilon }_{ij,T}^{p,lp}$, ${\alpha }_{ij,T}^{h,lh}$, ${\lambda }_{ij,T}^{h,lh}$, and ${\epsilon }_{ij,T}^{h,lh}$ are positive cost coefficients.

2.2 The interests of the function

The benefit of the energy body function revenue function and cost function are two parts, and the mathematical expression is as follows:

${\mathrm{\Psi }}_{i,T}{=\mathrm{O}}_{i,T}-C_{i,T}(34)$

Type: ${\mathrm{\Psi }}_{i,T}$ represents the ith a energy body in T time overall interests, ${\mathrm{O}}_{i,T}$ means the energy body in T moment ith total earnings, $C_{i,T}$ refers to the case of an energy body in T time ith the total cost. The specific expressions for the profit function and cost function in Eq. 34 are as follows:

${\mathrm{O}}_{i,T}={\mathrm{{\rm K}}}_{ij,T}^{use}+p{r}_T^p{P}_{i,T}^{ex}+p{r}_T^h{H}_{i,T}^{ex}+p{r}_T^g{G}_{i,T}^{ex}(35)$

$C_{i,T}=C\left(P_{ij,T}^{p,s}\right)+C\left(P_{ij,T}^{h,s}\right)+C\left(P_{ij,T}^{chp},H_{ij,T}^{chp}\right)(36)$

${\mathrm{{\rm K}}}_{ij,T}^{use}=-{\eta }_{ij}^p{\left(\mathrm{\Lambda }{P}_{ij,T}^r\right)}^2+{\nu }_{ij}^p\mathrm{\Lambda }{P}_{ij,T}^r-{\eta }_{ij}^h{\left(\mathrm{\Lambda }{H}_{ij,T}^r\right)}^2+{\nu }_{ij}^h\mathrm{\Lambda }{H}_{ij,T}^r(37)$

$C\left(P_{ij,T}^{p,s}\right)=C\left(P_{ij,T}^p\right)+C\left(P_{ij,T}^w\right)+C\left(P_{ij,T}^c\right)+C\left(P_{ij,T}^g\right)+C\left(P_{ij,T}^{es}\right)(38)$

$C\left(P_{ij,T}^{h,s}\right)=C\left(H_{ij,T}^p\right)+C\left(H_{ij,T}^c\right)+C\left(H_{ij,T}^g\right)+C\left(H_{ij,T}^{es}\right)(39)$

Type: ${\mathrm{{\rm K}}}_{ij,T}^{use}$ represents the energy utilization function for the energy system on the load side, ${\eta }_{ij}^p$, ${\nu }_{ij}^p$, ${\eta }_{ij}^h$, ${\nu }_{ij}^h$ are cost coefficients. $p{r}_T^p$, $p{r}_T^p$, $p{r}_T^p$ denote the electricity, heat, and gas prices at time T, respectively. $C\left(P_{ij,T}^{p,s}\right)$ and $C\left(P_{ij,T}^{h,s}\right)$ represent the cost of producing electricity and heat for all equipment except cogeneration units at time T.

2.3 The objective function

This study focuses on the optimization of an integrated energy system that aims to coordinate the use of different types of energy, such as electricity, gas, and heat, with the goal of reducing production costs and improving energy efficiency. Specifically, we investigate the collaborative optimization of three energy supply and demand types, namely, electricity, heat, and gas. The energy conversion model is employed to allow for price adjustments among the three types of energy (Yu-Shuai et al., 2020). We strive to achieve a globally optimal solution that takes full advantage of the complementary characteristics of various energy sources to obtain the most economic price, while ensuring the balance between energy supply and demand. The optimization problem is formulated as (34), using a modified version of Newton’s method, known as the difference Newton’s method, to speed up the algorithm iteration and reduce communication and computational pressure. The objective function is expressed as type (40), which represents the overall benefits of the entire energy system, while ensuring that the net energy value is zero, thus guaranteeing the balance between energy supply and demand. The function expression is presented below.

$\begin{array}{cc}\max & Object\end{array}={\displaystyle \sum _{i=1}^n}{\mathrm{\Psi }}_{i,T}(40)$

${\displaystyle \sum _{i=1}^n}{P}_{i,T}^{ex}=0,{\displaystyle \sum _{i=1}^n}{H}_{i,T}^{ex}=0,{\displaystyle \sum _{i=1}^n}{G}_{i,T}^{ex}=0(41)$

3 The algorithm design

3.1 The traditional Newton iteration method

The traditional numerical method referred to as Newton’s method is commonly utilized to solve nonlinear equations. Within integrated energy systems, collaborative optimization can utilize the traditional Newton’s method to solve complex optimization models. The basic idea of this method is to iteratively solve equations of zero and determine the direction of the next iteration through the first-order approximation of the equation. In practical applications, the traditional Newton method can achieve optimal cooperation among parties based on the integrated energy system states and parameters of continuous optimization. When addressing comprehensive power, heat, and gas optimization problems in energy systems, the traditional Newton method can be applied to solve conflicts and coordinate energy sources to realize optimal system synergy (Tan and Li, 2022).

3.2 DNEA algorithm design

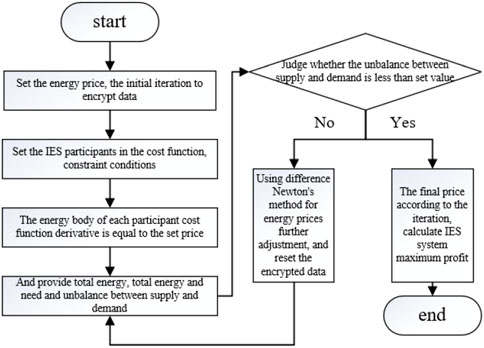
In integrated energy systems, each energy entity is equipped with its own processor. Nonetheless, the absence of a centralized system causes a distributed structure which lacks significant communication and computing power. Consequently, the computing capability of each processor in the energy entity is limited. When faced with the high-speed and high utilization of renewable energy, the conventional algorithm struggles to compute the parameters in a distributed energy system. To tackle this challenge, this study introduces the difference Newton’s method as a solution. This method is designed to resolve issues with slow calculation speed and communication and computing pressure. By applying the difference Newton’s method to every energy entity during the calculation process, the computational speed is significantly enhanced, while maintaining a balance between supply and demand and maximizing profit. The following outlines the design of the difference Newton’s method in the calculation process of the integrated energy system.

Due to the convex nature of the cost function designed in this paper, the derivative of the energy body’s benefit function for all participants is the iterative price $p{r}_T^p{\eta }_{ij}^p$, $p{r}_T^h$, $p{r}_T^g$. To ensure the maximization of the overall interests objective function of the energy system, this study assumes that each participant achieves the same benefits for the same unit of electricity and heat, namely, $p{r}_T^p=p{r}_T^h$. The specific algorithm design process is as follows:

$\frac{dC\left(P_{ij,T}^p\right)}{d{P}_{ij,T}^p}=\frac{dC\left(H_{ij,T}^p\right)}{d{H}_{ij,T}^p}=......=p{r}_{T,1}^{p,h}(42)$

Type: Given the goal of finding the optimal balance between supply and demand conditions for the maximum overall energy interests, the price of electricity and heat is assumed to be the same. Hence, the price of electricity and heat are represented by $p{r}_{T,1}^{p,h}$. The derivative of the cost function for the remaining energy body participants equals $p{r}_{T,1}^{p,h}$, which is not elaborated upon further to avoid redundancy. The sum of electricity and heat provided by all participants in the energy body is calculated as $S\left({\mathrm{\Lambda }}_{T,1}^{p,h}\right)$.

$S\left({\mathrm{\Phi }}_{T,1}^r\right)=S\left({\mathrm{\Phi }}_{T,1}^{p,r}\right)+S\left({\mathrm{\Phi }}_{T,1}^{h,r}\right)(43)$

Type: $S\left({\mathrm{\Phi }}_{T,1}^{p,r}\right)$, $S\left({\mathrm{\Phi }}_{T,1}^{h,r}\right)$ denote the sum of electricity and heat required by the load side participants at the given prices, respectively. This study assumes a 1:1 conversion efficiency for electricity and heat, resulting in the need for electricity and heat by the participants. The difference between supply and demand balance values is calculated using the following formula:

The difference between the value of ${\zeta }_{T,1}^{sd}$ between the supply and demand balance values at this time is calculated using the following formula:

${\zeta }_{T,1}^{sd}=\left|S\left({\mathrm{\Lambda }}_{T,1}^{p,h}\right)-S\left({\mathrm{\Phi }}_{T,1}^r\right)\right|(44)$

$\frac{dC\left(P_{ij,T}^p\right)}{d{P}_{ij,T}^p}=\frac{dC\left(H_{ij,T}^p\right)}{d{H}_{ij,T}^p}=......=p{r}_{T,2}^p(45)$

Assuming that the second energy iteration price is $p{r}_{T,2}^{p,h}$, the total energy provided by the participants is $S\left({\mathrm{\Lambda }}_{T,2}^{p,h}\right)$, the total energy required is $S\left({\mathrm{\Phi }}_{T,2}^r\right)$, the imbalance of supply and demand is ${\zeta }_{T,2}^{sd}$, and the second parameter is conceptually the same as the first parameter formula. The computation formula is as follows:

$p{r}_{T,3}^{p,h}=p{r}_{T,2}^{p,h}-{\zeta }_{T,2}^{sd}\frac{p{r}_{T,1}^{p,h}-p{r}_{T,2}^{p,h}}{{\zeta }_{T,1}^{sd}-{\zeta }_{T,2}^{sd}}(46)$

Type: according to the relationship between price and the imbalance between supply and demand, if all functions are linear and the balance between supply and demand is guaranteed, the energy price is $p{r}_{T,3}^{p,h}$. Due to the linear overtaking convex function, the imbalance of supply and demand and the demand for ${\zeta }_{T,3}^{sd}$ and $S\left({\mathrm{\Phi }}_{T,3}^r\right)$ are met, respectively. Using $p{r}_{T,2}^{p,h}$ and $p{r}_{T,3}^{p,h}$ as the new iteration prices, the next iteration price is found by repeating the process until meeting $\left|{\zeta }_{T,i}^{sd}\right|<{\upsilon }_{T,i}^a$: type: ${\zeta }_{T,i}^{sd}$ is the ith iteration imbalance between supply and demand, and ${\upsilon }_{T,i}^a$ is the allowed error range. For all participants in the energy body, the changes in electricity, heat, and gas provision correspond to the price changes of each iteration $p{r}_{T,i}^{p,h}$.

3.3 Ring signature algorithm design

This paper ensures privacy among all participants in the integrated energy system by initializing the encrypted energy data as $P{H}_T^{ed}$. For the first integrated energy system, the energy body’s privacy increases with each iteration, as each iteration process, $P{H}_T^{ed}$ modifies the initial encrypted data. This prevents the encrypted data from being guessed with increasing iteration numbers, thus avoiding privacy leaks for all participants in the integrated energy system. The ring signature algorithm is used as the basis for data transmission in integrated energy systems, with the formula as follows:

$P{H}_{ij,ki}^{ed}=P{H}_{ij,i-1}^{ed}+P{H}_T^{ed}(47)$

Type: In the first i-1 iterations, energy body information $P{H}_{ij,ki}^{ed}$ is introduced into the ith energy body, and $P{H}_{ij,i-1}^{ed}$ denotes the real information of the ith energy body. The information transfer direction is shown in Chart 1. This process strengthens privacy protection among energy bodies, ensuring each energy body's privacy and fully protecting the privacy of all agents in the system. This is an improvement compared to traditional privacy protection, which does not adequately protect privacy between integrated energy system energy bodies.

4 DNEA algorithm theory to prove

4.1 DNEA iteration speed

Setting parameters $\delta$, $\forall \delta \in R^{+}$, R⁺ denotes all positive values. The traditional iterative method using Newton’s method establishes an adjustment volume of each time as ${\zeta }_{T,i}^{sd,tra}$, and meeting ${\zeta }_{T,i}^{sd,tra}$, and $\forall \left|{\zeta }_{T,i}^{sd,tra}\right|<\delta$. Therefore, the average adjustment volume for the traditional iteration method is:

${\zeta }_{T,i,ave}^{sd,tra}={\displaystyle \sum _{i=1}^n}{\zeta }_{T,i}^{sd,tra}/N(48)$

Type: The total number N for iteration, ${\zeta }_{T,i}^{sd,tra}$ $\forall \left|{\zeta }_{T,i}^{sd,tra}\right|<\delta$. Then, N is the number of iterations, with $\forall \left|N\right|>\delta$. An inequality exists such that $\left|{\zeta }_{T,i,ave}^{sd,tra}\right|\le \delta$, and the iterative algorithm designed in this paper is based on the traditional Newton iteration method, employing the Newton difference method. In the early stages of the iterative algorithm presented in this paper, the adjustment of the imbalance of supply and demand ${\zeta }_{T,i}^{sd,ea}$ $p{r}_{T,3}^{p,h,ea}$ does not satisfy the price inequality $\forall \left|{\zeta }_{T,i}^{sd,ea}\right|<\delta$, $\forall \left|p{r}_{T,3}^{p,h,ea}\right|<\delta$, and the iteration process is repeated. Later in the iteration, the imbalance of supply and demand approaches ${\zeta }_{T,i}^{sd,la}$, and the iterative prices approach $p{r}_{T,3}^{p,h,la}$, $\forall \left|{\zeta }_{T,i}^{sd,ea}\right|<\delta$, and $\forall \left|p{r}_{T,3}^{p,h,ea}\right|<\delta$. Gradually, the material difference satisfies Equation ${\zeta }_{T,i,ave}^{sd}={\displaystyle \sum _{i=1}^n}{\zeta }_{T,i}^{sd}/N$, on average, it does not meet the equation for ${\zeta }_{T,i}^{sd}$ $\forall {\displaystyle \sum _{i=1}^n}{\zeta }_{T,i}^{sd}<\delta$, ${\zeta }_{T,i,ave}^{sd}$ does not meet the $\forall {\zeta }_{T,i,ave}^{sd}<\delta$. In summary, the iteration algorithm ${\zeta }_{T,i,ave}^{sd}>{\zeta }_{T,i,ave}^{sd,tra}$ designed in this paper improves upon the traditional Newton iteration method. This proof demonstrates that, within the same number of iterations, the difference Newton method achieves a smaller imbalance between supply and demand, significantly enhancing the iteration speed of the integrated energy system and reducing the amount of computation.

4.2 DNEA convergence is proved

Starting with the first iteration, $p{r}_{T,1}^{p,h}$, $p{r}_{T,2}^{p,h}$, are the calculated prices for the second iteration. Due to price changes, the imbalance of supply and demand alters the value of ${\zeta }_{T,1-2}^{sd}$. The corresponding relationship between price and the supply-demand imbalance assumes a linear characteristic between price and supply. The new iteration price $p{r}_{T,3}^{p,h}$ is determined when supply and demand are balanced. The first iteration point is connected to the second iteration point on the price and supply function, with a linear slope of $f_{p{r}_{T,12}^{p,h}}^{\prime }$. Lagrange’s theorem indicates that there is a point ${\epsilon }_1$ between the first and second iteration points with a slope satisfying $f_{{\epsilon }_1}^{\prime }=f_{p{r}_{T,12}^{p,h}}^{\prime }$. The second iteration point is connected to the third iteration point, with a linear slope of $f_{p{r}_{T,23}^{p,h}}^{\prime }$. Similarly, it can be found in the two point ${\epsilon }_2$, $f_{{\epsilon }_2}^{\prime }=f_{p{r}_{T,23}^{p,h}}^{\prime }$, by the nature of the convex function, the inequality of $f_{{\epsilon }_1}^{\prime }>f_{{\epsilon }_2}^{\prime }$, therefore, inequality $f_{p{r}_{T,12}^{p,h}}^{\prime }>f_{p{r}_{T,23}^{p,h}}^{\prime }$. It is also known that, ensuring that the units change with $\Delta p{r}_{T,i}^{p,h}$, $\Delta {\zeta }_{T,i}^{sd}$ , the change in becomes progressively smaller. Thus, the iteration points for the balance between supply and demand, obtained by linear prediction, do not exceed the supply and demand balance formed by the convex function.

4.3 DNEA optimality

In the energy body, a balance between supply and demand for electricity and heat must be maintained. Electricity and heat conversion are employed to compensate for energy deficiencies. Assuming equal prices for electricity and heat, if the energy body lacks a heat quantity of $H_{ij,T}^{now}$, $H_{ij,T}^{lack}$, the surplus electricity and power are $P_{ij,T}^{now}$, $P_{ij,T}^{lack}$, respectively. If electricity is not used for heat conversion, an increase in price for this portion of heat is required $p{r}_T^{h,ch}$, $p{r}_T^{h,unit}=H_{ij,T}^{lack}/p{r}_T^{h,ch}$, with and satisfying the equation. As the cost function of all participants in the energy body is convex, thus the $p{r}_T^{h,unit}>p{r}_{T,i}^{p,h}$, and the energy and power for the excess production unit price are $p{r}_T^{p,unit}$. The convex function properties indicate that the energy cost function has a larger slope for a larger y, with the slope representing the energy unit price. Therefore, the inequality $p{r}_T^{h,unit}>p{r}_{T,i}^{p,h}>p{r}_T^{p,unit}$ is obtained, ensuring that equal prices for electricity and heat result in the largest gains for the energy body.

4.4 DNEA kinetic behavior analysis

This section provides mathematical proof that the difference Newton iterative algorithm designed in this paper effectively avoids kinetic behavior. Based on the convergence proof, the difference Newton designed in this paper gradually tends toward a supply and demand balance of 0. Setting parameter ${\sigma }_T^{aisd}$ as the allowable maximum imbalance between supply and demand, the energy system is triggered from the beginning and iterates infinitely. The first time the supply and demand equilibrium is reached is at time T, and $\left|{\zeta }_{T,i}^{sd}\right|<{\sigma }_T^{aisd}$ satisfies the supply and demand imbalance ${\zeta }_{T,i}^{sd}$. It can be concluded that convergence has been achieved, eliminating the need for further triggering and avoiding infinite iterations within a limited time, thus preventing kinetic behavior.

5 DNEA algorithm simulation analysis

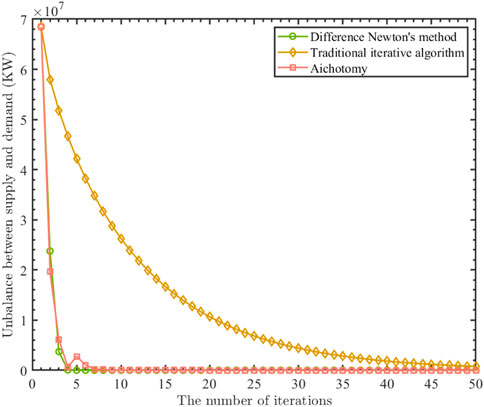
To verify the algorithm presented in this manuscript, a testing of a distributed algorithm based on differential points and Newton’s method was performed on an energy system described in Appendix 5, wherein the fundamental parameters of the simulation device are exhibited. Figure 1 portrays the integrated energy system under consideration. A condition is stipulated in this paper, wherein the energy supply and demand must remain within 10 kW of each other to achieve a balance between energy production and consumption. The algorithm was designed to accomplish this goal, and it achieved the desired balance within five iterations. The simulation process is as follows.

FIGURE 1

FIGURE 1. DNEA algorithmic trading structure.

5.1 DNEA simulation analysis iteration speed

A comparison between the iterative processes of the distributed algorithm based on differential points and Newton’s method and the traditional finite difference algorithm was conducted on five energy systems with unbalanced supply and demand. The simulation results, depicted in Figure 2, demonstrate that the differential points Newton algorithm achieved a supply and demand balance of less than 10 kW within the fifth iteration without causing any disturbances. In contrast, the traditional algorithm failed to reach the optimal balance even after 50 iterations. Dichotomy optimization for the iterative error is small, the eight time but also known from the analysis of the simulation, the final results, not avoid kino, cannot ensure the final iteration for optimal results. Simulation results depicted in Figure 2, Figure 3 indicate that all participants in the energy system, designed in this manuscript, achieved rapid convergence to the optimal forecast price point while ensuring a balance between supply and demand. These results verify the feasibility and effectiveness of the algorithm presented in this paper. The differential points Newton algorithm was employed to calculate the energy system under conditions of supply and demand balance, which yielded faster iteration speeds compared to traditional computing methods by several orders of magnitude. Consequently, energy losses, delays, and communication costs were considerably reduced, leading to more efficient energy systems.

FIGURE 2

FIGURE 2. IES difference flow chart of Newton’s method.

FIGURE 3

FIGURE 3. the balance between supply and demand iteration curve.

5.2 DNEA simulation convergence analysis

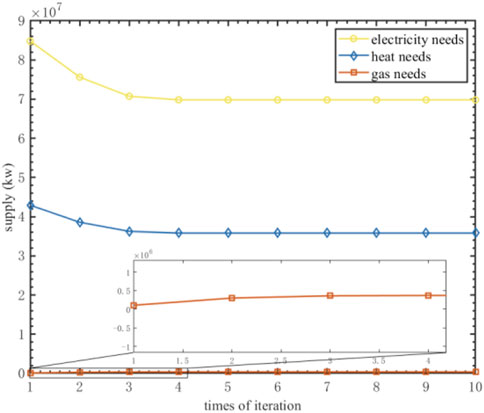
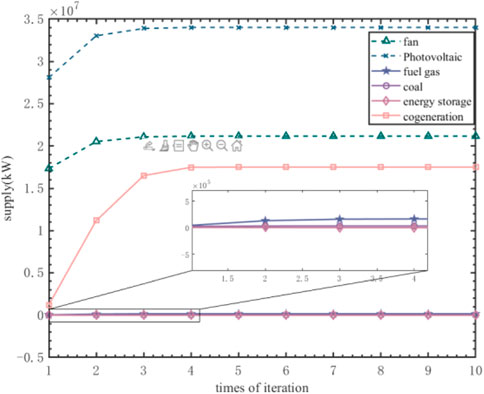
In this paper, an integrated energy system has been designed. The simulation diagram presented in Figure 4, Figure 5, Figure 6 depicts the supply side, and reveals that the total electricity generated is 69828694.93 kW. The final values of heat and gas are 35815789.39 kW and 368579.09 kW, respectively. The relevant parameters, such as the change of price and the fast convergence to phase, contribute to achieving a stable state. As a result, the aforementioned values remain practically unchanged.

FIGURE 4

FIGURE 4. electricity price, heat price change curve.

FIGURE 5

FIGURE 5. energy demand curve.

FIGURE 6

FIGURE 6. power supply curve to the participants.

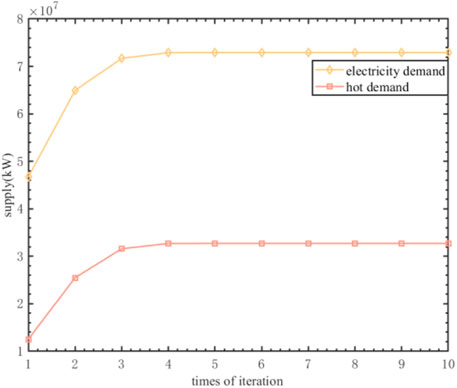
Furthermore, it is worth noting that Newton’s method, when used in this study, yields highly accurate and reliable calculation results. Moreover, it significantly reduces the communication and computation workload associated with the distributed energy system, facilitating a fast scheduling process and ensuring a steady state energy system. As shown in Figure 7, the power supply amounts to 72907191.36 kW, and the heating load reaches 32737316.53 kW, thereby achieving a balance between supply and demand.

FIGURE 7

FIGURE 7. heating participants curves of heating load.

Combining the simulation results presented in Figure 4, Figure 5, Figure 6, Figure 7, Figure 8, it can be concluded without surprise that by utilizing the difference Newton’s method, this study is capable of rapidly achieving a stable state, while simultaneously ensuring that the results remain stable post convergence.

FIGURE 8

FIGURE 8. load side can use change curve.

5.3 Ring to privacy protection analysis

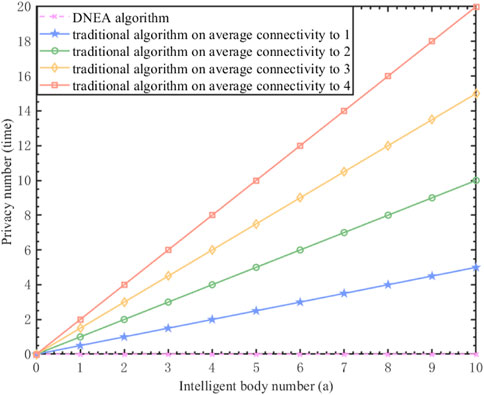
Traditional algorithm (Tan and Li, 2022) privacy often meet:

$M{\text{pl}}_T=\frac{A{c}_T*N{a}_T}{2}(49)$

Type: Mpl_T refers to privacy, and Ac_T, represents average connectivity, the term Na_T denotes an agent. Combined with the simulation Figure 9 shows in conventional privacy protection algorithms, an increase in the number of agents and average connectivity leads to a gradual enhancement in privacy levels. However, in this study, the researchers have designed a distinct Newton algorithm with a ring structure. In this approach, the growth in the number of agents and average connectivity does not result in elevated privacy levels, but rather maintains comprehensive privacy protection for the agents involved.

FIGURE 9

FIGURE 9. Privacy number and average number of connectivity and agent relationship diagram.

5.4 Usage scenarios and limit analysis of the algorithm

The utilization of the DNEA algorithmic approach is not applicable within the context of an integrated energy system, as the cost function follows a convex pattern. This system is characterized by interconnections, and it should not be employed in scenarios with high-quality energy standards, such as parks, intelligent buildings, hospitals, among others.

6 Conclusion

The calculation speed for the traditional iterative algorithm was evaluated multiple times, and each participant achieved the optimal convergence value. This confirmed the feasibility and stability of the proposed algorithm. However, it should be noted that this algorithm is not suitable for participants in the energy system with convex cost functions and constraints. Future scholars may explore non-convex cost functions and constraints to further develop the proposed algorithm. One limitation of this paper is that it did not address the non-convex cost function and constraints for the proposed algorithm.

Data availability statement

The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.

Author contributions

XC and XK has corrected the format and simulation prove. Other study is carried out by XL. All authors contributed to the article and approved the submitted version.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Supplementary material

The supplementary material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2023.1215786/full#supplementary-material

References

Chen, G., and Zhao, Z. Y. (2019). Delay effects on consensus-based distributed economic dispatch algorithm in microgrid. IEEE Trans. Power Syst. 33 (1), 602–612. doi:10.1109/tpwrs.2017.2702179

CrossRef Full Text | Google Scholar

Duan, J., and Chow, M. Y. (2019). A novel data integrity attack on consensus based distributed energy management algorithm using local information. IEEE Trans. Industrial Inf. 15 (3), 1544–1553. doi:10.1109/tii.2018.2851248

CrossRef Full Text | Google Scholar

Gao, S., He, J., Yang, S., and Xiao, B. (2022). En ergy management of interconnected microgrid bas ed on alternating direction method of multipliers method [J]. Grid Clean Energy 38 (06), 1 13–120.

Google Scholar

Hemamalini, S., and Simon, S. P. (2009). Maclaurin series-based Lagrangian method for economic dispatch with valve-point effect. IET Generation, Transm. Distribution 3 (9), 859–871. doi:10.1049/iet-gtd.2008.0499

CrossRef Full Text | Google Scholar

Huang, B. N., Liu, L. N., Zhang, H. W., Li, Y. S., and Sun, Q. Y. (2019). Distributed optimal economic dispatch for microgrids considering communication delays. IEEE Trans. Syst. Man, Cybern. Syst. 49 (8), 1634–1642. doi:10.1109/tsmc.2019.2900722

CrossRef Full Text | Google Scholar

Li, F. Y., Qin, J. H., and Kang, Y. (2019). Multi-agent system based distributed pattern search algorithm for non-convex economic load dispatch in smart grid. IEEE Trans. Power Syst. 34 (3), 2093–2102. doi:10.1109/tpwrs.2018.2889989

CrossRef Full Text | Google Scholar

Li, Y., Gao, D. W., Gao, W., Zhang, H., and Zhou, J. (2020). Double-mode energy management for multi-energy system via distributed dynamic event-triggered Newton-raphson algorithm. IEEE Trans. Smart Grid 11 (6), 5339–5356. doi:10.1109/tsg.2020.3005179

CrossRef Full Text | Google Scholar

Lin, C. E., and Viviani, G. L. (1984). Hierarchical economic dispatch for piece wise quadratic cost functions. IEEE Trans. Power Apparatus Syst. 6, 1170–1175. doi:10.1109/tpas.1984.318445

CrossRef Full Text | Google Scholar

Lv, H. (2022). Research on coordination method of multi-type demand response considering electrica l thermal coupling [D]. Jinan, China: Shandong University.

Google Scholar

Marty, F., Serra, S., Sochard, S., and Reneaume, J. M. (2017). Economic optimization of a combined heat and power plant: Heat vs electricity. Energy Procedia 116, 138–151. doi:10.1016/j.egypro.2017.05.062

CrossRef Full Text | Google Scholar

Munshi, A. A., and Mohamed, Y. A. R. I. (2019). Unsupervised nonintrusive extraction of electrical vehicle charging load patterns. IEEE Trans. Industrial Inf. 15 (1), 266–279. doi:10.1109/tii.2018.2806936

CrossRef Full Text | Google Scholar

Nie, Y., Peng, C., Hu, Y., He, Y., Ma, G., and Huang, C. (2023). Parallel distribute d optimal economic dispatch of high penetration microgrid based on edge computing [J/OL]. So uthern Power Grid Technol. 1-11. [2023-01-20]].

Google Scholar

Schfer, B., Beck, C., Aihara, K., Witthaut, D., and Timme, M. (2018). Non-Gaussian power grid frequency fluctuations characterized by Lévy-stable laws and superstatistics. Nat. Energy 3, 119–126. doi:10.1038/s41560-017-0058-z

CrossRef Full Text | Google Scholar

Tan, J., and Li, H. (2022). Annular directed distrib uted algorithm for energy internet. Int. Trans. Electr. Energy Syst. 2022. doi:10.1155/2022/7717605

CrossRef Full Text | Google Scholar

Tan, Z., Zhong, H., Wang, J., Xia, Q., and Kang, C. (2019). Enforcing intra-regional constraints in tie-line scheduling: A projection based framework. IEEE Trans. Power Syst. 34 (6), 4751–4761. doi:10.1109/tpwrs.2019.2913876

CrossRef Full Text | Google Scholar

Tan, Z., Zhong, H., Xia, Q., and Kang, C. (2021). Non-iterative multiarea coordinated dispatch via condensed system representation. IEEE Trans. Power Syst. 36, 1594–1604. doi:10.1109/tpwrs.2020.3019828

CrossRef Full Text | Google Scholar

Xie, Z., Lu, C., Wang, X., Wen-tao, Y., and Qi, C. (2022a). Microgrid based on distribute d resource cooperative contro research and appl ication of bidding strategy [J]. Electr. Age 10, 37–42.

Google Scholar

Xie, Z., Lu, C., wang, X., Wen-tao, Y., and Qi, C. (2022b). Microgrid based on distribute d resource cooperative contro research and appl ication of bidding strategy [J], the electrical age, 2022(10):37-42 control in dcmicrogrid based on linear matrix I nequalities [J], header-icon. J. Sol. Energy 43 (05), 45–52.

Google Scholar

Yang, M., and Wang, J. (2021). Optimal scheduling of islanded microgrid considering uncertain output of renewable energy[J]. Chin. J. Electri cal Eng. 41 (03), 973–985.

Google Scholar

Yang, Y., and Yang, P. (2022). The hierarchical modeling approach for centralized control microgrid cyber physical system [J]. Chin. J. Electr. Eng. 42 (19), 7088–7102.

Google Scholar

Yin, S., Qian, A., Zeng, S. Q., Wu, Q., Ran, H., and Jiang, D. (2018). Challenges and prospects of multi-energy distributed optimization for energy internet. Power Syst. Technol. 42 (5), 1–10.

Google Scholar

Yu-Shuai, L., Tian-yi, L., Gao, W., and Gao, W. (2020). Distributed collaborative optimization operati on approach for integrated energy system based on asynchronous and dynamic event-triggering C ommunication strategy [J]. J. Automation 46 (09), 1831–1843.

Google Scholar

Zhang, H., Li, Y., Gao, D. W., and Zhou, J. (2017). Distributed optimal energy management for energy internet. IEEE Trans. Industrial Inf. 13 (6), 3081–3097. doi:10.1109/tii.2017.2714199

CrossRef Full Text | Google Scholar

Zhang, N., Sun, Q., and Yang, L. (2020). A two-stage multi-objective optimal scheduling in the integrated energy system with we energy modeling. Energy 215, 119121. doi:10.1016/j.energy.2020.119121

CrossRef Full Text | Google Scholar

Zhang, Y., Lin, Y., Huang, G., Yang, X., Weng, G., and Zhou, Z. (2023). Rev iew on applications of deep reinforcement learning in regulation of microgrid systems [J/OL]. Power Grid Technol. 1-15. [2023-01-20].

Google Scholar

Zhang, Z., and Chow, M. Y. (2012). Convergence analysis of the incremental cost consensus algorithm under different communication net work topologies in a smart grid. IEEE Trans. Power Syst. 27 (4), 1761–1768. doi:10.1109/tpwrs.2012.2188912

CrossRef Full Text | Google Scholar

Zhao, C. C., He, J. P., Cheng, P., and Chen, J. M. (2016). Analysis of consensus based distributed economic dispatch under stealthy attacks. IEEE Trans. Industrial Electron. 64 (6), 5107–5117. doi:10.1109/tie.2016.2638400

CrossRef Full Text | Google Scholar

Zhong, Y., Zhou, Y., Gao, Z., Ton, J., and Yu, D. (2022). Optimal scheduling of micro grid based on ICA and NSGA-II compound algori thm [J]. Appl. Electr. 41 (11), 78–8 4.

Google Scholar

Zhu, Y., Zhang, J., Cheng, Q., Deng, K. F., Ma, K. J., Zhang, J. H., et al. (2022). Research progress of automatic diatom test by artificial intelligence. J. Mech. Inf. Technol. y 38 (07), 14–19. doi:10.12116/j.issn.1004-5619.2021.410404

CrossRef Full Text | Google Scholar