An islanding detection method for grid-connect inverter based on parameter optimized variational mode decomposition and deep learning

The rapid and effective islanding detection and disconnection of the microgrid are significant for preventing equipment from failure and safeguarding humanity’s safety. To address the drawbacks of active methods and passive methods, an intelligent islanding detection strategy based on parameter-optimized variational mode decomposition (VMD) and deep learning was developed. Firstly, the proposed adaptive variational mode decomposition (AVMD) strategy improves the optimal mode number and penalty term of VMD by utilizing the relative entropy between the original signal and the intrinsic mode functions (IMFs). Then, the Teager energy operator (TEO) further extracts sequence features to track the instantaneous energy of the IMFs. Finally, the AVMD-TEO-MPE -based features are used to train the one-dimensional convolutional neural network (1D-CNN) as a deep learning classifier. Simulation results indicate that the proposed method can effectively differentiate the islanding state under different working conditions with a testing accuracy level of 100% within a maximal detection time of 46.402 ms. It is also noise resistant to a degree. Comparative analysis confirms that the proposed method outperforms the existing method in distinguishing between islanding and non-islanding events.

1 Introduction

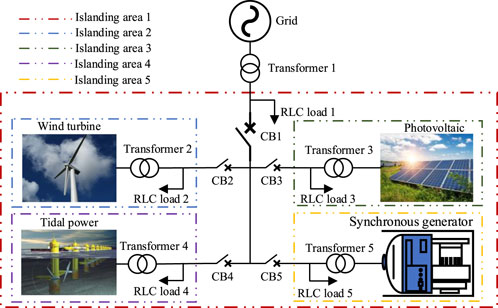
With the growing demand for global energy and the emissions of traditional fossil fuels, more and more countries have contributed to tackling climate change and energy demand by reducing their carbon footprints and moving towards carbon neutrality (Wang et al., 2022). China released a new development philosophy. The document includes creating a green, low-carbon, and circular economy, improving energy efficiency, increasing the share of non-fossil energy consumption, lowering carbon dioxide emissions, adjusting energy structures, and bolstering the development of new energy. Renewable energy sources such as solar and wind are being widely utilized to achieve the goals of peaking carbon dioxide emissions by 2023 and achieving carbon neutrality by 2060. Microgrids consisting of renewable energy power plants, energy storage and loads are widely implemented in China’s large-scale power systems due to their flexible power supply (Liu et al., 2024a). Compared to traditional grid interconnections, microgrids improve operating efficiency while reducing the additional costs and losses associated with new transmission lines. The power system is gradually transitioning to a low-carbon model. However, the rapid development of renewable energy sources presents significant challenges to the safety and stability of microgrids. Specifically, the chaotic, stochastic and intermittent nature of renewable energy sources like solar and wind pose technical challenges for control and protection, posing potential threats to power system reliability (Aljafari et al., 2024). Due to the characteristics of distributed energy described above, when the power system stops supplying power due to lines or tripping, the distributed power generation cannot detect its own island state in time and continues to transmit power to the grid, turning into an electrical island system, thus forming an unplanned island. Figure 1 depicts a typical example of the islanding scenario, including a synchronous generator and inverter-based distribution generation such as wind turbines and photovoltaic units, and tidal power generation. Once the CB1/CB2/CB3/CB4/CB5 is opened, the islanding scenario is formed.

Figure 1

Figure 1. Islanding scenario.

The unintentional islanding effect is when a grid fails due to overhaul or accidental failure and the distributed power generation system entering the grid cannot be detected and separated from the grid in time, resulting in a phenomenon where the load supply of an independent, integrated distributed power system (Yan et al., 2022). The undetected effect complicates power restoration, reduces power quality, threatens other distributed generators, and even poses a threat to humanity. During power system maintenance or outages, the islanding effect may cause the distributed power plant to continue supplying power, posing safety risks to maintenance personnel. When the power system is restored, the islanding condition may result in significant voltage and phase differences between the distributed power plant and the grid, potentially causing a large inrush current that could damage equipment. So, islanding detection is a non-trivial task and faces unprecedented challenges. The current GB/T33593-2017 and IEEE standards require that the distributed generators be separated from the grid within 2s, once the islanding scenario is formed. All islanding detection techniques strive toward swift detection with a minimal non-detection zone (NDZ) and zero spurious detections (Sankar and Sunitha, 2021). Therefore, studying an islanding detection method with high accuracy, short detection time, and low application cost for the microgrid is important.

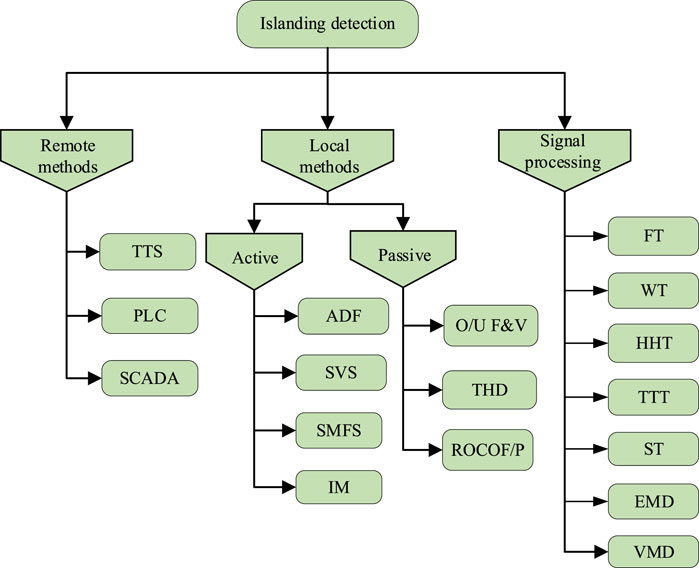
Islanding detection methods can be categorized into local, remote, and signal processing (Raza et al., 2015).

As depicted in Figure 2. The local method is further classified as passive and active. The active method injects deliberate disturbances to influence the output frequency of current or voltage and monitors the islanding state. Some of the common active methods are active frequency drift (AFD) (Liu et al., 2021), Sandia voltage shift (SCS) (Erick et al., 2020), impedance measurement (IM) (Jia et al., 2019), and sliding mode frequency shift (SMFS) (Zhang and Wai, 2022). A small NDZ, fast detection, and low error detection rate are advantages of the active method. However, external disturbance injection would cause both the complexity of the system, power quality, and noise problems. The passive method is based on system parameters at the point of common coupling (PCC). It detects the islanding state by comparing deviations from specified fault thresholds. Some examples of the passive method include the over/under frequency and voltage (O/U F&V) (Zeineldin and Kirtley, 2009), the rate of change of frequency/power (ROCOF/P) (Alam et al., 2019), and total harmonic detection (THD) (Wang et al., 2020). The issue of the active method affecting microgrid power quality is eliminated. However, it has a large NDZ in a power mismatch situation. The remote method is the communication link between the utility grid and the distributed generation system. The communication-based methods used in literature are the power line communication (PLC) (Miller et al., 2021), transfer trip scheme (TTS) (Mahela et al., 2021), and supervisory control and data acquisition (SCADA) (Zhaoxia et al., 2017). Compared with the local method, it achieves the purpose of a small NDZ and a rapid detection time. However, it is impractical for application because of the high-cost sensors, computational burden, and complexity. Signal processing can extract the input signal’s hidden features, lowering the NDZ of the passive method. However, the threshold varies significantly depending on the working conditions, making it difficult to determine the islanding state, and signal processing may not be able to eliminate the NDZ as the distributed power generation system becomes more complex. Various signal processing methods have been established for feature extraction. Some of these include Fourier transform (FT) (Baloch and Muhammad, 2021), wavelet transform (WT) (Allan and Morsi, 2021), S-transform (ST) (Papia et al., 2022), TT-transform (TTT) (Mohanty et al., 2012), Hilbert Huang transform (HHT) (Huang et al., 1971), empirical mode decomposition (EMD) (Khosravi et al., 2021) and variational mode decomposition (VMD) methods (Admasie et al., 2019). However, EMD is an algorithm in the feature extraction stage with modal aliasing, which leads to incomplete and inaccurate feature representation, which in turn affects the detection accuracy. Although the traditional method can basically and effectively carry out island detection, there are still some problems, such as long detection time, the large amount of calculation, and insufficient detection accuracy and accuracy.

Figure 2

Figure 2. Classification of islanding detection methods.

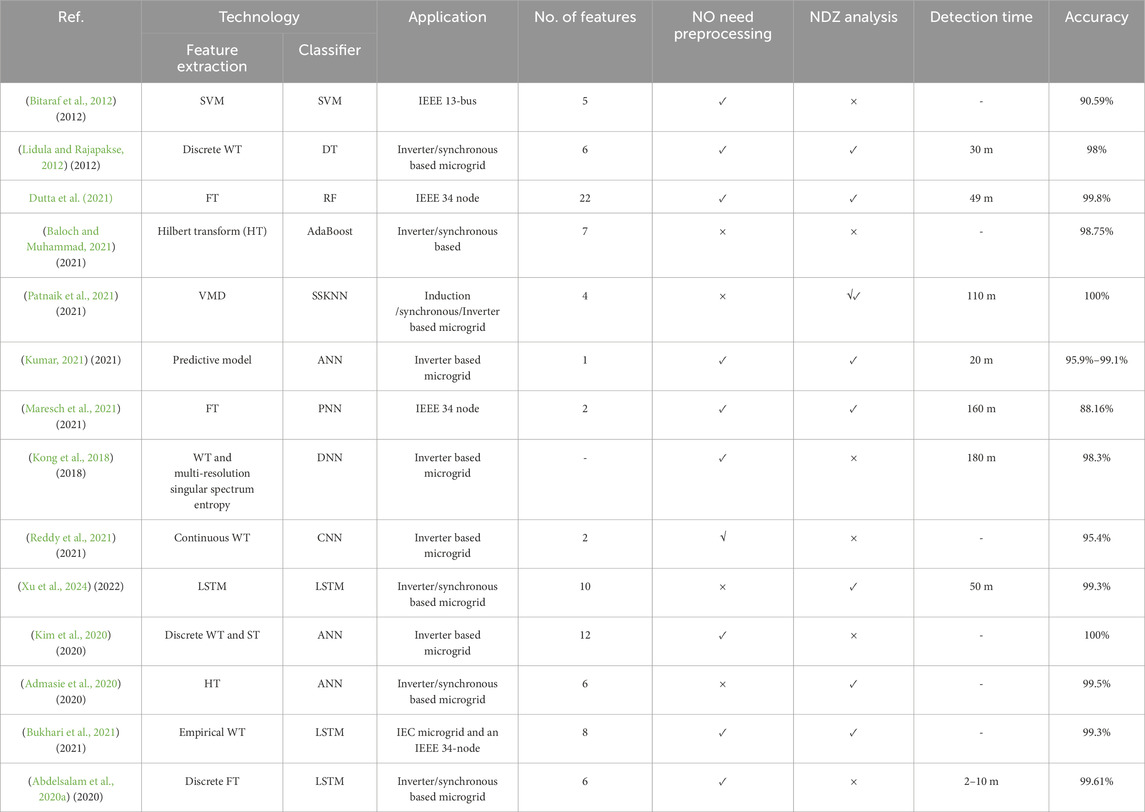
With the rapid development of machine learning (ML) and deep learning (DL) technology, intelligent islanding detection methods based on signal processing, ML, and DL have emerged as a new research avenue in light of the drawbacks of the above traditional detection methods (Dutta et al., 2018). The first step in intelligent islanding detection is to extract important features of the three-phase signal using signal preprocessing. In the second step, the signal preprocessing-based features are fed into ML and DL, which are then trained as classifiers. Some ML and DL schemes are most commonly presented in the literature which are based on support vector machines (SVM) (Bitaraf et al., 2012), decision tree (DT) (Lidula and Rajapakse, 2012), random forest (RF) (Dutta et al., 2021), AdaBoost (Baloch and Muhammad, 2021), K-nearest neighbor (KNN) (Patnaik et al., 2021), artificial neural network (ANN) (Kumar, 2021), perceptron neural network (PNN) (Maresch et al., 2021), deep neural network (DNN) (Kong et al., 2018), convolutional neural network (CNN) (Reddy et al., 2021) (Aljafari et al., 2024) (Xu et al., 2024), and long short-term memory (LSTM) (Xu et al., 2024). For quick and accurate islanding detection, in (Kim et al., 2020), two schemes are proposed of which one is based on discrete WT with ANN, and another one is based on ST with ANN. Those methods are more reliable and accurate. The authors used VMD and subspace KNN (SSKNN) to detect islanding events in (Patnaik et al., 2021). However, the dilution effect of different distributed power generation should be considered. The LSTM network has been used for islanding detection in (Özcanlı and Mustafa, 2022), (Bukhari et al., 2021), (Abdelsalam A. A. et al., 2020), which is used as the feature extractor and classifier, resulting in an accuracy detection that suffers from the LSTM structure. In (Admasie et al., 2020), the gray wolf optimized ANN model is trained as a deep learning classifier to classify islanding states by inputting the HHT-based features. However, the drawbacks are the effects of noise resistance (Özcanlı and Mustafa, 2022). used long and short-term neural networks as feature extractors and classifiers to extract PCC point voltage and current harmonic distortion features, and to train and detect them, this method has higher accuracy and lower loss, but it does not take into account that when islanding occurs at the instant of the converter output active and reactive power changes are very small, and the changes in the PCC point voltage and frequency in the islanding mode are very small, which results in difficulties in detecting the islanding state (Abdelsalam AA. et al., 2020). analyzes the symmetrical components in the second harmonic of voltage and current signals as inputs to a long-term and short term neural network to identify islanding events. Table 1 shows a detailed comparative analysis of the literature in recent years and strongly related literature in intelligent islanding detection. Among deep learning algorithms, 1D-CNN is widely used in power systems due to its excellent detection accuracy (Reddy et al., 2021). carries out island detection using 1D-CNN method, and the experimental results show that it is able to effectively discriminate between islanded and non-islanded states, which verifies the feasibility of 1D-CNN in the problem of island detection (Aljafari et al., 2024). uses 1D-CNN deep learning technique in PV grid-connected system fault detection, and combines it with IoT technology, and results show that 1D-CNN is able to effectively fault detection accuracy (Xu et al., 2024). improves 1D-CNN for acoustic processing scenarios and effectively improves the accuracy of detection by introducing an attention mechanism. These studies have shown that 1D-CNN is technically superior in many aspects of power system condition detection and sound signal processing, with advantage of wide applicability and high accuracy.

Table 1

Table 1. Comparison of the various intelligent islanding detection methods.

Based on these previous studies till 2021 in islanding detection, this paper introduces the concept of adaptive variational mode decomposition (AVMD) and presents a novel intelligent islanding detection based on AVMD, Teager energy operator (TEO), multi-scale permutation entropy (MPE), and one-dimensional convolutional neural network (1D-CNN). A binary classification model is established for intelligent recognition of islanding and non-islanding states. This model introduces relative entropy to optimize VMD parameters and represents the features of three-phase voltage and inverter output current using VMD. Meanwhile, to accurately track the instantaneous fluctuation of intrinsic mode functions (IMFs), the TEO is introduced to highlight the features of islanding, and the MPE reflects the complexity of islanding features at different scales. Finally, the AVMD-TEO-MPE-based features are used as the input of the 1D-CNN network to classify islanding events and non-islanding events. The algorithm’s performance is verified by indicators such as noise immunity, detection time, accuracy, precision, recall, and F1-score. The suggested intelligent islanding detection approach can effectively classify the islanding state under various working settings, and it has certain noise robustness, according to the simulation results. It solves the problems of long detection time and insufficient accuracy of traditional islanding detection methods.

The main contributions of this research work can be outlined as follows.

1. A parameter-optimized VMD algorithm, namely, AVMD, is proposed. More accurate islanding feature information can be obtained by adopting the relative entropy to obtain the optimal parameters of VMD.

2. A new islanding feature extraction based on AVMD-TEO-MPE is proposed, which can effectively extract the features of islanding and grid disturbance. By comparison, the method outperforms the WT, EMD, and VMD methods in feature extraction. The comparative results are discussed in Section 5.3.

3. The 1D-CNN trained as a deep learning classifier by inputting the AVMD-TEO-MPE-based features is first implemented to learn the features and classify islanding and grid disturbance, which is needless of a threshold value. The 1D-CNN method improves the classification effect compared with LSTM, BP, and SVM. The comparative results are discussed in Section 5.3.

4. The inverter control strategy-based model is simulated in MATLAB/SIMULINK. The proposed method can also be implemented on synchronous-based microgrids. Five case studies are presented to assess the performance of the proposed methodology in detecting the islanding. Such case studies include tripping a circuit breaker at PCC with the loaded quality factor quality factors of 1 and 2.5, all types of short-circuit faults at PCC, local load mutation, and capacitor mutation.

5. The proposed method can effectively differentiate the islanding state with a training accuracy level of 99.8% and a testing accuracy level of 100% within a maximal detection time of 46.402 m.

6. Compared to the active method, the proposed method does not disturb the quality of the power provided of the microgrid. The problem whereby the remote method needs high-cost sensors, computational burden, and complexity is avoided.

The structure of the study is as follows. Section 2 introduces the technology of islanding feature extraction of the microgrid; the basic theory of the AVMD is discussed in Section 2.1; the analysis of the islanding features of the AVMD-TEO-MPE is discussed in Sections 2.2, 2.3. Section 3 provides the details of the methodology presented in the paper. In Section 4, the simulation process used in the proposed method is presented, and the test system and data generation are discussed in Section 4.1. Section 4.2 introduces the experiment of 1D-CNN network parameters. Section 5 illustrates the performance analysis of the methodology. Finally, Section 6 summarizes the theory proposed in this paper.

2 Technology of islanding feature extraction

2.1 AVMD

2.1.1 Preprocessing of modal parameters

Given the different types of faults in the system, all three-phase signals should be considered when analyzing the islanding faults of the microgrid. Meanwhile, Equation 1 calculates the modal component of the voltage signal at PCC, and the converter outputs the current signal to reduce the analysis time of each phase and the computer memory (Ghanbari and Farjah, 2014).

$\left\{\begin{array}{l}{V}_m=q_1{V}_a+q_2{V}_b+q_3{V}_c\\ I_m=p_1{I}_a+p_2{I}_b+p_3{I}_c\end{array}\right.(1)$

Where V_m and I_m are modal components of voltage and current, respectively. q and p are modal coefficients. The subscripts a, b, and c refer to the a-phase, b-phase, and c-phase, respectively.

2.1.2 VMD

VMD proposed by Dragomiretskiy and Zosso is a signal processing technique in 2014, which consists of Wiener filtering, Hilbert transform, and frequency mixing as its fundamental components (Achlerkar et al., 2018). The VMD mathematical model for islanding detection in this paper of the microgrid is as follows. VMD decomposes the non-stationary input signal voltage V_m or modal current I_m into a series of IMFs with finite bandwidth and time-varying amplitude and frequency according to Equation 2

$u_k\left(t\right)={\displaystyle \sum _k}{A}_k\left(t\right)\cos \left({\varphi }_k\left(t\right)\right)(2)$

Where uk(t) is the modal function, Ak(t) is the instantaneous amplitude, ϕk(t) is the phase. For an input signal f in this paper is the voltage at PCC V_m or inverter output current I_m, its decomposition process is a constrained variational problem, which can be expressed as Equation 3

$\left\{\begin{array}{l}\underset{\left\{{\mathrm{u}}_{\mathrm{k}},{\mathrm{w}}_{\mathrm{k}}\right\}}{\min }\left\{{\displaystyle \sum _{\mathrm{k}}}{‖{\mathrm{\partial }}_{\mathrm{t}}\left[\left(\mathrm{\delta }\left(\mathrm{t}\right)+\frac{\mathrm{j}}{\pi \mathrm{t}}\right)*{\mathrm{u}}_{\mathrm{k}}\left(\mathrm{t}\right)\right]{\mathrm{e}}^{-\mathrm{j}{\mathrm{w}}_{\mathrm{k}}\mathrm{t}}‖}_2^2\right\}\\ \begin{array}{cc}\begin{array}{cc}\mathrm{s}.\mathrm{t}& {\displaystyle \sum _{\mathrm{k}}}{\mathrm{u}}_{\mathrm{k}}=\mathrm{f}\end{array}& \end{array}\end{array}\right.(3)$

Where $\mathrm{\delta }\left(\mathrm{t}\right)$ is the Dirac distribution, ${‖·‖}_2^2$ is square of two norms, u_k = {u₁,u₂ … u_k} is the set of all modes, w_k = {w₁,w₂ … w_k} is center frequencies of all modes, k is mode number, ${\mathrm{\partial }}_{\mathrm{t}}$ and $*$ denote gradient operation and convolution, respectively. The penalty term a and Lagrangian multipliers $\lambda$ are introduced to solve the constraint problem, which converts the constraint problem to the corresponding unconstrained problem as shown in Equation 4.

$\begin{array}{ll}\hfill & \hfill \mathrm{L}\left({\mathrm{u}}_{\mathrm{k}},{\mathrm{w}}_{\mathrm{k}},\mathrm{\lambda }\right)=\mathrm{a}\left\{{{\displaystyle \sum _{\mathrm{k}}}‖{\mathrm{\partial }}_{\mathrm{t}}\left[\left(\mathrm{\delta }\left(\mathrm{t}\right)+\frac{\mathrm{j}}{\pi \mathrm{t}}\right)*{\mathrm{u}}_{\mathrm{k}}\left(\mathrm{t}\right)\right]{\mathrm{e}}^{-\mathrm{j}{\mathrm{w}}_{\mathrm{k}}\mathrm{t}}‖}_2^2\right\}\\ \hfill & +{‖\mathrm{f}-{\displaystyle \sum _{\mathrm{k}}}{\mathrm{u}}_{\mathrm{k}}‖}_2^2+〈\mathrm{\lambda },\mathrm{f}-{\displaystyle \sum _{\mathrm{k}}}{\mathrm{u}}_{\mathrm{k}}〉\hfill \end{array}(4)$

To address the saddle point of the augmented Lagrangian function in Equation 4, the alternate direction method of multipliers is introduced to update u_k, w_k, and $\lambda$, as shown in Equations 5–7.

${\mathrm{u}}_{\mathrm{k}}^{\mathrm{n}+1}=\frac{\widehat{\mathrm{f}}\left(\mathrm{w}\right)-{\sum }_{\mathrm{i}<\mathrm{w}}{\widehat{\mathrm{u}}}_{\mathrm{i}}^{\mathrm{n}+1}\left(\mathrm{w}\right)-{\sum }_{\mathrm{i}>\mathrm{w}}{\widehat{\mathrm{u}}}_{\mathrm{i}}^{\mathrm{n}}+\widehat{\mathrm{\lambda }}\left(\mathrm{w}\right)/2}{1+2\mathrm{a}{\left(\mathrm{w}-{\mathrm{w}}_{\mathrm{k}}\right)}^2}(5)$

${\mathrm{w}}_{\mathrm{k}}^{\mathrm{n}+1}=\frac{{\int }_0^{\infty }\mathrm{w}{\left|{\widehat{\mathrm{u}}}_{\mathrm{k}}^{\mathrm{n}+1}\left(\mathrm{w}\right)\right|}^2\text{dw}}{{\int }_0^{\infty }{\left|{\widehat{\mathrm{u}}}_{\mathrm{k}}^{\mathrm{n}+1}\left(\mathrm{w}\right)\right|}^2\text{dw}}(6)$

${\widehat{\mathrm{\lambda }}}^{\mathrm{n}+1}\left(\mathrm{w}\right)={\widehat{\mathrm{\lambda }}}^{\mathrm{n}}\left(\mathrm{w}\right)+\mathrm{\tau }\left(\widehat{\mathrm{u}}\left(\mathrm{w}\right)-{\displaystyle \sum _{\mathrm{k}}}{\widehat{\mathrm{u}}}_{\mathrm{k}}^{\mathrm{n}+1}\left(\mathrm{w}\right)\right)(7)$

Where n is the number of iterations and is the noise tolerance. Equations 5–7 are continued until the convergence of Equation 8.

${\displaystyle \sum _{\mathrm{k}}}\frac{{‖{\widehat{\mathrm{u}}}_{\mathrm{k}}^{\mathrm{n}+1}-{\widehat{\mathrm{u}}}_{\mathrm{k}}^{\mathrm{n}}‖}_2^2}{{‖{\widehat{\mathrm{u}}}_{\mathrm{k}}^{\mathrm{n}}‖}^2}<\mathrm{\epsilon }(8)$

Where $\epsilon >0$ is the tolerance of the convergence criterion.

2.1.3 VMD parameters optimization based on relative entropy

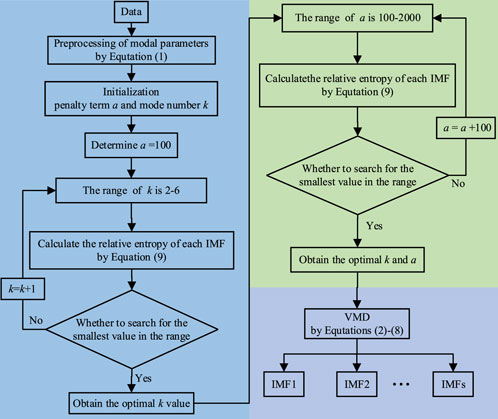
VMD algorithm avoids EMD limits of sensitivity to noise and sampling frequency. However, the mode number k and the penalty term a must be manually set, failing to match the actual parameters. When the preset parameters exceed the real parameters, over-decomposition occurs and new modes are generated. When the preset parameters are smaller than the actual parameters, important modes are not decomposed completely, resulting in the loss of important information. Due to the limitation of islanding detection time, a parameter optimization method with simple thinking, short time, and easy code writing is needed. VMD parameters optimization based on relative entropy is proposed in this work. Relative entropy, also known as Kullback-Leibler divergence, is a metric that expresses the dissimilarity of two sets of probability distributions (Yin et al., 2021). The greater the relative entropy, the greater the difference between the two sets of data distributions. The relative entropy between the original signal and each IMF is calculated by Equation 9, and the mode number and penalty term corresponding to the minimum relative entropy are determined to be the optimal parameters.

${\mathrm{D}}_{\text{KL}}\left(\mathrm{p}\Vert \mathrm{q}\right)={\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{N}}}\mathrm{p}\left({\mathrm{x}}_{\mathrm{i}}\right)\log \frac{\mathrm{p}\left({\mathrm{x}}_{\mathrm{i}}\right)}{\mathrm{q}\left({\mathrm{x}}_{\mathrm{i}}\right)}(9)$

Where p(x_i) is the modal components of voltage or current, q(x_i) is the corresponding modal component IMFs, N is the distribution length, x_i is a discrete random variable. Figure 3 illustrates a flowchart of VMD parameters optimization based on relative entropy. The specific steps for mode number k and penalty term a are as follows.

Step 1: Initialization parameters k = 0 and a = 0.

Step 2: Determine a = 100 and set the range of k as 2–6; the initial value is 2.

Step 3: Perform VMD and calculate the relative entropy of each IMF.

Step 4: If minimum relative entropy occurs, go to step 5, otherwise, k = k+1 and go to step 3.

Step 5: Obtain the optimal k value. Meanwhile, set the range of a as 100–2000.

Step 6: Calculate the relative entropy of each IMF.

Step 7: If minimum relative entropy occurs, go to step 8, otherwise, a = a+100 and go to step 6.

Step 8: Obtain the optimal k and a.

Figure 3

Figure 3. Flowchart of parameter optimized VMD.

2.2 TEO and its islanding feature

The TEO, a nonlinear difference operator, can quickly capture the instantaneous change of a signal, and its simple and fast calculation process is widely used in signal demodulation analysis (Deng et al., 2021). The IMFs obtained by AVMD of voltage at PCC and inverter output current are transformed by the TEO to obtain the frequency and amplitude information of islanding fault signals, and extract the instantaneous information of the signals. Therefore, the introduction of TEO into AVMD can improve the analysis performance of island fault. The process of the TEO to solve a continuous signal is shown in Equations 10, 11.

$\mathrm{\psi }\left[\mathrm{s}\left(\mathrm{t}\right)\right]={\stackrel{·}{\mathrm{s}}}^2\left(\mathrm{t}\right)-\mathrm{s}\left(\mathrm{t}\right)\stackrel{·}{\mathrm{s}} \left(\mathrm{t}\right)(10)$

$\left\{\begin{array}{l}\mathrm{f}\left(\mathrm{t}\right)=\frac{1}{4\mathrm{\pi }}\arccos \left[1-\frac{\mathrm{\psi }\left[\mathrm{s}\left(\mathrm{t}+1\right)-\mathrm{s}\left(\mathrm{t}-1\right)\right]}{2\mathrm{\psi }\left[\mathrm{s}\left(\mathrm{t}\right)\right]}\right]\\ \begin{array}{cc}\mathrm{a}\left(\mathrm{t}\right)=\frac{2\mathrm{\psi }\left[\mathrm{s}\left(\mathrm{t}\right)\right]}{\sqrt{\mathrm{\psi }\left[\mathrm{s}\left(\mathrm{t}+1\right)-\mathrm{s}\left(\mathrm{t}-1\right)\right]}}& \end{array}\end{array}\right.(11)$

Where $\psi \left[s\left(t\right)\right]$ is the instantaneous energy of the IMFs, $\stackrel{·}{s}\left(t\right)$ and $\stackrel{·}{\mathrm{s}} \left(t\right)$ are $\frac{\mathrm{d}s\left(t\right)}{\mathrm{d}t}$, $\frac{{\mathrm{d}}^{2}s\left(t\right)}{\mathrm{d}{t}^2}$, respectively. t is time, f (t) is the frequency of the IMFs, and a(t) is the amplitude of the IMFs. For the discrete signal s(n), the corresponding TEO expression is shown in Equation 12.

$\psi \left[s\left(n\right)\right]=s^2\left(n\right)-s\left(n+1\right)s\left(n-1\right)(12)$

To validate the performance of the proposed algorithm in feature extraction under different working conditions, taking the voltage as an example to illustrate the feature extraction process of AVMD-TEO. The loaded quality factor Q_f is used to measure the resonance capability of the local load, the greater the load quality factor, the stronger the resonance capability of the local load, and can be used to assess the reliability and robustness of detection methods (Panigrahi et al., 2021), it is defined as Equation 13.

$Q_f=R\sqrt{\frac{C}{L}}(13)$

Where Q_f is the loaded quality factor, R, C, and L are resistance, capacitance, and inductance. In the load quality factor Q_f = 1, the voltage at PCC does not fluctuate significantly. The resonance capability of the local load is exactly equal to the system frequency 50Hz, and the power required by the local load is provided totally by the inverter. In the circumstances, neither the O/U F&V protection methods can effectively detect islanding events. The feature waveforms with the load quality factor Q_f = 1 are shown in Figure 4 when a circuit breaker at PCC suddenly trips at 0.8s. The test system is difficult to detect islanding events under the most severe conditions. Figure 4a displays the voltage curves at PCC, IMF1, IMF2, and IMF3. The modal function extracted by AVMD does not fluctuate significantly at 0.8s, which cannot accurately represent the islanding feature. To detect the transient impact of the modal function, the energy conversion is carried out at t = 0.8s, Qf = 1, at this time, the active power and reactive power are equal, and the most serious islanding event occurs, which can maximize the detection of its effectiveness. The energy sequence is transformed by TEO (as shown in Figure 4b) and obviously distorted at 0.8s.

Figure 4

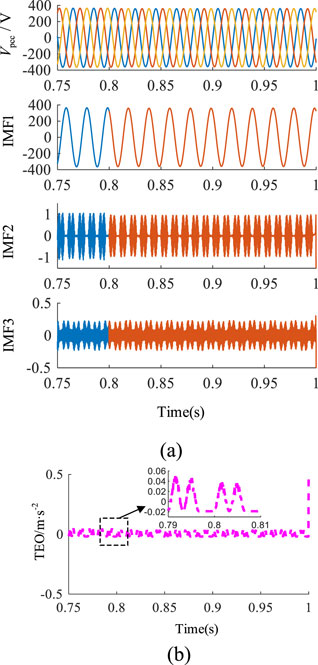
Figure 4. Feature waveforms with load quality factor Q_f = 1: (a) The voltage at PCC and its IMFs; (b) TEO of IMF1.

Meanwhile, Figure 5 shows that under the loaded quality factor Q_f of 2.5, a circuit breaker at PCC suddenly trips at 0.8s. As shown in Figure 5a, the voltage at PCC changes significantly when the circuit breaker is disconnected at 0.8s, showing a three-phase unbalanced state. Figure 5 shows that the AVMD-TEO can be well-represented by islanding features.

Figure 5

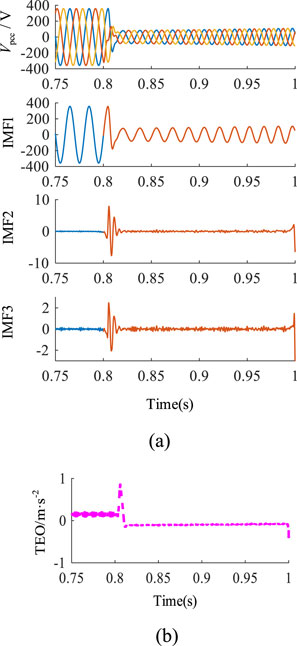
Figure 5. Feature waveforms with load quality factor Qf = 2.5: (a) The voltage at PCC and its IMFs; (b) TEO of IMF1.

As shown in Figure 6, a new parallel RLC load is added at 0.8s, its parameters are R = 0.64, C = 4.97mF, and L = 2.04 mH. Since the inverter is working in a normal state, Figure 6 displays that the load mutation’s features extracted by AVMD-TEO do not fluctuate significantly. Figure 7 also shows feature waveforms when a PCC three-phase short circuit. The voltage shows an obvious three-phase unbalanced state. Figure 7a shows that the modal functions IMF2 and IMF3 decomposed by AVMD have a sudden fluctuation at 0.8s. In order to highlight the fluctuation of IMF1, the energy sequence is transformed by TEO, which can effectively represent the islanding features, as shown in Figure 7b. Figure 8 shows the feature waveforms with capacitor mutation.

Figure 6

Figure 6. Feature waveforms when local load suddenly changes: (a) The voltage at PCC and its IMFs; (b) TEO of IMF1.

Figure 7

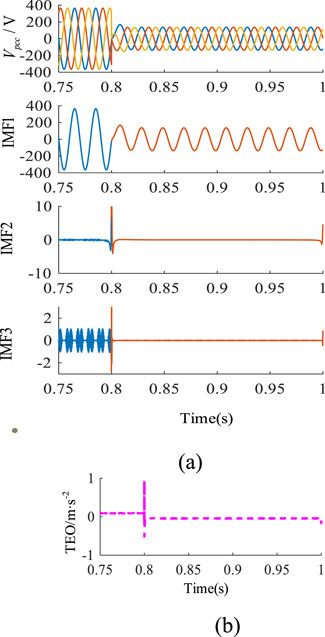
Figure 7. Feature waveforms when PCC fault conditions: (a) The voltage at PCC and its IMFs; (b) TEO of IMF1.

Figure 8

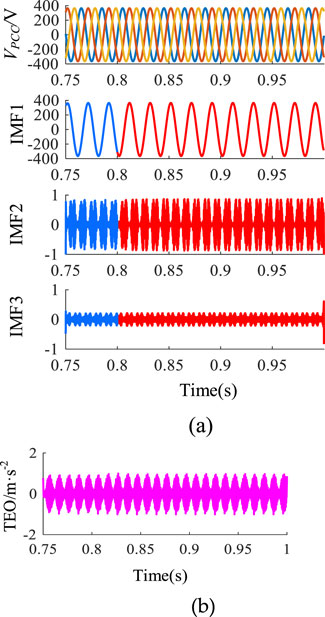
Figure 8. Feature waveforms when capacitor mutation: (a) The voltage at PCC and its IMFs; (b) TEO of IMF1.

2.3 MPE and its islanding feature

The MPE calculates the permutation entropy at different scales from the energy sequences derived from TEO, which aims to reflect the complexity of islanding features at different scales and facilitate the extraction of islanding feature vectors. Firstly, the IMFs components are coarse-grained to obtain multiple coarse-grained sequences y_j^(s), The multiple coarse-grained sequences y_j^(s) are transformed by increasing the length of IMFs, and the computation process is shown in Equation 14.

$y_j^{\left(s\right)}=\frac{1}{s}{\displaystyle \sum _{i=\left(j-1\right)s+1}^{js}}{x}_i,j=1,2\cdots ,\left[N/s\right](14)$

Where s is the scale factor, N is the length of IMFs [N/s] denotes the round-off number. Y_l^(s) was obtained by m-dimensional reconstruction of coarse-grained sequence y_j^(s), which is calculated as Equation 15.

$Y_l^{\left(s\right)}=\left\{y_l^{\left(s\right)},y_{l+\tau }^{\left(s\right)},\cdots ,y_{l+\left(m-1\right)t}^{\left(s\right)}\right\}(15)$

Where t is time-lag, l is reconstruction component l = 1,2, … , N-(m-1)t. Then the reconstructed components l are arranged in ascending order to obtain the sign sequence L(r) = (j₁,j₂, … ,j_m), where r = 1,2, … ,k, and k $\le$ m! Calculating the probability Pr for each symbol, and the permutation entropy of each coarse-grained sequence is calculated, and MPE = $-{\displaystyle \sum _{r=1}^R}{P}_r\ln P_r$ is obtained. The islanding features are transformed by normalization, as shown in Equation 16.

$0\le MPE=-{\displaystyle \sum _{r=1}^R}{P}_r\ln P_r/\ln \left(m!\right)\le 1(16)$

According to the MPE definition, four important parameters need to be set in this paper: an embedding dimension m, scale factor s, time-lag t, and length of IMFs N. In this paper, the length of IMFs N is equal to 9,000. As shown in Figure 9a, when the scale factor s is 12, the MPE value tends to be stable, so s is selected as 12. The time-lag t has little influence on the calculation of time series and is generally set to 1. When N = 9,000, s = 12, t = 1, the influences of different embedding dimensions on MPE values are analyzed. It can be seen from Figure 9b that if the m value is too large and the MPE value is too small, the mutability of IMFs cannot be accurately represented. On the contrary, the islanding information is close to randomization. Therefore, we select N = 9,000, s = 12, t = 1, and m = 6 in this paper to analyze the MPE of IMFs, as shown in Figure 9c. The results show that AVMD-MPE can effectively characterize the characteristics of islanding information.

Figure 9

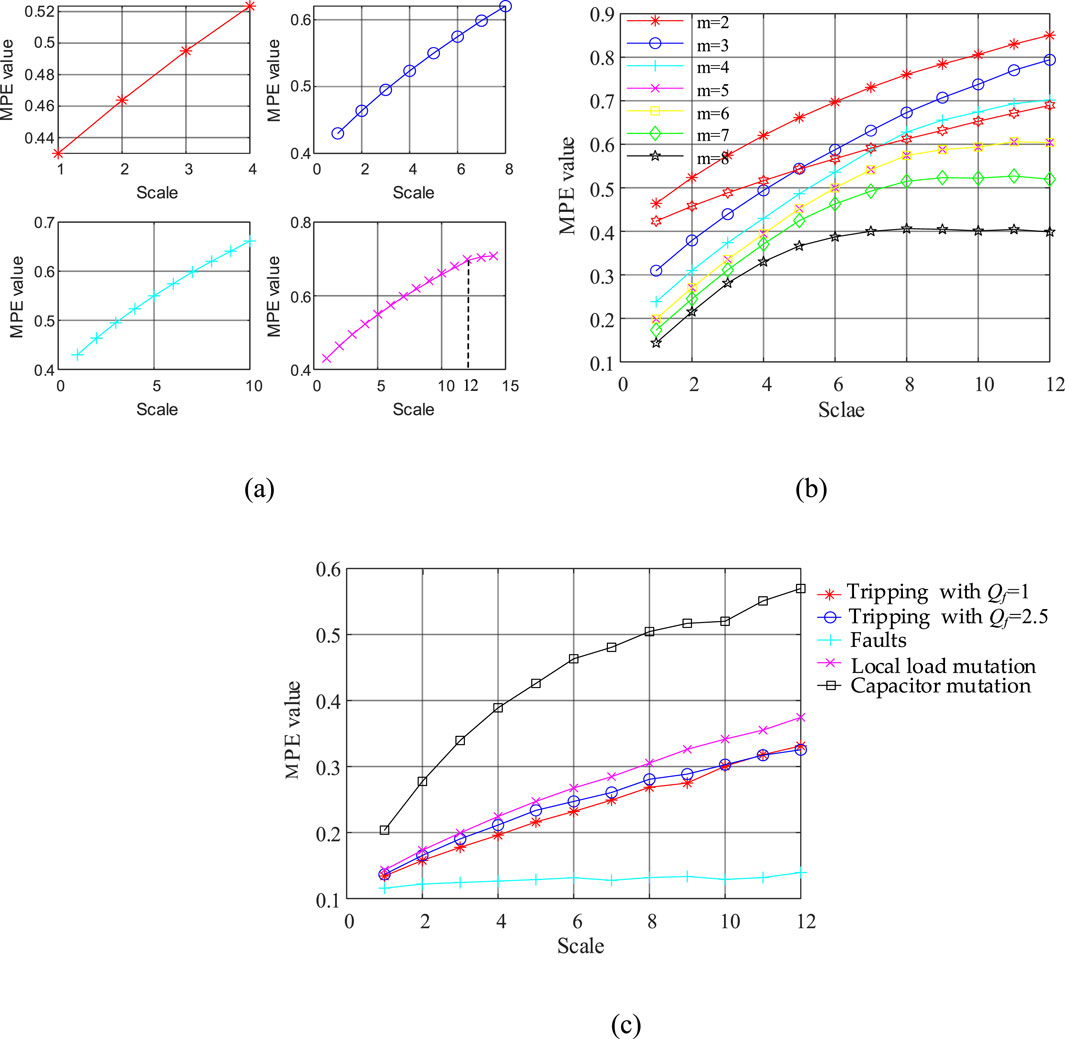
Figure 9. The results of MPE: (a) the different scale factor s; (b) the different embedding dimensions m; (c) the different events.

3 Proposed intelligent research methodology based on deep learning

3.1 1D-CNN

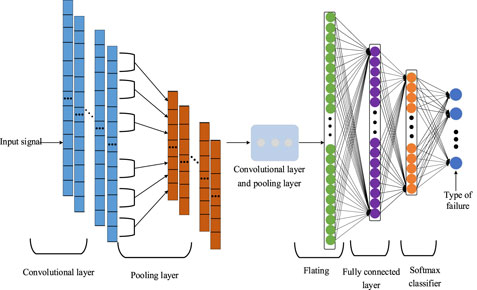
The features extracted by the AVMD-TEO-MPE change significantly under different working conditions, which are also affected by factors such as voltage fluctuations and harmonics. It is difficult to detect the islanding status by setting the threshold. Therefore, a strong pattern recognition algorithm is needed. Convolutional Neural Network has been successfully applied in the fields of natural language processing (Alawad et al., 2021), speech recognition (Han et al., 2021), and image processing (Tian et al., 2021), and has advantages in many engineering applications. The input of a 1D-CNN is a one-dimensional vector, its convolution kernel is also a one-dimensional structure, and each convolutional layer and pooling layer outputs a one-dimensional vector. A typical 1D-CNN generally includes an input, convolutional, pooling, fully connected, and output layer (Wang et al., 2021), as shown in Figure 10. Meanwhile, some techniques are introduced into 1D-CNN, such as batch normalization, dropout, etc. These techniques help to increase the algorithm’s learning performance and operating efficiency.

(1) The convolutional layer: the convolution kernel convolves the input signal to extract the features of the local area and uses the nonlinear activation function to reconstruct the output feature in the convolutional layer. The output of each layer is the result of the convolution of multiple input features. The advantage of the convolution kernel is that it can obtain the characteristics of rotation invariance, and its mathematical expressions are as shown in Equations 17, 18.

${\mathrm{y}}_{\mathrm{i}}^{\mathrm{l}+1}\left(\mathrm{j}\right)={\mathrm{K}}_{\mathrm{i}}^{\mathrm{l}}*{\mathrm{x}}^{\mathrm{l}}\left(\mathrm{j}\right)+{\mathrm{b}}_{\mathrm{i}}^{\mathrm{l}}(17)$

${\mathrm{a}}_{\mathrm{i}}^{\mathrm{l}+1}\left(\mathrm{j}\right)=\mathrm{f}\left({\mathrm{y}}_{\mathrm{i}}^{\mathrm{l}+1}\left(\mathrm{j}\right)\right)=\frac{\exp \left(\mathrm{x}\right)-\exp \left(-\mathrm{x}\right)}{\exp \left(\mathrm{x}\right)+\exp \left(-\mathrm{x}\right)}(18)$

Figure 10

Figure 10. Structure of 1D-CNN.

Where x^l_(j) designates the jth local region at layer l. $*$ is a convolution operation. y_i^l+1(j) designates jth feature map of x^l_(j). K_i^l and b_i^l designate the weights of the ith convolution kernel at layer l and the bias of the ith convolution kernel at layer l, respectively. In order to enhance the nonlinear ability of the input signal, the convolutional layer combined with the back propagation learning method adjusts the parameters to speed up the convergence. Activation function after the convolutional layer is added. As shown in Equation 18, f ($·$) is the tanh activation function.

(2) The pooling layer: effectively reducing the parameters of the neural network and preventing over-fitting are the purposes of the pooling layer. The max-pooling commonly used can halve the sequence length. The max-pooling formula is represented in Equation 19.

${\mathrm{P}}_{\mathrm{i}}^{\mathrm{l}+1}\left(\mathrm{j}\right)=\underset{\left(\mathrm{j}-1\right)\mathrm{W}+1\le \mathrm{t}\le \text{jW}}{\max }\left\{{\mathrm{q}}_{\mathrm{i}}^{\mathrm{l}}\left(\mathrm{t}\right)\right\}(19)$

Where q_i^l(t) denotes the value of the tth output of a neuron in the ith feature at layer l. W denotes the width of the pooling layer.

(3) The fully connected layer: the fully connected layer is composed of multiple hidden layers, and each neuron is fully linked to all the neurons in the previous layer, which can further realize the abstraction and combination of global features. Construct the output of the previous pooling layer into a one-dimensional vector as the input of the fully connected layer, described as Equation 20

${\mathrm{z}}^{\mathrm{l}+1}\left(\mathrm{j}\right)=\mathrm{f}\left({\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{m}}}{\displaystyle \sum _{\mathrm{t}=1}^{\mathrm{n}}}{\mathrm{W}}_{\text{itj}}^{\mathrm{l}}{\mathrm{a}}_{\mathrm{i}}^{\mathrm{l}}\left(\mathrm{t}\right)+{\mathrm{b}}_{\mathrm{j}}^{\mathrm{l}}\right)(20)$

Where W_itj^l and b_i^l are the weights and bias of the fully connected layer, respectively. a_i^l(t) is the output of the previous layer l.

(4) The output layer: the softmax classifier used for multi-classification is used as the output layer. It is an extension of logistic regression, and its expression is represented in Equation 21.

$\mathrm{Q}\left(\mathrm{j}\right)=\text{softmax}\left({\mathrm{z}}^{\mathrm{o}}\left(\mathrm{j}\right)\right)=\frac{{\mathrm{e}}^{{\mathrm{z}}^{\mathrm{o}}\left(\mathrm{j}\right)}}{{\sum }_{\mathrm{k}=1}^{\mathrm{M}}{\mathrm{e}}^{{\mathrm{z}}^{\mathrm{o}}\left(\mathrm{k}\right)}}(21)$

Where M is the number of categories, z⁰(j) is the logits of the output of the jth neuron.

3.2 The proposed islanding detection algorithm

A novel algorithm is proposed in this paper for the feature extraction and classification of islanding detection. The AVMD-TEO-MPE has the powerful capability of feature extraction in the power system. The feature extraction ensures that the extracted features can accurately represent islanding information and improve detection accuracy. The features extracted by AVMD-TEO-MPE can be automatically processed by the alternating convolutional layer and pooling layer in the 1D-CNN, and a fully connected layer outputs feature learning results.

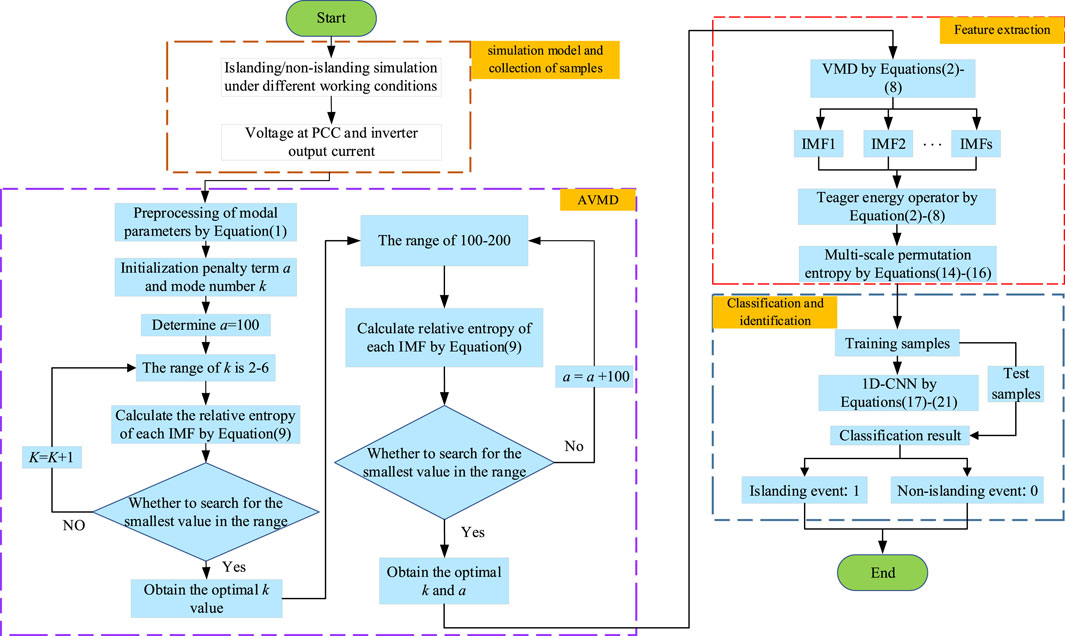
The proposed islanding detection algorithm includes the establishment of a simulation model and the collection of the data set, optimization of parameters, feature extraction, classification, and identification. Figure 11 shows the entire structure of the adaptive AVMD-TEO-MPE-based 1D-CNN islanding detection algorithm. The details are listed as follows.

Step 1: Establishment of the simulation model and collection of samples. Building a microgrid model in MATLAB/Simulink based on a three-phase voltage source inverter. Meanwhile, simulating the system operation under different islanding or non-islanding conditions, such case studies include circuit breaker tripping under different quality factors, all types of short-circuit faults at PCC, local load change, and capacitor mutation. Collecting voltage and current data.

Step 2: VMD parameters optimization based on relative entropy. The range of mode number k is set to 2-6, and the step size is 1. The inverter output current and voltage at PCC are transformed by AVMD, generating a set of IMFs. The relative entropy between the original signal and each IMF was calculated, and the K corresponding to the minimum relative entropy was determined to be the optimal mode number. Meanwhile, the range of penalty term a is set to 100–2000, and the step size is 100. The relative entropy of each IMF is calculated accordingly, and the one corresponding to the minimum relative entropy is determined as the optimal penalty term.

Step 3: Feature extraction. According to Step 2, the optimal mode number k is 3 and the penalty factor is 1,500. Selecting IMF1, IMF2, IMF3. Meanwhile, the TEO further extracts sequence features to track the instantaneous energy of the IMF1, IMF2, and IMF3. MPE transforms the extracted energy features.

Step 4: Classification and identification. The algorithm only classifies and recognizes the islanding state and the non-islanding state (“label 1″represents islanding, “label 0″represents non-islanding), and the number of output layer nodes is set to 2. The energy feature extracted by AVMD-TEO-MPE was randomly divided into training and testing samples in the ratio of 7:3. The training samples are used as the input of the 1D-CNN network. After plenty of training and experimentation, attain the optimal settings (Section 4.2). The test samples verify the classification performance of the 1D-CNN network and obtain the classification results. If the classification result is an islanded state, then output the grid-connected circuit breaker trip signal to interrupt the islanded state; if it is a non-islanded state, then do not output the signal, and the circuit breaker does not operate.

Figure 11

Figure 11. The architecture of the proposed islanding detection algorithm.

4 Simulation

4.1 Test system and data generation

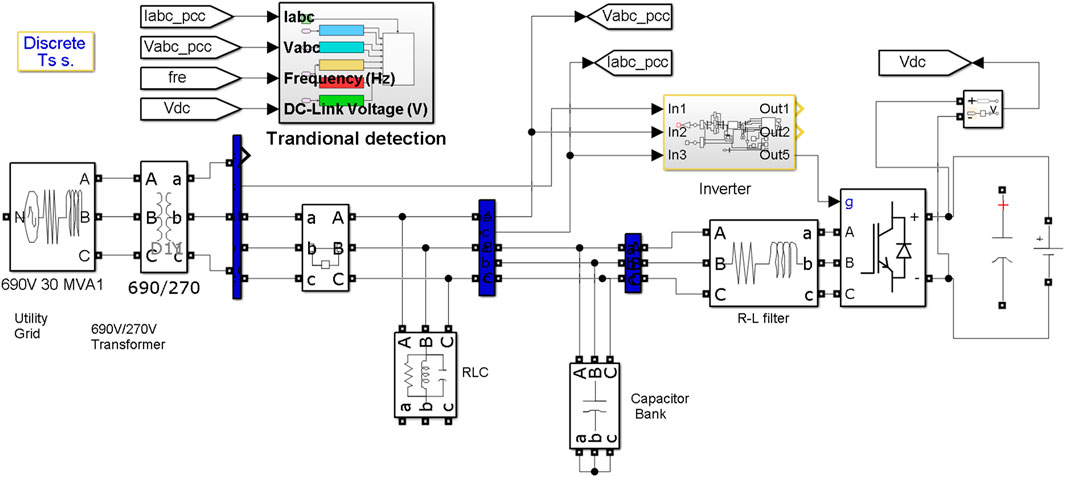
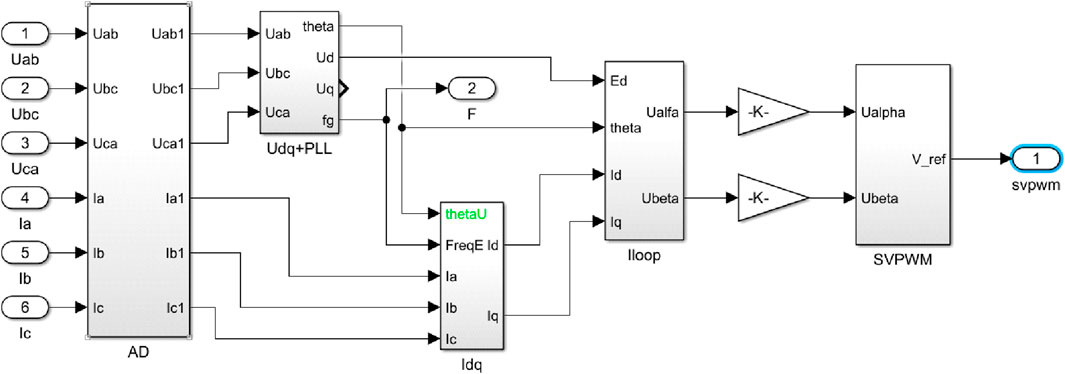
The photovoltaic inverter control strategy-based model is simulated on MATLAB/Simulink as drawn in Figure 12. As the current source in the distributed power, the inverter adopts single current loop control with a given output current, and the modulation algorithm of the inverter adopts space vector pulse width modulation technology (SVPWM), as shown in Figure 13. A single synchronous reference frame software phase-locked loop (SSRF-SPLL) outputs the sampled current frequency and voltage vector. The output voltage and output power of the inverter-based distributed power are 400V and 100kW, respectively. The inverter output filter reactor is 0.3 mH, and the filter capacitor is 960 μF. The grid line voltage is 270V. The details of the test system are as follows.

• Utility grid: Phase-to-phase voltage (Vrms) = 690V, Frequency = 50Hz, Rated short circuit Mva = 3MVA.

• Transformer: Nominal power = 63Mva, Frequency = 50Hz, V1 Ph-Ph (Vrms) = 690V, V2 Ph-Ph (Vrms) = 270V.

• Three-phase parallel RLC branch: Resistance (R) = 0.64 $\mathrm{\Omega }$, Capacitance (C) = 4.97 mF and Inductance (L) = 2.04 mH.

• R-L filter: R = $1\times {10}^{-3}\mathrm{\Omega }$, L = 0.15 mH.

• Universal Bridge: IGBT-Diode bridge, DC voltage = 400V.

• The inverter: Three-phase bridge topology, SVPWM modulation algorithm.

• The test system can operate in island mode with a three-phase circuit breaker opened or grid-connected mode with a three-phase circuit breaker closed.

Figure 12

Figure 12. Simulink diagram of test system considered in this study.

Figure 13

Figure 13. Simulink diagram of the control.

When the frequency of the parallel RLC load is exactly equal to the grid voltage frequency, islanding event detection is the most difficult. The parameters of the parallel RLC load are R = 0.64 $\mathrm{\Omega }$, C = 4.97mF, and L = 2.04mH, its loaded quality factor is 1, frequency is 50Hz, which verifies the performance of the algorithm under the condition that the absorbed power of the load is equal to the output power of the inverter.

The data sample is the basis of the training of the 1D-CNN, so four case studies are presented to assess the performance of the proposed methodology in detecting the islanding. Such case studies include tripping a circuit breaker at PCC with the loaded quality factors of 1 and 2.5, all types of short-circuit faults at PCC, local load mutation, and capacitor mutation, as shown in Table 2. Based on these previous different working conditions, the sampled data within 9 m is selected for AVMD. The test system is implemented in MATLAB/SIMULINK, and the proposed 1D-CNN network was constructed in Python.

Table 2

Table 2. The type of data.

4.2 Experiment: 1D-CNN network parameters

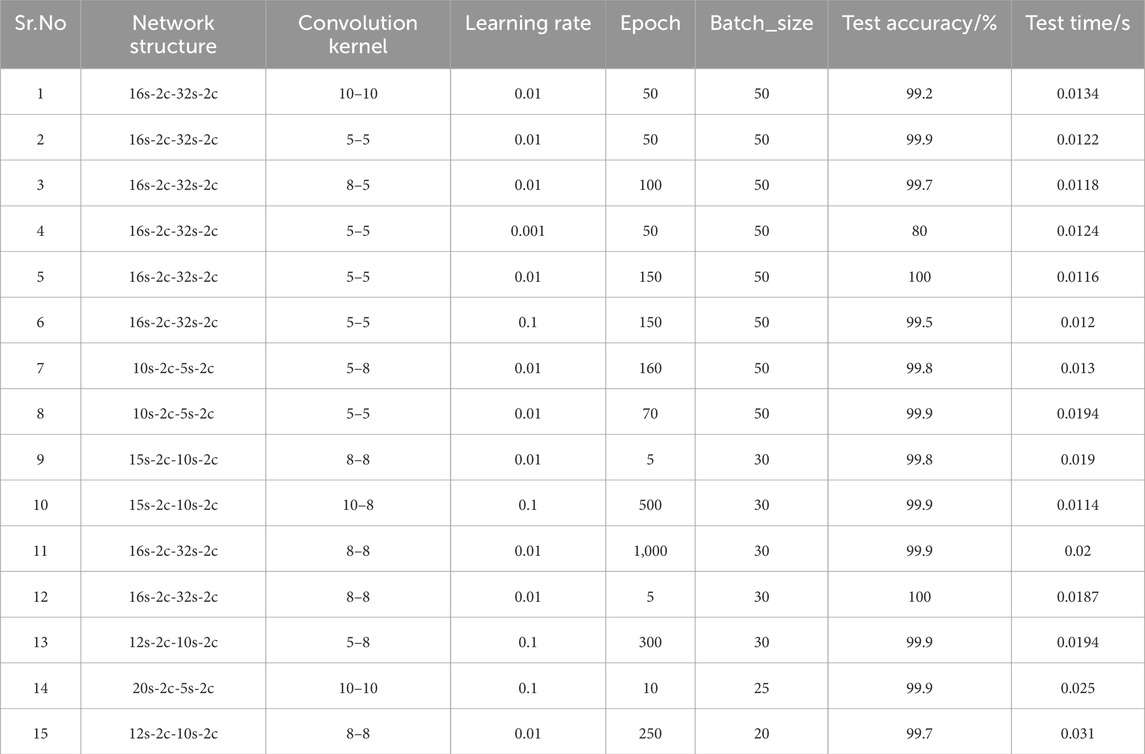
In order to truly unleash the classification and recognition characteristics of the 1D-CNN network, the 1D-CNN with different network structures is tested to determine the best structure of the network, as shown in Table 3. Taking serial number 1 as an example, the 16s in the network structure 16s-2c-32s-2c means that the first convolutional layer has 16 convolution kernels, and 2c means that the size of the first pooling layer is 2. The convolution kernel 10–10 indicates the size of the first and second convolution layer convolution kernels. The size of variation of the network and the number of input samples are the learning rate and batch size, respectively.

Table 3

Table 3. Test results of different 1D-CNN network structures.

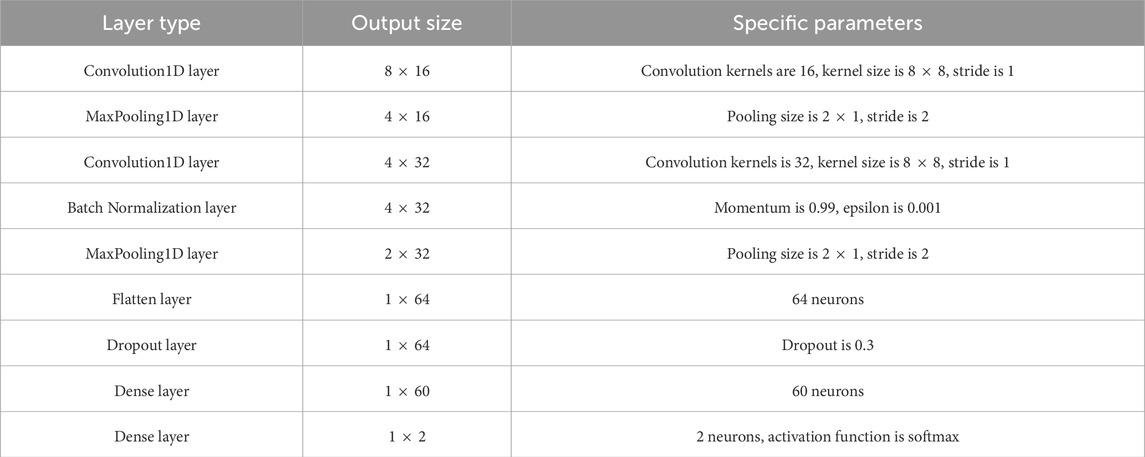
Setting the convolution kernel as a single variable, and found that when the convolution kernel is smaller, the accuracy is higher compared with serial numbers 1–3. Setting the learning rate to a single variable found that the lower the learning rate, the lower the accuracy rate. Comparing serial numbers 7–15 shows that the network structure has a greater impact on classification and recognition. Only through a large number of experiments and training can the appropriate experimental parameters be determined, so that the classification and recognition characteristics of the 1D-CNN network can be fully utilized. Meanwhile, Table 1 shows that serial numbers 5 and 12 have equivalent network structures, and their experimental test accuracy reaches 100%. Due to the short test time of serial number 5, serial number 5 is selected for this experiment’s 1D-CNN network structure parameters, and the specific parameters are shown in Table 4.

Table 4

Table 4. Specific parameters of 1D-CNN.

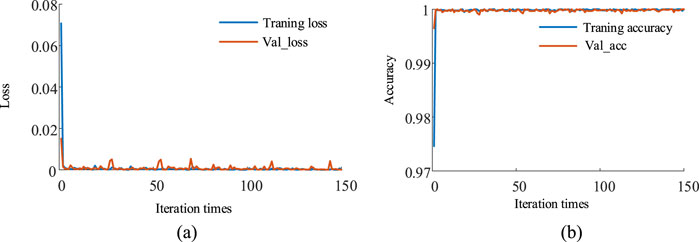
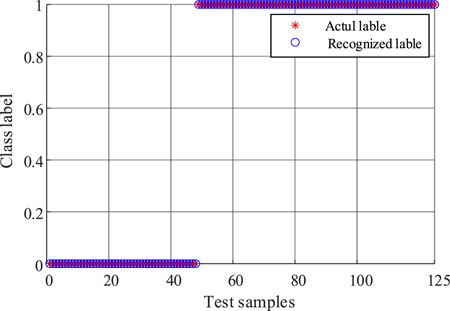
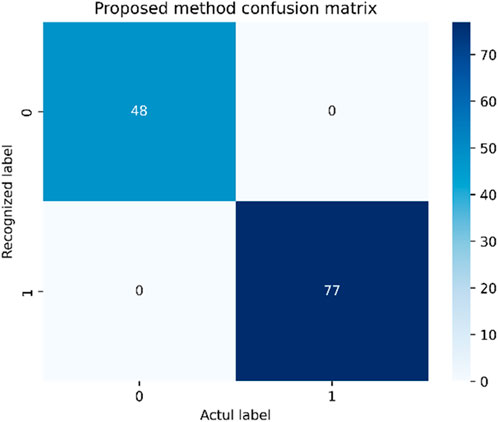
The AVMD-TEO-MPE-based features are input into the selected 1D-CNN network for islanding detection. Figure 14 shows the accuracy and loss of the 1D-CNN algorithm with a training accuracy of 99.8% and a training loss value of 0.000068. Meanwhile, the value of accuracy validation (val_accuracy) and loss validation (val_loss) are excellent with a val_accuracy of 100% and val_loss value of 0.00017. The islanding detection result and confusion matrix of the proposed method are shown in Figures 15, 16. The main diagonal elements in the confusion matrix can represent the number of correctly identified samples. The proposed method can correctly classify test samples of 125, which demonstrates the effectiveness of the proposed method for islanding detection.

Figure 14

Figure 14. The accuracy and loss of the 1D-CNN algorithm: (a) the accuracy; (b) the loss.

Figure 15

Figure 15. Identification results of the proposed method.

Figure 16

Figure 16. Confusion matrix of the proposed method.

5 Performance analysis and discussion

5.1 Anti-noise performance

In order to analyze the robustness of the proposed strategy, white Gaussian noise with different signal-to-noise ratios is used to simulate the possible measurement inaccuracies or interference in the real operation through the noise and to validate the effectiveness of the proposed strategy under real conditions (Hussain et al., 2023). By adding noise to the voltage signal at PCC to verify the anti-noise performance of the islanding detection algorithm, the Signal-to-noise ratio (SNR) describes the pollution degree of noise, as shown in Equation 22.

$\text{SNR}=10{\log }_{10}\frac{{\mathrm{p}}_{\text{sig}}}{{\mathrm{p}}_{\text{noi}}}(22)$

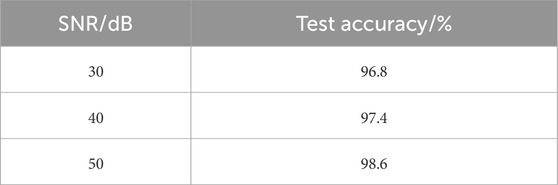
Where P_noi is noise signal power, P_sig is the raw signal power. The commonly used SNR is 40 dB in islanding detection (Ribeiro et al., 2013). Three new data sets with SNR of 30dB, 40dB, and 50 dB were generated by adding white Gaussian noise, which were tested using the 1D-CNN classifier trained on the noise-free data set. Table 5 shows that the test accuracy of the proposed algorithm is 96.8% and 98.6% under 30 dB and 50dB, and the method can work in a noisy environment. In turn, it is proved that the proposed strategy has good robustness.

Table 5

Table 5. Algorithm Performance under noise interference.

5.2 Detection time

According to GB/T33593-2017, the maximum detection time of islanding detection is not more than 2s. The detection time of the proposed islanding detection algorithm consists of sampling time, signal preprocessing time, feature extraction time, and test time. The transient variation of the islanding fault is about 2.5–3 m, and the sampling time of the simulation model is 1us. It takes about 9 m to capture 9,000 samples. In the signal preprocessing step, the average time to complete the AVMD feature extraction task is 10 m, the average time to complete the TEO and MPE detection tasks is 0.032 m and 2.77 m, respectively. Since the network does not need to be trained again in subsequent experiments after the training is completed, it takes about 24.6 m to classify in the test step of the classifier. In summary, the detection time is about 9 + 10+0.032 + 2.77+24.6 = 46.402 m, which is much shorter than the time specified in GB/T33593-2017.

5.3 Comparative performance analysis

A comparison is made from two perspectives (feature extraction and classifier) to verify the effectiveness of the proposed islanding detection method based on AVMD-TEO-MPE and 1D-CNN. Meanwhile, this paper introduces the accuracy, precision, recall and F1-score. The four criteria are described as

$\text{Acc}=\frac{\text{TP}+\text{TN}}{\text{TP}+\text{FP}+\text{TN}+\text{FN}}(23)$

Where TP, TN, FN, and FP are true positive, true negative, false negative, and false positive, respectively. Acc denotes the accuracy of the classifier. It is the ratio of the number of all correctly classified samples to the total number of samples, and is the most intuitive performance indicator of a model’s predictive power.

$\mathrm{Pr}e=\frac{TP}{TP+FP}(24)$

Pre is an indicator of precision, which measures the proportion of samples with positive predictions that are truly positive.

$\text{Re}\mathrm{c}=\frac{\mathrm{TP}}{\text{TP}+\mathrm{FN}}(25)$

Rec is the model recall, which measures the ability of the model of find all positive samples.

$\mathrm{F}1=\frac{2·\mathrm{Pre}·\text{Rec}}{\mathrm{Pre}+\text{Re}\mathrm{c}}(26)$

The F1 score is a reconciled average of Pre and Rec, which is suitable for category imbalance scenarios and provides a more accurate assessment of model performance metrics (Cui et al., 2025), it is based on the actual alignment, not the projected quantity itself.

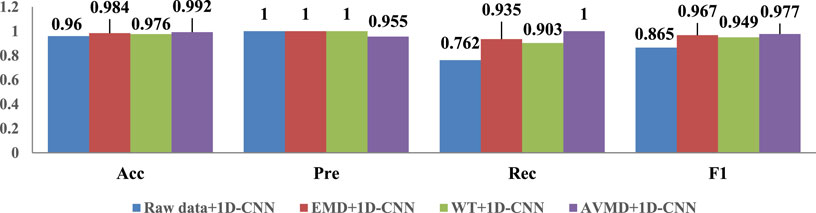
The feature extraction is used as a single variable to verify the performance of AVMD-TEO-MPE, as shown in Figure 17. The 1D-CNN is trained and tested using the features extracted by AVMD, the features extracted by EMD, the features extracted by WT, and the proposed method, respectively. Islanding detection is examined by calculating and analyzing the Acc, Pre, Rec, and F1 score as shown in Equations 23–26 respectively. The comparison results demonstrate the superiority of AVMD by evaluating several feature extraction algorithms. Meanwhile, the islanding detection results are shown in Figure 18, and the confusion matrix of different methods is illustrated in Figure 19. Due to the existence of category imbalance in prediction, the F1 score, which is not affected by category distribution, is mainly analysed. According to Figure 17, it can be seen that the F1 score under the proposed feature extraction strategy is better than the rest of the strategies when the 1D-CNN algorithm is also used, with an improvement of 12.9%, 1.0%, and 2.9%, respectively, compared the remaining three extraction methods. The superiority of the proposed feature extraction method can be verified.

Figure 17

Figure 17. Comparison of the results of different feature extraction approaches.

Figure 18

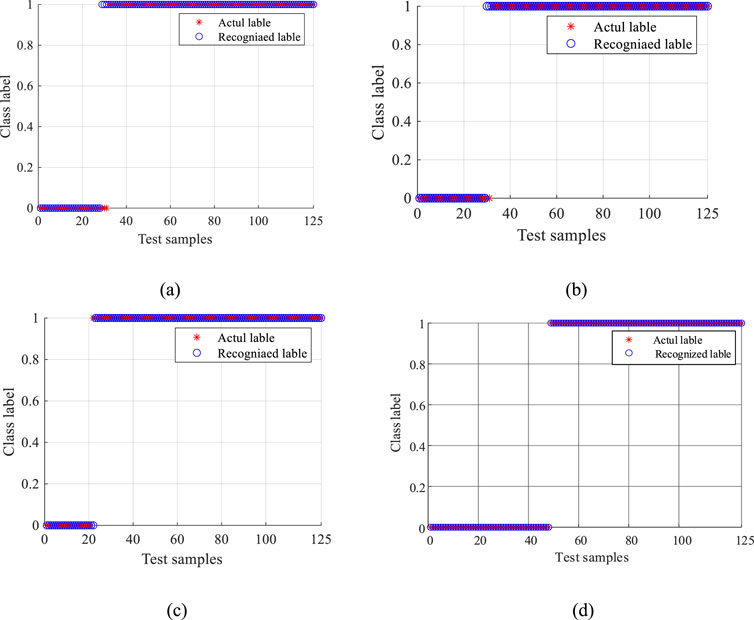
Figure 18. Islanding detection results: (a) WT+1D-CNN; (b) EMD+1D-CNN; (c) AVMD+1D-CNN; (d) Proposed method.

Figure 19

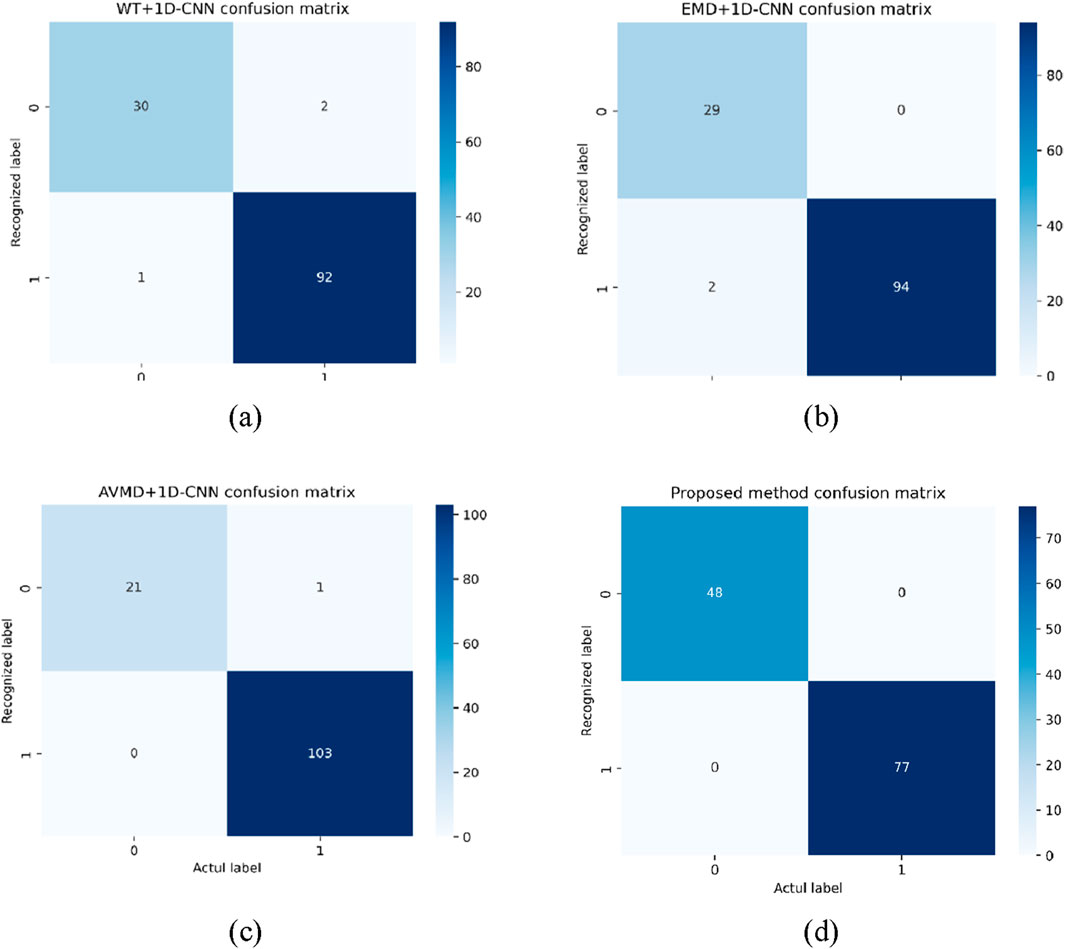
Figure 19. Confusion matrix of different methods: (a) WT+1D-CNN confusion matrix; (b) EMD+1D-CNN confusion matrix; (c) AVMD+1D-CNN confusion matrix; (d) Proposed method confusion matrix.

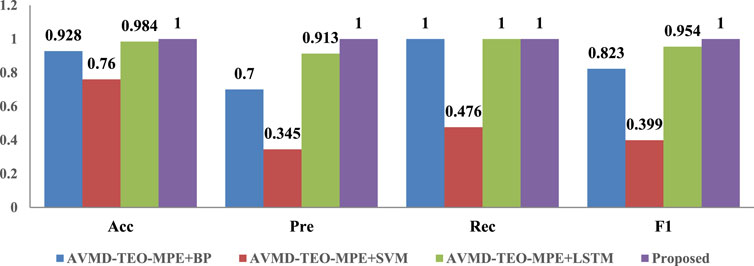
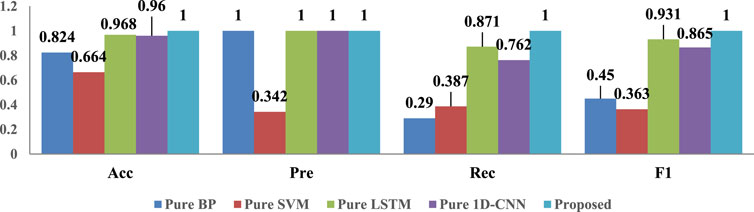
The classifier is implemented as a single-variable system as illustrated in Figure 20. To validate the performance of our proposed 1D-CNN classifier, comprehensive comparative experiments were conducted using Back Propagation (BP) neural networks, SVM, LSTM, and the proposed method, all trained and tested on feature vectors extracted through the AVMD-TEO-MPE framework. Quantitative evaluations reveal significant performance enhancements achieved by our proposed method across multiple metrics. Specifically, the proposed method maintains complete dominance in the F1-score (1.0) compared to LSTM’s 0.954. These experimental results substantiate that our 1D-CNN-based approach exhibits comprehensive advantages over traditional machine learning methods (BP, SVM) and shows particular improvement in precision metrics when compared with other deep learning architectures like LSTM. The systematic classifier comparison effectively highlights the technical superiority and practical value of our proposed methodology.

Figure 20

Figure 20. Comparison of the results of different classifier approaches.

Four groups of comparative experiments from the perspective of pure neural networks are designed to illustrate the importance of signal processing in feature extraction. The comparative results are shown in Figure 21. The F1 score of the proposed strategy is much higher than the rest of the deep learning algorithms due to the incorporation of better performing feature extraction methods, especially compared to the BP, SVM algorithms, the percentage of improvement reaches 122.2% and 175.4%, and compared to the more advanced LSTM and 1D-CNN methods, the percentage of improvement also reaches 7.4% and 15.6%, respectively. It also proves the superiority of the proposed algorithm.

Figure 21

Figure 21. Comparison of the results different pure other algorithms.

6 Conclusion

This paper analyzes a detailed review of islanding detection for the microgrid, especially intelligent islanding detection. The concept of AVMD was extended to extract features from the three-phase voltage and current signals. The AVMD-TEO-MPE-based index is proposed for the microgrid for the measured electrical characteristics. Exploiting the excellent properties of AVMD-Teager energy operator-MSPE for characterizing transient changes in power systems and the ability of 1D-CNN to extract the underlying information. This method overcomes the passive method in the load absorbed power and converter output power, completely matching the detection of the blind spot that exists in the case of large problems. At the same time, there is no impact on power quality as no disturbance current is injected into the system. , Theoretical derivation and simulation show that the algorithm is able to accurately detect islanded events and non-islanded events, and effectively reduce the detection blind zone and detection time, with a detection accuracy of up to 100%, 0.000068 of loss value within maximal detection time 46.402 m, confirmed the validity of the method proposed in this paper.

Additionally, due to the high training speed of 1D-CNN, the microgrid applied to the technology proposed has the function of quick online judgment and warning. Future work is to verify and further study the application performance of the proposed method in islanding detection based on the real distributed generation system experimental platform to be built.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

YX: Writing – original draft, Writing – review and editing. YL: Writing – review and editing. FY: Writing – original draft, Writing – review and editing. YiqY: Writing – review and editing. YilY: Writing – review and editing, Conceptualization. WL: Writing – review and editing. KL: Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This work is partially supported by Hydrogen Energy and Multi-energy Complementary Microgrid Engineering Technology Research Center of Sichuan Province (2024DWNY006), Sichuan Science and Technology Program (2022SZYZF01), and Opening Fund of Key Laboratory of Higher Education of Sichuan Province for Enterprise Informationalization and Internet of Things (2023WYJ01). This work was supported by the School of Automation and Information Engineering and Sichuan University of Science and Technology.

Conflict of interest

Authors WL and YilY were employed by Zonergy Co., Ltd. Author FY was employed by Zigong Branch of China Telecom Co., Ltd.

The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Abdelsalam, A. A., Ahmed, A., Oda, E. S., and Eldesouky, A. A. (2020b). Islanding detection of microgrid incorporating inverter based DGs using long short-term memory network. IEEE Access 8: 106471–106486. doi:10.1109/access.2020.3000872

CrossRef Full Text | Google Scholar

Abdelsalam, A. A., Salem, A. A., Oda, E. S., and Eldesouky, A. A. (2020a). Islanding detection of microgrid incorporating inverter based DGs using long short-term memory network. IEEE Access 8, 106471–106486. doi:10.1109/access.2020.3000872

CrossRef Full Text | Google Scholar

Achlerkar, P. D., Samantaray, S. R., and Manikandan, M. S. (2018). Variational mode decomposition and decision tree based detection and classification of power quality disturbances in grid-connected distributed generation system. IEEE Trans. Smart Grid 9 (4), 3122–3132. doi:10.1109/tsg.2016.2626469

CrossRef Full Text | Google Scholar

Admasie, S., Bukhari, S. B. A., Gush, T., Haider, R., and Kim, C. H. (2020). Intelligent islanding detection of multi-distributed generation using artificial neural network based on intrinsic mode function feature. J. Mod. Power Syst. Clean Energy 3 (8), 511–520. doi:10.35833/MPCE.2019.000255

CrossRef Full Text | Google Scholar

Admasie, S., Bukhari, S. B. A., Haider, R., Gush, T., and Kim, C. H. (2019). A passive islanding detection scheme using variational mode decomposition-based mode singular entropy for integrated microgrids. Electr. Power Syst. Res. 177, 105983. doi:10.1016/j.epsr.2019.105983

CrossRef Full Text | Google Scholar

Alam, M. R., Begum, M. T. A., and Muttaqi, K. M. (2019). Assessing the performance of ROCOF relay for anti-islanding protection of distributed generation under subcritical region of power imbalance. IEEE Trans. Industry Appl. 55 (5), 5395–5405. doi:10.1109/tia.2019.2927667

CrossRef Full Text | Google Scholar

Alawad, M., Yoon, H. J., Gao, S., Mumphrey, B., Wu, X. C., Durbin, E. B., et al. (2021). Privacy-preserving deep learning NLP models for cancer registries. IEEE Trans. Emerg. Top. Comput. 9 (3), 1219–1230. doi:10.1109/tetc.2020.2983404

PubMed Abstract | CrossRef Full Text | Google Scholar

Aljafari, B., Satpathy, P. R., Thanikanti, S. B., and Nwulu, N. (2024). Supervised classification and fault detection in grid-connected PV systems using 1D-CNN: simulation and real-time validation. Energy Rep. 12: 2156–2178. doi:10.1016/j.egyr.2024.08.008

CrossRef Full Text | Google Scholar

Allan, O. A., and Morsi, W. G. (2021). A new passive islanding detection approach using wavelets and deep learning for grid-connected photovoltaic systems. Electr. Power Syst. Res. 199, 107437. doi:10.1016/j.epsr.2021.107437

CrossRef Full Text | Google Scholar

Baloch, S., and Muhammad, M. S. (2021). An intelligent data mining-based fault detection and classification strategy for microgrid. IEEE Access 9, 22470–22479. doi:10.1109/access.2021.3056534

CrossRef Full Text | Google Scholar

Bitaraf, H., Sheikholeslamzadeh, M., Ranjbar, A. M., and Mozafari, B. (2012). A novel SVM approach of islanding detection in micro grid. IEEE PES Innov. Smart Grid Technol., 1–5. doi:10.1109/isgt-asia.2012.6303335

CrossRef Full Text | Google Scholar

Bukhari, S. B. A., Mehmood, K. K., Wadood, A., and Park, H. (2021). Intelligent islanding detection of microgrids using long short-term memory networks. Energies 18 (14), 5762. doi:10.3390/en14185762

CrossRef Full Text | Google Scholar

Cui, F., He, S. F., Luo, Z., Zong, C., Li, H. D., Ma, L. Q., et al. (2025). Research on multi-index early warning of rock burst based on bayesian optimization algorithm and machine learning. J. China Coal Soc. 1–17. doi:10.13225/j.cnki.jccs.2024.1499

CrossRef Full Text | Google Scholar

Deng, F., Zu, Y., Huang, Y., Zeng, X., Li, W., Xu, F., et al. (2021). Research on single-ended fault location method based on the dominant frequency component of traveling wave full-waveform. Proc. CSEE 41 (6), 2156–2168. doi:10.13334/j.0258-8013.pcsee.191995

CrossRef Full Text | Google Scholar

Dutta, S., Olla, S., and Sadhu, P. K. (2021). A secured, reliable and accurate unplanned island detection method in a renewable energy based microgrid. Eng. Sci. Technol. Int. J. 24 (5), 1102–1115. doi:10.1016/j.jestch.2021.01.015

CrossRef Full Text | Google Scholar

Dutta, S., Sadhu, P. K., Reddy, M. J. B., and Mohanta, D. K. (2018). Shifting of research trends in islanding detection method - a comprehensive survey. Prot. Control Mod. Power Syst. 3 (1), 1. doi:10.1186/s41601-017-0075-8

CrossRef Full Text | Google Scholar

Erick, V., Vazquez, N., and Femat, R. (2020). Modified Sandia voltage shift anti-islanding scheme for distributed power generator systems. IET Power Electron. 13 (18), 4226–4234. doi:10.1049/iet-pel.2020.0735

CrossRef Full Text | Google Scholar

Ghanbari, T., and Farjah, E. (2014). A multiagent-based fault-current limiting scheme for the microgrids. IEEE Trans. Power Deliv. 29 (2), 525–533. doi:10.1109/tpwrd.2013.2282917

CrossRef Full Text | Google Scholar

Han, K. J., Pan, J., Tadala, V. K. N., Ma, T., and Povey, D. (2021). “Multistream CNN for robust acoustic modeling,” in Proc. Of IEEE international conf. On acoustics, speech and signal processing (ICASSP). Toronto, ON, Canada, 6873–6877. doi:10.1109/ICASSP39728.2021.9414639

CrossRef Full Text | Google Scholar

Huang, N. E., Shen, Z., Long, S. R., Wu, M. C., Shih, H. H., Zheng, Q., et al. (1971). The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A 454, 903–995. doi:10.1098/rspa.1998.0193

CrossRef Full Text | Google Scholar

Hussain, A., Mirza, S., and Kim, C. H. (2023). Islanding detection and classification of non-islanding disturbance in multi-distributed generation power system using deep neural networks. Electr. Power Syst. Res. 224: 109807. doi:10.1016/j.epsr.2023.109807

CrossRef Full Text | Google Scholar

Jia, K., Zhu, Z., Zhao, Q., Zhe, Y., and Bi, T. (2019). Islanding detection method of multi-port photovoltaic DC micro grid based on harmonic impedance measurement. IET Renew. Power Gener. 13 (14), 2604–2611. doi:10.1049/iet-rpg.2019.0271

CrossRef Full Text | Google Scholar

Khosravi, H., Samet, H., and Tajdinian, M. (2021). Empirical mode decomposition based algorithm for islanding detection in microgrids. Electr. Power Syst. Res. 201, 107542. doi:10.1016/j.epsr.2021.107542

CrossRef Full Text | Google Scholar

Kim, S. C., Ray, P., and Salkut, S. R. (2020). Islanding detection in a distribution network with distributed generators using signal processing techniques. Int. J. Power Electron. Drive Syst. 11 (4), 2099. doi:10.11591/ijpeds.v11.i4.pp2099-2106

CrossRef Full Text | Google Scholar

Kong, X., Xu, X., Yan, Z., Chen, S., Yang, H., and Han, D. (2018). Deep learning hybrid method for islanding detection in distributed generation. Appl. Energy 210, 776–785. doi:10.1016/j.apenergy.2017.08.014

CrossRef Full Text | Google Scholar

Kumar, D. (2021). Islanding detection in microgrid compromising missing values using NI sensors. IEEE Syst. J., 1–10. doi:10.1109/JSYST.2021.3055566

CrossRef Full Text | Google Scholar

Li, H., Deng, J., Feng, P., Pu, C., Arachchige, D. D. K., and Cheng, Q. (2021). Short-term nacelle orientation forecasting using bilinear transformation and ICEEMDAN framework. Front. Energy Res. 9. doi:10.3389/fenrg.2021.780928

CrossRef Full Text | Google Scholar

Lidula, N. W. A., and Rajapakse, A. D. (2012). A pattern-recognition approach for detecting power islands using transient signals-Part II: performance evaluation. IEEE Trans. Power Deliv. 27 (3), 1071–1080. doi:10.1109/tpwrd.2012.2187344

CrossRef Full Text | Google Scholar

Liu, M., Zhao, W., Wang, Q., Huang, S., and Shi, K. (2021). A solution to the parameter selection and current static error issues with frequency shift islanding detection methods. IEEE Trans. Industrial Electron. 68 (2), 1401–1411. doi:10.1109/tie.2020.2970684

CrossRef Full Text | Google Scholar

Liu, Y., Han, X., Xing, Z., Liu, H., and Jiang, Z. (2024b). Research on control strategy of hybrid superconducting energy storage based on reinforcement learning algorithm. IEEE Trans. Appl. Supercond. 34, 1, 4. doi:10.1109/tasc.2024.3420314

CrossRef Full Text | Google Scholar

Liu, Y., Li, P., Xing, Z., Han, X., Fu, Q., and Jiang, Z. (2024a). Research on microgrid superconductivity-battery energy storage control strategy based on adaptive dynamic programming. IEEE Trans. Appl. Supercond., 34, 1, 4. doi:10.1109/tasc.2024.3420296

CrossRef Full Text | Google Scholar

Mahela, O. P., Sharma, Y., Ali, S., Khan, B., and Garg, A. R. (2021). Voltage-based hybrid algorithm using parameter variations and stockwell transform for islanding detection in utility grids. Informatics 8 (2), 21. doi:10.3390/informatics8020021

CrossRef Full Text | Google Scholar

Maresch, K., Marchesan, G., and Freitas-Gutierres, L. F. (2021). Passive islanding detection based on angular velocity harmonic patterns with perceptron neural network. IEEE Lat. Am. Trans. 19 (10), 1665–1673. doi:10.1109/tla.2021.9477269

CrossRef Full Text | Google Scholar

Miller, D., Mirzaeva, G., Townsend, C. D., and Goodwin, G. C. (2021). The use of power line communication in standalone microgrids. IEEE Trans. Industry Appl. 57 (3), 3029–3037. doi:10.1109/tia.2021.3057343

CrossRef Full Text | Google Scholar

Mohanty, S. R., Kishor, N., Ray, P. K., and Catalão, J. P. S. (2012). “Islanding detection in a distributed generation based hybrid system using intelligent pattern recognition techniques,” in 2012 3rd IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe). IEEE, 1–15. doi:10.1109/ISGTEurope.2012.6465689

CrossRef Full Text | Google Scholar

Özcanlı, A. K., and Mustafa, B. (2022). A novel Multi-LSTM based deep learning method for islanding detection in the microgrid. Electr. Power Syst. Res. 202, 107574. doi:10.1016/j.epsr.2021.107574

CrossRef Full Text | Google Scholar

Panigrahi, B. K., Bhuyan, A., Shukla, J., Ray, P. K., and Pati, S. (2021). A comprehensive review on intelligent islanding detection techniques for renewable energy integrated power system. Int. J. Energy Res. 45(10): 14085–14116. doi:10.1002/er.6641

CrossRef Full Text | Google Scholar

Papia, R., Reddy, S. S., and Monalisa, B. (2022). Two accurate hybrid islanding detection schemes for distribution network. J. Intelligent and Fuzzy Syst. 42 (2), 755–766. doi:10.3233/jifs-189746

CrossRef Full Text | Google Scholar

Patnaik, B., Mishra, M., and Jen, R. K. (2021). Variational mode decomposition-subspace-K-nearest neighbour based islanding detection in distributed generation system. Electr. energy Syst. 6 (31), e12490. doi:10.1109/APSIT52773.2021.9641279

CrossRef Full Text | Google Scholar

Raza, S., Mokhlis, H., Arof, H., Laghari, J. A., and Wang, L. (2015). Application of signal processing techniques for islanding detection of distributed generation in distribution network: a review. Energy Convers. Manag. 96, 613–624. doi:10.1016/j.enconman.2015.03.029

CrossRef Full Text | Google Scholar

Reddy, C. R., Reddy, K. H., and Goud, B. S. (2021). “A deep learning approach for islanding detection of integrated DG with CWT and CNN,” in Proc. Of the international conf. On sustainable energy and future electric transportation (SEFET). Hyderabad, India, 1–7.

Google Scholar

Ribeiro, P. F., Duque, C. A., Ribeiro, P. M., and Cerqueira, A. S. (2013). Power systems signal processing for smart grids. New York: Wiley.

Google Scholar

Sankar, A., and Sunitha, R. (2021). Synchrophasor data driven islanding detection, localization and prediction for microgrid using energy operator. IEEE Trans. Power Syst. 36 (5), 4052–4065. doi:10.1109/tpwrs.2021.3060763

CrossRef Full Text | Google Scholar

Tian, C., Xu, Y., Zuo, W., Lin, C. W., and Zhang, D. (2021). Asymmetric CNN for image superresolution. IEEE Trans. Syst. Man, Cybern. Syst., 1–13. doi:10.1109/TSMC.2021.3069265

CrossRef Full Text | Google Scholar

Wang, G., Gao, F., Liu, J., Li, Q., and Zhao, Y. (2020). Design consideration and performance analysis of a hybrid islanding detection method combining voltage unbalance/total harmonic distortion and bilateral reactive power variation. CPSS Trans. Power Electron. Appl. 5 (1), 86–100. doi:10.24295/cpsstpea.2020.00008

CrossRef Full Text | Google Scholar

Wang, M., Wang, P., Wu, L., Yang, R., Feng, X., Zhao, M., et al. (2022). Criteria for assessing carbon emissions peaks at provincial level in China. Adv. Clim. Change Res. 13 (1), 131–137. doi:10.1016/j.accre.2021.11.006

CrossRef Full Text | Google Scholar

Wang, X., Mao, D., and Li, X. (2021). Bearing fault diagnosis based on vibro-acoustic data fusion and 1D-CNN network. Measurement 173, 108518. doi:10.1016/j.measurement.2020.108518

CrossRef Full Text | Google Scholar

Xu, H., Tian, Y., Ren, H., and Liu, X. (2024). A lightweight channel and time attention enhanced 1D CNN model for environmental sound classification. Expert Syst. Appl. 249: 123768. doi:10.1016/j.eswa.2024.123768

CrossRef Full Text | Google Scholar

Yan, X., Yu, F., Xiong, X., Huang, Q., and Zhou, Q. (2022). A novel microgrid islanding detection algorithm based on a multi-feature improved LSTM. Energies 15 (8), 2810. doi:10.3390/en15082810

CrossRef Full Text | Google Scholar

Yin, J., Chen, X., Li, S., Shao, L., Li, J., and Liu, H. (2021). Singal denoising based on optimized VMD and NLM. Comput. Eng. Des. 42 (4), 1135–1142. doi:10.16208/j.issn1000-7024.2021.04.034

CrossRef Full Text | Google Scholar

Zeineldin, H. H., and Kirtley, J. L. (2009). Performance of the OVP/UVP and OFP/UFP method with voltage and frequency dependent loads. IEEE Trans. Power Deliv. 24 (2), 772–778. doi:10.1109/tpwrd.2008.2002959

CrossRef Full Text | Google Scholar

Zhang, Q. Q., and Wai, R. J. (2022). Distributed secondary control of islanded micro-grid based on adaptive fuzzy-neural-network-inherited total-sliding-mode control technique. Int. J. Electr. Power and Energy Syst. 137, 107792. doi:10.1016/j.ijepes.2021.107792

CrossRef Full Text | Google Scholar

Zhaoxia, X., Zhijun, G., Guerrero, J. M., and Hongwei, F. (2017). “SCADA system for islanded DC microgrids,” in Proc. Of the IECON 2017-43rd annual conference of the. Beijing, China: IEEE Industrial Electronics Society, 2669–2674.

CrossRef Full Text | Google Scholar