- 1State Grid TaiZhou Power Supply Company, Taizhou, China
- 2State Grid ZheJiang Electric Power Corporation, Hangzhou, China
In order to accurately describe the impact of the volatility and randomness of renewable energy output power on the operation of industrial park microgrids, a data-driven robust optimization method for industrial park microgrids is proposed. Firstly, based on the traditional interval set, the uncertain parameters of renewable energy output are modeled using a polyhedral set. Then, an ellipsoidal uncertainty set is established using historical data of renewable energy output. By connecting high-dimensional ellipsoidal vertices, a data-driven convex hull polyhedron set is established. Then, the uncertain parameters are better enveloped by scaling the convex hull set. A data-driven robust optimization model for industrial park microgrid was further established, and the column and constraint (C&CG) generation algorithm was used to solve the model. Finally, simulation comparisons were conducted through examples, and the results showed that the data-driven industrial park microgrids robust optimization method can reduce conservatism and improve the robustness of optimization results, demonstrating the effectiveness of the proposed method.
1 Introduction
With the increasingly prominent environmental and climate issues caused by excessive reliance on traditional fossil fuels, accelerating energy transition and sustainable development on a global scale has become a widely accepted consensus (Farh et al., 2024). To address the challenges of energy supply diversity and the intermittency of renewable energy sources, the industrial park microgrids featuring complementary and coupled forms of multiple energy supplies has emerged (Ishaq and Dincer, 2024). However, due to the instability of renewable energy outputs, power generation is affected by various factors such as climate, weather, and seasons, leading to significant fluctuations in power supply. These fluctuations can potentially trigger instability or even collapse of the industrial park microgrids, posing significant challenges to its safety and stability (Poodeh et al., 2025).
Existing research on the industrial park microgrids operation planning focuses on energy utilization efficiency and enhancing system stability. For instance, in Arooj (2024), system stability is improved by adopting demand-side response under the premise of considering flexible resources. In Rezazadeh and Avami (2024), a comprehensive energy system with detailed power-to-gas conversion and carbon cycling is established through the utilization of the carbon trading market. In Rahman et al. (2025), the grid partitioning of the integrated energy system is optimized by taking into account the characteristics of the load, thereby achieving cost reduction. Synthesizing these studies, there is a noticeable lack of consideration given to the uncertainty of renewable energy output.
To address the issue of uncertainty in renewable energy output, existing uncertainty optimization methods are mainly categorized into two types: stochastic optimization methods (Davidsdottir et al., 2024; Son and Kim, 2024; Aliasghar et al., 2022) and robust optimization methods (Vulusala and Madichetty, 2018; Stewart and Bingham, 2016). Robust optimization methods typically use a set-based approach to describe the distribution range of uncertain parameters. Unlike stochastic methods, robust optimization does not require the probability distribution of uncertain parameters and avoids the high-dimensional problems introduced by numerous scenarios. Consequently, it has gained increasing attention in the optimal operation of industrial park microgrids.
To enhance the reliability of robust optimization results and describe the correlations among uncertain parameters, recent studies have employed historical data of uncertain variables to explore the relationships between the variations of random variables, leading to the proposal of data-driven uncertainty sets (Sulaiman et al., 2024; Freitas et al., 2007; Ibraheemi and Janabi, 2024). For instance (Zhang et al., 2024a), constructed the uncertainty of photovoltaic power generation using historical data from smart meters and phasor measurement units to solve the problem of voltage regulation (Zhang et al., 2024b). constructed an uncertainty set using historical vehicle travel data to analyze the impact of large-scale transportation electrification on power systems (Lorca and Sun, 2015). established a polyhedral uncertainty set based on historical wind power data for economic dispatch modeling, analysis, and optimization (Jalilvand-Nejad et al., 2016). Proposed a correlated polyhedral uncertainty set model by bending the boundaries of a polyhedral set through mathematical analysis, building on the polyhedral set approach (Hamed and Rasoul, 2021). further refined the approach of Jalilvand-Nejad et al. (2016) by constructing a generalized correlated polyhedral uncertainty set model, allowing the polyhedral set to better envelop the range of uncertain parameters (Degefa et al., 2015). Constructed an ellipsoidal set to describe photovoltaic (PV) output and proposed an affine adjustable robust optimization strategy for active distribution networks. Although the ellipsoidal set effectively considers the correlations among uncertain parameters, its nonlinear structure increases the difficulty of solving the model. While Lorca and Sun (2015), Jalilvand-Nejad et al. (2016), Hamed and Rasoul (2021), and Degefa et al. (2015) consider the correlations within the uncertainty sets, the broader coverage of the uncertainty sets they establish can lead to increased conservatism in decision-making.
In addition to polyhedral and ellipsoidal sets, another common method is constructing uncertainty sets based on extreme scenarios. In Moradian et al. (2024) and Akter et al. (2025), historical data is first selected to form the uncertainty set. Then, extreme scenarios are identified based on the historical data, and convex hull sets are constructed from these scenarios. An appropriate scaling factor is introduced to cover all historical data, and finally, a robust optimization model based on extreme scenarios is established. The method in Ayene and Yibre (2024) and Bifei et al. (2022) does not predefine the shape of the uncertainty set but represents it as the convex hull of historical scenarios. These studies have made improvements regarding the conservativeness of polyhedral sets. However, although the uncertainty sets based on extreme scenarios can address the conservatism issue, they have a large number of vertices, making them difficult to solve. Therefore, this paper proposes a data-driven convex hull uncertainty set model. This model can not only reduce the conservatism of the solution but also decrease the difficulty of solving.
Against this research backdrop, considering the lack of attention to uncertain energy inputs in industrial park microgrids, this paper proposes a data-driven robust optimization method for industrial park microgrids. First, traditional polyhedral set modeling is conducted based on interval sets. Then, ellipsoidal sets are constructed based on historical scenarios, and the vertices of the ellipsoids are connected to form convex hull polyhedral sets. Finally, the constructed convex hull set is scaled to cover all historical scenarios. Furthermore, the data-driven convex hull model is embedded into the robust optimization model of the industrial park microgrids. The effectiveness of iu-the proposed method is verified through a case study of an integrated energy system in a specific region.
This paper will mainly make contributions in the following aspects:
1. In view of the current situation that the integrated energy system insufficiently considers the injection of uncertain energy sources, a data-driven robust optimization method for industrial park microgrids is proposed.
2. Aiming at the deficiencies of traditional uncertain set modeling, traditional polyhedron set modeling is first carried out on the interval set. Then, an elliptical set is constructed based on historical scenarios. Subsequently, the vertices of the ellipse are connected to construct a convex hull polyhedron set, and all historical scenarios are covered by scaling, thus establishing a unique data-driven modeling method.
3. The well-constructed data-driven convex hull set model is successfully embedded into the robust optimization model of the industrial park microgrids. Moreover, with the help of an example of an industrial park microgrid in a certain region, the effectiveness of the proposed method is verified.
The rest of this article is organized as follows: Section 2 introduces the different uncertain set modeling. The industrial park microgrid optimization model is introduced in Section 3. In Section 4, the specific objective function and constraints is presented. Section 5 studies the robust optimization method for microgrid in industrial park. Finally, Section 6 concludes.
2 Uncertain set modeling
2.1 Traditional uncertain set modeling
In this paper, the budget uncertainty set U is used to express the range of fluctuations in the magnitude of PV as well as wind power output. The specific expression is shown in Equation 1:
where
When there is no spatiotemporal correlation between uncertain variables, to better represent the range of variation of uncertain variables, this paper first characterizes them using traditional box sets and polyhedral sets, as shown below.
2.1.1 Box set
The specific expression for a box set can be given as:
where
From Equation 2, it can be seen that the box set is merely an interval representation of the uncertain variable, and under normal circumstances, the values are often taken at the boundaries. However, since the extreme conditions corresponding to the boundary values have a lower probability of occurrence, the box set fails to accurately represent most other cases. Therefore, a polyhedral set is often required.
2.1.2 Polyhedral set
The specific expression is shown in Equation 3:
where
2.2 Data-driven modeling of uncertain set
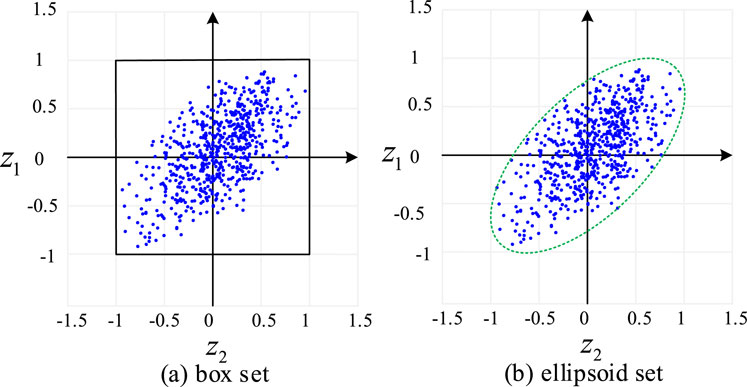
When there is spatiotemporal correlation among uncertain parameters, envelope lines can be adopted to represent different sets based on the scatter plots formed by the historical data of uncertain renewable energy output. Figure 2 illustrates the difference in envelope ranges when using box sets and ellipsoid sets.
As can be seen in Figure 2a, the box set envelopes all possible outcomes of distributed PV and wind power generation. However, due to the inherent spatiotemporal correlation of distributed PV at different times and locations, the PV output data predominantly clusters around the y = x and y = −x function lines. In this scenario, using a box set to describe the uncertainty of PV output may lead to overly conservative optimization solutions, since the box set not only encompasses all possible fluctuations but also covers areas with low probability of occurrence, which are essentially blank spaces. Therefore, it is necessary to adopt a more suitable modeling approach for uncertain sets.
2.2.1 Ellipsoid set
The specific expression is shown in Equation 4:
where
As illustrated in Figure 2b, the ellipsoid set, similar to the box set, envelopes all possible outcomes of distributed power generation. Unlike the box set, however, the ellipsoid set reduces the envelopment of blank areas with low probability of fluctuation occurrence, thereby decreasing the conservativeness of the decision results. However, due to the quadratic form of the ellipsoid set’s expression, it introduces complexity in the robust optimization process, increasing the difficulty of the solution.
2.2.2 Generalized convex hull set
Building upon this (Moradian et al., 2024), proposed a generalized convex hull set, which not only effectively reduces the conservativeness of optimization outcomes but also avoids the introduction of quadratic forms during the modeling process. Thus, based on Moradian et al. (2024), this paper constructs a data-driven uncertain set, with the modeling process illustrated in Figure 3.
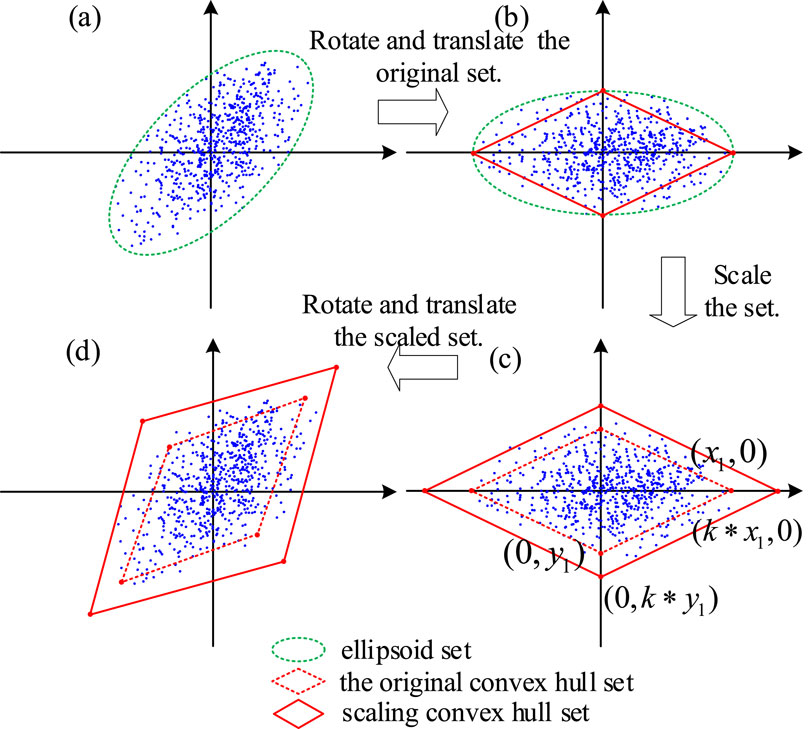
Figure 3. The modeling process for the convex hull uncertainty set (parts (a–d) illustrate key transformation steps).
Step (1): Firstly, construct a high-dimensional ellipsoidal uncertainty set that covers all historical data fluctuations with minimal volume, as illustrated in Figure 3a. The specific representation is given by Equation 5, which is:
Step (2): On the basis of the original high-dimensional ellipsoid, perform an orthogonal decomposition of the positive definite matrix
where
Given the diagonal matrix
where
Step (3): Due to the high-dimensional linear polyhedral set obtained from step 2, a small number of data points fall outside the envelope. Therefore, a scaling process is necessary for the original set, as shown by the solid lines in Figure 3c. After scaling, the vertices of the high-dimensional linear polyhedron are shown in Equation 9:
At this point, the scaled high-dimensional linear polyhedral uncertainty set
where
The scaling factor influences the degree to which the convex hull set envelops data points. When
Step (4): Rotate and translate the scaled high-dimensional linear polyhedron so that it conforms to the original data points’ range. From Equation 7, it is known that after rotation and translation, the high-dimensional linear polyhedral uncertainty set
In summary, when the box set is used to describe the fluctuation of photovoltaic output, because it is an interval set, as shown in the black box square box line in Figure 4. Although it completely envelopes all the possibilities of photovoltaic output, due to the existence of a large number of blank areas, the results obtained by using this set are conservative to a certain extent. When the convex hull set is used, it is shown in the color diamond box in Figure 4. Since it is connected by the endpoints of the elliptical set and the polyhedron set obtained by scaling, it has a good ability to describe the historical output points of the photovoltaic, and reduces the envelope of the blank area while completely enveloping. This solves the disadvantage of high conservatism brought by the box set.
3 Industrial park microgrid optimization modeling
3.1 Industrial park microgrid system
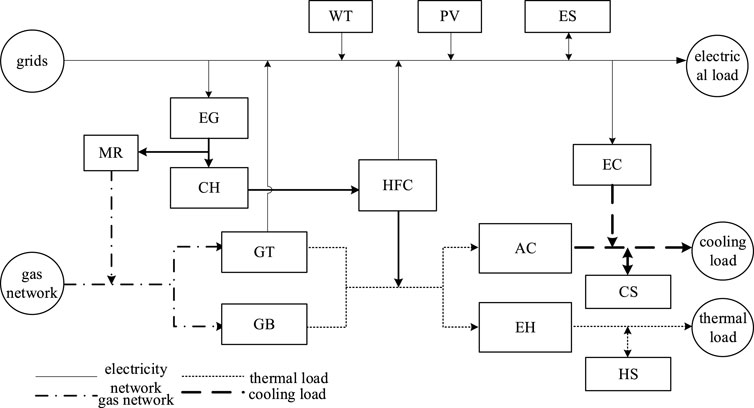
The power-to-gas industrial park microgrid system is an integrated system that combines electricity, thermal energy, and gas energy, typically involving various energy conversion and utilization technologies, aiming to achieve efficient energy utilization and complementarity.
The typical power-to-gas industrial park microgrid system established in this paper consists of the following components, and the industrial park microgrid system diagram is shown in Figure 5.
Renewable energy facilities, including solar photovoltaic (PV) systems and wind turbine generation (WT) systems, which primarily convert renewable energy such as solar and wind power into electricity to supply electric loads; energy storage facilities, including battery energy storage systems (ES), heat storage systems (HS), and cold storage systems (CS), which not only provide energy to the system but also store excess energy for future use; heating equipment, such as gas boilers (GB) and excess heat boilers (EH); cooling equipment, such as absorption refrigerators (AC); and various energy conversion equipment, including gas turbines (GT), electroliers (EG), methane reactors (MR), hydrogen storage tanks (CH), hydrogen fuel cells (HFC), and electric chillers (EC).
3.2 Demand-side response model
In order to better accommodate clean energy and enhance the stability and economic efficiency of the system, a demand-side response model needs to be established on the load side. The model is constructed as follows:
where
3.3 IDR model
However, the demand-side response model only focuses on making response strategies for a single type of demand-side resource, in the power-to-gas industrial park microgrid system, due to the coordinated operation of multiple energy forms and equipment, the demand-side response model is difficult to coordinate the operation of multiple types of energy and equipment, an efficient adjustment model is needed to manage and optimize the operation of the system. Therefore, this paper adopts the Integrated Demand Response (IDR) model.
where
4 Objective function and constraints
4.1 Objective function
In this paper, we consider the electricity-gas multi-energy complementary microgrid model that minimizes the integrated cost of energy purchase cost, operation and maintenance cost, IDR cost, and standby cost, and is shown in Equation 18:
where
where
where
where
4.2 Constraint condition
4.2.1 Energy balance constraints
The expression for the electrical power balance of the system is shown in Equation 23:
where
The gas balance expression for the system is shown in Equation 24:
where
The heat balance expression of the system is shown in Equation 25:
where
The cold balance expression of the system is shown in Equation 26:
where
4.2.2 Energy coupling constraints
Electricity - gas conversion mainly includes two aspects of electricity hydrogen and hydrogen methanization, the system of electricity - gas conversion coupling constraints expression is shown in Equation 27:
where
The heat-cooling conversion is mainly to convert part of the input thermal power of the system into cold power, and the expression of the coupling constraints of heat-cooling conversion of the system is as follows
where
4.2.3 Operation constraints of energy supply equipment
The operation constraints of each device in the system are expressed as Equations 29, 30
where
4.2.4 Energy storage operation constraints
where
4.2.5 Hydrogen storage tank operation constraints
Similar to the battery energy storage, the hydrogen storage tank can also be regarded as an energy storage device.
where
4.2.6 Power exchange constraints in large power grids
where
4.2.7 Constraint on reserve capacity
In order to ensure the reasonable reserve capacity of the system, the constraints are set as Equations 41–43.
where
4.2.8 Constraint on output of renewable energy
The constraints of renewable energy are as Equations 44, 45.
5 Robust optimization method for microgrid in industrial park
5.1 Robust optimization model establishment
Let the renewable energy constraint variable of the system be vector
where
For a two-stage robust optimization model like Equation 47, since it contains both continuous variables and integer variables, and the second stage of the model contains uncertain parameter
5.2 C&CG iterative solution method
The master-slave problem corresponding to Equation 47 is modeled as
The main problem MP1 corresponding to Equation 48 is solved first, at this point, MP1 belongs to the mixed-integer second-order cone programming problem. After solving the first-stage variable solution
5.2.1 Sub-problem solution method
Equation 49 is a max-min optimization problem, therefore, in this paper, the pairwise theorem is used to convert the inner min problem of Equation 49 into its pairwise form to merge it into a maximization problem, which is shown in the form of Equation 50.
in Equation 50, there exists a bilinear term
where MP2 and SP2 are used to solve the upper and lower bounds of Equation 38, respectively,
6 Example analysis
This section is validated using the IEEE-RTS 24 node example system. To reflect the planning requirements of the power generation and transmission system, the load will be increased by 1.4 times. At the same time, 400 MW wind farms were connected at nodes 3, 6, 15, 18, and 23, respectively. According to Equation 28, the predicted wind power output value is about 115 MW, and the fluctuation of wind power output is ±30% of the predicted value. The typical value of sub transient reactance for all units is 0.1 (standard value). This example has two voltage levels, namely, 138 kV and 230 kV, and the maximum allowable current of the circuit breaker is 31.5 kA and 35 kA, respectively. The abandonment cost and load shedding cost are $150/(MWh) and $5,000/(MWh) respectively. This article considers N-1 random faults in power generation and transmission, and the convergence threshold of the C&CG algorithm ζ Set to 0.001.
6.1 Example setting
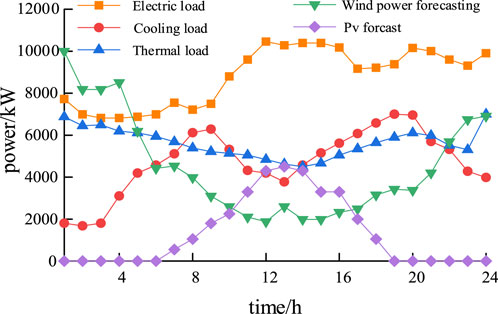
In order to verify the effectiveness of the data-driven industrial park microgrids robust optimization method established in this paper, this section cites a 24-h operation example of an industrial park in Hubei Province for verification. The equipment installed in the industrial park includes wind power, photovoltaic, gas boiler and waste heat boiler. Absorption chillers, gas turbines, electroliers, methane reactors, hydrogen storage tanks, hydrogen fuel cells, electric chillers, energy storage systems, etc. Among them, the wind power, photovoltaic prediction and load size of the system are shown in Figure 6. The operating parameters of each device are shown in. The operating parameters of each device are shown in Schedule A1. According to the calculation method given in (Hamed and Rasoul, 2021), the value
6.2 Result analysis and verification
6.2.1 The influence of scaling factor k on the optimization results
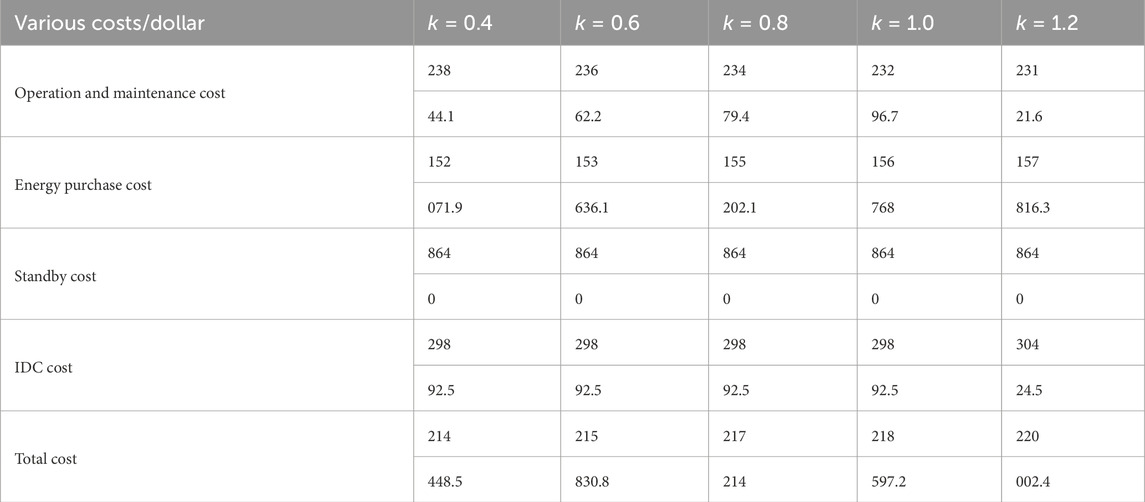
The impact of the scaling factor on the robust optimization of the industrial park microgrid is shown in Table 2. The size of the scaling factor determines the extent to which the constructed convex hull set covers historical data. As seen from Table 2, with the increase of the scaling factor, the system’s operational cost gradually decreases, while the energy purchase cost continues to increase. This is because the increase in the scaling factor expands the envelope range of the convex hull uncertainty set over the historical output data, meaning that the fluctuation range of renewable energy output becomes larger, making the worst-case scenario more likely to occur. When volatile renewable energies such as distributed photovoltaics and wind power continuously inject into the distribution network, in order to maintain supply-demand balance and reduce disturbances caused by the injection of uncertain energy, the system needs to filter out a large portion of the power injected by distributed photovoltaics and wind power. This leads to a reduction in the maintenance cost of photovoltaic and wind power equipment, and as a result, the overall operational cost decreases. Meanwhile, since the injection of distributed energy is reduced, more injection power from the grid is needed to meet the system’s electricity supply, thereby gradually increasing the energy purchase cost. Reserve cost refers to the margin cost incurred to account for the system’s response to possible random events and depends on the system’s contingency plan for the worst-case scenario. Therefore, regardless of changes in the scaling factor, the reserve cost shows little variation. Similar to the reserve cost, the IDR (Interruptible Demand Response) cost is an added cost to enhance the system’s stability margin. When the scaling factor is less than or equal to 1, the convex hull set does not envelop the extreme worst-case conditions, and thus the IDR cost remains unchanged. However, when the scaling factor exceeds 1, the convex hull set covers all possible scenarios, including the worst-case scenario. To improve the overall efficiency of the system, users need to appropriately shed load, which results in an increase in IDR cost.
6.2.2 The influence of robust adjustment coefficient β on the optimization results
Figure 7 demonstrates the influence of the robust adjustment coefficient β on the results of the robust optimization of the industrial park microgrid. From the figure, it can be seen that as the robust adjustment coefficient increases, each of the costs changes more or less, except for the standby cost, which is unaffected by system changes, which stays constant at $8640. When the robust adjustment coefficient of the system is small, the uncertain energy injected into the system at this time will be approximated as deterministic energy, the various equipment of the system will operate stably, and the photovoltaic and wind power equipment of the system will operate at full efficiency, so the operation and maintenance cost is the largest, and at the same time, due to the injection of the deterministic energy, the system purchased energy from the port decreases, so the system’s purchased energy cost is the smallest, and with the increase in the robust adjustment coefficient, this uncertainty energy injection will rise and the amount of energy purchased by the system from the port will keep on rising, which in turn leads to the rise of the system’s energy purchase cost and the decrease of the O&M cost. For the IDR cost, when
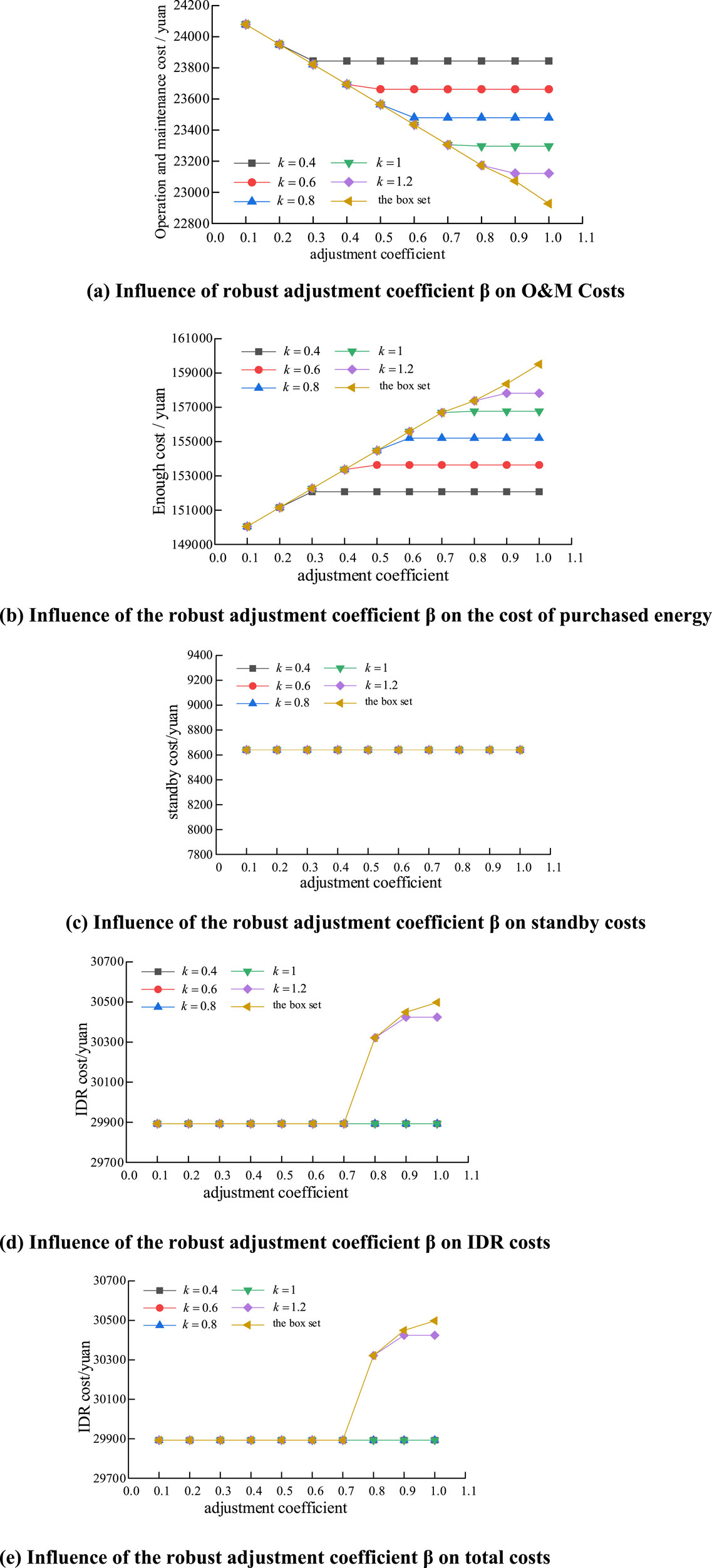
Figure 7. Influence of robust adjustment coefficient β on each cost. (a) Influence of robust adjustment coefficient β on O&M costs. (b) Influence of the robust adjustment coefficient β on the cost of purchased energy. (c) Influence of the robust adjustment coefficient β on standby costs. (d) Influence of the robust adjustment coefficient β on IDR costs. (e) Influence of the robust adjustment coefficient β on total costs.
As the robust adjustment coefficient increases, the magnitude of the change in the cost of purchased energy and O&M cost will remain stable when the convex packet ensemble is used, specifically, when the deflation multiplier increases from 0.4 to 1.2, the magnitude of the change in the cost of purchased energy and O&M cost will be stabilized at the time when the robust adjustment coefficient is equal to 0.3, 0.4, 0.6, 0.7, and 0.8, which is related to the renewable energy equipment’s power output situation. When β is small, the system is poorly adapted to the renewable energy perturbation and the cost does not change much no matter what kind of ensemble is used, on the contrary, when β is large, the system is better adapted to the distributed PV perturbation. However, when the convex packet ensemble is used, the envelope range of the convex packet ensemble is different due to different deflation multiples. When the deflation multiplier
6.2.3 The influence of the three aggregations on individual costs
The effects of the three uncertainty sets on each cost are further compared when the deflation multiplier
6.2.4 Output of each device in three pools
Figure 8 gives the output of each device at the electric power balance under the three uncertainty sets. From the figure, it can be seen that in the multi-energy complementary microgrid system, the individual devices coordinate with each other and work together to maintain the electric power balance. In the PV big hairy time period (12–16 h), the system purchases the lowest electric power from the ports, the polyhedral ensemble is the second, and the box ensemble is the most when the convex packet ensemble is used, which is the same as the conclusion obtained in the previous paper, and further verifies that the use of the convex packet ensemble enhances the robustness of the solution results and reduces the conservatism.
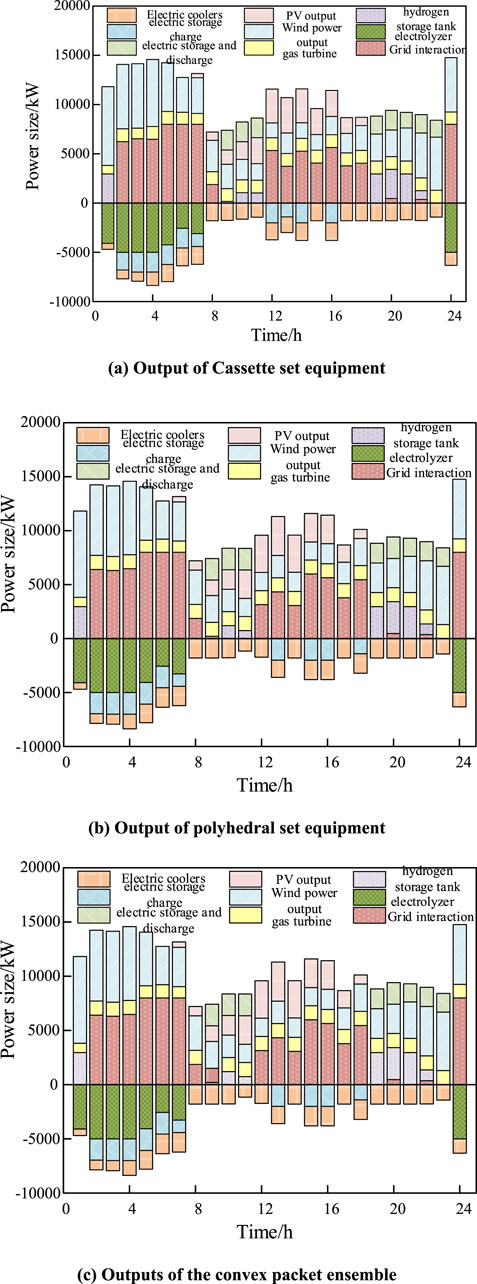
Figure 8. Output of each device under three aggregations. (a) Output of Cassette set equipment. (b) Output of polyhedral set equipment. (c) Outputs of the convex packet ensemble.
6.2.5 Computational efficiency analysis
To verify the computational efficiency of the convex hull uncertainty set, we supplemented simulation analyses comparing the convex hull set method with scenario-based stochastic optimization in the revised manuscript. The comparative results are shown in the table below.
As shown in Table 4, when handling problems of the same scale, the convex hull set method proposed in this paper exhibits significant computational efficiency advantages over scenario-based stochastic optimization. Even as the problem scale increases, the convex hull set method still outperforms scenario-based stochastic optimization in computational efficiency.
7 Conclusion
In this paper, a research model of the industrial park microgrids robust optimization method based on data-driven is constructed and solved by C&CG algorithm. Finally, by comparing the industrial park microgrids robust optimization methods under different sets, the simulation results show that:
1. Compared with the interval set which can only take extreme conditions at the boundary, the polyhedron set has a better envelope for the range of uncertain parameters, which makes the operation result more robust.
2. When the robust adjustment coefficient is the same, the total system cost of using the convex hull set is 0.71% lower than that of the box set and 0.53% lower than that of the polyhedron set. For the convex hull set with different scaling multiples, this not only increases the envelope of the region with higher distribution of uncertain parameters, but also reduces the envelope of the blank region with low probability. Therefore, compared with the polyhedral set, the industrial park microgrids robust optimization method using the convex hull set is less conservative and more robust.
In the future, we will explore the comparative analysis between convex hull sets and advanced data-driven methods such as distributionally robust optimization and machine learning-based uncertainty sets, with a view to providing more comprehensive and forward-looking research results for the field of multi-energy microgrid optimization.
Data availability statement
The original contributions presented in the study are included in the article/Supplementary Material, further inquiries can be directed to the corresponding author.
Author contributions
CR: Investigation, Methodology, Writing – original draft. LL: Investigation, Methodology, Writing – original draft. JL: Validation, Writing – review and editing. BJ: Validation, Writing – review and editing.
Funding
The author(s) declare that financial support was received for the research and/or publication of this article. This work is supported by Science and Technology Project of State Grid Zhejiang Electric Power Co., Ltd. (No. 5211TZ230002).
Conflict of interest
Authors CR, JL, and BJ were employed by State Grid TaiZhou Power Supply Company.
Author LL was employed by State Grid ZheJiang Electric Power Corporation.
The authors declare that this study received funding from State Grid Zhejiang Electric Power Co. The funder participated in the research design phase. During this phase, combining the actual operation requirements of industrial park microgrids, it put forward relevant suggestions on the research direction (e.g., the industrial load characteristics that need to be focused on in microgrid robust optimization) and the practicality of the technical framework.
Generative AI statement
The author(s) declare that no Generative AI was used in the creation of this manuscript.
Any alternative text (alt text) provided alongside figures in this article has been generated by Frontiers with the support of artificial intelligence and reasonable efforts have been made to ensure accuracy, including review by the authors wherever possible. If you identify any issues, please contact us.
Publisher’s note
All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fenrg.2025.1535211/full#supplementary-material
References
Akter, K., Rahman, M., Islam, R. M., Sheikh, M. R. I., and Hossain, M. (2025). Attack-resilient framework for wind power forecasting against civil and adversarial attacks. Electr. Power Syst. Res. 238, 238111065–111065. doi:10.1016/j.epsr.2024.111065
Aliasghar, B., Baseem, K., and Navid, P. (2022). Guest editorial: introduction to the special section on application of advanced machine/deep learning in electrical power and energy systems (VSI-mlep). Comput. Electr. Eng., 102. doi:10.1016/j.compeleceng.2022.108245
Arooj, Q. (2024). FedWindT: Federated learning assisted transformer architecture for collaborative and secure wind power forecasting in diverse conditions. Energy 309, 133072–133072. doi:10.1016/j.energy.2024.133072
Ayene, M. S., and Yibre, M. A. (2024). Wind power prediction based on deep learning models: the case of adama wind farm. Heliyon 10 (21), e39579. doi:10.1016/j.heliyon.2024.e39579
Bifei, T., Haoyong, C., and Xiaodong, Z. (2022). Two-stage robust optimization dispatch for multiple microgrids with electric vehicle loads based on a novel data-driven uncertainty set. Int. J. Electr. Power Energy Syst., 134. doi:10.1016/j.ijepes.2021.107359
Davidsdottir, B., Ásgeirsson, I. E., Fazeli, R., Gunnarsdottir, I., Leaver, J., Shafiei, E., et al. (2024). Integrated energy systems modeling with multi-criteria decision analysis and stakeholder engagement for identifying a sustainable energy transition. Energies 17 (17), 4266. doi:10.3390/en17174266
Degefa, M., Lehtonen, M., Millar, R., Alahäivälä, A., and Saarijärvi, E. (2015). Optimal voltage control strategies for day-ahead active distribution network operation. Electr. Power Syst. Res. 127, 12741–12752. doi:10.1016/j.epsr.2015.05.018
Farh, H. M. H., Shamma'a, A. A. A., Alaql, F., Omotoso, H. O., Alfraidi, W., and Mohamed, M. A. (2024). Optimization and uncertainty analysis of hybrid energy systems using monte carlo simulation integrated with genetic algorithm. Comput. Electr. Eng. 120 (PC), 109833. doi:10.1016/j.compeleceng.2024.109833
Freitas, W., Asada, N. E., Zobaa, F. A., and McConnach, J. S. (2007). Policy and economic issues of electrical power and energy systems. Int. J. Glob. Energy Issues 27 (3), 253–261. doi:10.1504/ijgei.2007.014347
Hamed, D., and Rasoul, S. (2021). A new correlated polyhedral uncertainty set for robust optimization. Comput. Industrial Eng., 157. doi:10.1016/j.cie.2021.107346
Ibraheemi, A. Z., and Janabi, A. S. (2024). Sustainable energy: advancing wind power forecasting with grey wolf optimization and GRU models. Results Eng. 24, 102930–102930. doi:10.1016/j.rineng.2024.102930
Ishaq, M., and Dincer, I. (2024). Development of a novel renewable energy-based integrated system coupling biomass and H2S sources for clean hydrogen production. Renew. Energy 237 (PC), 121642. doi:10.1016/j.renene.2024.121642
Jalilvand-Nejad, A., Shafaei, R., and Shahriari, H. (2016). Robust optimization under correlated polyhedral uncertainty set. Comput. Industrial Eng., 92. doi:10.1016/j.cie.2015.12.006
Lorca, A., and Sun, X. A. (2015). Adaptive robust optimization with dynamic uncertainty sets for multi-period economic dispatch under significant wind. IEEE Trans. Power Systems: A Publ. Power Eng. Soc. 30 (4), 1702–1713. doi:10.1109/tpwrs.2014.2357714
Michos, D., Catthoor, F., Foussekis, D., and Kazantzidis, A. (2024). Ultra-short-term wind power forecasting in complex terrain: a physics-based approach. Energies 17 (21), 5493. doi:10.3390/en17215493
Moradian, S., Gharbia, S., and Nezhad, M. M. (2024). Enhancing the accuracy of wind power projections under climate change using geospatial machine learning models. Energy Rep., 123353–123363. doi:10.1016/j.egyr.2024.09.007
Nayak, K. A., Sharma, C. K., Bhakar, R., and Tiwari, H. (2025). Probabilistic online learning framework for short-term wind power forecasting using ensemble bagging regression model. Energy Convers. Manag. 323 (PA), 119142. doi:10.1016/j.enconman.2024.119142
Poodeh, S. M., Hooshmand, A. R., and Khah, S. M. (2025). Reliability-constrained configuration optimization for integrated power and natural gas energy systems: a stochastic approach. Reliab. Eng. Syst. Saf. 254, 110600. doi:10.1016/j.ress.2024.110600
Rahman, J., Jacob, A. R., and Zhang, J. (2025). Multi-timescale power system operations for electrolytic hydrogen generation in integrated nuclear-renewable energy systems. Appl. Energy 377 (PA), 124346. doi:10.1016/j.apenergy.2024.124346
Rezazadeh, A. A., and Avami, A. (2024). An integrated policy approach for sustainable decarbonization pathways of energy system in a city under climate change scenarios. Energy Policy 195, 114394. doi:10.1016/j.enpol.2024.114394
Son, G. Y., and Kim, Y. S. (2024). Optimal planning and operation of integrated energy systems in South Korea: introducing a novel ambiguity set based distributionally robust optimization. Energy 307, 132503. doi:10.1016/j.energy.2024.132503
Stewart, P., and Bingham, C. (2016). Electrical power and energy systems for transportation applications. Energies 9 (7), 545. doi:10.3390/en9070545
Sulaiman, H. M., Mustaffa, Z., Saari, M. M., and Abas, M. F. (2024). Wind power forecasting with metaheuristic-based feature selection and neural networks. Clean. Energy Syst. 9, 100149. doi:10.1016/j.cles.2024.100149
Vulusala, V. S., and Madichetty, S. (2018). Application of superconducting magnetic energy storage in electrical power and energy systems: a review. Int. J. Energy Res. 42 (2), 358–368. doi:10.1002/er.3773
Zhang, Q., Bu, F., Guo, Y., and Wang, Z. (2024a). Tractable data enriched distributionally robust chance-constrained conservation voltage reduction. IEEE Trans. Power Syst. 39 (1), 821–835. doi:10.1109/tpwrs.2023.3244895
Keywords: industrial park microgrids, data-driven, robust optimization, convex hull set, column and constraint generation algorithm
Citation: Ru C, Li L, Lu J and Jiang B (2025) Data-driven industrial park microgrids robust optimization method. Front. Energy Res. 13:1535211. doi: 10.3389/fenrg.2025.1535211
Received: 27 November 2024; Accepted: 06 August 2025;
Published: 28 August 2025.
Edited by:
ZhaoYang Dong, City University of Hong Kong, Hong Kong SAR, ChinaReviewed by:
Qianzhi Zhang, Cornell University, United StatesJun Yang, Northeastern University, China
Copyright © 2025 Ru, Li, Lu and Jiang. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Chuanhong Ru, MTUyNzEwMjM3ODhAMTYzLmNvbQ==
 Chuanhong Ru
Chuanhong Ru Lei Li2
Lei Li2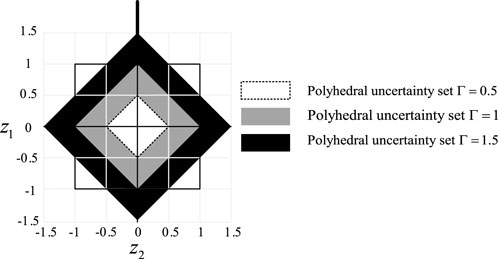
![Scatter plot with blue points and multiple polygons centered on the origin. Polygons represent different convex polyhedrons: solid black for \( k_{\text{min}} \), solid grey for \( k=1 \), dashed for \( k=[0,1] \), and dotted for \( k=[1, k_{\text{min}}] \). The box set is in a bold black outline. Axes labeled \( Z_1 \) and \( Z_2 \) from \(-1.5\) to \(1.5\).](https://www.frontiersin.org/files/Articles/1535211/fenrg-13-1535211-HTML-r1/image_m/fenrg-13-1535211-g004.jpg)