A coordinated optimization model for analysis of electric vehicle acceptance capacity considering compensation units

Introduction: Promoting the adoption of Electric Vehicles (EVs) is widely recognized as an effective strategy for addressing environmental challenges. Consequently, the expansion of EV charging infrastructure is necessary to enhance the user experience and accommodate the increasing demand. However, without careful consideration of optimal site selection and capacity planning, the integration of EV charging loads may induce significant overcapacity and voltage fluctuating issues.

Methods: This paper presents a coordinated optimization model for assessing the integration acceptance capacity of EV charging loads within distribution networks. The model is based on linear power flow equations and incorporates the compensatory capabilities of the distribution network.

Results and discussion: A case study is conducted to evaluate the acceptance capacity of two distinct types of EV charging loads within the IEEE 33-bus benchmark network. Additionally, the paper examines the impact of various system expansion strategies on the acceptance capacity, considering the aggregation of different units. The results indicate that energy storage systems (ESSs) and static var generators (SVGs) exert the most significant influence on the network’s ability to accommodate EV charging loads.

1 Introduction

Carbon emissions have become a critical environmental concern, driving global efforts to mitigate their adverse impacts on climate change and public health. Increasing attention has been directed towards the development and promotion of EVs (Fesli and Ozdemir, 2024). The transition to EVs is considered a pivotal measure in reducing carbon footprints, as these vehicles provide a cleaner alternative to traditional fossil fuel-powered transportation. Powered by the electricity stored in batteries, EVs can significantly lower carbon emissions compared to internal combustion engine vehicles (Li et al., 2024). This reduction is particularly pronounced when accounting for well-to-wheel emissions, which encompass the entire lifecycle of energy production, distribution, and consumption. Furthermore, when EVs are charged using renewable energy sources, such as wind or photovoltaic (PV) power, carbon emissions can be reduced even further (Hung et al., 2014; Yadav et al., 2022). The integration of EVs with renewable energy sources presents a promising approach to achieving a sustainable transportation sector by minimizing dependence on non-renewable energy and reducing greenhouse gas emissions. Therefore, the operational requirements for smart grids are higher than those for existing distribution networks (Lei et al., 2024; Xu et al., 2024).

However, the large-scale integration of EV charging stations into the power grid may have significant implications for power system operations (Tu et al., 2019; Arya and Das, 2023). The sudden surge in charging demand can place considerable strain on the existing infrastructure, particularly if not managed effectively. When EV users concentrate their charging activities within a short time window, such as during evening hours after work, the charging load can peak, potentially resulting in voltage drops or even violations of voltage limits within a short time frame (Dias Vasconcelos et al., 2024; Jie et al., 2024). These fluctuations can undermine the stability and reliability of the power grid, highlighting the critical need for strategic planning and management of EV charging infrastructure.

To mitigate the impact of EV charging loads on the power system, it is essential to properly plan the capacity of EV charging stations integrated into the grid. Numerous studies have focused on the capacity design of EV charging stations. For example (Zhao et al., 2021), optimized the charging station capacity by considering the EV arrival and service rates to enhance the quality of service. Li et al. (2021) proposed a planning model that accounts for EV battery capacity, while (Bayram, 2022) introduced a capacity planning framework that incorporates the overstay behavior of EV users. Although these studies primarily address the characteristics of EV users, the impact on the power system itself is often overlooked. Liu et al. (2022) employed particle swarm optimization to calculate the acceptance capacity of EV charging loads in residential areas. Li et al. (2020) formulated an optimization problem with equilibrium constraints to consider energy coordination in the planning of EV charging stations. Cui et al. (2019) proposed a placement method for EV charging stations that considers the driving range of EV users. However, while these studies provide valuable insights, they do not fully address the contribution of compensation units in the integration of EV charging stations.

To address the challenges posed by EV charging loads, it is essential to integrate compensation units with fast and flexible response capabilities to support power system operations. Energy storage systems (ESS) are particularly well-suited for this purpose, as they can provide both active and reactive power compensations. During peak load periods, ESS can discharge stored energy to supply active power, while during load valley periods, it can consume active power to recharge its batteries (Kharrich et al., 2021). This bidirectional functionality enables ESS to effectively mitigate the compensation challenges associated with the integration of aggregated EV charging loads (Chen et al., 2018; Yan and Chen, 2023). In this way, the ESS could reduce the risks of overcapacity and voltage fluctuations effectively.

Recent studies on EV charging station planning, such as (Zhao et al., 2021; Li et al., 2021; Bayram, 2022), largely overlooked the impacts on the power system, while others, such as (Liu et al., 2022; Li et al., 2020; Cui et al., 2019), neglected the role of compensation units. The capacity assessment method proposed by the authors in (Dai et al., 2023) enables the IEEE 33 benchmark distribution network to accommodate a total of 1.2 MW of EV charging load capacity. The work in (Lepolesa et al., 2024), through optimization algorithms, increases the capacity of EV charging loads to 2.75 MW. To bridge these gaps, this study proposes a coordinated optimization model for analyzing EV charging load capacity, incorporating compensation units such as ESS, SVG, and PV power generation. The proposed model aims to provide distribution network managers with the maximum EV charging load access capacity on different buses, considering compensatory devices. It also analyzes the contribution of various compensatory devices to enhancing EV access capabilities, thereby assisting managers in the planning of the distribution network. Considering the limitations of the traditional power flow function in convex optimization frameworks, we employ the Branch Power Flow (BPF) function. The BPF equations are linear power flow equations based on phase angle relaxation and second-order conic relaxation. They focus on the relationship between the square of the node voltage magnitude and the power injections at each node (Farivar and Low, 2013a; Farivar and Low, 2013b). In the case studies, various scenarios are designed to evaluate the integration of ESS, SVG, PV power generation, and transmission line capacity, demonstrating the effectiveness of the proposed optimization model in addressing the complexities of EV integration. The main contributions of this paper were listed as follows,

1. A coordinated optimization model is proposed, utilizing linear power flow functions to accurately assess the maximum acceptance capacity of EV charging loads across different buses. This approach ensures the rapid calculation of the maximum accessible capacity for EV charging loads.

2. Voltage Violation and Compensation Units: The proposed model takes into account voltage violation constraints and incorporates the support provided by compensatory units, considering the synergistic effects between compensation systems within the optimization model. Consequently, the effectiveness of various compensatory devices (including ESS and SVG) can be quantitatively evaluated. The contribution of different compensatory devices to enhancing the accessible capacity of EVs is assessed in the case study analysis.

3. Evaluation of EV Acceptance Capacity: The system evaluates the acceptance capacity of electric vehicles under various operational scenarios, with particular attention to the differences in access capacity across different buses. Case study results are presented and discussed, leading to general conclusions regarding the operation of electric vehicles in the context of grid integration.

This paper is organized as follows: Section 2 presents the mathematical models for compensation units, while Section 3 introduces the proposed optimization model. In Section 4, case studies with various scenarios are conducted and discussed, using an enhanced IEEE 33-bus benchmark test system. Finally, Section 5 provides the concluding remarks.

2 Mathematical model

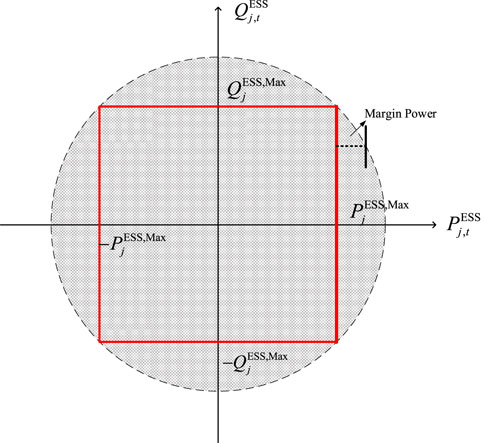
As previously mentioned, ESS can provide both active and reactive power compensation, with these output power variables constrained by its rated capacity. The operational boundary of ESS forms a circular region, as illustrated in Figure 1. However, since the circle boundary is nonlinear, an inscribed quadrilateral is used to approximate the circle, represented by the red line. The maximum values of active power and reactive power of ESS are denoted by $P_j^{\text{ESS},\mathrm{Max}}$ and $Q_j^{\text{ESS},\mathrm{Max}}$ respectively. The inscribed quadrilateral, with two boundaries parallel to the horizontal and vertical axes, allows for the decoupling of active and reactive power. The simplified ESS operational boundaries reduce the rated output power of the ESS, thereby allowing the ESS to provide more active power compensation during the actual operation of the power system. This approximation reveals that there is a margin in the output power, and in practical scenarios, limiting the power output may be more realistic and beneficial. Under conservative estimates, the simplified operational boundaries of the ESS have minimal significant impact on the analysis of EV integration capacity.

Figure 1

Figure 1. The operating boundary of ESS.

The ESS can operate either in a charging state or a discharging state. To represent these operational modes, two binary auxiliary variables are introduced. The mathematical model of the ESS can thus be expressed as Equations 1–4,

$B_{j,t}^{\text{ESS},\text{Cha}}+B_{j,t}^{\text{ESS},\text{Dis}}\le 1,\forall t\in T,\forall j(1)$

$0\le P_{j,t}^{\text{ESS},\text{Dis}}\le B_{j,t}^{\text{ESS},\text{Dis}}{P}_j^{\text{ESS},\mathrm{Max}},\forall t\in T,\forall j(2)$

$0\le P_{j,t}^{\text{ESS},\text{Cha}}\le B_{j,t}^{\text{ESS},\text{Cha}}{P}_j^{\text{ESS},\mathrm{Max}},\forall t\in T,\forall j(3)$

$0\le Q_{j,t}^{\text{ESS},\text{Dis}}\le Q_j^{\text{ESS},\mathrm{Max}},\forall t\in T,\forall j(4)$

where $P_{j,t}^{\text{ESS},\text{Dis}}$ and $P_{j,t}^{\text{ESS},\text{Cha}}$ represent the discharging and charging power of the ESS located at bus j during time interval t, respectively. Additionally, $Q_{j,t}^{\text{ESS},\text{Dis}}$ represents the reactive compensation power of the ESS. $B_{j,t}^{\text{ESS},\text{Cha}}$ and $B_{j,t}^{\text{ESS},\text{Dis}}$ are dimensionless variables denote the operational state of ESS.

Furthermore, when the ESS compensates for active power, the battery will be consumed, leading to a reduction in its SOC. Let $SO{C}_{j,t}^{\text{ESS}}$ denote the SOC of the ESS at bus j at time t, and let $E_j^{\text{ESS}}$ represent the rated capacity of the ESS. Let ${\eta }^{\text{Cha}}$ denote the charging efficiency of the ESS. Assuming that the output of the ESS, $P_{j,t}^{\text{ESS}}$, is positive when the ESS is discharging, the SOC constraints of ESS can be expressed as Equations 5, 6,

$SO{C}_{j,t+1}^{\text{ESS}}{E}_j^{\text{ESS}}=SO{C}_{j,t}^{\text{ESS}}{E}_j^{\text{ESS}}+P_{j,t}^{\text{ESS},\text{Cha}}{\eta }^{\text{Cha}}\Delta t-P_{j,t}^{\text{ESS},\text{Dis}}\Delta t,\forall t\in T,\forall j(5)$

$0\le SO{C}_{j,t}^{\text{ESS}}\le 1,\forall t\in T,\forall j(6)$

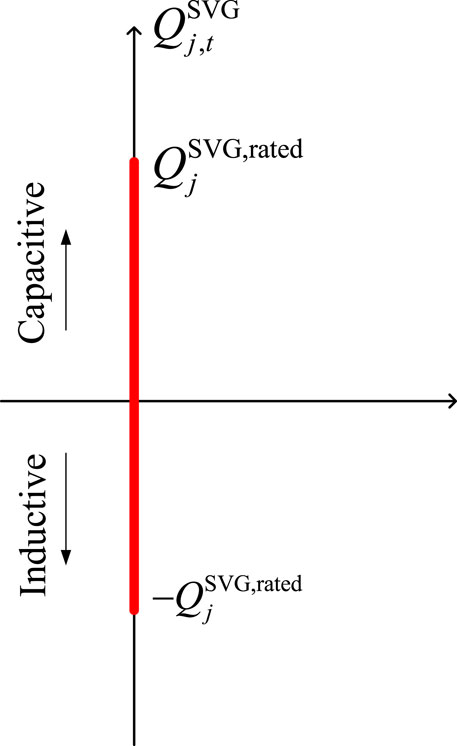
The SVG is capable of providing continuously adjustable reactive power, both inductive and capacitive. However, the output power must be constrained within the rated power range. It is assumed that a positive value represents capacitive reactive power. The operational boundary of the SVG is illustrated in Figure 2.

Figure 2

Figure 2. The operating boundary of SVG.

Let $Q_j^{\text{SVG},\text{rated}}$ denote the rated power of the SVG at bus j, and let $Q_{j,t}^{\text{SVG}}$ represent the output power of the SVG during time interval t. The mathematical model of the SVG can be described as Equation 7,

$-Q_j^{\text{SVG},\text{rated}}\le Q_{j,t}^{\text{SVG}}\le Q_j^{\text{SVG},\text{rated}},\forall t\in T,\forall j(7)$

3 Optimization model

In this paper, a coordinated optimization model is proposed for evaluating the acceptance capacity of the EV charging load. A capacity variable, $S^{\text{EV}}$, is introduced to account for the injected power. The objective function aims to maximize the capacity variable while minimizing network losses. The evaluation problem is formulated as an optimization problem, where the objective function is expressed as Equation 8,

$\min {\omega }_1{\displaystyle \sum _{t\in T}}{\displaystyle \sum _{i,j\in \epsilon }}\left(r_{ij}+x_{ij}\right)l_{ij,t}-{\omega }_2{S}_k^{\text{EV}}(8)$

where $r_{ij}$ and $x_{ij}$ represent the resistance and reactance of the transmission line between buses i and j, respectively., $l_{ij,t}$ is an auxiliary variable used in the BPF function, and the product $\left(r_{ij}+x_{ij}\right)l_{ij,t}$ represents the network loss on the transmission line between bus i and j. ${\omega }_1$ and ${\omega }_2$ are the weight of power losses and capacity variable. And k is the number of the bus aggregated the EV charging station.

The BPF function is employed to establish the power flow constraints, which can be expressed as Equations 9–12,

$V_{j,t}=V_{i,t}-2\left(r_{ij}{P}_{ij,t}+x_{ij}{Q}_{ij,t}\right)+\left(r_{ij}^2+x_{ij}^2\right)l_{ij,t},\forall \left(i,j\right)\in \epsilon ,\forall t\in T(9)$

${\displaystyle \sum _{k:j\to k}}{P}_{jk,t}-{\displaystyle \sum _{k:j\to k}}\left(P_{ij,t}-r_{ij}{l}_{ij,t}\right)=P_{j,t},\forall j,\forall t\in T(10)$

${\displaystyle \sum _{k:j\to k}}{Q}_{jk,t}-{\displaystyle \sum _{k:j\to k}}\left(Q_{ij,t}-x_{ij}{l}_{ij,t}\right)=Q_{j,t},\forall j,\forall t\in T(11)$

${‖\begin{array}{l}2P_{ij,t}\\ 2Q_{ij,t}\\ l_{ij,t}-V_{i,t}\end{array}‖}_2\le l_{ij,t}+V_{i,t},\forall \left(i,j\right)\in \epsilon ,\forall t\in T(12)$

where j represents the bus index, $V_{i,t}$ denotes the square of the voltage at bus i during time interval t, and $P_{ij,t}$ and $Q_{ij,t}$ represent the active and reactive power transmitted through the transmission line between buses i and j, respectively. $P_{j,t}$ and $Q_{j,t}$ represent the injected active and reactive power, respectively.

Equations 2–4 represent the power flow constraints on the transmission line, while Equation 5 defines the second-order rotating cone relaxation constraint. The derivation of the BPF function is provided in (Farivar and Low, 2013a) and (Farivar and Low, 2013b).

The node’s injected power consists of residential load and compensation power. When calculating the active power demand, the acceptance capacity of the EV charging load is also considered. Let $P_t^{\text{EV}}$ denote the EV charging demand variable for an EV charging station with a 1 MWh capacity at time t. Therefore, the injected power at the node can be expressed as Equations 13, 14,

$P_{j,t}=-P_{j,t}^{\text{Load}}+P_{j,t}^{\text{PV}}+P_{j,t}^{\text{ESS}}-S_k^{\text{EV}}{P}_t^{\text{EV}},\forall j,\forall t\in T(13)$

$Q_{j,t}=-Q_{j,t}^{\text{Load}}+Q_{j,t}^{\text{ESS}}+Q_{j,t}^{\text{SVG}},\forall j,\forall t\in T(14)$

where $P_{j,t}^{\text{Load}}$ and $Q_{j,t}^{\text{Load}}$ represent the active and reactive power of the residential load, respectively, while $P_{j,t}^{\text{PV}}$ represents the power output from the PV generation. Let ${\eta }^{\text{Dis}}$ denote the discharging efficiency of the ESS. Assuming the output power of the ESS when discharging is $P_{j,t}^{\text{ESS},\text{Dis}}$, the output of the ESS can be expressed as Equation 15,

$P_{j,t}^{\text{ESS}}=P_{j,t}^{\text{ESS},\text{Dis}}{\eta }^{\text{Dis}}-P_{j,t}^{\text{ESS},\text{Cha}},\forall t\in T,\forall j(15)$

The compensation unit constraints include functions (1) to (7). Let $V_{\max }$ and $V_{\min }$ represent the maximum and minimum permissible values of the voltage squared, respectively. The voltage violation constraint can then be expressed as Equation 16,

$V_{\min }\le V_{i,t}\le V_{\max },\forall \left(i,j\right)\in \epsilon ,\forall t\in T(16)$

4 Case studies

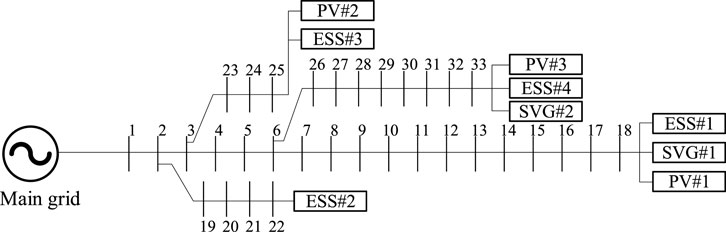
In this paper, the enhanced IEEE 33-bus benchmark distribution network, as proposed in (Farivar and Low, 2013a), is utilized for the case study. The topology of the network is shown in Figure 3, and the resistance and reactance parameters are provided in (Dolatabadi et al., 2021). To accommodate the EV charging load, the rated residential load is set to 80% of the values presented in (Dolatabadi et al., 2021).

Figure 3

Figure 3. The enhanced IEEE 33-bus distribution test system.

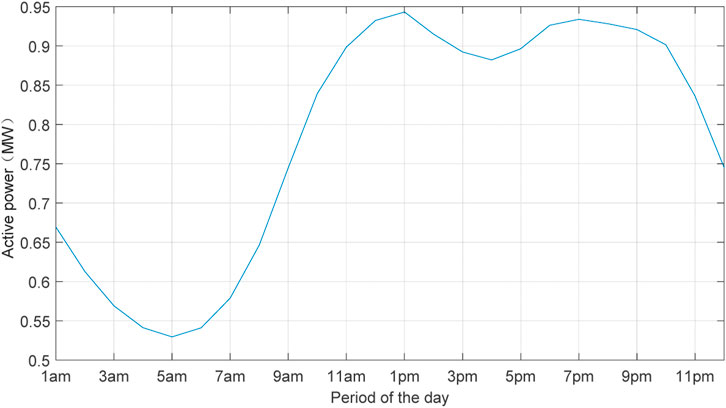
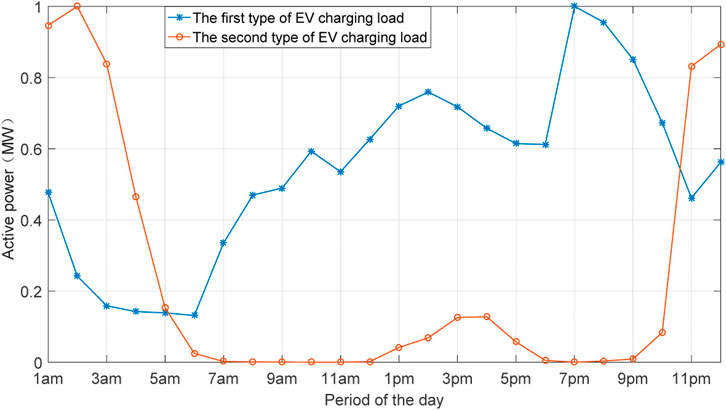
The daily residential load curve is shown in Figure 4, while two types of EV charging load curves are illustrated in Figure 5. The parameters of these load curves are derived by normalizing and fitting them to the actual daily load profiles of a Chinese residential consumer and two EV charging stations. The residential load is characterized by a prolonged peak period, with the valley power demand being approximately 50% of the peak value. This paper considers a conservative estimate of EV charging loads, meaning that in most cases, the charging demands of randomly distributed EVs will be lower than the provided data values.

Figure 4

Figure 4. Residential daily load curve.

Figure 5

Figure 5. EV charging daily load curves.

The first type of EV charging load reaches its peak during the daytime, with charging demand decreasing after 10 pm. The second type of EV charging load peaks at night, specifically between 11 pm and 3 am. These two types of EV charging loads represent distinct charging patterns. The first type reflects the charging demand in commercial areas, where users do not follow a specific charging schedule, resulting in charging demand throughout the day, particularly in the afternoon and evening. The second type reflects the charging demand in residential areas, where users tend to charge at night to take advantage of lower electricity prices, resulting in no charging demand during the morning and afternoon.

Four ESSs, all with the same parameters, are located at buses #18, #22, #25, and #33, denoted as ESS #1, #2, #3, and #4, respectively. Two SVGs are located at buses #18 and #33, denoted as SVG #1 and #2, respectively. Three PV power generation systems are integrated into the network, located at buses #18, #25, and #33, denoted as PV #1, #2, and #3, respectively. The PV output power is assumed to be positively correlated with solar radiation intensity. Therefore, the solar radiation intensity data provided in (Hung et al., 2014) are used to estimate the PV output power in this paper. This paper also considers a conservative estimate of PV generation power, implying that in most cases, the PV generation power, which is randomly distributed, will be higher than the provided data values. The integration locations for compensatory units and PV systems align with the references provided in the typical IEEE 33 distribution network model as detailed in (Dolatabadi et al., 2021).

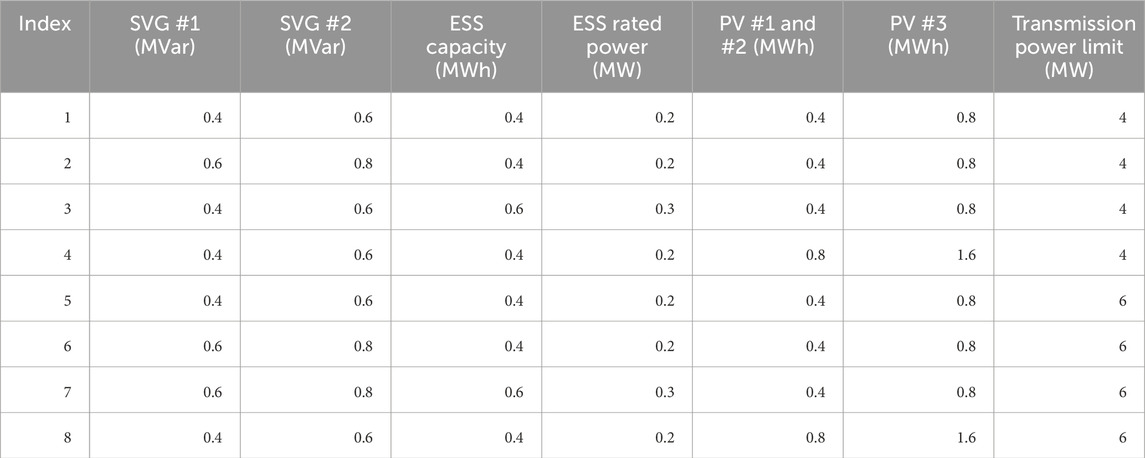
Several scenarios are designed to analyze the impact of different aggregated units on the system’s acceptance capacity. The parameters of the compensation units, PV generation systems, and transmission lines vary across these scenarios, as shown in Table 1. In Scenario 2, a larger capacity of SVGs is aggregated compared to Scenario 1. Scenario 3 aggregates a larger capacity of ESS compared to Scenario 1. Scenario 4 aggregates a larger capacity of PV generation systems compared to Scenario 1. Scenarios 5, 6, 7, and 8 are similar to the first four scenarios, but with higher transmission power limits. The weight values ${\omega }_1$ and ${\omega }_2$ in the objective function (1) are set to 0.1 and 0.9, respectively. Given the primary focus on the charging capacity of EVs, a higher weight value ${\omega }_2$ is assigned in the settings to emphasize this aspect. The optimization of network losses is given a lower weight ${\omega }_1$ due to the fact that the introduction of BPF equations, which involve second-order conic relaxation, tends to amplify line power losses.

Table 1

Table 1. Parameters of units in different scenarios.

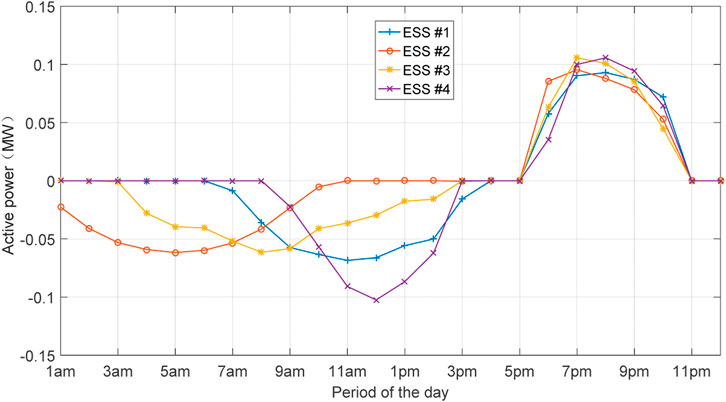
The coordinated optimization results for the first scenario, without considering the EV charging load curve, are depicted in Figures 6, 7. The data in Figure 6 indicate that the ESS units provide active power compensation during the final hours of the peak load period, influenced by photovoltaic PV power generation. Specifically, ESS #1, ESS #2, and ESS #3 recharge their batteries during the early morning hours, which coincide with the load valley period. In contrast, ESS#4, located at bus 33, recharges its battery when the PV output power reaches its peak. The charging schedules of the other ESS units further demonstrate the impact of PV generation on the coordinated charging strategy of the ESS.

Figure 6

Figure 6. Output power of ESS.

Figure 7

Figure 7. Reactive compensation power.

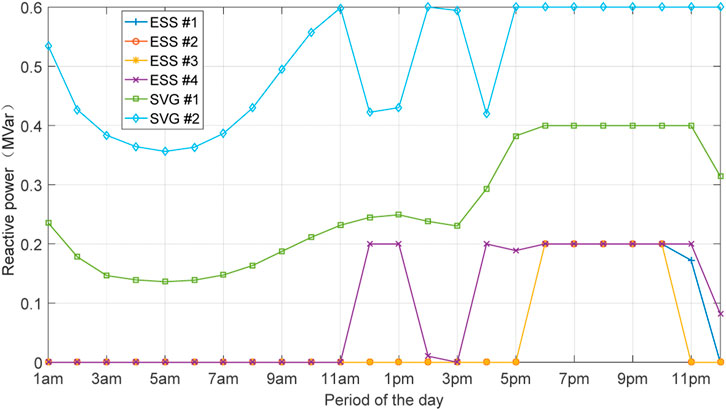
Regarding reactive power compensation, Figure 7 demonstrates that the reactive compensation units are coordinated to mitigate voltage drops, ensuring that the voltage remains within the permissible range. This coordination is essential for maintaining voltage stability and ensuring that the distribution network operates within safe limits. The reactive power compensation strategy optimizes the operation of the distribution network by accounting for variations in load and generation profiles, particularly those influenced by renewable energy sources such as PV.

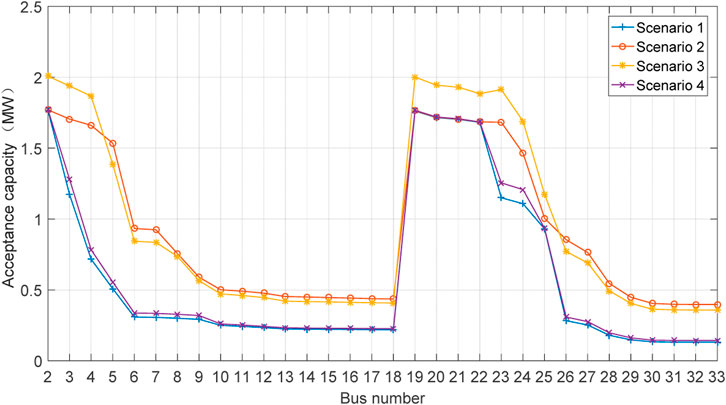
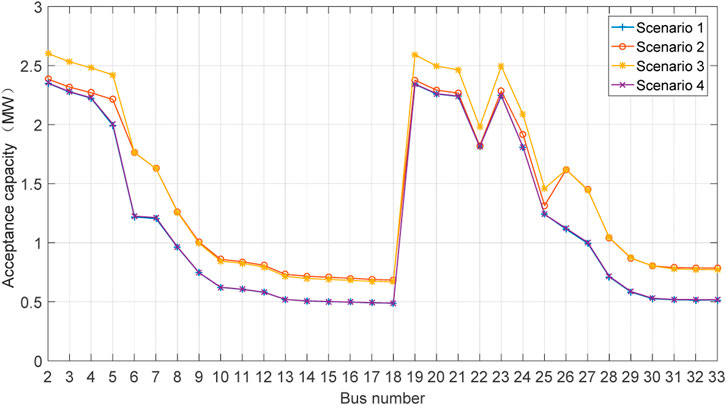
In each scenario, two types of EV charging loads are distributed across buses #2 to #33. The acceptance capacity for the first four scenarios, for both types of EV charging loads, is shown in Figures 8, 9, respectively. Analysis of the data in these figures reveals that both types of EV charging loads exhibit maximum acceptance capacity at buses #2 and #19, which are closest to the substation, and minimum acceptance capacity at buses #18 and #33, which are farthest from the substation. This highlights the significant impact of electrical distance on the acceptance of EV charging loads.

Figure 8

Figure 8. The first EV charging load acceptance capacity in the first four scenarios.

Figure 9

Figure 9. The second EV charging load acceptance capacity in the first four scenarios.

Overall, the acceptance capacity for the second type of EV charging load is higher than that of the first type, as the peak period of the first type overlaps more with residential load profiles. It is observed that the acceptance capacity for the second type of EV charging load decreases more sharply along transmission lines leading to buses #22 and #25, compared to the first type, suggesting that the second type is more sensitive to electrical distance.

Regarding the impact of compensation and PV generation system expansion on EV charging load acceptance capacity, both ESS and SVG contribute more significantly to capacity enhancement than the PV generation system for both types of EV charging loads.

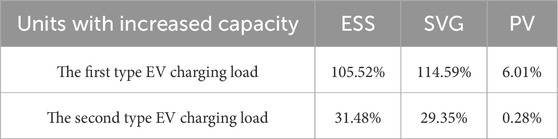
The detailed numerical results regarding the mean growth rate of acceptance capacity are presented in Table 2. The expansion of SVG has a more pronounced effect on the first type of EV charging load, resulting in a growth rate of 114.59%, while the expansion of ESS has a greater impact on the second type, with a growth rate of 31.48%. However, the differences observed between the two types of EV charging loads and their respective compensation units are not significantly distinct. Furthermore, the PV generation system does not contribute to enhancing the acceptance capacity for the second type of EV charging load, due to discrepancies in peak periods.

Table 2

Table 2. The mean growth rate of acceptance capacity in the first four scenarios.

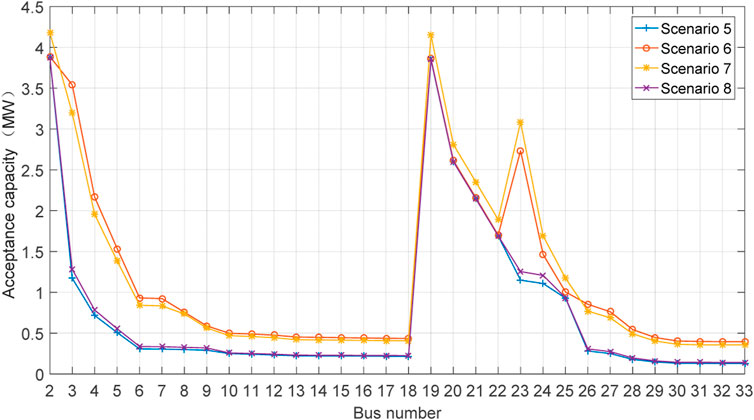
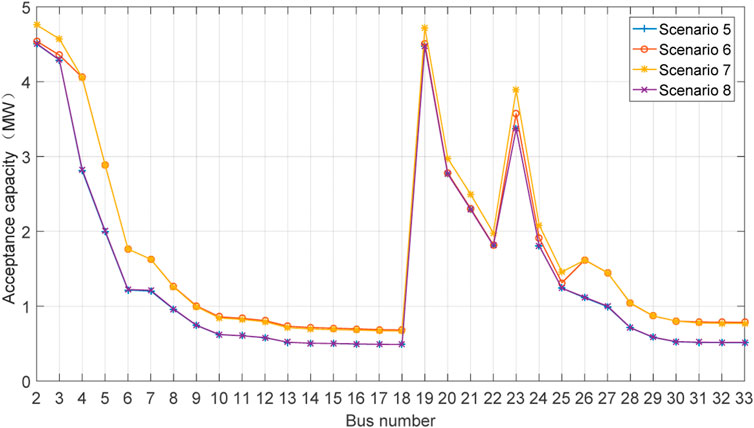
The acceptance capacity for the final scenario, for both types of EV charging loads, is depicted in Figures 10, 11, respectively. A comparison with the data in Figures 8, 9 shows that the maximum acceptance capacity for both types of EV charging loads has increased by more than 90%, while the minimum acceptance capacity remains unchanged.

Figure 10

Figure 10. The first EV charging load acceptance capacity in the last four scenarios.

Figure 11

Figure 11. The second EV charging load acceptance capacity in the last four scenarios.

Analysis of the data in Figures 10, 11 reveals that the capacity reduction along the lines leading to buses #22 and #25 has increased for the first type of EV charging load, indicating that the transmission line capacity in the first four scenarios limits the acceptance capacity at these buses. Additionally, it is observed that the expansion of PV generation does not contribute significantly to the integration of EV charging loads. However, the enhancement of both ESS and SVG continues to improve the acceptance capacity for both types of EV charging loads.

Although different types of EV charging loads were used compared to those in references (Chen et al., 2018) and (Yan and Chen, 2023), the coordinated framework proposed in this paper allows the IEEE 33 distribution network to accommodate a larger capacity of EV charging loads without causing voltage violations in the distribution network. In both EV charging load scenarios, the accessible capacity exceeds the 1.2 MW capacity mentioned in reference (Dai et al., 2023). Compared to the 2.75 MW capacity in reference (Lepolesa et al., 2024), although the maximum accessible capacities of 2MW and 2.5 MW shown in Figures 8, 9 are lower, the residential load capacity in reference (Lepolesa et al., 2024) is significantly lower than that in the case study analysis of this paper, accounting for only 25% of the total load capacity.

The detailed numerical results regarding the mean growth rate of acceptance capacity are presented in Table 3. The expansion of SVG significantly benefits the first type of EV charging load, resulting in a substantial growth rate of 111.76%, while the expansion of ESS has a more pronounced impact on the second type, contributing to a growth rate of 32.76%. An increase in the transmission line power limit amplifies the influence of compensation units on acceptance capacity; however, it does not enhance the impact of the PV power generation system.

Table 3

Table 3. The mean growth rate of acceptance capacity in the last four scenarios.

5 Conclusion

This paper investigates the integration of EV charging loads and proposes a coordinated optimization model to analyze the acceptance capacity of EV charging loads under various scenarios. The case study results indicate that a shorter electrical distance is associated with a higher acceptance capacity. Additionally, the transmission line capacity can limit the acceptance capacity at buses closer to the substation. Regarding compensation units, both ESS and SVG expansions lead to similar improvements in acceptance capacity. However, ESS has a more significant impact on the acceptance capacity for the second type of EV charging load, while SVG is more effective for the first type. PV generation systems, on the other hand, contribute minimally to the integration of EV charging loads. The research presented in this paper provides theoretical support for the practical planning of EV charging stations in a city in China.

The limitations of this paper lie in the use of conservative estimates for load demand and PV generation power, lacking consideration for the volatility of EV charging loads and PV generation power. Future research will focus on the impact of the inherent intermittency of renewable energy sources and EV charging loads on the accessible capacity of EV charging loads.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author contributions

SC: Conceptualization, Project administration, Supervision, Writing–original draft. HZ: Investigation, Methodology, Writing–review and editing. ZC: Software, Writing–review and editing. SL: Resources, Writing–review and editing. TF: Methodology, Writing–review and editing. YS: Validation, Writing–review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. The research was funded by Guizhou Power Grid Science and Technology Special Project, grant number is 060000KC23110059 and the APC was funded by the same funding. The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Conflict of interest

Authors SC, HZ, ZC, and TF were employed by Guizhou Power Grid Corporation. Authors SL and YS were employed by Dongfang Electronics Co., Ltd.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Arya, H., and Das, M. (2023). Fast charging station for electric vehicles based on DC microgrid. IEEE J. Emerg. Sel. Top. Industrial Electron. 4 (4), 1204–1212. doi:10.1109/jestie.2023.3285535

CrossRef Full Text | Google Scholar

Bayram, I. S. (2022). “Probabilistic capacity planning framework for electric vehicle charging stations with overstay,” in 2022 IEEE International Conference on Communications, Control, and Computing Technologies for Smart Grids (SmartGridComm), Singapore, 25-28 October 2022, 193–198. doi:10.1109/smartgridcomm52983.2022.9960993

CrossRef Full Text | Google Scholar

Chen, H., Hu, Z., Zhang, H., and Luo, H. (2018). Coordinated charging and discharging strategies for plug-in electric bus fast charging station with energy storage system. IET Gener. Transm. Distrib. 12, 2019–2028. doi:10.1049/iet-gtd.2017.0636

CrossRef Full Text | Google Scholar

Cui, Q., Weng, Y., and Tan, C.-W. (2019). Electric vehicle charging station placement method for urban areas. IEEE Trans. Smart Grid 10 (6), 6552–6565. doi:10.1109/tsg.2019.2907262

CrossRef Full Text | Google Scholar

Dai, W., Wang, C., Goh, H. H., Zhao, J., and Jian, J. (2023). Hosting capacity evaluation method for power distribution networks integrated with electric vehicles. J. Mod. Power Syst. Clean Energy 11 (5), 1564–1575. doi:10.35833/mpce.2022.000515

CrossRef Full Text | Google Scholar

Dias Vasconcelos, S., Filho da Costa Castro, J., Gouveia, F., Venancio de Moura Lacerda Filho, A., Fonseca Buzo, R., Henrique Alves de Medeiros, L., et al. (2024). Assessment of electric vehicles charging grid impact via predictive indicator. IEEE Access 12, 163307–163323. doi:10.1109/access.2024.3482095

CrossRef Full Text | Google Scholar

Dolatabadi, S. H., Ghorbanian, M., Siano, P., and Hatziargyriou, N. D. (2021). An enhanced IEEE 33 bus benchmark test system for distribution system studies. IEEE Trans. Power Syst. 36 (3), 2565–2572. doi:10.1109/tpwrs.2020.3038030

CrossRef Full Text | Google Scholar

Farivar, M., and Low, S. H. (2013a). Branch flow model: relaxations and convexification—Part I. IEEE Trans. Power Syst. 28 (3), 2554–2564. doi:10.1109/tpwrs.2013.2255317

CrossRef Full Text | Google Scholar

Farivar, M., and Low, S. H. (2013b). Branch flow model: relaxations and convexification—Part II. IEEE Trans. Power Syst. 28 (3), 2565–2572. doi:10.1109/tpwrs.2013.2255318

CrossRef Full Text | Google Scholar

Fesli, U., and Ozdemir, M. B. (2024). Electric vehicles: a comprehensive review of technologies, integration, adoption, and optimization. IEEE Access 12, 140908–140931. doi:10.1109/access.2024.3469054

CrossRef Full Text | Google Scholar

Hung, D. Q., Mithulananthan, N., and Lee, K. Y. (2014). Determining PV penetration for distribution systems with time-varying load models. IEEE Trans. Power Syst. 29 (6), 3048–3057. doi:10.1109/tpwrs.2014.2314133

CrossRef Full Text | Google Scholar

Jie, B., Baba, J., and Kumada, A. (2024). Contribution to V2G system frequency regulation by charging/discharging control of aggregated EV group. IEEE Trans. Industry Appl. 60 (1), 1129–1140. doi:10.1109/tia.2023.3292814

CrossRef Full Text | Google Scholar

Kharrich, M., Mohammed, O. H., Kamel, S., Aljohani, M., Akherraz, M., and Mosaad, M. I. (2021). “Optimal design of microgrid using chimp optimization algorithm,” in 2021 IEEE International Conference on Automation/XXIV Congress of the Chilean Association of Automatic Control (ICA-ACCA), Valparaíso, Chile, 22-26 March 2021, 1–5. doi:10.1109/icaacca51523.2021.9465336

CrossRef Full Text | Google Scholar

Lei, C., Bu, S., Wang, Q., and Liang, L. (2024). Observability defense-constrained distribution network reconfiguration for cyber-physical security enhancement. IEEE Trans. Smart Grid 15 (2), 2379–2382. doi:10.1109/tsg.2023.3334078

CrossRef Full Text | Google Scholar

Lepolesa, L. J., Adetunji, K. E., Ouahada, K., Liu, Z., and Cheng, L. (2024). Optimal EV charging strategy for distribution networks load balancing in a smart grid using dynamic charging price. IEEE Access 12, 47421–47432. doi:10.1109/access.2024.3382124

CrossRef Full Text | Google Scholar

Li, S., Zhao, P., Gu, C., Bu, S., Li, J., and Cheng, S. (2024). Integrating incentive factors in the optimization for bidirectional charging of electric vehicles. IEEE Trans. Power Syst. 39 (2), 4105–4116. doi:10.1109/tpwrs.2023.3308233

CrossRef Full Text | Google Scholar

Li, Y., Ni, Z., Zhao, T., Zhong, T., Liu, Y., Wu, L., et al. (2020). Supply function game based energy management between electric vehicle charging stations and electricity distribution system considering quality of service. IEEE Trans. Industry Appl. 56 (5), 5932–5943. doi:10.1109/tia.2020.2988196

CrossRef Full Text | Google Scholar

Li, Y., Zheng, N., Zhang, J., Cai, Q., Zhong, Z., and Qian, X. (2021). “Planning model for electric vehicle charging station considering battery capacity,” in 2021 IEEE 5th Conference on Energy Internet and Energy System Integration (EI2), Taiyuan, China, 22-24 October 2021, 3768–3771. doi:10.1109/ei252483.2021.9713435

CrossRef Full Text | Google Scholar

Liu, G., Yu, H., Lv, Z., Kang, K., Li, H., and Zhang, J. (2022). “Analysis of charging load acceptance capacity of electric vehicles in residential distribution network,” in 2022 IEEE 5th International Electrical and Energy Conference (CIEEC), Nangjing, China, 27-29 May 2022, 1945–1950. doi:10.1109/cieec54735.2022.9846518

CrossRef Full Text | Google Scholar

Tu, H., Feng, H., Srdic, S., and Lukic, S. (2019). Extreme fast charging of electric vehicles: a technology overview. IEEE Trans. Transp. Electrification 5 (4), 861–878. doi:10.1109/tte.2019.2958709

CrossRef Full Text | Google Scholar

Xu, M., Lei, S., Wang, C., Liang, L., Zhao, J., and Peng, C. (2024). Resilient dynamic microgrid formation by deep reinforcement learning integrating physics-informed neural networks. Eng. Appl. Artif. Intell. 138, 109470. doi:10.1016/j.engappai.2024.109470

CrossRef Full Text | Google Scholar

Yadav, L. K., Verma, M. K., and Joshi, P. (2022). Novel real valued improved coral-reef optimization algorithm for optimal integration of classified distributed generators. IEEE Access 10, 80623–80638. doi:10.1109/access.2022.3194894

CrossRef Full Text | Google Scholar

Yan, D., and Chen, Y. (2023). Distributed coordination of charging stations with shared energy storage in a distribution network. IEEE Trans. Smart Grid 14 (6), 4666–4682. doi:10.1109/tsg.2023.3260096

CrossRef Full Text | Google Scholar

Zhao, Z., Xu, M., and Lee, C. K. (2021). Capacity planning for an electric vehicle charging station considering fuzzy quality of service and multiple charging options. IEEE Trans. Veh. Technol. 70 (12), 12529–12541. doi:10.1109/tvt.2021.3121440

CrossRef Full Text | Google Scholar