Multi-objective coordinated control and optimization for photovoltaic microgrid scheduling

The stability and economic dispatch efficiency of photovoltaic (PV) microgrids is influenced by various internal and external factors, and they require a well-designed optimization plan to enhance their operation and management. This paper proposes a multi-objective coordinated control and optimization system for PV microgrids. To address the challenges of slow convergence and local optima in traditional PV microgrid scheduling methods, this study introduced an improved multiple objective particle swarm optimization (IMOPSO) algorithm that integrates an adaptive inertia weight adjustment strategy based on optimal similarity and a multi-directional iterative Pareto solution archive update mechanism. A tri-objective optimization model is formulated to minimize operational costs, environmental pollution, and grid output fluctuation variance, with decision-making supported by the Entropy Weight TOPSIS method. The proposed algorithm is validated through a practical case study of a PV microgrid located in Suzhou, China, and the results demonstrate that IMOPSO achieves a 4.4% reduction in total operational costs under time-of-use pricing (from 50.73 USD to 48.49 USD) and a 4.6% reduction under fixed pricing (from 54.93 USD to 52.38 USD), alongside a maximum safety variance reduction of 45% (from 22.16 to 12.15). The Pareto front distribution exhibits enhanced diversity and uniformity compared to the original MOPSO. While single-objective optimization yields lower costs in isolated scenarios (e.g., 28.50 USD for economic cost minimization), it significantly compromises environmental performance (20.44 USD) and grid stability (14.05 variance). In contrast, IMOPSO ensures coordinated control and effectively balances economic efficiency, environmental sustainability, and operational safety. This study provides a robust framework for multi-objective coordinated control and microgrid scheduling, advancing sustainable energy transition.

1 Introduction

The global energy crisis and escalating environmental concerns have propelled renewable energy systems to the forefront of sustainable development strategies. This urgency has driven governments and industries worldwide to accelerate the transition from fossil fuel dependency to decentralized clean energy infrastructure. Among these, photovoltaic (PV) microgrids have emerged as a promising solution for distributed power generation due to their scalability and carbon-neutral attributes. A PV microgrid typically comprises components such as photovoltaic arrays, energy storage systems, load equipment, controller and other ancillary devices (He et al., 2023). It functions as an autonomous power system which is capable of self-control and management, integrating complete functionalities of power generation, distribution, and consumption. This enables effective energy optimization within the grid and represents a critical component of smart grid systems (Boscaino et al., 2024). However, the variability in lighting conditions, coupled with the inherent intermittency of photovoltaic power generation and random fluctuations influenced by meteorological factors, pose significant challenges to grid stability and economic dispatch efficiency (Keisang et al., 2021). Therefore, a well-designed optimization plan is essential to enhance the management and operation of PV microgrids.

Extensive research efforts have been dedicated to optimizing PV microgrid scheduling through advanced computational intelligence. Various intelligent algorithms, ranging from evolutionary and metaheuristic computation techniques like genetic algorithms (GA) (Burhan et al., 2016; Raghavan et al., 2020; Shan et al., 2018; Torkan et al., 2022), differential evolution (DE) (Hemmati et al., 2014; Jiie et al., 2024; Qian et al., 2020; Ramli et al., 2018), and particle swarm optimization (PSO) to machine learning approaches such as deep reinforcement learning (Jiang et al., 2023; Liang et al., 2024; Upadhyay et al., 2024), artificial neural networks (ANN), and others (Keddouda et al., 2023; Indira et al., 2024; Rezaeimozafar et al., 2024), have been developed to address the complex multi-objective optimization challenges in microgrid operation. For instance, Duong et al. (Phuc Duong et al., 2025) employed the Black Kite algorithm, equilibrium optimizer and the Secretary Bird Optimization algorithm to optimize the placement of electric vehicle charging stations, wind turbine stations, photovoltaic units and capacitor banks in the IEEE 69-node distribution power grid, achieving the effects of reducing power loss in the grid and enhancing voltage stability. Recently, multiple objective particle swarm optimization (MOPSO) algorithm has shown promising performance in balancing competing objectives, including operational cost minimization, renewable energy utilization maximization, and system reliability enhancement. Recent studies highlight several advancements in this field (Borhanazad et al., 2014; Aguilar et al., 2024). Gholami et al. (Gholami and Dehnavi, 2019) improved MOPSO to address optimal power sharing among multiple power grids within the microgrid framework, such as wind power, photovoltaic power, and combined heat and power plants. This method optimizes and schedule sources in the microgrid with the goal of minimizing costs while accounting for uncertainties. Awad et al. (Awad et al., 2020) adopted the total solar power generation of the photovoltaic system and the power generation of each component as objective functions, using the inclination angle and pitch spacing of photovoltaic components as constraints. They employed the MOPSO method for optimization and verified the reliability of the output results through an empirical example. Li et al. (Multi-objective Optimization dispatching of microgrid based onimproved particle swarm algorithm, 2021) constructed a multi-objective optimal scheduling model for grid-connected microgrids, considering operation cost and environmental protection cost as objectives. The proposed model was solved using the MOPSO algorithm, effectively reducing electricity costs and environmental pollution, thereby promoting optimal microgrid operation. Guo et al. (2025) proposed a three-objective scheduling strategy for islanded microgrids based on an improved MOPSO algorithm. By enhancing parameter adjustment strategies and introducing adaptive and fuzzy identification methods, they achieved optimal solutions. Compared to single-objective optimization, their method reduces costs by 11.15% and improved satisfaction by 4.76%. He et al. (2024) introduced a novel metaheuristic MOPSO to address complex multi-objective optimization challenges in microgrids. Their approach avoids local Pareto frontier concentration through a random selection strategy, expanding the selection range of multiple objectives. Additionally, they established a comprehensive multi-objective optimization dispatch model for microgrids, considering operating costs and power fluctuations. Parvin et al. (2023) conducted multi-objective optimization for microgrids using MOPSO, with objective functions being the loss of power supply probability and the cost of energy per unit. Results indicated that high solar irradiation levels significantly reduce grid-provided power load. Calculated scenarios showed energy costs of 0.266 USD, 0.235 USD, and 0.247 USD per unit, respectively, with corresponding power outage interruption values of 0.285, 0.3218, and 0.207. Qu and Ye (2023) considered daily operation costs, carbon emissions, and primary energy consumption as optimization goals. They proposed an improved weighted fuzzy method to transform the multi-objective model into a single-objective one, solvable by MOPSO. This method enhances comprehensive coordination among multiple objectives and improves algorithm robustness, optimizing device outputs.

Existing MOPSO frameworks have been successfully applied to optimize energy storage coordination and demand response strategies in hybrid microgrid configurations, demonstrating their effectiveness in handling medium-scale optimization problems. However, significant limitations remain when addressing the high-dimensional optimization spaces characteristic of modern microgrid systems, particularly those incorporating multiple renewable energy sources, diverse load profiles, and complex grid interconnection requirements. Specifically, the convergence rate of the algorithm deteriorates markedly when dealing with non-convex Pareto fronts in these complex scenarios, primarily due to the increased computational complexity and solution space dimensionality (He et al., 2024). Furthermore, premature convergence to local optima persists as a critical challenge, stemming from insufficient maintenance of population diversity throughout the iterative optimization process, which ultimately compromises the quality and comprehensiveness of the obtained solutions.

Keeping in view these limitations, this study proposed an improved MOPSO algorithm (IMOPSO) for multi-objective coordinated control and optimization in PV microgrids integrating an adaptive inertia weight adjustment strategy based on optimal similarity and a multi-directional iterative Pareto solution archive update mechanism. Therein, a tri-objective optimization model is formulated to minimize operational costs, environmental pollution, and grid output fluctuation variance, with decision-making supported by the TOPSIS method. The proposed algorithm is validated through a practical case study of a photovoltaic microgrid located in Suzhou, China under both time-of-use and fixed electricity pricing models, and the results demonstrate its effectiveness in terms of operational cost, environment friendliness and grid output stability. Moreover, a comparison with single-objective optimization strategy and original MOPSO with tri-objective optimization shows that the proposed improved IMOPSO algorithm ensures coordinated control and balances economic efficiency, environmental sustainability, and operational safety more effectively. This study can help in addressing optimal scheduling challenges of PV microgrid leading to enhanced utilization of PV energy, reduced operating cost, enhanced electric grid resilience, reduced environmental footprint, and effective management.

2 Models

This section deals with modeling details of Improved MOPSO algorithm (IMOPSO) and photovoltaic microgrid system.

2.1 Improved MOPSO algorithm (IMOPSO)

2.1.1 Improvement measures

The general MOPSO suffers from problems such as slow convergence speed, random initialization and easy falling into local optimum (Xingshen et al., 2021). To address these issues, this paper proposes the following two improvement measures.

2.1.1.1 Adaptive adjustment of inertia weight

This paper adopts an adaptive adjustment strategy of inertia weight based on the optimal similarity. The inertia weight value is dynamically adjusted according to the similarity between the current particle and the optimal particle. When the similarity value is large, it indicates that the current particle is closer to the optimal particle, and the inertia weight value is appropriately reduced; when the optimal similarity exceeds the set value, the MC (Wu et al., 2014) operation is introduced to enhance the local optimization and local overflow ability of the particles; when the similarity value is small, it shows that the current particle is far from the optimal particle, and the inertia weight value is appropriately increased, which can enhance the global search ability of the particles. Perform dimensionless processing on the position of particles. Here, the original matrix X = [X₁, X₂, X₃.X_d] and the normalized matrix Y = [Y₁, Y₂, Y₃.Y_d] are defined. The processing method is given in Equation 1.

$y_{ij}=\frac{x_{ij}-\min X_j}{\max X_j-\min X_j}(1)$

where d is population particle dimension, i is row number, j is column number,y_ij represent the elements in matrix Y, x_ij represent the elements in matrix X, and X_j is column vectors of matrix X. The dissimilarity between particles is given in Equation 2.

${\mathit{cos}}_i=\frac{Z_i·g{x}^{\prime }}{\left|Z_i\right|·\left|g{x}^{\prime }\right|}(2)$

where cos_i is the dissimilarity value between particle i and the optimal particle, within [0, 1], the larger the value is, the higher the similarity degree will be. Z_i is row vectors of matrix Y, and gx’ is normalized position vector of the global optimal particle.

According to the adaptive adjustment strategy of the inertia weight, the variation curve is formulated as Equation 3.

$W_i=\frac{2\left(W_{up}-W_{down}\right)}{1+e^{6\left({\mathit{cos}}_i-1\right)}}+\left(2W_{down}-W_{up}\right)(3)$

where W_i is intertia weight of particle i, W_up is upper limit of intertia weight value, 0.9, and W_down is lower limit of intertia weight value, 0.4.

2.1.1.2 Pareto solution set update strategy

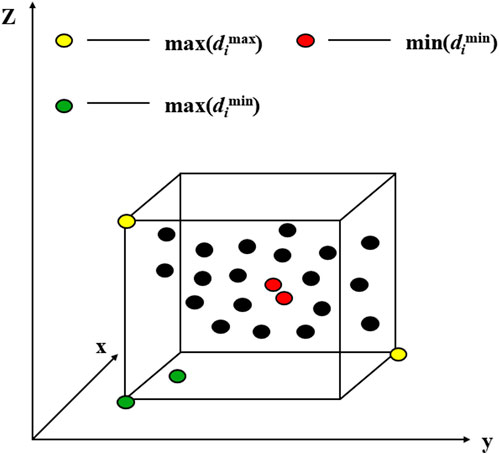
It includes adopting the dynamic update strategy of Pareto solution set in multiple iterative directions, as shown in Figure 1, by using the dimension box to determine whether the Pareto solution set exceeds the scale. If it does, each time, randomly delete one of the two particles with the smallest value in the vector group of the minimum particle distance (marked in red), and adjust in this way continuously until the Pareto solution set conforms to the scale. Finally, the two particles with the largest values in the vector group of the minimum particle distance and the two particles with the largest values in the vector group of the maximum particle distance (marked in yellow and green) are regarded as the optimal particles.

Figure 1

Figure 1. Pareto solution set update strategy diagram.

Before operating on this method, it is necessary to perform dimensionless processing on the fitness of each particle, and define and calculate the minimum particle distance vector group and the maximum particle distance vector group as given in Equations 4–6.

$f_{ik}^{\prime }=\frac{f_k^{\max }-f_{ik}}{f_k^{\max }-f_k^{\min }}(4)$

$d_i^{\mathit{min}}=\mathit{min}\sqrt{{\displaystyle \sum _{k=1}^m}\left({\left(f_{ik}^{\prime }-f_{jk}^{\prime }\right)}^2\right)}(5)$

$d_i^{m\text{ax}}=\mathit{max}\sqrt{{\displaystyle \sum _{k=1}^m}\left({\left(f_{ik}^{\prime }-f_{jk}^{\prime }\right)}^2\right)}(6)$

where m is size of the Pareto solution set, f^’_ik is scaled objective function values, f_k^max is absolute positive ideal solutions of the k^th objective function, f_ik is actual objective function values of particle i at the k^th dimension, f_k^min is absolute negative ideal solutions of the k^th objective function, d_i^min is ith elements of the minimum particle distance vector group, and d_i^max is ith elements of the maximum particle distance vector group.

2.1.2 IMOPSO model workflow

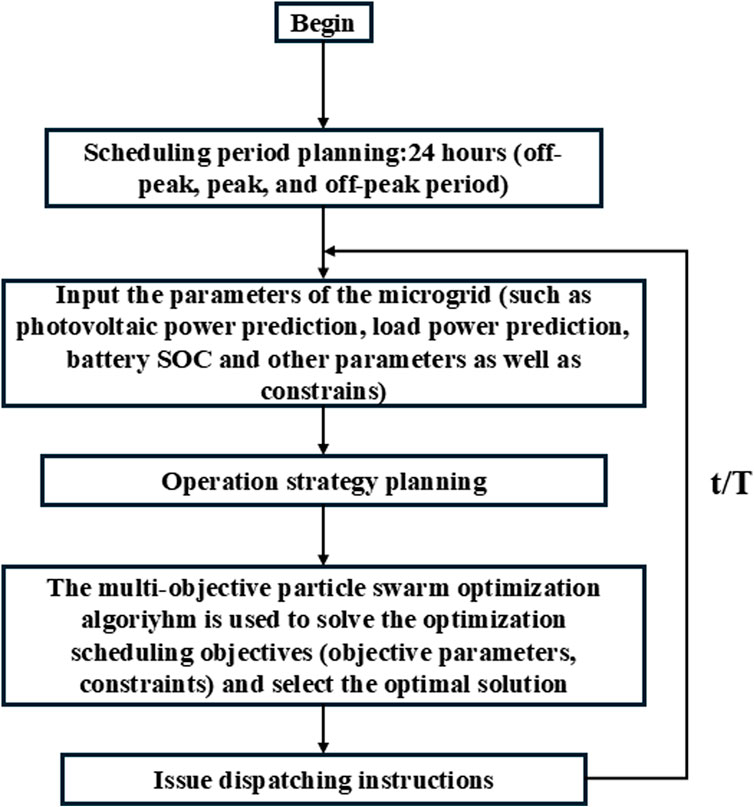
The process of the improved MOPSO (IMOPSO) algorithm is shown in Figure 2. From initializing the population to convergence, it includes different steps dealing with pareto solution set update, personal and global best position update, inertia weight update and others.

Figure 2

Figure 2. Improved MOPSO (IMOPSO) model workflow.

2.1.3 Improved MOPSO (IMOPSO) performance testing

This paper adopts the numerical experiments comparing the distances between the solutions obtained by the improved MOPSO and the real Pareto front, as well as the distribution of non-dominated solution sets on the Pareto front, as the evaluation indicators for the algorithm performance. They are given in Equations 7, 8.

$C\left(P\right)=\frac{\left({\displaystyle {\sum }_{i=1}^{\left|P\right|}}{d}_i\right)}{\left|P\right|}(7)$

$d_i=\underset{1\le j\le \left|P\right|}{\mathit{min}}\sqrt{{\displaystyle \sum _{k=1}^m}{\left(\frac{f_k\left(X_i\right)-f_k\left(X_j\right)}{f_k^{\mathit{max}}-f_k^{\mathit{min}}}\right)}^2}(8)$

In Equations 7, 8, k is number of objective functions, f_k^min is minimum value of objective function, and f_k^max is maximum value of objective function. The smaller C(P) is, the better the convergence property of the algorithm is.

The main metric for the uniformity of the solution set is to measure the variance of the distances between adjacent target vectors. According to the following model (Equations 9, 10), the calculation is carried out.

$SP=\sqrt{\frac{1}{\left|P\right|-1}{\displaystyle \sum _{i=1}^{\left|P\right|}}{\left(\overline{d}-d_i\right)}^2}(9)$

$d_i=\underset{1\le j\le \left|P\right|}{\mathit{min}}\left\{{\displaystyle \sum _{k=1}^{\mathrm{m}}}\left|f_k\left(X_i\right)-f_k\left(X_j\right)\right|\right\}(10)$

where $\overline{d}$ is average value of d_i, and m is the number of functions. The smaller the value of SP, the better the uniformity of the solution distribution and the higher the diversity of the solution set.

The following standard test functions (ZDT-1, ZDT-2, and ZDT-3) were selected to conduct algorithm performance tests (Chase et al., 2025), and analyze the performance of Improved MOPSO (IMOPSO) and MOPSO algorithms.

ZDT-1:

$\left\{\begin{array}{l}\mathit{min}{f}_1\left(x_1\right)=x_1\\ \mathit{min}{f}_2\left(x\right)=g\left(x\right)\left(1-\sqrt{\left(\frac{f_1}{g}\right)}\right)\\ g\left(x\right)=1+9{\displaystyle \sum _{i=2}^m}\frac{x_i}{m-1}\\ s.t.0\le x_i\le 1,i=1,2,...,30\end{array}\right.$

ZDT-2:

$\left\{\begin{array}{l}\mathit{min}{f}_1\left(x_1\right)=x_1\\ \mathit{min}{f}_2\left(x\right)=g\left(x\right)\left(1-{\left(\frac{f_1}{g}\right)}^2\right)\\ g\left(x\right)=1+9{\displaystyle \sum _{i=2}^m}\frac{x_i}{m-1}\\ s.t.0\le x_i\le 1,i=1,2,...,30\end{array}\right.$

ZDT-3:

$\left\{\begin{array}{l}\mathit{min}{f}_1\left(x\right)=\mathit{cos}\left(\frac{\pi }{2}{x}_1\right)\mathit{cos}\left(\frac{\pi }{2}{x}_2\right)\left(1+g\left(x\right)\right)\\ \mathit{min}{f}_2\left(x\right)=\mathit{cos}\left(\frac{\pi }{2}{x}_1\right)\mathit{sin}\left(\frac{\pi }{2}{x}_2\right)\left(1+g\left(x\right)\right)\\ \mathit{min}{f}_3\left(x\right)=\mathit{sin}\left(\frac{\pi }{2}{x}_1\right)\left(1+g\left(x\right)\right)\\ g\left(x\right)={\displaystyle \sum _{i=3}^m}{\left(x_i-0.5\right)}^2\\ s.t.0\le x_i\le 1,i=1,2,...,12\end{array}\right.$

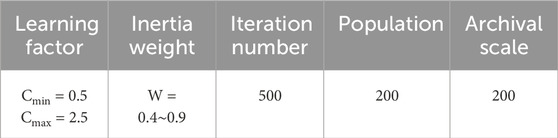
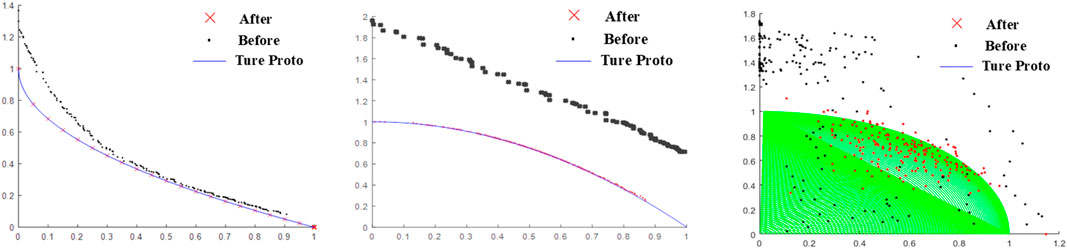
The parameters are given in Table 1. Since this type of algorithm is essentially iterative and has relatively high randomness; therefore, in order to demonstrate the test accuracy, this paper records the cumulative results of 20 tests. To show the convergence and stability of the algorithm, the quantitative and qualitative comparison results are given in Table 2; Figure 3 respectively.

Table 1

Table 1. Algorithm parameters setting.

Table 2

Table 2. Quantitative Comparison at different testing functions.

Figure 3

Figure 3. Qualitative comparison chart (Left) ZDT-1, (Center) ZDT-2, (Right) ZDT-3.

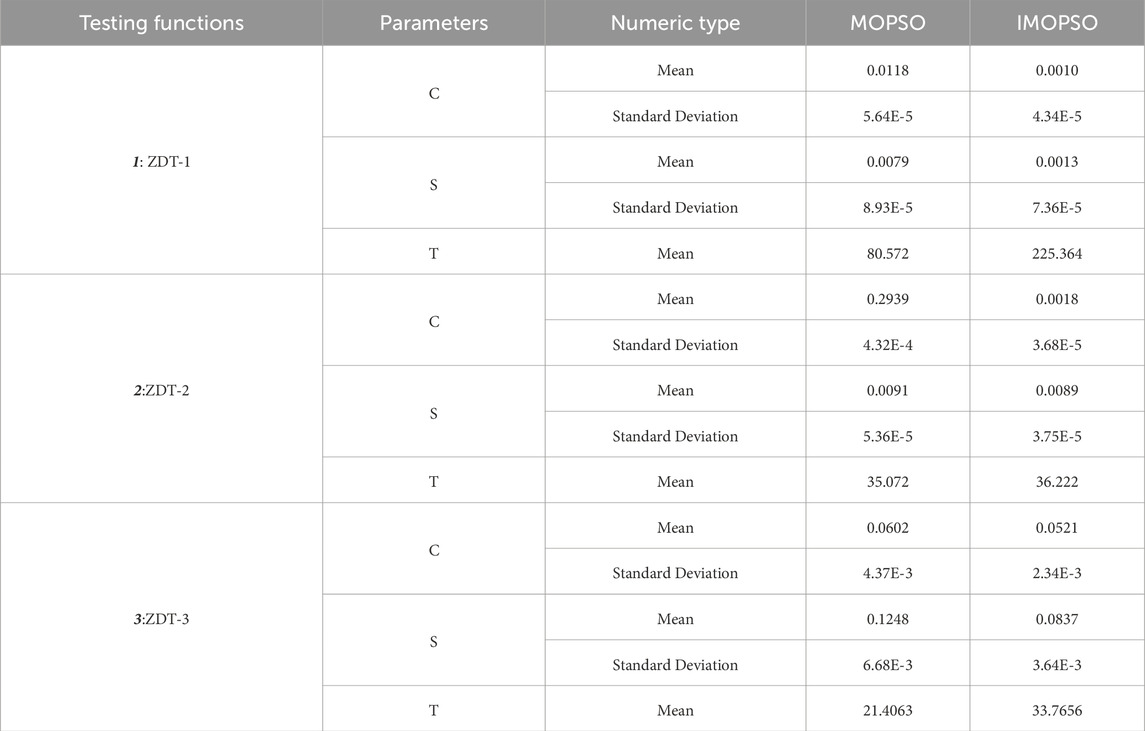
The evaluation of the calculation results is conducted from both qualitative and quantitative perspectives. The performance parameters used are: (i) C representing the distance from the estimated front to the real front found by the algorithm, (ii) S indicating the uniformity of the algorithm’s performance, and (iii) T denoting the time for the algorithm to converge once.

The above comparison results show: (1) Enhancement of convergence: In the ZDT-1 test, the mean value of C is decreased from 0.0118 to 0.0010 for IMOPSO (Table 2), a reduction of two orders of magnitude; in the ZDT-2 test, the mean value of C is decreased from 0.2939 to 0.0018. The smaller the C value is, the shorter the average distance between the solution set and the real Pareto front is, indicating that the convergence of the algorithm has been significantly improved, and (2) Avoiding local minima: In the ZDT-1 test, IMOPSO achieved a significant improvement in the mean value of S (from 0.0079 to 0.0013 in Table 2) and the standard deviation also decreased significantly (from 8.93E-5 to 7.36E-5 in Table 2), indicating a better uniformity of the solution set and higher population diversity, thereby reducing the risk of local optima.

In Table 2, although the running time (T) of IMOPSO is higher than that of MOPSO. This is because the improved algorithm incorporates mechanisms such as matrix operations to enhance the global search ability. Although it sacrifices some computational efficiency, it effectively avoids the problem of local minima. Secondly, the lower C value and better solution set quality indicate that this algorithm achieves better convergence effect within a limited number of iterations (500 times). The improved convergence characteristics directly reflect the enhancement of algorithm efficiency.

2.1.4 Construction of the optimization objective functions

The objective of optimizing scheduling is to achieve comprehensive efficiency scheduling under the condition of ensuring stable operation of the system and meeting the load demand. In this paper, the active power output of distributed power sources is taken as the optimization variable, and the optimization objective based on the economic cost, environmental friendliness and safety of the system operation is established and the target model is solved.

2.1.4.1 Objective function-I economic cost: minimizing the operating cost of the microgrid

The general operating costs of a microgrid system include: operating costs of micro-power sources, bidirectional power exchange cost of the grid, load compensation cost. This paper combines the photovoltaic microgrid system. Since this power station is established based on existing conditions, this paper does not consider the initial construction cost of system devices for the time being, only considering maintenance cost, depreciation cost and grid exchange cost. The operating cost objective function is established, given in Equation 11.

$\mathit{min}N={\sum }_{t=1}^T\left({\sum }_{i=1}^N\left(K_{OM\left(i\right)}{P}_i\left(t\right)+\frac{C_i}{8760K_i}·\frac{d_i{\left(1+d_i\right)}^{r_i}}{{\left(1+d_i\right)}^{r_i}-1}·P_i\left(t\right)\right)+a{C}_{grid}\left(t\right)\right)(11)$

where T is the scheduling period, N is the number of types of distributed power sources, K_OM(i) is the maintenance coefficient of distributed power source i, P_i(t) is the active power output at time t, C_i is the unit capacity installation cost, K_i is capacity factor, 8700K_i is annual power generation, d_i is annual depreciation rate, and r_i is depreciation period. Then, overall cost for grid is given in Equation 12.

$C_{grid}\left(t\right)=C_{buy}\left(t\right)P_{buy}\left(t\right)-C_{\text{sell}}\left(t\right)P_{\text{sell}}\left(t\right)(12)$

where C_buy(t) and C_sell(t) represent the purchase and sale prices of electricity from the power grid by the system in the tth period. P_buy(t) and P_sell(t) are the power exchanged between the photovoltaic microgrid and the power grid. a is the operating mode coefficient. when a = 1, it is the grid-connected state, and electricity is purchased from the grid at this time; when a = −1, electricity is sold to the grid at this point; when a = 0, it is the off-grid state, and no power exchange occurs between the two.

2.1.4.2 Objective function-II environmental friendliness: minimize the cost of pollutant generation by the microgrid

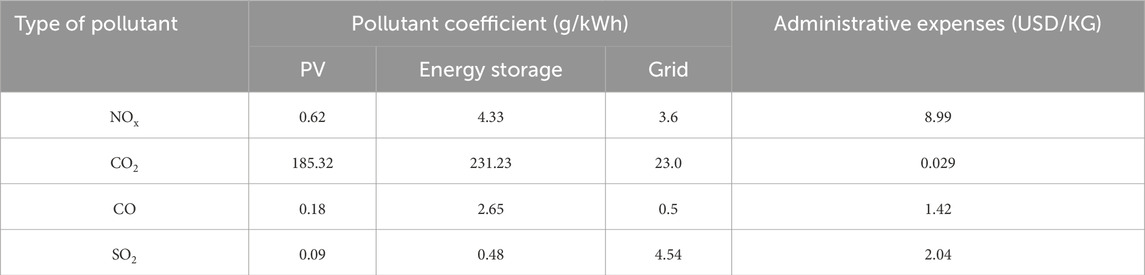
Photovoltaic power generation belongs to clean energy. However, during its operation, it still emits certain pollutants. Therefore, this paper takes into account the pollution control costs generated during the operation of photovoltaic power generation, batteries and the power grid. The main pollutants are CO, CO₂, SO₂ and NO_x. The function expression considering environmental costs is given in Equation 13.

$\mathit{min}C={\sum }_{t=1}^T\left[{\sum }_{k=1}^K{10}^{-3}{C}_k\left({\sum }_{i=1}^N{r}_{i,k}{P}_i\left(t\right)+r_{grid,k}{P}_{sell}\left(t\right)\right)\right](13)$

where C is the total environmental cost over the T period, C_k is the cost required for controlling each kilogram of k-type pollutants, K is pollutant category, r_i,k is mass of pollutants k produced per unit of active power, r_grid,k is mass of pollutants k generated by the large grid when it transmits unit electricity to the photovoltaic microgrid in the grid-connected mode.

2.1.4.3 Objective function-III safety of the system operation: minimizing the variance of output fluctuation of microgrid

For microgrids, since both photovoltaic power sources and loads in the system are predictive in nature, there will be fluctuation errors. These errors will have certain impacts on the microgrid’s grid-connected operation and may cause certain degrees of impact on the power grid. Usually, certain energy storage devices are configured in the system as backups. Therefore, it is necessary to consider from the perspective of safety and stability and define the safety formula, given in Equation 14.

$\mathit{min}S=\frac{1}{T}{\sum }_{t=1}^T{\left(\left|P_{grid}\left(t\right)\right|-\overline{P_{grid}}\right)}^2(14)$

where S represents the safety variance, and $\overline{P_{grid}}$ is the average value of the power output of the grid within one T-cycle in the grid-connected mode.

2.1.5 Operating constraints

Due to the limitations imposed by the physical factors such as the structure and working characteristics of the microgrid system, its operation must comply with the requirements of the actual working range. Therefore, for the microgrid system, system constraints must be established. The following is the analysis of the system constraints for the photovoltaic microgrid system in this paper. Each constraint condition is based on the actual photovoltaic power station.

(1) Balance power constraint is given in Equation 15.

$P_i^{\mathit{min}}\le P_i\left(t\right)\le P_i^{\mathit{max}}(15)$

where P_i^min and P_i^max represent the minimum and maximum values of the active power output of distributed power sources respectively. The power balancing provides Equation 16.

$a{P}_{grid}\left(t\right)+P_{pv}\left(t\right)=P_{chu}\left(t\right)+P_L\left(t\right)(16)$

where a = ±1, it is the grid-connected power balance; when a = 0, it is the off-grid power balance. Among them, P_chu(t) is the power of energy storage charging and discharging, P_pv(t) is the active power output of photovoltaic, and P_L(t) is the load power.

(2) Constraints on charging and discharging power of energy storage batteries and constraints on capacity and state-of-charge (SOC) of batteries, as given in Equation 17.

$P_{bat}^{\mathit{min}}\le P_{chu}\left(t\right)\le P_{bat}^{\mathit{max}}(17)$

where P_bat^min、P_bat^max are upper and lower limits for charging and discharging of the battery respectively, P_chu(t) represents the charging and discharging power during the t period.

During charging, it can be written as in Equation 18.

$E_{chu}\left(t\right)=E_{chu}\left(t-1\right)+P_{chu}\left(t\right)\Delta T{n}_d,P_{chu}\left(t\right)>0(18)$

During discharging, it can be written as in Equations 19 and 20.

$E_{chu}\left(t\right)=E_{chu}\left(t-1\right)+P_{chu}\left(t\right)\Delta T/n_c,P_{chu}\left(t\right)\le 0(19)$

$E_{rong}SO{C}_{\mathit{min}}\le E_{chu}\left(t\right)\le E_{rong}SO{C}_{\mathit{max}}(20)$

where E_rong represents the rated capacity of the battery, and SOC_min and SOC_max represent the lower and upper limits of SOC respectively. E_chu(t) is the battery capacity at time t, and E_chu(t-1) is the battery capacity at time t-1, that is, the previous time. If the start and end of the energy storage capacity within a scheduling period are equal, then, it provides Equation 21.

$E_{chu}\left(0\right)=E_{chu}\left(T\right)(21)$

(3) Power exchange constraint

When a microgrid operates in parallel with the grid, it conducts power exchange. During this process, it is subject to the power constraints of the tie lines themselves. It is given in Equation 22.

$P_{grid}^{\mathit{min}}\le P_{grid}\left(t\right)\le P_{grid}^{\mathit{max}}(22)$

where P_grid^min, and P_grid^max represent the minimum and maximum values of the exchanged power respectively.

(4) Slope power constraint

To ensure the smooth operation of the system, it is necessary to limit the variation range of the output power of distributed power sources in the system. It is given in Equation 23.

$\left|P_i\left(t\right)-P_i\left(t-1\right)\right|\le r(23)$

where r represents the constant of the limit value for the variation amplitude.

2.2 Photovoltaic microgrid system model with IMOPSO

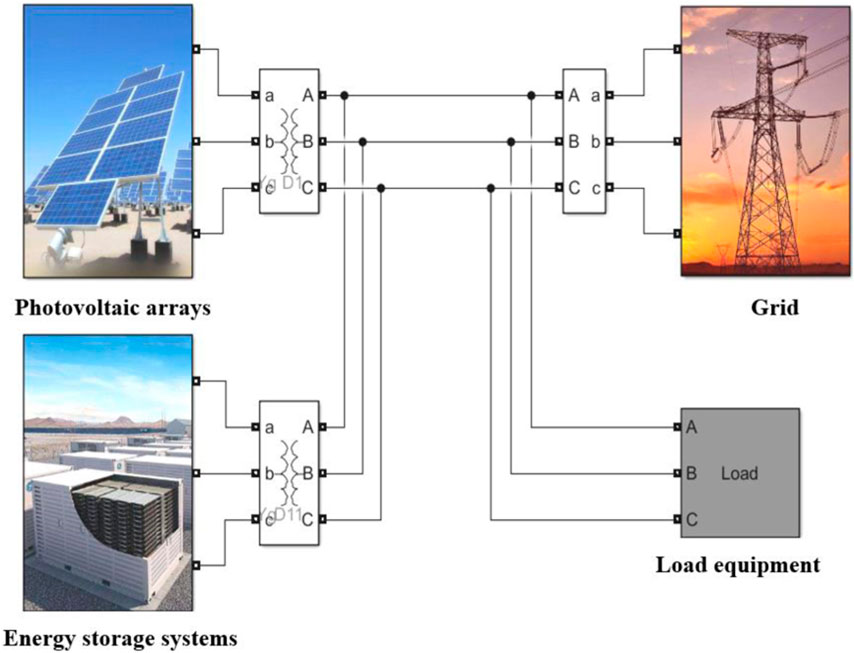
The composition of the PV microgrid system is shown in the Figure 4. Based on the aforementioned multi-objective optimization scheduling function, constraints, operation strategies and algorithms, the optimization scheduling model of the photovoltaic microgrid is established as shown in the Figure 4 and workflow of the IMOPSO algorithm for this PV microgrid is shown in Figure 5.

Figure 4

Figure 4. PV microgrid system.

Figure 5

Figure 5. Workflow of the IMOPSO algorithm for PV microgrid.

2.3 Entropy Weight TOPSIS decision-making framework

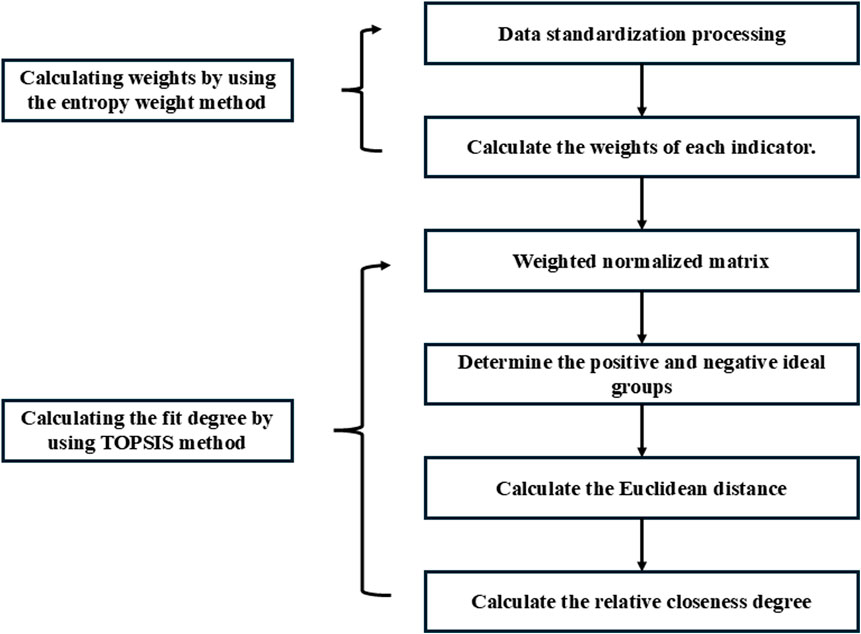
This method is actually the result of combining the Entropy Weight Method and the TOPSIS Method. The Entropy Weight Method is used for objectively weighting the indicators, and when the degree of change of a certain object in the tested system is greater, the amount of information contained behind it is also greater, and accordingly, a greater weight is assigned. The TOPSIS Method is used to quantify the comprehensive scores of each object to be evaluated. The principle is to determine the optimal solution and the worst solution among the indicators of each object to be evaluated, and calculate the Euclidean distance between each object and the optimal solution, thereby obtaining the relative proximity degree of each object and sorting them. The introduction of the Entropy Weight Method compensates for the limitations of the TOPSIS Method that it cannot highlight important indicators, and can enhance the scientific nature of the evaluation results (Zhihu, 2025). The analysis steps are given in Figure 6.

Figure 6

Figure 6. Entropy weight TOPSIS method analysis Route Map.

In this study, the selection of the optimal output scheme for the microgrid is a multi-level decision-making problem. The method of determining weights based on information entropy is relatively objective and appropriate. The calculation model is as follows:

Firstly, the fitness of each particle is normalized to eliminate the influence of different scales, as given in Equation 24.

$f_{ik}^{\prime }=\frac{f_k^{\mathit{max}}-f_{ik}}{f_k^{\mathit{max}}-f_k^{\mathit{min}}}(24)$

Secondly, the weights of each indicator are determined, as given in Equations 25–27.

${\lambda }_k=\frac{1-E_k}{n-{\sum }_{i=1}^n{E}_k}(25)$

$E_k=-\frac{1}{\mathit{ln}\left(n\right)}\left({\sum }_{i=1}^n{P}_{ij}·\mathit{ln}\left(P_{ij}\right)\right)(26)$

$P_{ik}=\frac{f_{ik}^{\prime }}{{\sum }_{i=1}^n{f}_{ik}^{\prime }}(27)$

where E_K is information entropy, and λ_K is attribute weight.

Then, the distance scale and the degree of fit are calculated, as given in Equations 28–30.

${S_i}^{+}=\sqrt{{\displaystyle \sum _{k=1}^m}{\left({\lambda }_k{f}_{ik}^{\prime }-{\lambda }_k{f}_{k+}^{\prime }\right)}^2}(28)$

${S_i}^{-}=\sqrt{{\displaystyle \sum _{k=1}^m}{\left({\lambda }_k{f}_{ik}^{\prime }-{\lambda }_k{f}_{k-}^{\prime }\right)}^2}(29)$

$C_i=\frac{{S_i}^{-}}{{S_i}^{+}-{S_i}^{-}}(30)$

where S_i⁺ and S_i⁻ represent the expected distance values of the particles, and C_i is the degree of fit. The larger the value is, the better it is, indicating the optimal output scheme of the current microgrid optimization scheduling.

The relative closeness degree C_i of each evaluation index object to the optimal object is calculated according to the above formula. They are sorted based on the relative closeness degree. According to the principle of TOPSIS method, the larger the relative closeness degree is, the closer the object is to the optimal solution.

3 Case illustration

The proposed IMOPSO algorithm is tested on data obtained from a PV micro-grid power station. This station is located in a science and technology park in Suzhou, Jiangsu Province. Through the mixed power supply of grid electricity, photovoltaic power and energy storage, it achieves peak shaving and valley filling, and optimizes the control of the power load in the park. The first phase of this project is designed with a photovoltaic installed capacity of 100 kW, an outdoor container energy storage capacity of 200 kW, and the installation of AC and DC charging piles. The system can switch between grid-connected and off-grid operation modes, and can also realize functions such as system emergency and peak shaving. The details of the system and data used are given subsequently.

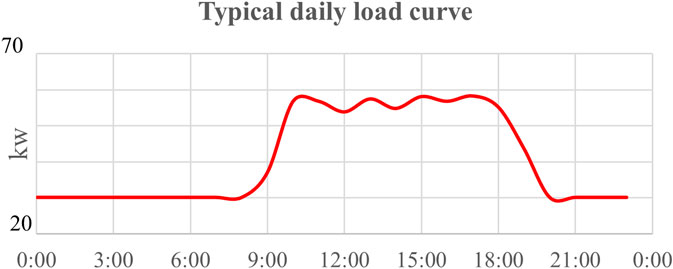
(1) Load operation status: The typical daily load data graph of this power station is shown in Figure 7.

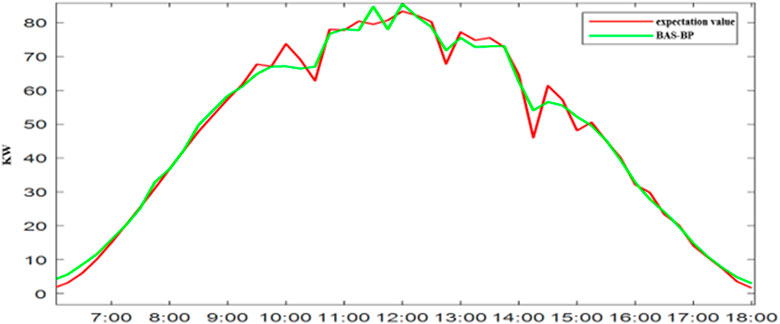
(2) PV power generation: The typical daily photovoltaic power generation of this power station is shown in Figure 8.

(3) Electricity prices: The photovoltaic micro-grid can purchase and sell electricity from the grid. According to the load demand and the demand for time-of-use electricity prices, the whole day is divided into three periods: off-peak, peak and flat. The specific information is shown in Table 3.

Figure 7

Figure 7. 24 h load curve during a typical day.

Figure 8

Figure 8. Daily active power output of photovoltaic system.

Table 3

Table 3. Electricity Prices (ToU and fixed).

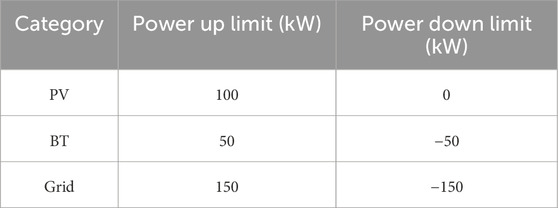
(4) Parameters: The parameters related to distributed power sources, limit values, and emission coefficients are given in Table 4–6 respectively.

Table 4

Table 4. Parameters related to distributed power sources.

Table 5

Table 5. Limit values for active power of micro-power sources.

Table 6

Table 6. Emission coefficients of pollutants and treatment costs.

4 Results and discussion

The simulation and analysis of power station optimal dispatching are carried out using MATLAB-Simulink. In this paper, the simulation of optimal output of the system under the grid-connected mode and the solution of the optimal dispatching function are conducted for time-of-use and fixed electricity prices. Moreover, a comparison between multi-objective optimization and single-objective optimization is also carried out for both prices.

4.1 System optimal dispatching considering time-of-use (ToU) electricity prices

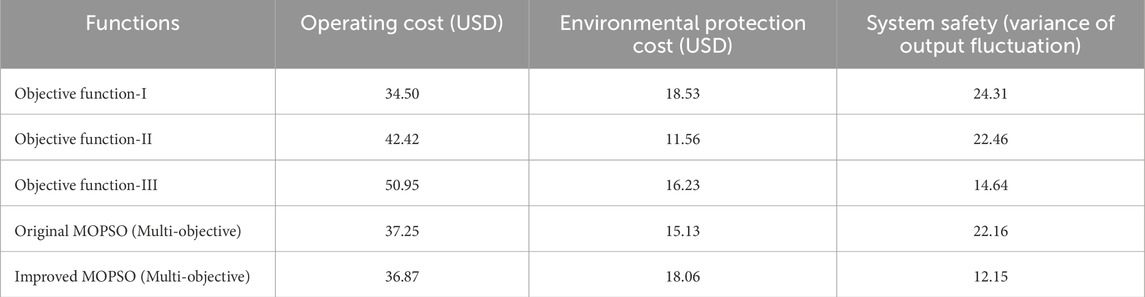
The optimal outputs of the multi-objective system considering time-of-use (ToU) electricity prices of the original MOPSO algorithm and improved MOPSO algorithm (IMOPSO) are shown in Figure 9 respectively. The IMOPSO algorithm significantly reduces output fluctuations in the PV and battery systems compared to the original algorithm. Specifically, the modified algorithm achieves smoother transitions between charging and discharging phases of the battery, particularly during peak and off-peak electricity price periods.

Figure 9

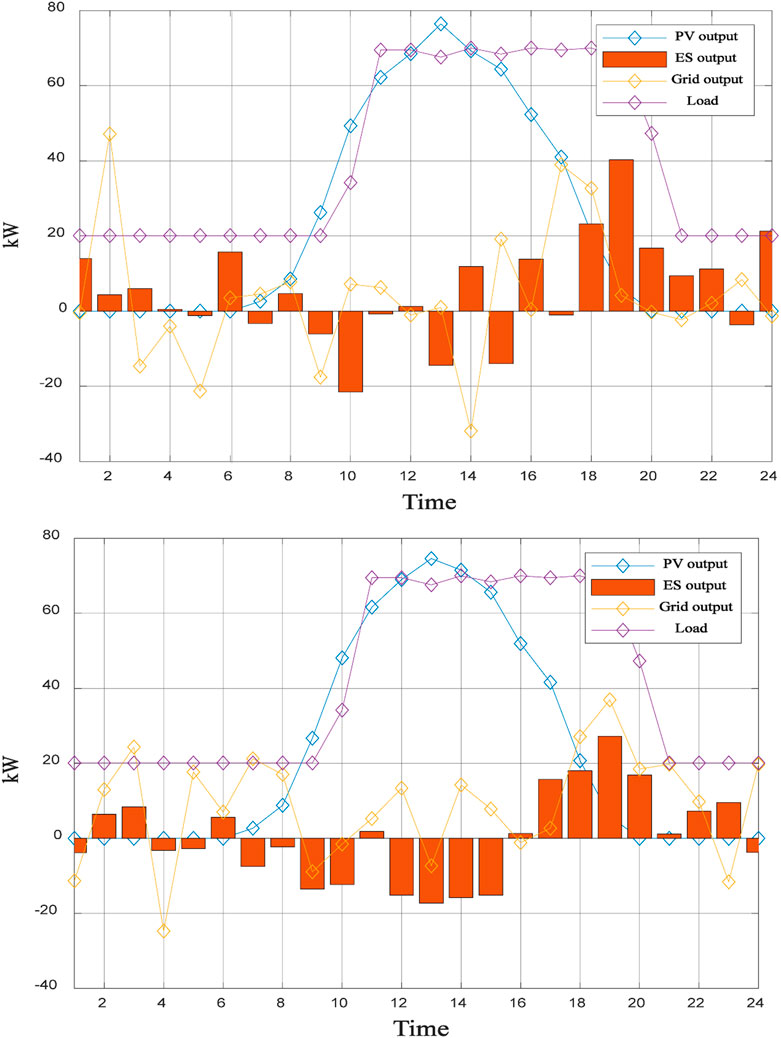
Figure 9. Comparison of Optimization Results for original and improved MOPSO algorithms (ToU price case) (Top) Original MOPSO algorithm, (Bottom) Improved MOPSO (IMOPSO) algorithm.

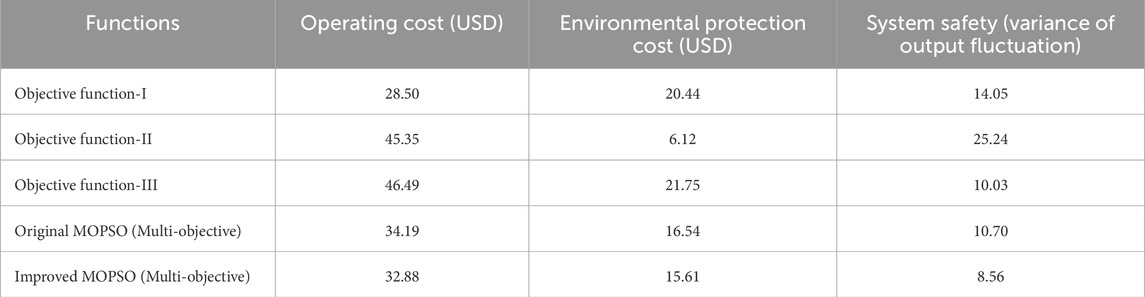
The Pareto front in Figure 10 illustrates the trade-offs between three objective functions i.e., operational cost, environmental cost, and system safety. For instance, Figure 10 (Objective function-1 to minimize operational cost) shows aggressive battery utilization during low-price periods, leading to reduced grid dependency. However, this strategy increases environmental costs (20.44 USD vs. 6.12 USD in Objective function-II shown in Table 7) due to frequent battery cycling, which indirectly raises lifecycle emissions. In Figure 10 (Objective function-II to minimize the cost of pollutant) and Figure 10 (Objective function-III to minimize the variance of output fluctuation), the grid dependency increases.

Figure 10

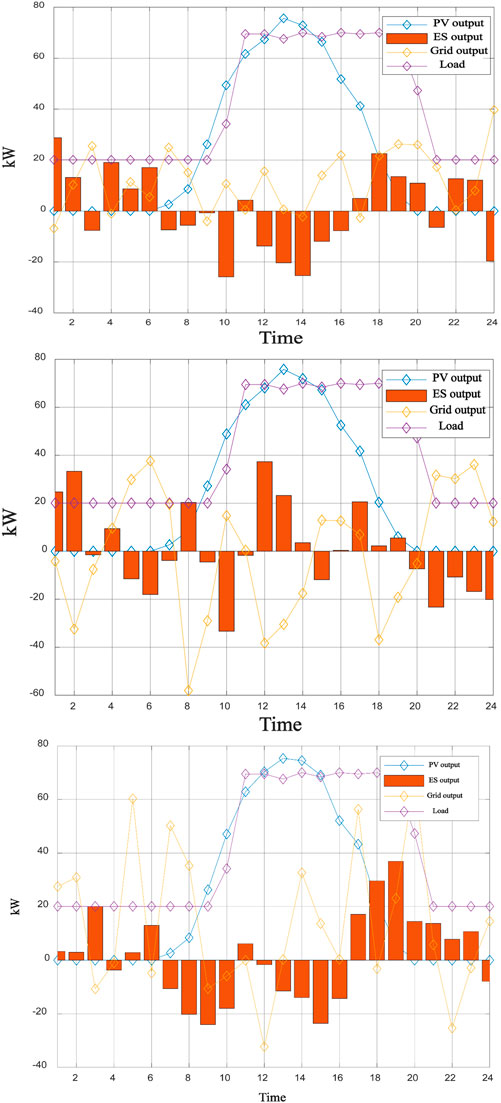
Figure 10. Optimal outputs of system for 3 objective functions (ToU price case) (Left) objective function-I, (Center) objective function-II, (Right) objective function-III.

Table 7

Table 7. Summary of optimization results for three objective functions (ToU price case).

In Table 7, the operation costs, environmental protection costs and variance of system output fluctuation for photovoltaic microgrid under different objective functions are presented. From the table, it can be seen that the microgrid optimal scheduling under multi-objective constraints has a total cost of 50.73 USD for original MOPSO algorithm (before improvement) and 48.49 USD for IMOPSO (after improvement). Moreover, the grid connection security is also higher after improvement, indicating that the improved multi-objective optimization has algorithmic advantages and proves that the improvement is effective. In the scenario based on single-objective optimization, the total cost is actually less than that of multi-objective optimization i.e., the results under multi-objective constraints are not as good as in case of single-objective optimization for some target values. However, when compared comprehensively, multi-objective constraints are more in line with the actual needs and are more objective.

4.2 System optimal dispatching under fixed electricity prices

The optimal outputs of the multi-objective system considering fixed electricity prices of the original MOPSO algorithm and improved MOPSO algorithm (IMOPSO) are shown in Figure 11 respectively. The IMOPSO algorithm demonstrates enhanced stability in grid power exchange.

Figure 11

Figure 11. Comparison of Optimization Results for original and improved MOPSO algorithms (fixed price case) (Top) Original MOPSO (Bottom) Improved IMOPSO.

The optimal solutions in Figure 12 illustrates the trade-offs between three objective functions i.e., operational cost, environmental cost, and system safety for fixed electricity price case.

Figure 12

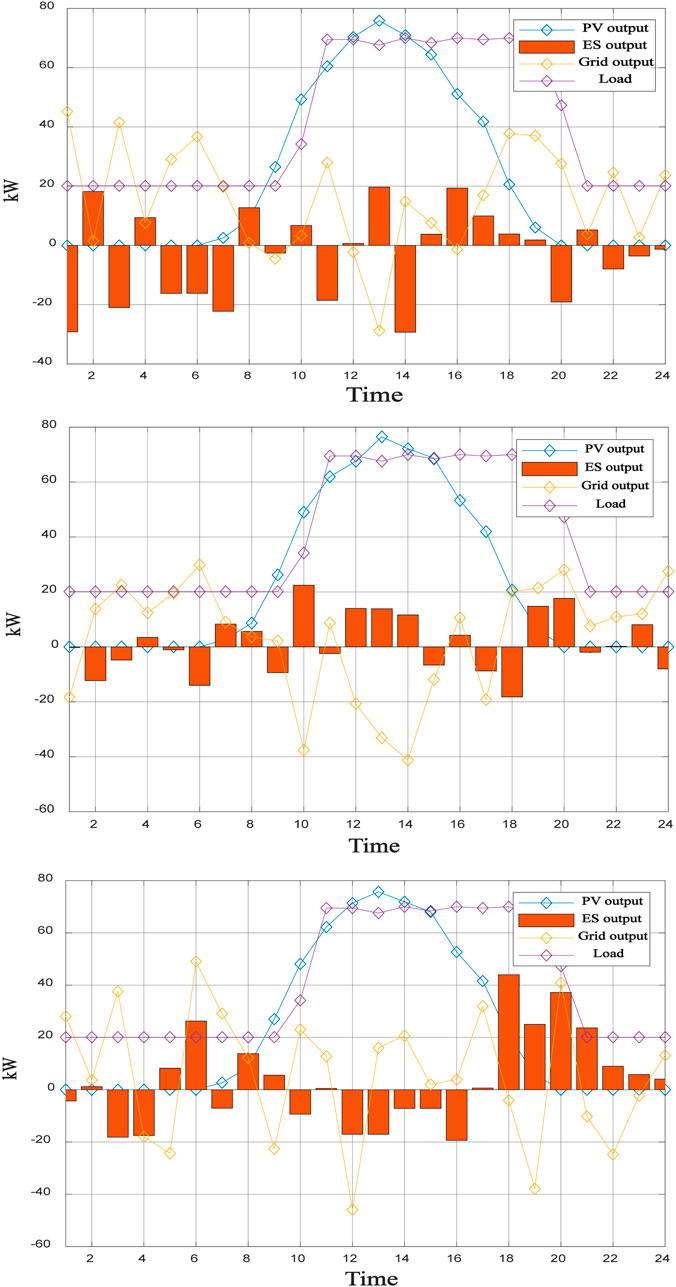
Figure 12. Optimal outputs of the system for three objective functions (fixed price case) (Left) objective function-I, (Center) objective function-II, (Right) objective function-III.

The optimization results for fixed price case are summarized in Table 8. It shows that under Objective 3 (minimizing grid fluctuation), the safety variance decreases from 14.64 (single-objective) to 12.15 (improved multi-objective), indicating a 17% improvement in system stability. However, this comes at the expense of higher operational costs (50.95 USD vs. 37.25 USD), as the battery compensates for grid variability through frequent bidirectional energy exchange.

Table 8

Table 8. Summary of optimization results for three objective functions (fixed price case).

It can also be seen from the table that before the improvement of the microgrid optimal scheduling algorithm under multi-objective constraints, the total cost was 54.93 USD, and after the improvement, it was 52.38 USD. Moreover, the grid connection security was higher, indicating that the improved multi-objective optimization algorithm has an algorithmic advantage and proves that the improvement is effective. However, in the scenario based on single-objective optimization, the total cost is actually less than that of multi-objective optimization. But when compared comprehensively, multi-objective constraints are more in line with the actual needs and are more objective.

4.3 Comparative analysis of both pricing cases

Under the conditions of fixed electricity price and time-of-use electricity price, the comparative analysis of the system output under grid connection conditions can be summarized as:

(1) With the optimization objective function-I (considering the minimum system operation cost): During the photovoltaic power generation stage, the battery in the system continuously charges. When there is no photovoltaic power generation, it continuously discharges to maintain normal power supply for the night load, and the grid output is relatively smooth. This indicates that the battery has played a significant role in offsetting the purchase cost, but it also caused the battery output burden.

(2) With the optimization objective function-II (considering environment friendliness of the system operation i.e., low environmental cost): It can be clearly seen in the system that in order to reduce the battery output, the grid output is larger. Because the pollution degree of the grid itself is much lower than that of the battery. But this also led to large fluctuations in grid output and reduced system safety.

(3) With the optimization objective function-III (considering the minimum impact of grid fluctuations during grid connection): In order to reduce the grid output fluctuations, the battery charges and discharges to the greatest extent during the day and night, so as to maintain the load operation. But this also led to an increase in system operation cost and environmental cost.

(4) Under the condition of comprehensive multi-objective optimization (considering the optimization of all objective functions): In order to balance the multi-objective optimization purpose, it can be seen that both the battery and the grid in the system show low-amplitude fluctuations. Through continuous bidirectional power exchange with the grid, the load is maintained in normal operation.

5 Conclusion

This study proposes an improved multi-objective particle swarm optimization (IMOPSO) algorithm for coordinated control and optimizing photovoltaic microgrid dispatch under grid-connected mode. The proposed IMOPSO algorithm is based on the inertia weight adaptive adjustment method of optimal similarity degree and the Pareto solution archive update strategy of multi-directional iteration. It is also tested on a practical case that shows its coordinated control and effectiveness in terms of minimizing operational cost, environment friendliness and reducing variance of output fluctuation. The following conclusions are drawn from this study.

(1) The integration of adaptive inertia weight and dynamic Pareto solution updating significantly improves convergence speed and solution diversity. Experimental results confirm a 3.8%–4.2% reduction in total costs and a 17%–24% improvement in safety metrics compared to the original MOPSO.

(2) While single-objective optimization achieves lower costs in isolated scenarios, the improved multi-objective framework better aligns with real-world requirements by balancing cost, environmental impact, and grid stability. For instance, safety variance decreases by 20% under fixed pricing without substantial cost escalation.

(3) The proposed model enables effective “peak shaving and valley filling” through coordinated battery-grid interactions, reducing dependance on fossil-fuel-based grid power during peak periods. This strategy supports sustainable energy transitions while maintaining economic viability.

5.1 Limitations and future work

The current system used for testing is a medium-sized microgrid system. The installed capacity of photovoltaic power generation is only 100 kW, and the energy storage capacity is 200 kW. This microgrid system is relatively simple in its overall structure and is mainly used for experimental testing purposes. It cannot fully reflect the complexity and diversity of modern power systems. During the experimental process, safety and the convenience of management are the primary important considerations. But, the application to large-scale microgrid system with thousands of variables is very important. After building a next-generation digital twin platform for microgrids in the future, we will further conduct real-time simulation and hardware testing to comprehensively explore the feasibility and scalability of this algorithm.

This study assumes the ideal weather conditions for photovoltaic output. In subsequent research, random factors of renewable energy generation and demand uncertainty should be included to enhance the practicability of the model from the perspectives of multi-energy synergy, multi-dimensional optimization, and demand-side randomness. In addition, real-time hardware-in-the-loop verification should be expanded to enhance the robustness of the algorithm.

Data availability statement

The raw data supporting the conclusions of this article will be made available by the authors, without undue reservation.

Author contributions

DY: Writing - original draft, Methodology, Data curation. KH: Writing - review and editing, Conceptualization, Methodology. XL: Writing – review and editing, Methodology. GC: Writing – review and editing, Investigation. XS: Writing – review and editing, Investigation. WW: Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. This project was supported by China southern power grid corporation science and technology project funding (Grant No. GDKJXM20220335). The funder was not involved in the study design, collection, analysis, interpretation of data, the writing of this article, or the decision to submit it for publication.

Conflict of interest

Authors DY, XL, and WW were employed by Electric Power Dispatching and Control Center of Guangdong Power Grid Co., Ltd. Authors KH, GC, and XS were employed by NARI Technology Co., Ltd.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Aguilar, D., Quinones, J. J., Pineda, L. R., Ostanek, J., and Castillo, L. (2024). Optimal scheduling of renewable energy microgrids: a robust multi-objective approach with machine learning-based probabilistic forecasting. Appl. Energy 369, 123548. doi:10.1016/j.apenergy.2024.123548

CrossRef Full Text | Google Scholar

Awad, H., Emtiaz Salim, K. M., and Gül, M. (2020). Multi-objective design of grid-tied solar photovoltaics for commercial flat rooftops using particle swarm optimization algorithm. J. Build. Eng. 28, 101080. doi:10.1016/j.jobe.2019.101080

CrossRef Full Text | Google Scholar

Borhanazad, H., Mekhilef, S., Ganapathy, V. G., Modiri-Delshad, M., and Mirtaheri, A. (2014). Optimization of micro-grid system using MOPSO. Renew. Energy 71, 295–306. doi:10.1016/j.renene.2014.05.006

CrossRef Full Text | Google Scholar

Boscaino, V., Ditta, V., Marsala, G., Panzavecchia, N., Tinè, G., Cosentino, V., et al. (2024). Grid-connected photovoltaic inverters: grid codes, topologies and control techniques. Renew. Sustain. Energy Rev. 189, 113903. doi:10.1016/j.rser.2023.113903

CrossRef Full Text | Google Scholar

Burhan, M., Chua, K. J. E., and Ng, K. C. (2016). Sunlight to hydrogen conversion: design optimization and energy management of concentrated photovoltaic (CPV-Hydrogen) system using micro genetic algorithm. Energy 99, 115–128. doi:10.1016/j.energy.2016.01.048

CrossRef Full Text | Google Scholar

Chase, N., Rademacher, M., Goodman, E., et al. (2025). A benchmark study of Multi-objective optimization methods. Red. Cedar Technol. Rev. 06.09.

Google Scholar

Gholami, K., and Dehnavi, E. (2019). A modified particle swarm optimization algorithm for scheduling renewable generation in a micro-grid under load uncertainty. Appl. Soft Comput. J. 78, 496–514. doi:10.1016/j.asoc.2019.02.042

CrossRef Full Text | Google Scholar

Guo, Z., Luo, J., Song, N., and Shu, J. (2025). Multi-objective optimal dispatch of island microgrid considering a novel scheduling resource. Electr. Power Syst. Res. 241, 111378. doi:10.1016/j.epsr.2024.111378

CrossRef Full Text | Google Scholar

He, G., Su, R., Yang, J., Huang, Y., Chen, H., Zhang, D., et al. (2023). Optimal location and sizing of distributed generator via improved multi-objective particle swarm optimization in active distribution network considering multi-resource. Energy Eng. 120 (9), 2133–2154. doi:10.32604/ee.2023.029007

CrossRef Full Text | Google Scholar

He, Y., Wu, X., Sun, K., Liu, X. Y., Wang, H. P., Zeng, S. M., et al. (2024). A novel MOWSO algorithm for Microgrid multi-objective optimal dispatch. Electr. Power Syst. Res. 232, 110374. doi:10.1016/j.epsr.2024.110374

CrossRef Full Text | Google Scholar

Hemmati, M., Amjady, N., and Ehsan, M. (2014). System modeling and optimization for islanded micro-grid using multi-cross learning-based chaotic differential evolution algorithm. Int. J. Electr. Power and Energy Syst. 56, 349–360. doi:10.1016/j.ijepes.2013.11.015

CrossRef Full Text | Google Scholar

Indira, G., Bhavani, M., Brinda, R., and Zahira, R. (2024). Electricity load demand prediction for microgrid energy management system using hybrid adaptive barnacle-mating optimizer with artificial neural network algorithm. Energy Technol. 12 (5), 2301091. doi:10.1002/ente.202301091

CrossRef Full Text | Google Scholar

Jiang, W., Liu, Y., Fang, G., and Ding, Z. (2023). Research on short-term optimal scheduling of hydro-wind-solar multi-energy power system based on deep reinforcement learning. J. Clean. Prod. 385, 135704. doi:10.1016/j.jclepro.2022.135704

CrossRef Full Text | Google Scholar

Jiie, H., Guo, X., Li, Y., and Wu, T. (2024). Uncertain scheduling of the power system based on wasserstein distributionally robust optimization and improved differential evolution algorithm. Energies 17 (15), 3846. doi:10.3390/en17153846

CrossRef Full Text | Google Scholar

Keddouda, A., Ihaddadene, R., Ali, B., Atia, A., Arıcı, M., Lebbihiat, N., et al. (2023). Solar photovoltaic power prediction using artificial neural network and multiple regression considering ambient and operating conditions. Energy Convers. Manag. 288, 117186. doi:10.1016/j.enconman.2023.117186

CrossRef Full Text | Google Scholar

Keisang, K., Bader, T., and Samikannu, R. (2021). Review of operation and maintenance methodologies for solar photovoltaic microgrids. Front. Energy Res. 9, 730230. doi:10.3389/fenrg.2021.730230

CrossRef Full Text | Google Scholar

Liang, T., Chai, L., Cao, X., Tan, J., Jing, Y., and Lv, L. (2024). Real-time optimization of large-scale hydrogen production systems using off-grid renewable energy: scheduling strategy based on deep reinforcement learning. Renew. Energy 224, 120177. doi:10.1016/j.renene.2024.120177

CrossRef Full Text | Google Scholar

Multi-objective Optimization dispatching of microgrid based on improved particle swarm algorithm (2021). Electr. Power Sci. Eng. 37(3):1–7.

Google Scholar

Parvin, M., Yousefi, H., and Noorollahi, Y. (2023). Techno-economic optimization of a renewable micro grid using multi-objective particle swarm optimization algorithm. Energy Convers. Manag. 277, 116639. doi:10.1016/j.enconman.2022.116639

CrossRef Full Text | Google Scholar

Phuc Duong, M., Le, M.-Ha, Nguyen, T. T., and Doan, A. T. (2025). Economic and technical aspects of power grids with electric vehicle charge stations, sustainable energies, and compensators. Sustainability 17, 376. doi:10.3390/su17010376

CrossRef Full Text | Google Scholar

Qian, X., Yang, Y., Li, C., and Tan, S. C. (2020). Operating cost reduction of dc microgrids under real-time pricing using adaptive differential evolution algorithm. IEEE Access 8, 169247–169258. doi:10.1109/access.2020.3024112

CrossRef Full Text | Google Scholar

Qu, H., and Ye, Ze (2023). Multi-objective optimization operation of micro energy network with energy storage system based on improved weighted fuzzy method. Energy Rep. 9, 1995–2003. doi:10.1016/j.egyr.2023.04.125

CrossRef Full Text | Google Scholar

Raghavan, A., Maan, P., and Shenoy, A. K. B. (2020). Optimization of Day-ahead energy storage system scheduling in microgrid using genetic algorithm and particle swarm optimization. IEEE Access 8, 173068–173078. doi:10.1109/access.2020.3025673

CrossRef Full Text | Google Scholar

Ramli, M. A. M., Bouchekara, H. R. E. H., and Alghamdi, A. S. (2018). Optimal sizing of PV/wind/diesel hybrid microgrid system using multi-objective self-adaptive differential evolution algorithm. Renew. Energy 121, 400–411. doi:10.1016/j.renene.2018.01.058

CrossRef Full Text | Google Scholar

Rezaeimozafar, M., Duffy, M., Monagha, R. F. D., and Barrett, E. (2024). Residential PV-battery scheduling with stochastic optimization and neural network-driven scenario generation. Energy Rep. 12, 418–429. doi:10.1016/j.egyr.2024.06.017

CrossRef Full Text | Google Scholar

Shan, H., Liu, H., Wu, L., Feng, Z., Wang, M., Yang, L., et al. (2018). Economic optimisation of microgrid based on improved quantum genetic algorithm. J. Eng. 2019, 1167–1174. doi:10.1049/joe.2018.8849

CrossRef Full Text | Google Scholar

Torkan, R., Ilinca, A., and Ghorbanzadeh, M. (2022). A genetic algorithm optimization approach for smart energy management of microgrids. Renew. Energy 197, 852–863. doi:10.1016/j.renene.2022.07.055

CrossRef Full Text | Google Scholar

Upadhyay, S., Ahmed, I., and Mihet-Popa, L. (2024). Energy management system for an industrial microgrid using optimization algorithms-based reinforcement learning technique. Energies 17 (16), 3898. doi:10.3390/en17163898

CrossRef Full Text | Google Scholar

Wu, X., Liu, Z., Liting, T., Dong, D., and Shuili, Y. (2014). Energy storage device locating and sizing for distribution network based on improved multi-objective particle swarm optimizer. Power Syst. Technol. 38 (12), 3405–3411.

Google Scholar

Xingshen, L., Jing, Z., Yu, H., Ying, Z., Ying, L., and Kaifeng, Y. (2021). Multi-objective optimization dispatching of microgrid based on improved particle swarm algorithm. Electr. Power Sci. Eng. 37 (3), 1–7.

Google Scholar

Zhihu (2025). What is meant by TOPSIS comprehensive evaluation method based on entropy weight? EB/OL. Available online at: http://www.zhihu.com/question/546564958.

Google Scholar