- 1Hydrostructural Pedology, Centre de Recherche Ile de France, IRD France Nord, Institut de Recherche pour le Développement, Bondy, France
- 2Department of Biological and Agricultural Engineering, Zachry Department of Civil Engineering, Texas A&M University, College Station, TX, USA
Current soil water models do not take into account the internal organization of the soil medium and consequently ignore the physical interaction between the water film at the surface of solids that form the soil structure and the structure itself. In this sense, current models deal empirically with the physical soil properties, which are all generated from this soil water and soil structure interaction. As a result, the thermodynamic state of the soil water medium, which constitutes the local physical conditions of development for all biological and geochemical processes within the soil medium, is still not well defined and characterized. This situation limits modeling and coupling the different processes in the soil medium since they all thermodynamically linked to the soil water cycle. The objective of this article is to present a complete framework for characterizing and modeling the internal soil organization and its hydrostructural properties resulting from interaction of its structure with the soil water dynamics. The paper builds on the pedostructure concept, which allowed the integration of the soil structure into equations of water equilibrium and movement in soils. The paper completes the earlier framework by introducing notions of soil-water thermodynamics that were developed in application to the concept of the Structural Representative Elementary Volume (SREV). Simulation of drainage after infiltration in the Yolo loam soil profile, as compared to measured moisture profile using the measured soil characteristic parameters, showed a high degree of agreement. This new modeling framework opens up new prospects in coupling agro-environmental models with the soil medium, recognizing that the soil organization, hydro-structural, and thermodynamic properties are the foundation for such coupling.
Introduction
Representing the structured medium of top soil, with special attention to its hierarchy of scales, is imperative for understanding and modeling the dynamics of water flow and storage in the vadose zone. This is of importance in hydrology, agronomy, and geochemistry, and in studies involving the environmental fate of solutes at field, farm, and watershed scales. Single pore representation of the soil water medium is very common in agronomic models such as GRASIM (Mohtar et al., 1997) or CropSyst (Stöckle et al., 2003). The tendency in modeling water flow and solute transport in structured soil is to distinguish two domains, micro- and macro-pore, in an implicit soil horizon REV (Representative Elementary Volume) of the soil medium (Othmer et al., 1991; Chen et al., 1993; Gerke and van Genuchten, 1993; Katterer et al., 2001; Logsdon, 2002; Simunek et al., 2003, 2008).
However, none of these models consider the soil medium as a structured medium with aggregates, and thus, they are unable to take into account the notion of primary peds, which represent the first level of organization of the primary particles into aggregates (Brewer, 1964), and the notion of pedostructure (Braudeau et al., 2004) which is constituted by their assembly. Consequently, the swelling-shrinkage properties of the primary peds within the soil structure that were quantified by Braudeau and Bruand (1993), and also the resulting hydro-structural properties of the soil medium (Braudeau et al., 2004, 2005; Braudeau and Mohtar, 2006), cannot be considered and modeled in the current agro-environmental modeling.
Thus, as long as the hydro-structural behavior of soil organization and structure remain undefined, the modeling of the numerous biophysical and chemical processes that take place within the soil medium cannot be fully physically modeled. It is why Braudeau and Mohtar (2009) introduced a new paradigm for modeling soil water on the basis of two new concepts in soil science: the pedostructure concept and the Structure Representative Elementary Volume (SREV) concept. The latter allows transformation of the pedostructure organization into a thermodynamic system consisting of two nested and complementary pore sub-systems (micro and macro) that refer to the inside and outside of the primary ped media. These micro- and macro-pore systems are in a quasi-equilibrium state of water retention when slow changes in water content (such as by evaporation or drainage) occur, whatever the water content.
A computer model simulating the multi scale hydro-structural functioning of the pedon, named Kamel®, was introduced by Braudeau et al. (2009) based on the pedostructure concept only, i.e., without integrating the recent advances in soil water thermodynamics following application of the SREV concept to the pedostructure organization. The objective of the paper is to present the complete theory behind Kamel® updated with the recent thermodynamic development of its state equations of equilibrium. Specifically, we will introduce (i) the basic principles of the soil-water modeling framework represented by Kamel®, including the pedostructure concept, the SREV concept, and the new thermodynamics equations resulting from it; and (ii) the implementation of equations into the computer model using the Simile® software environment. Application of this framework is presented followed by a discussion on the novelty of this modeling framework and its potential applications to current environmental issues.
Theory
Pedon Representation
Primary peds and pedostructure
Brewer (1964) introduced the concepts of peds, primary ped, and the S-matrix. He defined a ped as “an individual natural soil aggregate consisting of a cluster of primary particles and separated from adjoining peds by surfaces of weakness which are recognizable as natural voids or by occurrence of cutans.” Primary peds are the simplest peds occurring in a soil material. They are not divided into smaller peds, but they may be packed together to form compound peds of higher level of organization. The S-matrix of a soil material “is the material within the simplest (primary) peds, or composing apedal soil materials, in which the pedological features occur; it consists of plasma, skeleton grains, and voids that do not occur in pedological features other than plasma separations.”
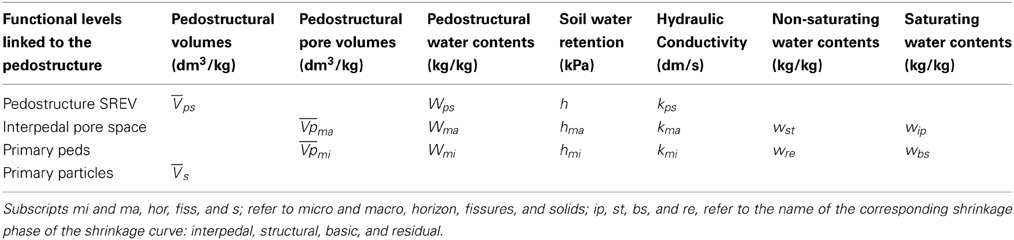
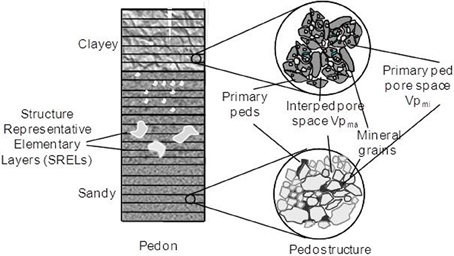
Braudeau et al. (2004) completed this morphological definition of primary peds with a hydro-functional definition based on the determination of an air entry point in the clayey plasma using the shrinkage curve that was continuously measured by the apparatus detailed in Braudeau et al. (1999). They introduced the term “pedostructure” which is the assembly of primary peds that is represented by two nested and complementary pore systems named as micropore and macropore corresponding respectively to the intra and inter primary ped pore space. Furthermore, Braudeau and Mohtar (2009) proposed the notion of “Structural Representative Elementary Volume” (SREV) to introduce the pedostructure concept in the systemic approach of the natural organization of the “soil-plant-atmosphere” continuum. The new paradigm generated enables characterization and modeling of the hydrostructural properties of soil horizons as hydro-functional elements of the pedon, itself representative of the soil mapping unit as schematized on Figure 1.
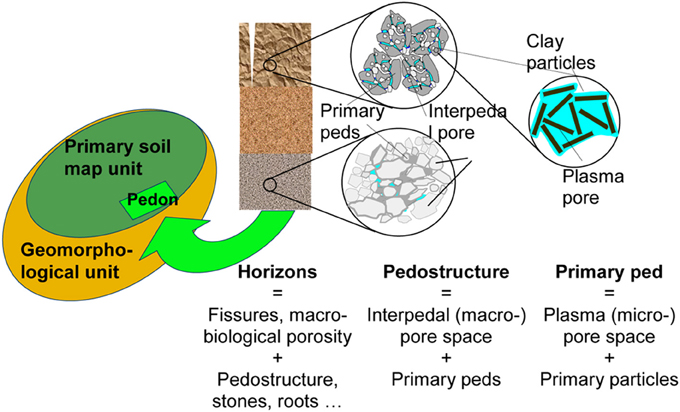
Figure 1. Internal and external hydro-functional hierarchy of the soil organization (Braudeau and Mohtar, 2009).
According to this new paradigm a new system of descriptive variables and characteristic parameters were defined for the two distinct media of the pedostructure: micro and macro pore volumes corresponding to the inside and outside of the primary peds. The pedostructure variables are listed in Table 1: Vmi, Vpmi, Wmi, hmi, kmi, Vma, Vpma, Wma, hma, kma (nomenclature and definitions are given in the text below).
Structural representative elementary volume (SREV) of the pedostructure
Unlike REV, SREV is virtually delimited by an enclosure permeable to air, water, and solute fluxes, but not to the solid particles that compose the structure and of which the mass (structural mass, Ms) contained in the SREV stays constant. This description defines any SREV as a volume V, virtually sampled in the homogeneous medium that it represents, and such that its structural mass, Ms, and the relative organization of solids particles between them remain unchanged with a change in water content. This allows taking Ms as reference to which all specific extensive variables of the SREV are reported; for example in Table 1, the total water content (W = Mw/Ms) and the pedostructural specific volume (Vps = Vps/Ms). We notice that this latter variable cannot exist in the REV-based system of variables since the volume itself of the REV is taken as reference for its extensive variables. Moreover, not only the organizational variables are reported to the structural mass Ms, but also the thermodynamic functions that are specific of the considered SREV. For example, U is the total internal energy, and Gwl, the total Gibbs free energy of water in its liquid phase, both contained in the SREV of pedostructure considered and reported to the structural mass Ms of this SREV. These properties are called, respectively: (i) pedostructural (instead of specific) internal energy, and (ii) pedostructural Gibbs free energy of the liquid water phase, counted positively (Braudeau et al., 2014):
and
where [S = S/Ms; V = V/Ms; Gwmi = Gwmi/Ms; Gwma = Gwma/Ms; Wmi = Mwmi/Ms; Wma = Mwma/Ms] are the extensive variables of the pedostructure divided by its structural mass Ms; related to the water components (micro and macro) of the liquid phase, respectively: the pedostructural entropy, volume, Gibbs free energy of the micro and macro liquid water phases and pedostructural micro and macro water contents. The intensive variables T, P, μwmi and μwma, and μair, are respectively: the absolute temperature, the pressure exerted on the considered SREV, the water chemical potential (<0) inside and outside of primary peds, and the chemical potential of the air.
A decrease in water content from water saturation induces a water suction pressure, or water retention, hmi and hma, in the both complementary pore systems of the pedostructure SREV. They are defined such as:
where μwmiSat and μwmaSat are the water chemical potential at saturation.
Equations (1) determine the hydrostructural and thermodynamic equilibrium states of any pedostructure SREV defined in a soil medium and under the controlled variables: T, P, W, and μair. Braudeau et al. (2014) and Assi et al. (2014) could then show the two following points: (i) Gwl, Gwmi, and Gwma stay constant with any change in water content, and (ii) at each equilibrium state depending of W, there is necessarily equality between the water retention inside and outside of primary peds, such that: hmi = hma = h at any value of W at equilibrium. They could deduce then the physical equations of the pedostructural shrinkage curve and the water retention curve that will be presented in the next section.
This new approach leads to the following qualifications and properties of the soil medium in each horizon of the pedon, considering that, at the global scale of the soil horizon, the pedostructure is only a component of the soil medium organization but which imposes to the horizon its hydrostructural properties:
(1) The soil medium is physically described by its pedostructural state variables S, V, A, Wmi, and Wma as functions of the pedostructural water content W at equilibrium under the intensive variables T, P, hmi, hma, and μair. These intensive variables are assumed to have the same value within each of the successive layers that have been discretized as horizontal SREVs in the soil horizon (see next section) and named SRELs (Table 1).
(2) The homogeneity of the soil medium in a soil horizon can be defined as the stability all over the horizon, of parameters of the pedostructural state equations: S(W), V(W), A(W), and h(W), as parametric functions of the variable W at T, P, and μa constant. Practically, knowing that A/ρ0air = V − W/ρ0w − Vs for the pedostrucure (Vs being the pedostructural volume of the solid phase), a soil horizon will be considered structurally homogeneous in regard to its physical properties with water if the three functions: the pedostructural entropy curve, S(W), shrinkage curve, V(W) and water retention curve, h(W), keep their hydrostructural parameters constant everywhere in the medium of the horizon, for given P and T. From the thermodynamic point of view, and in contrary to the current vision of the soil characterization, there is not only one soil moisture characteristic curve [the water retention curve h(W)], but at least three soil moisture characteristic curves that are the equations of state of the free energy equation at equilibrium depending on W: S(W), V(W) and h(W) = hmi(Wmi) = hma(Wma).
(3) Every pedostructural extensive (or organizational) variable of a SREV, is hierarchically nested inside the SREV with respect to the hierarchical organization of the medium represented by the SREV. This allows us to define the descriptive variables of the soil medium at its various functional levels, namely; the pedon, horizon, pedostructure, primary peds, and primary particles (Figure 1, Braudeau and Mohtar, 2009).
Discretization of the pedon according to the SREV concept
Simulation of the gravimetric water transfer and related processes within and through the pedon requires discretization of the medium into representative elementary layers. Assuming that a soil horizon has homogenous hydro-structural properties, and that it is a SREV of the corresponding horizon in the soil mapping unit, then each soil horizon can be discretized into thin horizontal layers that have the physical properties (pedostructure parameters) of the horizon considered, and that are at different equilibrium states depending on the water content all over the width of the pedon (Figure 2). These layers are called Structural Representative Elementary Layers (SRELs). In general, fine layers having a minimum thickness of 0.2 dm can be considered for the simulation of water transfer in soils. Moreover, the pedon must be wide enough so it can be representative of the soil with regards to pedologic features such as fissures, stones, etc., that may be observed at the pedon scale in the field.
Descriptive variables of an SREL include those of the pedostructure plus other features such as roots, biogenic macro-pores, stones, etc., whose volumes are related to the total pedostructure mass of the layer (MpsL). Table 2 presents the different hydro-functional subsystems of the pedon, like the SRELs, of which variables and parameters should be defined with respect to the SREV concept to be compatible with the other levels of organization of the pedon. In particular, the mass of pedostructure included in the SREL is conveniently taken as reference rather than the total mass of solids belonging to the layer. This allows us to keep the variables and properties of the pedostructure as part of the new SREL set of variables. For example, suppose that an SREL in one soil horizon consists of a certain volume of pedostructure and other organizational volumes like volumes of stones, roots, biogenic macro-pores, etc., all these volumes, including also the pedostructure volume, should be estimated as fractions of the total volume of the SREL, while the pedostructure mass contained in the SREL, MpsL, should be used as mass of reference for extensive variables of the SREL. Therefore, all SRELs of the horizon should have the same characteristic parameters of the entire horizon.
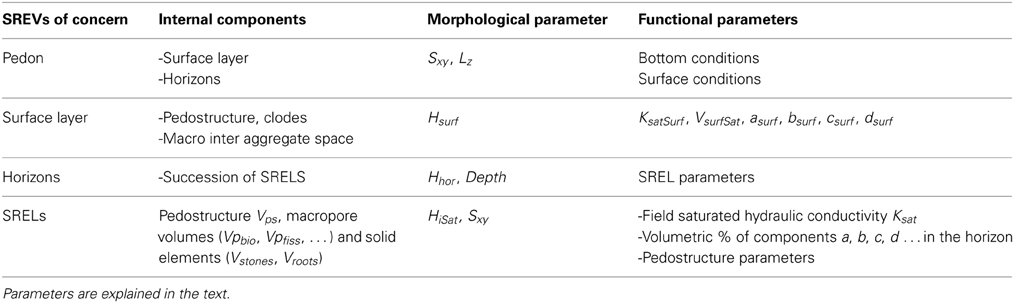
Table 2. List of the hydro-functional subsystems of a pedon SREV, their internal components, and the corresponding parameters.
If that a = (Vps + Vfiss)/Vhorizon is the volumetric proportion of pedostructure and fissures due to shrinkage in the considered horizon SREV, and Vps = Vps/Mps (dm3/kg), is the pedostructure specific volume measured in the laboratory on a soil sample representing the pedostructure in this horizon's SREV, then, the pedostructure mass in the discretized layer volume Vlay, SREL of the horizon, will be:
where MpsL is all the pedostructure mass in the layer, Vlay is the volume of the SREL, and Vps is the specific volume of the pedostructure. Accordingly, if we set b, the volumetric fraction of stones in the horizon, c, the volumetric fraction of biological voids, d, the proportion of roots, etc., therefore the specific volume of a SREL of the horizon will be:
Setting:
defines coefficients a, b, c, d as parameters of a horizon at the pedon scale that have to be determined by observations of soil profiles in-situ; they are such that their sum is equal to 1. As well as we have distinguished the poral volumes Vpfiss and Vpbio of the layer, in addition to the poral volumes Vpmi and Vpma of the pedostructural volume Vps, we distinguish also the water contents in these volumes, such as, respectively, Wfiss, Wbio, and Wps. Among the specific volumes in equations (3) only (Vps + Vpfiss) is directly dependent on the pedostructural water content Wps according to the pedostructural shrinkage curve Vps(Wps).
Hydro-Thermodynamic Equilibrium of the Pedostructure
The pedostructural water retention curve
Braudeau et al. (2014) derived the expressions of the pedostructure water retention inside and outside of primary peds (hmi and hma) from Equations (1) stated above. The pedostructure water retention h at equilibrium, such that h = hmi = hma, is determined by the constant (stable) repartition of the surface charges of the solids particles between inside and outside of primary peds (Emi and Ema) when the water content is changing:
where ρ0w is the specific density of water; Emi and Ema are the total potential energies (positive) relative to a fixed number of the surface charges of the solid particles (clays) inside of primary peds (for Emi) and outside at their surface in the interpedal macropore space (for Ema). Emi and Ema are in joules/kg of solids equal to the corresponding Gibbs free energies Gmi and Gma developed in the water phase surrounding the clay particles of the pedostructure. Both parameters WmiSat and WmaSat are, respectively, the micro and the macro water content of the pedostructure at saturation, when Wps = WpsSat. Thus, neglecting for Kamel the contribution hip of the saturation interpedal water content Wip which appear in certain soils weakly structured (Braudeau et al., 2014), parameters of the soil (pedostructure) water retention curve are Emi, Ema, WmiSat, and WmaSat.
Pedostructural micro and macro water contents at equilibrium
The equality of hmi and hma (Equations 4, 5) at each value of Wps is the condition for a reversible and slow change in water content that can be considered as a suit of hydro structural equilibrium states function of Wps. Braudeau et al. (2014) derived the unique solution of equality of Equations (4, 5), the couple [Weqma(W); Weqmi(W)], the equations of which are given below:
Considering that:
and
Weqma is the positive solution of the quadratic equation:
leading to:
then
Equations (9) and (10) give values of Weqmi and Weqma at equilibrium for each value of W. That means that, when they are reported in Equations (4, 5) of hmi and hma, these last have exactly the same value h. Figure 3 shows, as example, a measured soil water retention curve by tensiometer with the fitted curve h(Wps) and the corresponding curves of micro and macro pedostructural water contents at equilibrium.
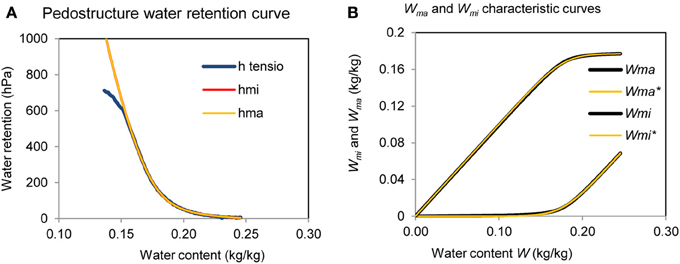
Figure 3. (A) Example of measured soil water retention curve using a tensiometer (h(W)) fitted by the theoretical water retention curve at equilibrium (h = hma = hmi); and (B), the corresponding curves Weqma(W) and Weqmi(W) at equilibrium of suction pressures, calculated from Equations (9, 10), and W*ma and W*mi, from Equations (A2b) and the sum (A2c, A2d).
Physical equations and parameters of the pedostructure hydrostructural equilibrium
According to the new developments in thermodynamics of the soil medium presented here above, the pedostructure shrinkage curve already modeled in Kamel using equations developed by Braudeau et al. (2004) were updated with the thermodynamic equations of Weqmi and Weqma. This update of the shrinkage curve is described in Supplementary Material, Appendix 2. A recapitulation of the whole equations and parameters describing the hydrostructural equilibrium states of the pedostructure in terms of its water content Wps is presented in Table 3.
Soil Water Dynamics at the Pedostructure Scale
The richards equation for the pedostructure medium
There are two types of water movement that are considered in the pedostructure and correlatively in the SRELs of the soil profile: (1) a local micro-macro transport corresponding to the water exchange between both pore systems, inside and outside of primary peds of the pedostructure, and (2) a transport through the pedostructure and between SRELs that involves only the interpedal water, Wma. The transfer equations are presented by Braudeau and Mohtar (2009); Braudeau et al. (2009):
and
where z is the depth (upwardly positive); hmi and hma are the water retention (positive values) inside and outside primary peds expressed in dm of water height (equivalent to a pressure in kPa), z in dm and kma in dm/s. The water pressures hmi and hma are determined by Equations (4, 5) in terms of Wmi and Wma out of equilibrium; equation and parameters for kma(Wma) and kmi are given here after.
Pedostructural hydraulic conductivity equation
The hydraulic conductivity kma in Equation (11) is exclusively related to the macro-pore water content Wma of the pedostructure. The water present outside of the pedostructure, such as the one present in fissures and biogenic pores defined in Equation (3) for the SREL at the horizon scale, does not constitute any part of the pedostructural water content Wps. Thus, we can assume that the movement of water within the pedostructural part of the horizon is always slow enough to consider changes in organization as a suit of equilibrium states in the same manner that the shrinkage and the soil retention curves were considered as Wps-dependent characteristics of equilibrium states of the soil medium.
Summing up Equations (11, 12) leads to a new shape of the Richards equation, not only concerning the use of SREV instead of REV variables, but also the controlling variables themselves: hma and kma that should be expressed in terms of Wma. Following Davidson et al. (1969) who showed that the unsaturated hydraulic conductivity, from saturation to field capacity, is well described by an exponential equation of W, instead of h (Gardner, 1958) generally used today (Bruckler et al., 2002), we experimentally observed the following equation for kma that wil be called pedostructural hydraulic conductivity kps (Assi et al., Submitted):
or
where k0ps = kpsSat/exp(αpsWmaSat) and α0 are the two characteristic parameters of this equation.
Equation (13) can also be expressed in terms of h such as, according to Equation (5):
of form: kps = k0psexp(αh/(h + βh))
where αh = αps ρw Ema, βh = ρwEma/WmaSat and k0ps = kpsSat/exp(αh/βh)
Equation (13b) is used in Kamel® for the unsaturated hydraulic conductivity of the pedostructure in terms of Wma limited to Wst, that means excluding the contribution of the saturated interpedal water Wip. The latter will be taken into account while measuring the saturated hydraulic conductivity by one of the standard laboratory methods such as falling head or constant head permeability tests.
Swelling rate of the pedostructure
The swelling and shrinkage dynamics of the pedostructure are governed by the same conceptual process that governs the water exchange between the primary peds and the interpedal pore space. Braudeau and Mohtar (2006) validated a particular case (aggregates immersed in water) of Equation (12) expressing the water exchange between the two media as proportional to the difference in their swelling pressure. In this equation, kmi is the transfer rate coefficient (kgwater kg−1soil kPa−1s−1) for the absorption-desorption of the interped water by the primary peds. This coefficient expresses the velocity of the last layer of water on the surface of the clay particles entering or leaving the primary peds. We assume that kmi is constant in the entire range of water content, from saturation to the micro air entry point B of the shrinkage curve (Figure 4) and that Equation (12) can be generalized to the shrinkage (dwbs/dt < 0) as well as the swelling (dwbs/dt > 0).
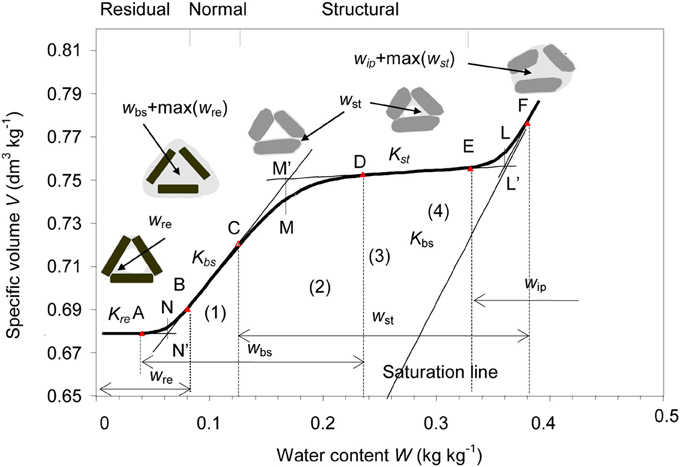
Figure 4. Different configurations of air and water partitioning into the two pore systems, inter and intra primary peds, related to the shrinkage phases of a standard Shrinkage Curve. The various water pools, wre, wbs, wst, wip, are represented with their domain of variation. The linear and curvilinear shrinkage phases are delimited by the transition points (A, B, C, D, E, and F). Points N′, M′, and L′ are the intersection points of the tangents at those linear phases of the SC (Braudeau et al., 2004).
Soil Structure and Water Pools Dynamics at the Horizon and Pedon Scale
Discretization of the pedon into SRELs allows us to model the internal processes that could not be modeled using the classical REV concept, where structural volumes are not defined and determined. Equations (3) define the different specific volumes of pore spaces that can be observed complementarily to the pedostructure at the horizon or pedon scale. Fissures and cracks are directly linked to the hydrostructural state of the pedostructure while pores of biological origin are generally fixed, which induces different kinds of hydraulic conductivity that should be distinguished from the pedostructural hydraulic conductivity.
Vertical fissures
The opening of the vertical porosity (Vpfiss) when a wetted soil is drying is modeled as follows in the new Kamel® which has to take into account the volume of pore systems other than that of the pedostructure in a pedon SREL. Actually, position (z = ΣHi) and thickness (Hi) of the SRELs are governed by Vlayer = Hi · S (where S is a fixed section of the pedon) which is calculated through equations (3) in which Vpfiss and Vps can be known in terms of Wps according to the pedostructure shrinkage curve Equation A.2 (in Supplementary Material, Appendix 2).
When the water is removed by evaporation or drainage, from the soil medium initially water saturated, vertical fissures appear at the soil surface, then through the SRELs with depth, when the water content decreases under Wps corresponding to the end of the saturated interpedal shrinkage phase, of slope Kip = 1, and the beginning of shrinkage of the primary peds in the pedostructure with the decrease of Weqmi.
Because of the difference between the one-dimensional volume change of the SRELs, according to their content in pedostructural volume Vps, and the three-dimensional volume change of the pedostructure itself, the relationship between the two nested SREVs (soil layer and pedostructure) is, according to Equation (3d) and assuming an isotropic shrinkage of the pedostructure:
where Hps and Sps are the height and surface of the volume occupied by the pedostructure in the layer. Since the shrinkage of Vps + Vpfiss is only vertical, the horizontal section of this volume stays constant with the change of Hps such that Sps = SpsL in Equation (15).
The shrinkage of the pedostructure is tri-dimensional, so:
and
Combining Equations (15, 17) leads to:
and
Thus, the pedostructural volume of the fissures present in a layer representative of a soil horizon is directly related to the pedostructural volume Vps.
Hydraulic conductivity of a SREL at the pedon scale
When the soil surface is subject to rain or irrigation, the vertical porosity, Vpfiss and the biological macropores (Vpbio) must be taken into account in the water infiltration balance. Both are different and must be treated separately. Actually, in a SREL, the fissural pore volume, Vpfiss is directly dependent on Vps. (Equation 19) and thus is function of the pedostructural water content Wps while the biological macropores volume Vpbio can be considered constant. The latter can be morphologically highlighted and measured in the field (Abou Najm et al., 2010; Sanders et al., 2012).
Water movement in biological macropores, (Wpbio). This water is considered moving out of the pedostructure but in contact with it in the SREL. Out of the pedostructure the water is free and submitted to gravity. The hydraulic conductivity kpbio can be assumed, according to the works of Chen and Wagenet (1992) and Chen et al. (1993), proportional to the saturation level of the biological porosity and equal to:
where KSat is the traditional hydraulic conductivity of the soil at saturation which is measured on saturated soil samples large enough to include the macrobiological porosity.
Thus, the movement of the free water in this poral system is the sum of two fluxes: a vertical Darcian flux in the gravitational field and a lateral flux due to the absorption of this free water by the pedostructural macroporosity:
where ybio is a length (dm) parameter, representing a mean distance between the biological porosity and the pedostructure medium.
Water movement in fissures and cracks, (Wfiss). The presence of water in the fissures created by the pedostructure shrinkage does not play any role in the vertical transfer of the pedostructural water Wps through the pedostructure and the biological macroporosity of the SRELs. This water stored in the pedostructural fissures after a rain or irrigation will be locally absorbed by primary peds of the pedostructure. Let Wlay the water content of a SREL as the sum of Wps and Wpbio, excluding the water stored in cracks and fissures Wfiss which is considered as external to the soil medium organization. Absorption of this water by the soil medium of the SRELi can be written such as:
where hfiss_i is the pressure head in the fissural water at the depth zi of the SRELi considered. Therefore, Wfiss, must be distinguished from the other SREL water contents and in particular from Wlay, the calculation of hfiss_i being a function of the rainfall intensity, the open volume of fissures at the soil surface, Vfissi = 0, and the fissural water storage at time t: . We can notice that during this lateral absorption of Wfiss by the pedostructure, the height of the water in fissures stays the same, the absorbed water being replaced by a same volume of the pedostructure swelling.
Implementation of the Theory in Soil Water Modeling
Update of the Soil Water Model Kamel
The earlier version of Kamel® (Braudeau et al., 2009) was based on the pedostructure concept which took into account the hydro-functionality of primary peds and of their assembly; it followed the system's approach for the definition of the hierarchically nested variables listed in Table 1. Thus, its update taking account of the advances in thermodynamics of the soil medium presented here above consists of two improvements:
(1) Replacing the previous equations of the pedostructure hydrostructural functioning by the new equations of thermodynamic origin, in particular for V(W); h(W); Weqmi; Weqma and Wip. This update will provide what we call Kamel-Core, for a use in laboratory, modeling the thermodynamic equilibriums of the soil medium (pedoclimate) as the conditions of development of the biological processes studied in laboratory.
(2) Introducing the new organization variables needed for the description of subsystems other than the pedostructure that compose a soil horizon and thus, the SRELs: such as the volumes of stones, roots, biological macropores, etc. This improvement will lead to a soil water model for field applications, named Kamel-field. It can simulate a pedon, organized in horizons containing subsystems surrounded by the pedostructure, like they are usually described in a soil profile on the field, in particular for the estimation of the field parameters like coefficients a, b, c, etc. and the dimensions of the horizons according to Table 2. Thus, the modeling of a pedon by Kamel-field can be considered as a physical modeling of the soil mapping unit of which the pedon is representative. This means that a soil map should contain all the parameters used by Kamel-field, at both pedostructure and horizon scales, to be totally characterized and modeled in the soil-plant-atmosphere system.
In both cases, the pedostructure parameters are needed; Table 3 recapitulates the new equations along with their respective parameters. These parameters could be obtained by fitting the new equations on simulated characteristic curves obtained using pedotransfer functions. However, the physical approach is of course to measure the 4 characteristic curves of the pedostructure: shrinkage curve, water retention curve, soil swelling rate, and hydraulic conductivity, and extract their parameters by adjustment with the theoretical equations of these curves. Implementation of the theory concerns not only the model in itself but also the methodology of measurement of the parameters required. The next section presents the new methodology used for getting the Kamel parameters.
Specific Methodology for the Kamel Parameters Determination
We have to distinguish between the pedostructural parameters that all can be measured in the laboratory on standard soil samples of near 100 cm3, and the pedon parameters that must be estimated in the field.
Pedostructure parameters
A complete hydrostructural characterization of the pedostructure for Kamel® requires the accurate and continuously measurement in laboratory of the four pedostructural characteristic curves mentioned above: shrinkage curve Vps(Wps), water retention curve h(Wps), conductivity curve kps(Wps) and the time dependent swelling curve Vps(t). Their equations and parameters are summarized in Table 3.
Hydrostructural equilibrium parameters. These are 12 parameters:
Vops, Kbs, Kst, Kip, kN, WN, Ema, Emi, WmiSat, WmaSat, kL, and WL
for the two hydro structural soil moisture characteristic curves (pedostructural shrinkage curve and water retention curve).
A new apparatus TypoSoil™ (Bellier and Braudeau, 2013) has been recently built to fulfill standards conditions of measurement of the shrinkage curve and the water retention curve (using micro-tensiometers). Measures of weight, water tension pressure, diameter and high of the sample, are made simultaneously and almost continuously (10 min of intervals) on a unconfined cylindrical soil sample (5 cm diameter, 5 cm in height), from water saturation to the dry state. Braudeau et al. (2014) and Assi et al. (Submitted), described the theory and accordingly the whole procedure using TypoSoil™ for preparing the samples, measuring the characteristic curves and for extracting the 12 parameters representing the two curves, whatever the shape of the shrinkage curve.
Hydrostructural dynamic parameters. These are k°ps and αps of the Equation (13a) and kmi of Equation (12). Parameters k°ps and αps can be measured accurately using the HypropTM device (Assi et al., Submitted) or using the wind method (Wendroth et al., 1993) in condition of having preliminarily the pedostructural parameters of the sample analyzed by these methods.
As for kmi, Braudeau and Mohtar (2006) showed how the micro-macro water exchange coefficient, kmi, can be determined from the measurement of the swelling rate of a soil sample immersed in water.
Reference mass of solids for the SREV variables
According to the SREV and SREL definitions, the reference mass of solids in a layer is its pedostructural mass, Mps; that is, the mass of solids in the total volume of pedostructure Vps, present in the considered layer of volume Vlayer. Thus, each layer has a fixed Mps, depending on its delimitation, when the horizon is discretized in layers. Therefore, this discretization of the pedon in layers (Figure 2) must be conducted in such a manner that the pedostructural mass of solids in each layer can be calculated. Given that the section, Sxy, of the pedon is constant and that the position (depth, zi) and thickness (Hi) of SRELs are variables controlled by the specific volume of layers (Vlayer), the horizons in the pedon must be considered, for discretization, at the total water saturation state (WlaySat), where no fissure due to shrinkage is open and where all state variables are assumed homogeneously distributed in the horizons. Accordingly, Mpsl could be calculated such as:
where the horizontal section of the pedon (Slay), the volumetric proportion of pedostructure in the horizon (a), and the chosen thickness of the layers at saturation of the horizons (HiSat), are the three organizational parameters of the pedon required to determine the pedostructural mass of solids present in each SREL i.
SREL and pedon parameters
Parameters of the pedon, its horizons and the SRELs coming from the discretization of the horizons, have already been presented in Table 2, separately from parameters of the pedostructure (Table 3). They describe the internal organization of the pedon into horizons and SRELs according to observations made at the field scale on a soil profile. These parameters characterize the soil surface boundaries, the volumetric fractions a, b, c, etc. of each of the terms of Equation (3a) for each horizon. Aside these morphological or organizational parameters, the hydrodynamic parameters like the saturated hydraulic conductivity at field scale of the soil horizons must be measured through field measurements (Libardi et al., 1980; Angulo-Jamarillo et al., 2000).
Algorithm of Simulation
Updating Kamel®-Core using Kamel® original algorithm where only the equations of the hydrostructural functioning of the pedostructure are updated, does not require changes in the algorithm used in Kamel® (Braudeau et al., 2009) for simulating the water movement in the soil horizons. This is because there are no other systemic components sharing the space inside the SRELS with the pedostructure. On the other hand, in the development of Kamel®-Field using Kamel®, the organizational variables such as Wps; Vps; Wfiss etc. should be specified in the equations used in the simulation of the different water fluxes and their contribution to the pedostructural water cycle.
The discretization of the soil horizons into soil layers and the nomenclature used are shown in Figure 5, where the fluxes F1 and F2 are represented for each layer at every time step along with the thickness Hi, the water pressure hi (= hma > 0) and the conductivity ki (= kps) of the pedostructure in the layer.
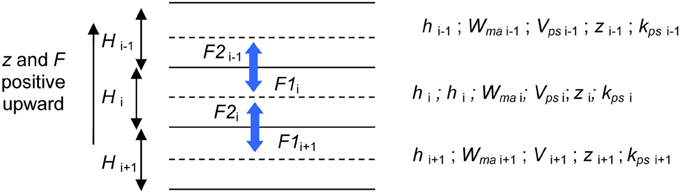
Figure 5. Representation of the Darcian flow of the pedostructural macro pore water (Wma) through the structural representative elementary layers (SRELs) of the discretized pedon.
Each layer is small enough (2 cm thick is recommended) such that the state variables kept the same values everywhere in the layer and the resulting conductivity of the portion delimited by two dashed lines (ki − 1/2 or ki + 1/2) can be approximated by the arithmetic average of the two corresponding conductivities:
At each time step, for the layer i, fluxes through the upper and lower surfaces of the soil layer i, F1i, and F2i are calculated:
and
The conditions are such that F2i − 1 = F1i and F2i = F1i + 1, and that F2 and F1 cannot be greater than the available space in the receiving layer nor can they extract more water than possible from the providing layer. At the inferior limit of the profile (i = end), F2end is calculated as if the layer outside has the same characteristics as the last layer of the profile but with k and h being taken as kend and hend calculated at the previous time step ti − 1.
Under these conditions, changes in Wps_i due to F1 and F2 for each step is then calculated using:
noticing that Vps should be used here instead of Vlayer in the earlier version in which the pedostructure occupied all the volume of the layer.
The change in Wps is initially considered as a change in Wma, which provokes temporarily a change in hma and then an imbalance between the retention of Wmi and Wma. There is therefore, during the time step, a transfer of water between the two pore systems which is calculated using the following equation:
During the same time step, we may have an eventual contribution to Wma coming from the Wpbio cycle and also to Wmi coming from Wfiss, as it is mentioned above.
Model Evaluation
This section presents Kamel® evaluation (old version) based on field observation of moisture profile as well as comparison with Hydrus 1D model. The intent is to show evidence of the model utility in characterization and modeling soil water medium. More detailed assessment of the model is available in Braudeau et al. (2009) and Singh et al. (2012).
Kamel® was first applied by Braudeau et al. (2009) to a case study of a field experiment of internal drainage published by Davidson et al. (1969). Estimation of parameters for the pedostructural shrinkage curve, water retention curve, and hydraulic conductivity curve was fully detailed in Braudeau et al. (2009). Kamel® was further evaluated at the field scale in comparison to the soil water model Hydrus-1D (Simunek et al., 2008) by Singh et al. (2012). In this new version of Kamel® the formulation of the four hydro-structural characteristic curves of the pedostructure have been changed but the descriptive variables used and the shape of these curves are all the same. Therefore, the results obtained in these evaluations suffice for the evaluation of the updated version. These evaluations are summarized hereafter. They show high level of agreement between Kamel® simulations and field measurements and Hydrus 1-D simulations. The sections below describe both evaluations:
Comparison with Moisture Profile Field Data
Figure 6 shows the computed moisture profiles of Kamel® at 0, 1, 5, 20, and 60 days of drainage, without evaporation from the surface and starting from the saturated state after infiltration. The figure also shows the field measured data of Davidson et al. (1969); the soil water content at 30, 60, 90, and 120 cm depth after 1 day, 5, 20, and 60 days of drainage without evaporation for comparison. The simulation were conducted without any calibration, simulation results show a good agreement with measured values where the first day, the difference between simulated and observed water content is ΔW 1day = −0.006 at 60 cm and 0.02 kg/kg at 120 cm. Less than 0.01 kg/kg are observed at 5 and 20 days for horizons 3 and 4 (90 and 120 cm) (Braudeau et al., 2009).
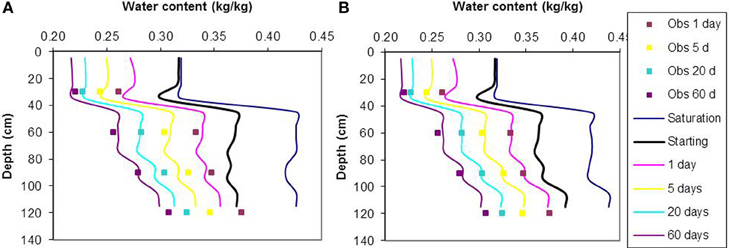
Figure 6. Simulation of drainage after infiltration up to equilibrium (black line “starting”) in the Yolo loam soil profile (Davidson et al., 1969). Squares represent the measured observations and lines represent the simulated moisture profile using the measured soil characteristic parameters given in the article: (A) without any change of these parameters and (B) with a correction of the parameter KpsSat for the second and fourth horizon corresponding to the deviation of water content at one day observed on the first graph (−0.006 and +0.02 kg/kg, respectively); (Braudeau et al., 2009).
Comparison with Hydrus-1D
Measured and predicted soil moisture by Kamel® and Hydrus-1D® at the 5 cm depth for the 4 month time period are presented in Figure 7 (Singh et al., 2012). Rainfall during this period is plotted on the secondary Y-axis. Since this is the surface layer, measured water content responds quickly to rainfall and evapotranspiration. The figure shows that Hydrus-1D® soil moisture prediction was in good agreement with observed water content.
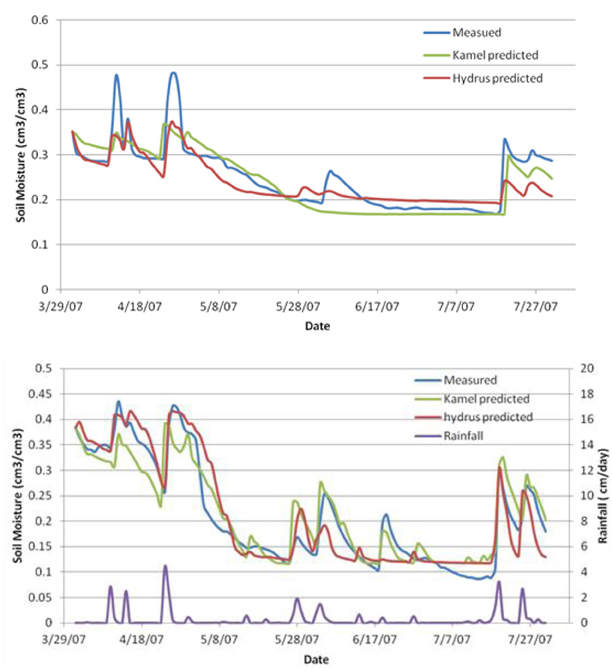
Figure 7. Comparison of measured, Kamel® predicted and Hydrus-1D® predicted water content at 5 and 20 cm depth; (Singh et al., 2012).
Conclusion
The principal function of Kamel® is to be a computational model that represents a soil pedon and its internal hydrological functioning at the different levels of hydro-functional organization of the soil medium. Integrating these levels of hydro-functional organization is significant in linking the internal functioning of the soil to its behavior and properties with the other elements of eco- or agro systems when subject to external climatic conditions. The update of Kamel® planned here introduces new prospects in multi-scale modeling of the natural environment discussed hereafter.
(1) As portrayed, Kamel® is a model that simulates two physical phenomena: (i) the hydrostructural and thermodynamic equilibrium states of the pedostructure, depending on the pedostructural water content, and (ii) the joint dynamics of the water and the soil structure at the different functional scales of the pedon (soil hydro-structural dynamics).
(2) Accordingly, Kamel®'s parameters and equations must be physically-based according to a new paradigm that can be called “hydrostructural pedology” where all the hydrostructural properties of the soil medium are thermodynamically defined and quantified. In this way, a soil mapping unit can be characterized by its representative pedon providing with the hydrostructural parameters of its horizons.
(3) Moreover, using this paradigm, the thermodynamic definition of the pedostructure system allowed us to quantitatively distinguish the two kinds of water fluxes inside and outside of the pedostructure within the soil horizons.
(4) Thus, Kamel® differentiates between two kinds of water, a pedostructural water, the water that takes part in the hydro-thermodynamic equilibrium of the soil-plant-water natural continuum, and a free water that is only subject to gravity out of the thermodynamic conditions laid down by the pedostructure.
(5) This distinction between a pedostructural water and a free water in the soil medium that could not be separated and modeled as such before. This distinction allows for the differentiation of what have been called green water and blue water resources.
(6) Finally, the soil as it will be modeled by Kamel®-field, constitutes the lieu of transformation of the blue water, driven down by gravity, to the green water or thermodynamic water of the soil plant atmosphere continuum. Therefore, Kamel® is a computer model that integrates hydrology and pedology in modeling the transfer of both types of water in the soil, the free water coming from rainfall or irrigation and the pedostructural water consumed by plants or evaporating at the soil surface to the atmosphere. This modeling determines the availability of space, water and air in the soil medium that condition the development of biotic and abiotic soil processes.
Conflict of Interest Statement
This article is an extension and an update (some fundamental equations) of an old version of the Kamel model which was registered at AP Paris in 2006 by IRD: Braudeau, E. F., 2006. Kamel® Simile version. Agence pour la Protection des Programmes, Paris, IDDN.FR.001.390019.000.S.P.2006.000.31500
Acknowledgments
The authors express their appreciation to the Graduate Research Associates Amjad Assi and Guy Bou Lahdou for their involvement in this project. The authors also wish to acknowledge QScience.com and Dr. Christopher Leonard for their assistance in editing the manuscript.
Supplementary Material
The Supplementary Material for this article can be found online at: http://www.frontiersin.org/journal/10.3389/fenvs.2014.00024/abstract
References
Abou Najm, M., Jabro, J., Iverson, W., Mohtar, R., and Evans, R. (2010). New method for the characterization of three-dimensional preferential flow paths in the field. Water Resour. Res. 46, 1–18. doi: 10.1029/2009WR008594
Angulo-Jamarillo, R., Vandervaere, J. P., Roulier, S., Thony, J. L., Gaudet, J. P., and Vauclin, M. (2000). Field measurement of soil surface hydraulic properties by disc and ring infiltrometers: a review and recent developments. Soil Till. Res. 55, 1–29. doi: 10.1016/S0167-1987(00)00098-2
Assi, A., Accola, J., Hovhannissian, G., Mohtar, R. H., and Braudeau, E. (2014). Physics of the soil medium organization part2: pedostructure characterization through measurement and modeling of the soil moisture characteristic curves. Front. Environ. Sci. 2:5. doi: 10.3389/fenvs.2014.00005
Bellier, G., and Braudeau, E. (2013). Device for Measurement Coupled with Water Parameters of Soil. WO 2013/004927 A1. Geneva: World Intellectual Property Organization, WIPO.
Braudeau, E., Assi, A. T., Boukcim, H., and Mohtar, R. H. (2014). Physics of the soil medium organization part 1: thermodynamic formulation of the pedostructure water retention and shrinkage curves. Front. Environ. Sci. 2:4. doi: 10.3389/fenvs.2014.00004
Braudeau, E., and Bruand, A. (1993). Détermination de la courbe de retrait de la phase argileuse à partir de la courbe de retrait établie sur échantillon de sol non remanié. C. R. Acad. Sci. Paris 316, 685–692.
Braudeau, E., Costantini, J., Bellier, G., and Colleuille, H. (1999). New device and method for soil shrinkage curve measurement and characterization. Soil Sci. Soc. Am. J. 63, 525–535. doi: 10.2136/sssaj1999.03615995006300030015x
Braudeau, E., Frangi, J. P., and Mohtar, R. H. (2004). Characterizing non-rigid dual porosity structured soil medium using its Shrinkage Curve. Soil Sci. Soc. Am. J. 68, 359–370. doi: 10.2136/sssaj2004.3590
Braudeau, E., and Mohtar, R. H. (2006). Modeling the swelling curve for packed soil aggregates using the pedostructure concept. Soil Sci. Soc. Am. J. 70, 494–502. doi: 10.2136/sssaj2004.0211
Braudeau, E., and Mohtar, R. (2009). Modeling the soil system: bridging the gap between pedology and soil-water physics. Glob. Planet. Change J. 67, 51–61. doi: 10.1016/j.gloplacha.2008.12.002
Braudeau, E., Mohtar, R. H., El Ghezal, N., Crayol, M., Salahat, M., and Martin, P. (2009). A multi-scale “soil water structure” model based on the pedostructure concept. Hydrol. Earth Syst. Sci. Discuss. 6, 1111–1163. doi: 10.5194/hessd-6-1111-2009
Braudeau, E., Sene, M., and Mohtar, R. H. (2005). Hydrostructural characteristics of two African tropical soils. Eur. J. Soil Sci. 56, 375–388. doi: 10.1111/j.1365-2389.2004.00679.x
Bruckler, L., Bertzzi, P., Angulo-Jamarillo, R., and Ruy, S. (2002). Testing an infiltration method for estimating soil hydraulic properties in the laboratory. Soil Sci. Soc. Am. J. 66, 384–395. doi: 10.2136/sssaj2002.3840
Chen, C., Thomas, D. M., Green, R. E., and Wagenet, R. J. (1993). Two-domain estimation of hydraulic properties in macropore soils. Soil Sci. Soc. Am. J. 57, 680–686. doi: 10.2136/sssaj1993.03615995005700030008x
Chen, C., and Wagenet, R. J. (1992). Simulation of water and chemicals in macropore soils. Part I Representation of the equivalent macropore influence and its effect on soil water flow. J. Hydrol. 130, 105–126. doi: 10.1016/0022-1694(92)90106-6
Davidson, J. M., Stone, L. R., Nielson, D. R., and Larue, M. E. (1969). Field measurement and use of soil water properties. Water Resour. Res. 5, 1312–1321. doi: 10.1029/WR005i006p01312
Gardner, W. R. (1958). Some steady-state solutions of the unsaturated moisture flow equation with application to evaporation from a water table. Soil Sci. 85, 228–232. doi: 10.1097/00010694-195804000-00006
Gerke, H., and van Genuchten, M. (1993). A dual-porosity model for simulating the preferential movement of water and solutes in structured porous media. Water Resour. Res. 29, 305–319. doi: 10.1029/92WR02339
Katterer, T., Schmied, B., Abbaspour, K. C., and Schulin, R. (2001). Single- and dual-porosity modelling of multiple tracer transport through soil columns: effects of initial moisture and mode of application. Eur. J. Soil Sci. 52, 25–36. doi: 10.1046/j.1365-2389.2001.00355.x
Libardi, P. L., Reichardt, K., Nielsen, D. R., and Biggar, J. W. (1980). Simple field method for estimating soil hydraulic conductivity. Soil Sci. Soc. Am. J. 44, 3–7. doi: 10.2136/sssaj1980.03615995004400010001x
Logsdon, S. D. (2002). Determination of preferential flow model parameters. Soil Sci. Soc. Am. J. 66, 1095–1103. doi: 10.2136/sssaj2002.1095
Mohtar, R. H., Jabro, J. D., and Buckmaster, D. (1997). A grazing simulation model: GRASIM B: Field Testing. Trans. ASABE 40, 1495–1500.
Othmer, H., Diekkrüger, B., and Kutilek, M. (1991). Bimodal porosity and unsaturated hydraulic conductivity. Soil Sci. 152, 139–149. doi: 10.1097/00010694-199109000-00001
Sanders, E. C., Abu Najm, M. R., Mohtar, R. H., Kladivco, E., and Shulze, D. (2012). Field method for separating the contribution of surface-connected preferential flow pathways from flow through the soil matrix. Water Resour. Res. 48. doi: 10.1029/2011WR011103
Simunek, J., Jarvis, N. J., van Genuchten, M. T., and Gardenas, A. (2003). Review and comparison of models for describing non-equilibrium and preferential flow and transport in the vadose zone. J. Hydrol. 272, 14–35. doi: 10.1016/S0022-1694(02)00252-4
Simunek, J., Sejna, M., Saito, H., Sakai, M., and van Genuchten, M. (2008). The HYDRUS-1D Software Package for Simulating the Movement of Water, Heat, and Multiple Solutes in Variably Saturated Media, Version 4.08, HYDRUS Software Series 3. Riverside, CA: Department of Environmental Sciences, University of California Riverside.
Singh, J., Mohtar, R., Braudeau, E., Heathmen, G., Jesiek, J., and Singh, D. (2012). Field evaluation of the pedostructure-based model (Kamel®). Comput. Electron. Agr. 86, 4–14. doi: 10.1016/j.compag.2012.03.001
Keywords: soil water modeling, multi-scale soil water processes, pedostructure, hydrostructural soil properties, soil hydrodynamics, soil water thermodynamics
Citation: Braudeau EF and Mohtar RH (2014) A framework for soil-water modeling using the pedostructure and Structural Representative Elementary Volume (SREV) concepts. Front. Environ. Sci. 2:24. doi: 10.3389/fenvs.2014.00024
Received: 23 February 2014; Accepted: 03 June 2014;
Published online: 20 June 2014.
Edited by:
Juergen Pilz, Alpen-Adria Universität Klagenfurt, AustriaReviewed by:
Yuichi S. Hayakawa, The University of Tokyo, JapanShawn P. Serbin, Brookhaven National Laboratory, USA
Copyright © 2014 Braudeau and Mohtar. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Erik F. Braudeau, Institut de Recherche pour le Développement, Pédologie Hydrostructurale, 32 Avenue Henri Varagnat, 93140 Bondy, France e-mail:ZXJpay5icmF1ZGVhdUBpcmQuZnI=
 Erik F. Braudeau
Erik F. Braudeau Rabi H. Mohtar
Rabi H. Mohtar