Climate change and persistent high temperatures: does it matter?

Introduction

The effect of climate change on earth systems has been reported to be significant in the Intergovernmental Panel on Climate Change (IPCC) studies (IPCC, 2013). When compared to the period of record keeping on these events and the period of human existence on earth during the preindustrial and industrial period, more recent acceleration of observed increases in world temperatures is occurring over a very short period of time and possibly at an increased rate (IPCC, 2013). Within this short period of recorded environmental system behavior, the near unanimous consensus among scientists is that these changes are due to anthropogenic greenhouse gas (GHG) emissions, and that they are significant and persistent (Solomon et al., 2009). The identification of tolerable levels of climate change and thus tolerable levels of GHGs in the atmosphere have always been the concern with respect to the behavior of ecosystems and their response to these stressors (Guzmán et al., 2009; Guan et al., 2013). The purpose here is to discuss the potential effect of this persistent behavior from the perspective of world population dynamics, and see if the world population could experience drastic impacts under these climatic conditions. One such persistent impact was identified in the IPCC studies (Hansen et al., 2006; Meehl et al., 2007; Solomon et al., 2007; IPCC, 2013) as the 2°C global warming scenario by the year 2100. This scenario was characterized to be an upper limit of temperature change beyond which nonlinear and rapid degradation of ecosystems would occur (Solomon et al., 2007). It was claimed that beyond this global warming level the carrying capacity of world systems will be affected and thus stable world population levels would be shifted. The 2°C scenario of IPCC was later lowered to a 1°C level indicating that at these levels drastic sea level changes and extinction of species would be expected (Hansen et al., 2006; IPCC, 2013). Independent studies including the physical models of IPCC have also confirmed the expected higher sea levels at these temperatures and that this would involve significant policy impacts (Meehl et al., 2007; Rahmstorf, 2007; Guzmán et al., 2009; Aral, 2013; Chang et al., 2013; Guan et al., 2013). More recently, in reference to climatic temperature trends another important concern was raised; even if drastic cuts in GHG emissions are implemented worldwide it is expected that the current levels of GHG in the atmosphere would persist over long periods and we should expect to see persistent levels of high temperatures for a long period of time (Wigley, 2005; Solomon et al., 2009). This is an important observation and the purpose of this commentary is to examine the implications of this prediction from the perspective of human global population dynamics.

The world population dynamics is discussed here from a historical perspective along with the mathematical models proposed to analyze this behavior in the current literature (Brown and Kane, 1994; Cohen, 1995; Aral, 2013). The purpose of this commentary is not to claim that the population models used here will accurately reflect the near or long term influence of climate change on population dynamics. As indicated in Aral (2013) that would be a rather difficult proposition since: (i) the overarching world population-climate dynamic system is very complex; (ii) the interactive behavior of world population within earth systems is highly nonlinear; (iii) the predictive process involves many interactive sub-processes which is hard to characterize in a population model; and, (iv) there are not enough data to calibrate this complex behavior for various climate and population changes that may potentially occur in the future, i.e., the characteristic signature data may not be currently available. We also acknowledge that there is no alternative to computer simulations if one wants to predict future. However, since—in this case—there is no way to validate them, the forecasts become more a matter of faith than a fact. Given these restrictions and observations, the purpose here is to discuss the possibility of occurrence of the statements made on potential effects of climate change on population dynamics by analyzing the behavior of “relative change” that may be observed in human population system behavior under persistent climatic conditions. For example, scientists have reached to the conclusion that global warming relative to year 2000 will persist for long periods of time even if the GHG emissions are reduced drastically (Solomon et al., 2009). If there is such an expectation then it may be important to see the relative effect of persistent and high temperature levels on human population dynamics using a model which may provide an insight to the “stability behavior” of population trends. Thus, the purpose here is to briefly review the historical perspectives on this subject and discuss the potential effect of persistent high temperatures on population dynamics. In this review temperature is selected as the climate change indicator parameter. If there is a potential for persistent temperature levels (Solomon et al., 2009) to trigger human population shifts, than these models may reflect that behavior in terms of the stability characteristics of the population system in the long term. The assumption made in this discussion is that fluctuations on temperature may cause temporal variations on global population trends in the short term, but these short term trends in temperature may not change the evolution of the long term population trends if the general trend in temperature is rising or decreasing. The purpose in this commentary is not to predict these short term trends but instead analyze the stability behavior of population trends based on persistent behavior of “increasing temperature” trends which is identified as the main outcome of climate change on earth.

World Population Models

The origins of the discussion on population dynamics are philosophical and it goes back to 16th and 17th centuries. According to Marquis de Condorcet (1743–1794) one line of thought is that: “Human mind is capable of eliminating all obstacles to human progress, thus all limitations to population growth can be overcome through technological advances that human mind can create.” Since the generation of new technologies, and thus the elimination of obstacles, is proportional to the population, according to this line of thought, higher the population higher will be the possibility of creation of new technologies to overcome the limitations to population growth. This perspective was the first in introducing the concept of carrying capacity of earth systems and acknowledging its link to human population as a function of knowledge accumulation. Condorcet's argument was that population growth in itself would not create a limitation or restriction since humans are so smart that they will find ways to overcome all possible carrying capacity limitations to population growth. This line of thought by Condorcet is useful, but it is important to mention here that innovative solutions that is adopted by humans may not necessarily be favorable for human survival as well, arguably the climate change issue is one of them. On the other side of this argument there was the Thomas Robert Malthus' (1766–1834) perspective which was: “Ecosystems have a finite carrying capacity. However, smart humans are this carrying capacity can only be expanded to a limit which is still arguably a function of population.” Given this limit eventually the population growth will win the race and human populations may become unsustainable. Now that we are in the 21st century with exponentially increasing population levels of 7 billion, so far it seems that Condorcet's argument is still winning. Although both points of view have their merit, it seems they are also deficient since they were only looking at the problem of population growth and arguing if the carrying capacity of earth would be sufficient to sustain or not sustain that growth. In the context of this commentary, it seems both philosophies have ignored the effect of the extreme and rapid change in environmental systems and the potential adverse human impacts of this change. When we look at the problem from this perspective and if the carrying capacity will not be the limiting factor, although it will still be an influencing factor, will there be other factors that need to be considered that may limit sustainable population growth. The question then becomes, if there is such a factor, can humans adapt to these extreme and rapid changes that might occur due to climate change independent of the influence of carrying capacity on population dynamics. We find the answer to that question in the teachings of Charles Darwin (1809–1882). According to Darwin: “Species always breed beyond available resources. Favorable variations would make organisms better at surviving under adverse conditions and passing the variations on to their offspring as a means of survival, while unfavorable variations would be lost which in essence is the extinction of species due to adverse and unsustainable conditions.” According to this observation, it seems human species still has some hope to adjust but this adjustment can only happen in Darwinian time scales. Than the question becomes is the climate change effects on humans are occurring on Darwinian time scales as well giving humans a chance to adjust. The answer to that question would be a definite “No.” The climate change observations indicate that not only the climate changes effects are occurring over a much shorter period of time when compared to Darwinian time scales, but also these climate change periods are getting shorter, and shorter given the level of the change that are being observed on earth (IPCC, 2013).

It is also possible to look at these historical perspectives from a mathematical modeling point of view. The Condorcet's and Malthus' arguments can be combined under the same mathematical model (Brown and Kane, 1994; Cohen, 1995) where the Malthus model takes the form,

$\begin{array}{cc}\frac{dP\left(t\right)}{dt}=c_1{\left(P\left(t\right)\right)}^2\left[K\left(t\right)-P\left(t\right)\right]& \left(1\right)\end{array}$

where P(t) is the population, K(t) is the carrying capacity, c₁ is the Malthus' constant and t is time. According to Malthus' principle the carrying capacity is to be assumed to be a constant but in this case, in order to introduce the Condorcet's principle into Equation (1), we will chose it to be time dependent. According to Condorcet's principle the time rate of change of K(t) is proportional to time rate of change of population. Thus, this definition can be introduced as,

$\begin{array}{cc}\frac{dK\left(t\right)}{dt}=c_2\frac{dP\left(t\right)}{dt}& \left(2\right)\end{array}$

where c₂ is the Condorcet's proportionality constant. Based on the value of c₂ the carrying capacity may change in several different ways. For (c₂ > 1) each member of the population will add to carrying capacity more than to cover his own consumption. Thus, the carrying capacity will grow faster than population and eventually according to Equation (1) the population will also grow faster than exponentially and will become infinite very quickly. For (c₂ = 1) each member of the population will add to carrying capacity as much as he consumes. For this case the increase in carrying capacity is directly proportional to population growth and according to Equation (1) the population growth will be exponential and will eventually reach infinity albeit at a much slower rate when compared to the previous case. For the case of (0 < c₂ < 1) each member of the population will add to the carrying capacity but less than he consumes. In this case, according to Equation (1) the population will grow logistically (Boccara, 2004), and eventually the growth rate decreases to zero. When (c₂ = 0) the population growth rate will not have any influence on the growth of the carrying capacity. In this case the carrying capacity is constant and this represents the Malthus principle and population levels will diminish over time. For (c₂ < 0) the population growth reduces the growth of the carrying capacity in which case the population will eventually collapse.

Given this interpretation of the Condorcet's and Malthus principles, the interpretation of the growth or the decay of the carrying capacity and the population dynamics that is associated with that behavior is possible. Using these principles several authors have demonstrated that the historical data on world population over the entire period of human existence up to the year 2000 can be accurately described by the use of empirical mathematical models (von Foerster et al., 1960; Kapitza, 1996; Lee et al., 2008; Dolgonosov, 2009, 2012; Akaev and Sadovnichii, 2012). A comprehensive review of these models and the lineage among them was discussed in Aral (2013), which will not be repeated here. One should also acknowledge that none of these models address the question we have posed earlier. That is: Observations indicate that the adverse effects of climate change are increased temperatures on earth, and this is being observed over short periods of time and these time scales are getting shorter and shorter given the level of the changes that are being observed. How will this affect the population dynamics as a function of the behavior of the carrying capacity of earth systems? To answer that question we will begin with the human population model that includes a climate change variant as proposed by Aral (2013). This model was based on earlier studies that included a logistic function that represents the world population carrying capacity that is identified as the homogeneous carrying capacity, i.e., Condorcet's principle. The temperature dependent human population carrying capacity was later introduced to this model as the heterogeneous carrying capacity representing the climate change effects (Aral, 2013). The population model that represents both the homogeneous and heterogeneous carrying capacity of human population systems is given in Equation (3) (Aral, 2013).

$\begin{array}{cc}\begin{array}{l}\frac{dP}{dt}=r{P}^2\left(t-{\tau }_1\right)\left[1-\frac{P\left(t\right)}{K\left(P,{\tau }_2,{\tau }_3\right)}\right]-\left(\frac{P\left(t-{\tau }_3\right)}{\left(P_c+P\left(t-{\tau }_3\right)\right)}\right)\\ {\left(\frac{\beta T\left(t-{\tau }_3\right)}{T_o}\right)}^2\end{array}& \left(3\right)\end{array}$

In this model P is the world population, T is global average world temperature, t is time in years and r is the coefficient of world population growth. The general structure of this model is tied to the earlier observation that the world population growth would be parabolic as represented by the square of the population term of Equation (3) (von Foerster et al., 1960; Kapitza, 1996). It is assumed that this growth would be limited by the homogenous carrying capacity of population growth characterized by the carrying capacity function K(P, τ₂, τ₃) given as Equation (4) which follows Equation (2). This carrying capacity term follows the information accumulation concept of Condorcet (Dolgonosov, 2009; Akaev and Sadovnichii, 2012). This is followed by the heterogeneous logistic function defined in terms of the carrying capacity that is associated with changing climatic conditions in association to population and temperature change. The introduction of this last term enables us to calibrate the model using the historical data on world temperature and also population. After calibration it is possible to see the “relative effect” of the future climatic conditions (temperature changes) on the dynamic behavior of human population (Solomon et al., 2009).

$\begin{array}{cc}\begin{array}{l}K\left(P,{\tau }_2,{\tau }_3\right)=P_c+\gamma \left(P\left(t-{\tau }_2\right)-P_o\right)\\ \exp \left(-\kappa \left(P\left(t-{\tau }_3\right)-P_o\right)\right)\end{array}& \left(4\right)\end{array}$

In Equations (3) and (4), P_c is identified as the current population density which is tied to the rate of information accumulation of humans which influence the population growth in the sense of Condorcet (Dolgonosov, 2009; Akaev and Sadovnichii, 2012). In Equations (3) and (4) the constant P_o = 1 billion is defined as the static biocapacity of earth (Akaev and Sadovnichii, 2012), which was exceeded during 1980s, κ and γ are rate constants, τ₁ ≈ 20−50 years which represents the mean reproductive age, τ₂ ≈ 10−100 years which represents the time of diffusion of basis technologies within human population which influence population growth (Gorshkov, 1995), and τ₃ = 25−100 years can be chosen as the time delay in the biospheric response of earth systems to anthropogenic loads. A discussion of the theoretical analysis of the reasons behind the choice of these parameters can be found in Dolgonosov (2009) and Akaev and Sadovnichii (2012). The second logistic function that introduces the temperature effects into the population model is introduced with a scaling factor β which may be used to describe the increase or decrease in world temperatures relative to a scenario such as the IPCC 2°C scenario beyond the year 2000 or any other temperature scenario may also be used here to define the future temperature trend (Solomon et al., 2009). If a predicted temperature scenario is directly used as input values for the temperature than the scaling factor β should be selected as one beyond the year 2000. The second logistic term in Equation (3) includes a temperature term which is introduced as the square of the non-dimensional form relative to the temperature T_o at the beginning of the historical data (1880) that is used in the analysis for calibration. This term also includes the temperature time lag, which is assumed to be the same as the time lag used to represent our expectation of the period it will take for the environmental systems to adjust to changing climate conditions as suggested in Akaev and Sadovnichii (2012). Although this time lag can be chosen in the range 25–100 years, as indicated above, this selection is actually a calibration parameter which can be adjusted when the world population data collected increases in the future. The temperature ratio is introduced into the model as a percentage and the square term allows the representation of the increase or decrease of temperatures relative toT_o. The population term of the second logistic function has the range [0, 1] forP [0, ∞] and uses the same time lag of the temperature term. For the calibration period, t < 2000 years and β = 1, historical data on temperature (Aral et al., 2012) and population data obtained from World Bank is used (World Bank, 2013). Further details of the development of this model are given in Aral (2013) along with the calibration and predictions for various scenarios which will not be repeated here. This model will be used here to discuss the effect of persistent and high global temperatures on relative world population levels. The persistent GHGs in its effects on temperature were reported in the recent literature (Solomon et al., 2009).

Persistent Temperature Trends and Its Effect on Population Dynamics

The mathematical model given in Equation (3) is calibrated using the historical population data for the period 1000–2000 (World Bank, 2013) and the global temperature data for the period 1880–2000 that is available in the literature (Aral et al., 2012). For predictions the starting time of computation is selected as t = 1900 yr. Prior to that year the Kapitza model output is used as initial estimates of population and the two year moving average of the historical temperature data is utilized to represent the temperature trends since the model in Equation (3) requires a time lag computation of about 25–100 years for some of the scenarios given below. P_c = 7.0 billion was selected to reflect current world population and P_o = 1.0 billion for all cases (Akaev and Sadovnichii, 2012). The other parameters of the model are chosen as reported in Akaev and Sadovnichii (2012) and as shown in Table 1. In Table 1 the lag time values in bold font are selected for Cases 1, 2, 3, 4.

TABLE 1

Table 1. Model parameters for Equation (3) and (4).

The focus of the discussion here is on the effect of persistent and high future temperatures as predicted by Solomon et al. (2009) which is reported in Figures 1, 2 of their paper. In that analysis the climate system responses are given for a ramp of CO₂ emissions at a rate of 2%/year to peak CO₂ values at 450, 550, 650, 750, 850, and 1200 ppmv and this was followed by zero emissions beyond 2100. Based on these scenarios the global temperature trends, among other parameters, are calculated using Atmosphere–Ocean General Circulation Models (AOGCMs). The temperature data predicted in that study was made available to the writer by the authors of that study and is used here without change (Solomon et al., 2009).

FIGURE 1

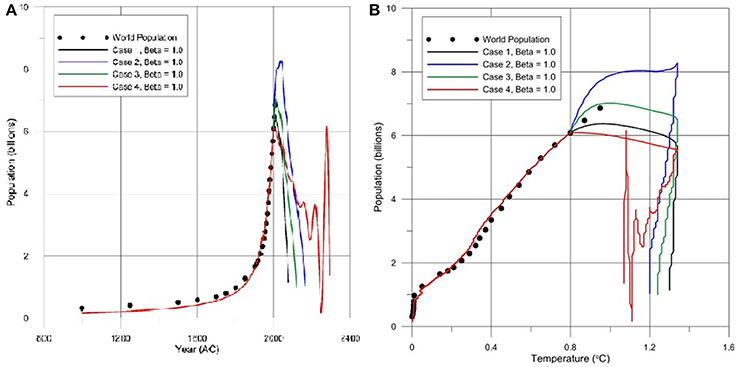
Figure 1. World population stability estimates for 2%/year peak of CO₂ to level of 450 ppmv until year 2050 at P_c = 7 billion and persistent global temperatures beyond 2050 as predicted in Solomon et al. (2009): (A) Time series plot; and, (B) Stability phase plane diagram.

FIGURE 2

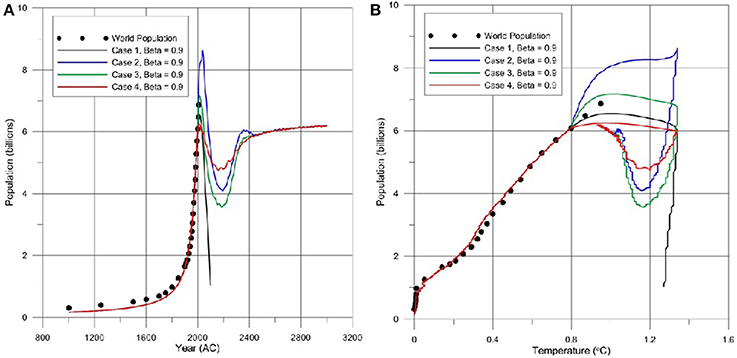
Figure 2. World population stability estimates for 90% of the 2%/year peak of CO₂ to level of 450 ppmv until year 2050 at P_c = 7 billion and persistent global temperatures beyond 2050 as predicted in Solomon et al. (2009): (A) Time series plot; and, (B) Stability phase plane diagram.

For the purposes of our discussion the population trends for only 2%/year to peak CO₂ values to 450 ppmv followed by zero emissions case will be discussed since the other higher CO₂ peak values resulted in much worse conditions with respect to the predicted population trends. The results shown in Figure 1A indicate that the model in Equation (3) fits the historical population data rather well with coefficient of determination (R = 0.99)but predicts an unstable world population for all cases that are described in Table 1 for the 450 ppmv peak CO₂ temperature scenario of Solomon et al. (2009). The general trend is that for all cases the world population collapses beyond year ~2100. Only Case 4 shows some oscillatory trend until year ~2200 after which that case also collapses. The phase plane diagram of this trend is shown in Figure 1B.

When we limit the temperature trend predicted in Solomon et al. (2009) to 90% of their levels, β = 0.9, than Case 1 still indicates an unstable world population but Cases 2, 3, 4 indicate a stable trend for world population as shown in Figure 2A. The phase plane diagram for this case is shown in Figure 2B. As can be seen in Figures 1, 2 there is an offshoot of population level in all cases at around year ~2000 which reflects the inertia of the historical population growth. It is important to note that in Figures 1B, 2B the inertia effect of world population rise is within the range of the calibration parameters used for Cases 1, 2, 3, 4. Thus, a more realistic population inertia effect can be calibrated when more accurate inertia trends in the population data will become available in the future. Currently it seems that the selected parameters for Case 3 is indicating a good fit Figure 1B. After the maximum is reached the stable population is expected to occur at the estimated sustainable population level defined by the logistic equation (Aral, 2013). This stability cannot be achieved for the temperature scenarios described in Solomon et al. (2009) for all cases Figure 1. For the 90% level of this scenario Case 1 is still unstable but an oscillatory convergence can be observed for Cases 2, 3, 4, Figure 2. For this case the sustainable level of population is much lower which is around ~6 billion and may be reached at ~2800. Under normal circumstances the stable population levels would be around ~7 billion for these cases. Thus, a loss of ~1 billion people is predicted for this scenario by the year ~2800. The temperature scenario discussed above has to be scaled down by 74.8% (β = 0.748) to reach the temperature limit for which all cases are stable. For this case the predicted stability level is still around ~6 billion as shown in Figure 3A for the time trend and the phase plane diagram as shown in Figure 3B. A loss of ~1 billion people is still expected for this case indicating that the carrying capacity of earth systems will still be affected.

FIGURE 3

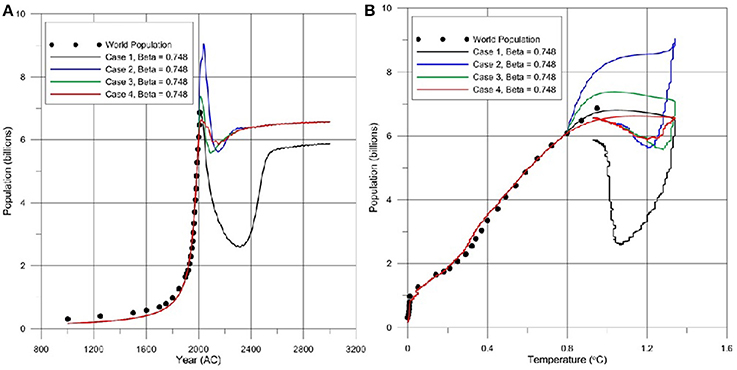
Figure 3. World population stability estimates for 74.8% of the 2%/year peak of CO₂ to level of 450 ppmv until year 2050 at P_c = 7 billion and persistent global temperatures beyond 2050 as predicted in Solomon et al. (2009): (A) Time series plot; and, (B) Stability phase plane diagram.

The stability behavior of the world population, Equation (3), improves as the current stable world population limit P_c is increased. The results of this is case is shown in Figure 4 for P_c = 8 billion, in which the temperature scenario used in Figure 1 is repeated, i.e., β = 1.0. For this data Case 1 population scenario is still unstable however Case 2, 3, 4 scenarios become stable. These scenarios were not yielding a stable outcome for P_c = 7 billion. For this case the stable world population level drops to ~7 billion from 8 billion indicating that a loss of ~1 billion people is still expected for the persistent and high temperatures by the year 3000. However, the selected P_c value should not be interpreted as the current world population but it is associated with the carrying capacity of earth systems and knowledge accumulation factor of humans as it is defined in Dolgonosov (2009); Aral (2013) which can be argued that information accumulation factor of humans due to technological advances is changing and thus increase in P_c to higher population levels is possible.

FIGURE 4

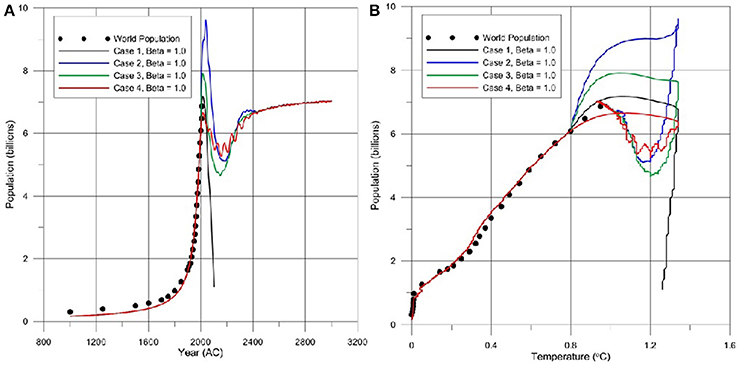
Figure 4. World population stability estimates for 2%/year peak of CO₂ to level of 450 ppmv until year 2050 at P_c = 8 billion and persistent global temperatures beyond 2050 as predicted in Solomon et al. (2009): (A) Time series plot; and, (B) Stability phase plane diagram.

Using this model regional or stability of individual country populations may also be investigated as suggested in Akaev and Sadovnichii (2012) and also used in Lee et al. (2008). For these cases the stationary population of individual country or the region should be used which can be estimated by dividing the current stationary world population, in this case P_c = 7.0 billion, by the country's anthropogenic load index such as CO₂ metric tons emissions per capita (World Bank, 2013). In this case regional temperature increase data need to be used to estimate the impact of climate change on the country's population.

The sustainable limit of population trends can be adjusted by the selection of appropriate constants for the parameters of the model and several time lag alternatives can be considered to fit the model to the inertia effects that may be observed in the historical or the future population data. As new world population data is collected the inertia effect can be calibrated better by the choice of appropriate parameters. The choices for these parameters that may be used to reflect the population inertia effect will not significantly affect the stability behavior of the population model (Aral, 2013), but the period of oscillations will be influenced. So far this exercise indicates that the use of the logistic function, Equation (3), may be a reasonable way to interpret sustainability of world population under changing climatic conditions and it is possible to work with quantitative population models to estimate the relative population trends for various climatic stresses.

Given the novel concept of introduction temperature change to population models, the author acknowledges that the current model is still at its infancy in predicting human population dynamics. For example the introduction of human health effects or epidemics that may be triggered with increases in temperatures are not considered in this model. Further, temperature increases will not be uniform across all regions of the world. This may trigger migration patterns over the world which is also not considered in this model. Speaking about the availability of resources i.e., spatial “carrying capacity” concept and how heterogeneous this distribution could be. Under such circumstances there could be an increasing tendency for the development of resource rich, resource-poor ecological ‘meta-populations’ or “islands.” They may have weak or strong boundaries depending on aspects of social, environmental and economic inequality. Coupling adaptive capacity (competitive vs. collaborative) type of human adaptive responses, various stable and unstable areas may develop and persist. This is a very different picture than the ‘homogenous’ landscape that is assumed in the current model. Thresholds of cumulative effects is also an important variant in this analysis. Certain thresholds may trigger sudden shifts in population levels, i.e., the population trends may not be smooth. One of the very important characteristic of societies is their collective resilience and collective adaptation capacity. This aspect of the human behavior when introduced into the model as a quantifiable process than the model introduced here would be a more reliable tool to work with in the sense of resilience analysis (Gunderson and Pritchard, 2002). In this context the discussion of the effects internal dynamics between urbanization-education-economics is very important as discussed in Jiang (2014). Introduction of quantifiable and computational aspects of these concepts to population models would enhance the analysis significantly.

Conclusions

In this commentary effect of climate change on population dynamics is discussed within a historical perspective of different philosophies that contributed to this subject. When the question is posed from the perspective of climate change effects on population and not from the perspective of effects of carrying capacity on population dynamics none of the earlier models seem to answer that question appropriately.

Given this limitation of the approach selected, to demonstrate the future trends in population in response to the effects of persistent climatic changes (Solomon et al., 2009) we have used the model proposed by Aral (2013). In this model temperature is chosen as the indicator parameter of climate change and the effect of the global warming trend is used to analyze the “relative” world population stability in aggregate. The proposed model is calibrated using the historical population (World Bank, 2013) and temperature data (Meehl et al., 2007; Solomon et al., 2007; Aral et al., 2012). The predictions made indicate that the proposed model reflects the historical world population trend rather well as a function of temperature (Aral, 2013). Keeping the simplicity of the model used and the potential enhancements that may be introduced to the model as discussed in the previous section in mind, the proposed model is then used to demonstrate the population stability trends using the temperature trend given in Solomon et al. (2009) beyond 2000. This data represents the persistent increase in temperature trends as expected even after the world wide reduction of GHG emissions is implemented. The purpose in this analysis is not to predict the expected population levels in the near term or even in the long term. Instead the goal is limited to the evaluation of world population stability conditions. The results indicate that for the temperature data where a 2%/year peak of CO₂ including and beyond 550 ppmv would yield unstable world population levels in the future. The world population levels for a ramp of 450 ppmv would only show a stable population trend at 90% of the temperature levels predicted by Solomon et al. (2009) for Case 2, 3, 4 and Case 1 is still unstable at this level. All cases show a stable population trend at 74.8% levels of the 450 ppmv scenario given in this temperature trend. Interestingly enough this temperature level corresponds to a persistent 1.3°C scenario over the long term which is within the recommended levels of temperature of the IPCC studies in order to avoid drastic impact to ecological systems on earth (IPCC, 2013). In that sense the outcome predicted here is consistent with earlier IPCC studies. For the 550 ppmv data reported in Solomon et al. (2009) stable populations can be observed at 60% levels. For this case Case 2, 3, 4 applications yield stable outcomes and Case 1 is still unstable. The percentage reductions need to be lower than 40% for the temperature ramp up cases 650 ppmv and beyond, which are not presented here. The resilience of world population levels improve as the current population value, P_c, increases. However, this value should not be interpreted as the current world population but it is associated with the information accumulation rate of humans and the carrying capacity of earth systems as it is defined in Dolgonosov (2009); Akaev and Sadovnichii (2012); Aral (2013), which should arguably increase by definition. These observations may indicate the urgency of imposing controls over increasing temperatures worldwide sooner. The conclusions presented here are reached within the limitations of the empirical population model developed in Aral (2013) and the hypothetical temperature scenarios developed in Solomon et al. (2009).

Conflict of Interest Statement

The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

References

Akaev, A. A., and Sadovnichii, V. A. (2012). Mathematical model of population dynamics with the world population size stabilizing about a stationary level. Dokl. Math. 82, 978–981. doi: 10.1134/S1064562410060360

CrossRef Full Text | Google Scholar

Aral, M. M. (2013). Climate change and human population dynamics. J. Water Qual. Expos. Health 6, 53–62. doi: 10.1007/s12403-013-0091-5

CrossRef Full Text | Google Scholar

Aral, M. M., Guan, J., and Chang, B. (2012). A Dynamic System Model to Predict Global Sea-Level Rise and Temperature Change. ASCE J. Hydrol. Eng. 17, 237–242. doi: 10.1061/(ASCE)HE.1943-5584.0000447

CrossRef Full Text | Google Scholar

Boccara, N. (2004). Modeling Complex Systems. New York, NY: Springer-Verlag Publishers.

Google Scholar

Brown, L. R., and Kane, H. (1994). Full House: Reassessing the Earth's Population Carrying Capacity. New York, NY: Norton.

Google Scholar

Chang, B., Guan, J., and Aral, M. M. (2013). Modeling spatial variations of sea level rise and corresponding inundation impacts: a case study for Florida, U.S.A. J. Water Qual. Expos. Health 6, 39–51. doi: 10.1007/s12403-013-0099-x

CrossRef Full Text | Google Scholar

Cohen, J. E. (1995). Population growth and earth's human carrying capacity. Science 269, 341–346. doi: 10.1126/science.7618100

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Dolgonosov, B. M. (2009). Nonlinear Dynamics of Ecological and Hydrological Processes. Moscow: Librocom/URSS.

Dolgonosov, B. M. (2012). Knowledge production, hyperbolic growth and phase transition in biosystems. Studia UBB Geographia LVII. 2, 5–36.

von Foerster, H., Mora, P. M., and Amiot, L. W. (1960). Doomsday: friday, 13 november, A.D. 2026. Science 132, 1291–1295. doi: 10.1126/science.132.3436.1291

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Gorshkov, V. G. (1995). Physical and Biological Bases of Life Stability: Mass, Biaota, Environment. Berlin: Springer Verlag.

Guan, J., Chang, B., and Aral, M. M. (2013). “A dynamic control system model for global temperature change and sea level rise in response to CO₂ emissions.” Clim. Res. 58, 55–66. doi: 10.3354/cr01189

CrossRef Full Text | Google Scholar

Gunderson, L. H., and Pritchard, L. (2002). Resilience and the Behavior of Large-Scale Systems. London: Island Press.

Google Scholar

Guzmán, M. J., Martine, G., McGranahan, G., Schensul, D., and Tacoli, C. (eds.). (2009). Population Dynamics–Climate Change. London: United Nations Population Fund; International Institute for Environment and Development.

Hansen, J., Sato, M., Ruedy, R., Lo, K., Lea, D. W., and Medina-Elizade, M. (2006). Global temperature change. PNAS 103, 14288–14293. doi: 10.1073/pnas.0606291103

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

IPCC. (2013). Summary for Policymakers. Available online at: http://www.ipcc.ch/report/ar5/wg1/ (Accessed November, 2013).

Jiang, L. (2014). Internal consistency of demographic assumptions in the shared socio economic pathways. Popul. Environ. 35, 261–285. doi: 10.1007/s11111-014-0206-3

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Kapitza, S. P. (1996). The phenomenological theory of world population growth. Phys. Usp. 39, 57–71. doi: 10.1070/PU1996v039n01ABEH000127

CrossRef Full Text | Google Scholar

Lee, H. F., Fok, L., and Zhang, D. D. (2008). Climatic change and Chinese population growth dynamics over the last millennium. Clim. Change 88, 131–156. doi: 10.1007/s10584-007-9329-1

CrossRef Full Text | Google Scholar

Meehl, G. A., Stocker, T. F., Collins, W. D., Friedlingstein, P., Gaye, A. T., Gregory, J. M., et al. (2007). “Global climate projections' in climate change: the physical science basis—contribution of working group I to the fourth assessment rep. of the intergovernmental panel on climate change. chapter 10,” in Projections of Global Average Sea Level Change for the 21st Century, eds S. Solomon, D. Qin, M. Manning, Z. Chen, M. Marquis, K. B. Averyt, et al. (Cambridge: Cambridge University Press), 820.

Rahmstorf, S. A. (2007). A semi-empirical approach to projecting future sea-level rise. Science 315, 368–370. doi: 10.1126/science.1135456

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Solomon, S., Qin, D., Manning, M., Chen, Z., Marquis, M., Averyt, K. B., et al. (eds.). (2007). Climate Change 2007: the Physical Science Basis. Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge: New York, NY: Cambridge University Press), 996.

Solomon, S., Plattner, G.-K., Knutti, R., and Friedlingstein, P. (2009). Irreversible climate change due to carbon dioxide emissions. PNAS 106, 1704–1709. doi: 10.1073/pnas.0812721106

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

Wigley, T. M. L. (2005). The climate change commitment. Science 307, 1766–1769. doi: 10.1126/science.1103934

Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar

World Bank. (2013). Available online at: http://www.worldbank.org/ (Accessed February, 2013).