- European Organisation for the Exploitation of Meteorological Satellites (EUMETSAT), Darmstadt, Germany
In this paper the algorithms to retrieve atmospheric aerosol properties using spaceborne observations are reviewed. The main focus is on the algorithms based on simultaneous measurements of the intensity and degree of polarization of reflected solar light at the top-of-atmosphere.
Introduction
Remote sensing of atmospheric aerosol from space is a comparatively new technique emerged with the development of satellite technology in the second half of the last century (Lee et al., 2009; Kokhanovsky, 2013). The atmospheric aerosol influences air quality and relevant for climate change studies. It also serves as an important source of iron for ocean. Therefore, it has an effect on the ocean bio-productivity. It is believed that the increase in the aerosol production due to human activities has reduced the possible high rise in ground temperatures due to increase in the concentration of greenhouse gasses. It also means that more effective and clean production chains and technologies will reduce the aerosol vertical load thereby increasing the climate warming signal. The aerosol can also influence local weather modifying cloud properties and rain probability.
Therefore, there is a great interest in understanding the global atmospheric aerosol, its sources, transport, and deposition. The global properties of aerosol can be understood only using satellite observations.
Lazarev et al. (1987) gave a comprehensive overview of the first instrumental observations of the Earth (aerosols, clouds, etc.) from manned spacecrafts. The first detection of aerosols from an un-manned spacecraft was achieved by the Multi Spectral Scanner (MSS) onboard the Earth Resources Technology Satellite (ERTS-1) (Griggs, 1975; Fraser, 1976; Mekler et al., 1977) and the first operational aerosol products were generated from the TIROS-N satellite launched on 19 October 1978. In these first investigations the intensity of backscattered solar light has been used to assess the amount of atmospheric aerosol suspended in atmosphere. Griggs (1975) was the first to derive the aerosol optical thickness from satellite measurements. Initially, only spectral measurements have been used. However, the subsequent studies (Mishchenko and Travis, 1997; Mishchenko et al., 2007; Kokhanovsky et al., 2010a) have shown the importance of multi-angular spectral measurements of both intensity and polarization characteristics of the reflected solar light. Several groups (see Kokhanovsky and de Leeuw, 2009; Dubovik et al., 2011; Hasekamp et al., 2011) have applied their algorithm to the Polarization and Directionality of the Earth's Reflectances (POLDER) and Research Scanning Polarimeter (RSP) data. The retrievals have shown that the quality of the aerosol products is essentially improved, if not only intensity but also multi-angular measurements of the backscattered solar light polarization are analyzed. The task of this paper is to review current aerosol retrieval techniques based both on intensity and polarization of reflected light measurements.
Aerosol Microphysical and Optical Properties
Atmospheric aerosol is composed of liquid and solid particles suspended in air (Hinds, 1999). They can be of different origin including solid or liquid particles wind-blown from the surface (e.g., sea salt and road dust), the particles produced in atmosphere due to aerosol nucleation bursts, particles emitted by industry, or even particles of a cosmic origin (debris of meteorits, etc.). The particles can be composed of organic and inorganic matter. Depending on the season and location, biological aerosols (spores, fungi, etc.) can dominate the total aerosol mass concentration. Usually aerosol particles are homogeneously mixed in the atmospheric boundary layer. However, in some cases (dust outbreaks, volcanic eruptions, fires, and industrial plumes) the concentration of aerosol particles is at maximum at a certain height (or heights) above the ground.
The aerosol properties of interest are:
- the vertical distribution of aerosol concentration N0(z)(m−3), where z is the vertical coordinate,
- the aerosol columnar concentration N = ∫zTOA0 N0 (z) dz (m−2), where zTOA is the position of the top-of-atmosphere (TOA),
- the aerosol chemical composition, type, and the aerosol refractive index,
- the aerosol size distribution, the shape and internal structure of the particles.
The aerosol optical properties such as the aerosol extinction and absorption coefficients, aerosol single scattering albedo (SSA), and aerosol phase matrix (PM) are of interest as well.
The complete characterization of the atmospheric aerosol requires the knowledge of the spatial distribution of the aerosol concentration N0(), the aerosol size distribution f(,), the particulate matter shape/internal structure distribution, and chemical composition (e.g., the spectral complex refractive index m()). Here is the vector signifying the position of the particle in the atmosphere and is the vector-parameter of geometrical dimensions of particles (e.g., the semi-axis of the ellipsoids or the radius for spheres). These parameters can be used to calculate the aerosol optical properties. The aerosol optical thickness (AOT) τ can be found from the following relationship:
Here Cext is the extinction cross section of the aerosol particle with the radius a. An important fact is that AOT can be directly measured from the ground using sunphotometers. Many satellite aerosol retrieval algorithms focus on the AOT determination using reflected solar light as detected on a satellite (Kokhanovsky and de Leeuw, 2009). Clearly, the intensity of the reflected solar light is influenced not only by AOT but also by aerosol phase function (PF)/phase matrix, the single scattering albedo, and underlying surface reflectance (USR). Therefore, the retrieval algorithms are often based on the assumptions with respect to the SSA, USR, and PF/PM. The ultimate goal is to develop the algorithm, which retrieves not only AOT but also SSA, PF/PM and underlying surface characteristics. This can be done successfully only using multi-angular polarimetric measurements (Kokhanovsky et al., 2010a; Knobelspiesse et al., 2012) performed at several wavelengths (e.g., from the UV to NIR).
To simplify the solution of the inverse problem, it is usually (but not always!) assumed that the atmospheric aerosol is homogeneously distributed in the boundary layer (say, 1 km depth) and composed of two fractions (fine mode with the mode radius a0 around 0.1 μm and coarse mode with the mode radius around 1 μm). It is assumed that each mode is characterized by the spectral complex refractive index m (mf for the fine mode and mc for the coarse mode). The particle size distribution for the both modes is assumed to be lognormal:
where s is the half-width parameter. The distribution is broader for larger values of s. The effective radius aef and the effective variance vef of particle size distribution are related to a0 and s with the following equations (Kokhanovsky, 2006): aef = a0 exp(2.5s2), vef = exp(s2) − 1.
The parameters for the inverse problem solution are a0, s, and the column number density of particles N in both modes. One needs to derive 6 parameters to characterize aerosol microstructure plus spectral complex refractive index m = n − ik for both modes. This is already quite a complex problem even if all particles are assumed to be spherical. Simultaneously with the aerosol state vector (ASV) (a0, s, N, n, k) (for both modes), the underlying surface spectral reflectance must be retrieved or eliminated (e.g., the use of spectral ratios, etc.).
In the assumption that the aerosol is distributed in a single homogeneous layer of a geometrical thickness L and has two modes (fine, coarse), we derive from Equation (1):
Here cf = Nf/N is the fine mode fraction, Nf is the columnar number density of particles in the fine mode, τf and τc are AOTs for the fine and coarse modes, respectively. Because the boundary layer thickness is generally not known, only the total surface aerosol concentration N = N0 L can be retrieved. The value of N0 can be found only if the boundary layer height is known in advance. The aerosol mass concentration can be derived from the following relationship: M = Nm, where m = ρ v is the average mass of an aerosol particle and v is the average volume of particles, ρ is the density of aerosol matter.
The Aerosol Retrieval Algorithms Based on the Measurements of the Stokes Vector of Reflected Solar Light
There are several retrieval algorithms based on the measurements of the Stokes vector of reflected solar light (I, Q, U, V) at several observation angles and spectral channels. They differ with respect to the general methodology (the use of pre-calculated look-up-tables, on-the-fly radiative transfer calculations, the selection of the inversion method (statistical roptimization, optimal estimation, etc.), the selection of input and output data, a priori assumptions, and the ways to deal with generally unknown underlying surface reflectance. Usually the Normalized Stokes Vector (NSV) (r, q, u, v) = π(I, Q, U, V)/E0μ0 is used in the retrievals. It has the following components: r = πI/E0μ0, q =πQ/E0μ0, u = πU/E0μ0, v = πV/E0μ0. Here μ0 is the cosine of the solar zenith angle, E0 is the extraterrestrial solar flux on the unit area perpendicular to the incident solar beam, Q = Il − Ir (Il, Ir are reflected intensity components parallel and perpendicular to the meridional plane containing the normal to the layer and viewing direction), , sin δ, δ is the phase difference between the electric vector components along two perpendicular axes (Perrin, 1942). It should be pointed out that the value of v = πV/E0μ0 is very small in the terrestrial atmosphere (see Kokhanovsky et al., 2010b) and, therefore, is not used in the retrievals. Sometimes the third Stokes vector component is used in the aerosol retrievals (Dubovik et al., 2011), sometimes—not (Knobelspiesse et al., 2011a). This is due to the fact the value of u is usually a small number and can be actually expressed via q, if the measurements are transferred to the scattering plane (Schutgens et al., 2004). Therefore, most of information on the aerosol comes from the measurements of r and q in the retrieval process. The value of r is positive by definition and q is the signed quantity being negative for the case of oscillations of the electric vector perpendicular to the meridional plane containing the normal to the scattering layer and the observation direction. The value of q makes more effective use of the observed neutral points as compared to the so-called polarized reflectance defined as .
The satellite aerosol retrieval algorithms have been developed specifically to process data from existing satellite and airborne spectropolarimeters (see Table 1). The ground-based and ship-based measurements of the Stokes vector of the transmitted light are used to characterize atmospheric aerosol as well.
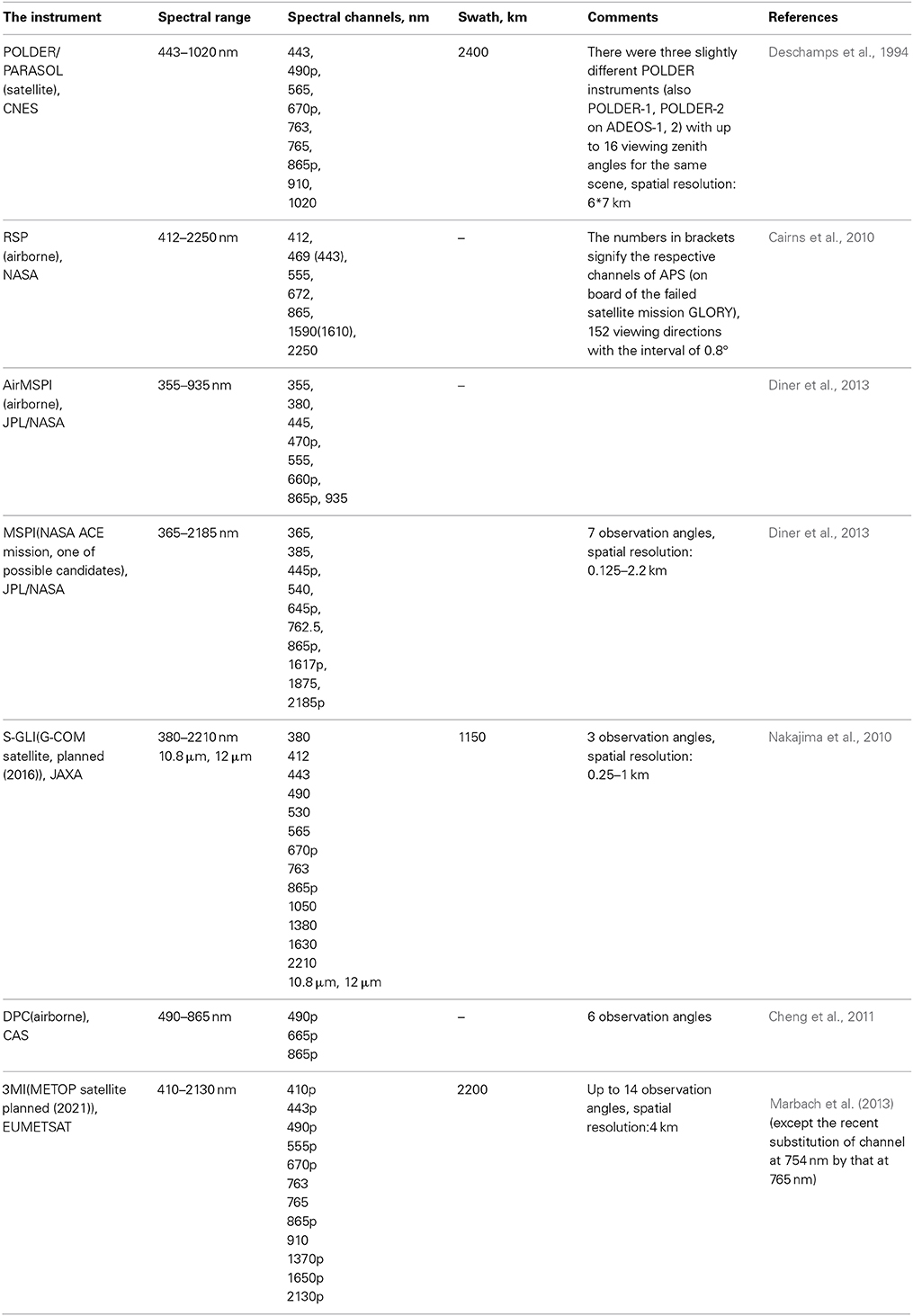
Table 1. The characteristics of airborne and spaceborne polarimeters (the index “p” means that the measurements of I, Q, U are performed at a given spectral channel).
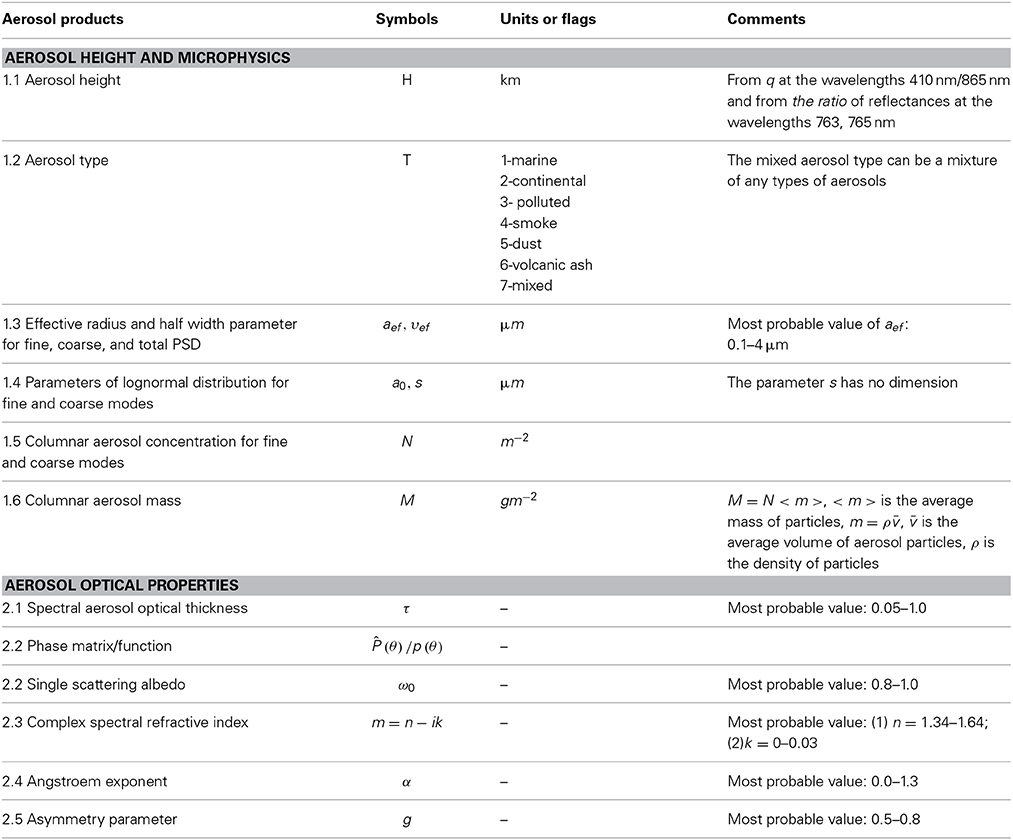
The summary of the algorithms is given in Table 2. The aerosol products are presented in Table 3. The algorithms and respective products are discussed in the next sections.
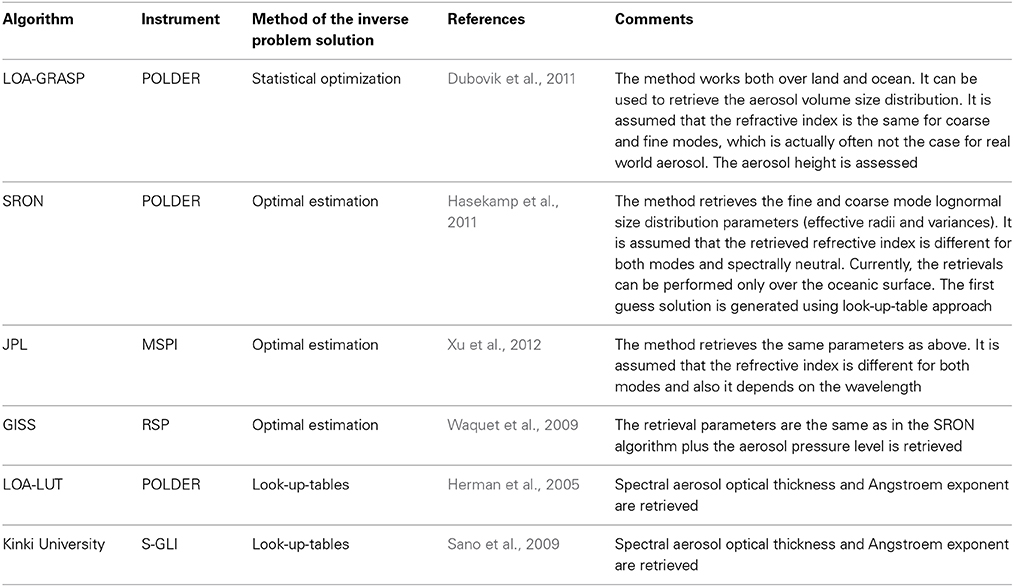
Table 2. The current aerosol retrieval algorithms based on the measurements of the intensity and polarization of backscattered light.
The GRASP Algorithm
The GRASP algorithm has been developed at Lille University (LOA) and published by Dubovik et al. (2011). The retrieval of aerosol properties is based on the POLDER measurements and rigorous statistical optimization. The algorithm fits the complete set of POLDER/PARASOL observations (see Table 1) in all spectral channels (except 763, 765, and 910 nm dominated by gaseous absorption) for up to 16 observation geometries including both measurements of total radiances and linear polarization (degree of linear polarization and the orientation of the plane of polarization with respect to the meridional plane). The retrieval parameters are the aerosol volume size distribution (in bins), the total volume concentration of aerosol, the complex aerosol refractive index (assumed to be the same for both modes), mean height of aerosol layer, and the fraction of nonspherical scatterers. Then these retrieved parameters are also used to calculate the total aerosol optical thickness, single scattering albedo and aerosol phase matrix. In addition, the surface reflectance parameters are also retrieved simultaneously with aerosol properties. The retrieval is designed as a rather elaborated fit providing statistically optimized solution. A number of a priori constrained are used including smoothness limitation on variability of size distribution and on spectral variability of all retrieved spectrally dependent parameters (complex refractive index and all spectrally dependent parameters of surface reflectance models). In addition, a new multi-pixel retrieval concept was realized in the algorithm: a simultaneous statistically optimized fitting of a large group of pixels within one or several images. Such, multi-pixel retrieval regime takes an advantage from known limitations on spatial and temporal variability in both aerosol and surfaces properties. Specifically the pixel-to-pixel or day-to-day variations of the retrieved parameters are enforced to be smooth by additional a priori constraints. This new concept is expected to provide retrieval of higher consistency for aerosol retrievals from satellites by enriching the retrieval over each single scene by co-incident aerosol information from neighboring pixels and also from the information about surface reflectance (over land) obtained in preceding and consequent observations over the same scenes. The algorithm is not based on look-up-tables. Instead it relies upon the direct radiative transfer (RT) calculations of various parameters and their derivatives. It is assumed that the aerosol vertical distribution follows the Gaussian law with the fixed half-width. The position of aerosol layer is derived during the inversion as well.
The SRON Algorithm
The SRON algorithm (Hasekamp et al., 2011) derives the following parameters: the effective radius, the effective variance, the refractive index (assumed to be spectrally neutral) in both modes and also AOTs for the fine and coarse modes. The algorithm fits POLDER observations at selected wavelengths and observation geometries simultaneously. The algorithm is based on direct radiative transfer calculations during the retrieval process. The derivatives are calculated using the solution of the adjoint radiative transfer equation. The Tikhonov regularization method is used in the retrieval process.
In particular, the following equation is used in the retrieval process:
where n = Wxn, a = Wxa, x is the vector of unknowns to be found, xa is the a priori vector of unknowns, W is the diagonal weighting matrix with the elements Wjj = 1/xa,j, b = S−1/2y (ymeas − ymod(xn)), ymes is the vector containing results of measurements (e.g., Stokes vector of reflected light at several wavelengths and observation directions), ymod is the vector containing the modeling results at a given value of the vector of unknowns in the n-th iteration xn, S−1/2y is the diagonal measurement error covariance matrix, which contains the measurement error estimate, , I is the unity matrix, γ is the regularization parameter, , Λ = (1 + ς)−1. The filter parameter ς is equal to 15 on the first iteration step. Then the update of the state vector is small (see Equation 4). The parameter ς is increased or decreased following an empirically found scheme similar to Levenberg-Marquardt strategies during the iterations (Rodgers, 2000).
Only the Stokes vector at 490, 670, 865, and 1020 nm is used in the retrieval process. The LUT constructed for 48 models for the fine mode and 2 models for the coarse mode is used to get the first guess of the solution. The 48 aerosol models are prepared assuming the effective radii 0.05, 0.1, 0.2, 0.3 (4 radii), the effective variance of 0.19, the real part of the refractive indices 1.35, 1.45, 1.55, and 1.65 (4 cases), and the imaginary part of refractive index equal to 0.001, 0.02, 0.1. The two aerosol models for the coarse mode components are given as (2.0, 0.43, 1.55, 0.00128) and (1.0, 0.43, 1.39, 0.0001) (in terms of the vector-parameter (aef, vef, n, κ) assuming the spectrally neutral complex refractive index).
The underlying surface reflectance is retrieved during the inverse problem solution as well.
The LOA LUT Algorithm
Underlying surface: ocean
The LOA LUT algorithm (over ocean) was presented by Deuzé et al. (2000). It relies on LUTs built for 12 aerosol models: for the three values of m and four values of the Angstrom exponent α (0.0, 0.3, 0.8, 1.4). It is assumed that the light absorption by aerosol particles is weak and can be neglected, which is a good approximation for the marine aerosol in the visible. The Angstrom exponent is calculated at s = 0.864 and the values of a0, which are functions of m, for the monomodal aerosol size distribution. The LUT is calculated at the values of AOT at 865 nm equal to 0.075, 0.15, 0.3, and 0.6 for various solar zenith angles, relative azimuths, and viewing zenith angles. The computations are performed with the successive order of scattering method taking into account molecular scattering, aerosol scattering, and specular reflectance from the sea surface according to the Cox and Munk (1954) model with the constant wind speed of 5 m/s. The molecular scattering is estimated according to standard atmosphere, and the aerosol and molecules are distributed according to the exponential density profiles with 2 and 8 km scale heights, respectively. Deuzé et al. (2000) have reported the differences up to 3% between the cases of a homogeneous and vertically inhomogeneous atmospheres (1% for the polarized radiance). Therefore, the accurate retrievals require a priori information on the aerosol vertical profiles (or the determination of the profiles during the retrieval process).
During the retrieval process the radiance and polarized radiance measurements at the wavelengths 670 and 865 nm, where water leaving radiance can be neglected, are compared with the theoretical radiances of the LUT until the best fit obtained for all observation geometries. This provides the parameters α, τ for the best fit, which serve as an output for the algorithm.
The modification of the algorithm using a nonspherical particle model was reported by Herman et al. (2005). They have used the bimodal size distribution instead of a mono-modal size distribution as it was done in the first version of the algorithm. For each N+M fine and coarse modes, the LUT was constructed for different values of AOTs at the wavelengths 670 and 865 nm, where the contribution of the water leaving radiance can be neglected. The Stokes vector corresponding to the mixture of fine (f) and coarse (c) modes are represented as a linear combination of the Stokes vectors for fine and coarse modes:
where γf = τf/τ. This reduces the size of LUTs because only the values of the Stokes vector for M fine mode and N coarse mode fractions must be stored and not their various combinations. The approach is an approximate one and strictly valid only in the case of single scattering. Usually, the aerosol optical thickness over ocean is low and the approach is well justified. The accuracy of approach depends on the number of fine and coarse modes. Herman et al. (2005) used 9 coarse modes and 33 fine modes. The couple (fine and coarse), which gives the best residual Δ between measurements and observations, is selected as the solution of the inverse problem. The residual at a given wavelength λ, ΔI(λ), for the J angular observations of the first Stokes component is calculated as follows:
and in a similar way for other components of the Stokes vector. Here rmeas (μj, λ) and rmod (μj, λ) are the measured and modeled reflectances, μj is the cosine of the observation angle. The final residual error is calculated as:
where λ1 = 670 nm, λ2 = 865 nm. The errors ΔQ (λ), ΔU(λ) are calculated using Equation (6) except for the second and the third component of the Stokes vector.
In the construction of LUTs, the value of a0 varies from 0.02 to 0.17 μm for the fine mode. It is equal to 0.5, 0.75, 1.0 for the coarse mode. The refractive index is assumed to be equal to 1.35, 1.45, or 1.6 for the fine mode. It is 1.35, 1.4, 1.45 for the coarse mode. The value of s is fixed (0.46 for the fine mode and 0.7 for the coarse mode).
The application of a similar algorithm combined with the dense dark vegetation approach (Kaufman and Sendra, 1988) to the measurements over East China has been reported by Wang et al. (2012).
Herman et al. (2005) also used the phase matrix of nonspherical scatterers to represent the possible presence of nonspherical scatterers in the atmospheric air. The 37 coarse modes are used in the construction of the LUTs with different proportions of nonspherical particles (for 4 values of the dissymmetry index defined as the ratio of the AOT at 865 nm for the nonspherical particles to the total AOT) and spherical particles from the 9 coarse modes used in the model of spherical scatterers. The output of the algorithm includes the AOT for the fine mode and also the AOT for the coarse mode (separately for spherical and nonspherical scatterers in the coarse mode).
Clearly, the correct retrievals can not be expected if nonspherical particles (say, dust from the deserts) are present in air but not included in the retrieval algorithm. Herman et al. (2005) found that an average model of the phase matrix of dust measured by Volten et al. (2001) in the laboratory can be used for the remote sensing purposes. The measurements of Volten do not contain the results in the small angle scattering range (below 5° scattering angle) due to the limitations of their experimental setup. Therefore, Herman et al. (2005) were not able to perform exact radiative transfer calculations for the respective phase matrix. Instead, the delta-approximation (Potter, 1970) was used. It is known that such an approximation is highly accurate with errors below the POLDER calibration errors.
The application of the algorithm (in slightly modified form) to the MICROPOL measurements (490–2200 nm spectral range) has been reported by Waquet et al. (2005).
When the aerosol load is low, the solution of the inverse problem becomes difficult and, therefore, a fixed aerosol model is considered, for which the aerosol optical thickness is derived. The retrieval of the refractive indices and modal radii of the small and large spherical particles depends on the viewing conditions since it requires a scattering angle coverage larger than 125–155°.
Underlying surface: land
Herman et al. (1997) and Deuzé et al. (2001) presented the main features of LOA LUT algorithm over land. They assumed that the reflected solar light as measured on a satellite is linearly polarized and can be characterized by the intensity, degree of polarization, and the angle between the polarization direction and the meridional plane. Indeed the ellipticity of the reflected light is usually small and can be neglected in most of cases (Kokhanovsky et al., 2010b). It is assumed that the aerosol PSD is a monomodal one with s = 0.864. Three values of the real refractive index are assumed (1.33, 1.4, 1.5) in the construction of the respective LUTs. For each value of the refractive index, a0 is adjusted to provide Angstrom exponents (AE) in the range 0.3–2.5. Given 2K measurements (2 wavelengths (670 and 865 nm) and K (usually equal to 16) viewing angles), for each aerosol model the deviation:
is calculated. Here Q is the second component of the Stokes vector. The function δ (τ) is minimized and the value of AOT, where δ (τ) has a minimum is reported in the output of the algorithm. Simultaneously, the Angstrom exponent α for the best fit aerosol model and also aerosol index i = ατ are reported. The fit of the calculated and measured reflected light intensity and the polarization angle ψ is not performed. This is because, as reported by the authors, the value of ψ is close to zero or 90° in most of cases and the intensity is influenced by the unknown surface reflectance. The Stokes vector component Q is less influenced by the surface reflectance because the polarizing power of terrestrial underlying surfaces is usually small and almost spectrally neutral. The authors have used the model of Nadal and Breon (1999) for the polarized surface reflectance in the retrieval process. The use of Q for remote sensing of fine mode aerosol contribution is well justified. However, the use of Q is more problematic in the case of large particles, where the degree of polarization is close to zero in most of observation geometries. Deuzé et al. (2001) confirmed a high accuracy of the algorithm for the case of biomass burning aerosols, where the fine mode fraction dominates. The results are less accurate in the case of coarse-mode dominated aerosols.
There are several versions of the respective LUTs with the most recent one containing accumulation mode aerosols with a0 in the range 50–150 nm, s = 0.403, and m = 1.47–0.01i. The output of the algorithm is the spectral AOT and the Angstrom Exponent of the fine mode only.
The extension of the algorithm to MICROPOL (670–2200 nm) over land measurements is reported by Waquet et al. (2007). The upwelling polarized radiance is modeled in the single scattering approximation. This is possible because primary scattering dominates the polarized light at typical values of AOT for the wavelengths above 670 nm. Therefore, only the wavelengths 670, 865, and 1600 nm are used in the retrieval process. The atmospheric contribution to the satellite signal is low at 2200 nm and this wavelength was used to assess the surface contribution to the polarized radiance, which is assumed to be spectrally neutral.
The polarized radiance is modeled as follows:
Here μ, μ0 are the cosines of the observation and solar zenith angles, ω0 is the single scattering albedo, τ is the AOT, τm is the molecular scattering optical thickness (low in the near infrared), qa is the aerosol polarized phase function and qm = 0.75(1 − cos2θ) is the molecular scattering polarized phase function, θ is the scattering angle, qs is the polarized surface reflectance. The transmission term in Equation (9) can be calculated as:
It is assumed that β lies between 0.3 and 0.6 depending on the aerosol model and γ = 0.9 (Lafrance and Herman, 1998).
A similar algorithm, with some modifications based on the use of the dark target approach (Kaufman et al., 1997a,b) and spectral mixture and separation techniques (von Hoyningen-Huene et al., 2003; Katsev et al., 2009), has been applied to the retrieval of aerosol properties over East Asia (Xie et al., 2013). The six aerosol models based on AERONET observations in the region under study have been used in the construction of LUTs. The authors state that in addition to the polarized reflectance, the total reflectance at 490 nm must be used in the retrievals. This is because the surface reflectance is low at this wavelength and the aerosol reflectance at 490 nm is higher as compared to the polarized reflectances (especially, for dust-loaded atmospheres).
The JPL Algorithm
The JPL aerosol optical thickness retrieval algorithm is based on the Levenberg-Marquardt inversion scheme. It currently adopts the multiplicative strategy for updating the damping factor. Starting with an initial guess x0, the optimized solution is approached through following iterations:
where Jk is the Jacobian matrix evaluated from the iterative solution xk and the weighting matrix W is diagonal with Wii = 1/σ2s,i, where σs is the standard deviation of I or Q measurements. The damping factor λk is chosen and adjusted in a multiplicative way until a solution xk+1 = xk + Δxk produces a significantly better fit to the measured data ymod, or in other words, the following chi-squared error function is reduced:
where ymod is the measured data vector containing r, q in the ith spectral/angle channel (i = 1, 2, … N, with N = 36 for 4 bands (443, 550, 670, and 865 nm) × 9 angles) and yk + 1 contains the fits for the reflectance and polarization data by the solution xk + 1 during the iteration. At the current stage, the weighting matrix is not considered and the iteration stops when the average fitting error F(xk + 1) = χ2 (xk + 1)/2N drops below a threshold value 1.0e-7 or the iteration exceeds kmax = 50 steps.
To start the retrieval, the same initial guess x0 for all 48 data sets is used, which means, the aerosol properties are m = 1.690, a0 = 0.125 μm, s = 0.3 and τ = 0.1 for the fine mode and m = 1.520, a0 = 0.7 μm, s = 1.0, τ = 0.07 for the coarse mode. The surface albedos rs are initialized to be 0.05, 0.05, 0.03, and 0.5 for 4 spectral bands mentioned above. The initial guess is obtained from a number of single scattering based retrievals (with slight manual adjustments so that starting from the same initial guess the retrieval gives similar aerosol properties for one group of data). As outer bounds on these parameters, it is assumed that 1.20 ≤ Re(m)≤ 1.70, 0.0 ≤ Im(m) ≤ 0.20, 0.02 ≤ a0 ≤ 1.00, 1.1 ≤ s ≤ 3.0, and 1.0E-4 ≤ τ ≤ 5.0 for both modes and 0 < rs < 1 for the four surface albedos.
The forward model used is the vectored Markov chain method recently developed at JPL. Currently it assumes bimodal lognormal distribution of aerosols and contains 3 types of surface, (i): depolarizing surface described by the modified RPV (mRPV) model (ii): polarizing surface described by the Cox-Munk's model and (iii): Mixed surface by (i) and (ii).
By setting k = 1 and b = 0, the surface described by mRPV reduces to be Lambertian surface with only the surface albedo remaining for retrieval. With the assumed MISR wavelengths 443, 560, 670, 865 nm, 6 parameters for bimodal log-normal aerosol size distribution are retrieved (a0, s, and N for each mode). In addition, the complex refractive index for each mode and surface albedo at 4 wavelengths is retrieved.
The algorithm for MSPI (see Table 1) is currently in preparation and is based on the GRASP algorithm with some minor changes including the introduction of the first guess using WRF-Chem model.
The GISS Algorithm
Waquet et al. (2009) reported the algorithm for the aerosol remote sensing over land based exclusively on the polarized reflectance measurements. The algorithm is based on the use of an optimal estimation method. The principle of an optimal estimation method is to determine the most probable atmospheric state conditional on the value of the measurements and some a priori knowledge of this medium (Rodgers, 2000). The following cost function is minimized:
where Y is the measurement vector, F is the simulation vector, X is the atmospheric state vector, Xa is the a priori atmospheric state vector, C−1T is the total error covariance matrix, C−1a is the a priori error covariance matrix.
The first term in Equation (13) corresponds to a weighted least squares error term that measures the distance between the measured polarized reflectances Rp = −πQ/μ0E0 and the modeled polarized reflectances. Here Q = Il − Ir is the second Stokes parameter defined with respect to the scattering plane, which contains the incident and observation directions. The polarized reflectance is positive, when the direction of polarization is perpendicular to the normal to the scattering plane. The total reflectances are not used in the retrieval process. This enables the better treatment of the underlying surface properties because surface polarized reflectances are generally low and almost spectrally neutral. The parameter U is not used because this parameter is close to zero, if the Stokes vector is defined with respect to the scattering plane and the polarized surface reflectance is similar to that caused by Fresnel reflection (Breon et al., 1995). The following bands are used: 410, 470, 550, 670, 865, and 1600 nm.
The second term in Equation (13) is a penalty function that constrains the solution to lie near the a priori state. It is assumed as the first guess: a0 = 150 nm, s = 0.4 for the fine mode and a0 = 800 nm, s = 0.6 for the coarse mode with refractive indices 1.47–0.01i and 1.53–0.005i for the fine and coarse modes, respectively. The LUTs are used to make the first rough estimate of the aerosol model and aerosol optical thickness. In total, 10 aerosol parameters are retrieved (a0, s, N and the spectrally neutral refractive index m = n − iκ for each mode) plus the pressure level that corresponds to the height, where the top of the aerosol layer is located.
Waquet et al. (2009) have shown that the surface-atmosphere reflection matrix can be described approximately as:
Here Ra is the reflection function of atmosphere bounded by the absolutely black surface underneath, Rs is the surface reflectance matrix, T1 is the total atmospheric transmittance from the TOA to the surface and T2 is the total atmospheric transmittance from the surface to the satellite. This approximation works quite well, if only the polarized reflectance is of concern. This is mostly due to the low ability of the terrestrial surfaces to polarize the incident sunlight. Also the second term in Equation (14) can be parameterized as follows: T2RsT1 = tRs, where t is given by Equation (10). Then it follows from Equation (14):
An important point is to separate the contribution of the aerosol and surface to the spectral TOA reflectance. This can be done in many ways. For instance, one may assume that the contribution of aerosol is low at 2200 nm and the polarized surface reflectance is almost spectrally neutral. Then the signal at 1600 nm can be modeled as:
Another opportunity is to use the approximation that the ratios of the bidirectional surface reflectance distribution matrix (BRDM) Rs at two viewing directions do not depend on the wavelength. Then Rs can be illuminated from Equation (15) and the retrieval becomes less influenced by the surface reflectance. There are also several parameterizations for the surface BRDM. In particular, Waquet et al. (2009) used the following approximation for the polarized surface reflectance (Breon et al., 1995):
where the Fresnel polarized RFp is calculated with a surface refractive index of 1.4 (the value of 1.5 is also used sometimes). The spectrally neutral scaling factor ξ depends on the observation angle and it is estimated from the measurements at 2200 nm, where the aerosol contribution is generally low.
Knobelspiesse et al. (2011b) have used the GISS algorithm (with some modifications) to the combined retrievals of boreal forest fire aerosol properties with a polarimeter and a lidar. The value of q at six wavelengths centered at 410, 470, 555, 670, 865, and 1590 nm was used in the retrievals at several observation geometries. The 2250 nm band was used to characterize the total and polarized surface reflectance for the radiative transfer model. The total radiance at 410 nm was used in the retrieval process. This is because the surface reflectance is low at this wavelength. The surface reflectance at 410 nm was estimated using the approach as described by Kaufman et al. (1997b). It is based on observations at 2250 nm. The authors have retrieved all components of the aerosol state vector—parameter (AVP) (a0, s, N, n, k) for the fine and coarse modes and also the aerosol height. The by-products have been derived as well. In particular, the scattering, extinction, and absorption cross sections, single scattering albedo, AOT, Angstroem parameter, backscatter-extinction ratio, and phase function at backscatter have been found for the case under study. The authors have used (a0, s) and not (aef, vef) as fitting parameters because the retrieval of the set (aef, vef) is more noisy due to the fact the effective parameters are the functions of the higher moments of the PSD. It was assumed that the refractive index is spectrally neutral, which is a valid assumption for the fire aerosol properties in the spectral range under study. Knobelspiesse et al. (2011a) have modified the approach described above to allow the imaginary part of aerosol refractive index to vary and have performed the simultaneous retrievals of aerosol and cloud properties during the MILARGO field campaign. It was assumed that the value of k for the fine mode can be presented as:
where ξk,f (λ) = (λ + 0.445)−10 and λ is the wavelength in microns. Such a modification is needed to allow for the increase in absorption at shorter wavelengths due to the “brown carbon” (BrC, absorbing organic carbon aerosols). The shortcoming of the method is due to the fact that the function ξ (λ) is purely empirical. Equation (18) can be generalized to account for the spectral dependence of the real part of the refractive index of fine aerosol mode:
where the function ξn,f (λ) can be selected using several retrieval tests. Another opportunity is determination of the functions ξn,f (λ) and ξκ,f (λ) from the retrieval itself. In a similar way, the spectral dependence of the complex refractive index of the coarse mode can be presented as:
The influence of aerosol vertical inhomogeneity on aerosol retrievals for RSP have been studied by Zhai et al. (2013) in the framework of the Levenberg-Marquardt algorithm for least squares fitting to minimize the following cost function:
Here Δri and Δqi are the differences between the measurements and calculations of r and q, respectively, for a given aerosol state. The index i is used to denote the functional dependence on the wavelength, the viewing zenith angle (for M measurements). The constants α and β are instrument—specific. They account for the RSP sensitivity.
The input for the algorithm is the Stokes vector measured at several angles and the wavelengths by the RSP and the output is the aerosol state vector (a0, s, N, n, k) for the monomodal PSD (and also aerosol height information). The initial guess is found using the LUT approach looking through 4500 cases with different aerosol states. The radiative transfer model is the successive-orders-of-scattering code.
Additional Algorithms: Brief Overview
Sano et al. (2009) has been developed an aerosol retrieval algorithm based on simultaneous intensity and polarization of reflected light measurements. It is based on the planned measurements of the S-GLI instrument on board Japanese GCOM-C SGLI (launch: 2016). The characteristics of the instrument are given in Table 1. The algorithm utilizes the measurements of the intensity of reflected light at the wavelengths 380, 670, 870 nm, and also the parameters (Q,U) at 670 and 870 nm. It is a simple look up table approach, where the parameters (a0, s) for the fine and coarse modes are fixed (a0 = 135 nm, s = 0.43 for the fine mode and a0 = 2365 nm, s = 0.63 for the coarse mode). The total aerosol optical thickness, the ratio of the fine mode AOT to the coarse mode AOT, the Angstroem exponent, and also the aerosol single scattering albedo are the output parameters. The surface reflectance is estimated using the minimal reflectance method.
Cheng et al. (2011) has developed the algorithm based on the measurements of the airborne Directional Polarimetric Camera (DPC). The camera performs measurements of the intensity, the degree of polarization, and the plane of polarization direction of reflected solar light at three wavelengths (490, 665, and 865 nm) and six viewing directions. The AOT and AE are retrieved using LUT approach based on Stokes vector measurements at 665 and 865 nm. The LUT is prepared using local aerosol properties and the surface reflectance measured at the ground. The aerosol scale height was determined using Raman lidar. The following cost function is minimized:
Here ΔRp,i,j is the difference between the measured and calculated (for a given aerosol state) polarized reflectance. The index i counts the wavelengths and the index j counts the observation angles.
Masuda et al. (2000) have retrieved the AOT and Angstroem coefficient using POLDER measurements. The degree of polarization measurements at the wavelengths 443 and 865 nm have been used. Masuda et al. (2000) reported that the AOT retrieval methods based on the polarization are more influenced by the assumption on the size of particles and also their refractive index as compared to the radiance only method in the case, if the wavelengths 670 and 865 nm are used. The same is true with respect to the shape of particles (Quenzel, 1983). Cheng et al. (2011) demonstrated the potential of AOT retrievals (including fine mode and nonspherical scatterers fractions) based on the radiance and polarization measurements (multi-angular) at a single wavelength 865 nm.
Lebsock et al. (2007) have developed the algorithm based on the measurements of reflected light intensity and degree of polarization by POLDER onboard PARASOL. They used the optimal estimation approach (Rodgers, 2000) and derived three aerosol parameters (AOT, effective refractive index, and the logarithm of the ratio Γ of the number concentration of two modes). They argue that only three pieces of information [e.g., AOT, Re(m), and Γ(oraef)] can be uniquely determined from POLDER measurements. They also have shown that the measurements of the degree of polarization are essential for the evaluation of the aerosol refractive index. The use of polarization in aerosol remote sensing is especially important in the case of underlying land surfaces.
Conclusions
It follows from this survey that all aerosol retrieval algorithms can be separated in two large categories: (1) the algorithms based on the LUT-approach, (2) the advanced algorithms based on various optimization, minimization and regularization methods. The second category of the algorithms is based on—the fly radiative transfer calculations and performs the search of the aerosol state vector in the continuous space of the solutions. The first type algorithms are more quick but they are based on the discrete space of the solutions. Therefore, the second-type algorithms are more accurate. However, they currently require a lot of processing time and not suitable for the operational processing. There are various attempts to speed the type 2 algorithms (e.g., using the LUTs for the generation of the first guess). However, the respective algorithms are still not mature enough to produce the speed of calculations needed for the operational processing.
Some retrieval algorithms are specifically designed for the retrievals over ocean and can not be used for the estimation of aerosol propertries over land. Other types of algorithms (e.g., GRAPS) are of universal nature and can be used both over land and ocean. The quality of retrievals of aerosol properties by different algorithms depend on the aerosol type. For instance, GRASP currently assumes the same refractive indices for both fine and coarse modes. However, this is not the case for the smoke and dust aerosol mixtures and also for some other cases. Then the quality of retrievals detoriarates. The SRON algorithm is free from this assumption and more suitable for the retrievals of mixed aerosol types. Some algorithms can deal with nonspherical scatterers and others assume that the signals as measured by an optical instrument is primarily from particles of spherical shape.
Most of algorithms include the estimation of corresponding errors of retrievals. This is especially easily done in the framework of optimal estimation methods. The problem of optimal estimation based algorithms discussed in this paper is computational time. This problem can be avoided using fast forward operators (e.g., LUTs in combinations with approximate analytical solutions of the vector radiative transfer equation valid for both small and large vertical columns of suspended particulate matter).
Conflict of Interest Statement
The Associate Editor Thomas Nauss declares that, despite having collaborated with author Alexander Kokhanovsky, the review process was handled objectively and no conflict of interest exists. The author declares that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The author thanks J. Weigt for the help in the literature search. He is also grateful to two reviewers and also to B. Cairns, O. Dubovik, O. Hasekamp, I. Sano, E. Zege, F. Xu, V. Budak, R. Munro for the discussions on aerosol remote sensing and review of this document or its parts. This work was supported by EUMETSAT.
Abbreviations
3MI, Multi-viewing Multi-channel Multi-polarization Imager (EUMETSAT mission); ACE, Aerosol-Cloud-Environment (Tier 2 NASA Decadal Survey mission); ADEOS, ADvanced Earth Observing Satellite (JAXA satellite series); AirMSPI, Airborne MSPI; DPC, Directional Polarimetric Camera; EUMETSAT, European Meteorological Satellite (organization); GRASP, Generalized Retrieval of Aerosol & Surface Properties; GCOM, Global Change Observation Mission (JAXA satellite series); JAXA, Japanese space agency; JPL, Jet Propulsion Laboratory (NASA Center); LOA, Laboratoire d'Optique Atmosphérique (CNRS research unit at Université Lille 1); MSPI, Multiangle SpectroPolarimetric Imager; NASA, National Aeronautics and Space Agency; PARASOL, Polarization and Anisotropy of Reflectances for Atmospheric Science coupled with Observations from a Lidar; POLDER, Polarization and Directionality of Earth Reflectance; RSP, Research Scanning Polarimeter; S-GLI, Second generation GLobal Imager; SRON, Netherlands Institute for Space Research.
References
Breon, F. M., Tanre, D., Leconte, P., and Herman, M. (1995). Polarized reflectance of bare soils and vegetation: measurements and models. IEEE Trans. Geosci. Remote Sens. 33, 487–499.
Cairns, B., Waquet, F., Knobelspiesse, K., Chowdhary, J., and Deuze, J.-L. (2010). “Polarimetric remote sensing of aerosols over land surfaces,” in Satellite Aerosol Remote Sensing Over Land, eds A. A. Kokhanovsky and G. de Leeuw (Chichester: Springer-Praxis), 295–325.
Cheng, T. H., Gu, X. F., Xie, D. H., Li, Z. Q., Yu, T., and Chen, X. F. (2011). Simultaneous retrieval of aerosol optical properties over the Pearl River Delta, China using multi-angular, multi-spectral, and polarized measurements. Remote Sens. Env. 115, 1643–1652. doi: 10.1016/j.rse.2011.02.020
Cox, C., and Munk, W. (1954). Measurements of the roughness of the sea surfacefrom the photographs of Sun's glitter. JOSA 44, 838–850.
Diner, D. J., Xu, F., Garay, M. J., Martonchik, J. V., Rheingans, B. E., Geier, S., et al. (2013). The airborne multiangle spectropolarimetric imager (AirMSPI): a new tool for aerosol and cloud remote sensing. Atmos. Meas. Tech. 6, 2007–2025. doi: 10.5194/amt-6-2007-2013
Deschamps, P. Y., Bréon, F. M., Leroy, M., Podaire, A., Bricaud, A., Buriez, J. C., et al. (1994). The POLDER mission; Instrument characteristics and scientific objectives'. IEEE Trans. Geosci. Remote Sens. 32, 598–615.
Deuzé, J. L., Bréon, F. M., Devaux, C., Goloub, P., Herman, M., Lafrance, B., et al. (2001). Remote sensing of aerosols over land surfaces from POLDER-ADEOS-1 polarized measurements. J. Geophys. Res. 106, 4913–4926. doi: 10.1029/2000JD900364
Deuzé, J. L., Goloub, P., Herman, M., Marchand, A., Perry, G., Susana, S., et al. (2000). Estimate of the aerosol properties over the ocean with POLDER. J. Geophys. Res. 105, 15329–15346. doi: 10.1029/2000JD900148
Dubovik, O., Herman, M., Holdak, A., Lapyonok, T., Tanré, D., Deuzé, J. L., et al. (2011). Statistically optimized inversion algorithm for enhanced retrieval of aerosol properties from spectral multi-angle polarimetric satellite observations. Atmos. Meas. Tech. 4, 975–1018. doi: 10.5194/amt-4-975-2011
Fraser, R. S. (1976). Satellite measurement of mass of Sahara dust in the atmosphere. Appl. Opt. 15:24.
Griggs, M. (1975). Measurements of atmospheric aerosol optical thickness over water using ERTS-1 data. J. Air Pollut. Control. Assoc. 25, 622–626.
Hasekamp, O. P., Litvinov, P., and Butz, A. (2011). Aerosol properties over the ocean from PARASOL multiangle photopolarimetric measurements. J. Geophys. Res. 116, D14204. doi: 10.1029/2010JD015469
Herman, M., Deuzé, J. L., Devaux, C., Goloub, P., Bréon, F. M., and Tanré, D. (1997). Remote sensing of aerosols over land surfaces including polarization measurements and application to POLDER measurements. J. Geophys. Res. 102, 17039–17049. doi: 10.1029/96JD02109
Herman, M., Deuzé, J.-L., Marchand, A., Roger, B., and Lallart, P. (2005). Aerosol remote sensing from POLDER/ADEOS over the ocean: improved retrieval using a nonspherical particle model. J. Geophys. Res. 110, D10SD02. doi: 10.1029/2004JD004798
Hinds, W. C. (1999). Aerosol Technology: Properties, Behaviour, and Measurement of Airborne particles. New York, NY: Wiley.
Katsev, I. L., Prikhach, A. S., Zege, E. P., Ivanov, A. P., and Kokhanovsky, A. A. (2009). “Iterative procedure for retrieval of spectral aerosol optical thickness and surface reflectance from satellite data using fast radiative transfer code and its application to MERIS measurements,” in Satellite Aerosol Remote Sensing Over Land, eds A. A. Kokhanovsky and G. de Leeuw (Berlin: Springer-Praxis), 101–134.
Kaufman, Y. J., and Sendra, C. (1988). Algorithm for automatic atmospheric corrections to visible and near-IR satellite imagery. Int. J. Remote Sens. 9, 1357–1381.
Kaufman, Y. J., Tanre, D., Nakajima, T., Lenoble, J., Frouin, R., Grassl, H., et al. (1997a). Passive remote sensing of tropospheric aerosol and atmospheric correction for the aerosol effect. J. Geophys. Res. 102, 16815–16830.
Kaufman, Y. J., Wald, A. E., Remer, L. A., Gao, B.-C., Li, R., and Flynn, L. (1997b). The MODIS 2.1 mm channel—Correlation with visible reflectance for use in remote sensing of aerosol, IEEE Trans. Geosci. Remote Sens. 35, 1286–1298.
Knobelspiesse, K., Cairns, B., Mishchenko, M., Chowdhary, J., Tsigaridis, K., van Diedenhoven, B., et al. (2012). Analysis of fine-mode aerosol retrieval capabilities by different passive remote sensing instrument designs. Opt. Exp. 20, 21457–21484. doi: 10.1364/OE.20.021457
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Knobelspiesse, K., Cairns, B., Ottaviani, M., Ferrare, R., Hair, J., Hostetler, C., et al. (2011b). Combined retrievals of boreal forest fire aerosol properties with a polarimeter and lidar. Atmos. Chem. Phys. 11, 7045–7067. doi: 10.5194/acp-11-7045-2011
Knobelspiesse, K., Cairns, B., Redemann, J., Bergstrom, R. W., and Stohl, A. (2011a). Simultaneous retrieval of aerosol and cloud properties during the MILAGRO field campaign. Atmos. Chem. Phys. 11, 6245–6263. doi: 10.5194/acp-11-6245-2011
Kokhanovsky, A. A., Budak, V. P., Cornet, C., Duan, M., Emde, C., Katsev, I. L., et al. (2010b). Benchmark results in vector atmospheric radiative transfer. JQSRT 111, 1931–1946. doi: 10.1016/j.jqsrt.2010.03.005
Kokhanovsky, A. A., Deuzé, J. L., Diner, D. J., Dubovik, O., Ducos, F., Emde, C., et al. (2010a). The intercomparison of major aerosol retrieval algorithms using simulated intensity and polarization characteristics of reflected light. Atmos. Meas. Tech. 3, 909–932. doi: 10.5194/amt-3-909-2010
Kokhanovsky, A. A. (2013). Remote sensing of atmospheric aerosol using spaceborne optical observations. Earth Sci. Rev. 116, 95–108. doi: 10.1016/j.earscirev.2012.10.008
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Kokhanovsky, A. A., and de Leeuw, G. (2009). Satellite Aerosol Remote Sensing Over Land. Berlin: Springer-Praxis.
Lafrance, B., and Herman, M. (1998). Correction of the stratospheric aerosol radiative influence in the POLDER measurements. IEEE Trans. Geosci. Remote Sens. 36, 1599–1608.
Lazarev, A. I., Kovalenok, V. V., and Avakyan, S. V. (1987). Investigation of Earth from Manned Spacecraft. Leningrad: Gidrometeoizdat.
Lebsock, M. D., L'Ecuyer, T., S., and Stephens, G. L. (2007). Information content of near-infrared spaceborne multiangular polarization measurements for aerosol retrievals. J. Geophys. Res. 112, D14206. doi: 10.1029/2007JD008535
Lee, K. H., Li, Z., Kim, Y. J., and Kokhanovsky, A. (2009). “Atmospheric aerosol monitoring from satellite observations: a history of three decades,” in Atmospheric and Biological Environmental Monitoring, eds Y. J. Kim, U. Platt, M. B. Gu, and H. Iwahashi (Berlin: Springer), 13–38.
Marbach, T., Phillips, P., Lacan, A., and Schlussel, P. (2013). “The Multi-Viewing, -Channel, -Polarisation Imager (3MI) of the EUMETSAT polar system—second generation (EPS-SG) dedicated to aerosol characterisation,” in Proceeding of SPIE 8889, Sensors, Systems, and Next-Generation Satellites XVII (Bellingham, WA). doi: 10.1117/12.2028221
Masuda, K., Takashima, T., Kawata, Y., Yamazaki, A., and Sasaki, M. (2000). Retrieval of aerosol optical properties over teh ocean using multispectral polarization measurements from space. Appl. Mathem. Comp. 116, 103–114. doi: 10.1016/S0096-3003(99)00198-8
Mekler, Y., Quenzel, H., Ohring, G., and Marcus, I. (1977). Relative atmospheric aerosol content from ERTS observations. J. Geophys. Res. 82, 967–972.
Mishchenko, M. I., Cairns, B., Kopp, G., Schueler, C. F., Fafaul, B. A., Hansen, J. E., et al. (2007). Accurate monitoring of terrestrial aerosols and total solar irradiance: introducing the Glory Mission. Bull. Amer. Meteorol. Soc. 88, 677–691. doi: 10.1175/BAMS-88-5-677
Mishchenko, M. I., and Travis, L. D. (1997). Satellite retrieval of aerosol properties over the ocean using measurements of reflected sunlight: effect of instrumental errors and aerosol absorption. J. Geophys. Res. 102, 13543–13553.
Nadal, F., and Breon, F.-M. (1999). Parameterization of surface polarized reflectance derived from POLDER spaceborne measurements. IEEE Trans. Geosci. Remote Sens. 37, 1709–1718.
Nakajima, T. Y., Kuji, M., Sano, I., Schutgens, N., Mano, Y., Riedi, J., et al. (2010). Observations of cloud and aerosol from GCOM-C SGLI. Int. Arch. Photogr. Remote Sens. Spat. Inf. Sci. XXXVIII, 30–34.
Perrin, F. (1942). Polarization of light scattered by isotropic opalescent media. Phys. J. Chem. 10, 415–427.
Potter, J. (1970). Delta function approximation in radiative transfer theory. J. Atmos. Sci. 27, 943–949.
Quenzel, H. (1983). Passive aerosol remote sensing from space now and in the future. Adv. Space Res. 2, 19–28.
Rodgers, C. (2000). Inverse Methods for Atmospheric Sounding. Theory and Practice. Singapore: World Scientific.
Sano, I., Okada, Y., Mukai, M., and Mukai, S. (2009). Retrieval algorithm based on combined use of POLDER and GLI data for biomass aerosols. J. Remote Sens. Soc. Jpn. 29, 54–59.
Schutgens, N. A. J., Tilstra, L. G, and Stammes, P. (2004). On the relationship between Stokes parameters Q and U of atmospheric ultraviolet/visible/near-infrared radiation. J. Geophys. Res. 109, D09205, doi: 10.1029/2003/JD004081
Volten, H., Muñoz, O., de Haan, J. F., Vassen, W., Hovenier, J. W., Muinonen, K., et al. (2001). Scattering matrices of mineral aerosol particles at 441.4 nm and 632.8 nm. J. Geophys. Res. 106, 17375–17401. doi: 10.1029/2001JD900068
von Hoyningen-Huene, W., Freitag, M., and Burrows, J. B. (2003). Retrieval of aerosol optical thickness over land surfaces from top-of-atmosphere radiance. J. Geophys. Res. 108, D94260. doi: 10.1029/2001JD002018
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Wang, Z., Chen, L., Li, Q., Li, S., Jiang, Z., and Wang, Z. (2012). Retrieval of aerosol size distribution from multi-angle polarized measurements assisted by intensity measurements over East China. Remote Sens. Environ. 124, 679–688. doi: 10.1016/j.rse.2012.06.021
Waquet, F., Cairns, B., Knobelspiesse, K., Chowdhary, J., Travis, L. D., Schmid, B., et al. (2009). Polarimetric remote sensing of aerosols over land. J. Geophys. Res. 114, D01206. doi: 10.1029/2008JD010619
Waquet, F., Goloub, P., Deuzé, J.-L., Léon, J.-F., Auriol, F., Verwaerde, C. et al. (2007). Aerosol retrieval over land using a multiband polarimeter and comparison with path radiance method. J. Geophys. Res. 112, D11214. doi: 10.1029/2006JD008029
Waquet, F., Léon, J.-F., Goloub, P., Pelon, J., Tanré, D., and Deuzé, J.-L. (2005). Maritime and dust aerosol retrieval from polarized and multispectral active and passive sensors. J. Geophys. Res. 110, D10S10. doi: 10.1029/2004JD004839
Xie, D., Cheng, T., Zhang, W., Yu, J., and Li, X. (2013). Aerosol type over east Asian retrieval using total and polarized remote sensing. JQSRT 129, 15–30. doi: 10.1016/j.jqsrt.2013.05.028
Xu, F., Davis, A. B., Sanghavi, S. V., Martonchik, J. V., and Diner, D. J. (2012). Linearization of Markov chain formalism for vector radiative transfer in a plane-parallel atmosphere/surface system. Appl. Opt. 51, 3491–3507. doi: 10.1364/AO.51.003491
Pubmed Abstract | Pubmed Full Text | CrossRef Full Text | Google Scholar
Keywords: remote sensing, atmospheric aerosol, polarimetry, inverse problems, atmospheric optics, radiative transfer
Citation: Kokhanovsky AA (2015) The modern aerosol retrieval algorithms based on the simultaneous measurements of the intensity and polarization of reflected solar light: a review. Front. Environ. Sci. 3:4. doi: 10.3389/fenvs.2015.00004
Received: 08 July 2014; Accepted: 16 January 2015;
Published online: 11 February 2015.
Edited by:
Thomas Nauss, Philipps Universität Marburg, GermanyReviewed by:
Alessandro Battaglia, University of Leicester, UKIrina Melnikova, St.Petersburg State University, Russia
Copyright © 2015 Kokhanovsky. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Alexander A. Kokhanovsky, European Organisation for the Exploitation of Meteorological Satellites (EUMETSAT), Eumetsat Allee 1, D64295 Darmstadt, Germany e-mail:YWxleGFuZGVyLmtva2hhbm92c2t5QGV1bWV0c2F0LmludA==
 Alexander A. Kokhanovsky
Alexander A. Kokhanovsky