- 1Discipline of Computer Science, School of Science and Technology, University of New England, Armidale, NSW, Australia
- 2Epidemiology and One Health Program, Animal Health Policy Branch, Department of Agriculture, Canberra, ACT, Australia
Foot-and-mouth disease (FMD) is a highly contagious and economically important viral disease of cloven-hoofed animals. Australia's freedom from FMD underpins a valuable trade in live animals and animal products. An outbreak of FMD would result in the loss of export markets and cause severe disruption to domestic markets. The prevention of, and contingency planning for, FMD are of key importance to government, industry, producers and the community. The spread and control of FMD is complex and dynamic due to a highly contagious multi-host pathogen operating in a heterogeneous environment across multiple jurisdictions. Epidemiological modeling is increasingly being recognized as a valuable tool for investigating the spread of disease under different conditions and the effectiveness of control strategies. Models of infectious disease can be broadly classified as: population-based models that are formulated from the top-down and employ population-level relationships to describe individual-level behavior; individual-based models that are formulated from the bottom-up and aggregate individual-level behavior to reveal population-level relationships; and hybrid models which combine the two approaches into a single model. The Australian Animal Disease Spread (AADIS) hybrid model employs a deterministic equation-based model (EBM) to model within-herd spread of FMD, and a stochastic, spatially-explicit agent-based model (ABM) to model between-herd spread and control. The EBM provides concise and computationally efficient predictions of herd prevalence and clinical signs over time. The ABM captures the complex, stochastic and heterogeneous environment in which an FMD epidemic operates. The AADIS event-driven hybrid EBM/ABM architecture is a flexible, efficient and extensible framework for modeling the spread and control of disease in livestock on a national scale. We present an overview of the AADIS hybrid approach, a description of the model's epidemiological capabilities, and a sample case study comparing two strategies for the control of FMD that illustrates some of AADIS's functionality.
Introduction
An outbreak of foot-and-mouth disease (FMD) in Australia would have a major economic and social impact. This includes disruption of the domestic market for livestock and products, loss of access to international markets, severe production and income losses in livestock and related industries, and the financial, political and social pressures of eradicating the disease (Carpenter et al., 2011; Matthews, 2011; Rushton et al., 2012). The present value of total direct economic losses from an outbreak of FMD in Australia are estimated at $5.6 to $52.2 billion AUD over 10 years, depending on the size of the outbreak and the effectiveness of control (Buetre et al., 2013).
Disease managers are faced with a number of challenges when responding to incursions of serious disease such as FMD. These include: what control measures to adopt; trade and economic implications of different control measures; how to manage resources such as personnel, equipment and vaccine; access to appropriate technology such as diagnostic tools; animal welfare issues; consumer concerns, and possible public health ramifications (Garner et al., 2007). The choice of control measures can be a compromise between the requirement for large-scale implementation and what is logistically and economically feasible (Tildesley et al., 2006). Disease models are increasingly being employed as decision support tools for outbreak planning and response (Garner and Hamilton, 2011). Models are especially useful when a country has not recently experienced the disease of concern (Bates et al., 2003b), for example, the last outbreak of FMD in Australia occurred in 1872 (Bunn et al., 1998).
Models of disease spread range from simple deterministic mathematical models (Haydon et al., 1997), through to complex spatially-explicit stochastic microsimulations (Garner and Beckett, 2005; Harvey et al., 2007; Stevenson et al., 2013). Models can be distinguished on the basis of how they handle time (discrete/continuous), space (spatially-explicit/non-spatial), and chance and uncertainty (deterministic/stochastic) (Taylor, 2003). Another way of classifying models is whether they are population-based, individual-based or a combination of both. A population-based model is formulated from the top-down and employs population-level relationships to describe individual-level behavior. An example is a traditional equation-based model (EBM) which uses a system of ordinary differential equations (ODEs) to prescribe ratios of infection states in a population over time (Keeling and Rohani, 2008). The model concisely and efficiently describes how a population ‘flows’ between Susceptible, Exposed, Infectious and Recovered (SEIR) compartments. Compartmental EBMs carry a general assumption of homogeneous contact rates and susceptibility, i.e., individuals mix uniformly and randomly, and have an equal likelihood of contracting a disease.
While simple mathematical models can provide useful insights into disease dynamics and epidemic behavior they tend to ignore the spatial, environmental, and social dimensions of epidemiology (Perez and Dragicevic, 2009). Assumptions of homogeneous mixing of the population and model parameters not varying over the solution interval understate the complexity of an epidemic. From a disease manager's perspective, outbreaks occur in a physical, economic, technological, management, and socio-political context (Garner and Hamilton, 2011). An epidemic environment is irregular and subject to probabilistic events that dynamically reshape the spread of disease (Bansal et al., 2007; Garner and Hamilton, 2011). Spatial effects, population heterogeneity, contact structures and social behavior all influence the course of an outbreak (Caraco et al., 2001; Hagenaars et al., 2004; Galvani and May, 2005; Lloyd-Smith et al., 2005; Bansal et al., 2007; James et al., 2007).
An individual-based model is formulated from the bottom-up and aggregates individual-level behavior to reveal population-level dynamics. Relationships between individuals emerge over time, as opposed to a population-based model where the relationships are prescribed as inputs. An example is a spatially-explicit agent-based model (ABM) where autonomous individuals with independent infection states interact within an environment. In this case, the emergent behavior of the model is the spatio-temporal spread of disease across a population. Individual-based models are well-suited to complex environmental systems due to their affinity for capturing heterogeneity, stochasticity, spatiality, social systems, and policy (Hare and Deadman, 2004), and subtle interactions between individuals that are especially important during the initial and final stages of an outbreak (Germann et al., 2006; Bansal et al., 2007). A data-driven, individual-based, modeling approach has proven popular in the field of animal health policy development with stochastic, spatially-explicit, state-transition microsimulations such as AusSpread (Garner and Beckett, 2005), InterSpread Plus (ISP) (Stevenson et al., 2013), and the North American Animal Disease Spread Model (NAADSM) (Harvey et al., 2007).
In this paper, we describe the Australian Animal Disease Spread (AADIS) model. AADIS is a national-scale hybrid model of livestock disease spread and control designed to support emergency animal disease planning in Australia. For this context, we narrow the definition of a hybrid model to one that employs both population-based and individual-based modeling techniques. AADIS models within-herd spread with a deterministic EBM and between-herd spread with a spatially-explicit stochastic ABM. The model architecture and software architecture were specifically developed for efficient handling of the national livestock population. Computational efficiency is especially important for large-scale stochastic models. It is often desirable to re-run a particular scenario hundreds, possibly thousands, of times to see if patterns emerge from the underlying stochastic processes. Although the AADIS architecture supports any pathogen, FMD is the development test-case.
Modeling Context
Foot-and-Mouth Disease
FMD is an acute, highly contagious viral disease of domestic and wild cloven-hoofed animals. The disease is clinically characterized by the formation of vesicles and erosions in the mouth and nostrils, on the teats, and on the skin between and above the hoofs (Meyer and Knudsen, 2001; Animal Health Australia, 2014a). The FMD virus spreads between hosts through direct contact (e.g., movement of live animals between farms, and between farms and markets), indirect contact (e.g., livestock products, byproducts, and fomites), and aerosol (Meyer and Knudsen, 2001). Australia is a significant livestock producer and a major exporter of livestock, livestock products, and livestock genetic material. An outbreak of FMD would have severe economic consequences for the economy, in particular the loss of export markets (Buetre et al., 2013). Because of the serious consequences of an FMD outbreak, Australia invests considerable resources in prevention and planning.
Australia's approach to managing an incursion of FMD is described in the Australian Veterinary Emergency Plan—AUSVETPLAN (Animal Health Australia, 2014a). In brief, the policy is to eradicate the disease as quickly as possible using stamping out, which involves culling and disposal of infected and exposed animals. Standard zoo-sanitary measures and movement restrictions are also applied, with a minimum 3-day national livestock stand-still and the establishment of control zones around infected premises (IPs) and dangerous contact premises (DCPs). Vaccination is identified as an option under some circumstances in AUSVETPLAN.
Livestock Production Systems
Livestock production in Australia is largely based on extensive grazing and is dominated by wool, sheepmeat, beef, and dairy. Australia also has smaller intensive pig and poultry industries (Animal Health Australia, 2014b). The livestock industry is diverse and extends from the beef cattle areas of tropical north Queensland to the sheep areas of temperate southern Tasmania, and from the dairying areas of coastal New South Wales to the merino wool producing areas of Western Australia (Garner et al., 2002). The main industries that would be directly affected by FMD are beef, dairy, wool, sheepmeat, and pigs. Australia has approximately 74 million sheep, 28 million cattle and 2 million pigs on approximately 78,000 commercial farms (Australian Bureau of Statistics, 2012), with a further estimated 104,000 smallholder/lifestyle farms. From a disease transmission perspective, the key unit of interest is a herd, defined as a group of animals of the same species that is managed as a single group. Commercial farms in Australia can be large and may consist of more than one herd of the same or different species, e.g., sheep-beef farms.
Australia is a federation made up of six states and two mainland territories. The Australian Government is responsible for quarantine, disease reporting, export certification, and trade government. State and territory governments are responsible for animal health services within their respective jurisdictions. This means that while there are national policies for managing diseases like FMD, the actual control measures are administered by the jurisdictions under their own legislation. For disease control purposes, it is the farming enterprise rather than the herd that is the key unit.
AADIS Hybrid Approach
To study FMD in Australia on a national scale, a model needs to handle approximately 240,000 herds across a variety of species and production systems, as well as incorporating regional heterogeneity in disease transmission and jurisdictional variations in control measures and resourcing. To address this complexity, AADIS employs a hybrid model architecture that combines population-based modeling with individual-based modeling. This approach provides computationally efficient within-herd spread and captures the rich heterogeneous environment in which between-herd spread operates. For modeling purposes, the Australian livestock population has been categorized into 11 herd types and 10 farm types (Table 1). A herd has static attributes such as type, size, location, jurisdiction, and local government area, and dynamic attributes such as infection status. A farm is made up of one or more herds. Spatially, a farm and its constituent herds are defined as a point identified by latitude and longitude. The herd population is synthesized from agricultural census data (Australian Bureau of Statistics, 2012) and industry reports and data.
Equation-Based Modeling of Within-Herd Disease Spread
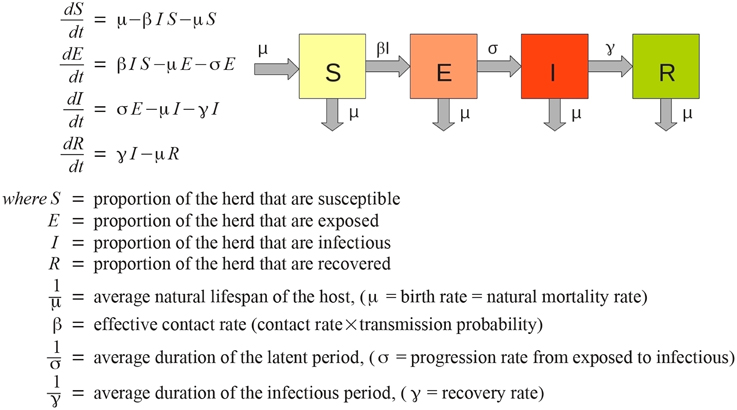
AADIS considers a herd to be well-mixed from a disease transmission point of view, i.e., all members of the herd are equally likely to contract a disease. This is a reasonable simplification for modeling the spread of disease at a national-scale, and one that lends itself to a population-based approach (Bradhurst et al., 2013). AADIS employs a non-spatial, deterministic SEIR compartmental EBM to represent within-herd spread of FMD (Figure 1). The approach is similar to that described by Keeling and Rohani (2008).
Each herd has its own ODE system customized for the herd type and the pathogen under study (Figure 2). AADIS simplifies a herd's size by considering it to be constant in the absence of culling. When a susceptible herd becomes infected the ODE system is solved numerically via a fourth-order Runge Kutta method (Cash and Karp, 1990), to yield the SEIR compartmental ratios over time. The EBM generates curves describing the prevalence and clinical signs of the infected herd. The EBM approach is computationally efficient as the solution remains in place up until an external asynchronous event acts upon the herd. If a herd is vaccinated and immunity levels increase, the EBM reacts by resolving the ODE system to yield updated SEIR compartment ratios from that point in time onwards (Figure 3). The EBM thus adapts and provides a dynamic representation of the within-herd infection state and presence of clinical signs.
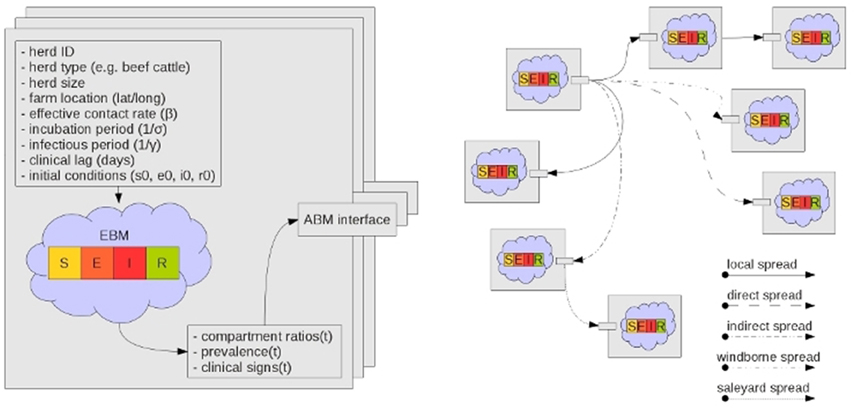
Figure 2. Each herd instance has a customized SEIR ODE-based EBM. The ABM stochastically establishes infection connection paths between herds (Bradhurst et al., 2013).
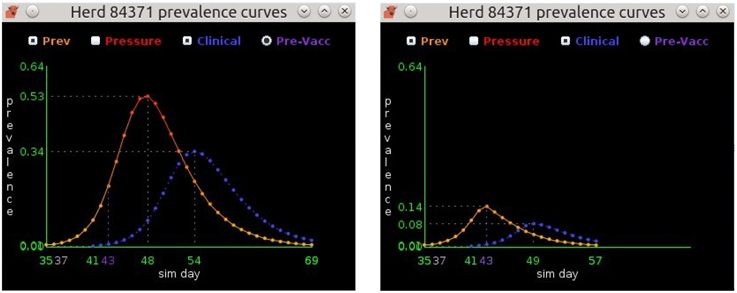
Figure 3. The prevalence curves on the left depict the EBM solution for a non-vaccinated beef herd. Infection starts on day 35, peaks at 53% prevalence on day 48, and ends on day 69. The prevalence curves on the right show the same herd, but with vaccination occurring on day 37. Susceptible animals in the herd achieve immunity on day 43 resulting in a greatly diminished peak prevalence of 14% and an earlier end to infection on day 57.
Agent-Based Modeling of Between-Herd Disease Spread and Control
Whilst a herd is viewed as a population for within-herd disease spread, it is somewhat paradoxically also viewed as an individual for between-herd spread (Figure 2). Aggregated herd-level infectious, latent (exposed), and clinical prevalence generated by the EBM, are inputs for modeling disease spread between herds. This is a sensible simplification for a model of national-scale, especially for a highly contagious disease such as FMD that when introduced into a susceptible herd will typically progress unchecked (Meyer and Knudsen, 2001; Carpenter et al., 2003). A herd is thus viewed as an atomic agent participating in an ABM for the purposes of between-herd spread.
While within-herd disease spread is deterministic and non-spatial, between-herd disease spread is highly stochastic and spatially-explicit. This is achieved through a rich ABM environment comprising disease spread pathways and control measures. The spread of disease is modeled with the following pathways:
• Direct contact – movement of live animals between premises,
• Market/saleyard spread – movement of live animals in and out of markets/saleyards,
• Indirect contact – movement of animal products, byproducts or fomites between herds,
• Local spread – proximity-based contact, e.g., over a boundary fence shared by adjoining premises,
• Airborne transmission – virus excreted by animals in aerosol form that remains viable in the air.
Each spread pathway has an algorithm that determines on any given simulation day whether disease transfers from an infectious herd to susceptible herd(s). AADIS introduces stochasticity through Monte Carlo sampling of probability distribution functions (Vose, 2008). The spread of disease between heterogeneous herds is well-suited to an individual-based model such as an ABM.
The control of disease is also part of the ABM environment. This includes movement restrictions, surveillance and tracing, IP operations, resource management and vaccination. The emergent behavior of the ABM is the spatiotemporal spread of disease across the population and the subsequent activities to control and eradicate the disease. The disease spread pathways and control measures can be thought of as components of the ABM environment. A component has autonomous logic, its own thread of execution and a blocking queue for receiving asynchronous events. Each component of the AADIS ABM environment operates independently and concurrently.
AADIS Functional Description
Transmission Pathways
AADIS models five independent means by which FMD can be transmitted between herds:
Direct Contact Spread
Direct contact spread is driven by the movements of live animals between herds. The expected number, size and destination of daily movements into and out of herds, stratified by month, is derived from various reports and industry sources (AusVet Animal Health Services, 2005, 2006; Hassall and Associates, 2006; Kokic and Mues, 2006; East and Foreman, 2011; East et al., 2014). AADIS only models movements from infected herds since it would be computationally prohibitive to consider all movements from all herds. For each infected herd, the daily likelihood of a movement, the type of herd the movement is directed to, and the movement distance and direction is determined stochastically. This is based on configuration data that includes movement frequencies, distance distributions and contact matrices.
Transmission depends on the prevalence of infection in the source herd and the consignment size. The probability that a consignment contains at least one exposed or infectious animal is given by:
where, pi = probability of infection, p(t) = prevalence of infection in the source herd at time t, where prevalence is defined as the proportion of infectious and exposed animals in the herd (per the EBM), n = consignment size.
When a susceptible herd becomes infected an EBM is created and solved with initial conditions based on the proportion of infectious and exposed animals in the consignment, and the size of the destination herd.
Saleyard/Market Spread
Markets and saleyards have the potential to greatly amplify an outbreak prior to the disease being recognized and controls implemented (Gibbens et al., 2001; Mansley et al., 2003). This is because disease transmission is greatly facilitated by the large number of susceptible animals, and the degree of mixing and partitioning of animals into consignments. Outgoing consignments may then be moved to multiple, widely dispersed locations.
AADIS provides two options for simulating saleyard spread, depending on the availability of data. A simplified module takes into account the frequency and destination of consignments from different herd types. On any given day the likelihood that an infected herd sends animals to a saleyard is determined stochastically. Each infected consignment to a saleyard generates multiple infected outgoing consignments based on beta pert distributions. A more explicit representation of saleyard spread is available which takes into account the type, frequency and timing of livestock sales. This approach is driven by specific buying and selling patterns at individual livestock sales (Hassall and Associates, 2007). AADIS models plausible sale events during a simulation. If a sale happens to involve an infected herd, then a series of stochastic decisions are made to determine the number of outgoing infected consignments, the consignment destination types (herd, feedlot or abattoir), and destination locations. Infection is transmitted to the destination herds with a force relative to the viral load in the consignment.
Indirect Contact Spread
Indirect contact transmission arises from the movement between herds of contaminated animal products, byproducts, and fomites such as equipment, people and vehicles. Potential sources include veterinarians, shearing contractors, artificial insemination technicians, milk tankers, and feed delivery vehicles. Indirect contacts can be categorized as high, medium or low according to their potential for transmitting infection (Nielen et al., 1996; Bates et al., 2001; Sanson, 2005; Noremark et al., 2013). In the interests of computational efficiency, AADIS only uses a single category of indirect contacts with a specified average (baseline) probability of transmission. The user can parameterize this to represent different risk profiles. Compared to direct contacts, there is limited data on indirect contacts. The type and location of exposed herds is determined stochastically using a contact matrix and distance distributions by herd type.
If a herd is exposed through indirect contact, the probability of transmission depends on the viral load of the source herd, the relative infectiousness of the source herd (based on species and herd size), environmental conditions that influence virus survival, biosecurity practices, and relative susceptibility of the exposed herd (based on species and herd size).
where, pi = probability that an indirect contact results in an infection, Pb = baseline probability that any indirect contact results in infection, p(t) = normalized prevalence of the source herd at time t, wi = infectivity weight of the source herd, ws = susceptibility weight of the destination herd, wb = biosecurity weight of the destination herd, wx = seasonal weight.
Local Spread
Local spread covers the transmission of disease from an infected herd to susceptible herds in close proximity (default within 3 km). The actual means of transmission is poorly understood and could involve local aerosol spread across fences, straying of stock, vehicles, people, run off, sharing of equipment between neighbors, etc. (Gibbens et al., 2001). AADIS uses a spatial kernel approach to represent local spread, with all susceptible herds inside the local spread radius at risk. The probability of transmission for at-risk herds is decided stochastically taking into account infectious prevalence in the source herd, infectivity of the source herd (based on species and size), susceptibility of the destination herd, biosecurity measures in place at the destination premises, and distance between the source and destination herds. The influence of distance between the source herd and target herds is described by a linear decay function—the closer a herd is to the source, the greater the probability of transmission. Local spread can also occur between herds that are co-resident on the same farm, with the probability of transmission increased to reflect the higher potential for local contact between herds managed on the same farm.
where pi = probability that a local contact results in an infection, Pb = baseline probability that a local contact between farms results in infection, p(t) = normalized prevalence of the source herd at time t, wi = infectivity weight of the source herd, ws = susceptibility weight of the destination herd, wb = biosecurity weight of the destination herd, wx = seasonal weight, wd = distance weight, wn = detection weight.
Airborne Spread
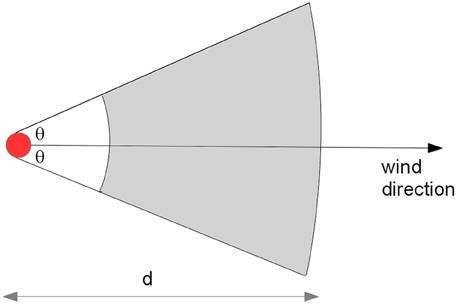
Airborne spread is the infection of susceptible animals by virus conveyed on the wind. Pigs pose the greatest threat for airborne spread because of their potential to excrete large quantities of virus relative to other species. Airborne spread requires a concentrated source of virus, appropriate weather conditions and susceptible animals downwind (Donaldson and Alexandersen, 2002). AADIS assumes that only pig herds are capable of transmitting FMD by airborne spread beyond a distance of 3 km. Aerosol transmissions within 3 km are captured by the local spread pathway. For each simulation day, the weather station closest to each infected pig herd is queried for conditions conducive to airborne spread (Garner et al., 2006). If suitable, a sector is constructed at the infected herd's location in the prevailing wind direction, subtended by a configurable angle (Figure 4). The sector radius represents the extent of the viral plume on that day and is determined by the number of infectious pigs in the source herd (Donaldson et al., 2001). Susceptible herds within the sector are identified, excluding those within 3 km. The probability of transmission takes into account the susceptible herd species, the size of the herd, and the distance of the susceptible herd from the infected herd.
where, pi = probability that a susceptible herd will become infected, Psp = probability that a single animal of the susceptible species will become infected, n = size of the susceptible herd, wd = distance weight.
The distance weight models the diffusion of the plume over distance from the source herds, and hence the diminishing risk of transmission. Distance weight is configurable as either a linear or exponential decay function.
Disease Control
Australia's FMD policy is to eradicate the disease in the shortest possible time using a combination of strategies, while minimizing economic impact, (Animal Health Australia, 2014a). Mandatory control strategies include:
• quarantine and movement controls of animals, animal products and fomites in declared areas in order to minimize the spread of infection
• tracing and surveillance to determine the source and extent of infection
• valuation and destruction of animals on infected premises and potentially on dangerous contact premises
• disposal of destroyed animals and infected animal products, and decontamination of depopulated premises.
Optional control strategies include:
• vaccination to reduce susceptibility of animals to infection and clinical disease, and potentially reduce virus excretion
• pre-emptive destruction of susceptible animals in order to minimize the spread of infection
• zoning and/or compartmentalization (to support trade)
• risk-based movement controls.
The farm is the population unit of interest for disease control. An AADIS farm has static attributes such as type and constituent herds, and dynamic attributes such as premises classification and declared area. The main simulated control strategies are movement restrictions, surveillance, tracing, IP operations and vaccination. The control and eradication phase of an outbreak commences after the declaration of the first infected premises. The day of first detection is either determined stochastically (using pre-configured probabilities of reporting by herd type, and clinical prevalence), or occurs on a fixed day at a specific or randomly selected farm.
Movement Restrictions
A national livestock standstill (minimum of 3 days), is implemented immediately following detection of the first IP. AADIS models livestock standstill by restricting the direct and saleyard spread pathways. The level of restriction depends on standstill status, type of control area, and the spread pathway being throttled. A compliance percentage for each pathway is defined in the AADIS configuration data to allow for the possibility of illegal movements during the standstill. The AADIS configuration data defines the length of the national standstill by jurisdiction. This reflects how individual jurisdictions may extend a standstill beyond the initial 3-day national period.
Controlled areas are established around each infected premises in order to restrict the movement of livestock, products and other material. The controlled areas are defined and enforced per-jurisdiction, and may be designated areas (local government, state/territory), or radius-based per IP. There are two levels of control: Restricted Areas (RAs) that immediately enclose IPs, and Control Areas (CAs) that enclose RAs. RAs have the highest level of control while CAs have a lower level of control (Animal Health Australia, 2014a). AADIS models the imposition of controlled areas in a staged manner. Larger controlled areas are enforced at the start of an outbreak. As the control program progresses, the dimensions of the controlled areas are reduced according to per-jurisdictional preferences. A radius-based controlled area is clipped to fall within the jurisdictional boundaries of the subject IP. When IPs are clustered a meta-RA and meta-CA are formed from the union of the constituent RAs and CAs.
Surveillance and Tracing
Surveillance is the process by which new infections are identified and declared. During an FMD outbreak, surveillance is used to detect new outbreaks, define the extent of infection, and demonstrate freedom in uninfected areas (Animal Health Australia, 2014a).
AADIS allows for reporting of suspect cases on an ad hoc basis by owners/inspectors or others. This represents one of the most important mechanisms for finding new IPs (McLaws et al., 2007). AADIS commences suspect case reporting the day after the first IP has been declared, and allows for both true positive and false positive reports. False positive reports identify herds that are exhibiting symptoms but are not actually infected with FMD. True positive reports are generated stochastically based on an infected herd's clinical prevalence, the probability of reporting and the expected time to report. The latter two parameters are defined per herd-type in the AADIS configuration data. The number of false positive reports generated is proportional to an n-day (default 3), moving average number of true positive reports. The default ratio of false to true reports is 2.34 based on McLaws et al. (2007). The modeling of both true and false reports facilitates more realistic modeling of surveillance, i.e., team resources are consumed regardless of whether a surveillance visit yields a positive assessment or not. AADIS also models the active inspection of premises within RAs. All farms within a designated distance of IPs are subject to a configurable inspection schedule (number and frequency of inspections).
Tracing is the identification of movements onto and off IPs in order to ascertain where infection may have come from, or gone to. AUSVETPLAN provides minimum periods over which tracing should be carried out (Animal Health Australia, 2014a). Tracing includes animals, products, equipment, vehicles and people. Traced premises may be true cases (and thus infected), or false (not infected). AADIS can readily identify true traces by following infection chains during a simulation, allowing for variable tracing effectiveness by herd type and pathway (direct contact vs. indirect contact), and tracing duration. False forward traces are obtained by applying the direct and indirect spread pathways to a premises of interest within the forward tracing window. False backward traces are obtained by reversing the direct and indirect spread pathways over the backwards tracing window (i.e., modeling movements onto the premises of interest). This approach results in a set of plausible false traces, i.e., premises of a suitable type and location that could well have been sources or destinations of movements of concern.
Premises that require visits by surveillance teams are identified through tracing, active inspection of premises within RAs, and reporting of suspect premises. Laboratory samples are taken when needed. Surveillance visits are prioritized according to risk (Animal Health Australia, 2014a). AADIS maintains a resource-constrained dynamic queue of premises awaiting a surveillance visit. Visits are prioritized according to a configurable scheme that takes into account premises classification, declared area and herd type. If multiple premises have the same priority, then arbitration is based on how long a premises has been waiting for a visit. The visit duration (based on herd type), visit frequency (based on priority), and overall surveillance period are configurable.
IP Operations
IP Operations is comprised of the valuation, destruction and disposal of animals (stamping out), and decontamination of premises. Stamping out is Australia's default initial policy for controlling an outbreak of FMD (Animal Health Australia, 2014a). It is considered the fastest way to reduce viral excretions on IPs and thus dampen spread. Stamping out is implemented on all IPs, and potentially on DCPs, subject to risk assessment.
Premises undergoing IP Operations transition through the following states: cull pending, cull in progress, disposal pending, disposal in progress, decontamination pending, decontamination in progress, and resolved. Each jurisdiction has separate pools of teams for culling, disposal and decontamination. When a pool is exhausted (i.e., all of the teams are on assignment), pending jobs are held in a queue. Visits to premises are prioritized based on premises classification, herd/species priority, herd size, time in queue, and proximity to an IP. The times required for a premises to undergo culling, disposal and decontamination are defined by herd type in the AADIS configuration data.
Vaccination
Vaccination is one of the available options to support stamping out of an FMD outbreak. The decision to vaccinate and the specific role of vaccination in an FMD response varies according to the specific outbreak scenario (Animal Health Australia, 2014a). Vaccination strategies include:
• Suppressive – vaccination is carried out inside known infected areas (RAs) in order to suppress virus production in at-risk and exposed herds to reduce further spread.
• Protective – vaccination is carried out outside known infected areas in order to protect susceptible animals from infection.
• Mass – vaccination is carried out across a broad area to large numbers of animals. This strategy could be applied if an outbreak is not under control and there is a risk of spread escalating.
AADIS provides two triggers for commencing a vaccination program: on a configurable day into the control program, or once a configurable number of IPs has been declared. AADIS models all vaccination policies with an annulus of configurable inner and outer radii. The inner radius is set to zero for suppressive and mass vaccination. A vaccination annulus is established around each target IP, and eligible premises inside the annulus are scheduled for vaccination. The user can select to only vaccinate around IPs found on or after the day the vaccination program begins, or around all new and previously identified IPs. The vaccination candidates inside each annulus are prioritized according to herd type, herd size, and proximity to the nearest IP. It is also possible to omit certain herd types from vaccination. The direction of vaccination (from the outside in, or from the inside out), is set in the AADIS configuration data.
The effect of vaccination is to increase herd immunity (i.e., reduce a herd's susceptibility to infection) over time. When a partially immune herd is exposed to infection, the virus production profile generated by the EBM reflects that some of the animals have protective immunity.
As with surveillance and IP operations, the ability to implement a vaccination program depends on the availability of resources. Each jurisdiction has a separate pool of vaccination teams. When a pool is exhausted (i.e., all of the teams are on assignment), pending jobs are held in a queue. Visits to premises are prioritized according to herd type, herd size, time in queue, and proximity to an IP. The time required for a premises to undergo vaccination is defined by herd type in the AADIS configuration data.
Resourcing
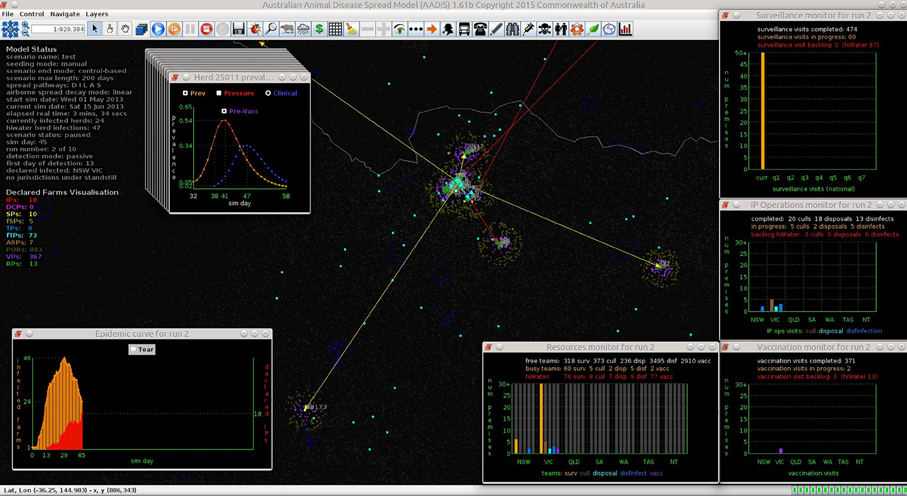
The resources required to manage an emergency animal disease outbreak include personnel (e.g., veterinarians, animal health officers, control center staff), equipment (e.g., vehicles), facilities (e.g., laboratories) and consumables (e.g., vaccine, disinfectant). Some aspects of disease control and eradication are resource-intensive and the lack of resources can severely hamper the response to an outbreak (Matthews, 2011; Roche et al., 2014). AADIS models the personnel resources required for key operational activities: surveillance, culling, disposal, decontamination, and vaccination. As state and territory governments are responsible for emergency animal disease management within their own boundaries (Animal Health Australia, 2014a), the teams are organized into pools by jurisdiction, i.e., each jurisdiction has five pools. It is anticipated that resource levels ramp up over time, so initially the pools are small and increase in a linear manner up to the maximum size. The starting point, duration of the ramp-up and maximum pool size are defined in the AADIS configuration data by resource type and by jurisdiction. AADIS tracks the availability and allocation of resources to provide immediate feedback as to whether/where the control program is resource constrained (Figure 5).
Model Implementation
AADIS is implemented in Java (Oracle, 2014) and employs open-source products such as PostgreSQL (PostgreSQL, 2014) and OpenMap (BBN, 2014). AADIS runs under either Linux™ or Windows™ and has an asynchronous software architecture with concurrency achieved through Java threads. This takes good advantage of the inexpensive parallelism available on the quad-core x64 target machine. Although C and C++ are perhaps more typical language choices for computationally intense applications, Java offers the advantage of platform-independence and a rich collection of utility libraries. Parker and Epstein (2011) describe how the Java-based GSAM pandemic model scales up to 6.5 billion agents distributed across a 32-node high-performance computing (HPC) cluster.
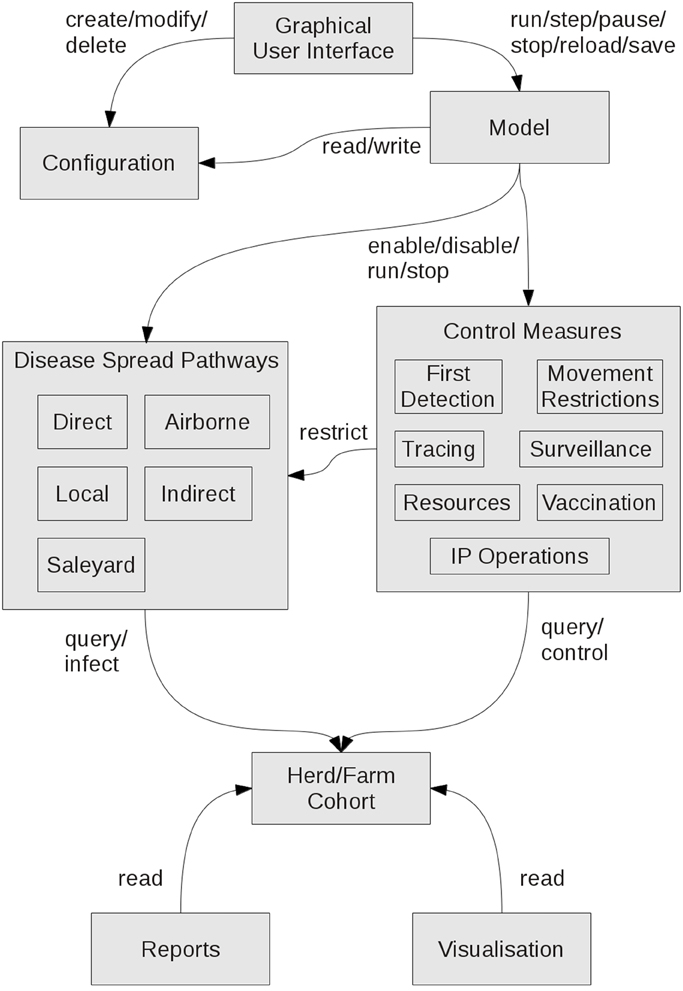
AADIS is able to run complex disease spread and control scenarios across the entire Australian population of FMD-susceptible herds efficiently on a single desktop platform. For example, a 100-day national outbreak with all disease spread pathways enabled, all control measures deployed, dynamic resourcing, report writing, and real-time visualization takes around 10 s to complete on a quad-core laptop with 16 GB RAM. This is achieved through several strategies including the hybrid model architecture, asynchronous software architecture, a grid-based spatial indexing system (in lieu of geospatial Structured Query Language (SQL) exchanges with the database server), and lightweight agents. Implementation and performance details of interest will feature in a future paper. Figure 6 provides a summary of the AADIS subsystems and the main relationships between them.
Simulation Flow
AADIS operates in discrete time steps of a day. At the start of a simulation day, the disease spread components and the control components access the herd/farm initial conditions for the day. All components then independently and concurrently proceed with their daily processing, making various stochastic decisions on the spread and control of disease. As each component finishes its daily processing, a set of herd/farm update requests are sent asynchronously to the ABM component scheduler where they are queued. When all updates have been received, they are collated and submitted to the cohort of herd/farm agents. The new herd/farm reality is then available for all components at the start of the next simulation day. This concurrent approach is computationally efficient and reflects the reality that spread and control proceed independently and in parallel during an outbreak. The scheduler arbitrates whenever one or more components attempt to act upon the same herd/farm on the same day. The arbitration may be random or rule-based. For example, if the direct and indirect spread pathways both attempt to infect the same herd on the same day, then the scheduler randomly selects one pathway to succeed. On the other hand, if for example, the IP Operations component and the Vaccination component both attempt to control the same farm on the same day, then the scheduler always gives priority to IP Operations.
Configuration Data
AADIS has three levels of configuration:
• Project data for the study at hand includes the herd population, weather data, movement patterns and pathogen specific parameters. This data typically does not change often and may be large with cross-dependencies. The project data is stored in a relational database (PostgreSQL, 2014), and any changes require a database rebuild (which ensures referential integrity).
• Scenario-specific data is stored in a Java properties file that is persistent across multiple invocations of the model. The data is stored outside the database and so changes do not trigger a database rebuild.
• The graphical user interface can be used to make short-term adjustments of selected configuration data. The changes only last for the current invocation of the model.
Outputs
As AADIS is a stochastic model, it generates a range of possible outcomes when run with the same starting parameters. When modeling a specific scenario, multiple model runs (iterations) are used to generate a probability distribution of potential outcomes. Results of individual runs and summaries of groups of runs are produced. AADIS provides both tabular and graphical outputs.
Tabular
The formal outputs of an AADIS scenario run are comma-separated values (CSV) files. These contain a range of metrics at the herd, farm and scenario level, and are used for subsequent epidemiological analysis.
Graphical
AADIS provides three modes for visualizing an outbreak in progress:
• Within-herd spread (EBM) – infected herds are represented as heat-colored dots reflecting the viral load.
• Between-herd spread (ABM) – infected herds are represented as color-coded dots reflecting the particular pathway that triggered the infection. There is an option of displaying each pathway connection as a vector – thus depicting the entire infection network.
• Control (ABM) – farms are represented as color-coded dots reflecting the current premises classification.
AADIS provides a range of graphical utilities for the dynamic display of herd prevalence curves, epidemic curves, convex hull of infection, controlled areas, traces, resource usage, resource backlog, and peak resource levels (Figure 5).
Sample Case Study
The following simple epidemiological case study is provided to illustrate how AADIS can be used to address policy issues.
Outbreak Scenario
The south-east of Australia is an agriculturally intensive area that has previously been identified as vulnerable to an FMD outbreak (East et al., 2013). The Goulburn Valley is a 14,287 km2 sub-region of Victoria with significant cattle and horticultural sectors (Regional Development Victoria, 2010). The dairy industry in this region comprises around 3000 farms and accounts for approximately 13% of Australia's milk production (Department of Environment and Primary Industries, 2015). Other livestock-based sectors in the region include beef, wool, sheepmeat, and pigs.
We assume FMD is introduced into the Goulburn Valley with the primary case occurring on a pig farm with a population of 3209 pigs. The farm has 20 neighboring farms within a 3 km radius. The outbreak occurs in May when the usual cool weather favors the survival of FMD virus outside a host. Detection of the index case occurs 21 days after the primary infection. Table 2 lists some of the key EBM parameter values.
Two strategies for controlling the outbreak were assessed:
• Stamping out of infected premises (SO),
• Stamping out of infected premises plus suppressive ring vaccination (SORV).
Selected parameter settings for the control strategies are provided in Table 3. Note that this is a simplification of the model setup as only a subset of key parameters are described.
Method
The simulation was run 500 times for each control strategy and the following outputs compared:
• duration of the outbreak (defined as the number of days from when the index case was declared to when the last infected premises was resolved)
• cumulative number of infected premises
• cumulative number of culled premises
• cumulative number of culled animals
• cumulative number of vaccinated premises
• cumulative number of vaccinated animals
In addition, a simple sensitivity analysis was carried out on selected parameters under strategy SO.
• time to first detection (7, 14, 21, 28 days)
• duration of the national standstill (0, 3, 7, 10 days)
The test hardware platform was a quad-core laptop with 16 GB RAM running 64-bit Kubuntu Linux™.
The Stata/IC statistical package (Stata, 2014) was used to analyse the distributions of the key model outputs. Data sets were imported into Stata and checked for normality. Non-parametric statistical methods were used throughout this analysis as some data sets were non-normal and could not be transformed to normality by standard transformation techniques. The number of infected premises, outbreak duration, number of culled animals, number of vaccinated premises and number of vaccinated animals were analyzed using the Kruskal-Wallis test for comparison of multiple independent groups of data. Post hoc analysis to identify differences between strategies was conducted using the Kruskal-Wallis test with the significance level adjusted per the Bonferroni correction for multiple pairwise comparisons. Model outcomes were expressed as medians with 90% confidence intervals.
Results
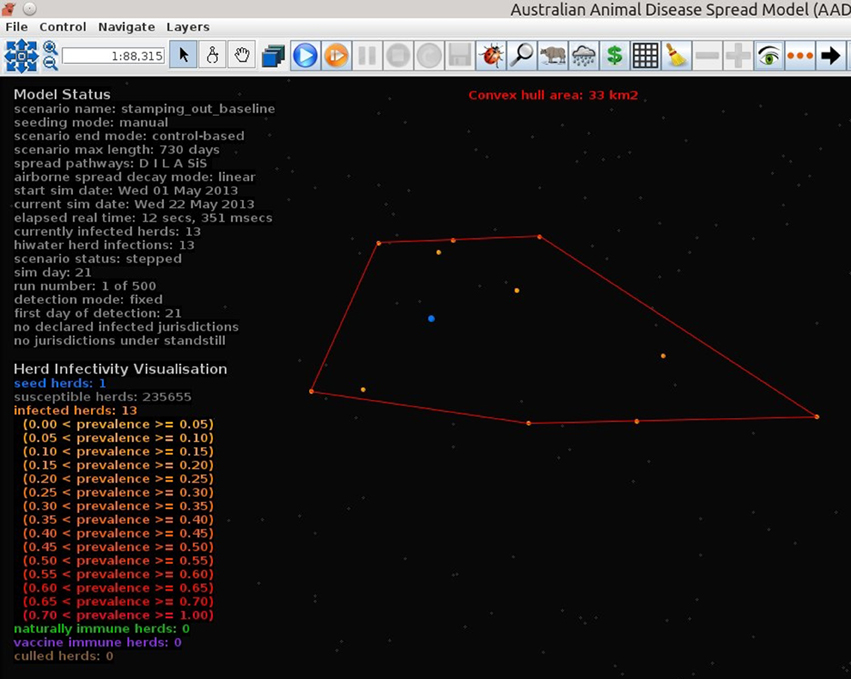
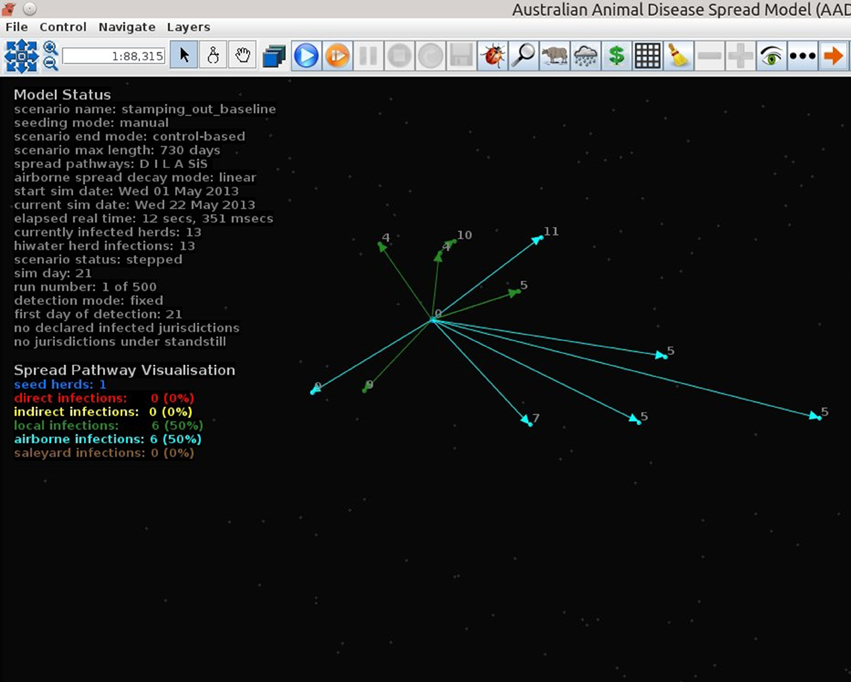
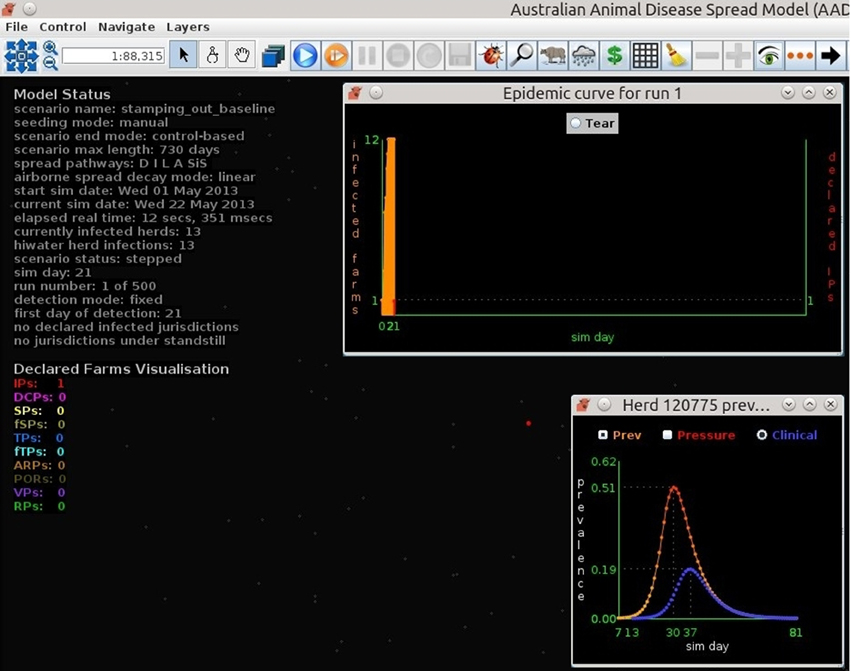
Figures 7–9 provide visualization snapshots at day 21 of run number 1 (of 500) of the baseline stamping out scenario. Figure 7 shows how within-herd spread is represented as heat-colors reflecting prevalence levels generated by the EBM of each infected herd. Figure 7 also illustrates the optional display of the convex hull area of infection, in this case 33 km2. Figure 8 shows the infection network generated by the ABM, with color-coded vectors reflecting the particular spread pathway that triggered. At this stage in the outbreak there is only local (green) and airborne (cyan) spread emanating from the primary case pig herd. Figure 9 shows the outbreak from a disease management point of view. Despite there being 13 infected herds on day 21, there is only one known infected premises (red). Figure 9 also shows two optional popup windows: the prevalence curves for a herd (in this case the index case), and the epidemic curve depicting declared infected premises vs. actual infected premises. These outputs demonstrate the potential of AADIS as a training tool that provides various visualizations of disease transmission, and also contrasts a disease manager's incomplete view of an outbreak (what is known), with the physical reality (infected herds in the population).
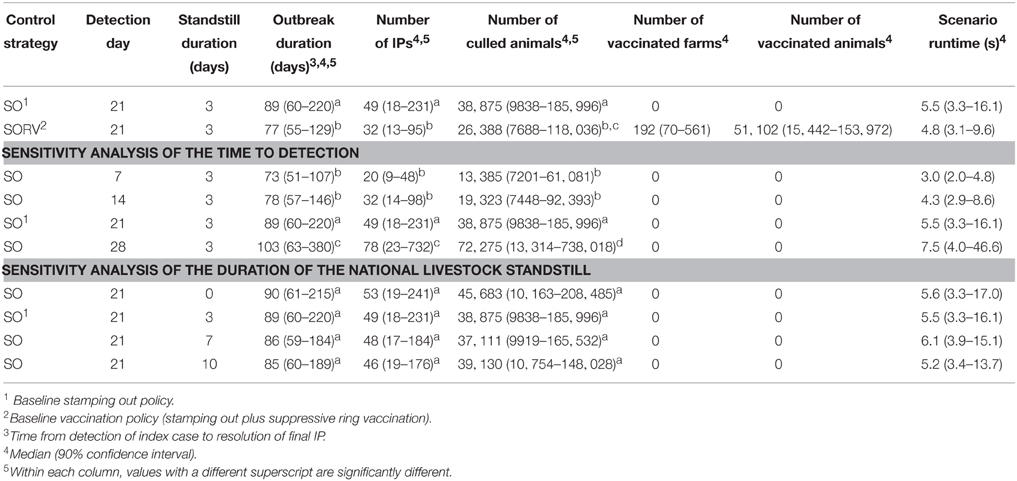
In this study we investigated the effect of incorporating suppressive ring vaccination into the control program for an FMD outbreak. Strategy SORV was effective in reducing both the size and duration of an outbreak when compared to the baseline SO strategy. There were significantly less IPs, significantly shorter outbreaks, and significantly less culled animals than stamping out alone (p < 0.05) (Figure 10 and Table 4). SORV was particularly effective in reducing the likelihood of a very large outbreak, which could be an important consideration for a disease manager.
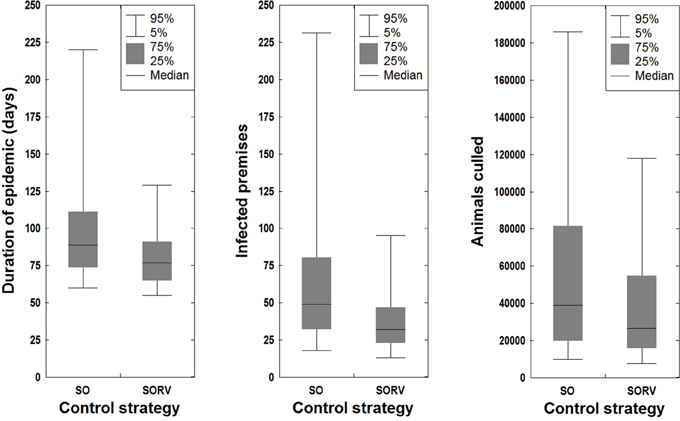
Figure 10. Effect of control strategy on outbreak duration, outbreak size, and number of culled animals.
The sensitivity analyses showed that findings are significantly influenced by the time to first detection. Varying the time to detection for strategy SO produced strongly correlated changes to the number of IPs, outbreak duration, and number of culled animals (p < 0.05) (Table 4). The findings were less sensitive to the duration of the national livestock standstill with only a 0-day standstill and a 10-day standstill producing significantly different outcomes (p < 0.05). This suggests that for the outbreak scenario, there is perhaps not a significant advantage in extending the default 3-day standstill.
Discussion
An incursion of FMD into Australia would have severe economic consequences and Australia thus invests heavily in prevention and contingency planning. The control and eradication of FMD is challenging due to the complexities of a highly contagious and multi-host pathogen operating in a heterogeneous environment across multiple jurisdictions. Models of disease spread and control are increasingly recognized as valuable tools for informing policy. Population-based approaches and individual-based approaches have both been used to model the spread and control of FMD and inform policy makers and disease managers. The hybrid approach of AADIS combines the advantages of population-based and individual-based approaches in order to efficiently model the spread and control of FMD on a national scale.
Advantages and Disadvantages of Population-Based Modeling
Livestock epidemics can occur in highly heterogeneous environments. Take for example, an outbreak of FMD within an extensive beef production system in a northern Australian jurisdiction, compared to one in an intensive dairy production system in a southern Australian jurisdiction. Despite the same pathogen and the same host species, there are significant differences in livestock density, farming practices, market systems and climate. The probability of disease detection and reporting varies with the level of contact between owners/inspectors and livestock. State/territory jurisdictions are responsible for their own disease control policies and resourcing. This results in distinct disease spread dynamics and control environments between the two regions.
Population-based models carry a general assumption of homogeneous contact rates and susceptibility. In the case of a compartmental SEIR EBM, individuals within any given compartment are indiscernible. The subtle contributions of specific individuals to the dynamics of an outbreak are thus lost in a population-based model. This is a limitation if the population and environment being modeled is heterogeneous. Complex environmental systems are typically multi-scale, non-linear and heterogeneous—characteristics that are ill-suited to an aggregated population-based modeling approach (Bansal et al., 2007; D'Souza et al., 2009; Parker and Epstein, 2011; Vincenot et al., 2011a). Although computationally efficient, an EBM can become complex and less tractable as more variables are factored into the mathematical abstraction (Miller, 1976; Parunak et al., 1998; Bobashev et al., 2007).
Advantages and Disadvantages of Individual-Based Modeling
Individual-based models are better suited to complex environmental systems due to their natural affinity for capturing heterogeneity, stochasticity, spatial relationships, social systems and policy (Hare and Deadman, 2004). The ability to distinguish between individuals in a population is especially important during the initial and final stages of an outbreak (Germann et al., 2006; Bansal et al., 2007). A data-driven, individual-based modeling approach has proven popular in the field of veterinary epidemiology with stochastic, spatially-explicit, state-transition models such as AusSpread, ISP and NAADSM. Individual-based models tend to be complex with a large number of parameters for which data may not always be available. Individual-based models may not scale well for large populations. Consider individual-based models of human pandemics in populations of millions or even billions. Such models have considerable computational requirements and typically require highly parallel platforms such as HPC clusters (Carley et al., 2006; Germann et al., 2006) or general purpose computing on graphics processing units (D'Souza et al., 2009) and custom software implementations (Parker and Epstein, 2011).
Advantages of Hybrid Models
Hybrid epidemiological models incorporate a population-based approach and an individual-based approach into a single model. Epidemics across a meta-population are multi-scale in the sense that the mechanisms and rates of within-site spread are distinct from those of between-site spread. In the case of a livestock epidemic, once infection is introduced into a farm the rate of within-farm propagation is dependent on the specifics of the pathogen and the farm. Factors include the host species, livestock density, livestock numbers, production system, and biosecurity measures. The spread of disease between farms is influenced by more irregular factors such as contact networks between farms (direct and indirect), market practices, distance between farms and environmental conditions (including weather).
Bobashev et al. (2007) describe a stage-based hybrid model of global human influenza that dynamically switches between an ABM and an EBM based on the number of cases. Within-city spread is initially simulated by an ABM in order to capture subtle interactions between individuals early in an epidemic. When a cases threshold is reached, the ABM is halted and a snapshot of agent states is used as initial conditions for an EBM. Although the granularity of modeling decreases to population-level, it occurs at a point in the outbreak when the number of cases is sufficient to support a population-averaged approach. Moreover, the overall performance of the model is maintained due to the computationally efficient EBM. When the number of cases in a city falls below a threshold value, the model switches back to an ABM in order to capture subtle interactions between individuals as the epidemic wanes.
Network-based hybrid models employ a multi-scale approach to modeling the spread of disease across a meta-population. A population-based model handles the spread of disease within each meta-population site while an individual-based model handles the spread of disease between sites. An example is provided by Vincenot and Moriya (2011b) where a system dynamics-based EBM is used for within-site spread and a contact network is used for between-site spread. A compartment-based EBM is a good match for a closed homogeneous site while a data-driven spatially-explicit individual-based model captures heterogeneity in the epidemic environment. The edges of a contact network topology are formed from the potential conduits of disease across the meta-population. Network-based hybrid models have proven tractable in the study of human pandemics—driven by local and international mobility patterns derived from such sources as census data, surveys and the International Air Transport Association (IATA) database (Bansal et al., 2007; Balcan et al., 2009; Yu et al., 2010; Parker and Epstein, 2011; Van den Broeck et al., 2011; Yoneyama et al., 2012). Hybrid models used in the field of veterinary epidemiology include:
• The Davis Animal Disease Simulation Model (DADS) (Bates et al., 2003a) and DTU-DADS (Boklund et al., 2013) where within-herd spread of FMD is modeled with a Reed-Frost EBM (Fine, 1977), and between-herd spread modeled with a stochastic spatially-explicit contact network.
• The Netherlands FMD model (Backer et al., 2012) where within-herd spread is handled by an SEIR-based EBM and between-herd spread is modeled with a spatial kernel driven by probabilities derived from the 2001 outbreak in the Netherlands.
• Nickbakhsh et al. (2013) where within-flock spread of highly pathogenic avian influenza (HPAI) is modeled with a SEIR-based EBM and between-flock spread with a stochastic contact network.
• LaBute et al. (2014) where within-herd spread of FMD and HPAI are modeled with a compartmental SIR EBM and between-herd spread with a spatially-explicit contact network.
How AADIS differs from Other Hybrid Models
AADIS extends the network-based hybrid approach by employing an event-driven ABM in lieu of a contact network. The meta-population under study is heterogeneous, reflecting the multiple species of domestic cloven-hoofed animals that are susceptible to FMD. The network by which meta-population sites (i.e., herds) can ‘connect’ is multi-layer, reflecting how FMD spreads via direct contact (animal movements between herds and between herds and markets), indirect contact (livestock products, by-products and fomites) and aerosols.
The AADIS ABM also models the control and eradication of FMD. Each disease spread pathway and control measure operates as an autonomous concurrent ‘component’ of the ABM environment. The decoupled component approach is robust, flexible and extensible. Components can be added/removed/modified with minimal impact on other components.
How AADIS Differs from Other Major Models of FMD Spread and Control
The AADIS EBM predicts a herd's prevalence and clinical signs over time based on the pathogen, herd type and herd size. These values dynamically feed into ABM decisions on the spread of disease between herds, the probability of detection, and the control of disease. In its role as an agent in the ABM, a herd reacts to environmental events such as culling and vaccination by resolving the EBM ODE system which in turn yields updated predictions for prevalence and clinical signs (Figure 3). The decoupling of within-herd spread and between-herd spread reflects the multi-scale nature of livestock epidemics (Carpenter et al., 2003; Keeling, 2005). Stochastic state-transition microsimulations such as AusSpread, ISP and NAADSM simplify intra-farm transmission as transitions through atomic infection states according to durations sampled from probability distributions. A state-transition approach to within-herd spread doesn't naturally capture the dynamics of intra-herd transmission. A simple herd state of ‘infectious’ doesn't distinguish between the infectiousness of a herd with 1% of the animals infected and that of a herd with 100% of the animals infected. This leads to a loss of prevalence information that is relevant to between-herd spread, and a loss of information on clinical signs that influences the detection and control of disease (Carpenter et al., 2003). It is possible to augment infection states with transmission probabilities that vary over time (Stevenson et al., 2013). However, this is less intuitive than the AADIS organic EBM approach. An architectural advantage of decoupling within-herd spread and between-herd spread is that alternative EBMs can be readily employed as required for the specific pathogen under study. This is awkward to accomplish when intra-herd spread and inter-herd spread are tightly coupled in a pure individual-based model such as a state-transition microsimulation.
Other distinguishing functional features of AADIS include:
• The configuration and deployment of control measures are decentralized to the separate state/territory jurisdictions. This permits realistic modeling of an epidemic that may spread across borders and require control at the jurisdictional level.
• The resources available for disease control and eradication are configurable by jurisdiction. This improves model realism as resource levels and priorities may vary considerably between jurisdictions. The AADIS ABM also allows resource requirements to emerge from a scenario as opposed to a top-down modeling approach that prescribes resourcing levels ahead of time. The inclusion of false positive suspect premises reports and traces provides more realistic modeling of surveillance as it reflects how resources are consumed regardless of the result of a surveillance visit.
• AADIS provides detailed graphical visualization modes that allow a user to dynamically view an outbreak unfolding in ‘real’ time. The graphical user interface allows a user to interact with an epidemic, for example to pause a scenario and view details of any herd/farm in the population. It is also possible to manually adjust the declared state of any farm. AADIS has potential as not only a predictive tool that informs policy, but also as a vivid training tool for disease managers.
• The multi-threaded asynchronous AADIS architecture offers significant performance improvements over a single-threaded state-transition approach. As all AADIS spread and control tasks proceed concurrently the length of a simulation day is only limited by the longest individual task. Computational efficiency is an important consideration for a stochastic model of national-scale as complex scenarios are re-run hundreds if not thousands of times to allow trends to emerge.
• Most of the current microsimulation models use a farm as the epidemiological unit of interest. AADIS's use of the herd captures heterogeneity in the spread of disease involving farms with co-located but separately managed herds, for example mixed beef/sheep farms.
• The national set of herds can be viewed abstractly as nodes in a network (Dube et al., 2011; Noremark et al., 2011). A network topology forms over time when spread pathways trigger and create edges (Figures 2, 8). The topology takes the form of a directed acyclic graph, until such time as recovered herds lose their immunity. Network paths can subsequently be traversed forward to determine the downstream impact of an infected herd, and backward to trace the historical infection route. The network topology thus captures the spatiotemporal history of the simulated epidemic. The infection network can be mathematically analyzed to identify topological features of interest such as sinks and spreaders.
It should be noted that specific functional advantages of one model over another can be short-lived. Models such as AusSpread, ISP, NAADSM, DADS, DTU-DADS, and the Netherlands model (Backer et al., 2012) are active and continue to evolve. The principle innovation of AADIS is perhaps architectural, i.e., the movement away from the state-transition microsimulation approach of AusSpread, ISP and NAADSM to a hybrid EBM/ABM model. Network-based hybrid models tend to have single species meta-population and single layer contact network. AADIS expands this genre of models to a multi-species meta-population and a multi-layer contact network.
Limitations
The realism of data-driven models of disease spread hinges on the quality of the underlying data. This includes population data, contact structures, environmental data and pathogen data. Inadequate data can be replaced with assumptions/expert opinion but this has the potential to introduce bias into a model. In countries such as Australia where agriculture is of great importance to the economy, there is increasing availability of spatially-based data on livestock and livestock products. An example is the National Livestock Identification System (NLIS) which tracks livestock from property of birth to place of slaughter/export (Meat and Livestock Australia, 2011). The NLIS database is a rich source of livestock movement data and takes into account species, production system and region. For AADIS to be used in a jurisdiction with a paucity of data, the spread and control components would need to be simplified. For example, a complex spread pathway based on animal movement data could be replaced with a simple distance kernel-based spread module.
AADIS has extensive configuration data spread across 40 tables in a relational database and three ASCII configuration files. This allows for detailed configuration of a heterogeneous environment and population, and pathogen under study. A result of this complexity is that the parameterization of the model requires a good understanding of the epidemiological system being modeled.
An artifact of the concurrent architecture adopted by AADIS is that thread scheduling arbitrarily influences the order that components request random numbers. This means that it is not possible to replay scenarios by specifying the pseudo-random number generator seed (and thus control the stream of random numbers used to sample from probability distributions). The ability to control the random number stream makes a stochastic model temporarily deterministic, and allows specific aspects of a scenario to be isolated. For example, a specific control measure such as vaccination can be varied and the impact on the scenario outcome directly observed (in the absence of variability introduced through stochasticity). The implication of this for AADIS is that a greater number of scenario runs may be required before results converge.
Concluding Remarks
Disease managers have to take into account technical, socio-political, economic and logistical issues when developing policies for disease control. Often there are conflicting objectives to balance, for example, to eradicate the disease as soon as possible and regain export markets, while minimizing the costs of control and compensation, and reducing impacts on other industries. Epidemiological modeling is emerging as an important contributor to the complex task of policy development.
Population-based models represent the spread of disease in a closed homogeneous population in a concise and computationally efficient manner. Individual-based models have a natural affinity for incorporating stochasticity, population heterogeneity, spatial effects, social factors and jurisdictional differences. This flexibility and realism has led to a strong interest in microsimulations for the purposes of informing official policy on disease control. Hybrid models have the modeling advantages of an individual-based approach but are also computationally efficient, which is particularly important when dealing with large livestock populations. The AADIS assumption that a herd is homogeneous is reasonable given that livestock are typically managed as single species cohorts that share a single contact network whilst on a farm. The AADIS SEIR-based EBM provides computationally efficient and adaptive predictions of herd prevalence and clinical signs over time. The AADIS ABM is well-suited to the complex, stochastic and heterogeneous environment in which an FMD epidemic operates.
There is an increasing availability of livestock movement and marketing data (including spatially-referenced data), through livestock identification, and tracing systems. This allows data-driven disease models such as AADIS to realistically simulate production system dynamics and contact structures.
The AADIS asynchronous hybrid EBM/ABM architecture has thus far shown itself as a flexible, efficient and extensible framework for modeling the spread and control of FMD in livestock on a national scale.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
AADIS is a joint research venture between the Australian Department of Agriculture and the University of New England (UNE). The authors acknowledge both organizations for their support of the project. The authors would like to thank Dr. A.S.M. Sajeev who was a strong supporter of the project whilst Professor of Computer Science at UNE. The authors would also like to thank Dr. Rachel Iglesias of the Department of Agriculture for providing helpful comments on the manuscript. This work is funded under the Australian Government's Animal Biosecurity Response and Reform Program.
Abbreviations
AADIS, Australian Animal Disease Spread model; ABARES, Australian Bureau of Agricultural and Resource Economics and Sciences; ABM, Agent-based model; ABS, Australian Bureau of Statistics; AUD, Australian dollar; AUSVETPLAN, Australian Veterinary Emergency Plan (Animal Health Australia, 2014a); CA, Control Area—a controlled area enclosing an RA and subject to lower levels of movement restrictions than those applied in RAs; CSV, Comma-Separated Values; DADS, Davis Animal Disease Simulation model (Bates et al., 2003a); DCP, Dangerous Contact Premises—a premises that, based on a risk assessment, is considered highly likely to contain an FMD-infected animal(s) or contaminated animal products, equipment or other material.; DTU-DADS, Technical University of Denmark—Davis Animal Disease Simulation model (Boklund et al., 2013); EBM, Equation-based model; FMD, Foot-and-mouth disease; GIS, Geographic Information System; GSAM, Global-Scale Agent Model (Parker and Epstein, 2011); HPAI, Highly Pathogenic Avian Influenza; HPC, High-Performance Computing; ISP, InterSpread Plus (Stevenson et al., 2013); IP, Infected Premises—a premises where infection has been confirmed.; NAADSM, North American Animal Disease Spread Model (Harvey et al., 2007).; NLIS, National Livestock Identification System; ODE, Ordinary Differential Equation; RA, Restricted Area—a controlled area surrounding an IP and subject to the highest level of movement restrictions; SEIR, Susceptible Exposed Infectious Recovered; SO, Stamping Out; SORV, Stamping Out plus suppressive Ring Vaccination; SQL, Structured Query Language.
References
Animal Health Australia. (2014a). Disease Strategy: Foot-and-Mouth Disease (Version 3.4). Australian Veterinarian Emergency Plan (AUSVETPLAN), 3rd Edn. Canberra, ACT: Standing Council on Primary Industries.
Animal Health Australia. (2014b). Animal Health in Australia 2013. Canberra, ACT: Animal Health Australia.
Australian Bureau of Statistics. (2012). Agricultural Commodities, Australia. Available online at: http://www.abs.gov.au/ausstats/abs@.nsf/mf/7121.0
AusVet Animal Health Services. (2005). A Review of the Structure and Dynamics of the Australian Dairy Cattle Industry. Report prepared for the Department of Agriculture, Fisheries and Forestry, Canberra, ACT, Australia.
AusVet Animal Health Services. (2006). A Review of the Structure and Dynamics of the Australian Beef Cattle Industry. Report prepared for the Department of Agriculture, Fisheries and Forestry, Canberra, ACT, Australia.
Backer, J. A., Hagenaars, T. J., Nodelijk, G., and van Roermund, H. J. W. (2012). Vaccination against foot-and-mouth disease I: epidemiological consequences. Prev. Vet. Med. 107, 27–40. doi: 10.1016/j.prevetmed.2012.05.012
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Balcan, D., Colizza, V., Goncalves, B., Hu, J., Ramasco, J. J., and Vespignani, A. (2009). Multiscale mobility networks and the spatial spreading of infectious diseases. Proc. Natl. Acad. Sci. U.S.A. 106, 21484–21489. doi: 10.1073/pnas.0906910106
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Bansal, S., Grenfell, B. T., and Ancel Meyers, L. (2007). When individual behaviour matters: homogeneous and network models in epidemiology. J. R. Soc. Interface 4, 879–891. doi: 10.1098/rsif.2007.1100
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Bates, T. W., Thurmond, M. C., and Carpenter, T. E. (2001). Direct and indirect contact rates among beef, dairy, goat, sheep and swine herds in three California counties, with reference to control of potential foot-and-mouth disease transmission. Am. J. Vet. Res. 62, 1121–1129. doi: 10.2460/ajvr.2001.62.1121
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Bates, T. W., Thurmond, M. C., and And Carpenter, T. E. (2003a). Description of an epidemic simulation model for use in evaluating strategies to control an outbreak of foot-and-mouth disease. Am. J. Vet. Res. 64, 195–204. doi: 10.2460/ajvr.2003.64.195
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Bates, T. W., Thurmond, M. C., and And Carpenter, T. E. (2003b). Results of epidemic simulation modeling to evaluate strategies to control an outbreak of foot-and-mouth disease. Am. J. Vet. Res. 64, 205–210. doi: 10.2460/ajvr.2003.64.205
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
BBN. (2014). OpenMap. BBN Technologies. Available online at: http://openmap.bbn.com/
Bobashev, G. V., Goedecke, D. M., Yu, F., and Epstein, J. M. (2007). “A hybrid epidemic model: combining the advantages of agent-based and equation-based approaches,” in Proceedings of the 2007 Winter Simulation Conference (Washington, DC), 1532–1537.
Boklund, A., Halasa, T., Christiansen, L. E., and And Enoe, C. (2013). Comparing control strategies against foot-and-mouth disease: will vaccination be cost-effective in Denmark? Prevent. Vet. Med. 111, 206–219. doi: 10.1016/j.prevetmed.2013.05.008
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Bradhurst, R. A., Roche, S. E., Garner, M. G., Sajeev, A. S. M., and Kwan, P. (2013). “Modelling the spread of livestock disease on a national scale: the case for a hybrid approach,” in Proceedings of the 20th International Congress on Modelling and Simulation (MODSIM2013), Modelling and Simulation Society of Australia and New Zealand (Adelaide, SA), 345–351.
Buetre, B., Wicks, S., Kruger, H., Millist, N., Yainshet, A., Garner, G., et al. (2013). Potential Socio-Economic Impacts of an Outbreak of Foot-and-Mouth Disease in Australia. Research Report 13.11, October 2013, Australian Bureau of Agricultural and Resource Economics and Sciences (ABARES).
Bunn, C. M., Garner, M. G., and Cannon, R. M. (1998). The 1872 outbreak of foot-and-mouth disease in Australia – why didn't it become established? Aust. Vet. J. 76, 262–269. doi: 10.1111/j.1751-0813.1998.tb10157.x
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Caraco, T., Duryea, M. C., and Glavavakov, S. (2001). Host spatial heterogeneity and the spread of vector-borne infection. Theor. Popul. Biol. 59, 185–206. doi: 10.1006/tpbi.2000.1517
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Carley, K. M., Fridsma, D. B., Casman, E., Yahja, A., Altman, N., Chen, L., et al. (2006). BioWar: Scalable agent-based model of bioattacks. IEEE Trans. Syst. Man Cybern. A Syst. Hum. 36, 252–265. doi: 10.1109/TSMCA.2005.851291
Carpenter, T. E., Bates, T. W., and Thurmond, M. C. (2003). “The importance of including intra-herd transmission in a foot-and-mouth disease model,” in Proceedings of the 10th Symposium of the International Society for Veterinary Epidemiology and Economics, Vina del Mar, Chile, November 2003, New Concepts – Modelling Session,” 249–251.
Carpenter, T. E., O'Brien, J. M., Hagerman, A. D., and McCarl, B. A. (2011). Epidemic and economic impacts of delayed detection of foot-and-mouth disease: a case study of a simulated outbreak in California. J. Vet. Diagn. Invest. 23, 26–33. doi: 10.1177/104063871102300104
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Cash, J. R., and Karp, A. R. (1990). A variable order Runge-Kutta method for initial value problems with rapidly varying right-hand sides. ACM Trans. Math. Softw. 16, 201–222. doi: 10.1145/79505.79507
Department of Environment and Primary Industries. (2015). Goulburn Valley Regional Overview. State Government of Victoria. Available online at: http://www.depi.vic.gov.au/agriculture-and-food/food-and-fibre-industries/region-overviews/goulburn
Donaldson, A. I., Alexandersen, A., Sorensen, J. H., and Mikkelsen, T. (2001). Relative risks of the uncontrollable (airborne) spread of FMD by different species. Vet. Rec. 148, 602–604. doi: 10.1136/vr.148.19.602
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Donaldson, A. I., and Alexandersen, A. (2002). Predicting the spread of foot and mouth disease by airborne spread. Rev. Sci. Tech. 21, 569–575.
D'Souza, R. M., Marino, S., and Kirschner, D. (2009). “Data-parallel algorithms for agent-based model simulation of tuberculosis on graphics processing units,” in Proceedings of the 2009 Spring Simulation Multiconference (SpringSim '09), Society for Computer Simulation International (San Diego, CA), 1–12.
Dube, C., Ribble, C., Kelton, D., and McNab, B. (2011). Introduction to network analysis and its implications for animal disease modelling. Rev. Sci. Tech. 30, 425–436.
East, I. J., and Foreman, I. (2011). The structure, dynamics and movement patterns of the Australian sheep industry. Aust. Vet. J. 89, 477–489. doi: 10.1111/j.1751-0813.2011.00852.x
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
East, I. J., Wicks, R. M., Martin, P. A. J., Sergeant, E. S. G., Randall, L. A., and Garner, M. G. (2013). Use of a multi-criteria analysis framework to inform the design of risk based general surveillance systems for animal disease in Australia. Prev. Vet. Med. 112, 230–247. doi: 10.1016/j.prevetmed.2013.09.012
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
East, I. J., Davis, J., Sergeant, E. S. G., and Garner, M. G. (2014). Structure, dynamics and movement patterns of the Australian pig industry. Aust. Vet. J. 92, 52–57. doi: 10.1111/avj.12141
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Fine, P. E. M. (1977). A commentary on the mechanical analogue to the Reed-Frost epidemic model. Am. J. Epidemiol. 106, 87–100.
Galvani, A. P., and May, R. M. (2005). Dimensions of superspreading. Nature 438, 293–294. doi: 10.1038/438293a
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Garner, M. G., and Beckett, S. D. (2005). Modelling the spread of foot-and-mouth disease in Australia. Aust. Vet. J. 83, 758–766. doi: 10.1111/j.1751-0813.2005.tb11589.x
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Garner, M. G., Dube, C., Stevenson, M. A., Sanson, R. L., Estrada, C., and Griffen, J. (2007). Evaluating alternative approaches to managing animal disease outbreaks – the role of modelling in policy formulation. Vet. Ital. 43, 285–298.
Garner, M. G., and Hamilton, S. A. (2011). Principles of epidemiological modelling. Rev. Sci. Tech. 30, 407–416.
Garner, M. G., Hess, G. D., and Yang, X. (2006). An integrated modelling approach to assess the risk of wind-borne spread of foot-and-mouth disease virus from infected premises. Environ. Model. Assess. 11, 195–207. doi: 10.1007/s10666-005-9023-5
Garner, M. G., Murray, J. G., and Fisher, B. S. (2002). Economic aspects of foot and mouth disease: perspectives of a free country, Australia. Rev. Off. Int. Epizoot. 21, 625–635. doi: 10.1016/j.prevetmed.2013.07.013
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Germann, T. C., Kadau, K., Longini, I. M., and And Macken, C. A. (2006). Mitigation strategies for pandemic influenza in the United States. Proc. Natl. Acad. Sci. U.S.A. 103, 5935–5940. doi: 10.1073/pnas.0601266103
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Gibbens, J. C., Sharpe, C. E., Wilesmith, J. W., Mansley, L. M., Michalopoulou, E., Ryan, J. B., et al. (2001). Descriptive epidemiology of the 2001 foot-and-mouth disease epidemic in Great Britain: the first five months. Vet. Rec. 149, 729–743.
Hagenaars, T. J., Donnelly, C. A., and Ferguson, N. M. (2004). Spatial heterogeneity and the persistence of infectious diseases. J. Theor. Biol. 229, 349–359. doi: 10.1016/j.jtbi.2004.04.002
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Hare, M., and Deadman, P. (2004). Further towards a taxonomy of agent-based simulation models in environmental management. Math. Comput. Simul. 64, 25–40. doi: 10.1016/S0378-4754(03)00118-6
Harvey, N., Reeves, A., Schoenbaum, M. A., Zagmutt-Vergara, F. J., Dubé, C., Hill, A. E., et al. (2007). The North American Animal Disease Spread Model: a simulation model to assist decision making in evaluating animal disease incursions, Prevent. Vet. Med. 82, 176–97. doi: 10.1016/j.prevetmed.2007.05.019
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Hassall and Associates. (2006). The Structure and Dynamics of Australia's Sheep Population. Report prepared for the Department of Agriculture, Fisheries and Forestry, Canberra, ACT, Australia.
Hassall and Associates. (2007). A Review and Analysis of Saleyard Marketing in Australia. Report prepared for the Department of Agriculture, Fisheries and Forestry, Canberra, ACT, Australia.
Haydon, D. T., Woolhouse, M. E., and Kitching, R. P. (1997). An analysis of foot-and-mouth-disease epidemics in the UK. IMAJ. Math. Appl. Med. Biol. 14, 1–9. doi: 10.1093/imammb/14.1.1
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
James, A., Pitchford, J. W., and Plank, M. J. (2007). An event-based model of superspreading in epidemics. Proc. R. Soc. B Biol. Sci. 274, 741–747. doi: 10.1098/rspb.2006.0219
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Keeling, M. J. (2005). Models of foot-and-mouth disease. Proc. R. Soc. B Biol. Sci. 272, 1195–1202. doi: 10.1098/rspb.2004.3046
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Keeling, M. J., and Rohani, P. (2008). Modeling Infectious Diseases in Humans and Animals. Princeton; Oxford. Princeton University Press.
Kokic, P., and Mues, C. (2006). Cattle Movements. Research Report. Australian Bureau of Agricultural and Resource Economics and Sciences (ABARES).
LaBute, M. X., McMahon, B. H., Brown, M., Manore, C., and Fair, J. M. (2014). A flexible spatial framework for modeling spread of pathogens in animals with biosurveillance and disease control applications. ISPRS Int. J. Geo-Inform. 3, 638–661. doi: 10.3390/ijgi3020638
Lloyd-Smith, J. O., Schreiber, S. J., Hopp, P. E., and Getz, W. M. (2005). Superspreading and the effect of individual variation on disease emergence. Nature 438, 355–359. doi: 10.1038/nature04153
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Mansley, L. M., Dunlop, P. J., Whiteside, S. M., and Smith, R. G. H. (2003). Early dissemination of FMD virus through sheep marketing in February 2001. Vet. Rec. 153, 43–50. doi: 10.1136/vr.153.2.43
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Matthews, K. (2011). A Review of Australia's Preparedness for the Threat of Foot-and-Mouth Disease. Australian Government Department of Agriculture, Fisheries and Forestry, Canberra, ACT. Available online at: http://www.agriculture.gov.au/animal-plant-health/pests-diseases-weeds/animal/fmd/review-foot-and-mouth-disease
McLaws, M., Ribble, C., Stephen, C., McNab, B., and Barrios, P. R. (2007). Reporting of suspect cases of foot-and-mouth disease during the 2001 epidemic in the UK, and the herd sensitivity and herd specificity of clinical diagnosis. Prevent. Vet. Med. 78, 12–23. doi: 10.1016/j.prevetmed.2006.09.001
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Meat and Livestock Australia. (2011). National Livestock Identification Scheme Database. Available online at: http://www.mla.com.au/Meat-safety-and-traceability/National-Livestock-Identification-System
Meyer, R. F., and Knudsen, R. C. (2001). Foot-and-mouth disease: a review of the virus and the symptoms. J. Environ. Health 64, 21–23.
Miller, W. M. (1976). “A state-transition model of epidemic foot-and-mouth disease,” in Proceedings of the International Symposia on Veterinary Epidemiology and Economics (ISVEE 1), New Techniques in Veterinary Epidemiology and Economics. Reading: University of Reading, Descriptive Modelling Session, 56–72.
Nickbakhsh, S., Matthews, L., Dent, J. E., Innocent, G. T., Arnold, M. E., Reid, S. W. J., et al. (2013). Implications of within-farm transmission for network dynamics: consequences for the spread of avian influenza. Epidemics 5, 67–76. doi: 10.1016/j.epidem.2013.03.001
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Nielen, M., Jalvingh, A. W., Horst, H. S., Dijkhisen, A. A., Maurice, H., Schut, B. H., et al. (1996). Quantification of contacts between Dutch farms to assess the potential risk of foot-and-mouth disease spread. Prevent. Vet. Med. 28, 143–158. doi: 10.1016/0167-5877(96)01042-2
Noremark, M., Hakansson, N., Sternberg Lewerin, S., Lindberg, A., and Jonsson, A. (2011). Network analysis of cattle and pig movements in Sweden: measures relevant for disease control and risk based surveillance. Prevent. Vet. Med. 99, 78–90. doi: 10.1016/j.prevetmed.2010.12.009
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Noremark, M., Frossling, J., and Sternberg Lewerin, S. (2013). A survey of visitors on Swedish livestock farms with reference to the spread of animal diseases. BMC Vet. Res. 9:184. doi: 10.1186/1746-6148-9-184
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Oracle. (2014). Java. Oracle Corporation. Available online at: http://www.java.com/en/
Parker, J., and Epstein, J. M. (2011). A distributed platform for global-scale agent-based models of disease transmission. ACM Trans. Model. Comput. Simul. 22:2. doi: 10.1145/2043635.2043637
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Parunak, H. V. D., Savit, R., and Riolo, R. L. (1998). “Agent-based modeling vs. equation-based modeling: a case study and users' guide,” in Proceedings of Multi-Agent Systems and Agent-Based Simulation (MABS'98), 10–25.
Perez, L., and Dragicevic, S. (2009). An agent-based approach for modeling dynamics of contagious disease spread. Int. J. Health Geogr. 8:50. doi: 10.1186/1476-072X-8-50
PostgreSQL. (2014). PostgreSQL. The PostgreSQL Global Development Group. Available online at: http://www.postgresql.org/
Regional Development Victoria. (2010). Goulburn Valley sub-regional plan – The Hume Strategy for sustainable communities 2010-2010. State Government of Victoria. Available online at: http://www.rdv.vic.gov.au/victorian-regions/hume
Roche, S. E., Garner, M. G., Wicks, R. M., East, I. J., and de Witte, K. (2014). How do resources influence control measures during a simulated outbreak of foot and mouth disease in Australia? Prevent. Vet. Med. 113, 436–446. doi: 10.1016/j.prevetmed.2013.12.003
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Rushton, J., Knight Jones, T. J. D., Donaldson, A. I., de Leeuw, P. W., Ferrari, G., and Domenech, J. (2012). The Impact of Foot and Mouth Disease – Supporting Document N° 1. Paper prepared for the FAO/OIE Global Conference on Foot and Mouth Disease Control, Bangkok (Thailand), 27 to 29 June 2012.
Sanson, R. L. (2005). A survey to investigate movements off sheep and cattle farms in New Zealand, with reference to the potential transmission of foot-and-mouth disease. N. Z. Vet. J. 53, 223–233. doi: 10.1080/00480169.2005.36550
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Stata. (2014). STATA Intercooled Software v11.0. Stata Corporation. Available online at: http://www.stata.com/products/which-stata-is-right-for-me/#IC
Stevenson, M. A., Sanson, R. L., Stern, M. W., O'Leary, B. D., Sujau, M., Moles-Benfell, N., et al. (2013). InterSpread Plus: a spatial and stochastic simulation model of disease in animal populations. Prevent. Vet. Med. 109, 10–24. doi: 10.1016/j.prevetmed.2012.08.015
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Taylor, N. (2003). Review of the Use of Models in Informing Disease Control Policy Development and Adjustment. School of Agriculture, Policy and Development, The University of Reading.
Tildesley, M. J., Savill, N. J., Shaw, D. J., Deardon, R., Brooks, S. P., Woolhouse, M. E. J., et al. (2006). Optimal reactive vaccination strategies for a foot-and-mouth outbreak in the UK. Nature 440, 83–86. doi: 10.1038/nature04324
PubMed Abstract | Full Text | CrossRef Full Text | Google Scholar
Van den Broeck, W., Gioannini, C., Gonçalves, B., Quaggiotto, M., Colizza, V., and Vespignani, A. (2011). The GLEaMviz computational tool, a publicly available software to explore realistic epidemic spreading scenarios at the global scale. BMC Infect. Dis. 11:37. doi: 10.1186/1471-2334-11-37
Vincenot, C. E., Giannino, F., Rietkerk, M., Moriya, K., and Mazzoleni, S. (2011a). Theoretical considerations on the combined use of System Dynamics and individual-based modeling in ecology. Ecol. Modell. 222, 210–218. doi: 10.1016/j.ecolmodel.2010.09.029
Vincenot, C. E., and Moriya, K. (2011b). Impact of the topology of metapopulations on the resurgence of epidemics rendered by a new multiscale hybrid modeling approach. Ecol. Inform., 6, 177–186. doi: 10.1016/j.ecoinf.2011.04.002
Vose, D. (2008). Risk Analysis: A Quantitative Guide, 3rd Edn. Chichester: John Wiley and Sons, Ltd.
Yoneyama, T., Das, S., and Krishnamoorthy, M. (2012). A hybrid model for disease spread and an application to SARS pandemic. J. Artif. Soc. Soc. Simul. 15, 5.
Yu, B., Wang, J., McGowan, M., Vaidyanathan, G., and Younger, K. (2010). “Gryphon: A hybrid agent-based modeling and simulation platform for infectious diseases. Advances in Social Computing,” in Third International Conference on Social Computing, Behavioural Modeling and Prediction, SBP 2010, Proceedings, LNCS 6007 (Bethesda, MD), 199–207.
Keywords: AADIS, FMD, epidemiological model, hybrid model, spatiotemporal model
Citation: Bradhurst RA, Roche SE, East IJ, Kwan P and Garner MG (2015) A hybrid modeling approach to simulating foot-and-mouth disease outbreaks in Australian livestock. Front. Environ. Sci. 3:17. doi: 10.3389/fenvs.2015.00017
Received: 05 December 2014; Paper pending published: 14 January 2015;
Accepted: 24 February 2015; Published: 19 March 2015.
Edited by:
Christian E. Vincenot, Kyoto University, JapanReviewed by:
Jagdish Krishnaswamy, Ashoka Trust for Research in Ecology and the Environment, IndiaFabrizio Carteni, University of Naples Federico II, Italy
Copyright © 2015 Bradhurst, Roche, East, Kwan and Garner. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Richard A. Bradhurst, Discipline of Computer Science, School of Science and Technology, University of New England, Armidale, NSW 2351, AustraliacmJyYWRodXJAbXl1bmUuZWR1LmF1
 Richard A. Bradhurst
Richard A. Bradhurst Sharon E. Roche2
Sharon E. Roche2 Iain J. East
Iain J. East Paul Kwan
Paul Kwan