- 1Environmental Sciences Group, Wageningen University and Research Centre, Wageningen, Netherlands
- 2Department of Environmental Sciences, The University of Sydney, Sydney, NSW, Australia
The English polymath Lewis Fry Richardson (1881–1953) made important contributions to many fields, including numerical weather prediction, finite difference solutions of partial differential equations, turbulent flow and diffusion, fractals, and the cause and evolution of conflicts. His first papers in 1908 concerned unconfined flow of water in saturated soil, arising in the design of required ditch spacing for draining peat. He developed and used a graphical method to solve this problem. This and other practical problems stimulated his interest in numerical methods and soon led him to the challenge of numerical weather prediction. In 1922 he published the book Weather Prediction by Numerical Process. He did the research for this book under difficult circumstances just before, during, and right after World War I. The book was received positively, but methods like those proposed in it were not successfully implemented until the invention of fast digital computers around 1950. Posthumously, most of Richardson's contributions in various fields received considerable attention. Important exceptions are his contributions to soil science and hydrology, on which we focus in this paper. In his 1922 book, Richardson formulated an elaborate model for transport processes in the atmosphere. For the lower boundary of his atmospheric model, he needed to understand the movement of liquid water, water vapor, and heat in the upper layer of the soil, and at the soil-atmosphere and plant-atmosphere interfaces. Finding little previous work on this, he first of all formulated the partial differential equation for transient, vertical flow of liquid water in soil. We argue that the resulting equation can rightly be called the Richardson-Richards equation. In addition he formulated equations for simultaneous transfer of liquid water and water vapor, for transfer of heat in soil, and for the balances of water and energy at the soil-atmosphere and plant-atmosphere interfaces. Finite difference versions of all the equations were incorporated in the numerical weather forecasting model. Unfortunately, his results were hardly noticed by soil physicists and hydrologists, likely because they were too effectively buried in an intimidating book on weather prediction.
1. Introduction
There are already several published articles in journals and chapters in books about the scientific work of Lewis Fry Richardson. In the following brief biography we explain why the world of science needs this article (Ashford et al., 1993a; Charnock, 1993; Drazin, 1993; Hunt, 1998; Lynch, 2006, 2007). We conclude this introduction with an outline of this paper.
Lewis Fry Richardson (Figure 1) was born on October 11, 1881 at Newcastle, as the youngest of the seven children of his Quaker parents David and Catherine Richardson (Ashford, 1985; Drazin, 1986; Hunt, 1993). LFR (throughout this paper we will frequently use this abbreviation of L. F. Richardson's name) attended Newcastle Preparatory School. Next he was sent to Bootham School, a Quaker boarding school at York, where his interest in science was fostered and his high moral standards were formed. In 1898 he entered Newcastle University, where he took courses in mathematical physics, chemistry, botany, and zoology. In 1900 he moved on to King's College at the University of Cambridge, where he graduated as physicist in 1903.

Figure 1. Lewis Fry Richardson (1881–1953), after a photograph taken in 1931 by Walter Stoneman, reproduced with permission from the National Portrait Gallery in London.
In the following 10 years he held numerous successive research posts at government and industrial laboratories, and at universities. In 1906–1907 he held an appointment as chemist at the National Peat Industry Ltd. His responsibility was to design a layout of ditches that would drain the peat in a predictable manner. To find answers, he formulated a theory describing the flow of water in peat, involving the Laplace equation (Richardson, 1908b). To solve this equation, he first devised a graphic method for determining the stream lines and equipotential lines (Richardson, 1908a). The two 1908 papers showed that he could handle flows in complicated geometries, for which it would be difficult or impossible to find analytical solutions.
Following this early success, he set out to solve computational problems by a more versatile finite difference method. In a pioneering paper in numerical analysis (Richardson, 1910), he used as illustration the determination of stresses in a masonry dam. Hunt (1998) describes the difficulty Richardson had in getting this work published in The Philosophical Transactions of the Royal Society and that it was also not appreciated at Cambridge, where he unsuccessfully sought a Fellowship to allow him to do research and teach.
During a brief period in 1912–1913, he was Demonstrator and Lecturer at Manchester College of Technology. That College was later incorporated in the University of Manchester, where the School of Mathematics lists LFR among its fourteen “Distinguished minds.” In 1913 LFR joined the Meteorological Office as Superintendent of Eskdalemuir Observatory at a remote location in Scotland. It is there that he started his work in meteorology, initially as a proving ground for his finite difference method (cf. item 7 in Richardson, 1949). A first draft of a book entitled Weather Prediction by Arithmetical Finite Differences was communicated in May 1916 by Sir Napier Shaw to the Royal Society, which voted 100 pounds toward its publication (see Hunt, 1998 and also the Preface of Richardson, 1922). But then World War I interfered. In May 1916 LFR resigned from the Meteorological Office to offer his services by joining the Society of Friends' Ambulance Unit, thus remaining true to his pacifist principles (Hunt, 1998). At the Western Front in France, he became a driver for the Section Sanitaire Anglaise attached to a French infantry division.
In his spare time in France, LFR performed meteorological experiments and continued working on his book. He also became deeply interested in the psychology of war. To understand initiation, development, and resolution of conflicts, he formulated mathematical models. Much of his motivation can be found in Mathematical Psychology of War (Richardson, 1919), which he dedicated to “my Comrades of the motor ambulance convoy known as S.S. Anglaise 13, in whose company this essay was mainly written.” This and many of his other publications on war and peace are good reading, also for the not mathematically inclined. Volume 2 of the Collected Works of LFR is devoted entirely to quantitative psychology, especially studies of conflict (Ashford et al., 1993b). At the centennial of the start of World War I, Berreby (2014) fluently described LFR's simultaneous interest in prediction of the weather and of conflicts.
In 1919 LFR rejoined the Meteorological Office, then at Benson, Oxfordshire, “nominally in charge of experiments in the computation of the sequence of weather by numerical processes.” A new, final draft of the book resulted, with the title Weather Prediction by Numerical Process (Richardson, 1922). The 1922 book concerns mainly atmospheric transport processes, but our interest here is the brief treatment of four subsurface and surface processes that served as boundary conditions for the atmospheric model. Two of those processes are soil related, one soil-atmosphere related, and one plant-atmosphere related:
• water movement in unsaturated soil;
• heat transfer in soil;
• the balances of water and energy at the soil-atmosphere interface;
• the balances of water and energy at the plant-atmosphere interface.
The book was published in 1922 by Cambridge University Press. The book received widespread attention from reviewers, not only from British reviewers, but also in Monthly Weather Review by Woolard (1922) from the Weather Bureau, Washington, D.C. and in Geographical Review by the Harvard meteorologist McAdie (1923). The latter wrote prophetically: “[it] is a remarkable book, perhaps the most remarkable of all meteorological treatises. It can have but a limited number of readers and will probably be quickly placed upon a library shelf and allowed to rest undisturbed by most of those who purchase a copy. It is a strikingly bold attempt to wake up weather forecasters; indeed, to make forecasting a science rather than an art.” Following the initial attention, it became very quiet. A recent search in Web of Science reveals only 12 citations of Richardson (1922) in the three decades after its publication.
Post-World War II developments in numerical weather prediction eventually led to serious interest (Platzman, 1967) and a reprint of the 1922 book was published by Dover, with a new introduction by the British mathematician and geophysicist Sydney Chapman. Also in the last two decades the interest has been intense. A second edition, with a new introduction by Peter Lynch, was again published by Cambridge University Press. Since LFR died in 1953 at age 71, the importance of his contributions has been recognized widely: Richardson Peace Institute at Lancaster University, founded in 1959; Richardson Wing of the Meteorological Office at Bracknell, opened in 1972; Annual LF Richardson Prize for early-career members of the Royal Meteorological Society, since late 1970s; Annual Lewis Fry Richardson medal of European Geosciences Union (EGU) Division of Nonlinear Processes in Geophysics, since late 1990s. Yet, despite all this attention, the contributions by LFR to soil physics and hydrology practically remained unnoticed, very likely because they were too effectively buried in an intimidating book on weather prediction.
In this paper we do describe in detail the contributions by Richardson to soil physics and hydrology. Throughout the paper we comment on inspiration from earlier work and for later developments. Section 2 deals with his study of ditch drainage of peat for the National Peat Industry Ltd. In section 3 it will be shown in considerable detail how Richardson in his 1922 book dealt with movement of water in unsaturated soil, heat transfer in soil, and the balances of water and energy at the soil-atmosphere and plant-atmosphere interfaces. In section 4 we briefly discuss Richardson's contributions to numerical analysis, with emphasis on their direct and indirect influence in soil physics.
2. Flow to Ditches in Saturated Peat
2.1. Introductory Remarks
In 1906 and 1907, LFR was employed by the young, small company National Peat Industries Ltd at Newcastle upon Tyne (see Ashford, 1985, p. 21). According to the company prospectus issued in August 1905, the purpose was “to deal in a scientific way with peat and its various products and uses, and for that purpose to acquire, combine, and consolidate certain businesses, properties and interests, and to acquire peat mosses, patent rights, licenses, plant and machinery.” LFR and his father were shareholders in the company. Several years after LFR had left, the company suffered losses related to property in Ireland and defalcations by the management team. As a result the company failed and in 1916 was taken over by Umeras Peat Ltd. For LFR the company brought financial loss, but also early experience with a practical problem requiring both the formulation of a new physico-mathematical model and the development of new methods to solve the equations.
At the National Peat Industry Ltd., Richardson was faced with the questions (Richardson, 1908b):
Given the annual rainfall, how must the drains be cut in order to remove just the right amount of water? Or conversely, What will be the effect of any given cutting?
In his analysis of the drainage of peat, LFR decided to treat the peat as a continuous medium and to explicitly disregard complications from presence of air, heterogeneity, anisotropy, and swelling. As LFR writes: “In this present imperfect stage of the theory of drainage, there is no need to apologize for taking a simplified case.”
In Richardson (1908b), the bibliography sheds some light on the sources of inspiration. The earliest reference is a 1889 book on irrigation and drainage by Franklin Hiram King, Professor of Agricultural Physics at the University of Wisconsin (Tanner and Simonson, 1993). We have only seen the 1907, fifth edition of this book (King, 1907), which seemingly was the same as the 1889 first edition, except for some corrections. King's Figure 134, which also appears as Figure 14 in King (1899), shows a “Diagram of lines of flow of water in the drainage of a river valley,” with strictly vertical flow above the water table and a realistic pattern of streamlines below the water table. The diagram is perhaps based on discussions of King with Charles Slichter.
Another source of inspiration was a paper by Pennink (1905). Pennink's Figure 8, reproduced here as Figure 2A, was based on streamlines and equipotentials inferred, respectively, from injected dyes and piezometer data. The flow pattern is comparable to that in the diagram of King for the drainage of a river valley. Pennink's Figure 12, reproduced here as Figure 2B, shows clear evidence of lateral flow in the capillary fringe. In fact, that figure may well be the first documentation of lateral flow in the capillary fringe. It appears that this was not noticed by Richardson who, like King, appears to regard the flow above the water table as strictly vertical.
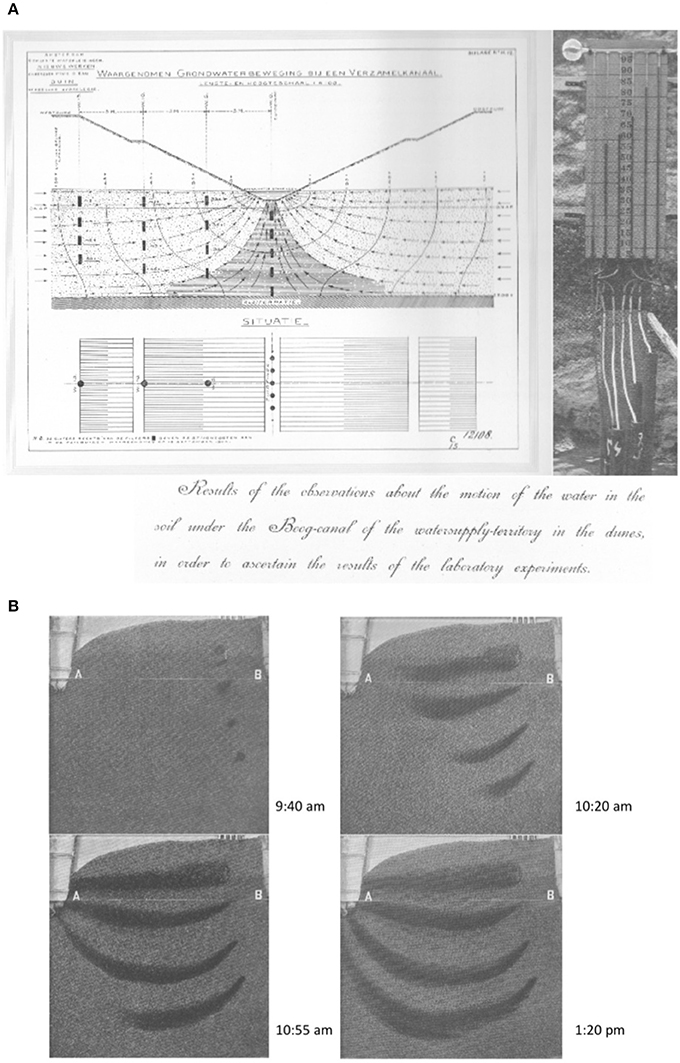
Figure 2. (A) Flow pattern based on observed total head in a field, and (B) streamlines made visible with Indian ink in a sand tank model, both copied from Pennink (1905), with permission from the Royal Netherlands Society of Engineers (KIVI).
Perhaps most important for Richardson were recent papers by Joseph Valentin Boussinesq (1842–1929). He cites seven contributions in the Comptes Rendues, Acad. Sci., Paris and also two in the Journal de Mathematiques, Paris covering more or less the same material. Boussinesq (1904) made use of the so-called Dupuit-Forchheimer assumption, allowing him to treat flows as horizontal in either one dimension or two dimensions. As a result of this simplification, Boussinesq could only deal with relatively shallow flows.
2.2. Formulation of the Problem
Richardson (1908b) starts with an experiment intended to demonstrate the validity of Darcy's law for peat. To determine the hydraulic conductivity, he used the falling head method, first proposed by Darcy (1856). Unfortunately, the variable diameter of the small sample used by Richardson and his incorrect identification of the driving force make the execution and interpretation of the experiment problematical. But apart from this, he realized that the disturbed sample was not representative “of the peat as it lies in the bog.” Later, we will see how he resolved this problem.
Richardson felt that the Dupuit-Forchheimer shallow flow assumption was not justified for the situations he wished to consider. Therefore, he formulated a fully three-dimensional theory by applying the principles of balance of mass and balance of forces to the water at any point in the peat (Figure 3, left column). Assuming the pore volume fraction and the density of the water to be uniform and constant, he expressed the balance of mass by the divergence of the velocity of the water v being zero. In the balance of forces for the water, he neglected the acceleration and equated the total force exerted on the water to the resistance force exerted by the peat. The total force exerted is the sum of the pressure gradient force and the gravitational force. Assuming K—which Richardson calls “porosity”—to be constant, he defined the velocity potential ϕ by ϕ = K(gρz − p), and showed that the velocity v is equal to the gradient of ϕ and that, hence, the motion of the water is irrotational. Combining the mass balance and the force balance, he found that ϕ satisfies the Laplace equation. Note that p/(gρ) and Kgρ correspond to what are now called “pressure head” and “hydraulic conductivity.” The handling of the forces driving the flow of the water by LFR is better than that given earlier by King (1899) and Slichter (1899). LFR also formulated appropriate boundary conditions, namely the no-flow, free surface, and seepage surface conditions given, respectively, by Equations (6–8) in the right column of Figure 3.

Figure 3. Differential equations (Left column) and boundary conditions (Right column) for flow of water in saturated soil, copied from Richardson (1908b), with permission from the Royal Dublin Society (RDS).
2.3. Graphical Solution of the Problem
Prompted by the drainage problem at the National Peat Industry Ltd, in a separate paper Richardson (1908a) explored the potential of graphical methods for solving partial differential equations. He was pessimistic about using available analytical methods to deal with the equations, boundary conditions, and geometries arising in practice. He motivated exploring graphical methods for such problems as follows (Richardson, 1908a, p. 89):
…the time required to arrive at the desired result by analytical methods cannot be foreseen with any certainty. It may come out in a morning, it may be unfinished at the end of a month. It is no wonder that the practical engineer is shy of anything so risky.
With regard to the origin of his graphical method, Richardson (1908a, p. 90), wrote:
Maxwell in section 92 of his “Elementary Treatise on Electricity and Magnetism” speaks of tentative methods of altering known solutions of the Laplacian equation by drawing diagrams on paper and selecting the least improbable. The object of the present thesis is to point out that this method can do far more than merely alter known results, and that it may be so far from tentative as to yield an accuracy at one percent of the range.
It appears that Richardson was not aware of the fact that, already two decades earlier, Forchheimer (1886) proposed the graphical method to solve the Dupuit-Forchheimer equation for horizontal flow. This may be related to the fairly low profile German journal and to the relatively remote location where LFR worked.
Richardson (1908a) went on to develop a graphical method for solving the Laplace equation for geometries and boundary conditions of interest. Specifically, for the plane flow version of a theory such as described above, he proved that for the network—or checkerboard as he calls it—formed by streamlines and equipotentials, each drawn at equal intervals, all checkers are curvilinear rectangles and have the same checker ratio, i.e., the same ratio of length in the direction of the flow and width perpendicular to the flow.
Richardson (1908b) used these orthogonality and constant checker ratio properties to construct by freehand drawing flow patterns for drainage problems with realistic geometries and boundary conditions, including a seepage surface. For a peat with a particular value of K, Figures 4A,C show the results for flow to a “drain” for, respectively, low rainfall with W/(Kgρ) = 0.085 and high rainfall with W/(Kgρ) = 0.96. Presumably, by “drain” he means free outflow into a vertical boundary reaching an impermeable bottom. For low rainfall, Figure 4A shows a water table separating the saturated and unsaturated peat and outflow at a seepage surface. Figure 4B shows flow to a drain as in Figure 4A, calculated by a modern variational method (Knight, 1984; Van der Hoek et al., 1984). For high rainfall, Figure 4C shows a seepage face reaching to nearly the top of the peat; Richardson remarks that “the form of the water surface is indeterminate by this method in this instance.”
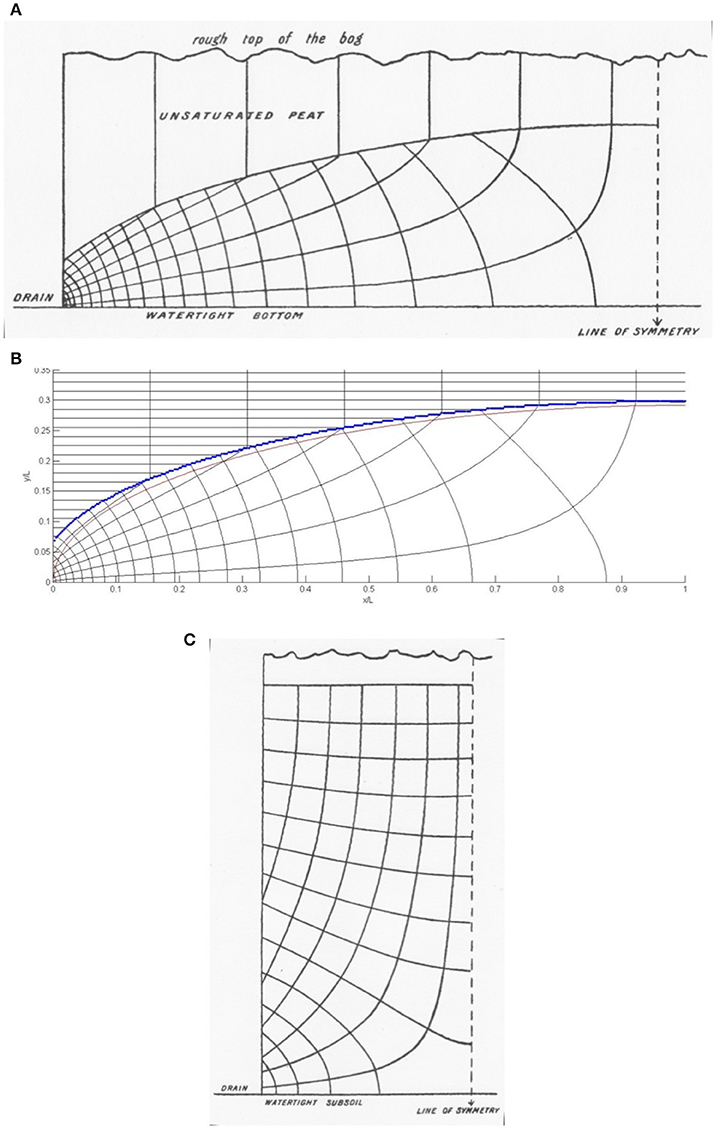
Figure 4. Flow nets (A) for flow to drain with W/(Kgρ) = 0.085, (B) for flow to drain, calculated by a variational method (Knight, 1984; Van der Hoek et al., 1984), (C) for flow to drain with W/(Kgρ) = 0.96. Parts (A,C) copied from, respectively, Figures 3, 4 in Richardson (1908b), with permission from the Royal Dublin Society (RDS).
Again for peat with a particular value of K, Figures 5A,B show the results for flow to a ditch for, respectively, low rainfall with W/(Kgρ) = 0.068 and high rainfall W/(Kgρ) = 0.226. For high rainfall a much larger fraction of the water enters the ditch via the seepage surface along the vertical boundary of the ditch.
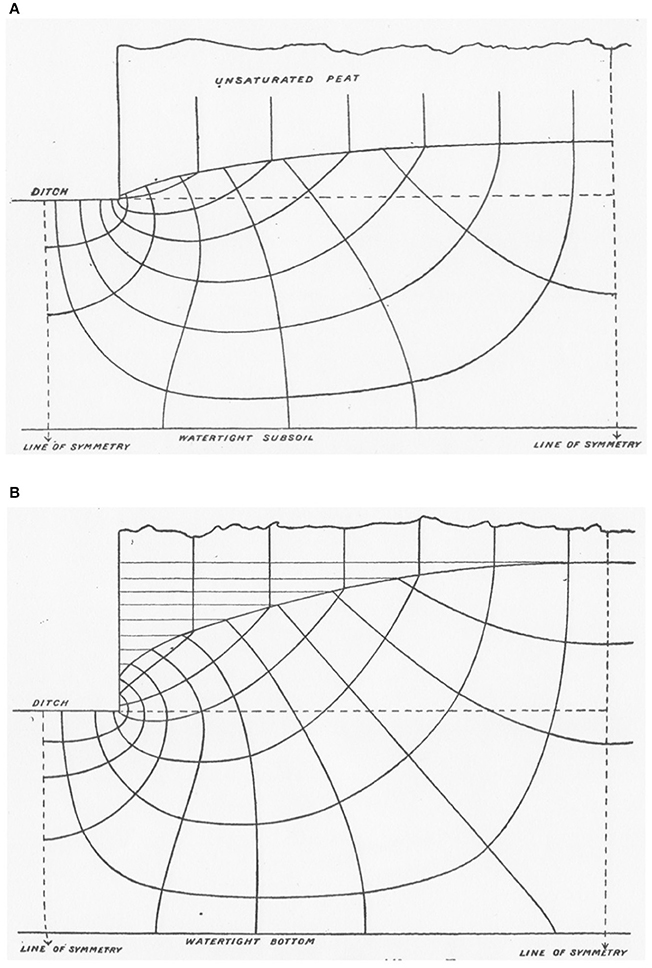
Figure 5. Flow nets (A) for flow to ditch with W/(Kgρ) = 0.068, (B) for flow to drain with W/(Kgρ) = 0.226. Parts (A,B) copied, respectively, from Figures 5, 6 in Richardson (1908b), with permission from the Royal Dublin Society (RDS).
Recall that in connection with his not too satisfactory attempt to measure the hydraulic conductivity, Richardson had remarked that the disturbed sample used was a problem. Near the end of his paper, he presents an imaginative method for determining the hydraulic conductivity of a large sample “of the peat, as it lies in the bog”: see Figure 6. In the separate paper, Richardson (1908a) already had worked out for this axisymmetric case the necessary adjustment of the dependence of the checker ratio as function of the distance from the axis.
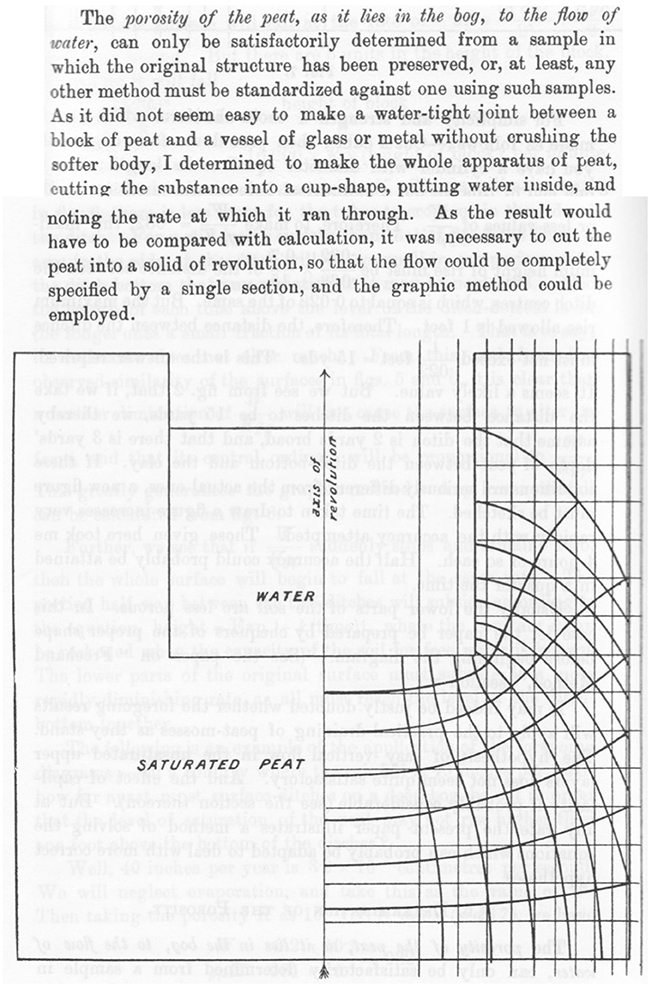
Figure 6. Determination of hydraulic conductivity, using a cylindrical sample with water delivery hole. Copied from text and Figure 7 in Richardson (1908b), with permission from the Royal Dublin Society (RDS).
Concerning LFR's drainage research, Ashford (1985, p. 23) wrote: “By a simple experiment he confirmed that some already known equations could be applied with appropriate modifications, and he then went on to solve the equations approximately by a freehand graphic method.” It appears that by referring to “some already known equations,” Ashford underestimates the difference between the shallow flow approach of Boussinesq and the approach of LFR described above involving a three dimensional Laplace equation with a combination of no-flow, free surface, and seepage surface boundary conditions. A complete history of the use of such boundary conditions in the first half of the twentieth century remains to be written.
3. Water Movement and Heat Transfer in Unsaturated Soil
3.1. Introductory Remarks
In his book Weather Prediction by Numerical Process (Richardson, 1922), the primary interest of LFR is the atmosphere. But in view of the large capacity of the soil and the seas for water and heat, he also believes that “The atmosphere and the upper layers of the soil or sea form together a united system.” He points out that two approaches present themselves:
• directly estimate the earth-atmosphere interface conditions as function of time of the day and year;
• derive the interface conditions needed from a detailed analysis of transfer processes below the surface of the earth.
LFR considers, successively, four types of lower boundaries of the atmosphere: sea, bare soil, earth covered with vegetation, and snow and ice. With regard to the sea-atmosphere interface, he believes that the first approach—i.e., direct use of measured sea-atmosphere interface temperature as function of time of the day in the course of the year—is the practical choice. Nevertheless, he leaves open the possibility that some day a prediction of the sea surface temperature on the basis of long-wave and solar radiation, turbulence in the sea and the air, and atmospheric and ocean currents might be considered. For the snow- and ice-atmosphere interface, he refers to observations on specific radiative and thermal conductive properties of snow.
Our chief interest is in LFR's treatment of bare soil and of earth covered with vegetation. Although LFR was certainly not frightened by the prospect of elaborate computations, he closed the subsection “General” with a proposal to use a spatial discretization grid that becomes coarser with depth in the soil. On the basis of estimated damping of thermal fluctuations, he proposed to transform the depth as:
and thus later for computational purposes to use the substitutions:
and
3.2. Movement of Water in Bare Soil
In Chapter 4 of Weather Prediction by Numerical Process (Richardson, 1922), at the beginning of section 10.2 on “The bare soil,” LFR clearly states his objective in developing a theory for the motion of water and heat in soil (page 107):
In winter great areas of arable land are bare. As in the case of the sea, we require to forecast the temperature and humidity of the air in immediate contact with the surface of the soil.
To the second sentence he could have added, “as lower boundary conditions for the atmosphere.” The main source of inspiration he cites is the book Lectures on Some of the Physical Properties of Soil (Warington, 1900).
LFR starts by noting that lysimeter observations at Rothamsted have shown that in the six winter months, October to March, evaporation is practically identical with that from a water surface (see page 108 in Warington, 1900), so that presumably in that period the bare soil surface is so wet that the air in contact with it is saturated. Nevertheless LFR proceeds to develop an equation for the motion of water in soil that is applicable in summer as well as winter. He aims at a description at the macroscopic level (page 107):
In this equation it will be convenient to regard the soil as a continuous medium, that is to say the “infinitesimal” differences of the coordinates must be large compared with the soil particles and yet small enough to give a good representation of the variation of moisture with position.
LFR notes that the theory of percolation in saturated soils had already been put in mathematical form by Boussinesq, as discussed in section 2 above. In a footnote (page 107) he refers to his own Dublin paper on drainage (Richardson, 1908b) and to the sources of inspiration for that paper (King, 1899; Boussinesq, 1904; Pennink, 1905). LFR continues (page 107):
For unsaturated soil, such as is often found near the surface, I have not found the equation anywhere. It may be developed from the ideas of Briggs, according to whom the water in unsaturated soil may be typified by a waist-shaped piece partly filling the crevice between two soil spherical particles. If the amount of water in the waist decreases, the curvature of its surface becomes more strongly concave, and the negative pressure in the water is thereby decreased. If the water in all the crevices is continuous with itself, the pressure will tend to become everywhere equal, in the absence of gravity.
The reference to Briggs in this quote can be traced to pages 93–94 in Warington (1900) and from there to a report published at age 23 by the American physicist Lyman J. Briggs (1874–1963) as a bulletin of the USDA Bureau of Soils (Briggs, 1897; Landa and Nimmo, 2003). Briggs discusses in great detail the relationships between distribution of water in soil, surface tension of air-water interfaces, and water pressure. Briggs on the whole takes a pore scale point of view.
After having mentioned his sources of inspiration, LFR immediately switches from the pore scale point of view to the porous medium point of view. He writes (pages 107–108):
Denote the mass of water per volume of soil by w. From the point of view of our large infinitesimals, the pressure in the water will be a single valued continuous function of position, and will depend on w. Denote the pressure of the water by ψ(w). The form of the function ψ can be determined, for any particular soil, by experiments similar to those of Loughridge. He put air-dried soil into vertical metal pipes closed at their lower ends by muslin.Water was supplied through the muslin and rose by capillarity. From the mode of its entry this water was probably all continuous. When the steady state was established, samples taken at different heights were weighed, dried and reweighed. This gave w. At the same time ψ(w) is equal to g times the height of the sample above the free water level outside the tube, as the density of the water is unity.
This is a clear definition of the soil water retention characteristic, as we now call it, and the description of a method to determine this characteristic. From pages 97–100 of Warington (1900), the original source of the data on the equilibrium distribution of water following capillary rise can be traced to Loughridge (Report Agricultural Experiment Stations 1892-3-4, p. 91). Note that LFR seems aware of the fact that “the mode of its entry” may affect the distribution of the water at the pore scale. In view of his experiences with peat, this is hardly surprising.
After having dealt with the equilibrium of the water in a vertical tube and having proposed to use it to determine the ψ(w) relationship, LFR continues (page 108; in Equations 4, 5 and elsewhere I have replaced Richardson's Coptic letter shai by k):
In the more general case, when there is not equilibrium, will be the unbalanced pressure gradient producing a flow upwards. Since the flow is in very narrow channels it is non-turbulent. It is therefore proportional to the unbalanced pressure gradient, and varies inversely as the viscosity. The flow also depends on the dimensions of the channels. These are bounded in part by water-air surfaces, with the result that the conductance of the channels diminishes rapidly with diminishing w. Denote the conductance of the channels connecting the opposite faces of a centimeter cube of soil by k, which is the Coptic letter pronounced “shai.” Then the flow of water upwards is, in cm3 s−1 per horizontal cm2,
So the rate at which water accumulates to any point by creeping is
Note that the coordinate z is positive in the downward direction and that therefore an upward flux is negative. Equation (5) describing flow of water in the vertical direction is obtained by inserting the expression for the volumetric flux given by Equation (4), obtained from the force balance for the water, in the volumetric mass balance for the water. Thus, as in his Dublin paper for flow of water in saturated peat, LFR's theory for flow of water in unsaturated soils is based on the balance of mass and the balance of forces for the water. Note that the “unbalanced pressure gradient” corresponds, in now commonly used terminology in soil physics, to the “gradient of the total head.”
Next LFR proposes an experiment to determine the dependence of the conductivity k upon the volumetric water content w (page 108):
The conductivity k could, I think, be determined experimentally as a function of w by means of apparatus similar to that which gives the pressure ψ. For let a uniform slow current of water be established, either down the tube by dropping water on the top, or up the tube by promoting evaporation at the top. Let the current be measured and be maintained constant until a steady state has become established throughout the tube; and then let w be determined at a series of heights by drying samples. From the distribution of w, that of the pressure ψ(w) could be found, since the form of ψ is known from the previous experiment. Taking the gradient of the pressure ψ(w) and inserting it along with the constant flow in (4) we should have the conductivity k for a series of values of w.
LFR is aware of its possible complications and limitations, for he writes (page 108):
ψ and k depend on the temperature in known ways; if, as usually happens, the soil is not uniform, they also depend on the depth. The possibility of the existence of isolated water must not be forgotten, although no way of treating it mathematically may be at hand. Nor must the loss of water by surface drainage, root-holes and fissures be overlooked.
LFR's theory for movement of liquid water in unsaturated soil has much in common with Buckingham (1907), who also describes how the hydrostatic vertical equilibrium can be used to obtain the water retention characteristic, extends Darcy's law to unsaturated soils, and verbally introduces the principle of mass balance. Buckingham calculated the diffusivity, the hydraulic conductivity, and the water capacity as a function of the water content. Buckingham's inspiration came, on the one hand, from Poiseuille flow in tubes, Fourier's law for flow of heat, and Ohm's law for electric currents, and on the other hand from his thorough familiarity with thermodynamics. Especially the latter enabled him to devise the concept of capillary potential.
Despite all this, Buckingham (1907) did not manage to formulate a clearcut physical-mathematical flow theory that quickly inspired other soil physicists. Gardner (1919) and Gardner and Widtsoe (1921) gave it another try, but got bogged down in details and ended up with something very special. It took a person like Richardson, with wide experience of continuum mechanical theories (fluid mechanics, theory of elasticity) to formulate a clearcut theory in a very direct manner. But, as it has turned out, Richardson's formulation was never noticed by soil physicists.
This completes the discussion of LFR's theory for the vertical movement of liquid water in unsaturated soils and the description of associated experimental methods. LFR in essence formulates the rudiments of the Surface Tension-Viscous Flow (STVF)-theory of Miller and Miller (1956). The equation for movement of water in unsaturated soil of Richardson (1922) is comparable to the well known equation of Richards (1931). Based on this, for several years we have been suggesting that the Richards equation for movement of water in unsaturated soil might also be called the Richardson equation. But a reviewer has pointed out that another British physicist named Owen Richardson (1929 Nobel Prize in Physics) in the early twentieth century studied thermionic emission and that in connection with that there already exists a Richardson equation. This proves once more that naming laws, equations, and principles after persons is risky! A sustainable alternative is to speak from now on of the Richardson-Richards equation.
Next LFR turns his attention to the diffusion of water vapor, the “distillation of vapor” as he calls it. He argues that the vapor density ρv, for which Richardson uses the symbol F, depends on the temperature θ and the volumetric water content w, for liquid water as well as adsorbed water. The “mass of water distilling upwards per unit of time and of horizontal area” he writes as
where D denotes the vapor diffusivity, which LFR calls “the porosity to water vapor” and for which he uses the Coptic letter janja pronounced “janja.” Note again that the coordinate z is positive in the downward direction and that therefore an upward flux is negative. For peat dust, LFR determined the dependence of D on the volumetric water content w. Quite surprisingly, LFR's attention for vapor diffusion was noticed by Danderon (1969). But he merely writes “According to Richardson's experimental data, the coefficient of water vapor diffusion (D) in soil is approximately the same as in motionless air.” To obtain the total water flux, LFR simply adds the fluxes for liquid water and water vapor. Substitution of this total flux in the mass balance gives the final equation for combined flow of water in the liquid and gaseous phases:
In subsection 8/2/12 on page 169 on evaporation from bare soil, Richardson (1922) transforms the gradients of ψ and ρv to gradients of the vapor concentration μ, giving for the total flux Ξsoil of liquid water and water vapor:
Next LFR observes that since the water content w and the humidity μ are functionally related, Equation (8) can be written as:
where
Richardson stopped short of also transforming w on the left hand side of Equation (7) to μ so as to obtain a flow equation fully in terms of μ. But apart from that, the treatment of simultaneous flow of liquid water and water vapor by is quite comparable to that by Philip (1955b). We return to the expression (9) for the total flux Ξsoil in section 3.4 on flux of water from vegetation and from bare soil to the atmosphere.
LFW closes the subsubsection on the motion of water in soils as follows (page 110):
The flow of water across the surface z=0 depends on precipitation and evaporation, and can be calculated at the initial instant, at which w is given, according to the methods of Ch 4/6, Ch 4/8/5, Ch 4/9/6. Then the appropriate distribution of w after δt can be found from (7).
3.3. Transfer of Heat in Soil
In LFR's subsubsection on the motion of heat in soil on pages 110–111 of Richardson (1922), the main novelty is the comprehensibility of the processes considered: conductive transfer and convective heat transfer associated with the flux of liquid water and water vapor. Conductive transfer of heat was intensely studied throughout the nineteenth century, also in soil.
LFR derives the following expression for the time rate of change of the temperature:
where u is the thermal capacity of the soil per unit volume, κ is the thermal conductivity, and 4.7 × 107 in the last term on the right hand side is the specific heat of liquid water in ergs gram−1 degree−1. On the right hand side, the three terms reflect the three causes of the temporal change in temperature θ: (1) the first term reflects the contribution from the divergence of the heat flux by conduction; (2) the second term reflects the contribution from the divergence of the latent heat associated with the vapor flux; (3) the third term reflects the contribution from the divergence of the latent heat associated with the liquid water flux. LFR notes that, in addition to the processes accounted for in Equation (11), “The latent heat of fusion of ice in the soil may be regarded as a very large increase in the thermal capacity in the immediate neighborhood of the freezing point.”
At the end of the discussion of the motion of water and heat, LFR emphasizes that in order to calculate the radiation and the evaporation from bare soil, it is desirable that values of θ and w at the soil surface should be tabulated, rather than mean values for the upper layer in the numerical model, which is 1.7 cm thick; note that in Equation (1) depth z = 1.7 cm corresponds to j = 1.
3.4. Flux of Water From Vegetation and From Bare Soil to the Atmosphere
After having treated the movement of water and transfer of heat in bare soil, Richardson (1922) turned in subsection 4/10/3 (pages 111–114) his attention to earth covered by vegetation. He did not attempt to generalize the partial differential Equations (5) and (7) for movement of water by including a sink term for the uptake of water by plant roots. Instead he seems to tacitly assume that such uptake occurs right at the soil surface and focuses on the water and heat balances at the soil surface and in the plant canopy, making use of earlier work by Brown and Escombe (1900, 1905a,b,c) and Brown and Wilson (1905).
LFR points out that there is not much room for water to accumulate in the air in the stomata and in the canopy space between the leaves, and that therefore a description of the quasi-steady flux of water Ξ in terms resistances in series is appropriate. The equality of the rates at which water evaporates inside the stomates, diffuses out of the stomates, and is carried off into the atmosphere above the plant canopy allows him to express the flux Ξplants from the leaves to the canopy and on to the atmosphere above the plant canopy as:
where the humidity μ is mass of water substance per unit mass of moist atmosphere, A is the stomatal resistance, B is the canopy resistance, and (A+B) is the total resistance. The stomatal resistance A was studied in great detail by Brown and Escombe (1900, 1905a,b,c) and Brown and Wilson (1905). For the canopy resistance LFR relied on his description of turbulent transfer in other parts of his book.
Richardson (1922) formulated in subsubsection 8/2/12 on page 169 a similar model for evaporation from bare soil to the atmosphere. First he writes the expression for the total flux Ξsoil near the soil surface in finite difference form as:
Assuming continuity of the humidity μ and of the flux of water Ξ at the soil surface, and using Equation (12), LFR wrote by analogy with Equation (9) expressions for evaporation Ξsoil from bare soil:
where f(μ) is given by Equation (10) and z11/f(μ) is the analog of the stomatal resistance in Equation (12). Richardson points out that in Equation (14) the gravitational term −k(μ)gz11/f(μ) “corresponds to the potential difference due to a battery in the circuit.”
Richardson points out that in saturated soil dψ(μ)/dμ is very large so that f(μ) defined by Equation (10) is also very large and the soil resistance z11/f(μ) in Equation (14) is very small. Equation (14) then simplifies to:
The main subject of Richardson (1922) is the dynamics of the atmosphere. Equations (12)–(15) allowed him to account for inputs from vegetated soil and bare soil. Richardson's description of the flux of water from vegetation to the atmosphere may well the earliest version of such a model with stomatal and canopy resistances in series. In essence Richardson formulated a forerunner of the Soil-Plant-Atmosphere Continuum (SPAC) initiated by Philip (1957b). Entekhabi (1995) emphasized Richardson's key role in describing the transpirational flux of water vapor.
4. Richardson's Contributions to Numerical Analysis and Their Indirect and Direct Influence on Solutions of the Richards Equation
The experience with the freehand graphical method motivated Richardson to look for other approximate methods of solving partial differential equations. In one paper he explored the use of integration over a surface as a basis for improving a graphic guess (Richardson, 1911). But around the same time he was switching to purely numerical methods. Richardson (1910) distinguished between “marching” and “jury” finite difference methods for solving partial differential equations. “Marching” methods are suitable for parabolic equations, e.g., the diffusion and convection-diffusion equations, and for hyperbolic equations, e.g., the wave equation. Weather prediction also belongs to the “marching” class, “at least if you believe that future weather is determined by present weather together with astronomical events which are foreknown” (Richardson, 1925). “Jury” methods are suitable for elliptic equations, e.g., the Laplace and Poisson equations. The adjective “jury” refers to the requirement that all values together have to satisfy simultaneously everywhere the partial differential equation and the boundary conditions, “just as the verdict has to satisfy all the jurymen seated round the table” (Richardson, 1925). Instead of the adjective “jury,” the adjective “relaxation” is most often used nowadays.
The drainage problem, which Richardson (1908b) treated by a graphical method (see section 2 above), belongs to the “jury” class. The graphic method for solving the Laplace equation became rather popular (e.g., Dachler, 1936; Van Deemter, 1950; Bromhead, 2007), but was eventually superseded by efficient numerical methods. A method competing with Richardson's iterative method was Southwell's relaxation method. For LFR's contact with Southwell see Ashford (1985, pp. 116–117, 244). Southwell's relaxation method figures prominently in mid-twentieth century drainage research (see e.g., Van Deemter, 1950; Childs, 1969, ch. 15). Scarborough (1950) in his chapter XII compares the iterative and relaxation methods.
The fundamental paper on “marching” and “jury” methods (Richardson, 1910) played a key role in later developments in numerical analysis by Liebmann (1918), Shortley and Weller (1938), Fox (1993), and Lynch (2007) and others, this despite the difficulty LFR had to get this paper published. Although in his 1910 paper LFR concentrated on the “jury” method, in paragraph 2.2 he gives as an example the “marching” solution of an initial value problem for the diffusion or heat equation with time and one space dimension. His solution of this problem was later found to be numerically unstable by Crank and Nicolson (1947) and others. Richardson used a central difference in time to construct a method which was explicit in time and gave values at any time level in terms of values at the previous two time levels. To obtain starting values for what he called “the troublesome first step,” he used a stable central difference method with two time levels, which required the solution of a system of linear equations. Richardson carried out calculations only for five time steps up to a dimensionless time of 0.005, not enough to show the instability. Fox (1993) pointed out that the highly successful method of Crank and Nicolson (1947) was identical to the method of Richardson for the first step, but also used Richardson's stable starting method for all later steps. Having devised his stable starting method, Richardson also could then have used it for subsequent steps. Unaware of the instability, he presumably preferred his three step method because it was explicit and did not require the extra calculation involved in solving a system of equations at every time step. The stable method, as used by Richardson for his first step and by Crank and Nicolson for all steps, could justifiably be called the Crank-Nicolson-Richardson method.
Hanks and Bowers (1962) and Whisler and Klute (1965, 1967) used modifications of the Crank-Nicolson method in finite difference solutions of the Richards equation for various cases of infiltration of water into soil. The paper of Hanks and Bowers is an early example of users of the Crank-Nicolson method not actually citing Crank and Nicolson (1947), but Crank (1956), and spelling “Nicolson” incorrectly. Recent Google searches for “Crank Nicolson,” “Crank Nicholson,” “Crank Nicolsen” and “Crank Nicholsen” found 199 k, 520 k, 0.9 k, and 9 k results respectively, compared to a total of 1,567 citations of Crank and Nic(h)olson (1947) in Web of Science as of February 2018.
The method of deferred approach to the limit or h2-extrapolation is another important contribution by Richardson (1927). The central difference approximation to the derivatives used by Richardson implies that the difference of the discrete and continuous solutions is a power series in h2, h being the mesh size. Using only the first term of the series, a better approximate solution can be obtained by solving the discrete problem for two values of h and then eliminate the h2 contribution. Philip devised semi-analytical, semi-numerical solutions of the nonlinear diffusion equation (Philip, 1955a) and of the Richards equation (Philip, 1957a), and used the Richardson (1927) h2-extrapolation to speed the convergence.
5. Concluding Remarks
The intent of our paper is to highlight the contributions by Lewis Fry Richardson to soil science and hydrology. In the past these contributions have received hardly any attention. Ashford (1985) wrote a biography for the general reader, emphasizing the life and connections of LFR, rather than the details of his research. In the Preface he wrote:
As the biography is intended for a wide variety of readers, I have refrained from entering into highly technical details and, to the extent possible, from using mathematics. My aim is not to explain to professional meteorologists the significance of Richardson's contributions to meteorology, nor to psychologists the way in which he helped to advance their science.
In his fascinating book on numerical weather prediction, Lynch (2006) on page 30 did take notice of the topics discussed in section 3:
Finally, Richardson discusses the interaction between the atmosphere and the sea and land surfaces beneath it. He suggests that climatological sea temperatures may suffice, but also discusses how the sea surface temperature might be predicted. He considers heat and moisture transports within the soil and discusses at some length the influence of vegetation: “Leaves, when present, exert a paramount influence on the interchanges of moisture and heat” (Richardson, 1922, p. 111). Clearly, Richardson is thinking far beyond short-range forecasting here, and has entered the realm of climate modeling.
Richardson was able to pioneer all aspects of a problem: formulation of a model, graphical and numerical analysis based on the model, suggestion and to some extent performing related experiments (Ashford et al., 1993a). The drainage problem treated in Chapter 2 is not quite as important than the treatment of the soil-plant-atmosphere continuum in Chapter 3. Nevertheless, Chapter 2 does reveal the origin of some of the concepts used in Chapter 3. Comparing the 1908 drainage paper with the treatment of the soil-plant-atmosphere-continuum in the 1922 book shows that LFR in the intervening 15 years became an experienced writer.
Author Contributions
PR and JK jointly planned the paper. JK made the calculation by a modern variational method shown in Figure 4B. PR wrote the first draft and both authors contributed to successive revisions.
Funding
This paper arose from the authors' interest in the history of science.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
PR likes to acknowledge the help from librarians at the University of Groningen in The Netherlands. See further the credits given in the legends of the Figures. Suggestions by Frontiers Editor Philippe Baveye and two reviewers led to numerous improvements in the manuscript.
References
Ashford, O. M. (1985). Prophet or Professor? The Life and Work of Lewis Fry Richardson. Bristol: Adam Hilger.
Ashford, O. M., Charnock, H., Drazin, P. G., Hunt, J. C. R., Smoker, P., and Sutherland, I. (eds.). (1993a). Collected Papers, Volume 1: Meteorology and Numerical Analysis. Cambridge: Cambridge University Press.
Ashford, O. M., Charnock, H., Drazin, P. G., Hunt, J. C. R., Smoker, P., and Sutherland, I. (eds.). (1993b). Collected Papers, Volume 2: Quantitative Psychology and Studies of Conflict. Cambridge: Cambridge University Press.
Berreby, D. (2014). Lewis Fry Richardson's Weather Forecasts Changed the World. But Could His Predictions of War Do the Same? The Independent Online. Available online at: http://www.independent.co.uk/news/world/lewis-fry-richardsons-weather-forecasts-changed-the-world-but-could-his-predictions-of-war-do-the-9679295.html, http://nautil.us/issue/15/turbulence/cloudy-with-a-chance-of-war (Accessed August 19, 2014).
Boussinesq, J. (1904). Recherches théoriques sur l'écoulement des nappes d'eau infiltrées dans le sol et sur le débit des sources. J. Math. Pures Appl. 10, 5–78.
Briggs, L. J. (1897). The Mechanics of Soil Moisture. Washington, DC: Bulletin 10, USDA Bureau of Soils.
Bromhead, E. N. (2007). Flow nets and textbooks. Geotech. Eng. 160, 203–207. doi: 10.1680/geng.2007.160.4.203
Brown, H. T., and Escombe, F. (1900). Static diffusion of gases and liquids in relation to the assimilation of carbon and translocation in plants. Philos. Trans. R. Soc. Lond. Ser. B 193, 223–291. doi: 10.1098/rstb.1900.0014
Brown, H. T., and Escombe, F. (1905a). Researches on some of the physiological processes of green leaves, with special reference to the interchange of energy between the leaf and its surroundings. Proc. R. Soc. Lond. B 76, 29–111. doi: 10.1098/rspb.1905.0002
Brown, H. T., and Escombe, F. (1905b). On a new method for the determination of atmospheric carbon dioxide, based on its absorption by a free surface of a solution of caustic alkali. Proc. R. Soc. Lond. B 76, 112–117. doi: 10.1098/rspb.1905.0003
Brown, H. T., and Escombe, F. (1905c). On the variations in the amount of carbon dioxide in the air of Kew in the years 1898-1901. Proc. R. Soc. Lond. B 76, 118–121. doi: 10.1098/rspb.1905.0004
Brown, H. T., and Wilson, W. E. (1905). On the thermal emissivity of a green leaf in still and moving air. Proc. R. Soc. Lond. B 76, 122–137. doi: 10.1098/rspb.1905.0005
Buckingham, E. (1907). Studies on the Movement of Soil Moisture. Washington, DC: Bulletin 38, USDA Bureau of Soils.
Charnock, H. (1993). “Meteorology,” in Collected Papers of Lewis Fry Richardson. Vol 1, Meteorology and Numerical Analysis, ed P. G. Drazin (Cambridge: Cambridge University Press), 29–36.
Crank, J., and Nicolson, P. (1947). A practical method for numerical evaluation of solutions of partial differential equations of the heat conduction type. Proc. Camb. Philos. Soc. 43, 50–67. doi: 10.1017/S0305004100023197
Danderon, Z. D. (1969). Experimental determination of the coefficient of water vapour diffusion in soil. Pochvovedeniye 10, 69–75.
Darcy, H. (1856). Les Fontaines Publiques de la Ville de Dijon. APPENDICE. - NOTE D. Détermination des Lois d'Écoulement de l'Eau à Travers le Sable. [The Public Fountains of the City of Dijon. APPENDIX. - NOTE D. Determination of the laws of water flow through sand.] Paris: Dalmont.
Drazin, P. G. (1986). Review of Ashford (1985). Brit. J. Hist. Sci. 19:217. doi: 10.1017/S0007087400023074
Drazin, P. G. (ed.). (1993). “Fractals,” in Collected Papers of Lewis Fry Richardson, Vol. 1, Meteorology and Numerical Analysis (Cambridge: Cambridge University Press), 45.
Entekhabi, D. (1995). Recent advances in land-atmosphere interaction research. Rev. Geophys. 33, 995–1003. doi: 10.1029/95RG01163
Forchheimer, P. (1886). Über die Ergiebigkeit von Brunnen-Anlagen und Sickerschlitzen. Z. Architekt. Ing.-Ver. Hannover 32, 539–563.
Fox, L. (1993). “Numerical analysis,” in Collected Papers of Lewis Fry Richardson. Vol 1, Meteorology and Numerical Analysis, ed P. G. Drazin (Cambridge: Cambridge University Press), 36–44.
Gardner, W. (1919). The movement of moisture in soil by capillarity. Soil Sci. 7, 313–317. doi: 10.1097/00010694-191904000-00008
Gardner, W., and Widtsoe, J. A. (1921). The movement of soil moisture. Soil Sci. 11, 215–232. doi: 10.1097/00010694-192103000-00003
Hanks, R. J., and Bowers, S. A. (1962). Numerical solution of the moisture flow equation for infiltration into layered soils. Soil Sci. Soc. Amer. Proc. 26, 530–534.
Hunt, J. C. R. (1993). “A general introduction to the life and work of L. F. Richardson,” in Collected Papers of Lewis Fry Richardson, Vol 1, Meteorology and Numerical Analysis, ed P. G. Drazin (Cambridge: Cambridge University Press), 1–27.
Hunt, J. C. R. (1998). Lewis Fry Richardson and his contributions to mathematics, meteorology, and models of conflict. Annu. Rev. Fluid Mech. 30, xiii–xxxvi. doi: 10.1146/annurev.fluid.30.1.0
King, F. H. (1899). “Principles and conditions of the movements of ground waters,” in 19th Annual Report, Part II, United States Geological Survey (Washington, DC: Government Printing Office), 59–294.
King, F. H. (1907). Irrigation and Drainage. Principles and Practice of Their Cultural Phases, 5th Edn., Reprinted with Corrections from the 1889 First Edn. New York, NY: Macmillan.
Knight, J. H. (1984). “Numerical solution of a free surface drainage problem using a variational inequality method,” in Computational Techniques and Applications: CTAC-83, eds J. Noye and C. Fletcher (Amsterdam: North-Holland), 597–603.
Landa, E. R., and Nimmo, J. R. (2003). The life and scientific contributions of Lyman. J. Briggs. Soil Sci. Soc. Am. J. 67, 681–693. doi: 10.2136/sssaj2003.0681
Liebmann, H. (1918). Die angenährte Ermittelung harmonischer Functionen und konformer Abbildungen. Sitzungsberichte der Mathematisch-NaturwissenschaftlichenKlasse der Bayerischen Akademie der Wissenschaften zu München, 385–416.
Lynch, P. (2006). The Emergence of Numerical Weather Prediction: Richardson's Dream. Cambridge: Cambridge University Press.
Lynch, P. (2007). The origins of computer weather prediction and climate modeling. J. Comput. Phys. 227, 3431–3444. doi: 10.1016/j.jcp.2007.02.034
McAdie, A. (1923). Weather-forcasting reduced to a science; review of Richardson (1922). Geograph. Rev. 13, 324–325. doi: 10.2307/208464
Miller, E. E., and Miller, R. D. (1956). Physical theory of capillary flow phenomena. J. Appl. Phys. 27, 324–332. doi: 10.1063/1.1722370
Pennink, J. M. K. (1905). Over de beweging van grondwater [About the movement of ground water]. De Ingenieur 20, 482–492.
Philip, J. R. (1955a) Numerical solution of equations of the diffusion type with diffusivity concentration-dependent. Trans. Faraday Soc. 51, 885–892. doi: 10.1039/tf9555100885
Philip, J. R. (1955b). The concept of diffusion applied to soil water. Proc. Natl. Acad. Sci. India Sect. A 24, 93–104.
Philip, J. R. (1957a). Numerical solution of equations of the diffusion type with diffusivity concentration-dependent, II. Aust. J. Phys. 10, 29–42. doi: 10.1071/PH570029
Philip, J. R. (1957b). “The physical principles of soil water movement during the irrigation cycle,” in Proceedings of the International Congress of Irrigation and Drainage, 3rd, Vol. 8 (San Francisco, CA), 125–153.
Platzman, G. W. (1967). A retrospective view of Richardson's book on weather prediction. Bull. Am. Meteorol. Soc. 48, 514–550.
Richards, L. A. (1931). Capillary conduction of liquids through porous mediums. Physics 1, 318–333. doi: 10.1063/1.1745010
Richardson, L. F. (1908a). A freehand graphic way of determining stream lines and equipotentials. Proc. Phys. Soc. Lond. 21, 88–124; Also Philos. Mag. Ser. 6, 15 237–269; Also: in Collected Papers of Lewis Fry Richardson. Vol. 1, Meteorology and Numerical Analysis, ed P. G. Drazin, 55–93.
Richardson, L. F. (1908b). The lines of flow of water in saturated soils: explaining a simple method for determining the relation between the distance apart of ditches and the height to which the saturating water will rise with a given rainfall, special reference being made to the draining of peat-mosses. Scient. Proc. R. Dubl. Soc. 11, 295–316; Also: in Collected Papers of Lewis Fry Richardson. Vol. 1, Meteorology and Numerical Analysis, ed P. G. Drazin, 95–118.
Richardson, L. F. (1910). The approximate arithmetical solution by finite differences of physical problems involving differential equations, with an application to the stresses in a masonry dam. Philos. Trans. R. Soc. Lond. Ser. A 210, 307–357; Also: in Collected Papers of Lewis Fry Richardson. Vol. 1, Meteorology and Numerical Analysis, ed P. G. Drazin, 119–171.
Richardson, L. F. (1911). The approximate solution of various boundary problems by surface integration combined with freehand graphs. Proc. Phys. Soc. Lond. 23, 75–85; Also: in Collected Papers of Lewis Fry Richardson. Vol. 1, Meteorology and Numerical Analysis, ed P. G. Drazin, 173–186.
Richardson, L. F. (1919). “Mathematical psychology of war,” in Collected Papers of Lewis Fry Richardson. Vol 1, Meteorology and Numerical Analysis, ed P. G. Drazin (Cambridge: Cambridge University Press), 61–100.
Richardson, L. F. (1922). Weather Prediction by Numerical Process. Cambridge: Cambridge University Press. (Reprinted by Dover Publications, New york, 1965, with a new introduction by S. Chapman, xvi+236; 2d Edn. by Cambridge University Press, 2007, with a new introduction by P. Lynch.).
Richardson, L. F. (1925). How to solve differential equations approximately by arithmetic. Math. Gazette 12, 415–421; Also: in Collected Papers of Lewis Fry Richardson. Vol. 1, Meteorology and Numerical Analysis, ed P. G. Drazin, 511–519.
Richardson, L. F. (1927). The deferred approach to the limit. Part I Single Lattice. Philos. Trans. R. Soc. Lond. Ser. A 226, 299–349; Also: in Collected Papers of Lewis Fry Richardson. Vol. 1, Meteorology and Numerical Analysis, ed P. G. Drazin, 625–677.
Richardson, L. F. (1949). Meteorological publications by L.F. Richardson as they appear to him in October 1948. Weather Lond. 4, 6–9; Also: in Collected Papers of Lewis Fry Richardson. Vol. 1, Meteorology and Numerical Analysis, ed P. G. Drazin, 893-898.
Scarborough, J. B. (1950). Numerical Mathematical Analysis. 2nd Edn. Baltimore: The Johns Hopkins Press.
Shortley, G. H., and Weller, R. (1938). The numerical solution of Laplace's equation. J. Appl. Phys. 9, 334–344.
Slichter, C. S. (1899). “Theoretical investigation of the motion of ground waters,” in 19th Annual Report, Part II, United States Geological Survey (Washington, DC: Government Printing Office), 295–384.
Tanner, C. B., and Simonson, R. W. (1993). Franklin Hiram King - pioneer scientist. Soil Sci. Soc. Amer. J. 57, 286–292.
Van Deemter, J. J. (1950). Theoretische en numerieke behandeling van ontwaterings- en infiltratie-stromingsproblemen (Theoretical and numerical treatment of flow problems connected with drainage and irrigation). Bijdragen tot de kennis van enige natuurkundige grootheden van de grond No. 11. Verslagen van Landbouwkundige Onderzoekingen 56.7. VIII+67.
Van der Hoek, J., Barnes, C. J., and Knight, J. H. (1984). A free surface problem arising in the drainage of a uniformly irrigated field: existence and uniqueness results. J. Aust. Math. Soc. Ser. A 36, 389–403.
Whisler, F. D., and Klute, A. (1965). The numerical analysis of infiltration, considering hysteresis, into a vertical soil column at equilibrium under gravity. Soil Sci. Soc. Amer. Proc. 29, 489–494.
Whisler, F. D., and Klute, A. (1967). Rainfall infiltration into a vertical soil column. Trans. Amer. Soc. Agr. Engs. 10, 391–395.
Keywords: water movement, saturated soils, unsaturated soils, numerical analysis, history of science
Citation: Raats PAC and Knight JH (2018) The Contributions of Lewis Fry Richardson to Drainage Theory, Soil Physics, and the Soil-Plant-Atmosphere Continuum. Front. Environ. Sci. 6:13. doi: 10.3389/fenvs.2018.00013
Received: 29 December 2017; Accepted: 02 March 2018;
Published: 04 April 2018.
Edited by:
Philippe C. Baveye, AgroParisTech Institut des Sciences et Industries du Vivant et de L'environnement, FranceReviewed by:
Wilfred Otten, Cranfield University, United KingdomMilena Cislerova, Czech Technical University, Czechia
Copyright © 2018 Raats and Knight. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Peter A. C. Raats, cGFjLnJhYXRzQGhvbWUubmw=
 Peter A. C. Raats
Peter A. C. Raats John H. Knight
John H. Knight