- 1Institut National de la Recherche Scientifique, Eau-Terre-Environnement, Quebec City, QC, Canada
- 2Natural Resources Canada, Geological Survey of Canada, Quebec City, QC, Canada
Hydrogeophysics is increasingly used to understand groundwater flow and contaminant transport, essential basis for groundwater resources forecast, management, and remediation. It has proven its ability to improve the characterization of the hydraulic conductivity (K) when used along with hydrogeological knowledge. Geophysical tools and methods provide high density information of the spatial distribution of physical properties in the ground at relatively low costs and in a non-destructive manner. Amongst them, the Electrical Resistivity Tomography (ERT) has been widely used for its high spatial coverage and for the strong theoretical links between electrical resistivity (ρ) and key hydrogeological parameters, such as K. Historically, ERT data processing was based on isotropic hypothesis. However, the unconsolidated aquifers in Canada reveal in most cases a strong anisotropic behavior for K both with in situ or laboratory measurements. Recently, electrical anisotropy has been considered model-wise, but it is seldom considered as an interpretation tool or in the characterization process of the anisotropy of K. In order to evaluate the potential of ERT to assess the anisotropy of electrical resistivity, we developed a forward and inverse modeling code. These codes have been validated and tested on a realistic synthetic case reproducing the behavior of a real aquifer extensively characterized, the site of Saint-Lambert-de-Lauzon in Quebec (Canada). On this site, innovative in situ hydraulic tomography has revealed a strong anisotropy, with up to three orders of magnitude between horizontal and vertical K components. In order to confirm the link between in situ K- and ρ-anisotropies, an ERT survey has been performed, using the same wells as for the hydraulic tomography. The inversion confirms a strong link between K- and ρ-anisotropies. It demonstrates the suitability of the anisotropic ERT approach coupled with well measurements to provide better estimates of K and its anisotropy at the scale of a site.
1. Introduction
Understanding groundwater flow and contaminant transport in the subsurface for water management and aquifer remediation generally requires a good knowledge of the spatial distribution of hydraulic properties within the aquifers. The hydraulic conductivity (K) is a key parameter to assess as it affects both the direction and velocity of flow and contaminant in aquifers. K can also vary over several orders of magnitude within a same geological unit, which highlights the importance of having accurate high-resolution and high-coverage estimates to reduce errors in groundwater flow and mass transport (de Marsily et al., 2005) and improve groundwater management. While several methods have shown their potential to estimate K at different scales (Butler, 2005), few have been focused on the characterization of its anisotropy that can greatly affect the outcomes of different hydrogeological in situ problems, such as groundwater recharge (e.g., Hart et al., 2006) well capture zone (e.g., Barry et al., 2009), and spreading of contaminant plumes (e.g., Falta et al., 2005).
Indeed, K-anisotropy can be obtained from laboratory permeameters on sediment or rock samples collected in the field (Wenzel and Fishel, 1942). However, the difficulties in the experimental procedures related to sample collection and manipulation may restrict reliable estimations of K-anisotropy for certain kinds of materials. Moreover, permeameter estimates may require an up-scaling to field conditions to be representative. In order to overcome this burdens, several authors have proposed different hydraulic tests in wells to estimate K-anisotropy, such as the dipole-flow test using in one well (Kabala, 1993; Zlotnik and Ledder, 1996; Xiang and Kabala, 1997; Zlotnik and Zurbuchen, 1998; Hvilshøj et al., 2000; Sutton et al., 2000; Zlotnik et al., 2001) or two wells (Goltz et al., 2008), the single-well vertical interference test (Burns Jr et al., 1969; Hirasaki et al., 1974; Onur et al., 2002; Sheng, 2009; Paradis and Lefebvre, 2013), and hydraulic tomography (Paradis et al., 2015a, 2016a,b).
While previous hydraulic tests were shown to provide invaluable estimates of K-anisotropy in real field conditions, these methods are time consuming to operate and can thus only provide very local information. In this study, we propose using geophysical data to complement hydraulic tests as geophysical methods can provide broad pictures of the subsurface in a considerably shorter amount of time than hydraulic methods. Electrical methods, in particular direct current (DC) methods, are frequently used to infer porosity and K (Archie, 1942; Lesmes and Friedman, 2005). However, only a few studies have been done to study the anisotropy of the resistivity of unconsolidated sediments. Anisotropy of electrical conductivity (ρ) is a well-known phenomenon (Maillet, 1947) but its accurate in situ estimation has only been studied recently (Greenhalgh et al., 2010; Kenkel and Kemna, 2016; Gernez et al., 2018). Moreover, there is a theoretical equivalence between K-anisotropy and ρ-anisotropy in unconsolidated sediments were the electric current flows in the conductive saturated pores (Hubbard and Rubin, 2005). Recently, laboratory investigations have demonstrated strong similarities between ρ- and K-anisotropies on core samples (Adams et al., 2016). In addition, recent field works have shown that taking into account ρ-anisotropy in DC surveys leads to more accurate estimations of both ρ values and structures (Pekşen and Yas, 2018), and have shown reasonable estimates of hydraulic anisotropy in slightly anisotropic aquifer systems (Yeboah-Forson and Whitman, 2014).
The objective of this paper is to demonstrate the ability of DC methods to quantify ρ-anisotropy and to illustrate how it compares with K-anisotropy in a real case study. After introducing the study area (section 2) and presenting theoretical considerations related to ρ-anisotropy (section 3), we provide methodological insights, through a synthetic case, related to DC data acquisition to ascertain the presence of ρ-anisotropy (section 4). Then, the methodology is applied for a real case study known to be highly heterogeneous, and ρ-anisotropy estimated through anisotropic inversion is compared to K-anisotropy obtained with hydraulic tests at the study site to strengthen the reliability of the proposed approach (section 5). This study exposes the capacity of DC surveys to improve hydrogeological characterization.
2. Study Area and Evidences of Anisotropic Conditions
The study area is located in Saint-Lambert-de-Lauzon (SLdL), 30 km south of Quebec City, Canada (Figure 1). The SLdL study area is a 12 km2 sub-watershed surrounding a decommissioned sanitary landfill site in an unconfined granular aquifer. The surficial sediments composing the aquifer consists primarily of Late Quaternary sandy and silty sediments that were deposited in the receding Champlain Sea, which was an arm of the Atlantic Ocean that invaded the St-Lawrence Valley at the time of the last deglaciation (Bolduc, 2003). Deposition of the Saint-Lambert site was controlled mainly by longshore currents that redeposited in littoral and sublittoral settings that supplied the Chaudière River paleodelta. This geological depositional environment leads thus to sediment size ranging from fine sand to very fine silt with poor to very poor grain-size sorting. Furthermore, this environment shows minor proportions of clay (generally < 20%). Clay in major proportions (>50%) is only present below the cross-section studied. The resulting superposition of finely layered sand and silt sediments create very heterogeneous distribution of sediments at centimetric to decametric scales along with more gradual lateral transitions in these littoral and sublittoral sediments as a result of changing energy levels along the Champlain Sea shorelines. The depth of the granular aquifer varies in depth between 0 and 22 m, the water table is generally within 2 m from the surface (Paradis et al., 2014; Tremblay et al., 2014).
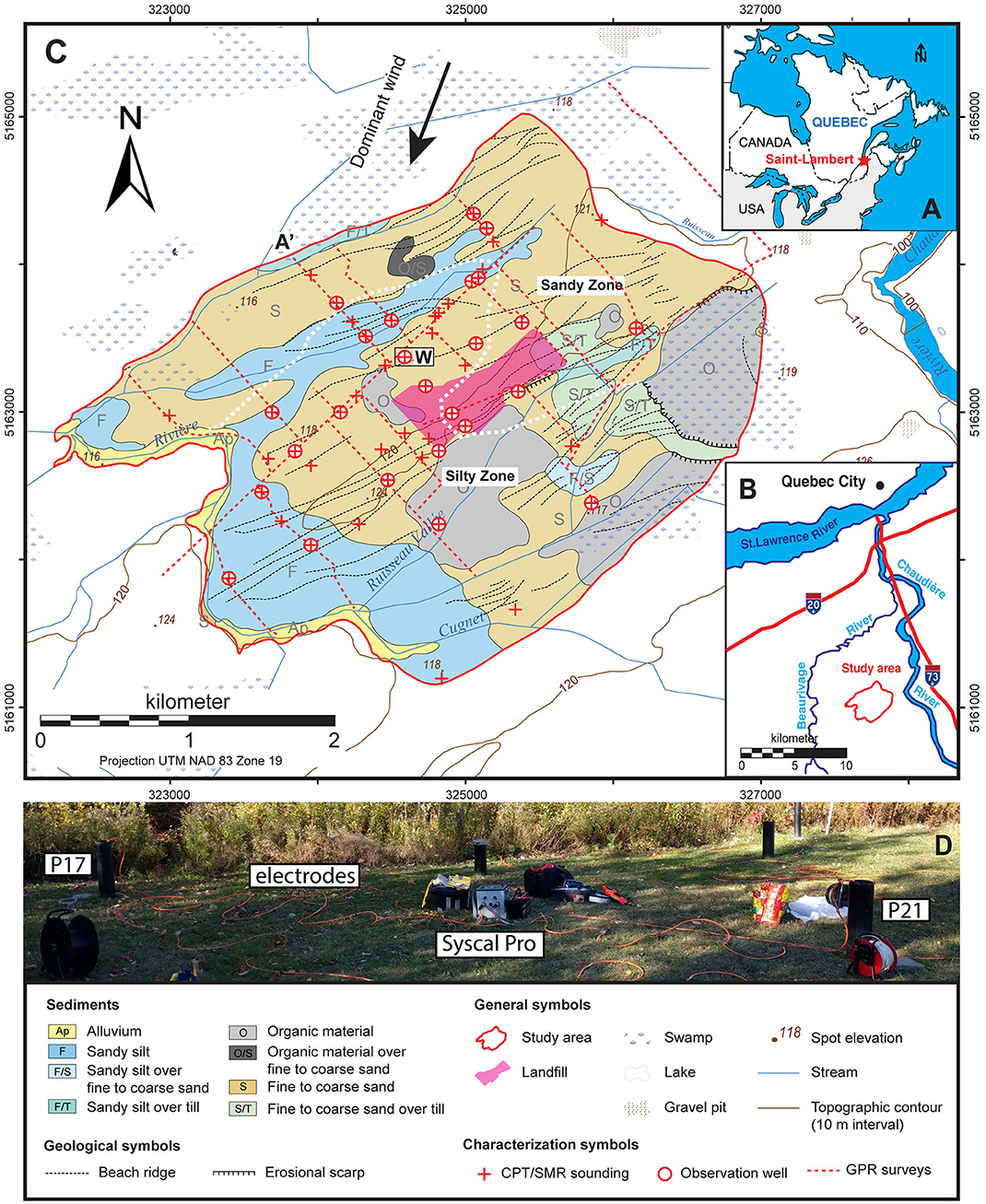
Figure 1. Saint-Lambert-de-Lauzon (SLdL) study area. It is located (A) in Québec, Canada, (B) 30 km south of Québec City between to the Chaudière and Beaurivage rivers. (C) Geology and characterization details of the study area. (D) Anisotropic hydraulic and electrical tomography site corresponding to the “W” on (C). ERT acquisition is done using an IRIS Syscal Pro system. Nine and Eight electrodes are, respectively, immersed in P17 and P21. Seventeen electrodes are planted between P17 and P21. P17 and P21 are separated by 8 m, electrodes separation is 1 m inside the wells and 0.5 m at the surface. Adapted from Paradis et al. (2015b).
This site has been extensively characterized by previous studies using different techniques, such as Ground Penetrating Radar (GPR) and resistivity surveys, Cone Penetrometer Test—Soil Moisture Resistivity soundings (CPT/SMR), hydraulic tests in wells and logging (Paradis et al., 2014; Tremblay et al., 2014). These data allowed to obtain valuable information on the structure of the aquifer system (aquifer and aquitard layers) including information on its heterogeneity. Particularly, several observations suggest that the heterogeneous nature of the sediments at a fine scale may induce anisotropy at larger scale posing challenges to the interpretation of flow and transport processes in this environment. Anisotropy can be due to the microscopic scale organization of the minerals (micro or intrinsic anisotropy, e.g., crystals ordered structure or oblong grains) or, as is the case here, to the macroscopic structural elements of the ground (macro or extrinsic anisotropy, e.g., fractures or alternating heterogeneous beds). First, the comparison of 59 vertical hydraulic conductivity (KV) estimates made on 15 cm undisturbed sediment samples with a laboratory permeameter to horizontal hydraulic conductivity (KH) values obtained from high-resolution multi-level slug tests on similar intervals reveals a strong K-anisotropy even at this small scale. K-anisotropy (or the ratio of KH on KV, KH/KV) was indeed up to two orders of magnitude (Paradis and Lefebvre, 2013). Then, numerical inversion of vertical interference slug tests and hydraulic tomography experiments indicate that K-anisotropy should be considered to match hydraulic responses measured in wells (Paradis and Lefebvre, 2013; Paradis et al., 2016a). For a 60 cm vertical resolution of the numerical grid, KH/KV values ranged from near isotropy (1) to more than 100. Moreover, comparison of high-resolution cone-based ρ measurements (SMR probe) with collocated estimates of the ρ computed with surface-based surveys (ERT) revealed a bias between the two data sets (Ruggeri et al., 2014). For instance, the magnitudes of the SMR probe data are generally higher than those of the ERT surveys. This suggests that given the SMR probe sense essentially the horizontal component of ρ due to the configuration of its electrodes (spaced vertically by 9 cm), lower ρ values from ERT surveys are the results of the influence of the ρ-anisotropy induced by the heterogeneous nature of the sediments (section 3.2.2). Finally, those evidences motivate the need to develop a geophysical approach able to handle this anisotropy to provide insights about K-anisotropy in order to better characterize aquifer systems for groundwater flow and contaminant transport studies.
3. Electrical Resistivity Anisotropy
3.1. Theoretical Considerations and Definitions
Electrical anisotropy refers to the directional dependence of electrical conductivity or resistivity which results in the directional dependence of the measured potential fields. This means that the current can preferentially flow in certain directions compared to others. Ohm's law establishes the relationship between an injected electric current in the ground and the induced potential field (Dey and Morrison, 1979). In order to take into account the 2D electrical anisotropy, the scalar conductivity σ in Ohm's law is replaced by the conductivity tensor (or its inverse, the resistivity tensor ), with σH and σV being the conductivity values in the horizontal and vertical directions, respectively (Greenhalgh et al., 2009). Anisotropic Poisson's equation has the following expression in the 2.5D case, i.e., 2-D resistivity structure (plane invariance) and 3-D current flow (Zhou et al., 2009):
where is the potential in the frequential domain, ky is the wavenumber, r(x, z) are the coordinates in the computational domain or on its boundaries, I is the current source intensity located at rs(xs, zs) and δ is the Dirac function. The coefficient of anisotropy is defined as : anisotropy increases as λ departs from the value of 1 (λ = 1 corresponds to isotropy). In this study, we will consider an H/V anisotropy. More complex geometries are handleable by the numerical modeling tool we developed to this end (AIM4RES), but they will not be investigated in this study.
3.2. Diagnosis of Electrical Anisotropy
The next sections aim at demonstrating the effects of electrical anisotropy on the interpretation of ERT data using isotropic ERT inversion. We take advantage of three particular effects to propose an electrical diagnosis to detect anisotropy on measured electric potentials. These effects are observable without the need for a complete characterization study, both in terms of field and numerical resources.
3.2.1. Importance of Data Acquisition Protocols
The measured electric potential field is linked to the amount of electric current passing through the different heterogeneous part of the ground. Hence, in the case of surface ERT measurements, a thin conductive anisotropic layer and a thicker less conductive isotropic layer can produce the same electric potential differences (equivalence principle, Maillet, 1947). In other words, it is impossible to distinguish between isotropic layer response from anisotropic layer response using surface ERT data. Consequently, isotropic ERT inversion (Loke, 2001; Bouchedda, 2010) of surface anisotropic data always converge to an equivalent resistivity model which is not representative of the true electrical state of the ground, leading to erroneous resistivity model of the earth. To overcome this problem, anisotropic ERT acquisition and inversion should be used. To address the data directionnality problem, we unavoidably need borehole electrodes along with surface electrodes. In that way, anisotropic ERT inversion requires an optimization of the acquisition protocol, in order to converge toward the true solution.
Nevertheless, in presence of anisotropy, isotropic inversion of ERT directional data leads to unrealistic solutions. It is explained by the fact that there is no physical isotropic solution fitting both surface and inhole data. To demonstrate this effect, two data experiments were simulated using only surface electrodes in the first one and both borehole and surface electrodes in the second one. The resistivity model consists of two horizontally anisotropic layers (Figure 2A). The first layer has a thickness h = 4 m with ρH = 100 Ω.m and ρV = 400 Ω.m. The second layer is a semi-infinite space with ρH = 10 Ω.m and ρV = 40 Ω.m. For the whole section, the anisotropy coefficient λ is 2.
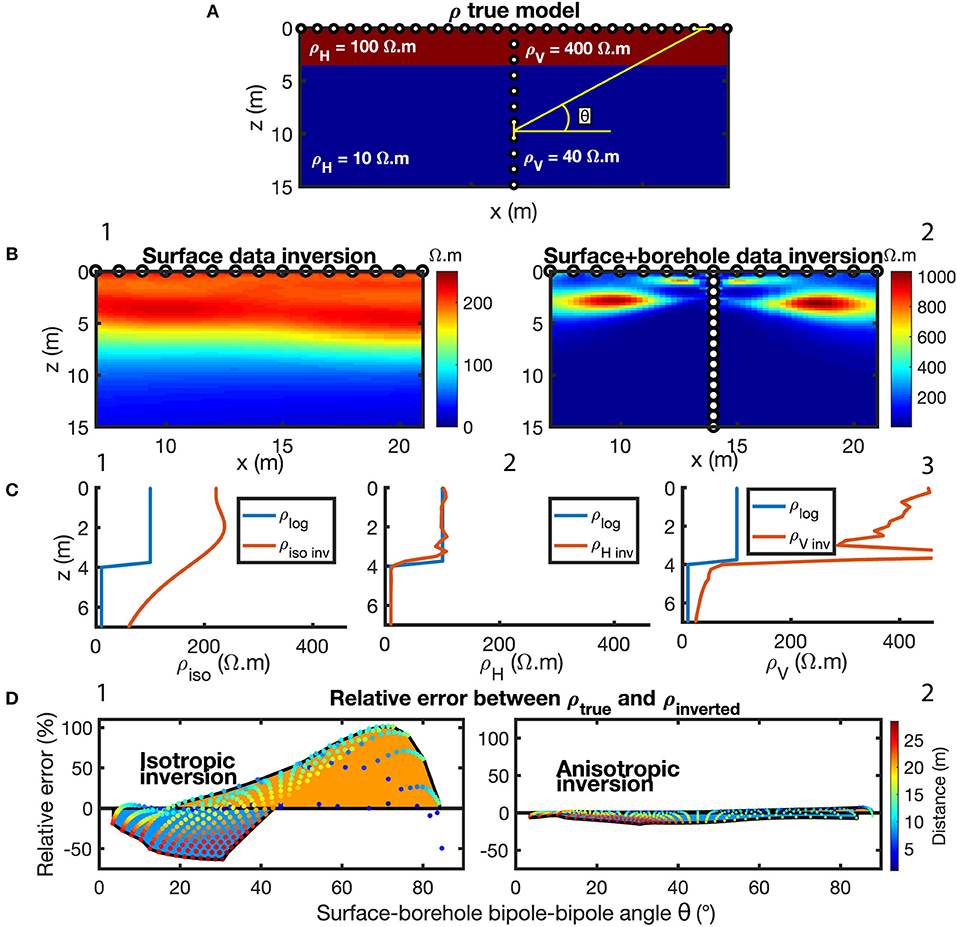
Figure 2. (A) Synthetic model, constituted of an anisotropic layer over an anisotropic semi-infinite space. Upper layer: ρH = 100 Ω.m and ρV = 400 Ω.m. Semi-infinite space: ρH = 10 Ω.m and ρV = 40 Ω.m. λ = 2 for the whole model. Electrodes (white dots) are located at the surface and in-hole borehole at x = 14m. In yellow is shown an example of surface-borehole measure angle (D). (B) (section 3.2.1) Isotropic inversions of potentials acquired using (B.1) only surface electrodes and (B.2) surface and borehole electrodes (borehole at x = 14 m). (C) (section 3.2.2) Comparison between logged (ρlog, blue curve) and inverted (ρinv, red curves) resistivities: (C.1) isotropically inverted resistivity. (C.2) ρH from inversion vs. ρlog. (C.3) ρV from inversion vs. ρlog (borehole at x = 20 m). The logged resistivity is the direct resistivity measurement at x = 20 m, therefore the blue curve is the same for all (C.1–3) graphs. (D) (section 3.2.3) Relative error behavior as a function of the measure angle θ. The points are the error values, their color represents the associated dipole-dipole distance. Orange area represents a positive error, blue area represents a negative error. (D.1) Relative error from an isotropic inversion of data acquired on an anisotropic model, displaying a sigmoid shape. (D.2) Relative error from an anisotropic inversion of data acquired on an anisotropic model, relative error is close to zero and is not angle dependant (borehole at x = 25 m).
The first experiment was performed using only surface Wenner array data. We assumed the convergence is reached as the RMSE values are very low (0.0026%), but the inverted model (Figure 2B.1) is not consistent with the true resistivity model (Figure 2A) neither in terms of amplitude of the resistivity nor in terms of geology. According to the theory, the resistivity of the upper layer appears to be m and the resistivity of the semi-infinite space appears to be m. In addition, the thickness of the upper layer appears to be λ·h = 8m.
In addition to the previous Wenner surface array, a dipole-dipole array in the borehole and a mixed surface-borehole array were added to the acquisition protocol in the second experiment. The isotropic ERT inversion result of these data sets are presented in the Figure 2B.2. It can be clearly seen that isotropic inversion of directional ERT data leads to unrealistic solutions. Furthermore, the final misfit between measured data and predicted data is high (RMSE = 22.1%) for isotropic inversion in comparison to anisotropic inversion (0.002%), showing that directional data are unable to fit an isotropic solution. This can be used as an evidence of electrical anisotropy.
3.2.2. Effect of Anisotropy on ERT Measurements
In the case of horizontally anisotropic resistivity model, it has been pointed out by Maillet (1947) and Keller and Frischknecht (1966) that the measurements made in the horizontal direction are equal to geometric mean of horizontal and vertical resistivity components, while the measurements made in the vertical direction are equal to the horizontal resistivity components. This is the paradox of electrical resistivity anisotropy: measurements along vertical profiles in the case of layered anisotropic model are sensitive to horizontal component as shown in our synthetic model example. For formal demonstration please see Lüling (2013). Indeed, electrical resistivity logs can be used as in situ measurements of the horizontal resistivity ρH that can be introduced as a constraint in the inversion system or employed in combination of surface ERT data to diagnose the anisotropy.
In our case, the electrical resistivity logging was measured using a CPT-SMR instrument which does not require a well installation, simplifying its implementation. The probe is 5 cm thick and 9 cm long. Note that the small probe diameter and the small electrodes separation make the hole effect negligible and the measured resistivity is only sensitive to ρH.
In order to demonstrate the effectiveness of resistivity well logs as anisotropy diagnosis tool, let us compare well logs resistivities and estimated resistivities from isotropic ERT inversion of surface data obtained on an anisotropic resistivity models. When isotropic ground is considered, both resistivities are expected to be similar. For horizontally anisotropic ground (as in SLdL), well log resistivities are equal to horizontal resistivity components whereas isotropic ERT inversion returns an equivalent resistivity model which combines both horizontal and vertical resistivity components (equivalence and paradox effects). In other words, the difference between the two resistivities can be very important depending on the value of anisotropy coefficient. Consequently, any difference between the two resistivities is an indication of the presence of anisotropy.
To illustrate the anisotropy diagnosis using synthetic model let consider the previous two layered anisotropic model (Figure 2A). Figure 2C.1 shows the comparison between the electrical resistivity logging (blue curve, e.g., obtained with a CPT-SMR logging at x = 14 m) and the corresponding resistivity (red curve) estimated using the isotropic ERT inversion of surface data. Both curves depart from each other, indicating the presence of anisotropy. Figures 2C.2,C.3 show the comparison between the same electrical resistivity logging and collocated horizontal and vertical resistivities obtained from anisotropic ERT inversion of surface and borehole data. As logged resistivity is carried along a vertical profile, it is only sensitive to the horizontal resistivity component of the ground and thus departs from the estimated vertical resistivity of anisotropic medium which confirms the validity of our methodological approach to quantify the anisotropy. Please see references for more details.
3.2.3. Relative Error vs. Array Angle
To assess the effect of anisotropy on data misfit error of isotropic ERT inversion, we consider the same two layered synthetic model as in sections 3.2.1 and 3.2.2. The data acquisition is simulated using only surface-borehole data. The current electrodes are located in wells and the potential electrodes are located at the surface. Array configuration were made using 50 surface electrodes and 15 boreholes electrodes. Electrode spacing is 1 m. Centers of each bipole describe a skew line with the horizontal, forming an angle θ (Figure 2A). The simulated potential data (ϕtrue) are isotropically inverted. The data misfit relative error is computed as the normalized difference between the potential data calculated using the inverted model (ϕcalc) and the simulated potential data (ϕtrue):
Figure 2D displays scatter plots of data misfit relative error as function of array angle θ for isotropic and anisotropic ERT inversion. For angles between 0 and 45°, the relative errors are mostly negative, meaning that ϕcalc are underestimated (blue area in Figure 2D.1). The errors become positive for angles between 45 and 90° (orange area in Figure 2D.1). This sigmoid error shape is expected when an isotropic inversion is used to invert ERT data of horizontally anisotropic media. The horizontal resistivity component ρH is lower than the vertical resistivity component ρV. At low acquisition angles, current flow is mainly driven by ρH, and isotropic inversion underestimate the apparent resistivity values. Conversely, current flow is mainly driven by ρV at high angles and isotropic inversion overestimate the apparent resistivity values. The underestimations (blue area at low angles) compensate overall the overestimations (orange area at high angles). The sigmoid shape arises for any borehole dipole depth. For a given angle value, the more space is integrated—i.e., the deeper the borehole dipole–, they higher the local relative error (as represented by the colored points in Figure 2D.1). The total mean error of the measures is −2%. The same relative error computation is made with anisotropically inverted data. It shows an error close to zero (−2.75%) and independent of array angles (Figure 2D.2). A sigmoid relative error shape between true data and calculated data resulting from isotropic ERT inversion is then a strong indication of anisotropy existence in the ground.
The points addressed by section 3.2 give various ways to detect electrical anisotropy by analyzing ERT data. It can be difficult to gather information from multiple sources on the field: lack of outcrops, incapacity of drilling numerous wells (e.g., as needed for hydraulic tomography), or even total absence of well. We propose this preliminary methodological qualitative study to ascertain the presence of electrical anisotropy, and then a fortiori to ascertain the presence of hydraulic anisotropy. A full quantitative anisotropic study, in terms of data acquisition and processing, represents more time, resources and costs than a common isotropic study. Nevertheless, processes comprehension and interpretations suffer greatly from the lack of trustful data, and anisotropy consideration might be unavoidable to produce better forecasts, reducing the uncertainties and then the risks on the investigation or engineering works.
The next sections methodologically demonstrate the ability of anisotropic ERT campaigns to quantify the electrical and hydraulic ground anisotropies.
4. Anisotropic Electrical Resistivity Inversion for a Synthetic Case
Before starting the real case study, a synthetic electrical model is created on the basis of hydraulic tomography results. Forward modeling is performed on this model to generate synthetic electric potentials to simulate data acquisition in the field. After that, anisotropic ERT inversion is used to reconstruct ρH and ρV fields. The comparison between anisotropically inverted fields and the original synthetic model will allow to assess the robustness of the proposed approach to estimate ρ-anisotropy. The section describes the synthetic model (section 4.1), the optimal data acquisition protocol for anisotropic characterization of the subsurface (section 4.2), and the details of the forward and inverse modeling procedures (section 4.3) along with the performances of inversion (section 4.4).
4.1. Synthetic Model
The synthetic model used in this numerical experiment mimics the K fields model obtained from the hydraulic tomography experiment measured between wells P21 and P17 (see Figure 1 for location) by Paradis et al. (2016a). The two wells are separated by 8 m and the aquifer thickness is 9 m, which corresponds to the approximate length of the wells. The K fields were directly transformed in σ values by increasing K by a factor 105, which were inverted to obtain ρ values, to make it realistic of earth materials at the site (values between 102 and 105 Ω.m, Figure 3). This transformation leads to log(ρH)∈[1.30;2.52]log(Ω.m) (Figure 3A), log(ρV)∈[2.44;4.60]log(Ω.m) (Figure 3B), and log(ρV/ρH)∈[1;3] (Figures 3C,D), which could be qualified as a moderate anisotropic field. For the synthetic simulation, 34 electrodes (black dots in Figure 3) were placed around the synthetic model: every 1 m inside the wells and every 0.5 m at the surface.
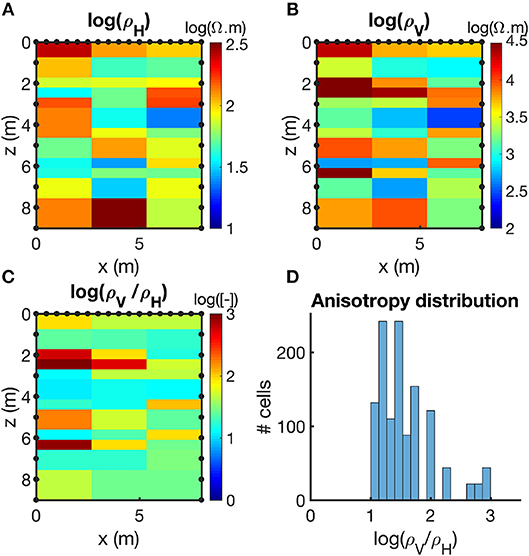
Figure 3. Electrical resistivity synthetic model based on real case hydraulic study results from Paradis et al. (2016a). The horizontal (A) and vertical (B) resistivities ρH and ρV are the components of the anisotropic resistivity tensor . The anisotropy (C) shows locally up to three orders of magnitude. Black dots represent the electrodes locations. The distribution of anisotropy is represented on the histogram (D).
4.2. Optimal Data Acquisition Protocol
As in the isotropic case presented in section 3, it is crucial to adapt the data acquisition protocol given that electrode configurations are not necessarily sensitive to the same subsurface features. Different electrodes configurations do not have the same sensitivity to anisotropy (Wiese et al., 2009; Greenhalgh et al., 2010; Kenkel and Kemna, 2016). In particular, Bing and Greenhalgh (2000) have detailed the use of cross-hole ERT. Thus, configurations not sensitive to anisotropy should be avoided as using them will lead the inversion toward an isotropic (hence wrong) inverted solution. Using the synthetic model previously described (Figure 3), nine quadrupoles configurations were tested (Figure 4) to assess their ability to detect anisotropy (Figure 5). Those quadrupoles use different combinations of electrodes placed in wells and at the soil surface. The following arrays were tested:
• Two inline borehole protocols with the four electrodes in the left (IB1) or right (IB2) borehole,
• One surface protocol with the four electrodes at the surface (S),
• Two cross-hole protocols with the current electrodes in the same (XH1) or separated (XH2) boreholes,
• Two surface-borehole protocols using left (SB1, SB2) or right (SB3, SB4) borehole, with both current electrodes (or indifferently potential electrodes) in the borehole, the other two electrodes at the surface (SB1 or SB3) or with one current electrode and one potential electrode in the borehole, and one current electrode and one potential electrode at the surface (SB2 or SB4).
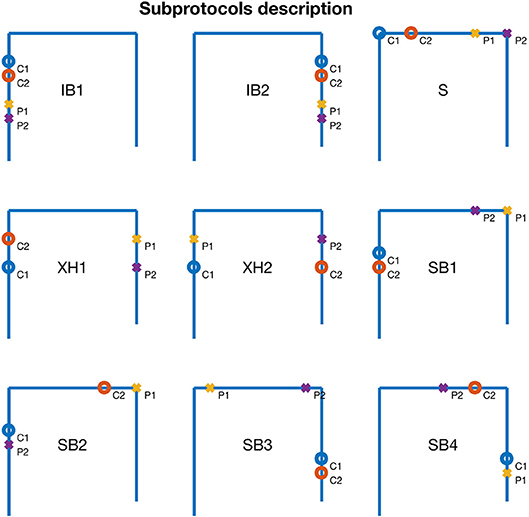
Figure 4. Representation of the different subprotocols used during this study in boreholes and at the surface. For each subprotocol, ◦ represent the current electrodes C1 and C2 and × represent the potential electrodes P1 and P2.
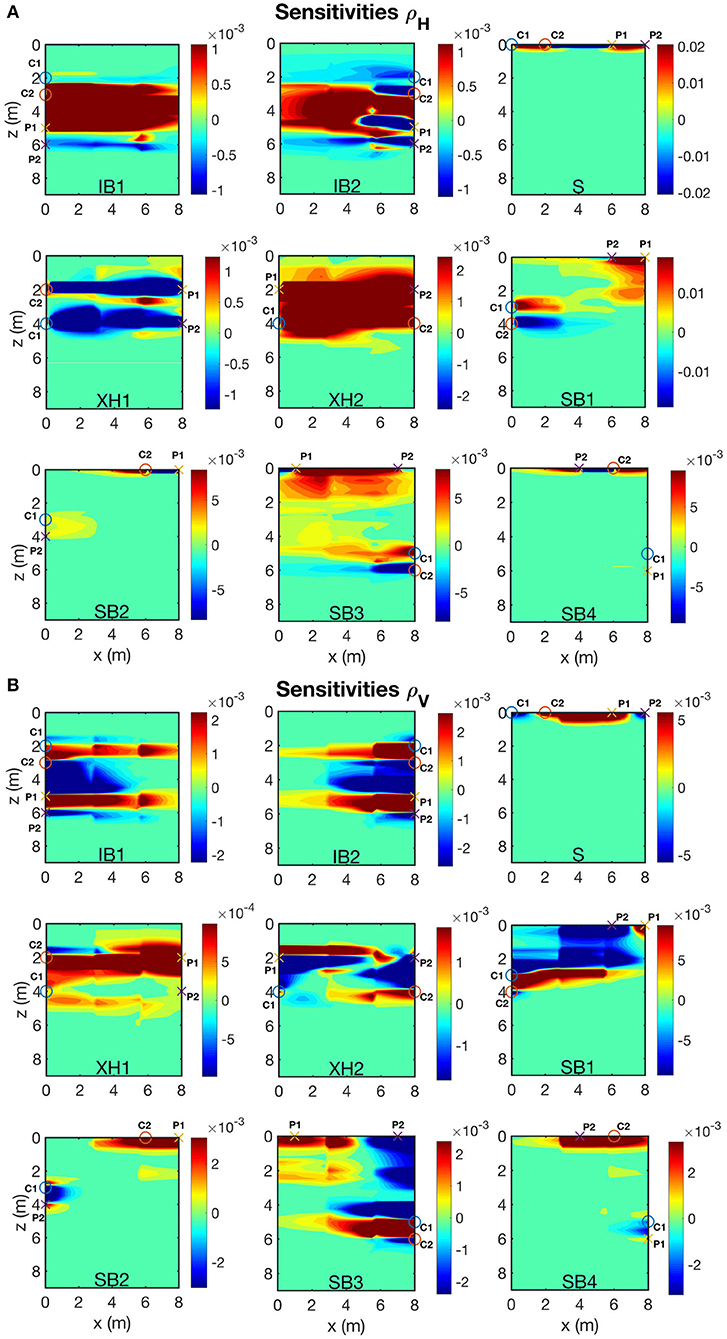
Figure 5. The sensitivity pattern is obtained from the Jacobian matrix (matrix of the potential derivatives according to the resistivity values of the model) computation of the electrode quadrupoles on the synthetic model from Figure 3. (A) Sensitivity pattern relative to ρH and (B) Sensitivity pattern relative to ρV. Same subprotocols as Figure 4. ◦ represent the current electrodes C1 and C2 and × represent the potential electrodes P1 and P2.
For each of these quadrupoles, the sensitivity of the electric potentials to ρH and ρV was analyzed using values of the Jacobian matrix, which is the matrix of the potential derivatives according to the resistivity values of the model (Greenhalgh et al., 2009).
As each quadrupole have a distinct sensitivity pattern, several observations can be made from Figure 5. First, inline borehole (IB1, 1B2) and surface (S) configurations show larger sensitivities close to the location of the electrodes, which limit the area of investigation of the surveys performed with those quadrupoles. On the other hand, crosshole (XH1, XH2) and surface-borehole (SB1, SB2, SB3, SB4) quadrupoles are sensitive to much larger areas. However, the magnitude of the sensitivities is larger for S, SB1, and SB3 quadrupoles, which can better resolve ρH and ρV in the associated sensitive areas using those configurations. Then, the sensitivity patterns for symmetric configurations (IB1 and IB2, SB1 and SB3, SB2 and SB4) show similar behavior despite the electrodes being located in different materials due to the heterogeneous nature of the synthetic model. The contrast in ρ material seems thus to have less impact on sensitivities than the electrode configuration itself. Also, sensitivity patterns for ρH and ρV are different. This means that a quadrupole can be more influenced by one component of than by the other. Quadrupoles configuration should be thus chosen accordingly to avoid bias in the measurements.
Given the previous observations, the S, IB1, IB2, XH1, XH2, SB1, and SB3 quadrupoles were then found the most informative and useful for an anisotropic inversion. IB1, IB2, XH1, XH2, SB1, and SB3 quadrupoles were chosen because they appear to be more sensitive to the central region of the investigated section, far from the surface and the wells. They provide information on the whole section. The S quadrupoles, even not significantly sensitive in depth, have been considered because they provide constraints for the model. This further constraints are particularly important since the surficial cells are not well-constrained by borehole electrode configurations and have an important effect on the inversion. Amongst the chosen subprotocols, electrode configurations might be sensitive to the same parts of the characterized section, incorporate redundancy. This redundancy is to be avoided in order to ease convergence of an inverted solution.
4.3. Forward and Inverse Modeling
In this section, the forward- and inverse-modeling (Dey and Morrison, 1979) adapted for anisotropic conditions (Gernez et al., 2018) is used to compute both forward and inverse modeling of ERT data on a numerical grid made of 8,970 squared cells of 25 × 25 cm. The forward modeling on the synthetic model used a protocol made of 755 quadrupoles chosen to be sensitive to the anisotropy (IB1[73], IB2[63], S[39], XH2[220], SB1[118], SB3[242]). The synthetic potentials are transformed on equivalent apparent resistivities ρapp and were then inverted to reconstruct ρH and ρV fields. For this reason, XH1 has not been considered since most of its apparent resistivities were negative. To reduce the risk of the model to converge toward a local minimum, homogeneous and anisotropic ρ values were also used to initialize the inverted model (lnρH = 4.75 ln Ω.m, ln λ = 6.2146). A weak first-order Tikhonov constraint (α) on the vertical direction was used (αV/αH = 0.5) in order to promote horizontal structures (which is consistent which geological information and GPR data). This horizontal smoothing is used to favor a layered inverted model. Conversely, a ratio departing too much from 1 will show horizontal artifacts. By rule of thumb, we choose 0.1 < αV/αH < 1. Refining is done by trial and error. A regularized iterative Gauss-Newton method was used to tackle the non-linear inverse problem.
4.4. Inversion Performances
The Figure 6C presents a histogram of the relative error between synthetic and inverted potential values after convergence of the model at the seventh iteration. With most of the relative error centered on zero and an overall low RMSE of 1.7%, the inversion is considered to fit almost perfectly the synthetic potentials.
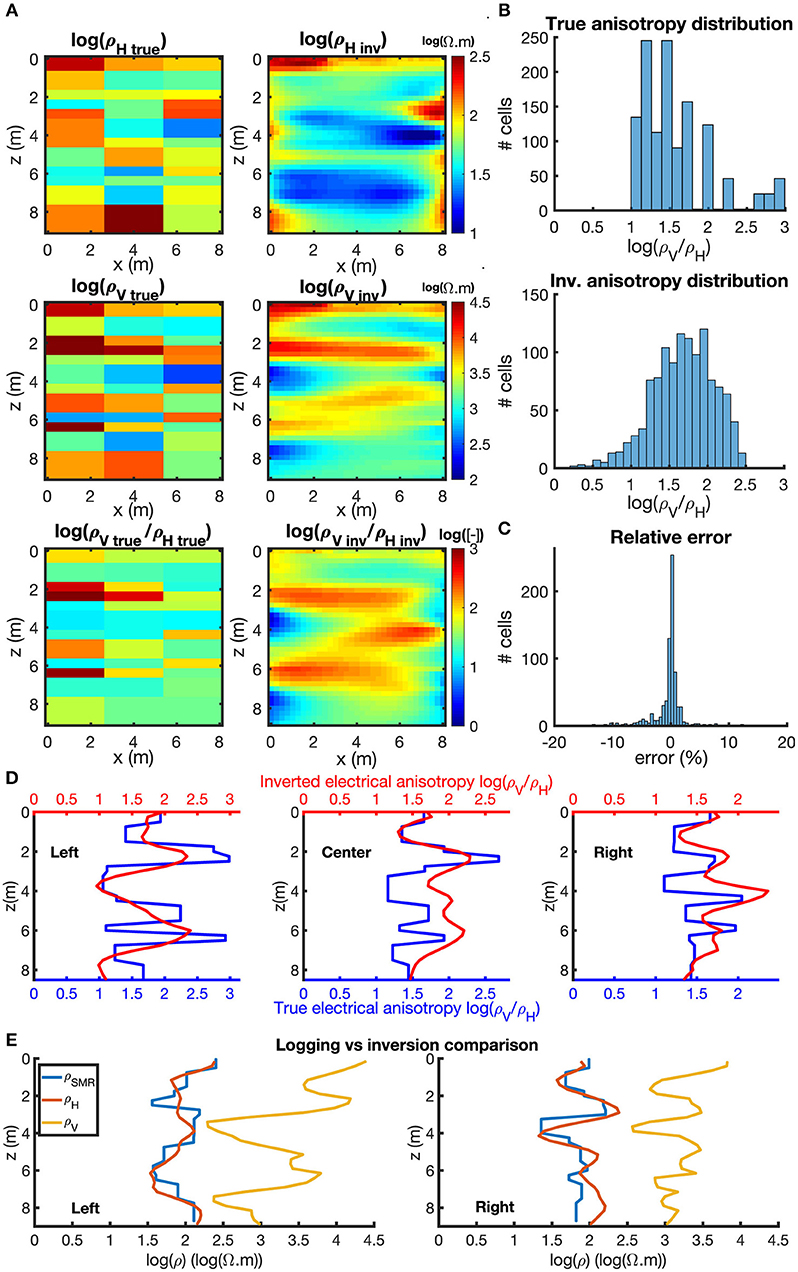
Figure 6. Synthetic study anisotropic inversion results displaying logarithmic inverted resistivities. Unless otherwise stated, ρH and ρV represent the components of the inverted resistivity ρHinv and ρVinv. (A) True and inverted resistivity models (wells at x = 0 m and x = 8 m). (B) Histograms of the true and inverted anisotropy distributions. (C) Histogram of the relative error between measured and inverted ρapp. (D) Comparison between true (blue curves) and inverted (red curves) anisotropies. To compensate the resolution difference, the inverted anisotropy is averaged on the 2.5 m around the wells and in the center of the modeled section. (E) Comparison between the logged (ρSMR, blue curves), and the inverted horizontal (ρH, red curves) and vertical (ρV, yellow curves) resistivities (corresponding to the left and right resistivities section). Notice the similarities between ρSMR and ρH.
Moreover, the Figure 6A (right) shows ρ fields resulting from the inversion. While the ρ fields are smoother than the synthetic model [Figure 3, 6A (left)], the main features of the subsurface are reproduced, such as alternations of low and high ρ layers and overall range of ρ variations. Also, the analysis of the frequency distributions of synthetic and inverted ρ-anisotropy reveals similarities with quasi-normal distributions (Figures 3D, 6B). Examination of rho profiles along the depth (Figure 6D) illustrates more specifically the good agreement between synthetic and inverted fast alternations between low and high values of rho-anisotropy: both the trends and magnitudes of the synthetic and inverted profiles are well-reproduced. Finally, inverted ρH matches well the logged rho (Figure 6E), in agreement with the paradox of electrical resistivity anisotropy detailed in section 3.2.2.
Given the above model performances, we have shown that anisotropic inverse modeling is able to reconstruct ρ fields, particularly ρ-anisotropy, even for a very challenging aquifer with moderate heterogeneity and anisotropy.
5. Field Case Study: Comparison Between Electrical and Hydraulic Anisotropies
Through the synthetic study presented in section 4.1, we demonstrated the ability of our methodology to characterize an electrically anisotropic environment using an adapted ERT survey (acquisition and inversion), without further external information. In this section, we want to verify with in situ measurements the possibility to characterize K-anisotropy from ERT anisotropic inversion.
The wells used for ERT were installed by direct-push technique in order to minimize skin effects around wells during testing (Paradis et al., 2011). Conventional well installation procedures indeed require the use of sand-pack to fulfill the space between the drilling hole and the screen, which may hinder the electrical response of the natural formation behind it. Direct-push well installation procedure allows the screen to be in direct contact with the aquifer with minimal disturbances to the surrounding sediments. The screen of the wells is open to the entire thickness of the aquifer allowing for multi-level hydrogeological and geophysical surveys. The screens ensure the free flow of water with slotted openings of 2.5 mm spaced vertically at every centimeter and covering over half of the circumference of the screens. The wells are also made of electrical insulator material (PVC) to ensure the integrity of electrical measurements.
The ERT setup is displayed in Figure 1. It consists of 17 inhole electrodes (9 in P17 and 8 in P21) and 17 surface electrodes located around the plane formed by P17 and P21 wells. P17 and P21 are separated by 8 m, electrodes separation is 1 m inside the wells and 0.5 m at the surface. Using this configuration, 18,936 electric potentials were measured with an IRIS Syscal Pro system. In addition, high resolution horizontal resistivity log data are available, acquired along P17 and P21 with the CPT-SMR probe. The SMR probe measures the resistivity using two ring electrodes 9 cm apart at a 1 kHz frequency to reduce polarization effects (Shinn et al., 1998; Paradis et al., 2015b). The log is 10.41 m deep at P17 and 9.96 m deep at P21, and ρH is measured over a 5 cm interval.
Before getting to the inversion, a quality control was done on the data using the reciprocal data. Interchanging the two electrodes inside a pair (current or potential) should only alter the sign of the measured potential data. Alternatively, interchanging the two pairs (current with electrodes) should provide the same measured potential data by principle of reciprocity (Slater et al., 2000). During our survey, 5369 data has been acquired to that end. Amongst them, 89.6% of these data show a difference of < 15%, and that 84.5% show a difference of < 5%. These values show an overall good quality data set. From the whole data set, we can extract the data used for the inversion (section 5.2). Inverse modeling is computed on a numerical grid made of 8,970 squared cells of 25 × 25 cm, similarly to the synthetic case (section 4).
5.1. Anisotropy Diagnosis of Real Case Study ERT Data
In section 3.2 two different approaches were presented to assess the electrical anisotropy by analyzing ERT data. In the following, anisotropy diagnosis of real case study ERT data is studied by performing isotropic ERT inversion. After removing negative ρapp data and poor quality data, 12,933 resistance data measurements were considered for the inversion. The isotropic ERT inversion converges after 10 iterations with an acceptable RMSE of 8.3%. Nevertheless, numerous erratic structures that do not correspond to the known geology of the site (section 2) appear on the isotropic resistivity image (ρiso, Figure 7A). More precisely, few small resistivity structures are close to the electrodes, where the inverted section is usually better resolved as shown in Figure 2B.2.
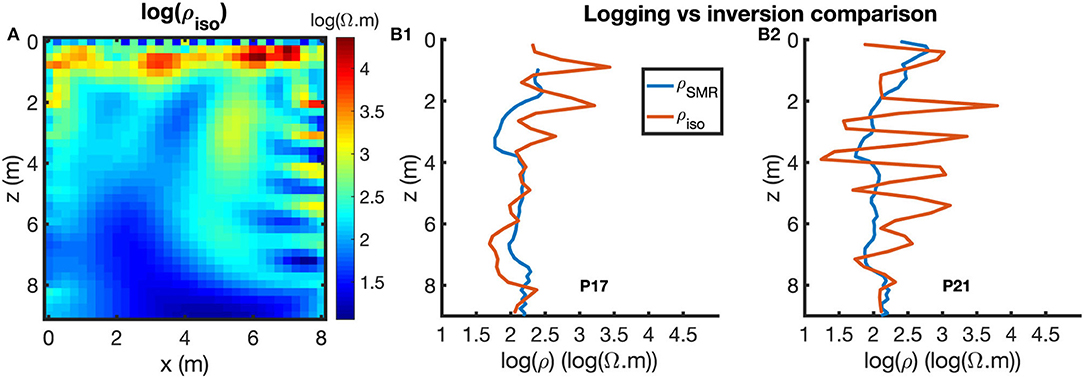
Figure 7. Real case study isotropic inversion results displaying logarithmic inverted resistivities. (A) Inverted results from the apparent resistivities acquired between P17 (x = 0 m) and P21 (x = 8 m) on the tomography site (Figure 1). (B) Comparison between the logged (ρSMR, blue curves) and the inverted isotropic (ρH, red curves) resistivities (corresponding to the P17 [B1] and P21 [B2] resistivities).
When ρiso is compared to the logged ρ in P17 and P21 wells (Figure 7B), ρiso shows very high frequency variations on both wells, and its values do not correspond to ρ values. As we have shown before (section 3 and Figure 3C), this is due to anisotropy. We then established the presence of anisotropy using a very fast approach in comparison to hydrogeological experiments. In fact, ERT data are carried out in less than a few hours, whereas several weeks are needed for anisotropic hydrogeological tomography data acquisition. Therefore, electrical anisotropy diagnosis approaches can be used as an assisting tool to help taking hydraulic decisions.
5.2. Anisotropic Inversion of Anisotropic ERT Data
As for the synthetic case, XH1, SB2, and SB4 arrays are not considered. The used protocol is made of 975 measures (IB1[75], IB2[64], S[38], XH2[436], SB1[186], SB3[176]), based on the result obtained in the synthetic study. Homogeneous and anisotropic ρ values were used to initialize the inverted model with an initial ρH value corresponding to the median of the measured apparent resistivities and an initial anisotropy value of λ = 10. The convergence is reached after 6 iterations, after which misfit or RMSE slightly decrease, but do not improve significantly anymore. At this point, the inverted model starts integrating the noise held in the data, so further iterations are ignored. The relative error between the measured and the computed ρapp from the inverted model is shown in Figure 8B. The histogram displays a slight bias of 4.3% in the relative error and a standard deviation of 10.83%. Unlike the synthetic case study, detailed information of the ground structure is unavailable, making hard the building of an optimized protocol. The chosen protocol was inspired from the synthetic case study since the latter was based on the hydraulic characterization of the ground. The residual error can be explained by the difficulty it met to reconcile its different sensitivities, whose preliminary examination is not achievable. Nevertheless, the final error (9.3%) combined with the relative error are considered low in a noisy real case study context.
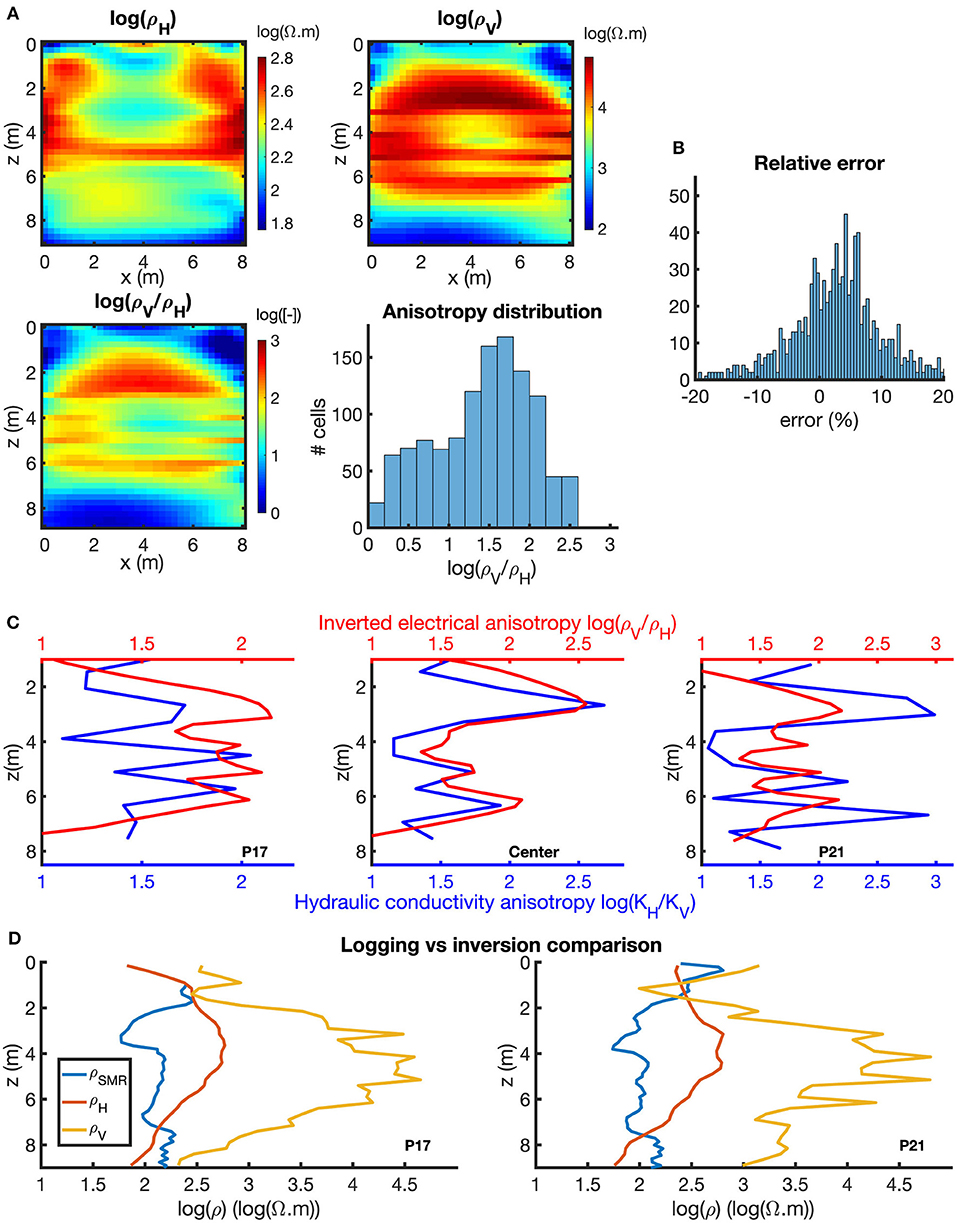
Figure 8. Real case study inversion results displaying logarithmic inverted resistivities. (A) Inverted results from the apparent resistivities acquired between P17 (x = 0 m) and P21 (x = 8 m) on the tomography site (Figure 1). (B) Histogram of the relative error between measured and inverted ρapp. (C) Comparison between inverted hydraulic (blue curves) and electrical (red curves) anisotropies. Hydraulic data starts at z = 1 m (saturated depth). To compensate the resolution difference, the inverted resistivities are averaged on the 2.5 m around the wells and in the center of the modeled section. (D) Comparison between the logged (ρSMR, blue curves), and the inverted horizontal (ρH, red curves) and vertical (ρV, yellow curves) resistivities (corresponding to the P17 and P21 resistivities).
The inverted sections are shown in Figure 8A. Both ρH and ρV sections show subhorizontal structures, as expected from our geological and hydrogeological knowledge of SLdL. The comparison between K (blue curve in Figure 8C) and ρ (red curve Figure 8C) anisotropies show strong similarities in their patterns and their amplitudes. It indicates the ability of anisotropic ERT inversion to characterize K-anisotropy. Finally, CPT-SMR resistivity is compared to anisotropic ERT inversion results (Figure 8D). Similarly to the synthetic case, the graphs display the collocated logged (ρSMR, blue curve), horizontal (ρH, red curve) and vertical (ρV, yellow curve) resistivities on wells P17 and P21. On the contrary to isotropic ERT inversion, horizontal resistivities at P17 and P21 are smooth which is consistent with CPT-SMR resistivities. However, there is a gap between the two curves. More precisely, horizontal resistivities are several times higher than CPT-SMR resistivities. This difference is due to the fully-screened wells effect on ERT data. CPT-SMR data measurement is carried out by direct-push before fully-screened well installation. Its coupling is very good, the electrodes being in direct contact with the undisturbed investigated underground. In the ERT case, acquisition is done using electrodes immersed into water in the screened well. Due to this aqueous environment, a part of the current is channelized along the well and affects the inverted model. The use of packers could prevent this channeling. Unfortunately, we were not able to implement this experiment during the campaign acquisition. Moreover, to our knowledge, the borehole effect has been studied in the isotropic case when the electrodes are mounted on the electrically insulated borehole casing (Doetsch et al., 2010; Wagner et al., 2015; Lee et al., 2016). This effect is important only for large resistivity contrasts between the rock formation and borehole fluid and for large borehole diameters (Doetsch et al., 2010). Furthermore, sensitivity is very high close to the electrode. Impact of close objects or structures are important (Binley and Kemna, 2005). According to us, because the ERT method is very sensitive to the resistivity variations close to the electrodes, the screened borehole casing impacts the resistivity model. In our opinion, borehole effect in our case is substantially handled by anisotropic inversion because hydraulic tomography shows approximately the same anisotropy variations as electrical resistivity tomography. On the contrary, isotropic inversion shows a lot of artifacts around the boreholes.
If Figures 8C,D show the comparison between various linked parameters, a direct proportionality relation between ρ and K anisotropies is hard to achieve. The sensitivities of the geophysical and hydraulic methods are not the same. Moreover, both anisotropy sections are inverted sections, coming from two different inversions (in terms of grid size, regularization, etc.). To obtain a direct proportionality relation between ρ and K anisotropies, or even directly between ρ and K values, further investigations are needed to that goes beyond the framework of this work (use of packers to prevent current channeling, use 3-D finite elements code to more efficiently remove the well effects, etc.).
6. Conclusions
Hydraulic anisotropy has a major influence on the groundwater flow and mass transport. Its consideration is essential when it exists. Through this study, we pointed out: 1. the ability of isotropic ERT modeling to assess the presence of ρ-anisotropy, 2. the ability of anisotropic ERT modeling to quantify ρ-anisotropy and 3. the strong relationship existing between K- and ρ-anisotropies through an in situ survey. To achieve this work, we developed a new methodology based on an innovative anisotropic ERT modeling tool. To overcome the equivalence problem, electrodes were placed inside a fully screened borehole along with surface electrodes. Anisotropic ERT inversion is then carried out to estimate the ρ-anisotropic model. The latter suggest a strong link with the collocated K-anisotropic characterization: even though the setup used does not allow a direct proportionality relation, the proposed geophysical method is able to provide proxy of the in-situ hydraulic anisotropy.
In this study, we have shown that the anisotropic electrical resistivity surveys are helpful for anisotropic hydrogeologic parameters characterization, which paves the way for large scale hydrogeophysical characterization campaigns, even in challenging anisotropic environments. Integrated hydrogeophysical studies can therefore be powerful approaches in the understanding processes in order to produce more reliable forecasts.
Author Contributions
EG funded the project. DP and EG conceived the idea of linking the in situ resistivity and hydraulic anisotropies. AB, DP, and EG supervised the project. AB and SG developed the physical and numerical theory, worked on data curation and analysis, and designed the computational modeling framework. AB encouraged further investigation on the data selected for the inversion, contributed to the interpretation of the results, and proposed further methodological experiments to improve data interpretation and final conclusion. SG conceived and carried out the synthetic and field experiments and wrote the manuscript draft. SG, EG, AB, and DP provided review, editing, and final approving on the manuscript.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The field data considered in this paper were acquired through the support of the Régie Intermunicipale de gestion des déchets des Chutes-de-la-Chaudière. The authors would like to acknowledge the participation of students for fieldwork. The authors would also like to thank the two reviewers that helped to improve the initial manuscript. This is LMS contribution number 20180391.
References
Adams, A. L., Nordquist, T. J., Germaine, J. T., and Flemings, P. B. (2016). Permeability anisotropy and resistivity anisotropy of mechanically compressed mudrocks. Can. Geotech. J. 53, 1474–1482. doi: 10.1139/cgj-2015-0596
Archie, G. E. (1942). The electrical resistivity log as an aid in determining some reservoir characteristics. Petrol. Technol. 146, 54–62.
Barry, F., Ophori, D., Hoffman, J., and Canace, R. (2009). Groundwater flow and capture zone analysis of the Central Passaic River Basin, New Jersey. Environ. Geol. 56, 1593–1603. doi: 10.1007/s00254-008-1257-5
Bing, Z., and Greenhalgh, S. (2000). Cross-hole resistivity tomography using different electrode configurations. Geophys. Prospect. 48, 887–912. doi: 10.1046/j.1365-2478.2000.00220.x
Binley, A., and Kemna, A. (2005). “DC resistivity and induced polarization methods,” in Hydrogeophysics, eds Y. Rubin, and S. S. Hubbard (Dordrecht: Springer), 129–156.
Bolduc, A.-M. (2003). Géologie des Formations Superficielles. Charny, QC: Commission géologique du Canada.
Bouchedda, A. (2010). >Inversion Conjointe des Données Électriques et de Radar en Forage. Ph.D. thesis, École Polytechnique de Montréal, Université de Montréal.
Burns, W. A. Jr. (1969). New single-well test for determining vertical permeability. J. Petrol. Technol. 21, 743–752.
Butler, J. J. (2005). “Hydrogeological methods for estimation of spatial variations in hydraulic conductivity,” in Hydrogeophysics, eds Y. Rubin, and S. S. Hubbard (Dordrecht: Springer), 23–58.
de Marsily, G., Delay, F., Gonçalvès, J., Renard, P., Teles, V., and Violette, S. (2005). Dealing with spatial heterogeneity. Hydrogeol. J. 13, 161–183. doi: 10.1007/s10040-004-0432-3
Dey, A., and Morrison, H. (1979). Resistivity modelling for arbitrarily shaped two-dimensional structures. Geophys. Prospect. 27, 106–136.
Doetsch, J. A., Coscia, I., Greenhalgh, S., Linde, N., Green, A., and Günther, T. (2010). The borehole-fluid effect in electrical resistivity imaging. Geophysics 75, F107–F114. doi: 10.1190/1.3467824
Falta, R. W., Basu, N., and Rao, P. S. (2005). Assessing impacts of partial mass depletion in DNAPL source zones: II. Coupling source strength functions to plume evolution. J. Contam. Hydrol. 79, 45–66. doi: 10.1016/j.jconhyd.2005.05.012
Gernez, S., Bouchedda, A., Gloaguen, E., and Paradis, D. (2018). “Comparison between hydraulic conductivity anisotropy and electrical resistivity anisotropy from tomography inverse modelling,” in 80th EAGE Conference and Exhibition 2018 (Copenhagen). doi: 10.3997/2214-4609.201800828
Goltz, M. N., Huang, J., Close, M. E., Flintoft, M. J., and Pang, L. (2008). Use of tandem circulation wells to measure hydraulic conductivity without groundwater extraction. J. Contam. Hydrol. 100, 127–136. doi: 10.1016/j.jconhyd.2008.06.003
Greenhalgh, S., Wiese, T., and Marescot, L. (2010). Comparison of dc sensitivity patterns for anisotropic and isotropic media. J. Appl. Geophys. 70, 103–112. doi: 10.1016/j.jappgeo.2009.10.003
Greenhalgh, S. A., Zhou, B., Greenhalgh, M., Marescot, L., and Wiese, T. (2009). Explicit expressions for the fréchet derivatives in 3d anisotropic resistivity inversion. Geophysics 74, F31–F43. doi: 10.1190/1.3111114
Hart, D. J., Bradbury, K. R., and Feinstein, D. T. (2006). The vertical hydraulic conductivity of an aquitard at two spatial scales. Groundwater 44, 201–211. doi: 10.1111/j.1745-6584.2005.00125.x
Hirasaki, G. J. (1974). Pulse tests and other early transient pressure analyses for in-situ estimation of vertical permeability. Soc. Petrol. Eng. J. 14, 75–90.
Hubbard, S. S., and Rubin, Y. (2005). “Introduction to hydrogeophysics,” in Hydrogeophysics, eds Y. Rubin, and S. S. Hubbard (Dordrecht: Springer), 3–21.
Hvilshøj, S., Jensen, K., and Madsen, B. (2000). Single-well dipole flow tests: Parameter estimation and field testing. Groundwater 38, 53–62. doi: 10.1111/j.1745-6584.2000.tb00202.x
Kabala, Z. J. (1993). The dipole flow test: a new single-borehole test for aquifer characterization. Water Resour. Res. 29, 99–107.
Keller, G. V., and Frischknecht, F. C. (1966). Electrical Methods in Geophysical Prospecting. Pergamon Press.
Kenkel, J., and Kemna, A. (2016). Sensitivity of 2-d complex resistivity measurements to subsurface anisotropy. Geophys. J. Int. 208, 1043–1057. doi: 10.1093/gji/ggw353
Lee, K.-S., Cho, I.-K., and Kim, Y.-J. (2016). Borehole effect in 2.5D crosshole resistivity tomography. J. Appl. Geophys. 135, 212–222. doi: 10.1016/j.jappgeo.2016.10.015
Lesmes, D. P., and Friedman, S. P. (2005). “Relationships between the electrical and hydrogeological properties of rocks and soils,” in Hydrogeophysics, eds Y. Rubin, and S. S. Hubbard (Dordrecht: Springer), 87–128.
Loke, M. H. (2001). “Constrained time-lapse resistivity imaging inversion,” in Symposium on the Application of Geophysics to Engineering and Environmental Problems 2001 (Denver, CO). doi: 10.4133/1.2922877
Lüling, M. G. (2013). The paradox of anisotropy in electric logging: a simple proof and extensions to other physics domains. Geophysics 78, W1–W8. doi: 10.1190/geo2012-0123.1
Onur, M., Hegeman, P. S., and Kuchuk, F. J. (2002). “Pressure-pressure convolution analysis of multiprobe and packer-probe wireline formation tester data,” in SPE Annual Technical Conference and Exhibition (San Antonio, TX: Society of Petroleum Engineers).
Paradis, D., Gloaguen, E., Lefebvre, R., and Giroux, B. (2015a). Resolution analysis of tomographic slug test head data: two-dimensional radial case. Water Resour. Res. 51, 2356–2376. doi: 10.1002/2013WR014785
Paradis, D., Gloaguen, E., Lefebvre, R., and Giroux, B. (2016a). A field proof-of-concept of tomographic slug tests in an anisotropic littoral aquifer. J. Hydrol. 536, 61–73. doi: 10.1016/j.jhydrol.2016.02.041
Paradis, D., and Lefebvre, R. (2013). Single-well interference slug tests to assess the vertical hydraulic conductivity of unconsolidated aquifers. J. Hydrol. 478, 102–118. doi: 10.1016/j.jhydrol.2012.11.047
Paradis, D., Lefebvre, R., Gloaguen, E., and Giroux, B. (2016b). Comparison of slug and pumping tests for hydraulic tomography experiments: a practical perspective. Environ. Earth Sci. 75:1159. doi: 10.1007/s12665-016-5935-4
Paradis, D., Lefebvre, R., Gloaguen, E., and Rivera, A. (2015b). Predicting hydrofacies and hydraulic conductivity from direct-push data using a data-driven relevance vector machine approach: Motivations, algorithms, and application. Water Resour. Res. 51, 481–505. doi: 10.1002/2014WR015452
Paradis, D., Lefebvre, R., Morin, R. H., and Gloaguen, E. (2011). Permeability profiles in granular aquifers using flowmeters in direct-push wells. Groundwater 49, 534–547. doi: 10.1111/j.1745-6584.2010.00761.x
Paradis, D., Tremblay, L., Lefebvre, R., Gloaguen, E., Rivera, A., Parent, M., et al. (2014). Field characterization and data integration to define the hydraulic heterogeneity of a shallow granular aquifer at a sub-watershed scale. Environ. Earth Sci. 72, 1325–1348. doi: 10.1007/s12665-014-3318-2
Pekşen, E., and Yas, T. (2018). Resistivity inversion of transversely isotropic media. Turkish J. Earth Sci. 27, 152–166. doi: 10.3906/yer-1702-6
Ruggeri, P., Gloaguen, E., Lefebvre, R., Irving, J., and Holliger, K. (2014). Integration of hydrological and geophysical data beyond the local scale: application of bayesian sequential simulation to field data from the Saint-Lambert-de-Lauzon site, Québec, canada. J. Hydrol. 514, 271–280. doi: 10.1016/j.jhydrol.2014.04.031
Sheng, J. J. (2009). A new technique to determine horizontal and vertical permeabilities from the time-delayed response of a vertical interference test. Transport Porous Media 77, 507–527. doi: 10.1007/s11242-008-9274-0
Shinn, J. D., Timian, D. A., Morey, R. M., Mitchell, G., Antle, C. L., and Hull, R. (1998). Development of a CPT deployed probe for in situ measurement of volumetric soil moisture content and electrical resistivity. Field Anal. Chem. Technol. 2, 103–109.
Slater, L., Binley, A., Daily, W., and Johnson, R. (2000). Cross-hole electrical imaging of a controlled saline tracer injection. J. Appl. Geophys. 44, 85–102. doi: 10.1016/S0926-9851(00)00002-1
Sutton, D., Kabala, Z., Schaad, D., and Ruud, N. (2000). The dipole-flow test with a tracer: a new single-borehole tracer test for aquifer characterization. J. Contam. Hydrol. 44, 71–101. doi: 10.1016/S0169-7722(00)00083-8
Tremblay, L., Lefebvre, R., Paradis, D., and Gloaguen, E. (2014). Conceptual model of leachate migration in a granular aquifer derived from the integration of multi-source characterization data (St-Lambert, Canada). Hydrogeol. J. 22, 587–608. doi: 10.1007/s10040-013-1065-1
Wagner, F. M., Bergmann, P., Rücker, C., Wiese, B., Labitzke, T., Schmidt-Hattenberger, C., et al. (2015). Impact and mitigation of borehole related effects in permanent crosshole resistivity imaging: an example from the ketzin CO2 storage site. J. Appl. Geophys. 123, 102–111. doi: 10.1016/j.jappgeo.2015.10.005
Wenzel, L. K., and Fishel, V. C. (1942). Methods for Determining Permeability of Water-Bearing Materials, With Special Reference to Discharging-Well Methods, With a Section on Direct Laboratory Methods and Bibliography on Permeability and Laminar Flow. US Geological Survey, United States Department of the Interior. doi: 10.3133/wsp887
Wiese, T., Greenhalgh, S., and Marescot, L. (2009). DC resistivity sensitivity patterns for tilted transversely isotropic media. Near Surf. Geophys. 7, 125–139. doi: 10.3997/1873-0604.2009003
Xiang, J., and Kabala, Z. (1997). Performance of the steady-state dipole flow test in layered aquifers. Hydrol. Process. 11, 1595–1605.
Yeboah-Forson, A., and Whitman, D. (2014). Electrical resistivity characterization of anisotropy in the biscayne aquifer. Groundwater 52, 728–736. doi: 10.1111/gwat.12107
Zhou, B., Greenhalgh, M., and Greenhalgh, S. A. (2009). 2.5-D/3-D resistivity modelling in anisotropic media using Gaussian quadrature grids. Geophys. J. Int. 176, 63–80. doi: 10.1111/j.1365-246x.2008.03950.x
Zlotnik, V., and Ledder, G. (1996). Theory of dipole flow in uniform anisotropic aquifers. Water Resour. Res. 32, 1119–1128.
Zlotnik, V. A., and Zurbuchen, B. R. (1998). Dipole probe: design and field applications of a single-borehole device for measurements of vertical variations of hydraulic conductivity. Groundwater 36, 884–893.
Keywords: hydrogeophysics, anisotropy, electrical resistivity tomography, hydraulic conductivity, modeling, groundwater
Citation: Gernez S, Bouchedda A, Gloaguen E and Paradis D (2019) Comparison Between Hydraulic Conductivity Anisotropy and Electrical Resistivity Anisotropy From Tomography Inverse Modeling. Front. Environ. Sci. 7:67. doi: 10.3389/fenvs.2019.00067
Received: 19 September 2018; Accepted: 06 May 2019;
Published: 04 June 2019.
Edited by:
Philippe Renard, Université de Neuchâtel, SwitzerlandReviewed by:
Renaud Toussaint, Université de Strasbourg, FranceAbderrahim Jardani, Université de Rouen, France
Copyright © 2019 Gernez, Bouchedda, Gloaguen and Paradis. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) and the copyright owner(s) are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Simon Gernez, c2ltb24uZ2VybmV6QGV0ZS5pbnJzLmNh
 Simon Gernez
Simon Gernez Abderrezak Bouchedda
Abderrezak Bouchedda Erwan Gloaguen
Erwan Gloaguen Daniel Paradis
Daniel Paradis