The Tripartite Regulation Game of Carbon Financial Products Based on the Prospect Theory

Introduction

Achieving the carbon-reduction goal associated with climate change and environmental treatment requires enormous economic investment (Xu et al., 2019; Zhao X. et al., 2020). Issuing carbon finance products (CFPs) is an important economic measure aimed at effectively filling the gap between demand for low-carbon investment and financial resources. In this paper, we define CFPs broadly in terms of the financial nature of products that have been developed in carbon finance markets. As one specific dimension of green finance with the attributes of financial risks and speculative opportunities, a range of essential CFPs and derivatives, including carbon forwards, futures, options, loans, and so on, have been released to curb carbon emissions based on “carbon emission rights” (Ji and Zhang, 2019). The European Union Emissions Trading System (EU ETS), Chicago Climate Exchange, and China’s carbon finance market are the crucial platforms in trading and investment for CFPs. Even so, investment in low-carbon sectors is still far from what is needed according to estimates, i.e., ranging from 650 billion to 1 trillion US dollars (IEA, 2012; WEF, 2013). What is worse, investment in CFPs is currently declining (BNEF, 2014).

One of the critical reasons for this low investment is due to the existence of market failures that may lead financial institutions—the most important source—not to respond as expected to price signals. Financial institutions may infringe on investors’ rights because of the externalities and asymmetric information. For example, in 2010, the Australian Transaction Reports and Analysis Centre reported a fake carbon credit investment scheme, in which investors lost 3.5 million Australian dollars in an investment scam by an Australian green energy company (Australian Transaction Reports and Analysis Centre (AUSTRAC), 2011). This severe problem also happened to the EU ETS. Regarding investors’ actual activity, when they face market risks caused by the financial institutions, they not only pursue the maximization of expected profits but also consider the impact of profit fluctuations. Due to these irregularity risks, investors find it difficult to purchase CFPs without regulation by governments, which is a severe problem in practice and needs to be solved urgently.

Many research mostly focused on the optimal strategy charged by governments and financial institutions. Investors as important players are rarely analyzed. Regulation of CFPs involves cooperation among governments, investors, and financial institutions. Actually, this is a tripartite game under the participation of governments. Only by coordinating the interests of all three stakeholders will it become possible to choose the optimal regulation. Meanwhile, the game players in the previous studies were homogeneous and perfectly rational. Therefore, this paper studies the impact of government regulation strategy on the development of CFPs. Specifically, the problems are as follows:

(1) What is the interaction game mechanism among the governments, financial institutions, and investors?

(2) How does the heterogeneity of governments, financial institutions, and investors influence their strategy choices?

(3) Considering attitudes to risk, what are the decisions for governments, financial institutions, and investors under bounded rationality?

By addressing the above questions, this paper makes several contributions. The first contribution is that the theoretical relationship among governments, financial institutions, and investors is analyzed. Based on this, we develop the tripartite regulation game model which accounts for all stakeholders. Second, considering the characteristics of heterogeneous participants of CFPs, the players are divided into two types: tough and weak ones. We compare different strategy selection for tough or weak game players. Third, the bounded rationality of game players is explored by incorporating the prospect theory. The prospective value is replaced with the perceived value function. Finally, based on the realization conditions of the deterrence game equilibrium, suggestions to enhance the quality of CFPs are put forward.

The remainder of this paper is organized as follows. The literature is reviewed in the section “Literature Review.” In the Section “Problem Description and Research Hypotheses,” we explain the relationship of game players, present our model assumptions, and construct the tripartite regulation game for CFPs. The behavioral strategy selection and the conditions of different game equilibrium are presented in the section “Model Solution and Analysis.” Finally, in the section “Conclusion and Managerial Implications,” we summarize our concluding remarks and point out some managerial implications.

Literature Review

We reviewed here the key studies related to our research, which can be divided into three subsections: policies of the carbon financial market, regulation game of different products, and analysis of heterogeneous game players.

Policies of the Carbon Financial Market

In recent years, the carbon finance market has drawn considerable attention for its potential to curb carbon emissions (Lu and Shao, 2016; Shu et al., 2017). Related research has become promising areas of investigation, such as mechanisms, models, and policies (Li et al., 2020; Yang et al., 2020; Zhang et al., 2020). Considering the characteristics of the carbon finance market, many researchers also pointed out its disadvantages. For example, Li L. et al. (2019) showed that carbon financial information disclosure was very low by looking at listed enterprises in China’s heavy pollution industry from 2009 to 2013. Campiglio (2016) argued that market failures may lead commercial banks not to respond as expected to price signals, and pointed out that the main challenges in the development of the carbon finance were the lack of sound policies, regulations, and legal systems.

Many papers simultaneously focus on governmental regulation of the carbon financial market. Layfield (2013) proposed that there should be tighter regulation of carbon markets, which should go further rather than simply relying on market-based instruments to achieve reductions in carbon emissions. Munnings et al. (2016) also believed that the implementation of a carbon-emissions trading system has become a major challenge for governments to effectively regulate the market. Girod (2016) reviewed and evaluated policy evolution over the past decade in terms of both measures implemented and emissions addressed, and proposed that current product-oriented climate policies need to be reinforced. Eyraud et al. (2013) demonstrated that regulation policies of carbon-pricing schemes have a positive and significant impact on green investment. Raberto et al. (2019) found that appropriate banking and regulatory policies can push the banking sector into shifting from speculative lending to green investments lending. Given the strengthening of carbon regulations and the launch of emission trading scheme in China, Zhou et al. (2020) empirically demonstrated the influence of carbon risk management on corporate competitive advantages.

Since the implementation of regulation for CFPs, relationships between stakeholders have been the key of research. Xu et al. (2016) studied the joint production and pricing problem of a manufacturing firm with multiple products under cap-and-trade and carbon tax regulations. Van de Broek et al. (2019) developed a qualitative model to assess how agricultural soils function with respect to the climate regulation of different stakeholders. Liao and Shi (2018) examined the determinants of green investment in China from the perspective of public appeal and proposed that public appeal promotes local governments’ enforcement of stricter environmental regulation.

This literature review reveals that previous studies, which have highlighted the role of governments in CFPs, mainly focused on the objectives of government regulation, without considering the synergy of financial institutions and investors. Therefore, when a given strategy damages the interests of one or more members of CFPs, it is necessary to coordinate their interests to find ways to compensate for the damage.

Regulation Game for Different Products

The game theory has been widely used to study the decision-making behaviors of stakeholders, such as the regulation of green products, new energy products, and low-carbon products (Hu et al., 2020). Regarding the quality of new energy products, Liu and Xia (2020) used the evolutionary game model to analyze the impact factors of strategic selection between customers and manufacturers. Lou et al. (2020) developed game-theoretic models of green products in a two-echelon dual-channel supply chain under government subsidies. Zhao N. et al. (2020) analyzed the subsidy-related deception behavior in energy-saving products based on the game theory and indicated that government regulation is necessary to keep manufacturers honest. Zhang S.Y. et al. (2019) constructed models of the evolutionary game between governments and manufacturers and analyzed the impacts of government policy on the decisions of manufacturers and the dynamic tendency of the cap-and-trade market. Zhao X. et al. (2020) proposed a tripartite evolutionary game theory to examine the behavioral strategies of government, banks, and grid enterprises in the low-carbon power grid technology innovation cooperation.

Many scholars have employed the general game theory to discuss the impacts of government intervention on manufacturers’ decisions, such as the Nash bargaining game, the Stackelberg game, etc. However, to the best of our knowledge, there are few studies on the analysis of CFPs with a dynamic multistage game, especially in terms of the settlement of rights-protection disputes.

Analysis of Heterogeneous Game Players

Most studies have investigated whether the heterogeneity of players affected the strategic choice and performance of the game. In green development aspects, Li J.J. et al. (2019) examined whether gender inequality affects a household’s decision to adopt green-consumption behavior in China, and indicated that promoting gender equality can have a favorable impact on green development. Li and Li (2016) investigated that the consumers’ preferences for low-carbon products is a critical factors for manufacturers to promote products. Centered on the heterogeneity of enterprises, Sun and Zhang (2019) built an evolutionary game to analyze the evolutionarily stable strategy of heterogeneous enterprises in preventing greenwashing. Zhang L.H. et al. (2019) studied how consumer environmental awareness and concerns about retailers’ fairness affect environmental quality.

The heterogeneity of financial institutions is manifested as liquidity, solvency, and riskiness. Berger et al. (2009) indicated that banks of different ownership types react differently and with different speeds to changes in the regulatory environment. Casu et al. (2013) found that state-owned banks performed better than private-sector banks, and medium-sized state-owned banks are more likely to operate at higher levels of efficiency and have, on average, less nonperforming loans. Badunenko and Kumbhakar (2017) built a model to control for bank heterogeneity, introduced persistent and time-varying inefficiency, and found that the scale economies of state-owned banks are unaffected by regulation. Raberto et al. (2019) investigated the banking regulatory provision that differentiates the capital adequacy ratio according to the type of lending. Zhou et al. (2018) showed that private firms with high positive media attention were more sensitive and less tolerant to environmental regulations.

The abovementioned studies discuss the heterogeneity of players from different aspects. However, few scholars investigate the heterogeneity of multiple subjects, and they only analyze single individuals. On the other hand, our study focuses on multiple participants with heterogeneity: governments, financial institutions, and investors in the regulation of CFPs. In addition, the subjectivity of players causes the differences between expected and real actions. The prospect theory is an effective descriptive theory for the behavior of players and also adequately describes situations in which players face exogenous risk (Brunner et al., 2019; Vahid-Pakdel et al., 2019). This study fills this research gap by incorporating the prospect theory into a dynamic game model with heterogeneous participants.

Problem Description and Research Hypotheses

In this section, the background of the model is described, and research hypotheses are proposed. Additionally, the parameters involved in the models are accurately defined.

Problem Description

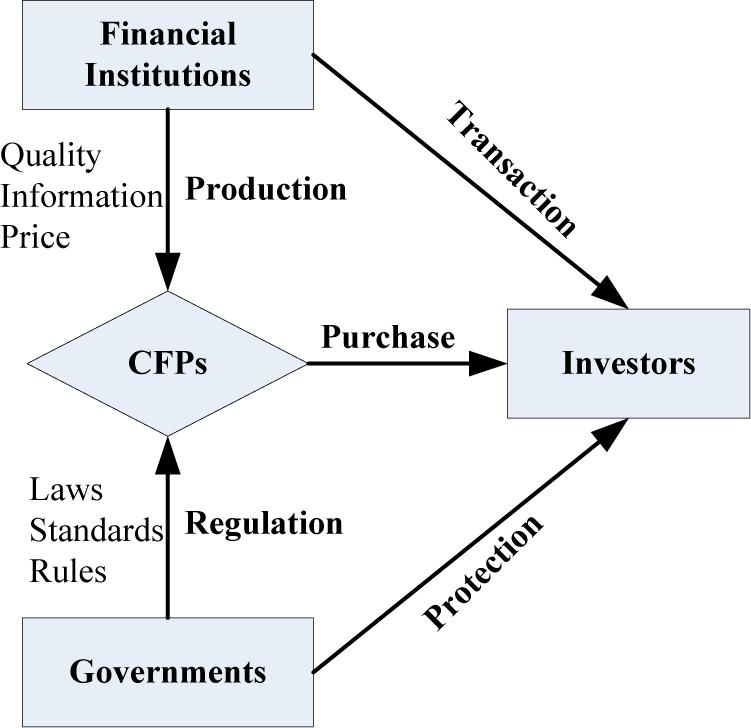
The carbon finance market is a place for transactions of CFPs, including all the institutional arrangements and policy systems. The design, circulation, and trading platform of CFPs are the game result of governments, financial institutions, and investors. The governments have effectively promoted the construction of market systems such as regulation laws and rules, trading platform, access requirements, and trading institution for CFPs. The policies of governments not only improve the quality of CFPs but also stimulate the demand for investors. Financial institutions include commercial banks, financial companies, third-party organizations, etc. They have to observe laws and disciplines to get the administrative licensing. Actually, because the price and cost of CFPs is private information, financial institutions also can manipulate the market and violate regulatory policies to infringe investor rights. As for the investors, the rapid improvement of environmental awareness promotes the increasing demand for CFPs. However, CFPs bring unsatisfactory returns to investors and sometimes even lead to losses. Therefore, investors need to be protected by governments. The relationship among CFP stakeholders is visualized in Figure 1.

FIGURE 1

Figure 1. The relationship among CFPs stakeholders.

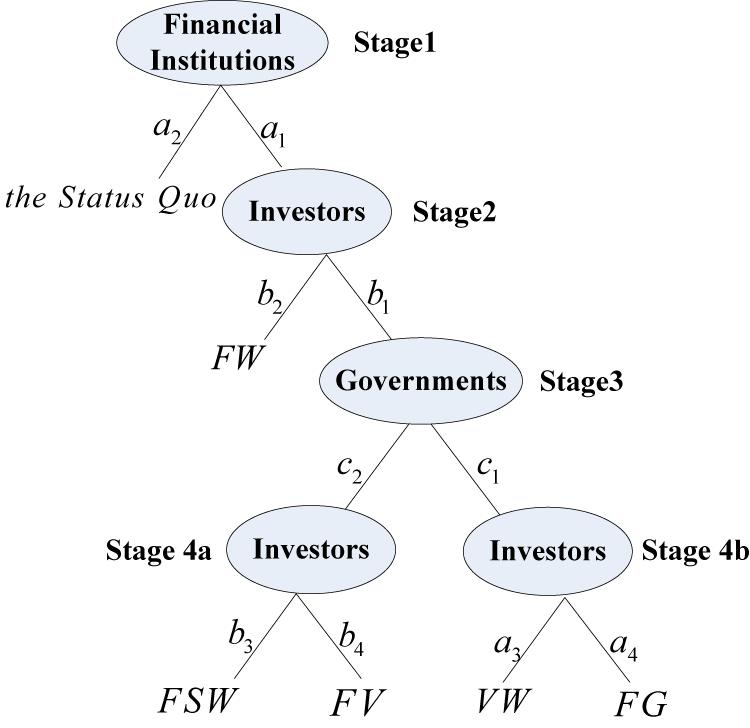
Using the game theory, this paper presents the whole process of the tripartite regulation game, which includes four stages.

In stage 1, financial institutions launch CFPs. The financial institutions’ behavior set to the investors is (a₁,a₂) = (infringement, non-infringement). If the financial institutions choose a₂, the game ends with the “status quo.” If not, the game enters stage 2.

In stage 2, investors have two strategies, the set of behavior is (b₁,b₂) = (complaint, non-complaint). When investors choose the “non-complaint” strategy, the result of game is “financial institutions win” (FW). Otherwise, the game continues.

In stage 3, the governments’ behavior set is (c₁,c₂) = (regulation, non-regulation). When governments choose the “non-regulatory” strategy, investors make the choice at stage 4a. If governments choose the “regulatory” strategy, financial institutions make the choice at stage 4b.

In stage 4a, due to the fact that the investors’ complaint is beyond the jurisdiction, governments choose strategy c₂. At this time, an optional set of behavior for investors is (b₃,b₄) = (settlement, non-settlement). This corresponds to the result of “financial institutions slightly win (FSW)” or “conflict between financial institutions and investors (FV).” FSW means that, in order to reach a settlement with investors, financial institutions may pay some compensation to investors, but still get the extra benefit brought by infringement.

In stage 4b, financial institutions have two options, which is defined as (a₃,a₄) = (stop infringement, continue infringement). When financial institutions choose strategyVB₄, the game ends in “investors win” (VW). The other scenario is “conflict between financial institutions and governments (FG),” that is, financial institutions do not implement regulatory decisions or evade regulation.

Above all, in stage 1, financial institutions determine the quality of CFPs. In stage 2, investor determines its optimal decisions, and then in stage 3, governments choose the strategy. Financial institutions and investors select the strategies in stage 4. So, the model description is visually shown in Figure 2.

FIGURE 2

Figure 2. The process of the tripartite regulation game in CFPs.

Model Hypotheses

According to the whole regulation process of CFPs, the game model is abstracted from reality and involves three participants: “the challenger”—financial institutions, “the protectors”—investors, and “the defender”—governments. To conduct a better analysis of tripartite regulation game in CFPs, we assume that all players of the game are under bounded rationality. Two strategies for each member are considered in the game. The parameters involved in the model are accurately defined.

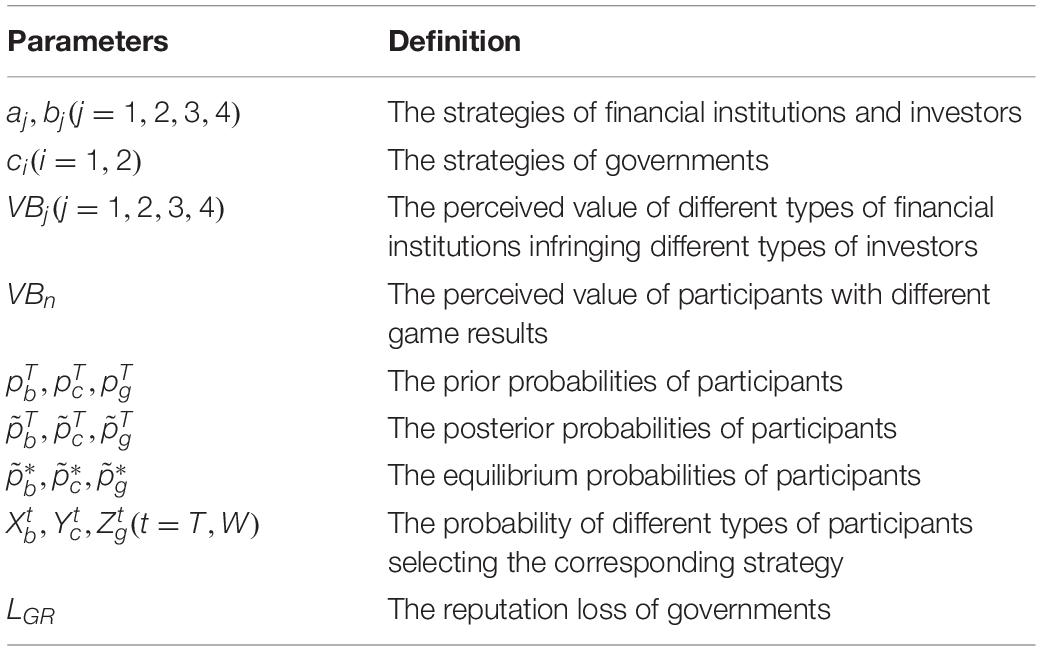
Assumption 1: Financial institutions, investors, and governments all have two types: tough and weak ones, t = (T,W) _{X_b^t} is the probability of financial institutions choosing strategy a₁. Let $Y_c^t$ be the probability of investors choosing strategy b₁. The probability of governments choosing strategy c₁ is $Z_g^t$.

Assumption 2: Let VB_n, VC_n, and VG_n denote the perceived value of financial institutions, investors, and governments, where n is the different results of the game. The perceived value of game players depends on their type. For example, VG_VW is denoted as the perceived value of the result VW, while $V{G}_{FG}^T$ and $V{G}_{FG}^W$ are the perceived values of the tough and weak governments, respectively.

Assumption 3: L_GR is the perceived value of reputation loss suffered by governments due to “non-regulation”; herein, L_GR > 0. When governments choose strategy c₂, the deterrent effect will be weakened and it may suffer from reputation risk. At this time, the perceived value is denoted by VG_SQ−L_GR.

Assumption 4: We assume that $p_b^T$, $p_c^T$, and $p_g^T$ are the prior probabilities of financial institutions, investors, and governments. The posterior probability of financial institutions being tough after selecting strategy a₁ is ${\tilde{p}}_b^T$, while ${\tilde{p}}_c^T$ is the posterior probability of the tough investors after choose b₁ strategy at stage 2. The belief updating of the game participants is carried out in accordance with the Bayesian rule. We get ${\tilde{p}}_b^T=\frac{p_b^{T}p(a_1|T)}{p_b^{T}p(a_1|T)+(1-p_b^T)p(a_1|W)}$, ${\tilde{p}}_c^T=\frac{p_c^{T}p(b_1|T)}{p_b^{T}p(b_1|T)+(1-p_b^T)p(b_1|W)}$.

Assumption 5: ${\tilde{P}}_b^{*}$, ${\tilde{P}}_c^{*}$, and ${\tilde{P}}_g^{*}$ are the equilibrium probabilities of the financial institutions, investors and governments. Table 1 summarizes the major parameters we will use in our model development.

TABLE 1

Table 1. The main parameters of the game model.

Model Solution and Analysis

Model Solution

The behavioral strategy of participants in the tripartite regulation game is discussed in this section.

The Behavioral Strategy of Governments

In stage 3, when governments choose the “non-regulation” strategy, it may suffer from reputation loss. The perceived value is denoted by VG_SQ−L_GR. When governments adopt the “regulation” strategy, the tough financial institutions will choose to “continue the infringement,” while the weak financial institutions will “stop the infringement,” then the perceived value of governments is $V{G}_{FG}^W<V{G}_{SQ}-L_{GR}<V{G}_{FG}^T<V{G}_{VW}$.

When governments are tough, the strategy c₁ is a dominant strategy, namely$Z_g^T=1$. When governments are weak, the strategy depends on the comparison of the perceived value of different strategies. When the perceived value of c₁ and c₂ is equal, solving the equation ${\tilde{p}}_b^{*}V{G}_{FG}^W+(1-{\tilde{p}}_b^{*})V{G}_{VW}=V{G}_{SQ}-L_{GR}$, we can obtain the equilibrium probability which is ${\tilde{p}}_b^{*}=\frac{V{G}_{VW}+L_{GR}-V{G}_{SQ}}{V{G}_{VW}-V{G}_{FG}^W}$.

Then, the strategic behavior of the weak governments in stage 3 is:

$$Z_g^W=\{\begin{array}{cc}\hfill 1\hfill & \hfill {\tilde{p}}_b^T<{\tilde{p}}_b^{*}\hfill \\ \hfill [0,1]\hfill & \hfill {\tilde{p}}_b^T={\tilde{p}}_b^{*}\hfill \\ \hfill 0\hfill & \hfill {\tilde{p}}_b^T>{\tilde{p}}_b^{*}\hfill \end{array}$$

The Behavioral Strategy of Investors

In stage 4a, of the two game results, the tough investors prefer FV, because of $V{C}_{FV}^T>V{C}_{FSW}$, and will choose the “non-settlement” strategy. However, the weak investors prefer FSW and will select the “settlement” strategy, i.e., $V{C}_{FV}^W<V{C}_{FSW}$. To sum up, there is $V{C}_{FV}^W<V{C}_{FSW}<V{C}_{FV}^T$. For investors, VW is the best outcome and FSW is the worst. We can get

$$V{C}_{FV}^W<V{C}_{FG}^W<V{C}_{FSW}<V{C}_{FW}<V{C}_{FV}^T<V{C}_{FG}^T<V{C}_{VW}.$$

In stage 2, when investors choose “complaint” and if governments choose “non-regulation,” the tough investors will choose “non-settlement,” because $V{C}_{FV}^T>V{C}_{FSW}$. If governments choose “regulation,” no matter what strategy financial institutions take, the investors’ perceived value of VW or FG is higher than FW when they choose “non-complaint.” Therefore, the tough investors will choose the “complaint” strategy at stage 2, i.e., $Y_c^T=1$.

When the weak investors choose “complaint” and if governments choose “non-regulation,” the perceived value of investors for FSW is lower than the perceived value of FW, which means $V{C}_{FSW}^W<V{C}_{FW}^W$; then, investors will choose “non-complaint.” If governments choose “regulation” (governments are weak, the “regulation” strategy should be adopted, at this time, ${\tilde{p}}_b^T<{\tilde{p}}_b^{*}$), the outcome depends on the type of financial institutions. In other words, the tough financial institutions will choose the “continuing infringement” strategy with the result of FG; the weak financial institutions will choose the “stop infringement” strategy and end up with VW. When there is no difference in the perceived value of “complaint” and “non-complaint,” we have:

$$p_g^T\left[{\tilde{p}}_b^{**}V{C}_{FG}+(1-{\tilde{p}}_b^{**})V{C}_{VW}\right]+(1-p_g^T)V{C}_{FSW}=V{C}_{FW}.$$

According to the equation, it can be obtained that

$${\tilde{p}}_b^{**}=\frac{V{C}_{FW}-p_g^{T}V{C}_{VW}-(1-p_g^T)V{C}_{FSW}}{p_g^T(V{C}_{FG}-V{C}_{VW})}.$$

Therefore, the weak investors should meet two conditions when choosing the “complaint” strategy in stage 2: governments are weak and “regulatory,” which meets the condition of ${\tilde{p}}_b^T<{\tilde{p}}_b^{*}$; meanwhile, the posterior probability of the tough financial institution is less than the equilibrium probability, under the condition ${\tilde{p}}_b^T<{\tilde{p}}_b^{**}$, $Y_c^W=1$. Otherwise, there will be “non-complaint,” at this time, $Y_c^W=0$.

The Behavioral Strategy of Financial Institutions

In stage 4b, the tough financial institutions prefer FG and will choose the “continuing infringement” strategy, that is, $V{B}_{FG}^T>V{B}_{VW}$. The weak financial institutions prefer VW and will choose the “stop infringement” strategy, namely $V{B}_{FG}^W>V{B}_{VW}$. Above all, $V{B}_{FG}^W<V{B}_{VW}<V{B}_{FG}^T$.

In stage 1, FW is the best outcome for financial institutions, and FSW, SQ is the second best result; FV, FG, and VW are the poor outcomes. The perceived value of financial institutions to FG depends on the type of financial institutions. Therefore, we can get

$$V{B}_{FG}^W<V{B}_{VW}<V{B}_{FG}^T<V{B}_{FV}<V{B}_{SQ}<V{B}_{FSW}<V{B}_{FW}.$$

For the tough financial institutions, when there is no difference between “infringement” and “non-infringement” in stage 1, we have

$${\tilde{p}}_c^{*}V{B}_1+(1-{\tilde{p}}_c^{*})V{B}_2=V{B}_{SQ}.$$

We calculate that ${\tilde{p}}_c^{*}=\frac{V{B}_2-V{B}_{SQ}}{V{B}_2-V{B}_1}$, where VB₁ and VB₂ are the perceived values of tough financial institutions when they meet the tough and weak investors, respectively.

The tough investors always choose the “complaint” or “non-settlement” strategy. When ${\tilde{p}}_b^T>{\tilde{p}}_b^{*}$, the weak governments will choose the “non-regulation” strategy, VB₁ = VB_FV; otherwise, no matter whether tough or weak, governments will choose the “regulation” strategy at stage 3, $V{B}_1=p_g^{T}V{B}_{FG}+(1-p_g^T)V{B}_{FV}$.

To the weak investors, at stage 2, if ${\tilde{p}}_b^T<{\tilde{p}}_b^{*}$ and ${\tilde{p}}_b^T<{\tilde{p}}_b^{**}$ are satisfied, they will choose the “complaint” strategy, $V{B}_2=p_g^{T}V{B}_{FG}+(1-p_g^T)V{B}_{FSW}^T$; otherwise, the weak investors will choose the “non-complaint” strategy, VB₂ = VB_FW.

The strategic choice of the tough financial institutions at stage 1 is as follows:

$$X_b^T=\{\begin{array}{c}\hfill 1\hfill \\ \hfill [0,1]\hfill \\ \hfill 1\hfill \end{array}\begin{array}{c}\\ \end{array}\begin{array}{c}\hfill \stackrel{\sim \phantom{T}}{p_c^T}<\stackrel{\sim \phantom{*}}{p_c^{*}}\hfill \\ \hfill \stackrel{\sim \phantom{T}}{p_c^T}=\stackrel{\sim \phantom{*}}{p_c^{*}}\hfill \\ \hfill \stackrel{\sim \phantom{T}}{p_c^T}>\stackrel{\sim \phantom{*}}{p_c^{*}}\hfill \end{array}.$$

For the weak financial institution, when there is no difference between “infringement” and “non-infringement” strategies in stage 1, ${\tilde{p}}_c^{**}V{B}_3+(1-{\tilde{p}}_c^{**})V{B}_4=V{B}_{SQ}$. We can obtain ${\tilde{p}}_c^{**}=\frac{V{B}_4-V{B}_{SQ}}{V{B}_4-V{B}_3}$. VB₃ and VB₄, respectively, are the perceived value of the outcome when the weak financial institutions meet tough and weak investors.

The tough investors always choose the “complaint” or “non-settlement” strategies. When ${\tilde{P}}_b^{\text{T}}>{\tilde{P}}_b^{*}$, the weak governments will choose the “non-regulation” strategy, VB₃ = VB_FV; otherwise, no matter whether tough or weak, governments will choose the “regulation” strategy at stage 3, $V{B}_3=p_g^{T}V{B}_{VW}+(1-p_g^T)V{B}_{FV}$.

The weak investors may choose the “complaint” strategy or “non-complaint” strategy. If ${\tilde{P}}_b^{\text{T}}<{\tilde{P}}_b^{*}$ and ${\tilde{P}}_b^{\text{T}}<{\tilde{P}}_b^{**}$, weak investors will choose the “complaint” strategy in stage 2, $V{B}_4=p_g^{T}V{B}_{VW}+(1-p_g^T)V{B}_{FSW}$; otherwise, they will choose the “non-complaint” strategy, VB₄ = VB_FW.

Then the strategic choice of the weak financial institutions at stage 1 is as follows:

$$X_b^W=\{\begin{array}{c}\hfill 1\hfill \\ \hfill [0,1]\hfill \\ \hfill 1\hfill \end{array}\begin{array}{c}\\ \end{array}\begin{array}{c}\hfill \stackrel{\sim \phantom{T}}{p_c^T}<\stackrel{\sim \phantom{**}}{p_c^{**}}\hfill \\ \hfill \stackrel{\sim \phantom{T}}{p_c^T}=\stackrel{\sim \phantom{**}}{p_c^{**}}\hfill \\ \hfill \stackrel{\sim \phantom{T}}{p_c^T}>\stackrel{\sim \phantom{**}}{p_c^{**}}\hfill \end{array}.$$

Analysis of the Different Equilibriums

We have analyzed the strategic choices and conditions of game players in the four stages. Next, we will discuss the different equilibriums in the tripartite regulation game.

Deterrence Equilibrium

When$X_b^T=X_b^W=0$, both the tough and weak financial institutions are constrained by the “status quo.” They will choose the “non-infringement” strategy. The equilibrium of deterrence at this time means the successful deterrence of governments. The deterrence equilibrium exists only if ${\tilde{P}}_c^{\text{T}}>{\tilde{P}}_c^{*}$ and ${\tilde{P}}_c^{\text{T}}>{\tilde{P}}_c^{**}$.

Challenge Equilibrium

When $X_b^T=X_b^W=1$, no matter whether financial institutions are tough or weak, they will choose the “infringement” strategy to reach the challenge balance, which means that the deterrence of governments fails. The conditions for the challenge equilibrium are ${\tilde{P}}_c^{\text{T}}<{\tilde{P}}_c^{*}$ and ${\tilde{P}}_c^{\text{T}}<{\tilde{P}}_c^{**}$.

Separation Equilibrium

When $X_b^T=1$ and $X_b^W=0$, different types of financial institutions will choose different strategies. The tough financial institutions will choose the “infringement” strategy, while the weak financial institutions will choose the “non-infringement” strategy. So as to achieve the separation equilibrium, governments successfully deter the weak financial institutions, but fail to deter the tough ones. The conditions for the existence of this equilibrium are ${\tilde{P}}_c^{\text{T}}<{\tilde{P}}_c^{*}$ and ${\tilde{P}}_c^{\text{T}}>{\tilde{P}}_c^{**}$.

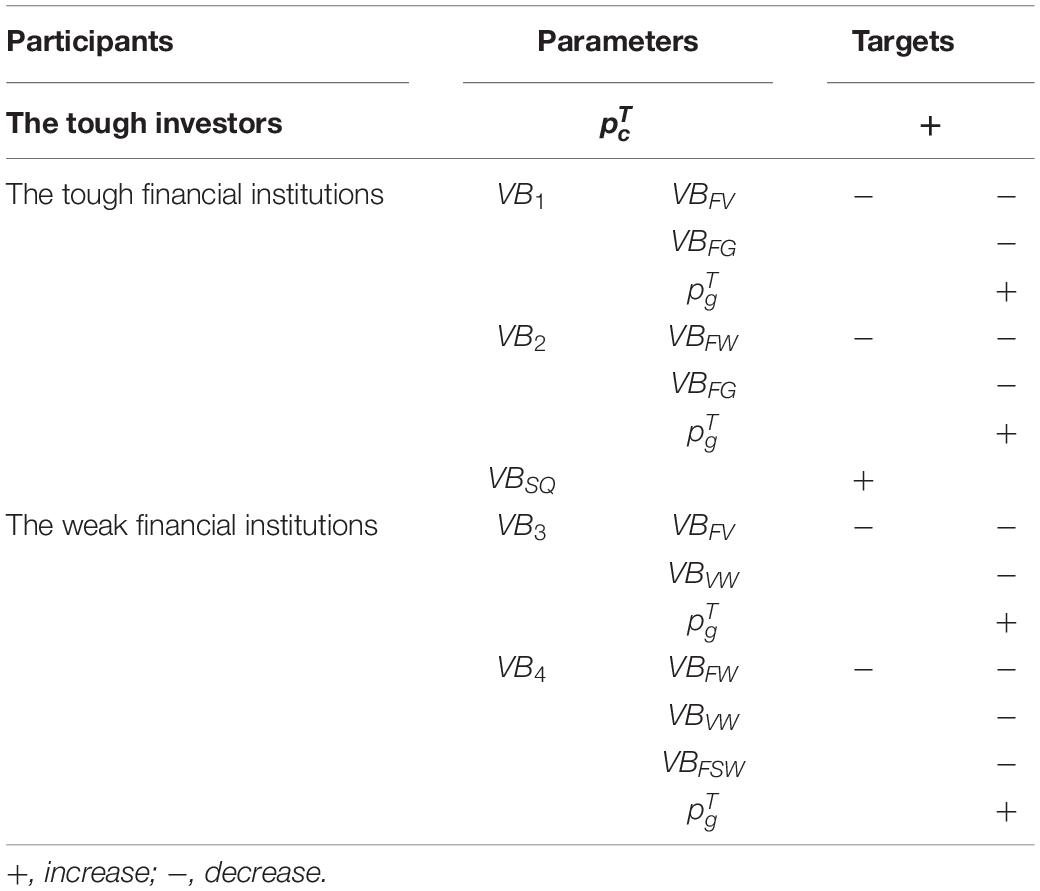
According to the analysis of the game model, the deterrence equilibrium is the optimal equilibrium scenario that governments want to achieve. At this time, no matter whether tough or weak ones, financial institutions will no longer choose infringement. Governments maximize the protection of investors and guaranteed the quality of CFPs. In summary, the condition of the deterrence equilibrium in the regulation game with model parameters is given in Table 2. It not only shows the critical influencing factors, but also demonstrates the relationship between the equilibrium strategies and the model parameters.

TABLE 2

Table 2. The conditions of the deterrence equilibrium in the regulation game.

Conclusion and Managerial Implications

In this paper, we theoretically analyzed the relationship of governments, financial institutions, and investors in CFPs, and then the tripartite regulation game of CFPs was explored. Moreover, taking bounded rationality into account, we also combined the prospect theory with the risk attitude of participants on the strategy selection. This study enriches the literature on the protection of investors and the validity of regulation for CFPs. Based on the perspective of governments, suggestions for improving the quality of CFPs are proposed as follows.

First, in terms of strategies for cultivating the tough investors, when the prior probability $P_c^T$ increased, it is beneficial for the realization of the deterrence equilibrium. The behavior characteristic of the tough investors is that they insist on safeguarding their rights and have a comprehensive understanding of the legality of their behaviors. The improvement of $P_c^T$ mainly depends on investors accurately grasping the information of CFPs.

Governments should encourage the tough investors so as to provide professional technical consultation systems for those involved in carbon trading to analyze, assess, and circumvent products and transaction risks. On the one hand, it is necessary to pay attention to the standardization of relevant knowledge. The intelligibility and content of products should be enhanced. When rights are infringed, investors have knowledge of rights protection and effectively identify the improper behaviors of financial institutions. On the other hand, to enhance the rights-protection awareness of investors, governments should publicize the knowledge of CFPs and build dispute mechanisms for rights protection. New media should also be fully utilized to enhance public participation and penetration.

Prospective interventional regulation of CFPs can be implemented, such as the selection of representative investors to carry out presale tracking evaluation, as a prerequisite for access, to reduce the asymmetry of market information. Furthermore, the evaluation of a regulatory index needs to be strengthened, incorporating the performance of financial institutions.

Second, regarding strategies for the tough financial institutions, when the perceived value VB₁ of them infringing rights of tough investors decreases, ${\tilde{p}}_c^{*}$ can be reduced, which is conducive to the realization of the deterrence equilibrium. The reduction of VB₁ can be achieved by reducing VB_FV, VB_FG, and increasing $p_g^T$.

To reduce VB_FV, the information from investors about the behavior of financial institutions needs to be collected. For example, an information database of rights protection can be established through targeted and random questionnaire surveys of the public, so as to dynamically grasp the situation regarding financial institutions’ infringement behaviors. The disposition of infringement incidents of financial institutions will be included in regulatory rating and linked to market access to form a continuous deterrent.

To decrease VB_FG, regulatory penalties should be increased. Once refusal to rectify or repeatedly checking infringement is found, accountability should be strictly implemented in accordance with the law, such as multidimensional accountability, confiscating illegal gains, and imposing fines. Penalties on financial institutions and holding those responsible accountable should be imposed at the same time. It is necessary to conduct a special regulation over financial institutions with serious problems, such as restricting market access and narrowing the scope of their business operations.

To increase $p_g^T$, governments should pay attention to public interests in order to evaluate the effectiveness of regulation. While improving the channels for handling disputes about rights protection, daily deterrence should be formed by various regulation methods, for example, being held strictly accountable for the dereliction of duty in the handling of disputes through disciplinary action and other means, so as to force regulators to fulfill their duties.

When the perceived value VB₂ decreases, ${\tilde{p}}_c^{*}$ can be reduced. Therefore, the deterrence equilibrium can be achieved by decreasing VB_FW, VB_FG, and increasing $p_g^T$ to lower VB₂. The initiative to rectify problems is an important indicator, which encourages them to take the initiative to make up for investors’ loss after infringement. Meanwhile, financial institutions should also examine their similar problems and increase initiatives to solve them.

When the perceived value of financial institutions VB_SQ is enhanced, ${\tilde{p}}_c^{*}$ can be reduced, which is conducive to realization of the deterrence equilibrium. The organizational behavior and management of financial institutions should be evaluated. Follow-up evaluations, including that of organizational culture, behavior management systems, post restriction, leadership style, and employee behavior performance, can be carried out. This will improve expectations about financial institutions regarding safeguarding rights of investors and implement reputation recognition with excellent work, which is closely related to products, and the tenure of senior executives.

Third, regarding strategies for the weak financial institutions, when the perceived value VB₃ decreases, ${\tilde{p}}_c^{**}$ can be reduced, so that the reduction of VB_FV and VB_VW, and the increase of $p_g^T$ are conducive to the realization of the deterrence equilibrium.

The reputations of financial institutions should be enhanced, paying attention to both infringement incidents and their handling of rights protection, and penalties should be reduced as appropriate for financial institutions that actively rectify problems. To strengthen evaluation of financial institutions, the effect of responding to lawsuits and investors’ satisfaction with rights protection should be taken seriously. Meanwhile, attention should also be paid to financial institutions’ internal transmission efficiency when responding to complaints, so as to improve the management level of similar products.

When the weak financial institutions infringe on weak investors, the perceived value VB₄ decreases, and ${\tilde{p}}_c^{**}$ can be reduced. VB₄ can be reduced by reducingVB_FW, VB_VW, and VB_FSW and increasing $p_g^T$, which is conducive to the realization of the deterrence equilibrium. To reduce the perceived value VB_FSW of financial institutions, investors should be regularly informed about the disposition of rights-protection disputes, so that they can dispel the fluke mentality. There is a need to keep track of settlement results of disputes and make investors’ rights protection effectively.

In this paper, we studied the tripartite game among stakeholders involved in CFPs and discussed their strategy. This study provides a theoretical basis and lays the foundation for improving the quality of CFPs. Future research can use the insights of this study to discuss the difference among specific regulation policies, such as subsidy and carbon credit. Additionally, games among stakeholders of CFPs are repeated, and the repeated games also need to be researched. Moreover, it would be interesting to use relevant cases to conduct an empirical application and analysis of the game models.

Data Availability Statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding author.

Author Contributions

All authors contributed to the study conception, design, read, and approved the final manuscript.

Funding

This research was funded by the Shandong Provincial Natural Science Foundation (Grant Nos. ZR2017QG003 and ZR2016GM10), the National Natural Science Foundation of China (Grant No. 41801173), the Shandong Provincial Social Science Foundation (Grant No. 17DGLJ09), and the China Postdoctoral Science Foundation (Grant No. 2017M622265).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

We gratefully acknowledge the helpful comments and suggestions of the reviewers, which have improved the presentation.

References

Australian Transaction Reports and Analysis Centre (AUSTRAC) (2011). AUSTRAC Typologies and Case Studies Report 2011. Canberra: Australian Government, 28–29.

Google Scholar

Badunenko, O., and Kumbhakar, S. C. (2017). Economies of scale, technical change and persistent and time-varying cost efficiency in Indian banking: do ownership, regulation and heterogeneity matter? Eur. J. Operat. Res. 260, 789–803. doi: 10.1016/j.ejor.2017.01.025

CrossRef Full Text | Google Scholar

Berger, A. N., Hasan, I., and Zhou, M. M. (2009). Bank ownership and efficiency in China: what will happen in the world’s largest nation? J. Bank. Finance 33, 113–130. doi: 10.1016/j.jbankfin.2007.05.016

CrossRef Full Text | Google Scholar

BNEF (2014). Global Trends in Clean Energy Investment. New York, NY: Financial information service provider.

Google Scholar

Brunner, T., Reiner, J., Natter, M., and Skierab, B. (2019). Prospect theory in a dynamic game: theory and evidence from online pay-per-bid auctions. J. Econ. Behav. Organ. 164, 215–234. doi: 10.1016/j.jebo.2019.05.032

CrossRef Full Text | Google Scholar

Campiglio, E. (2016). Beyond carbon pricing: the role of banking and monetary policy in financing the transition to a low-carbon economy. Ecol. Econ. 121, 220–230. doi: 10.1016/j.ecolecon.2015.03.020

CrossRef Full Text | Google Scholar

Casu, B., Ferrari, A., and Zhao, T. S. (2013). Regulatory reform and productivity change in indian banking. Rev. Econ. Stat. 95, 1066–1077. doi: 10.1162/REST_a_00298

CrossRef Full Text | Google Scholar

Eyraud, L., Clements, B., and Wane, A. (2013). Green investment: trends and determinants. Energy Policy 60, 852–865. doi: 10.1016/j.enpol.2013.04.039

CrossRef Full Text | Google Scholar

Girod, B. (2016). Product-oriented climate policy: learning from the past to shape the future. J. Clean. Product. 128, 209–220. doi: 10.1016/j.jclepro.2015.07.010

CrossRef Full Text | Google Scholar

Hu, M., Zhang, D. Y., Ji, Q., and Wei, L. J. (2020). Macro factors and the realized volatility of commodities: a dynamic network analysis. Resour. Policy 68:101813. doi: 10.1016/j.resourpol.2020.101813

CrossRef Full Text | Google Scholar

IEA (2012). Energy Technology Perspectives 2012. Paris: International Energy Agency.

Google Scholar

Ji, Q., and Zhang, D. Y. (2019). How much does financial development contribute to renewable energy growth and upgrading of energy structure in China? Energy Policy 128, 114–124. doi: 10.1016/j.enpol.2018.12.047

CrossRef Full Text | Google Scholar

Layfield, D. (2013). Turning carbon into gold: the financialisation of international climate policy. Environ. Polit. 22, 901–917. doi: 10.1080/09644016.2012.737252

CrossRef Full Text | Google Scholar

Li, L., Liu, Q. Q., Wang, J., and Hong, X. F. (2019). Carbon information disclosure, marketization, and cost of equity financing. Int. J. Environ. Res. Public Health 16:150. doi: 10.3390/ijerph16010150

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, X., and Li, Y. J. (2016). Chain-to-chain competition on product sustainability. J. Clean. Product. 112, 2058–2065. doi: 10.1016/j.jclepro.2014.09.027

CrossRef Full Text | Google Scholar

Li, X. Y., Zhang, D. Y., Zhang, T., Ji, Q., and Lucey, B. (2020). Awareness, energy consumption and pro-environmental choices of Chinese households. J Clean. Product. 279:123734. doi: 10.1016/j.jclepro.2020.123734

CrossRef Full Text | Google Scholar

Li, J. J., Zhang, J., Zhang, D., and Ji, Q. (2019). Does gender inequality affect household green consumption behaviour in China? Energy Policy 135:111071. doi: 10.1016/j.enpol.2019.111071

CrossRef Full Text | Google Scholar

Liao, X. C., and Shi, X. P. (2018). Public appeal, environmental regulation and green investment: evidence from China. Energy Policy 119, 554–562. doi: 10.1016/j.enpol.2018.05.020

CrossRef Full Text | Google Scholar

Liu, C. Y., and Xia, T. S. (2020). Strategy analysis of governments and new energy product manufacturers and consumers based on evolutionary game model. Soft Comput. 24, 6445–6455. doi: 10.1007/s00500-019-04571-6

CrossRef Full Text | Google Scholar

Lou, Z. K., Lou, X. M., and Dai, X. Z. (2020). Game-theoretic models of green products in a two-echelon dual-channel supply chain under government subsidies. Math. Problems Eng. 2020:2425401. doi: 10.1155/2020/2425401

CrossRef Full Text | Google Scholar

Lu, Z. J., and Shao, S. (2016). Impacts of government subsidies on pricing and performance level choice in energy performance contracting: a two-step optimal decision model. Appl. Energy 184, 1176–1183. doi: 10.1016/j.apenergy.2016.05.106

CrossRef Full Text | Google Scholar

Munnings, C., Morgenstern, R. D., Wang, Z. M., and Liu, X. (2016). Assessing the design of three carbon trading pilot programs in China. Energy Policy 96, 688–699. doi: 10.1016/j.enpol.2016.06.015

CrossRef Full Text | Google Scholar

Raberto, M., Ozel, B., Ponta, L., Teglio, A., and Cincotti, S. (2019). From financial instability to green finance: the role of banking and credit market regulation in the Eurace model. J. Evol. Econ. 29, 429–465. doi: 10.1007/s00191-018-0568-2

CrossRef Full Text | Google Scholar

Shu, T., Peng, Z. Z., Chen, S., Wang, S. Y., Lai, K. K., and Yang, H. L. (2017). Government subsidy for remanufacturing or carbon tax rebate: which is better for firms and a low-carbon economy. Sustainability 9, 1–22. doi: 10.3390/su9010156

CrossRef Full Text | Google Scholar

Sun, Z. Y., and Zhang, W. W. (2019). Do government regulations prevent greenwashing? An evolutionary game analysis of heterogeneous enterprises. J. Clean. Product. 231, 1489–1502. doi: 10.1016/j.jclepro.2019.05.335

CrossRef Full Text | Google Scholar

Vahid-Pakdel, M. J., Ghaemi, S., Mohammadi-ivatloo, B., Salehi, J., and Siano, P. (2019). Modeling Noncooperative Game of GENCOs’ participation in electricity markets with prospect theory. IEEE Trans. Ind. Inform. 15, 5489–5496. doi: 10.1109/tii.2019.2902172

CrossRef Full Text | Google Scholar

Van de Broek, M., Henriksen, C. B., Ghaley, B. B., Lugato, E., Kuzmanovski, V., Trajanov, A., et al. (2019). Assessing the climate regulation potential of agricultural soils using a decision support tool adapted to stakeholders’ needs and possibilities. Front. Environ. Sci. 7:131. doi: 10.3389/fenvs.2019.00131

CrossRef Full Text | Google Scholar

WEF (2013). The Green Investment Report. Geneva: World Economic Forum.

Google Scholar

Xu, X. F., Wei, Z. F., Ji, Q., Wang, C. L., and Gao, G. W. (2019). Global renewable energy development: influencing factors, trend predictions and countermeasures. Resour. Policy 63:101470. doi: 10.1016/j.resourpol.2019.101470

CrossRef Full Text | Google Scholar

Xu, X. Y., Xu, X. P., and He, P. (2016). Joint production and pricing decisions for multiple products with cap-and-trade and carbon tax regulations. J. Clean. Product. 112, 4093–4106. doi: 10.1016/j.jclepro.2015.08.081

CrossRef Full Text | Google Scholar

Yang, M., Hou, Y. R., Ji, Q., and Zhang, D. Y. (2020). Assessment and optimization of provincial CO2 emissions reduction scheme in China: an improved ZSG-DEA approach. Energy Econ. 91:e104931. doi: 10.1016/j.eneco.2020.104931

CrossRef Full Text | Google Scholar

Zhang, D. Y., Li, J., and Ji, Q. (2020). Does better access to credit help reduce energy intensity in China? Evidence from manufacturing firms. Energy Policy 145:111710. doi: 10.1016/j.enpol.2020.111710

CrossRef Full Text | Google Scholar

Zhang, L. H., Zhou, H., Liu, Y. Y., and Lu, R. (2019). Optimal environmental quality and price with consumer environmental awareness and retailer’s fairness concerns in supply chain. J. Clean. Product. 213, 1063–1079. doi: 10.1016/j.jclepro.2018.12.187

CrossRef Full Text | Google Scholar

Zhang, S. Y., Wang, C. X., and Yu, C. (2019). The evolutionary game analysis and simulation with system dynamics of manufacturer’s emissions abatement behavior under cap-and-trade regulation. Appl. Math. Comput. 355, 343–355. doi: 10.1016/j.amc.2019.02.080

CrossRef Full Text | Google Scholar

Zhao, N., Xia, T. S., Yu, T., and Liu, C. Y. (2020). Subsidy-related deception behavior in energy-saving products based on game theory. Front. Energy Res. 7:154. doi: 10.3389/fenrg.2019.00154

CrossRef Full Text | Google Scholar

Zhao, X., Bai, Y., Ding, L. L., and Wang, L. (2020). Tripartite Evolutionary Game Theory Approach for Low-Carbon Power Grid Technology Cooperation With Government Intervention. IEEE Access 8, 47357–47369. doi: 10.1109/access.2020.2974666

CrossRef Full Text | Google Scholar

Zhou, Z. F., Zhang, L. Y., Lin, L., Zeng, H. X., and Chen, X. H. (2020). Carbon risk management and corporate competitive advantages: “Differential promotion” or “cost hindrance”? Bus. Strategy Environ. 29, 1764–1784. doi: 10.1002/bse.2468

CrossRef Full Text | Google Scholar

Zhou, Z. F., Zhang, T., Wen, K., Zeng, H. X., and Chen, X. H. (2018). Carbon risk, cost of debt financing and the moderation effect of media attention: evidence from Chinese companies operating in high-carbon industries. Bus. Strategy Environ. 27, 1131–1144. doi: 10.1002/bse.2056

CrossRef Full Text | Google Scholar