Quantifying Cooperation Benefits for New Dams in Transboundary Water Systems Without Formal Operating Rules

Introduction

Growing food, water and energy demand is fuelling the expansion of water resources infrastructure such as dams (Zarfl et al., 2014; Siciliano et al., 2018; Gerlak et al., 2020). New infrastructure can modify a river’s flow regime impacting benefits and services provided by existing downstream infrastructure and natural assets like wetlands or floodplains. These often play a central role in the functioning of aquatic ecosystems and of local communities by providing food and drinking water supply services (Mul et al., 2017). Furthermore, new infrastructure can generate or intensify conflicts between different basin stakeholders, especially in transboundary river basins without cooperative water management arrangements (Sadoff and Grey, 2009; Basheer et al., 2018; Wheeler et al., 2018). In this context, water resource systems models can be used to identify and quantify the potential impacts of new infrastructure and different operating policies of existing and new infrastructure (Loucks, 1992; Thiessen and Loucks, 1992).

Motivated by the need to identify the best possible approaches to share transboundary waters, optimisation models have often been used to filter through the nearly unlimited ways water sharing rules could be structured and parametrised. Different methods have been applied including linear optimisation (e.g., Kucukmehmetoglu and Guldmann, 2004, 2010; Porse et al., 2015), stochastic dynamic programming and stochastic dual dynamic programming (e.g., Tilmant and Kinzelbach, 2012; Tilmant et al., 2012; Arjoon et al., 2014; Kahsay et al., 2019). Kucukmehmetoglu and Guldmann (2004) use a linear optimisation model to identify optimal allocation of water resources in the Euphrates and Tigris river basin considering water demands for irrigation, urban consumption and hydropower generation, where the economic consequences of different strategies with cooperative and non-cooperative scenarios were assessed. Arjoon et al. (2014) use a stochastic dual dynamic programming model to assess the hydro-economic risk of the Grand Ethiopian Renaissance Dam (GERD) in the eastern Nile river basin, where they demonstrated that if the riparian countries (Ethiopia, Sudan, and Egypt) agree to cooperative management in the basin, the GERD would increase the basin-wide benefits, increasing water security in Sudan and Egypt during dry years.

Other scholars have sought to more realistically represent institutional realities and motivations within models. Methods used in this vein include for example agent-based models (e.g., Becker and Easter, 1999; Kilgour and Dinar, 2001; Giuliani and Castelletti, 2013; Yoon et al., 2021) and game theory (e.g., Bennett et al., 1998; Bhaduri and Liebe, 2013; Bhagabati et al., 2014). Giuliani and Castelletti (2013) presented a multiagent decision-analytic framework to model and analyse different levels of cooperation and information exchange among multiple decision makers in the Zambezi river basin. Bhagabati et al. (2014) investigated the net benefits of hydropower developments and water resource utilisation in the Mekong transboundary river basin using a game theory approach where different adaptation strategies that benefit all riparian countries were proposed. A potential advantage of game theory or agent-based methods is their ability to represent more realistic scenarios of non-cooperation and non-centralised management in transboundary systems, involving multiple institutional or stakeholder interests. These methods assume each agent or institution can give priority to their own objectives and the interactions between parties can be identified and described (Madani, 2010; Giuliani and Castelletti, 2013). Optimisation techniques typically assume all parties are willing to cooperate and exchange information to achieve better system-wide outcomes; in practice this can be unrealistic given the political and institutional contexts within transboundary river basins (Giuliani and Castelletti, 2013).

Classical optimization, agent-based and game theory methods may however be difficult to apply when representing large-scale complex systems including non-linear physical and institutional processes. In this case rule-based simulation of water resources systems (Loucks, 1992; Loucks and Van Beek, 2005; Matrosov et al., 2011) can be helpful because they do not require assuming optimising behaviours and they can be applied to large-scale complex real-world non-linear water systems, coupling hydrological complexity with the complexity of human water management rules. Simulation models allow to test and refine management strategies through scenario simulation and can incorporate water management impact information from ecology, economics and stakeholder-informed metrics of performance (Wurbs, 1993; Loucks and Van Beek, 2005; Harou et al., 2009; Voinov et al., 2016). Water resource management simulation models can help improve stakeholder understanding of large-scale and complex systems and thereby contribute to their design, management, and operation (Hall et al., 2019).

In the last decade hybrid simulation-optimisation methods have become popular; this involves simulating a variety of behaviours (without necessarily assuming optimising agents), then linking simulators to external independent search algorithms which help filter through the numerous system design and management options whilst considering the motivation and behaviours of simulated agents. Linking water resources system simulators to multi-objective evolutionary algorithms (MOEAs) has proven effective at allowing water manager and planners to assess trade-offs among conflicting objectives and explore strategies under multiple plausible future scenarios (e.g., Kasprzyk et al., 2009; Herman et al., 2014; Zeff et al., 2014; Matrosov et al., 2015; Huskova et al., 2016; Giuliani et al., 2018; Wheeler et al., 2018; Geressu and Harou, 2019; Wild et al., 2019). MOEAs use search techniques to approximate a multidimensional Pareto front identifying a non-dominated (“best achievable”) set of intervention strategies (Reed and Kasprzyk, 2009; Maier et al., 2014, 2018). For the different system design and/or management alternatives identified in the Pareto front, an incremental change made to improve one objective will come at the expense of one or more other objectives (i.e., the system has reached a level of system performance where any further improvement will necessarily come at a cost). The resulting multi-objective trade-off analysis can assist stakeholders in managing or planning river system infrastructure and services. Example applications, several of which are in Africa, include (e.g., Hurford and Harou, 2014; Smith et al., 2015; Zeff et al., 2016; Geressu et al., 2020; Hurford et al., 2020a,b).

To date, there have been relatively few multi-objective trade-off studies in transboundary water systems seeking to assess whether a new development in one country may or may not conflict with benefits in others (Geressu and Harou, 2015; Wheeler et al., 2018). For example, Giuliani et al. (2016a) explored the impact of different climate projections on existing infrastructure in the Red river basin, shared by China and Vietnam. They used many-objective Direct Policy Search (Giuliani et al., 2014) to identify optimal reservoir operations that offset possible negative impacts on hydropower generation in the basin. Wheeler et al. (2018) presented a framework to evaluate the impact of the GERD in Ethiopia on the downstream infrastructure in the eastern Nile basin. They coupled the Borg MOEA (Hadka and Reed, 2013) with a hydro policy model of the basin to explore different management infrastructure strategies under different levels of cooperation between the riparian countries. Schmitt et al. (2019) proposed a multi-objective optimisation-based framework for planning dams in the transboundary Mekong basin considering trade-offs between sediment and hydropower.

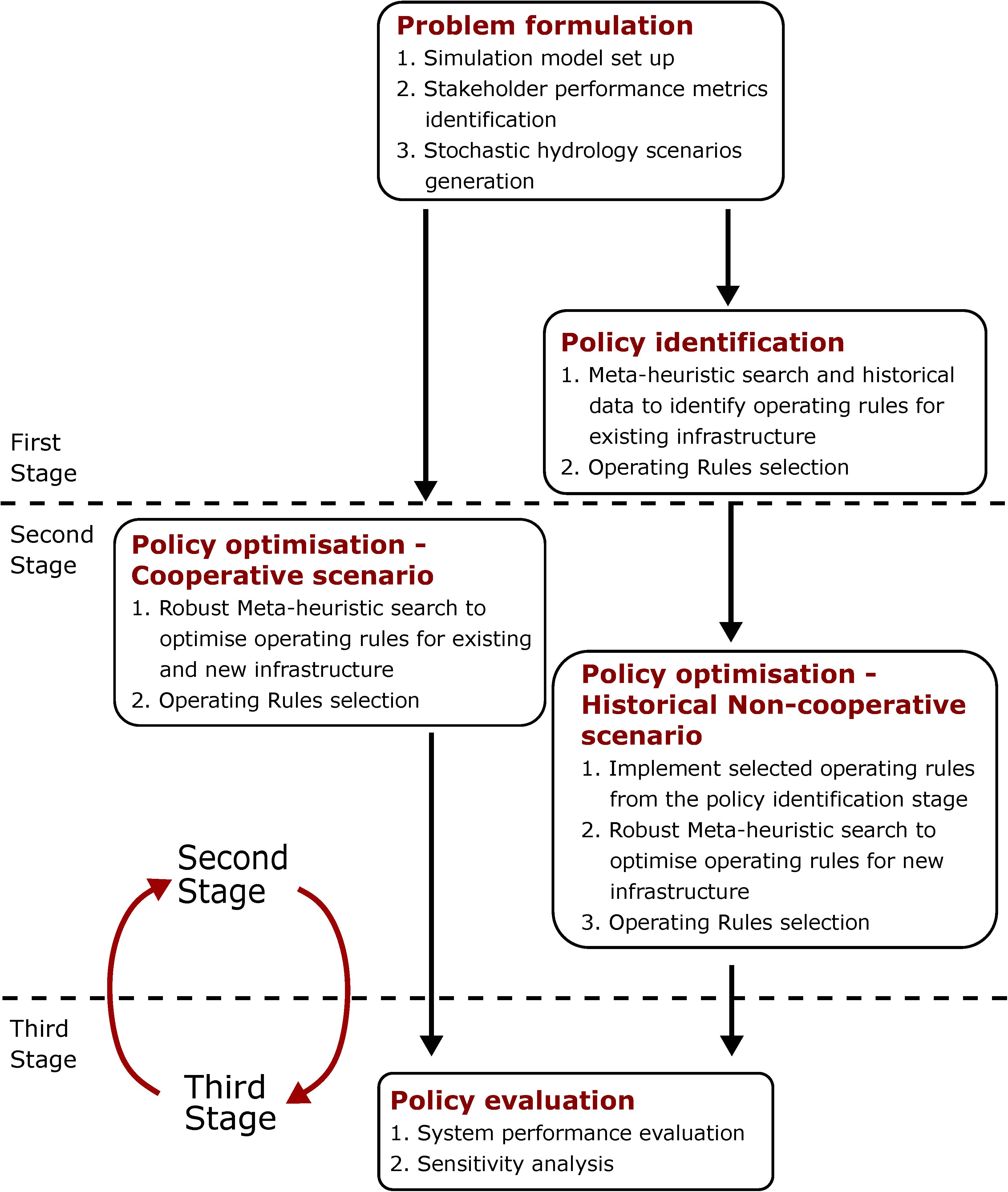
This study builds on the multi-objective water system design literature contributing a multi-objective framework for evaluating impacts of new dams on the performance of existing natural and built transboundary basin systems with poorly codified operating rules. The proposed methodology is divided into three stages. Stage one uses a policy identification approach (Giuliani et al., 2014), based on many-objective direct policy search, to identify historical operating policies for existing infrastructure using observed operational data (observed flow and storage volume); stage two, based on two scenarios, cooperative and historical non-cooperative, identifies optimal operational strategies for new infrastructure; finally, in stage three, a stochastic evaluation of the operating policies identified in stages one and two is conducted. The cooperative scenario assumes transparent coordination between the riparian countries and infrastructure operators through a central water management institution in the basin. The historical non-cooperative scenario omits coordination of historical operations with new infrastructure. The framework is applied to the new Pwalugu Multipurpose Dam (PMD), in Ghana, within the Volta river basin. The new dam is designed to produce hydropower, provide flood protection, food production and employment via a new irrigation scheme. Our application aims to demonstrate how formal synergistic operation of new and existing infrastructure in the transboundary, multi-reservoir Volta basin could improve water resource system ecosystem services for multiple actors.

The paper is organised as follows: section “The Volta River Basin Context” presents a description of the Volta river basin; section “Methods and Tools” introduces the Volta river basin simulation model and describes the methods. Section “Results and Discussion” presents and discusses results and section “Conclusion” concludes.

The Volta River Basin Context

Basin Description

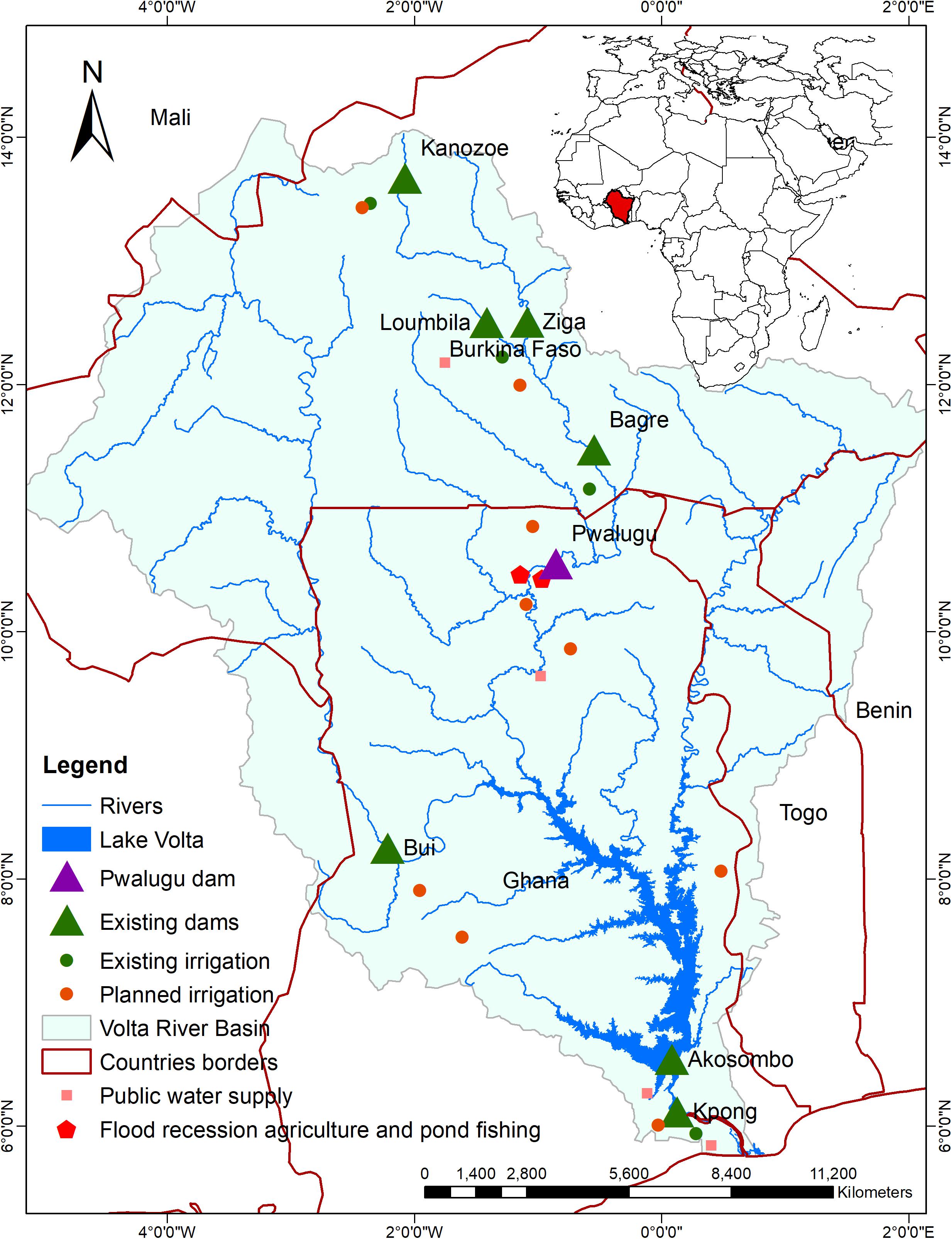
The Volta river basin (Figure 1) is located in West Africa and is shared by six riparian countries where Ghana and Burkina Faso make up the largest area of 42 and 43%, respectively, while the remaining 15% is distributed between Benin, Côte d’Ivoire, Mali and Togo (Mul et al., 2015). The Volta’s total average annual flow is approximately 40,400 [Mm³ year^–1] and making it one of the major rivers of Africa (McCartney et al., 2012). The Volta’s water resources are used for irrigation, hydropower generation, fisheries, domestic, industrial, mining, livestock, and water transport. According to Mul et al. (2015), and Baah-Kumi and Ward (2020) different factors such as high population growth, climate change, floods in wet seasons, and increased economic activity have motivated new infrastructure to regulate flow in the basin. Proposed infrastructure includes single and multi-purpose dams for hydropower, large-scale irrigation schemes and public water supply.

FIGURE 1

Figure 1. Volta river basin. Location of infrastructure in the six-country river basin.

Figure 1 shows the most relevant built and natural assets (existing and planned) in the basin. Existing built infrastructure includes the Kanozoe, Ziga, Loumbila, Bagre Dams in the White Volta, Kompienga dam in the Oti, Bui dam in the Black Volta, and Akosombo and Kpong dams in the Lower Volta, and associated irrigation schemes. Existing natural assets includes the floodplain downstream of Pwalugu, which floods annually when the White Volta river overflows, distributing water and sediments beyond the riverbanks. The floodplain supports local communities’ livelihoods enabling flood recession agriculture (FRA), pond fishing, year-round domestic water supply and grazing grounds for livestock during the dry season (Mul et al., 2017).

The PMD is being implemented in the White Volta sub-basin in the Upper East region of Ghana, downstream of the Bagre Dam in Burkina Faso (Mosello et al., 2017; Baah-Kumi and Ward, 2020). The project is managed by the Volta River Authority (VRA), in collaboration with the Ghana Irrigation Development Authority (GIDA) and funded by the Ghanaian government. The PMD is expected to contribute to the development of Northern Ghana, one of the countries’ poorest regions (Darko et al., 2019). According to Volta River Authority (2018) the PMD has the potential to irrigate 20,000 ha and to produce 176 GWh. Another function of the PMD would be flood protection resulting from intense rainfall events in northern Ghana, exacerbated by spills from the Bagre Dam (Darko et al., 2019).

Context for the Development of Pwalugu Dam

The Volta river basin in West Africa is shared between six countries with Ghana and Burkina Faso covering over 80% of the area and where most of the large water infrastructures in the basin are found (Mul et al., 2015). Water resources in the basin provide essential services that support the economies of its riparian communities and wider countries (Mul et al., 2015, 2017). Ecosystem services and water resources infrastructure in the basin facilitate food production, access to renewable and cheap energy via hydropower, flood protection and provision of water for industrial and domestic use (Baah-Kumi and Ward, 2020). In the last two decades Ghana and Burkina Faso have experienced significant economic and population growth putting increased pressure on their water resources. This led the two governments and the transboundary basin agency, the Volta Basin Authority (VBA), to consider developing some new infrastructure to control and increase water availability in the basin as well as provide other benefits such as increased food production via formal irrigation schemes and hydropower. The VBA is a basin-wide institution that, among other mandates, is developing a transboundary cooperative institutional framework to guide future water use in the multi-country basin (Baah-Kumi and Ward, 2020).

The PMD is located on the White Volta sub-basin close to the Pwalugu village in the Upper East region of Ghana, downstream of the Bagre Dam in Burkina Faso (Mosello et al., 2017; Baah-Kumi and Ward, 2020). The main benefit of the dam is considered to be hydropower production, which is aimed at increasing energy connectivity in the northern regions of the country. The dam will also, provide flood protection, food production and employment via a new irrigation scheme. As an energy exporting country, Ghana would benefit from increasing overall hydropower production, which also supplies Burkina Faso. However, while providing these benefits, the PMD could disrupt the current flow regime which allows FRA and pond fishing (Mul et al., 2017). Also, reduced downstream water availability because of increased water storage, evaporation and irrigation water use may reduce hydropower production downstream at Akosombo (Baah-Kumi and Ward, 2020). Furthermore, the PMD itself could be impacted by the operation of the existing Bagre Dam or expansion of the irrigated area upstream in Burkina Faso. Ideally these dams would be operated jointly to maximise the benefits to both countries and to limit negative impacts. However, despite the existence of the transboundary VBA basin-wide agency, current management and development initiatives amongst the riparian countries are relatively uncoordinated (Baah-Kumi and Ward, 2020). For example, historically, more than 80% of the annual inflow into the Bagre Dam is spilt during peaks flow periods (August/September) (Mul et al., 2017; Darko et al., 2019) contributing to flooding in Northern Ghana. Floods in Northern Ghana have led to the deaths of more than 63 people and displaced over 100,000 in addition to causing widespread damage to farmlands, roads, houses, and bridges (Davies, 2018; IFRC, 2019). According to Baah-Kumi and Ward (2020), Ghana and Burkina Faso have agreed that Burkina Faso will provide 2 weeks’ notice before the start of annual Bagre Dam spillage in late August or early September, allowing Ghana take mitigation measures to reduce flood damage.

Methods and Tools

The framework presented in this study (Figure 2) is composed of three stages. Stage 1 formulates the planning and management problem and identifies historical operating rules when information about them is not available. The policy identification step calibrates a river basin simulation model representing existing infrastructure to available historical data via many-objective optimisation; in the literature this has also been referred to as “direct policy search” (Giuliani et al., 2014). This identifies operating policies for existing infrastructure that reproduce the system’s historical operation under the observed inflow, release, and storage volume time series. In Stage 2, two scenarios, cooperative and historical non-cooperative, are defined and a robust many-objective direct policy search is implemented to design new infrastructure operating policies for both existing and planned assets. In Stage 3 evaluation of the operational policies over an ensemble of plausible futures and sensitivity analysis are conducted.

FIGURE 2

Figure 2. Schematic of the proposed framework.

The cooperative scenario represents a situation where there is a central water management institution in the basin (as is the case of the Volta river basin) and where the countries and the infrastructure operators agree management strategies of existing and future infrastructure. This scenario also assumes all data is shared (inflows, water demands, water withdrawals, and future developments) across the basin. This assumption is not always met in practice given the political and institutional settings in many transboundary basins (Giuliani and Castelletti, 2013). However, according to Sadoff and Grey (2009) an integration scenario that recognises the opportunities for distribution of benefits and costs, and the different alternatives of cooperation, is a worthy goal of integrated water resources management. The historical non-cooperative scenario assumes there is no cooperation between the riparian countries and infrastructure operators with regards to reservoir operation. Here, the upstream countries maximise their benefits without consideration of the impacts on the downstream countries built or natural assets.

Volta River Basin Simulation Model

The river basin simulation uses the Python Water Resources model (Pywr), a Python-based water resources system simulator freely available as an open-source Python library (Tomlinson et al., 2020). Pywr is an optimisation-driven simulator and solves a linear program at every simulation time-step to allocate water to different nodes by minimising allocation penalties. The model can be summarised by a mass balance equation Eq. (1) solved at each node in the network representing incremental catchment inflow and water demands at ecosystem service delivery and infrastructure locations:

$$S_{t+1,n}=S_{t,n}+q_{t,n}-e_{t,n}\left(h_{t,n}\right){\text{C}}^{\text{R}}\left(\sum _{\forall i}{u}_{t,n}^i-s{p}_{t,n}\right)\mathit{\hspace{1em}}\forall t,n(1)$$

where, S_t,n is the volume of water stored in the reservoirs at node n, in time-step t; $u_{t,n}^i$ represents the water allocation for the water uses (i) in the system, namely public water supply (pws), hydropower (hp), and irrigation schemes (is). Irrigation demand is defined by the water demand of each crop (ct) integrating an irrigation scheme whilst sp_t,n denotes spill flows from reservoirs; q_t,n represents the inflows to the nodes and e(⋅)_t,n represent evaporation, which uses on the water level h_t,n in the reservoir to determine its real-time surface area using a bathymetry curve. C^R is the network connectivity matrix in the system [${\text{C}}_{\mathrm{j},\mathrm{k}}^{\text{R}}=1\left(-1\right)$ where node j receives water from (to) node k]. For releases to consumptive water uses (mainly irrigation uses), the network connectivity matrix tracks possible flows that return to the network as a fraction of the release.

Figure 3 shows the network schematic of the Volta river basin simulation model, and a screenshot of an online model deployment (Knox et al., 2019) which allows its access by collaborating parties. The model includes the existing infrastructure in the basin and the proposed PMD project (Table 1). Existing built infrastructure in Burkina Faso includes the Kanozoe dam and attached Yako irrigation scheme; the Loumbila dam that provides water to an irrigation scheme and public water supply to Ouagadougou the capital of Burkina Faso; the Ziga dam provides most of the public water supply to Ouagadougou and the Bagre Dam that produces hydropower and provides water to an existing irrigation scheme. Modelled existing infrastructure in Ghana includes the Bui dam and attached irrigation scheme; the Akosombo dam and the Kpong run-of-river hydropower plant and an irrigation scheme associated to Kpong. Also, aggregated public water supply for the Ghana Water Company Limited is modelled downstream of the PMD near the city of Tamale as well as aggregated abstractions from Lake Volta and an abstraction downstream of Kpong for Accra.

FIGURE 3

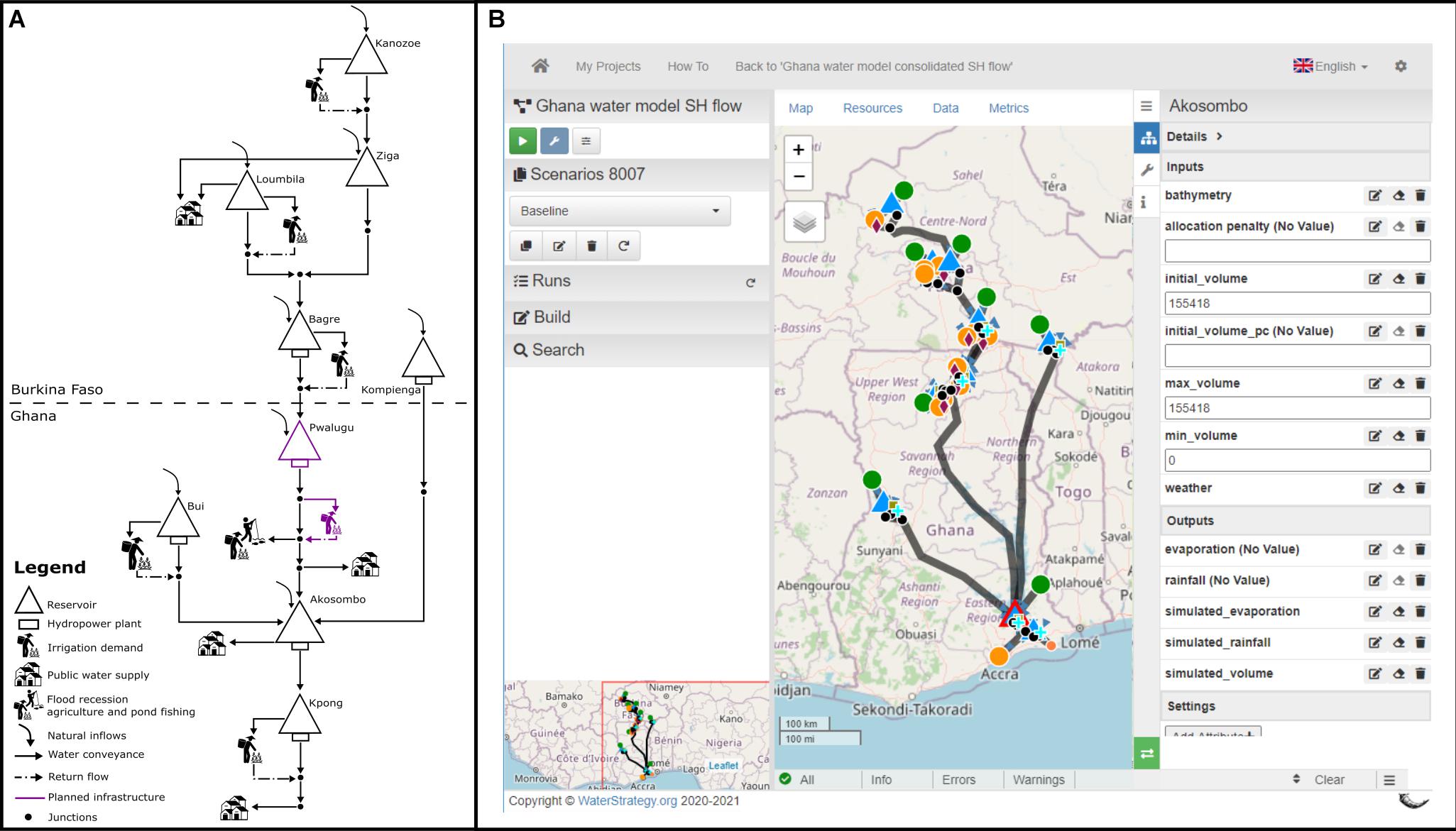
Figure 3. Panel (A) shows the Volta river basin simulation model schematic, and panel (B) shows a screenshot of the WaterStrategy online interface (Knox et al., 2019) which allows collaborative development and use of the Python water resource simulation model (Pywr).

TABLE 1

Table 1. Summary of the existing and future built and natural infrastructure.

Modelled natural assets include FRA and pond fishing, downstream of the PMD. These benefits are made possible by the annual flood that occurs during the rainy season. Floods deposit nutrients that replenish the soil, enabling the practice of FRA by the local inhabitants. As the flood recedes, depressions in the banks are left with residual floodwater containing fish, allowing residents to perform pond fishing during an annual ceremony (Mul et al., 2017).

Performance Metrics

Performance metrics quantify the benefits generated by the built and natural assets in the Volta river basin. Metrics include annual and firm hydropower production, irrigation yield, prescribed environmental flows downstream of the PMD, and FRA benefits. The flood recession pond fishing benefit was considered in the simulation model, however, it was not incorporated in the optimisation process. The impact analysis on natural assets was focused on FRA because this activity represented greater financial benefits compared to the flood recession and pond fishing benefits.

Hydropower Generation

The Volta water model quantifies the average Annual Energy production [GWh year^–1], and the Firm Power at 90% exceedance of each hydropower dam:

$$H{P}_{t,n}=\mathrm{\eta }g{\mathrm{\gamma }}_w{h}_{t,n}{u}_{t,n}^{hp}(2)$$

$$f_n^{AE}=max\left[\underset{\mathrm{\Xi }}{mean}\left(\frac{1}{T}\sum _{t=1}^{T}H{P}_{t,n}\right)\right](3)$$

$$f_n^{FP}=max\left[\underset{\mathrm{\Xi }}{mean}(H{P}_{90,n}:P(H{P}_{t,n}=H{P}_{90,n})=0.90)\right](4)$$

where, HP_t,n is the hydropower generation; η is the turbine efficiency [%] (Akosombo = 0.93, Kompienga = 0.85, Bagre = 0.8, Bui = 0.85, Pwalugu = 0.9 and Kpong = 0.93); g is the gravitational acceleration constant, 9.8m s^–2; γ_w is the water density [kg m^–3]; h_t,n is the net hydraulic head [m]; T is the simulation time horizon and Ξ represents the hydrological ensemble. Finally, $f_n^{AE}$ and $f_n^{FP}$ are the average Annual Energy and Firm Power metrics, respectively.

Irrigation

Benefits of formal irrigation schemes are represented by irrigation yield. Each scheme’s irrigation water demand and yield are estimated by using the Crop Water Requirements method proposed by the FAO (Allen et al., 1998):

$$CW{R}_{t,(ct\in n)}=max(0,K{c}_{t,(ct\in n)}(ET{o}_{t,(ct\in n)}-R_{t,n})A_{(ct\in n)})(5)$$

$$IW{R}_{t,n}=\sum _{ct\in n}\frac{CW{R}_{t,(ct\in n)}}{{\mathrm{\alpha }}_{ct}{\mathrm{\beta }}_{ct}}(6)$$

$$C{R}_{t,n}=\frac{u_{t,n}^{is}}{IW{R}_{t,n}}(7)$$

$$f_n^Y=mean\left[\underset{\mathrm{\Xi }}{mean}\left(\frac{1}{T}\sum _{t=1}^{T}C{R}_{t,n}\left(A_n{y}_n\right)\right)\right](8)$$

where, CWR_t,n is the crop water requirement per node (irrigation scheme) and per month (m ∈ t). Kc_{t,(ct ∈ n)}, ETo_{t,(ct ∈ n)}, and R_t,n are the monthly crop water coefficient, effective evapotranspiration [mm day^–1] per crop and effective precipitation [mm day^–1], obtained from Sadick et al. (2015), respectively. A_(ct∈n) is the area [ha] reserved for each crop type. IWR_t,n is the monthly irrigation water requirement per irrigation scheme, α_ct and β_ct are the overall irrigation and conveyance efficiencies, assumed to be 0.8 and 0.7, respectively. CR_t,n is a curtailment ratio, y_n is the annual yield [ton/ha] per irrigation scheme. Finally, $f_n^Y$ is the average irrigation yield metric per irrigation scheme.

Environmental Flow

The environmental flow was calculated as a minimum flow that is exceeded 95% of the time according to PMD feasibility study (Volta River Authority, 2018), Eq. (9).

$$f_n^{EF}=max\left[\underset{\mathrm{\Xi }}{mean}(q_{95,n}:P(q_{t,n}\le q_{95,n})=0.95)\right](9)$$

where, q_t,n is the flow downstream [Mm³ day^–1] of the PMD and $f_n^{EF}$is the environmental flow metric, maximised in the policy identification process under the hydrological ensemble Ξ.

Flood Recession Agriculture

Flood recession agriculture is dependent on the seasonal flooding of the floodplain during the peak of the rainy season (July–September). The magnitude of the annual peak (August or September) determines the total area sown by locals each year (Balana et al., 2015). Low flood peaks do not result in the river overflowing the banks, preventing FRA activities. Once the flooding threshold is breached, the flooded area increases with increasing flood peak. Extreme floods can negatively affect FRA by removing the fertile topsoil. Therefore, the area suitable for FRA reduces to zero for extreme flows (95% exceedance probability).

$$q_n^{FRA}=\frac{1}{T}\sum _{t}max(q_{\left(Aug\right)\mathrm{ϵ}t,n},q_{(Sep)\mathrm{ϵ}t,n})(10)$$

$$Y_n=A_n(q_n^{FRA})f_{FRA}{C}_y(11)$$

$$f_n^{FRA}=max\left[\underset{\mathrm{\Xi }}{mean}\left({\mathrm{\beta }}_{FRA}\times Y_n\right)\right](12)$$

where, $q_n^{FRA}$ is the average annual flow in August or September during the simulation horizon; q_{t, n} is the flow in August and September; A_n(⋅) is the flooded area [ha]; f_FRA is a suitability factor (Balana et al., 2015); C_y is the crop yield [ton ha^–1] assuming a typical FRA crop mix of maize, beans, Bambara beans, soya, millet and groundnuts (Sidibé et al., 2016); Y_n is the total FRA yield [ton year^–1]; β_FRA is the average regional market price of the crops at $1,222 ton^–1 (Pettinotti, 2017). Finally, $f_n^{FRA}$ is the benefit of the FRA activity.

Policy Identification

To evaluate the impact of new infrastructure operation it is necessary to identify and simulate the historical operational strategy of the existing infrastructure in the basin. Here, we use an explicit policy identification approach (Khadem et al., 2020), which requires a historical time series to estimate the operating rules of the existing infrastructure. The policy identification uses many-objective direct policy search to approximate operating rules of existing infrastructure using quantitative statistics metrics as objectives (Moriasi et al., 2007).

Operating Rules

We employed Gaussian radial basis functions (RBF) to model system operating rules. RBFs have shown good performance representing functions for a large class of problems, including reservoir storage and time into release decisions (Giuliani et al., 2014, 2016b; Zatarain Salazar et al., 2017; Geressu and Harou, 2019). The Gaussian RBF is defined by Eq. (13).

$$\mathrm{\phi }\left(\mathbf{x}\right)=\sum _{i=1}^l{w}_i\times exp\left[-\sum _{j=1}^m\frac{{\left(x_j-c_{j,i}\right)}^2}{b_{j,i}^2}\right](13)$$

where m = 2 is the number of input variables x (namely time and reservoir level); l is the number of RBFs (l = 4); w_i is the weight of the ith RBF (φ_i); c_j,i, and b_j,i are the m-dimensional centres and radius vectors of the ith RBF, respectively. The centres and radius include: $c_{j,\text{i}}\in [-1,1]b_{j,\text{i}}\in [0,1]w_{j,\text{i}}\in [0,1]{\sum }_{i=1}^n{w}_i=1.$ The parameter vector θ is defined as θ = [c_j,i,b_j,i,w_i]. For more details we refer the reader to Giuliani et al. (2014).

Historical Many-Objective Optimisation

Similar to Giuliani et al. (2016a) this study applies direct policy search, where the operating policy is parametrised using Gaussian RBF and then the parameters of the RBF are optimised using many-objective optimisation using the system’s performance metrics (section “Performance Metrics”) as objectives. In this work, in addition to optimising the operating policy parameters to maximise the system’s metrics, we used the Nash-Sutcliffe efficiency metric to calibrate the operating policy parameters such that they reproduce observed reservoir volume time-series. Using observed historical data, we attempt to identify historical operating policies:

$$\mathbf{\text{F}}\left({\mathrm{\theta }}_n\right)=(f_n^{AE},f_n^{FP},f_n^{NS})n=Bagre,Bui,Kompienga,andAkosombo(14)$$

where, $f_n^{NS}$ is the Nash-Sutcliffe objective; θ_n is the vector of decision variables which are the parameters for the reservoir operating rules. The objective function F(⋅) vector is obtained by simulating the Volta river basin simulation model over the horizon T and the historical hydrologic scenario under the set of operating rules (θ_n) defined by the search algorithm.

Policy Optimisation

Historical Non-cooperative Scenario

The historical non-cooperative scenario is based on the Policy identification stage, where operating rules for existing dams were identified under historical hydrological conditions. This scenario assumes business as usual with dam operators focussing maximising their own benefits. In this scenario, the PMD maximises its benefits without consideration of the impacts on the downstream built infrastructure. We represent this scenario by a many-objective robust optimisation formulation that maximises the benefits generated by the operation of the new PMD and the downstream natural assets over a hydrological ensemble. In this study, robust optimisation is employed where the performance metric values of the simulations over hydrological scenario ensemble are aggregated into a single percentile value statistically (Herman et al., 2015; Kwakkel et al., 2016; McPhail et al., 2018). In this formulation the operating policies for existing infrastructure identified in stage 1 are static. Eq. (15) present the objective vector to be optimised:

$$\mathbf{\text{F}}\left({\mathrm{\theta }}_n\right)=(f_n^{AE},f_n^{FP},f_n^Y,f_n^{EF},q_n^{FRA})n=PMD(15)$$

where, θ_n is the vector of decision variables which are the parameters of the PMD operating rules. The objective function F(⋅) vector is obtained by simulating the Volta river basin simulation model over the horizon T and the hydrological ensemble Ξ under the set of operating rules (θ_n) defined by the search algorithm.

Cooperative Scenario

This scenario assumes practical coordination and collaboration amongst the riparian countries and infrastructure operators, where institutional integration allows revising and possibly modifying the operation of existing dams to maximise basin-wide benefits. For the analysis, we only considered the Bagre and Akosombo dams because these two dams are upstream and downstream, respectively, of the PMD. The operation for the Bui and the Kompienga dams is considered static and uses operating rules identified in Stage 1. Eq. (16) present the objective vector to be optimised.

$$\mathbf{\text{F}}\left({\mathrm{\theta }}_n\right)=(f_n^{AE},f_n^{FP},f_{PMD}^Y,f_{PMD}^{EF},q_{PMD}^{FRA})n=Bagre,PMD,andAkosombo(16)$$

where, θ_n is the vector of decision variables of the operating rules for the Bagre, PMD, and Akosombo reservoirs. Note, that the cooperative scenario formulation only includes the objectives $f_n^Y$, $f_n^{EF}$, and $q_n^{FRA}$ for the PMD, whilst the $f_n^{AE}$ and $f_n^{FP}$ objectives are calculated for the Bagre, PMD and Akosombo reservoirs. Similar to the historical non-cooperative scenario, the objective function F(⋅) vector is obtained by simulating the Volta river basin simulation model over the horizon T and the hydrological ensemble Ξ under the set of operating rules (θ_n) defined by the search algorithm.

Hydrological Inputs

The Volta river basin simulation model requires historical inflow time-series and possible future hydrological scenarios to perform the Policy identification and the Policy optimisation, respectively. The historical inflow scenario is used to simulate and identify the historical system operation. Meanwhile, the possible future scenarios are used to evaluate the alternative policies over a wide range of hydrological conditions.

For the historical inflow scenario, given the lack of long-term observational flow data at all upstream reservoir locations, we used a reconstruction of the monthly historical naturalised river flows in the basin derived from a hydrological model, following Lin et al. (2019). We used the incremental flows at each dam location to represent the inflows to the reservoirs. Additionally, this historical scenario was used to generate a stochastic ensemble (Ξ) of hydrologic realisations for each reservoir located in the basin. We used the synthetic streamflow generation method proposed by Kirsch et al. (2013), which relies on Cholesky decomposition to maintain autocorrelation, and a bootstrap resampling technique to preserve multisite correlation (Herman et al., 2016).

Computational Experiment

For the Policy identification and the Policy optimisation we linked the Volta river basin simulation model to the Borg MOEA (Hadka and Reed, 2013) algorithm to solve the many-objective optimisation problem. This identifies the Pareto-approximate (“best achievable for any combination of priorities between objectives”) set of reservoir system operating rules and quantifies the trade-offs between performance objectives that they imply. Borg has been shown to successfully handle complex, non-linear, and non-concave problems when searching for non-dominated solutions (Hadka and Reed, 2012; Zatarain Salazar et al., 2016). We used the default algorithm parametrisation, with an initial population of 100 individuals. Additionally, we set epsilon values equal to 1.0 for annual energy production, 0.1 for firm power, 0.05 for irrigation yield, 0.05 for environmental flow and 0.05 for FRA.

The Volta basin simulation model runs on a weekly time step (t) over a 20-year time horizon (T = 20 years) for both the historical and 30-member future ensemble (Ξ). The Policy identification and the Policy optimisation were run for 10 random seeds where each seed was run over 400,000 function evaluations (i.e., 4,000,000 simulations for the hydrological ensemble). The final Pareto-approximate curve is obtained as the set of non-dominated solutions from the combined results of all optimisations.

Results and Discussion

First Stage: Historical Operation Identification

We use historical observed reservoir storage time series to identify the historical policy operating of existing infrastructure. Daily data were available for the Akosombo reservoir (01/01/1991 to 12/31/2010) and monthly data for the Bagre reservoir (01/01/2000 to 12/31/2010). In addition to the Nash-Sutcliffe efficiency objectives used to identify the reservoir operation for Akosombo and Bagre, we use system performance metrics (see section “Performance Metrics”) to identify the operation for the reservoirs Bui and Kompienga, where historical time series were not available.

Figure 4 shows the historical observed versus the simulated volume for the Akosombo and Bagre reservoirs. The operating policy for the existing reservoirs was selected based on the maximum values for the Nash-Sutcliffe metric obtained in the optimisation process, 0.75 and 0.63 for the Akosombo and Bagre Nash-Sutcliffe metrics, respectively. According to Moriasi et al. (2007), these results are classified as good and satisfactory, respectively. In general, the historical operating policy can reproduce the seasonality of both reservoirs. The storage volume is reduced every year almost to the minimum operating level in July and reservoirs fill in the wet season. However, in some years modelled storage is overestimated or underestimated and in the case of the Bagre reservoir, modelled storage reaches lower troughs as compared to the observed data. This is because the inflow time-series used by the simulation model are taken from the hydrological model and are subject to errors in their year-to-year variability.

FIGURE 4

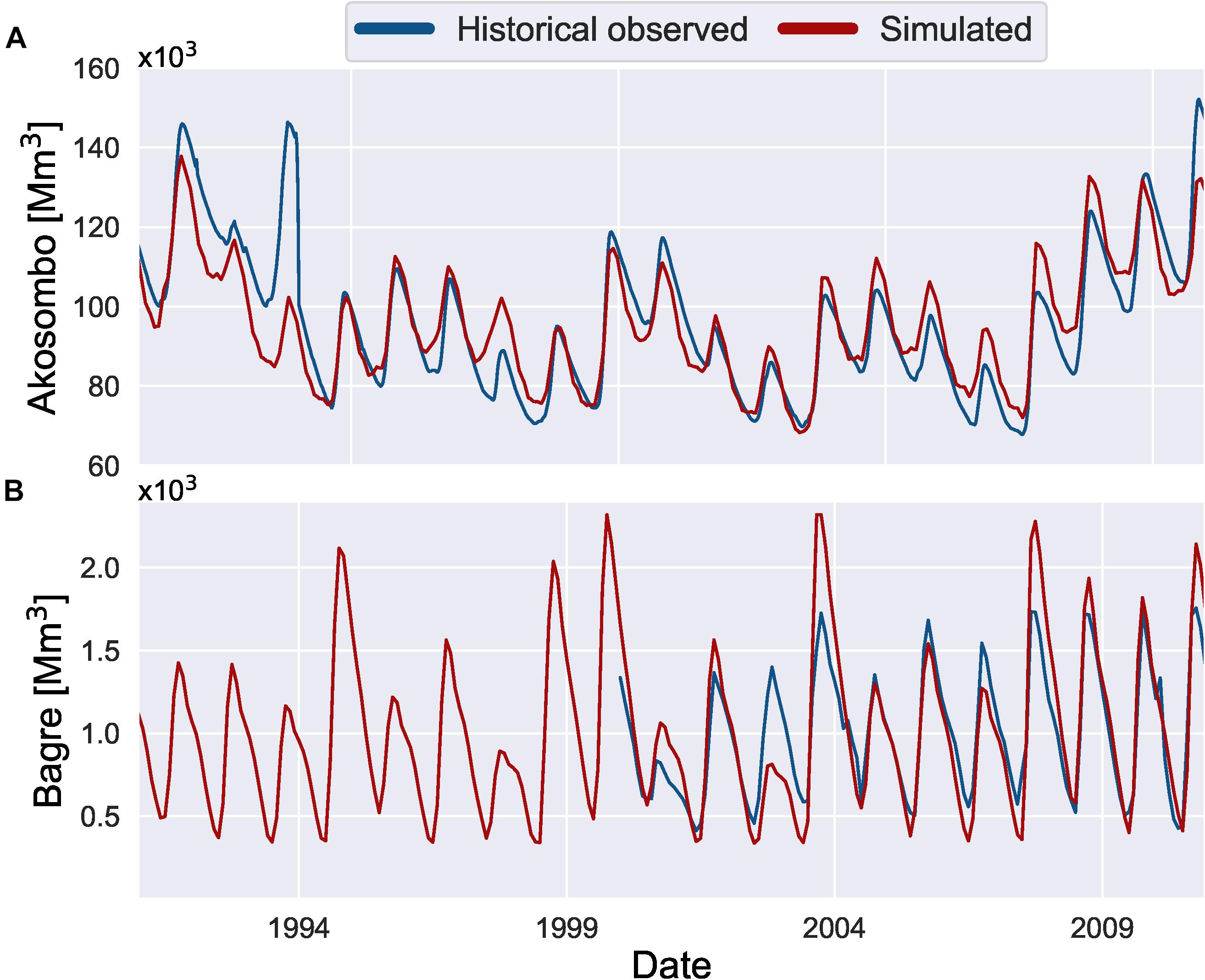
Figure 4. Comparison of observed and simulated reservoir volumes used for policy identification. Panel (A) shows the observed and simulated volume for the Akosombo reservoir, and panel (B) shows the observed and simulated volume for the Bagre reservoir.

Second Stage: Design and Adaptation of System Infrastructure Operation Policies

In the second phase of the method, we identify Pareto-approximate PMD reservoir release operating rules under two scenarios, historical non-cooperative and cooperative, where, in the non-cooperative, the Bagre and the Akosombo operating policies are held constant. Whilst in the cooperative we allowed Bagre and Akosombo operating policies to adapt to the new built infrastructure (the PMD) to maximise overall basin benefits. Results of the historical non-cooperative and cooperative scenarios (Figure 5) are visualised using a parallel plot (Inselberg, 1997). In Figure 5, each vertical axis represents an objective in the optimisation formulation whilst each coloured line represents a non-dominated operating policy portfolio for each new and existing dam. That point at which each coloured line intersects each respective vertical axis represents the performance of that policy in that objective. An ideal solution in the figure would lead to a straight horizontal line that intersects every axis at the top. Crossing lines between axes indicate trade-offs between two adjacent objectives. The “Ghana Average Energy” axis represents a non-optimised metric which is the sum of the Pwalugu and Akosombo average energy objectives. This metric is visualised in the figure to show the impacts of the upstream reservoirs’ operation (Bagre and Pwalugu) on the overall energy production in Ghana.

FIGURE 5

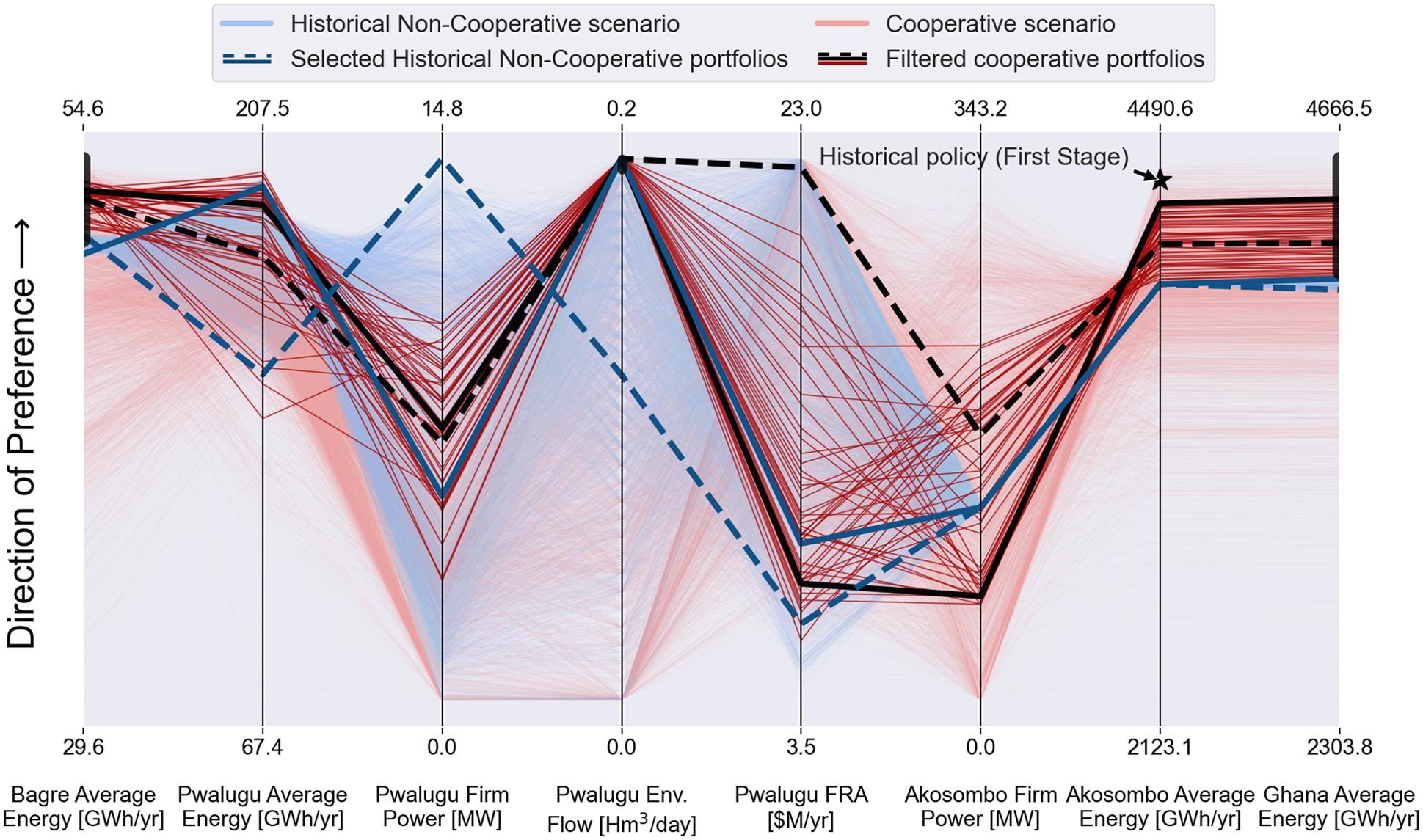
Figure 5. Parallel axis plot comparing the historical non-cooperative and cooperative scenario. Light blue and light red are the full set of non-dominated solutions for the historical non-cooperative and cooperative scenario, respectively. Blue solid and dashed lines are selected portfolios of the historical non-cooperative scenario and the black and solid red lines are filtered portfolios of the cooperative scenario. Vertical thick black bars over parts of the first, fourth and eighth axes are “filters” which allow selecting a subset of the efficient designs in the plot. The Akosombo average energy [4,457.8 GWh year^–1] of the historical policy, identified in the First Stage, is shown with a black star.

The full set of non-dominated portfolios for the historical non-cooperative and cooperative scenarios are presented in light blue and light red, respectively. We selected two policy portfolios from the historical non-cooperative scenario (solid and dashed line in blue) to evaluate in detail. The portfolio represented by the solid blue line achieves the highest PMD average energy 197.2 [GWh year^–1] in the set of historical non-cooperative portfolios, whilst at the same time the flow (at 95% exceedance) downstream of the PMD is greater than the minimum environmental flow (0.18 Mm³ day^–1) requirement (Volta River Authority, 2018). The dashed line corresponds to an operating policy that achieves the highest PMD firm power 13.5 [MW]. Both operating policies, however, fall in the lower range of FRA benefits generating 9.3 [$M year^–1] and 6.3 [$M year^–1] for the portfolios represented by the solid and dashed lines, respectively. As under in the historical non-cooperative scenario we employed static operating policies for the Bagre and Akosombo dams (identified in the Policy identification stage), their range of performance is small across all Pareto-approximate policies.

Cooperation between the two riparian countries is more likely to occur if both countries receive a net benefit as a result of the cooperation (Sadoff and Grey, 2009; Jeuland et al., 2017). The solutions for the cooperative scenario are filtered such that those that only increase energy generation from Bagre in Burkina Faso 51.1 [GWh year^–1], and energy generation in Ghana 4151.3 [GWh year^–1] as compared to the historical non-cooperative scenario are seen in bold colours. We also filter out all policies that result in flows downstream of the PMD that are greater than 0.18 [Mm³ day^–1], the minimum environmental flow identified in Volta River Authority (2018). Amongst the remaining cooperative solutions, we select two the “Built Infrastructure portfolio” represented by the solid black line maximises Ghana Average energy (producing 4490.7 [GWh year^–1]) whilst the “compromise portfolio” represented by the dashed black line maximises ecosystem services in Northern Ghana by maximising FRA benefits (generating 22.5 [$M year^–1]).

Figure 5 shows how that energy generation and firm power from the Akosombo dam may be impacted if the historical operating policies of existing dams are not adapted to the new flow regime resulting from PMD development (blue lines). The filtered cooperative portfolios (red lines) show that implementing cooperative operating policies results in Akosombo hydropower benefits (average energy and firm power) being less negatively impacted than if non-cooperative policies were implemented. In addition, hydropower benefits at Bagre can be increased, and environmental flows downstream of the PMD can be maintained.

According to Baah-Kumi and Ward (2020), the PMD development may impact Akosombo operation because the inflows to Lake Volta could be reduced due to increasing water storage, water demands and evaporation upstream of Lake Volta. Our analysis confirms this conclusion; however, Figure 5 shows that the negative impact of Akosombo could be greater without the coordinated infrastructure management. For example, Akosombo average energy is reduced by 11.5% from the energy generated historically (black star in Figure 5), in the selected non-cooperative scenarios. However, if cooperative policies are implemented this impact is reduced to only 3.6% (solid black line in the Figure 5). This policy achieves a positive net energy production of 0.74% in Ghana and 6.2% for Bagre in Burkina Faso (see Figure 5). The FRA benefits are reduced by 63.5% from the historical 25.2 [$M year⁻¹], in the selected non-cooperative portfolio (solid blue line). Whilst under the cooperative portfolio, which maximises hydropower benefits (solid black line) the FRA benefits are reduced by 69.4%. However, note that under the compromise operating policy (dashed black line), the FRA benefits could be reduced only by 10.7%.

Third Stage: Implications for Infrastructure Operation on the Volta River Basin

To investigate the possible range of benefits generated in the Volta basin with the identified operating policies we performed a sensitivity analysis by simulating the system over 100 hydrological scenarios. Policies considered in this analysis include the selected cooperative and non-cooperative policies as well as those in the entire cooperative filtered set in Figure 5.

Figure 6 shows the exceedance curves for the different metrics and different operating policies. Figures 6A,B visualize the PMD hydropower metrics while Figures 6C,D show metrics related to the new irrigation scheme and the impact to the environmental services – FRA – downstream of the PMD at Pwalugu in the Upper East Region of Ghana. Finally, Figures 6C,F show the average energy produced at Bagre and Akosombo, respectively. In general, the exceedance curves show that the operating policies identified by the cooperative scenario perform better according to almost all metrics for all hydrological scenarios. The selected cooperative policy that maximises Ghana Average energy (solid black line in Figure 6) shows that the Pwalugu average energy and firm power (Figures 6A,B) is 162.7 [GWh year^–1] and 5.1 [MW] at 90% of exceedance, respectively. Note that the PMD was designed to produce 176 [GWh year^–1] with a firm power of 16 [MW]. According to our results the designed annual energy is achieved at only 77% exceedance under the same cooperative policy (Figure 6A).

FIGURE 6

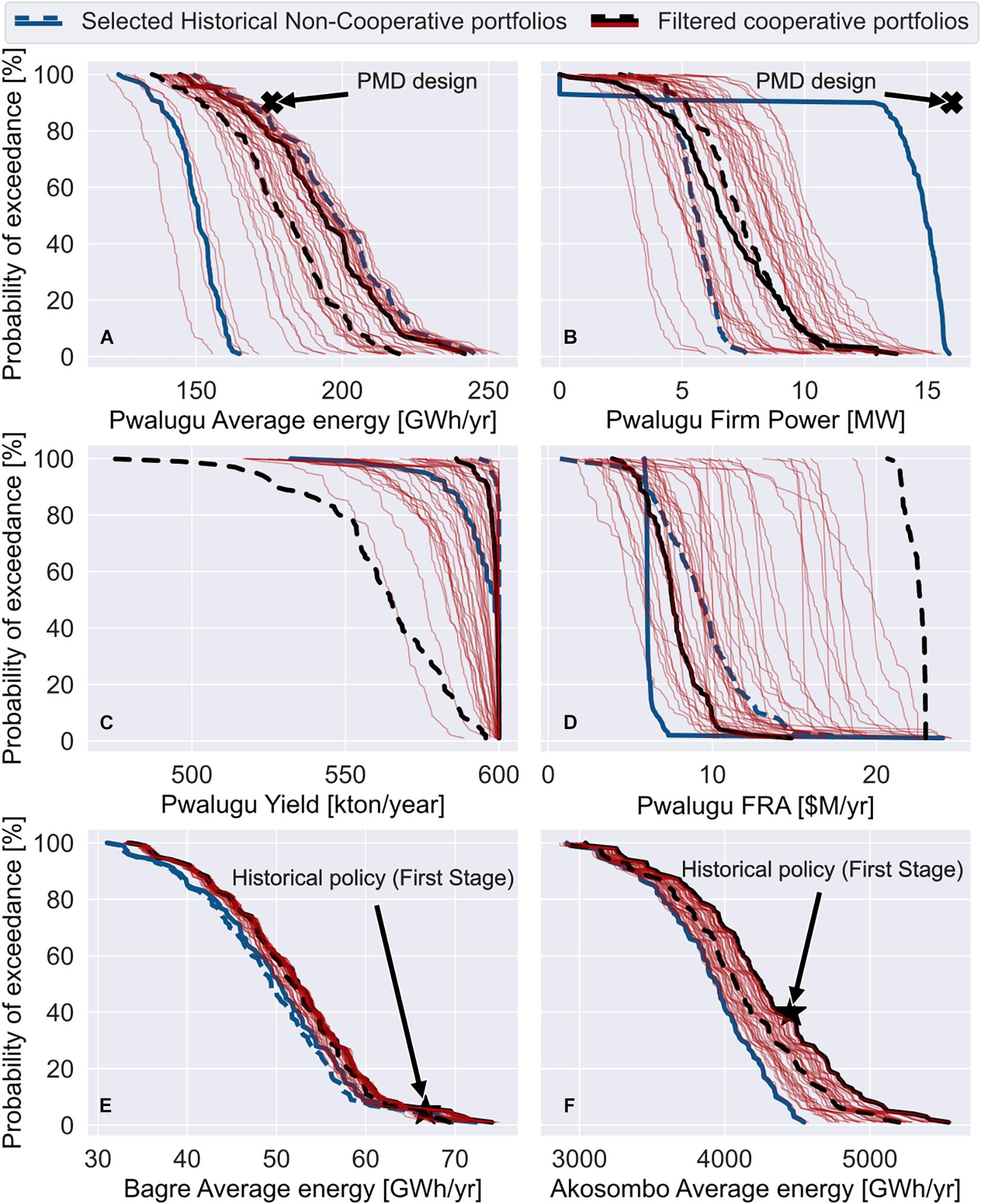
Figure 6. Probability of exceedance curves for different metrics in the system. Panel (A) shows the Pwalugu Average energy, panel (B) shows the Pwalugu Firm Power, panel (C) shows the Pwalugu Irrigation Yield, panel (D) shows the Pwalugu Flood Recession Agriculture (FRA), panel (E) shows the Bagre Average energy, and panel (F) shows the Akosombo Average energy. The PMD average energy and firm power design (Volta River Authority, 2018) is displayed in panels (A,B), respectively.

Figures 6C,D, show that a trade-off exists between irrigation yield and FRA downstream the PMD. Policies that result in higher benefits in FRA in Pwalugu result in lower irrigation yields from the formal irrigation scheme associated with the PMD. For example, if the selected cooperative policies (solid and dashed black lines) are compared, the formal irrigation yield under the cooperative policy that maximises Ghana Average energy is 596.0 [kton year^–1] at 90% of exceedance whilst the FRA benefit is 8.7 [$M year^–1]. However, under the portfolio that maximises the FRA benefits, the formal irrigation yield is reduced to 526.9 [kton year^–1] and the FRA benefits increase to 21.6 [$M year^–1]. The flood recession ecosystem services benefits occur downstream of the PMD in the floodplains. The irrigation system abstracts water downstream of the PMD hydropower releases. These abstractions result in smaller downstream floods and lower overall flood recession benefits, implying there is direct competition between formal and informal irrigation. Figures 6E,F show the Bagre and the Akosombo average energy production in the cooperative scenario outperform the energy production in the historical non-cooperative scenario under all hydrologic scenarios.

Figure 7 shows five-operation-years for the Bagre, Pwalugu, and Akosombo reservoirs, for the operating policy represented by the black and blue solid lines under the hydrological scenarios. Figures 7A,C,E show the mean value under the scenarios and the standard deviation (light blue and grey area in Figure 7) for the simulated reservoir volume in Bagre, Pwalugu, and Akosombo, respectively. While Figures 7B,D,F show the same information but for the simulated energy production for the Bagre, Pwalugu, and Akosombo dams.

FIGURE 7

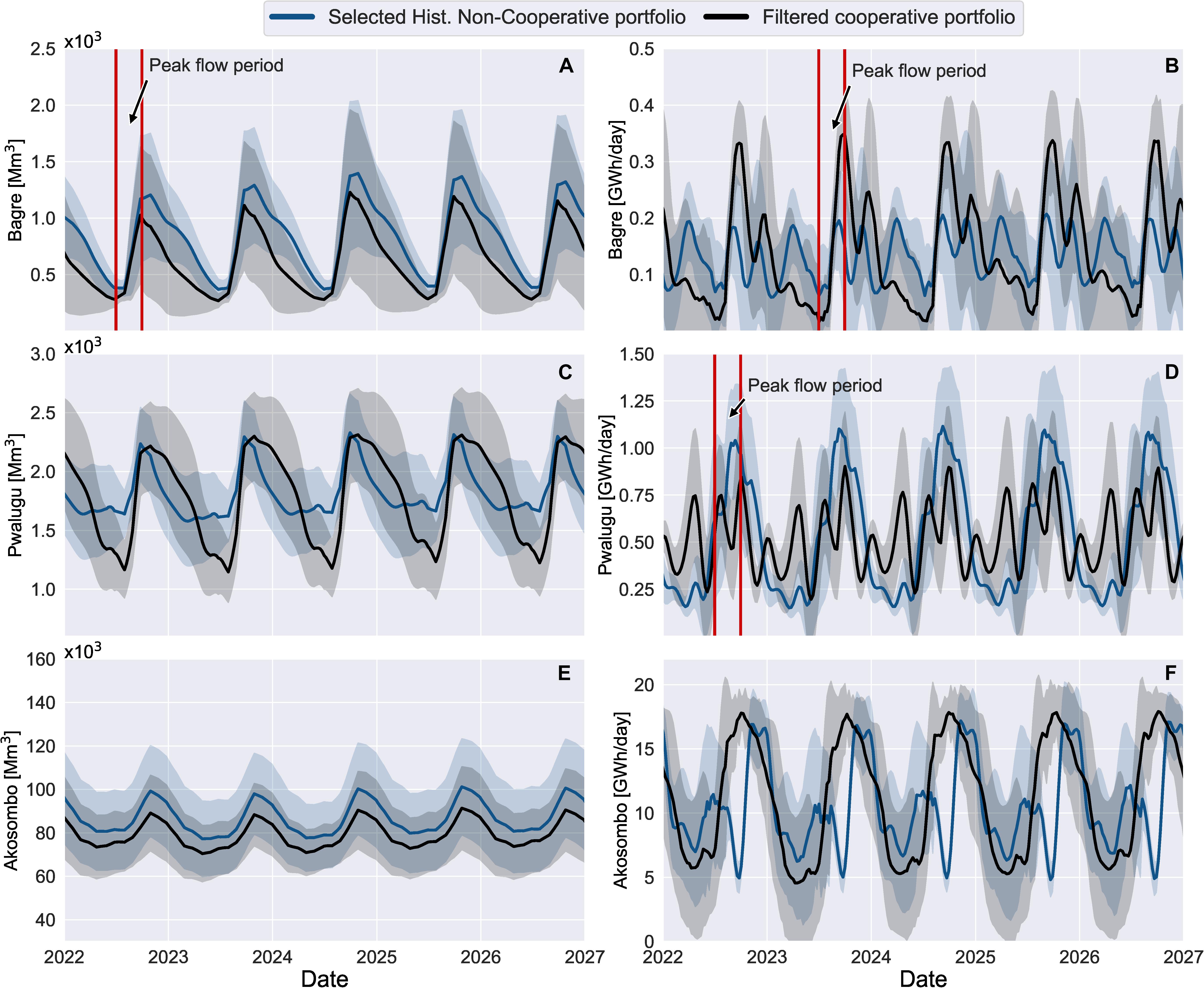
Figure 7. Reservoirs operation. Panel (A,C,E) show the mean value under the hydrological scenarios and the standard deviation (light blue and grey area) of the stimulated reservoir volume in Bagre, Pwalugu, and Akosombo, respectively. Panel (B,D,F) show the mean value under the hydrological scenarios and the standard deviation of the simulated energy production for the Bagre, Pwalugu, and Akosombo dams, respectively.

According to Figures 7A,E, the mean volume for Akosombo and Bagre follow a similar seasonal operating pattern as compared to the historical operation of both reservoirs (see section “First Stage: Historical Operation Identification”), where reservoir storages reduce to lower volumes in the dry season and fill in the wet season. However, building and operating the PMD under the selected cooperative policy (black line) results in lower volumes in Akosombo in all seasons compared to the historical operation without the PMD development (see Figure 4). This results from the increase in upstream storage, water consumption, and evaporation and the increased hydropower generation in peak flow periods (see Figure 7F) to maintain historical energy generation levels. The Pwalugu reservoir operation follows a similar seasonal pattern to the Bagre reservoir, where the storage volume is reduced every year almost to the minimum operating level in July and reservoirs fill in the wet season. However, this operation for Pwalugu is more pronounced (lower reservoir volumes) in the cooperative scenario. This could potentially reduce flood peaks downstream of the PMD by increasing Pwalugu’s capacity to buffer possible spills from Bagre protecting from floods in Northern Ghana. However reducing the flood peak would also reduce the ecosystem-services derived from this flood (i.e., FRA) (see Figure 7D) and (Figure 6D), as well as increase risks that the dam is not able to refill in some years.

Under the cooperative policy (black line), on average Bagre operates at a lower volume and increases its hydropower generation during peak flow periods, as compared to the historical non-cooperative scenario (see Figures 7A,B). This added to steady Pwalugu hydropower releases (see Figure 7D) increases the water availability downstream minimising the negative impacts on the Akosombo energy production, as compared to the non-cooperative scenario. However, increasing energy production in Bagre during peak flows reduce its ability to generate hydropower during off-peak flows periods (Figure 7B). This could possibly increase energy import dependency in Burkina Faso during these periods despite total annual generation by Bagre being greater in the cooperative scenario. This possible negative impact for Burkina Faso could be offset by increasing energy trades between Ghana and Burkina Faso during those periods.

Future Work and Limitations

The analysis presented in this paper considers hydrologic uncertainty within the robust optimisation. The stochastic ensemble used in the optimisation process is based on the historical flow regime in the basin. Climate change may modify this flow regime and could impact the long-term robustness of the operating policies identified in the study. Future studies could apply the proposed framework under climate change uncertainty to identify cooperative water strategies that are robust to climate change and support long-term sustainable water resources management. Another potential direction for future research could be to explore the impacts of political or economic uncertainty or the consequences of deviation from operating agreements by each party via optimisation or sensitivity analysis.

Conclusion

This paper explores the multiple potential impacts of the proposed Pwalugu Multipurpose Dam (PMD) could have on existing infrastructure and water services of the Volta river basin. We presented a novel framework that links river basin simulation to many-objective search to approximate existing operating rules and design new ones in the presence of complex multi-actor trade-offs. The approach identifies benefits of collaborative management in systems where current river management is not codified in formal regulations, as is the case in many multi-region river basins in the global south. We evaluated the possible impacts that new development could impose on ecosystem services and downstream infrastructure and how the PMD itself could be impacted by different operating strategies of the existing upstream Bagre Dam in Burkina Faso under two alternative scenarios assuming cooperation and non-cooperation.

Results indicate that the PMD has the potential to reduce inflows into the Akosombo dam. This would likely have a negative impact on hydropower generation from Akosombo, with up to 11.5% reduction in energy generation compared to the case without the PMD. However, if cooperative infrastructure operation is adopted, the impact could be reduced by only 3.6%, and result in a positive net energy production of 0.74% in Ghana overall and a 6.2% increase for Bagre Dam hydropower production in Burkina Faso. Environmental services in Northern Ghana may also be impacted in a non-cooperative operation scenario decreasing floods downstream of the PMD and possibly reducing benefits to local communities that depend directly on flood recession activities. Under a cooperative scenario, the Bagre reservoir could increase hydropower releases during peak flow periods increasing its total net annual generation. This operative strategy could increase water availability downstream of the PMD minimising the negative impacts on Akosombo energy production, resulting in net positive energy production in Ghana even after constructing the PMD. However, such a strategy could reduce Bagre energy generation during low flow periods increasing Burkina Faso’s dependence on energy imports from Ghana during the dry season, despite the higher overall total annual generation. Results showed there is room for riparian countries to negotiate cooperative strategies to offset possible negative impacts generated by the new PMD. The PMD provides an opportunity for the VBA to implement cooperative operational water management strategies in the basin.

Data Availability Statement

The raw data supporting the conclusions of this article will be made available by the authors upon consultation with the relevant national authorities who own the data.

Author Contributions

JG: conceptualization, methodology, software, formal analysis, writing – original draft, and visualization. EM: conceptualization, methodology, software, formal analysis, and writing – review and editing. EO, AB-B, and JD: conceptualization, and writing – review and editing. MM, LP, SG, and JS: methodology and writing – review and editing. DS: conceptualization, writing – review and editing, and funding acquisition. JH: conceptualization, supervision, and writing – review and editing, and funding acquisition. All authors contributed to the article and approved the submitted version.

Funding

The authors acknowledge UKRI research funding through the “Future Design and Assessment of water-energy-food-environment Mega Systems” (FutureDAMS) research project (ES/P011373/1).

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Acknowledgments

The authors thank the national and regional stakeholders who contributed to the BMU (Germany) funded IUCN-led WISE-UP to Climate project (http://www.waterandnature.org/initiatives/wise-climate). The authors acknowledge the use of the Computational Shared Facility of the University of Manchester and associated support services.

References

Allen, R. G., Pereira, L. S., Raes, D., and Smith, M. (1998). Crop Evapotranspiration –Guidelines for Computing Crop Water Requirements. FAO Irrigation and Drainage Paper 56. Rome: Food and Agriculture Organization.

Google Scholar

Arjoon, D., Mohamed, Y., Goor, Q., and Tilmant, A. (2014). Hydro-economic risk assessment in the eastern Nile River basin. Water Resour. Econ. 8, 16–31. doi: 10.1016/j.wre.2014.10.004

CrossRef Full Text | Google Scholar

Baah-Kumi, B., and Ward, F. A. (2020). Poverty mitigation through optimized water development and use: insights from the Volta Basin. J. Hydrol. 582:124548. doi: 10.1016/j.jhydrol.2020.124548

CrossRef Full Text | Google Scholar

Balana, B., Mul, M., Williams, T., Ghansah, B., Gyanfuah-Owusu, A., and Amarnath, G. (2015). Analysis of Historical Flood Inundation and Recession Patterns; Implications for Flood Recession Agriculture in Northern Ghana. IWMI-IFRI Project Report, 30 September 2015. Accra: IWMI.

Google Scholar

Basheer, M., Wheeler, K. G., Ribbe, L., Majdalawi, M., Abdo, G., and Zagona, E. A. (2018). Quantifying and evaluating the impacts of cooperation in transboundary river basins on the Water-Energy-Food nexus: the Blue Nile Basin. Sci. Total Environ. 630, 1309–1323. doi: 10.1016/j.scitotenv.2018.02.249

PubMed Abstract | CrossRef Full Text | Google Scholar

Becker, N., and Easter, K. W. (1999). Conflict and cooperation in managing international water resources such as the great lakes. Land Econ. 75:233. doi: 10.2307/3147008

CrossRef Full Text | Google Scholar

Bennett, L. L., Ragland, S. E., and Yolles, P. (1998). “Facilitating International agreements through an interconnected game approach: the case of river Basins,” in Conflict and Cooperation on Trans-Boundary Water Resources, eds R. E. Just and S. Netanyahu (Boston, MA: Springer US), 61–85. doi: 10.1007/978-1-4615-5649-7_4

CrossRef Full Text | Google Scholar

Bhaduri, A., and Liebe, J. (2013). Cooperation in transboundary water sharing with issue linkage: game-theoretical case study in the Volta Basin. J. Water Resour. Plan. Manag. 139, 235–245. doi: 10.1061/(ASCE)WR.1943-5452.0000252

PubMed Abstract | CrossRef Full Text | Google Scholar

Bhagabati, S., Kawasaki, A., Babel, M., Rogers, P., and Ninsawat, S. (2014). A cooperative game analysis of transboundary hydropower development in the lower mekong: case of the 3S sub-basins. Water Resour. Manag. 28, 3417–3437. doi: 10.1007/s11269-014-0594-2

CrossRef Full Text | Google Scholar

Darko, D., Kpessa-Whyte, M., Obuobie, E., Siakwah, P., Torto, O., and Tsikata, D. (2019). The Context and Politics of Decision Making on Large Dams in Ghana: An Overview. FutureDAMS Working Paper 002. Manchester: The University of Manchester.

Google Scholar

Davies, R. (2018). Ghana – Dozens Killed by Flooding in Northern Regions. Available online at: http://floodlist.com/africa/ghana-floods-northern-regions-september-2018 (accessed July 20, 2020).

Google Scholar

Geressu, R., Siderius, C., Harou, J. J., Kashaigili, J., Pettinotti, L., and Conway, D. (2020). Assessing river basin development given water-energy-food-environment interdependencies. Earths Futur. 8:e2019EF001464. doi: 10.1029/2019EF001464

CrossRef Full Text | Google Scholar

Geressu, R. T., and Harou, J. J. (2015). Screening reservoir systems by considering the efficient trade-offs—informing infrastructure investment decisions on the Blue Nile. Environ. Res. Lett. 10:125008. doi: 10.1088/1748-9326/10/12/125008

CrossRef Full Text | Google Scholar

Geressu, R. T., and Harou, J. J. (2019). Reservoir system expansion scheduling under conflicting interests. Environ. Model. Softw. 118, 201–210. doi: 10.1016/j.envsoft.2019.04.002

CrossRef Full Text | Google Scholar

Gerlak, A. K., Saguier, M., Mills-Novoa, M., Fearnside, P. M., and Albrecht, T. R. (2020). Dams, Chinese investments, and EIAs: a race to the bottom in South America? Ambio 49, 156–164. doi: 10.1007/s13280-018-01145-y

PubMed Abstract | CrossRef Full Text | Google Scholar

Giuliani, M., Anghileri, D., Castelletti, A., Vu, P. N., and Soncini-Sessa, R. (2016a). Large storage operations under climate change: expanding uncertainties and evolving tradeoffs. Environ. Res. Lett. 11:035009. doi: 10.1088/1748-9326/11/3/035009

CrossRef Full Text | Google Scholar

Giuliani, M., and Castelletti, A. (2013). Assessing the value of cooperation and information exchange in large water resources systems by agent-based optimization. Water Resour. Res. 49, 3912–3926. doi: 10.1002/wrcr.20287

CrossRef Full Text | Google Scholar

Giuliani, M., Castelletti, A., Pianosi, F., Mason, E., and Reed, P. M. (2016b). Curses, tradeoffs, and scalable management: advancing evolutionary multiobjective direct policy search to improve water reservoir operations. J. Water Resour. Plan. Manag. 142:04015050. doi: 10.1061/(ASCE)WR.1943-5452.0000570

PubMed Abstract | CrossRef Full Text | Google Scholar

Giuliani, M., Herman, J. D., Castelletti, A., and Reed, P. (2014). Many-objective reservoir policy identification and refinement to reduce policy inertia and myopia in water management. Water Resour. Res. 50, 3355–3377. doi: 10.1002/2013WR014700

CrossRef Full Text | Google Scholar

Giuliani, M., Quinn, J. D., Herman, J. D., Castelletti, A., and Reed, P. M. (2018). Scalable multiobjective control for large-scale water resources systems under uncertainty. IEEE Trans. Control Syst. Technol. 26, 1492–1499. doi: 10.1109/TCST.2017.2705162

CrossRef Full Text | Google Scholar

Hadka, D., and Reed, P. (2012). Diagnostic assessment of search controls and failure modes in many-objective evolutionary optimization. Evol. Comput. 20, 423–452. doi: 10.1162/EVCO_a_00053

CrossRef Full Text | Google Scholar

Hadka, D., and Reed, P. (2013). Borg: an auto-adaptive many-objective evolutionary computing framework. Evol. Comput. 21, 231–259.

Google Scholar

Hall, J. W., Borgomeo, E., Mortazavi-Naeini, M., and Wheeler, K. (2019). “Water resource system modelling and decision analysis,” in Water Science, Policy, and Management, eds S. J. Dadson, D. E. Garrick, E. C. Penning-Rowsell, J. W. Hall, R. Hope, and J. Hughes (Hoboken, NJ: John Wiley & Sons Ltd), doi: 10.1002/9781119520627

CrossRef Full Text | Google Scholar

Harou, J. J., Pulido-Velazquez, M., Rosenberg, D. E., Medellín-Azuara, J., Lund, J. R., and Howitt, R. E. (2009). Hydro-economic models: concepts, design, applications, and future prospects. J. Hydrol. 375, 627–643. doi: 10.1016/j.jhydrol.2009.06.037

CrossRef Full Text | Google Scholar

Herman, J. D., Reed, P. M., Zeff, H. B., and Characklis, G. W. (2015). How should robustness be defined for water systems planning under change? J. Water Resour. Plan. Manag. 141:04015012. doi: 10.1061/(ASCE)WR.1943-5452.0000509

PubMed Abstract | CrossRef Full Text | Google Scholar

Herman, J. D., Zeff, H. B., Lamontagne, J. R., Reed, P. M., and Characklis, G. W. (2016). Synthetic drought scenario generation to support bottom-up water supply vulnerability assessments. J. Water Resour. Plan. Manag. 142:04016050. doi: 10.1061/(ASCE)WR.1943-5452.0000701

PubMed Abstract | CrossRef Full Text | Google Scholar

Herman, J. D., Zeff, H. B., Reed, P. M., and Characklis, G. W. (2014). Beyond optimality: multistakeholder robustness tradeoffs for regional water portfolio planning under deep uncertainty. Water Resour. Res. 50, 7692–7713. doi: 10.1002/2014WR015338

CrossRef Full Text | Google Scholar

Hurford, A., Harou, J. J., Bonzanigo, L., Ray, P. A., Karki, P., Bharati, L., et al. (2020a). Efficient and robust hydropower system design under uncertainty – a demonstration in Nepal. Renew. Sustain. Energy Rev. 132:109910. doi: 10.1016/j.rser.2020.109910

CrossRef Full Text | Google Scholar

Hurford, A., McCartney, M. P., Harou, J. J., Dalton, J., Smith, D. M., and Odada, E. (2020b). Balancing services from built and natural assets via river basin trade-off analysis. Ecosyst. Serv. 45:101144. doi: 10.1016/j.ecoser.2020.101144

CrossRef Full Text | Google Scholar

Hurford, A. P., and Harou, J. J. (2014). Balancing ecosystem services with energy and food security &ndash assessing trade-offs from reservoir operation and irrigation investments in Kenya’s Tana Basin. Hydrol. Earth Syst. Sci. 18, 3259–3277. doi: 10.5194/hess-18-3259-2014

CrossRef Full Text | Google Scholar

Huskova, I., Matrosov, E. S., Harou, J. J., Kasprzyk, J. R., and Lambert, C. (2016). Screening robust water infrastructure investments and their trade-offs under global change: a London example. Glob. Environ. Chang. 41, 216–227. doi: 10.1016/j.gloenvcha.2016.10.007

CrossRef Full Text | Google Scholar

IFRC (2019). Ghana/Upper East: Floods Emergency Plan of Action DREF Operation n° MDRGH016. Available online at: https://reliefweb.int/report/ghana/ghana-upper-east-floods-emergency-plan-action-dref-operation-n-mdrgh016 (accessed July 20, 2020).

Google Scholar

Inselberg, A. (1997). “Multidimensional detective,” in Proceedings of VIZ’97: Visualization Conference, Information Visualization Symposium and Parallel Rendering Symposium (Phoenix, AZ: IEEE Computer Society), 100–107. doi: 10.1109/INFVIS.1997.636793

CrossRef Full Text | Google Scholar

Jeuland, M., Wu, X., and Whittington, D. (2017). Infrastructure development and the economics of cooperation in the Eastern Nile. Water Int. 42, 121–141. doi: 10.1080/02508060.2017.1278577

CrossRef Full Text | Google Scholar

Kahsay, T. N., Arjoon, D., Kuik, O., Brouwer, R., Tilmant, A., and van der Zaag, P. (2019). A hybrid partial and general equilibrium modeling approach to assess the hydro-economic impacts of large dams – The case of the Grand Ethiopian Renaissance Dam in the Eastern Nile River basin. Environ. Model. Softw. 117, 76–88. doi: 10.1016/j.envsoft.2019.03.007

CrossRef Full Text | Google Scholar

Kasprzyk, J. R., Reed, P. M., Kirsch, B. R., and Characklis, G. W. (2009). Managing population and drought risks using many-objective water portfolio planning under uncertainty. Water Resour. Res. 45, 1–18. doi: 10.1029/2009WR008121

CrossRef Full Text | Google Scholar

Khadem, M., Roug, C., and Harou, J. J. (2020). What do economic water storage valuations reveal about optimal vs. historical water management? Water Resour. Econ. 32:100158. doi: 10.1016/j.wre.2020.100158

CrossRef Full Text | Google Scholar

Kilgour, D. M., and Dinar, A. (2001). Flexible water sharing within an international river basin. Environ. Resour. Econ. 18, 43–60. doi: 10.1023/A:1011100130736

CrossRef Full Text | Google Scholar

Kirsch, B. R., Characklis, G. W., and Zeff, H. B. (2013). Evaluating the impact of alternative hydro-climate scenarios on transfer agreements: practical improvement for generating synthetic streamflows. J. Water Resour. Plan. Manag. 139, 396–406. doi: 10.1061/(ASCE)WR.1943-5452.0000287

PubMed Abstract | CrossRef Full Text | Google Scholar

Knox, S., Tomlinson, J., Harou, J. J., Meier, P., Rosenberg, D. E., Lund, J. R., et al. (2019). An open-source data manager for network models. Environ. Model. Softw. 122:104538. doi: 10.1016/j.envsoft.2019.104538

CrossRef Full Text | Google Scholar

Kucukmehmetoglu, M., and Guldmann, J.-M. (2004). International water resources allocation and conflicts: the case of the euphrates and Tigris. Environ. Plan. A Econ. Sp. 36, 783–8>801. doi: 10.1068/a3670

CrossRef Full Text | Google Scholar

Kucukmehmetoglu, M., and Guldmann, J.-M. (2010). Multiobjective allocation of transboundary water resources: case of the Euphrates and Tigris. J. Water Resour. Plan. Manag. 136, 95–105. doi: 10.1061/(ASCE)0733-94962010136:1(95)

CrossRef Full Text | Google Scholar

Kwakkel, J. H., Haasnoot, M., and Walker, W. E. (2016). Comparing robust decision-making and dynamic adaptive policy pathways for model-based decision support under deep uncertainty. Environ. Model. Softw. 86, 168–183. doi: 10.1016/j.envsoft.2016.09.017

CrossRef Full Text | Google Scholar

Lin, P., Pan, M., Beck, H. E., Yang, Y., Yamazaki, D., Frasson, R., et al. (2019). Global reconstruction of naturalized river flows at 2.94 million reaches. Water Resour. Res. 55, 6499–6516. doi: 10.1029/2019WR025287

PubMed Abstract | CrossRef Full Text | Google Scholar

Loucks, D. P. (1992). Water resource systems models: their role in planning. J. Water Resour. Plan. Manag. 118, 214–223. doi: 10.1061/(ASCE)0733-94961992118:3(214)

CrossRef Full Text | Google Scholar

Loucks, D. P., and Van Beek, E. (2005). Water Resources Systems Planning and Management An Introduction to Methods, Models and Applications. Paris: United Nations Educational, Scientific and Cultural Organization.

Google Scholar

Madani, K. (2010). Game theory and water resources. J. Hydrol. 381, 225–238. doi: 10.1016/j.jhydrol.2009.11.045

CrossRef Full Text | Google Scholar

Maier, H. R., Kapelan, Z., Kasprzyk, J., Kollat, J., Matott, L. S., Cunha, M. C., et al. (2014). Evolutionary algorithms and other metaheuristics in water resources: current status, research challenges and future directions. Environ. Model. Softw. 62, 271–299. doi: 10.1016/j.envsoft.2014.09.013

CrossRef Full Text | Google Scholar

Maier, H. R., Razavi, S., Kapelan, Z., Matott, L. S., Kasprzyk, J., and Tolson, B. A. (2018). Introductory overview: optimization using evolutionary algorithms and other metaheuristics. Environ. Model. Softw. 114, 195–213. doi: 10.1016/j.envsoft.2018.11.018

CrossRef Full Text | Google Scholar

Matrosov, E. S., Harou, J. J., and Loucks, D. P. (2011). A computationally efficient open-source water resource system simulator – application to London and the Thames Basin. Environ. Model. Softw. 26, 1599–1610. doi: 10.1016/j.envsoft.2011.07.013

CrossRef Full Text | Google Scholar

Matrosov, E. S., Huskova, I., Kasprzyk, J. R., Harou, J. J., Lambert, C., and Reed, P. M. (2015). Many-objective optimization and visual analytics reveal key trade-offs for London’s water supply. J. Hydrol. 531, 1040–1053. doi: 10.1016/j.jhydrol.2015.11.003

CrossRef Full Text | Google Scholar

McCartney, M., Forkuor, G., Sood, A., Amisigo, B., and Hattermann, F. (2012). The Water Resource Implications of Changing Climate in the Volta River Basin. IWMI Research Report 146. Colombo: International Water Management Institute, 40. doi: 10.5337/2012.219

CrossRef Full Text | Google Scholar

McPhail, C., Maier, H. R., Kwakkel, J. H., Giuliani, M., Castelletti, A., and Westra, S. (2018). Robustness metrics: how are they calculated, when should they be used and why do they give different results? Earths Futur. 6, 169–191. doi: 10.1002/2017EF000649

CrossRef Full Text | Google Scholar

Moriasi, D. N., Arnold, J. G., Van Liew, M. W., Bingner, R. L., Harmel, R. D., and Veith, T. L. (2007). Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 50, 885–900. doi: 10.13031/2013.23153

CrossRef Full Text | Google Scholar

Mosello, B., Adamtey, R., and Obuobie, E. (2017). Making Water Infrastructure Investment Decisions in a Changing Climate A Political Economy Study of River Basin Development in Ghana. London: Overseas Development Institute, 45.

Google Scholar

Mul, M., Obuobie, E., Appoh, R., Kankam-Yeboah, K., Bekoe-Obeng, E., Amisigo, B., et al. (2015). Water Resources Assessment of the Volta River Basin. Colombo: International Water Management Institute, doi: 10.5337/2015.220

CrossRef Full Text | Google Scholar

Mul, M., Pettinotti, L., Amonoo, N. A., Bekoe-Obeng, E., and Obuobie, E. (2017). Dependence of Riparian Communities on Ecosystem Services in Northern Ghana. IWMI Working Paper 179. Colombo: International Water Management Institute, 43. doi: 10.5337/2018.201

PubMed Abstract | CrossRef Full Text | Google Scholar

Pettinotti, L. (2017). Baseline Valuation of Ecosystem Services Based Activities Underpinning the Livelihood of the Pwalugu communities – Northern Ghana. Project report. WISE-UP to Climate project. Gland: International Union for Conservation of Nature.

Google Scholar

Porse, E. C., Sandoval-Solis, S., and Lane, B. A. (2015). Integrating environmental flows into multi-objective reservoir management for a transboundary, water-scarce river basin: Rio Grande/Bravo. Water Resour. Manag. 29, 2471–2484. doi: 10.1007/s11269-015-0952-8

CrossRef Full Text | Google Scholar

Reed, P. M., and Kasprzyk, J. (2009). Water resources management: the myth, the wicked, and the future. J. Water Resour. Plan. Manag. 135, 411–413. doi: 10.1061/(ASCE)WR.1943-5452.0000047

PubMed Abstract | CrossRef Full Text | Google Scholar

Sadick, A., Ansah, I. O., Badu, A. O., Nketia, K. A., Asamoah, E., Asaana, J., et al. (2015). Estimation of potential evapotranspiration at botanga irrigation scheme in the Northern Region of Ghana. Environ. Res. Eng. Manag. 70:7752. doi: 10.5755/j01.erem.70.4.7752

CrossRef Full Text | Google Scholar

Sadoff, C. W., and Grey, D. (2009). Cooperation on International rivers A continuum for securing and sharing benefits. Water Int. 30, 420–427. doi: 10.1080/02508060508691886

CrossRef Full Text | Google Scholar

Schmitt, R. J. P., Bizzi, S., Castelletti, A., Opperman, J. J., and Kondolf, G. M. (2019). Planning dam portfolios for low sediment trapping shows limits for sustainable hydropower in the Mekong. Sci. Adv. 5:eaaw2175. doi: 10.1126/sciadv.aaw2175

PubMed Abstract | CrossRef Full Text | Google Scholar

Siciliano, G., Urban, F., Tan-Mullins, M., and Mohan, G. (2018). Large dams, energy justice and the divergence between international, national and local developmental needs and priorities in the global South. Energy Res. Soc. Sci. 41, 199–209. doi: 10.1016/j.erss.2018.03.029

CrossRef Full Text | Google Scholar

Sidibé, Y., Williams, T. O., and Kolavalli, S. (2016). Flood Recession Agriculture for Food Security in Northern Ghana opportunities. GSSP Working Paper 42. Washington, DC: International Food Policy Research Institute.

Google Scholar

Smith, R., Kasprzyk, J., and Zagona, E. (2015). Many-objective analysis to optimize pumping and releases in multireservoir water supply network. J. Water Resour. Plan. Manag. 142:04015049. doi: 10.1061/(asce)wr.1943-5452.0000576

PubMed Abstract | CrossRef Full Text | Google Scholar

Thiessen, E. M., and Loucks, D. P. (1992). Computer assisted negotiation of multiobjective water resources conflicts. J. Am. Water Resour. Assoc. 28, 163–177. doi: 10.1111/j.1752-1688.1992.tb03162.x

CrossRef Full Text | Google Scholar

Tilmant, A., and Kinzelbach, W. (2012). The cost of noncooperation in international river basins. Water Resour. Res. 48:1503. doi: 10.1029/2011WR011034

CrossRef Full Text | Google Scholar

Tilmant, A., Kinzelbach, W., Juizo, D., Beevers, L., Senn, D., and Casarotto, C. (2012). Economic valuation of benefits and costs associated with the coordinated development and management of the Zambezi river basin. Water Policy 14, 490–508. doi: 10.2166/wp.2011.189

CrossRef Full Text | Google Scholar

Tomlinson, J. E., Arnott, J. H., and Harou, J. J. (2020). A water resource simulator in Python. Environ. Model. Softw. 126:104635. doi: 10.1016/j.envsoft.2020.104635

CrossRef Full Text | Google Scholar

Voinov, A., Kolagani, N., McCall, M. K., Glynn, P. D., Kragt, M. E., Ostermann, F. O., et al. (2016). Modelling with stakeholders – Next generation. Environ. Model. Softw. 77, 196–220. doi: 10.1016/j.envsoft.2015.11.016

CrossRef Full Text | Google Scholar

Volta River Authority (2018). Pwalugu Multipurpose Dam Project: Technical Feasibility Study. Internal VRA Report. Accra: Volta River Authority.

Google Scholar

Wheeler, K. G., Hall, J. W., Abdo, G. M., Dadson, S. J., Kasprzyk, J. R., Smith, R., et al. (2018). Exploring cooperative transboundary river management strategies for the Eastern Nile Basin. Water Resour. Res. 54, 9224–9254. doi: 10.1029/2017WR022149

PubMed Abstract | CrossRef Full Text | Google Scholar

Wild, T. B., Reed, P. M., Loucks, D. P., Mallen-Cooper, M., and Jensen, E. D. (2019). Balancing hydropower development and ecological impacts in the mekong: tradeoffs for Sambor Mega Dam. J. Water Resour. Plan. Manag. 145:05018019. doi: 10.1061/(ASCE)WR.1943-5452.0001036

PubMed Abstract | CrossRef Full Text | Google Scholar

Wurbs, R. A. (1993). Reservoir-system simulation and optimization models. J. Water Resour. Plan. Manag. 119, 455–472. doi: 10.1061/(ASCE)0733-94961993119:4(455)

CrossRef Full Text | Google Scholar

Yoon, J., Klassert, C., Selby, P., Lachaut, T., Knox, S., Avisse, N., et al. (2021). A coupled human-natural system analysis of freshwater security under climate and population change. Proc. Natl. Acad. Sci. 118:e2020431118. doi: 10.1073/pnas.2020431118

PubMed Abstract | CrossRef Full Text | Google Scholar

Zarfl, C., Lumsdon, A. E., Berlekamp, J., Tydecks, L., and Tockner, K. (2014). A global boom in hydropower dam construction. Aquat. Sci. 77, 161–170. doi: 10.1007/s00027-014-0377-0

CrossRef Full Text | Google Scholar

Zatarain Salazar, J., Reed, P. M., Herman, J. D., Giuliani, M., and Castelletti, A. (2016). A diagnostic assessment of evolutionary algorithms for multi-objective surface water reservoir control. Adv. Water Resour. 92, 172–185. doi: 10.1016/j.advwatres.2016.04.006

CrossRef Full Text | Google Scholar

Zatarain Salazar, J., Reed, P. M., Quinn, J. D., Giuliani, M., and Castelletti, A. (2017). Balancing exploration, uncertainty and computational demands in many objective reservoir optimization. Adv. Water Resour. 109, 196–210. doi: 10.1016/j.advwatres.2017.09.014

CrossRef Full Text | Google Scholar

Zeff, H. B., Herman, J. D., Reed, P. M., and Characklis, G. W. (2016). Cooperative drought adaptation: Integrating infrastructure development, conservation, and water transfers into adaptive policy pathways. Water Resour. Res. 52, 7327–7346. doi: 10.1002/2016WR018771

CrossRef Full Text | Google Scholar

Zeff, H. B., Kasprzyk, J. R., Herman, J. D., Reed, P. M., and Characklis, G. W. (2014). Navigating financial and supply reliability tradeoffs in regional drought management portfolios. Water Resour. Res. 50, 4906–4923. doi: 10.1002/2013WR015126

CrossRef Full Text | Google Scholar