New model for predicting terminal settling velocity and drag coefficient of the Oncomelania

This paper presents a study of the terminal settling velocity and drag coefficient of the Oncomelanias with highly irregular shape in the range of particle Reynolds number (10 < R_ep < 600). The movement characteristics of the Oncomelanias with horizontal and slant postures are revealed using image analysis and wavelet analysis. The shape features of Oncomelanias with different dimensions are quantified and formulated. The authors propose a new model for predicting the drag coefficient of the dormant and active Oncomelanias, which is proven to be better than several widely-used formulas. Further, a simple settling velocity model that can predict the terminal velocity of the Oncomelanias fairly with several easy-to-measure parameters is developed. These findings provide a basis for the further improvement for the hydraulic schistosomiasis control project and supply reference for the settling characteristics and drag coefficient of cone-shaped particles.

Introduction

Schistosomiasis is a parasitic infectious disease that is harmful to human health and restricts the development of the economy and society. It is prevalent mainly in 73 countries of Asia, Africa, and Latin America, and the number of patients affected is approximately 200 million (Mcmanus et al., 2011). The Oncomelania is the only intermediate host of Schistosoma japonicum, and its distribution is consistent with that of S. japonicum. One of the most key issues for schistosomiasis control is the dispersal of the snail intermediate host along rivers and irrigation schemes (Cheng et al., 2016). Thus, the hydraulic schistosomiasis control project can be considered an effective measure to control the epidemic spreading of S. japonicum, one of the keys of which is the physical traits and settling characteristics of the Oncomelania.

The settling process of solid particle occurs in many natural and industrial processes, such as the deposition of hydrochorous seeds and fish eggs (Jia et al., 2020; Liu et al., 2018; Zhu et al., 2017), transportation of drilling cuttings and fracturing proppants (Chien, 1994), chemical and powder processing (Chhabra and Richardson, 2011), alluvial channel (Hvitved-Jacobsen et al., 1998), and pipeline transportation of mining and coal particles (Delleur, 2001).

Although the settlement of the sphere is the basis of all settlement issues in practical applications, the most commonly encountered particles are non-spherical and the knowledge of drag coefficient and settling velocity for non-spherical particles is of fundamental significance (Song et al., 2017).

The settling mechanism of spherical particle has been deeply investigated. Stokes (1851) presented the standard drag coefficient curves from the experimental data. Meanwhile, Chhabra et al. (1999) developed a terminal velocity prediction model, which was suitable for different particle sizes and fluid characteristics. Barry and Parlange (2018) proposed an expression of drag coefficient for spherical particle, drop, or bubble in an infinite homogeneous liquid. Terminal settling velocity and drag coefficient can be predicted accurately under different Reynolds numbers (Ma et al., 2020; Wang et al., 2020).

However, natural and artificial particles, such as organisms (Chambert and James., 2009), coal (Zhou et al., 2020), pulp (Bhutani and Brito-Parada, 2020), and fiber (Roegiers and Denys, 2019), have different shapes and sizes. Owing to the higher surface area to volume ratio, drag coefficient of the non-spherical particles is greater than those of spherical particles (Wang et al., 2014). The error occurs as the published prediction formula was applied in non-spherical particles (Ren et al., 2011), especially for particles with a high Reynolds number. Yin et al. (2003) studied the movement of columnar particles and revealed that particles will rotate when their pressure centers were inconsistent with the mass center. The flow mechanism of the non-spherical particles has not been fully understood because further research on the measuring devices and methods of particle identification and tracking was needed. Establishing precise prediction models of terminal velocity and drag coefficient for non-spherical particles remains a challenge.

Many different methods described the shape of non-spherical particles, including sphericity, circularity, flatness, and the Corey shape factor. In particular, Dellino et al. (2005) proposed a shape descriptor defined as the ratio between sphericity and circularity, which is suitable for highly irregular pumice particles. These shape factors have been used to understand and formulate the effect of particle shape on the drag better.

Few models for the prediction accuracy of terminal settling velocity and drag coefficient cover the wide range of differences in particle properties with a low prediction inaccuracy. The prediction accuracy of the models was derived for non-spherical particles (Ganser, 1993; Haider and Levenspiel, 1989; Hölzer and Sommerfeld, 2008; Ouchene et al., 2016), using the sphericity as a shape descriptor, was not significantly improved for drinking-water-related granules (Kramer et al., 2021).

In the present study, a comprehensive analytical and experimental investigation on settling process and drag coefficient of highly irregular-shaped Oncomelania is conducted, which is a research gap of predicting the drag coefficient and terminal settling velocity of the cone-shaped organism accurately. The settling trajectories of the Oncomelanias are extracted using image recognition, and the movement characteristics of the settling process are analyzed. The shape features of the Oncomelania are quantified. Finally, the authors develop a drag coefficient model of the Oncomelania and propose an explicit expression of the settling velocity.

Settling experiments and shape features

Experiment setup

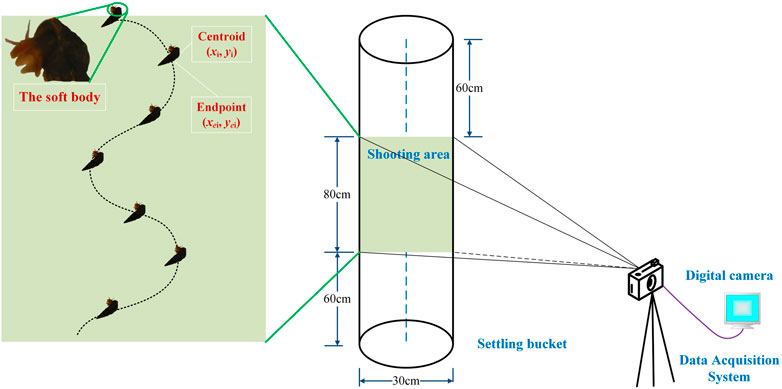
Settling experiments were carried out in the vertical Plexiglas cylinder with a height of 200 cm and an inner diameter of 30 cm, as shown in Figure 1. All experiments were conducted at atmospheric pressure and at the controlled room temperatures of 17°C–20°C for all the solutions to ensure that the rheological properties of the solutions did not change greatly due to temperature variation. The cylinders were filled with the liquid solution at least 24 h prior to each experimental session to allow the escape of air bubbles.

FIGURE 1

FIGURE 1. Schematic diagram of the experimental set-up and settling trajectory of the Oncomelania.

By testing, different sized Oncomelanias can attain equilibrium condition after sinking 50 cm, and the trajectories with terminal settling velocities, including settling trajectories, orientation angle, and settling velocity, are collected and analyzed. The velocity in the vertical direction was obtained by center difference method from three consecutive frames.

After the settling experiment, a MATLAB program was used to analyze the images recorded by the camera to obtain various data. The temporal resolution, which depended on the reciprocal of the camera frame, was 0.04 s.

The MATLAB program can identify the centroid of the Oncomelania in each frame, and the movement characteristic values was calculated by center difference method.

${u_{s,}}_i=\frac{x_{i+1}-x_{i-1}}{2\Delta t}\begin{array}{cc},& w_{\mathrm{s},i}=\frac{y_{i+1}-y_{i-1}}{2\Delta t}\end{array},{\theta }_i=\arctan \left(\left|\frac{y_i-y_{ei}}{x_{ei}-x_i}\right|\right)(1)$

where u_s,i and w_s,i were the longitudinal and transversal instantaneous velocity of floating particles, respectively; (x_i+1, y_i+1) was the centroid coordinate in (i+1)th frame of images; (x_i-1, y_i-1) was the centroid coordinate in (i-1)th frame of images; (x_ei, y_ei) was the right endpoint in (i)th frame of images; Δt was the time interval between the two frame; and θ_i was an instantaneous vector angular.

Trajectory extraction

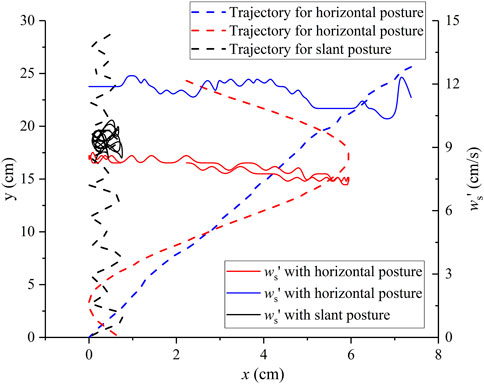
Owing to the fixed proportional relationship between pixels and actual size, the pixel unit was calibrated in advance. Based on the video image acquisition and coordinate extraction using a MATLAB program, the settling trajectories of the Oncomelania can be obtained. The stable settling postures of Oncomelanias were independent on the initial posture as water enters, most of samples sink with stable horizontal posture, some samples sink with slant posture first and last to horizontal posture, and others sink with stable slant posture.

As depicted in Figure 2, the red and blue dotted denote the sinking trajectory for the horizontal posture, and the black denotes that for the slant posture. The characteristic of trajectories can be decided by the settling posture, all of the samples sink in helix-type and only have difference in terms of stability and helical diameter. The trajectories of samples sinking with horizontal posture is instable w_s’ and have lager helical diameters (twice more than the length of samples), and the trajectories of the samples sinking with slant posture are more stable w_s’ and have smaller helical diameter (less than half of the length of samples).

FIGURE 2

FIGURE 2. Trajectories and w_s’ of the Oncomelania with horizontal and slant postures.

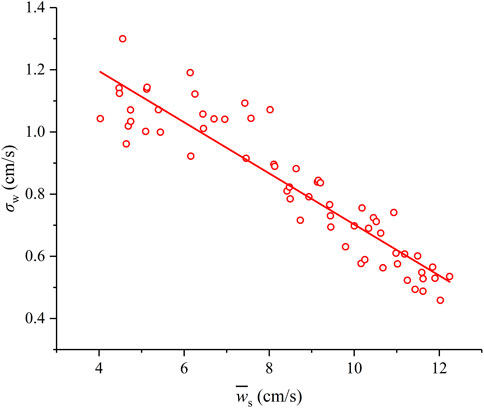
The vertical time-average velocity and turbulent intensity are defined as

${\overline{w}}_s=\frac{1}{N_d}{\displaystyle \sum }_1^{N_d}{w}_s^{\prime }(2)$

${\sigma }_w=\sqrt{\frac{1}{N_d}{\displaystyle \sum }_1^{N_d}{\left(w_s^{\prime }-{\overline{w}}_s\right)}^2}(3)$

where N_d is the number of trajectory dots. As shown in Figure 3, ${\sigma }_w$ and ${\overline{w}}_s$ have a significantly negative linear correlation,

${\sigma }_w=-0.0822{\overline{w}}_s+1.5244(4)$

with the correlation coefficient R² = 0.922. The variation relationship is in contrast to that of open channel flow, where the turbulent intensity is proportional with discharge and the time-average velocity (Akan and Lyer, 2021). For heavy particles that sink in stable water, the faster the settling velocity, the higher conversion efficiency of gravitational potential energy to kinetic energy.

FIGURE 3

FIGURE 3. The correlation between time-average settling velocity and turbulent intensity.

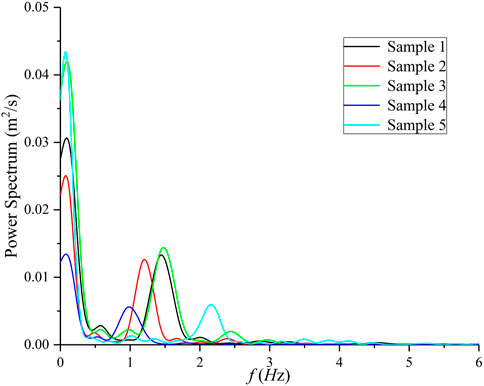
The power spectrum distribution of instantaneous settling velocities of the five samples is analyzed using wavelet analysis, as shown in Figure 4. Each sample has two peaks, the low-peak indicates the helical sinking process, and the corresponding frequency of different samples are almost same, ranging from 0.12 to 0.13 H_Z. The high-peak indicates the fluctuation around the average, and the lower time-average velocity, the corresponding frequency becomes higher. The settling postures of Oncomelanias affect the amplitude of helical trajectories, but have no effect on the frequency of oscillation that only depends on the shape structure of Oncomelanias. Analogous to stem-scale turbulence in vegetated open channel flows associated with the diameter of vegetation and flow velocity, the high-peak means the fine-scale disturbance and determined by the physical characteristics and settling velocity of Oncomelanias.

FIGURE 4

FIGURE 4. The power spectrum distribution of instantaneous settling velocities of five samples.

Shape features of the Oncomelania

In this study, the Oncomelanias are sampled from the Jingzhou fragment (the middle reach) of Changjiang River, China, as shown in Figure 5. The Oncomelania is amphibian, the young lives in water, and the adult generally lives on bottomland and wetland with rich nutrients. The sampling regions includes typical habitats (lake, bottomland, riverside) in the Yangtze River basin, where different growth state of Oncomelanias can be sampled. The shape features of the Oncomelania are obtained by the photographs of different angles with image processing using the MATLAB program, which mainly includes preprocessing, binarization, and morphological operation (Brueck and Wildenschild, 2020). The density of the Oncomelanias is measured using the Archimedes method.

FIGURE 5

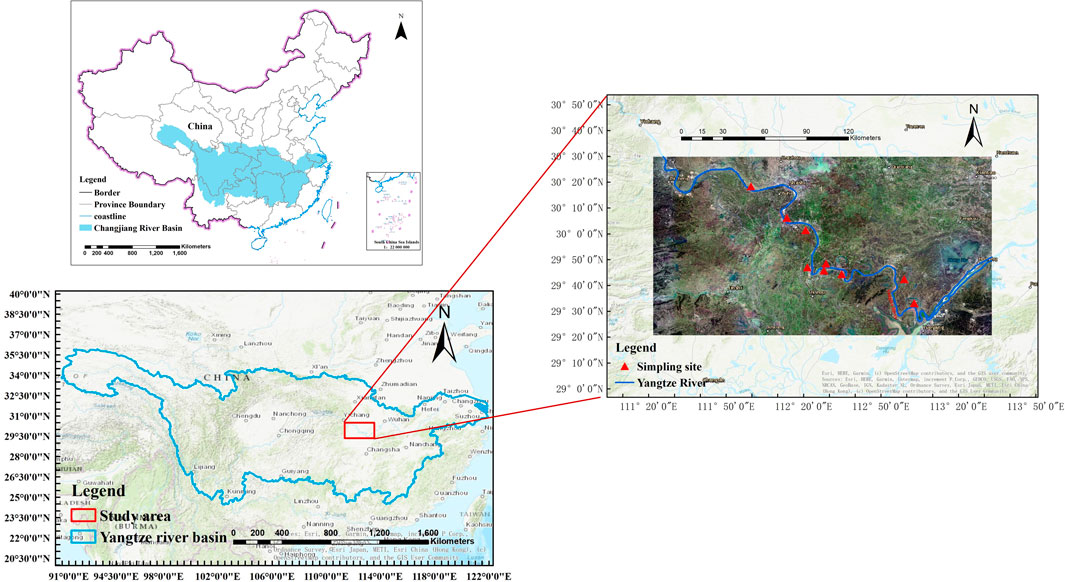
FIGURE 5. Sampling sites of experimental Oncomelanias of the Jingzhou fragment (the middle reach) of Changjiang River.

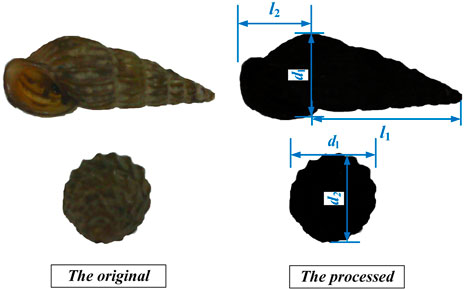
The body of the Oncomelania can be divided into two parts at the maximum diameter, one is half a quasi-spheroid toward the mouth of the Oncomelania, and the other is a quasi-cone. As shown in Figure 6, the three axial lengths of the quasi-spheroid are d₁, d₂, and 2l₂. Cross section of the quasi-spheroid approximates circle, d₁ is considered to be equivalent to d₂. The height and diameter of the quasi-cone are l₁ and d₁. The maximum and minimum project areas are the front and side of the Oncomelania respectively, and the maximum project area can be estimated as

$A_{pm}=\frac{k_p{d}_1}{2}\left(\frac{\pi }{2}{l}_2+l_1\right)(5)$

where k_p is the correction coefficient. For consistency, the total length of the Oncomelania is defined as 0.5πl₂+l₁, and the diameter of the Oncomelania is d₁, which is approximately equal to d₂.

FIGURE 6

FIGURE 6. Main shape parameters of the Oncomelania with the original and processed images.

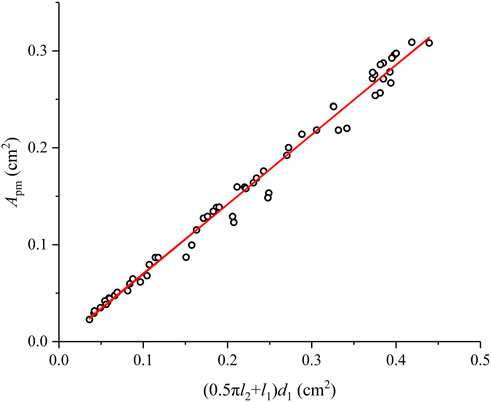
As shown in Figure 7, the parameter A_pm increases linearly with parameter (0.5πl₂+l₁)d₁, and k_p is a constant for the Oncomelania and equals to 1.424 with the correlation coefficient R² = 0.966.

FIGURE 7

FIGURE 7. The linear relationship between A_pm and parameter (0.5πl₂+l₁)d₁.

The weight distribution and density of the Oncomelania depend on the proportion of the quasi-cone. Thus, the ratio $\gamma =l_1/l_2$ is introduced to describe the shape feature, accordingly, Eq. 5 can be written as

$A_{pm}=0.712\left(\gamma +\frac{\pi }{2}\right)l_2{d}_1(6)$

To obtain a definite diameter, the diameter of the volume-equivalent sphere is introduced,

$d_e={\left(6V_p/\pi \right)}^{1/3}(7)$

Owing to the shape structure of the Oncomelanias being fixed, d_e is found to be proportion to the total length, as shown in Figure 8, the relationship between d_e and (0.5πl₂+l₁) can be described as,

$d_e=0.0765\left(0.5\pi l_2+l_1\right)+0.235(8)$

with the correlation coefficient R² = 0.988.

FIGURE 8

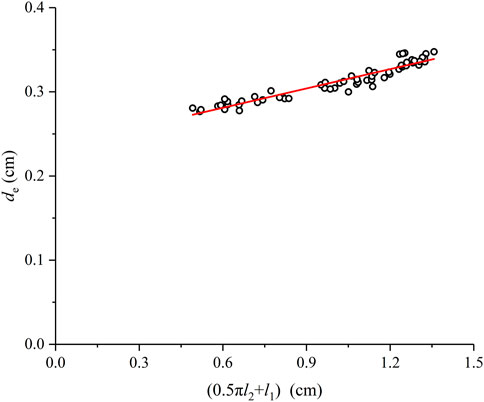
FIGURE 8. The variation relationship between the total length and the he diameter of the volume-equivalent sphere.

Sphericity is defined as the ratio between the surface area of the equivalent sphere A_eq and that of the actual particle A_s, which can be written as follows,

$\varphi =\frac{A_{eq}}{A_s}(9)$

Sphericity is a measure of the degree to which the shape of a particle approximates that of a true sphere, and it is very difficult to be evaluated for highly irregular particles because measuring A_s is difficult. Thus, the surface area of the Oncomelania is estimated, referring to quasi-spheroid and quasi-spheroid,

$A_s=\frac{2\pi }{3}\left(d_1{d}_2/4+d_1{l}_2/2+d_2{l}_2/4\right)+\frac{d_1}{2}\sqrt{l_1^2+d_1^2/4}(10)$

The sphericity of the Oncomelania can be expressed as,

$\varphi =\frac{\pi {\left[0.0765\left(0.5\pi l_2+l_1\right)+0.235\right]}^3}{4\pi \left(d_1{d}_2/4+d_1{l}_2/2+d_2{l}_2/4\right)+\frac{d_1}{2}\sqrt{l_1^2+d_1^2/4}}(11)$

For highly irregular particles, the parameter Ψ, which is the ratio between phericity ϕ and a newly defined inverse circularity χ, is an effective shape descriptor.

$\chi =\frac{P_p}{P_s}(12)$

where P_p is the maximum projection perimeter of the actual particle, and P_s is the perimeter of the circle equivalent to the maximum projection area A_s. χ is sensible to the irregularity of the contour of particles and is very suitable in evaluating the particle shape with sharp corners with large obtuse angles (Büttner et al., 2002).

Combining with Eqs 10–12, χ can be written as,

$\chi =\frac{2\sqrt{l_1^2+d_1^2/4}+\pi d_1/4+2\left(l_2-d_1/2\right)}{\sqrt{2.8484\pi d_1(\frac{\pi }{2}{l}_2+l_1)}}(13)$

which is a 2D shape factor and sensible to the irregularity of the contour of particles, and very suitable for evaluating the particle shape with sharp corners of large obtuse angles.

Models and discussion

Settling velocity model

The forces on a single particle that sinks in balance include the buoyancy force (F_b), gravitational force (F_g), and the particle-liquid interaction force (F_D). According to Newton’s equation of motion, the motion of the sinking particle can be presented as

$F_{\mathrm{g}}=F_D+F_b(14)$

The gravitational force and buoyancy force are calculated respectively as

$F_g={\rho }_p{V}_{p}g(15)$

$F_b={\rho }_w{V}_{p}g(16)$

where V_p is the volume of the Oncomelania, ρ_p is the density of the Oncomelania, and ρ_w is the density of the fluid. For the Oncomelania uniformly settling in static water, the particle–liquid interaction force is considered the drag force, which is defined as the parallel component of the combined shear and pressure forces that act on the surface of the immersed Oncomelania (Fox et al., 2020) and generally expressed in terms of the drag coefficient C_D,

$F_D=\frac{1}{2}{C}_D{\rho }_w{A}_p{w}_r^2(17)$

where w_r is the relative velocity between particle and fluid, w_r = w_s for sinking in static water, and A_p is the projected surface area of the Oncomelania normal to the direction of its motion. For sinking with horizontal posture, A_p equals to the maximum projected area, which is estimated by Eq. 6; for sinking with slant posture, A_p is the projected area along the settling orientation.

The force balance between the drag force and the net gravitational force (the difference of the particle weight and the particle buoyancy) is expressed as

$\frac{1}{2}{C}_D{\rho }_w{A}_p{w}_s^2=\left({\rho }_p-{\rho }_w\right)g{V}_p(18)$

For convenient application, this study attempts to develop an explicit settling velocity equation that is suitable for different sized Oncomelanias.

The particle Reynolds number is defined with d_e and w_s,

$R_{ep}=\frac{{\rho }_w{w}_s{d}_e}{\mu }(19)$

where μ is the dynamic viscosity coefficient of the fluid. Combining with Eq. 7, C_D can be written as

$C_D=\frac{\pi g\left({\rho }_p-{\rho }_w\right)d_e^3}{3{\rho }_w{A}_p{w}_s^2}(20)$

For the prediction of terminal settling velocity of particles of given properties, the quantity C_DR²_ep is introduced and convenient to be obtained, which is independent of settling velocity and can be evaluated from the physical properties of the Oncomelanias and the liquid (Wang et al., 2018). Combining with Eq. 19, C_DR²_ep can be written as,

$C_D{R}_{ep}^2=\frac{\pi g{\rho }_w\left({\rho }_p-{\rho }_w\right)d_e^5}{3\mu A_p}(21)$

To reveal the effect of the physical characteristic and shape feature on the settling process and determine the terminal settling velocity of the Oncomelania, the variation relationship between the main influencing factor and C_D should be further discussed.

Drag coefficient for the Oncomelanias

Drag coefficient plays a core role in determining the drag F_D, which is a dimensionless parameter, however, that of the cone-shaped particle is rarely investigated.

According to previous studies (Dioguardi and Mele, 2015; Govindan et al., 2021; Song et al., 2017; Zhou et al., 2022), particle diameter, particle length, particle sphericity, and particle Reynolds number take effect on the drag coefficient. Thus, the drag coefficient should be the function of these effects, and can be expressed as,

$C_D=f\left(l,d,{\rho }_{p,}{\rho }_w,w_s,A_p,\varphi \right)(22)$

Three dimensionless parameters are refined to represent the above mentioned parameters. The shape factor ψ is defined as the ratio of the sphericity and χ, χ represents the deviation of the particle shape from the circle, and $\gamma =\left(l_1+l_2\right)/d_1$ represents the flatness ratio of the maximum projection plane. Eq. 22 can be simplified as

$C_D=f\left(\psi ,\gamma ,R_{ep},S\right)(23)$

To apply the smooth sphere formula to irregularly-shaped particles, a shape factor needs to be introduced in the equation. Several proven methods can be referenced, where the effect of the irregular particle shape can be considered using parameter ψ in the form of power function (Dellino et al., 2005; Dioguardi and Mele, 2015; Wang et al., 2018; Zhu et al., 2017).

As shown in Figure 9, the influence of the shape feature on the variation of drag coefficient and terminal settling velocity becomes more noticeable as R_ep increases, which is compatible with that of Loth (2008) and Khatmullina and Isachenko (2017).

FIGURE 9

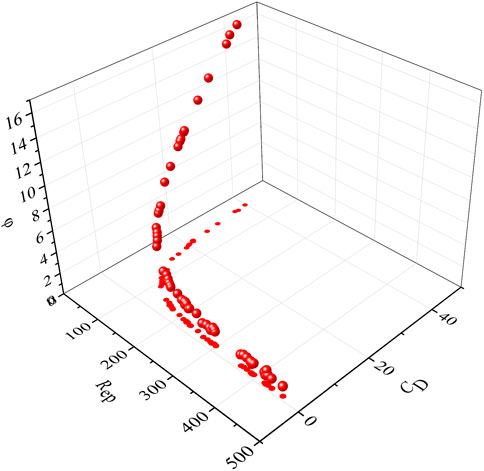
FIGURE 9. The variation relationship among the particle Reynold number, drag coefficient and Sphericity.

The drag coefficient of smooth sphere (C_D,sph) proposed by Clift and Gauvin (1971) is adopted in this study, which has been valid for 0 < R_ep < 3 × 10⁵,

$C_{\mathrm{D}\mathrm{s}\mathrm{p}\mathrm{h}}=\frac{24}{R_{e\mathrm{p}}}{\left(1+0.15R_{ep}\right)}^{0.687}+\raisebox{1ex}{$0.42$}\!\left/ \!\raisebox{-1ex}{$\left(1+42500R_{ep}^{-1.16}\right)$}\right.(24)$

Eq. 24 is appropriate for spherical particles. According to present experimental results, R_ep of the Oncomelania ranges from 30 to 400, the boundary layer around the particle separates and produces vortex shedding and wake formation, which lead to higher pressure drag and may cause the effect of shape and roundness to be dominant. To apply it to irregularly shaped particles, shape factors need to be introduced in the equation, and the effect of shape factors on C_D is affected by R_ep (Zhou et al., 2022). Thus, the ratio of C_D to C_{D, sph} can be described as,

$\frac{C_D}{C_{D\mathrm{s}\mathrm{p}\mathrm{h}}}=f\left(\psi ,\gamma ,R_{ep},S\right)(25)$

Further, the expression form of R_ep and ψ has been determined (Kramer et al., 2021; Wang et al., 2018),

$\frac{C_D}{C_{D\mathrm{s}\mathrm{p}\mathrm{h}}}\sim {\psi }^m{R}_{ep}^n(26)$

where m and n are undetermined coefficients.

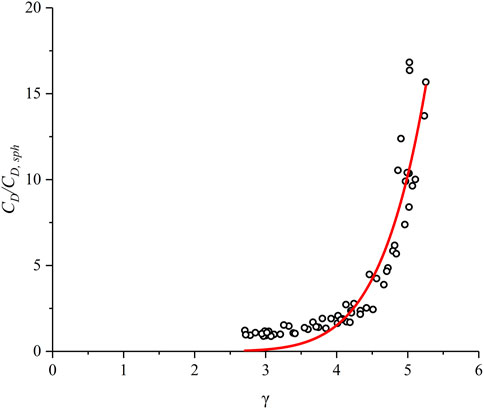
As shown in Figure 10, C_D/C_{D, sph} increases with the increase of γ in the form of approximate power law function, thus, the best fit is obtained by a power form with a high correlation coefficient. Eq. 25 can be expressed as

$\frac{C_D}{C_{D,\mathrm{s}\mathrm{p}\mathrm{h}}}=k{\psi }^m{R}_{ep}^n{\gamma }^p(27)$

where p is the undetermined coefficient, and k is the scale factor.

FIGURE 10

FIGURE 10. The variation relationship between parameter γ and C_D/C_{D, sph}.

Considering that the terminal settling velocity are obtained from the experiments, the measured drag coefficient (C_D,meas) is determined using Eq. 9. The drag coefficient of smooth sphere (C_D,sph) is calculated by Eq. 24. The calculated drag coefficient (C_D,calc) can be obtained through the analysis of the best fitting parameters of the experimental data.

$C_D/C_{D,sph}={\psi }^{1.72}{\gamma }^{0.93}{R}_{ep}^{0.23}(28)$

The average relative error is evaluated as,

$r=\frac{1}{N}{\displaystyle \sum }_{i=1}^N\frac{\left|C_{D,calc}-C_{D,meas}\right|}{C_{D,meas}}\times 100\%(29)$

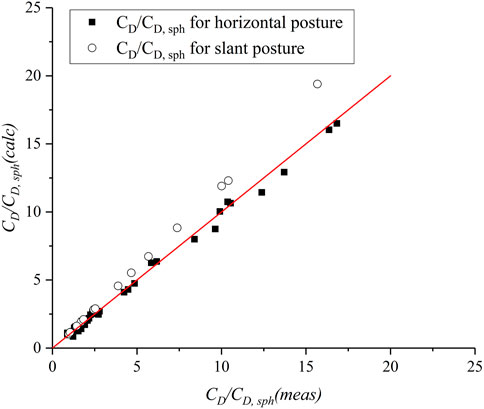
where N is the total number of data points. As shown in Figure 11, the calculated and measured C_D/C_D,sph for horizontal posture match well with r = 5.2%, and the calculated C_D/C_D,sph for slant posture is significantly greater than the measured ones, suggesting that the effect of settling orientation cannot be ignored. Thus, the effect of settling orientation is represented by S, which is the ratio between equivalent sphere area (S_e) and the projected area of particle settling direction (A_p).

$S=\frac{S_e}{A_p}(30)$

FIGURE 11

FIGURE 11. Comparison of the measured C_D/C_{D, sph} to that of the calculated.

Thus, Eq. 30 can be further written as

$\frac{C_D}{C_{D\mathrm{s}\mathrm{p}\mathrm{h}}}=k{\psi }^m{R}_{ep}^n{\gamma }^p{S}^{\mathrm{q}}(31)$

where q is the undetermined coefficient, and q = 0 is for the horizontal posture. Through nonlinear fitting with the experimental data of the slant posture, the following relationships can been derived,

$C_D/C_{D,sphere}=0.946{\psi }^{1.72}{\gamma }^{0.93}{R}_{ep}^{0.23}{S}^{-0.07}(32)$

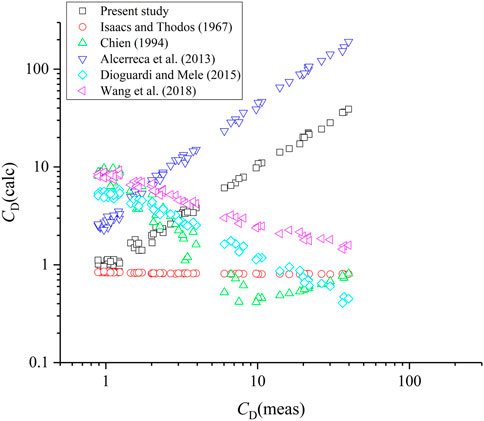
The average relative error of Eq. 32 is r = 1.2%. To evaluate the accuracy and rationality of the present formula compared with other models, we evaluated C_D of the Oncomelania with other well-known laws available in the literature.

Isaacs and Thodos (1967) studied the free settling of cylindrical particles in the turbulent regime. The authors used the equal volume sphere as the characteristic dimension and found that the drag coefficient was independent of R_ep. The drag coefficient depended on the particle/fluid density ratio (ρ_p/ρ_w) and the aspect ratio (E, defined as L/d_c),

$C_D=0.99{\left({\rho }_p/{\rho }_w\right)}^{-0.12}{E}^{-0.08}\left(200<R_{\mathrm{e}}\le 60000\right)(33)$

Chien (1994) reanalyzed the data available in the petroleum engineering and processing literature and proposed the following drag expression,

$C_D=\frac{30}{R_{ep}}+\frac{67.289}{e^{5.030\Phi }}(34)$

where C_D and R_ep are based on the equal-volume sphere diameter. Eq. 34 was stated to be valid in the ranges 0.2 < ϕ < 1 and R_ep < 5000.

Alcerreca et al. (2013) derived a new equation for the computation of particle settling velocity for calcareous sand,

$C_D=\frac{4d_e^3\left[\frac{g}{{\nu }^2}\left({\rho }_p/{\rho }_w-1\right)\right]}{3R_{ep}^2}(35)$

where ν is kinematic viscosity of water.

Dioguardi and Mele (2015) investigated the drag of non-spherical rough particles in a wide range of Reynolds numbers (0.03–10,000), the correlation has the functional form of a power law with particle Reynolds number and the shape factor. For 50 < R_ep < 10,000, the drag coefficient can be easily written as.

$C_D=0.931R_{ep}^{-0.079}{\psi }^{-1.6}(36)$

Wang et al. (2018) developed a new model for predicting the drag coefficient of natural particles of highly irregular shapes in a wide range of particle Reynolds number (0.01–3700).

$C_D=0.945\frac{C_{Dshp}}{{\psi }^{0.641R_{ep}^{0.153}}}{R}_{ep}^{-0.01}(37)$

As shown in Figure 12, the other formulas of cylindrical particles (Isaacs and Thodos, 1967) and approximate isometric calcareous particles (Chien, 1994; Dioguardi and Mele, 2015; Wang et al., 2018) are not applicable for the Oncomelania (cone-shaped particle). The predicting values of Alcerreca et al. (2013) and Dioguardi and Mele (2015) significantly lower than the measured, the basic reason of which are the flow structure around cone-shaped particle is more complicated and skin friction coefficient is higher. The average relative errors between present experimental data and predicting formula that applied to isometric calcareous particles are larger than 100%, and the trends of C_D and R_ep are inconsistent with the results obtained in the present experiments. Only sphericity and circularity being considered as shape factors is not enough, especially for the irregular-shape particle with asymmetrical weight distribution. Therefore, parameter γ is essential to weight the proportion of disc-shaped and cone-shaped parts. The formula proposed by Alcerreca et al. (2013), which considered all calcareous sand types and demonstrated the best performance in predicting the settling velocity, is comparatively applicative.

FIGURE 12

FIGURE 12. Comparisons between measured and calculated C_D for present and other related studies.

In general, the drag coefficient of the Oncomelania with different status can be written as

$C_D=C_{D,sph}{R}_{ep}^{0.23}\times \{\begin{array}{l}{\psi }^{1.72}{\gamma }^{0.93}for\begin{array}{c}\_the\_domant\end{array}\\ 0.946{\psi }^{1.72}{\gamma }^{0.93}{S}^{-0.07}for\_\begin{array}{c}the\_\begin{array}{c}active\end{array}\end{array}\end{array}(38)$

The particle Reynold number of the Oncomelania ranges from 36 to 470, and the reported R_ep of the Oncomelania is in the range of 10–600. The relationship between the drag coefficient of smooth sphere proposed by Clift and Gauvin (1971) and R_ep is plotted in Figure 13. Significantly, the variation of C_D,sph with R_ep for 10 < R_ep < 600 can be well fitted with power function, which can be described as,

$C_{D,\mathrm{s}\mathrm{p}\mathrm{h}}=8.7R_{ep}^{-0.359}10<R_{ep}<600(39)$

with the correlation coefficient R² = 0.9915.

FIGURE 13

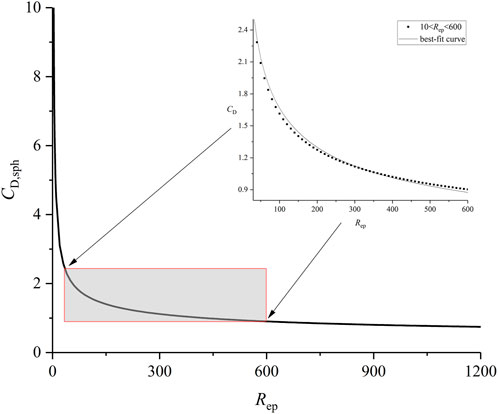
FIGURE 13. The relationship between C_{D, sph} and R_ep for smooth sphere, the top right-hand corner indicates the best-fit curve with 10 < R_ep < 600.

An explicit formula needs to be developed to facilitate practical application. Combining Eqs. 39, 38 can be written as:

$C_D=\{\begin{array}{l}8.7R_{ep}^{-0.129}{\psi }^{1.72}{\gamma }^{0.93}for\begin{array}{c}\_the\_domant\end{array}\\ 8.23R_{ep}^{-0.129}{\psi }^{1.72}{\gamma }^{0.93}{S}^{-0.07}for\_\begin{array}{c}the\_\begin{array}{c}active\end{array}\end{array}\end{array}(40)$

Further, combining with Eq. 21, the explicit formula of w_s for the Oncomelania can be reorganized as:

$w_s=\{\begin{array}{l}\frac{2.725g^{-0.5345}{d}_e^{-2.601}{\rho }_w^{-1.5345}{\left({\rho }_p-{\rho }_w\right)}^{-0.5345}}{{\mu }^{-2.069}{\psi }^{-0.9193}{\gamma }^{-0.4971}}\begin{array}{c}for\begin{array}{c}\_the\_domant\end{array}\end{array}\\ \frac{2.646g^{-0.5345}{d}_e^{-2.601}{\rho }_w^{-1.5345}{\left({\rho }_p-{\rho }_w\right)}^{-0.5345}}{{\mu }^{-2.069}{\psi }^{-0.9193}{\gamma }^{-0.4971}{S}^{-0.0374}}\begin{array}{c}for\_\begin{array}{c}the\_\begin{array}{c}active\end{array}\end{array}\end{array}\end{array}(41)$

Given that the experiments in the terminal settling velocities (w_{s, exp}) are obtained using Eq. 20, the predicted terminal settling velocities (w_{s, pre}) are determined using Eq. 41. As shown in Figure 14, 95% of data points lies within the predicting error of 10%, the average relative error between the predicted and the experimental of the dormant Oncomelanias using Eq. 29 is 3.72%, and that of the active Oncomelanias is 0.48%. A general good performance of the proposed explicit formula enables the prediction of fall velocity values within the range of 10 < R_ep < 600.

FIGURE 14

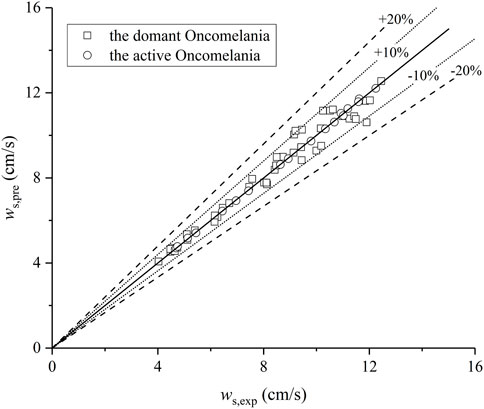
FIGURE 14. Comparison of measured and predicted settling velocity calculated by using explicit terminal settling velocity of Eq. 41.

Conclusion

In this study, a new model for predicting the settling velocity and drag coefficient of different sized Oncomelanias is developed. These findings cover the particle Reynolds number range of 10–600, which are suitable for young and mature Oncomelanias, and can offer references for millimeter-sized cone-shaped and disc-shaped particles. The stable settling postures of Oncomelanias do not depend on the initial posture as entering the water, the Oncomelania in dormant state will sink in horizontal posture, the Oncomelania in active state will sink in slant posture. Turbulent intensity and time-average sinking velocity have a significantly negative linear correlation. The settling postures of Oncomelanias affect the amplitude of helical trajectories, but have no effect on the frequency of oscillation that only depends on the shape structure of Oncomelanias.

The body of the Oncomelania can be divided into the quasi-spheroid and the quasi-cone. Accordingly, the authors define three axial lengths. Three dimensionless shape parameters are selected using the defined lengths to predict the drag coefficient of the Oncomelania. As R_ep increases, the influence of shape features on the particle drag coefficient and terminal settling velocity become increasingly evident. The proposed model performs better in predicting drag coefficient compared with several widely used formulas. Finally, combining with the predicting formula of C_D and Eqs 20, 21 with parameters ρ_p, l₁, l₂, d_1, and d₂, an explicit formula for settling velocity is developed with several easy-to-measure parameters is and proven to be a high-precision prediction formula of settling velocity for the dormant (r = 3.72%) and active Oncomelanias (r = 0.48%).

This study focuses on the research gap of predicting the drag coefficient and terminal settling velocity of the cone-shaped organism accurately, and can provide a basis for further improvement for the hydraulic schistosomiasis control project.

Data availability statement

The datasets presented in this study can be found in online repositories. The names of the repository/repositories and accession number(s) can be found in the article/supplementary material.

Author contributions

XL: Conceptualization, Methodology, Formal analysis, Resources, Investigation, Writing, Validation; JW: Methodology, Formal analysis, Writing, Supervision, Funding acquisition; ZC: Formal analysis, Writing, Supervision, Funding acquisition; XJ: Methodology, Formal analysis, Supervision; KZ: Formal analysis, Supervision; JD: Formal analysis, Supervision.

Funding

This work was mainly supported by the Fundamental Research Funds for Central Public Welfare Research Institutes (Grant Nos CKSF2021438/HL and CKSF2021530/HL), Open Foundation from the State Key Laboratory of Water Resources and Hydropower Engineering Science (Grant No. 2021HLG02), the National Natural Science Foundation of China (Grant Nos. 10802013 and 51809012) and the Program of the National Key Research and Development Plan (Grant No. 2018YFC0407803). The data that support the findings of this study is available on request from the corresponding author.

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Akan, A. O., and Iyer, S. S. (2021). Open channel hydraulics. Oxford, United Kingdom: Butterworth-Heinemann.

Google Scholar

Alcerreca, J. C., Silva, R., and Mendoza, E. (2013). Simple settling velocity formula for calcareous sand. J. hydraulic Res. 51 (2), 215–219. doi:10.1080/00221686.2012.753645

CrossRef Full Text | Google Scholar

Barry, D. A., and Parlange, J. Y. (2018). Universal expression for the drag on a fluid sphere. Plos one 13 (4), e0194907. doi:10.1371/journal.pone.0194907

PubMed Abstract | CrossRef Full Text | Google Scholar

Bhutani, G., and Brito-Parada, P. R. (2020). A framework for polydisperse pulp phase modelling in flotation. Sep. Purif. Technol. 236, 116252. doi:10.1016/j.seppur.2019.116252

CrossRef Full Text | Google Scholar

Brueck, C. L., and Wildenschild, D. (2020). A proximity‐based image‐processing algorithm for colloid assignment in segmented multiphase flow datasets. J. Microsc. 277 (2), 118–129. doi:10.1111/jmi.12874

PubMed Abstract | CrossRef Full Text | Google Scholar

Büttner, R., Dellino, P., La Volpe, L., Lorenz, V., and Zimanowski, B. (2002). Thermohydraulic explosions in phreatomagmatic eruptions as evidenced by the comparison between pyroclasts and products from Molten Fuel Coolant Interaction experiments. J. Geophys. Res. 107 (B11), ECV 5-1–ECV 5-14. doi:10.1029/2001jb000511

CrossRef Full Text | Google Scholar

Chambert, S., and James, C. S. (2009). Sorting of seeds by hydrochory. River Res. Appl. 25, 48–61. doi:10.1002/rra.1093

CrossRef Full Text | Google Scholar

Cheng, G., Li, D., Zhuang, D., and Wang, Y. (2016). The influence of natural factors on the spatio-temporal distribution of Oncomelania hupensis. Acta Trop. 164, 194–207. doi:10.1016/j.actatropica.2016.09.017

PubMed Abstract | CrossRef Full Text | Google Scholar

Chhabra, R. P., Agarwal, L., and Sinha, N. K. (1999). Drag on non-spherical particles: An evaluation of available methods. Powder Technol. 101 (3), 288–295. doi:10.1016/s0032-5910(98)00178-8

CrossRef Full Text | Google Scholar

Chhabra, R. P., and Richardson, J. F. (2011). Non-Newtonian flow and applied rheology: Engineering applications. Elsevier Science, Butterworth-Heinemann.

Google Scholar

Chien, S. F. (1994). Settling velocity of irregularly shaped particles. SPE Drill. Complet. 9 (04), 281–289. doi:10.2118/26121-pa

CrossRef Full Text | Google Scholar

Clift, R., and Gauvin, W. H. (1971). Motion of entrained particles in gas streams. Can. J. Chem. Eng. 49 (4), 439–448. doi:10.1002/cjce.5450490403

CrossRef Full Text | Google Scholar

Delleur, J. W. (2001). New results and research needs on sediment movement in urban drainage. J. Water Resour. Plan. Manag. 127 (3), 186–193. doi:10.1061/(asce)0733-9496(2001)127:3(186)

CrossRef Full Text | Google Scholar

Dellino, P., Mele, D., Bonasia, R., Braia, G., La Volpe, L., and Sulpizio, R. (2005). The analysis of the influence of pumice shape on its terminal velocity. Geophys. Res. Lett. 32 (21), L21306. doi:10.1029/2005gl023954

CrossRef Full Text | Google Scholar

Dioguardi, F., and Mele, D. (2015). A new shape dependent drag correlation formula for non-spherical rough particles. Experiments and results. Powder Technol. 277, 222–230. doi:10.1016/j.powtec.2015.02.062

CrossRef Full Text | Google Scholar

Fox, R. W., McDonald, A. T., and Mitchell, J. W. (2020). Fox and McDonald's introduction to fluid mechanics. Hoboken, NJ, USA: John Wiley & Sons.

Google Scholar

Ganser, G. H. (1993). A rational approach to drag prediction of spherical and nonspherical particles. Powder Technol. 77 (2), 143–152. doi:10.1016/0032-5910(93)80051-b

CrossRef Full Text | Google Scholar

Govindan, B., Mohanmani, P., Jakka, S. C. B., Tiwari, A. K., Kalburgi, A. K., Sudhakar, T. M., et al. (2021). Shape descriptors-settling characteristics of irregular shaped particles. Chem. Eng. Commun. 208 (3), 295–303. doi:10.1080/00986445.2019.1710494

CrossRef Full Text | Google Scholar

Haider, A., and Levenspiel, O. (1989). Drag coefficient and terminal velocity of spherical and nonspherical particles. Powder Technol. 58 (1), 63–70. doi:10.1016/0032-5910(89)80008-7

CrossRef Full Text | Google Scholar

Hölzer, A., and Sommerfeld, M. (2008). New simple correlation formula for the drag coefficient of non-spherical particles. Powder Technol. 184 (3), 361–365. doi:10.1016/j.powtec.2007.08.021

CrossRef Full Text | Google Scholar

Hvitved-Jacobsen, T., Vollertsen, J., and Tanaka, N. (1998). Wastewater quality changes during transport in sewers—an integrated aerobic and anaerobic model concept for carbon and sulfur microbial transformations. Water Sci. Technol. 38 (10), 257–264. doi:10.2166/wst.1998.0409

CrossRef Full Text | Google Scholar

Isaacs, J. L., and Thodos, G. (1967). The free‐settling of solid cylindrical particles in the turbulent regime. Can. J. Chem. Eng. 45 (3), 150–155. doi:10.1002/cjce.5450450306

CrossRef Full Text | Google Scholar

Jia, W. F., Zhang, S. H., Yang, Y. F., and Yi, Y. J. (2020). A laboratory investigation of the transport mechanism of floating fish eggs: A case study of asian carps. Aquaculture 519, 734855. doi:10.1016/j.aquaculture.2019.734855

CrossRef Full Text | Google Scholar

Khatmullina, L., and Isachenko, I. (2017). Settling velocity of microplastic particles of regular shapes. Mar. Pollut. Bull. 114 (2), 871–880. doi:10.1016/j.marpolbul.2016.11.024

PubMed Abstract | CrossRef Full Text | Google Scholar

Kramer, O. J., de Moel, P. J., Raaghav, S. K., Baars, E. T., van Vugt, W. H., Breugem, W. P., et al. (2021). Can terminal settling velocity and drag of natural particles in water ever be predicted accurately? Drink. Water Eng. Sci. 14 (1), 53–71. doi:10.5194/dwes-14-53-2021

CrossRef Full Text | Google Scholar

Liu, X., Zeng, Y., and Huai, W. (2018). Modeling of interactions between floating particles and emergent stems in slow open channel flow. Water Resour. Res. 54 (9), 7061–7075. doi:10.1029/2018wr022617

CrossRef Full Text | Google Scholar

Loth, E. (2008). Drag of non-spherical solid particles of regular and irregular shape. Powder Technol. 182 (3), 342–353. doi:10.1016/j.powtec.2007.06.001

CrossRef Full Text | Google Scholar

Ma, L., Xu, S., Li, X., Guo, Q., Gao, D., Ding, Y., et al. (2020). Particle tracking velocimetry of porous sphere settling under gravity: Preparation of the model porous particle and measurement of drag coefficients. Powder Technol. 360, 241–252. doi:10.1016/j.powtec.2019.09.058

CrossRef Full Text | Google Scholar

McManus, D. P., Gray, D. J., Ross, A. G., Williams, G. M., He, H. B., and Li, Y. S. (2011). Schistosomiasis research in the dongting lake region and its impact on local and national treatment and control in China. PLoS Negl. Trop. Dis. 5 (8), e1053. doi:10.1371/journal.pntd.0001053

PubMed Abstract | CrossRef Full Text | Google Scholar

Ouchene, R., Khalij, M., Arcen, B., and Tanière, A. (2016). A new set of correlations of drag, lift and torque coefficients for non-spherical particles and large Reynolds numbers. Powder Technol. 303, 33–43. doi:10.1016/j.powtec.2016.07.067

CrossRef Full Text | Google Scholar

Ren, B., Zhong, W., Jin, B., Lu, Y., Chen, X., and Xiao, R. (2011). Study on the drag of a cylinder-shaped particle in steady upward gas flow. Ind. Eng. Chem. Res. 50 (12), 7593–7600. doi:10.1021/ie102263u

CrossRef Full Text | Google Scholar

Roegiers, J., and Denys, S. (2019). CFD-modelling of activated carbon fibers for indoor air purification. Chem. Eng. J. 365, 80–87. doi:10.1016/j.cej.2019.02.007

CrossRef Full Text | Google Scholar

Song, X., Xu, Z., Li, G., Pang, Z., and Zhu, Z. (2017). A new model for predicting drag coefficient and settling velocity of spherical and non-spherical particle in Newtonian fluid. Powder Technol. 321, 242–250. doi:10.1016/j.powtec.2017.08.017

CrossRef Full Text | Google Scholar

Stokes, G. G. (1851). On the effect of the internal friction of fluids on the motion of pendulums. Cambridge, UK: Pitt Press, Cambridge Philosophical Society.

Google Scholar

Wang, L., Zheng, K., Ding, Z., Yan, X., Zhang, H., Cao, Y., et al. (2020). Drag coefficient and settling velocity of fine particles with varying surface wettability. Powder Technol. 372, 8–14. doi:10.1016/j.powtec.2020.05.102

CrossRef Full Text | Google Scholar

Wang, Y., Zhou, L., Wu, Y., and Yang, Q. (2018). New simple correlation formula for the drag coefficient of calcareous sand particles of highly irregular shape. Powder Technol. 326, 379–392. doi:10.1016/j.powtec.2017.12.004

CrossRef Full Text | Google Scholar

Wang, Z., Ren, S., and Huang, N. (2014). Saltation of non-spherical sand particles. Plos one 9 (8), e105208. doi:10.1371/journal.pone.0105208

PubMed Abstract | CrossRef Full Text | Google Scholar

Yin, C., Rosendahl, L., Kær, S. K., and Sørensen, H. (2003). Modelling the motion of cylindrical particles in a nonuniform flow. Chem. Eng. Sci. 58 (15), 3489–3498. doi:10.1016/s0009-2509(03)00214-8

CrossRef Full Text | Google Scholar

Zhou, C., Su, J., Chen, H., and Shi, Z. (2022). Terminal velocity and drag coefficient models for disc-shaped particles based on the imaging experiment. Powder Technol. 398, 117062. doi:10.1016/j.powtec.2021.117062

CrossRef Full Text | Google Scholar

Zhou, E., Lu, J., Wang, Q., Lv, G., Zhao, Y., Dong, L., et al. (2020). Mixing and migration rule of binary medium in vibrated dense medium fluidized bed for fine coal separation. Adv. Powder Technol. 31 (8), 3420–3432. doi:10.1016/j.apt.2020.06.029

CrossRef Full Text | Google Scholar

Zhu, X., Zeng, Y. H., and Huai, W. X. (2017). Settling velocity of non-spherical hydrochorous seeds. Adv. Water Resour. 103, 99–107. doi:10.1016/j.advwatres.2017.03.001

CrossRef Full Text | Google Scholar