Pricing and coordination in a green supply chain with a risk-averse manufacturer under the reference price effect

This paper considers a green supply chain using manufacturers and retailers as the research objects. The pricing and coordination strategy of the green supply chain, considering a risk-averse manufacturer, is investigated under the reference price effect. We establish centralized, decentralized, and cost-sharing contract decision-making models and then provide the optimal balancing strategy for each model. Further, we analyzed the optimal equilibrium strategy of different models. In the end, validate them through numerical simulation. We have found that the cost-sharing contract model is better than the decentralized decision model. Besides, manufacturers’ degree of risk avoidance affects the wholesale price, product greenness, retail prices, and profits of supply chain members. It is verified that the cost-sharing contract can coordinate the supply chain system to increase the profit of members of the supply chain.

Introduction

In recent years, consumer awareness of the environment has increased worldwide, and corresponding laws and regulations have been improved (Shen et al., 2013). Consumers often consider the level of the greenness of products when purchasing them, and the stronger the environmental awareness of consumers, the stronger their willingness to pay for green products. Based on the influence of environmental awareness, different scholars have proposed the concept of a green supply chain (Nagel, 2000; Sarkis, 2012; Fahimnia et al., 2015). From a business and leadership viewpoint, Nagel (2000) investigated the applicability of environmental supply chain management and green purchasing to supply chains and concluded that green purchasing would predominate in green supply chains. While previous researchers have frequently used the term “industrial environmental management” to describe green supply chains, Sarkis (2012) completed a review of related literature, redefined the concept’s parameters, and offered a framework for future research in the field. Fahimnia et al. (2015) used bibliometric tools and a network topology map approach to analyze the green supply chain research area, identify current and potential future research directions, and provide specific green supply chain research lines. The earliest research on green supply chains can be traced back to 1996 at Michigan State University (Corbett and Klassen, 2006).

Currently, green supply chains have been widely researched, and most scholars focus on two aspects of green supply chain research: product pricing and coordination mechanism design. On green supply chain product pricing, Heydari (2020) investigates the issue from the perspective of customer environmental awareness for a green supply chain made up of a single manufacturer and retailer. Li et al. (2021) study the pricing strategy of a green supply chain consisting of two competing retailers and one manufacturer. From the perspectives of channel competition, government subsidies, and uncertain market demand, some researchers have studied the optimal product price problems in green supply chains (Li et al., 2016; Rahmani and Yavari, 2018; Lou et al., 2020; Yao and Shao, 2022; Yang and Xiao, 2017). Furthermore, some researchers have created manufacturer-direct sales channels based on traditional retail channels to investigate pricing issues in green supply chains. For example, Wang et al. (2020) consider a closed-loop green supply chain product pricing problem using a dual channel of the manufacturer’s direct sales channel and retail channel, considering consumer-customized products. Mondal et al. (2020) examine pricing and greening strategies under three decentralized scenarios, including manufacturer-led, retailer-led, and Nash equilibrium, for a dual-channel green supply chain with forward and reverse manufacturer’s channel and retail channel. A manufacturer-direct and retailer channels are used in a dual-channel sales model by Wang and Sun (2019) to explore static and dynamic wholesale pricing strategies in a green supply chain.

On the green supply chain coordination mechanism, unlike traditional supply chains, green supply chains focus on improving the greenness level of products and adopt various coordination contracts such as cost-sharing contracts, two-part price contracts, and benefit-sharing contracts to compensate manufacturers for their investment in the greenness level of products (Ghosh and Shah, 2015; Panja and Mondal, 2019; Yi et al., 2021), to coordinate the supply chain system and thus improve the profits of supply chain members. In a green supply chain coordination problem, Ghosh and Shah (2015) compare the effects of the cost-sharing contract and the retailer-manufacturer bargain on the cost-sharing contract on product greenness, green product price, and supply chain member profitability. In a two-level green supply chain with a manufacturer and a retailer, Taleizadeh et al. (2020) investigate the impacts of the cost-sharing contract and the repayment agreement on supply chain manufacturing and sales. Yang and Gong (2021) investigate the best supply chain decision-making under cost-sharing contracts by including retailers’ reciprocal preferences in a green supply chain. Our study uses cost-sharing contracts to coordinate green supply chain systems, similar to the scholars mentioned above. In addition to the cost-sharing contract, some researchers use a two-part price contract to coordinate green supply chains (Li et al., 2016; Zhang et al., 2017; Sant, 2022). Revenue-sharing contracts are also often used to coordinate green supply chain systems. Panja and Mondal (2019) consider a two-level green supply chain consisting of manufacturers and retailers and find that revenue-sharing contracts can increase manufacturer and retailer profits by comparing optimal supply chain decisions under three scenarios: centralized, decentralized, and revenue-sharing. Shen (2021) introduces uncertain market demand, uses a revenue-sharing pact to coordinate the supply chain system based on a two-level green supply chain, and shows that the contract can improve greenness and reduce retail prices. A revenue-sharing contract is used by Yang et al. (2020) to coordinate a cartel supply chain while adding uncertainty to the manufacturer’s product development environment.

The product’s greenness influences consumer purchases, and in addition, consumer behavioral factors play an essential role in decision-making. In fact, consumers are influenced by the prices of similar products in other channels when purchasing goods, i.e., the reference price effect. Some scholars use the reference price effect when describing consumer behavior characteristics and incorporate it into the study of supply chain pricing issues. Based on the study by Xu and Liu (2017), it is found that in the closed-loop supply chain decision problem considering the reference price effect, as the reference price increases, the profits of manufacturers and retailers decrease, and the profits of third parties increase. Further, Malekian and Rasti-Barzoki (2019) explore the impact of price and advertising promotions on the profits of supply chain members under the reference price effect. Unlike the above studies, Wang et al. (2021) investigated the issue of channel supply chain pricing strategies for two different structures of online and offline channels under the reference price effect.

In past studies, researchers have considered the issue of supply chain pricing strategies when consumers have reference price effects. However, green supply chains operate in a process where decision-makers are not entirely rational. Behavioral economics studies have shown that the psychological factors of decision-makers influence the decision-making process and lead to deviations between results and reality. For example, supply chain members adopt a more conservative strategy, i.e., risk aversion. The risk-aversion behavior of supply chain members affects the decision-making of the supply chain system. Researchers have considered risk-averse supply chain pricing strategies (Liu et al., 2016); other researchers investigate the impact of risk aversion on pricing and supply chain coordination from the perspectives of demand uncertainty and asymmetric information (Xiao and Yang, 2008; Li et al., 2017; Alamdar et al., 2019; Bai et al., 2020).

From the above literature, it can be seen that the reference price effect on consumers is an important research area in the current green supply chain. In fact, manufacturers frequently exhibit risk-aversion behavior when developing green products, which impacts the optimal supply chain decision. In summary, this paper combines the two to study the problem of green supply chain pricing and coordination, considering manufacturers’ risk aversion and reference price effects. Researchers investigated green supply chains under the supply chain members’ risk-averse behavior but neglected to consider the reference price effect (Liu et al., 2016; Li et al., 2017; Bai et al., 2020). Another group of scholars considered the green supply chain under reference prices but did not consider the supply chain members’ behavioral factors (Xu and Liu, 2017; Wang et al., 2021). However, we are clear that the pricing of products from the green supply chain is affected by both the reference price effect and the members’ risk-averse behavior. Further investigation into the pricing and coordination of the green supply chain, taking into account manufacturers’ risk-averse behavior under the reference price effect, could contribute to solutions for the collaboration of supply chain members.

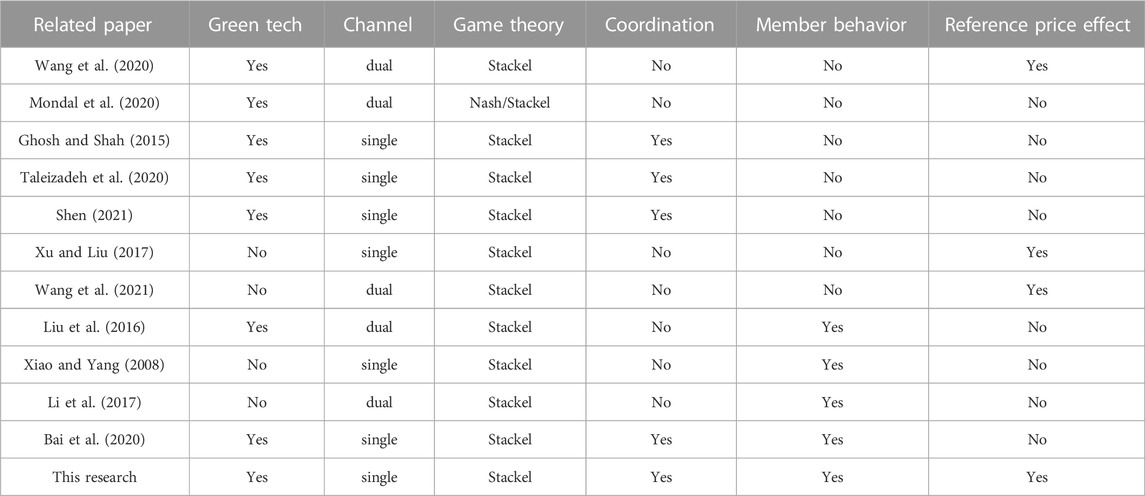
In this paper, we make the following contributions: First, based on the research already mentioned, we further investigate how supply chain members optimize profits by taking manufacturer risk aversion into account under the reference price effect. Investigate the patterns of parameters such as product greenness, retail pricing, and wholesale pricing that are affected by the level of manufacturer risk aversion. Second, we also propose improved coordination methods, using cost-sharing contracts to increase the overall profit of the green supply chain and the profit of each member, as well as to increase the level of product greenness. Finally, we compare and analyze the optimal decision-making in each of the three models of decision-making: centralized, decentralized, and cost-sharing. Moreover, verify by numerical experiments to provide some management insights for the green supply chain. Table 1 clearly shows the contribution of this paper and some related works.

TABLE 1

TABLE 1. Related works.

Table 1 lists the research gaps between this paper and other related works. “Green tech” indicates whether or not the research uses green technology. This paper investigated a green supply chain, where manufacturers invest in green product costs. “Channel” denotes whether the supply chain has only one channel. This paper is about a two-level supply chain consisting of a manufacturer and a retailer. Other scholars have also studied channels such as manufacturer direct sales channels, both online and offline channels (Liu et al., 2016; Li et al., 2017; Mondal et al., 2020; Wang et al., 2020; Wang et al., 2021). “Game theory” represents the game approach used, and the Stackelberg game is used in this paper.

2 Model assumptions

The research object of this article is a two-level supply chain composed of a manufacturer and a retailer. Manufacturers manufacture products at unit product cost $c$, and retailers purchase products from manufacturers at wholesale price $w$ and sell them to consumers at retail price $p$. Manufacturers dominate the supply chain; retailers follow manufacturers in the Stackelberg game; the information between the two sides is wholly shared. The relevant parameter symbols are shown in Table 2.

TABLE 2

TABLE 2. Relevant parameter symbols.

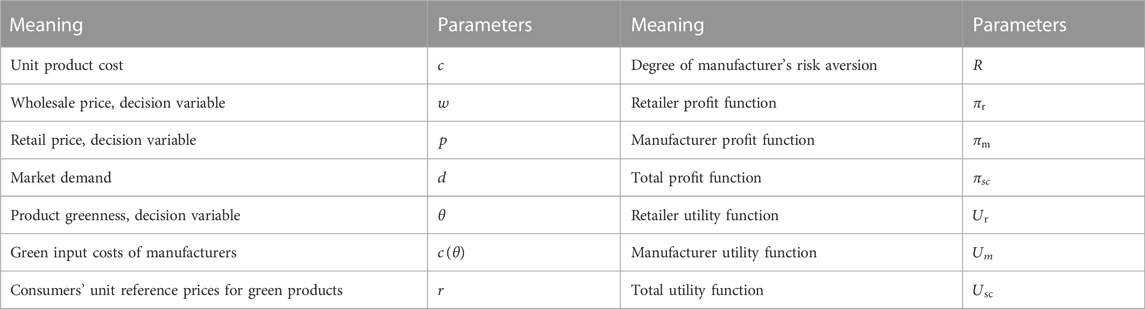
In Table 2, a list of the symbols and variables used in the study is shown. Retail pricing and product greenness make up the two parts of market demand, according to Xu and Liu (2014). Based on this, the model introduces reference price effects $\lambda \left(p-r\right)$ and manufacturer risk aversion coefficients $R$ (Xie et al., 2011). The profit functions of retailers and manufacturers were built under the two-level green supply chain. Similar to Wang et al. (2020), Ghosh and Shah (2015), and Shen (2021), the manufacturer and retailer play the Stackelberg game, where the manufacturer decides the wholesale price $w$ and the product’s degree of greenness $\theta$. The retailer will then decide on the retail price. Retailers and manufacturers compete for maximum profitability. $\pi$ represents profit, whereas subscript $r,m,\mathrm{s}\mathrm{c}$ represents the retailer, manufacturer, and supply chain system. $U$ represents utility since the retailer has no risk-averse behavior, i.e., $U_{\mathrm{r}}={\pi }_r$. The following assumptions mention the additional Table 2 parameters, so we will not repeat them here.

For the purpose of modeling, the following assumptions are made in this paper.

1) Market demand $d$ is a general linear function of the retail price $p$ and product greenness $\theta$ (Xu and Liu, 2014; Yao et al., 2022). Market demand is

$d=a-\beta p+k\theta -\lambda \left(p-r\right)(1)$

Where, $a$ indicates the potential market demand, $a=\alpha +\epsilon$, $\epsilon$ is a requirement random parameter that obeys a mean of zero and normal distribution with a variance of ${\sigma }^2$ (Tang, 2006; Yue and Liu, 2006). $\beta$ is the elasticity of market demand $d$ to the retail price $p$. $k$ is the elasticity coefficient of market demand $d$ on the greenness of the product $\theta$. $\lambda$ represents the elasticity coefficient of the difference between the consumer’s retail price $p$ and the reference price $r$ of the product.

2) The manufacturer has a risk-averse behavior, and the retailer has no risk behavior, i.e., the retail utility function $U_{\mathrm{r}}$ is equal to its profit function ${\pi }_{\mathrm{r}}$. A manufacturer’s utility function $U_m$ is an exponential function of its degree of risk aversion $R$, i.e.; $U_m=-e^{-R{\pi }_m}$; $R>0$. The manufacturer’s profit function ${\pi }_m$ follows a normal distribution: the mean is $E\left({\pi }_m\right)$, and the variance is $Var\left({\pi }_m\right)$. The manufacturer’s utility function is $U_m=E\left({\pi }_m\right)-RVar\left({\pi }_m\right)/2$ (Xie et al., 2011).

3) In order to produce green products, manufacturers need to invest a certain amount of money. It is a quadratic function between the manufacturers’ green input costs $c\left(\theta \right)$ and the product’s greenness $\theta$, i.e., $c\left(\theta \right)=\eta {\theta }^2/2$. Where, $\eta$ is the elasticity of the cost of green manufacturing inputs to product greenness.

As a result, manufacturers’ and retailers’ functions are

$U_r=\left(p-w\right)\left(\alpha -\beta p+k\theta -\lambda \left(p-r\right)\right)(2)$

Where $p-w$ represents the difference between the retail price and the wholesale price, i.e., the retailer’s revenue per unit of product. $\alpha -\beta p+k\theta -\lambda \left(p-r\right)$ denotes the market demand considering the product’s greenness and the reference price effect, which is the same as Eq. 1.

$U_m=\left(w-c\right)\left(\alpha -\beta p+k\theta -\lambda \left(p-r\right)\right)-\frac{1}{2}\eta {\theta }^2-\frac{1}{2}R{\left(w-c\right)}^2{\sigma }^2(3)$

Where $w-c$ represents the difference between the wholesale price and the cost of generation, i.e., the manufacturer’s revenue per unit of product. $\alpha -\beta p+k\theta -\lambda \left(p-r\right)$ is the same as Equation 1 above, indicating market demand. Manufacturers need to invest in the development costs to generate green products $\eta {\theta }^2/2$. $R{\left(w-c\right)}^2{\sigma }^2/2$ indicates the loss of revenue due to manufacturer risk aversion.

3 Model analysis

For ease of analysis, superscript $C$ denotes the equilibrium model under centralized decision-making, superscript $D$ denotes the equilibrium model under decentralized decision-making, and superscript $CS$ denotes the equilibrium model under cost-sharing contracts.

3.1 Centralized decision model

Under centralized decision-making, manufacturers and retailers are viewed as a whole, and make joint decisions to maximize the expected utility of the supply chain. The decision variables are wholesale price $w$, retail price $p$, and product greenness $\theta$. Then the total supply chain profit function under the centralized decision model is

${\pi }_{sc}=\left(p-c\right)\left(\alpha -\beta p+k\theta -\lambda \left(p-r\right)\right)-\frac{1}{2}\eta {\theta }^2-\frac{1}{2}R{\left(w-c\right)}^2{\delta }^2(4)$

Proposition 1 Under the centralized decision model, there is a single best solution for the total profit function of the supply chain when $k^2<2\eta \left(\lambda +\beta \right)$. The optimal decision is specified as follows

$w^C=c(5)$

${\theta }^C=\frac{k\left(c\lambda +c\beta -\alpha -r\lambda \right)}{k^2-2\lambda \eta -2\beta \eta }(6)$

$p^C=\frac{\eta \left(c\lambda +c\beta -\alpha -r\lambda \right)}{k^2-2\lambda \eta -2\beta \eta }+c(7)$

Proof of Proposition 1

Under the centralized decision model, the Hessian matrix of the total supply chain profit function ${\pi }_{sc}$ about the retail price $p$, the wholesale price $w$ and the product greenness $\theta$ is

$H^C=\left[\begin{array}{ccc}-2\lambda -2\beta & 0& k\\ 0& -R{\delta }^2& 0\\ k& 0& -\eta \end{array}\right](8)$

From the above Hesse matrix, the first-order principal subformula $-2\beta -2\lambda <0$, the second-order principal subformula $2R{\delta }^2\left(\lambda +\beta \right)>0$, and the third-order principal subformula $R{\delta }^2\left(k^2-\left(2\eta \lambda +2\eta \beta \right)\right)<0$ are obtained. Therefore, the Hesse matrix is a negative definite matrix. ${\pi }_{sc}$ is a joint concave function concerning the retail price $p$, the wholesale price $w$, and the product greenness $\theta$. So there is a single best solution for the total profit function of the supply chain ${\pi }_{sc}$. Under centralized decision-making, the optimal wholesale price $w^C$, the optimal retail price $p^C$ and the optimal product greenness ${\theta }^C$ are obtained by letting the first-order partial derivatives of ${\pi }_{sc}$ with respect to $p$, $w$ and $\theta$ be equal to zero. Proposition 1 is proven.

Substituting Eqs. 5, 6, and Eq. 7 into Eq. 4, the total supply chain profit function can be obtained

${\pi }_{sc}^C=\frac{\eta {\left(c\lambda +c\beta -\alpha -r\lambda \right)}^2}{2\left(2\lambda \eta +2\beta \eta -k^2\right)}(9)$

3.2 Decentralized decision model

Under the decentralized decision model, the manufacturer considers risk aversion, and the retailer is risk neutral. Furthermore, the retailer aims to maximize its own expected utility. Under the Stackelberg game, the manufacturer sets the wholesale price $w$ and the greenness of the product $\theta$ first. Above this, retailers set the retail price $p$ as followers of the manufacturer. The retailer’s profit function and the manufacturer’s profit function under decentralized decision-making are given by Eqs 2, 3.

${\pi }_r=\left(p-w\right)\left(\alpha -\beta p+k\theta -\lambda \left(p-r\right)\right)(10)$

${\pi }_m=\left(w-c\right)\left(\alpha -\beta p+k\theta -\lambda \left(p-r\right)\right)-\frac{1}{2}\eta {\theta }^2-\frac{1}{2}R{\left(w-c\right)}^2{\delta }^2(11)$

Proposition 2 Under the decentralized decision model, there is a single best solution for the supply chain. The optimal decision is

$w^D=\frac{2\eta \left(c\lambda +c\beta -\alpha -r\lambda \right)}{k^2-4\eta R{\delta }^2-4\eta \lambda -4\eta \beta }+c(12)$

${\theta }^D=\frac{k\left(c\lambda +c\beta -\alpha -r\lambda \right)}{k^2-4\eta R{\delta }^2-4\eta \lambda -4\eta \beta }(13)$

$p^D=\frac{\eta \left(2R{\delta }^2+3\lambda +3\beta \right)\left(c\lambda +c\beta -\alpha -r\lambda \right)}{\left(\lambda +\beta \right)\left(k^2-4\eta R{\delta }^2-4\eta \lambda -4\eta \beta \right)}+c(14)$

Proof of Proposition 2

The inverse solution approach is used to resolve the decentralized decision model. First, the retailer’s profit function ${\pi }_r$ concerning the retail price $p$ is discovered to be a first-order partial derivative. Let the value of this first-order condition be zero. And the optimal retail price response function is found as

$p^D=\frac{k\theta +w\left(\lambda +\beta \right)+\alpha +r\lambda }{2\left(\lambda +\beta \right)}(15)$

Second, the manufacturer’s profit function is produced by putting Eq. 15 into Eq. 11. ${\pi }_m$ concerning the wholesale price $w$ and the product greenness $\theta$ of the Hesse matrix is

$H^D=\left[\begin{array}{cc}-\lambda -\beta -R{\delta }^2& \frac{1}{2}k\\ \frac{1}{2}k& -\eta \end{array}\right](16)$

From the above Hesse matrix, we have the first-order principal subformula $-\lambda -\beta -R{\delta }^2<0$ , the second-order principal subformula $\eta \left(R{\delta }^2+\lambda +\beta \right)-k^2/4>0$. Therefore, the Hesse matrix is a negative definite matrix, ${\pi }_m$ is a joint concave function concerning the wholesale price $w$ and product’s greenness $\theta$, and ${\pi }_m$ has a single best solution. Under decentralized decision-making, the optimal wholesale price $w^D$ and the optimal product greenness ${\theta }^D$ are obtained by letting the first-order partial derivatives of ${\pi }_m$ with respect to $w$ and $\theta$ be equal to zero.

Finally, we obtain the optimal retail price $p^D$ by substituting $w^D$ and ${\theta }^D$ into Eq. 15. Proposition 2 is proven.

Putting Eqs 12, 13, 14 into Eqs 10, 11, the retailer profit function, the manufacturer profit function, and the total profit effect function can be obtained as

${\pi }_r^D=\frac{{\eta }^2{\left(2R{\delta }^2+\lambda +\beta \right)}^2{\left(c\lambda +c\beta -\alpha -r\lambda \right)}^2}{\left(\lambda +\beta \right){\left(k^2-4\eta R{\delta }^2-4\eta \lambda -4\eta \beta \right)}^2}(17)$

${\pi }_m^D=\frac{\eta {\left(c\lambda +c\beta -\alpha -r\lambda \right)}^2}{-2\left(k^2-4\eta R{\delta }^2-4\eta \lambda -4\eta \beta \right)}(18)$

${\pi }_{sc}^D=\frac{\eta {\left(c\lambda +c\beta -\alpha -r\lambda \right)}^{2}A}{2\left(\lambda +\beta \right){\left(k^2-4\eta R{\delta }^2-4\eta \lambda -4\eta \beta \right)}^2}(19)$

Among them

$A=8R^2{\delta }^4\eta +12R\beta {\delta }^2\eta +12R\lambda {\delta }^2\eta +12\lambda \beta \eta +6{\beta }^2\eta +6{\lambda }^2\eta -\lambda k^2-\beta k^2$

Proposition 3 Under the decentralized decision model, wholesale price $w$, product greenness $\theta$, and retail price $p$ are negatively related to the degree of risk aversion of the manufacturer $R$.

Proof of Proposition 3$w^D$, ${\theta }^D$ and $p^D$ are obtained by taking the first-order derivatives of $R$, respectively

$\frac{\partial w^D}{\partial R}=-\frac{8{\delta }^2{\eta }^2\left(\alpha +r\lambda -c\lambda -c\beta \right)}{{\left(k^2-4\eta R{\delta }^2-4\eta \lambda -4\eta \beta \right)}^2}<0(20)$

$\frac{\partial {\theta }^D}{\partial R}=-\frac{4k{\delta }^2\eta \left(\alpha +r\lambda -c\lambda -c\beta \right)}{{\left(k^2-4\eta R{\delta }^2-4\eta \lambda -4\eta \beta \right)}^2}<0(21)$

$\frac{\partial p^D}{\partial R}=-\frac{2{\delta }^2\eta \left(k^2+2\lambda \eta +2\beta \eta \right)\left(\alpha +r\lambda -c\lambda -c\beta \right)}{\left(\lambda +\beta \right){\left(k^2-4\eta R{\delta }^2-4\eta \lambda -4\eta \beta \right)}^2}<0(22)$

Proposition 3 is proven.

According to Proposition 3, as the level of manufacturer risk aversion reduces, optimal wholesale pricing, product greenness, and retail prices all rise. Manufacturers who are less risk averse, whose higher optimal wholesale prices correspond to reduced risk aversion, are encouraged to invest more in creating green products, which leads to a rise in the greenness of their products. Additionally, when manufacturers’ risk aversion declines, retail prices rise in response. This is because retailers decide to raise retail prices to enhance profits, and vice versa, as optimal wholesale prices rise.

Proposition 4 Under the decentralized decision model, the retailer profit function is positively related to manufacturer risk aversion when $k^2>4R{\delta }^2\eta$, and the manufacturer profit function and total profit function are negatively related to manufacturer risk aversion $R$.

Proof of Proposition 4${\pi }_r^D$, ${\pi }_m^D$ and ${\pi }_{sc}^D$ are obtained by taking the first-order derivatives of $R$, respectively

$\frac{{\pi }_r^D}{R}=\frac{4{\delta }^2{\eta }^2\left(2\lambda \eta +2\beta \eta -k^2\right)\left(2R\delta {}^2+\lambda +\beta \right){\left(\alpha +r\lambda -c\lambda -c\beta \right)}^2}{\left(\lambda +\beta \right){\left(4R{\delta }^2\eta +4\lambda \eta +4\beta \eta -k^2\right)}^3}>0(23)$

$\frac{{\pi }_m^D}{R}=-\frac{2{\delta }^2{\eta }^2{\left(\alpha +r\lambda -c\lambda -c\beta \right)}^2}{{\left(4R{\delta }^2\eta +4\lambda \eta +4\beta \eta -k^2\right)}^2}<0(24)$

$\frac{{\pi }_{sc}^D}{R}=-\frac{2{\delta }^2{\eta }^2{\left(\alpha +r\lambda -c\lambda -c\beta \right)}^2\left(4R{\delta }^2{k}^2+\left(\lambda +\beta \right)\left(k^2-4R{\delta }^2\eta \right)\right)}{\left(\lambda +\beta \right)\left(4R{\delta }^2\eta +4\lambda \eta +4\beta \eta -k^2\right)}<0(25)$

Proposition 4 is proven.

According to Proposition 4, the manufacturer’s profit function and total profit function decline as risk aversion rise, whereas the retailer’s profit function rises as it does. The manufacturer’s profit is also squeezed as its risk aversion level rises. In order to obtain more profit, the manufacturer takes measures to adjust the wholesale price and the level of product greenness so that it gains an advantageous position and minimizes the retailer’s profit. Retailers and manufacturers aim to maximize their profits, which has a double marginal impact. The risk aversion of manufacturers reduces the benefits of supply chain members, aggravating the double marginal effect of the supply chain and reducing the total profit. Therefore, it is essential to create a suitable contract to coordinate the behavior of supply chain participants to benefit both manufacturers and retailers and increase the total profit of the supply chain.

4 Contract coordination

In order to produce green products, manufacturers must make significant financial investments. Nevertheless, when manufacturers have a risk-averse effect, they will inevitably choose to increase the wholesale price or reduce the greenness of their products in order to maximize their profits. This will impact on the market’s demand for green products and lessen the advantages of supply chain participants, ultimately aggravating the double marginal utility. However, choosing a cost-sharing contract can lower the cost of manufacturers’ investments. This is because consumers’ preference for green products makes retailers willing to bear part of the cost of green products. The ratio of retailers bearing the input cost of green products is $g\left(0<g<1\right)$.

Under the cost-sharing contract model, the manufacturer and the retailer still follow the manufacturer-dominated Stackelberg game. The retailer’s profit function and the manufacturer’s profit function are

${\pi }_r=\left(p-w\right)\left(\alpha -\beta p+k\theta -\lambda \left(p-r\right)\right)-\frac{1}{2}\eta g{\theta }^2(26)$

${\pi }_m=\left(w-c\right)\left(\alpha -\beta p+k\theta -\lambda \left(p-r\right)\right)-\frac{1}{2}\eta \left(1-g\right){\theta }^2-\frac{1}{2}R{\left(w-c\right)}^2{\delta }^2(27)$

The inverse solution method is applied to Eqs 26, 27. First, solve ${\pi }_r$ for the first-order conditions of $p$ to derive the optimal price function, which can be expressed as

$p^{CS}=\frac{k\theta +w\left(\lambda +\beta \right)+\alpha +r\lambda }{2\left(\lambda +\beta \right)}(28)$

Next, the manufacturer’s profit function is obtained by putting Eq. 28 into Eq. 27. Solving ${\pi }_m^{CS}$ for the first order conditions on $w$ and $\theta$, we can get $w^{CS}$ and ${\theta }^{CS}$. Then $p^{CS}$ is brought by putting $w^{CS}$ and ${\theta }^{CS}$ into Eq. 28, which can be expressed as

$w^{CS}=\frac{2\left(1-g\right)\eta \left(c\lambda +c\beta -\alpha -r\lambda \right)}{k^2-4\left(1-g\right)\eta \left(R{\delta }^2+\lambda +\beta \right)}+c(29)$

${\theta }^{CS}=\frac{k\left(c\lambda +c\beta -\alpha -r\lambda \right)}{k^2-4\left(1-g\right)\eta \left(R{\delta }^2+\lambda +\beta \right)}(30)$

$p^{CS}=\frac{\left(1-g\right)\eta \left(2R{\delta }^2+3\lambda +3\beta \right)\left(c\lambda +c\beta -\alpha -r\lambda \right)}{\left(\lambda +\beta \right)\left(k^2-4\left(1-g\right)\eta \left(R{\delta }^2+\lambda +\beta \right)\right)}+c(31)$

The retailer’s profit function can be given by putting Eqs 29, 30, 31 into Eq. 26, which can be expressed as

${\pi }_r^{CS}=\frac{\left(2{\left(1-g\right)}^2{\eta }^2{\left(2R{\delta }^2+\lambda +\beta \right)}^2-\left(\lambda +\beta \right)g\eta k^2\right){\left(c\lambda +c\beta -\alpha -r\lambda \right)}^2}{2\left(\lambda +\beta \right){\left(k^2-4\left(1-g\right)\eta \left(R{\delta }^2+\lambda +\beta \right)\right)}^2}(32)$

Again, the retailer splits a particular percentage $g$ of the cost of manufacturing green products, but it determines the optimal $g$ to maximize profit. Solving ${\pi }_r^{CS}$ for the first-order condition on $g$, we get

$g=\frac{16R^2{\delta }^4\eta +12R{\delta }^2\lambda \eta +12R{\delta }^2\beta \eta +\lambda k^2+\beta k^2}{4\eta \left(4R^2{\delta }^4+5R{\delta }^2\lambda +5R{\delta }^2\beta +4\lambda \beta +2{\lambda }^2+2{\beta }^2\right)}(33)$

Putting $g$ into Eqs 29, 30, 31, we get

$w^{CS}=\frac{\left(\lambda +\beta \right)\left(\alpha +r\lambda -c\lambda -c\beta \right)\left(8R{\delta }^2\eta +8\lambda \eta +8\beta \eta -k^2\right)}{2B}+c(34)$

${\theta }^{CS}=\frac{k\left(\alpha +r\lambda -c\lambda -c\beta \right)\left(4R^2{\delta }^2+5R{\delta }^2\lambda +5R{\delta }^2\beta +4\lambda \beta +2{\lambda }^2+2{\beta }^2\right)}{B}(35)$

$p^{CS}=\frac{\left(2R{\delta }^2+3\lambda +3\beta \right)\left(\alpha +r\lambda -c\lambda -c\beta \right)\left(8R{\delta }^2\eta +8\lambda \eta +8\beta \eta -k^2\right)}{4B}+c(36)$

Among them

$B=\left(16R{\delta }^2\eta -3k^2\right){\left(\lambda +\beta \right)}^2+\left(8R^2{\delta }^4-6R{\delta }^2{k}^2+24\eta \lambda \beta \right)\left(\lambda +\beta \right)+8\eta {\lambda }^3+8\eta {\beta }^3-4R^2{\delta }^4{k}^2$

Finally, the manufacturer’s optimal profit, the retailer’s optimal profit, and the total supply chain profit can be given by putting Eqs 34, 35, 36 into ${\pi }_r$, ${\pi }_m$ and ${\pi }_{sc}$, which can be expressed as

${\pi }_r^{CS}=\frac{{\left(\alpha +r\lambda -c\lambda -c\beta \right)}^2\left(32R^2{\delta }^4\eta +\left(\lambda +\beta \right)\left(32R{\delta }^2\eta +8\eta \lambda +8\eta \beta +k^2\right)\right)}{16B}(37)$

${\pi }_m^{CS}=\frac{\left(\lambda +\beta \right){\left(\alpha +r\lambda -c\lambda -c\beta \right)}^2\left(8R{\delta }^2\eta +8\eta \lambda +8\eta \beta -k^2\right)}{8B}(38)$

${\pi }_{sc}^{CS}=\frac{{\left(\alpha +r\lambda -c\lambda -c\beta \right)}^2\left(32R^2{\delta }^4\eta +\left(\lambda +\beta \right)\left(48R{\delta }^2\eta +24\eta \lambda +24\eta \beta -k^2\right)\right)}{16B}(39)$

Proposition 5 When $4R{\delta }^2\eta >\eta \left(\lambda +\beta \right)$, manufacturer’s profit, retailer’s profit, and total profit are higher under the cost-sharing contract than decentralized decision-making.

Proof of Proposition 5

Compare the profits earned by the producer, the retailer, and the total profit.

$\frac{{\pi }_r^{CS}}{{\pi }_r^D}=1+\frac{k^2{\left(16R^2{\delta }^4\eta +12R{\delta }^2\eta \lambda +12R{\delta }^2\eta \beta +k^2\lambda +k^2\beta \right)}^2}{16{\eta }^2{\left(2R{\delta }^2+\lambda +\beta \right)}^{2}B}(40)$

$\frac{{\pi }_m^{CS}}{{\pi }_m^D}=1+\frac{k^2\left(16R^2{\delta }^4\eta +12R{\delta }^2\eta \lambda +12R{\delta }^2\eta \beta +k^2\lambda +k^2\beta \right)}{4\eta B}(41)$

$\frac{{\pi }_{sc}^{CS}}{{\pi }_{sc}^D}=\frac{\left(2\lambda +2\beta \right){\left(4R{\delta }^2\eta -k^2+4\eta \lambda +4\eta \beta \right)}^{2}F}{4\eta \left(F-3k^2\lambda -3k^2\beta \right)B}(42)$

Among them

$F=32R^2{\delta }^4\eta +48R{\delta }^2\eta \lambda +48R{\delta }^2\eta \beta -k^2\lambda -k^2\beta +24{\lambda }^2\eta +48\lambda \beta \eta +24{\beta }^2\eta$

${\pi }_r^{CS}>{\pi }_r^D$ and ${\pi }_m^{CS}>{\pi }_m^D$ can be obtained from Eqs 40, 41, which show that both the manufacturer’s and retailer’s profits are greater under the cost-sharing contract than under the decentralized decision.

From Eq. 42, we get

$\frac{{\pi }_{sc}^{CS}}{{\pi }_{sc}^D}>\frac{\left(2\lambda +2\beta \right){\left(4R{\delta }^2\eta -k^2+4\eta \lambda +4\eta \beta \right)}^2}{4\eta B}=1+\frac{k^2\left(8R^2{\delta }^4\eta +\left(\lambda +\beta \right)\left(4R{\delta }^2\eta +k^2-2\eta \left(\lambda +\beta \right)\right)\right)}{2\eta B}(43)$

Further when Further when $k^2>4R{\delta }^2\eta >\eta \left(\lambda +\beta \right)$, ${\pi }_{sc}^{CS}/{\pi }_{sc}^D>1$, so ${\pi }_{sc}^{CS}>{\pi }_{sc}^D$. i.e., the total profit of the supply chain under the cost-sharing contract is more significant than its profit under the decentralized decision.

Proposition 5 is proven.

Proposition 5 illustrates that a cost-sharing contract can coordinate supply chain coordination in a green supply chain that considers manufacturer risk aversion and reference price effects. Unlike decentralized decision-making, where the manufacturer’s profit, the retailer’s profit, and the total profit are compared, the retailer bears a portion of the cost of the green product input, allowing for the optimal decision-making between the two parties and the supply chain. This shows that cost-sharing contracts boost supply chain members’ profits and enhance their effectiveness.

5 Impact analysis

In this section, we analyze how manufacturer risk aversion affects supply chain profit, product greenness, and optimal pricing under the reference price effect and offer pertinent managerial revelations.

Proposition 6 The wholesale price under the cost-sharing contract and the wholesale price under the decentralized decision satisfy $w^{CS}>w^D$; the greenness of the product under the centralized decision, the greenness of the product under the decentralized decision, and the greenness of the product under the cost-sharing contract satisfy ${\theta }^C>{\theta }^{CS}>{\theta }^D$.

Proof of Proposition 6

By comparing $w^{CS}$ and $w^D$, we obtain

$\frac{w^{CS}}{w^D}=1+\frac{k^2\left(\alpha +r\lambda -c\lambda -c\beta \right)\left(16R^2{\delta }^2+12R{\delta }^2\eta \lambda +12R{\delta }^2\eta \beta +k^2\lambda +k^2\beta \right)}{\left(8R{\delta }^2\eta c+4r\eta \lambda +4\alpha \eta +2c\left(2\eta \lambda +2\eta \beta -k^2\right)\right)B}(44)$

$w^{CS}/w^D>1$ is given by Eq. 44, i.e., $w^{CS}>w^D$. By comparing ${\theta }^{CS}$ and ${\theta }^D$, we obtain

$\frac{{\theta }^{CS}}{{\theta }^D}=1+\frac{\left(R{\delta }^2+\lambda +\beta \right)\left(16R^2{\delta }^4\eta +12R{\delta }^2\eta \lambda +12R{\delta }^2\eta \beta +k^2\lambda +k^2\beta \right)}{B}(45)$

${\theta }^{CS}/{\theta }^D>1$ is given by Eq. 45, i.e., ${\theta }^{CS}>{\theta }^D$.By comparing ${\theta }^C$ and ${\theta }^{CS}$ , we obtain

$\frac{{\theta }^C}{{\theta }^{CS}}=1+\frac{\left(\lambda +\beta \right)\left(6R{\delta }^2\eta \lambda +6R{\delta }^2\eta \beta -R{\delta }^2{k}^2+\left(\lambda +\beta \right)\left(4\eta \lambda +4\eta \beta -k^2\right)\right)}{\left(2\eta \lambda +2\eta \beta -k^2\right)\left(4R^2{\delta }^2+5R{\delta }^2\lambda +5R{\delta }^2\beta +2{\lambda }^2+4\lambda \beta +2{\beta }^2\right)}(46)$

${\theta }^C/{\theta }^{CS}>1$ is given by Eq. 46, i.e., ${\theta }^C>{\theta }^{CS}$.

In summary, ${\theta }^C>{\theta }^{CS}>{\theta }^D$. Proposition 6 is proven.

According to proposition 6, cost-sharing contracts have a better product greenness than decentralized decision-making, indicating that they can improve product greenness. However, product greenness is higher under centralized decision-making rather than cost-sharing agreements, indicating that cost-sharing agreements only partially coordinate the supply chain mechanism between upstream and downstream businesses. Cost-sharing contracts do not lower the product’s wholesale price, resulting in higher wholesale prices than decentralized decision-making.

Proposition 7 The retail price under centralized decision, the retail price under decentralized decision, and the retail price under the cost-sharing contract satisfy $p^C>p^{CS}>p^D$.

Proof of Proposition 7

By comparing $p^{CS}$ and $p^C$, we obtain

$p^{CS}-p^C=\frac{\left(\alpha +r\lambda -c\lambda -c\beta \right)L}{\left(8\eta \lambda +8\eta \beta -4k^2\right)B}<0(47)$

Among them

$L=2R{\delta }^2{k}^2+\left(16R{\delta }^2{\eta }^2-18k^2\eta \right){\left(\lambda +\beta \right)}^2+\left(3k^4+48\lambda \beta {\eta }^2-20R{k}^2{\delta }^2\eta \right)\left(\lambda +\beta \right)+16{\eta }^2\left({\lambda }^3+{\beta }^3\right)$

From Eq. 47, we get $p^C>p^{CS}$.

Then by comparing $p^{CS}$ and $p^D$, we obtain

$\frac{p^{CS}}{p^D}=1+\frac{k^2\left(2R{\delta }^2+3\lambda +3\beta \right)\left(\alpha +r\lambda -c\lambda -c\beta \right)\left(16R^2{\delta }^4\eta +\left(12R{\delta }^2\eta +k^2\right)\left(\lambda +\beta \right)\right)}{HB}(48)$

Among them

$H=8R{\delta }^2\eta \left(\alpha +r\lambda \right)+\left(8R{\delta }^2\eta c+12r\eta \lambda +12\alpha \eta -4c{k}^2\right)\left(\lambda +\beta \right)+4c\eta {\left(\lambda +\beta \right)}^2$

From Eq. 48, we get $p^{CS}/p^D>1$, i.e., $p^{CS}>p^D$.

In summary, $p^C>p^{CS}>p^D$. Proposition 7 is proven.

Proposition 7 illustrates that different decision models significantly impact retailers’ decisions. Retail price is higher under centralized decision-making than under the cost-sharing contract and higher under decentralized decision-making. The relationship between retail prices and the degree of product greenness under various models continues to be consistent. This suggests that retail prices will increase as products become greener and product quality is assured.

Proposition 8 Total profit under centralized decision-making, total profit under decentralized decision-making, and total profit under the cost-sharing contract satisfy ${\pi }_{sc}^C>{\pi }_{sc}^{CS}>{\pi }_{sc}^D$.

Proof of Proposition 8 ${\pi }_{sc}^{CS}>{\pi }_{sc}^D$ follows from Proposition 5. In turn, by comparing ${\pi }_{sc}^C$ and ${\pi }_{sc}^{CS}$ , we obtain

$\frac{{\pi }_{sc}^C}{{\pi }_{sc}^{CS}}=1+\frac{\left(\lambda +\beta \right)\left(\left(32R{\delta }^2{\eta }^2+2k^2\eta \right)\left(\lambda +\beta \right)+16{\eta }^2{\left(\lambda +\beta \right)}^2-k^4\right)}{\left(2\eta \lambda +2\eta \beta -k^2\right)\left(32R^2{\delta }^4\eta +48R{\delta }^2\eta \lambda +48R{\delta }^2\eta \beta +24\eta {\left(\lambda +\beta \right)}^2-k^2\left(\lambda +\beta \right)\right)}$

Because $k^2<2\eta \left(\lambda +\beta \right)$, therefore, $k^4<4{\eta }^2{\left(\lambda +\beta \right)}^2$, $k^2\left(\lambda +\beta \right)<2\eta {\left(\lambda +\beta \right)}^2$. ${\pi }_{sc}^C/{\pi }_{sc}^{CS}>1$,i.e., ${\pi }_{sc}^C>{\pi }_{sc}^{CS}$.

In summary, ${\pi }_{sc}^C>{\pi }_{sc}^{CS}>{\pi }_{sc}^D$. Proposition 8 is proven.

According to proposition 8, the cost-sharing contract can produce higher supply chain profits than decentralized decision-making, which can help the supply chain system coordinate and boost member earnings. However, supply chain profits under centralized decision-making are higher than supply chain profits under the cost-sharing contract, indicating that the cost-sharing contract can only partially coordinate supply chain systems. The cost-sharing contract improves the profitability of the supply chain participants and the product’s greenness, even though it does not fully coordinate the system.

6 Simulation

We verified the relevant results using numerical simulations to explore further the effect of manufacturer risk aversion on green supply chain pricing and profitability under the reference price effect. It should be noted that, under a centralized decision-making model, the manufacturer and the retailer are in an ideal state when the optimal decision is that the manufacturer’s wholesale price is the same as the cost, i.e., $w=c$. The manufacturer’s risk aversion factor has no impact on the wholesale price, retail pricing and supply chain profit. The numerical simulations compare only the best decisions made under a cost-sharing contract and decentralized decision-making. Parameters: market demand $\alpha =1000$, retail price elasticity $\beta =2$, unit product cost $c=6$ ( for manufacturers and retailers to be profitable, the cost must be lower than retail price $p$ and reference price $r$), risk aversion variance $\delta =0.1$ (The risk aversion variance can be found in Yue and Liu (2006)), reference price $r=15$ (reference price is higher than cost), reference price elasticity $\lambda =0.5or0.8$ ( The range for the reference price effect $\lambda$ is from 0 to 1. The model is the situation of no reference price effect when the reference price effect $\lambda$ is 0.), product greenness elasticity $k=2$, input cost elasticity $\eta =1$.

The effect of manufacturer risk aversion on the optimal equilibrium strategy under the decentralized decision model and the cost-sharing contract model concerning the price effect is shown in Figures 1, 2, 3, 4, 5, 6.

FIGURE 1

FIGURE 1. $R$ impacts on wholesale prices.

FIGURE 2

FIGURE 2. $R$ impacts on the greenness of the product.

FIGURE 3

FIGURE 3. $R$ impacts on retail price.

FIGURE 4

FIGURE 4. $R$ impacts on retailer profit.

FIGURE 5

FIGURE 5. $R$ impacts on manufacturer profit.

FIGURE 6

FIGURE 6. $R$ impacts on total profit.

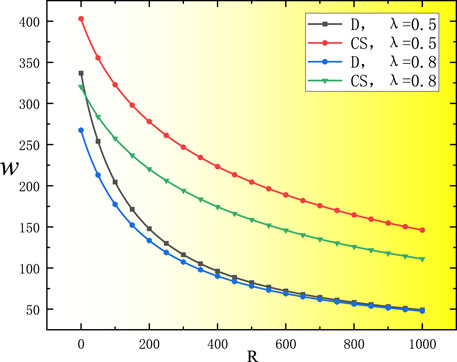
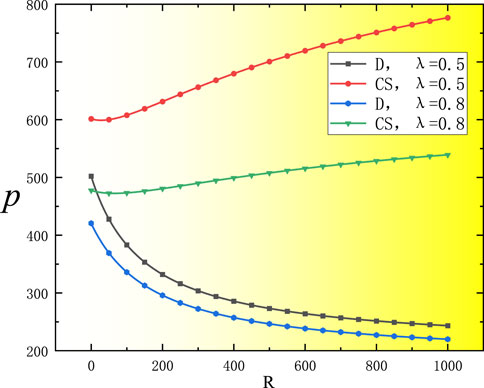
As shown in Figure 1, under the decentralized decision process, wholesale prices converge with the manufacturer’s degree of risk aversion when the degree of reference price effect is low. Under the cost-sharing contract, the wholesale price at $\lambda =0.5$ is higher than that at $\lambda =0.8$. Moreover, the wholesale price under decentralized decision-making and the cost-sharing contract decreases as the manufacturer’s risk aversion rises. The wholesale price under the cost-sharing contract is consistently more significant than the wholesale price under decentralized decision-making, which remains consistent with the conclusion of Proposition 6. However, the wholesale price under the cost-sharing contract declines at a noticeably slower rate, and the gap between the two continues to widen. This is so that risk-averse manufacturers can keep their competitive edge by adjusting wholesale pricing. It is also clear from the decreasing gap between the two that the cost-sharing contract coordinates the supply chain system.

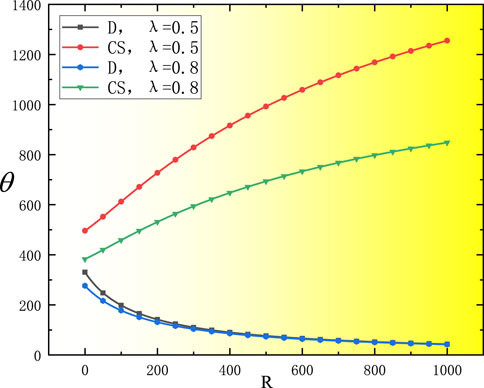
Figure 2, 3 show that under decentralized decision-making and cost-sharing contracts, product greenness and retail price at $\lambda =0.5$ are both higher than product greenness and retail price at $\lambda =0.8$. When the reference price effect is low, however, the level of greenness increases along with the level of manufacturer risk, which is consistent with the pattern of wholesale pricing seen in Figure 1. Under decentralized decision-making, the product’s greenness and retail price decrease as the manufacturer’s risk aversion increases, but under the cost-sharing contract, they are the opposite. It is also clear that the product’s greenness and retail price are higher under the cost-sharing contract than in decentralized decision-making, which is consistent with the conclusion of Proposition 6 and Proposition 7. This shows that under the cost-sharing contract, retailers share a portion of the cost of green products, thereby increasing the greenness of the products. Additionally, wholesale and retail prices rise, increasing producers’ and retailers’ profits.

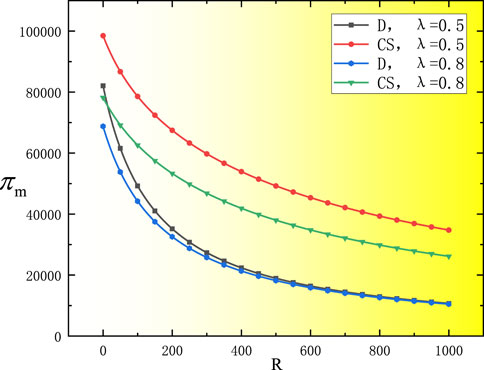
Figure 4 shows that under decentralized decision-making and cost-sharing contracts, retailer profit at $\lambda =0.5$ is higher than retailer profit at $\lambda =0.8$. As the manufacturer’s risk aversion rises, the retailer’s profit rises under decentralized decision-making and the cost-sharing contract. Additionally, retailers’ profit under the cost-sharing contract is consistently higher than it is under decentralized decision-making, and the gap between the two is widening, which is consistent with the conclusion of Proposition 5. This demonstrates that a cost-sharing contract can coordinate the supply chain. The retailer partially bears the cost of the green product, but this does not affect its profitability. Promoting profit motivates retailers to take on product green costs, and the product’s greenness has increased.

Figure 5 shows that under decentralized decision-making, the manufacturer’s profit tends to be consistent with the degree of risk aversion when the reference price effect is low. Manufacturer profit at $\lambda =0.5$ is higher than manufacturer profit at $\lambda =0.8$ under the cost-sharing contract. Manufacturers’ profit and wholesale pricing are consistent. The manufacturer’s profit under the cost-sharing contract and the decentralized decision-making declines as the manufacturer’s risk aversion rises. However, the manufacturer will profit more under the cost-sharing contract model than decentralized decision-making, which is consistent with the conclusion of Proposition 5. This means that manufacturers can bargain with retailers to bear a portion of the price of green products and select the cost-sharing contract. This can help them preserve their dominant position in the supply chain system and boost both sides’ profits to create a win-win scenario.

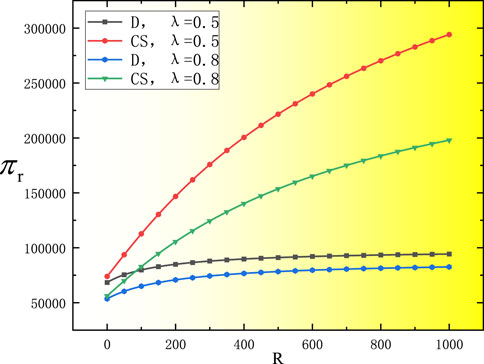
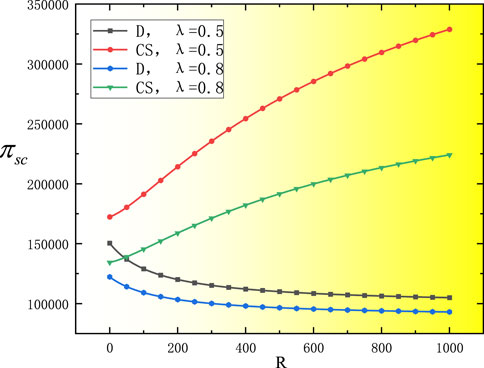
Figure 6 shows that under decentralized decision-making and cost-sharing contracts, the overall supply chain profit at $\lambda =0.5$ is higher than the total supply chain profit at time $\lambda =0.8$. The total supply chain profit under the cost-sharing contract increases as the manufacturer’s risk aversion rises. While the total supply chain profit under decentralized decision-making decreases, the difference between the two grows, which is consistent with the conclusion of Proposition 8. This is so because the cost-sharing contract coordinates the supply chain system, raising the product’s greenness while also improving the profits of the manufacturer, retailer, and supply chain.

7 Discussion

In this paper, we study green supply chains’ pricing and coordination decisions by considering that manufacturers have risk-averse preferences under the reference price effect. The optimal supply chain strategy under the centralized decision, decentralized decision, and cost-sharing contract is obtained using game theory. Further, discuss the coordination of the cost-sharing contract in the supply chain and analyze how manufacturer risk aversion affects supply chain member profits and optimal pricing.

Previous studies (Gan et al., 2004; Xie et al., 2011; Yang et al., 2018) have studied the pricing and coordination of risk-averse behavior in supply chains, but they have ignored the growing importance of green products among consumers and reality. Price factors also affect the purchase behavior of products. Based on the existing literature on the reference price effect (Malekian and Rasti-Barzoki, 2019; Ma and Hu, 2020) and risk aversion (Xiao and Yang, 2008; Zhang et al., 2022), this paper explored how supply chain participants adjust their optimal pricing strategies when manufacturer risk aversion occurs under the reference price effect. Therefore, this paper can offer product pricing and contract selection suggestions for green supply chain companies.

In the real-world business environment, market demand is uncertain, so companies make operational plans to make risk-averse decisions to minimize the loss of corporate revenue. However, the performance of the supply chain will be impacted by the decision-risk-averse maker’s behavior, and the enterprise loss is irreparable. For instance, China.com reported on 17 July 2014, that the total stock of 42 domestically listed classes of clothing and textile companies, including Li Ning, Anta, 361°, Tebu, and Pique, was as high as 48.3 billion yuan based on the financial records for the first half of the year. Additionally, it is acceptable practice in the apparel sector to keep stock at 45% of the total cost. In order to reduce risk, businesses increase stock, but doing so comes at a stock cost. Businesses that want to maximize profits take into account their ability to accept risks and adopt a more cautious approach, giving up certain benefits in the process. Additionally, as the 5G era approaches, people are becoming more and more careful when buying products. Unlike traditional purchase behavior, consumers buy products to compare with reference price. Typically, these reference price is found on websites (such as Jingdong and Taobao.), in recommendations from friends, and on advertising posters. The reference pricing effect influences the supply chain participants’ decision-making behavior. Complex settings impact how businesses make decisions, but there has not been any research on how manufacturer risk aversion affects supply chain decisions under the reference price effect. Studying manufacturers’ risk-averse behavior under the reference price effect can help supply chain members develop better pricing strategies and thus improve total profit.

We provided a detailed investigation by establishing three decision models—centralized decision, decentralized decision, and cost-sharing contract—and calculating the best strategy under each model. We obtained the following findings. First, the reference price effect affects the supply chain system. The higher the reference price effect, the lower the product greenness, wholesale price, retail price, supply chain members’ profit, and total profit. It is consistent with intuition. Because it makes intuitive sense that the higher the reference price effect, the more significant the gap between the retail price and the reference price, which can lower consumer desire and be harmful to both the greenness of the product and the profits of supply chain members (He et al., 2019). Second, with higher manufacturer risk aversion, decentralized decision-making decreases wholesale price, product greenness, retail price, manufacturer’s profit, and overall profit, but a slight increase in retailer profit. Among a cost-sharing contract, product greenness, retail pricing, retailer profit, and overall supply chain profit rise dramatically, whereas wholesale price and manufacturer profit decrease as manufacturer risk aversion rise. According to Shengju (2020), a cost-sharing contract leads to higher greening, wholesale price, retail price, and manufacturer profit. Finally, it is found that the optimal decisions under a cost-sharing contract are better than those under decentralized decisions after introducing a cost-sharing contract to coordinate the green supply chain. According to Yang and Gong (2021), using a cost-sharing contract for Pareto improvement of green supply chains was found to positively impact the chains’ performance and coordinate the chains effectively. This is congruent with the findings of Song et al. (2022), who found that a cost-sharing contract boosts the revenues of supply chain participants, and other scholars are consistent with this (Ghosh and Shah, 2015; Taleizadeh et al., 2018). It again demonstrates that a cost-sharing contract improves the environmental friendliness of products, the sustainability of supply chain members, and total profit.

The above finding makes it clear that, in any situation, the manufacturer’s risk-averse behavior in the decentralization decision results in a decrease in the supply chain’s efficiency. In other words, product greenness, wholesale price, manufacturer profit, and overall profit all decline. To avoid and reduce manufacturers’ risk-averse behavior, the government and business-related departments must adopt policies and measures. For instance, the government has enacted measures to protect product prices and subsidize green products. Further, the coordination mechanism between upstream and downstream enterprises can be strengthened to change the cooperation mode of enterprises, improve the efficiency of the supply chain, and increase the members’ benefits.

However, there are some limitations to this paper. It only considers the risk aversion of the manufacturer under the reference price effect, ignoring the risk preferences of the retailer and other behaviors. For the coordination of supply chain systems, only the cost-sharing contract is used, while additional coordination contracts may be included for comparative analysis. In addition, this paper consists of a second-order green supply chain system with one manufacturer and one retailer. Then the pricing and coordination research of a green supply chain system with numerous manufacturers and retailers can be considered.

8 Conclusion

Under the reference price effect, the pricing and coordination of a green supply chain with a risk-averse manufacturer are examined in this study. We explore the coordination of the cost-sharing contract on the supply chain and study the effects of manufacturer risk aversion on the pricing and profitability of the green supply chain. Through numerical simulations, we get the following findings.

1) Manufacturer profit, retailer profit, and total supply chain profit are all higher under the cost-sharing contract than under the decentralized decision. This shows that the cost-sharing contract can help the supply chain system work together, giving manufacturers, retailers, and the supply chain system the opportunity to all win. Because of this, companies can choose cost-sharing agreements to promote profits while making greener products.

2) In the cost-sharing contract, the total supply chain profit is less than it is under the centralized decision. As a result, it can be seen that the cost-sharing contract can only partially coordinate the supply chain system.

3) Product greenness increases with the manufacturer’s risk aversion and retail price under cost-sharing contracts, during product greenness and retail price increase in the opposite direction under decentralized decision-making. This shows that the cost-sharing contract raises retail pricing, boosts product quality, and increases the product’s greenness. A consistent relationship can be found between product greenness, retail pricing, and total supply chain profit. This implies that companies can promote green products more aggressively, raise customer acceptance, and educate consumers about green consumption to increase supply chain system profit.

Data availability statement

The raw data supporting the conclusion of this article will be made available by the authors, without undue reservation.

Author contributions

ZC: Conceptualization (lead); writing-original draft (lead); formal analysis (lead); writing-review and editing (equal); software (lead). LS: Conceptualization (supporting); writing-review and editing (equal). YW: formal analysis (supporting); writing-review and editing (equal).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Alamdar, S., Rabbani, M., and Heydari, J. (2019). Optimal decision problem in a three-level closed-loop supply chain with risk-averse players under demand uncertainty. Uncertain. Supply Chain Manag. 7 (2), 351–368. doi:10.5267/j.uscm.2018.7.002

CrossRef Full Text | Google Scholar

Bai, Q., Xu, J., and Chauhan, S. S. (2020). Effects of sustainability investment and risk aversion on a two-stage supply chain coordination under a carbon tax policy. Comput. Industrial Eng. 142, 106324. doi:10.1016/j.cie.2020.106324

CrossRef Full Text | Google Scholar

Corbett, C. J., and Klassen, R. D. (2006). Extending the horizons: Environmental excellence as key to improving operations. Manuf. Serv. Operations Manag. 8 (1), 5–22. doi:10.1287/msom.1060.0095

CrossRef Full Text | Google Scholar

Fahimnia, B., Sarkis, J., and Davarzani, H. (2015). Green supply chain management: A review and bibliometric analysis. Int. J. Prod. Econ. 162, 101–114. doi:10.1016/j.ijpe.2015.01.003

CrossRef Full Text | Google Scholar

Gan, X., Sethi, S. P., and Yan, H. (2004). Coordination of supply chains with risk-averse agents. Prod. Operations Manag. 13 (2), 135–149. doi:10.1111/j.1937-5956.2004.tb00150.x

CrossRef Full Text | Google Scholar

Ghosh, D., and Shah, J. (2015). Supply chain analysis under green sensitive consumer demand and cost sharing contract. Int. J. Prod. Econ. 164, 319–329. doi:10.1016/j.ijpe.2014.11.005

CrossRef Full Text | Google Scholar

He, J., Lei, Y., and Fu, X. (2019). Do consumer’s green preference and the reference price effect improve green innovation? A theoretical model using the food supply chain as a case. Int. J. Environ. Res. Public Health 16 (24), 5007. doi:10.3390/ijerph16245007

PubMed Abstract | CrossRef Full Text | Google Scholar

Heydari, J., Govindan, K., and Basiri, Z. (2020). Balancing price and green quality in presence of consumer environmental awareness: A green supply chain coordination approach. Int. J. Prod. Res. 59 (7), 1957–1975. doi:10.1080/00207543.2020.1771457

CrossRef Full Text | Google Scholar

Li, B., Zhu, M., Jiang, Y., and Li, Z. (2016). Pricing policies of a competitive dual-channel green supply chain. J. Clean. Prod. 112, 2029–2042. doi:10.1016/j.jclepro.2015.05.017

CrossRef Full Text | Google Scholar

Li, P., Rao, C., Goh, M., and Yang, Z. (2021). Pricing strategies and profit coordination under a double echelon green supply chain. J. Clean. Prod. 278, 123694. doi:10.1016/j.jclepro.2020.123694

CrossRef Full Text | Google Scholar

Li, Q., Li, B., Chen, P., and Hou, P. (2017). Dual-channel supply chain decisions under asymmetric information with a risk-averse retailer. Ann. Operations Res. 257 (1), 423–447. doi:10.1007/s10479-015-1852-2

CrossRef Full Text | Google Scholar

Liu, M., Cao, E., and Salifou, C. K. (2016). Pricing strategies of a dual-channel supply chain with risk aversion. Transp. Res. Part E Logist. Transp. Rev. 90, 108–120. doi:10.1016/j.tre.2015.11.007

CrossRef Full Text | Google Scholar

Lou, Z., Lou, X., and Dai, X. (2020). Game-Theoretic models of green products in a two-echelon dual-channel supply chain under government subsidies. Math. Problems Eng. 2020, 1–11. doi:10.1155/2020/2425401

CrossRef Full Text | Google Scholar

Malekian, Y., and Rasti-Barzoki, M. (2019). A game theoretic approach to coordinate price promotion and advertising policies with reference price effects in a two-echelon supply chain. J. Retail. Consumer Serv. 51, 114–128. doi:10.1016/j.jretconser.2019.05.028

CrossRef Full Text | Google Scholar

Mondal, C., Giri, B. C., and Maiti, T. (2020). Pricing and greening strategies for a dual-channel closed-loop green supply chain. Flexible Serv. Manuf. J. 32 (3), 724–761. doi:10.1007/s10696-019-09355-6

CrossRef Full Text | Google Scholar

Nagel, M. H. (2000). “Environmental supply-chain management versus green procurement in the scope of a business and leadership perspective,” in Proceedings of the 2000 IEEE International Symposium on Electronics and the Environment San Francisco, CA, USA, May 2000 (IEEE), 219–224. Cat. No. 00CH37082. doi:10.1109/isee.2000.857652

CrossRef Full Text | Google Scholar

Panja, S., and Mondal, S. K. (2019). Exploring a two-layer green supply chain game theoretic model with credit linked demand and mark-up under revenue sharing contract. J. Clean. Prod. 250, 119491. doi:10.1016/j.jclepro.2019.119491

CrossRef Full Text | Google Scholar

Rahmani, K., and Yavari, M. (2018). Pricing policies for a dual-channel green supply chain under demand disruptions. Comput. Industrial Eng. 127, 493–510. doi:10.1016/j.cie.2018.10.039

CrossRef Full Text | Google Scholar

Sant, T. G. (2022). Distribution channel coordination in green supply chain management in the presence of price premium effects. Int. J. Serv. Operations Manag. 41 (1-2), 142–162. doi:10.1504/IJSOM.2022.121725

CrossRef Full Text | Google Scholar

Sarkis, J. (2012). A boundaries and flows perspective of green supply chain management. Supply Chain Manag. Int. J. 17 (2), 202–216. doi:10.1108/13598541211212924

CrossRef Full Text | Google Scholar

Shen, J. (2021). Uncertain two-echelon green supply chain models based on revenue sharing contract. Int. J. Mach. Learn. Cybern. 12 (7), 2059–2068. doi:10.1007/s13042-021-01292-x

CrossRef Full Text | Google Scholar

Shen, L., Olfat, L., Govindan, K., Khodaverdi, R., and Diabat, A. (2013). A fuzzy multi criteria approach for evaluating green supplier's performance in green supply chain with linguistic preferences. Resour. Conservation Recycl. 74, 170–179. doi:10.1016/j.resconrec.2012.09.006

CrossRef Full Text | Google Scholar

Shengju, S. A. N. G., and Qiang, Z. H. A. N. G. (2020). Coordination mechanisms of green supply chain with reference price effect. J. Syst. Manag. 29 (5), 994. doi:10.3969/j.issn.1005-2542.2020.05.018

CrossRef Full Text | Google Scholar

Song, H., Chu, H., Yue, H., and Chen, Y. (2022). Green supply chain coordination with substitutable products under cost sharing contract. Procedia Comput. Sci. 199, 1112–1119. doi:10.1016/j.procs.2022.01.141

CrossRef Full Text | Google Scholar

Taleizadeh, A. A., Alizadeh-Basban, N., and Sarker, B. R. (2018). Coordinated contracts in a two-echelon green supply chain considering pricing strategy. Comput. Industrial Eng. 124, 249–275. doi:10.1016/j.cie.2018.07.024

CrossRef Full Text | Google Scholar

Taleizadeh, A. A., Noori-Daryan, M., and Sana, S. S. (2020). Manufacturing and selling tactics for a green supply chain under a green cost sharing and a refund agreement. J. Model. Manag. 15 (4), 1419–1450. doi:10.1108/jm2-01-2019-0016

CrossRef Full Text | Google Scholar

Tang, C. S. (2006). Perspectives in supply chain risk management. Int. J. Prod. Econ. 103 (2), 451–488. doi:10.1016/j.ijpe.2005.12.006

CrossRef Full Text | Google Scholar

Wang, N., Zhang, T., Zhu, X., and Li, P. (2020). Online-offline competitive pricing with reference price effect. J. Operational Res. Soc. 72 (3), 642–653. doi:10.1080/01605682.2019.1696154

CrossRef Full Text | Google Scholar

Wang, N., Zhang, T., Zhu, X., and Li, P. (2021). Online-offline competitive pricing with reference price effect. J. Operational Res. Soc. 72 (3), 642–653. doi:10.1080/01605682.2019.1696154

CrossRef Full Text | Google Scholar

Wang, Y., and Sun, X. (2019). Dynamic vs. static wholesale pricing strategies in a dual-channel green supply chain. Complexity 2019, 1–14. doi:10.1155/2019/8497070

CrossRef Full Text | Google Scholar

Xiao, T., and Yang, D. (2008). Price and service competition of supply chains with risk-averse retailers under demand uncertainty. Int. J. Prod. Econ. 114 (1), 187–200. doi:10.1016/j.ijpe.2008.01.006

CrossRef Full Text | Google Scholar

Xie, G., Yue, W., Wang, S., and Lai, K. K. (2011). Quality investment and price decision in a risk-averse supply chain. Eur. J. Operational Res. 214 (2), 403–410. doi:10.1016/j.ejor.2011.04.036

CrossRef Full Text | Google Scholar

Xu, J., and Liu, N. (2014). Research on closed loop supply chain with reference price effect. J. Intelligent Manuf. 28 (1), 51–64. doi:10.1007/s10845-014-0961-0

CrossRef Full Text | Google Scholar

Xu, J., and Liu, N. (2017). Research on closed loop supply chain with reference price effect. J. Intelligent Manuf. 28 (1), 51–64. doi:10.1007/s10845-014-0961-0

CrossRef Full Text | Google Scholar

Yang, D., and Xiao, T. (2017). Pricing and green level decisions of a green supply chain with governmental interventions under fuzzy uncertainties. J. Cleaner Prod. 149, 1174–1187. doi:10.1016/j.jclepro.2017.02.138

CrossRef Full Text | Google Scholar

Yang, F., Kong, J., Liu, T., and Ang, S. (2020). Cooperation and coordination in green supply chain with R&D uncertainty. J. Operational Res. Soc. 1, 481–496. –16. doi:10.1080/01605682.2020.1848359

CrossRef Full Text | Google Scholar

Yang, L., Cai, G., and Chen, J. (2018). Push, pull, and supply chain risk-averse attitude. Prod. Operations Manag. 27 (8), 1534–1552. doi:10.1111/poms.12881

CrossRef Full Text | Google Scholar

Yang, M., and Gong, X. M. (2021). Optimal decisions and Pareto improvement for green supply chain considering reciprocity and cost-sharing contract. Environ. Sci. Pollut. Res. 28 (23), 29859–29874. doi:10.1007/s11356-021-12752-w

PubMed Abstract | CrossRef Full Text | Google Scholar

Yao, Q., and Shao, L. (2022). Research on emission reduction strategies of building materials manufacturers and real estate developers in the context of carbon trading. Front. Environ. Sci. 10. doi:10.3389/fenvs.2022.848260

CrossRef Full Text | Google Scholar

Yao, Q., Shao, L., Yin, Z., Wang, J., and Lan, Y. (2022). Strategies of property developers and governments under carbon tax and subsidies. Front. Environ. Sci. 10. doi:10.3389/fenvs.2022.916352

CrossRef Full Text | Google Scholar

Yi, W., Feng, Z., Tan, C., and Yang, Y. (2021). Green supply chain management with Nash bargaining loss-averse reference dependence. Mathematics 9 (24), 3154. doi:10.3390/math9243154

CrossRef Full Text | Google Scholar

Yue, X., and Liu, J. (2006). Demand forecast sharing in a dual-channel supply chain. Eur. J. Operational Res. 174 (1), 646–667. doi:10.1016/j.ejor.2004.12.020

CrossRef Full Text | Google Scholar

Zhang, D., Zou, F., Li, S., and Zhou, L. (2017). Green supply chain network design with economies of scale and environmental concerns. J. Adv. Transp. 2017, 1–14. doi:10.1155/2017/6350562

CrossRef Full Text | Google Scholar

Zhang, J., Sethi, S. P., Choi, T. M., and Cheng, T. C. E. (2022). Pareto optimality and contract dependence in supply chain coordination with risk-averse agents. Prod. Operations Manag. 31, 2557–2570. doi:10.1111/poms.13701

CrossRef Full Text | Google Scholar