Application of a Novel Hybrid Machine Learning Algorithm in Shallow Landslide Susceptibility Mapping in a Mountainous Area

Landslides can be a major challenge in mountainous areas that are influenced by climate and landscape changes. In this study, we propose a hybrid machine learning model based on a rotation forest (RoF) meta classifier and a random forest (RF) decision tree classifier called RoFRF for landslide prediction in a mountainous area near Kamyaran city, Kurdistan Province, Iran. We used 118 landslide locations and 25 conditioning factors from which their predictive usefulness was measured using the chi-square technique in a 10-fold cross-validation analysis. We used the sensitivity, specificity, accuracy, F1-measure, Kappa, and area under the receiver operating characteristic curve (AUC) to validate the performance of the proposed model compared to the Artificial Neural Network (ANN), Logistic Model Tree (LMT), Best First Tree (BFT), and RF models. The validation results demonstrated that the landslide susceptibility map produced by the hybrid model had the highest goodness-of-fit (AUC = 0.953) and higher prediction accuracy (AUC = 0.919) compared to the benchmark models. The hybrid RoFRF model proposed in this study can be used as a robust predictive model for landslide susceptibility mapping in the mountainous regions around the world.

1 Introduction

In recent years, population growth and urban development have contributed to an increase in natural disasters in both developed and developing countries (Huppert and Sparks, 2006), but are generally more serious in developing countries (Alcántara-Ayala, 2002). Landslides are among the most common damaging geohazards, especially in the mountainous regions. Landslide is a general term for a variety of mass movements in soil or rock moving downslope by gravity (Malamud et al., 2004). Over the last century (1903-2004), landslides alone accounted for 17% of the world’s natural disasters, with the highest annual damage in Europe estimated at US$17 million (Koehorst et al., 2005). Landslides have resulted in hundreds of billions of dollars in damages to the built environment, thousands of fatalities, and numerous environmental impacts and are an important driver of landscape change (Aleotti and Chowdhury, 1999; Schuster and Highland, 2001; Geertsema et al., 2009; Fan et al., 2019; Kadirhodjaev et al., 2020). In developing countries, more than 0.5% of the Gross Domestic Product (GDP) is lost every year due to landslides (Chen et al., 2015).

The topic of landslide susceptibility mapping (LSM) has become increasingly popular over the last decade and is being continuously fine-tuned to mitigate landslide hazards, inform land use planning, and improve the prediction accuracy of upcoming landslides. The core idea of LSM has been to explore the association between historical landslides and different causing factors for the prediction of the likelihood of upcoming landslides. To analyze the associations between historical landslides and causing factors, researchers have suggested and used many methods that range from simple and straightforward expert-based and statistical methods to advanced and complex methods derived from machine learning. The expert knowledge methods such as analytical hierarchy process (AHP) (Althuwaynee et al., 2016) and spatial multicriteria evaluation (SMCE) (Meena et al., 2019) and bivariate and multivariate statistics such as frequency ratio (FR) (Chen et al., 2015), weights of evidence (WoE) (Razavizadeh et al., 2017), weighted linear combinations (WLC) (Hung et al., 2016), statistical index (SI) (Razavizadeh et al., 2017), certainty factor (CF) (Wang et al., 2019), index of entropy (IOE) (Chen et al., 2015), and logistic regression (LR) (Sun et al., 2021b) are the first generation methods used for LSM mapping worldwide, with clear processes and are easy to understand and interpret outcomes.

The next generation of the methods used for LSM has originated from machine learning that involves hundreds of algorithms such as artificial neural network (ANN) (Lucchese et al., 2021), adaptive neurofuzzy inference system (ANFIS) (Jaafari et al., 2017), random forest (RF) (Park and Kim, 2019), support vector machine (SVM) (Yao et al., 2008), decision tree (DT) (Dou et al., 2019a), Naïve Bayes (NB) (Nguyen and Kim, 2021), Bayesian logistic regression (BLR) (Abedini et al., 2019), best first decision tree (BFT) (Chen et al., 2018), and deep learning neural network (Ghasemian et al., 2022). With the improvement of artificial intelligence, machine learning becomes the most applied approach for LSM currently.

The other stream of research on machine learning modeling of LSM has combined different methods/algorithms to achieve more accurate prediction results. For example, Pham et al. (2017) reported that the rotation forest (RoF) technique improved the predictive ability of the Naïve Bayes tree landslide prediction. Nguyen et al. (2017) showed that the landslide predictive ability of the instance based learning classifier can be improved by the RoF technique. He et al. (2019) combined the Creedal Decision Tree with the RoF technique and achieved improved accuracy for landslide prediction. In a recent study, Fang et al. (2021) demonstrated that the performance of the decision tree models could be significantly improved when they were integrated with the RoF technique. The key advantage of the RoF technique as a meta classifier is that it can balance accuracy and diversity and decrease bias and overfitting of the modeling process.

Reliability and accuracy of future probabilities are the most important characteristics of a landslide susceptibility map. While machine learning is now widely used in LSM, there is no best method for accurately predicting landslides, especially not for the regions of varying levels of geoenvironmental complexity. However, the experience, to date, suggests comparing several different methods and selecting the optimal one to generate an accurate landslide susceptibility map for a given region. Furthermore, the evaluation of the usefulness of different conditioning factors via feature screening techniques and the optimization of different methods in terms of parameters are other important subjects in the field of landslide modeling (Sun et al., 2021a; Zhou X. et al., 2021).

Iran’s vast mountainous areas have been shaped and modified by ongoing tectonic forces, producing faults, fractures, and sensitive lithology, priming the country for landslides (Shafizadeh-Moghadam et al., 2019). Increased developmental activities and industrial and agricultural and human encroachment on the natural environment due to the extensive land use change in forested areas in recent decades have increased the vulnerability to landslides. Susceptibility mapping and understanding landslide mechanisms, in order to reduce or control landslide damage, are necessary.

In this study, we combined a metaclassifier algorithm with a standalone algorithm as a base classifier to increase the predictive power of the base classifier by reinforcing the parameters used in the model during the calibration phase. The main contribution of our study is to explore how the RoF classifier and a random forest (RF) decision tree classifier generate a hybrid predictive model, called RoFRF, that provides an opportunity to pilot hybrid modeling of LSM and insights into feature screening and selection and parameter optimization. We developed the hybrid RoFRF model using the datasets belonging to Asadi et al. (2022) and Ghasemian et al. (2022) from the Kamyaran area in the Kurdistan Province, Iran, but with a different set of algorithms and results.

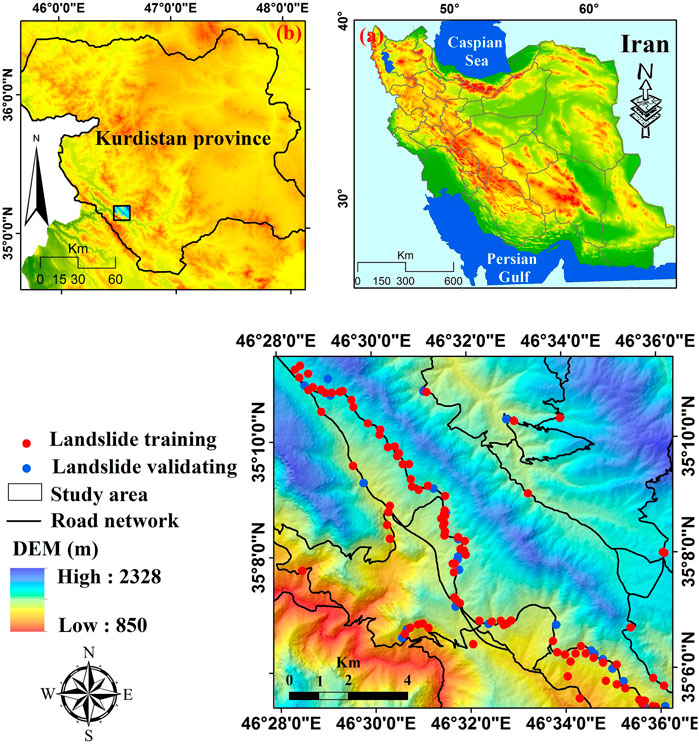
2 Study Area

The study area is in the southwest of the Kurdistan Province covering an area of about 150 km² (Figure 1). The minimum and maximum elevations of the study area are 850 and 2,328 m, respectively, with a height difference of 1,478 m (Figure 1). The average annual rainfall for the period from 2001 to 2019 ranges from 438 to 560 mm and the average annual temperature is 14.15°C. Based on the De Martonne climatic classification index, the climate of the study area is semi-arid climate (Asadi et al., 2022). Bedrock geology belongs to the structural zone of Sanandaj-Sirjan and the high Zagros zone, typified by basalts and shales with the intercalations of volcanic rocks. The six main land cover classes include dry farming, semi-dense forest, low-dense forest, semi-dense pasture, dense pasture, and woodland. The predominant land covers in the study area are semi-dense forests and dry farming (Ghasemian et al., 2022).

FIGURE 1

FIGURE 1. Study area location in (A) Iran and (B) Kurdistan Province.

The study area involved by active faults from the Zagros Main Recent Fault and its formations such as marl and shale and also due to the topographical conditions and geomorphological process (steep slopes and soil erosion) and also anthropogenic factor or improper human interferences (e.g., road construction on Kashtar to Yozidar route and the removal of slope bases) resulted in some landslides occurrence, considering the study area as one of the most susceptible regions of the Kurdistan Province and the country (Asadi et al., 2022). Landslides of the study area are typically shallow with the rupture surfaces less than 2–3 m depth. Figure 2 shows photos of a number of the landslides that occurred in the study area.

FIGURE 2

FIGURE 2. The photographs of the landslides occurred in the study area.

3 Methodology

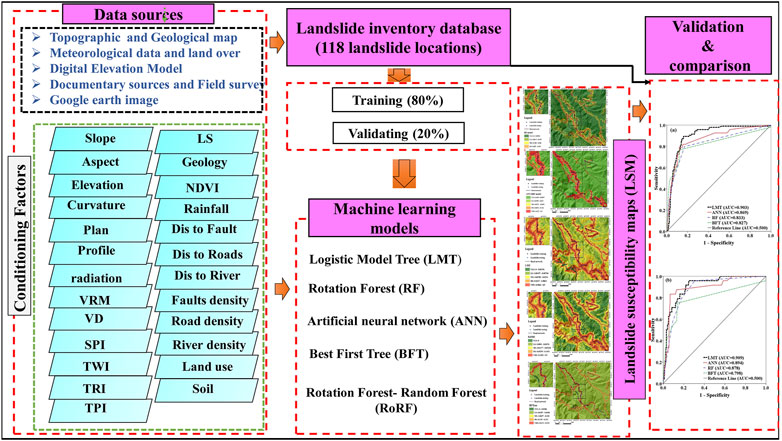
The methodology of this research is shown in Figure 3. We selected 25 conditioning factors for the terrain hosting landslides derived from the topographical, geological and land cover maps, meteorological data, digital elevation model (DEM), documentary sources, field surveys, and Google Earth Imagery. We classified our landslides into two groups; training landslides (80%) and validation landslides (20%) (Xie et al., 2021a; Xie et al., 2021b). We then developed the hybrid RoFRF model and compared its performance to the four benchmark models including RF, ANN, BFT, and logistic model tree (LMT) using area under ROC and other statistical measures. The main steps of the methodology are described in the following subsections.

FIGURE 3

FIGURE 3. Flowchart of the study.

3.1 Data Collection

3.1.1 Landslide Inventory

From a total of 118 landslide points detected in the study area, we subdivided the landslides into two datasets with 80% (94 landslides) in a training dataset and 20% (24 landslides) in a validation dataset. These 118 landslides were selected from the 175 landslides that have been previously used by Asadi et al. (2022) and Ghasemian et al. (2022).

3.1.2 Landslide Conditioning Factors

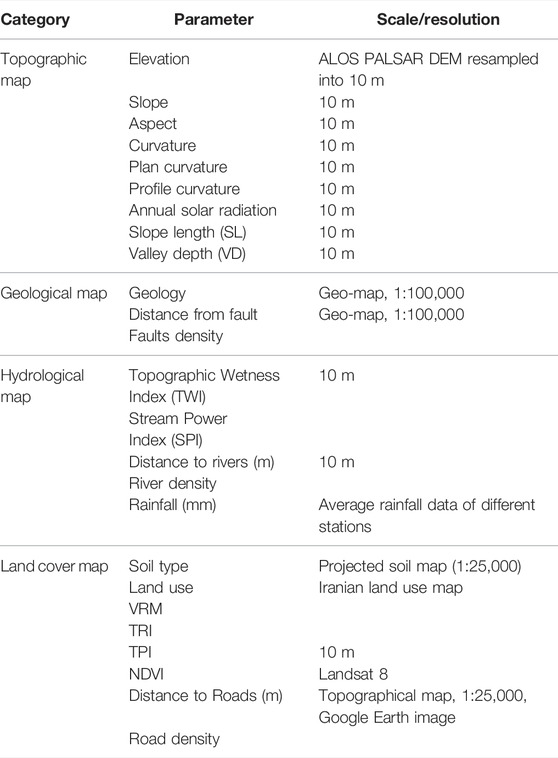
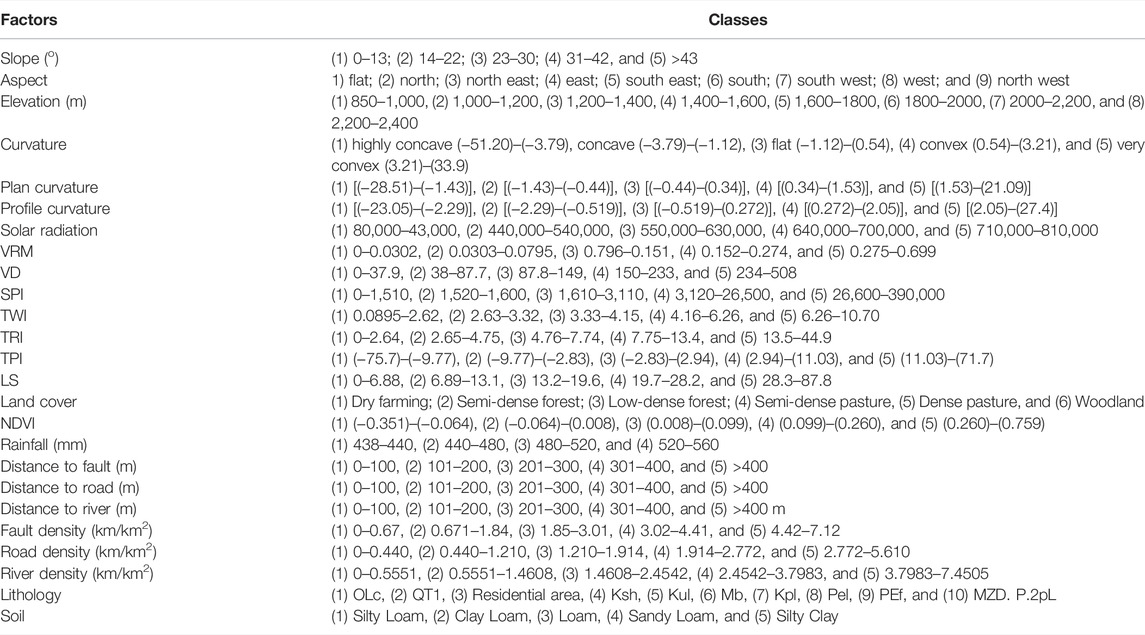
In this study, we selected 25 landslide conditioning factors that were, elevation, slope, aspect, annual solar radiation, curvature, plan curvature, profile curvature, valley depth, vector ruggedness measure (VRM), topographic wetness index (TWI), stream power index (SPI), slope length (LS), topographic position index (TPI), terrain ruggedness index (TRI), normalized difference vegetation index (NDVI), land use, lithology, soil texture, rainfall, fault density, road density, river density, and distance to faults, roads, and rivers (Table 1).

TABLE 1

TABLE 1. Data layers considered as effective factors in the analysis.

Topographic factors (slope, aspect, elevation, profile curvature, plan curvature, and slope length), that have been previously identified as the most influential landslide causing factors, were derived from a DEM of the study area (Zhang et al., 2019b; Wang et al., 2021). Another DEM-derived factor was annual solar radiation, which may affect the incidence of landslides. The land use and land cover were visually interpreted using the high-resolution satellite imagery. NDVI can show surface reflectance of the area and yield quantitative estimates of the vegetation biomass and growth (Li J. et al., 2021; Liu et al., 2022), which can influence landslides. TWI, SPI, TPI, VRM, and valley depth are the secondary DEM products that have been widely used for landslide prediction modeling (Li and Zhang, 2008; Zhang et al., 2019a; Dou et al., 2019b; Lan et al., 2021; Zhao et al., 2021). We incorporated the mean annual rainfall data from 2001 to 2019 to generate a rainfall map using the inverse distance weighted (IDW) method (Chao et al., 2021; de Jesus et al., 2021). The strength and permeability of soils and rocks are controlled in parts by structural variations and lithological formations (Jiang et al., 2021). We extracted lithological units from the geological maps (1:100,000 scale). Soil texture has a significant impact on landslide occurrence (Geertsema et al., 2009). The density maps that include fault density, road density, and river density were prepared using the GIS-based techniques to quantify their effects (Yin et al., 2022b; Chen et al., 2022) on landslide occurrences. The distance maps that include distance to rivers, distance to rivers, and distance to faults were also prepared using the GIS-based techniques (Lee et al., 2017) (Table 2).

TABLE 2

TABLE 2. Landslide conditioning factors with their classes.

3.2 Machine Learning Algorithms

3.2.1 Artificial Neural Networks

ANN is one of the widely used ML algorithms to capture complex trends in the multivariate datasets. The features in ANN use independent statistical distribution, self-learning, and interdependent memory (Zhang et al., 2021). Although not known as a black box model where the modeling processes are not specified, it has been widely used for pattern recognition, classification, and solving regression problems (Zhang et al., 2022). ANNs have multiple nodes that imitate biological neurons in the human brain and therefore the ANN model is often applied in the medical field. It is also being used in landslide susceptibility mapping and drawing relationships between landslides and a host of conditioning factors. The ANN approach has certain advantages over the other statistical techniques. ANNs have input layers (conditioning factors), hidden layers (with activation functions), and output layers (landslide and nonlandslide labels) (Yin et al., 2022a). The neurons process inputs by multiplying each entry with the corresponding weight and summing the product. In turn, the sum is processed using a nonlinear transfer function. ANNs learn by adjusting the weights between the neurons associated with errors between the actual output values and target output values. Then, a number of iterations and learning the neural network created a model that predicts target values from the given input values. We used a back propagation (BP) algorithm, learning in the ANN employing the error signal Es as a measure of the network’s performance.

An ANN becomes a more robust model when relationships between the training datasets are not known. The neurons connect these layers, each using a direct link to connect with other neurons. The links have weights that reflect the power of the outgoing signal (Zhou et al., 2022).

The neurons in each layer were linked to the front and rear neurons with each associated weight (Khandelwal et al., 2018). There are two kinds of networks used in ANN: recurrent neural networks and feed-forward neural networks (FNN). The FNN, based on BP, is a well-known network used in many studies with excellent performance (Luan et al., 2022). Therefore, in this study, FNN was selected for the prediction of the Cv. To validate the performance of FNN, we used different quantitative validation indexes, namely the root means square error (RMSE), the mean absolute error (MAE), and the coefficient of determination (R²) (Li et al., 2021b; Li et al., 2021a). A detailed description of such measurements is presented in several previously published works. These indexes are expressed as follows (Zhou et al., 2021a; Zhou et al., 2021b; Xu et al., 2021):

$\mathrm{MAE}=\frac{1}{m}{\displaystyle \sum _{i=1}^m\left(e_i-\overline{e_i}\right)},(1)$

$\mathrm{RMSE}=\sqrt{\frac{1}{m}{\displaystyle \sum _{i=1}^m{\left(e_i-\overline{e_i}\right)}^2}},(2)$

${\mathrm{R}}^2=1-\frac{{\displaystyle \sum _{i=1}^m\left(e_i-\overline{e_i}\right)}}{{\displaystyle \sum _{i=1}^m\left(e_i-\overline{e}\right)}},(3)$

where $e_i$ is the actual output, ${\overline{e}}_i$ infers the predicted output, $\overline{e}$ infers the mean of the $e_i$, and m infers the number of used samples (Li B. et al., 2021; Zhou W et al., 2021).

3.2.2 Logistic Model Tree

The LMT is a recently developed ML algorithm that combines the model trees and logistic regression functionality, especially for classification problems (Landwehr et al., 2005). Therefore, it is advantageous in selecting relevant features in the data, and it is considered an equivalent to the trees algorithm for categorical outcomes (Landwehr et al., 2005). A simplified version of the LMT equation is

$\mathrm{P}\left(\mathrm{M}|\mathrm{X}\right)={\displaystyle {\sum }_{\mathrm{M}=1}^{\frac{\exp \left({\mathrm{L}}_{\mathrm{M}}\left(\mathrm{X}\right)\right)}{D}}\exp \left({\mathrm{L}}_{\mathrm{M}}\left(\mathrm{X}\right)\right)},(4)$

where D is the outcome category, the LMT has also proven to be a better algorithm when dealing with spatial data extracted from the remote sensing images (Colkesen and Kavzoglu, 2017). It reduces the likelihood of overfitting by cross-validation and logistic regression at each node in the tree where the tree undergoes pruning (Breiman et al., 1984).

3.2.3 Best First Tree

BFT build binary trees in which each internal node has exactly two outgoing edges. Here, the splitting process selects the “best” node that reduces impurity among all the available nodes (Shi, 2007). Essential to BF trees is deciding which attribute to split on and how to do so. Here, information and Gini gains are employed. The information value is determined by an entropy function, expressed as follows:

$\mathrm{entropy}\left({\mathrm{p}}_1,{\mathrm{p}}_2,\dots ,{\mathrm{p}}_n\right)=-{\mathrm{p}}_1{\log }_{\mathrm{p}1}-{\mathrm{p}}_2{\log }_{\mathrm{p}2}\dots -{\mathrm{p}}_n{\log }_{\mathrm{pn}},(5)$

where pn, n = 1, 2,. . , n, is the probability of each class and the sum of the pn is 1 (Quinlan, 1986).

Discovering the maximal Gini gain or information gain for a split at a node demands the finding of minimal values of the weighted sum of the information values (Gini index) of its successor nodes (Shi, 2007). This process ends when all the nodes reach a specific number of expansions. The best first decision tree learning process handles both the categorical and numerical variables, expanding the “best” node first.

3.2.4 Rotation Forest

RoF is a widely used ensemble method that was first introduced by Rodriguez et al. (2006). In RoF, the Principal Component Analysis (PCA) is used to extract features to build the training sets. RoF can enhance the accuracy of base classifiers for both individual and diverse applications simultaneously (Rodriguez-Galiano et al., 2012). Because of this, the RF model is commonly used in LSM to achieve a higher accuracy of the prediction capacity (Hong et al., 2019). We assume that x = (x₁, x₂, … , x_n) is considered as the vector of the conditioning factors, while v = (v₁, v₂) is denoted as the vectors of landslides and nonlandslides, and H symbolizes the training set. E₁, E₂, and E_L are represented as classifiers in the ensemble, and R is designated as a feature set. First, R is separated into K subset, where each subset has the number of condition factors equal to T = n/k. Then, we can get R_ij (the jth landslide influencing factors) and H_ij (the training set for the R_ij features). According to the bootstrap technique, R’_ij is randomly generated from the original training set R_ij with 75% size. Subsequently, R’_ij will be converted to obtain a T × 1 coefficient vector, which can be presented as $\left\{b_{ij}^1,\dots ,b_{ij}^{T1}\right\}$. Then, by rearranging the matrix of R_i, the rotation matrix $R_i^a$ is formed as follows:

$R_i=\left[\begin{array}{cccc}{b}_{i,1}^{\left(1\right)},b_{i,1}^{\left(2\right)},\dots ,b_{i,1}^{\left(T_1\right)}& 0& \cdots & 0\\ 0& b_{i,2}^{\left(1\right)},b_{i,2}^{\left(2\right)},\dots ,b_{i,1}^{\left(T_2\right)}& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & b_{i,k}^{\left(1\right)},b_{i,k}^{\left(2\right)},\dots ,b_{i,k}^{\left(T_K\right)}\end{array}\right].(6)$

After that, for a specified test sample, the confidence (${\mu }_k\left(\delta \right)$) of each class is determined from the mean combination method as follows:

${\mu }_k\left(\delta \right)=\frac{1}{L}{\displaystyle \sum _{i=1}^L{\gamma }_{i,k}\left(\delta R_i^a\right),k=1,\dots ,c},(7)$

where ${\gamma }_{i,k}\left(\delta R_i^a\right)$ represents the probability produced by the classifier, E_i, assume that class k contains δ, and c denotes the sum of class number. In the end, the δ will be allocated to the class that has the highest confidence.

3.3 Model Performance Evaluation

To evaluate the model performance, we employed a variety of statistical index-based methods, including: Sensitivity (SST), Specificity (SPF), Accuracy (ACC), F1-Measure, Matthew’s correlation coefficient (MCC), Kappa, and Receiver operative characteristic (ROC). All the statistical metrics were computed based on the scores from true positives (TP), true negatives (TN), false positives (FP), and false negatives (FN). TP represents the number of pixels of landslides (value 1) that are correctly classified as landslides. TN represents the number of pixels of nonlandslides that are correctly classified as nonlandslides and FP is the number of nonlandslide pixels (value 0) that are incorrectly classified to be landslides while FN is defined as the number of landslide pixels that have been incorrectly classified as nonlandslide points (Zhou et al., 2022). These statistical index-based metrics are described from Eq. 8–15 as follows:

$\mathrm{\text{SST=}}\frac{\mathrm{TP}}{\mathrm{TP+FN}},(8)$

$\mathrm{\text{SPF=}}\frac{\mathrm{TN}}{\mathrm{FP+TN}},(9)$

$\mathrm{\text{ACC=}}\frac{\mathrm{TP+ TN}}{\mathrm{TP+TN+FN+FN}},(10)$

$F-measure=\frac{2\times precision\times recall}{recision+recall},(11)$

$Precision=\frac{\mathit{TP}}{\mathit{TP}+\mathit{FP}},(12)$

$MCC =\frac{TP\times TN\times FP\times FN}{\sqrt{\left(TP+FP\right)\left(TP+FN\right)\left(TN+FP\right)\left(TN+FN\right)}},(13)$

$\mathrm{\text{Kappa= }}\frac{{\mathrm{P}}_{\mathrm{c}}\mathrm{-}{\mathrm{P}}_{\exp }}{\mathrm{1-}{\mathrm{P}}_{\exp }},(14)$

$\mathrm{\text{Pexp=}}\frac{\left(\left(\mathrm{TP+FN}\right)\mathrm{\times }\left(\mathrm{TP+FP}\right)\mathrm{+}\left(\mathrm{FP+TN}\right)\mathrm{\times }\left(\mathrm{FN+TN}\right)\right)}{\sqrt{\left(\mathrm{TP+TN+FP+FN}\right)}},(15)$

$\mathrm{\text{AUC=}}\sum \mathrm{\text{TP+}}\sum \frac{\mathrm{TN}}{\mathrm{P}}\mathrm{+N,}(16)$

where SST is the ratio of landslide pixels that have been rightly classified as landslides and this indicates the good predictability of the landslide model for classifying the shallow landslide pixels (Zhou et al., 2022). SPF is the ratio of the number of landslide locations that are correctly classified as nonlandslides that indicate good predictability of the landslide model for classifying the nonlandslide pixels. ACC is the ratio of nonlandslide and landslide pixels that are correctly classified (Bennett et al., 2013). The ACC demonstrates how well the landslide model works. The F1-Measure is used to assess the landslide diagnosis function. The recall measure represents the number of rightly retrieved pixels divided by the number of relevant pixels from the test dataset. It is a way to combine and balance both precision and sensitivity into a single measure (Konishi and Suga, 2018). The precision measure is the ratio of the correctly retrieved pixels over the number of retrieved pixels.

Mathew’s Correlation Coefficient (MCC) is a correlation coefficient of the observed and predicted binary classifications that yields a value from −1 to +1 (+1 represents a perfect prediction, 0 no better than random, and −1 indicates total disagreement). The Kappa index is used to assess the acceptability of landslide models. The values of this index vary from −1 (unacceptability) to +1 (acceptability) (Bennett et al., 2013). The AUC is a measure used to assess the model performance (Fawcett, 2006). The ROC curve is built with sensitivity on the y-axis and 1-specificity on the x-axis with some cut-off thresholds. The area under the ROC curve (AUC) implies the capability of a model to distinguish between the shallow landslide and nonlandslide pixels. A model is ideal or perfect if AUC isone, and weak or inaccurate if AUC is near zero.

3.4 Chi-Square

A chi-squared test (χ2) is a statistical hypothesis test to determine whether there is a significant statistical difference between the model’s performance in one or more categories of variables or not. The two factors include the number of cells found in the table and the total number of observations of the main factors (Bryant and Satorra, 2012). For the evaluation of the value of landslide predictors by the chi-square algorithm, we defined the null hypothesis first. This hypothesis shows that understanding the level of a landslide predictor does not aid in the prediction of landslide incidence (Sarkar and Kanungo, 2004). The variables are independent.

H₁: There is no independent condition between variable X (e.g., aspect) and variable Y (e.g., landslide occurrence).

H₀: There is an independent condition between variable X (e.g., aspect) and variable Y (e.g., landslide occurrence). This method is calculated according to Eq. 16:

${\mathrm{\chi }}^2={\displaystyle \sum _{i=1}^n\frac{{\left(O_i-E_i\right)}^2}{E_i}},(17)$

where χ2 is the chi-square, $O_i$ is the observed value, and $E_i$ is the expected value.

4 Results and Analysis

4.1 The Most Important Factors in the Modeling Procedure

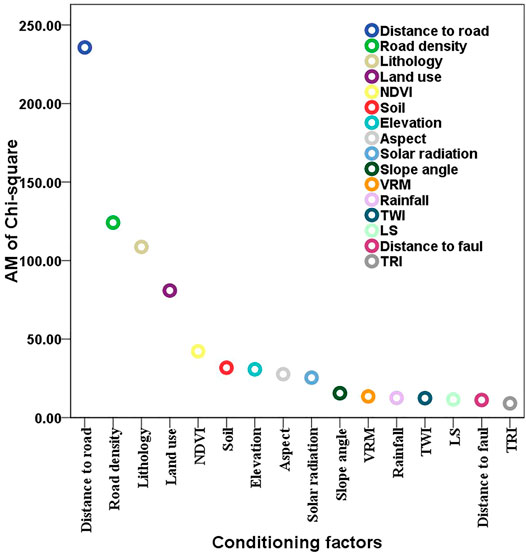
Figure 4 shows the role and relative importance of the conditioning factors on the shallow landslide occurrence in our study area based on the average merit (AM) of the chi-square feature selection technique in a 10-fold cross-validation analysis. The results indicate that the distance to road has the highest impact (AM = 235.737) on landslides in the study area, followed by road density (AM = 124.198), lithology (AM = 108.694), land use (AM = 80.921), NDVI (AM = 42.228), soil (AM = 31.774), elevation (AM = 30.733), aspect (AM = 27.662), annual solar radiation (AM = 25.426), slope (AM = 15.538), VRM (AM = 13.489), rainfall (AM = 12.521), TWI (AM = 12.391), LS (AM = 11.563), distance to fault (AM = 11.210), and TRI (AM = 9.064).

FIGURE 4

FIGURE 4. Factor selection using the chi-square technique with 10-fold cross-validation.

4.2 Model Result, Validation, and Comparison

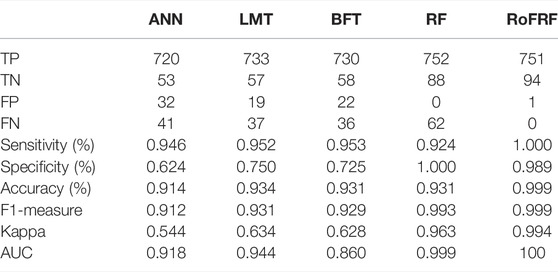
Table 3 shows the performance of the models using various statistical measures including specificity, sensitivity, accuracy, F1-measure, Kappa, and AUC obtained using the training dataset. The results show that the hybrid RoFRF model has the highest sensitivity (1.000), which points out that all of the landslide locations (100%) have been correctly classified as nonlandslide. However, RF has the highest specificity (1.000; 100%), indicating that 100% of the nonlandslide locations have been correctly classified and known as nonlandslide locations. This is followed by the RoFRF (0.989; 98.9%), LMT (0.750; 75%), BFT (0.725; 72.5%), and ANN (0.624; 62.4%) models. The accuracy metric state that the hybrid RoFRF model has the highest value (0.999; 99.9%), indicating that this model is able to correctly classify the landslide and nonlandslide locations as landslide and nonlandslide situations, respectively.

TABLE 3

TABLE 3. Model results using the training dataset.

The LMT model was ranked as the second with an accuracy = 0.934, followed by the RF, BFT (0.931), and ANN (0.914) models. F1-measure shows the highest value of 0.999 for the hybrid RoFRF model, and the least value of 0.912 for ANN. Moreover, this value for the RF, LMT, and BFT models are 0.993, 0.931, and 0.929, respectively. The lowest and highest Kappa values are 0.544 and 0.994, respectively for the RoFRF and ANN models. Meanwhile, RF (0.963), LMT (0.634), and BFT (0.628) was ranked in other positions. The AUC value of the hybrid RoFRF model is 100, which shows that the power performance or goodness-of-fit of the hybrid RoFRF model is the highest (100%), followed by the RF (0.999), LMT (0.944), ANN (0.918), and BFT (0.860) models (Table 3).

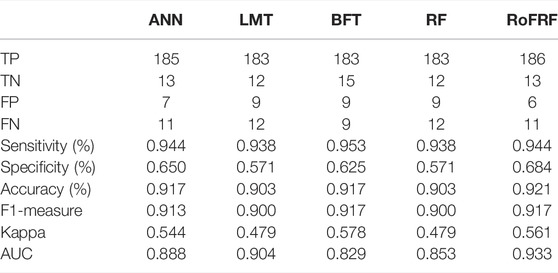
Table 4 shows the prediction accuracy of the five models of the study that were obtained based on the validating dataset. These results are important for assessing the power prediction, applicability, and robustness of the models. According to Table 4, the sensitivity values for BFT, RoFRF, ANN, RF, and LMT are 0.953, 0.944, and 0.938, respectively. However, specificity is the highest for the hybrid RoFRF model (0.684; 68.4%) and then for the ANN (0.650; 65%), BFT (0.625; 62.5%), LMT, and RF (571; 57.1%) models, respectively. The highest value of accuracy is 0.921 (92.1%) for the hybrid RoFRF model, next for the ANN and BFT (0.917; 91.7%) and the RF and LMT (0.903; 90.3%) models. The F1-measure for the hybrid RoFRF model and the BFT model is 0.917 as the highest value, whereas this value is 0.913 for ANN and 0.900 for RF and LMT. Although the BFT model has the highest Kappa (0.578), it had the lowest value of AUC (0.829). Hence, the hybrid RoFRF model with a Kappa value of 0.561 has the AUC value of 0.933, indicating that the power prediction of the hybrid model is 93.3%. This indicates that this model with an AUC of 93.3% is highly capable of predicting landslides. The LMT model has the second-highest value of AUC (0.904; 90.4%) and ANN, RF, and BFT have AUC equal to 0.888 (88.8%), 0.853 (85.3%), and 0.829 (82.9%), respectively (Table 4).

TABLE 4

TABLE 4. Model results using the validation dataset.

4.3 Parameter Optimization

In the modeling procedure, successful and reasonable results are thoroughly dependent on the values of the parameters that are defined by the users. The parameter’s tuning procedure is done by trial-and-error technique and checking the obtained results such as AUC (Janizadeh et al., 2019; Pham et al., 2020a; Hong et al., 2020). We have presented the values of the parameters employed in each model in Table 5.

TABLE 5

TABLE 5. Parameters of machine learning algorithms for shallow landslide susceptibility mapping.

4.4 Landslide Susceptibility Maps

We assigned the landslide susceptibility index (LSIs) computed for each pixel of our study area by using the probability distribution function in the machine learning models. In this study, we classified the LSIs of RoFRF and LMT maps using the quantile classification method and the BFTree, RF, and ANN using the geometric interval classification method. The LSIs were reclassified into five susceptibility classes including very low susceptibility (VLS; dark green color), low susceptibility (LS; light green color), moderate susceptibility (MS: yellow color), high susceptibility (HS: orange color), and very high susceptibility (VHS; red color). Figure 5 shows the landslide susceptibility maps produced by the hybrid RoFRF model and the benchmark models used in this study.

FIGURE 5

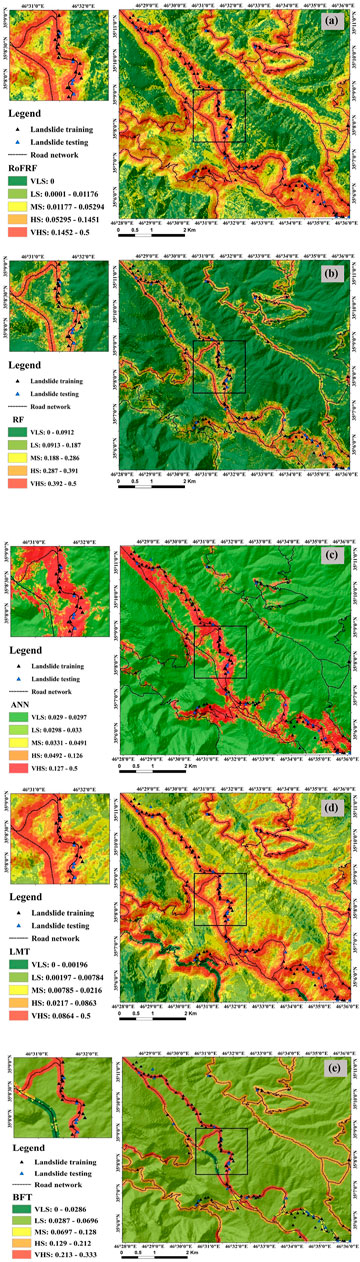
FIGURE 5. Landslide susceptibility maps produced using the (A) RoFRF, (B) RF, (C) ANN, (D) LMT, and (E) BFT.

Since the distance to road and road density factors were identified as the most important factors in the modeling process, the HS and VHS classes are located around the road networks. We enlarged a rectangle on the left side of the susceptibility maps to show graphically how many landslide occurrence locations (training and validation) are corresponding to the areas in terms of susceptibility to landslide occurrence.

4.5 Accuracy Assessment and Comparison

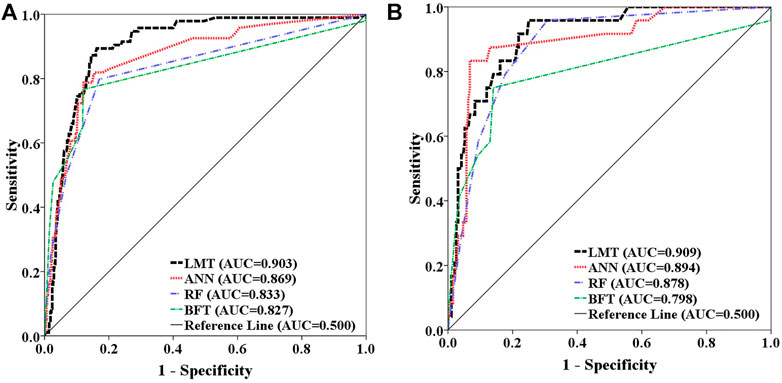
We tested and evaluated the performance and prediction accuracy of the hybrid model and the four soft computing benchmark models using the training and validating datasets, respectively (Figures 6, 7). From Figure 6A, the results indicate that the hybrid model with AUC equal to 0.953 (95.3%) has the highest performance compared with the other models, while according to Figure 6B, the power prediction of the hybrid model is 0.919 (91.9%). In comparison (Figures 7A,B), the hybrid RoFRF model is more capable in terms of both the performance and prediction accuracy than the LMT (AUC train = 0.903; AUC validating = 0.909), ANN (AUC train = 0.869; AUC validating = 0.894), RF (AUC train = 0.833; AUC validating = 0.878), and BFT (AUC train = 0.827; AUC validating = 0.798) models.

FIGURE 6

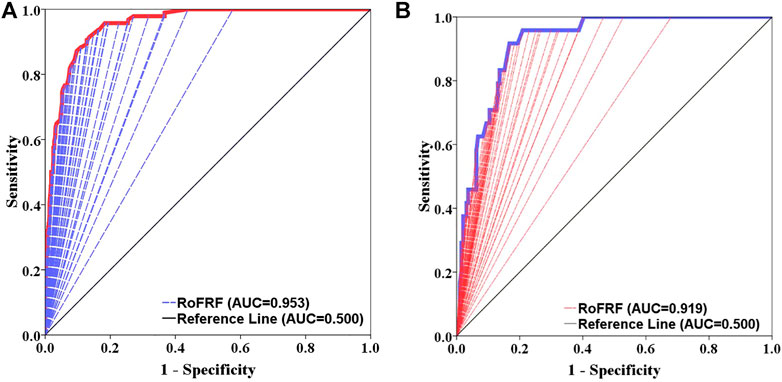
FIGURE 6. Performance and prediction accuracy of the RoFRF model using ROC curve (A) training dataset, (B) validation dataset.

FIGURE 7

FIGURE 7. Areas under the curve (AUC) for (A) training dataset, (B) validation dataset.

5 Discussion

The main objective of our study was to model the spatial distribution of landslide susceptibility and to produce a susceptibility map with high prediction reliability. Therefore, we focused on evaluating the performance of different machine learning methods as the crucial step of a landslide modeling project (Brenning, 2005; Reichenbach et al., 2018). While numerous methods have been suggested and used for landslide modeling over the past decades, machine learning methods have been preferred by many researchers (Merghadi et al., 2020). In recent years, the efficiency of ensemble learning techniques in improving the performance of the machine learning methods has been acknowledged by some researchers (Pham et al., 2020b; Nhu et al., 2020). To test the performance of single models against an ensemble model, we first measured the significance of the conditioning factors using the Chi-square technique with 10-fold cross-validation and identified the distance to roads and road density as the most significant factors related to landslide occurrences in the study area. Similar results have also been reported from other regions, where transport infrastructure cross-steep terrain (Jaafari et al., 2017; Schlögl and Matulla, 2018). Old road networks, which were once planned for low traffic and axle loads, are at extremely high risk of landslides. Hence, maintenance and landslide mitigation measures for these roads should be considered (Schlögl et al., 2019).

We assessed the models’ results via a validation process to compare the ability of four models developed to spatially predict landslides. 10 performance measures indicated that the RF model had a better goodness-of-fit (using the training dataset) and prediction ability (using the validation dataset) than that of the other three single models (i.e., ANN, LMT, and BFT). Many other studies have demonstrated the superiority of the RF model to other machine learning methods, such as best-first decision tree and Naïve Bayes tree (Chen et al., 2018), artificial neural network, and logistic regression (Smith et al., 2021). RF is a powerful nonlinear machine learning method intended for solving classification problems that can overcome the multicollinearity and nonlinear dependencies among the variables (Boulesteix et al., 2012). Being a nonparametric method, RF can be regarded as the most flexible machine learning method (James et al., 2021) with the ability to handle multiclass and skewed datasets (Guyennon et al., 2021). Given this superiority, we selected the RF model as the base model for combining it with the RoF technique to develop a hybrid predictive model, i.e., RoFRF. The new hybrid RoFRF model significantly improved the prediction performance of the base RF model. This is reasonable because the models developed based on the ensemble learning techniques can reduce both the variance and bias of the modeling process and avoid overfitting to gain the highest prediction performance (Nhu et al., 2020; Tran et al., 2020). The key point for the efficiency of the RoF technique is to increase the diversity and individual accuracy of the ensemble classifier simultaneously. Diversity is promoted via the principal component analysis (PCA) to perform feature extraction for the base classifier, whereas accuracy is achieved by using all the principal components and also the whole dataset to train the base classifier (Park et al., 2019). Similar studies have also shown that the RoF technique can improve the training performance (i.e., goodness-of-fit) and validation performance (i.e., predictive ability) of the base classifiers for landslide prediction. In sum, the RoF technique with a fast performance has a decent generalization capability and low implementation complexity, that make it a favored choice for developing powerful ensemble models for landslide prediction.

Overall, our study demonstrated that for a certain study area it is reasonable to select the most influential controlling factors via the feature screening methods and to identify the most accurate method via parameter optimization and comparing multiple models. A comparative approach allows for investigating the capability of multiple models for producing the most accurate and reliable susceptibility maps. This approach is an improvement to the traditional approach that often selects a single model and may ignore the other potentially better models for prediction. Therefore, the hybrid modeling provides a framework that accurately analyzes the historical landslides and conditional factors and improves the reliability of the prediction of future landslides.

6 Conclusion

The aim of this study was to perform a hybrid model of Rotation Forest - Random Forest (RoFRF) and its comparison with the Artificial Neural Network (ANN), Logistic Model Tree (LMT), Best First Tree (BFT), and Random Forest (RF) models to map landslide susceptibility in the part of Kamyaran area in Kurdistan Province, Iran. To achieve this goal based on different sources, 25 landslides affecting (or controlling) factors: elevation, slope angle, aspect, curvature, profile curvature, plan curvature, solar radiation, VRM, VD, SPI TWI, TRI, TPI, LS, NDVI, rainfall, distance to fault, distance to road, distance to river, fault density, road density, river density, lithology, land use, and soil were selected and applied as inputs to the models. Then, the relative importance of each factor was examined based on the Average Merit (AM) score. Among all the factors, 16 factors were importantly selected and used for the modeling procedure. In the next step, after drawing the landslide inventory map, a set of training and validation datasets were divided respectively, for modeling and evaluation processes. The hybrid proposed method can derive the benefits of basic classifiers using different group learning strategies. The present study demonstrated an efficient way to combine different types of landslide susceptibility methods, hybrid learning, and deep learning to obtain a more accurate map. Based on this, the most important findings of our study are summarized as follows:

1) Identifying the most influential controlling factors in the occurrence of shallow landslides and the preparation of susceptibility maps are the basic strategies to control this phenomenon and select the most appropriate and practical options. Although according to the AM score, 16 factors affected the occurrence of shallow landslides, and the most important factor was the distance to roads, followed by the road density factor. Our results demonstrated that more careful road construction, maintenance, and route planning needs to be considered to reduce future landslide occurrence.

2) The parameter optimization contributes to the best performance of the models, and thereby the prediction accuracy of future landslides.

3) Sensitivity, accuracy, specificity, Kappa, RMSE, and AUC metrics were used to evaluate the models that showed that the hybrid RoFRF model had a better goodness-of-fit and prediction accuracy than the ANN, LMT, BFT, and RF models. This model had a successful estimate and significant performance in predicting shallow landslide occurrence.

4) Our results showed that hybrid modeling using group techniques, such as RF is promising for the shallow landslide susceptibility mapping. This approach can then be used as a tool for shallow landslide hazard avoidance and mitigation worldwide.

Data Availability Statement

The original contributions presented in the study are included in the article/Supplementary Material. Further inquiries can be directed to the corresponding author.

Author Contributions

BG, HS, AS, NA-A, AJ, MG, AM, SS, and AA contributed equally to the work. BG, HS, and AS collected field data and conducted the landslide susceptibility analysis. BG, HS, AS, NA-A, SS, and AJ wrote the manuscript. MG, AM, SS, and AA provided critical comments in planning this article and edited the manuscript. All the authors discussed the results and edited the manuscript. All authors have read and agreed to the published version of the manuscript.

Funding

This research was supported by the University of Kurdistan, Iran, based on a grant number 00-9-34027-4469.

Conflict of Interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Publisher’s Note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors, and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

Acknowledgments

The authors would like to thank the Vice Chancellorship of Research and Technology, University of Kurdistan, Sanandaj, Iran, for supplying required data, reports, useful maps, and their nationwide geodatabase to the first author (BG) as a postdoctoral fellowship scheme.

References

Abedini, M., Ghasemian, B., Shirzadi, A., Shahabi, H., Chapi, K., Pham, B. T., et al. (2019). A Novel Hybrid Approach of Bayesian Logistic Regression and its Ensembles for Landslide Susceptibility Assessment. Geocarto Int. 34 (13), 1427–1457. doi:10.1080/10106049.2018.1499820

CrossRef Full Text | Google Scholar

Alcantara-Ayala, I. (2002). Geomorphology, Natural Hazards, Vulnerability and Prevention of Natural Disasters in Developing Countries. Geomorphology 47 (2-4), 107–124. doi:10.1016/S0169-555X(02)00083-1

CrossRef Full Text | Google Scholar

Aleotti, P., and Chowdhury, R. (1999). Landslide Hazard Assessment: Summary Review and New Perspectives. Bull. Eng. Geol. Env. 58 (1), 21–44. doi:10.1007/s100640050066

CrossRef Full Text | Google Scholar

Althuwaynee, O. F., Pradhan, B., and Lee, S. (2016). A Novel Integrated Model for Assessing Landslide Susceptibility Mapping Using CHAID and AHP Pair-Wise Comparison. Int. J. Remote Sens. 37 (5), 1190–1209. doi:10.1080/01431161.2016.1148282

CrossRef Full Text | Google Scholar

Asadi, M., Goli Mokhtari, L., Shirzadi, A., Shahabi, H., and Bahrami, S. (2022). A Comparison Study on the Quantitative Statistical Methods for Spatial Prediction of Shallow Landslides (Case Study: Yozidar-Degaga Route in Kurdistan Province, Iran). Environ. Earth Sci. 81 (2), 1–21. doi:10.1007/s12665-021-10152-4

CrossRef Full Text | Google Scholar

Bennett, N. D., Croke, B. F. W., Guariso, G., Guillaume, J. H. A., Hamilton, S. H., Jakeman, A. J., et al. (2013). Characterising Performance of Environmental Models. Environ. Model. Softw. 40, 1–20. doi:10.1016/j.envsoft.2012.09.011

CrossRef Full Text | Google Scholar

Boulesteix, A.-L., Janitza, S., Kruppa, J., and König, I. R. (2012). Overview of Random Forest Methodology and Practical Guidance with Emphasis on Computational Biology and Bioinformatics. WIREs Data Min. Knowl. Discov. 2 (6), 493–507. doi:10.1002/widm.1072

CrossRef Full Text | Google Scholar

Breiman, L., Friedman, J. H., Olshen, R. A., and Stone, C. J. (1984).Classification and Regression Trees, Int. Group. 432, 151–166. doi:10.1201/9781315139470

CrossRef Full Text | Google Scholar

Brenning, A. (2005). Spatial Prediction Models for Landslide Hazards: Review, Comparison and Evaluation. Nat. Hazards Earth Syst. Sci. 5 (6), 853–862. doi:10.5194/nhess-5-853-2005

CrossRef Full Text | Google Scholar

Bryant, F. B., and Satorra, A. (2012). Principles and Practice of Scaled Difference Chi-Square Testing. Struct. Equ. Model. A Multidiscip. J. 19 (3), 372–398. doi:10.1080/10705511.2012.687671

CrossRef Full Text | Google Scholar

Chao, L., Zhang, K., Wang, J., Feng, J., and Zhang, M. (2021). A Comprehensive Evaluation of Five Evapotranspiration Datasets Based on Ground and Grace Satellite Observations: Implications for Improvement of Evapotranspiration Retrieval Algorithm. Remote Sens. 13 (12), 2414. doi:10.3390/rs13122414

CrossRef Full Text | Google Scholar

Chen, W., Li, W., Hou, E., Bai, H., Chai, H., Wang, D., et al. (2015). Application of Frequency Ratio, Statistical Index, and Index of Entropy Models and Their Comparison in Landslide Susceptibility Mapping for the Baozhong Region of Baoji, China. Arab. J. Geosci. 8 (4), 1829–1841. doi:10.1007/s12517-014-1554-0

CrossRef Full Text | Google Scholar

Chen, W., Zhang, S., Li, R., and Shahabi, H. (2018). Performance Evaluation of the GIS-Based Data Mining Techniques of Best-First Decision Tree, Random Forest, and Naïve Bayes Tree for Landslide Susceptibility Modeling. Sci. Total Environ. 644, 1006–1018. doi:10.1016/j.scitotenv.2018.06.389

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, Z., Liu, Z., Yin, L., and Zheng, W. (2022). Statistical Analysis of Regional Air Temperature Characteristics before and after Dam Construction. Urban Clim. 41, 101085. doi:10.1016/j.uclim.2022.101085

CrossRef Full Text | Google Scholar

Colkesen, I., and Kavzoglu, T. (2017). The Use of Logistic Model Tree (LMT) for Pixel- and Object-Based Classifications Using High-Resolution WorldView-2 Imagery. Geocarto Int. 32 (1), 71–86. doi:10.1080/10106049.2015.1128486

CrossRef Full Text | Google Scholar

De Jesus, J. B., Kuplich, T. M., de Carvalho Barreto, Í. D., Da Rosa, C. N., and Hillebrand, F. L. (2021). Temporal and Phenological Profiles of Open and Dense Caatinga Using Remote Sensing: Response to Precipitation and its Irregularities. J. For. Res. 32 (3), 1067–1076. doi:10.1007/s11676-020-01145-3

CrossRef Full Text | Google Scholar

Dou, J., Yunus, A. P., Tien Bui, D., Merghadi, A., Sahana, M., Zhu, Z., et al. (2019a). Assessment of Advanced Random Forest and Decision Tree Algorithms for Modeling Rainfall-Induced Landslide Susceptibility in the Izu-Oshima Volcanic Island, Japan. Sci. total Environ. 662, 332–346. doi:10.1016/j.scitotenv.2019.01.221

PubMed Abstract | CrossRef Full Text | Google Scholar

Dou, J., Yunus, A. P., Xu, Y., Zhu, Z., Chen, C.-W., Sahana, M., et al. (2019b). Torrential Rainfall-Triggered Shallow Landslide Characteristics and Susceptibility Assessment Using Ensemble Data-Driven Models in the Dongjiang Reservoir Watershed, China. Nat. Hazards 97 (2), 579–609. doi:10.1007/s11069-019-03659-4

CrossRef Full Text | Google Scholar

Fan, X., Scaringi, G., Korup, O., West, A. J., Westen, C. J., Tanyas, H., et al. (2019). Earthquake‐Induced Chains of Geologic Hazards: Patterns, Mechanisms, and Impacts. Rev. Geophys. 57 (2), 421–503. doi:10.1029/2018rg000626

CrossRef Full Text | Google Scholar

Fang, Z., Wang, Y., Duan, G., and Peng, L. (2021). Landslide Susceptibility Mapping Using Rotation Forest Ensemble Technique with Different Decision Trees in the Three Gorges Reservoir Area, China. Remote Sens. 13 (2), 238. doi:10.3390/rs13020238

CrossRef Full Text | Google Scholar

Fawcett, T. (2006). An Introduction to ROC Analysis. Pattern Recognit. Lett. 27 (8), 861–874. doi:10.1016/j.patrec.2005.10.010

CrossRef Full Text | Google Scholar

Geertsema, M., Highland, L., and Vaugeouis, L. (2009). Landslides–disaster Risk Reduction. Berlin, Heidelberg: Springer, 589–607.

Google Scholar

Ghasemian, B., Shahabi, H., Shirzadi, A., Al-Ansari, N., Jaafari, A., Kress, V. R., et al. (2022). A Robust Deep-Learning Model for Landslide Susceptibility Mapping: a Case Study of Kurdistan Province, Iran. Sensors 22 (4), 1573. doi:10.3390/s22041573

PubMed Abstract | CrossRef Full Text | Google Scholar

Guyennon, N., Salerno, F., Rossi, D., Rainaldi, M., Calizza, E., and Romano, E. (2021). Climate Change and Water Abstraction Impacts on the Long-Term Variability of Water Levels in Lake Bracciano (Central Italy): A Random Forest Approach. J. Hydrology Regional Stud. 37, 100880. doi:10.1016/j.ejrh.2021.100880

CrossRef Full Text | Google Scholar

He, Q., Xu, Z., Li, S., Li, R., Zhang, S., Wang, N., et al. (2019). Novel Entropy and Rotation Forest-Based Credal Decision Tree Classifier for Landslide Susceptibility Modeling. Entropy 21 (2), 106. doi:10.3390/e21020106

PubMed Abstract | CrossRef Full Text | Google Scholar

Hong, H., Miao, Y., Liu, J., and Zhu, A.-X. (2019). Exploring the Effects of the Design and Quantity of Absence Data on the Performance of Random Forest-Based Landslide Susceptibility Mapping. Catena 176, 45–64. doi:10.1016/j.catena.2018.12.035

CrossRef Full Text | Google Scholar

Hong, H., Tsangaratos, P., Ilia, I., Loupasakis, C., and Wang, Y. (2020). Introducing a Novel Multi-Layer Perceptron Network Based on Stochastic Gradient Descent Optimized by a Meta-Heuristic Algorithm for Landslide Susceptibility Mapping. Sci. total Environ. 742, 140549. doi:10.1016/j.scitotenv.2020.140549

PubMed Abstract | CrossRef Full Text | Google Scholar

Hung, L. Q., Van, N. T. H., Duc, D. M., Ha, L. T. C., Van Son, P., Khanh, N. H., et al. (2016). Landslide Susceptibility Mapping by Combining the Analytical Hierarchy Process and Weighted Linear Combination Methods: a Case Study in the Upper Lo River Catchment (Vietnam). Landslides 13 (5), 1285–1301. doi:10.1007/s10346-015-0657-3

CrossRef Full Text | Google Scholar

Huppert, H. E., and Sparks, R. S. J. (2006). Extreme Natural Hazards: Population Growth, Globalization and Environmental Change. Phil. Trans. R. Soc. A 364 (1845), 1875–1888. doi:10.1098/rsta.2006.1803

PubMed Abstract | CrossRef Full Text | Google Scholar

Jaafari, A., Rezaeian, J., and Omrani, M. S. (2017). Spatial Prediction of Slope Failures in Support of Forestry Operations Safety. Croat. J. For. Eng. 38 (1), 107–118.

Google Scholar

James, G., Witten, D., Hastie, T., and Tibshirani, R. (2021). An Introduction to Statistical Learning. New York, USA: Springer, 15–57.

CrossRef Full Text | Google Scholar

Janizadeh, S., Avand, M., Jaafari, A., Phong, T. V., Bayat, M., Ahmadisharaf, E., et al. (2019). Prediction Success of Machine Learning Methods for Flash Flood Susceptibility Mapping in the Tafresh Watershed, Iran. Sustainability 11 (19), 5426. doi:10.3390/su11195426

CrossRef Full Text | Google Scholar

Jiang, S., Zuo, Y., Yang, M., and Feng, R. (2021). Reconstruction of the Cenozoic Tectono-Thermal History of the Dongpu Depression, Bohai Bay Basin, China: Constraints from Apatite Fission Track and Vitrinite Reflectance Data. J. Petroleum Sci. Eng. 205, 108809. doi:10.1016/j.petrol.2021.108809

CrossRef Full Text | Google Scholar

Kadirhodjaev, A., Rezaie, F., Lee, M.-J., and Lee, S. (2020). Landslide Susceptibility Assessment Using an Optimized Group Method of Data Handling Model. ISPRS. Int. J. Geo-Inf. 9 (10), 566. doi:10.3390/ijgi9100566

CrossRef Full Text | Google Scholar

Khandelwal, M., Marto, A., Fatemi, S. A., Ghoroqi, M., Armaghani, D. J., Singh, T. N., et al. (2018). Implementing an ANN Model Optimized by Genetic Algorithm for Estimating Cohesion of Limestone Samples. Eng. Comput. 34 (2), 307–317. doi:10.1007/s00366-017-0541-y

CrossRef Full Text | Google Scholar

Koehorst, B., Kjekstad, O., Patel, D., Lubkowski, Z., Knoeff, J., and Akkerman, G. (2005). Workpackage 6 Determination of Socio-Economic Impact of Natural Disasters. Assessing Socioeconomic Impact in Europe, 173

Google Scholar

Konishi, T., and Suga, Y. (2018). Landslide Detection Using COSMO-SkyMed Images: A Case Study of a Landslide Event on Kii Peninsula, Japan. Eur. J. remote Sens. 51 (1), 205–221.

CrossRef Full Text | Google Scholar

Lan, Z., Zhao, Y., Zhang, J., Jiao, R., Khan, M. N., Sial, T. A., et al. (2021). Long-term Vegetation Restoration Increases Deep Soil Carbon Storage in the Northern Loess Plateau. Sci. Rep. 11 (1), 1–11. doi:10.1038/s41598-021-93157-0

PubMed Abstract | CrossRef Full Text | Google Scholar

Landwehr, N., Hall, M., and Frank, E. (2005). Logistic Model Trees. Mach. Learn. 59 (1-2), 161–205. doi:10.1007/s10994-005-0466-3

CrossRef Full Text | Google Scholar

Lee, S., Hong, S.-M., and Jung, H.-S. (2017). A Support Vector Machine for Landslide Susceptibility Mapping in Gangwon Province, Korea. Sustainability 9 (1), 48. doi:10.3390/su9010048

CrossRef Full Text | Google Scholar

Li, B., Yang, J., Yang, Y., Li, C., and Zhang, Y. (2021). Sign Language/gesture Recognition Based on Cumulative Distribution Density Features Using UWB Radar. IEEE Trans. Instrum. Meas. 70, 1–13. doi:10.1109/tim.2021.3092072

PubMed Abstract | CrossRef Full Text | Google Scholar

Li, H., Deng, J., Feng, P., Pu, C., Arachchige, D. D., and Cheng, Q. (2021a). Short-Term Nacelle Orientation Forecasting Using Bilinear Transformation and ICEEMDAN Framework. Front. Energy Res. 697, 780928. doi:10.3389/fenrg.2021.780928

CrossRef Full Text | Google Scholar

Li, H., Deng, J., Yuan, S., Feng, P., and Arachchige, D. D. (2021b). Monitoring and Identifying Wind Turbine Generator Bearing Faults Using Deep Belief Network and EWMA Control Charts. Front. Energy Res. 9, 770. doi:10.3389/fenrg.2021.799039

CrossRef Full Text | Google Scholar

Li, J., Zhao, Y., Zhang, A., Song, B., and Hill, R. L. (2021). Effect of Grazing Exclusion on Nitrous Oxide Emissions during Freeze-Thaw Cycles in a Typical Steppe of Inner Mongolia. Agric. Ecosyst. Environ. 307, 107217. doi:10.1016/j.agee.2020.107217

CrossRef Full Text | Google Scholar

Li, Z.-J., and Zhang, K. (2008). Comparison of Three GIS-Based Hydrological Models. J. Hydrol. Eng. 13 (5), 364–370. doi:10.1061/(asce)1084-0699(2008)13:5(364)

CrossRef Full Text | Google Scholar

Liu, B., Spiekermann, R., Zhao, C., Püttmann, W., Sun, Y., Jasper, A., et al. (2022). Evidence for the Repeated Occurrence of Wildfires in an Upper Pliocene Lignite Deposit from Yunnan, SW China. Int. J. Coal Geol. 250, 103924 doi:10.1016/j.coal.2021.103924

CrossRef Full Text | Google Scholar

Luan, D., Liu, A., Wang, X., Xie, Y., and Wu, Z. (2022). Robust Two-Stage Location Allocation for Emergency Temporary Blood Supply in Postdisaster. Discrete Dyn. Nat. Soc., 2022. doi:10.1155/2022/6184170

CrossRef Full Text | Google Scholar

Lucchese, L. V., De Oliveira, G. G., and Pedrollo, O. C. (2021). Mamdani Fuzzy Inference Systems and Artificial Neural Networks for Landslide Susceptibility Mapping. Nat. Hazards 106 (3), 2381–2405. doi:10.1007/s11069-021-04547-6

CrossRef Full Text | Google Scholar

Malamud, B. D., Turcotte, D. L., Guzzetti, F., and Reichenbach, P. (2004). Landslide Inventories and Their Statistical Properties. Earth Surf. Process. Landforms 29 (6), 687–711. doi:10.1002/esp.1064

CrossRef Full Text | Google Scholar

Meena, S., Mishra, B., and Tavakkoli Piralilou, S. (2019). A Hybrid Spatial Multi-Criteria Evaluation Method for Mapping Landslide Susceptible Areas in Kullu Valley, Himalayas. Geosciences 9 (4), 156. doi:10.3390/geosciences9040156

CrossRef Full Text | Google Scholar

Merghadi, A., Yunus, A. P., Dou, J., Whiteley, J., Thaipham, B., Bui, D. T., et al. (2020). Machine Learning Methods for Landslide Susceptibility Studies: A Comparative Overview of Algorithm Performance. Earth-Science Rev. 207, 103225. doi:10.1016/j.earscirev.2020.103225

CrossRef Full Text | Google Scholar

Nguyen, B.-Q. -V., and Kim, Y.-T. (2021). Landslide Spatial Probability Prediction: a Comparative Assessment of Naïve Bayes, Ensemble Learning, and Deep Learning Approaches. Bull. Eng. Geol. Environ. 80 (6), 4291–4321. doi:10.1007/s10064-021-02194-6

CrossRef Full Text | Google Scholar

Nguyen, Q. K., Bui, D. T., Hoang, N. D., Trinh, P. T., Nguyen, V. H., and Yilmaz, I. (2017). A Novel Hybrid Approach Based on Instance Based Learning Classifier and Rotation Forest Ensemble for Spatial Prediction of Rainfall-Induced Shallow Landslides Using GIS. Sustain. Switz. 9 (5), 813. doi:10.3390/su9050813

CrossRef Full Text | Google Scholar

Nhu, V.-H., Shirzadi, A., Shahabi, H., Chen, W., Clague, J. J., Geertsema, M., et al. (2020). Shallow Landslide Susceptibility Mapping by Random Forest Base Classifier and its Ensembles in a Semi-arid Region of Iran. Forests 11 (4), 421. doi:10.3390/f11040421

CrossRef Full Text | Google Scholar

Park, S., Hamm, S.-Y., and Kim, J. (2019). Performance Evaluation of the GIS-Based Data-Mining Techniques Decision Tree, Random Forest, and Rotation Forest for Landslide Susceptibility Modeling. Sustainability 11 (20), 5659. doi:10.3390/su11205659

CrossRef Full Text | Google Scholar

Park, S., and Kim, J. (2019). Landslide Susceptibility Mapping Based on Random Forest and Boosted Regression Tree Models, and a Comparison of Their Performance. Appl. Sci. 9 (5), 942. doi:10.3390/app9050942

CrossRef Full Text | Google Scholar

Pham, B. T., Jaafari, A., Nguyen-Thoi, T., Van Phong, T., Nguyen, H. D., Satyam, N., et al. (2020a). Ensemble Machine Learning Models Based on Reduced Error Pruning Tree for Prediction of Rainfall-Induced Landslides. Int. J. Digital Earth 14, 1–22. doi:10.1080/17538947.2020.1860145

CrossRef Full Text | Google Scholar

Pham, B. T., Phong, T. V., Nguyen-Thoi, T., Trinh, P. T., Tran, Q. C., Ho, L. S., et al. (2020b). GIS-based Ensemble Soft Computing Models for Landslide Susceptibility Mapping. Adv. Space Res. 66 (6), 1303–1320. doi:10.1016/j.asr.2020.05.016

CrossRef Full Text | Google Scholar

Pham, B. T., Bui, D. T., Dholakia, M. B., Prakash, I., Pham, H. V., Mehmood, K., et al. (2017). A Novel Ensemble Classifier of Rotation Forest and Naïve Bayer for Landslide Susceptibility Assessment at the Luc Yen District, Yen Bai Province (Viet Nam) Using GIS. Geomatics, Nat. Hazards Risk 8 (2), 649–671. doi:10.1080/19475705.2016.1255667

CrossRef Full Text | Google Scholar

Quinlan, J. R. (1986). Induction of Decision Trees. Mach. Learn 1 (1), 81–106. doi:10.1007/bf00116251

CrossRef Full Text | Google Scholar

Razavizadeh, S., Solaimani, K., Massironi, M., and Kavian, A. (2017). Mapping Landslide Susceptibility with Frequency Ratio, Statistical Index, and Weights of Evidence Models: a Case Study in Northern Iran. Environ. Earth Sci. 76 (14), 1–16. doi:10.1007/s12665-017-6839-7

CrossRef Full Text | Google Scholar

Reichenbach, P., Rossi, M., Malamud, B. D., Mihir, M., and Guzzetti, F. (2018). A Review of Statistically-Based Landslide Susceptibility Models. Earth-Science Rev. 180, 60–91. doi:10.1016/j.earscirev.2018.03.001

CrossRef Full Text | Google Scholar

Rodriguez, J. J., Kuncheva, L. I., and Alonso, C. J. (2006). Rotation Forest: A New Classifier Ensemble Method. IEEE Trans. Pattern Anal. Mach. Intell. 28 (10), 1619–1630. doi:10.1109/tpami.2006.211

PubMed Abstract | CrossRef Full Text | Google Scholar

Rodriguez-Galiano, V. F., Ghimire, B., Rogan, J., Chica-Olmo, M., and Rigol-Sanchez, J. P. (2012). An Assessment of the Effectiveness of a Random Forest Classifier for Land-Cover Classification. ISPRS J. Photogrammetry Remote Sens. 67, 93–104. doi:10.1016/j.isprsjprs.2011.11.002

CrossRef Full Text | Google Scholar

Sarkar, S., and Kanungo, D. P. (2004). An Integrated Approach for Landslide Susceptibility Mapping Using Remote Sensing and GIS. Photogramm. Eng. remote Sens. 70 (5), 617–625. doi:10.14358/pers.70.5.617

CrossRef Full Text | Google Scholar

Schlögl, M., and Matulla, C. (2018). Potential Future Exposure of European Land Transport Infrastructure to Rainfall-Induced Landslides throughout the 21st Century. Nat. hazards earth Syst. Sci. 18 (4), 1121–1132. doi:10.5194/nhess-18-1121-2018

CrossRef Full Text | Google Scholar

Schlögl, M., Richter, G., Avian, M., Thaler, T., Heiss, G., Lenz, G., et al. (2019). On the Nexus between Landslide Susceptibility and Transport Infrastructure–An Agent-Based Approach. Nat. hazards earth Syst. Sci. 19 (1), 201–219. doi:10.5194/nhess-19-201-2019

CrossRef Full Text | Google Scholar

Schuster, R. L., and Highland, L. (2001). Socioeconomic and Environmental Impacts of Landslides in the Western Hemisphere. Citeseer, 1–48. doi:10.3133/ofr01276

CrossRef Full Text | Google Scholar

Shafizadeh-Moghadam, H., Minaei, M., Shahabi, H., and Hagenauer, J. (2019). Big Data in Geohazard; Pattern Mining and Large Scale Analysis of Landslides in Iran. Earth Sci. Inf. 12 (1), 1–17. doi:10.1007/s12145-018-0354-6

CrossRef Full Text | Google Scholar

Shi, H. (2007). Best-first Decision Tree Learning. Hamilton, New Zealand: The University of Waikato.

Google Scholar

Smith, H. G., Spiekermann, R., Betts, H., and Neverman, A. J. (2021). Comparing Methods of Landslide Data Acquisition and Susceptibility Modelling: Examples from New Zealand. Geomorphology 381, 107660. doi:10.1016/j.geomorph.2021.107660

CrossRef Full Text | Google Scholar

Sun, D., Shi, S., Wen, H., Xu, J., Zhou, X., and Wu, J. (2021a). A Hybrid Optimization Method of Factor Screening Predicated on GeoDetector and Random Forest for Landslide Susceptibility Mapping. Geomorphology 379, 107623. doi:10.1016/j.geomorph.2021.107623

CrossRef Full Text | Google Scholar

Sun, D., Xu, J., Wen, H., and Wang, D. (2021b). Assessment of Landslide Susceptibility Mapping Based on Bayesian Hyperparameter Optimization: A Comparison between Logistic Regression and Random Forest. Eng. Geol. 281, 105972. doi:10.1016/j.enggeo.2020.105972

CrossRef Full Text | Google Scholar

Tran, Q. C., Minh, D. D., Jaafari, A., Al-Ansari, N., Minh, D. D., Van, D. T., et al. (2020). Novel Ensemble Landslide Predictive Models Based on the Hyperpipes Algorithm: A Case Study in the Nam Dam Commune, Vietnam. Appl. Sci. 10 (11), 3710. doi:10.3390/app10113710

CrossRef Full Text | Google Scholar

Wang, Q., Guo, Y., Li, W., He, J., and Wu, Z. (2019). Predictive Modeling of Landslide Hazards in Wen County, Northwestern China Based on Information Value, Weights-Of-Evidence, and Certainty Factor. Geomatics, Nat. Hazards Risk 10 (1), 820–835. doi:10.1080/19475705.2018.1549111

CrossRef Full Text | Google Scholar

Wang, S., Zhang, K., Chao, L., Li, D., Tian, X., Bao, H., et al. (2021). Exploring the Utility of Radar and Satellite-Sensed Precipitation and Their Dynamic Bias Correction for Integrated Prediction of Flood and Landslide Hazards. J. Hydrology 603, 126964. doi:10.1016/j.jhydrol.2021.126964

CrossRef Full Text | Google Scholar

Xie, W., Li, X., Jian, W., Yang, Y., Liu, H., Robledo, L. F., et al. (2021a). A Novel Hybrid Method for Landslide Susceptibility Mapping-Based Geodetector and Machine Learning Cluster: A Case of Xiaojin County, China. ISPRS. Int. J. Geo-Inf. 10 (2), 93. doi:10.3390/ijgi10020093

CrossRef Full Text | Google Scholar

Xie, W., Nie, W., Saffari, P., Robledo, L. F., Descote, P.-Y., and Jian, W. (2021b). Landslide Hazard Assessment Based on Bayesian Optimization-Support Vector Machine in Nanping City, China. Nat. Hazards 109 (1), 931–948. doi:10.1007/s11069-021-04862-y

CrossRef Full Text | Google Scholar

Xu, J., Wu, Z., Chen, H., Shao, L., Zhou, X., and Wang, S. (2021). Study on Strength Behavior of Basalt Fiber-Reinforced Loess by Digital Image Technology (DIT) and Scanning Electron Microscope (SEM). Arab. J. Sci. Eng. 46 (11), 11319–11338. doi:10.1007/s13369-021-05787-1

CrossRef Full Text | Google Scholar

Yao, X., Tham, L. G., and Dai, F. C. (2008). Landslide Susceptibility Mapping Based on Support Vector Machine: a Case Study on Natural Slopes of Hong Kong, China. Geomorphology 101 (4), 572–582. doi:10.1016/j.geomorph.2008.02.011

CrossRef Full Text | Google Scholar

Yin, L., Wang, L., Keim, B. D., Konsoer, K., and Zheng, W. (2022a). Wavelet Analysis of Dam Injection and Discharge in Three Gorges Dam and Reservoir with Precipitation and River Discharge. Water 14 (4), 567. doi:10.3390/w14040567

CrossRef Full Text | Google Scholar

Yin, L., Wang, L., Zheng, W., Ge, L., Tian, J., Liu, Y., et al. (2022b). Evaluation of Empirical Atmospheric Models Using Swarm-C Satellite Data. Atmosphere 13 (2), 294. doi:10.3390/atmos13020294

CrossRef Full Text | Google Scholar

Zhang, K., Ali, A., Antonarakis, A., Moghaddam, M., Saatchi, S., Tabatabaeenejad, A., et al. (2019a). The Sensitivity of North American Terrestrial Carbon Fluxes to Spatial and Temporal Variation in Soil Moisture: An Analysis Using Radar‐Derived Estimates of Root‐Zone Soil Moisture. J. Geophys. Res. Biogeosci. 124 (11), 3208–3231. doi:10.1029/2018jg004589

CrossRef Full Text | Google Scholar

Zhang, K., Wang, S., Bao, H., and Zhao, X. (2019b). Characteristics and Influencing Factors of Rainfall-Induced Landslide and Debris Flow Hazards in Shaanxi Province, China. Nat. Hazards Earth Syst. Sci. 19 (1), 93–105. doi:10.5194/nhess-19-93-2019

CrossRef Full Text | Google Scholar

Zhang, K., Shalehy, M. H., Ezaz, G. T., Chakraborty, A., Mohib, K. M., and Liu, L. (2022). An Integrated Flood Risk Assessment Approach Based on Coupled Hydrological-Hydraulic Modeling and Bottom-Up Hazard Vulnerability Analysis. Environ. Model. Softw. 148, 105279. doi:10.1016/j.envsoft.2021.105279

CrossRef Full Text | Google Scholar

Zhang, Y., Liu, F., Fang, Z., Yuan, B., Zhang, G., Lu, J., et al. (2021). Learning from a Complementary-Label Source Domain: Theory and Algorithms. IEEE Transactions on Neural Networks and Learning Systems

Google Scholar

Zhao, X., Xia, H., Pan, L., Song, H., Niu, W., Wang, R., et al. (2021). Drought Monitoring over Yellow River Basin from 2003–2019 Using Reconstructed MODIS Land Surface Temperature in Google Earth Engine. Remote Sens. 13 (18), 3748. doi:10.3390/rs13152934

CrossRef Full Text | Google Scholar

Zhou, G., Long, S., Xu, J., Zhou, X., Song, B., Deng, R., et al. (2021a). Comparison Analysis of Five Waveform Decomposition Algorithms for the Airborne LiDAR Echo Signal. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 14, 7869–7880. doi:10.1109/jstars.2021.3096197

CrossRef Full Text | Google Scholar

Zhou, G., Zhang, R., and Huang, S. (2021b). Generalized Buffering Algorithm. IEEE Access 9, 27140–27157. doi:10.1109/access.2021.3057719

CrossRef Full Text | Google Scholar

Zhou, W., Lv, Y., Lei, J., and Yu, L. (2019). Global and Local-Contrast Guides Content-Aware Fusion for RGB-D Saliency Prediction. IEEE Trans. Syst. Man Cybern. Syst., 51(6), 3641–3649. doi:10.1109/tsmc.2019.2957386

CrossRef Full Text

Zhou, W., Guo, Q., Lei, J., Yu, L., and Hwang, J. (2021). IRFR-Net: Interactive Recursive Feature-Reshaping Network for Detecting Salient Objects in RGB-D Images. IEEE Trans. Neural Netw. Learn Syst., 1–13. doi:10.1109/TNNLS.2021.3105484

CrossRef Full Text

Zhou, X., Wen, H., Zhang, Y., Xu, J., and Zhang, W. (2021). Landslide Susceptibility Mapping Using Hybrid Random Forest with GeoDetector and RFE for Factor Optimization. Geosci. Front. 12 (5), 101211. doi:10.1016/j.gsf.2021.101211

CrossRef Full Text | Google Scholar

Zhou, Y., Xu, G., Tang, K., Tian, L., and Sun, Y. (2022). Video Coding Optimization in AVS2. Inf. Process. Manag. 59 (2), 102808. doi:10.1016/j.ipm.2021.102808

CrossRef Full Text | Google Scholar