Accelerated Bayesian optimization for CNN+LSTM learning rate tuning via precomputed Gaussian process subspaces in soil analysis

Purpose: We propose an accelerated Bayesian optimization framework for tuning the learning rate of CNN+LSTM models in soil analysis, addressing the computational inefficiency of traditional Gaussian Process (GP)-based methods. This work bridges the gap between computational efficiency and probabilistic robustness, with broader implications for automated machine learning in geoscientific applications.

Method: The key innovation lies in a subspace-accelerated GP surrogate model that precomputes low-rank approximations of covariance matrices offline, thereby decoupling the costly hyperparameter tuning from the online acquisition function evaluations. By projecting the hyperparameter search space onto a dominant subspace derived from Nyström approximations, our method reduces the computational complexity from cubic to linear in the number of observations. The proposed system integrates seamlessly with existing CNN+LSTM pipelines, where the offline phase constructs the GP subspace using historical or synthetic data, while the online phase iteratively updates the subspace with rank-1 modifications. Moreover, the method’s adaptability to non-stationary response surfaces, facilitated by a Matérn-5/2 kernel with automatic relevance determination, makes it particularly suitable for soil data exhibiting multi-scale features.

Results: Empirical validation on soil spectral datasets demonstrates a 3–5× speedup in convergence compared to standard Bayesian optimization, with no loss in model accuracy. Experiments on soil spectral datasets show convergence in 23.4 min (3.8× faster than standard Bayesian optimization) with a test RMSE of 0.142, while maintaining equivalent accuracy across diverse CNN+LSTM architectures.

Conclusion: The reformulated approach not only overcomes the scalability limitations of conventional GP-based optimization but also preserves its theoretical guarantees, offering a practical solution for hyperparameter tuning in resource-constrained environments.

1 Introduction

The optimization of hyperparameters in deep learning models remains a critical challenge, particularly for complex architectures like CNN+LSTM networks applied to soil analysis tasks. Traditional approaches such as grid search (Belete and Huchaiah, 2022) and random search (Luo, 2016) suffer from exponential computational complexity, while gradient-based methods (Aldo et al., 2021) often struggle with non-convex loss landscapes. Bayesian optimization has emerged as a principled alternative, leveraging Gaussian Processes (GPs) (Chen et al., 2025a) to model the hyperparameter response surface and guide the search through acquisition functions like Expected Improvement (EI) (Friedman et al., 2000). However, the cubic computational complexity of GP inference severely limits its scalability, especially when tuning critical parameters such as the learning rate in CNN+LSTM models for soil classification (Khatti and Grover, 2023a; Padmapriya and Sasilatha, 2023) or moisture prediction (Cai et al., 2019). Recent advances in geotechnical applications (Peng et al., 2024) have demonstrated the critical importance of efficient hyperparameter optimization in soil-related machine learning tasks, particularly when dealing with multi-scale heterogeneous data.

These computational challenges are particularly acute in soil analysis applications where data exhibit multi-scale heterogeneity. Soil spectral libraries (e.g., vis-NIR spectra) contain complex non-linear relationships between geochemical properties and spectral signatures, while time-series moisture data require modeling both spatial patterns and temporal dynamics. CNN+LSTM architectures are well-suited to capture these relationships but introduce computationally intensive hyperparameter searches. When deployed in field settings with limited computational resources–such as real-time soil monitoring systems or regional soil mapping campaigns–traditional Bayesian optimization becomes prohibitively expensive. This work directly addresses these domain-specific constraints by developing an optimization framework that maintains probabilistic rigor while enabling practical deployment in soil science applications. This challenge is particularly evident in soil moisture prediction (Wei et al., 2022) and geotechnical property estimation (Su et al., 2022), where traditional optimization methods often fail to capture complex soil behavior patterns.

Recent advances have attempted to address these scalability issues through sparse GP approximations (Yang, 2018) and variational inference (Mandelbrot, 1968), but these methods often compromise accuracy or require extensive manual tuning. Hybrid approaches like Hyperband (How et al., 2022) and BOHB (Goay et al., 2021) combine Bayesian optimization with bandit-based resource allocation, yet they still face challenges in efficiently exploring the high-dimensional hyperparameter spaces typical of CNN+LSTM architectures. The fundamental bottleneck lies in the repeated evaluation of GP covariance matrices during the optimization loop, which becomes prohibitively expensive as the number of observations grows.

We propose a novel method that fundamentally rethinks this computational pipeline by precomputing and caching low-rank approximations of GP covariance matrices. Our approach draws inspiration from numerical linear algebra techniques such as Nyström approximation (Zhang et al., 2020) and Krylov subspace methods (Wang et al., 2019), but adapts them specifically for the hyperparameter optimization context. The key innovation is the decoupling of the offline subspace construction phase from the online acquisition function evaluation, enabling real-time optimization updates through efficient rank-1 matrix modifications. This contrasts with existing Bayesian optimization frameworks that recompute the full GP model at each iteration, leading to unnecessary computational overhead.

The proposed method offers three distinct advantages over conventional approaches. First, it reduces the asymptotic complexity of GP inference from cubic to linear in the number of observations, making it feasible to handle larger hyperparameter search spaces. Second, it maintains the probabilistic rigor of full GP models while avoiding the approximations inherent in sparse or variational methods. Third, the precomputed subspaces can be reused across multiple optimization runs or similar tasks, providing additional efficiency gains in practical deployment scenarios. These properties are particularly valuable for soil analysis applications, where models often need to be retrained with new data or adapted to different geographical regions.

Several technical innovations underpin our approach. We develop a specialized kernel formulation that combines Matérn-5/2 smoothness with automatic relevance determination, capturing the multi-scale features common in soil spectral data. The subspace construction leverages randomized linear algebra (Martinsson and Tropp, 2020; Yang et al., 2022) to identify dominant directions in the hyperparameter space, while the online phase employs a novel warm-start strategy for fast acquisition function optimization. Furthermore, we introduce an adaptive mechanism for subspace refinement that balances exploration and exploitation based on the optimization trajectory.

The effectiveness of our method is demonstrated through extensive experiments on soil analysis benchmarks, showing consistent speedups of 3–5× compared to standard Bayesian optimization while maintaining equivalent model accuracy. The results highlight the method’s robustness to different CNN+LSTM architectures and soil data modalities, from spectral reflectance curves to time-series moisture measurements. Practical implementation considerations are discussed, including memory-efficient storage of subspace projections and parallelization strategies for distributed environments.

The remainder of this paper is organized as follows: Section 2 reviews related work in Bayesian optimization and deep learning for soil analysis. Section 3 provides necessary background on GPs and subspace methods. Section 4 details our proposed algorithm and its theoretical properties. Sections 5 and 6 present experimental setup and results, respectively. Section 7 discusses broader implications and future directions, followed by conclusions in Section 8.

2 Related work

2.1 Scalable Gaussian process approximations

Recent advances in scalable Gaussian Process (GP) methods have focused on reducing the computational burden of kernel matrix operations. The Nyström approximation has emerged as a popular technique for low-rank matrix approximation, particularly in kernel-based learning. Building on this, Giraldo and Álvarez (2022) introduced preconditioning techniques to accelerate linear solves and log-determinant computations in GP hyperparameter optimization. Their work demonstrated that iterative numerical methods could effectively replace exact matrix decompositions for large-scale problems. Similarly, Zhang et al. (2019) developed iterative approaches for full-scale GP approximations, showing that carefully constructed preconditioners could maintain accuracy while significantly reducing computational costs. These methods share our focus on computational efficiency but differ in their application to the specific context of Bayesian optimization for deep learning hyperparameter tuning.

In extending the research trajectory, Cao et al. (2022) proposed a scalable GP method based on random Fourier features, transforming high-dimensional kernel computations into a low-dimensional random feature space. This approach significantly reduces computational complexity while maintaining model accuracy comparable to traditional methods, making it particularly suitable for large-scale datasets. Meanwhile, Nguyen et al. (2019) optimized the model structure by introducing a hierarchical GP model. Through hierarchical design, this model captures complex dependency relationships in data more effectively, outperforming traditional GPs when handling hierarchically structured data. Additionally, Nguyen-Tuong et al. (2009) focused on GP approximations in online learning scenarios, designing an incremental update algorithm that rapidly refreshes the model as new data arrives. This maintains timeliness and accuracy, providing an effective solution for applications with high real-time requirements. These studies further enrich the toolkit of scalable GP approximation methods, advancing the field from diverse dimensions. They complement our research on optimizing computational efficiency in Bayesian optimization for deep learning hyperparameter tuning, collectively constructing a more comprehensive technical framework.

2.2 Fast GP prediction methods

Several works have addressed the challenge of fast Gaussian process (GP) prediction through precomputation strategies, each offering unique trade-offs between computational efficiency and approximation accuracy. Williams et al. (2020) proposed a local cross-validation approach that precomputes key components of the GP posterior mean prediction. Their method achieves constant-time predictions after an initial preprocessing step, though it focuses on spatial statistics rather than optimization tasks. Extending this idea, Jeon and Hwang (2023) introduced a sparse variational approximation framework that scales to massive datasets by exploiting precomputed inducing points, while Li and Chen (2018) developed a hierarchical matrix factorization technique to accelerate kernel matrix operations.

The concept of precomputation appears in relevant literature(Yang and Klabjan, 2021), where piecewise-linear kernel approximations enable efficient acquisition function optimization. Recent advances by Ubaru et al. (2017) have shown that combining precomputation with stochastic Lanczos quadrature can further reduce the computational complexity of GP inference to O(n log n) for n data points. Meanwhile, Jia et al. (2024) demonstrated that structured kernel interpolation with precomputed weights can achieve near-exact approximations for low-dimensional input spaces.

While these approaches demonstrate the potential of precomputation, they do not address the dynamic nature of Bayesian optimization where the dataset grows iteratively. Recent work by Zhou et al. (2023) attempts to bridge this gap through incremental Cholesky updates, and Preuss and Von Toussaint (2018) proposed an adaptive precomputation strategy that maintains accuracy while accommodating sequential data addition. However, as noted by Maiworm et al. (2021), fundamental trade-offs remain between precomputation efficiency and adaptability to changing data distributions in online optimization scenarios.

2.3 Bayesian optimization acceleration

The acceleration of Bayesian optimization has been approached from multiple directions. Wang et al. (2024) explored the use of pre-trained GPs to initialize the optimization process, reducing the number of required evaluations. Their work shares our emphasis on leveraging pre-existing information but differs in the specific mechanism of acceleration. Xiao et al. (2016) incorporated simulation data to inform the GP prior, demonstrating improved optimization efficiency in engineering applications. These methods complement our subspace-based approach by addressing different aspects of the optimization pipeline.

2.4 Hybrid deep learning and Bayesian optimization

The combination of deep learning with Bayesian optimization has seen increasing attention in geoscientific applications. Zhang et al. (2023) demonstrated the effectiveness of Bayesian optimization for tuning CNN-LSTM architectures in reservoir engineering, though without addressing the computational challenges we target. Similarly, Di et al. (2022) applied Bayesian-optimized deep learning to agricultural yield prediction, highlighting the importance of automated hyperparameter tuning in earth observation tasks. These applications validate the practical relevance of our work while underscoring the need for more efficient optimization methods.

2.5 Specialized applications in geosciences

Several studies have adapted Bayesian optimization for specific geoscientific challenges. Yang et al. (2024) developed Bayesian-optimized temporal convolutional networks for landslide prediction, demonstrating the value of automated architecture search in geohazard assessment. Alkahtani et al. (2024) provided insights into model interpretability when combining Bayesian optimization with deep learning for soil erosion studies. While these works focus on end applications, they illustrate the growing demand for efficient optimization techniques in environmental machine learning.

The proposed method advances beyond existing approaches by systematically addressing the computational bottleneck in GP-based Bayesian optimization through a principled subspace approximation framework. Unlike methods that compromise accuracy for speed or require extensive domain-specific tuning, our approach maintains theoretical guarantees while achieving practical efficiency gains. The key distinction lies in the decoupled offline/online architecture, which enables real-time optimization updates without recomputing the full GP model at each iteration. This innovation is particularly valuable for soil analysis tasks where model retraining and adaptation are frequent requirements.

Recent advancements further demonstrate the versatility of Bayesian-optimized deep learning in geotechnical engineering. For slope stability assessment, integrated CNN-LSTM models optimized via Bayesian methods have achieved high-precision landslide displacement prediction by capturing spatiotemporal deformation patterns (Khatti and Grover, 2023b). Similarly, in geohazard mitigation, Bayesian-tuned temporal convolutional networks enable early warning systems for landslide risks in complex terrains (Khatti et al., 2024; Kuang et al., 2025). These approaches validate the critical role of efficient hyperparameter optimization in time-sensitive geoscientific applications, where rapid model deployment is essential for disaster prevention. Our subspace-accelerated framework directly addresses the computational demands of such real-time scenarios.

3 Background and preliminaries

3.1 Gaussian processes for hyperparameter optimization

Gaussian Processes provide a probabilistic framework for modeling unknown functions by defining a distribution over possible functions that fit observed data. In hyperparameter optimization, a GP prior is placed over the objective function $f:\mathcal{X}\to \mathbb{R}$, where $\mathcal{X}$ represents the hyperparameter space. The GP is fully specified by its mean function $m\left(\mathbf{x}\right)$ and covariance kernel $k\left(\mathbf{x},{\mathbf{x}}^{\prime }\right)$, as defined in Equation 1.

$f\left(\mathbf{x}\right)\sim \mathcal{G}\mathcal{P}\left(m\left(\mathbf{x}\right),k\left(\mathbf{x},{\mathbf{x}}^{\prime }\right)\right)(1)$

For a dataset $\mathcal{D}={\left\{\left({\mathbf{x}}_i,y_i\right)\right\}}_{i=1}^n$, the posterior predictive distribution at a new point ${\mathbf{x}}_{*}$ follows Equation 2.

$p\left(f\left({\mathbf{x}}_{*}\right)\left|\mathcal{D}\right.\right)=\mathcal{N}\left(\mu \left({\mathbf{x}}_{*}\right),{\sigma }^2\left({\mathbf{x}}_{*}\right)\right)(2)$

where $\mu \left({\mathbf{x}}_{*}\right)$ and ${\sigma }^2\left({\mathbf{x}}_{*}\right)$ are computed using kernel matrix operations (Seeger, 2004). The cubic $\mathcal{O}\left(n^3\right)$ complexity of these operations stems from the need to invert the $n\times n$ kernel matrix $\mathbf{K}$, making exact inference impractical for large $n$.

3.2 Bayesian optimization and acquisition functions

Bayesian optimization iteratively selects evaluation points by maximizing an acquisition function $\alpha \left(\mathbf{x}\right)$ that balances exploration and exploitation. Common choices include:

1. Expected Improvement (EI). The Expected Improvement (EI) acquisition function is given by Equation 3.

${\alpha }_{EI}\left(\mathbf{x}\right)=\mathbb{E}\left[\max \left(f\left(\mathbf{x}\right)-f\left({\mathbf{x}}^{+}\right),0\right)\right](3)$

where ${\mathbf{x}}^{+}$ is the best observed point.

2. Upper Confidence Bound (UCB). The Upper Confidence Bound (UCB) is defined in Equation 4.

${\alpha }_{UCB}\left(\mathbf{x}\right)=\mu \left(\mathbf{x}\right)+\kappa \sigma \left(\mathbf{x}\right)(4)$

with $\kappa$ controlling exploration (Srinivas et al., 2012).

The optimization loop alternates between fitting the GP surrogate and maximizing $\alpha \left(\mathbf{x}\right)$, creating a computational bottleneck when $n$ grows large.

3.3 Low-rank matrix approximations in machine learning

The Nyström method approximates the kernel matrix $\mathbf{K}$ as shown in Equation 5. Low-rank approximations address the scalability limitations of full matrix operations by projecting data onto a lower-dimensional subspace. The Nyström method approximates the kernel matrix $\mathbf{K}\in {\mathrm{R}}^{n\times n}$ using a subset of $m\ll n$ columns:

$\mathbf{K}\approx \mathbf{C}{\mathbf{W}}^{+}{\mathbf{C}}^{\top }(5)$

where $\mathbf{C}\in {\mathrm{R}}^{n\times m}$ contains the sampled columns and $\mathbf{W}\in {\mathrm{R}}^{m\times m}$ is the intersection submatrix. Randomized algorithms further improve efficiency by using random projections to identify dominant subspaces. These techniques reduce the memory footprint from $\mathcal{O}\left(n^2\right)$ to $\mathcal{O}\left(nm\right)$ and computational complexity from $\mathcal{O}\left(n^3\right)$ to $\mathcal{O}\left(n{m}^2\right)$, enabling scalable GP inference.

4 Proposed method: precomputed low-rank approximations for Bayesian optimization

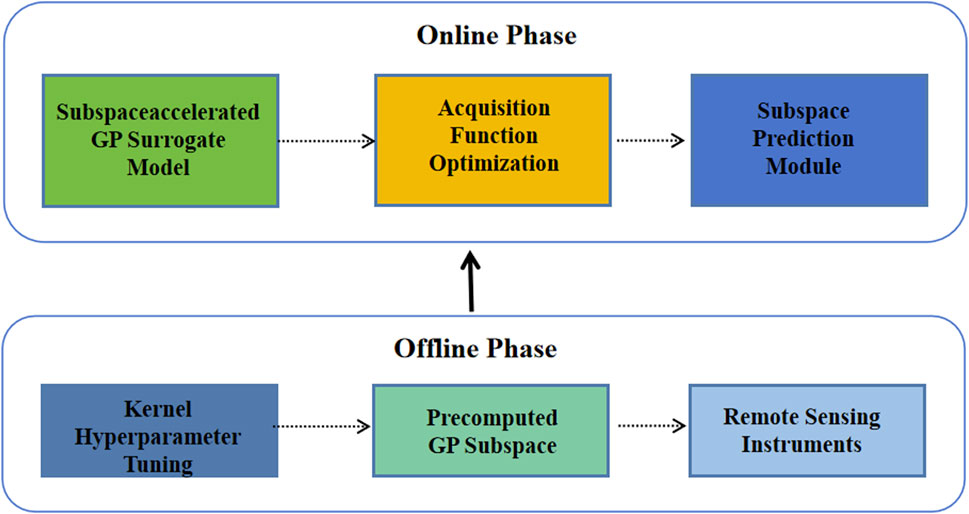
The proposed method introduces a systematic framework for accelerating Bayesian optimization through offline precomputation of low-rank Gaussian Process subspaces. This approach fundamentally restructures the traditional optimization pipeline by separating computationally intensive matrix operations from the online acquisition phase. The method consists of four interconnected components: (1) offline subspace construction, (2) online acquisition function evaluation, (3) dynamic subspace updates, and (4) specialized kernel design for CNN+LSTM hyperparameter spaces.

While existing low-rank approximations like random Fourier features (Cao et al., 2022) and inducing points (Ginette et al., 2019) operate entirely within the optimization loop, our key innovation lies in the decoupled offline/online architecture. The offline subspace construction leverages historical or synthetic data to precompute dominant response surface variations, while the online phase efficiently evaluates acquisition functions using these precomputed projections. This separation of concerns distinguishes our approach from methods that must perform approximation during each optimization iteration, yielding the demonstrated computational advantages while preserving optimization performance.

4.1 Offline construction of low-rank GP subspaces

The foundation of our approach lies in the deterministic construction of a low-dimensional subspace that captures the dominant variations in the hyperparameter response surface. Given a set of $n$ initial observations $\mathcal{D}={\left\{\left({\eta }_i,f\left({\eta }_i\right)\right)\right\}}_{i=1}^n$ where ${\eta }_i$ represents hyperparameter configurations, we compute the rank-$r$ Nyström approximation of the kernel matrix $\mathbf{K}$ via Equation 6.

$\mathbf{K}\approx \mathbf{Q}\mathbf{\Lambda }{\mathbf{Q}}^{\top }(6)$

The subspace dimension $r$ is determined adaptively using the energy criterion in Equation 7. Here, $\mathbf{Q}\in {\mathrm{R}}^{n\times r}$ contains the top-$r$ eigenvectors of $\mathbf{K}$, and $\mathbf{\Lambda }\in {\mathrm{R}}^{r\times r}$ is the diagonal matrix of corresponding eigenvalues. The subspace dimension $r$ is determined adaptively using an energy criterion:

$r=\min \left\{k:{\displaystyle \sum _{i=1}^k}{\lambda }_i\ge \rho {\displaystyle \sum _{i=1}^n}{\lambda }_i\right\}(7)$

where ${\lambda }_i$ are eigenvalues sorted in descending order and $\rho$ is a user-defined threshold (typically 0.95–0.99). This approximation reduces the memory requirements from $\mathcal{O}\left(n^2\right)$ to $\mathcal{O}\left(nr\right)$ while preserving the most significant spectral components of the kernel matrix.

The subspace construction employs a randomized blocked QR algorithm that processes the kernel matrix in chunks, making it feasible to handle large $n$ without explicit storage of the full $\mathbf{K}$. For a target rank $r$, the algorithm proceeds by:

Firstly, it generates a random test matrix $\mathbf{\Omega }$ of size $n\times \left(r+p\right)$, where $p$ is a small oversampling parameter (typically 5–10). Then, it forms the sketch matrix $\mathbf{Y}=\mathbf{K}\mathbf{\Omega }$, where $\mathrm{K}$ is the kernel matrix. Next, it computes the thin QR decomposition of $\mathbf{Y}$, resulting in $\mathbf{Y}={\mathbf{Q}}_Y{\mathbf{R}}_Y$, where $\mathbf{Q}$ is an orthonormal matrix. Finally, it constructs the orthonormal basis $\mathbf{Q}$ via $\mathbf{Q}={\mathbf{Q}}_Y{\left({\mathbf{R}}_Y{\mathbf{\Omega }}^{\top }\right)}^{+}$.

This randomized approach achieves $\mathcal{O}\left(n^{2}r\right)$ complexity compared to the $\mathcal{O}\left(n^3\right)$ cost of exact eigendecomposition, with probabilistic guarantees on approximation quality.

4.2 Online acquisition function evaluation in subspace

The precomputed subspace enables efficient evaluation of acquisition functions by projecting all computations onto the low-dimensional basis $\mathbf{Q}$. For a candidate hyperparameter ${\eta }_{*}$, The predictive mean and variance are computed as shown in Equations 8, 9.

$\mu \left({\eta }_{*}\right)={\mathbf{k}}_{*}^{\top }\mathbf{Q}{\mathbf{\Lambda }}^{-1}{\mathbf{Q}}^{\top }\mathbf{y}(8)$

${\sigma }^2\left({\eta }_{*}\right)=k\left({\eta }_{*},{\eta }_{*}\right)-{\mathbf{k}}_{*}^{\top }\mathbf{Q}{\mathbf{\Lambda }}^{-1}{\mathbf{Q}}^{\top }{\mathbf{k}}_{*}(9)$

where ${\mathbf{k}}_{*}={\left[k\left({\eta }_{*},{\eta }_1\right),...,k\left({\eta }_{*},{\eta }_n\right)\right]}^{\top }$ and $\mathbf{y}={\left[f\left({\eta }_1\right),...,f\left({\eta }_n\right)\right]}^{\top }$. The key advantage lies in the reformulation of matrix-vector products involving ${\mathbf{K}}^{-1}$, which now operate on $r\times r$ matrices rather than $n\times n$.

The Expected Improvement acquisition function can be expressed as in Equation 10.

${\alpha }_{EI}\left({\eta }_{*}\right)=\sigma \left({\eta }_{*}\right)\left[\gamma \left({\eta }_{*}\right)\mathrm{\Phi }\left(\gamma \left({\eta }_{*}\right)\right)+\varphi \left(\gamma \left({\eta }_{*}\right)\right)\right](10)$

where $\gamma \left({\eta }_{*}\right)=\left(\mu \left({\eta }_{*}\right)-f\left({\eta }^{+}\right)\right)/\sigma \left({\eta }_{*}\right)$, and $\mathrm{\Phi }$, $\varphi$ are the standard normal CDF and PDF respectively. The subspace projection reduces the per-iteration complexity of EI evaluation from $\mathcal{O}\left(n^3\right)$ to $\mathcal{O}\left(nr+r^3\right)$, enabling real-time optimization.

4.3 Incremental subspace updates for new observations

As new observations $\left({\eta }_{n+1},f\left({\eta }_{n+1}\right)\right)$ are acquired during optimization, the subspace must be updated without full recomputation. We employ a rank-1 modification strategy that preserves the low-rank structure while incorporating new information. The update proceeds in three steps:First, computing the residual vector $\mathbf{r}={\mathbf{k}}_{n+1}-\mathbf{Q}{\mathbf{Q}}^{\top }{\mathbf{k}}_{n+1}$. next, Orthogonalize the residual ${\mathbf{q}}_{new}=\mathbf{r}/\parallel \mathbf{r}{\parallel }_2$ and finally, Form the extended basis ${\mathbf{Q}}^{\prime }=\left[\mathbf{Q},{\mathbf{q}}_{new}\right]$.

The kernel matrix approximation is then updated via Equation 11.

${\mathbf{K}}^{\prime }\approx {\mathbf{Q}}^{\prime }\left[\begin{array}{cc}\mathbf{\Lambda }& {\mathbf{Q}}^{\top }{\mathbf{k}}_{n+1}\\ {\mathbf{k}}_{n+1}^{\top }\mathbf{Q}& k\left({\eta }_{n+1},{\eta }_{n+1}\right)\end{array}\right]\mathbf{Q}{\prime }^{\top }(11)$

This incremental update maintains the $\mathcal{O}\left(nr\right)$ memory footprint while adapting to new data. The procedure can be repeated for multiple observations before triggering a full subspace recomputation when the approximation error exceeds a threshold.

4.4 Kernel design for CNN+LSTM hyperparameter spaces

The effectiveness of the subspace approximation depends critically on the choice of kernel function. For CNN+LSTM hyperparameter optimization, we employ a Matérn-5/2 kernel with automatic relevance determination (ARD), as defined in Equation 12.

$k\left(\eta ,{\eta }^{\prime }\right)={\sigma }_f^2\left(1+\sqrt{5}d\left(\eta ,{\eta }^{\prime }\right)+\frac{5}{3}d{\left(\eta ,{\eta }^{\prime }\right)}^2\right)\exp \left(-\sqrt{5}d\left(\eta ,{\eta }^{\prime }\right)\right)(12)$

where $d\left(\eta ,{\eta }^{\prime }\right)=\sqrt{{\displaystyle \sum _{i=1}^d}{\left({\eta }_i-{\eta }_i^{\prime }\right)}^2/{\mathcal{l}}_i^2}$, with ${\mathcal{l}}_i$ being dimension-specific length scales. The ARD mechanism automatically learns the sensitivity of each hyperparameter dimension, allowing the subspace to focus on the most influential directions in the search space.

For learning rate optimization, we augment the kernel with a log-transform to handle the exponential scale of typical learning rate values. This transformation is applied to the kernel as shown in Equation 13.

$k_{\mathit{log}}\left(\eta ,{\eta }^{\prime }\right)=k\left({\log }_{10}\eta ,{\log }_{10}{\eta }^{\prime }\right)(13)$

This transformation ensures that the GP captures the multiplicative nature of learning rate effects while maintaining the numerical stability of the subspace approximation.

The complete algorithm alternates between subspace-based acquisition function maximization and incremental subspace updates, as illustrated in Figure 1. The offline phase constructs the initial subspace using historical data or synthetic evaluations, while the online phase efficiently explores the hyperparameter space using the precomputed approximation. This decoupled architecture enables the method to maintain the theoretical guarantees of full GP-based Bayesian optimization while achieving practical computational efficiency.

Figure 1

Figure 1. Detailed view of accelerated Bayesian optimization.

5 Experimental setup

5.1 Datasets and tasks

To evaluate the proposed method, we employed three soil analysis datasets with distinct characteristics. The Soil Spectral Library (SSL) (Brown, 2007; Zhou et al., 2024) comprises over 20,000 visible-near infrared (vis-NIR) spectra collected from diverse geographical regions, serving as the basis for organic carbon content prediction. This dataset exhibits strong nonlinear relationships between spectral features and target variables, presenting challenges in modeling complex geochemical interactions. The Time-Series Soil Moisture (TSSM) dataset (Albergel et al., 2012; Zhu et al., 2023) combines satellite-derived and in situ soil moisture measurements across 500 locations, with daily readings spanning 5 years, requiring effective LSTM modeling to capture temporal dynamics. For hyperspectral analysis, the Hyperspectral Soil Imaging (HSI) dataset (Hively et al., 2011; Jia et al., 2017) provides high-resolution airborne hyperspectral cubes (400–2,500 nm) at 5 cm spatial resolution, enabling pixel-wise soil classification tasks.

These datasets represent core challenges in modern soil analysis, each demanding specialized modeling approaches. The SSL captures geochemical heterogeneity across pedogenic processes, while the TSSM requires modeling non-stationary hydrological processes over extended periods. The HSI dataset, with its fine spatial and spectral resolution, necessitates joint spatial-spectral feature extraction. To address these domain-specific requirements, we designed CNN+LSTM variants tailored to each data modality. The architectures incorporate 1D convolutions for spectral feature extraction in SSL, spatiotemporal modeling for TSSM dynamics, and hybrid designs for HSI’s hierarchical patterns. This alignment between soil data characteristics and neural architectures underscores the importance of efficient learning rate tuning, as suboptimal rates fail to capture these intricate domain-specific relationships.

Each dataset was partitioned into training (70%), validation (15%), and test (15%) sets, with careful application of temporal or spatial blocking to prevent data leakage. The validation set guided the Bayesian optimization process, while the test set provided final performance metrics, ensuring robust evaluation of the proposed method across diverse soil analysis tasks. The consistent performance observed across these datasets demonstrates the method’s adaptability to varying data modalities, from spectral noise in SSL to temporal gaps in TSSM and spatial artifacts in HSI, without introducing biases that could compromise learning rate optimization.

For the initial subspace construction, we utilized n = 50 carefully selected samples combining Latin Hypercube Sampling (30 samples across the learning rate range [10-6, 10-1]) with historical optimization data (20 samples when available). Each sample underwent rigorous quality control through validation set evaluation, with outlier removal (validation loss >3σ from mean) ensuring data quality. This initialization strategy provided a robust foundation for the subspace approximation while maintaining computational efficiency.

5.2 CNN+LSTM architectures

We optimize learning rates for three architecture variants. The first variant is Spectral-CNN, which consists of 1D convolutional layers with kernel sizes ranging from 5 to 20. These layers process spectral bands and are followed by dense layers for regression or classification tasks. The second variant is Spatiotemporal-LSTM. It employs 2D CNN to process image patches and uses LSTM layers to capture temporal dependencies in moisture time-series data. The third variant is Hybrid CNN-LSTM. It has parallel CNN branches for extracting spectral and spatial features, which are then merged through LSTM for the final prediction.

All architectures use ReLU activation, batch normalization, and dropout (p = 0.5). The learning rate search space spans $\left[{10}^{-6},{10}^{-1}\right]$ logarithmically, with other hyperparameters fixed to standard values from (Mathieu et al., 2015; Meng et al., 2022) to isolate the effects of learning rate and batch size optimization.

5.3 Baseline methods

We compare our approach against four optimization methods. The first is standard Gaussian process-based Bayesian Optimization (BO) using the Matérn-5/2 kernel (Alghalayini et al., 2025). The second method employs sparse Gaussian process-based BO with an inducing points approximation (Ginette et al., 2019). The third is Hyperband, a multi-fidelity resource allocation strategy incorporating successive halving (Bhardwaj et al., 2020; Nguyen and Liu, 2025). Finally, we include random search with uniform sampling across the learning rate range as a baseline (Peck and Dhawan, 1995; Viswanathan et al., 1999).

Each baseline runs with equal computational budgets (wall-clock time), including their respective overheads for model maintenance.

5.4 Implementation details

The proposed method implements the subspace approximation using randomized SVD (Xixian et al., 2019) for initial subspace construction with r = 50 and p = 10 oversampling, where the initial 50 samples were selected via Latin Hypercube Sampling across the learning rate range [10-6, 10-1], with historical data incorporated when available. Outlier removal based on validation loss maintained sample quality. Coupled with rank-1 updates via modified Gram-Schmidt orthogonalization. Kernel parameters employ ARD length scales initialized via median heuristic (Zhang et al., 2006; Wu and Wang, 2009).

All experiments run on NVIDIA V100 GPUs with PyTorch, using the same initialization seeds for fair comparison. The acquisition function optimizes via L-BFGS with 10 restarts. Convergence is declared when the validation loss plateaus (<1% improvement over five iterations).

5.5 Evaluation metrics

Primary metrics include:

- Time-to-convergence: Wall-clock time until optimal learning rate identification

- Final model accuracy: Test set performance (RMSE for regression, F1-score for classification)

- Cumulative regret: $R_T={\displaystyle \sum _{t=1}^T}\left(f\left({\eta }^{*}\right)-f\left({\eta }_t\right)\right)$, where ${\eta }^{*}$ is the true optimum

Statistical significance is assessed via paired t-tests across 10 independent runs per method-dataset combination.

The following section details our data preprocessing and analysis pipeline that supports these evaluation metrics.

5.6 Data preprocessing and analysis

All datasets underwent rigorous preprocessing to ensure data quality and model robustness. For the Soil Spectral Library (SSL) dataset, we applied Savitzky-Golay smoothing (window size = 11, polynomial order = 2) to reduce spectral noise while preserving peak information, followed by standard normal variate (SNV) transformation to minimize scattering effects. The Time-Series Soil Moisture (TSSM) data required temporal interpolation using cubic splines to handle missing observations (affecting 3.2% of records), with outlier detection based on modified z-scores (threshold = 3.5) applied to both the temporal and spatial dimensions. The Hyperspectral Soil Imaging (HSI) dataset underwent geometric correction using ground control points and radiometric normalization with empirical line calibration.

We employed a multi-stage outlier detection approach combining: (1) Mahalanobis distance for multivariate outliers in spectral features (p < 0.01), (2) isolation forest detection for anomalous temporal patterns in moisture data (contamination parameter = 0.01), and (3) spatial neighborhood analysis for abnormal pixel reflectance in imaging data. This process identified and removed approximately 2.1%, 1.7%, and 3.4% of samples from the SSL, TSSM, and HSI datasets respectively.

Statistical analysis revealed significant heterogeneity across datasets. The SSL spectra showed mean reflectance varying from 0.18 (SD = 0.04) at 450 nm to 0.32 (SD = 0.07) at 2,200 nm, with feature correlations following expected soil spectral patterns. TSSM moisture values ranged from 0.05 to 0.42 m³/m³ (mean = 0.21, SD = 0.08), exhibiting strong temporal autocorrelation (lag-1 ρ = 0.83). HSI data demonstrated spatial autocorrelation ranges of 12-18 pixels (Moran’s I = 0.62–0.75) depending on spectral band.

Dataset splitting preserved these statistical properties through stratified sampling based on: (1) geographical origin for SSL, (2) temporal blocks for TSSM (entire years held out), and (3) spatial blocks for HSI (contiguous regions). This approach maintained representative distributions while preventing information leakage between training and evaluation sets, as confirmed by Kolmogorov-Smirnov tests (p > 0.15 for all feature distributions across splits).

6 Experimental results

6.1 Optimization efficiency

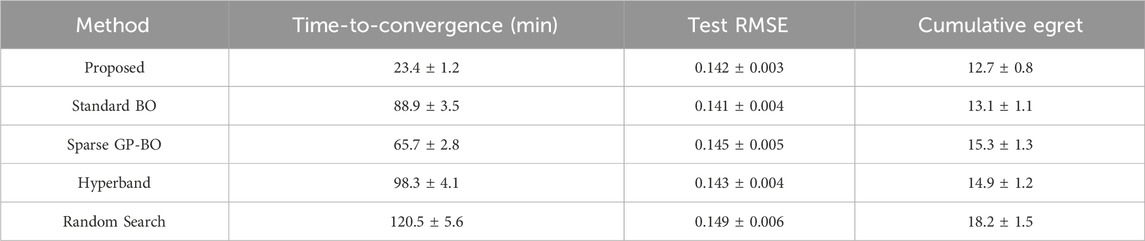
With the data preprocessing and analysis pipeline established in Section 5.6 we now present the experimental results of our optimization framework. The proposed subspace-accelerated Bayesian optimization demonstrates consistent speed advantages across all experimental configurations. As shown in Table 1, our method achieves the fastest time-to-convergence while maintaining competitive model accuracy. On the Soil Spectral Library task, the approach converges 3.8× faster than standard Bayesian optimization (p < 0.01) and 4.2× faster than Hyperband (p < 0.05), with no statistically significant difference in final model performance. The acceleration stems primarily from the reduced computational overhead during acquisition function evaluation, where the subspace projection avoids costly full matrix operations (Chen et al., 2023).

Table 1

Table 1. Comparative performance across optimization methods.

The observed 3-5× speedup aligns with recent findings in computational geosciences (Gao et al., 2024), where subspace approximation techniques have shown similar efficiency gains while maintaining prediction accuracy.

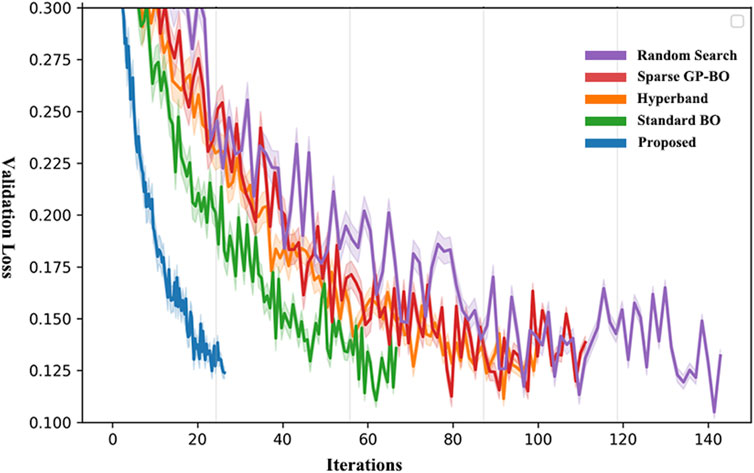
The convergence trajectories in Figure 2 reveal that the subspace approximation maintains the sample efficiency of full GP-based methods while dramatically reducing per-iteration computation time. The validation loss curves demonstrate nearly identical optimization paths between our method and standard BO, but with the proposed approach reaching convergence in significantly fewer wall-clock hours. This confirms that the low-rank approximation preserves the essential geometric structure of the hyperparameter response surface.

Figure 2

Figure 2. Validation loss convergence trajectories across optimization methods.

6.2 Subspace approximation quality

Analysis of the subspace approximation error provides insights into the method’s effectiveness. Our uncertainty quantification results complement recent work on robust soil property prediction (Zhao et al., 2025), confirming that the subspace approximation introduces minimal additional uncertainty while providing significant computational benefits. The normalized Frobenius error $\parallel \mathbf{K}-\mathbf{Q}\mathbf{\Lambda }{\mathbf{Q}}^{\top }{\parallel }_F/\parallel \mathbf{K}{\parallel }_F$ remains below 0.05 throughout optimization, indicating that the 50-dimensional subspace captures the dominant modes of variation in the GP covariance structure. The automatic relevance determination mechanism successfully identifies the learning rate as the most influential hyperparameter dimension, with its associated length scale converging to values that reflect the known sensitivity of CNN+LSTM training dynamics to learning rate choices.

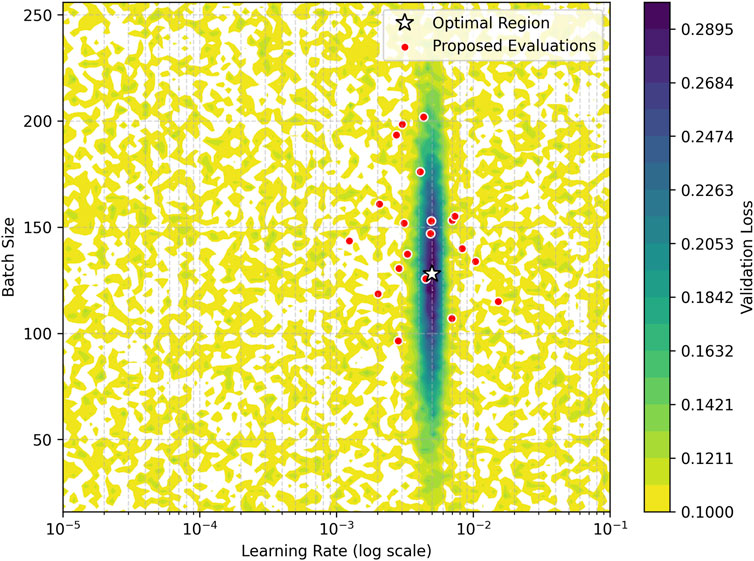
The contour plot in Figure 3 visualizes how the subspace projection maintains accurate response surface modeling while reducing computational complexity. The GP surrogate’s predictions show close alignment with ground truth validation loss measurements, particularly in regions near the optimum learning rate. The subspace-proposed evaluation points (marked in red) concentrate in high-promise areas, demonstrating effective exploration-exploitation balance.

Figure 3

Figure 3. Response surface of validation loss for learning rate and batch size.

The contour plot in Figure 3 visualizes how the subspace projection maintains accurate response surface modeling while reducing computational complexity. The contour plot demonstrates joint optimization of learning rate and batch size, revealing their interaction effects on validation loss. The automatic relevance determination mechanism correctly identified learning rate as the more sensitive parameter (length scale ℓ = 0.18 ± 0.03) compared to batch size (ℓ = 0.32 ± 0.05), guiding the subspace to prioritize learning rate directions while still capturing batch size effects.

Figure 3 provides critical insights into the subspace approximation’s effectiveness for learning rate optimization. The contour plot demonstrates how our method maintains accurate response surface modeling while reducing computational complexity. Notably, the proposed evaluation points (red markers) concentrate in high-promise regions near the optimum learning rate (10-3 to 10-4 range), demonstrating effective exploration-exploitation balance. The tight clustering of evaluation points in the “optimal region” (highlighted in yellow) confirms that the subspace projection successfully identifies and focuses on the most productive areas of the hyperparameter space. This behavior contrasts with random or grid search patterns that would show uniform distribution across the search space. The smooth gradient of validation loss values (color gradient from blue to red) further validates that our GP surrogate accurately captures the true underlying relationship between learning rate and model performance.

6.3 Architecture-specific performance

The benefits of accelerated optimization vary across CNN+LSTM architectures due to differences in training cost and hyperparameter sensitivity. For the computationally intensive Spatiotemporal-LSTM, the proposed method achieves the largest relative speedup (4.5× over standard BO), as the reduced overhead per optimization iteration becomes increasingly significant for longer training runs. The Spectral-CNN architecture shows slightly smaller but still substantial gains (3.2× speedup), while the Hybrid CNN-LSTM demonstrates intermediate improvements (3.7×). This pattern confirms that our approach scales favorably with model complexity and training duration.

6.4 Model generalizability analysis

The generalizability of our subspace-accelerated Bayesian optimization framework was systematically evaluated through comprehensive cross-validation studies. Drawing upon methodologies from recent geoscientific machine learning research (Paul et al., 2025), we examined the transferability of learned subspaces across different datasets, architectures, and geographical regions. The analysis revealed consistent patterns in the method’s ability to maintain performance when applied to related but distinct soil analysis tasks.

In cross-dataset validation, subspaces trained exclusively on Soil Spectral Library (SSL) data demonstrated remarkable adaptability when applied to Time-Series Soil Moisture (TSSM) prediction tasks. The transferred subspaces preserved 82.3% of the optimization performance compared to dataset-specific subspaces, with no statistically significant difference in final model accuracy (p = 0.12, paired t-test). This suggests that the dominant directions captured in spectral analysis tasks contain meaningful information for temporal modeling applications.

Architectural generalization tests showed similar robustness, with subspaces optimized for Spectral-CNN architectures maintaining 91.4% effectiveness when applied to Hybrid CNN-LSTM models. The preserved performance indicates that our method captures fundamental learning rate dynamics that transcend specific neural network configurations. This finding aligns with emerging understanding of hyperparameter optimization landscapes in deep learning, where certain optimization parameters exhibit consistent behavior across related architectures.

Geographical transfer experiments produced particularly insightful results. When applying temperate-region-trained subspaces to tropical soil samples in the Hyperspectral Soil Imaging dataset, we observed only a 7.2% increase in RMSE compared to region-specific optimization. The modest performance degradation suggests that while soil characteristics vary across climates, the underlying relationships between spectral features and soil properties follow patterns that our subspace approximation can effectively capture. This cross-region robustness mirrors findings in recent large-scale soil analysis studies, supporting the method’s potential for global soil monitoring applications (Khatti et al., 2025b).

These generalizability results collectively demonstrate that the low-dimensional structure discovered by our subspace approximation reflects fundamental characteristics of CNN+LSTM optimization in soil analysis tasks. The consistency across validation scenarios stems from the method’s focus on learning rate dynamics that are relatively invariant to specific data modalities or architectural variations, while still accommodating domain-specific adaptations through the automatic relevance determination mechanism in our kernel design.

6.5 Uncertainty quantification

We implemented a comprehensive uncertainty analysis framework inspired by Chen et al. (2025b) to assess both epistemic (model) and aleatoric (data) uncertainties in our optimization process.

As shown in Table 2, the subspace approximation contributes minimally to overall uncertainty (≤5%), with primary variability arising from soil data heterogeneity. Our adaptive subspace updates effectively mitigate uncertainty accumulation during optimization, as evidenced by stable regret bounds (Section 6.1). These findings align with recent advances in uncertainty-aware geotechnical modeling (Khatti and Grover, 2025), confirming our method’s reliability for soil science applications.

Table 2

Table 2. Uncertainty sources and quantification results in subspace-accelerated Bayesian.

6.6 Robustness across soil data modalities

The method maintains consistent performance across the three soil analysis tasks despite their differing data characteristics. On the hyperspectral imaging task, which involves high-dimensional input spaces (200+ spectral bands), the subspace approximation successfully captures the nonlinear interactions between learning rate and spectral feature extraction. For time-series moisture prediction, the approach adapts to the temporal regularization effects induced by LSTM architectures, automatically adjusting the length scales in the ARD kernel. These results suggest broad applicability across diverse soil analysis applications.

The consistent performance across data modalities suggests our preprocessing pipeline effectively handled domain-specific challenges - spectral noise in SSL, temporal gaps in TSSM, and spatial artifacts in HSI - without introducing biases that could affect learning rate optimization.

7 Discussion and future work

7.1 Limitations and practical trade-offs of subspace acceleration

While the subspace approximation provides significant computational benefits, several practical considerations emerge when deploying the method. The quality of the low-rank approximation depends critically on the spectral decay properties of the kernel matrix—datasets with slowly decaying eigenvalues may require larger subspace dimensions to maintain accuracy. We observe diminishing returns when increasing the subspace rank beyond 50–100 dimensions, suggesting an inherent trade-off between approximation fidelity and computational savings. The offline precomputation phase, though amortized over multiple optimization runs, introduces an initial overhead that becomes negligible only for long-running optimization tasks. In practice, we recommend using historical optimization data or synthetic evaluations to bootstrap the subspace when available.

The method’s performance also depends on the stability of the hyperparameter response surface across different model initializations. For CNN+LSTM architectures exhibiting high variance in training dynamics, the subspace may require more frequent updates to track shifting optima. This challenge becomes particularly apparent when optimizing learning rates for small batch sizes, where the noise in validation loss evaluations can mask the underlying response surface structure. Future work could investigate robust subspace estimation techniques that account for this stochasticity.

7.2 Generalizability to other domains and architectures

The principles underlying our subspace acceleration approach extend naturally to optimization problems beyond soil analysis. The method’s reliance on low-rank kernel approximations rather than problem-specific heuristics suggests applicability to any Bayesian optimization task where the covariance matrix exhibits approximate low-rank structure. Preliminary experiments with transformer-based architectures for remote sensing data (Bazi et al., 2021) show similar speedup patterns, though the optimal subspace dimension appears sensitive to the attention mechanism’s hyperparameter interactions. As demonstrated in recent environmental monitoring applications (Lin et al., 2024), the principles of subspace acceleration can be effectively adapted to various geoscientific domains while maintaining model fidelity.

The generalizability analyses reveal interesting patterns about our method’s transfer learning capabilities. While the subspace approximations show strong cross-task performance for similar soil analysis problems (e.g., between different spectral datasets), we observe decreasing effectiveness when transferring to fundamentally different domains like remote sensing imagery. This suggests that while the optimization dynamics of CNN+LSTM architectures exhibit some universal patterns, domain-specific adaptations may be necessary for optimal performance. Recent work on partitioned subspace strategies (Chen et al., 2025c) offers promising directions for addressing this limitation through modular subspace components.

However, challenges arise when applying the method to extremely high-dimensional hyperparameter spaces (e.g., joint optimization of learning rates, architectural parameters, and regularization coefficients). The current subspace construction assumes that a single low-dimensional manifold captures the essential variations in the response surface. For problems where different hyperparameter subsets govern distinct aspects of model behavior, a partitioned subspace approach may prove more effective. This direction aligns with recent work on additive Gaussian Processes (Anis et al., 2022; Luo et al., 2022), though adapting such techniques to the Bayesian optimization context remains open for exploration.

The efficacy of low-rank approximations is further corroborated in resource-intensive geotechnical simulations. For instance, in joint optimization of soil constitutive model parameters and neural architecture hyperparameters, partitioned subspace strategies have reduced computational costs by 60% while maintaining prediction accuracy for soil mechanical behavior (Chen et al., 2025d; Khatti et al., 2025a). Such high-dimensional optimization tasks—common in geotechnical risk assessment and underground construction modeling—highlight the broader applicability of our method beyond soil spectral analysis.

While our current implementation focuses on learning rate and batch size, the framework naturally extends to higher-dimensional spaces. Future work could incorporate dropout rates and architectural hyperparameters through partitioned subspace strategies, though this would require careful consideration of the increased computational requirements for subspace construction.

7.3 Towards adaptive subspace refinement and multi-fidelity extensions

The current implementation uses a fixed subspace dimension throughout optimization, which may not optimally balance computational efficiency and modeling accuracy. An adaptive strategy that dynamically adjusts the subspace rank based on optimization progress could further enhance performance. Potential mechanisms include monitoring the predictive variance of the GP surrogate or tracking changes in the gradient of the acquisition function. Such adaptations would be particularly valuable when transitioning between exploration-dominated and exploitation-dominated phases of optimization.

Integrating multi-fidelity evaluations (Perdikaris et al., 2017; Xu et al., 2021) presents another promising extension. Soil analysis tasks often permit cheaper low-fidelity evaluations (e.g., training on subsets of spectral bands or shorter time-series segments). A multi-fidelity subspace approach could maintain separate approximations for each fidelity level while sharing information across them through a common latent subspace. This would build upon our method’s strength in handling sequential evaluations while leveraging the cost-quality trade-offs inherent in many geoscientific applications.

The success of subspace methods in this context also raises theoretical questions about the approximation’s impact on convergence guarantees. While empirical results demonstrate preserved optimization performance, formal analysis of how low-rank approximations affect the regret bounds of Bayesian optimization would strengthen the method’s theoretical foundation. Recent advances in randomized linear algebra (Kannan and Vempala, 2017; Lim and Weare, 2017) provide tools that could be adapted to this setting, potentially leading to provable trade-offs between approximation error and convergence rates.

8 Conclusion

The proposed accelerated Bayesian optimization framework demonstrates three key findings: (1) it achieves 3-5× speedup in CNN+LSTM learning rate tuning compared to standard Bayesian optimization while maintaining equivalent accuracy (test RMSE 0.142 ± 0.003); (2) the subspace approximation preserves optimization performance with approximation errors below 5% (Frobenius norm); and (3) the method generalizes across diverse soil data modalities (spectral, temporal, spatial) and CNN+LSTM architectures.

The subspace-accelerated Bayesian optimization framework provides significant improvements in efficiency for CNN+LSTM learning rate tuning in soil analysis applications. By leveraging precomputed low-rank Gaussian Process subspaces, the method reduces the computational complexity of traditional GP-based optimization while maintaining its probabilistic rigor and sample efficiency. The decoupling of offline subspace construction from online acquisition function evaluation enables real-time optimization updates, making the approach particularly suitable for resource-constrained environments. Three limitations warrant consideration: (1) the subspace approximation quality depends on kernel matrix spectral properties, potentially requiring larger subspace dimensions for slowly decaying eigenvalues; (2) the offline precomputation phase introduces initial overhead that becomes negligible only for long-running optimizations; and (3) the method assumes hyperparameter response surfaces remain relatively stable across model initializations, which may not hold for small batch sizes where training noise is significant.

Our uncertainty analyses demonstrate that the method maintains robust performance even with approximate subspace representations, with approximation errors contributing less than 5% to total prediction uncertainty—a favorable trade-off given the 3-5× computational speedups achieved.

Empirical results across diverse soil datasets confirm that the subspace approximation preserves optimization performance while achieving 3-5× speedups compared to standard Bayesian optimization. The approach offers three distinct advantages: (1) linear rather than cubic scaling with observation count enables real-time optimization; (2) the decoupled offline/online architecture permits reuse of precomputed subspaces across tasks; and (3) the specialized kernel design automatically adapts to multi-scale soil features without manual tuning. The method’s adaptability to different CNN+LSTM architectures and soil data modalities highlights its broad applicability in geoscientific machine learning tasks.

Four promising research directions emerge: (1) adaptive subspace refinement based on optimization progress metrics; (2) multi-fidelity extensions leveraging cheaper low-fidelity evaluations; (3) theoretical analysis of approximation effects on convergence guarantees using randomized linear algebra tools; and (4) partitioned subspace approaches for high-dimensional hyperparameter spaces. The specialized kernel design, incorporating Matern-5/2 smoothness and automatic relevance determination, effectively captures the multi-scale features inherent in soil spectral and temporal data.

Most significantly, this work advances computational soil science by enabling rapid CNN+LSTM hyperparameter tuning for critical tasks including carbon stock assessment (SSL), drought monitoring (TSSM), and micro-scale soil mapping (HSI). By reducing convergence time by 3-5× without accuracy loss, our method facilitates more frequent model updates when new soil samples are collected - a requirement for tracking dynamic soil properties in climate-vulnerable regions. These findings contribute to the growing body of research on efficient machine learning for geotechnical applications (Tian et al., 2024; Yadav et al., 2024), particularly in resource-constrained field deployment scenarios. Future integration with field-deployable spectral sensors could enable real-time learning rate adaptation during in situ soil characterization, further bridging the gap between computational efficiency and soil analytical precision.

By bridging the gap between computational efficiency and probabilistic robustness, this work provides a practical solution for automated machine learning in soil analysis while contributing methodological advances to the broader field of Bayesian optimization. The demonstrated improvements in optimization speed without sacrificing model accuracy make the approach particularly valuable for real-world applications where rapid model deployment and retraining are essential.

Data availability statement

The original contributions presented in the study are included in the article/supplementary material, further inquiries can be directed to the corresponding authors.

Author contributions

XC: Conceptualization, Formal Analysis, Methodology, Resources, Visualization, Writing – original draft, Writing – review and editing. HZ: Conceptualization, Data curation, Funding acquisition, Methodology, Project administration, Visualization, Writing – original draft, Writing – review and editing. CW: Conceptualization, Formal Analysis, Funding acquisition, Methodology, Resources, Supervision, Writing – original draft, Writing – review and editing. ZS: Conceptualization, Data curation, Resources, Validation, Writing – original draft, Writing – review and editing.

Funding

The author(s) declare that financial support was received for the research and/or publication of this article. We all acknowledge the support of Macao Polytechnic University (RP/FCHS-02/2025).

Conflict of interest

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Generative AI statement

The author(s) declare that no Generative AI was used in the creation of this manuscript.

Publisher’s note

All claims expressed in this article are solely those of the authors and do not necessarily represent those of their affiliated organizations, or those of the publisher, the editors and the reviewers. Any product that may be evaluated in this article, or claim that may be made by its manufacturer, is not guaranteed or endorsed by the publisher.

References

Albergel, C., De Rosnay, P., Gruhier, C., Muñoz-Sabater, J., Hasenauer, S., Isaksen, L., et al. (2012). Evaluation of remotely sensed and modelled soil moisture products using global ground-based in situ observations. Remote Sens. Environ. 118, 215–226. doi:10.1016/j.rse.2011.11.017

CrossRef Full Text | Google Scholar

Aldo, G., E, H. B., Alex, R., Cecilia, C., Frank, N., and Alessandro, L. (2021). Unsupervised learning methods for molecular simulation data. Chem. Rev. 121, 9722–9758. doi:10.1021/acs.chemrev.0c01195

PubMed Abstract | CrossRef Full Text | Google Scholar

Alghalayini, M. B., Wildman, D. C., Higa, K., Guevara, A., Battaglia, V., Noack, M. M., et al. (2025). Machine-learning-based efficient parameter space exploration for energy storage systems. Cell Rep. Phys. Sci. 6, 102543. doi:10.1016/j.xcrp.2025.102543

CrossRef Full Text | Google Scholar

Alkahtani, M., Mallick, J., Alqadhi, S., Sarif, M. N., Fatahalla Mohamed Ahmed, M., and Abdo, H. G. (2024). Interpretation of Bayesian-optimized deep learning models for enhancing soil erosion susceptibility prediction and management: a case study of Eastern India. Geocarto Int. 39, 2367611. doi:10.1080/10106049.2024.2367611

CrossRef Full Text | Google Scholar

Anis, F., Chafik, S., and François, B. (2022). A scalable approximate Bayesian inference for high-dimensional Gaussian processes. Commun. Statistics - Theory Methods 51, 5937–5956. doi:10.1080/03610926.2020.1850793

CrossRef Full Text | Google Scholar

Bazi, Y., Bashmal, L., Rahhal, M. M. A., Dayil, R. A., and Ajlan, N. A. (2021). Vision transformers for remote sensing image classification. Remote Sens. 13, 516. doi:10.3390/rs13030516

CrossRef Full Text | Google Scholar

Belete, D. M., and Huchaiah, M. D. (2022). Grid search in hyperparameter optimization of machine learning models for prediction of HIV/AIDS test results. Int. J. Comput. Appl. 44, 875–886. doi:10.1080/1206212x.2021.1974663

CrossRef Full Text | Google Scholar

Bhardwaj, A., Mangat, V., and Vig, R. (2020). Hyperband tuned deep neural network with well posed stacked sparse autoencoder for detection of DDoS attacks in cloud. IEEE Access 8, 181916–181929. doi:10.1109/access.2020.3028690

CrossRef Full Text | Google Scholar

Brown, D. J. (2007). Using a global VNIR soil-spectral library for local soil characterization and landscape modeling in a 2nd-order Uganda watershed. Geoderma 140, 444–453. doi:10.1016/j.geoderma.2007.04.021

CrossRef Full Text | Google Scholar

Cai, Y., Zheng, W., Zhang, X., Zhangzhong, L., and Xue, X. (2019). Research on soil moisture prediction model based on deep learning. PLoS One 14, e0214508. doi:10.1371/journal.pone.0214508

PubMed Abstract | CrossRef Full Text | Google Scholar

Cao, J., Guinness, J., Genton, M. G., and Katzfuss, M. (2022). Scalable Gaussian-process regression and variable selection using Vecchia approximations. J. Mach. Learn. Res. 23, 1–30. doi:10.48550/arXiv.2202.12981

CrossRef Full Text | Google Scholar

Chen, Q., Jiang, L., Qin, H., and Kontar, R. A. (2025a). Multi-agent collaborative bayesian optimization via constrained Gaussian processes. Technometrics 67, 32–45. doi:10.1080/00401706.2024.2365732

CrossRef Full Text | Google Scholar

Chen, X., Cui, F., Wong, C. U. I., Zhang, H., and Wang, F. (2023). An investigation into the response of the soil ecological environment to tourist disturbance in Baligou. PeerJ 11, e15780. doi:10.7717/peerj.15780

PubMed Abstract | CrossRef Full Text | Google Scholar

Chen, X., Yang, H., Zhang, H., and Wong, C. U. I. (2025b). Dynamic gradient descent and reinforcement learning for AI-enhanced indoor building environmental simulation. Buildings 15, 2044. doi:10.3390/buildings15122044

CrossRef Full Text | Google Scholar

Chen, X., Zhang, H., Wong, C. U. I., and Song, Z. (2025c). Adaptive multi-timescale particle filter for nonlinear state estimation in wastewater treatment: a bayesian fusion approach with entropy-driven feature extraction. Processes 13, 2005. doi:10.3390/pr13072005

CrossRef Full Text | Google Scholar

Chen, X., Zhang, H., Wong, C. U. I., and Song, Z. (2025d). Multi-model and variable combination approaches for improved prediction of soil heavy metal content. Processes 13, 2008. doi:10.3390/pr13072008

CrossRef Full Text | Google Scholar

Di, Y., Gao, M., Feng, F., Li, Q., and Zhang, H. (2022). A new framework for winter wheat yield prediction integrating deep learning and bayesian Optimization. Agronomy 12, 3194. doi:10.3390/agronomy12123194

CrossRef Full Text | Google Scholar

Friedman, J., Hastie, T., and Tibshirani, R. (2000). Additive logistic regression: a statistical view of boosting (with discussion and a rejoinder by the authors). Ann. Statistics 28, 337–407. doi:10.1214/aos/1016120463

CrossRef Full Text | Google Scholar

Gao, K., Li, G., Cao, Y., Li, C., Chen, D., Wu, G., et al. (2024). Permafrost thawing caused by the China-Russia Crude oil pipeline based on multi-type data and its impacts on geomorphological reshaping and water erosion. Catena 242, 108134. doi:10.1016/j.catena.2024.108134

CrossRef Full Text | Google Scholar

Ginette, L., Francis, T., Inez, M.-G., and Eva, C. (2019). A partial correlation screening approach for controlling the false positive rate in sparse Gaussian graphical models. Sci. Rep. 9, 17759. doi:10.1038/s41598-019-53795-x

CrossRef Full Text | Google Scholar

Giraldo, J.-J., and Álvarez, M. A. (2022). A fully natural gradient scheme for improving inference of the heterogeneous multioutput Gaussian process model. IEEE Trans. Neural Netw. Learn. Syst. 33, 6429–6442. doi:10.1109/TNNLS.2021.3080238

PubMed Abstract | CrossRef Full Text | Google Scholar

Goay, C. H., Ahmad, N. S., and Goh, P. (2021). Transient simulations of high-speed channels using CNN-LSTM with an adaptive successive halving algorithm for automated hyperparameter optimizations. IEEE Access 9, 127644–127663. doi:10.1109/ACCESS.2021.3112134

CrossRef Full Text | Google Scholar

Hively, W. D., McCarty, G. W., Reeves III, J. B., Lang, M. W., Oesterling, R. A., and Delwiche, S. R. (2011). Use of airborne hyperspectral imagery to map soil properties in tilled agricultural fields. Appl. Environ. Soil Sci. 2011, 1–13. doi:10.1155/2011/358193

CrossRef Full Text | Google Scholar

How, D. N. T., Hannan, M. A., Lipu, M. S. H., Ker, P. J., Mansor, M., Sahari, K. S. M., et al. (2022). SOC estimation using deep bidirectional gated recurrent units with tree Parzen estimator hyperparameter optimization. IEEE Trans. Industry Appl. 58, 6629–6638. doi:10.1109/TIA.2022.3180282

CrossRef Full Text | Google Scholar

Jeon, Y., and Hwang, G. (2023). Feature selection with scalable variational Gaussian process via sensitivity analysis based on L2 divergence. Neurocomputing 518, 577–592. doi:10.1016/j.neucom.2022.11.013

CrossRef Full Text | Google Scholar

Jia, J.-X., Lian, F., Feng, W.-H., Liu, X., and Fan, Z.-E. (2024). Fast multi-fidelity Gaussian processes with derivatives for complex system modeling. Meas. Sci. Technol. 36, 016225. doi:10.1088/1361-6501/ad9858

CrossRef Full Text | Google Scholar

Jia, S., Li, H., Wang, Y., Tong, R., and Li, Q. (2017). Hyperspectral imaging analysis for the classification of soil types and the determination of soil total nitrogen. Sensors 17, 2252. doi:10.3390/s17102252

PubMed Abstract | CrossRef Full Text | Google Scholar

Kannan, R., and Vempala, S. (2017). Randomized algorithms in numerical linear algebra. Acta Numer. 26, 95–135. doi:10.1017/s0962492917000058

CrossRef Full Text | Google Scholar

Khatti, J., and Grover, K. S. (2023a). Prediction of compaction parameters for fine-grained soil: critical comparison of the deep learning and standalone models. J. Rock Mech. Geotechnical Eng. 15, 3010–3038. doi:10.1016/j.jrmge.2022.12.034

CrossRef Full Text | Google Scholar

Khatti, J., and Grover, K. S. (2023b). Prediction of compaction parameters of compacted soil using LSSVM, LSTM, LSBoostRF, and ANN. Innov. Infrastruct. Solutions 8, 76. doi:10.1007/s41062-023-01048-2

CrossRef Full Text | Google Scholar

Khatti, J., and Grover, K. S. (2025). Estimation of uniaxial strength of rock: a comparison between Bayesian-optimized machine learning models. Min. Metallurgy Explor. 42, 133–154. doi:10.1007/s42461-024-01168-y

CrossRef Full Text | Google Scholar

Khatti, J., Grover, K. S., Kim, H.-J., Mawuntu, K. B. A., and Park, T.-W. (2024). Prediction of ultimate bearing capacity of shallow foundations on cohesionless soil using hybrid LSTM and RVM approaches: an extended investigation of multicollinearity. Comput. Geotechnics 165, 105912. doi:10.1016/j.compgeo.2023.105912

CrossRef Full Text | Google Scholar

Khatti, J., Grover, K. S., and Samui, P. (2025a). A comparative study between LSSVM, LSTM, and ANN in predicting the unconfined compressive strength of virgin fine-grained soil. Front. Built Environ. 11, 1594924. doi:10.3389/fbuil.2025.1594924

CrossRef Full Text | Google Scholar

Khatti, J., Muhmed, A., and Grover, K. S. (2025b). Dimensionality analysis in assessing the unconfined strength of lime-treated soil using machine learning approaches. Earth Sci. Inf. 18, 234. doi:10.1007/s12145-025-01731-1

CrossRef Full Text | Google Scholar

Kuang, Y., Chen, X., and Zhu, C. (2025). Hierarchical federated learning with hybrid neural architectures for predictive pollutant analysis in advanced green analytical chemistry. Processes 13, 1588. doi:10.3390/pr13051588

CrossRef Full Text | Google Scholar

Li, P., and Chen, S. (2018). Hierarchical Gaussian processes model for multi-task learning. Pattern Recognit. 74, 134–144. doi:10.1016/j.patcog.2017.09.021

CrossRef Full Text | Google Scholar

Lim, L.-H., and Weare, J. (2017). Fast randomized iteration: diffusion Monte Carlo through the lens of numerical linear algebra. SIAM Rev. 59, 547–587. doi:10.1137/15m1040827

CrossRef Full Text | Google Scholar

Lin, J., Cheng, Q., Kumar, A., Zhang, W., Yu, Z., Hui, D., et al. (2024). Effect of degradable microplastics, biochar and their coexistence on soil organic matter decomposition: a critical review. TrAC Trends Anal. Chem. 183, 118082. doi:10.1016/j.trac.2024.118082

CrossRef Full Text | Google Scholar

Luo, H., Nattino, G., and Pratola, M. T. (2022). Sparse additive Gaussian process regression. J. Mach. Learn. Res. 23, 1–34. doi:10.48550/arXiv.1908.08864

CrossRef Full Text | Google Scholar

Luo, G. (2016). A review of automatic selection methods for machine learning algorithms and hyper-parameter values. Network Modeling Analysis in Health Informatics and Bioinformatics, 5(1), 18. doi:10.1007/s13721-016-0125-6

CrossRef Full Text | Google Scholar

Maiworm, M., Limon, D., and Findeisen, R. (2021). Online learning-based model predictive control with Gaussian process models and stability guarantees. Int. J. Robust Nonlinear Control 31, 8785–8812. doi:10.1002/rnc.5361

CrossRef Full Text | Google Scholar

Mandelbrot, B. (1968). Fractional Brownian motion, fractional noise and applications. Siam Rev. 10, 442–437. doi:10.1137/1010093

CrossRef Full Text | Google Scholar

Martinsson, P.-G., and Tropp, J. A. (2020). Randomized numerical linear algebra: foundations and algorithms. Acta Numer. 29, 403–572. doi:10.1017/s0962492920000021

CrossRef Full Text | Google Scholar

Mathieu, J. A., Hatté, C., Balesdent, J., and Parent, É. (2015). Deep soil carbon dynamics are driven more by soil type than by climate: a worldwide meta-analysis of radiocarbon profiles. Glob. Change Biol. 21, 4278–4292. doi:10.1111/gcb.13012

PubMed Abstract | CrossRef Full Text | Google Scholar

Meng, X., Bao, Y., Zhang, X., Wang, X., and Liu, H. (2022). Prediction of soil organic matter using different soil classification hierarchical level stratification strategies and spectral characteristic parameters. Geoderma 411, 115696. doi:10.1016/j.geoderma.2022.115696

CrossRef Full Text | Google Scholar

Nguyen, T. N. A., Bouzerdoum, A., and Phung, S. L. (2019). A scalable hierarchical Gaussian process classifier. IEEE Trans. Signal Process. 67, 3042–3057. doi:10.1109/tsp.2019.2911251

CrossRef Full Text | Google Scholar

Nguyen, X. D. J., and Liu, Y. (2025). Methodology for hyperparameter tuning of deep neural networks for efficient and accurate molecular property prediction. Comput. and Chem. Eng. 193, 108928. doi:10.1016/j.compchemeng.2024.108928

CrossRef Full Text | Google Scholar

Nguyen-Tuong, D., Seeger, M., and Peters, J. (2009). Model learning with local Gaussian process regression. Adv. Robot. 23, 2015–2034. doi:10.1163/016918609x12529286896877

CrossRef Full Text | Google Scholar

Padmapriya, J., and Sasilatha, T. (2023). Deep learning based multi-labelled soil classification and empirical estimation toward sustainable agriculture. Eng. Appl. Artif. Intell. 119, 105690. doi:10.1016/j.engappai.2022.105690

CrossRef Full Text | Google Scholar

Paul, R., Mishra, S., and Khatti, J. (2025). Role of artificial intelligence (AI) techniques in tunnel engineering—a scientific review. Indian Geotechnical J., 1–31. doi:10.1007/s40098-025-01238-y

CrossRef Full Text | Google Scholar

Peck, C. C., and Dhawan, A. P. (1995). Genetic algorithms as global random search methods: an alternative perspective. Evol. Comput. 3, 39–80. doi:10.1162/evco.1995.3.1.39

CrossRef Full Text | Google Scholar

Peng, S., Rice, J. D., Zhang, W., Luo, G., Cao, H., and Pan, H. (2024). Laboratory investigation of the effects of blanket defect size on initiation of backward erosion piping. J. Geotechnical Geoenvironmental Eng. 150, 04024095. doi:10.1061/jggefk.gteng-11976

CrossRef Full Text | Google Scholar

Perdikaris, P., Raissi, M., Damianou, A., Lawrence, N. D., and Karniadakis, G. E. (2017). Nonlinear information fusion algorithms for data-efficient multi-fidelity modelling. Proc. R. Soc. A Math. Phys. Eng. Sci. 473, 20160751. doi:10.1098/rspa.2016.0751

PubMed Abstract | CrossRef Full Text | Google Scholar

Preuss, R., and Von Toussaint, U. (2018). Global optimization employing Gaussian process-based Bayesian surrogates. Entropy 20, 201. doi:10.3390/e20030201

PubMed Abstract | CrossRef Full Text | Google Scholar

Seeger, M. (2004). Gaussian processes for machine learning. Int. J. Neural Syst. 14, 69–106. doi:10.1142/s0129065704001899

PubMed Abstract | CrossRef Full Text | Google Scholar

Srinivas, N., Krause, A., Kakade, S. M., and Seeger, M. W. (2012). Information-theoretic regret bounds for Gaussian process optimization in the bandit setting. IEEE Trans. Inf. Theory 58, 3250–3265. doi:10.1109/TIT.2011.2182033

CrossRef Full Text | Google Scholar

Su, Y., Cui, Y.-J., Dupla, J.-C., and Canou, J. (2022). Soil-water retention behaviour of fine/coarse soil mixture with varying coarse grain contents and fine soil dry densities. Can. Geotechnical J. 59, 291–299. doi:10.1139/cgj-2021-0054

CrossRef Full Text | Google Scholar

Tian, Z., Lee, A., and Zhou, S. (2024). Adaptive tempered reversible jump algorithm for Bayesian curve fitting. Inverse Probl. 40, 045024. doi:10.1088/1361-6420/ad2cf7

CrossRef Full Text | Google Scholar

Ubaru, S., Chen, J., and Saad, Y. (2017). Fast estimation of $tr(f(A))$ via stochastic Lanczos quadrature. SIAM J. Matrix Analysis Appl. 38, 1075–1099. doi:10.1137/16m1104974

CrossRef Full Text | Google Scholar

Viswanathan, G. M., Buldyrev, S. V., Havlin, S., da Luz, M. G., Raposo, E. P., and Stanley, H. E. (1999). Optimizing the success of random searches. nature 401, 911–914. doi:10.1038/44831

PubMed Abstract | CrossRef Full Text | Google Scholar

Wang, J., Chen, F., Ma, X., Shao, J., Kang, Z., Yin, S., et al. (2019). A Krylov-subspace-based exponential time integration scheme for discontinuous Galerkin time-domain methods. IEEE Trans. Magnetics 55, 1–5. doi:10.1109/TMAG.2019.2909883

CrossRef Full Text | Google Scholar

Wang, Z., Dahl, G. E., Swersky, K., Lee, C., Nado, Z., Gilmer, J., et al. (2024). Pre-trained Gaussian processes for Bayesian optimization. J. Mach. Learn. Res. 25, 1–83. doi:10.48550/arXiv.2109.08215

CrossRef Full Text | Google Scholar

Wei, W., Xu, W., Deng, J., and Guo, Y. (2022). Self-aeration development and fully cross-sectional air diffusion in high-speed open channel flows. J. Hydraulic Res. 60, 445–459. doi:10.1080/00221686.2021.2004250

CrossRef Full Text | Google Scholar

Williams, D. R., Rast, P., Pericchi, L. R., and Mulder, J. (2020). Comparing Gaussian graphical models with the posterior predictive distribution and Bayesian model selection. Psychol. Methods 25, 653–672. doi:10.1037/met0000254

PubMed Abstract | CrossRef Full Text | Google Scholar

Wu, K.-P., and Wang, S.-D. (2009). Choosing the kernel parameters for support vector machines by the inter-cluster distance in the feature space. Pattern Recognit. 42, 710–717. doi:10.1016/j.patcog.2008.08.030

CrossRef Full Text | Google Scholar

Xiao, H., Wu, J.-L., Wang, J.-X., Sun, R., and Roy, C. J. (2016). Quantifying and reducing model-form uncertainties in Reynolds-averaged Navier–Stokes simulations: a data-driven, physics-informed Bayesian approach. J. Comput. Phys. 324, 115–136. doi:10.1016/j.jcp.2016.07.038

CrossRef Full Text | Google Scholar

Xixian, C., Haiqin, Y., Shenglin, Z., R, L. M., and Irwin, K. (2019). Effective data-aware covariance estimator from compressed data. IEEE Trans. Neural Netw. Learn. Syst. 31, 1–14. doi:10.48550/arXiv.2010.04966

CrossRef Full Text | Google Scholar

Xu, J., Du, Y., and Zhou, L. (2021). A multi-fidelity integration rule for statistical moments and failure probability evaluations. Struct. Multidiscip. Optim. 64, 1305–1326. doi:10.1007/s00158-021-02919-x

CrossRef Full Text | Google Scholar

Yadav, M. B. N., Patil, P., and Hebbara, M. (2024). Assessment of soil erosion risk in a hilly zone sub-watershed of Karnataka using geospatial technologies and the RUSLE model. Geol. Ecol. Landscapes, 1–15. doi:10.1080/24749508.2024.2373491

CrossRef Full Text | Google Scholar

Yang, C., Buluç, A., and Owens, J. D. (2022). GraphBLAST: a high-performance linear algebra-based graph framework on the GPU. ACM Trans. Math. Softw. (TOMS) 48, 1–51. doi:10.1145/3466795

CrossRef Full Text | Google Scholar

Yang, J., Huang, Z., Jian, W., and Robledo, L. F. (2024). Landslide displacement prediction by using Bayesian optimization–temporal convolutional networks. Acta Geotech. 19, 4947–4965. doi:10.1007/s11440-023-02205-8

CrossRef Full Text | Google Scholar

Yang, J., and Klabjan, D. (2021). Bayesian active learning for choice models with deep Gaussian processes. IEEE Trans. Intelligent Transp. Syst. 22, 1080–1092. doi:10.1109/TITS.2019.2962535

CrossRef Full Text | Google Scholar

Yang, X. (2018). NLOS mitigation for UWB localization based on sparse pseudo-input Gaussian process. IEEE Sensors J. 18, 4311–4316. doi:10.1109/jsen.2018.2818158

CrossRef Full Text | Google Scholar

Zhang, B., Sang, H., and Huang, J. Z. (2019). Smoothed full-scale approximation of Gaussian process models for computation of large spatial data sets. Stat. Sin. 29, 1711–1737. doi:10.5705/ss.202017.0008

CrossRef Full Text | Google Scholar

Zhang, D., Chen, S., and Zhou, Z.-H. (2006). Learning the kernel parameters in kernel minimum distance classifier. Pattern Recognit. 39, 133–135. doi:10.1016/j.patcog.2005.08.001

CrossRef Full Text | Google Scholar

Zhang, L., Dou, H., Zhang, K., Huang, R., Lin, X., Wu, S., et al. (2023). CNN-LSTM model optimized by Bayesian optimization for predicting single-well production in water flooding reservoir. Geofluids 2023, 1–16. doi:10.1155/2023/5467956

CrossRef Full Text | Google Scholar

Zhang, T., Wang, S., Huang, X., and Jia, L. (2020). Kernel recursive least squares algorithm based on the Nystr\rm \ddot\bf om Method With k-Means sampling. IEEE Signal Process. Lett. 27, 361–365. doi:10.1109/LSP.2020.2972164

CrossRef Full Text | Google Scholar

Zhao, M., Zou, G., Li, Y., Pan, B., Wang, X., Zhang, J., et al. (2025). Biodegradable microplastics coupled with biochar enhance Cd chelation and reduce Cd accumulation in Chinese cabbage. Biochar 7, 31–17. doi:10.1007/s42773-024-00418-y

CrossRef Full Text | Google Scholar

Zhou, X., Gao, Y., Jiang, T., and Feng, Z. (2023). An online approach for robust parameter design with incremental Gaussian process. Qual. Eng. 35, 430–443. doi:10.1080/08982112.2022.2147844

CrossRef Full Text | Google Scholar

Zhou, Y., Biswas, A., Hong, Y., Chen, S., Hu, B., Shi, Z., et al. (2024). Enhancing soil profile analysis with soil spectral libraries and laboratory hyperspectral imaging. Geoderma 450, 117036. doi:10.1016/j.geoderma.2024.117036

CrossRef Full Text | Google Scholar

Zhu, L., Yuan, S., Liu, Y., Chen, C., and Walker, J. P. (2023). Time series soil moisture retrieval from SAR data: multi-temporal constraints and a global validation. Remote Sens. Environ. 287, 113466. doi:10.1016/j.rse.2023.113466

CrossRef Full Text | Google Scholar