- 1Dipartimento di Scienze della Terra, dell'Ambiente e delle Risorse, Università degli Studi di Napoli Federico II, Naples, Italy
- 2Dipartimento di Bioscienze e Territorio, University of Molise, Campobasso, Italy
The geographic range sizes frequency distribution (RFD) within clades is typically right-skewed with untransformed data, and bell-shaped or slightly left-skewed under the log-transformation. This means that most species within clades occupy diminutive ranges, whereas just a few species are truly widespread. A number of ecological and evolutionary explanations have been proposed to account for this pattern. Among the latter, much attention has been given to the issue of how extinction and speciation probabilities influence RFD. Numerous accounts now convincingly demonstrate that extinction rate decreases with range size, both in living and extinct taxa. The relationship between range size and speciation rate, though, is much less obvious, with either small or large ranged species being proposed to originate more daughter taxa. Herein, we used a large fossil database including 21 animal clades and more than 80,000 fossil occurrences distributed over more than 400 million years of marine metazoans (exclusive of vertebrates) evolution, to test the relationship between extinction rate, speciation rate, and range size. As expected, we found that extinction rate almost linearly decreases with range size. In contrast, speciation rate peaks at the large (but not the largest) end of the range size spectrum. This is consistent with the peripheral isolation mode of allopatric speciation being the main mechanism of species origination. The huge variation in phylogeny, fossilization potential, time of fossilization, and the overarching effect of mass extinctions suggest caution must be posed at generalizing our results, as individual clades may deviate significantly from the general pattern.
Introduction
The extent of the geographical range is one of the most important biological attributes of a species. Species occupying large ranges may have better dispersal ability (Shanks et al., 2003; Lester et al., 2007), usually have larger populations (Gaston et al., 1997; Blackburn and Gaston, 2003; Carotenuto et al., 2010), and engender wider niche (Williams et al., 2009; Slatyer et al., 2013; Saupe et al., 2015), as compared to small-ranged species. Large population size, good dispersal ability and large range size, in turn, significantly decrease the chance of stochastic extinction. Therefore, perhaps unsurprisingly, large-ranged species have been repeatedly demonstrated to endure lower extinction risk, or longer duration in the fossil record (e.g., Hawkins et al., 2000; Cardillo et al., 2005; Foote and Miller, 2013). The relationship between range size and speciation rate is much less obvious. On the one hand, large-ranged species may have greater chance to produce daughter species (Wagner and Erwin, 1995), either by peripheral isolation (Glazier, 1987; Rosenzweig, 1995), or microvicariance (Cracraft and Prum, 1988). However, assuming most originations occur by allopatric speciation, the likelihood that a barrier is large enough to break a species' range into smaller pieces is arguably low for the largest-ranged taxa (Gaston, 2003). This suggests that even under allopatry speciation probability might be a peaked function of species range size (Jablonski and Roy, 2003). However, it must be noted that since species with large range might be expected to live for longer (because of the positive effect of range size on survival), they will likely leave more descendants in the fossil record (Wagner and Erwin, 1995).
Such diversification dynamics significantly affect the range size-frequency distribution (Gaston, 1998, 2003; Blackburn and Gaston, 2003). In most animal groups, the RFD is strongly right-skewed, meaning that most species within a clade have restricted ranges, and a very few of them are extremely widespread (Blackburn and Gaston, 2003). The evolutionary process producing RFD at the clade level ultimately depends on the distribution of speciation and extinction rates along the range size spectrum. If small-to-medium ranged species produce more daughter species, most speciation occurs by vicariance (Gaston, 1998, 2003), and the right hand of the RFD is populated by the few long-living species escaping range division (i.e., by allopatric speciation). This would imply a negative, or no relationship either, between speciation rate and range size. This pattern is also consistent with the notion of range transformation, which is the peaked trajectory of range size over time since origination that most species, and even entire clades, seem to follow (DeGusta and Vrba, 2003; Raia et al., 2006; Foote, 2009). On the other hand, if speciation rate increases with range size, the left hand of the RFD must be populated with species deriving from highly asymmetrical range splits in large ranged species, according to the peripheral isolation speciation mode. Under this scenario, the relationship between range size and speciation rate should be positive and significant. Finally, if most speciation occurs by allopatric speciation, extinction rate should significantly decrease with range size for the RFD distribution to hold a constant shape, because small-ranged species are bound to appear more often than large-ranged species to maintain the right skew.
In this study, we computed range size at species and clade level, as well as per capita speciation and extinction rates for 21 extinct clades of marine metazoans. We tested whether speciation and extinction rates were significantly affected by the average range size of species within their clades, partitioned into consecutive, non-overlapping temporal bins. Then, we inferred from the shape of the speciation rate vs. range size curve whether the dominant mode of speciation in the fossil record has been either peripheral isolation or simple vicariance, either. This is feasible because with the former, speciation rate should be higher in larger ranged species, whereas under the latter, the rate should peak at intermediate ranges, or show no relationship with range size, either.
Materials and Methods
We used fossil occurrence data provided by the Paleobiology Database (www.paleodb.org), regarding 21 clades of marine metazoans belonging to five animal phyla (Arthropoda, Brachiopoda, Bryozoa, Cnidaria, Mollusca). The fossil record spans from Late Cambrian to Late Cretaceous, initially including more than 20,000 species occurrences. For each clade, occurrence records were divided into consecutive time bins of constant duration. Time bin duration was set separately for each clade, as to obtain as many bins as possible, while avoiding creating bins with little species diversity (we only considered bins including at least 3 species ranges). Within each bin, we only included species with at least 3 fossil occurrences, this being the minimum number of occurrences required to draw the polygon representing a species geographic range. In addition, we dropped species and genera lacking a continuous stratigraphic range or affected by uncertain taxonomic classification (e.g., sp., cf.). Albeit the quality of the fossil record in terrestrial settings may be very good in some instances (e.g., Laurin and Soler-Gijón, 2010) herein we focused on the marine realm, because of the usually finer and more continuous fossilization in marine sediments, and because the calculation of the speciation and extinction rates is more robust under better sampling (Foote, 2000). Given our focus on diversification dynamics, we feel it is important to notice that we refer to no particular species concept, and used nominal species which are generally separated on morphological grounds (morphospecies).
The final dataset obtained after applying these filtering criteria included 14,427 species and 84,453 occurrences. This fossil occurrence database was originally presented in Raia et al. (2016) and we therefore address the reader to that paper for further details.
The Range Size Metric and Its Proficiency
A variety of approaches exist in both the neontological and the paleontological literature to compute species geographic range sizes. Most measures of range extension are based on occurrence data in individual plots, or on counting the geographic cells where a species is present (i.e., site occupancy, Gaston, 2003). Herein, we used the minimum convex polygon approach (MCP, Carotenuto et al., 2010, 2015). MCP is the smallest possible convex polygon drawn as to include all the occurrences of a species (Figure 1). The area of the polygon represents the species geographic range size. We first calculated a single MCP for each species within each temporal bin (Table S1). Subsequently, a MCP was also calculated for the entire clade in a given time bin, by pooling together all the occurrences of the species belonging to the clade (Figure 1, Table S1). MCPs were calculated with the software Quantum Gis 2.14 (www.qgis.org/it/site). Since we considered only marine species, we removed land portions (as included in MCPs) that would overestimate the species geographic ranges. For this purpose, we used the digitized version of 19 world maps displaying the reconstructed position and geographic extent of landmasses in the past (http://deeptimemaps.com/) choosing for each time bin the map whose age is closest to the time bin absolute age. For each time bin, we selected the appropriate geographic projection, depending on the distribution of occurrences. Three different projection systems were considered. Specifically, when a MCP was comprised within 180 decimal degrees in longitude, we applied the Lambert Azimuthal Equal Area projection. For MCPs exceeding 180 decimal degrees and ranging within ±60 latitudinal degrees, we applied the Mollweide Equal Area projection. Alternatively, if the range fell outside the ±30 decimal degrees of latitude from the equator, we applied the Albers Equal Area projection. In a few cases the species occurrences cannot be easily accommodated with any of these criteria. To cope with them, we split the polygons and projected the resulting portions by using Lambert Azimuthal Equal Area projection. The MCP area was expressed in squared kilometers.
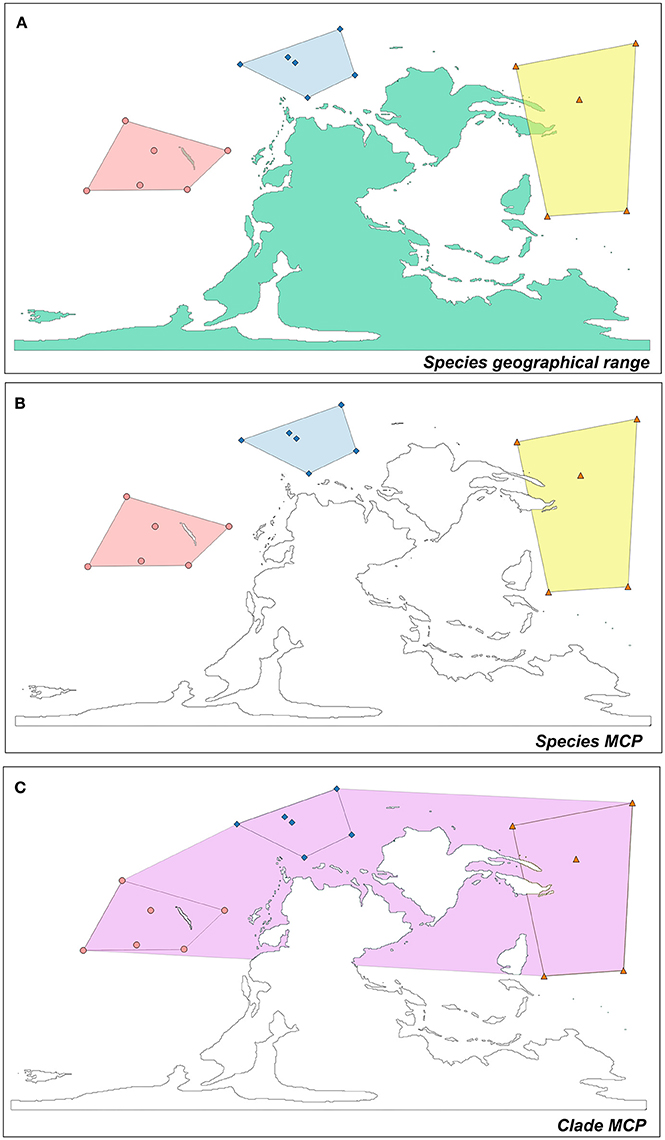
Figure 1. Criteria for clade and species range size estimation. (A) The computation of the MCP of three different species in a temporal bin. The colors (yellow, pink, and light red) indicate the different geographical distribution of the species. In (B) land portions are removed in order to compute species MCPs. (C) The calculation of clade-level MCP, considering all the occurrences of all the species belonging to the clade in a given temporal bin.
Speciation and extinction rates were calculated for each clade within each time bin (see below). Consequently, we had to use an “average” representation of the species geographic range per time bin in order to assess the effect of range size on the rates. To this aim, we took the average range size computed over all of the species within a clade and a given time bin, and divided this average area by the clade range size, obtaining a “standard average range size” (hereafter simply standard range, SR). The size of a clade geographic range is mostly influenced by the range sizes of the largest-ranged species it includes. Since the range size difference between the largest- and smallest-ranged species increases with the skew of the RFD, there should be an inverse relationship between SR and skew. This means that SR should, in principle, be low when the RFD contains a disproportionate number of small-ranged species, and high otherwise. We set up a simulation experiment to demonstrate this point. We originated 100,000 random, right-skewed distributions of 100 species, each time sampling from a beta distribution with a small fixed value of the a, and large, random values of the b parameter. The beta distribution is defined by the equation:
Then, before computing the SR of species, we have to draw their clade MCP. In theory, the clade range size may span from a value as small as the range of its largest-ranged species (an ideal situation where all the species of the clade are sympatric and geographically contained within the range of the largest-ranged species), to a value several times the algebraic sum of species range sizes (in the case of species having disjunctive ranges). In the simulations, at each repetition we drew at random the clade range size (i.e., its MCP) from a uniform distribution, spanning from the MCP of the largest species range within the clade up to a value 5 times the algebraic sum of all species range sizes. Then, we counted how many species MCPs (out of 100) are smaller than one tenth the clade MCP (i.e., the number of small-ranged species), and the number of ranges larger than 90% of the clade MCP (i.e., the number of large-ranged species). Eventually, we regressed these percentages against SR.
We used the same simulations set to test for the effect of sympatry on such relationship, by regressing the percentage of small ranged species against both SR and the degree of sympatry (computed as the ratio between the algebraic sum of species ranges and the clade MCP) in a multiple regression model.
The Computation of Speciation and Extinction Rates. Pradel Models
To compute speciation and extinction rates, we applied Pradel models (Pradel, 1996), which belongs to the Jolly-Seber family of capture-mark-recapture (CMR) models. We preferred this method over more traditional approaches (2008; 2000) as it is recommended for paleontological data, especially under heterogeneous and incomplete sampling (Liow and Finarelli, 2014). In fact, under the Pradel approach the absence of a species from a time bin is interpreted as either real absence or as failed-to recognize presence. Hence, sampling probability is estimated jointly with other parameters.
With Pradel models, four distinct parameters are fitted to the data. Survival probability(φi) is the probability of a species surviving from the interval i to the interval i+1. Thus, the complement of this term (1-φi) is the probability of extinction from time i to time i+1.
Seniority (γi) is the probability that a species extant at interval i was already present during the interval i−1. Thus, the complement of this term (1–γi) is the speciation probability from time i−1 to time i. This parameter is related to recruitment, fi, which is the number of new species appearing at interval i+1 divided by the number of species present at interval i. Recruitment is computed as:
Growth rate (λi) is defined as the ratio between the number of species at intervals i+1 and i. It can be also computed as: λi = fi + φi. Therefore, the net per capita diversification rate is:
Eventually, sampling probability (pi) is the probability for a species actually extant during interval i to be sampled in that very interval.
We built two types of Pradel models, one based on the estimation of “survival and seniority” (which fits extinction, speciation, and sampling rates) and the other on the estimation of “survival and population growth” (which fits extinction, diversification, and sampling rates). The application of two different models is necessary because the parameters are linear functions of each other (i.e., they are defined by a family of linear equations). For each model, we assumed that sampling was allowed to change from one time bin to the next. The motivation was that sampling affects diversification metrics, and it is hard to tell whether sampling follows a random walk path, or is highly variable among intervals.
Given we used morphospecies, it is important to emphasize that the extinction events we record are not always true extinctions, and some speciation events are actually the continuation in time of some genome that from some point on receives a different name. There are methods being implemented that allow accounting for pseudo-extinction (i.e., distinguishing between “budding” speciation and cladogenesis, Didier et al., 2017) and pseudo-speciation (i.e., by accounting for ancestor-descendant relationships, Bapst, 2013), but they require explicit phylogenetic information that is unavailable in the present context.
The rate analyses were run using the software “MARK” and the R package “RMark” (www.phidot.org/software/mark). First, we took the entire fossil record of each clade and partitioned it into time bins (the same bins as per the calculation of MCPs. Consequently, within each clade we created a matrix of presence-absence of each species per bin, representing the specific “encounter” history in the fossil record. At this point, we allowed all four variables of Pradel's models [Survival probability (φi), Seniority (γi), Growth rate (λi), Sampling probability (pi)] to vary across bins. Eventually, we used the rates of all four variables to calculate speciation and extinction rates of each clade over time (Table S2).
Effect of SR on Diversification Rates
To test the statistical relationship between diversification rates estimated by Pradel models and SR, we used generalized linear mixed models (GLMM; McCullagh and Nelder, 1989) implemented in the R package “lme4” (Bates et al., 2015). As response variables, we used alternatively the two rates (i.e., extinction and speciation) as estimated by Pradel's models (see above) and SR as explanatory variable. As extinction and speciation rates represent probabilities (Liow and Finarelli, 2014; Finarelli and Liow, 2016), we converted them into “number of successes” or “number of failures” and included into GLMMs with a binomial distribution of errors and logit link function. In both regression models, linear and quadratic terms between SR and the response variables were calculated. Besides, we considered the interaction between time interval and clade as random effect. Specifically, we allowed the model to change the intercept according to this factor to take into account non-independence of data between clades per time intervals. We also run GLMMs considering only linear terms and only quadratic terms, separately.
Regression models including species traits should account for phylogenetic non-independence (Felsenstein, 1985). Although there is increasing recognition of the importance of producing phylogenies for fossil species (Diniz-Filho et al., 2013; Didier et al., 2017), this was not possible in the present study, because there may simply not be any available phylogeny for many of the studied taxa.
The goodness-of-fit of the models was assessed by calculating the conditional coefficient of determination for GLMM (R2), which is interpreted as the variance explained by both fixed and random factors (Nakagawa and Schielzeth, 2013).
Results
Appropriateness of SR as an Indicator of the Presence of Extremely Small-Ranged, and Large-Ranged Species
As expected, there is a significant negative relationship between SR and the proportion of small ranged species (slope = −2.430, p = 8 * 10−4), and a significant positive relationship between SR and the proportion of large ranged species (slope = 0.639, p = 2 * 10−5). The relationship between SR and the skewness of the simulated RFDs is significant and negative (slope = −0.219, p = 1 * 10−5). Finally, we found that the degree of sympatry has no bearing on the proportion of small ranged species (SR: slope = −3.038, p = 2 * 10−4; degree of sympatry: SR: slope = −0.021, p = 0.11). These results indicate that SR is a very good proxy to describe the degree of asymmetry of the RFD distribution. More importantly in the present context, it correlates to the proportion of species with very small range size, hence arguably under higher extinction risk.
Pradel Models
None of the simulations performed was affected by unsuccessful convergence. Therefore, we were able to extract survival probability, preservation, seniority, and growth rate for each model. The AICc values strongly support the “survival and population growth” in 19 out of 21 clades. Orthida and Productida showed instead the best AICc for the “survival and seniority” model (Table 1). For each clade, we derived extinction, speciation and diversification rates from the best model (Table 1).
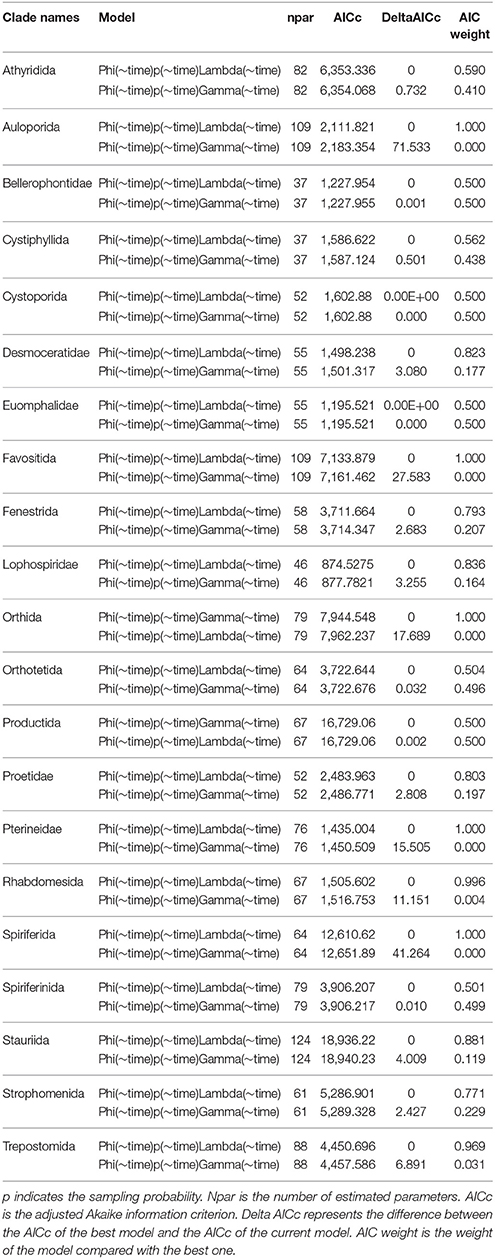
Table 1. Results of “survival (Phi) and seniority (Gamma)” and “survival (Phi) and population growth (Lambda)” models simulations for all the 21 clades.
Effect of SR on Diversification Rates
Regression models reported a significant, negative relationship between extinction rate and SR. Both terms were significant (Table 2). A significant, positive relationship occurs between speciation rate and SR (both linear and quadratic terms were significant, Table 2). The regressions including only linear terms showed similar results, with the extinction rate being significantly and negatively related to SR, and speciation rate reporting a significant, positive relationship with SR (Table 3). For both rate metrics, models including both linear and quadratic terms reported lower AIC values than those including only linear terms (i.e., quadratic models perform better, Table 2). Eventually, the purely quadratic models show the least fit to the data (Table 4).
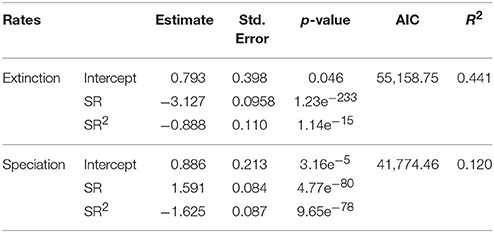
Table 2. Linear and quadratic regression coefficients quantifying the relationship between diversification rates (i.e., extinction and speciation) and SR.
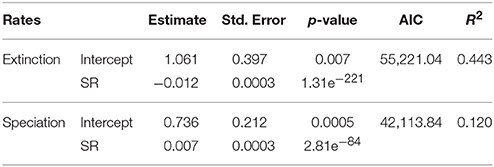
Table 3. Regression coefficients based only on linear models quantifying the relationship between diversification rates (i.e., extinction and speciation) and SR.
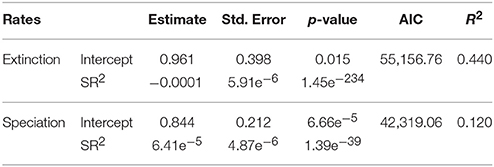
Table 4. Regression coefficients based only on quadratic models quantifying the relationship between diversification rates (i.e., extinction and speciation) and SR.
At the level of individual clades, the polynomial still performs best in describing extinction rates, outperforming the other two models 16 times out of 21 (Table S3a). However, there is strong variation in the trend of extinction rate with almost an equal number of instances of rate increase or decrease with SR. With speciation rate, the polynomial model still works better than other models fifteen times, but the positive trend of speciation rate with SR is only marginally more common than the opposite (Table S3b). We urge the reader to consider that clade level regression results must be taken with caution, because there are little valid bins for several groups, and because of the unique effect of mass extinctions on the calculation of rates (time bin age was in fact used as a covariate in the full model).
Discussion
The geographic distribution of a species depends on how individuals are organized in space, how much they tolerate environmental variation, and ultimately how they interact with each other to occupy the territory. The geographic range size is intimately linked to dispersal ability, which, in turn, is influenced by organisms' physiological tolerance. The range size frequency distribution thus depends on how all of these features vary across species within a clade (Blackburn and Gaston, 2003). The RFD is a right-skewed unimodal distribution when using raw data for most of the studied living and fossil clades. This means that clades include mostly species with small range size, and just a few species that were environmentally tolerant and good at dispersing enough as to occupy a large space.
By using a hefty, extinct metazoan clades dataset, spanning over more than 400 Myr of evolution, we were able to demonstrate that speciation rate is positively related to average range size, and extinction rate negatively associated to such average range size, especially when a quadratic term is added to the equation (Figure 2B). The latter result is nothing but a confirmation of the strongly hold notion that having a wide geographic range favors species survival (Jablonski, 1986; Rosenfield, 2002; Gaston, 2003; McKinney, 2003; Cardillo et al., 2005, 2008; Jablonski and Hunt, 2015). Our measure of range size, SR, is not range size per se, but a metric that correlates to the presence of (many) extremely small and (few) extremely large ranged species within the RFD. According to the simulations we performed, low SR means that extremely small-ranged species are overrepresented in the RFD, which provides a plain ecological explanation for the relationship between SR and extinction (Figures 2B,D).
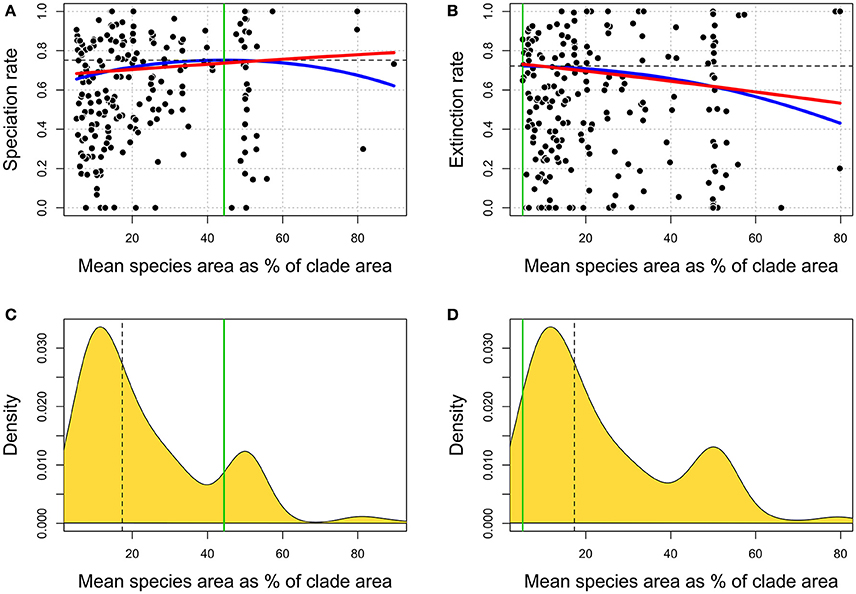
Figure 2. Plot showing the fitted statistical models for both the speciation rate (left column) and the extinction rate (right). On the top, statistical relationships between speciation (A) and extinction rates (B) and SR. Blue lines refer to regression models including both linear and quadratic terms. Red lines indicate regression models including linear terms only. The green and the black dashed lines mark SR and diversification rates values where the quadratic regression models reach the inflection point. On the bottom, densities of SR values used as explanatory variables in regression models against speciation (C) and extinction (D) rates. Dashed black lines indicate the median value. Green lines mark SR values where the quadratic regression models reach the inflection point.
The relationship between SR and speciation rate is positive and significant, but more difficult to interpret. According to the peripheral isolation mode of allopatric speciation (Glazier, 1987; Gaston, 1998), the rate should increase linearly with range size. However, although at high skew values species with extremely large ranges are expected to appear, the number of such large-ranged species in the RFD decreases, which means that the total number of daughter species produced by such large-ranged species is not expected to peak at the highest range class. This might explain why we found that the addition of a negative quadratic term to the speciation rate vs. SR regression increases the model likelihood. It is important to notice this does not mean speciation is a peaked function of range size (as expected under the vicariance model). First, if species with small to medium range originate more species (Jablonski and Roy, 2003), the speciation rate to range size regression should be negative or non-significant, whereas we obtained a significant and positive relationship (Figure 2A). Secondly, the peak in speciation rate is at some 44% of the SR distribution (Figure 2C), which is much higher than the modal SR class. Again, this suggests that large, but not the largest size class produces more daughter species.
In the context of RFD, Gaston (1998) discussed two different mechanisms describing the process of species generation via allopatry: the vicariance and the peripheral isolation models. According to the vicariance model, wide ranged species can give birth to one or more daughter species and then disappear. This implies an increase in the number of small-ranged species that must be balanced by their greater proclivity to extinction in order to maintain the shape of RFD constant. We tested this latter notion (constancy of the RFD shape vs. time) for the individual clades included in this study, by regressing the skew of the distribution vs. the age of time bins (actually the midpoint age of bins duration). The regression is non-significant in 19 out of 21 clades (Table S4), indicating that the right-skewed shape of the RFD is a very pervasive pattern in the distribution of species range sizes throughout clades history. However, the negative relationship between range size and extinction rate opposes the interpretation of the vicariance as the dominant mode of speciation.
According to the peripheral isolation mode we support here (Figure 3), species with wide geographical extension may originate daughters at the boundary of their distribution, either because of small barriers intervening to break the continuity of the parental species range at its borders, or by waif dispersal. Under this model, the formation of geographic barriers or the dispersal ability of propagules are pivotal to genetic isolation. If a range is large enough, the likelihood that barriers may divide it into halves is much smaller than the probability of a small barrier occurring at the range periphery. However, a widespread species is also likely to be tolerant, which could prevent the formation of demographic isolates (Jablonski and Roy, 2003; Roy et al., 2009).
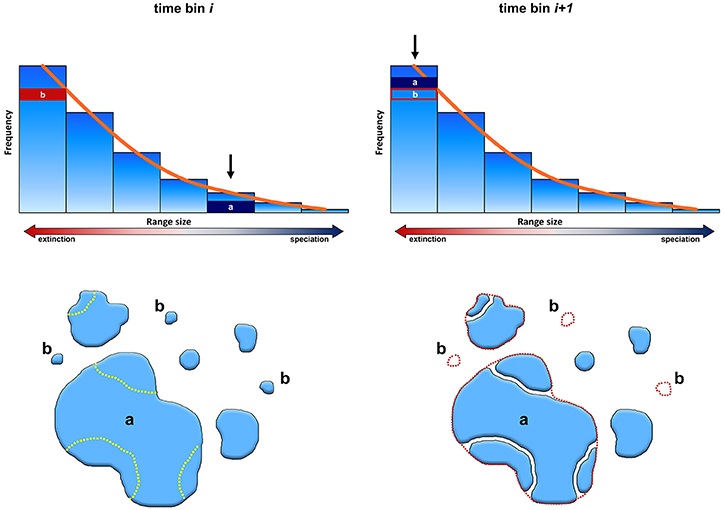
Figure 3. Evolution of the frequency range size distribution over two consecutive time bins. According to our results, during time i (left column) large-ranged species (dark blue box, indicated with the lower case letter a) have higher probability of speciation, and tend to split at their range periphery giving small ranged daughter species (lower row, left). On the contrary, small ranged species (indicated with the lower case letter b) have higher extinction rates. As a consequence, in the succeeding time bin (i+1 right column) species deriving from “a” occupy the small-range size class, replacing species “b,” now extinct.
In this study, we dealt with marine species, many of them had planktonic larval stages capable of wide dispersal. A positive association between dispersal ability and gene flow is well supported in marine clades (Kittiwattanawong, 1999; Bohonak, 2015; Jablonski and Hunt, 2015). Thus, in terms of speciation probability, very widespread marine species may be insensitive to even large geographic barriers, like oceanic ridges. This means that although we do not support the notion that small ranged clades are more speciose, it is still possible that speciation rate peaks at large, not the largest range size classes. There is one additional caveat to consider in interpreting species ranges as correlating to speciation probability. Since the evidence for an inverse relationship between range size and extinction rate is supported here and is a very general assumption in ecological and evolutionary studies, it might be true that large-ranged species simply originate more species because they live for longer (Wagner and Erwin, 1995; Wagner, 2010). Albeit true in principle, the importance of this caveat here is most probably limited, because the record is divided into discrete time bins, meaning that not all of the potential daughter species of a wide ranged parent are expected to be part of the same RFD.
So far, we have taken the range of species as fixed, which is feasible working with time bins, but untrue from the perspective of range size evolution. It has been demonstrated that the range of both species and clades follows a symmetrical, peaked trajectory, with the maximum range size value reached almost midway between a taxon appearance and its disappearance in the fossil record (Jernvall and Fortelius, 2004; Vrba and DeGusta, 2004; Raia et al., 2006; Foote, 2009). While this could be an artifact or statistical necessity (Pigot et al., 2012), a recent account demonstrates that such pattern has feasible ecological explanations (Foote, 2014). Within a RFD, there are species at different stages of the peaked range size trajectory. To the left hand of the RFD, newly formed species may show exceptionally small ranges (Vrba and DeGusta, 2004), which agrees with the peripheral isolation mode of speciation. This would provide further evidence in favor of such allopatric mode of origination, which it is certainly worth testing in the future. To the right hand, species with exceptionally large ranges are expected to be roughly halfway between their origination and extinction moments. We believe proving this statement true would be important as well.
We are aware of the huge variation in history, duration, range size, ecological characteristics, environmental and physiological preferences of the species included in this study. Our aim was to provide a simple, general representation of the influence of range size on speciation and extinction rates, and of these diversification metrics on RFD. New studies should address, in the future, the huge residual variation that is present in the data, singling out the potential effects of habitat extension, mass extinctions, and phylogeny on RFD shape and its evolution.
Author Contributions
SC, AM, MM, and CS collected the data. SC, AM, MM computed the evolutionary rate. AM, FC, and MD computed the geographic ranges and the GLM models. PR, SC, and AM conceived the study. PR lead the writing.
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
We are grateful to Daniele Silvestro, Mikael Fortelius, Michael Rosenzweig, and Lorenzo Rook for sharing us ideas and for methodological advices.
Supplementary Material
The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fevo.2017.00147/full#supplementary-material
Table S1. Species occurrence list with mid-age, paleo-coordinates, collection, species area, and clade area.
Table S2. Extinction, preservation, speciation rates per time bin for each clade, as estimated by Pradel models.
Table S3. Regression coefficients and AIC values for linear, quadratic, and polynomial regression models, run separately for each clade. (A) extinction rates vs. SR, (B) speciation rates vs. SR.
Table S4. Regression coefficients of skewness vs. midpoint age of bins, run separately for each clade.
References
Bapst, D. W. (2013). A stochastic rate-calibrated method for time-scaling phylogenies of fossil taxa. Methods Ecol. Evol. 4, 724–733. doi: 10.1111/2041-210X.12081
Bates, D., Mächler, M., Bolker, B. M., and Walker, S. C. (2015). Fitting linear mixed-effects models using lme4. J. Stat. Soft. 67, 1–48. doi: 10.18637/jss.v067.i01
Blackburn, T. M., and Gaston, K. J. (2003). Macroecology: Concepts and Consequences: 43rd Symposium of the British Ecological Society, Vol. 43. Cambridge: Cambridge University Press.
Bohonak, A. J. (2015). Dispersal, gene flow, and population structure. Q. Rev. Biol. 74, 21–45. doi: 10.1086/392950
Cardillo, M., Mace, G. M., Gittleman, J. L., Jones, K. E., Bielby, J., and Purvis, A. (2008). The predictability of extinction: biological and external correlates of decline in mammals. Proc. R. Soc. B 275, 1441–1448. doi: 10.1098/rspb.2008.0179
Cardillo, M., Mace, G. M., Jones, K. E., Bielby, J., Bininda-Emonds, O. R. P., Sechrest, W., et al. (2005). Multiple causes of high extinction risk in large mammal species. Science 309, 1239–1241. doi: 10.1126/science.1116030
Carotenuto, F., Barbera, C., and Raia, P. (2010). Occupancy, range size, and phylogeny in Eurasian Pliocene to Recent large mammals. Paleobiology 36, 399–414. doi: 10.1666/09059.1
Carotenuto, F., Diniz-Filho, J. A. F., and Raia, P. (2015). Space and time: the two dimensions of Artiodactyla body mass evolution. Palaeogeogr. Palaeoclimatol. Palaeoecol. 437, 18–25. doi: 10.1016/j.palaeo.2015.07.013
Cracraft, J., and Prum, R. O. (1988). Patterns and processes of diversification: speciation and historical congruence in some Neotropical birds. Evolution 42, 603–620. doi: 10.1111/j.1558-5646.1988.tb04164.x
DeGusta, D., and Vrba, E. (2003). A method for inferring paleohabitats from the functional morphology of bovid astragali. J. Archaeol. Sci. 30, 1009–1022. doi: 10.1016/S0305-4403(02)00286-8
Didier, G., Fau, M., and Laurin, M. (2017). Likelihood of tree topologies with fossils and diversification rate estimation. Syst. Biol. 66, 964–987. doi: 10.1093/sysbio/syx045
Diniz-Filho, J. A. F., Loyola, R. D., Raia, P., Mooers, A. O., and Bini, L. M. (2013). Darwinian shortfalls in biodiversity conservation. Trends Ecol. Evol. 28, 689–695. doi: 10.1016/j.tree.2013.09.003
Felsenstein, J. (1985). Phylogenies and the comparative method. Am. Nat. 125, 1–15. doi: 10.1086/284325
Finarelli, J. A., and Liow, L. H. (2016). Diversification histories for North American and Eurasian carnivorans. Biol. J. Linn. Soc. 118, 26–38. doi: 10.1111/bij.12777
Foote, M. (2000). Origination and extinction components of taxonomic diversity: general problems. Paleobiology 26, 74–102. doi: 10.1666/0094-8373(2000)26[74:OAECOT]2.0.CO;2
Foote, M. (2009). Symmetric waxing and waning of marine invertebrate genera. Paleobiology 33, 517–529. doi: 10.1666/06084.1
Foote, M. (2014). Environmental controls on geographic range size in marine animal genera. Paleobiology 40, 440–458. doi: 10.1666/13056
Foote, M., and Miller, A. I. (2013). Determinants of early survival in marine animal genera. Paleobiology 39, 171–192. doi: 10.1666/12028
Gaston, K. J. (1998). Species-range size distributions: products of speciation, extinction and transformation. Philos. Trans. R. Soc. Lond. B 353, 219–230. doi: 10.1098/rstb.1998.0204
Gaston, K. J. (2003). The Structure and Dynamics of Geographic Ranges. Oxford: Oxford University Press.
Gaston, K. J., Blackburn, T. M., and Lawton, J. H. (1997). Interspecific abundance-range size relationships: an appraisal of mechanisms. J. Anim. Ecol. 66:579. doi: 10.2307/5951
Glazier, D. S. (1987). Toward a predictive theory of speciation: the ecology of isolate selection. J. Theor. Biol. 126, 323–333. doi: 10.1016/S0022-5193(87)80239-4
Hawkins, J. P., Roberts, C. M., and Clark, V. (2000). The threatened status of restricted-range coral reef fish species. Anim. Conserv. 3, 81–88. doi: 10.1111/j.1469-1795.2000.tb00089.x
Jablonski, D. (1986). Larval ecology and macroevolution in marine invertebrates. Bull. Mar. Sci. 39, 565–587.
Jablonski, D., and Hunt, G. (2015). Larval ecology, geographic range, and species survivorship in cretaceous mollusks: organismic versus species-level explanations. Am. Nat. 168, 556–564. doi: 10.1086/507994
Jablonski, D., and Roy, K. (2003). Geographical range and speciation in fossil and living molluscs. Proc. Roy. Soc. B 270, 401–406. doi: 10.1098/rspb.2002.2243
Jernvall, J., and Fortelius, M. (2004). Maintenance of trophic structure in fossil mammal communities: site occupancy and taxon resilience. Am. Nat. 164, 614–624. doi: 10.1086/424967
Kittiwattanawong, K. (1999). The relation of reproductive modes to population differentiation in marine bivalves and gastropods. Phuket Mar. Biol. Center Spec. Publ. 19, 129–138.
Laurin, M., and Soler-Gijón, R. (2010). “Osmotic tolerance and habitat of early stegocephalians: indirect evidence from parsimony, taphonomy, paleobiogeography, physiology and morphology,” in The Terrestrialization Process: Modelling Complex Interactions at the Biosphere-Geosphere Interface, Vol. 339, eds M. Vecoli and G. Clément (London: The Geological Society of London), 151–179.
Lester, S. E., Ruttenberg, B. I., Gaines, S. D., and Kinlan, B. P. (2007). The relationship between dispersal ability and geographic range size. Ecol. Lett. 10, 745–758. doi: 10.1111/j.1461-0248.2007.01070.x
Liow, L. H., and Finarelli, J. A. (2014). A dynamic global equilibrium in carnivoran diversification over 20 million years. Proc. Roy. Soc. B 281:20132312. doi: 10.1098/rspb.2013.2312
McCullagh, P., and Nelder, J. A. (1989). Generalized Linear Models. London; New York, NY: Chapman and Hall.
McKinney, M. L. (2003). Extinction vulnerability and selectivity: combining ecological and paleontological views. Annu. Rev. Ecol. Syst. 28, 495–516. doi: 10.1146/annurev.ecolsys.28.1.495
Nakagawa, S., and Schielzeth, H. (2013). A general and simple method for obtaining R2 from generalized linear mixed-effects models. Meth. Ecol. Evol. 4, 133–142. doi: 10.1111/j.2041-210x.2012.00261.x
Pigot, A. L., Owens, I. P. F., and Orme, C. D. L. (2012). Speciation and extinction drive the appearance of directional range size evolution in phylogenies and the fossil record. PLoS Biol. 10:e1001260. doi: 10.1371/journal.pbio.1001260
Pradel, R. (1996). Utilization of capture-mark-recapture for the study of recruitment and population growth rate. Biometrics 52:703. doi: 10.2307/2532908
Raia, P., Carlo, M., Loy, A., and Barbera, C. (2006). Species occupancy and its course in the past: macroecological patterns in extinct communities. Evol. Ecol. Res. 8, 181–194.
Raia, P., Carotenuto, F., Mondanaro, A., Castiglione, S., Passaro, F., Saggese, F., et al. (2016). Progress to extinction: increased specialisation causes the demise of animal clades. Sci. Rep. 6, 30965–30911. doi: 10.1038/srep30965
Rosenfield, J. A. (2002). Pattern and process in the geographical ranges of freshwater fishes. Glob. Ecol. Biogeogr. 11, 323–332. doi: 10.1046/j.1466-822X.2002.00287.x
Rosenzweig, M. L. (1995). Species Diversity in Space and Time. Cambridge: Cambridge University Press. doi: 10.1017/CBO9780511623387
Roy, K., Hunt, G., Jablonski, D., Krug, A. Z., and Valentine, J. W. (2009). A macroevolutionary perspective on species range limits. Proc. Roy. Soc. B 276, 1485–1493. doi: 10.1098/rspb.2008.1232
Saupe, E. E., Qiao, H., Hendricks, J. R., Portell, R. W., Hunter, S. J., Soberón, J., et al. (2015). Niche breadth and geographic range size as determinants of species survival on geological time scales. Glob. Ecol. Biogeogr. 24, 1159–1169. doi: 10.1111/geb.12333
Shanks, A. L., Grantham, B. A., and Carr, M. H. (2003). Propagule dispersal distance and the size and spacing of marine reserves. Ecol. Appl. 13, S159–S169. doi: 10.1890/1051-0761(2003)013[0159:PDDATS]2.0.CO;2
Slatyer, R. A., Hirst, M., and Sexton, J. P. (2013). Niche breadth predicts geographical range size: a general ecological pattern. Ecol. Lett. 16, 1104–1114. doi: 10.1111/ele.12140
Vrba, E. S., and DeGusta, D. (2004). Do species populations really start small? New perspectives from the Late Neogene fossil record of African mammals. Philos. Trans. R. Soc. Lond. B 359, 285–292. discussion: 292–293. doi: 10.1098/rstb.2003.1397
Wagner, P. J. (2010). “Paleontological perspectives on morphological evolution,” in Evolution Since Darwin: The First 150 Years, ed J. S. Levinton (Sunderland, MA: Sinauer Associates Inc.), 451–478.
Wagner, P. J., and Erwin, D. H. (1995). “Phylogenetic patterns as tests of speciation models,” in New Approaches to Speciation in the Fossil Record, eds D. Erwin and R. L. Anstey (New York, NY: Columbia University Press), 87–122.
Keywords: range size frequency distribution, extinction rate, speciation rate, paleogeographic range, biodiversity
Citation: Castiglione S, Mondanaro A, Melchionna M, Serio C, Di Febbraro M, Carotenuto F and Raia P (2017) Diversification Rates and the Evolution of Species Range Size Frequency Distribution. Front. Ecol. Evol. 5:147. doi: 10.3389/fevo.2017.00147
Received: 14 September 2017; Accepted: 09 November 2017;
Published: 21 November 2017.
Edited by:
Rachid Cheddadi, Université de Montpellier, FranceReviewed by:
Michel Laurin, UMR7207 Centre de Recherche sur la Paléobiodiversité et les Paléoenvironnements (CR2P), FranceGilles Didier, UMR7373 Institut de Mathématiques de Marseille (I2M), France
Copyright © 2017 Castiglione, Mondanaro, Melchionna, Serio, Di Febbraro, Carotenuto and Raia. This is an open-access article distributed under the terms of the Creative Commons Attribution License (CC BY). The use, distribution or reproduction in other forums is permitted, provided the original author(s) or licensor are credited and that the original publication in this journal is cited, in accordance with accepted academic practice. No use, distribution or reproduction is permitted which does not comply with these terms.
*Correspondence: Pasquale Raia, cGFzcXVhbGUucmFpYUB1bmluYS5pdA==
 Silvia Castiglione
Silvia Castiglione Alessandro Mondanaro
Alessandro Mondanaro Marina Melchionna
Marina Melchionna Carmela Serio
Carmela Serio Mirko Di Febbraro
Mirko Di Febbraro Francesco Carotenuto
Francesco Carotenuto Pasquale Raia
Pasquale Raia